1. Introduction
Am stars are characterized by the absence of a large-scale magnetic field and show an overabundance of metals. The question of the formation of chemical anomalies in the atmospheres of Am stars remains unclear. It is believed that the origin of anomalies is associated with the processes of atomic diffusion, according to which the diffusion of atoms and ions of an element occurs under the action of gravity directed towards the centre of the star and radiation pressure forces that push particles into the outer layers of the atmosphere [
1]. To understand the mechanisms of formation of anomalies in chemical elements, it is necessary to determine accurately the abundances of elements from light CNO to rare earth elements (REE).
Observations [
2] and theory [
3] show that slow rotation (equatorial velocity below 120 km/s) favours the presence of chemical anomalies in A–B stars. There are two different atomic diffusion scenarios that attempt to explain the Am star phenomenon. Ref. [
4] suggested that the separation of chemical elements occurs directly below the hydrogen convection zone, in the radiative zone (see, e.g., [
5]), and it is assumed that a very small mass of a star has high abundance when the star is in the main sequence (MS) stage. Furthermore, when the star reaches the subgiant branch, there is a decrease in atmospheric abundances in the star’s atmosphere. In another model proposed by [
6], the separation of elements occurs much deeper in the star. Consequently, most of the mass has anomalous chemical abundances when the star is in the MS stage; furthermore, the anomalies presumably remain longer as the star evolves to the subgiant stage.
The majority of previous studies investigating the chemical composition of A-type and Am stars have been conducted under the assumption of local thermodynamic equilibrium (LTE) (e.g., [
7,
8]). However, deviations from LTE can have a significant impact on the accuracy of abundance determinations, which are essential for testing theories of atomic diffusion and for the correct interpretation of spectroscopic observations. The non-LTE (NLTE) approach accounts for these deviations by solving the equations of statistical equilibrium simultaneously with the radiative transfer equations, thereby providing more realistic level populations. Recent investigations have demonstrated that, in Am stars with effective temperatures exceeding 9300 K and surface gravities
< 4.0, elements such as calcium and scandium may appear overabundant relative to solar values when analysed in the non-LTE approach [
9].
Of particular interest is the study of binary systems with chemically anomalous components at different stages of their evolution, which makes it possible to study the processes of creating chemical anomalies in stellar atmospheres in more detail. Binary star systems are formed from the same interstellar medium; thus, they should have similar chemical abundances. However, recent studies have suggested that the component stars in a binary system may have different chemical abundances (e.g., [
10]), which means these differences are generated by processes during stellar evolution. Therefore, these studies may provide a clue to the understanding of the physical processes leading to the creation of anomalies in stellar atmospheres.
For this purpose, we chose the spectroscopic binary star
Equulei (HD 202447, HD 202448). Griffin and Griffin found that the primary component of the bright composite-spectrum binary
Equulei is a normal G7 giant, while the secondary is an Am star, classified as kA3hA4mA9 based on spectral disentangling [
11] (hereafter, GG02). The system’s well-determined visual orbit and high-resolution spectroscopy allowed for the precise measurement of the mass ratio (q = 1.15 ± 0.03) and component masses (2.3 M⊙ for the giant primary and 2.0 M⊙ for the dwarf secondary). Both stars fit a single 0.74 Gyr isochrone, with the primary on its first ascent of the red giant branch and the secondary evolving off the main sequence.
Equulei provides a rare opportunity to study the chemical composition and evolutionary status of an Am star in a well-characterised binary system.
The paper is organised as follows.
Section 2 describes the observations and data sources used in this study. The spectral disentangling procedure is presented in
Section 3. In
Section 4, we detail the model atmospheres and methods applied to determine the stellar parameters of both components. The abundance analysis is discussed in
Section 5. A comparison of our results with those from the literature is provided in
Section 6. Finally, we present conclusions in
Section 7.
2. Observations
We obtain high-resolution spectra from the SOPHIE spectrograph in HR mode (
, spectral range 3872–6943 Å) in all ranges of phases of radial velocities; so, we are able to disentangle spectra and do spectral analysis. Observational data are provided in
Table 1. Phases are calculated relative to
45,293.63 (GG02). Additional spectra are available from other archives: UVES (with a resolving power of
–
) and NARVAL (
). In the case of UVES, although the spectra cover a wide range of rotational phases, the signal-to-noise ratio is relatively low: approximately 50–170 for the 3282–4563 Å range, and 190–430 for the 4583–6686 Å range. In contrast, all NARVAL spectra are obtained during a single rotational phase, 0.491, when recalculated with respect to the
value adopted in the study by GG02. Therefore, we select the SOPHIE spectra for spectral disentangling.
3. Spectral Disentangling
We used a new technique of spectral disentangling introduced in our previous paper [
12]. It is based on the spectral line deconvolution (SLD) method, also developed by us, which consists of looking for the SLD function
, which provides the observed spectrum
after convolution with the theoretical profiles of individual spectral lines
:
where
is a set of multiplicative coefficients accounting for the fact that the profile of a blend is not necessarily a linear sum of the profiles of its individual components contributing to that blend. The
SLD function is a normalised broadening profile that includes all global physical and instrumental effects that determine the spectral line shape: rotation, turbulence, and spectral resolution. Equation (
1) can be generalised to spectroscopic double (SB2) and higher-order multiple systems. For SB2 systems in particular, two linear masks are used to identify two
SLD functions, each of which corresponds to a different component of the binary system. Applying this to binary systems also involves introducing an additional free parameter: the flux ratio of two stars.
The disentangling process is characterised by an iterative approach, which can be described as follows: (I) theoretical line masks for both stars were calculated based on an initial set of atmospheric parameters. (II) Equation (
1) was solved for the
SLD functions. Subsequently, we optimised the flux ratios of the two stars using the golden section method to determine the radius ratio, and line strength corrections were performed by introducing a scale factor for each spectral line across all utilised spectra during the simultaneous disentangling. (III) The obtained
SLD functions were convolved with improved line masks to produce disentangled spectra for the two components of the binary system. The convergence criterion in the search for the disentangled spectra was the simultaneous maximisation of the fit between the computed composite model spectra and the observed spectra across all phases. The resulting spectra, which were free from masking, were then analysed to refine the atmospheric parameters of the stars.
This entire process (steps I to III) is repeated until no significant changes are observed in the line strength corrections, flux ratios, and atmospheric parameters derived from the unmasked spectra.
The initial parameters were taken from the work of GG02. The radial velocities of the components were obtained using a two-dimensional mutual correlation method similar to that used in the
TODCOR code [
13]. This method was applied to the spectra used in the disentangling process.
For test purposes, we used artificial dual spectra mimicking the observed spectra. Synthetic spectra of each component, expressed in flux units, were folded to account for the shift in the wavelength scale according to the radial velocity of each component. These composite spectra were then convolved with an instrumental profile corresponding to
75,000, and noise was added to simulate the
ratio. Spectrum disentangling was performed under the perturbation of atmospheric parameters and showed insensitivity to their variations within the errors in the calculation of
SLD masks. As for the disentangling of the real observed spectra, two iterations were sufficient to obtain the final results.
Figure 1 shows the results of disentangling the observed spectra of the
Equulei system.
4. Stellar Fundamental Parameters
After each spectral disentangling into two component spectra, the atmospheric parameters of each component were determined using the spectroscopy made easy (
SME) software package [
14].
SME derives the effective temperature (
), surface gravity (
), metallicity ([M/H]), projected rotational velocity (
), microturbulent velocity (
), and macroturbulent velocity (
). The code computes synthetic spectra using precomputed grids of stellar atmosphere models within selected spectral regions and performs a fitting procedure to the observed spectra to determine the best-fit values of the adjustable parameters. In our analysis, we employed the LLmodels grid [
15]. Fitting was performed in the optical spectral range, including hydrogen lines that are particularly sensitive to variations in
, especially
.
The chosen spectral intervals contain approximately 300 Fe i and Fe ii lines spanning a wide range of excitation potentials and equivalent widths (EWs) from 3 to 110 mÅ. These lines are crucial for constraining and by ensuring ionisation balance, i.e., agreement in elemental abundance derived from lines of different ionisation stages, as well as for determining . The microturbulent velocity was derived by requiring the consistency of the iron abundance obtained from individual lines of varying equivalent widths.
The results of the atmospheric parameter determination based on
SME analysis of the observed spectra are presented in
Table 2. We used two independent methods to estimate the uncertainties of the free parameters. The first is the classical approach based on the covariance matrix of the least-squares fit, which yields small internal errors that do not exceed 5 K for
and 0.01 dex for the other parameters. Note that these uncertainties are not summarised in
Table 2. The second method is based on the analysis of cumulative probability distributions (see, e.g., [
14]), which accounts for observational noise, continuum normalisation, atomic data uncertainties, and other potential sources of systematic error. While the exact magnitude of these systematics is difficult to quantify, the true uncertainties likely lie between the estimates obtained from the two methods.
To check the adequacy of the chosen atmospheric model for the
SME solution for the stars of the first and second components, we plotted the dependence of the abundance of individual Fe
i–
ii lines on the reduced equivalent width
and ionisation potential
(
Figure 2). In the first case, the absence of dependence confirms the correctness of the obtained microturbulent velocity
; in the second case, the parameters of the atmosphere
and
. We also present the profiles of the
and
hydrogen lines with synthetic spectra calculated with the obtained from
SME solution atmospheric models (
Figure 3).
Another method for verifying the parameters is the spectral energy distribution (
SED) fitting. This involves fitting a theoretical
SED model to the observations by varying atmospheric parameters from an LLmodel grid, where absorption in each line is calculated taking into account the individual chemical composition. During the fitting process, parameters such as effective temperature (
), surface gravity (
), metallicity ([Fe/H]), and stellar radius (
) can be simultaneously adjusted. In this case, only the radius of each component in the binary star system was varied, as the other parameters were reasonably well determined using the SME method. The flux from each component was then calculated based on the radius contributions and compared to the observed data. The correction for interstellar reddening was applied according to the extinction curve from the paper [
16] with the
.
value was taken from the dust map from the EXPLORE (accessed on 21 July 2025) website
1 and for the distance 58 pc it equals 0.024.
As a result, we obtained
and
, which is consistent with the results presented in the GG02 paper. The
SED is shown in
Figure 4.
5. Abundance Analysis
The determination of chemical abundances was carried out by fitting synthetic spectral line profiles to the observed ones using the
BinMag6 code [
17]. This program allows for variation of the elemental abundance, macroturbulent velocity, projected rotational velocity (
), and radial velocity (
) of the star. We determined 25 abundances of elements from C to Nd. For elements up to barium, abundances were derived from lines of neutral atoms and first ions, while for the REEs, lines of first and second ions were used.
Synthetic spectra were computed with the
SynthVb code [
18], which enables the calculation of both LTE and non-LTE line profiles by incorporating b-factors (the ratio of atomic level populations in non-LTE to those in LTE), computed with the
DETAIL code ([
19,
20,
21]). Atomic data were taken from VALD3 [
22,
23].
Elemental abundances are provided on the standard logarithmic scale, , where and are the number densities of the element and hydrogen, respectively.
He, Al, S, V, Cr, Mn, Co, Ni, and REE abundances (La, Ce, and Nd) were derived in LTE. For C, O, Na, Mg, Si, K, Ca, Sc, Ti, Fe, Zn, Sr, Y, Zr, and Ba, we determined LTE and non-LTE abundances using model atoms. The model atoms and references to their detailed descriptions are summarized in
Table 3. The derived abundances of
Equulei components are presented in
Table 4 and shown in
Figure 5.
In the spectrum of the primary component, the following elements are represented by a single line: K i 5108 Å, Mn i 6205 Å and Ba i 6110 Å. The resonance line K i 7698 Å was not observed in the SOPHIE spectrum because the necessary band was missing. In the secondary component, the elements Al i 5557 Å, S i 5032 Å, and Co i 5483 Å are represented by a single line.
In the atmospheres of the investigated stars, the concentrations of Mg, Si, Ca, Sc, Ti, Cr, Mn, and Fe remain at equilibrium values. The abundances of heavy elements Zn, Sr, Y, Zr, and Ba in the primary component are represented by neutral atoms and ions. The non-LTE models of the atoms of the corresponding elements contain only the transitions of the once ionised element, and the non-LTE corrections do not exceed dex. Therefore, for neutral atoms, the non-LTE corrections are expected to be in approximately the same range. REEs are also observed in the primary component spectrum: La i, Ce i, and Nd i, where Ce i shows the maximum deviation from the solar values of 0.51 dex among the neighbouring elements. In the spectrum of the secondary component, the non-LTE corrections of the heavy elements do not exceed dex and differ from the solar values in the range from 0.88 to 1.26, while the REEs are represented only by Nd iii, which exceeds the solar value by 1.14 dex.
6. Discussion
The observed abundance pattern of chemical elements in the primary component is close to the solar values. The overall metallicity of the star is 0.09 ± 0.28, and the metallicity for elements from C to Cu is −0.02 ± 0.16. For the secondary component the metallicity are 0.35 ± 0.46 and for elements from C to Ni 0.09 ± 0.26, respectively.
Stars can be considered as normal if the abundance of the elements from He to Fe matches the solar values within 3
error and the abundance of heavier elements can be correlated with the effective temperature, as we demonstrate in our previous paper [
38]. The primary component of
Equulei has an almost solar abundance of elements from C to Cu, Zn show underabundance of 0.41 dex, and neutron-capture elements (n-capture) show overabundances from 0.41 dex for Zr
i to 0.74 dex for Ba
i. REEs are denoted by the elements Ce and Nd, and their relative abundances are estimated to be 0.35 and 0.51 dex greater than the solar values, respectively. Therefore, we conclude that the primary component of
Equulei is a normal star of the G spectral class.
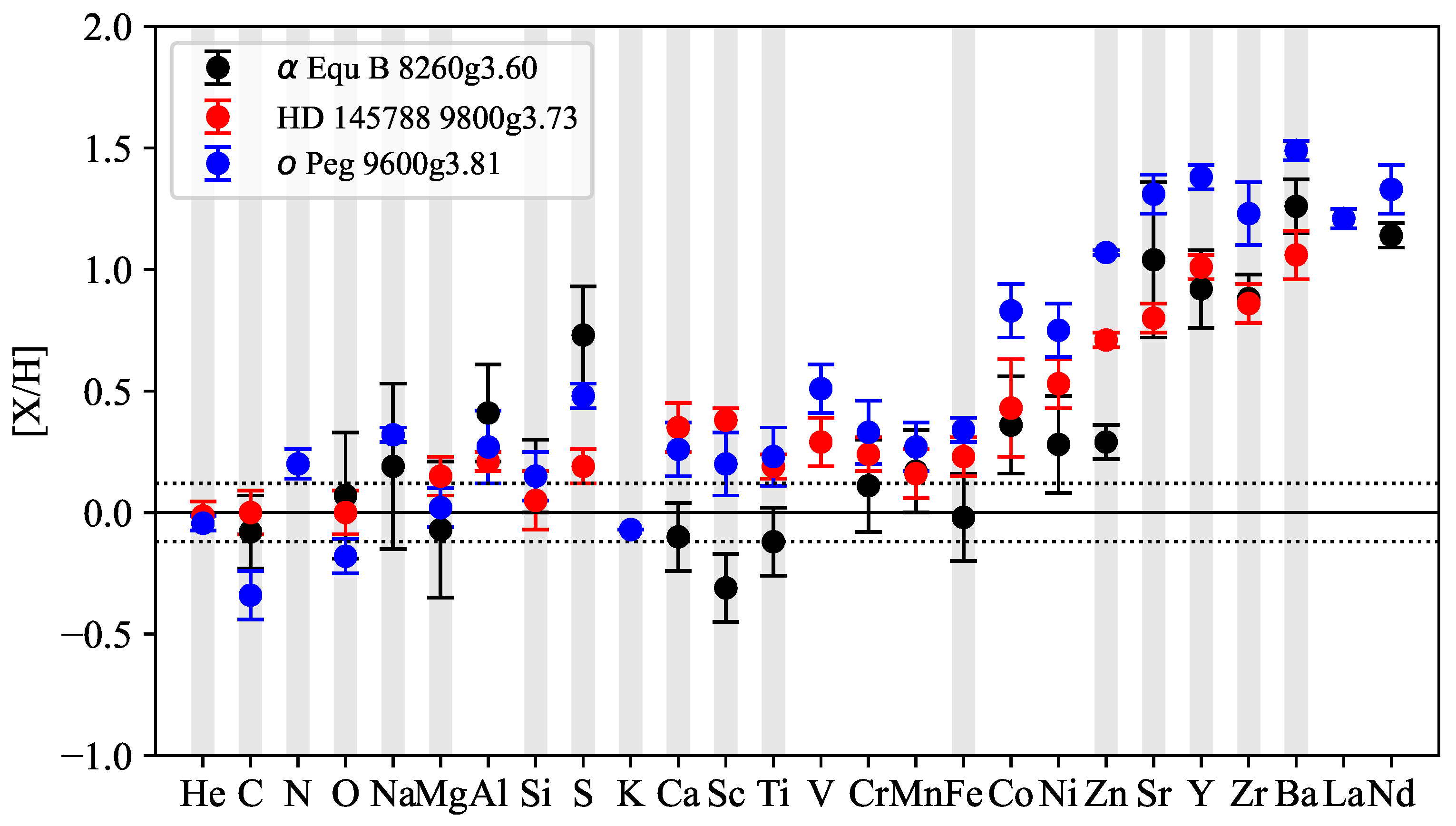
Since the secondary component exhibits a higher metallicity than the primary component, we investigated the differences in abundance between low-rotation Am-type stars in different evolutionary stages. To make this comparison, we selected stars with close fundamental parameters: star HD 145788, which is in the early stages of becoming an Am star, with atmospheric parameters of
= 9800 and
= 3.73 [
38], and the Am star
o Peg with
= 9600 and
= 3.81 [
36]. Both stars have well-determined LTE and non-LTE abundances, as well as reliably established atmospheric parameters. This makes them suitable benchmarks for comparison in
Figure 6. The RMS of overall metallicity is
between
Equulei B and HD 145788 and
between
Equulei B and
oPeg. The abundance pattern in the atmosphere of
Equulei B is close to that of HD 145788, despite the
discrepancy of 1540 K.
The abundances of elements Al and S are higher than in Am stars, but note that the abundances of both elements were derived from a single line. The abundances of elements from Sc to Zn are lower than in an Am star; however, the abundances of heavy elements Sr, Y, Zr, and Ba are close to the values observed in HD 145788 within errors. Non-LTE calculations from [
31] showed that in Am stars with
< 9000 K and
< 4 Ca and Sc have predominantly lower than solar abundances [
9]. In the secondary component
Equulei, the Ca and Sc abundances do not contradict the conclusions of the above paper. Zn shows an abundance close to that of normal stars, where a Zn excess of up to 0.75 dex is observed in the 9500 K effective temperature range. Therefore, we conclude that
Equulei B is in the early stages of becoming an Am.
7. Conclusions
In this study, we performed, for the first time, a self-consistent chemical abundance analysis of the eclipsing spectroscopic binary
Equulei, covering elements from C to Nd. The fundamental stellar parameters were refined using spectral disentangling and the SME package. Additionally we validated the fundamental parameters by demonstrating that the abundance of individual Fe
i–
ii lines does not depend on the reduced equivalent widths and ionisation potential, spectral energy distributions, or hydrogen line profile fitting. We determined the abundances of 25 chemical elements, applying non-LTE methods to 15 of them. The non-LTE abundances of C, O, Na, Mg, Si, K, Ca, Sc, Ti, Fe, Zn, Sr, Y, Zr, and Ba were obtained using the same non-LTE modelling approach as in [
36].
The primary component (G7-type) exhibited a typical abundance pattern for normal stars: the elements from He to Fe matched the solar values, and neutron-captured elements showed an overabundance average of up to 0.5 dex, relative to solar values. Despite this, non-LTE effects for the primary prove negligible (<0.1 dex) and can be safely disregarded in abundance analysis.
In contrast, the secondary component shows Am star characteristics, requiring non-LTE corrections for elemental abundances. Our results support the spectral type classifications of both components proposed in GG02. However, based on our comparison of chemical abundances in Am stars at different evolutionary stages, we conclude that Equulei B is an early stage Am star. We also detect Na, K, V, Cu, La, and Ce exclusively in the primary component, while S appears only in the secondary.
Since the atmospheric parameters we obtained match those in the GG02 paper, we also confirm the conclusion that these stars formed simultaneously. The observed differences in chemical abundance between the two components of the Equulei binary system suggest different diffusion processes in their stellar atmospheres. Our results support the idea that chemical anomalies in Am stars emerge during the main sequence and may decrease as the stars evolve toward the subgiant branch due to the deepening of the convective zone.
Author Contributions
Conceptualisation, A.R.; methodology, A.R. and S.Z.; software, A.R. and S.Z.; validation, A.R. and S.Z.; formal analysis, A.R. and S.Z.; investigation, A.R. and S.Z.; resources, A.R. and S.Z.; data curation, A.R.; writing original draft preparation, A.R.; writing review and editing, A.R. and S.Z.; visualisation, A.R. and S.Z.; supervision, A.R.; project administration, A.R.; funding acquisition, A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Spectra of
Equulei normalised to the continuum level are provided as
Supplementary Materials in the form of an ASCII file in CDS. The full table of used lines with
, excitation potentials
, LTE and non-LTE abundances, and references for oscillator strengths and hyperfine constants is available online.
Acknowledgments
The authors would like to express their gratitude to T. Sitnova for providing the results of non-LTE calculations for Fe, Ti, Y, and Zn and to L. Mashonkina for providing the results of non-LTE calculations for Sc ii. The authors would also like to acknowledge T. Ryabchikova for her constructive feedback on the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Acknowledgments Statement. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| SLD | Spectral Line Deconvolution |
| SME | Spectroscopy Made Easy |
| REE | Rare Earth Elements |
| MS | Main Sequence |
| LTE | Local Thermodynamic Equilibrium |
| SOPHIE | Spectrograph for the Observation of the Phenomena of Stellar Interiors and Exoplanets |
| HR mode | High-resolution Mode |
| UVES | Ultraviolet and Visual Echelle Spectrograph |
| LLmodels | Line-by-Line models |
| EWs | Equivalent Widths |
References
- Michaud, G. Diffusion Processes in Peculiar a Stars. Astrophys. J. 1970, 160, 641. [Google Scholar] [CrossRef]
- Preston, G.W. The chemically peculiar stars of the upper main sequence. Annu. Rev. Astron. Astrophys. 1974, 12, 257. [Google Scholar] [CrossRef]
- Michaud, G. Meridional circulation versus diffusion in stellar envelopes. Astrophys. J. 1982, 258, 349. [Google Scholar] [CrossRef]
- Watson, W.D. Particle Diffusion in Stars Having Shallow Convective Envelopes. Astron. Astrophys. 1971, 13, 263. [Google Scholar]
- Alecian, G. Fm-Am stars in open clusters as a tool for stellar physics. Astron. Astrophys. 1996, 310, 872. [Google Scholar]
- Richer, J.; Michaud, G.; Turcotte, S. The Evolution of AMFM Stars, Abundance Anomalies, and Turbulent Transport. Astrophys. J. 2000, 529, 338. [Google Scholar] [CrossRef]
- Trust, O.; Jurua, E.; De Cat, P.; Joshi, S.; Lampens, P. HERMES spectroscopy of normal A and Am stars. Mon. Not. R. Astron. Soc. 2021, 504, 5528. [Google Scholar] [CrossRef]
- Nasolo, Y.; Çalışkan, S. A search for chemical anomalies of seven A-type stars. Mon. Not. R. Astron. Soc. 2023, 521, 3699. [Google Scholar] [CrossRef]
- Mashonkina, L.I.; Fadeyev, Y.A. Revision of the Calcium and Scandium Abundances in Am Stars Based on Non-LTE Calculations and Comparison with Diffusion Stellar Evolution Models. Astron. Lett. 2024, 50, 373. [Google Scholar] [CrossRef]
- Paunzen, E.; Fedurco, M.; Hełminiak, K.G.; Pintado, O.I.; Hambsch, F.-J.; Hümmerich, S.; Niemczura, E.; Bernhard, K.; Konacki, M.; Hubrig, S.; et al. Orbital parameters and evolutionary status of the highly peculiar binary system HD 66051. Astron. Astrophys. 2018, 615, A36. [Google Scholar] [CrossRef]
- Griffin, R.E.M.; Griffin, R.F. Composite spectra Paper 11: α Equulei, an astrometric binary with an Am secondary. Mon. Not. R. Astron. Soc. 2002, 330, 288. [Google Scholar] [CrossRef]
- Ryabchikova, T.; Zvyagintsev, S.; Tkachenko, A.; Tsymbal, V.; Pakhomov, Y.; Semenko, E. Fundamental parameters and abundance analysis of the components in the SB2 system HD 60803. Mon. Not. R. Astron. Soc. 2022, 509, 202. [Google Scholar] [CrossRef]
- Mazeh, T.; Zucker, S.; Smith, H. TODCOR: A New Two-Dimensional Correlation Technique to Analyze Stellar Spectra in Search for Faint Companions. Am. Astron. Soc. Meet. Abstr. 1993, 25, 1425. [Google Scholar]
- Piskunov, N.; Valenti, J.A. Spectroscopy Made Easy: Evolution. Astron. Astrophys. 2017, 597, A16. [Google Scholar] [CrossRef]
- Shulyak, D.; Tsymbal, V.; Ryabchikova, T.; Stütz, C.; Weiss, W.W. Line-by-line opacity stellar model atmospheres. Astron. Astrophys. 2004, 428, 993. [Google Scholar] [CrossRef]
- Fitzpatrick, E.L. Correcting for the Effects of Interstellar Extinction. Publ. Astron. Soc. Pac. 1999, 111, 63. [Google Scholar] [CrossRef]
- Kochukhov, O. BinMag: Widget for Comparing Stellar Observed with Theoretical Spectra. Astrophysics Source Code Library. ascl:1805.015. 2018. Available online: https://ui.adsabs.harvard.edu/abs/2018ascl.soft05015K/abstract (accessed on 21 July 2025).
- Tsymbal, V.; Ryabchikova, T.; Sitnova, T. Software for NLTE Spectrum Fitting. Phys. Magn. Stars 2019, 518, 247. [Google Scholar]
- Giddings, J.R. Quantum Particles in Kerr-Newman Fields. Ph.D. Thesis, Moscow University, Moscow, Russia, 1981. [Google Scholar]
- Butler, K. A Non-LTE Study of NIII in O Stars. Ph.D. Thesis, University College London, London, UK, 1984. [Google Scholar]
- Przybilla, N.; Nieva, M.-F.; Butler, K. Testing common classical LTE and NLTE model atmosphere and line-formation codes for quantitative spectroscopy of early-type stars. J. Phys. Conf. Ser. 2011, 328, 012015. [Google Scholar] [CrossRef]
- Piskunov, N.E.; Kupka, F.; Ryabchikova, T.A.; Weiss, W.W.; Jeffery, C.S. VALD: The Vienna Atomic Line Data Base. Astron. Astrophys. Suppl. Ser. 1995, 112, 525. [Google Scholar]
- Pakhomov, Y.V.; Ryabchikova, T.A.; Piskunov, N.E. Hyperfine Splitting in the VALD Database of Spectral-line Parameters. Astron. Rep. 2019, 63, 1010. [Google Scholar] [CrossRef]
- Alexeeva, S.A.; Ryabchikova, T.A.; Mashonkina, L.I. NLTE carbon abundance determination in selected A- and B-type stars and the interpretation of C i emission lines. Mon. Not. R. Astron. Soc. 2016, 462, 1123. [Google Scholar] [CrossRef]
- Sitnova, T.M.; Mashonkina, L.I.; Ryabchikova, T.A. Influence of departures from LTE on oxygen abundance determination in the atmospheres of A-K stars. Astron. Lett. 2013, 39, 126. [Google Scholar] [CrossRef]
- Alexeeva, S.A.; Pakhomov, Y.V.; Mashonkina, L.I. Non-LTE sodium abundance in galactic thick- and thin-disk red giants. Astron. Lett. 2014, 40, 406. [Google Scholar] [CrossRef]
- Alexeeva, S.; Ryabchikova, T.; Mashonkina, L.; Hu, S. NLTE Line Formation for Mg i and Mg ii in the Atmospheres of B-A-F-G-K Stars. Astrophys. J. 2018, 866, 153. [Google Scholar] [CrossRef]
- Mashonkina, L. Non-local thermodynamic equilibrium line formation for Si i- ii- iii in A-B stars and the origin of Si ii emission lines in ι Her. Mon. Not. R. Astron. Soc. 2020, 493, 6095. [Google Scholar] [CrossRef]
- Sitnova, T.M.; Mashonkina, L.I.; Ryabchikova, T.A. A NLTE line formation for neutral and singly ionized calcium in model atmospheres of B-F stars. Mon. Not. R. Astron. Soc. 2018, 477, 3343. [Google Scholar] [CrossRef]
- Neretina, M.D.; Mashonkina, L.I.; Sitnova, T.M.; Yakovleva, S.A.; Belyaev, A.K. Influence of Collisions with Hydrogen Atoms on Non-LTE Effects for K i and Ca ii in Stellar Atmospheres. Astron. Lett. 2020, 46, 621. [Google Scholar] [CrossRef]
- Mashonkina, L. Influence of departures from LTE on determinations of the scandium abundances in A-B-type stars. Mon. Not. R. Astron. Soc. 2024, 527, 8234. [Google Scholar] [CrossRef]
- Sitnova, T.M.; Yakovleva, S.A.; Belyaev, A.K.; Mashonkina, L.I. Influence of Collisions with Hydrogen on Titanium Abundance Determinations in Cool Stars. Astron. Lett. 2020, 46, 120. [Google Scholar] [CrossRef]
- Sitnova, T.; Ryabchikova, T.; Alexeeva, S.; Mashonkina, L. NLTE abundances of C, O, Ca, Ti, and Fe in the reference BAF-type stars. Rediscovering Our Galaxy 2018, 334, 360. [Google Scholar] [CrossRef]
- Sitnova, T.M.; Yakovleva, S.A.; Belyaev, A.K.; Mashonkina, L.I. Non-LTE abundances of zinc in different spectral type stars and the Galactic [Zn/Fe] trend based on quantum-mechanical data on inelastic processes in zinc-hydrogen collisions. Mon. Not. R. Astron. Soc. 2022, 515, 1510. [Google Scholar] [CrossRef]
- Mashonkina, L.; Ryabchikova, T.; Alexeeva, S.; Sitnova, T.; Zatsarinny, O. Chemical diversity among A-B stars with low rotational velocities: Non-LTE abundance analysis. Mon. Not. R. Astron. Soc. 2020, 499, 3706. [Google Scholar] [CrossRef]
- Romanovskaya, A.M.; Ryabchikova, T.A.; Pakhomov, Y.V.; Korotin, S.A.; Sitnova, T.M. Non-LTE abundance analysis of A-B stars with low rotational velocities—ii. Do A-B stars with normal abundances exist? Mon. Not. R. Astron. Soc. 2023, 526, 3386. [Google Scholar] [CrossRef]
- Lodders, K. Relative Atomic Solar System Abundances, Mass Fractions, and Atomic Masses of the Elements and Their Isotopes, Composition of the Solar Photosphere, and Compositions of the Major Chondritic Meteorite Groups. Space Sci. Rev. 2021, 217, 44. [Google Scholar] [CrossRef]
- Romanovskaya, A.M.; Ryabchikova, T.A.; Mashonkina, L.I.; Sitnova, T.M.; Serebryakova, N. Non-LTE Abundance Analysis of Main-Sequence A–B Stars. iii. Normal-Star Criteria. Astron. Lett. 2025, 51, 1. [Google Scholar] [CrossRef]
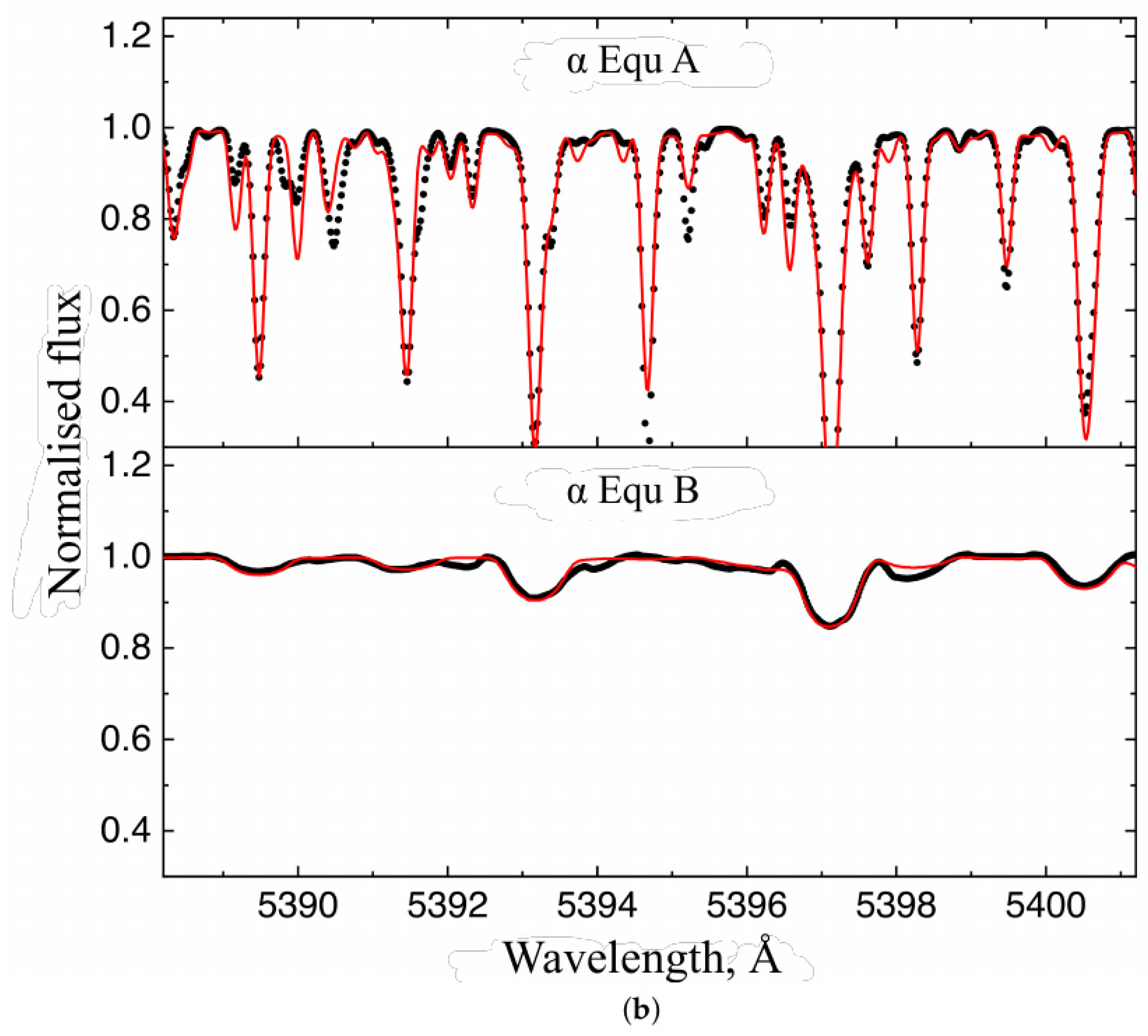
Figure 1.
(a) The quality of the fit to observed spectra of Equulei in two different orbital phases. The observations are indicated by black dots, the red line shows the best-fit composite profile, and the black line shows the residuals between the observations and the best-fit model. (b) Disentangled spectra of the components in the same spectral regions (black dots). The red lines show the fit of the synthetic spectra, which were calculated using the final atmospheric parameters, to the individual spectra of the components.
Figure 1.
(a) The quality of the fit to observed spectra of Equulei in two different orbital phases. The observations are indicated by black dots, the red line shows the best-fit composite profile, and the black line shows the residuals between the observations and the best-fit model. (b) Disentangled spectra of the components in the same spectral regions (black dots). The red lines show the fit of the synthetic spectra, which were calculated using the final atmospheric parameters, to the individual spectra of the components.
Figure 2.
Fe i (black dots) and Fe i (blue dots) abundances relative to the reduced equivalent widths and ionisation potential for the Equulei components. The solar Fe abundance is shown by the solid horizontal line. Dashed lines indicate differences of ±0.12 from the solar abundance. The r value in the graphs is the Pearson correlation coefficient.
Figure 2.
Fe i (black dots) and Fe i (blue dots) abundances relative to the reduced equivalent widths and ionisation potential for the Equulei components. The solar Fe abundance is shown by the solid horizontal line. Dashed lines indicate differences of ±0.12 from the solar abundance. The r value in the graphs is the Pearson correlation coefficient.
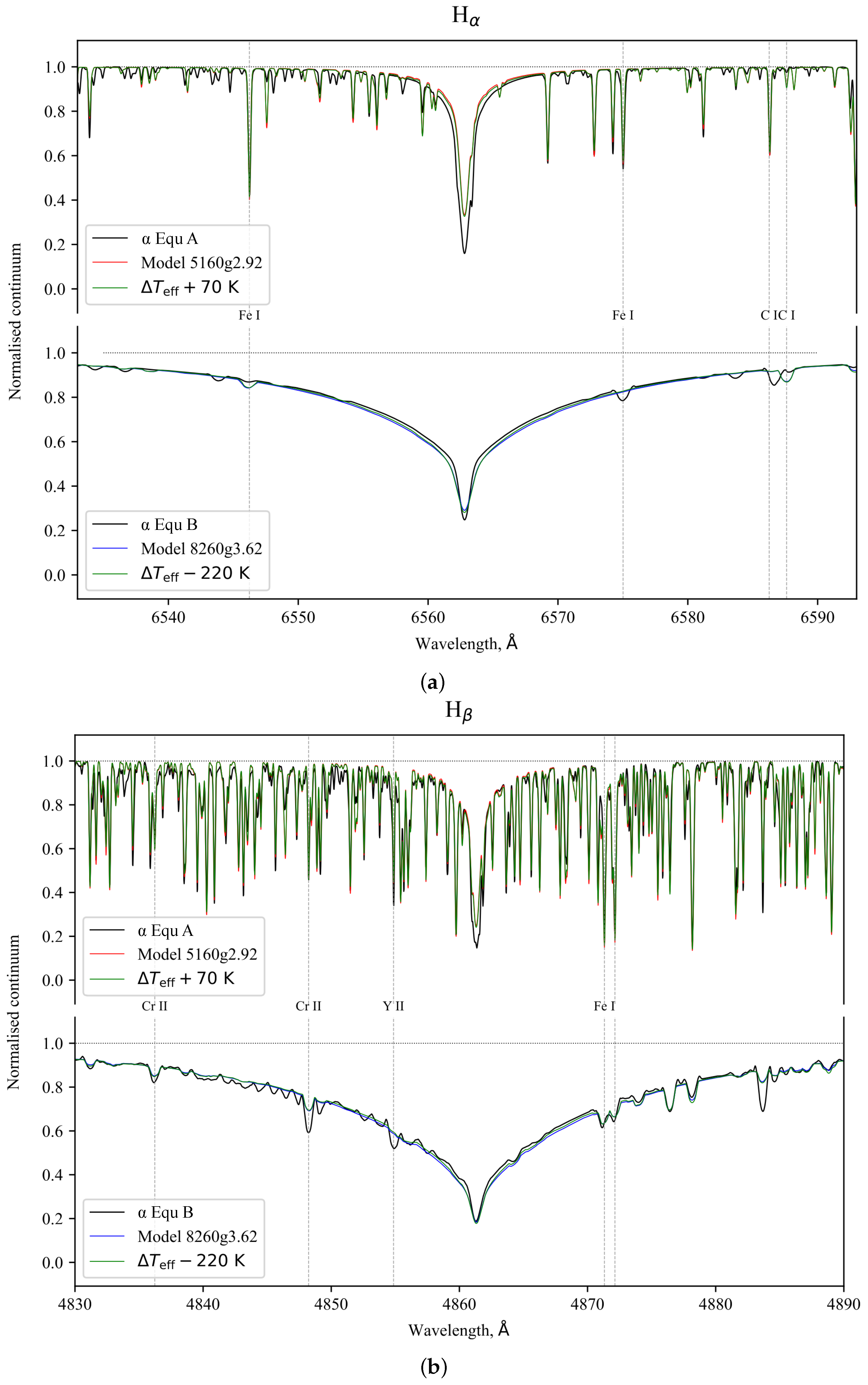
Figure 3.
Hydrogen line profiles in the atmosphere of two components of Equulei, (a)— and (b)—. Normalised continuum is indicated by a dashed line.
Figure 3.
Hydrogen line profiles in the atmosphere of two components of Equulei, (a)— and (b)—. Normalised continuum is indicated by a dashed line.
Figure 4.
Spectral energy distributions for Equulei. The black line represents the energy distribution obtained from calculations with the best-fit radius values of the primary and the secondary components; the red line represents the spectral energy distribution based on the SME solution for the primary component; the blue line refers to the secondary component. Radii are provided as the radius of the Sun.
Figure 4.
Spectral energy distributions for Equulei. The black line represents the energy distribution obtained from calculations with the best-fit radius values of the primary and the secondary components; the red line represents the spectral energy distribution based on the SME solution for the primary component; the blue line refers to the secondary component. Radii are provided as the radius of the Sun.
Figure 5.
Abundance pattern in Equulei relative to solar values, indicated by the solid line, with 3 errors shown as dashed lines. (a) Abundances of Equulei A with model 5160g3.90; (b) abundances of Equulei B with model 8260g3.60. For elements where both LTE and non-LTE abundances are available, the corresponding LTE values are shown using open symbols.
Figure 5.
Abundance pattern in Equulei relative to solar values, indicated by the solid line, with 3 errors shown as dashed lines. (a) Abundances of Equulei A with model 5160g3.90; (b) abundances of Equulei B with model 8260g3.60. For elements where both LTE and non-LTE abundances are available, the corresponding LTE values are shown using open symbols.
Figure 6.
Abundance comparison of the secondary component of Equulei B (black dots) to early Am star HD 145788 (red dots) and Am star o Peg (blue dots), relative to solar values, indicated by the solid line, with 3 errors shown as dashed lines. Grey lines indicate non-LTE abundances.
Figure 6.
Abundance comparison of the secondary component of Equulei B (black dots) to early Am star HD 145788 (red dots) and Am star o Peg (blue dots), relative to solar values, indicated by the solid line, with 3 errors shown as dashed lines. Grey lines indicate non-LTE abundances.
Table 1.
Observed spectra from the SOPHIE spectrograph. Phases calculated from 45,293.63.
Table 1.
Observed spectra from the SOPHIE spectrograph. Phases calculated from 45,293.63.
| Sequence Number | BJD | S/N | Phase |
|---|
| 2345960_s1d | 2458041.25604479 | 388 | 0.007 |
| 2253190_s1d | 2457967.50131843 | 385 | 0.260 |
| 1872770_s1d | 2457295.39394543 | 442 | 0.458 |
| 1877520_s1d | 2457305.35730816 | 234 | 0.559 |
| 2007640_s1d | 2457602.53160324 | 383 | 0.567 |
| 2016580_s1d | 2457622.53572631 | 326 | 0.769 |
| 2023130_s1d | 2457634.49218795 | 306 | 0.890 |
Table 2.
Atmospheric parameters of both components.
Table 2.
Atmospheric parameters of both components.
| Component | , | | [Fe/H] | | , | , | , |
|---|
| | K | | | | km s−1 | km s−1 | km s−1 |
|---|
| A | 5160 ± 65 | 2.94 ± 0.28 | 0.11 ± 0.06 | 9.20 ± 0.01 | 1.13 ± 0.14 | 0.0 | 5.53 ± 0.14 |
| B | 8260 ± 218 | 3.62 ± 0.37 | 0.14 ± 0.16 | 2.60 ± 0.03 | 4.22 ± 1.15 | 0.0 | 25.88 ± 3.45 |
Table 3.
Model atoms used for non-LTE calculations and corresponding references.
Table 3.
Model atoms used for non-LTE calculations and corresponding references.
| Element | Reference |
|---|
| C | Alexeeva, Ryabchikova, and Mashonkina [24] |
| O | Sitnova, Mashonkina, and Ryabchikova [25] |
| Na | Alexeeva, Pakhomov, and Mashonkina [26] |
| Mg | Alexeeva et al. [27] |
| Si | Mashonkina [28] |
| Ca | Sitnova, Mashonkina, and Ryabchikova [29] |
| K | Neretina et al. [30] |
| Sc | Mashonkina [31] |
| Ti | Sitnova et al. [32] |
| Fe | Sitnova et al. [33] |
| Zn | Sitnova et al. [34] |
| Sr, Zr, Ba | Mashonkina et al. [35] |
| Y | Romanovskaya et al. [36] |
Table 4.
Non-LT E and LTE abundances for atoms and ions in the atmosphere of both components of Equulei (A: 5160g2.90 and B: 8260g3.60), scaled to .
Table 4.
Non-LT E and LTE abundances for atoms and ions in the atmosphere of both components of Equulei (A: 5160g2.90 and B: 8260g3.60), scaled to .
| | | Equulei A | Equulei B | Sun |
|---|
| Element | | logϵ | [X/H] | nl | logϵ | [X/H] | nl | |
|---|
| C i | L | 8.11(07) | −0.36 | 2 | 8.43(16) | −0.04 | 5 | 8.47 |
| | N | 8.10(10) | −0.37 | | 8.39(15) | −0.08 | | |
| O i | L | | | | 8.86(26) | 0.13 | 9 | 8.73 |
| | N | | | | 8.80(26) | 0.07 | | |
| Na i | L | 6.32(13) | 0.05 | 4 | 6.76(43) | 0.49 | 4 | 6.27 |
| | N | 6.25(13) | −0.02 | | 6.46(34) | 0.19 | | |
| Mg i | L | 7.47(05) | −0.05 | 5 | 7.47(26) | −0.05 | 6 | 7.52 |
| | N | 7.61(07) | 0.09 | | 7.34(20) | −0.18 | | |
| Mg ii | L | | | | 7.68(26) | 0.16 | 4 | |
| | N | | | | 7.62(29) | 0.10 | | |
| N | 0.09(07) | −0.07(28) | |
| Al i | L | 6.29(09) | −0.13 | 3 | 6.83(20) | 0.41 | 1 | 6.42 |
| Si i | L | 7.55(14) | 0.04 | 12 | 7.78(04) | 0.27 | 5 | 7.51 |
| | N | 7.48(12) | −0.03 | | 7.73(03) | 0.22 | | |
| Si ii | L | | | | 7.51(18) | 0.00 | 5 | |
| | N | | | | 7.58(17) | 0.07 | | |
| N | −0.03(12) | 0.15(15) | |
| S i | L | | | | 7.35(16) | 0.20 | 4 | 7.15 |
| S ii | L | | | | 7.88(20) | 0.73 | 1 | |
| L | | 0.31(26) | |
| K i | L | 5.42(20) | 0.35 | 1 | | | | 5.07 |
| | N | 5.38(20) | 0.31 | | | | | |
| Ca i | L | 6.51(12) | 0.24 | 11 | 6.11(16) | −0.16 | 12 | |
| | N | 6.54(11) | 0.27 | | 6.17(15) | −0.10 | | |
| Ca ii | L | 6.20(11) | −0.07 | 3 | 6.20(11) | −0.07 | 5 | |
| | N | 6.18(12) | −0.09 | | 6.19(11) | −0.08 | | |
| N | 0.20(19) | −0.10(14) | |
| Sc i | L | 3.21(09) | 0.17 | 11 | | | | 3.04 |
| Sc ii | L | 3.00(05) | 0.04 | 7 | 2.74(16) | −0.30 | 6 | |
| | N | 3.02(12) | −0.02 | | 2.73(14) | −0.31 | | |
| L* | 0.12(14) | −0.30(14) | |
| Ti i | L | 5.02(12) | 0.12 | 75 | | | | 4.90 |
| | N | 4.99(14) | 0.09 | | | | | |
| Ti ii | L | 4.98(14) | 0.08 | 37 | 4.81(13) | −0.09 | 36 | |
| | N | 4.95(13) | 0.05 | | 4.78(14) | −0.12 | | |
| N | 0.08(14) | −0.12(14) | |
| V i | L | 4.06(11) | 0.11 | 24 | | | | 3.95 |
| | N | | | | | | | |
| Cr i | L | 5.69(25) | 0.06 | 9 | 5.77(19) | 0.14 | 8 | 5.63 |
| | N | | | | | | | |
| Cr ii | L | 5.74(20) | 0.11 | 21 | 5.73(19) | 0.10 | 28 | |
| | N | | | | | | | |
| L | 0.10(22) | 0.11(19) | |
| Mn i | L | 5.29(15) | −0.18 | 6 | 5.64(26) | 0.17 | 10 | 5.47 |
| Mn ii | L | 5.26(20) | −0.21 | 1 | 6.12(07) | 0.65 | 2 | |
| L | −0.18(14) | 0.25(30) | |
| Fe i | L | 7.41(14) | −0.04 | 24 | 7.43(18) | −0.02 | 19 | 7.45 |
| | N | 7.40(13) | −0.05 | | 7.40(20) | −0.05 | | |
| Fe ii | L | 7.36(14) | −0.09 | 26 | 7.44(16) | −0.01 | 40 | |
| | N | 7.35(14) | −0.10 | | 7.44(16) | −0.01 | | |
| N | −0.08(14) | −0.02(18) | |
| Co i | L | 4.83(16) | −0.03 | 13 | 5.22(20) | 0.36 | 1 | 4.86 |
| Ni i | L | 6.13(09) | −0.07 | 13 | 6.48(20) | 0.28 | 17 | 6.20 |
| Cu i | L | 4.04(07) | −0.14 | 3 | | | | 4.24 |
| Zn i | L | 4.26(07) | −0.35 | 3 | 4.86(07) | 0.25 | 3 | 4.61 |
| | N | 4.20(05) | −0.41 | | 4.90(07) | 0.29 | | |
| Sr i | L | 3.31(13) | 0.43 | 3 | | | | 2.88 |
| Sr ii | L | 3.00(06) | 0.12 | 3 | 3.99(31) | 1.11 | 3 | |
| | N | 3.02(08) | 0.14 | | 3.92(32) | 1.04 | | |
| L* | 0.28(19) | 1.11(31) | |
| Y i | L | 2.75(17) | 0.60 | 3 | | | | 2.15 |
| | N | 3.08(23) | 0.93 | | | | | |
| Y ii | L | 2.66(16) | 0.51 | 12 | 3.11(16) | 0.96 | 15 | |
| | N | 2.63(17) | 0.48 | | 3.07(16) | 0.92 | | |
| N | 0.57(25) | 0.92(16) | |
| Zr i | L | 3.16(08) | 0.61 | 2 | | | | 2.55 |
| Zr ii | L | 2.94(06) | 0.39 | 3 | 3.37(11) | 0.82 | 7 | |
| | N | 2.96(09) | 0.41 | | 3.43(10) | 0.88 | | |
| L* | 0.48(13) | 0.82(11) | |
| Ba i | L | 2.52(20) | 0.35 | 1 | | | | 2.17 |
| Ba ii | L | 2.94(12) | 0.77 | 5 | 3.58(19) | 1.41 | 5 | |
| | N | 2.91(10) | 0.74 | | 3.43(11) | 1.26 | | |
| L* | 0.70(19) | 1.41(19) | |
| La ii | L | 1.43(19) | 1.43 | 4 | | | | 1.17 |
| Ce ii | L | 2.09(19) | 0.51 | 11 | | | | 1.58 |
| Nd ii | L | 1.80(21) | 0.35 | 15 | | | | 1.45 |
| Nd iii | L | | | | 2.59(05) | 1.14 | 3 | |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).