Convective Boundary Mixing in Main-Sequence Stars: Theory and Empirical Constraints
Abstract
1. Introduction
- To provide context for investigators who need to employ CBM in their own studies.
- To summarize past works and provide launching points for future studies aimed at improving CBM prescriptions.
- To facilitate communication between observers, 1D modelers, and 3D numericists.
2. Theoretical (1D) Parametrizations
2.1. How Does CBM Modify Stellar Evolution?
2.2. Convective Boundaries
2.3. Internal Mixing Profiles
2.4. Overshoot or Overmixing
2.5. Convective Penetration
2.6. Extended Convective Penetration
2.7. Limiting the Extent of the CBM Region
2.8. Comparing Different CBM Parameters
2.9. The 1D Models Not Covered in This Review
3. 3D Hydrodynamical Perspectives of Convective Boundary Mixing
3.1. Nondimensional Fluid Parameters
3.2. Convective Overshoot
3.3. Convective Overshoot as Turbulent Diffusion
3.4. Entrainment
3.5. Convective Penetration
3.6. Rotational Constraint and Magnetic Pumping
4. Empirical Calibrations
4.1. Stellar Clusters
4.2. Apsidal Motion
4.3. Mass Discrepancy
4.3.1. A Search for Mass-Dependent CBM Using Binary Systems
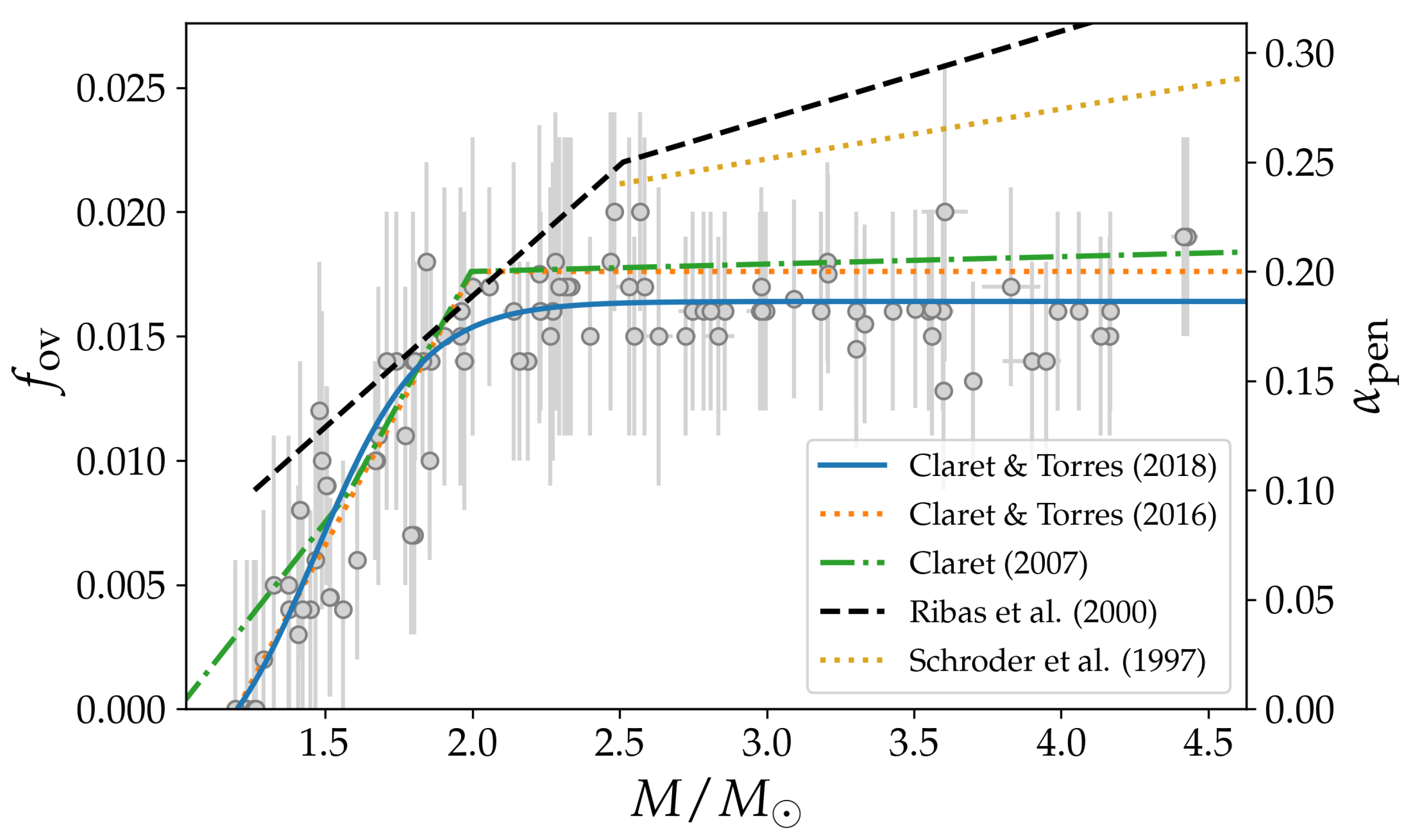
4.3.2. Evidence against Mass-Dependent CBM and Complications
4.4. Asteroseismology
4.4.1. Onset of the Convective Core
4.4.2. Extent of the CBM Region across the Main-Sequence
4.4.3. Differentiating between Different CBM Prescriptions
5. Discussion and Future Work
- First and foremost, it is valuable to “grow the catalogue” of CBM observations. More observational constraints will allow us to not only test and verify new models but also may allow us to understand how complications such as, e.g., rotation affect CBM.
- A uniform analysis of past observations using a consistent stellar structure and boundary mixing scheme should be performed.
- To ease comparisons in future work, authors should clearly state which quantities their CBM prescriptions mix. Specifically, does CBM adjust or not?
- Evidence for extended convective penetration (Section 2.6) is seen in hydrodynamical simulations, and this prescription should be included in more stellar structure codes and models.
- In main sequence intermediate- to high-mass stars, the mass and radius of the convective core should be clearly reported along with the mass and size of the CBM region. Whether the reported convective core mass does or does not include the mass in the CBM region should also be specified. This circumvents difficulties associated with making comparisons between codes using different CBM prescriptions and methods of limiting the size of the CBM region.
- When reporting ages of stars on the main sequence, also report a quantity such as the core hydrogen fraction for easier comparison across works.
- Whenever possible, 3D hydrodynamical simulations should strive to provide prescriptions that do not have free parameters but instead rely on stellar structure.
- For example, overshoot depth and turbulent diffusive mixing profiles should be carefully calibrated and parameterized so that overshoot can be evaluated as a function of stellar structure rather than a specified .
- The 1D prescriptions derived from 3D simulation data should be validated using the same initial conditions employed in the 3D simulations. If the 1D prescription produces a different result from the 3D data, this should be explored in detail.
- Simulations probing the thermal structure near a convective boundary should be evolved until thermal equilibrium is achieved. Performing short simulations which are initialized with CBM regions of various sizes can however qualitatively answer the question, “Which way does the convective boundary move?”
- It is not clear how to properly parameterize dissipation, but dissipation sets the size of a convective penetration region. Future studies should answer the following: what sets the magnitude of the viscous dissipation? How does rotation affect it? How does magnetism and the presence of Ohmic dissipation affect it?
- Entrainment is important when convective regions are first forming or when the convective luminosity or nuclear burning change rapidly compared to the convective overturn timescale. These evolutionary stages should be modeled by time-dependent convection (TDC) prescriptions [153]. Future work should test whether TDC models reproduce the entrainment rates at convective boundaries observed in simulations, and TDC models should be improved where they disagree with simulations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BSG | Blue supergiant |
| CBM | Convective boundary mixing |
| CZ | Convection zone |
| DDLEB | Detached double-lined eclipsing binary |
| eMSTO | Extended main-sequence turnoff |
| LHS | Left-hand side |
| RHS | Right-hand side |
| RZ | Radiative zone |
| PZ | Penetrative zone |
| TAMS | Terminal age main sequence |
| ZAMS | Zero-age main sequence |
| 1 | To account for the step taken inside of the convective core, one would usually add to the overshooting parameter. As an example, in MESA one would use overshoot_f, where overshoot_f is the name of the overshoot parameter in MESA. |
| 2 | We note that the authors of both of these studies of detached double-lined eclipsing binary systems [76,77] use in their notation, but they are actually assuming an adiabatic temperature gradient in the CBM region. In other words, while they talk about a step-based overshooting using the free parameter , they are in fact referring to convective penetration. |
| 3 | The Anelastic approximation models low Mach number flows and assumes that Equation (12) reduces to where is the “background” density. The Boussinesq approximation goes one step further and assumes incompressibility, or that is constant everywhere so that Equation (12) becomes ; under the Boussinesq approximation, small-density perturbations are allowed to exist in the buoyancy term in the momentum equation. |
| 4 | was often defined in terms of polytropic indices; thus, we use ≈ instead of = in our definition here. |
| 5 | |
| 6 | The spectroscopic masses are obtained from the spectroscopic values in combination with radius estimates from, e.g., relations between values, bolometric corrections, and spectral types (see [245]). |
| 7 | can be derived from the component masses and radii and was therefore held fixed for this comparison. |
| 8 | In the spectroscopic HR diagram, the luminosity is calculated as , thereby becoming independent of distance and extinction measurements. |
| 9 | The Spearman’s rank correlation coefficient for this sub-sample is 0.324 with a p-value of 0.0011, corresponding to strong evidence for a positive correlation between the CBM parameter and stellar mass. |
References
- Böhm-Vitense, E. Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. Z. Astrophys. 1958, 46, 108. [Google Scholar]
- Anders, E.H.; Jermyn, A.S.; Lecoanet, D.; Fraser, A.E.; Cresswell, I.G.; Joyce, M.; Fuentes, J.R. Schwarzschild and Ledoux are Equivalent on Evolutionary Timescales. Astrophys. J. Lett. 2022, 928, L10. [Google Scholar] [CrossRef]
- Chabrier, G.; Baraffe, I. Structure and evolution of low-mass stars. Astron. Astrophys. 1997, 327, 1039–1053. [Google Scholar]
- Chabrier, G.; Baraffe, I. Theory of Low-Mass Stars and Substellar Objects. Annu. Rev. Astron. Astrophys. 2000, 38, 337–377. [Google Scholar] [CrossRef]
- Jermyn, A.S.; Anders, E.H.; Lecoanet, D.; Cantiello, M. An Atlas of Convection in Main-sequence Stars. Astrophys. J. Suppl. Ser. 2022, 262, 19. [Google Scholar] [CrossRef]
- Pinsonneault, M. Mixing in Stars. Annu. Rev. Astron. Astrophys. 1997, 35, 557–605. [Google Scholar] [CrossRef]
- Carlos, M.; Meléndez, J.; Spina, L.; dos Santos, L.A.; Bedell, M.; Ramirez, I.; Asplund, M.; Bean, J.L.; Yong, D.; Yana Galarza, J.; et al. The Li-age correlation: The Sun is unusually Li deficient for its age. Mon. Not. R. Astron. Soc. 2019, 485, 4052–4059. [Google Scholar] [CrossRef]
- Dumont, T.; Palacios, A.; Charbonnel, C.; Richard, O.; Amard, L.; Augustson, K.; Mathis, S. Lithium depletion and angular momentum transport in solar-type stars. Astron. Astrophys. 2021, 646, A48. [Google Scholar] [CrossRef]
- Christensen-Dalsgaard, J.; Monteiro, M.J.P.F.G.; Rempel, M.; Thompson, M.J. A more realistic representation of overshoot at the base of the solar convective envelope as seen by helioseismology. Mon. Not. R. Astron. Soc. 2011, 414, 1158–1174. [Google Scholar] [CrossRef]
- Bergemann, M.; Serenelli, A. Solar Abundance Problem. In Determination of Atmospheric Parameters of B; Springer: Cham, Switzerland, 2014; pp. 245–258. [Google Scholar] [CrossRef]
- Basu, S. Global seismology of the Sun. Living Rev. Sol. Phys. 2016, 13, 2. [Google Scholar] [CrossRef]
- Hansen, C.J.; Kawaler, S.D.; Trimble, V. Stellar Interiors: Physical Principles, Structure, and Evolution; Springer: Cham, Switzerland, 2004. [Google Scholar]
- Cantiello, M.; Braithwaite, J. Envelope Convection, Surface Magnetism, and Spots in A and Late B-type Stars. Astrophys. J. 2019, 883, 106. [Google Scholar] [CrossRef]
- Jermyn, A.S.; Anders, E.H.; Cantiello, M. A Transparent Window into Early-type Stellar Variability. Astrophys. J. 2022, 926, 221. [Google Scholar] [CrossRef]
- Johnston, C. One size does not fit all: Evidence for a range of mixing efficiencies in stellar evolution calculations. Astron. Astrophys. 2021, 655, A29. [Google Scholar] [CrossRef]
- Kaiser, E.A.; Hirschi, R.; Arnett, W.D.; Georgy, C.; Scott, L.J.A.; Cristini, A. Relative importance of convective uncertainties in massive stars. Mon. Not. R. Astron. Soc. 2020, 496, 1967–1989. [Google Scholar] [CrossRef]
- Schootemeijer, A.; Langer, N.; Grin, N.J.; Wang, C. Constraining mixing in massive stars in the Small Magellanic Cloud. Astron. Astrophys. 2019, 625, A132. [Google Scholar] [CrossRef]
- Farrell, E.J.; Groh, J.H.; Meynet, G.; Eldridge, J.J.; Ekström, S.; Georgy, C. SNAPSHOT: Connections between internal and surface properties of massive stars. Mon. Not. R. Astron. Soc. 2020, 495, 4659–4680. [Google Scholar] [CrossRef]
- Pedersen, M.G.; Aerts, C.; Pápics, P.I.; Michielsen, M.; Gebruers, S.; Rogers, T.M.; Molenberghs, G.; Burssens, S.; Garcia, S.; Bowman, D.M. Internal mixing of rotating stars inferred from dipole gravity modes. Nat. Astron. 2021, 5, 715–722. [Google Scholar] [CrossRef]
- Claret, A.; Torres, G. The Dependence of Convective Core Overshooting on Stellar Mass: Additional Binary Systems and Improved Calibration. Astrophys. J. 2018, 859, 100. [Google Scholar] [CrossRef]
- Castro, N.; Fossati, L.; Langer, N.; Simón-Díaz, S.; Schneider, F.R.N.; Izzard, R.G. The spectroscopic Hertzsprung-Russell diagram of Galactic massive stars. Astron. Astrophys. 2014, 570, L13. [Google Scholar] [CrossRef]
- Higgins, E.R.; Vink, J.S. Massive star evolution: Rotation, winds, and overshooting vectors in the mass-luminosity plane. I. A calibrated grid of rotating single star models. Astron. Astrophys. 2019, 622, A50. [Google Scholar] [CrossRef]
- Martinet, S.; Meynet, G.; Ekström, S.; Simón-Díaz, S.; Holgado, G.; Castro, N.; Georgy, C.; Eggenberger, P.; Buldgen, G.; Salmon, S.; et al. Convective core sizes in rotating massive stars. I. Constraints from solar metallicity OB field stars. Astron. Astrophys. 2021, 648, A126. [Google Scholar] [CrossRef]
- Higgins, E.R.; Vink, J.S. Stellar age determination in the mass-luminosity plane. Mon. Not. R. Astron. Soc. 2023, 518, 1158–1169. [Google Scholar] [CrossRef]
- Meakin, C.A.; Arnett, D. Turbulent Convection in Stellar Interiors. I. Hydrodynamic Simulation. Astrophys. J. 2007, 667, 448–475. [Google Scholar] [CrossRef]
- Gilet, C.; Almgren, A.S.; Bell, J.B.; Nonaka, A.; Woosley, S.E.; Zingale, M. Low Mach Number Modeling of Core Convection in Massive Stars. Astrophys. J. 2013, 773, 137. [Google Scholar] [CrossRef]
- Cristini, A.; Meakin, C.; Hirschi, R.; Arnett, D.; Georgy, C.; Viallet, M.; Walkington, I. 3D hydrodynamic simulations of carbon burning in massive stars. Mon. Not. R. Astron. Soc. 2017, 471, 279–300. [Google Scholar] [CrossRef]
- Jones, S.; Andrassy, R.; Sandalski, S.; Davis, A.; Woodward, P.; Herwig, F. Idealized hydrodynamic simulations of turbulent oxygen-burning shell convection in 4π geometry. Mon. Not. R. Astron. Soc. 2017, 465, 2991–3010. [Google Scholar] [CrossRef]
- Andrassy, R.; Herwig, F.; Woodward, P.; Ritter, C. 3D hydrodynamic simulations of C ingestion into a convective O shell. Mon. Not. R. Astron. Soc. 2020, 491, 972–992. [Google Scholar] [CrossRef]
- Higl, J.; Müller, E.; Weiss, A. Calibrating core overshooting parameters with two-dimensional hydrodynamical simulations. Astron. Astrophys. 2021, 646, A133. [Google Scholar] [CrossRef]
- Rizzuti, F.; Hirschi, R.; Georgy, C.; Arnett, W.D.; Meakin, C.; Murphy, A.S. Realistic 3D hydrodynamics simulations find significant turbulent entrainment in massive stars. Mon. Not. R. Astron. Soc. 2022, 515, 4013–4019. [Google Scholar] [CrossRef]
- Brandenburg, A.; Svedin, A.; Vasil, G.M. Turbulent diffusion with rotation or magnetic fields. Mon. Not. R. Astron. Soc. 2009, 395, 1599–1606. [Google Scholar] [CrossRef]
- Anders, E.H.; Pedersen, M.G. Supplemental Materials for “Convective Boundary Mixing in Main-Sequence Stars: Theory and Empirical Constraints”; Zenodo: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Paxton, B.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Blinnikov, S.; Duffell, P.; Farmer, R.; Goldberg, J.A.; Marchant, P.; Sorokina, E.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Convective Boundaries, Element Diffusion, and Massive Star Explosions. Astrophys. J. Suppl. Ser. 2018, 234, 34. [Google Scholar] [CrossRef]
- Garaud, P. Double-Diffusive Convection at Low Prandtl Number. Annu. Rev. Fluid Mech. 2018, 50, 275–298. [Google Scholar] [CrossRef]
- Salaris, M.; Cassisi, S. Chemical element transport in stellar evolution models. R. Soc. Open Sci. 2017, 4, 170192. [Google Scholar] [CrossRef]
- Georgy, C.; Saio, H.; Meynet, G. Blue supergiants as tests for stellar physics. Astron. Astrophys. 2021, 650, A128. [Google Scholar] [CrossRef]
- Gabriel, M.; Noels, A.; Montalbán, J.; Miglio, A. Proper use of Schwarzschild Ledoux criteria in stellar evolution computations. Astron. Astrophys. 2014, 569, A63. [Google Scholar] [CrossRef]
- Zahn, J.P. Convective penetration in stellar interiors. Astron. Astrophys. 1991, 252, 179–188. [Google Scholar]
- Woo, J.H.; Demarque, P. Empirical Constraints on Convective Core Overshoot. Astron. J. 2001, 122, 1602–1606. [Google Scholar] [CrossRef]
- Freytag, B.; Ludwig, H.G.; Steffen, M. Hydrodynamical models of stellar convection. The role of overshoot in DA white dwarfs, A-type stars, and the Sun. Astron. Astrophys. 1996, 313, 497–516. [Google Scholar]
- Herwig, F. The evolution of AGB stars with convective overshoot. Astron. Astrophys. 2000, 360, 952–968. [Google Scholar]
- Weiss, A.; Schlattl, H. GARSTEC—the Garching Stellar Evolution Code. The direct descendant of the legendary Kippenhahn code. Astrophys. Space Sci. 2008, 316, 99–106. [Google Scholar] [CrossRef]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. Ser. 2011, 192, 3. [Google Scholar] [CrossRef]
- Paxton, B.; Cantiello, M.; Arras, P.; Bildsten, L.; Brown, E.F.; Dotter, A.; Mankovich, C.; Montgomery, M.H.; Stello, D.; Timmes, F.X.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Planets, Oscillations, Rotation, and Massive Stars. Astrophys. J. Suppl. Ser. 2013, 208, 4. [Google Scholar] [CrossRef]
- Paxton, B.; Marchant, P.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Cantiello, M.; Dessart, L.; Farmer, R.; Hu, H.; Langer, N.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Binaries, Pulsations, and Explosions. Astrophys. J. Suppl. Ser. 2015, 220, 15. [Google Scholar] [CrossRef]
- Paxton, B.; Smolec, R.; Schwab, J.; Gautschy, A.; Bildsten, L.; Cantiello, M.; Dotter, A.; Farmer, R.; Goldberg, J.A.; Jermyn, A.S.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Pulsating Variable Stars, Rotation, Convective Boundaries, and Energy Conservation. Astrophys. J. Suppl. Ser. 2019, 243, 10. [Google Scholar] [CrossRef]
- Roxburgh, I.W. A note on the boundary of convective zones in stars. Mon. Not. R. Astron. Soc. 1965, 130, 223. [Google Scholar] [CrossRef]
- Prather, M.J.; Demarque, P. Convective Overshoot Mixing in Old Open Clusters. Astrophys. J. 1974, 193, 109–112. [Google Scholar] [CrossRef]
- Dotter, A.; Chaboyer, B.; Jevremović, D.; Baron, E.; Ferguson, J.W.; Sarajedini, A.; Anderson, J. The ACS Survey of Galactic Globular Clusters. II. Stellar Evolution Tracks, Isochrones, Luminosity Functions, and Synthetic Horizontal-Branch Models. Astron. J. 2007, 134, 376–390. [Google Scholar] [CrossRef]
- Dotter, A.; Chaboyer, B.; Jevremović, D.; Kostov, V.; Baron, E.; Ferguson, J.W. The Dartmouth Stellar Evolution Database. Astrophys. J. Suppl. Ser. 2008, 178, 89–101. [Google Scholar] [CrossRef]
- Cassisi, S.; Salaris, M. A critical investigation on the discrepancy between the observational and the theoretical red giant luminosity function ‘bump’. Mon. Not. R. Astron. Soc. 1997, 285, 593–603. [Google Scholar] [CrossRef]
- Salaris, M.; Cassisi, S. A new analysis of the red giant branch ‘tip’ distance scale and the value of the Hubble constant. Mon. Not. R. Astron. Soc. 1998, 298, 166–178. [Google Scholar] [CrossRef]
- Pietrinferni, A.; Cassisi, S.; Salaris, M.; Castelli, F. A Large Stellar Evolution Database for Population Synthesis Studies. I. Scaled Solar Models and Isochrones. Astrophys. J. 2004, 612, 168–190. [Google Scholar] [CrossRef]
- Pietrinferni, A.; Cassisi, S.; Salaris, M.; Castelli, F. A Large Stellar Evolution Database for Population Synthesis Studies. II. Stellar Models and Isochrones for an α-enhanced Metal Distribution. Astrophys. J. 2006, 642, 797–812. [Google Scholar] [CrossRef]
- Cordier, D.; Pietrinferni, A.; Cassisi, S.; Salaris, M. A Large Stellar Evolution Database for Population Synthesis Studies. III. Inclusion of the Full Asymptotic Giant Branch Phase and Web Tools for Stellar Population Analyses. Astron. J. 2007, 133, 468–478. [Google Scholar] [CrossRef]
- Percival, S.M.; Salaris, M.; Cassisi, S.; Pietrinferni, A. A Large Stellar Evolution Database for Population Synthesis Studies. IV. Integrated Properties and Spectra. Astrophys. J. 2009, 690, 427–439. [Google Scholar] [CrossRef]
- Pietrinferni, A.; Cassisi, S.; Salaris, M.; Percival, S.; Ferguson, J.W. A Large Stellar Evolution Database for Population Synthesis Studies. V. Stellar Models and Isochrones with CNONa Abundance Anticorrelations. Astrophys. J. 2009, 697, 275–282. [Google Scholar] [CrossRef]
- Hui-Bon-Hoa, A. The Toulouse Geneva Evolution Code (TGEC). Astrophys. Space Sci. 2008, 316, 55–60. [Google Scholar] [CrossRef]
- Théado, S.; Alecian, G.; LeBlanc, F.; Vauclair, S. The new Toulouse-Geneva stellar evolution code including radiative accelerations of heavy elements. Astron. Astrophys. 2012, 546, A100. [Google Scholar] [CrossRef]
- Demarque, P.; Guenther, D.B.; Li, L.H.; Mazumdar, A.; Straka, C.W. YREC: The Yale rotating stellar evolution code. Non-rotating version, seismology applications. Astrophys. Space Sci. 2008, 316, 31–41. [Google Scholar] [CrossRef]
- Eggenberger, P.; Meynet, G.; Maeder, A.; Hirschi, R.; Charbonnel, C.; Talon, S.; Ekström, S. The Geneva stellar evolution code. Astrophys. Space Sci. 2008, 316, 43–54. [Google Scholar] [CrossRef]
- Viallet, M.; Meakin, C.; Prat, V.; Arnett, D. Toward a consistent use of overshooting parametrizations in 1D stellar evolution codes. Astron. Astrophys. 2015, 580, A61. [Google Scholar] [CrossRef]
- Michielsen, M.; Pedersen, M.G.; Augustson, K.C.; Mathis, S.; Aerts, C. Probing the shape of the mixing profile and of the thermal structure at the convective core boundary through asteroseismology. Astron. Astrophys. 2019, 628, A76. [Google Scholar] [CrossRef]
- Michielsen, M.; Aerts, C.; Bowman, D.M. Probing the temperature gradient in the core boundary layer of stars with gravito-inertial modes. The case of KIC 7760680. Astron. Astrophys. 2021, 650, A175. [Google Scholar] [CrossRef]
- Christensen-Dalsgaard, J. ASTEC—the Aarhus STellar Evolution Code. Astrophys. Space Sci. 2008, 316, 13–24. [Google Scholar] [CrossRef]
- Monteiro, M.J.P.F.G.; Christensen-Dalsgaard, J.; Thompson, M.J. Seismic study of overshoot at the base of the solar convective envelope. Astron. Astrophys. 1994, 283, 247–262. [Google Scholar]
- Demarque, P.; Woo, J.H.; Kim, Y.C.; Yi, S.K. Y2 Isochrones with an Improved Core Overshoot Treatment. Astrophys. J. Suppl. Ser. 2004, 155, 667–674. [Google Scholar] [CrossRef]
- Spada, F.; Demarque, P.; Kim, Y.C.; Boyajian, T.S.; Brewer, J.M. The Yale-Potsdam Stellar Isochrones. Astrophys. J. 2017, 838, 161. [Google Scholar] [CrossRef]
- Magic, Z.; Serenelli, A.; Weiss, A.; Chaboyer, B. On Using the Color-Magnitude Diagram Morphology of M67 to Test Solar Abundances. Astrophys. J. 2010, 718, 1378–1387. [Google Scholar] [CrossRef]
- Claret, A. Updating the theoretical tidal evolution constants: Apsidal motion and the moment of inertia. Astron. Astrophys. 2019, 628, A29. [Google Scholar] [CrossRef]
- Morel, P.; Lebreton, Y. CESAM: A free code for stellar evolution calculations. Astrophys. Space Sci. 2008, 316, 61–73. [Google Scholar] [CrossRef]
- Viani, L.S.; Basu, S. Examining the Relationship Between Convective Core Overshoot and Stellar Properties Using Asteroseismology. Astrophys. J. 2020, 904, 22. [Google Scholar] [CrossRef]
- Deheuvels, S. Probing core overshooting using asteroseismology. Bull. Soc. R. Sci. Liege 2019, 88, 84–105. [Google Scholar] [CrossRef]
- Moravveji, E.; Townsend, R.H.D.; Aerts, C.; Mathis, S. Sub-inertial Gravity Modes in the B8V Star KIC 7760680 Reveal Moderate Core Overshooting and Low Vertical Diffusive Mixing. Astrophys. J. 2016, 823, 130. [Google Scholar] [CrossRef]
- Claret, A.; Torres, G. The Dependence of Convective Core Overshooting on Stellar Mass: A Semi-empirical Determination Using the Diffusive Approach with Two Different Element Mixtures. Astrophys. J. 2017, 849, 18. [Google Scholar] [CrossRef]
- Tkachenko, A.; Pavlovski, K.; Johnston, C.; Pedersen, M.G.; Michielsen, M.; Bowman, D.M.; Southworth, J.; Tsymbal, V.; Aerts, C. The mass discrepancy in intermediate- and high-mass eclipsing binaries: The need for higher convective core masses. Astron. Astrophys. 2020, 637, A60. [Google Scholar] [CrossRef]
- Noels, A.; Montalban, J.; Miglio, A.; Godart, M.; Ventura, P. Overshooting and semiconvection: Structural changes and asteroseismic signatures. Astrophys. Space Sci. 2010, 328, 227–236. [Google Scholar] [CrossRef]
- Unno, W. Anisotropy of Solar Convection. Astrophys. J. 1957, 126, 259. [Google Scholar] [CrossRef]
- Böhm, K.H. The Mixing of Matter in the Layer Below the Outer Solar Convection Zone. Astrophys. J. 1963, 138, 297. [Google Scholar] [CrossRef]
- Saslaw, W.C.; Schwarzschild, M. Overshooting from Stellar Convective Cores. Astrophys. J. 1965, 142, 1468. [Google Scholar] [CrossRef]
- Zahn, J.P.; Toomre, J.; Latour, J. Nonlinear modal analysis of penetrative convection. Geophys. Astrophys. Fluid Dyn. 1982, 22, 159–193. [Google Scholar] [CrossRef]
- Straus, J.M.; Blake, J.B.; Schramm, D.N. Effects of convective overshoot on lithium depletion in main-sequence stars. Astrophys. J. 1976, 204, 481–487. [Google Scholar] [CrossRef]
- Spiegel, E.A. A Generalization of the Mixing-Length Theory of Turbulent Convection. Astrophys. J. 1963, 138, 216. [Google Scholar] [CrossRef]
- Shaviv, G.; Salpeter, E.E. Convective Overshooting in Stellar Interior Models. Astrophys. J. 1973, 184, 191–200. [Google Scholar] [CrossRef]
- Nordlund, A. On Convection in Stellar Atmospheres. Astron. Astrophys. 1974, 32, 407. [Google Scholar]
- Maeder, A. Stellar evolution III: The overshooting from convective cores. Astron. Astrophys. 1975, 40, 303–310. [Google Scholar]
- Cogan, B.C. Convective Overshooting in Main-Sequence Models. Astrophys. J. 1975, 201, 637–640. [Google Scholar] [CrossRef]
- Ulrich, R.K. A Nonlocal Mixing-Length Theory of Convection for Use in Numerical Calculations. Astrophys. J. 1976, 207, 564–573. [Google Scholar] [CrossRef]
- Langer, N. Non-local treatment of convection and overshooting from stellar convective cores. Astron. Astrophys. 1986, 164, 45–50. [Google Scholar]
- Marcus, P.S.; Press, W.H.; Teukolsky, S.A. Multiscale model equations for turbulent convection and convective overshoot. Astrophys. J. 1983, 267, 795–821. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Li, Y. Turbulent Convection Model in the Overshooting Region. I. Effects of the Convective Mixing in the Solar Overshooting Region. Astrophys. J. 2012, 746, 50. [Google Scholar] [CrossRef]
- Zhang, Q.S. A Simple Scheme to Implement a Nonlocal Turbulent Convection Model for Convective Overshoot Mixing. Astrophys. J. 2016, 818, 146. [Google Scholar] [CrossRef]
- Canuto, V.M. Stellar mixing. V. Overshooting. Astron. Astrophys. 2011, 528, A80. [Google Scholar] [CrossRef]
- Kupka, F.; Montgomery, M.H. A-star envelopes: A test of local and non-local models of convection. Mon. Not. R. Astron. Soc. 2002, 330, L6–L10. [Google Scholar] [CrossRef]
- Kupka, F.; Ahlborn, F.; Weiss, A. Stellar evolution models with overshooting based on 3-equation non-local theories I. Physical basis and the computation of the dissipation rate. arXiv 2022, arXiv:2207.12296. [Google Scholar]
- Chen, C.J. Response of an Optically Thin, Isothermal Atmosphere to a Convective Overshoot. Sol. Phys. 1974, 37, 53–62. [Google Scholar] [CrossRef]
- Renzini, A. Some embarrassments in current treatments of convective overshooting. Astron. Astrophys. 1987, 188, 49–54. [Google Scholar]
- Pratt, J.; Baraffe, I.; Goffrey, T.; Constantino, T.; Viallet, M.; Popov, M.V.; Walder, R.; Folini, D. Extreme value statistics for two-dimensional convective penetration in a pre-main sequence star. Astron. Astrophys. 2017, 604, A125. [Google Scholar] [CrossRef]
- Augustson, K.C.; Mathis, S. A Model of Rotating Convection in Stellar and Planetary Interiors. I. Convective Penetration. Astrophys. J. 2019, 874, 83. [Google Scholar] [CrossRef]
- Herwig, F.; Freytag, B.; Fuchs, T.; Hansen, J.P.; Hueckstaedt, R.M.; Porter, D.H.; Timmes, F.X.; Woodward, P.R. Convective and Non-Convective Mixing in AGB Stars. In Why Galaxies Care about AGB Stars: Their Importance as Actors and Probes; Kerschbaum, F., Charbonnel, C., Wing, R.F., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2007; Volume 378, p. 43. [Google Scholar]
- Spiegel, E.A.; Veronis, G. On the Boussinesq Approximation for a Compressible Fluid. Astrophys. J. 1960, 131, 442. [Google Scholar] [CrossRef]
- Lantz, S.R. Dynamical Behavior of Magnetic Fields in a Stratified, Convecting Fluid Layer. Ph.D. Thesis, Cornell University, New York, NY, USA, 1992. [Google Scholar]
- Braginsky, S.I.; Roberts, P.H. Equations governing convection in earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 1995, 79, 1–97. [Google Scholar] [CrossRef]
- Lantz, S.R.; Fan, Y. Anelastic Magnetohydrodynamic Equations for Modeling Solar and Stellar Convection Zones. Astrophys. J. Suppl. Ser. 1999, 121, 247–264. [Google Scholar] [CrossRef]
- Jones, C.A.; Kuzanyan, K.M.; Mitchell, R.H. Linear theory of compressible convection in rapidly rotating spherical shells, using the anelastic approximation. J. Fluid Mech. 2009, 634, 291. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics. 1987. Available online: https://www.sciencedirect.com/book/9780080339337/fluid-mechanics#book-info (accessed on 9 February 2023).
- Grossmann, S.; Lohse, D. Scaling in thermal convection: A unifying theory. J. Fluid Mech. 2000, 407, 27–56. [Google Scholar] [CrossRef]
- Jones, C.A.; Mizerski, K.A.; Kessar, M. Fully developed anelastic convection with no-slip boundaries. J. Fluid Mech. 2022, 930, A13. [Google Scholar] [CrossRef]
- Roxburgh, I.W. Integral constraints on convective overshooting. Astron. Astrophys. 1989, 211, 361–364. [Google Scholar]
- Käpylä, P.J.; Rheinhardt, M.; Brandenburg, A.; Arlt, R.; Käpylä, M.J.; Lagg, A.; Olspert, N.; Warnecke, J. Extended Subadiabatic Layer in Simulations of Overshooting Convection. Astrophys. J. Lett. 2017, 845, L23. [Google Scholar] [CrossRef]
- Anders, E.H.; Jermyn, A.S.; Lecoanet, D.; Fuentes, J.R.; Korre, L.; Brown, B.P.; Oishi, J.S. Convective Boundary Mixing Processes. Res. Notes Am. Astron. Soc. 2022, 6, 41. [Google Scholar] [CrossRef]
- Hurlburt, N.E.; Toomre, J.; Massaguer, J.M.; Zahn, J.P. Penetration below a Convection Zone. Astrophys. J. 1994, 421, 245. [Google Scholar] [CrossRef]
- Lecoanet, D.; Schwab, J.; Quataert, E.; Bildsten, L.; Timmes, F.X.; Burns, K.J.; Vasil, G.M.; Oishi, J.S.; Brown, B.P. Turbulent Chemical Diffusion in Convectively Bounded Carbon Flames. Astrophys. J. 2016, 832, 71. [Google Scholar] [CrossRef]
- Couston, L.A.; Lecoanet, D.; Favier, B.; Le Bars, M. Dynamics of mixed convective-stably-stratified fluids. Phys. Rev. Fluids 2017, 2, 094804. [Google Scholar] [CrossRef]
- Anders, E.H.; Jermyn, A.S.; Lecoanet, D.; Brown, B.P. Stellar Convective Penetration: Parameterized Theory and Dynamical Simulations. Astrophys. J. 2022, 926, 169. [Google Scholar] [CrossRef]
- Aerts, C.; Augustson, K.; Mathis, S.; Pedersen, M.G.; Mombarg, J.S.G.; Vanlaer, V.; Van Beeck, J.; Van Reeth, T. Rossby numbers and stiffness values inferred from gravity-mode asteroseismology of rotating F- and B-type dwarfs. Consequences for mixing, transport, magnetism, and convective penetration. Astron. Astrophys. 2021, 656, A121. [Google Scholar] [CrossRef]
- Kippenhahn, R.; Weigert, A.; Weiss, A. Stellar Structure and Evolution; Springer: Cham, Switzerland, 2013. [Google Scholar] [CrossRef]
- Brummell, N.H.; Clune, T.L.; Toomre, J. Penetration and Overshooting in Turbulent Compressible Convection. Astrophys. J. 2002, 570, 825–854. [Google Scholar] [CrossRef]
- Rogers, T.M.; Glatzmaier, G.A. Penetrative Convection within the Anelastic Approximation. Astrophys. J. 2005, 620, 432–441. [Google Scholar] [CrossRef]
- Browning, M.K.; Brun, A.S.; Toomre, J. Simulations of Core Convection in Rotating A-Type Stars: Differential Rotation and Overshooting. Astrophys. J. 2004, 601, 512–529. [Google Scholar] [CrossRef]
- Rempel, M. Overshoot at the Base of the Solar Convection Zone: A Semianalytical Approach. Astrophys. J. 2004, 607, 1046–1064. [Google Scholar] [CrossRef]
- Rogers, T.M.; Glatzmaier, G.A.; Jones, C.A. Numerical Simulations of Penetration and Overshoot in the Sun. Astrophys. J. 2006, 653, 765–773. [Google Scholar] [CrossRef]
- Brun, A.S.; Miesch, M.S.; Toomre, J. Modeling the Dynamical Coupling of Solar Convection with the Radiative Interior. Astrophys. J. 2011, 742, 79. [Google Scholar] [CrossRef]
- Singh, H.P.; Roxburgh, I.W.; Chan, K.L. A study of penetration at the bottom of a stellar convective envelope and its scaling relationships. Astron. Astrophys. 1998, 340, 178–182. [Google Scholar]
- Saikia, E.; Singh, H.P.; Chan, K.L.; Roxburgh, I.W.; Srivastava, M.P. Examination of Scaling Relationships Involving Penetration Distance at the Bottom of a Stellar Convective Envelope. Astrophys. J. 2000, 529, 402–413. [Google Scholar] [CrossRef]
- Hurlburt, N.E.; Toomre, J.; Massaguer, J.M. Nonlinear Compressible Convection Penetrating into Stable Layers and Producing Internal Gravity Waves. Astrophys. J. 1986, 311, 563. [Google Scholar] [CrossRef]
- Kiraga, M.; Jahn, K.; Muthsam, H.J.; Stȩpień, K. 2D Computer Simulations of Stellar Convection Using a Three-Layer Model. Acta Astron. 1995, 45, 685–704. [Google Scholar]
- Bazán, G.; Arnett, D. Two-dimensional Hydrodynamics of Pre–Core Collapse: Oxygen Shell Burning. Astrophys. J. 1998, 496, 316–332. [Google Scholar] [CrossRef]
- Dietrich, W.; Wicht, J. Penetrative Convection in Partly Stratified Rapidly Rotating Spherical Shells. Front. Earth Sci. 2018, 6, 189. [Google Scholar] [CrossRef]
- Cai, T. Upward Overshooting in Turbulent Compressible Convection. I. Effects of the Relative Stability Parameter, the Prandtl Number, and the Péclet Number. Astrophys. J. 2020, 888, 46. [Google Scholar] [CrossRef]
- Cai, T. Upward Overshooting in Turbulent Compressible Convection. II. Simulations at Large Relative Stability Parameters. Astrophys. J. 2020, 891, 49. [Google Scholar] [CrossRef]
- Tian, C.L.; Deng, L.C.; Chan, K.L. Numerical simulations of downward convective overshooting in giants. Mon. Not. R. Astron. Soc. 2009, 398, 1011–1022. [Google Scholar] [CrossRef]
- Käpylä, P.J. Overshooting in simulations of compressible convection. Astron. Astrophys. 2019, 631, A122. [Google Scholar] [CrossRef]
- Korre, L.; Garaud, P.; Brummell, N.H. Convective overshooting and penetration in a Boussinesq spherical shell. Mon. Not. R. Astron. Soc. 2019, 484, 1220–1237. [Google Scholar] [CrossRef]
- Brown, B.P.; Vasil, G.M.; Zweibel, E.G. Energy Conservation and Gravity Waves in Sound-proof Treatments of Stellar Interiors. Part I. Anelastic Approximations. Astrophys. J. 2012, 756, 109. [Google Scholar] [CrossRef]
- Herwig, F.; Freytag, B.; Hueckstaedt, R.M.; Timmes, F.X. Hydrodynamic Simulations of He Shell Flash Convection. Astrophys. J. 2006, 642, 1057–1074. [Google Scholar] [CrossRef]
- Woodward, P.R.; Herwig, F.; Lin, P.H. Hydrodynamic Simulations of H Entrainment at the Top of He-shell Flash Convection. Astrophys. J. 2015, 798, 49. [Google Scholar] [CrossRef]
- Turner, J.S. The behaviour of a stable salinity gradient heated from below. J. Fluid Mech. 1968, 33, 183–200. [Google Scholar] [CrossRef]
- Deardorff, J.W.; Willis, G.E.; Lilly, D.K. Laboratory investigation of non-steady penetrative convection. J. Fluid Mech. 1969, 35, 7–31. [Google Scholar] [CrossRef]
- Kato, H.; Phillips, O.M. On the penetration of a turbulent layer into stratified fluid. J. Fluid Mech. 1969, 37, 643–655. [Google Scholar] [CrossRef]
- Linden, P.F. The deepening of a mixed layer in a stratified fluid. J. Fluid Mech. 1975, 71, 385–405. [Google Scholar] [CrossRef]
- Fernando, H.J.S. The formation of a layered structure when a stable salinity gradient is heated from below. J. Fluid Mech. 1987, 182, 525–541. [Google Scholar] [CrossRef]
- Molemaker, M.J.; Dijkstra, H.A. The formation and evolution of a diffusive interface. J. Fluid Mech. 1997, 331, 199–229. [Google Scholar] [CrossRef]
- Leppinen, D.M. The erosion of a salinity step by distributed and localized heat sources. Numer. Heat Transf. Part A Appl. 2003, 44, 625–644. [Google Scholar] [CrossRef]
- Fuentes, J.R.; Cumming, A. Penetration of a cooling convective layer into a stably-stratified composition gradient: Entrainment at low Prandtl number. Phys. Rev. Fluids 2020, 5, 124501. [Google Scholar] [CrossRef]
- Toppaladoddi, S.; Wettlaufer, J.S. Penetrative convection at high Rayleigh numbers. Phys. Rev. Fluids 2018, 3, 043501. [Google Scholar] [CrossRef]
- Arnett, D.; Meakin, C.; Young, P.A. Turbulent Convection in Stellar Interiors. II. The Velocity Field. Astrophys. J. 2009, 690, 1715–1729. [Google Scholar] [CrossRef]
- Mocák, M.; Müller, E.; Weiss, A.; Kifonidis, K. The core helium flash revisited. II. Two and three-dimensional hydrodynamic simulations. Astron. Astrophys. 2009, 501, 659–677. [Google Scholar] [CrossRef]
- Cristini, A.; Hirschi, R.; Meakin, C.; Arnett, D.; Georgy, C.; Walkington, I. Dependence of convective boundary mixing on boundary properties and turbulence strength. Mon. Not. R. Astron. Soc. 2019, 484, 4645–4664. [Google Scholar] [CrossRef]
- Staritsin, E.I. Turbulent entrainment at the boundaries of the convective cores of main-sequence stars. Astron. Rep. 2013, 57, 380–390. [Google Scholar] [CrossRef]
- Scott, L.J.A.; Hirschi, R.; Georgy, C.; Arnett, W.D.; Meakin, C.; Kaiser, E.A.; Ekström, S.; Yusof, N. Convective core entrainment in 1D main-sequence stellar models. Mon. Not. R. Astron. Soc. 2021, 503, 4208–4220. [Google Scholar] [CrossRef]
- Jermyn, A.S.; Bauer, E.B.; Schwab, J.; Farmer, R.; Ball, W.H.; Bellinger, E.P.; Dotter, A.; Joyce, M.; Marchant, P.; Mombarg, J.S.G.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Time-Dependent Convection, Energy Conservation, Automatic Differentiation, and Infrastructure. arXiv 2022, arXiv:2208.03651. [Google Scholar] [CrossRef]
- Roxburgh, I.W. Convection and stellar structure. Astron. Astrophys. 1978, 65, 281–285. [Google Scholar]
- Roxburgh, I.W. Limits on convective penetration from stellar cores. Astron. Astrophys. 1992, 266, 291–293. [Google Scholar]
- Kitiashvili, I.N.; Kosovichev, A.G.; Mansour, N.N.; Wray, A.A. Dynamics of Turbulent Convection and Convective Overshoot in a Moderate-mass Star. Astrophys. J. Lett. 2016, 821, L17. [Google Scholar] [CrossRef]
- Baraffe, I.; Pratt, J.; Vlaykov, D.G.; Guillet, T.; Goffrey, T.; Le Saux, A.; Constantino, T. Two-dimensional simulations of solar-like models with artificially enhanced luminosity. I. Impact on convective penetration. Astron. Astrophys. 2021, 654, A126. [Google Scholar] [CrossRef]
- Singh, H.P.; Roxburgh, I.W.; Chan, K.L. Three-dimensional simulation of penetrative convection: Penetration below a convection zone. Astron. Astrophys. 1995, 295, 703. [Google Scholar]
- Brun, A.S.; Strugarek, A.; Varela, J.; Matt, S.P.; Augustson, K.C.; Emeriau, C.; DoCao, O.L.; Brown, B.; Toomre, J. On Differential Rotation and Overshooting in Solar-like Stars. Astrophys. J. 2017, 836, 192. [Google Scholar] [CrossRef]
- Käpylä, P.J.; Korpi, M.J.; Stix, M.; Tuominen, I. Effects of rotation and input energy flux on convective overshooting. In Convection in Astrophysics; Kupka, F., Roxburgh, I., Chan, K.L., Eds.; Cambridge University Press: Cambridge, UK, 2007; Volume 239, pp. 437–442. [Google Scholar] [CrossRef]
- Hotta, H. Solar Overshoot Region and Small-scale Dynamo with Realistic Energy Flux. Astrophys. J. 2017, 843, 52. [Google Scholar] [CrossRef]
- Baraffe, I.; Clarke, J.; Morison, A.; Vlaykov, D.G.; Constantino, T.; Goffrey, T.; Guillet, T.; Le Saux, A.; Pratt, J. A study of convective core overshooting as a function of stellar mass based on two-dimensional hydrodynamical simulations. Mon. Not. R. Astron. Soc. 2023, 519, stad009. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Viallet, M.; Meakin, C.; Arnett, D.; Mocák, M. Turbulent Convection in Stellar Interiors. III. Mean-field Analysis and Stratification Effects. Astrophys. J. 2013, 769, 1. [Google Scholar] [CrossRef]
- Currie, L.K.; Browning, M.K. The Magnitude of Viscous Dissipation in Strongly Stratified Two-dimensional Convection. Astrophys. J. Lett. 2017, 845, L17. [Google Scholar] [CrossRef]
- Julien, K.; Legg, S.; McWilliams, J.; Werne, J. Penetrative convection in rapidly rotating flows: Preliminary results from numerical simulation. Dyn. Atmos. Ocean. 1996, 24, 237–249. [Google Scholar] [CrossRef]
- Julien, K.; Knobloch, E.; Rubio, A.M.; Vasil, G.M. Heat Transport in Low-Rossby-Number Rayleigh-Bénard Convection. Phys. Rev. Lett. 2012, 109, 254503. [Google Scholar] [CrossRef]
- Aurnou, J.M.; Horn, S.; Julien, K. Connections between nonrotating, slowly rotating, and rapidly rotating turbulent convection transport scalings. Phys. Rev. Res. 2020, 2, 043115. [Google Scholar] [CrossRef]
- Pal, P.S.; Singh, H.P.; Chan, K.L.; Srivastava, M.P. Turbulent compressible convection with rotation—penetration above a convection zone. Astrophys. Space Sci. 2008, 314, 231–239. [Google Scholar] [CrossRef]
- Drobyshevski, E.M.; Yuferev, V.S. Topological pumping of magnetic flux by three-dimensional convection. J. Fluid Mech. 1974, 65, 33–44. [Google Scholar] [CrossRef]
- Tobias, S.M.; Brummell, N.H.; Clune, T.L.; Toomre, J. Transport and Storage of Magnetic Field by Overshooting Turbulent Compressible Convection. Astrophys. J. 2001, 549, 1183–1203. [Google Scholar] [CrossRef]
- Ziegler, U.; Rüdiger, G. Box simulations of rotating magnetoconvection. Effects of penetration and turbulent pumping. Astron. Astrophys. 2003, 401, 433–442. [Google Scholar] [CrossRef]
- Fisher, G.H.; McClymont, A.N.; Chou, D.Y. The Stretching of Magnetic Flux Tubes in the Convective Overshoot Region. Astrophys. J. 1991, 374, 766. [Google Scholar] [CrossRef]
- van Ballegooijen, A.A. The overshoot layer at the base of the solar convective zone and the problem of magnetic flux storage. Astron. Astrophys. 1982, 113, 99–112. [Google Scholar]
- Racine, R. Photometry of M67 to M_{v} = +12. Astrophys. J. 1971, 168, 393. [Google Scholar] [CrossRef]
- Torres-Peimbert, S. On the Ages of the Galactic Clusters NGC 188, M67 AND NGC 6791. Bol. Obs. Tonantzintla Tacubaya 1971, 6, 3–14. [Google Scholar]
- Bell, R.A. The reddening, distance modulus, chemical composition and age of the galactic cluster NGC 752. Mon. Not. R. Astron. Soc. 1972, 157, 147–156. [Google Scholar] [CrossRef]
- McClure, R.D.; Newell, B.; Barnes, J.V. PDS Photometry of the Open Cluster NGC 2420. Publ. Astron. Soc. Pac. 1978, 90, 170. [Google Scholar] [CrossRef]
- Demarque, P.; Sarajedini, A.; Guo, X.J. The Gap in the Color-Magnitude Diagram of NGC 2420: A Test of Convective Overshoot and Cluster Age. Astrophys. J. 1994, 426, 165. [Google Scholar] [CrossRef]
- Maeder, A.; Mermilliod, J.C. The extent of mixing in stellar interiors: Evolutionary models and tests based on the HR diagrams of 34 open clusters. Astron. Astrophys. 1981, 93, 136–149. [Google Scholar]
- Kozhurina-Platais, V.; Demarque, P.; Platais, I.; Orosz, J.A.; Barnes, S. The Age of NGC 3680 and a Test of Convective Overshoot. Astron. J. 1997, 113, 1045–1056. [Google Scholar] [CrossRef]
- Andersen, J.; Clausen, J.V.; Nordstrom, B. New Strong Evidence for the Importance of Convective Overshooting in Intermediate-Mass Stars. Astrophys. J. Lett. 1990, 363, L33. [Google Scholar] [CrossRef]
- Vallenari, A.; Chiosi, C.; Bertelli, G.; Meylan, G.; Ortolani, S. Star clusters of the large magellanic cloud. III. CCD-photometry of NGC 2164. Astron. Astrophys. Suppl. Ser. 1991, 87, 517–540. [Google Scholar]
- Vallenari, A.; Chiosi, C.; Bertelli, G.; Meylan, G.; Ortolani, S. Stars Clusters of the Large Magellanic Cloud: CCD Photometry of NGC 1831. Astron. J. 1992, 104, 1100. [Google Scholar] [CrossRef]
- Chiosi, C.; Bertelli, G.; Meylan, G.; Ortolani, S. Globular clusters in the Large Magellanic Cloud: NGC 1866, a test for convective overshoot. Astron. Astrophys. 1989, 219, 167–191. [Google Scholar]
- Bruntt, H.; Frandsen, S.; Kjeldsen, H.; Andersen, M.I. Strömgren photometry of the open clusters NGC 6134 and NGC 3680. Astron. Astrophys. Suppl. Ser. 1999, 140, 135–143. [Google Scholar] [CrossRef]
- Woo, J.H.; Gallart, C.; Demarque, P.; Yi, S.; Zoccali, M. Testing Intermediate-Age Stellar Evolution Models with VLT Photometry of Large Magellanic Cloud Clusters. II. Analysis with the Yale Models. Astron. J. 2003, 125, 754–769. [Google Scholar] [CrossRef]
- Mucciarelli, A.; Origlia, L.; Ferraro, F.R. The Intermediate-Age Globular Cluster NGC 1783 in the Large Magellanic Cloud. Astron. J. 2007, 134, 1813. [Google Scholar] [CrossRef]
- Girardi, L.; Rubele, S.; Kerber, L. Discovery of two distinct red clumps in NGC 419: A rare snapshot of a cluster at the onset of degeneracy. Mon. Not. R. Astron. Soc. 2009, 394, L74–L78. [Google Scholar] [CrossRef]
- Nordstrom, B.; Andersen, J. Open clusters under the microscope. Messenger 1991, 63, 34–37. [Google Scholar]
- Dinescu, D.I.; Demarque, P.; Guenther, D.B.; Pinsonneault, M.H. The Ages of the Disk Clusters NGC 188, M67, and NGC 752, Using Improved Opacities and Cluster Membership Data. Astron. J. 1995, 109, 2090. [Google Scholar] [CrossRef]
- Michaud, G.; Richard, O.; Richer, J.; VandenBerg, D.A. Models for Solar Abundance Stars with Gravitational Settling and Radiative Accelerations: Application to M67 and NGC 188. Astrophys. J. 2004, 606, 452–465. [Google Scholar] [CrossRef]
- Viani, L.; Basu, S. Isochrones of M67 with an Expanded Set of Parameters. Eur. Phys. J. Web Conf. 2017, 160, 05005. [Google Scholar] [CrossRef]
- Bressan, A.; Marigo, P.; Girardi, L.; Salasnich, B.; Dal Cero, C.; Rubele, S.; Nanni, A. PARSEC: Stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 2012, 427, 127–145. [Google Scholar] [CrossRef]
- Dotter, A. MESA Isochrones and Stellar Tracks (MIST) 0: Methods for the Construction of Stellar Isochrones. Astrophys. J. Suppl. Ser. 2016, 222, 8. [Google Scholar] [CrossRef]
- Choi, J.; Dotter, A.; Conroy, C.; Cantiello, M.; Paxton, B.; Johnson, B.D. Mesa Isochrones and Stellar Tracks (MIST). I. Solar-scaled Models. Astrophys. J. 2016, 823, 102. [Google Scholar] [CrossRef]
- Johnston, C.; Tkachenko, A.; Aerts, C.; Molenberghs, G.; Bowman, D.M.; Pedersen, M.G.; Buysschaert, B.; Pápics, P.I. Binary asteroseismic modelling: Isochrone-cloud methodology and application to Kepler gravity mode pulsators. Mon. Not. R. Astron. Soc. 2019, 482, 1231–1246. [Google Scholar] [CrossRef]
- Johnston, C.; Aerts, C.; Pedersen, M.G.; Bastian, N. Isochrone-cloud fitting of the extended main-sequence turn-off of young clusters. Astron. Astrophys. 2019, 632, A74. [Google Scholar] [CrossRef]
- Milone, A.P.; Marino, A.F.; Di Criscienzo, M.; D’Antona, F.; Bedin, L.R.; Da Costa, G.; Piotto, G.; Tailo, M.; Dotter, A.; Angeloni, R.; et al. Multiple stellar populations in Magellanic Cloud clusters - VI. A survey of multiple sequences and Be stars in young clusters. Mon. Not. R. Astron. Soc. 2018, 477, 2640–2663. [Google Scholar] [CrossRef]
- Goudfrooij, P.; Girardi, L.; Bellini, A.; Bressan, A.; Correnti, M.; Costa, G. The Minimum Mass of Rotating Main-sequence Stars and its Impact on the Nature of Extended Main-sequence Turnoffs in Intermediate-age Star Clusters in the Magellanic Clouds. Astrophys. J. Lett. 2018, 864, L3. [Google Scholar] [CrossRef]
- Milone, A.P.; Bedin, L.R.; Piotto, G.; Anderson, J. Multiple stellar populations in Magellanic Cloud clusters. I. An ordinary feature for intermediate age globulars in the LMC? Astron. Astrophys. 2009, 497, 755–771. [Google Scholar] [CrossRef]
- Yang, W.; Meng, X.; Bi, S.; Tian, Z.; Li, T.; Liu, K. The Contributions of Interactive Binary Stars to Double Main-sequence Turnoffs and Dual Red Clump of Intermediate-age Star Clusters. Astrophys. J. Lett. 2011, 731, L37. [Google Scholar] [CrossRef]
- Bastian, N.; de Mink, S.E. The effect of stellar rotation on colour-magnitude diagrams: On the apparent presence of multiple populations in intermediate age stellar clusters. Mon. Not. R. Astron. Soc. 2009, 398, L11–L15. [Google Scholar] [CrossRef]
- Yang, W.; Tian, Z. The Effects of the Overshooting of the Convective Core on Main-sequence Turnoffs of Young- and Intermediate-age Star Clusters. Astrophys. J. 2017, 836, 102. [Google Scholar] [CrossRef]
- Bastian, N.; Kamann, S.; Cabrera-Ziri, I.; Georgy, C.; Ekström, S.; Charbonnel, C.; de Juan Ovelar, M.; Usher, C. Extended main sequence turnoffs in open clusters as seen by Gaia - I. NGC 2818 and the role of stellar rotation. Mon. Not. R. Astron. Soc. 2018, 480, 3739–3746. [Google Scholar] [CrossRef]
- Marino, A.F.; Przybilla, N.; Milone, A.P.; Da Costa, G.; D’Antona, F.; Dotter, A.; Dupree, A. Different Stellar Rotations in the Two Main Sequences of the Young Globular Cluster NGC 1818: The First Direct Spectroscopic Evidence. Astron. J. 2018, 156, 116. [Google Scholar] [CrossRef]
- Sun, W.; de Grijs, R.; Deng, L.; Albrow, M.D. Stellar Rotation and the Extended Main-sequence Turnoff in the Open Cluster NGC 5822. Astrophys. J. 2019, 876, 113. [Google Scholar] [CrossRef]
- Kamann, S.; Bastian, N.; Gossage, S.; Baade, D.; Cabrera-Ziri, I.; Da Costa, G.; de Mink, S.E.; Georgy, C.; Giesers, B.; Göttgens, F.; et al. How stellar rotation shapes the colour-magnitude diagram of the massive intermediate-age star cluster NGC 1846. Mon. Not. R. Astron. Soc. 2020, 492, 2177–2192. [Google Scholar] [CrossRef]
- Kamann, S.; Saracino, S.; Bastian, N.; Gossage, S.; Usher, C.; Baade, D.; Cabrera-Ziri, I.; de Mink, S.E.; Ekstrom, S.; Georgy, C.; et al. The effects of stellar rotation along the main sequence of the 100-Myr-old massive cluster NGC 1850. Mon. Not. R. Astron. Soc. 2023, 518, 1505–1521. [Google Scholar] [CrossRef]
- von Zeipel, H. The radiative equilibrium of a rotating system of gaseous masses. Mon. Not. R. Astron. Soc. 1924, 84, 665–683. [Google Scholar] [CrossRef]
- Espinosa Lara, F.; Rieutord, M. Gravity darkening in rotating stars. Astron. Astrophys. 2011, 533, A43. [Google Scholar] [CrossRef]
- Lipatov, M.; Brandt, T.D.; Gossage, S. Rotational Variation Allows for Narrow Age Spread in the Extended Main-sequence Turnoff of Massive Cluster NGC 1846. Astrophys. J. 2022, 934, 105. [Google Scholar] [CrossRef]
- Russell, H.N. On the advance of periastron in eclipsing binaries. Mon. Not. R. Astron. Soc. 1928, 88, 641–643. [Google Scholar] [CrossRef]
- Claret, A.; Gimenez, A. The effect of core overshooting and mass loss on the internal density concentration of main sequence stars. Astron. Astrophys. 1991, 244, 319. [Google Scholar]
- Semeniuk, I.; Paczyński, B. Apsidal Motion in Binary Systems. III. Model Computations. Acta Astron. 1968, 18, 33. [Google Scholar]
- Stothers, R. The apsidal-motion test for models of main-sequence stars. Astrophys. J. 1974, 194, 651–655. [Google Scholar] [CrossRef]
- Mathis, J.S.; Odell, A.P. The apsidal constant and structure of alpha Virginis. Astrophys. J. 1973, 180, 517. [Google Scholar] [CrossRef]
- Odell, A.P. The structure of Alpha Virginis. II. The apsidal constant. Astrophys. J. 1974, 192, 417–424. [Google Scholar] [CrossRef]
- Shobbrook, R.R.; Herbison-Evans, D.; Johnston, I.D.; Lomb, N.R. Light variations in Spica. Mon. Not. R. Astron. Soc. 1969, 145, 131. [Google Scholar] [CrossRef]
- Shobbrook, R.R.; Lomb, N.R.; Herbison-Evans, D. The short period light and velocity variations in Alpha Virginis. Mon. Not. R. Astron. Soc. 1972, 156, 165. [Google Scholar] [CrossRef]
- Smith, M.A. The nonradial oscillations of Spica. I. Two commensurable modes. Astrophys. J. 1985, 297, 206–223. [Google Scholar] [CrossRef]
- Smith, M.A. The non-radial oscillations of Spica. II. A “quasi-toroidal” mode. Astrophys. J. 1985, 297, 224–232. [Google Scholar] [CrossRef]
- Harrington, D.; Koenigsberger, G.; Moreno, E.; Kuhn, J. Line-profile Variability from Tidal Flows in Alpha Virginis (Spica). Astrophys. J. 2009, 704, 813–830. [Google Scholar] [CrossRef]
- Tkachenko, A.; Matthews, J.M.; Aerts, C.; Pavlovski, K.; Pápics, P.I.; Zwintz, K.; Cameron, C.; Walker, G.A.H.; Kuschnig, R.; Degroote, P.; et al. Stellar modelling of Spica, a high-mass spectroscopic binary with a β Cep variable primary component. Mon. Not. R. Astron. Soc. 2016, 458, 1964–1976. [Google Scholar] [CrossRef]
- Bowman, D.M.; Vandenbussche, B.; Sana, H.; Tkachenko, A.; Raskin, G.; Delabie, T.; Vandoren, B.; Royer, P.; Garcia, S.; Van Reeth, T.; et al. The CubeSpec space mission. I. Asteroseismology of massive stars from time-series optical spectroscopy: Science requirements and target list prioritisation. Astron. Astrophys. 2022, 658, A96. [Google Scholar] [CrossRef]
- Claret, A.; Gimenez, A. The apsidal motion test of the internal stellar structure: Comparison between theory and observations. Astron. Astrophys. 1993, 277, 487–502. [Google Scholar]
- Claret, A. The role of the stellar rotation on the internal constitution of PV Cassiopeiae. Astron. Astrophys. 2008, 490, 1103–1107. [Google Scholar] [CrossRef]
- Wolf, M.; Zejda, M.; de Villiers, S.N. Apsidal motion in southern eccentric eclipsing binaries: GL Car, QX Car, NO Pup and V366 Pup. Mon. Not. R. Astron. Soc. 2008, 388, 1836–1842. [Google Scholar] [CrossRef]
- North, P.; Gauderon, R.; Barblan, F.; Royer, F. VLT multi-object spectroscopy of 33 eclipsing binaries in the Small Magellanic Cloud. New distance and depth of the SMC, and a record-breaking apsidal motion. Astron. Astrophys. 2010, 520, A74. [Google Scholar] [CrossRef]
- Bulut, İ. Apsidal motion elements of six eccentric eclipsing binaries: V799 Cas, CO Cep, V1136 Cyg, V345 Lac, V364 Lac and V402 Lac. New Astron. 2013, 21, 22–26. [Google Scholar] [CrossRef]
- Zasche, P.; Wolf, M. Apsidal motion and absolute parameters for five LMC eccentric eclipsing binaries. Astron. Astrophys. 2013, 558, A51. [Google Scholar] [CrossRef]
- Lacy, C.H.S.; Torres, G.; Fekel, F.C.; Muterspaugh, M.W.; Southworth, J. Absolute Properties of the Eclipsing Binary Star IM Persei. Astron. J. 2015, 149, 34. [Google Scholar] [CrossRef]
- Bakış, V. Young eccentric binary KL CMa revisited in the light of spectroscopy. New Astron. 2015, 40, 14–19. [Google Scholar] [CrossRef]
- Hong, K.; Lee, J.W.; Kim, S.L.; Koo, J.R.; Park, J.H.; Kim, C.H.; Lee, C.U.; Kim, H.W.; Kim, D.J.; Han, C. Absolute Dimensions and Apsidal Motions of Three Binary Systems in the Large Magellanic Cloud. Astron. J. 2019, 158, 185. [Google Scholar] [CrossRef]
- Andersen, J.; Clausen, J.V.; Nordstrom, B.; Popper, D.M. Absolute dimensions of eclipsing binaries. VIII. V760 Scorpii. Astron. Astrophys. 1985, 151, 329–339. [Google Scholar]
- Gimenez, A.; Kim, C.H.; Nha, I.S. Apsidal motion in the early-type eclipsing binaries CW Cephei, Y Cygni and AG Persei. Mon. Not. R. Astron. Soc. 1987, 224, 543–555. [Google Scholar] [CrossRef]
- Bakış, V.; Bakış, H.; Demircan, O.; Eker, Z. Absolute dimensions and apsidal motion of the eccentric binary PT Velorum. Mon. Not. R. Astron. Soc. 2008, 384, 1657–1667. [Google Scholar] [CrossRef]
- Deǧirmenci, Ö.L.; Gülmen, Ö.; Sezer, C.; Ibanoǧlu, C.; Çakırlı, Ö. Up-to-date UBV light and O-C curves analyses of the eclipsing binary V477 Cygni. Astron. Astrophys. 2003, 409, 959–967. [Google Scholar] [CrossRef]
- Bakiş, V.; Bulut, Á.; Bilir, S.; Bakiş, H.; Demircan, O.; Hensberge, H. Absolute Dimensions and Apsidal Motion of the Young Detached System LT Canis Majoris. Publ. Astron. Soc. Jpn. 2010, 62, 1291–1299. [Google Scholar] [CrossRef]
- Baroch, D.; Giménez, A.; Morales, J.C.; Ribas, I.; Herrero, E.; Perdelwitz, V.; Jordi, C.; Granzer, T.; Allende Prieto, C. Absolute dimensions and apsidal motion of the eclipsing binaries V889 Aquilae and V402 Lacertae. Astron. Astrophys. 2022, 665, A13. [Google Scholar] [CrossRef]
- Claret, A.; Giménez, A.; Baroch, D.; Ribas, I.; Morales, J.C.; Anglada-Escudé, G. Analysis of apsidal motion in eclipsing binaries using TESS data. II. A test of internal stellar structure. Astron. Astrophys. 2021, 654, A17. [Google Scholar] [CrossRef]
- Guinan, E.F.; Ribas, I.; Fitzpatrick, E.L.; Giménez, Á.; Jordi, C.; McCook, G.P.; Popper, D.M. Eclipsing Binaries as Astrophysical Laboratories: Internal Structure, Core Convection, and Evolution of the B-Star Components of V380 Cygni. Astrophys. J. 2000, 544, 409–422. [Google Scholar] [CrossRef]
- Claret, A. The massive and evolved EBS V380 Cygni: A case of critical evolution. Astron. Astrophys. 2003, 399, 1115–1119. [Google Scholar] [CrossRef]
- Rosu, S.; Rauw, G.; Nazé, Y.; Gosset, E.; Sterken, C. Apsidal motion in massive eccentric binaries: The case of CPD-41° 7742, and HD 152218 revisited. Astron. Astrophys. 2022, 664, A98. [Google Scholar] [CrossRef]
- Groenewegen, M.A.T.; Lamers, H.J.G.L.M.; Pauldrach, A.W.A. The winds of O-stars. II. The terminal velocities of stellar winds ofO-type stars. Astron. Astrophys. 1989, 221, 78–88. [Google Scholar]
- Herrero, A.; Kudritzki, R.P.; Vilchez, J.M.; Kunze, D.; Butler, K.; Haser, S. The mass and helium discrepancy in massive young stars. In The Atmospheres of Early-Type Stars; Heber, U., Jeffery, C.S., Eds.; Springer: Cham, Switzerland, 1992; Volume 401, p. 21. [Google Scholar] [CrossRef]
- Gronbech, B.; Gyldenkerne, K.; Jorgensen, H.E. Four-colour photometry of eclipsing binaries. VII. SZ Cen, light curves, photometric elements, absolute dimensions and determination of helium content. Astron. Astrophys. 1977, 55, 401–409. [Google Scholar]
- Clausen, J.V. Absolute dimensions of eclipsing binaries. XIX. BW Aquarii: A late F-typeindicator of overshooting. Astron. Astrophys. 1991, 246, 397. [Google Scholar]
- Fitzpatrick, E.L.; Garmany, C.D. The H-R Diagram of the Large Magellanic Cloud and Implications for Stellar Evolution. Astrophys. J. 1990, 363, 119. [Google Scholar] [CrossRef]
- Hunter, I.; Lennon, D.J.; Dufton, P.L.; Trundle, C.; Simón-Díaz, S.; Smartt, S.J.; Ryans, R.S.I.; Evans, C.J. The VLT-FLAMES survey of massive stars: Atmospheric parameters and rotational velocity distributions for B-type stars in the Magellanic Clouds. Astron. Astrophys. 2008, 479, 541–555. [Google Scholar] [CrossRef]
- Brott, I.; de Mink, S.E.; Cantiello, M.; Langer, N.; de Koter, A.; Evans, C.J.; Hunter, I.; Trundle, C.; Vink, J.S. Rotating massive main-sequence stars. I. Grids of evolutionary models and isochrones. Astron. Astrophys. 2011, 530, A115. [Google Scholar] [CrossRef]
- Vink, J.S.; Brott, I.; Gräfener, G.; Langer, N.; de Koter, A.; Lennon, D.J. The nature of B supergiants: Clues from a steep drop in rotation rates at 22 000 K. The possibility of Bi-stability braking. Astron. Astrophys. 2010, 512, L7. [Google Scholar] [CrossRef]
- Pavlovski, K.; Tamajo, E.; Koubský, P.; Southworth, J.; Yang, S.; Kolbas, V. Chemical evolution of high-mass stars in close binaries—II. The evolved component of the eclipsing binary V380Cygni. Mon. Not. R. Astron. Soc. 2009, 400, 791–804. [Google Scholar] [CrossRef]
- Tkachenko, A.; Degroote, P.; Aerts, C.; Pavlovski, K.; Southworth, J.; Pápics, P.I.; Moravveji, E.; Kolbas, V.; Tsymbal, V.; Debosscher, J.; et al. The eccentric massive binary V380 Cyg: Revised orbital elements and interpretation of the intrinsic variability of the primary component*. Mon. Not. R. Astron. Soc. 2014, 438, 3093–3110. [Google Scholar] [CrossRef]
- Fekel, F.C. Chromospherically Active Stars. VIII. HD 155683 = V972 Herculis: Observational Constraints on Evolutionary Theory. Astron. J. 1991, 101, 1489. [Google Scholar] [CrossRef]
- Andersen, J.; Clausen, J.V.; Nordstrom, B.; Gustafsson, B.; Vandenberg, D.A. Absolute dimensions of eclipsing binaries. XIII. AI Phoenicis: A casestudy in stellar evolution. Astron. Astrophys. 1988, 196, 128–140. [Google Scholar]
- Andersen, J.; Clausen, J.V.; Magain, P. Absolute dimensions of eclipsing binaries. XIV. UX Mensae. Astron. Astrophys. 1989, 211, 346–352. [Google Scholar]
- Claret, A.; Torres, G. The dependence of convective core overshooting on stellar mass. Astron. Astrophys. 2016, 592, A15. [Google Scholar] [CrossRef]
- Schroder, K.P.; Pols, O.R.; Eggleton, P.P. A critical test of stellar evolution and convective core ‘overshooting’ by means of zeta Aurigae systems. Mon. Not. R. Astron. Soc. 1997, 285, 696–710. [Google Scholar] [CrossRef]
- Ribas, I.; Jordi, C.; Giménez, Á. The mass dependence of the overshooting parameter determined from eclipsing binary data. Mon. Not. R. Astron. Soc. 2000, 318, L55–L59. [Google Scholar] [CrossRef]
- Claret, A. Does convective core overshooting depend on stellar mass?. Tests using double-lined eclipsing binaries. Astron. Astrophys. 2007, 475, 1019–1025. [Google Scholar] [CrossRef]
- Claret, A.; Torres, G. The Dependence of Convective Core Overshooting on Stellar Mass: Reality Check and Additional Evidence. Astrophys. J. 2019, 876, 134. [Google Scholar] [CrossRef]
- Costa, G.; Girardi, L.; Bressan, A.; Marigo, P.; Rodrigues, T.S.; Chen, Y.; Lanza, A.; Goudfrooij, P. Mixing by overshooting and rotation in intermediate-mass stars. Mon. Not. R. Astron. Soc. 2019, 485, 4641–4657. [Google Scholar] [CrossRef]
- Constantino, T.; Baraffe, I. Significant uncertainties from calibrating overshooting with eclipsing binary systems. Astron. Astrophys. 2018, 618, A177. [Google Scholar] [CrossRef]
- Meng, Y.; Zhang, Q.S. Calibrating the Updated Overshoot Mixing Model on Eclipsing Binary Stars: HY Vir, YZ Cas, χ2 Hya, and VV Crv. Astrophys. J. 2014, 787, 127. [Google Scholar] [CrossRef]
- Stancliffe, R.J.; Fossati, L.; Passy, J.C.; Schneider, F.R.N. Confronting uncertainties in stellar physics: Calibrating convective overshooting with eclipsing binaries. Astron. Astrophys. 2015, 575, A117. [Google Scholar] [CrossRef]
- Andersen, J. Accurate masses and radii of normal stars. Astron. Astrophys. Rev. 1991, 3, 91–126. [Google Scholar] [CrossRef]
- Valle, G.; Dell’Omodarme, M.; Prada Moroni, P.G.; Degl’Innocenti, S. Calibrating convective-core overshooting with eclipsing binary systems. The case of low-mass main-sequence stars. Astron. Astrophys. 2016, 587, A16. [Google Scholar] [CrossRef]
- Valle, G.; Dell’Omodarme, M.; Prada Moroni, P.G.; Degl’Innocenti, S. Statistical errors and systematic biases in the calibration of the convective core overshooting with eclipsing binaries. A case study: TZ Fornacis. Astron. Astrophys. 2017, 600, A41. [Google Scholar] [CrossRef]
- Valle, G.; Dell’Omodarme, M.; Prada Moroni, P.G.; Degl’Innocenti, S. Overshooting calibration and age determination from evolved binary systems. A statistical investigation on biases and random variability. Astron. Astrophys. 2018, 615, A62. [Google Scholar] [CrossRef]
- Pols, O.R.; Tout, C.A.; Schroder, K.P.; Eggleton, P.P.; Manners, J. Further critical tests of stellar evolution by means of double-lined eclipsing binaries. Mon. Not. R. Astron. Soc. 1997, 289, 869–881. [Google Scholar] [CrossRef]
- Mahy, L.; Sana, H.; Abdul-Masih, M.; Almeida, L.A.; Langer, N.; Shenar, T.; de Koter, A.; de Mink, S.E.; de Wit, S.; Grin, N.J.; et al. The Tarantula Massive Binary Monitoring. III. Atmosphere analysis of double-lined spectroscopic systems. Astron. Astrophys. 2020, 634, A118. [Google Scholar] [CrossRef]
- de Mink, S.E.; Cantiello, M.; Langer, N.; Pols, O.R.; Brott, I.; Yoon, S.C. Rotational mixing in massive binaries. Detached short-period systems. Astron. Astrophys. 2009, 497, 243–253. [Google Scholar] [CrossRef]
- Martins, F.; Mahy, L.; Hervé, A. Properties of six short-period massive binaries: A study of the effects of binarity on surface chemical abundances. Astron. Astrophys. 2017, 607, A82. [Google Scholar] [CrossRef]
- Pavlovski, K.; Southworth, J.; Tkachenko, A.; Van Reeth, T.; Tamajo, E. High-mass eclipsing binaries: A testbed for models of interior structure and evolution—Accurate fundamental properties and surface chemical composition for V1034 Sco, GL Car, V573 Car and V346 Cen. arXiv 2023, arXiv:2301.04215. [Google Scholar] [CrossRef]
- Graczyk, D.; Pietrzyński, G.; Thompson, I.B.; Gieren, W.; Pilecki, B.; Konorski, P.; Villanova, S.; Górski, M.; Suchomska, K.; Karczmarek, P.; et al. The Late-type Eclipsing Binaries in the Large Magellanic Cloud: Catalog of Fundamental Physical Parameters. Astrophys. J. 2018, 860, 1. [Google Scholar] [CrossRef]
- Eker, Z.; Bilir, S.; Soydugan, F.; Gökçe, E.Y.; Soydugan, E.; Tüysüz, M.; Şenyüz, T.; Demircan, O. The Catalogue of Stellar Parameters from the Detached Double-Lined Eclipsing Binaries in the Milky Way. Publ. Astron. Soc. Aust. 2014, 31, e024. [Google Scholar] [CrossRef]
- Veramendi, M.E.; González, J.F. Accurate absolute parameters of the binary system V4089 Sgr. New Astron. 2015, 34, 266–270. [Google Scholar] [CrossRef]
- Kjurkchieva, D.; Vasileva, D.; Atanasova, T. Orbital Parameters of the Eclipsing Detached Kepler Binaries with Eccentric Orbits. Astron. J. 2017, 154, 105. [Google Scholar] [CrossRef]
- Graczyk, D.; Pietrzyński, G.; Thompson, I.B.; Gieren, W.; Pilecki, B.; Konorski, P.; Udalski, A.; Soszyński, I.; Villanova, S.; Górski, M.; et al. The Araucaria Project. The Distance to the Small Magellanic Cloud from Late-type Eclipsing Binaries. Astrophys. J. 2014, 780, 59. [Google Scholar] [CrossRef]
- Pilecki, B.; Graczyk, D.; Pietrzyński, G.; Gieren, W.; Thompson, I.B.; Freedman, W.L.; Scowcroft, V.; Madore, B.F.; Udalski, A.; Soszyński, I.; et al. Physical parameters and the projection factor of the classical Cepheid in the binary system OGLE-LMC-CEP-0227. Mon. Not. R. Astron. Soc. 2013, 436, 953–967. [Google Scholar] [CrossRef]
- Pilecki, B.; Graczyk, D.; Gieren, W.; Pietrzyński, G.; Thompson, I.B.; Smolec, R.; Udalski, A.; Soszyński, I.; Konorski, P.; Taormina, M.; et al. The Araucaria Project: The First-overtone Classical Cepheid in the Eclipsing System OGLE-LMC-CEP-2532. Astrophys. J. 2015, 806, 29. [Google Scholar] [CrossRef]
- Gieren, W.; Pilecki, B.; Pietrzyński, G.; Graczyk, D.; Udalski, A.; Soszyński, I.; Thompson, I.B.; Prada Moroni, P.G.; Smolec, R.; Konorski, P.; et al. The Araucaria Project: A Study of the Classical Cepheid in the Eclipsing Binary System OGLE LMC562.05.9009 in the Large Magellanic Cloud. Astrophys. J. 2015, 815, 28. [Google Scholar] [CrossRef]
- Graczyk, D.; Pietrzyński, G.; Thompson, I.B.; Gieren, W.; Pilecki, B.; Udalski, A.; Soszyński, I.; Kołaczkowski, Z.; Kudritzki, R.P.; Bresolin, F.; et al. The Araucaria Project: An Accurate Distance to the Late-type Double-lined Eclipsing Binary OGLE SMC113.3 4007 in the Small Magellanic Cloud. Astrophys. J. 2012, 750, 144. [Google Scholar] [CrossRef]
- Pietrzyński, G.; Graczyk, D.; Gieren, W.; Thompson, I.B.; Pilecki, B.; Udalski, A.; Soszyński, I.; Kozłowski, S.; Konorski, P.; Suchomska, K.; et al. An eclipsing-binary distance to the Large Magellanic Cloud accurate to two per cent. Nature 2013, 495, 76–79. [Google Scholar] [CrossRef]
- Torres, G.; Claret, A.; Pavlovski, K.; Dotter, A. Capella (α Aurigae) Revisited: New Binary Orbit, Physical Properties, and Evolutionary State. Astrophys. J. 2015, 807, 26. [Google Scholar] [CrossRef]
- Hełminiak, K.G.; Graczyk, D.; Konacki, M.; Pilecki, B.; Ratajczak, M.; Pietrzyński, G.; Sybilski, P.; Villanova, S.; Gieren, W.; Pojmański, G.; et al. Orbital and physical parameters of eclipsing binaries from the ASAS catalogue - VIII. The totally eclipsing double-giant system HD 187669. Mon. Not. R. Astron. Soc. 2015, 448, 1945–1955. [Google Scholar] [CrossRef]
- Buzasi, D.; Catanzarite, J.; Laher, R.; Conrow, T.; Shupe, D.; Gautier, T.N.I.; Kreidl, T.; Everett, D. The Detection of Multimodal Oscillations on α Ursae Majoris. Astrophys. J. Lett. 2000, 532, L133–L136. [Google Scholar] [CrossRef]
- Walker, G.; Matthews, J.; Kuschnig, R.; Johnson, R.; Rucinski, S.; Pazder, J.; Burley, G.; Walker, A.; Skaret, K.; Zee, R.; et al. The MOST Asteroseismology Mission: Ultraprecise Photometry from Space. Publ. Astron. Soc. Pac. 2003, 115, 1023–1035. [Google Scholar] [CrossRef]
- Auvergne, M.; Bodin, P.; Boisnard, L.; Buey, J.T.; Chaintreuil, S.; Epstein, G.; Jouret, M.; Lam-Trong, T.; Levacher, P.; Magnan, A.; et al. The CoRoT satellite in flight: Description and performance. Astron. Astrophys. 2009, 506, 411–424. [Google Scholar] [CrossRef]
- Baglin, A.; Auvergne, M.; Barge, P.; Deleuil, M.; Michel, E.; CoRoT Exoplanet Science Team. CoRoT: Description of the Mission and Early Results. In Transiting Planets; Pont, F., Sasselov, D., Holman, M.J., Eds.; Cambridge University Press: Cambridge, UK, 2009; Volume 253, pp. 71–81. [Google Scholar] [CrossRef]
- Borucki, W.J.; Koch, D.; Basri, G.; Batalha, N.; Brown, T.; Caldwell, D.; Caldwell, J.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E.; et al. Kepler Planet-Detection Mission: Introduction and First Results. Science 2010, 327, 977. [Google Scholar] [CrossRef]
- Koch, D.G.; Borucki, W.J.; Basri, G.; Batalha, N.M.; Brown, T.M.; Caldwell, D.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E.; Dunham, E.W.; et al. Kepler Mission Design, Realized Photometric Performance, and Early Science. Astrophys. J. Lett. 2010, 713, L79–L86. [Google Scholar] [CrossRef]
- Howell, S.B.; Sobeck, C.; Haas, M.; Still, M.; Barclay, T.; Mullally, F.; Troeltzsch, J.; Aigrain, S.; Bryson, S.T.; Caldwell, D.; et al. The K2 Mission: Characterization and Early Results. Publ. Astron. Soc. Pac. 2014, 126, 398. [Google Scholar] [CrossRef]
- Weiss, W.W.; Rucinski, S.M.; Moffat, A.F.J.; Schwarzenberg-Czerny, A.; Koudelka, O.F.; Grant, C.C.; Zee, R.E.; Kuschnig, R.; Mochnacki, S.; Matthews, J.M.; et al. BRITE-Constellation: Nanosatellites for Precision Photometry of Bright Stars. Publ. Astron. Soc. Pac. 2014, 126, 573. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instrum. Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Aerts, C.; Christensen-Dalsgaard, J.; Kurtz, D.W. Asteroseismology; Springer: Cham, Switzerland, 2010. [Google Scholar] [CrossRef]
- Chaplin, W.J.; Miglio, A. Asteroseismology of Solar-Type and Red-Giant Stars. Annu. Rev. Astron. Astrophys. 2013, 51, 353–392. [Google Scholar] [CrossRef]
- Aerts, C.; Mathis, S.; Rogers, T.M. Angular Momentum Transport in Stellar Interiors. Annu. Rev. Astron. Astrophys. 2019, 57, 35–78. [Google Scholar] [CrossRef]
- Bowman, D.M. Asteroseismology of high-mass stars: New insights of stellar interiors with space telescopes. Front. Astron. Space Sci. 2020, 7, 70. [Google Scholar] [CrossRef]
- Holdsworth, D.L. The roAp Stars Observed by the Kepler Space Telescope. Front. Astron. Space Sci. 2021, 8, 31. [Google Scholar] [CrossRef]
- Christensen-Dalsgaard, J. Solar structure and evolution. Living Rev. Sol. Phys. 2021, 18, 2. [Google Scholar] [CrossRef]
- Aerts, C. Probing the interior physics of stars through asteroseismology. Rev. Mod. Phys. 2021, 93, 015001. [Google Scholar] [CrossRef]
- Guzik, J.A. Highlights of Discoveries for δ Scuti Variable Stars From the Kepler Era. Front. Astron. Space Sci. 2021, 8, 55. [Google Scholar] [CrossRef]
- Kurtz, D.W. Asteroseismology Across the Hertzsprung-Russell Diagram. Annu. Rev. Astron. Astrophys. 2022, 60, 31–71. [Google Scholar] [CrossRef]
- Houdek, G.; Gough, D.O. An asteroseismic signature of helium ionization. Mon. Not. R. Astron. Soc. 2007, 375, 861–880. [Google Scholar] [CrossRef]
- Roxburgh, I.W.; Vorontsov, S.V. Acoustic wave reflection by stellar cores: Can it be seen in the autocorrelation function of p-mode measurements? Mon. Not. R. Astron. Soc. 2007, 379, 801–806. [Google Scholar] [CrossRef]
- Cunha, M.S.; Metcalfe, T.S. Asteroseismic Signatures of Small Convective Cores. Astrophys. J. 2007, 666, 413–422. [Google Scholar] [CrossRef]
- Cunha, M.S.; Brandão, I.M. Probing tiny convective cores with the acoustic modes of lowest degree. Astron. Astrophys. 2011, 529, A10. [Google Scholar] [CrossRef]
- Silva Aguirre, V.; Basu, S.; Brandão, I.M.; Christensen-Dalsgaard, J.; Deheuvels, S.; Doğan, G.; Metcalfe, T.S.; Serenelli, A.M.; Ballot, J.; Chaplin, W.J.; et al. Stellar Ages and Convective Cores in Field Main-sequence Stars: First Asteroseismic Application to Two Kepler Targets. Astrophys. J. 2013, 769, 141. [Google Scholar] [CrossRef]
- Deheuvels, S.; Michel, E.; Goupil, M.J.; Marques, J.P.; Mosser, B.; Dupret, M.A.; Lebreton, Y.; Pichon, B.; Morel, P. Survival of a convective core in low-mass solar-like pulsator HD 203608. Astron. Astrophys. 2010, 514, A31. [Google Scholar] [CrossRef]
- Roxburgh, I.W. Present Problems of the Solar Interior. Sol. Phys. 1985, 100, 21. [Google Scholar] [CrossRef]
- Mowlavi, N. A peculiar effect of core overshooting on the internal structure of low mass stars. In IAU Colloq. 137: Inside the Stars; Weiss, W.W., Baglin, A., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 1993; Volume 40, p. 454. [Google Scholar]
- Moździerski, D.; Pigulski, A.; Kołaczkowski, Z.; Michalska, G.; Kopacki, G.; Carrier, F.; Walczak, P.; Narwid, A.; Stęślicki, M.; Fu, J.N.; et al. Ensemble asteroseismology of pulsating B-type stars in NGC 6910. Astron. Astrophys. 2019, 632, A95. [Google Scholar] [CrossRef]
- Deheuvels, S.; Brandão, I.; Silva Aguirre, V.; Ballot, J.; Michel, E.; Cunha, M.S.; Lebreton, Y.; Appourchaux, T. Measuring the extent of convective cores in low-mass stars using Kepler data: Toward a calibration of core overshooting. Astron. Astrophys. 2016, 589, A93. [Google Scholar] [CrossRef]
- Bellinger, E.P.; Angelou, G.C.; Hekker, S.; Basu, S.; Ball, W.H.; Guggenberger, E. Fundamental Parameters of Main-Sequence Stars in an Instant with Machine Learning. Astrophys. J. 2016, 830, 31. [Google Scholar] [CrossRef]
- Mombarg, J.S.G.; Van Reeth, T.; Aerts, C. Constraining stellar evolution theory with asteroseismology of γ Doradus stars using deep learning. Stellar masses, ages, and core-boundary mixing. Astron. Astrophys. 2021, 650, A58. [Google Scholar] [CrossRef]
- Dupret, M.A.; Thoul, A.; Scuflaire, R.; Daszyńska-Daszkiewicz, J.; Aerts, C.; Bourge, P.O.; Waelkens, C.; Noels, A. Asteroseismology of the β Cep star HD 129929. II. Seismic constraints on core overshooting, internal rotation and stellar parameters. Astron. Astrophys. 2004, 415, 251–257. [Google Scholar] [CrossRef]
- Ausseloos, M.; Scuflaire, R.; Thoul, A.; Aerts, C. Asteroseismology of the β Cephei star ν Eridani: Massive exploration of standard and non-standard stellar models to fit the oscillation data. Mon. Not. R. Astron. Soc. 2004, 355, 352–358. [Google Scholar] [CrossRef]
- Mazumdar, A.; Briquet, M.; Desmet, M.; Aerts, C. An asteroseismic study of the β Cephei star β Canis Majoris. Astron. Astrophys. 2006, 459, 589–596. [Google Scholar] [CrossRef]
- Briquet, M.; Morel, T.; Thoul, A.; Scuflaire, R.; Miglio, A.; Montalbán, J.; Dupret, M.A.; Aerts, C. An asteroseismic study of the β Cephei star θ Ophiuchi: Constraints on global stellar parameters and core overshooting. Mon. Not. R. Astron. Soc. 2007, 381, 1482–1488. [Google Scholar] [CrossRef]
- Desmet, M.; Briquet, M.; Thoul, A.; Zima, W.; De Cat, P.; Handler, G.; Ilyin, I.; Kambe, E.; Krzesinski, J.; Lehmann, H.; et al. An asteroseismic study of the β Cephei star 12 Lacertae: Multisite spectroscopic observations, mode identification and seismic modelling. Mon. Not. R. Astron. Soc. 2009, 396, 1460–1472. [Google Scholar] [CrossRef]
- Aerts, C.; Briquet, M.; Degroote, P.; Thoul, A.; van Hoolst, T. Seismic modelling of the β Cephei star HD 180642 (V1449 Aquilae). Astron. Astrophys. 2011, 534, A98. [Google Scholar] [CrossRef]
- Briquet, M.; Aerts, C.; Baglin, A.; Nieva, M.F.; Degroote, P.; Przybilla, N.; Noels, A.; Schiller, F.; Vučković, M.; Oreiro, R.; et al. An asteroseismic study of the O9V star HD 46202 from CoRoT space-based photometry. Astron. Astrophys. 2011, 527, A112. [Google Scholar] [CrossRef]
- Briquet, M.; Neiner, C.; Aerts, C.; Morel, T.; Mathis, S.; Reese, D.R.; Lehmann, H.; Costero, R.; Echevarria, J.; Handler, G.; et al. Multisite spectroscopic seismic study of the β Cep star V2052 Ophiuchi: Inhibition of mixing by its magnetic field. Mon. Not. R. Astron. Soc. 2012, 427, 483–493. [Google Scholar] [CrossRef]
- Walczak, P.; Daszyńska-Daszkiewicz, J.; Pamyatnykh, A.A.; Zdravkov, T. The hybrid B-type pulsator γ Pegasi: Mode identification and complex seismic modelling. Mon. Not. R. Astron. Soc. 2013, 432, 822–831. [Google Scholar] [CrossRef]
- Moravveji, E.; Aerts, C.; Pápics, P.I.; Triana, S.A.; Vandoren, B. Tight asteroseismic constraints on core overshooting and diffusive mixing in the slowly rotating pulsating B8.3V star KIC 10526294. Astron. Astrophys. 2015, 580, A27. [Google Scholar] [CrossRef]
- Schmid, V.S.; Aerts, C. Asteroseismic modelling of the two F-type hybrid pulsators KIC 10080943A and KIC 10080943B. Astron. Astrophys. 2016, 592, A116. [Google Scholar] [CrossRef]
- Daszyńska-Daszkiewicz, J.; Pamyatnykh, A.A.; Walczak, P.; Colgan, J.; Fontes, C.J.; Kilcrease, D.P. Interpretation of the BRITE oscillation data of the hybrid pulsator ν Eridani: A call for the modification of stellar opacities. Mon. Not. R. Astron. Soc. 2017, 466, 2284–2293. [Google Scholar] [CrossRef]
- Sánchez Arias, J.P.; Córsico, A.H.; Althaus, L.G. Asteroseismology of hybrid δ Scuti-γ Doradus pulsating stars. Astron. Astrophys. 2017, 597, A29. [Google Scholar] [CrossRef]
- Buysschaert, B.; Aerts, C.; Bowman, D.M.; Johnston, C.; Van Reeth, T.; Pedersen, M.G.; Mathis, S.; Neiner, C. Forward seismic modeling of the pulsating magnetic B-type star HD 43317. Astron. Astrophys. 2018, 616, A148. [Google Scholar] [CrossRef]
- Aerts, C.; Pedersen, M.G.; Vermeyen, E.; Hendriks, L.; Johnston, C.; Tkachenko, A.; Pápics, P.I.; Debosscher, J.; Briquet, M.; Thoul, A.; et al. Combined asteroseismology, spectroscopy, and astrometry of the CoRoT B2V target HD 170580. Astron. Astrophys. 2019, 624, A75. [Google Scholar] [CrossRef]
- Khalack, V.; Lovekin, C.; Bowman, D.M.; Kobzar, O.; David-Uraz, A.; Paunzen, E.; Sikora, J.; Lenz, P.; Kochukhov, O.; Holdsworth, D.L.; et al. Rotational and pulsational variability in the TESS light curve of HD 27463. Mon. Not. R. Astron. Soc. 2019, 490, 2102–2111. [Google Scholar] [CrossRef]
- Hendriks, L.; Aerts, C. Deep Learning Applied to the Asteroseismic Modeling of Stars with Coherent Oscillation Modes. Publ. Astron. Soc. Pac. 2019, 131, 108001. [Google Scholar] [CrossRef]
- Wu, T.; Li, Y. High-precision Asteroseismology in a Slowly Pulsating B Star: HD 50230. Astrophys. J. 2019, 881, 86. [Google Scholar] [CrossRef]
- Fedurco, M.; Paunzen, E.; Hümmerich, S.; Bernhard, K.; Parimucha, Š. Pulsational properties of ten new slowly pulsating B stars. Astron. Astrophys. 2020, 633, A122. [Google Scholar] [CrossRef]
- Wu, T.; Li, Y.; Deng, Z.m.; Lin, G.f.; Song, H.f.; Jiang, C. Asteroseismic Analyses of Slowly Pulsating B Star KIC 8324482: Ultraweak Element Mixing beyond the Central Convective Core. Astrophys. J. 2020, 899, 38. [Google Scholar] [CrossRef]
- Pedersen, M.G. On the Diversity of Mixing and Helium Core Masses of B-type Dwarfs from Gravity-mode Asteroseismology. Astrophys. J. 2022, 930, 94. [Google Scholar] [CrossRef]
- Niemczura, E.; Walczak, P.; Mikołajczyk, P.; Schöller, M.; Hummel, C.A.; Hubrig, S.; Różański, T. Seismic modelling of the pulsating mercury-manganese star HD 29589. Mon. Not. R. Astron. Soc. 2022, 514, 5640–5658. [Google Scholar] [CrossRef]
- Szewczuk, W.; Walczak, P.; Daszyńska-Daszkiewicz, J.; Moździerski, D. Seismic modelling of a very young SPB star - KIC 8264293. Mon. Not. R. Astron. Soc. 2022, 511, 1529–1543. [Google Scholar] [CrossRef]
- Pedersen, M.G. Internal Rotation and Inclinations of Slowly Pulsating B Stars: Evidence of Interior Angular Momentum Transport. Astrophys. J. 2022, 940, 49. [Google Scholar] [CrossRef]
- Angelou, G.C.; Bellinger, E.P.; Hekker, S.; Mints, A.; Elsworth, Y.; Basu, S.; Weiss, A. Convective boundary mixing in low- and intermediate-mass stars - I. Core properties from pressure-mode asteroseismology. Mon. Not. R. Astron. Soc. 2020, 493, 4987–5004. [Google Scholar] [CrossRef]
- Lecoanet, D.; Bowman, D.M.; Van Reeth, T. Asteroseismic inference of the near-core magnetic field strength in the main-sequence B star HD 43317. Mon. Not. R. Astron. Soc. 2022, 512, L16–L20. [Google Scholar] [CrossRef]
- Pedersen, M.G.; Aerts, C.; Pápics, P.I.; Rogers, T.M. The shape of convective core overshooting from gravity-mode period spacings. Astron. Astrophys. 2018, 614, A128. [Google Scholar] [CrossRef]
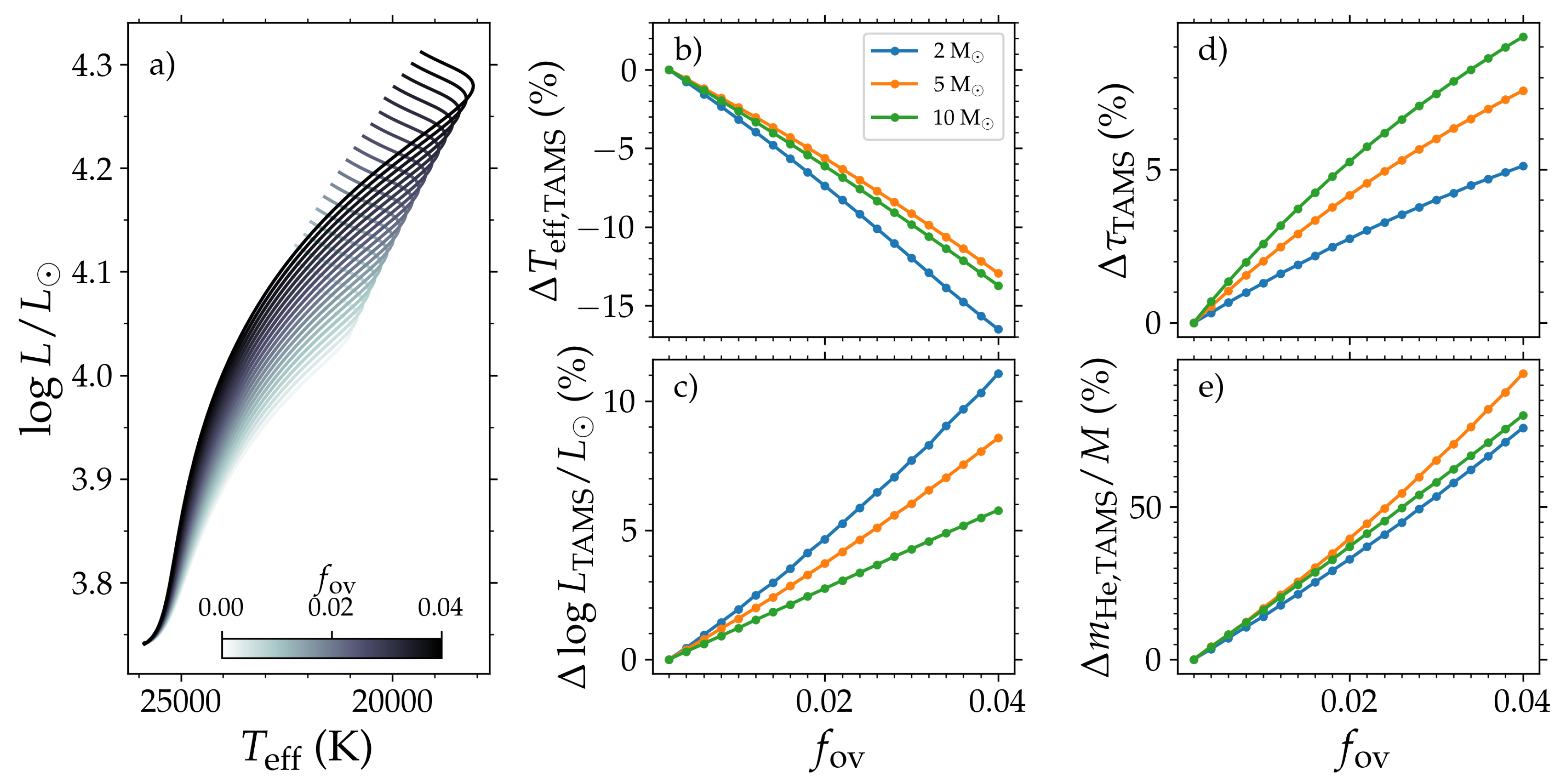
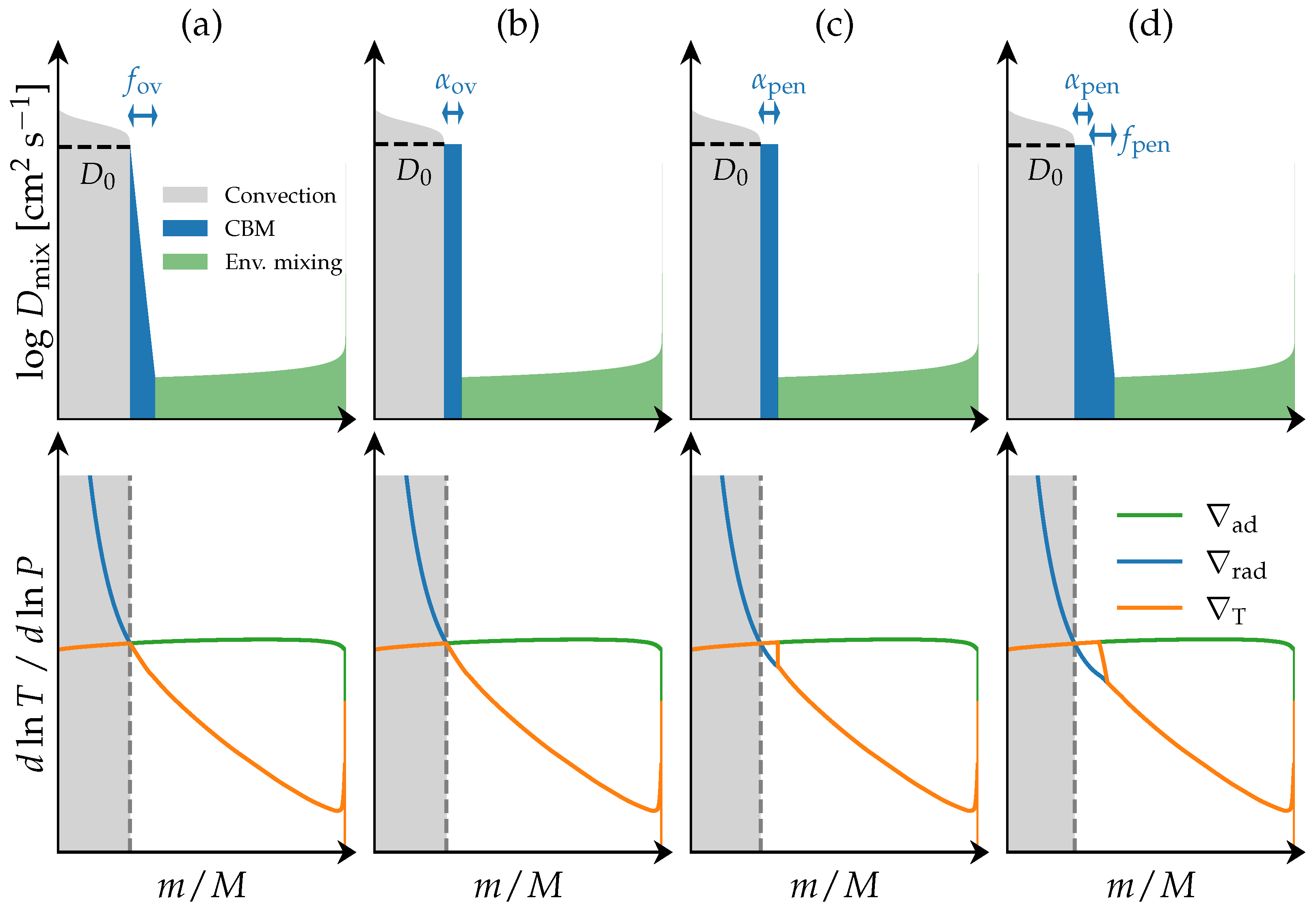
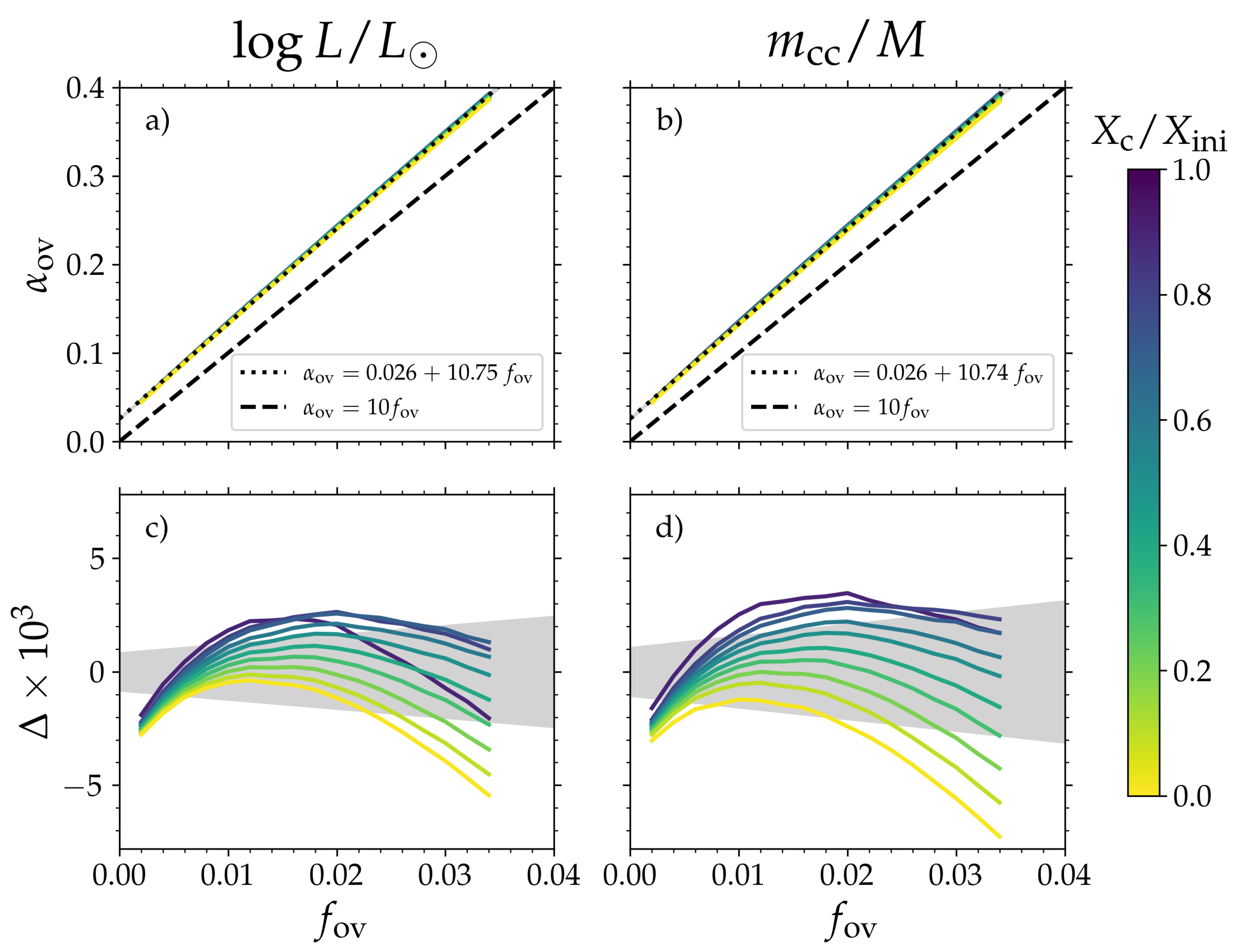
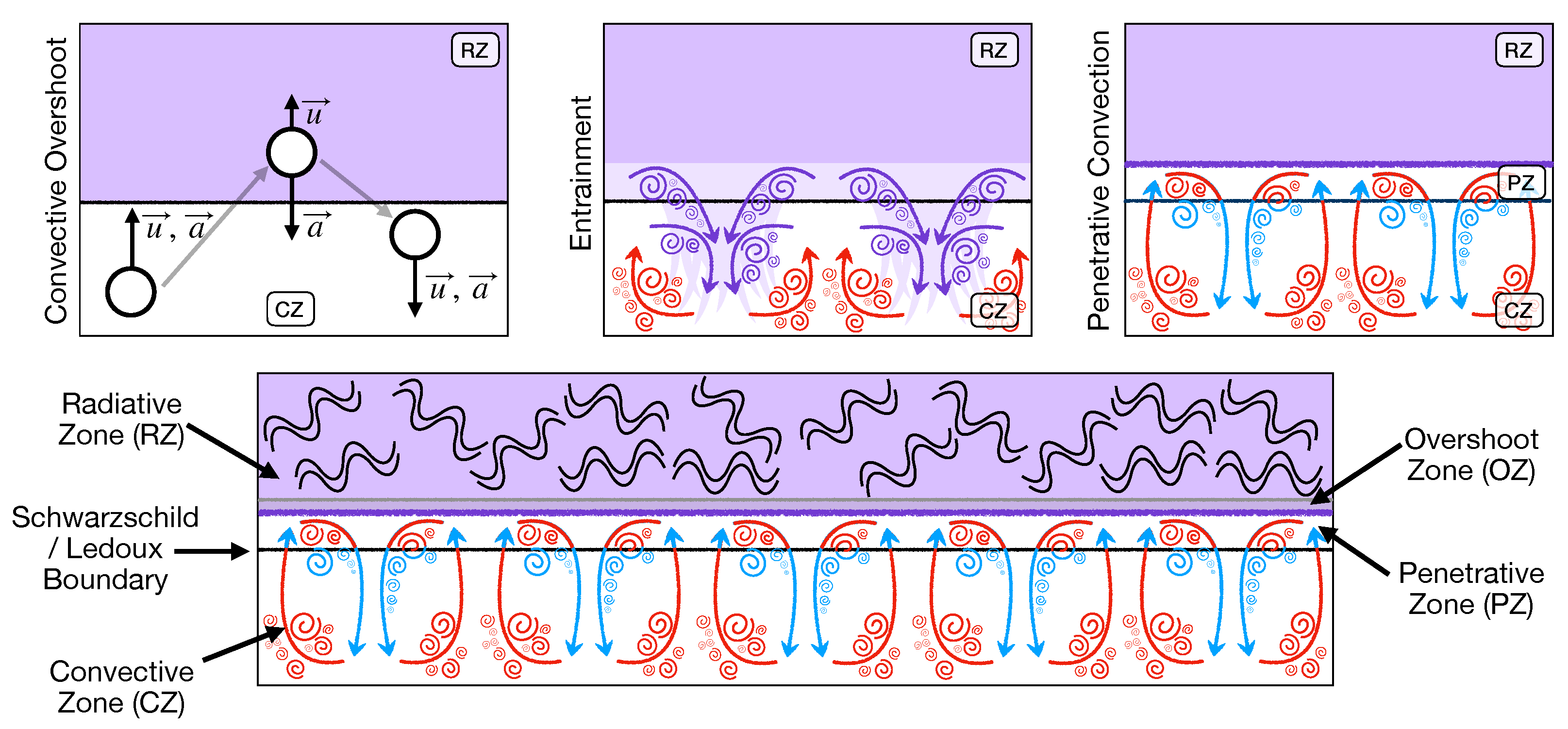
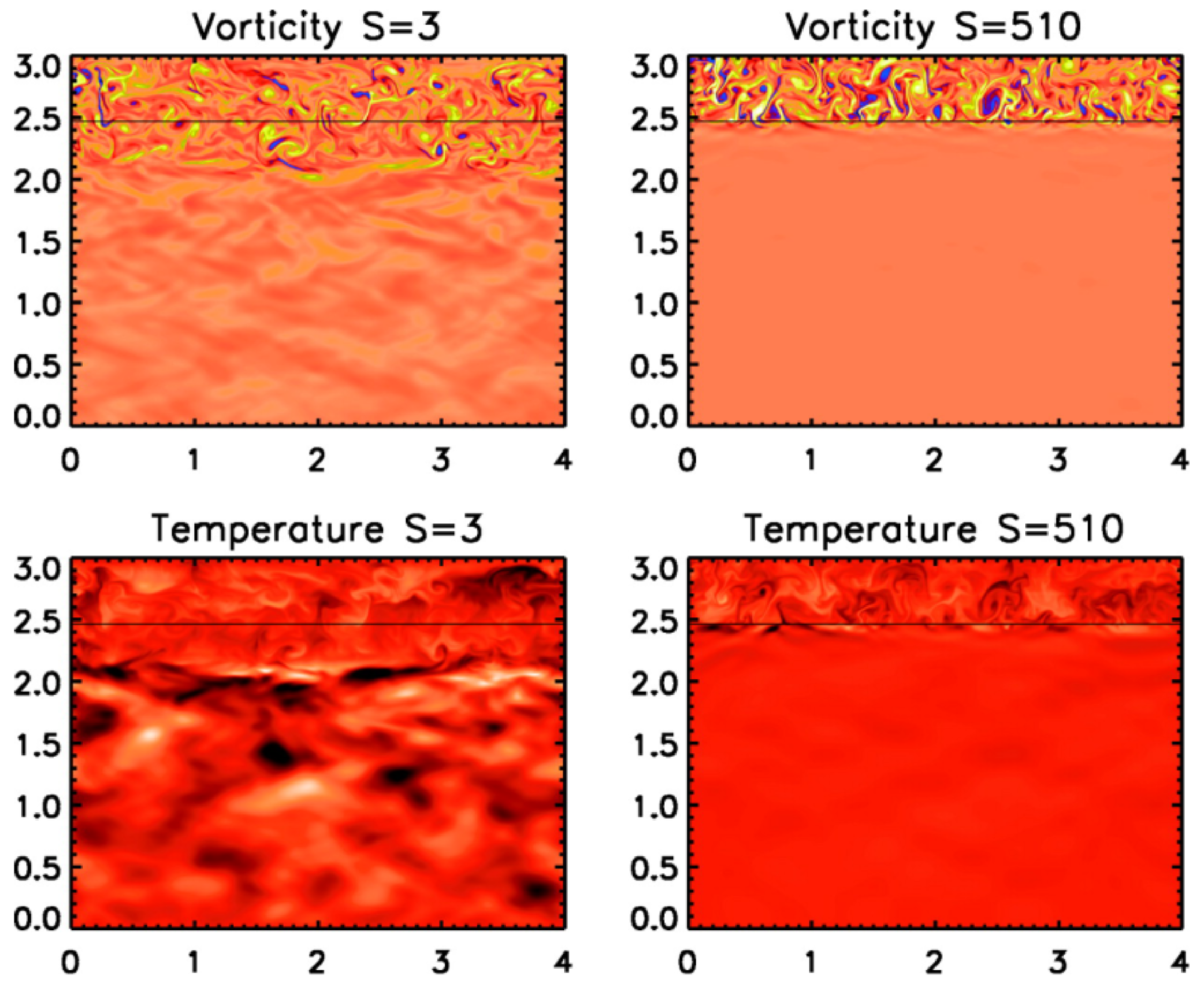
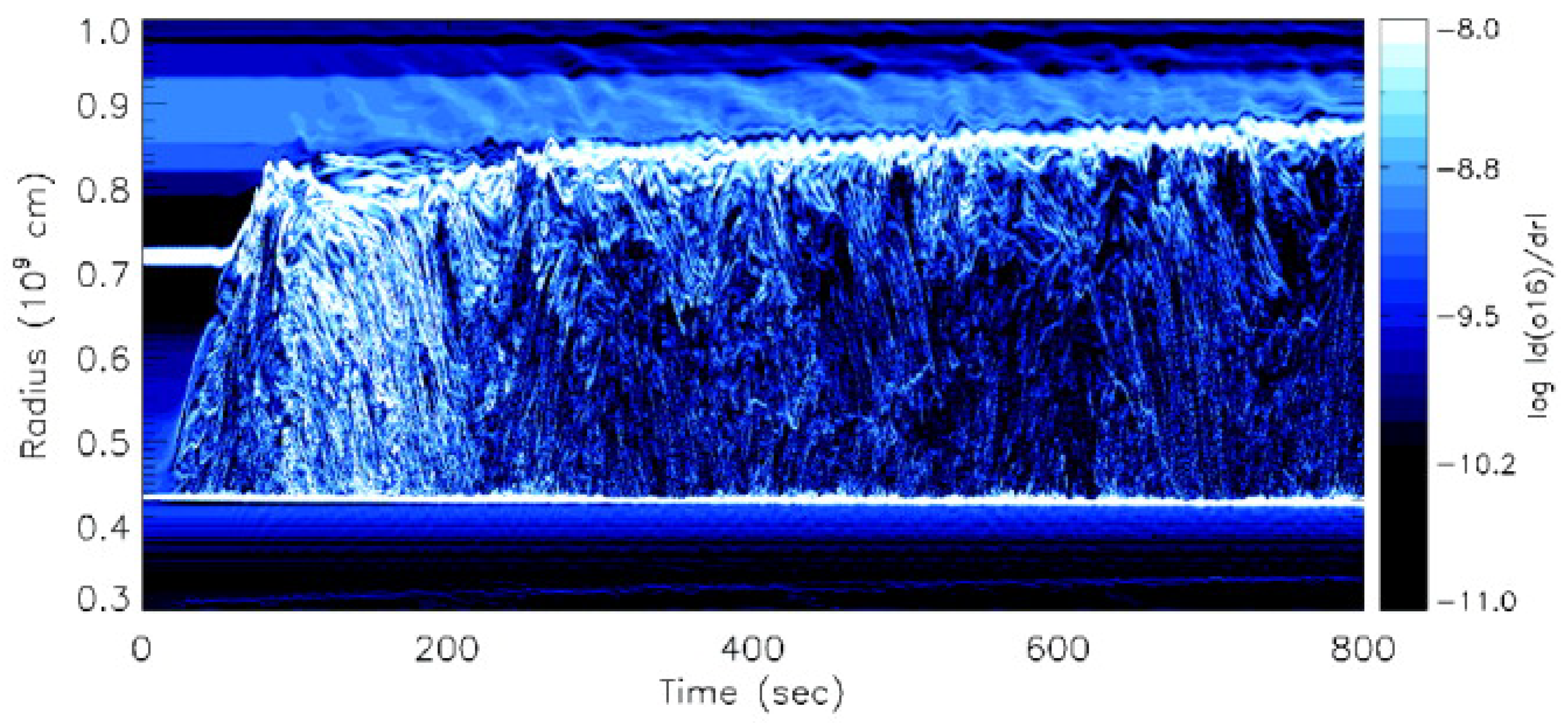
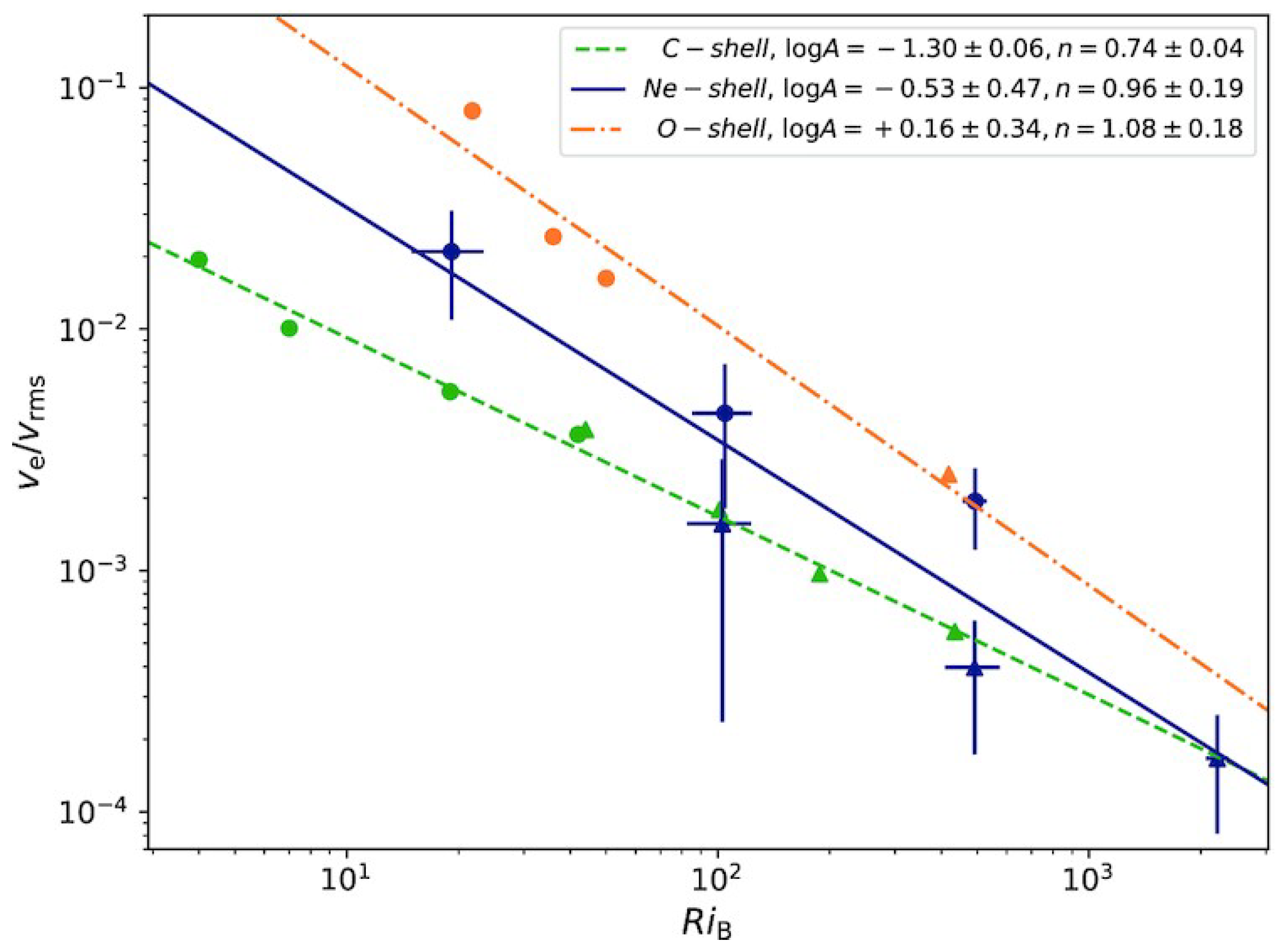
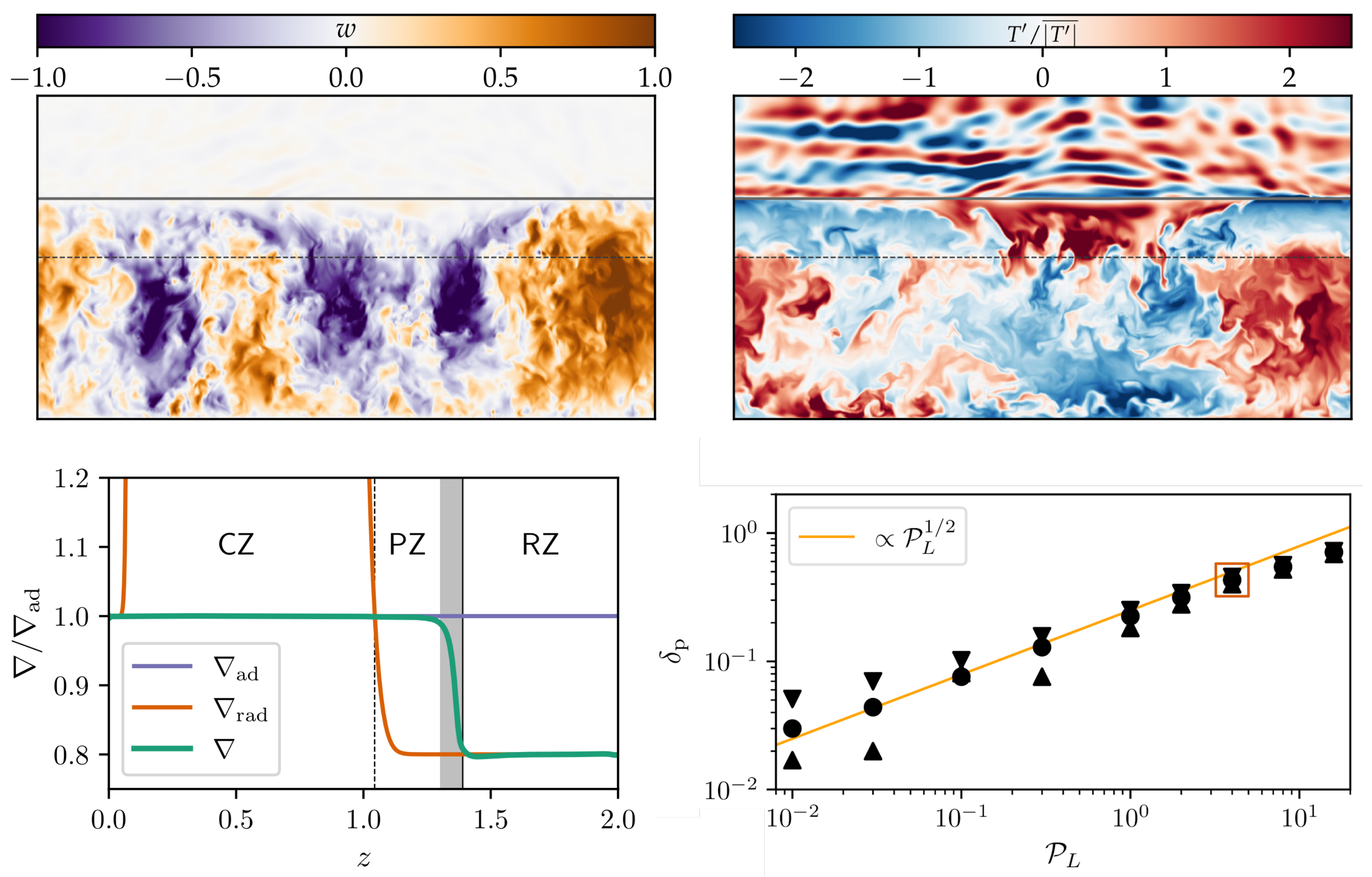
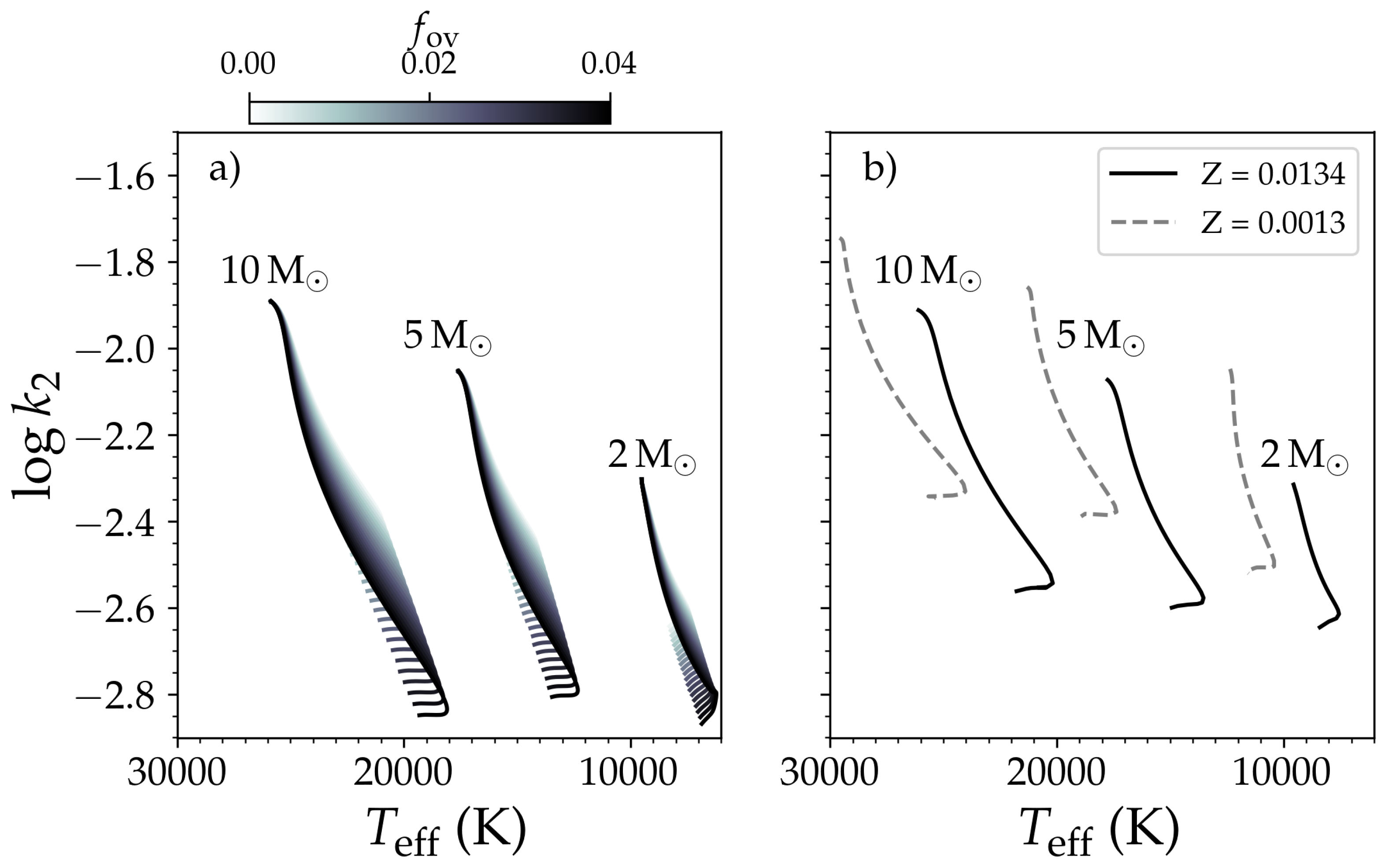
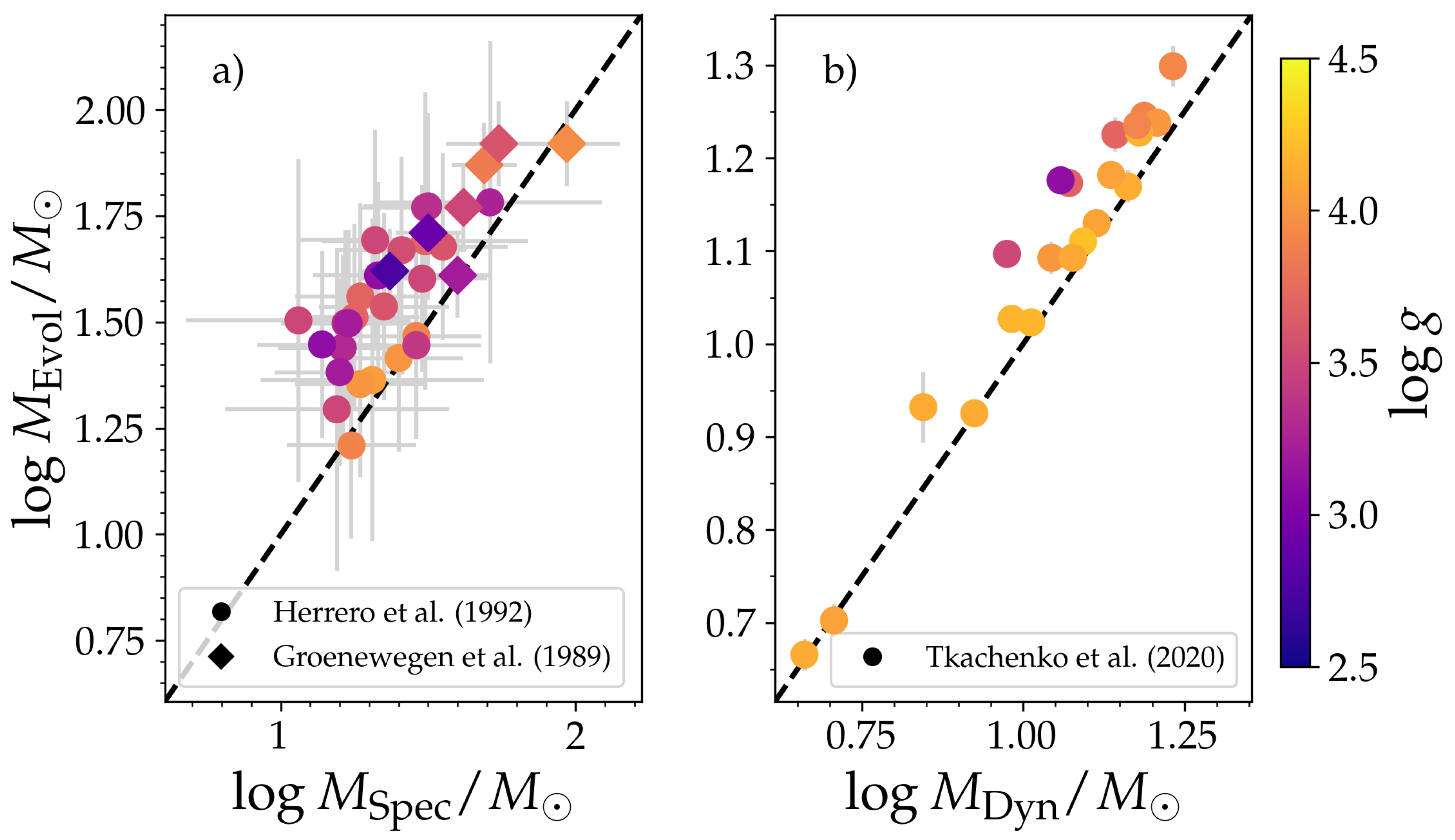
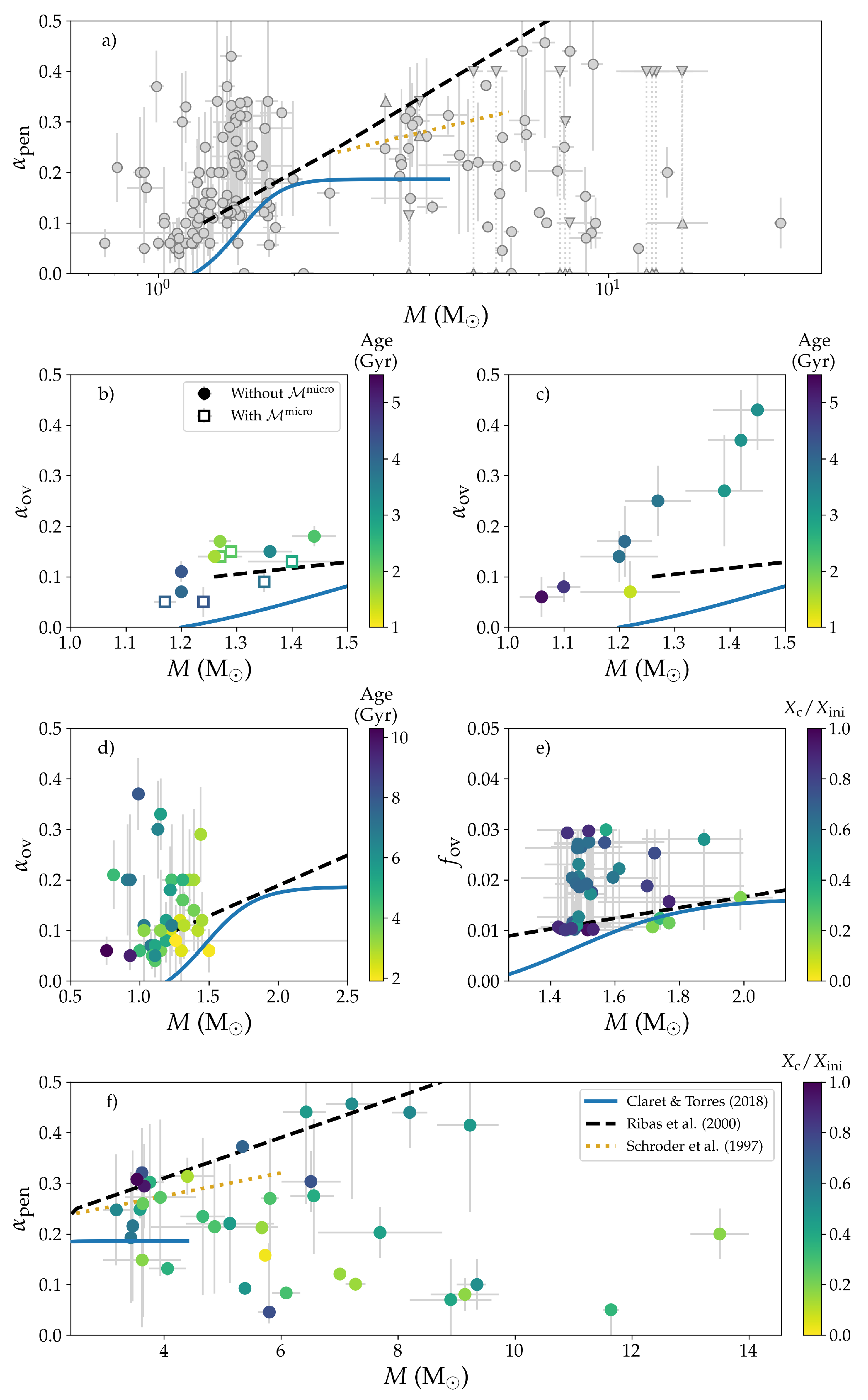
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anders, E.H.; Pedersen, M.G. Convective Boundary Mixing in Main-Sequence Stars: Theory and Empirical Constraints. Galaxies 2023, 11, 56. https://doi.org/10.3390/galaxies11020056
Anders EH, Pedersen MG. Convective Boundary Mixing in Main-Sequence Stars: Theory and Empirical Constraints. Galaxies. 2023; 11(2):56. https://doi.org/10.3390/galaxies11020056
Chicago/Turabian StyleAnders, Evan H., and May G. Pedersen. 2023. "Convective Boundary Mixing in Main-Sequence Stars: Theory and Empirical Constraints" Galaxies 11, no. 2: 56. https://doi.org/10.3390/galaxies11020056
APA StyleAnders, E. H., & Pedersen, M. G. (2023). Convective Boundary Mixing in Main-Sequence Stars: Theory and Empirical Constraints. Galaxies, 11(2), 56. https://doi.org/10.3390/galaxies11020056






