The Simplest Parametrization of the Equation of State Parameter in the Scalar Field Universe
Abstract
1. Introduction
2. Theoretical Model and Basic Equations
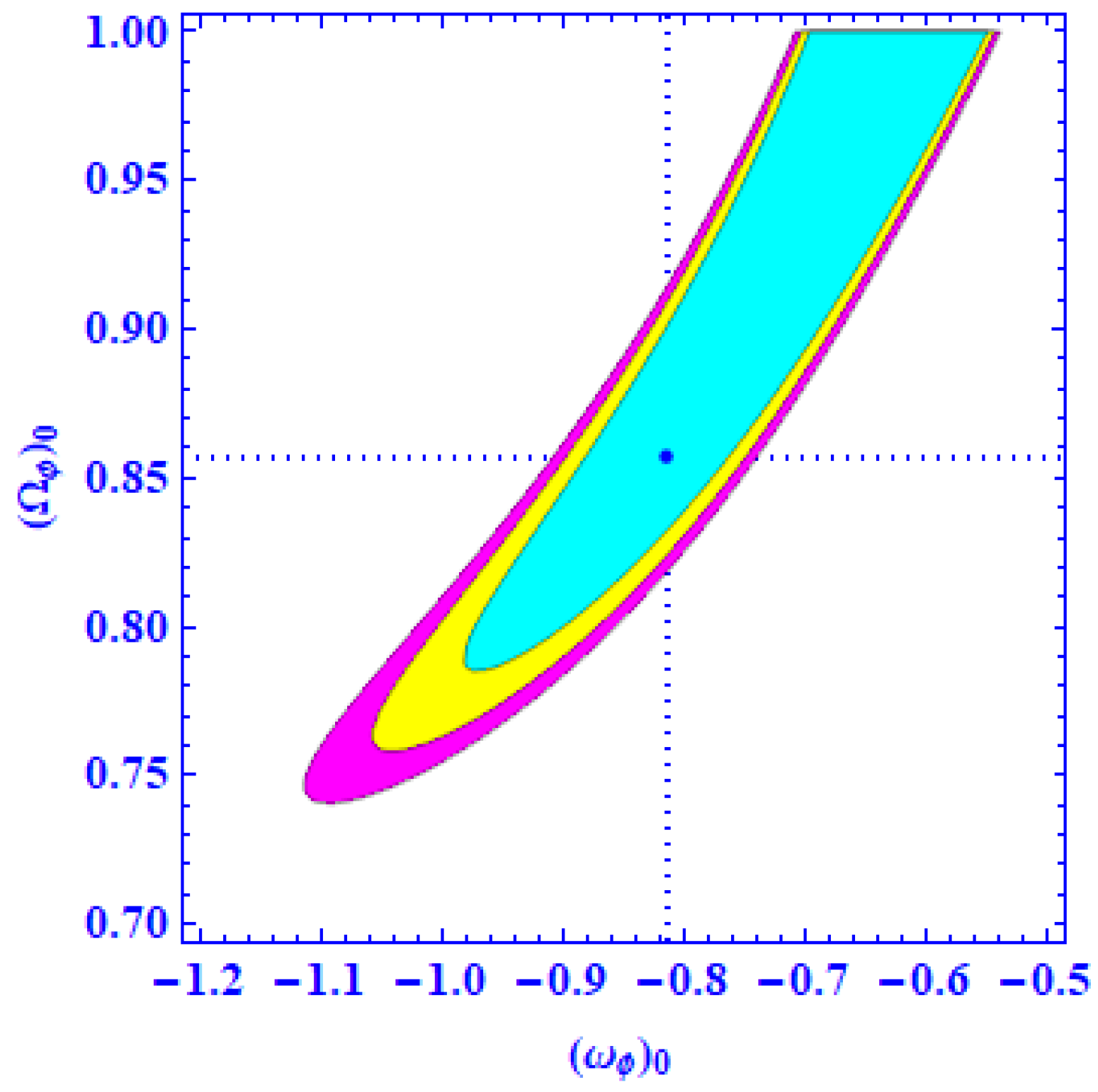
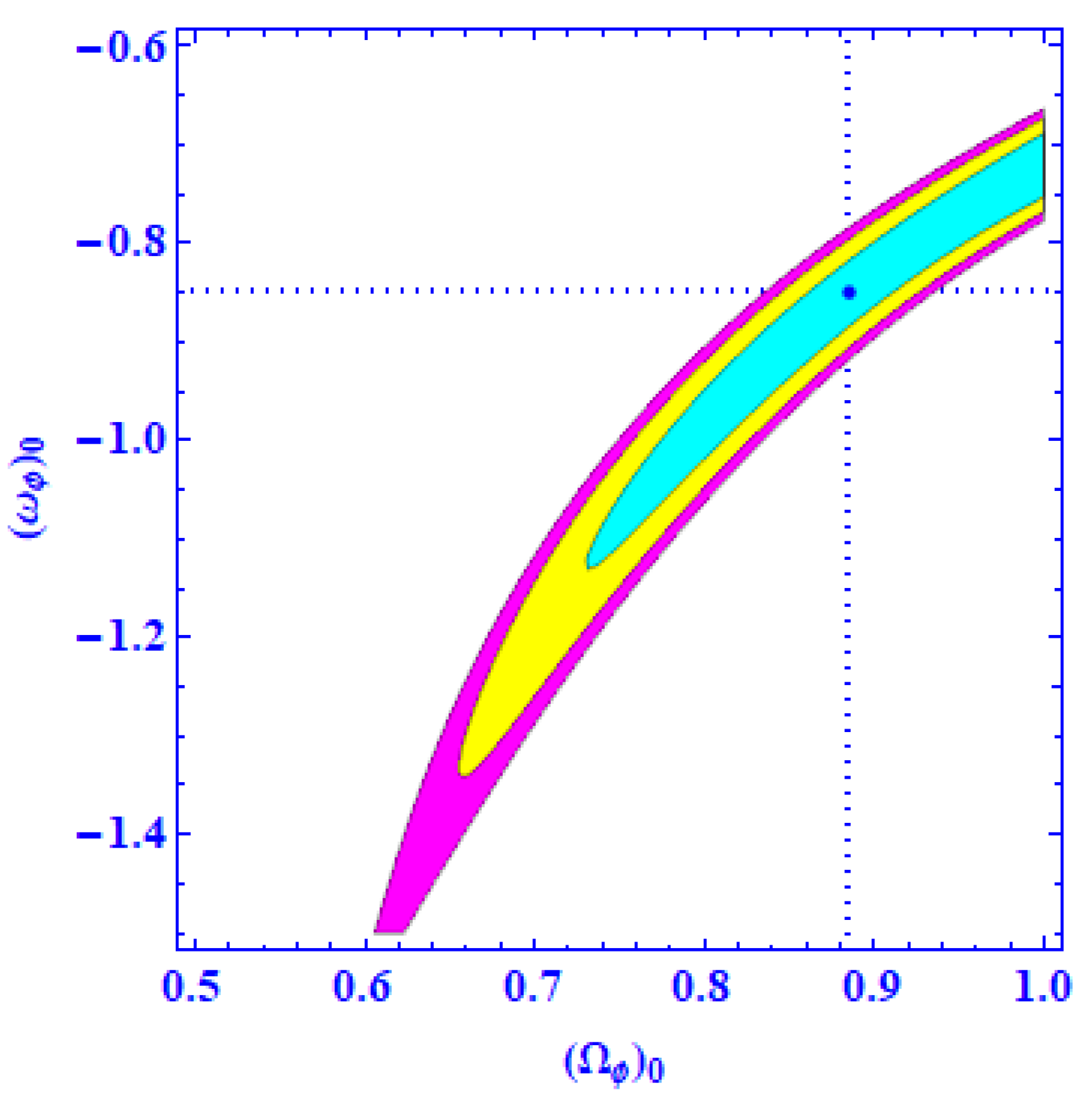
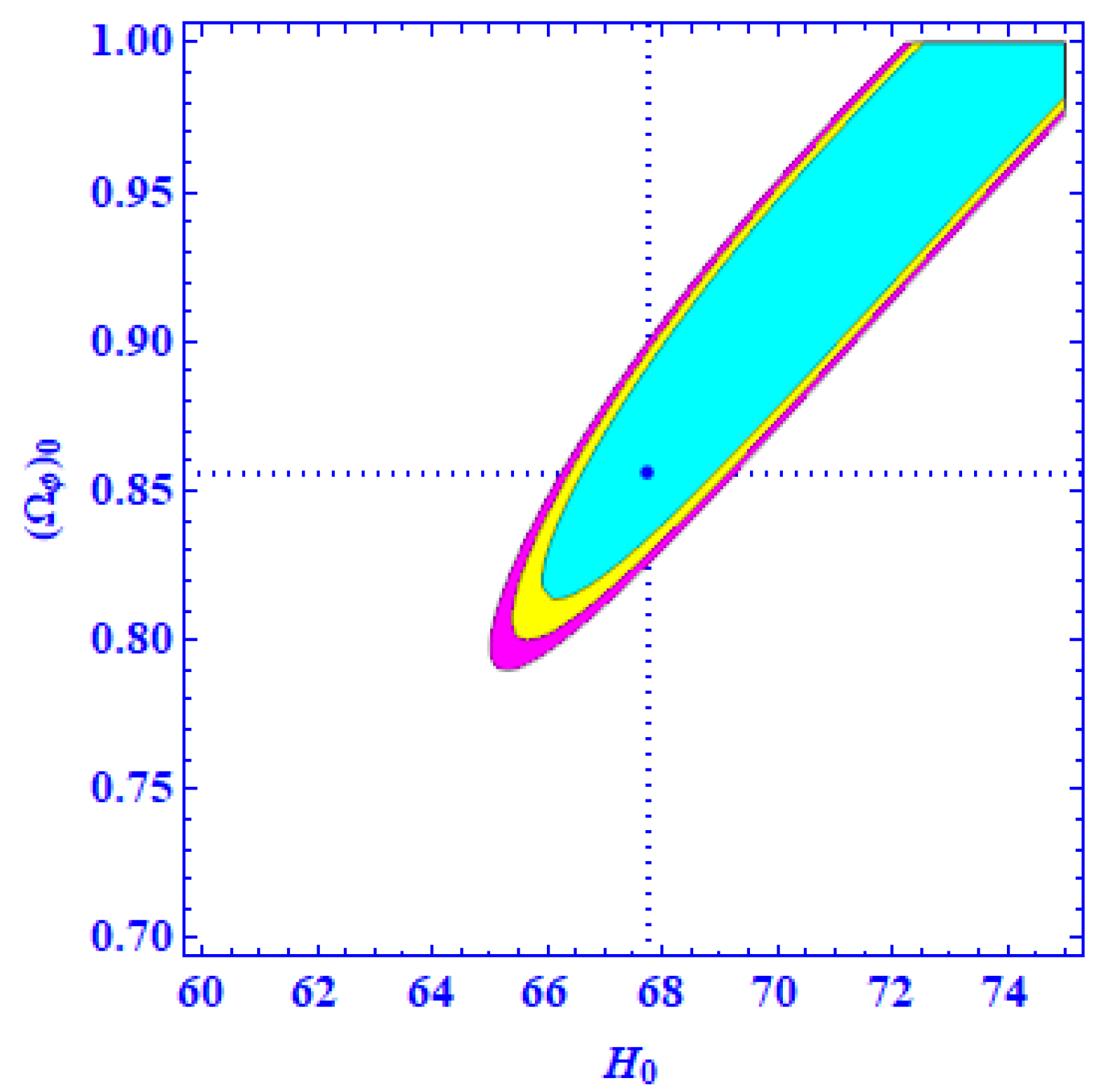
3. Observational Constraints
4. Physical Properties of The Model
4.1. Age of Universe
4.2. Deceleration Parameter
4.3. Statefinder Diagnostics
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| S. N. | z | H(z) | Method | References | |
|---|---|---|---|---|---|
| 1 | 0 | 67.77 | 1.30 | DA | [97] |
| 2 | 0.07 | 69 | 19.6 | DA | [98] |
| 3 | 0.09 | 69 | 12 | DA | [99] |
| 4 | 0.01 | 69 | 12 | DA | [100] |
| 5 | 0.12 | 68.6 | 26.2 | DA | [98] |
| 6 | 0.17 | 83 | 8 | DA | [100] |
| 7 | 0.179 | 75 | 4 | DA | [101] |
| 8 | 0.1993 | 75 | 5 | DA | [101] |
| 9 | 0.2 | 72.9 | 29.6 | DA | [98] |
| 10 | 0.24 | 79.7 | 2.7 | DA | [102] |
| 11 | 0.27 | 77 | 14 | DA | [100] |
| 12 | 0.28 | 88.8 | 36.6 | DA | [98] |
| 13 | 0.35 | 82.7 | 8.4 | DA | [103] |
| 14 | 0.352 | 83 | 14 | DA | [101] |
| 15 | 0.38 | 81.5 | 1.9 | DA | [104] |
| 16 | 0.3802 | 83 | 13.5 | DA | [105] |
| 17 | 0.4 | 95 | 17 | DA | [99] |
| 18 | 0.4004 | 77 | 10.2 | DA | [105] |
| 19 | 0.4247 | 87.1 | 11.2 | DA | [105] |
| 20 | 0.43 | 86.5 | 3.7 | DA | [102] |
| 21 | 0.44 | 82.6 | 7.8 | DA | [106] |
| 22 | 0.44497 | 92.8 | 12.9 | DA | [105] |
| 23 | 0.47 | 89 | 49.6 | DA | [107] |
| 24 | 0.4783 | 80.9 | 9 | DA | [105] |
| 25 | 0.48 | 97 | 60 | DA | [100] |
| 26 | 0.51 | 90.4 | 1.9 | DA | [104] |
| 27 | 0.57 | 96.8 | 3.4 | DA | [108] |
| 28 | 0.593 | 104 | 13 | DA | [101] |
| 29 | 0.6 | 87.9 | 6.1 | DA | [106] |
| 30 | 0.61 | 97.3 | 2.1 | DA | [104] |
| 31 | 0.68 | 92 | 8 | DA | [101] |
| 32 | 0.73 | 97.3 | 7 | DA | [106] |
| 33 | 0.781 | 105 | 12 | DA | [101] |
| 34 | 0.875 | 125 | 17 | DA | [101] |
| 35 | 0.88 | 90 | 40 | DA | [100] |
| 36 | 0.9 | 117 | 23 | DA | [100] |
| 37 | 1.037 | 154 | 20 | DA | [101] |
| 38 | 1.3 | 168 | 17 | DA | [100] |
| 39 | 1.363 | 160 | 33.6 | DA | [109] |
| 40 | 1.43 | 177 | 18 | DA | [100] |
| 41 | 1.53 | 140 | 14 | DA | [100] |
| 42 | 1.75 | 202 | 40 | DA | [100] |
| 43 | 1.965 | 186.5 | 50.4 | DA | [109] |
| 44 | 2.3 | 224 | 8 | DA | [110] |
| 45 | 2.34 | 222 | 7 | DA | [111] |
| 46 | 2.36 | 226 | 8 | DA | [112] |
References
- Kumar, S.; Yadav, A.K. Some Bianchi type V models of accelerating universe with dark energy. Mod. Phys. Lett. A 2011, 26, 647. [Google Scholar] [CrossRef]
- Yadav, A.K. Some anisotropic dark energy models in Bianchi type-V space-time. Astrophys. Space Sc. 2011, 335, 565. [Google Scholar] [CrossRef]
- Yadav, A.K. A transitioning universe with anisotropic dark energy. Astrophys. Space Sc. 2016, 361, 1. [Google Scholar] [CrossRef]
- Goswami, G.K.; Yadav, A.K.; Mishra, B. Probing kinematics and fate of Bianchi type V Universe. Mod. Phys. Lett. A 2020, 35, 2050224. [Google Scholar] [CrossRef]
- Amirhashchi, H.; Yadav, A.K.; Ahmad, N.; Yadav, V. Interacting Dark Sectors in Anisotropic Universe: Observational Constraints and H0 Tension. Phys. Dark Uni. 2022, 36, 2022. [Google Scholar] [CrossRef]
- Goswami, G.K.; Mishra, M.; Yadav, A.K.; Pradhan, A. Two Fluid Scenario in Bianchi Type-I Universe. Mod. Phys. Lett. A 2020, 33, 2050086. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, C.P. Anisotropic dark energy models with constant deceleration parameter. Gen. Relativ. Grav. 2011, 43, 1427. [Google Scholar] [CrossRef]
- Akarsu, Ö; Kılınc, C.B. Bianchi type III models with anisotropic dark energy. Gen. Relativ. Grav. 2010, 42, 763. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f (R, T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Prasad, R.; Gupta, L.K.; Goswami, G.K.; Yadav, A.K. Bulk viscous accelerating Universe in f(R,T) theory of gravity. Pramana J. Physics 2020, 94, 135. [Google Scholar] [CrossRef]
- Yadav, A.K.; Sahoo, P.K.; Bhardwaj, V. Bulk Viscous Bianchi-I Embedded Cosmological Model in f (R, T)=f1(R)+f2(R)f3(T) Gravity. Mod. Phys. Lett. A 2019, 34, 1950145. [Google Scholar] [CrossRef]
- Sharma, L.K.; Yadav, A.K.; Sahoo, P.K.; Singh, B.K. Non-Minimal Matter-Geometry Coupling in Bianchi-I Space-Time. Results Phys. 2018, 10, 738. [Google Scholar] [CrossRef]
- Perlmutter, S.; Gabi, S.; Goldhaber, G.; Goobar, A.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Pain, R.; et al. Measurements of the Cosmological Parameters Ω and Λ from the First Seven Supernovae at z ≥ 0.35. ApJ 1997, 483, 565. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Della Valle, M.; Deustua, S.; Ellis, R.S.; Fabbro, S.; Fruchter, A.; Goldhaber, G.; Groom, D.E.; Hook, I.M.; et al. Discovery of a supernova explosion at half the age of the Universe. Nature 1998, 391, 51. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. ApJ 1999, 517, 565. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.-G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia supernova discoveries at z > 1 from the Hubble space telescope: Evidence for past deceleration and constraints on dark energy evolution. ApJ 2004, 607, 665. [Google Scholar] [CrossRef]
- Blake, C.; Kazin, E.; Beutler, F.; Davis, T.; Parkinson, D.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; et al. The WiggleZ Dark Energy Survey: Mapping the distance-redshift relation with baryon acoustic oscillations. MNRAS 2011, 418, 1707. [Google Scholar] [CrossRef]
- Bennett, C.; Hill, R.S.; Hinshaw, G.; Nolta, M.R.; Odegard, N.; Page, L.; Spergel, D.N.; Weiland, J.L.; Wright, E.L.; Halpern, M.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Foreground Emission. ApJS 2003, 148, 1. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. [Planck Collaboration.] Planck 2015 results XIII Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Peebles, P.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large magellanic cloud cepheid standards provide a 1% foundation for the determination of the Hubble Constant and stronger evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with LambdaCDM. arXiv 2020, arXiv:2012.08534. [Google Scholar] [CrossRef]
- Valentino, E.D.; Pan, S.; Yang, W.; Anchordoqui, L.A. Touch of neutrinos on the vacuum metamorphosis: Is the H0 Solution Back? Phys. Rev. D 2021, 103, 123527. [Google Scholar] [CrossRef]
- Banerjee, A.; Cai, H.; Heisenberg, L.; Colgain, E.O.; Sheikh-Jabbari, M.M.; Yang, T. Hubble Sinks In The Low-Redshift Swampland. Phys. Rev. D 2021, 103, 081305. [Google Scholar] [CrossRef]
- Capozziello, S.; Carloni, S.; Troisi, A. Quintessence without scalar fields. Recent Res. Dev. Astron. Asrophys. 2003, 1, 625. [Google Scholar]
- Harko, T. Thermodynamic interpretation of the generalized gravity models with geometry-matter coupling. Phys. Rev. D 2014, 90, 044067. [Google Scholar] [CrossRef]
- Bhardwaj, V.K.; Yadav, A.K. Some Bianchi type V accelerating cosmological models in f (R, T) = f1(R) + f2(T) formalism. Int. J. Geom. Meth. Mod. Phys. 2020, 7, 2050159. [Google Scholar] [CrossRef]
- Yadav, A.K.; Mondal, M.; Rahaman, F. Singularity-free nonexotic compact star in f(R,T) gravity. Pramana J. Phys. 2020, 94, 90. [Google Scholar] [CrossRef]
- Sharma, L.K.; Yadav, A.K.; Singh, B.K. Power-law solution for homogeneous and isotropic universe in f(R, T) gravity. New Astron. 2020, 79, 101396. [Google Scholar] [CrossRef]
- Singla, N.; Gupta, M.K.; Yadav, A.K. Accelerating model of flat universe in f (R, T) gravity. Grav. Cosmol. 2020, 26, 144. [Google Scholar] [CrossRef]
- Yadav, A.K.; Ali, A.T. Invariant Bianchi type I models in f(R,T) Gravity. Int. J. Geom. Methods. Mod. Phys. 2018, 15, 1850026. [Google Scholar] [CrossRef]
- Yadav, A.K.; Srivastava, P.K.; Yadav, L. Hybrid expansion law for dark energy dominated universe in f(R,T) Gravity. Int. J. Theor. Phys. 2015, 54, 1671. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f (R) cosmic acceleration that evade solar system tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Dark energy and dark matter as curvature effects. JCAP 2006, 0608, 001. [Google Scholar]
- Martins, C.F.; Salucci, P. Analysis of Rotation Curves in the framework of Rn gravity. Mon. Not. R. Astron. Soc. 2007, 381, 1103. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Harko, T.; Lobo, F.S.N. Dark matter as a geometric effect in f (R) gravity. Astropart. Phys. 2008, 29, 386. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Harko, T.; Lobo, F.S.N. Generalized virial theorem in f(R) gravity. JCAP 2008, 03, 024. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. Construction of cosmologically viable f (G) gravity models. Phys. Lett. B 2009, 675, 1. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Finite-time future singularities in modified Gauss-Bonnet and F(R, G) gravity and singularity avoidance. Eur. Phys. J. C 2010, 67, 295. [Google Scholar] [CrossRef]
- Bahamonde, S.; Zubair, M.; Abbas, G. Thermodynamics and cosmological reconstruction in f (T, B gravity. Phys. Dark Univ. 2018, 19, 78. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rept. 2017, 692, 1. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Rescaled Einstein-Hilbert gravity from F(R) gravity: Inflation, dark energy, and the swampland criteria. Phys. Rev. D 2021, 103, 124028. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Unifying inflation with early and late dark energy epochs in axion F(R) gravity. Phys. Rev. D 2021, 103, 044036. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Geometric inflation and dark energy with axion F(R) gravity. Phys. Rev. D 2020, 101, 044009. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Unification of inflation with dark energy in F(R) gravity and axion dark matter. Phys. Rev. D 2019, 99, 104070. [Google Scholar] [CrossRef]
- Yousaf, Z. Stellar filaments with Minkowskian core in the Einstein - Λ gravity. Eur. Phys. J. Plus 2017, 132, 71. [Google Scholar] [CrossRef]
- Yousaf, Z. On the role of f (G, T) terms in structure scalars. Eur. Phys. J. Plus 2019, 134, 245. [Google Scholar] [CrossRef]
- Yousaf, Z.; Bamba, K.; Bhatti, M.Z. Causes of irregular energy density in f(R,T) gravity. Phys. Rev. D 2016, 93, 124048. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological Imprint of an Energy Component with General Equation of State. Phys. Rev. Lett 1998, 80, 1582. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Joyce, M. Cosmology with a primordial scaling field. Phys. Rev. D 1998, 58, 023503. [Google Scholar] [CrossRef]
- Copel, E.J.; Liddle, A.R.; Wands, D. Exponential potentials and cosmological scaling solutions. Phys. Rev. D 1998, 57, 4686. [Google Scholar]
- Liddle, A.R.; Scherrer, R.J. Classification of scalar field potentials with cosmological scaling solutions. Phys. Rev. D 1998, 59, 023509. [Google Scholar] [CrossRef]
- Dodleson, S.; Kaplinghat, M.; Stewart, E. Solving the Coincidence Problem: Tracking Oscillating Energy. Phys. Rev. Lett. 2000, 85, 5276. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.; Steinhardt, P.J. Quintessence, Cosmic Coincidence, and the Cosmological Constant. Phys. Rev. Lett. 1999, 82, 896. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wang, L.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504. [Google Scholar] [CrossRef]
- Johri, V.B. Search for tracker potentials in quintessence theory. Class. Quant. Grav. 2002, 19, 5959. [Google Scholar] [CrossRef]
- Johri, V.B. Genesis of cosmological tracker fields. Phys. Rev. D 2001, 63, 103504. [Google Scholar] [CrossRef]
- Sahni, V. Dark matter and dark energy. Lect. Notes Phys. 2004, 653, 141. [Google Scholar]
- Sahni, V.; Starobinsky, A. The Case for a Positive Cosmological Lambda-term. Int. J. Mod. Phys. D 2000, 9, 373. [Google Scholar] [CrossRef]
- Chimento, L.P.; Jakubi, A.S. Scalar field cosmologies with perfect fluid in Robertson-Walker metric. Int. J. Mod. Phys. D 1996, 5, 71. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Wave function of the Universe. Phys. Rev. D 1983, 28, 2960. [Google Scholar] [CrossRef]
- Hawking, S.W. The quantum state of the universe. Nucl. Phys. B 1984, 239, 257. [Google Scholar] [CrossRef]
- Vilenkin, A. Creation of universes from nothing. Phys. Lett. B 1982, 117, 25. [Google Scholar] [CrossRef]
- Barvinsky, A.O. Unitarity approach to quantum cosmology. Phys. Rep. 1993, 230, 237. [Google Scholar] [CrossRef]
- Spokoiny, B.L. Inflation and generation of perturbations in broken-symmetric theory of gravity. Phys. Lett. B 1984, 147, 39. [Google Scholar] [CrossRef]
- Salopek, D.S.; Bond, J.R.; Bardeen, J.M. Designing density fluctuation spectra in inflation. Phys. Rev. D 1989, 40, 1753. [Google Scholar] [CrossRef]
- Khalatnikov, I.M.; Mezhlumian, A. The classical and quantum cosmology with a complex scalar field. Phys. Lett. A 1992, 169, 308. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, Y. Probing the curvature and dark energy. Phys. Rev. D 2005, 72, 043518. [Google Scholar] [CrossRef]
- Sharov, G.S.; Vasiliev, V.O. How predictions of cosmological models depend on Hubble parameter data sets. Math. Model. Geom. 2018, 6, 1. [Google Scholar] [CrossRef]
- Biswas, P.; Roy, P.; Biswas, R. Posing constraints on the free parameters of a new model of dark energy EoS: Responses through cosmological behaviours. arXiv 2019, arXiv:1908.00408. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Heath Jones, D.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon acoustic oscillations and the local Hubble constant. MNRAS 2011, 416, 3017. [Google Scholar] [CrossRef]
- Padmanabhan, N.; Xu, X.; Eisenstein, D.J.; Scalzo, R.; Cuesta, A.J.; Mehta, K.T.; Kazin, E. A 2 percent distance to z=0.35 by reconstructing baryon acoustic oscillations - I. Methods and application to the Sloan Digital Sky Survey. MNRAS 2012, 427, 2132. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Bizyaev, D.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; Cuesta, A.J.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Release 9 spectroscopic galaxy sample. MNRAS 2013, 427, 3435. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Davis, T.; Drinkwater, M.J.; Forster, K.; Gilbank, D.; et al. The WiggleZ Dark Energy Survey: The growth rate of cosmic structure since redshift z=0.9. MNRAS 2011, 415, 2876. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- Bond, H.E.; Nelan, E.P.; VandenBerg, D.A.; Schaefer, G.H.; Harmer, D. HD 140283: A star in the solar neighborhood that formed shortly after big bang. Astrophys. J. 2013, 765, L12. [Google Scholar] [CrossRef]
- Masi, S.; Ade, P.A.R.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Contaldi, C.R.; Crill, B.P.; De Bernardis, P.; et al. The BOOMERanG experiment and the curvature of the universe. Prog. Part. Nucl. Phys. 2002, 48, 243. [Google Scholar] [CrossRef]
- Yadav, A.K.; Alshehri, A.M.; Ahmad, N.; Goswami, G.K.; Kumar, M. Transitioning universe with hybrid scalar field in Bianchi I space-time. Phys. Dark Uni. 2021, 31, 100738. [Google Scholar] [CrossRef]
- Renzini, A.; Bragaglia, A.; Ferraro, F.R. The white dwarf distance to the globular cluster NGC 6752 (and its age) with the HUBBLE SPACE TELESCOPE. Astrophys. J. 1996, 465, L23. [Google Scholar] [CrossRef]
- Valentino, E.D.; Anchordoqu, L.A.; Akarsu, Ö.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgar, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Cosmology Intertwined IV The Age of the Universe and its Curvature. Astropart. Phys. 2021, 131, 102607. [Google Scholar] [CrossRef]
- Capozziello, S.; Agostino, R.D.; Luongo, O. High-redshift cosmography: Auxiliary variables versus Pade polynomials. Mon. Not. Roy. Astron. Soc. 2020, 494, 2576. [Google Scholar] [CrossRef]
- Cunha, C.E.; Lima, M.; Oyaizu, H.; Frieman, J.; Lin, H. Estimating the redshift distribution of photometric galaxy samples – II. Applications and tests of a new method. Mon. Not. Roy. Astron. Soc. 2009, 396, 2379. [Google Scholar] [CrossRef]
- Jesus, J.F.; Valentim, R.; Escobal, A.A.; Pereira, S.H. Gaussian process estimation of transition redshift. J. Cosm. Astrop. Phys. 2020, 04, 053. [Google Scholar] [CrossRef]
- Singla, N.; Gupta, M.K.; Yadav, A.K.; Goswami, G.K. Accelerating universe with binary mixture of bulk viscous fluid and dark energy. Int. J. Mod. Phys. A 2021, 36, 2150148. [Google Scholar] [CrossRef]
- Prasad, R.; Gupta, L.K.; Yadav, A.K. Lyra’s cosmology of homogeneous and isotropic universe in Brans-Dicke theory. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150029. [Google Scholar] [CrossRef]
- Prasad, R.; Gupta, L.K.; Beeshan, A.; Goswami, G.K.; Yadav, A.K. Bianchi type I universe: An extension of ΛCDM model. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150069. [Google Scholar] [CrossRef]
- Prasad, R.; Yadav, A.K.; Yadav, A.K. Constraining Bianchi type V universe with recent H(z) and BAO observations in Brans–Dicke theory of gravitation. Eur. Phys. J. Plus 2020, 135, 297. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder - a new geometrical diagnostic of dark energy. JETP Lett. 2003, 77, 201. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Saini, T.D.; Starobinsky, A.A. Exploring the Expanding Universe and Dark Energy using the Statefinder Diagnostic. Mon. Not. R. Astron. Soc. 2003, 344, 1057. [Google Scholar] [CrossRef]
- Tsagas, C.G. The deceleration parameter in ‘tilted’ universes: Generalising the Friedmann background. Euro. Phys. J. C 2022, 82, 521. [Google Scholar] [CrossRef]
- Bouali, A.; Chaudhary, H.; Debnath, U.; Roy, T.; Mustafa, G. Constraints on the Parameterized Deceleration Parameter in FRW Universe. arXiv 2023, arXiv:2301.12107. [Google Scholar]
- Macaulay, E.; Nichol, R.C.; Bacon, D.; Brout, D.; Davis, T.M.; Zhang, B.; Bassett, B.A.; Scolnic, D.; Moller, A.; D’Andrea, C.B.; et al. First cosmological results using Type Ia supernovae from the Dark Energy Survey: Measurement of the Hubble constant. arXiv 2018, arXiv:1811.02376. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Yuan, S.; Liu, S.; Zhang, T.J.; Sun, Y.C. Four New Observational H(z) Data From Luminous Red Galaxies of Sloan Digital Sky Survey Data Release Seven. Res. Astron. Astrophys. 2014, 14, 1221. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic chronometers: Constraining the equation of state of dark energy I: H(z) measurements. JCAP 2010, 1002, 008. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H. et al. Improved constraints on the expansion rate of the Universe up to z∼1.1 from the spectroscopic evolution of cosmic chronometers. JCAP 2012, 8, 006. [Google Scholar] [CrossRef]
- Gaztanaga, E.; Cabre, A.; Hui, L. Clustering of Luminous Red Galaxies IV: Baryon Acoustic Peak in the Line-of-Sight Direction and a Direct Measurement of H(z). MNRAS 2009, 399, 1663. [Google Scholar] [CrossRef]
- Chuang, D.H.; Wang, Y. Modelling the anisotropic two-point galaxy correlation function on small scales and single-probe measurements of H(z), DA(z) and f (z)σ8(z) from the Sloan Digital Sky Survey DR7 luminous red galaxies. MNRAS 2013, 435, 255. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. MNRAS 2016, 470, 2617. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. JCAP 2016, 5, 014. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z <1. MNRAS 2012, 425, 405. [Google Scholar]
- Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Vaisanen, P. Age-dating luminous red galaxies observed with the Southern African Large Telescope. MNRAS 2017, 467, 3239. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, É.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. MNRAS 2014, 441, 24. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z∼2. MNRAS 2015, 450, L16. [Google Scholar] [CrossRef]
- Busca, N.G.; Delubac, T.; Rich, J.; Bailey, S.; Font-Ribera, A.; Kirkby, D.; Le Goff, J.-M.; Pieri, M.M.; Slosar, A.; Aubourg, É.; et al. Baryon acoustic oscillations in the Lyα forest of BOSS quasars. Astron. Astrophys. 2013, 552, A96. [Google Scholar] [CrossRef]
- Rich, J. Which fundamental constants for cosmic microwave background and baryon-acoustic oscillation? Astron. Astrophys. 2015, 584, A69. [Google Scholar] [CrossRef]
- Font-Ribera, A.; Kirkby, D.; Busca, N.; Miralda-Escude, J.; Ross, N.P.; Slosar, A.; Rich, J.; Aubourg, E.; Bailey, S.; Bhardwaj, V.; et al. Quasar-Lyman α forest cross-correlation from BOSS DR11: Baryon Acoustic Oscillations. JCAP 2014, 1405, 027. [Google Scholar] [CrossRef]









| S. N. | z | References | |
|---|---|---|---|
| 1 | 0.106 | 0.336 | [76] |
| 2 | 0.35 | 0.113 | [77] |
| 3 | 0.57 | 0.073 | [78] |
| 4 | 0.44 | 0.0916 | [79] |
| 5 | 0.60 | 0.0726 | [79] |
| 6 | 0.73 | 0.0592 | [17] |
| Parameters | + Pantheon | + BAO | |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrivastava, P.; Khan, A.J.; Kumar, M.; Goswami, G.; Singh, J.K.; Yadav, A.K. The Simplest Parametrization of the Equation of State Parameter in the Scalar Field Universe. Galaxies 2023, 11, 57. https://doi.org/10.3390/galaxies11020057
Shrivastava P, Khan AJ, Kumar M, Goswami G, Singh JK, Yadav AK. The Simplest Parametrization of the Equation of State Parameter in the Scalar Field Universe. Galaxies. 2023; 11(2):57. https://doi.org/10.3390/galaxies11020057
Chicago/Turabian StyleShrivastava, Preeti, Abdul Junaid Khan, Mukesh Kumar, Gopikant Goswami, Jainendra Kumar Singh, and Anil Kumar Yadav. 2023. "The Simplest Parametrization of the Equation of State Parameter in the Scalar Field Universe" Galaxies 11, no. 2: 57. https://doi.org/10.3390/galaxies11020057
APA StyleShrivastava, P., Khan, A. J., Kumar, M., Goswami, G., Singh, J. K., & Yadav, A. K. (2023). The Simplest Parametrization of the Equation of State Parameter in the Scalar Field Universe. Galaxies, 11(2), 57. https://doi.org/10.3390/galaxies11020057







