Magnetism in High-Mass Stars
Abstract
1. Introduction
2. Observations
2.1. Historical Perspective
2.2. From Ap/Bp to OBA Stars
2.3. Neutron Stars and Magnetars
3. Theoretical Background
3.1. Fossil vs. Dynamo Fields
3.2. Time Evolution of Magnetic Fields
3.2.1. Fossil Fields
3.2.2. Dynamo Fields
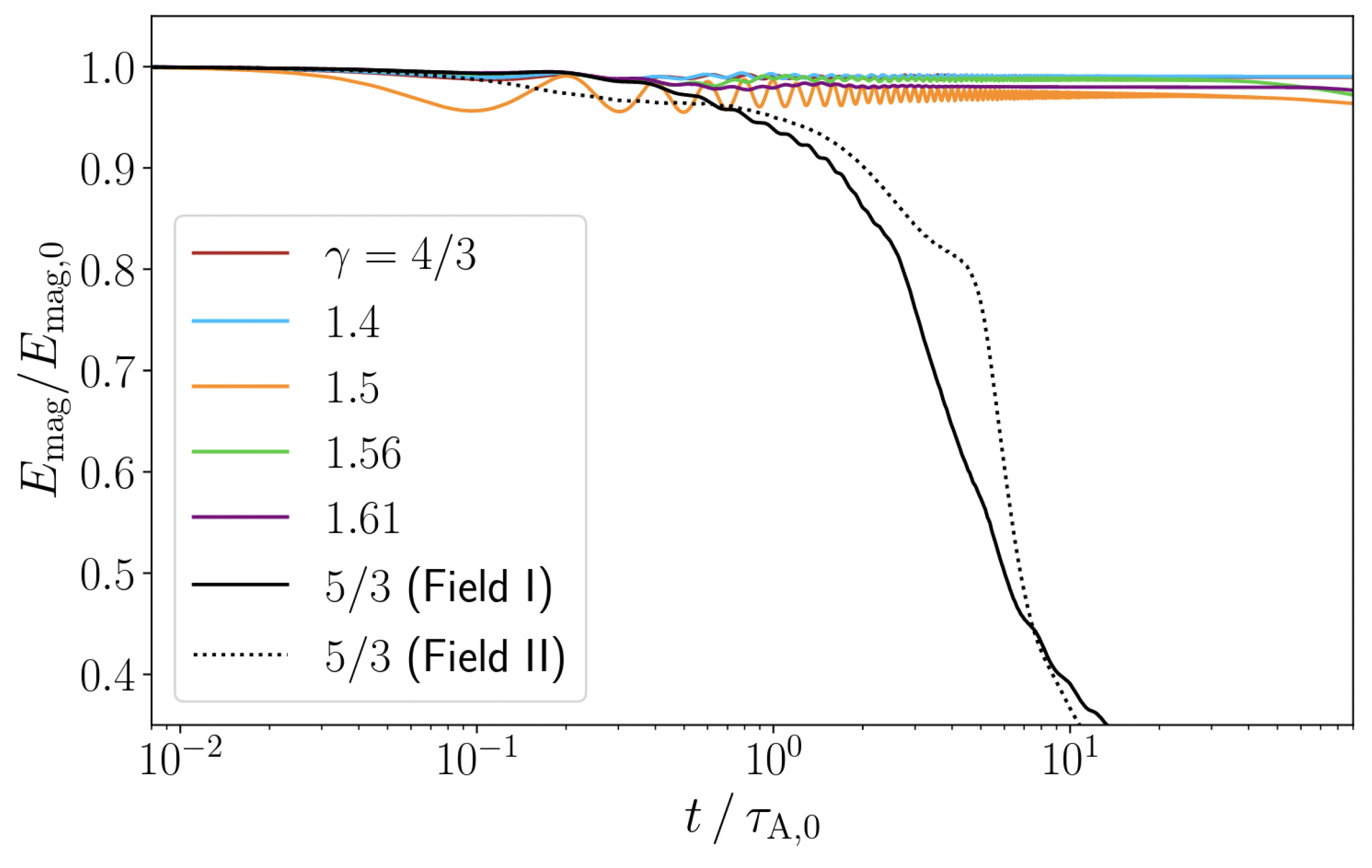
3.3. Stability Criteria for Fossil Fields
3.3.1. Momentum Equation
3.3.2. Convective Expulsion and Inhibition of Convection
3.3.3. Rotational Expulsion and Inhibition of Differential Rotation
3.4. Angular Momentum Transport and Loss
4. Modelling Approaches
4.1. Dynamos in the Stellar Core
4.2. Dynamos in Convective Shells
4.3. Dynamos in the Stably Stratified Envelope
4.3.1. Tayler Instability
4.3.2. Magneto-Rotational Instability
4.3.3. Mean-Field Dynamos
4.3.4. Adaptation in Evolutionary Models
4.4. Fossil Field in the Stably Stratified Envelope
4.4.1. Magneto-Convection
4.4.2. Surface Magnetic Braking
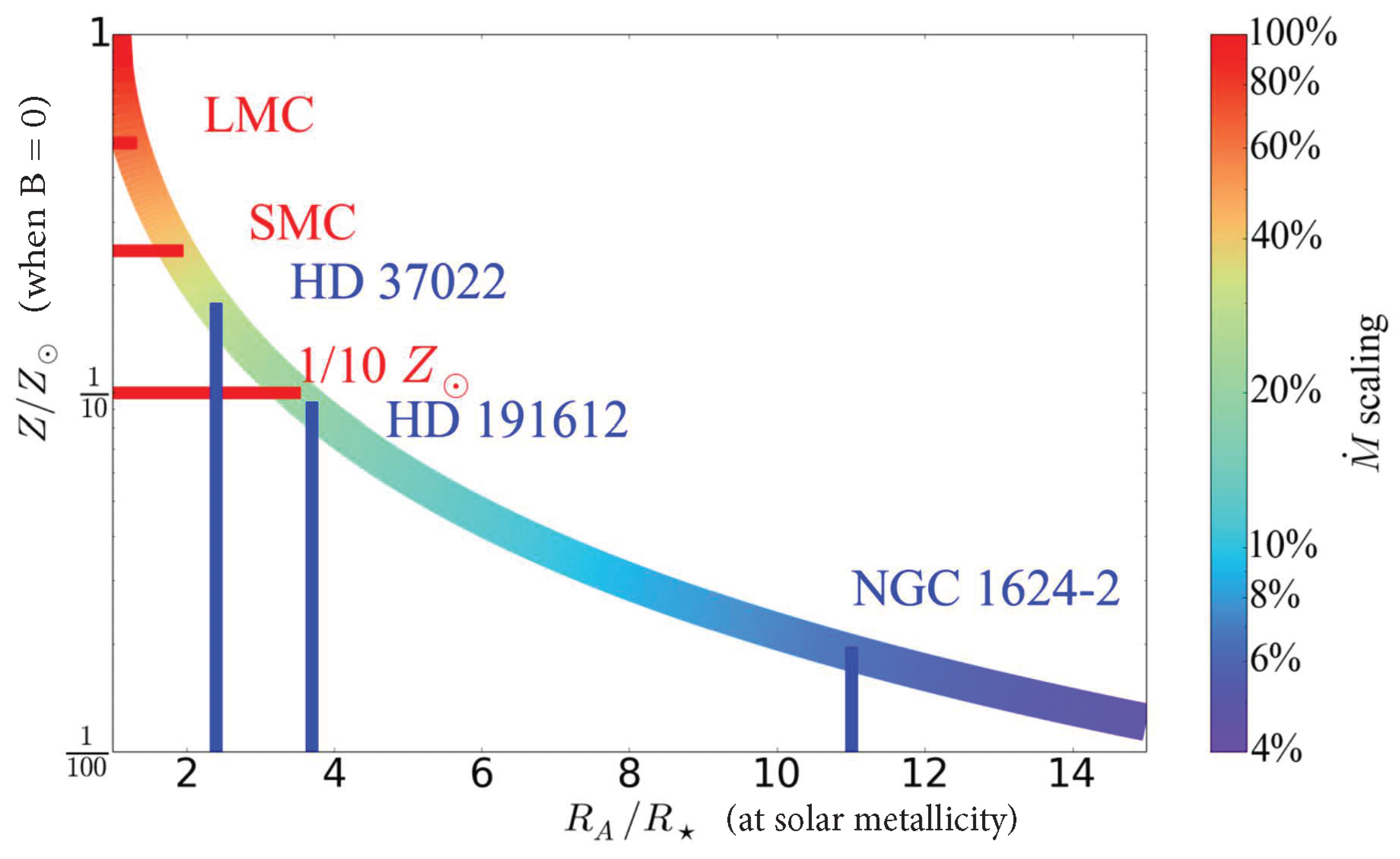
4.4.3. Mass-Loss Quenching
4.5. Stellar Mergers
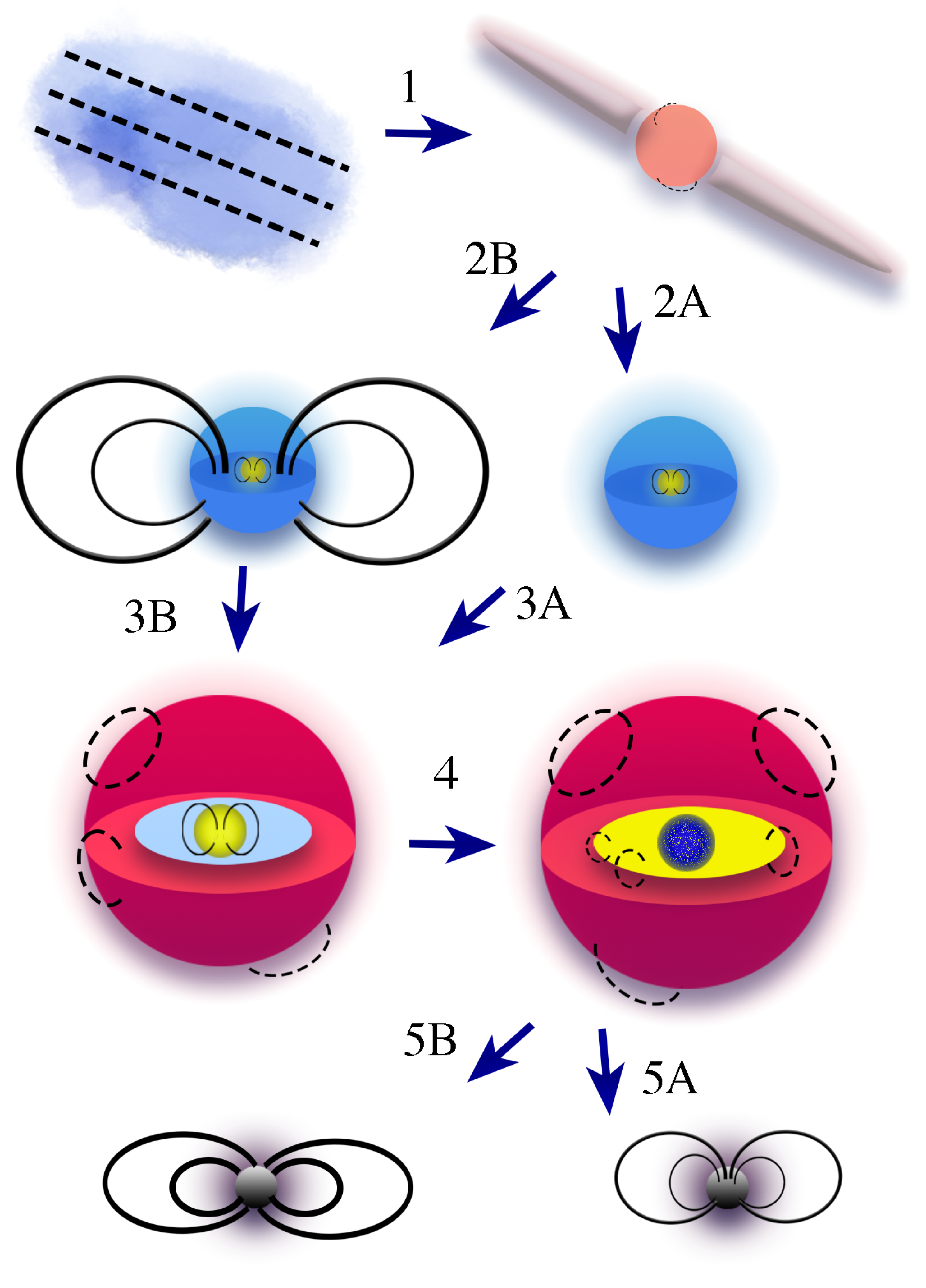
5. Overall Picture of Magnetic Field Evolution in a High-Mass Star
- Phase 1: Collapse of the Molecular Cloud
- Phase 2A: Observably “Non-Magnetic” OB Star
- Phase 2B: “Magnetic” OB Star
- Phase 3A: Red Supergiant with a Convective Core
- Phase 3B: Red Supergiant with a Convective Core
- Phase 4: Advanced Shell Burning Stage
- Phase 5A: Formation of a Typical Neutron Star
- Phase 5B: Formation of a Magnetar
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vidotto, A.A.; Jardine, M.; Morin, J.; Donati, J.F.; Lang, P.; Russell, A.J.B. Effects of M dwarf magnetic fields on potentially habitable planets. Astron. Astrophys. 2013, 557, A67. [Google Scholar] [CrossRef]
- Varela, J.; Brun, A.S.; Strugarek, A.; Réville, V.; Zarka, P.; Pantellini, F. MHD study of the planetary magnetospheric response during extreme solar wind conditions: Earth and exoplanet magnetospheres applications. Astron. Astrophys. 2022, 659, A10. [Google Scholar] [CrossRef]
- Commerçon, B.; Hennebelle, P.; Henning, T. Collapse of Massive Magnetized Dense Cores Using Radiation Magnetohydrodynamics: Early Fragmentation Inhibition. Astrophys. J. Lett. 2011, 742, L9. [Google Scholar] [CrossRef]
- Seifried, D.; Walch, S.; Weis, M.; Reissl, S.; Soler, J.; Klessen, R.; Joshi, P. From parallel to perpendicular—On the orientation of magnetic fields in molecular clouds. Mon. Not. R. Astron. Soc. 2020, 497, 4196–4212. [Google Scholar] [CrossRef]
- Kaspi, V.M.; Beloborodov, A.M. Magnetars. Annu. Rev. Astron. Astrophys. 2017, 55, 261–301. [Google Scholar] [CrossRef]
- Enoto, T.; Kisaka, S.; Shibata, S. Observational diversity of magnetized neutron stars. Rep. Prog. Phys. 2019, 82, 106901. [Google Scholar] [CrossRef]
- Reisenegger, A. Stable magnetic equilibria and their evolution in the upper main sequence, white dwarfs, and neutron stars. Astron. Astrophys. 2009, 499, 557–566. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Untwisting Magnetospheres of Neutron Stars. Astrophys. J. Lett. 2009, 703, 1044–1060. [Google Scholar] [CrossRef]
- Akahori, T.; Nakanishi, H.; Sofue, Y.; Fujita, Y.; Ichiki, K.; Ideguchi, S.; Kameya, O.; Kudoh, T.; Kudoh, Y.; Machida, M.; et al. Cosmic magnetism in centimeter- and meter-wavelength radio astronomy. Publ. Astron. Soc. Jpn. 2018, 70, R2. [Google Scholar] [CrossRef]
- Cowling, T.G. On the Sun’s general magnetic field. Mon. Not. R. Astron. Soc. 1945, 105, 166. [Google Scholar] [CrossRef]
- Spitzer, L.J. Theoretical Problems of Stellar Magnetism. In Electromagnetic Phenomena in Cosmical Physics; Lehnert, B., Ed.; Cambridge University Press: Cambridge, UK, 1958; Volume 6, p. 169. [Google Scholar]
- Nomoto, K.; Kobayashi, C.; Tominaga, N. Nucleosynthesis in Stars and the Chemical Enrichment of Galaxies. Annu. Rev. Astron. Astrophys. 2013, 51, 457–509. [Google Scholar] [CrossRef]
- Geen, S.; Bieri, R.; Rosdahl, J.; de Koter, A. The geometry and dynamical role of stellar wind bubbles in photoionized H II regions. Mon. Not. R. Astron. Soc. 2021, 501, 1352–1369. [Google Scholar] [CrossRef]
- Kim, J.G.; Ostriker, E.C.; Filippova, N. Star Formation Efficiency and Dispersal of Giant Molecular Clouds with UV Radiation Feedback: Dependence on Gravitational Boundedness and Magnetic Fields. Astrophys. J. Lett. 2021, 911, 128. [Google Scholar] [CrossRef]
- Bochenek, C.D.; Ravi, V.; Belov, K.V.; Hallinan, G.; Kocz, J.; Kulkarni, S.R.; McKenna, D.L. A fast radio burst associated with a Galactic magnetar. Nature 2020, 587, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Andersen, B.C. et al. [CHIME/FRB Collaboration]. A bright millisecond-duration radio burst from a Galactic magnetar. Nature 2020, 587, 54–58. [Google Scholar] [CrossRef]
- Petroff, E.; Hessels, J.W.T.; Lorimer, D.R. Fast radio bursts at the dawn of the 2020s. Astron. Astrophys. Rev. 2022, 30, 2. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- del Toro Iniesta, J.C. Introduction to Spectropolarimetry; Cambridge University Press: Cambridge, UK, 2003; ISBN 0521818273. [Google Scholar]
- Donati, J.F.; Landstreet, J.D. Magnetic Fields of Nondegenerate Stars. Annu. Rev. Astron. Astrophys. 2009, 47, 333–370. [Google Scholar] [CrossRef]
- Kochukhov, O. Magnetic fields of M dwarfs. Astron. Astrophys. Rev. 2021, 29, 1. [Google Scholar] [CrossRef]
- Hale, G.E. On the Probable Existence of a Magnetic Field in Sun-Spots. Astrophys. J. Lett. 1908, 28, 315. [Google Scholar] [CrossRef]
- Parker, E.N. Dynamics of the Interplanetary Gas and Magnetic Fields. Astrophys. J. Lett. 1958, 128, 664. [Google Scholar] [CrossRef]
- Weiss, N.O.; Tobias, S.M. Physical Causes of Solar Activity. Space Sci. Rev. 2000, 94, 99–112. [Google Scholar] [CrossRef]
- Spruit, H.C. Dynamo action by differential rotation in a stably stratified stellar interior. Astron. Astrophys. 2002, 381, 923–932. [Google Scholar] [CrossRef]
- Mohanty, S.; Basri, G. Rotation and Activity in Mid-M to L Field Dwarfs. Astrophys. J. Lett. 2003, 583, 451–472. [Google Scholar] [CrossRef]
- Mathias, P.; Aurière, M.; López Ariste, A.; Petit, P.; Tessore, B.; Josselin, E.; Lèbre, A.; Morin, J.; Wade, G.; Herpin, F.; et al. Evolution of the magnetic field of Betelgeuse from 2009–2017. Astron. Astrophys. 2018, 615, A116. [Google Scholar] [CrossRef]
- Babcock, H.W. Zeeman Effect in Stellar Spectra. Astrophys. J. Lett. 1947, 105, 105. [Google Scholar] [CrossRef]
- Landstreet, J.D.; Borra, E.F. Discovery of magnetic fields in three short-period Ap stars. Astrophys. J. Lett. 1977, 212, L43–L46. [Google Scholar] [CrossRef]
- Borra, E.F.; Landstreet, J.D. The magnetic fields of the AP stars. Astrophys. J. Suppl. Ser. 1980, 42, 421–445. [Google Scholar] [CrossRef]
- Hümmerich, S.; Paunzen, E.; Bernhard, K. A plethora of new, magnetic chemically peculiar stars from LAMOST DR4. Astron. Astrophys. 2020, 640, A40. [Google Scholar] [CrossRef]
- Giarrusso, M.; Cecconi, M.; Cosentino, R.; Munari, M.; Ghedina, A.; Ambrosino, F.; Boschin, W.; Leone, F. Twenty-year monitoring of the surface magnetic fields of chemically peculiar stars. Mon. Not. R. Astron. Soc. 2022, 514, 3485–3509. [Google Scholar] [CrossRef]
- Hajduk, M.; Leto, P.; Vedantham, H.; Trigilio, C.; Haverkorn, M.; Shimwell, T.; Callingham, J.R.; White, G.J. Radio detection of chemically peculiar stars with LOFAR. Astron. Astrophys. 2022, 665, A152. [Google Scholar] [CrossRef]
- Kobzar, O.; Khalack, V.; Bohlender, D.; Mathys, G.; Shultz, M.E.; Bowman, D.M.; Paunzen, E.; Lovekin, C.; David-Uraz, A.; Sikora, J.; et al. Analysis of eight magnetic chemically peculiar stars with rotational modulation. Mon. Not. R. Astron. Soc. 2022, 517, 5340–5357. [Google Scholar] [CrossRef]
- Semenko, E.; Romanyuk, I.; Yakunin, I.; Kudryavtsev, D.; Moiseeva, A. Spectropolarimetry of magnetic Chemically Peculiar stars in the Orion OB1 association. Mon. Not. R. Astron. Soc. 2022, 515, 998–1011. [Google Scholar] [CrossRef]
- Alecian, E.; Wade, G.A.; Catala, C.; Grunhut, J.H.; Landstreet, J.D.; Böhm, T.; Folsom, C.P.; Marsden, S. A high-resolution spectropolarimetric survey of Herbig Ae/Be stars—II. Rotation. Mon. Not. R. Astron. Soc. 2013, 429, 1027–1038. [Google Scholar] [CrossRef]
- Villebrun, F.; Alecian, E.; Hussain, G.; Bouvier, J.; Folsom, C.P.; Lebreton, Y.; Amard, L.; Charbonnel, C.; Gallet, F.; Haemmerlé, L.; et al. Magnetic fields of intermediate-mass T Tauri stars. I. Magnetic detections and fundamental stellar parameters. Astron. Astrophys. 2019, 622, A72. [Google Scholar] [CrossRef]
- Lavail, A. et al. [BinaMIcS Collaboration]. The large-scale magnetic field of the eccentric pre-main-sequence binary system V1878 Ori. Mon. Not. R. Astron. Soc. 2020, 497, 632–642. [Google Scholar] [CrossRef]
- Kholtygin, A.F.; Tsiopa, O.A.; Doronina, Y.A.; Tumanova, I.M.; Ryspaeva, E.B.; Merkulova, O.A. Accretion and Magnetic Fields of Herbig Ae/Be Stars. Astrophysics 2021, 64, 54–60. [Google Scholar] [CrossRef]
- Conti, P.S. On the Accretion of Material by Theta Orionis C. Astrophys. J. Lett. 1972, 174, L79. [Google Scholar] [CrossRef]
- Stahl, O.; Kaufer, A.; Rivinius, T.; Szeifert, T.; Wolf, B.; Gaeng, T.; Gummersbach, C.A.; Jankovics, I.; Kovacs, J.; Mandel, H.; et al. Phase-locked photospheric and stellar-wind variations of θ1 Orionis C. Astron. Astrophys. 1996, 312, 539–548. [Google Scholar]
- Wade, G.A.; Fullerton, A.W.; Donati, J.F.; Landstreet, J.D.; Petit, P.; Strasser, S. The magnetic field and confined wind of the O star θ1 Orionis C. Astron. Astrophys. 2006, 451, 195–206. [Google Scholar] [CrossRef]
- Babel, J.; Montmerle, T. X-ray emission from Ap-Bp stars: A magnetically confined wind-shock model for IQ Aur. Astron. Astrophys. 1997, 323, 121–138. [Google Scholar]
- ud-Doula, A.; Owocki, S.P. Dynamical Simulations of Magnetically Channeled Line-driven Stellar Winds. I. Isothermal, Nonrotating, Radially Driven Flow. Astrophys. J. Lett. 2002, 576, 413–428. [Google Scholar] [CrossRef]
- Gagné, M.; Oksala, M.E.; Cohen, D.H.; Tonnesen, S.K.; ud-Doula, A.; Owocki, S.P.; Townsend, R.H.D.; MacFarlane, J.J. Chandra HETGS Multiphase Spectroscopy of the Young Magnetic O Star Theta1 Orionis C. Astrophys. J. Lett. 2005, 628, 986–1005. [Google Scholar] [CrossRef]
- Cohen, D.H.; de Messières, G.E.; MacFarlane, J.J.; Miller, N.A.; Cassinelli, J.P.; Owocki, S.P.; Liedahl, D.A. High-Resolution Chandra Spectroscopy of τ Scorpii: A Narrow-Line X-ray Spectrum from a Hot Star. Astrophys. J. Lett. 2003, 586, 495–505. [Google Scholar] [CrossRef]
- Nazé, Y.; Petit, V.; Rinbrand, M.; Cohen, D.; Owocki, S.; ud-Doula, A.; Wade, G.A. X-ray Emission from Magnetic Massive Stars. Astrophys. J. Suppl. Ser. 2014, 215, 10. [Google Scholar] [CrossRef]
- Fletcher, C.L.C. X-rays from Magnetic B-Type Stars. Ph.D. Thesis, Florida Institute of Technology, Melbourne, FL, USA, 2018. [Google Scholar]
- Donati, J.F.; Babel, J.; Harries, T.J.; Howarth, I.D.; Petit, P.; Semel, M. The magnetic field and wind confinement of θ1 Orionis C. Mon. Not. R. Astron. Soc. 2002, 333, 55–70. [Google Scholar] [CrossRef]
- Petit, V. et al. [MiMeS Collaboration]. A magnetic confinement versus rotation classification of massive-star magnetospheres. Mon. Not. R. Astron. Soc. 2013, 429, 398–422. [Google Scholar] [CrossRef]
- Morel, T.; Castro, N.; Fossati, L.; Hubrig, S.; Langer, N.; Przybilla, N.; Schöller, M.; Carroll, T.; Ilyin, I.; Irrgang, A.; et al. The B Fields in OB Stars (BOB) Survey. In Proceedings of the New Windows on Massive Stars, Geneva, Switzerland, 23–27 June 2014; Meynet, G., Georgy, C., Groh, J., Stee, P., Eds.; Cambridge University Press: Cambridge, UK, 2015; Volume 307, IAU Symposium. pp. 342–347. [Google Scholar] [CrossRef]
- Fossati, L. et al. [BOB Collaboration]. B fields in OB stars (BOB): Low-resolution FORS2 spectropolarimetry of the first sample of 50 massive stars. Astron. Astrophys. 2015, 582, A45. [Google Scholar] [CrossRef]
- Fossati, L.; Castro, N.; Morel, T.; Langer, N.; Briquet, M.; Carroll, T.A.; Hubrig, S.; Nieva, M.F.; Oskinova, L.M.; Przybilla, N.; et al. B fields in OB stars (BOB): On the detection of weak magnetic fields in the two early B-type stars β CMa and ϵ CMa. Possible lack of a “magnetic desert” in massive stars. Astron. Astrophys. 2015, 574, A20. [Google Scholar] [CrossRef]
- Fossati, L.; Schneider, F.R.N.; Castro, N.; Langer, N.; Simón-Díaz, S.; Müller, A.; de Koter, A.; Morel, T.; Petit, V.; Sana, H.; et al. Evidence of magnetic field decay in massive main-sequence stars. Astron. Astrophys. 2016, 592, A84. [Google Scholar] [CrossRef]
- Wade, G.A.; Neiner, C.; Alecian, E.; Grunhut, J.H.; Petit, V.; Batz, B.D.; Bohlender, D.A.; Cohen, D.H.; Henrichs, H.F.; Kochukhov, O.; et al. The MiMeS survey of magnetism in massive stars: Introduction and overview. Mon. Not. R. Astron. Soc. 2016, 456, 2–22. [Google Scholar] [CrossRef]
- Neiner, C.; Oksala, M.E.; Georgy, C.; Przybilla, N.; Mathis, S.; Wade, G.; Kondrak, M.; Fossati, L.; Blazère, A.; Buysschaert, B.; et al. Discovery of magnetic A supergiants: The descendants of magnetic main-sequence B stars. Mon. Not. R. Astron. Soc. 2017, 471, 1926–1935. [Google Scholar] [CrossRef]
- Grunhut, J.H. et al. [MiMeS Collaboration]. The MiMeS survey of Magnetism in Massive Stars: Magnetic analysis of the O-type stars. Mon. Not. R. Astron. Soc. 2017, 465, 2432–2470. [Google Scholar] [CrossRef]
- Sikora, J.; Wade, G.A.; Power, J.; Neiner, C. A volume-limited survey of mCP stars within 100 pc II: Rotational and magnetic properties. Mon. Not. R. Astron. Soc. 2019, 483, 3127–3145. [Google Scholar] [CrossRef]
- Shultz, M.E. et al. [MiMeS, and BinaMIcS Collaboration]. The magnetic early B-type stars—III. A main-sequence magnetic, rotational, and magnetospheric biography. Mon. Not. R. Astron. Soc. 2019, 490, 274–295. [Google Scholar] [CrossRef]
- Neiner, C. et al. [BinaMIcS and MiMeS Collaborations]. The Origin of Magnetic Fields in Hot Stars; Nagendra, K.N., Bagnulo, S., Centeno, R., Jesús Martínez González, M., Eds.; Cambridge University Press: Cambridge, UK, 2015; Volume 305, IAU Symposium; pp. 61–66. [Google Scholar] [CrossRef]
- David-Uraz, A.; Petit, V.; Shultz, M.E.; Fullerton, A.W.; Erba, C.; Keszthelyi, Z.; Seadrow, S.; Wade, G.A. New observations of NGC 1624-2 reveal a complex magnetospheric structure and underlying surface magnetic geometry. Mon. Not. R. Astron. Soc. 2021, 501, 2677–2687. [Google Scholar] [CrossRef]
- Shultz, M.E. et al. [MiMeS and BinaMIcS Collaboration]. The magnetic early B-type stars I: Magnetometry and rotation. Mon. Not. R. Astron. Soc. 2018, 475, 5144–5178. [Google Scholar] [CrossRef]
- Lander, S.K.; Jones, D.I. Non-rigid precession of magnetic stars. Mon. Not. R. Astron. Soc. 2017, 467, 4343–4382. [Google Scholar] [CrossRef]
- Lander, S.K.; Jones, D.I. Neutron-star spindown and magnetic inclination-angle evolution. Mon. Not. R. Astron. Soc. 2018, 481, 4169–4193. [Google Scholar] [CrossRef]
- Donati, J.F.; Howarth, I.D.; Jardine, M.M.; Petit, P.; Catala, C.; Landstreet, J.D.; Bouret, J.C.; Alecian, E.; Barnes, J.R.; Forveille, T.; et al. The surprising magnetic topology of τ Sco: Fossil remnant or dynamo output? Mon. Not. R. Astron. Soc. 2006, 370, 629–644. [Google Scholar] [CrossRef]
- Kochukhov, O.; Wade, G.A. Magnetic field topology of τ Scorpii. The uniqueness problem of Stokes V ZDI inversions. Astron. Astrophys. 2016, 586, A30. [Google Scholar] [CrossRef]
- Wade, G.A.; Maíz Apellániz, J.; Martins, F.; Petit, V.; Grunhut, J.; Walborn, N.R.; Barbá, R.H.; Gagné, M.; García-Melendo, E.; Jose, J.; et al. NGC 1624-2: A slowly rotating, X-ray luminous Of?cp star with an extraordinarily strong magnetic field. Mon. Not. R. Astron. Soc. 2012, 425, 1278–1293. [Google Scholar] [CrossRef]
- Lignières, F.; Petit, P.; Böhm, T.; Aurière, M. First evidence of a magnetic field on Vega. Towards a new class of magnetic A-type stars. Astron. Astrophys. 2009, 500, L41–L44. [Google Scholar] [CrossRef]
- Petit, P.; Böhm, T.; Folsom, C.P.; Lignières, F.; Cang, T. A decade-long magnetic monitoring of Vega. Astron. Astrophys. 2022, 666, A20. [Google Scholar] [CrossRef]
- Blazère, A.; Petit, P.; Lignières, F.; Aurière, M.; Ballot, J.; Böhm, T.; Folsom, C.P.; Gaurat, M.; Jouve, L.; Lopez Ariste, A.; et al. Detection of ultra-weak magnetic fields in Am stars: β Ursae Majoris and θ Leonis. Astron. Astrophys. 2016, 586, A97. [Google Scholar] [CrossRef]
- Blazère, A.; Petit, P.; Neiner, C.; Folsom, C.; Kochukhov, O.; Mathis, S.; Deal, M.; Landstreet, J. Magnetic geometry and surface differential rotation of the bright Am star Alhena A. Mon. Not. R. Astron. Soc. 2020, 492, 5794–5810. [Google Scholar] [CrossRef]
- Moss, D. The survival of fossil magnetic fields during pre-main sequence evolution. Astron. Astrophys. 2003, 403, 693–697. [Google Scholar] [CrossRef]
- Braithwaite, J.; Spruit, H.C. A fossil origin for the magnetic field in A stars and white dwarfs. Nature 2004, 431, 819–821. [Google Scholar] [CrossRef] [PubMed]
- Mestel, L.; Moss, D. The evolution of stable magnetic fields in stars: An analytical approach. Mon. Not. R. Astron. Soc. 2010, 405, 1845–1853. [Google Scholar] [CrossRef]
- Ferrario, L.; Melatos, A.; Zrake, J. Magnetic Field Generation in Stars. Space Sci. Rev. 2015, 191, 77–109. [Google Scholar] [CrossRef]
- Aurière, M.; Wade, G.A.; Silvester, J.; Lignières, F.; Bagnulo, S.; Bale, K.; Dintrans, B.; Donati, J.F.; Folsom, C.P.; Gruberbauer, M.; et al. Weak magnetic fields in Ap/Bp stars. Evidence for a dipole field lower limit and a tentative interpretation of the magnetic dichotomy. Astron. Astrophys. 2007, 475, 1053–1065. [Google Scholar] [CrossRef]
- Lignières, F.; Petit, P.; Aurière, M.; Wade, G.A.; Böhm, T. The dichotomy between strong and ultra-weak magnetic fields among intermediate-mass stars. Proc. Int. Astron. Union 2013, 302, 338–347. [Google Scholar] [CrossRef]
- Petit, V. et al. [MiMeS Collaboration]. The MiMeS survey of magnetism in massive stars: Magnetic properties of the O-type star population. Mon. Not. R. Astron. Soc. 2019, 489, 5669–5687. [Google Scholar] [CrossRef]
- Buysschaert, B.; Aerts, C.; Bowman, D.M.; Johnston, C.; Van Reeth, T.; Pedersen, M.G.; Mathis, S.; Neiner, C. Forward seismic modeling of the pulsating magnetic B-type star HD 43317. Astron. Astrophys. 2018, 616, A148. [Google Scholar] [CrossRef]
- Pfeffer, C.M.; McSwain, M.V. Modeling the Photometric Variability of Alpha2 CVn with a Dynamical Magnetosphere. Astrophys. J. Lett. 2022, 935, 145. [Google Scholar] [CrossRef]
- Shen, D.X.; Liu, J.Z.; Zhu, C.H.; Lü, G.L.; Zhang, Y.; Lü, C.L.; Wang, H.Z.; Li, L.; Lu, X.Z.; Yu, J.L.; et al. Photometric Properties and Stellar Parameters of the Rapidly Rotating Magnetic Early-B Star HD 345439. Res. Astron. Astrophys. 2023, 23, 015002. [Google Scholar] [CrossRef]
- David-Uraz, A.; Neiner, C.; Sikora, J.; Bowman, D.M.; Petit, V.; Chowdhury, S.; Handler, G.; Pergeorelis, M.; Cantiello, M.; Cohen, D.H.; et al. Magnetic OB[A] Stars with TESS: Probing their Evolutionary and Rotational properties (MOBSTER)—I. First-light observations of known magnetic B and A stars. Mon. Not. R. Astron. Soc. 2019, 487, 304–317. [Google Scholar] [CrossRef]
- Eikenberry, S.S.; Chojnowski, S.D.; Wisniewski, J.; Majewski, S.R.; Shetrone, M.; Whelan, D.G.; Bizyaev, D.; Borish, H.J.; Davenport, J.R.A.; Ebelke, G.; et al. Discovery of Two Rare Rigidly Rotating Magnetosphere Stars in the APOGEE Survey. Astrophys. J. Lett. 2014, 784, L30. [Google Scholar] [CrossRef]
- Oksala, M.E.; Grunhut, J.H.; Kraus, M.; Borges Fernandes, M.; Neiner, C.; Condori, C.A.H.; Campagnolo, J.C.N.; Souza, T.B. An infrared diagnostic for magnetism in hot stars. Astron. Astrophys. 2015, 578, A112. [Google Scholar] [CrossRef]
- Wisniewski, J.P.; Chojnowski, S.D.; Davenport, J.R.A.; Bartz, J.; Pepper, J.; Whelan, D.G.; Eikenberry, S.S.; Lomax, J.R.; Majewski, S.R.; Richardson, N.D.; et al. Characterizing the Rigidly Rotating Magnetosphere Stars HD 345439 and HD 23478. Astrophys. J. Lett. 2015, 811, L26. [Google Scholar] [CrossRef]
- Leto, P.; Trigilio, C.; Krtička, J.; Fossati, L.; Ignace, R.; Shultz, M.E.; Buemi, C.S.; Cerrigone, L.; Umana, G.; Ingallinera, A.; et al. A scaling relationship for non-thermal radio emission from ordered magnetospheres: From the top of the main sequence to planets. Mon. Not. R. Astron. Soc. 2021, 507, 1979–1998. [Google Scholar] [CrossRef]
- Das, B.; Chandra, P.; Shultz, M.E.; Leto, P.; Mikulášek, Z.; Petit, V.; Wade, G.A. Testing a scaling relation between coherent radio emission and physical parameters of hot magnetic stars. Mon. Not. R. Astron. Soc. 2022, 517, 5756–5769. [Google Scholar] [CrossRef]
- Erba, C.; Ignace, R. Radio Spectral Energy Distributions for Single Massive Star Winds with Free-Free and Synchrotron Emission. Astrophys. J. Lett. 2022, 932, 12. [Google Scholar] [CrossRef]
- Owocki, S.P.; Shultz, M.E.; ud-Doula, A.; Chandra, P.; Das, B.; Leto, P. Centrifugal breakout reconnection as the electron acceleration mechanism powering the radio magnetospheres of early-type stars. Mon. Not. R. Astron. Soc. 2022, 513, 1449–1458. [Google Scholar] [CrossRef]
- Shultz, M.E.; Owocki, S.P.; ud-Doula, A.; Biswas, A.; Bohlender, D.; Chandra, P.; Das, B.; David-Uraz, A.; Khalack, V.; Kochukhov, O.; et al. MOBSTER—VI. The crucial influence of rotation on the radio magnetospheres of hot stars. Mon. Not. R. Astron. Soc. 2022, 513, 1429–1448. [Google Scholar] [CrossRef]
- Morin, J.; Bouret, J.C.; Neiner, C.; Aerts, C.; Bagnulo, S.; Catala, C.; Charbonnel, C.; Evans, C.; Fossati, L.; Garcia, M.; et al. Stellar Physics with High-Resolution UV Spectropolarimetry. arXiv 2019, arXiv:1908.01545. [Google Scholar] [CrossRef]
- Shultz, M.E.; Casini, R.; Cheung, M.C.M.; David-Uraz, A.; del Pino Alemán, T.; Erba, C.; Folsom, C.P.; Gayley, K.; Ignace, R.; Keszthelyi, Z.; et al. Ultraviolet Spectropolarimetry with Polstar: Using Polstar to test Magnetospheric Mass-loss Quenching. Astrophys. Space Sci. 2022, 367, 120. [Google Scholar] [CrossRef]
- Folsom, C.P.; Ignace, R.; Erba, C.; Casini, R.; del Pino Alemán, T.; Gayley, K.; Hobbs, K.; Manso Sainz, R.; Neiner, C.; Petit, V.; et al. Ultraviolet Spectropolarimetry: Investigating stellar magnetic field diagnostics. Astrophys. Space Sci. 2022, 367, 125. [Google Scholar] [CrossRef]
- Bagnulo, S.; Nazé, Y.; Howarth, I.D.; Morrell, N.; Vink, J.S.; Wade, G.A.; Walborn, N.; Romaniello, M.; Barbá, R. First constraints on the magnetic field strength in extra-Galactic stars: FORS2 observations of Of?p stars in the Magellanic Clouds. Astron. Astrophys. 2017, 601, A136. [Google Scholar] [CrossRef]
- Bagnulo, S.; Wade, G.A.; Nazé, Y.; Grunhut, J.H.; Shultz, M.E.; Asher, D.J.; Crowther, P.A.; Evans, C.J.; David-Uraz, A.; Howarth, I.D.; et al. A search for strong magnetic fields in massive and very massive stars in the Magellanic Clouds. Astron. Astrophys. 2020, 635, A163. [Google Scholar] [CrossRef]
- Ferrario, L.; Wickramasinghe, D. Origin and evolution of magnetars. Mon. Not. R. Astron. Soc. 2008, 389, L66–L70. [Google Scholar] [CrossRef]
- Zhou, P.; Vink, J.; Safi-Harb, S.; Miceli, M. Spatially resolved X-ray study of supernova remnants that host magnetars: Implication of their fossil field origin. Astron. Astrophys. 2019, 629, A51. [Google Scholar] [CrossRef]
- Makarenko, E.I.; Igoshev, A.P.; Kholtygin, A.F. Testing the fossil field hypothesis: Could strongly magnetized OB stars produce all known magnetars? Mon. Not. R. Astron. Soc. 2021, 504, 5813–5828. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. Neutron Star Dynamos and the Origins of Pulsar Magnetism. Astrophys. J. Lett. 1993, 408, 194. [Google Scholar] [CrossRef]
- Masada, Y.; Takiwaki, T.; Kotake, K. Convection and Dynamo in Newly Born Neutron Stars. Astrophys. J. Lett. 2022, 924, 75. [Google Scholar] [CrossRef]
- Reboul-Salze, A.; Guilet, J.; Raynaud, R.; Bugli, M. A global model of the magnetorotational instability in protoneutron stars. Astron. Astrophys. 2021, 645, A109. [Google Scholar] [CrossRef]
- Aloy, M.Á.; Obergaulinger, M. Magnetorotational core collapse of possible GRB progenitors—II. Formation of protomagnetars and collapsars. Mon. Not. R. Astron. Soc. 2021, 500, 4365–4397. [Google Scholar] [CrossRef]
- Obergaulinger, M.; Aloy, M.Á. Magnetorotational core collapse of possible gamma-ray burst progenitors—IV. A wider range of progenitors. Mon. Not. R. Astron. Soc. 2022, 512, 2489–2507. [Google Scholar] [CrossRef]
- Reboul-Salze, A.; Guilet, J.; Raynaud, R.; Bugli, M. MRI-driven α − Ω dynamos in protoneutron stars. Astron. Astrophys. 2022, 667, A94. [Google Scholar] [CrossRef]
- Barrère, P.; Guilet, J.; Reboul-Salze, A.; Raynaud, R.; Janka, H.T. A new scenario for magnetar formation: Tayler-Spruit dynamo in a proto-neutron star spun up by fallback. arXiv 2022, arXiv:2206.01269. [Google Scholar] [CrossRef]
- Mestel, L. Stellar Magnetism; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 1999; ISBN 0198526725. [Google Scholar]
- Kulsrud, R.M. Plasma Physics for Astrophysics; Princeton University Press: Princeton, NJ, USA, 2005; ISBN 9780691120737. [Google Scholar]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 2005, 417, 1–209. [Google Scholar] [CrossRef]
- Goedbloed, J.P.; Keppens, R.; Poedts, S. Advanced Magnetohydrodynamics; Cambridge University Press: Cambridge, UK, 2010; ISBN 9781107123922. [Google Scholar]
- Walder, R.; Folini, D.; Meynet, G. Magnetic Fields in Massive Stars, Their Winds, and Their Nebulae. Space Sci. Rev. 2012, 166, 145–185. [Google Scholar] [CrossRef]
- Braithwaite, J.; Spruit, H.C. Magnetic fields in non-convective regions of stars. R. Soc. Open Sci. 2017, 4, 160271. [Google Scholar] [CrossRef] [PubMed]
- Augustson, K.C. Magnetism in Massive Stars. In Proceedings of the Stellar Magnetism: A Workshop in Honour of the Career and Contributions of John D. Landstreet, London, ON, Canada, 8–11 July 2019; Wade, G., Alecian, E., Bohlender, D., Sigut, A., Eds.; Polish Astronomical Society: Warzsawa, Poland, 2020; Volume 11, pp. 105–116. [Google Scholar]
- Braithwaite, J. On the magnetic flux problem in star formation. Mon. Not. R. Astron. Soc. 2012, 422, 619–628. [Google Scholar] [CrossRef]
- Braithwaite, J.; Nordlund, Å. Stable magnetic fields in stellar interiors. Astron. Astrophys. 2006, 450, 1077–1095. [Google Scholar] [CrossRef]
- Braithwaite, J. On non-axisymmetric magnetic equilibria in stars. Mon. Not. R. Astron. Soc. 2008, 386, 1947–1958. [Google Scholar] [CrossRef]
- Braithwaite, J. Axisymmetric magnetic fields in stars: Relative strengths of poloidal and toroidal components. Mon. Not. R. Astron. Soc. 2009, 397, 763–774. [Google Scholar] [CrossRef]
- Becerra, L.; Reisenegger, A.; Valdivia, J.A.; Gusakov, M. Stability of axially symmetric magnetic fields in stars. Mon. Not. R. Astron. Soc. 2022, 517, 560–568. [Google Scholar] [CrossRef]
- Becerra, L.; Reisenegger, A.; Valdivia, J.A.; Gusakov, M.E. Evolution of random initial magnetic fields in stably stratified and barotropic stars. Mon. Not. R. Astron. Soc. 2022, 511, 732–745. [Google Scholar] [CrossRef]
- Charbonneau, P.; MacGregor, K.B. Magnetic Fields in Massive Stars. I. Dynamo Models. Astrophys. J. Lett. 2001, 559, 1094–1107. [Google Scholar] [CrossRef]
- Vidal, J.; Cébron, D.; ud-Doula, A.; Alecian, E. Fossil field decay due to nonlinear tides in massive binaries. Astron. Astrophys. 2019, 629, A142. [Google Scholar] [CrossRef]
- Alfvén, H. Existence of Electromagnetic-Hydrodynamic Waves. Nature 1942, 150, 405–406. [Google Scholar] [CrossRef]
- Martin, A.J.; Neiner, C.; Oksala, M.E.; Wade, G.A.; Keszthelyi, Z.; Fossati, L.; Marcolino, W.; Mathis, S.; Georgy, C. First results from the LIFE project: Discovery of two magnetic hot evolved stars. Mon. Not. R. Astron. Soc. 2018, 475, 1521–1536. [Google Scholar] [CrossRef]
- Keszthelyi, Z.; Meynet, G.; Shultz, M.E.; David-Uraz, A.; ud-Doula, A.; Townsend, R.H.D.; Wade, G.A.; Georgy, C.; Petit, V.; Owocki, S.P. The effects of surface fossil magnetic fields on massive star evolution—II. Implementation of magnetic braking in MESA and implications for the evolution of surface rotation in OB stars. Mon. Not. R. Astron. Soc. 2020, 493, 518–535. [Google Scholar] [CrossRef]
- Keszthelyi, Z.; de Koter, A.; Götberg, Y.; Meynet, G.; Brands, S.A.; Petit, V.; Carrington, M.; David-Uraz, A.; Geen, S.T.; Georgy, C.; et al. The effects of surface fossil magnetic fields on massive star evolution: IV. Grids of models at Solar, LMC, and SMC metallicities. Mon. Not. R. Astron. Soc. 2022, 517, 2028–2055. [Google Scholar] [CrossRef]
- Landin, N.R.; Mendes, L.T.S.; Vaz, L.P.R.; Alencar, S.H.P. Rossby numbers of fully and partially convective stars. Mon. Not. R. Astron. Soc. 2023, 519, 5304–5314. [Google Scholar] [CrossRef]
- Tayler, R.J. The adiabatic stability of stars containing magnetic fields-I.Toroidal fields. Mon. Not. R. Astron. Soc. 1973, 161, 365. [Google Scholar] [CrossRef]
- Akgün, T.; Reisenegger, A.; Mastrano, A.; Marchant, P. Stability of magnetic fields in non-barotropic stars: An analytic treatment. Mon. Not. R. Astron. Soc. 2013, 433, 2445–2466. [Google Scholar] [CrossRef]
- Flowers, E.; Ruderman, M.A. Evolution of pulsar magnetic fields. Astrophys. J. Lett. 1977, 215, 302–310. [Google Scholar] [CrossRef]
- Markey, P.; Tayler, R.J. The adiabatic stability of stars containing magnetic fields. II. Poloidal fields. Mon. Not. R. Astron. Soc. 1973, 163, 77–91. [Google Scholar] [CrossRef]
- Wright, G.A.E. Pinch instabilities in magnetic stars. Mon. Not. R. Astron. Soc. 1973, 162, 339–358. [Google Scholar] [CrossRef]
- Prendergast, K.H. The Equilibrium of a Self-Gravitating Incompressible Fluid Sphere with a Magnetic Field. I. Astrophys. J. Lett. 1956, 123, 498. [Google Scholar] [CrossRef]
- Duez, V.; Mathis, S. Relaxed equilibrium configurations to model fossil fields. I. A first family. Astron. Astrophys. 2010, 517, A58. [Google Scholar] [CrossRef]
- Duez, V.; Braithwaite, J.; Mathis, S. On the Stability of Non-force-free Magnetic Equilibria in Stars. Astrophys. J. Lett. 2010, 724, L34–L38. [Google Scholar] [CrossRef]
- Yoshida, S.; Yoshida, S.; Eriguchi, Y. Twisted-Torus Equilibrium Structures of Magnetic Fields in Magnetized Stars. Astrophys. J. Lett. 2006, 651, 462–474. [Google Scholar] [CrossRef]
- Yoshida, S.; Eriguchi, Y. Equilibrium Configurations of Magnetized Rotating Polytropes: Effects of Strong Toroidal Magnetic Fields in Addition to Poloidal Magnetic Fields. Astrophys. J. Suppl. Ser. 2006, 164, 156–172. [Google Scholar] [CrossRef]
- Kaufman, E.; Lecoanet, D.; Anders, E.H.; Brown, B.P.; Burns, K.J.; Oishi, J.S.; Vasil, G.M. The stability of prendergast magnetic fields. Mon. Not. R. Astron. Soc. 2022, 517, 3332–3340. [Google Scholar] [CrossRef]
- Lander, S.K.; Jones, D.I. Are there any stable magnetic fields in barotropic stars? Mon. Not. R. Astron. Soc. 2012, 424, 482–494. [Google Scholar] [CrossRef]
- Armaza, C.; Reisenegger, A.; Valdivia, J.A. On Magnetic Equilibria in Barotropic Stars. Astrophys. J. Lett. 2015, 802, 121. [Google Scholar] [CrossRef]
- Mitchell, J.P.; Braithwaite, J.; Reisenegger, A.; Spruit, H.; Valdivia, J.A.; Langer, N. Instability of magnetic equilibria in barotropic stars. Mon. Not. R. Astron. Soc. 2015, 447, 1213–1223. [Google Scholar] [CrossRef]
- Stift, M.J.; Leone, F. Zeeman Doppler mapping revisited: Force-free fields, regularisation functions, and abundance maps. Astron. Astrophys. 2022, 659, A33. [Google Scholar] [CrossRef]
- Gough, D.O.; Tayler, R.J. The influence of a magnetic field on Schwarzschild’s criterion for convective instability in an ideally conducting fluid. Mon. Not. R. Astron. Soc. 1966, 133, 85. [Google Scholar] [CrossRef]
- Sundqvist, J.O. et al. [MiMeS Collaboration]. On magnetic inhibition of photospheric macroturbulence generated in the iron-bump opacity zone of O-stars. Mon. Not. R. Astron. Soc. 2013, 433, 2497–2501. [Google Scholar] [CrossRef]
- MacDonald, J.; Petit, V. Magnetic inhibition of convection in O-star envelopes. Mon. Not. R. Astron. Soc. 2019, 487, 3904–3913. [Google Scholar] [CrossRef]
- Lydon, T.J.; Sofia, S. A Method for Incorporating the Effects of Large-Scale Magnetic Fields in the Study of Stellar Structure and Variability. Astrophys. J. Suppl. Ser. 1995, 101, 357. [Google Scholar] [CrossRef]
- MacDonald, J.; Mullan, D.J. Magnetic Modeling of Inflated Low-mass Stars Using Interior Fields No Larger than ∼10 kG. Astrophys. J. Lett. 2017, 850, 58. [Google Scholar] [CrossRef]
- Weiss, N.O. The Expulsion of Magnetic Flux by Eddies. Proc. R. Soc. Lond. Ser. A 1966, 293, 310–328. [Google Scholar] [CrossRef]
- Spruit, H.C. Convective collapse of flux tubes. Sol. Phys. 1979, 61, 363–378. [Google Scholar] [CrossRef]
- Schüssler, M.; Knölker, M. Magneto-Convection. In Proceedings of the Magnetic Fields Across the Hertzsprung-Russell Diagram, Santiago, Chile, 15–19 January 2001; Mathys, G., Solanki, S.K., Wickramasinghe, D.T., Eds.; Astronomical Society of the Pacific Conference Series: San Francisco, CA, USA, 2001; Volume 248, p. 115. [Google Scholar]
- Spruit, H.C. Differential rotation and magnetic fields in stellar interiors. Astron. Astrophys. 1999, 349, 189–202. [Google Scholar]
- Ferraro, V.C.A. The non-uniform rotation of the Sun and its magnetic field. Mon. Not. R. Astron. Soc. 1937, 97, 458. [Google Scholar] [CrossRef]
- Woltjer, L. Hydromagnetic Equilibrium IV. Axisymmetric Compressible Media. Astrophys. J. Lett. 1959, 130, 405. [Google Scholar] [CrossRef]
- Rüdiger, G.; Gellert, M.; Spada, F.; Tereshin, I. The angular momentum transport by unstable toroidal magnetic fields. Astron. Astrophys. 2015, 573, A80. [Google Scholar] [CrossRef]
- Fuller, J.; Piro, A.L.; Jermyn, A.S. Slowing the spins of stellar cores. Mon. Not. R. Astron. Soc. 2019, 485, 3661–3680. [Google Scholar] [CrossRef]
- Schneider, F.R.N.; Ohlmann, S.T.; Podsiadlowski, P.; Röpke, F.K.; Balbus, S.A.; Pakmor, R.; Springel, V. Stellar mergers as the origin of magnetic massive stars. Nature 2019, 574, 211–214. [Google Scholar] [CrossRef]
- Aerts, C.; Mathis, S.; Rogers, T.M. Angular Momentum Transport in Stellar Interiors. Annu. Rev. Astron. Astrophys. 2019, 57, 35–78. [Google Scholar] [CrossRef]
- Potter, A.T.; Chitre, S.M.; Tout, C.A. Stellar evolution of massive stars with a radiative α-Ω dynamo. Mon. Not. R. Astron. Soc. 2012, 424, 2358–2370. [Google Scholar] [CrossRef]
- Mathis, S.; de Brye, N. Low-frequency internal waves in magnetized rotating stellar radiation zones. II. Angular momentum transport with a toroidal field. Astron. Astrophys. 2012, 540, A37. [Google Scholar] [CrossRef]
- Fuller, J.; Cantiello, M.; Stello, D.; Garcia, R.A.; Bildsten, L. Asteroseismology can reveal strong internal magnetic fields in red giant stars. Science 2015, 350, 423–426. [Google Scholar] [CrossRef] [PubMed]
- Lecoanet, D.; Bowman, D.M.; Van Reeth, T. Asteroseismic inference of the near-core magnetic field strength in the main sequence B star HD 43317. arXiv 2022, arXiv:2202.03440. [Google Scholar] [CrossRef]
- Weber, E.J.; Davis, L., Jr. The Angular Momentum of the Solar Wind. Astrophys. J. Lett. 1967, 148, 217–227. [Google Scholar] [CrossRef]
- Mestel, L. Magnetic braking by a stellar wind-I. Mon. Not. R. Astron. Soc. 1968, 138, 359. [Google Scholar] [CrossRef]
- Parker, E.N. Interplanetary Dynamical Processes; Interscience Publishers: New York, NY, USA, 1963. [Google Scholar]
- ud-Doula, A.; Owocki, S.P.; Townsend, R.H.D. Dynamical simulations of magnetically channelled line-driven stellar winds—II. The effects of field-aligned rotation. Mon. Not. R. Astron. Soc. 2008, 385, 97–108. [Google Scholar] [CrossRef]
- ud-Doula, A.; Owocki, S.P.; Townsend, R.H.D. Dynamical simulations of magnetically channelled line-driven stellar winds—III. Angular momentum loss and rotational spin-down. Mon. Not. R. Astron. Soc. 2009, 392, 1022–1033. [Google Scholar] [CrossRef]
- ud-Doula, A.; Owocki, S.P.; Russell, C.; Gagné, M.; Daley-Yates, S. 3D MHD models of the centrifugal magnetosphere from a massive star with an oblique dipole field. Mon. Not. R. Astron. Soc. 2023, 520, 3947–3954. [Google Scholar] [CrossRef]
- MacGregor, K.B.; Cassinelli, J.P. Magnetic Fields in Massive Stars. II. The Buoyant Rise of Magnetic Flux Tubes through the Radiative Interior. Astrophys. J. Lett. 2003, 586, 480–494. [Google Scholar] [CrossRef]
- MacDonald, J.; Mullan, D.J. Magnetic fields in massive stars: Dynamics and origin. Mon. Not. R. Astron. Soc. 2004, 348, 702–716. [Google Scholar] [CrossRef]
- Brun, A.S.; Browning, M.K.; Toomre, J. Simulations of Core Convection in Rotating A-Type Stars: Magnetic Dynamo Action. Astrophys. J. Lett. 2005, 629, 461–481. [Google Scholar] [CrossRef]
- Featherstone, N.A.; Browning, M.K.; Brun, A.S.; Toomre, J. Effects of Fossil Magnetic Fields on Convective Core Dynamos in A-type Stars. Astrophys. J. Lett. 2009, 705, 1000–1018. [Google Scholar] [CrossRef]
- Augustson, K.C.; Brun, A.S.; Toomre, J. The Magnetic Furnace: Intense Core Dynamos in B Stars. Astrophys. J. Lett. 2016, 829, 92. [Google Scholar] [CrossRef]
- Varma, V.; Müller, B. 3D simulations of oxygen shell burning with and without magnetic fields. Mon. Not. R. Astron. Soc. 2021, 504, 636–647. [Google Scholar] [CrossRef]
- Meakin, C.A.; Arnett, D. Active Carbon and Oxygen Shell Burning Hydrodynamics. Astrophys. J. Lett. 2006, 637, L53–L56. [Google Scholar] [CrossRef]
- Müller, B.; Viallet, M.; Heger, A.; Janka, H.T. The Last Minutes of Oxygen Shell Burning in a Massive Star. Astrophys. J. Lett. 2016, 833, 124. [Google Scholar] [CrossRef]
- Yoshida, T.; Takiwaki, T.; Kotake, K.; Takahashi, K.; Nakamura, K.; Umeda, H. One-, Two-, and Three-dimensional Simulations of Oxygen-shell Burning Just before the Core Collapse of Massive Stars. Astrophys. J. Lett. 2019, 881, 16. [Google Scholar] [CrossRef]
- McNeill, L.O.; Müller, B. Differential rotation in a 3D simulation of oxygen shell burning. Mon. Not. R. Astron. Soc. 2022, 509, 818–830. [Google Scholar] [CrossRef]
- Pitts, E.; Tayler, R.J. The adiabatic stability of stars containing magnetic fields. IV—The influence of rotation. Mon. Not. R. Astron. Soc. 1985, 216, 139–154. [Google Scholar] [CrossRef]
- Goldstein, J.; Townsend, R.H.D.; Zweibel, E.G. The Tayler Instability in the Anelastic Approximation. Astrophys. J. Lett. 2019, 881, 66. [Google Scholar] [CrossRef]
- Ji, S.; Fuller, J.; Lecoanet, D. Magnetohydrodynamic Simulations of the Tayler Instability in Rotating Stellar Interiors. arXiv 2022, arXiv:2209.08104. [Google Scholar]
- Zahn, J.P.; Brun, A.S.; Mathis, S. On magnetic instabilities and dynamo action in stellar radiation zones. Astron. Astrophys. 2007, 474, 145–154. [Google Scholar] [CrossRef]
- Denissenkov, P.A.; Pinsonneault, M. A Revised Prescription for the Tayler-Spruit Dynamo: Magnetic Angular Momentum Transport in Stars. Astrophys. J. Lett. 2007, 655, 1157–1165. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A Powerful Local Shear Instability in Weakly Magnetized Disks. I. Linear Analysis. Astrophys. J. Lett. 1991, 376, 214. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Stability of Non-Dissipative Couette Flow in Hydromagnetics. Proc. Natl. Acad. Sci. USA 1960, 46, 253–257. [Google Scholar] [CrossRef] [PubMed]
- Masada, Y.; Takiwaki, T.; Kotake, K.; Sano, T. Local Simulations of the Magnetorotational Instability in Core-collapse Supernovae. Astrophys. J. Lett. 2012, 759, 110. [Google Scholar] [CrossRef]
- Reichert, M.; Obergaulinger, M.; Aloy, M.A.; Gabler, M.; Arcones, A.; Thielemann, F.K. Magnetorotational supernovae: A nucleosynthetic analysis of sophisticated 3D models. arXiv 2022, arXiv:2206.11914. [Google Scholar] [CrossRef]
- Wheeler, J.C.; Kagan, D.; Chatzopoulos, E. The Role of the Magnetorotational Instability in Massive Stars. Astrophys. J. Lett. 2015, 799, 85. [Google Scholar] [CrossRef]
- Jouve, L.; Gastine, T.; Lignières, F. Three-dimensional evolution of magnetic fields in a differentially rotating stellar radiative zone. Astron. Astrophys. 2015, 575, A106. [Google Scholar] [CrossRef]
- Jouve, L.; Lignières, F.; Gaurat, M. Interplay between magnetic fields and differential rotation in a stably stratified stellar radiative zone. Astron. Astrophys. 2020, 641, A13. [Google Scholar] [CrossRef]
- Griffiths, A.; Eggenberger, P.; Meynet, G.; Moyano, F.; Aloy, M.Á. The magneto-rotational instability in massive stars. Astron. Astrophys. 2022, 665, A147. [Google Scholar] [CrossRef]
- Quentin, L.G.; Tout, C.A. Rotation and magnetism in intermediate-mass stars. Mon. Not. R. Astron. Soc. 2018, 477, 2298–2309. [Google Scholar] [CrossRef]
- Kissin, Y.; Thompson, C. Rotation and Magnetism of Massive Stellar Cores. Astrophys. J. Lett. 2018, 862, 111. [Google Scholar] [CrossRef]
- Takahashi, K.; Langer, N. Modeling of magneto-rotational stellar evolution. I. Method and first applications. Astron. Astrophys. 2021, 646, A19. [Google Scholar] [CrossRef]
- Petitdemange, L.; Marcotte, F.; Gissinger, C. Hidden dynamo spins down radiative stars. arXiv 2022, arXiv:2206.13819. [Google Scholar]
- Skoutnev, V.; Squire, J.; Bhattacharjee, A. On large-scale dynamos with stable stratification and the application to stellar radiative zones. Mon. Not. R. Astron. Soc. 2022, 517, 526–542. [Google Scholar] [CrossRef]
- Maeder, A.; Meynet, G. Stellar evolution with rotation and magnetic fields. II. General equations for the transport by Tayler-Spruit dynamo. Astron. Astrophys. 2004, 422, 225–237. [Google Scholar] [CrossRef]
- Bowman, D.M.; Burssens, S.; Simón-Díaz, S.; Edelmann, P.V.F.; Rogers, T.M.; Horst, L.; Röpke, F.K.; Aerts, C. Photometric detection of internal gravity waves in upper main-sequence stars. II. Combined TESS photometry and high-resolution spectroscopy. Astron. Astrophys. 2020, 640, A36. [Google Scholar] [CrossRef]
- Burssens, S.; Simón-Díaz, S.; Bowman, D.M.; Holgado, G.; Michielsen, M.; de Burgos, A.; Castro, N.; Barbá, R.H.; Aerts, C. Variability of OB stars from TESS southern Sectors 1–13 and high-resolution IACOB and OWN spectroscopy. Astron. Astrophys. 2020, 639, A81. [Google Scholar] [CrossRef]
- Van Beeck, J.; Prat, V.; Van Reeth, T.; Mathis, S.; Bowman, D.M.; Neiner, C.; Aerts, C. Detecting axisymmetric magnetic fields using gravity modes in intermediate-mass stars. Astron. Astrophys. 2020, 638, A149. [Google Scholar] [CrossRef]
- Dhouib, H.; Mathis, S.; Bugnet, L.; Van Reeth, T.; Aerts, C. Detecting deep axisymmetric toroidal magnetic fields in stars. The traditional approximation of rotation for differentially rotating deep spherical shells with a general azimuthal magnetic field. Astron. Astrophys. 2022, 661, A133. [Google Scholar] [CrossRef]
- Petermann, I.; Langer, N.; Castro, N.; Fossati, L. Blue supergiants as descendants of magnetic main sequence stars. Astron. Astrophys. 2015, 584, A54. [Google Scholar] [CrossRef]
- Cantiello, M.; Langer, N.; Brott, I.; de Koter, A.; Shore, S.N.; Vink, J.S.; Voegler, A.; Lennon, D.J.; Yoon, S.C. Sub-surface convection zones in hot massive stars and their observable consequences. Astron. Astrophys. 2009, 499, 279–290. [Google Scholar] [CrossRef]
- Simón-Díaz, S.; Godart, M.; Castro, N.; Herrero, A.; Aerts, C.; Puls, J.; Telting, J.; Grassitelli, L. The IACOB project. III. New observational clues to understand macroturbulent broadening in massive O- and B-type stars. Astron. Astrophys. 2017, 597, A22. [Google Scholar] [CrossRef]
- Aerts, C.; Puls, J.; Godart, M.; Dupret, M.A. Collective pulsational velocity broadening due to gravity modes as a physical explanation for macroturbulence in hot massive stars. Astron. Astrophys. 2009, 508, 409–419. [Google Scholar] [CrossRef]
- Oksala, M.E.; Wade, G.A.; Townsend, R.H.D.; Owocki, S.P.; Kochukhov, O.; Neiner, C.; Alecian, E.; Grunhut, J. Revisiting the Rigidly Rotating Magnetosphere model for σ Ori E—I. Observations and data analysis. Mon. Not. R. Astron. Soc. 2012, 419, 959–970. [Google Scholar] [CrossRef]
- Townsend, R.H.D.; Oksala, M.E.; Cohen, D.H.; Owocki, S.P.; ud-Doula, A. Discovery of Rotational Braking in the Magnetic Helium-strong Star Sigma Orionis E. Astrophys. J. Lett. 2010, 714, L318–L322. [Google Scholar] [CrossRef]
- Mikulášek, Z.; Krtička, J.; Henry, G.W.; Janík, J.; Zverko, J.; Žižňovský, J.; Zejda, M.; Liška, J.; Zvěřina, P.; Kudrjavtsev, D.O.; et al. Surprising variations in the rotation of the chemically peculiar stars CU Virginis and V901 Orionis. Astron. Astrophys. 2011, 534, L5. [Google Scholar] [CrossRef]
- Meynet, G.; Eggenberger, P.; Maeder, A. Massive star models with magnetic braking. Astron. Astrophys. 2011, 525, L11. [Google Scholar] [CrossRef]
- Keszthelyi, Z.; Meynet, G.; Georgy, C.; Wade, G.A.; Petit, V.; David-Uraz, A. The effects of surface fossil magnetic fields on massive star evolution: I. Magnetic field evolution, mass-loss quenching, and magnetic braking. Mon. Not. R. Astron. Soc. 2019, 485, 5843–5860. [Google Scholar] [CrossRef]
- Aerts, C.; Molenberghs, G.; Kenward, M.G.; Neiner, C. The Surface Nitrogen Abundance of a Massive Star in Relation to its Oscillations, Rotation, and Magnetic Field. Astrophys. J. Lett. 2014, 781, 88. [Google Scholar] [CrossRef]
- Martins, F. et al. [Mimes Collaboration]. Observational effects of magnetism in O stars: Surface nitrogen abundances. Astron. Astrophys. 2012, 538, A29. [Google Scholar] [CrossRef]
- Martins, F.; Hervé, A.; Bouret, J.C.; Marcolino, W.; Wade, G.A.; Neiner, C.; Alecian, E.; Grunhut, J.; Petit, V. The MiMeS survey of magnetism in massive stars: CNO surface abundances of Galactic O stars. Astron. Astrophys. 2015, 575, A34. [Google Scholar] [CrossRef]
- Lennon, D.J.; Dufton, P.L.; Crowley, C. More nitrogen rich B-type stars in the SMC cluster, NGC 330. Astron. Astrophys. 2003, 398, 455–466. [Google Scholar] [CrossRef]
- Ramírez-Agudelo, O.H.; Sana, H.; de Mink, S.E.; Hénault-Brunet, V.; de Koter, A.; Langer, N.; Tramper, F.; Gräfener, G.; Evans, C.J.; Vink, J.S.; et al. The VLT-FLAMES Tarantula Survey. XXI. Stellar spin rates of O-type spectroscopic binaries. Astron. Astrophys. 2015, 580, A92. [Google Scholar] [CrossRef]
- Dufton, P.L.; Thompson, A.; Crowther, P.A.; Evans, C.J.; Schneider, F.R.N.; de Koter, A.; de Mink, S.E.; Garland, R.; Langer, N.; Lennon, D.J.; et al. The VLT-FLAMES Tarantula Survey. XXVIII. Nitrogen abundances for apparently single dwarf and giant B-type stars with small projected rotational velocities. Astron. Astrophys. 2018, 615, A101. [Google Scholar] [CrossRef]
- Dufton, P.L.; Evans, C.J.; Lennon, D.J.; Hunter, I. The NGC 346 massive star census. Nitrogen abundances for apparently single, narrow lined, hydrogen core burning B-type stars. Astron. Astrophys. 2020, 634, A6. [Google Scholar] [CrossRef]
- Owocki, S.P.; ud-Doula, A. The Effect of Magnetic Field Tilt and Divergence on the Mass Flux and Flow Speed in a Line-driven Stellar Wind. Astrophys. J. Lett. 2004, 600, 1004–1015. [Google Scholar] [CrossRef]
- Owocki, S.P.; ud-Doula, A.; Sundqvist, J.O.; Petit, V.; Cohen, D.H.; Townsend, R.H.D. An ‘analytic dynamical magnetosphere’ formalism for X-ray and optical emission from slowly rotating magnetic massive stars. Mon. Not. R. Astron. Soc. 2016, 462, 3830–3844. [Google Scholar] [CrossRef]
- Townsend, R.H.D.; Owocki, S.P. A rigidly rotating magnetosphere model for circumstellar emission from magnetic OB stars. Mon. Not. R. Astron. Soc. 2005, 357, 251–264. [Google Scholar] [CrossRef]
- Bard, C.; Townsend, R.H.D. Effect of a magnetic field on massive-star winds—I. Mass-loss and velocity for a dipole field. Mon. Not. R. Astron. Soc. 2016, 462, 3672–3688. [Google Scholar] [CrossRef]
- Shultz, M.E. et al. [MiMeS and BinaMIcS Collaboration]. The magnetic early B-type stars—IV. Breakout or leakage? H α emission as a diagnostic of plasma transport in centrifugal magnetospheres. Mon. Not. R. Astron. Soc. 2020, 499, 5379–5395. [Google Scholar] [CrossRef]
- Owocki, S.P.; Shultz, M.E.; ud-Doula, A.; Sundqvist, J.O.; Townsend, R.H.D.; Cranmer, S.R. How the breakout-limited mass in B-star centrifugal magnetospheres controls their circumstellar H α emission. Mon. Not. R. Astron. Soc. 2020, 499, 5366–5378. [Google Scholar] [CrossRef]
- Driessen, F.A.; Sundqvist, J.O.; Wade, G.A. First empirical constraints on the low Hα mass-loss rates of magnetic O-stars. IAU Symp. 2019, 346, 45–48. [Google Scholar] [CrossRef]
- Keszthelyi, Z.; Wade, G.A.; Petit, V. The evolution of magnetic hot massive stars: Implementation of the quantitative influence of surface magnetic fields in modern models of stellar evolution. Proc. Int. Astron. Union 2016, 12, 250–254. [Google Scholar] [CrossRef]
- Keszthelyi, Z. The Role of Surface Fossil Magnetic Fields in Massive Star Evolution. Ph.D. Thesis, Queens University, Kingston, ON, Canada, 2019. Available online: http://hdl.handle.net/1974/26465 (accessed on 28 February 2023).
- Deal, M.; Cunha, M.S.; Keszthelyi, Z.; Perraut, K.; Holdsworth, D.L. Fundamental properties of a selected sample of Ap stars: Inferences from interferometric and asteroseismic constraints. Astron. Astrophys. 2021, 650, A125. [Google Scholar] [CrossRef]
- Petit, V.; Keszthelyi, Z.; MacInnis, R.; Cohen, D.H.; Townsend, R.H.D.; Wade, G.A.; Thomas, S.L.; Owocki, S.P.; Puls, J.; ud-Doula, A. Magnetic massive stars as progenitors of ‘heavy’ stellar-mass black holes. Mon. Not. R. Astron. Soc. 2017, 466, 1052–1060. [Google Scholar] [CrossRef]
- Georgy, C.; Meynet, G.; Ekström, S.; Wade, G.A.; Petit, V.; Keszthelyi, Z.; Hirschi, R. Possible pair-instability supernovae at solar metallicity from magnetic stellar progenitors. Astron. Astrophys. 2017, 599, L5. [Google Scholar] [CrossRef]
- Groh, J.H.; Farrell, E.J.; Meynet, G.; Smith, N.; Murphy, L.; Allan, A.P.; Georgy, C.; Ekstroem, S. Massive Black Holes Regulated by Luminous Blue Variable Mass Loss and Magnetic Fields. Astrophys. J. Lett. 2020, 900, 98. [Google Scholar] [CrossRef]
- Castor, J.I.; Abbott, D.C.; Klein, R.I. Radiation-driven winds in Of stars. Astrophys. J. Lett. 1975, 195, 157–174. [Google Scholar] [CrossRef]
- Pauldrach, A.; Puls, J.; Kudritzki, R.P. Radiation-driven winds of hot luminous stars. Improvements of the theory and first results. Astron. Astrophys. 1986, 164, 86–100. [Google Scholar]
- Vink, J.S.; de Koter, A.; Lamers, H.J.G.L.M. Mass-loss predictions for O and B stars as a function of metallicity. Astron. Astrophys. 2001, 369, 574–588. [Google Scholar] [CrossRef]
- Puls, J.; Vink, J.S.; Najarro, F. Mass loss from hot massive stars. Astron. Astrophys. Rev. 2008, 16, 209–325. [Google Scholar] [CrossRef]
- Mokiem, M.R.; de Koter, A.; Vink, J.S.; Puls, J.; Evans, C.J.; Smartt, S.J.; Crowther, P.A.; Herrero, A.; Langer, N.; Lennon, D.J.; et al. The empirical metallicity dependence of the mass-loss rate of O- and early B-type stars. Astron. Astrophys. 2007, 473, 603–614. [Google Scholar] [CrossRef]
- Sander, A.A.C.; Vink, J.S.; Hamann, W.R. Driving classical Wolf–Rayet winds: A Γ- and Z-dependent mass-loss. Mon. Not. R. Astron. Soc. 2020, 491, 4406–4425. [Google Scholar] [CrossRef]
- Sander, A.A.C.; Vink, J.S. On the nature of massive helium star winds and Wolf–Rayet-type mass-loss. Mon. Not. R. Astron. Soc. 2020, 499, 873–892. [Google Scholar] [CrossRef]
- Higgins, E.R.; Sander, A.A.C.; Vink, J.S.; Hirschi, R. Evolution of Wolf–Rayet stars as black hole progenitors. Mon. Not. R. Astron. Soc. 2021, 505, 4874–4889. [Google Scholar] [CrossRef]
- Pauldrach, A.W.A.; Vanbeveren, D.; Hoffmann, T.L. Radiation-driven winds of hot luminous stars XVI. Expanding atmospheres of massive and very massive stars and the evolution of dense stellar clusters. Astron. Astrophys. 2012, 538, A75. [Google Scholar] [CrossRef]
- Hirai, R.; Podsiadlowski, P.; Owocki, S.P.; Schneider, F.R.N.; Smith, N. Simulating the formation of η Carinae’s surrounding nebula through unstable triple evolution and stellar merger-induced eruption. Mon. Not. R. Astron. Soc. 2021, 503, 4276–4296. [Google Scholar] [CrossRef]
- Vigna-Gómez, A.; Liu, B.; Aguilera-Dena, D.R.; Grishin, E.; Ramirez-Ruiz, E.; Soares-Furtado, M. Mergers prompted by dynamics in compact, multiple-star systems: A stellar-reduction case for the massive triple TIC 470710327. Mon. Not. R. Astron. Soc. 2022, 515, L50–L55. [Google Scholar] [CrossRef]
- Ferrario, L.; Pringle, J.E.; Tout, C.A.; Wickramasinghe, D.T. The origin of magnetism on the upper main sequence. Mon. Not. R. Astron. Soc. 2009, 400, L71–L74. [Google Scholar] [CrossRef]
- Wickramasinghe, D.T.; Tout, C.A.; Ferrario, L. The most magnetic stars. Mon. Not. R. Astron. Soc. 2014, 437, 675–681. [Google Scholar] [CrossRef]
- Schneider, F.R.N.; Podsiadlowski, P.; Langer, N.; Castro, N.; Fossati, L. Rejuvenation of stellar mergers and the origin of magnetic fields in massive stars. Mon. Not. R. Astron. Soc. 2016, 457, 2355–2365. [Google Scholar] [CrossRef]
- Schneider, F.R.N.; Ohlmann, S.T.; Podsiadlowski, P.; Röpke, F.K.; Balbus, S.A.; Pakmor, R. Long-term evolution of a magnetic massive merger product. Mon. Not. R. Astron. Soc. 2020, 495, 2796–2812. [Google Scholar] [CrossRef]
- Caiazzo, I.; Burdge, K.B.; Fuller, J.; Heyl, J.; Kulkarni, S.R.; Prince, T.A.; Richer, H.B.; Schwab, J.; Andreoni, I.; Bellm, E.C.; et al. A highly magnetized and rapidly rotating white dwarf as small as the Moon. Nature 2021, 595, 39–42. [Google Scholar] [CrossRef]
- Keszthelyi, Z.; Meynet, G.; Martins, F.; de Koter, A.; David-Uraz, A. The effects of surface fossil magnetic fields on massive star evolution—III. The case of τ Sco. Mon. Not. R. Astron. Soc. 2021, 504, 2474–2492. [Google Scholar] [CrossRef]
- Shultz, M.E.; Johnston, C.; Labadie-Bartz, J.; Petit, V.; David-Uraz, A.; Kochukhov, O.; Wade, G.A.; Pepper, J.; Stassun, K.G.; Rodriguez, J.E.; et al. MOBSTER—III. HD 62658: A magnetic Bp star in an eclipsing binary with a non-magnetic ‘identical twin’. Mon. Not. R. Astron. Soc. 2019, 490, 4154–4165. [Google Scholar] [CrossRef]
- Shultz, M. et al. [BinaMIcS Collaboration]. Detection of magnetic fields in both B-type components of the ϵ Lupi system: A new constraint on the origin of fossil fields? Mon. Not. R. Astron. Soc. 2015, 454, L1–L5. [Google Scholar] [CrossRef]
- Moe, M.; Di Stefano, R. Mind Your Ps and Qs: The Interrelation between Period (P) and Mass-ratio (Q) Distributions of Binary Stars. Astrophys. J. Suppl. Ser. 2017, 230, 15. [Google Scholar] [CrossRef]
- de Mink, S.E.; Langer, N.; Izzard, R.G.; Sana, H.; de Koter, A. The Rotation Rates of Massive Stars: The Role of Binary Interaction through Tides, Mass Transfer, and Mergers. Astrophys. J. Lett. 2013, 764, 166. [Google Scholar] [CrossRef]
- Mathys, G. A search for magnetic fields in blue stragglers of M67. Messenger 1988, 53, 39–42. [Google Scholar]
- Freytag, B.; Steffen, M.; Dorch, B. Spots on the surface of Betelgeuse—Results from new 3D stellar convection models. Astron. Nachrichten 2002, 323, 213–219. [Google Scholar] [CrossRef]
- Tessore, B.; Lèbre, A.; Morin, J.; Mathias, P.; Josselin, E.; Aurière, M. Measuring surface magnetic fields of red supergiant stars. Astron. Astrophys. 2017, 603, A129. [Google Scholar] [CrossRef]
- Keszthelyi, Z. Reproduction package for the paper “The effects of surface fossil magnetic fields on massive star evolution: IV. Grids of models at Solar, LMC, and SMC metallicities”. Zenodo 2022, 7069766. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keszthelyi, Z. Magnetism in High-Mass Stars. Galaxies 2023, 11, 40. https://doi.org/10.3390/galaxies11020040
Keszthelyi Z. Magnetism in High-Mass Stars. Galaxies. 2023; 11(2):40. https://doi.org/10.3390/galaxies11020040
Chicago/Turabian StyleKeszthelyi, Zsolt. 2023. "Magnetism in High-Mass Stars" Galaxies 11, no. 2: 40. https://doi.org/10.3390/galaxies11020040
APA StyleKeszthelyi, Z. (2023). Magnetism in High-Mass Stars. Galaxies, 11(2), 40. https://doi.org/10.3390/galaxies11020040






