Hydrodynamic Simulations of a Relativistic Jet Interacting with the Intracluster Medium: Application to Cygnus A
Abstract
1. Introduction
2. Methods
2.1. Physics
2.2. Code
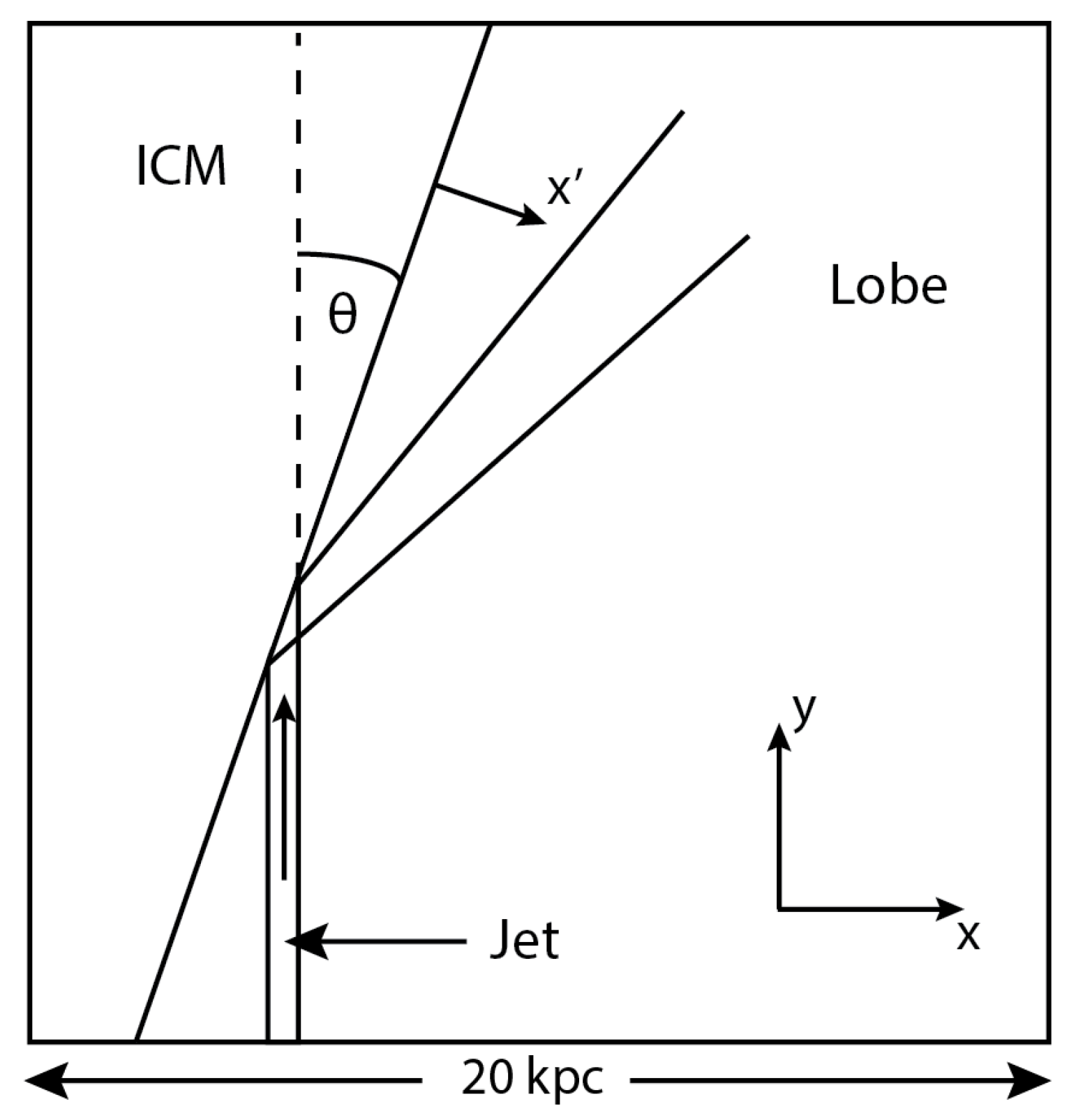
2.3. Simulation Setup
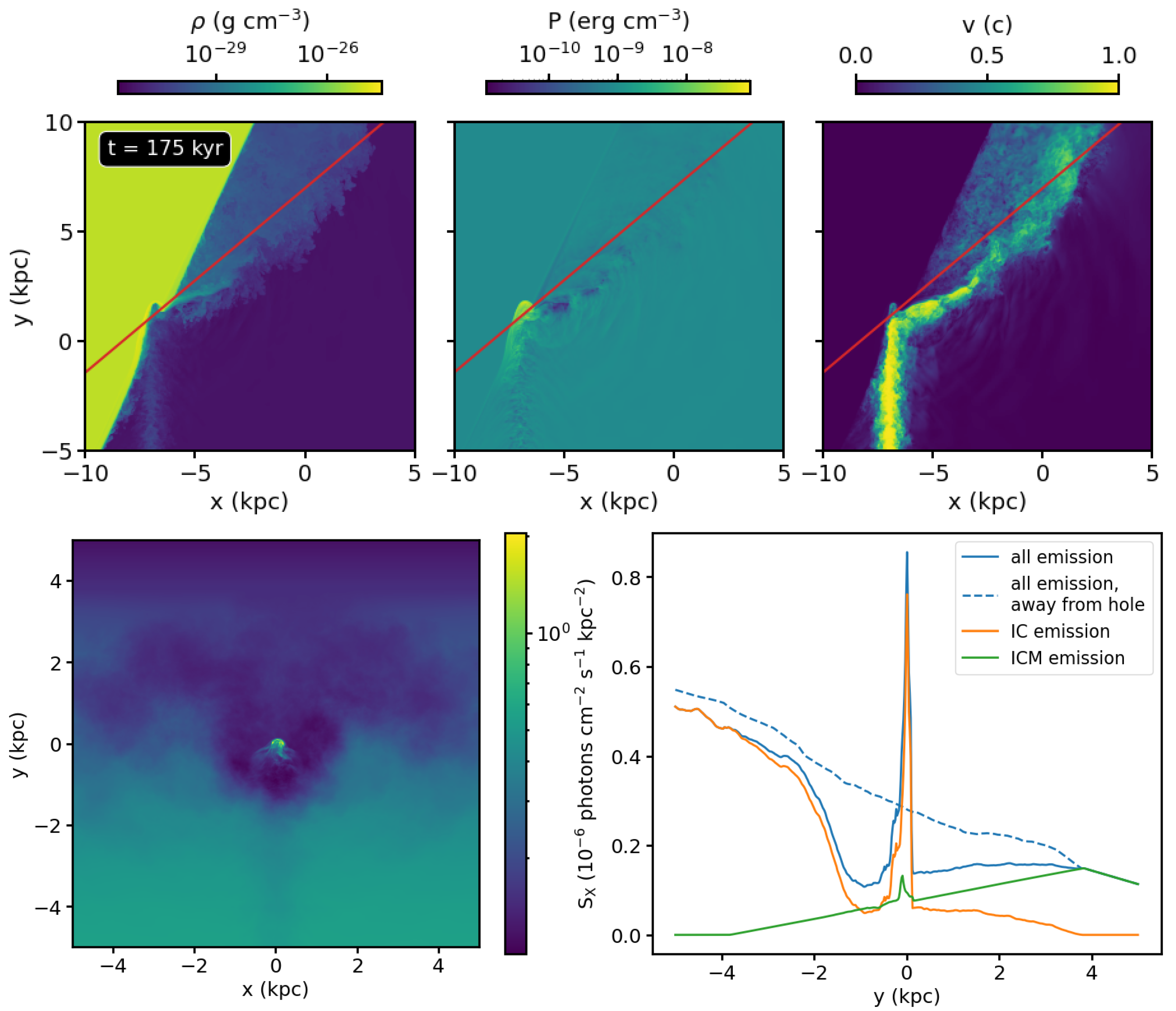
3. Results
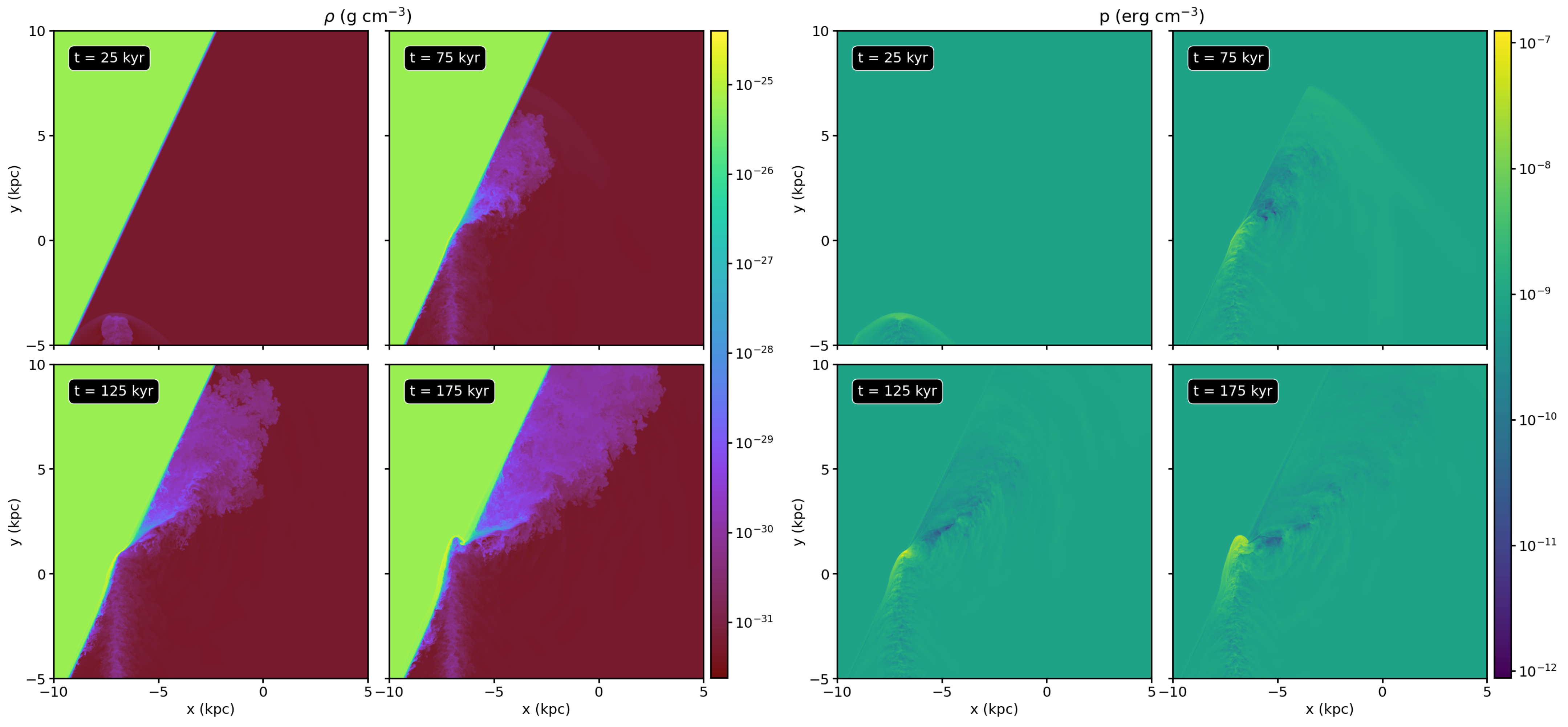
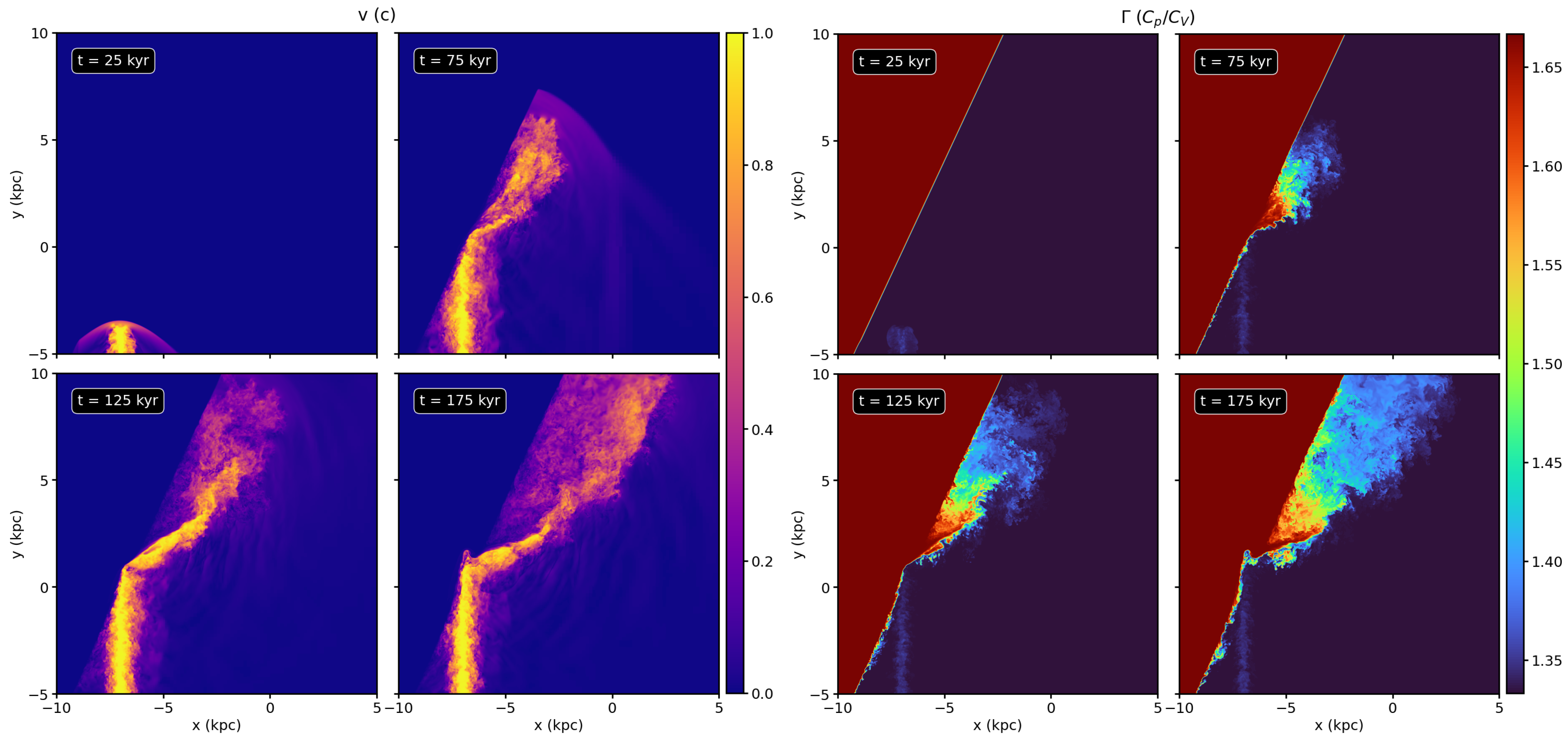
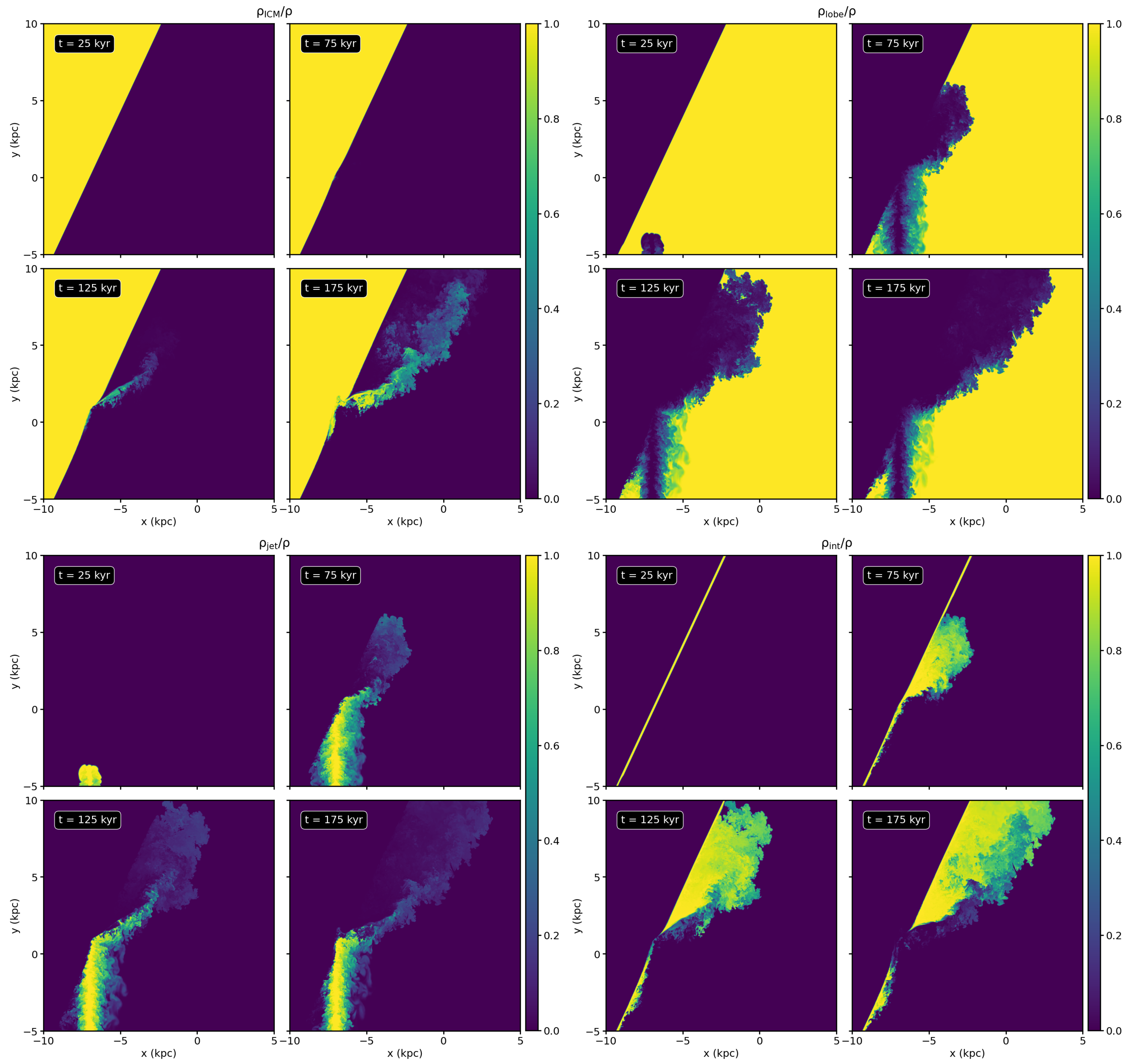
3.1. Fiducial Run: Slices
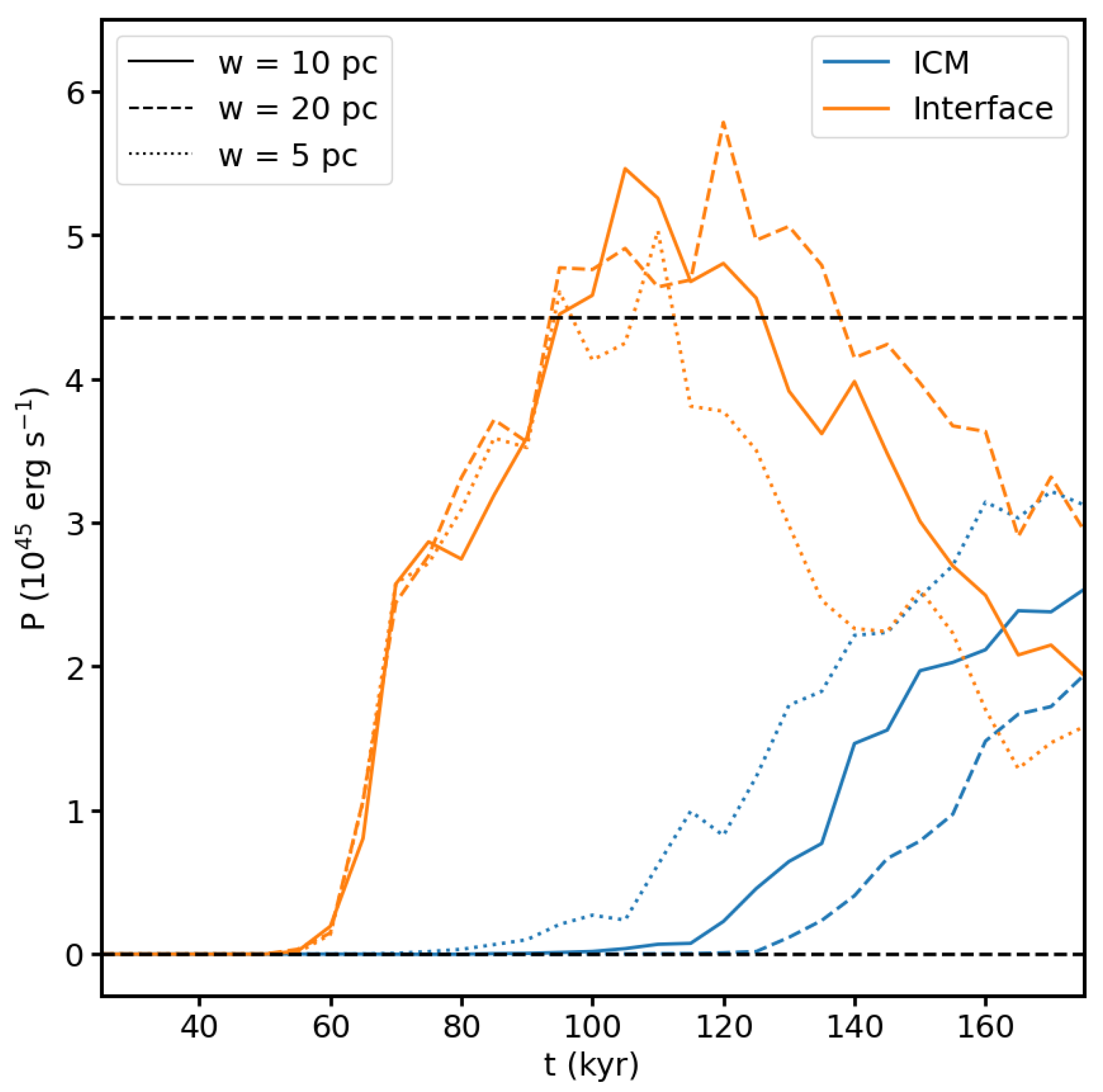
3.2. Fiducial Run: Jet Power
3.3. Varying the Width of the Interface
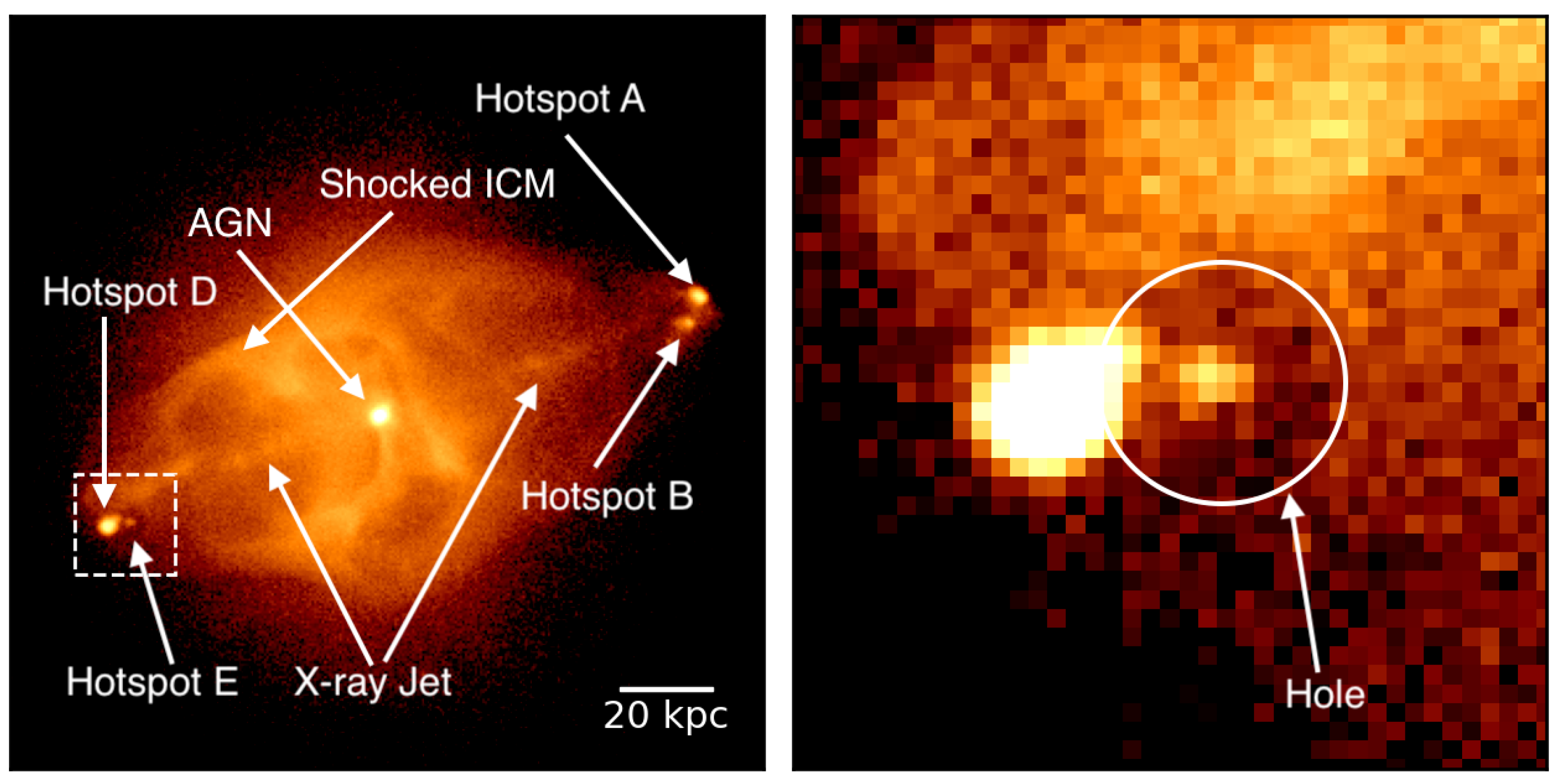
3.4. Carving a Hole: Projected X-ray Emission
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
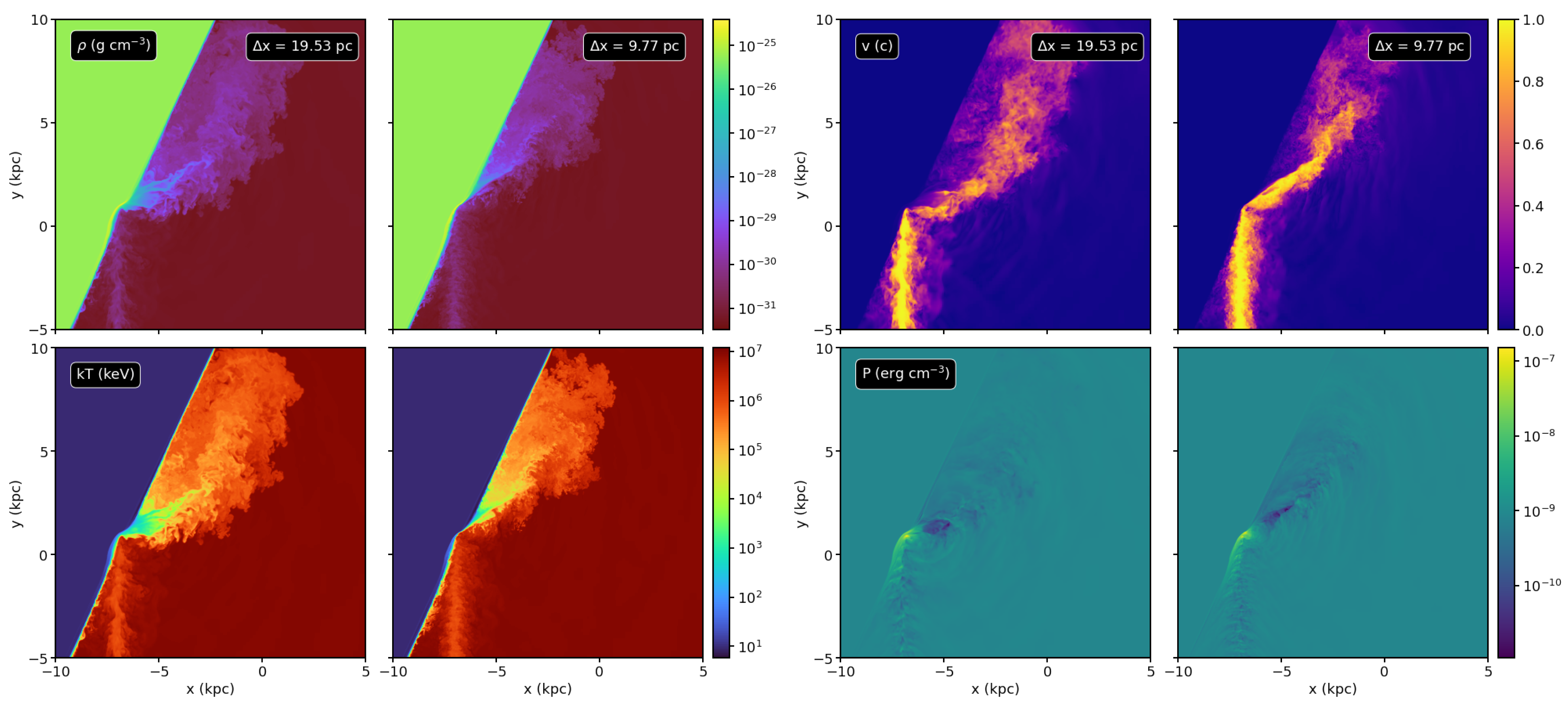
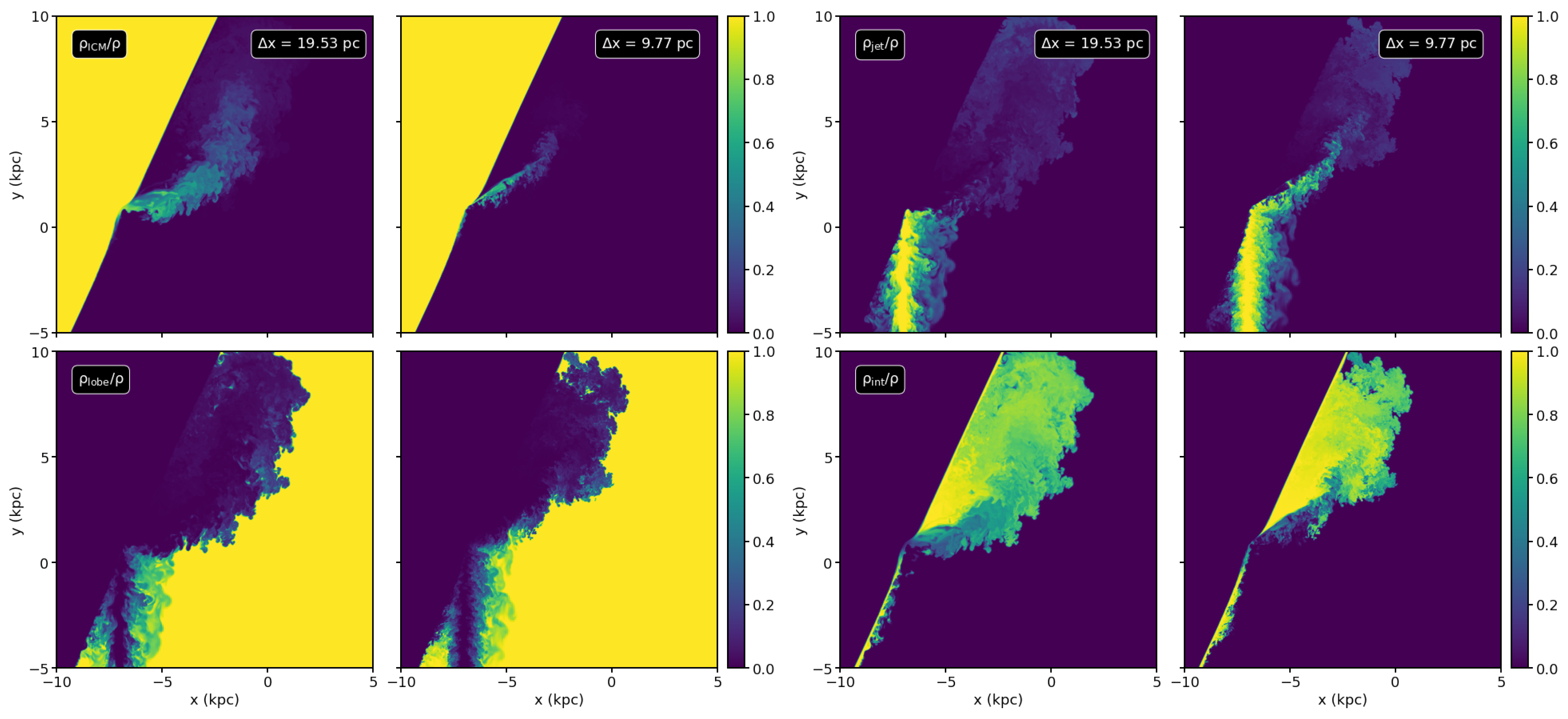
Appendix A. Resolution Test
References
- Fanaroff, B.L.; Riley, J.M. The morphology of extragalactic radio sources of high and low luminosity. Mon. Not. R. Astron. Soc. 1974, 167, 31P–36P. [Google Scholar] [CrossRef]
- Carilli, C.L.; Barthel, P.D. Cygnus A. Astron. Astrophys. Rev. 1996, 7, 1–54. [Google Scholar] [CrossRef]
- Godfrey, L.E.H.; Shabala, S.S. AGN Jet Kinetic Power and the Energy Budget of Radio Galaxy Lobes. Astrophys. J. 2013, 767, 12. [Google Scholar] [CrossRef]
- Snios, B.; Nulsen, P.E.J.; Wise, M.W.; de Vries, M.; Birkinshaw, M.; Worrall, D.M.; Duffy, R.T.; Kraft, R.P.; McNamara, B.R.; Carilli, C.; et al. The Cocoon Shocks of Cygnus A: Pressures and Their Implications for the Jets and Lobes. Astrophys. J. 2018, 855, 71. [Google Scholar] [CrossRef]
- Croton, D.J.; Springel, V.; White, S.D.M.; De Lucia, G.; Frenk, C.S.; Gao, L.; Jenkins, A.; Kauffmann, G.; Navarro, J.F.; Yoshida, N. The many lives of active galactic nuclei: Cooling flows, black holes and the luminosities and colours of galaxies. Mon. Not. R. Astron. Soc. 2006, 365, 11–28. [Google Scholar] [CrossRef]
- McNamara, B.R.; Nulsen, P.E.J. Heating Hot Atmospheres with Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2007, 45, 117–175. [Google Scholar] [CrossRef]
- Fabian, A.C. Observational Evidence of Active Galactic Nuclei Feedback. Annu. Rev. Astron. Astrophys. 2012, 50, 455–489. [Google Scholar] [CrossRef]
- Gitti, M.; Brighenti, F.; McNamara, B.R. Evidence for AGN Feedback in Galaxy Clusters and Groups. Adv. Astron. 2012, 2012, 950641. [Google Scholar] [CrossRef]
- Hardcastle, M.J.; Croston, J.H. Radio galaxies and feedback from AGN jets. New Astron. Rev. 2020, 88, 101539. [Google Scholar] [CrossRef]
- Steenbrugge, K.C.; Blundell, K.M.; Duffy, P. Multiwavelength study of Cygnus A-II. X-ray inverse-Compton emission from a relic counterjet and implications for jet duty cycles. Mon. Not. R. Astron. Soc. 2008, 388, 1465–1472. [Google Scholar] [CrossRef]
- Croston, J.H.; Hardcastle, M.J.; Harris, D.E.; Belsole, E.; Birkinshaw, M.; Worrall, D.M. An X-ray Study of Magnetic Field Strengths and Particle Content in the Lobes of FR II Radio Sources. Astrophys. J. 2005, 626, 733–747. [Google Scholar] [CrossRef]
- de Vries, M.N.; Wise, M.W.; Huppenkothen, D.; Nulsen, P.E.J.; Snios, B.; Hardcastle, M.J.; Birkinshaw, M.; Worrall, D.M.; Duffy, R.T.; McNamara, B.R. Detection of non-thermal X-ray emission in the lobes and jets of Cygnus A. Mon. Not. R. Astron. Soc. 2018, 478, 4010–4029. [Google Scholar] [CrossRef]
- Snios, B.; Johnson, A.C.; Nulsen, P.E.J.; Kraft, R.P.; de Vries, M.; Perley, R.A.; Sebokolodi, L.; Wise, M.W. The X-ray Cavity Around Hotspot E in Cygnus A: Tunneled by a Deflected Jet. Astrophys. J. 2020, 891, 173. [Google Scholar] [CrossRef]
- Blandford, R.D.; Rees, M.J. A “twin-exhaust” model for double radio sources. Mon. Not. R. Astron. Soc. 1974, 169, 395–415. [Google Scholar] [CrossRef]
- Harris, D.E.; Carilli, C.L.; Perley, R.A. X-ray emission from the radio hotspots of Cygnus A. Nature 1994, 367, 713–716. [Google Scholar] [CrossRef]
- Tseng, P.H.; Schive, H.Y.; Chiueh, T. An adaptive mesh, GPU-accelerated, and error minimized special relativistic hydrodynamics code. Mon. Not. R. Astron. Soc. 2021, 504, 3298–3315. [Google Scholar] [CrossRef]
- Taub, A.H. Relativistic Rankine-Hugoniot Equations. Phys. Rev. 1948, 74, 328–334. [Google Scholar] [CrossRef]
- Mathews, W.G. The Hydromagnetic Free Expansion of a Relativistic Gas. Astrophys. J. 1971, 165, 147. [Google Scholar] [CrossRef]
- Mignone, A.; Bodo, G. An HLLC Riemann solver for relativistic flows—I. Hydrodynamics. Mon. Not. R. Astron. Soc. 2005, 364, 126–136. [Google Scholar] [CrossRef]
- Synge, J.L.; Morse, P.M. The Relativistic Gas. Phys. Today 1958, 11, 56. [Google Scholar] [CrossRef]
- Schive, H.Y.; ZuHone, J.A.; Goldbaum, N.J.; Turk, M.J.; Gaspari, M.; Cheng, C.Y. GAMER-2: A GPU-accelerated adaptive mesh refinement code—Accuracy, performance, and scalability. Mon. Not. R. Astron. Soc. 2018, 481, 4815–4840. [Google Scholar] [CrossRef]
- Toro, E.F.; Spruce, M.; Speares, W. Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 1994, 4, 25–34. [Google Scholar] [CrossRef]
- Colella, P.; Woodward, P.R. The Piecewise Parabolic Method (PPM) for Gas-Dynamical Simulations. J. Comput. Phys. 1984, 54, 174–201. [Google Scholar] [CrossRef]
- Worrall, D.M. The X-ray jets of active galaxies. Astron. Astrophys. Rev. 2009, 17, 1–46. [Google Scholar] [CrossRef]
- Smith, R.K.; Brickhouse, N.S.; Liedahl, D.A.; Raymond, J.C. Collisional Plasma Models with APEC/APED: Emission-Line Diagnostics of Hydrogen-like and Helium-like Ions. Astrophys. J. 2001, 556, L91–L95. [Google Scholar] [CrossRef]
- Lind, K.R.; Blandford, R.D. Semidynamical models of radio jets: Relativistic beaming and source counts. Astrophys. J. 1985, 295, 358–367. [Google Scholar] [CrossRef]
- Liu, W.; Sun, M.; Nulsen, P.E.J.; Worrall, D.M.; Birkinshaw, M.; Sarazin, C.; Forman, W.R.; Jones, C.; Ge, C. AGN feedback in the FR II galaxy 3C 220.1. Mon. Not. R. Astron. Soc. 2020, 492, 3156–3168. [Google Scholar] [CrossRef]
- Schive, H.Y.; Tsai, Y.C.; Chiueh, T. GAMER: A Graphic Processing Unit Accelerated Adaptive-Mesh-Refinement Code for Astrophysics. Astrophys. J. Suppl. Ser. 2010, 186, 457–484. [Google Scholar] [CrossRef]
- Robitaille, T.P. et al. [Astropy Collaboration] Astropy: A community Python package for astronomy. Astron. Astrophys. 2013, 558, A33. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Turk, M.J.; Smith, B.D.; Oishi, J.S.; Skory, S.; Skillman, S.W.; Abel, T.; Norman, M.L. yt: A Multi-code Analysis Toolkit for Astrophysical Simulation Data. Astrophys. J. 2011, 192, 9. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| g cm | |
| 9.52 keV | |
| g cm | |
| p | erg cm |
| w | 10 pc |
| g cm | |
| 0.25 kpc | |
| erg s | |
| 25 | |
| −4.482c | |
| 7.342c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
ZuHone, J.A.; Nulsen, P.E.J.; Tseng, P.-H.; Schive, H.-Y.; Jones, T.W. Hydrodynamic Simulations of a Relativistic Jet Interacting with the Intracluster Medium: Application to Cygnus A. Galaxies 2023, 11, 51. https://doi.org/10.3390/galaxies11020051
ZuHone JA, Nulsen PEJ, Tseng P-H, Schive H-Y, Jones TW. Hydrodynamic Simulations of a Relativistic Jet Interacting with the Intracluster Medium: Application to Cygnus A. Galaxies. 2023; 11(2):51. https://doi.org/10.3390/galaxies11020051
Chicago/Turabian StyleZuHone, John A., Paul E. J. Nulsen, Po-Hsun Tseng, Hsi-Yu Schive, and Tom W. Jones. 2023. "Hydrodynamic Simulations of a Relativistic Jet Interacting with the Intracluster Medium: Application to Cygnus A" Galaxies 11, no. 2: 51. https://doi.org/10.3390/galaxies11020051
APA StyleZuHone, J. A., Nulsen, P. E. J., Tseng, P.-H., Schive, H.-Y., & Jones, T. W. (2023). Hydrodynamic Simulations of a Relativistic Jet Interacting with the Intracluster Medium: Application to Cygnus A. Galaxies, 11(2), 51. https://doi.org/10.3390/galaxies11020051






