Gravitational-Wave Instabilities in Rotating Compact Stars
Abstract
:1. Introduction
2. Equation of State of Dense Neutron Star Matter
2.1. Choice of Lagrangian
2.2. Dyson Equation and Baryon Self-Energies
2.3. Equation of State in Standard RMF Theory
2.4. Density-Dependent RMF Models
2.5. A Polytropic Model for the EoS of Ultradense Matter
3. The Model Parameters of the RMF Models
4. Stellar Structure Equations
4.1. Non-Rotating Compact Stellar Objects
4.2. Rotating Compact Stellar Objects
5. Gravitational-Radiation Reaction Driven Instabilities
6. Shear and Bulk Viscosity
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DDRMF | Density-dependent relativistic mean-field |
| EoS | Equation of state |
| GRR | Gravitational-radiation reaction |
| RMF | Relativistic mean-field |
| SNM | Symmetric nuclear matter |
| TOV | Tolman-Oppenheimer-Volkoff |
| HPf | Hypernulcear Potential fit |
References
- Janka, H.T.; Langanke, K.; Marek, A.; Martínez-Pinedo, G.; Müller, B. Theory of core-collapse supernovae. Phys. Rep. 2007, 442, 38–74. [Google Scholar] [CrossRef]
- Becker, W. Neutron Stars and Pulsars; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Blaschke, D.; Chamel, N. Phases of Dense Matter in Compact Stars. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 337–400. [Google Scholar]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. Lett. 1975, 195, L51–L53. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Taylor, J.H. The Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis. In Astronomical Society of the Pacific Conference Series, Proceedings of the Binary Radio Pulsars; Aspen, Colorado, 2004; Rasio, F.A., Stairs, I.H., Eds.; ASP: San Francisco, CA, 2005; Volume 328, p. 25. [Google Scholar]
- Malfatti, G.; Orsaria, M.G.; Ranea-Sandoval, I.F.; Contrera, G.A.; Weber, F. Delta baryons and diquark formation in the cores of neutron stars. Phys. Rev. D 2020, 102, 063008. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Alford, M.; Sedrakian, A. Compact Stars with Sequential QCD Phase Transitions. Phys. Rev. Lett. 2017, 119, 161104. [Google Scholar] [CrossRef]
- Blaschke, D.; Alvarez-Castillo, D.E.; Ayriyan, A.; Grigorian, H.; Largani, N.K.; Weber, F. Astrophysical Aspects of General Relativistic Mass Twin Stars. In Topics on Strong Gravity; World Scienfitic: Singapore, 2020; pp. 207–256. [Google Scholar]
- Friedman, J.L.; Schutz, B.F. Secular instability of rotating Newtonian stars. Astrophys. J. 1978, 222, 281–296. [Google Scholar] [CrossRef]
- Lindblom, L. Estimates of the Maximum Angular Velocity of Rotating Neutron Stars. Astrophys. J. 1986, 303, 146. [Google Scholar] [CrossRef]
- Andersson, N.; Kokkotas, K.D.; Schutz, B.F. Gravitational Radiation Limit on the Spin of Young Neutron Stars. Astrophys. J. 1999, 510, 846–853. [Google Scholar] [CrossRef]
- Andersson, N.; Kokkotas, K.D. The r-mode instability in rotating neutron stars. Int. J. Mod. Phys. D 2001, 10, 381–441. [Google Scholar] [CrossRef]
- Lindblom, L. Phase transitions and the mass-radius curves of relativistic stars. Phys. Rev. D 1998, 58, 024008. [Google Scholar] [CrossRef] [Green Version]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics (Series in High Energy Physics, Cosmology and Gravitation); CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar] [CrossRef]
- Lindblom, L. The Structure and Evolution of Neutron Stars. In Instabilities in Rotating Neutron Stars; Pines, D., Tamagaki, R., Tsuruta, S., Eds.; Addison-Wesley: New York, NY, USA, 1992; p. 122. [Google Scholar]
- Orsaria, M.G.; Malfatti, G.; Mariani, M.; Ranea-Sandoval, I.F.; García, F.; Spinella, W.M.; Contrera, G.A.; Lugones, G.; Weber, F. Phase transitions in neutron stars and their links to gravitational waves. J. Phys. G Nucl. Part. Phys. 2019, 46, 073002. [Google Scholar] [CrossRef]
- Ipser, J.R.; Lindblom, L. The Oscillations of Rapidly Rotating Newtonian Stellar Models. II. Dissipative Effects. Astrophys. J. 1991, 373, 213. [Google Scholar] [CrossRef]
- Friedman, J.L. Upper Limit on the Frequency of Pulsars. Phys. Rev. Lett. 1983, 51, 11–14. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Glendenning, N. Compact Stars: Nuclear Physics, Particle Physics and General Relativity; Astronomy and Astrophysics Library; Springer: New York, NY, USA, 2012. [Google Scholar]
- Spinella, W.; Weber, F. Dense Baryonic Matter in the Cores of Neutron Stars. In Topics on Strong Gravity; World Scientific: Singapore, 2020; pp. 85–152. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H. Relativistic mean field calculations with density-dependent meson-nucleon coupling. Nucl. Phys. A 1999, 656, 331–364. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A. Relativistic calculation of nuclear matter and the nuclear surface. Nucl. Phys. A 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Boguta, J.; Stocker, H. Systematics of nuclear matter properties in a non-linear relativistic field theory. Phys. Lett. B 1983, 120, 289–293. [Google Scholar] [CrossRef] [Green Version]
- Horowitz, C.J.; Piekarewicz, J. Neutron radii of 208Pb and neutron stars. Phys. Rev. C 2001, 64, 062802. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Piekarewicz, J. Neutron Star Structure and the Neutron Radius of 208Pb. Phys. Rev. Lett. 2001, 86, 5647–5650. [Google Scholar] [CrossRef]
- Chen, W.C.; Piekarewicz, J. Building relativistic mean field models for finite nuclei and neutron stars. Phys. Rev. C 2014, 90, 044305. [Google Scholar] [CrossRef]
- Müller, H.; Serot, B.D. Relativistic mean-field theory and the high-density nuclear equation of state. Nucl. Phys. A 1996, 606, 508–537. [Google Scholar] [CrossRef]
- Weber, F.; Farrell, D.; Spinella, W.M.; Malfatti, G.; Orsaria, M.G.; Contrera, G.A.; Maloney, I. Phases of Hadron-Quark Matter in (Proto) Neutron Stars. Universe 2019, 5, 169. [Google Scholar] [CrossRef]
- Farrell, D.; Alp, A.; Spinella, W.; Weber, F.; Malfatti, G.; Orsaria, M.G.; Ranea-Sandoval, I.F. Hot Neutron Star Matter and Proto-Neutron Stars. In New Phenomena and New States of Matter in the Universe: From Quarks to the Cosmos; World Scientific: Singapore, 2022; in press. [Google Scholar]
- Spinella, W.M. A Systematic Investigation of Exotic Matter in Neutron Stars. Ph.D. Thesis, Claremont Graduate University, Claremont, CA, USA, San Diego State University, San Diego, CA, USA, 2017; pp. 145–150. [Google Scholar] [CrossRef]
- Typel, S. Relativistic Mean-Field Models with Different Parametrizations of Density Dependent Couplings. Particles 2018, 1, 3–22. [Google Scholar] [CrossRef]
- Fuchs, C.; Lenske, H.; Wolter, H.H. Density dependent hadron field theory. Phys. Rev. C 1995, 52, 3043–3060. [Google Scholar] [CrossRef]
- Malfatti, G.; Orsaria, M.G.; Contrera, G.A.; Weber, F.; Ranea-Sandoval, I.F. Hot quark matter and (proto-) neutron stars. Phys. Rev. C 2019, 100, 015803. [Google Scholar] [CrossRef]
- Mellinger, R.; Weber, F.; Spinella, W.M.; Contrera, G.A.; Orsaria, M.G. Quark Deconfinement in Rotating Neutron Stars. Universe 2017, 3, 5. [Google Scholar] [CrossRef] [Green Version]
- Lattimer, J.M.; Lim, Y. Constraining the symmetry parameters of the nuclear interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Steiner, A.W. Constraints on the symmetry energy using the mass-radius relation of neutron stars. Eur. Phys. J. A 2014, 50, 40. [Google Scholar] [CrossRef]
- Lattimer, J.M. Neutron Star Mass and Radius Measurements. Universe 2019, 5, 159. [Google Scholar] [CrossRef]
- Cavagnoli, R.; Menezes, D.P.; Providência, C.m.c. Neutron star properties and the symmetry energy. Phys. Rev. C 2011, 84, 065810. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 2014, 922, 1–70. [Google Scholar] [CrossRef]
- Providência, C.; Rabhi, A. Interplay between the symmetry energy and the strangeness content of neutron stars. Phys. Rev. C 2013, 87, 055801. [Google Scholar] [CrossRef]
- Providência, C.; Avancini, S.S.; Cavagnoli, R.; Chiacchiera, S.; Ducoin, C.; Grill, F.; Margueron, J.; Menezes, D.P.; Rabhi, A.; Vidaña, I. Imprint of the symmetry energy on the inner crust and strangeness content of neutron stars. Eur. Phys. J. A 2014, 50, 44. [Google Scholar] [CrossRef]
- Drago, A.; Lavagno, A.; Pagliara, G.; Pigato, D. Early appearance of Δ isobars in neutron stars. Phys. Rev. C 2014, 90, 065809. [Google Scholar] [CrossRef]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef] [Green Version]
- Zdunik, J.L.; Bejger, M.; Haensel, P.; Gourgoulhon, E. Phase transitions in rotating neutron stars cores: Back bending, stability, corequakes, and pulsar timing. A&A 2006, 450, 747–758. [Google Scholar]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Typel, S. Relativistic model for nuclear matter and atomic nuclei with momentum-dependent self-energies. Phys. Rev. C 2005, 71, 064301. [Google Scholar] [CrossRef]
- Rijken, T.A.; Nagels, M.M.; Yamamoto, Y. Baryon-Baryon Interactions—Nijmegen Extended-Soft-Core Models—. Prog. Theor. Phys. Suppl. 2010, 185, 14–71. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Zubairi, O.; Weber, F. Structure and stability of deformed compact stars. In Centennial of General Relativity: A Celebration; World Scientific: Singapore, 2017; pp. 73–95. [Google Scholar] [CrossRef]
- Zubairi, O.; Wigley, D.; Weber, F. Stellar Structure Models of Deformed Neutron Stars. Int. J. Mod. Phys. Conf. Ser. 2017, 45, 1760029. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.L.; Ipser, J.R.; Parker, L. Rapidly Rotating Neutron Star Models. Astrophys. J. 1986, 304, 115. [Google Scholar] [CrossRef]
- Thirring, H. Über die Wirkung rotierender ferner Massen in der Einsteinschen Gravitationstheorie. Phys. Z. 1918, 19, 33. [Google Scholar]
- Thirring, H. Berichtigung zu meiner Arbeit “Über die Wirkung rotierender ferner Massen in der Einsteinschen Gravitationstheorie”. Phys. Z. 1921, 22, 19. [Google Scholar]
- Lense, J.; Thirring, H. Über den Einfluss der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Relativitätstheorie. Phys. Z. 1921, 19, 156. [Google Scholar]
- Pfister, H. On the history of the so-called Lense-Thirring effect. Gen. Relativ. Gravit. 2007, 39, 1735–1748. [Google Scholar] [CrossRef]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars—I. Numerical method and its application to uniformly rotating polytropes. Mon. Not. R. Astron. Soc. 1989, 237, 355–379. [Google Scholar] [CrossRef]
- Cook, G.B.; Shapiro, S.L.; Teukolsky, S.A. Rapidly Rotating Polytropes in General Relativity. Astrophys. J. 1994, 422, 227. [Google Scholar] [CrossRef]
- Hartle, J.B. Slowly Rotating Relativistic Stars. I. Equations of Structure. Astrophys. J. 1967, 150, 1005. [Google Scholar]
- Hartle, J.B.; Thorne, K.S. Slowly Rotating Relativistic Stars. II. Models for Neutron Stars and Supermassive Stars. Astrophys. J. 1968, 153, 807. [Google Scholar]
- Weber, F.; Glendenning, N.K. Application of the Improved Hartle Method for the Construction of General Relativistic Rotating Neutron Star Models. Astrophys. J. 1992, 390, 541. [Google Scholar] [CrossRef]
- Hessels, J.W.T.; Ransom, S.M.; Stairs, I.H.; Freire, P.C.C.; Kaspi, V.M.; Camilo, F. A Radio Pulsar Spinning at 716 Hz. Science 2006, 311, 1901–1904. [Google Scholar] [CrossRef]
- Ipser, J.R.; Lindblom, L. The Oscillations of Rapidly Rotating Newtonian Stellar Models. Astrophys. J. 1990, 355, 226. [Google Scholar]
- Cutler, C.; Lindblom, L. The Effect of Viscosity on Neutron Star Oscillations. Astrophys. J. 1987, 314, 234. [Google Scholar]
- Ipser, J.R.; Lindblom, L. Oscillations and stability of rapidly rotating neutron stars. Phys. Rev. Lett. 1989, 62, 2777–2780, Erratum in Phys. Rev. Lett. 1989, 63, 1327. [Google Scholar] [PubMed]
- Lindblom, L.; Owen, B.J.; Morsink, S.M. Gravitational Radiation Instability in Hot Young Neutron Stars. Phys. Rev. Lett. 1998, 80, 4843–4846. [Google Scholar]
- Flowers, E.; Itoh, N. Transport properties of dense matter. Astrophys. J. 1976, 206, 218–242. [Google Scholar]
- Flowers, E.; Itoh, N. Transport properties of dense matter. II. Astrophys. J. 1979, 230, 847–858. [Google Scholar] [CrossRef]
- Sawyer, R.F. Bulk viscosity of hot neutron-star matter and the maximum rotation rates of neutron stars. Phys. Rev. D 1989, 39, 3804–3806. [Google Scholar]
- Lin, Z.; Bratton, E.; Weber, F.; Orsaria, M.G.; Ranea-Sandoval, I.F. Gravitational radiation-reaction driven instabilities in rotating neutron stars. Astron. Nachrichten 2021, 342, 799–807. [Google Scholar]
- Sotani, H.; Tominaga, K.; Maeda, K.I. Density discontinuity of a neutron star and gravitational waves. Phys. Rev. D 2001, 65, 024010. [Google Scholar] [CrossRef]
- Miniutti, G.; Pons, J.A.; Berti, E.; Gualtieri, L.; Ferrari, V. Non-radial oscillation modes as a probe of density discontinuities in neutron stars. Mon. Not. R. Astron. Soc. 2003, 338, 389–400. [Google Scholar] [CrossRef]
- Vásquez Flores, C.; Lugones, G. Discriminating hadronic and quark stars through gravitational waves of fluid pulsation modes. Class. Quantum Gravity 2014, 31, 155002. [Google Scholar] [CrossRef]
- Ranea-Sandoval, I.F.; Guilera, O.M.; Mariani, M.; Orsaria, M.G. Oscillation modes of hybrid stars within the relativistic Cowling approximation. J. Cosmol. Astropart. Phys. 2018, 2018, 031. [Google Scholar] [CrossRef]
- Tonetto, L.; Lugones, G. Discontinuity gravity modes in hybrid stars: Assessing the role of rapid and slow phase conversions. Phys. Rev. D 2020, 101, 123029. [Google Scholar] [CrossRef]
- Rodríguez, M.C.; Ranea-Sandoval, I.F.; Mariani, M.; Orsaria, M.G.; Malfatti, G.; Guilera, O.M. Hybrid stars with sequential phase transitions: The emergence of the g2 mode. J. Cosmol. Astropart. Phys. 2021, 2021, 009. [Google Scholar] [CrossRef]
- Lai, D. Secular instability of g-modes in rotating neutron stars. Mon. Not. R. Astron. Soc. 1999, 307, 1001–1007. [Google Scholar] [CrossRef]
- Wei, W.; Salinas, M.; Klähn, T.; Jaikumar, P.; Barry, M. Lifting the Veil on Quark Matter in Compact Stars with Core g-mode Oscillations. Astrophys. J. 2020, 904, 187. [Google Scholar] [CrossRef]
- Friedman, J.L.; Ipser, J.R.; Sorkin, R.D. Turning Point Method for Axisymmetric Stability of Rotating Relativistic Stars. Astrophys. J. 1988, 325, 722. [Google Scholar] [CrossRef]


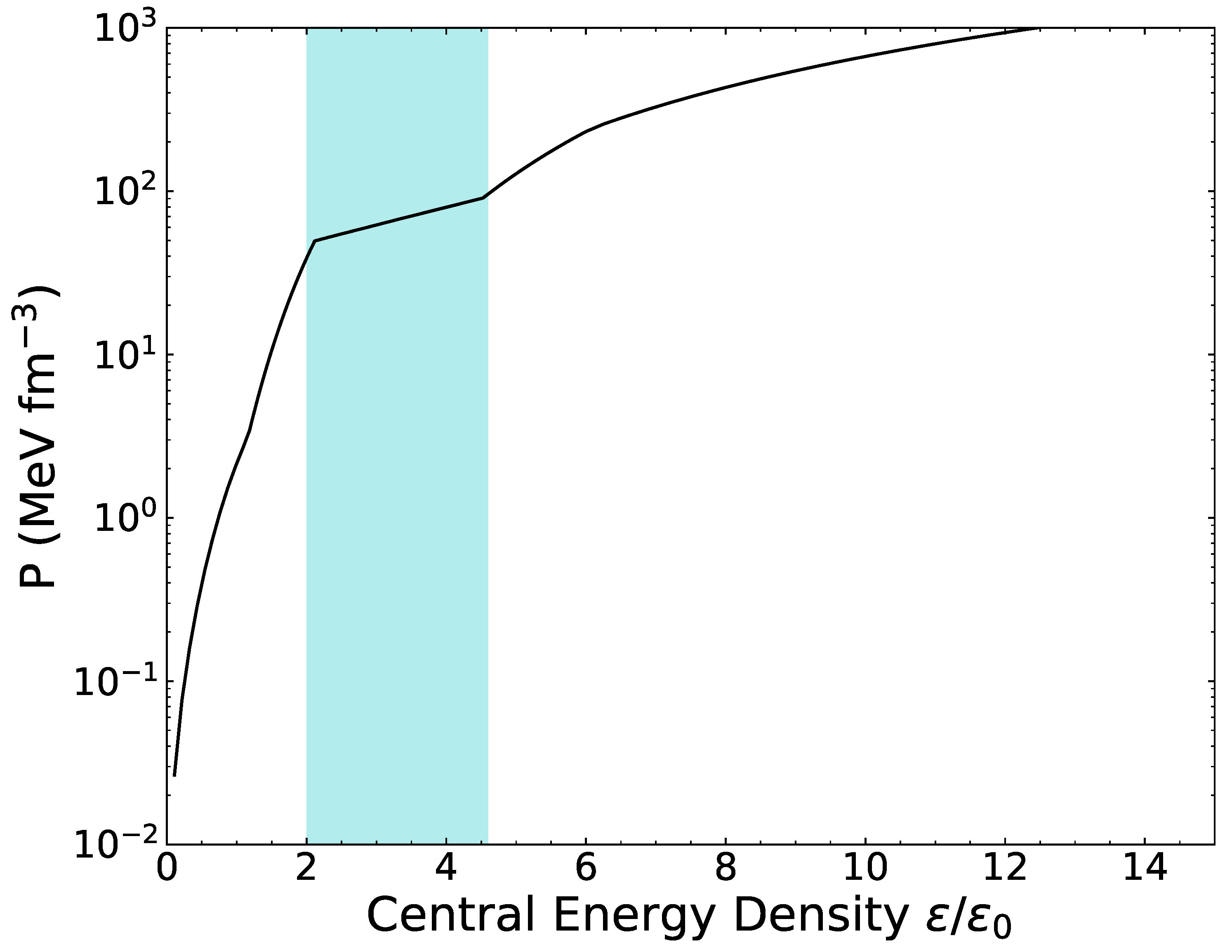
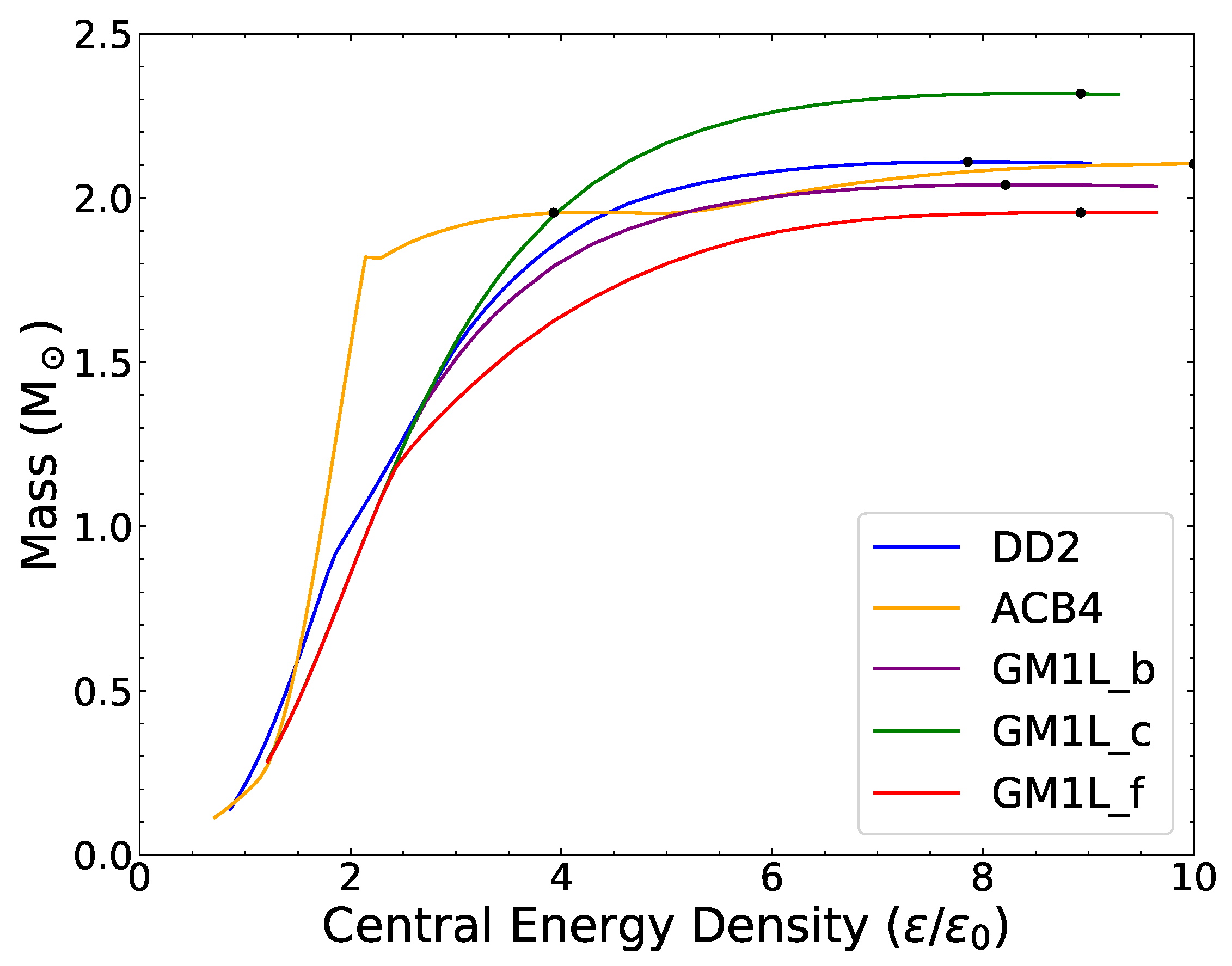
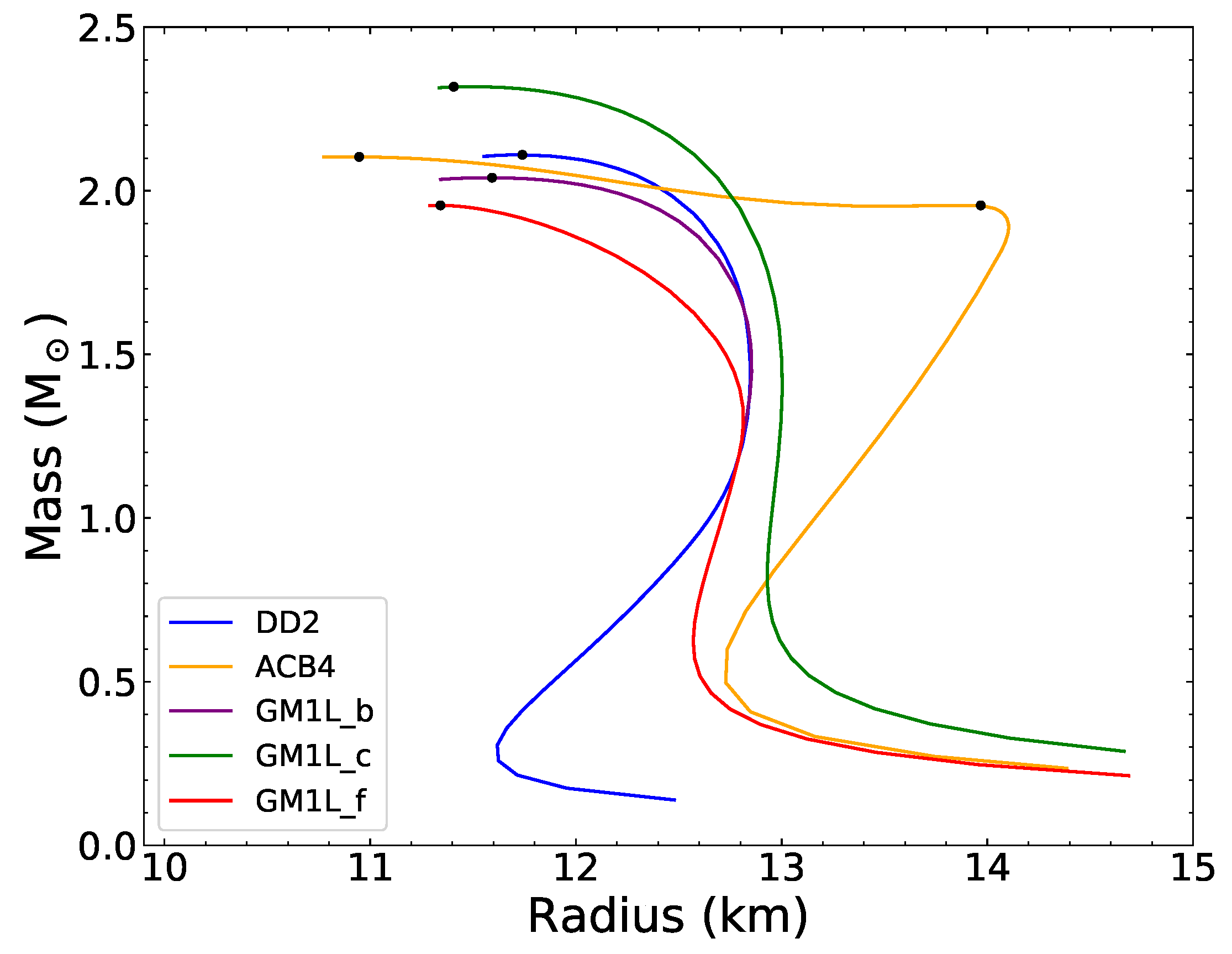
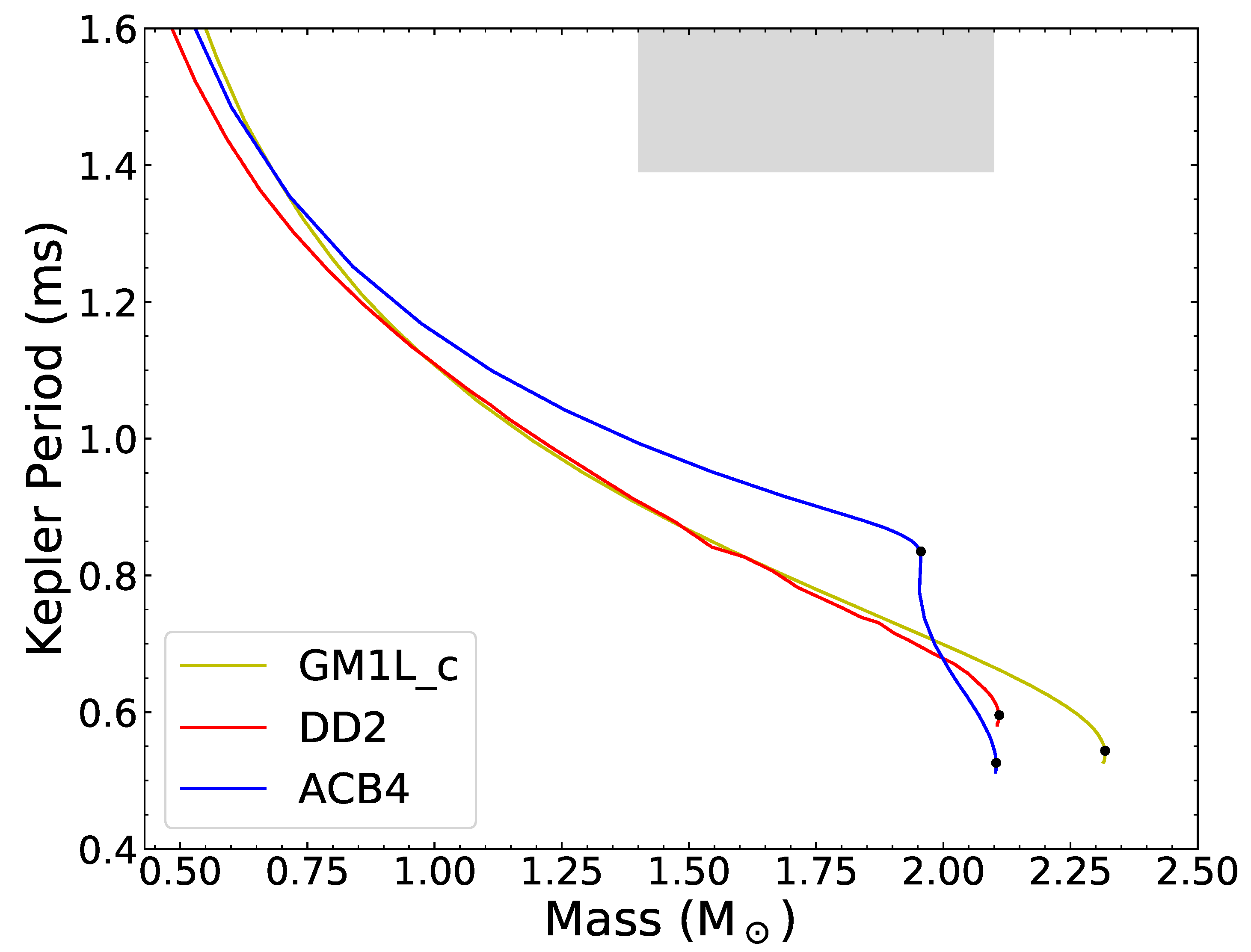
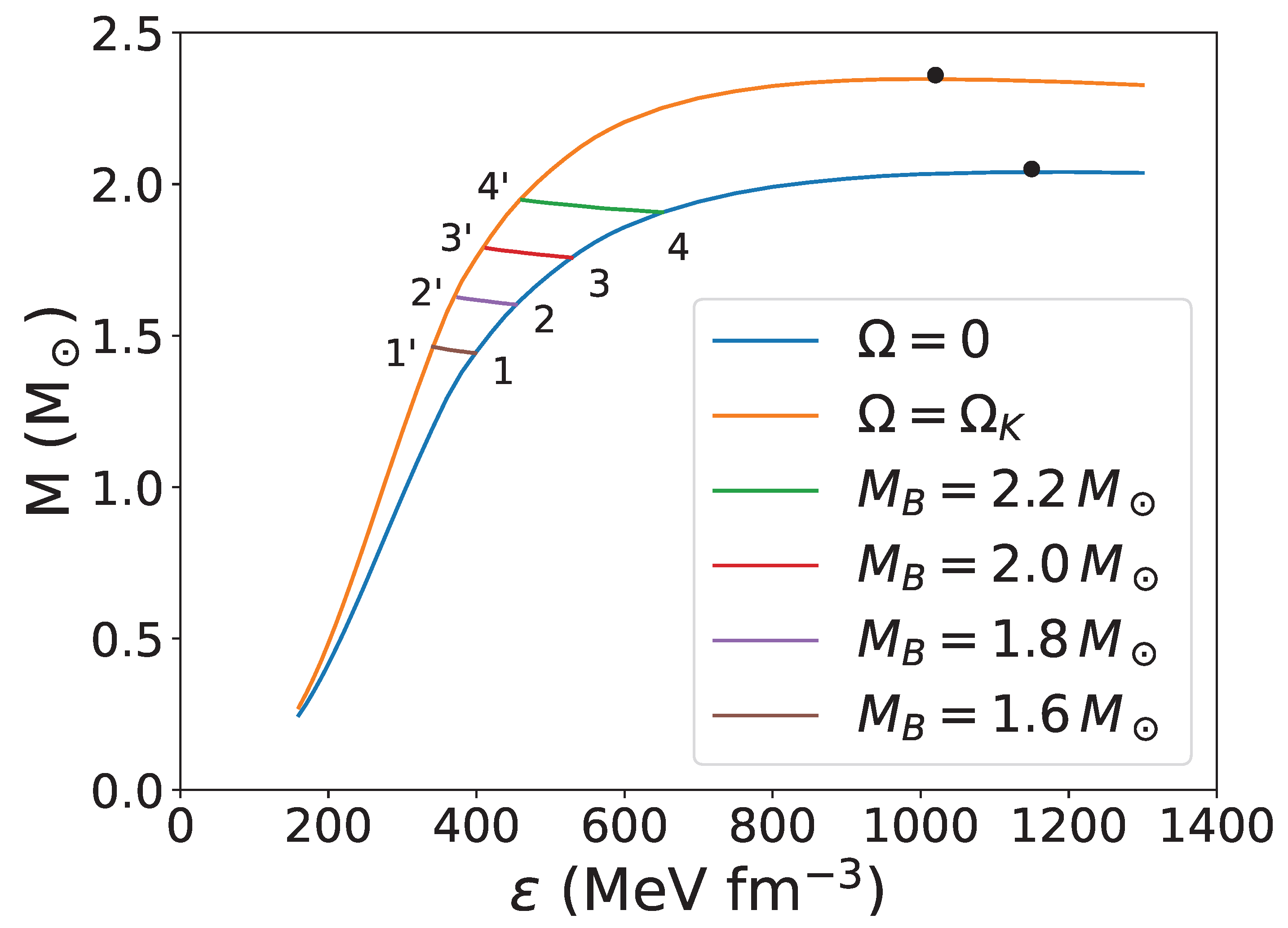
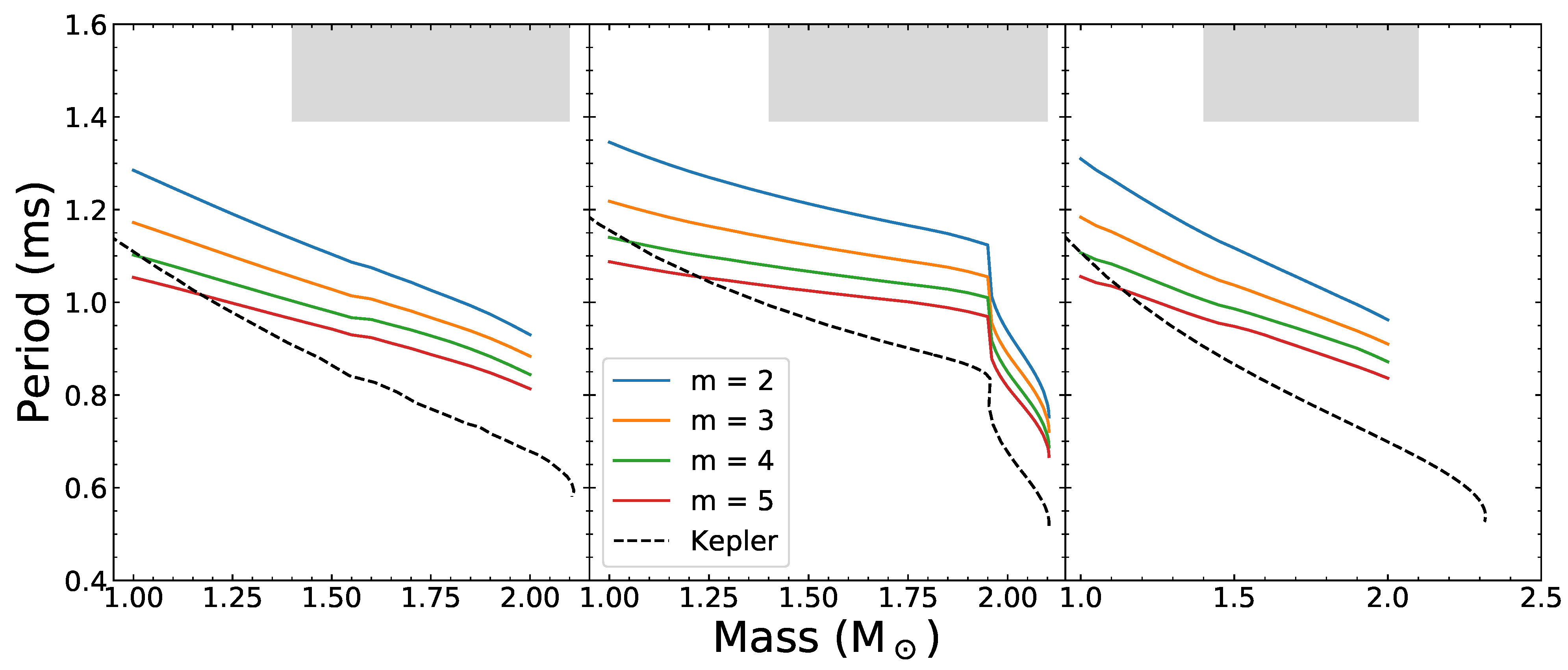
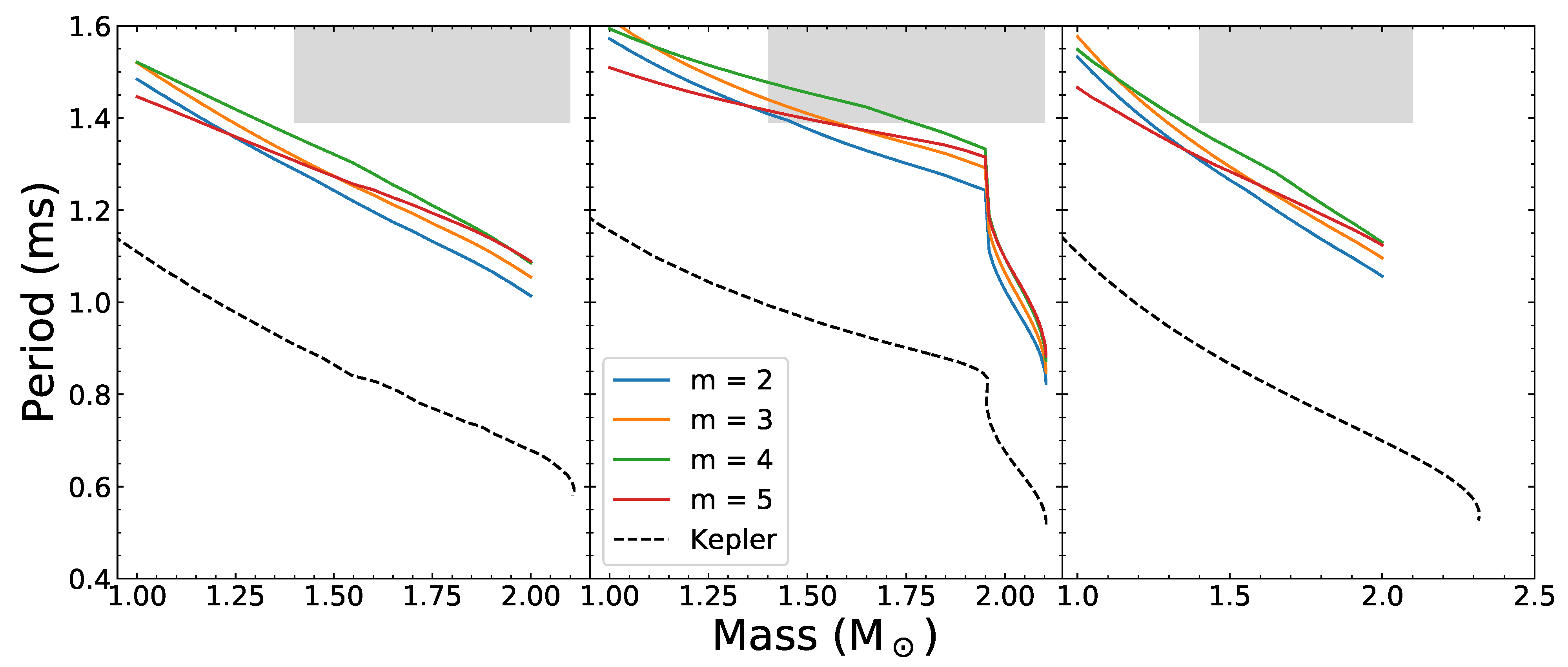
| i | (MeV/fm) | n (fm) | m (MeV) | |
|---|---|---|---|---|
| 1 | 4.921 | 2.1680 | 0.1650 | 939.56 |
| 2 | 0.0 | 63.178 | 0.3174 | 939.56 |
| 3 | 4.000 | 0.5075 | 0.5344 | 1031.2 |
| 4 | 2.800 | 3.2401 | 0.7500 | 958.55 |
| Saturation Properties | Units | DD2 Model | GM1L Model |
|---|---|---|---|
| MeV | |||
| MeV | 242.7 | 300.0 | |
| − | 0.56 | 0.70 | |
| J | MeV | 32.8 | 32.5 |
| MeV | 55.3 | 55.0 | |
| 0.149 | 0.153 | ||
| MeV | 75.2 | 65.6 |
| Parameter | Units | DD2 Model | GM1L Model |
|---|---|---|---|
| GeV | 0.5462 | 0.550 | |
| GeV | 0.783 | 0.783 | |
| GeV | 0.763 | 0.770 | |
| − | 10.687 | 9.5722 | |
| − | 13.342 | 10.618 | |
| − | 3.6269 | 8.983 | |
| − | − | 0.0029 | |
| − | − | ||
| − | 1.3576 | − | |
| − | 0.6344 | − | |
| − | 1.0054 | − | |
| − | 0.5758 | − | |
| − | 1.3697 | − | |
| − | 0.4964 | − | |
| − | 0.8177 | − | |
| − | 0.6384 | − | |
| − | 0.5189 | 0.3898 |
| Model | p | n | e | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GM1L_b | • | • | • | • | • | • | • | • | HPf | SU(3) | 1 | 1.2 | 1.2 | 1.2 |
| GM1L_c | • | • | − | − | − | − | • | • | − | − | − | − | − | − |
| GM1L_f | • | • | • | • | • | • | • | • | HPf | SU(3) | 1 | 0.8 | 0.8 | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bratton, E.L., II; Lin, Z.; Weber, F.; Orsaria, M.G.; Ranea-Sandoval, I.F.; Saavedra, N. Gravitational-Wave Instabilities in Rotating Compact Stars. Galaxies 2022, 10, 94. https://doi.org/10.3390/galaxies10050094
Bratton EL II, Lin Z, Weber F, Orsaria MG, Ranea-Sandoval IF, Saavedra N. Gravitational-Wave Instabilities in Rotating Compact Stars. Galaxies. 2022; 10(5):94. https://doi.org/10.3390/galaxies10050094
Chicago/Turabian StyleBratton, Eric L., II, Zikun Lin, Fridolin Weber, Milva G. Orsaria, Ignacio F. Ranea-Sandoval, and Nathaniel Saavedra. 2022. "Gravitational-Wave Instabilities in Rotating Compact Stars" Galaxies 10, no. 5: 94. https://doi.org/10.3390/galaxies10050094
APA StyleBratton, E. L., II, Lin, Z., Weber, F., Orsaria, M. G., Ranea-Sandoval, I. F., & Saavedra, N. (2022). Gravitational-Wave Instabilities in Rotating Compact Stars. Galaxies, 10(5), 94. https://doi.org/10.3390/galaxies10050094







