On Low Hubble Expansion Rate from Planck Data Anomalies
Abstract
1. Introduction
2. The Induced Four–Dimensional Equations in an Embedded Space–Time
3. Embedded Four-Dimensional FLRW Cosmology
4. Scalar Perturbations in Newtonian Gauge
5. On Evolution of H(z) and
6. Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results V. CMB power spectra and likelihoods. A&A 2020, 641, A5. [Google Scholar]
- Sahni, V.; Starobinsky, A. Reconstructing Dark Energy. Int. J. Mod. Phys. 2006, D15, 2105. [Google Scholar] [CrossRef]
- Percival, W.J.; Cole, S.; Eisenstein, D.J.; Nichol, R.C.; Peacock, J.A.; Pope, A.C.; Szalay, A.S. Measuring the Baryon Acoustic Oscillation scale using the Sloan Digital Sky Survey and 2dF Galaxy Redshift Survey. Mon. Not. R. Astron. Soc. 2007, 381, 1053. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617. [Google Scholar] [CrossRef]
- Kowalski, M.; Rubin, D.; Aldering, G.; Agostinho, R.J.; Amadon, A.; Amanullah, R.; Balland, C.; Barbary, K.; Blanc, G.; Challis, P.J.; et al. Improved Cosmological Constraints from New, Old, and Combined Supernova Data Sets. Astrophys. J. 2008, 686, 749. [Google Scholar] [CrossRef]
- Jaffe, A.H.; Ade, P.A.R.; Balbi, A.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; de Bernardis, P.; et al. Cosmology from MAXIMA-1, BOOMERANG, and COBE DMR Cosmic Microwave Background Observations. Phys. Rev. Lett. 2001, 86, 3475. [Google Scholar] [CrossRef]
- Izzo, L.; Muccino, M.; Zaninoni, E.; Amati, L.; Valle, M.D. New measurements of Ωm from gamma-ray bursts. Astron. Astrophys. 2015, 582, A115. [Google Scholar] [CrossRef]
- Efstathiou, G.; Lemos, P. Statistical inconsistencies in the KiDS-450 data set. Mon. Not. Roy. Astron. Soc. 2017, 476, 151. [Google Scholar] [CrossRef]
- Allen, S.W.; Rapetti, D.A.; Schmidt, R.W.; Ebeling, H.; Morris, R.G.; Fabian, A.C. Improved constraints on dark energy from Chandra X-ray observations of the largest relaxed galaxy clusters. Mon. Not. R. Astron. Soc. 2008, 383, 879. [Google Scholar] [CrossRef]
- Baxter, E.; Clampitt, J.; Giannantonio, T.; Dodelson, S.; Jain, B. Joint measurement of lensing–galaxy correlations using SPT and DES SV data. Mon. Not. R. Astron. Soc. 2016, 461, 4099. [Google Scholar] [CrossRef]
- Chávez, R.; Plionis, M.; Basilakos, S.; Terlevich, R.; Terlevich, E.; Melnick, J.; Bresolin, F.; González-Morán, A.L. Constraining the dark energy equation of state with H II galaxies. Mon. Not. R. Astron. Soc. 2016, 462, 2431. [Google Scholar] [CrossRef]
- Nemiroff, R.J.; Joshi, R.; Patla, B.R. An exposition on Friedmann cosmology with negative energy densities. J. Cosmol. Astropart. Phys. 2016, 006. [Google Scholar] [CrossRef]
- Santos, B.; Coley, A.A.; Devi, N.C.; Alcaniz, J.S. Testing averaged cosmology with type Ia supernovae and BAO data. J. Cosmol. Astropart. Phys. 2017, 002, 047. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, C.P. New agegraphic dark energy model in Brans-Dicke theory with logarithmic form of scalar field. Astrophys. Space Sci. 2017, 362, 52. [Google Scholar] [CrossRef]
- Velten, H.E.S.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological “coincidence problem”. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Sultana, J. The Rh=ct universe and quintessence. Mon. Not. R. Astron. Soc. 2016, 457, 212. [Google Scholar] [CrossRef][Green Version]
- Sivanandam, N. Is the cosmological coincidence a problem? Phys. Rev. D 2013, 87, 083514. [Google Scholar] [CrossRef]
- Nozari, K.; Behrouz, N.; Rashidi, N. Interaction between Dark Mat-ter and Dark Energy and the Cosmological Coincidence Problem. Adv. High Energy Phys. 2014, 569702. [Google Scholar]
- Maia, M.D.; Monte, E.M. Geometry of brane-worlds. Phys. Lett. A 2002, 297, 9. [Google Scholar] [CrossRef][Green Version]
- Maia, M.D.; Monte, E.M.; Maia, J.M.F.; Alcaniz, J.S. On the geometry of dark energy. Class. Quantum Grav. 2005, 22, 1623. [Google Scholar] [CrossRef]
- Maia, M.D.; Silva, N.; Fernandes, M.C.B. Brane-world quantum gravity. J. High En. Phys. 2007, 04, 047. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. The hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 1998, 429, 263. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. Large Mass Hierarchy from a Small Extra Dimension. Phys. Rev. Lett. 1999, 83, 3370. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An Alternative to Compactification. Phys. Rev. Lett. 1999, 83, 4690. [Google Scholar] [CrossRef]
- Dvali, G.; Gabadadze, G.; Porrati, M. 4D Gravity on a Brane in 5D Minkowski Space. Phys. Lett. B 2000, 485, 208. [Google Scholar] [CrossRef]
- Battyea, R.A.; Carter, B. Generic junction conditions in brane-world scenarios. Phys. Lett. B 2001, 509, 331. [Google Scholar] [CrossRef]
- Heydari-Farda, M.; Sepangi, H.R. Anisotropic brane gravity with a confining potential. Phys. Lett. B 2007, 649, 1. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Mehrnia, M.; Sepangi, H.R. Classical tests in brane gravity. Class. Quant. Grav. 2009, 26, 155007. [Google Scholar] [CrossRef][Green Version]
- Maia, M.D. Geometry of the Fundamental Interactions; Springer: New York, NY, USA, 2011; p. 166. [Google Scholar]
- Maia, M.D.; Capistrano, A.J.S.; Alcaniz, J.S.; Monte, E.M. The deformable universe. Gen. Rel. Grav. 2011, 10, 2685. [Google Scholar] [CrossRef][Green Version]
- Ranjbar, A.; Sepangi, H.R.; Shahidi, S. Asymptotically Lifshitz Brane-World Black Holes. Ann. Phys. 2012, 327, 3170. [Google Scholar] [CrossRef][Green Version]
- Capistrano, A.J.S.; Cabral, L.A. Geometrical aspects on the dark matter problem. Ann. Phys. 2014, 384, 64. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Rostami, T. Covariant extrinsic gravity and the geometric origin of dark energy. Int. J. Mod. Phys. D 2015, 24, 1550027. [Google Scholar] [CrossRef]
- Capistrano, A.J.S. Constraints on cosmokinetics of smooth deformations. Mon. Not. Roy. Astron. Soc. 2015, 448, 1232. [Google Scholar] [CrossRef][Green Version]
- Capistrano, A.J.S.; Cabral, L.A. Evolving extrinsic curvature and the cosmological constant problem. Phys. Scr. 2016, 91, 105001. [Google Scholar] [CrossRef][Green Version]
- Capistrano, A.J.S.; Cabral, L.A. Implications on the cosmic coincidence by a dynamical extrinsic curvature. Class. Quantum Grav. 2016, 33, 245006. [Google Scholar] [CrossRef][Green Version]
- Capistrano, A.J.S.; Gutiérrez-Piñeres, A.C.; Ulhoa, S.C.; Amorim, R.G.G. On classical thermal stability of black holes with a dynamical extrinsic curvature. Ann. Phys. 2017, 380, 106. [Google Scholar] [CrossRef]
- Capistrano, A.J.S. Evolution of Density Parameters on a Smooth Embedded Universe. Ann. Phys. 2017, 1700232. [Google Scholar] [CrossRef]
- Capistrano, A.J.S. Lukewarm black holes in the Nash-Greene framework. Phys. Rev. D 2019, 100, 064049-1. [Google Scholar] [CrossRef]
- Capistrano, A.J.S. Linear Nash perturbations with a CMB+Pantheon+H(z) and BAO+DES Y1 joint analysis of cosmic growth expansion. Phys. Rev. D 2021, 103, 043527. [Google Scholar] [CrossRef]
- Capistrano, A.J.S. Sub-horizon modes and growth index in a linear scalar cosmological perturbations. Eur. Phys. J. 2021, 81, 550. [Google Scholar] [CrossRef]
- Capistrano, A.J.S. Fluid approach of linear cosmological Nash-Greene perturbations. Phys. Dark Universe 2021, 33, 100872. [Google Scholar] [CrossRef]
- Capistrano, A.J.S.; Seidel, P.T.Z.; Duarte, H.R. Subhorizon linear Nash-Greene perturbations with constraints on and the deceleration parameter. Phys. Dark Universe 2021, 31, 100760. [Google Scholar] [CrossRef]
- Capistrano, A.J.S.; Cabral, L.A.; Marão, J.A.P.F.; Araújo, C.H.C. Linear Nash-Greene fluctuations on the evolution of S8 and H0 tensions. Eur. Phys. J. C 2022, 82, 1. [Google Scholar] [CrossRef]
- Fan, X.; Bahcall, N.A.; Cen, R. Determining the Amplitude of Mass Fluctuations in the Universe. Astrophy. J. Lett. 1997, 490, 123. [Google Scholar] [CrossRef][Green Version]
- Brinckmann, T.; Lesgourgues, J. MontePython 3: Boosted MCMC sampler and other features. Phys. Dark Universe 2019, 24, 100260. [Google Scholar] [CrossRef]
- Audren, B.; Lesgourgues, J.; Benabed, K.; Prunet, S. Conservative constraints on early cosmology with MontePython. J. Cosmol. Astropart. Phys. 2013, 1302, 001. [Google Scholar] [CrossRef]
- Audren, B.; Lesgourgues, J.; Benabed, K.; Prunet, S. Monte python: Monte Carlo code for CLASS in Python. Astrophys. Source Code Libr. 2013, ascl-1307. Available online: http://ascl.net/1307.002 (accessed on 30 October 2022).
- Lesgourgues, J. CLASS I: Overview. arXiv 2011, arXiv:1104.2932. [Google Scholar] [CrossRef]
- Blas, D.; Lesgourgues, J.; Tram, T. The Cosmic Linear Anisotropy Solving System (CLASS). Part II: Approximation schemes. J. Cosmol. Astropart. Phys. 2011, 7, 034. [Google Scholar] [CrossRef]
- Dio, E.D.; Montanari, F.; Lesgourgues, J.; Durrer, R. The CLASSgal code for Relativistic Cosmological Large Scale Structure. J. Cosmol. Astropart. Phys. 2013, 11, 044. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon acoustic oscillations and the local Hubble constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 2014, 441, 24–62. [Google Scholar] [CrossRef]
- Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The clustering of the SDSS DR7 main Galaxy sample–I. A 4 per cent distance measure at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 835–847. [Google Scholar] [CrossRef]
- Buen-Abad, M.A.; Schmaltz, M.; Lesgourgues, J.; Brinckmann, T. Interacting dark sector and precision cosmology. J. Cosmol. Astropart. Phys. 2018, 1801, 008. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M. A 2.4& determination of the local value of Hubble constant. Astrophys. J. 2016, 826, 56. [Google Scholar]
- Samushia, L.; Percival, W.J.; Raccanelli, A. Interpreting large-scale redshift-space distortion measurements. Mon. Not. R. Astron. Soc. 2012, 420, 2102. [Google Scholar] [CrossRef]
- Howlett, C.; Ross, A.J.; Samushia, L.; Percival, W.J.; Manera, M. The clustering of the SDSS main galaxy sample–II. Mock galaxy catalogues and a measurement of the growth of structure from redshift space distortions at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 848. [Google Scholar] [CrossRef]
- Feix, M.; Nusser, A.; Branchini, E. Growth Rate of Cosmological Perturbations at z∼0.1 from a New Observational Test. Phys. Rev. Lett. 2015, 115, 011301. [Google Scholar] [CrossRef]
- Huterer, D.; Shafer, D.; Scolnic, D.; Schmidt, F. Testing ΛCDM at the lowest redshifts with SN Ia and galaxy velocities. J. Cosmol. Astropart. Phys. 2017, 015, 1705. [Google Scholar] [CrossRef]
- Hudson, M.J.; Turnbull, S.J. The growth rate of cosmic structure from peculiar velocities at low and high redshifts. Astrophys. J. Lett. 2013, 751, L30. [Google Scholar] [CrossRef]
- Turnbull, S.J.; Hudson, M.J.; Feldman, H.A.; Hicken, M.; Kirshner, R.P.; Watkins, R. Cosmic flows in the nearby universe from Type Ia supernovae. Mon. Not. R. Astron. Soc. 2012, 420, 447. [Google Scholar] [CrossRef]
- Davis, M.; Nusser, A.; Masters, K.L.; Springob, C.; Huchra, J.; Lemson, G. Local gravity versus local velocity: Solutions for β and non-linear bias. Mon. Not. R. Astron. Soc. 2011, 413, 2906. [Google Scholar] [CrossRef]
- Song, Y.S.; Percival, W.J. Reconstructing the history of structure formation using redshift distortions. J. Cosmol. Astropart. Phys. 2009, 0910, 004. [Google Scholar] [CrossRef]
- Blake, C.; Baldry, I.K.; Bland-Hawthorn, J.; Christodoulou, L.; Colless, M.; Conselice, C.; Driver, S.P.; Hopkins, A.M.; Liske, J.; Loveday, J.; et al. Galaxy And Mass Assembly (GAMA): Improved cosmic growth measurements using multiple tracers of large-scale structure. Mon. Not. R. Astron. Soc. 2013, 436, 3089. [Google Scholar] [CrossRef]
- Sanchez, A.G.; Montesano, F.; Kazin, E.A.; Aubourg, E.; Beutler, F.; Brinkmann, J.; Brownstein, J.R.; Cuesta, A.J.; Dawson, K.S.; Eisensteinet, D.J.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological implications of the full shape of the clustering wedges in the data release 10 and 11 galaxy samples. Mon. Not. R. Astron.Soc. 2014, 440, 2692. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z<1. Mon. Not. R. Astron. Soc. 2012, 425, 405. [Google Scholar]
- Pezzotta, A.; de la Torre, S.; Bel, J.; Granett, B.R.; Guzzo, L.; Peacock, J.A.; Garilli, B.; Scodeggio, M.; Bolzonella, M.; Abbas, U.; et al. The VIMOS Public Extragalactic Redshift Survey (VIPERS): The growth of structure at 0.5<z<1.2 from redshift-space distortions in the clustering of the PDR-2 final sample. Astron. Astrophys. 2017, 604, A33. [Google Scholar]
- Okumura, T.; Hikage, C.; Totani, T.; Tonegawa, M.; Okada, H.; Glazebrook, K.; Blake, C.; Ferreira, P.G.; More, S.; Taruya, A.; et al. The Subaru FMOS galaxy redshift survey (FastSound). IV. New constraint on gravity theory from redshift space distortions at z∼1.4. Publ. Astron. Soc. Jap. 2016, 68, 38. [Google Scholar] [CrossRef]
- Zarrouk, P.; Burtin, E.; Gil-Marín, H.; Ross, A.J.; Tojeiro, R.; Pâris, I.; Dawson, K.S.; Myers, A.D.; Percival, W.J.; Chuang, C.-H.; et al. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: Measurement of the growth rate of structure from the anisotropic correlation function between redshift 0.8 and 2.2. Mon. Not. R. Astron. Soc. 2018, 477, 1639. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Evolution of the fσ8 tension with the Planck 15/ΛCDM determination and implications for modified gravity theories. Phys. Rev. D 2018, 97, 103503. [Google Scholar] [CrossRef]
- Gil-Marín, H.; Guy, J.; Zarrouk, P.; Burtin, E.; Chuang, C.-H.; Percival, W.J.; Ross, A.J.; Tojeiro, R.; Zhao, G.-B.; Wang, Y.; et al. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: Structure growth rate measurement from the anisotropic quasar power spectrum in the redshift range 0.8 < z < 2.2. Mon. Not. R. Astron. Soc. 2018, 477, 1604–1638. [Google Scholar]
- Hou, J.; Sánchez, A.G.; Scoccimarro, R.; Salazar-Albornoz, S.; Burtin, E.; Gil-Marín, H.; Percival, W.J.; Ruggeri, R.; Zarrouk, P.; Zhao, G.-B.; et al. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: Anisotropic clustering analysis in configuration space. Mon. Not. R. Astron. Soc. 2018, 480, 2521–2534. [Google Scholar] [CrossRef]
- Zhao, G.-B.; Wang, Y.; Saito, S.; Gil-Marín, H.; Percival, W.J.; Wang, D.; Chuang, C.-H.; Ruggeri, R.; Mueller, E.-M.; Zhu, F.; et al. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: A tomographic measurement of cosmic structure growth and expansion rate based on optimal redshift weights. Mon. Not. R. Astron. Soc. 2019, 482, 3497–3513. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z∼1.1 from the spectroscopic evolution of cosmic chronometers. J. Cosmol. Astropart. Phys. 2012, 1208, 006. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, X. Constraining dark energy with Hubble parameter measurements: An analysis including future redshift-drift observations. Eur. Phys. J. C 2016, 76, 163. [Google Scholar] [CrossRef]
- Donaldson, S.K. Smooth 4-manifolds with definite intersection form. Contemp. Math. (AMS) 1984, 35, 201. [Google Scholar]
- Taubes, C.H. An introduction to self-dual connections. Contemp. Math. (AMS) 1984, 35, 493. [Google Scholar]
- Lim, C.S. The Higgs particle and higher-dimensional theories. Prog. Theor. Exp. Phys. 2014, 02A101. [Google Scholar] [CrossRef][Green Version]
- Nash, J. The Imbedding Problem for Riemannian Manifolds. Ann. Math. 1956, 63, 20. [Google Scholar] [CrossRef]
- Greene, R. Isometric Embeddings of Riemannian and Pseudo-Riemannian Manifolds. Memoirs Amer. Math. Soc. 1970, 97. [Google Scholar] [CrossRef]
- Einsenhart, L.P. Non-Riemannian Geometry; Dover: New York, NY, USA, 2005. [Google Scholar]
- Choquet-Bruhat, Y.; York, J.J. Mathematics of Gravitation; Institute of Mathematics, Polish Academy of Sciences: Warsaw, Poland, 1997. [Google Scholar]
- Turner, M.S.; White, M. CDM models with a smooth component. Phys. Rev. D 1987, 56, 4439. [Google Scholar] [CrossRef]
- Zheng, R.; Huang, Q.-G. Growth factor in f(T) gravity. J. Cosmol. Astropart. Phys. 2011, 1103, 002. [Google Scholar] [CrossRef]
- Nesseris, S.; Basilakos, S.; Saridakis, E.N.; Perivolaropoulos, L. Viable f(T) models are practically indistinguishable from ΛCDM. Phys. Rev. D 2013, 88, 103010. [Google Scholar] [CrossRef]
- Lewis, A. GetDist: A Python Package for Analysing Monte Carlo Samples. arXiv 2019, arXiv:1910.13970. [Google Scholar] [CrossRef]
- Lewis, A.; Bridle, S. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. D 2002, 66, 103511. [Google Scholar] [CrossRef]
- Lewis, A. Efficient sampling of fast and slow cosmological parameters. Phys. Rev. D 2013, 87, 103529. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457. [Google Scholar] [CrossRef]
- Uzan, J.-P. Varying Constants, Gravitation and Cosmology. Living Rev. Rel. 2011, 14, 2. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; de Cruz Pérez, J. First Evidence of Running Cosmic Vacuum: Challenging the Concordance Model. Astrophys. J. 2017, 836, 43. [Google Scholar] [CrossRef]
- Copi, C.J.; Davis, A.N.; Krauss, L.M. New Nucleosynthesis Constraint on the Variation of G. Phys. Rev. Lett. 2004, 92, 171301. [Google Scholar] [CrossRef] [PubMed]
- Nesseris, S.; Perivolaropoulos, L. Limits of extended quintessence. Phys. Rev. D 2007, 75, 023517. [Google Scholar] [CrossRef]
- Nesseris, S.; Pantazis, G.; Perivolaropoulos, L. Tension and constraints on modified gravity parametrizations of Geff(z) from growth rate and Planck data. Phys. Rev. D 2017, 96, 023542. [Google Scholar] [CrossRef]
- Philcox, O.H.E.; Sherwin, B.D.; Farren, G.S.; Baxter, E.J. Determining the Hubble constant without the sound horizon: Measurements from galaxy surveys. Phys. Rev. D 2021, 103, 023538. [Google Scholar] [CrossRef]
- Dutcher, D.; Balkenhol, L.; Ade, P.A.R.; Ahmed, Z.; Anderes, E.; Anderson, A.J.; Archipley, M.; Avva, J.S.; Aylor, K.; Barry, P.S.; et al. Measurements of the E-mode polarization and temperature-E-mode correlation of the CMB from SPT-3G 2018 data. Phys. Rev. D 2021, 104, 022003. [Google Scholar] [CrossRef]
- Valentino, E.D.; Giarè, W.; Melchiorri, A.; Silk, J. Health checkup test of the standard cosmological model in view of recent cosmic microwave background anisotropies experiments. Phys. Rev. D 2022, 106, 103506. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Transact. Autom. Control 1974, 19, 716. [Google Scholar] [CrossRef]
- Liddle, A.R. Information criteria for astrophysical model selection. Mon. Not. R. Astron. Soc. 2007, 377, L74–L78. [Google Scholar] [CrossRef]
- Sugiura, N. Further analysis of the data by Akaike’s information criterion and the finite corrections. Commun. Stat. A 1978, 7, 13. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability, 3rd ed.; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Das, S.; Souradeep, T. SCoPE: An efficient method of Cosmological Parameter Estimation. J. Cosmol. Astropart. Phys. 2014, 07, 018. [Google Scholar] [CrossRef][Green Version]
- Hollenstein, L.; Sapone, D.; Crittenden, R.; Schaefer, B.M. Constraints on early dark energy from CMB lensing and weak lensing tomography. J. Cosmol. Astropart. Phys. 2009, 0904, 012. [Google Scholar] [CrossRef]
- Kuijken, K.; Heymans, C.; Hildebrandt, H.; Nakajima, R.; Erben, T.; de Jong, J.T.A.; Viola, M.; Choi, A.; Hoekstra, H.; Miller, L.; et al. Gravitational lensing analysis of the Kilo-Degree Survey. Mon. Not. R. Astron. Soc. 2015, 454, 3500. [Google Scholar] [CrossRef]
- Hildebrandt, H.; Viola, M.; Heymans, C.; Joudaki, S.; Kuijken, K.; Blake, C.; Erben, T.; Joachimi, B.; Klaes, D.; Miller, L.; et al. KiDS-450: Cosmological parameter constraints from tomographic weak gravitational lensing. Mon. Not. R. Astron. Soc. 2017, 465, 1454. [Google Scholar] [CrossRef]
- Conti, I.F.; Herbonnet, R.; Hoekstra, H.; Merten, J.; Miller, L.; Viola, M. Calibration of weak-lensing shear in the Kilo-Degree Survey. Mon. Not. R. Astron. Soc. 2017, 467, 1627. [Google Scholar] [CrossRef]
- Heymans, C.; Tröster, T.; Asgari, M.; Blake, C.; Hildebrandt, H.; Joachimi, B.; Kuijken, K.; Lin, C.-A.; Sánchez, A.J.; van den Busch, J.L.; et al. KiDS-1000 Cosmology: Multi-probe weak gravitational lensing and spectroscopic galaxy clustering constraints. A&A 2021, 646, A140. [Google Scholar]
- Abbott, T.M.C.; Abdalla, F.B.; Alarcon, A.; Aleksić, J.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S. Dark Energy Survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2018, 98, 043526. [Google Scholar] [CrossRef]
- Troxel, M.A.; MacCrann, N.; Zuntz, J.; Eifler, T.F.; Krause, E.; Dodelson, S.; Gruen, D.; Blazek, J.; Friedrich, O.; Samuroff, S.; et al. Dark Energy Survey Year 1 results: Cosmological constraints from cosmic shear. Phys. Rev. D 2018, 98, 043528. [Google Scholar] [CrossRef]
- Heymans, C.; van Waerbeke, L.; Miller, L.; Erben, T.; Hildebrandt, H.; Hoekstra, H.; Kitching, T.D.; Mellier, Y.; Simon, P.; Bonnett, C.; et al. CFHTLenS: The Canada–France–Hawaii Telescope Lensing Survey. Mon. Not. R. Astron. Soc. 2012, 427, 146. [Google Scholar] [CrossRef]
- Erben, T.; Hildebrandt, H.; Miller, L.; van Waerbeke, L.; Heymans, C.; Hoekstra, H.; Kitching, T.D.; Mellier, Y.; Benjamin, J.; Blake, C.; et al. CFHTLenS: The Canada–France–Hawaii Telescope Lensing Survey–imaging data and catalogue products. Mon. Not. R. Astron. Soc. 2013, 433, 2545. [Google Scholar] [CrossRef]
- Joudaki, S.; Blake, C.; Heymans, C.; Choi, A.; Harnois-Deraps, J.; Hildebrandt, H.; Benjamin, J.; Johnson, A.; Mead, A.; Parkinson, D.; et al. CFHTLenS revisited: Assessing concordance with Planck including astrophysical systematics. Mon. Not. R. Astron. Soc. 2017, 465, 2033. [Google Scholar] [CrossRef]
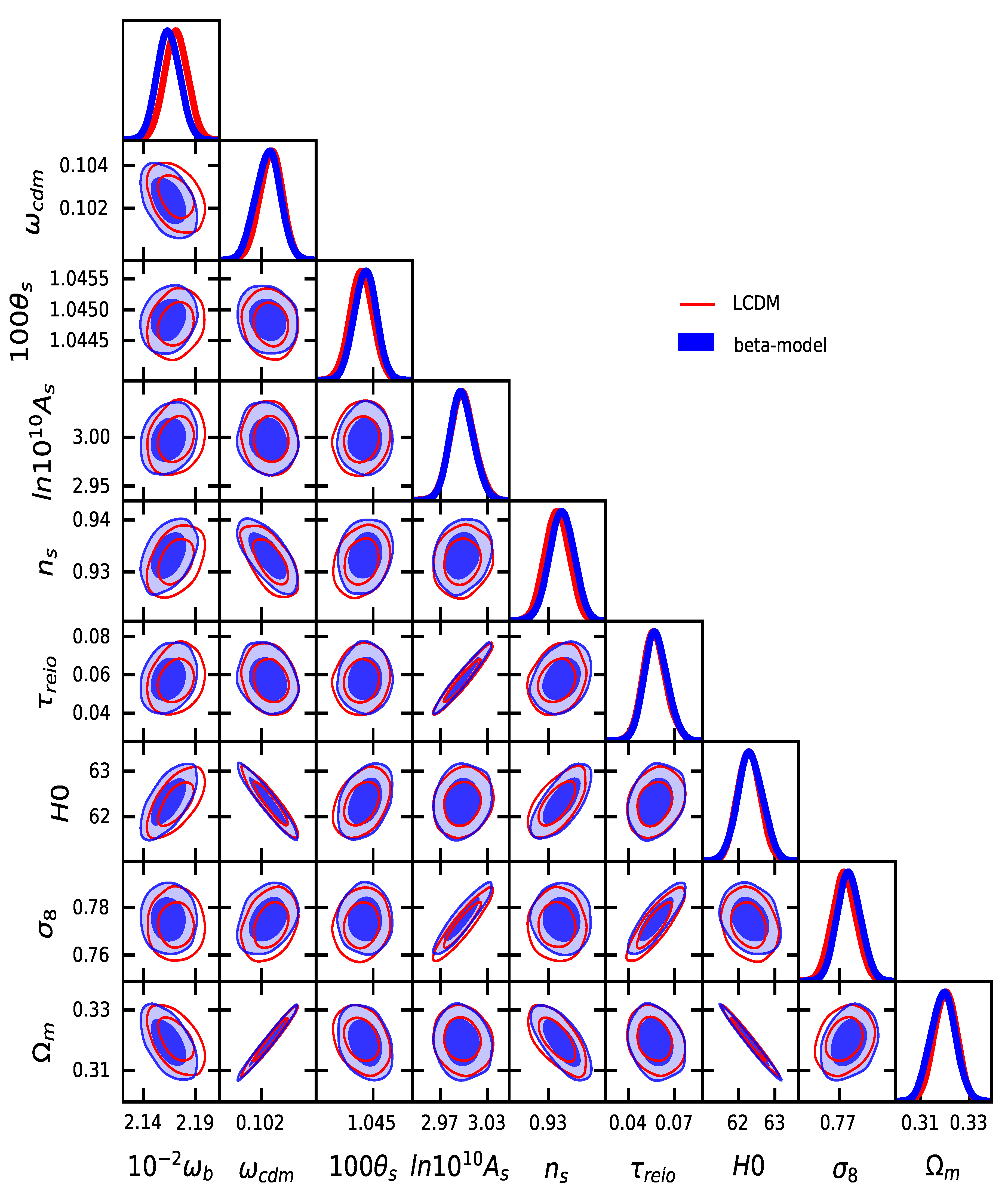
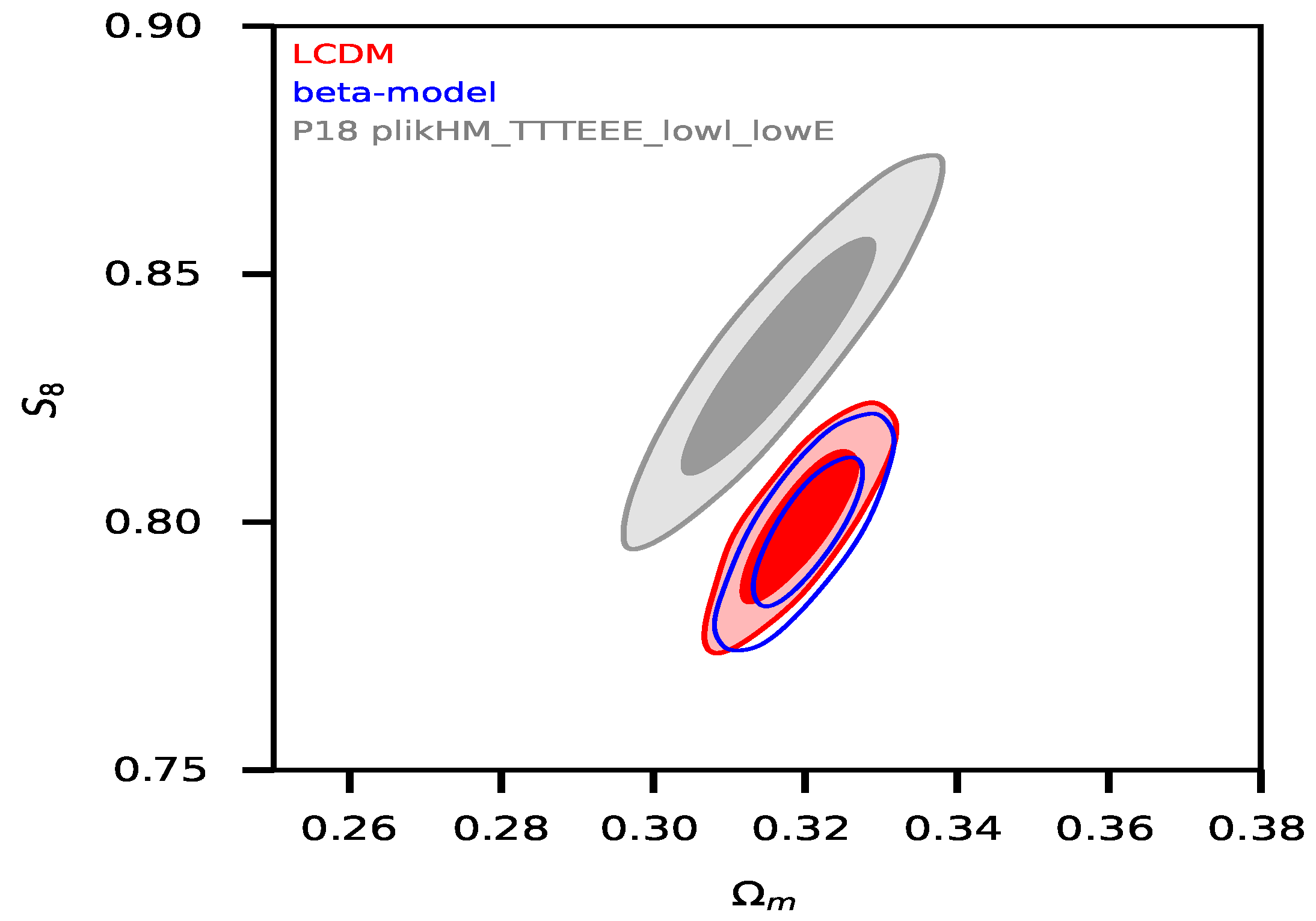
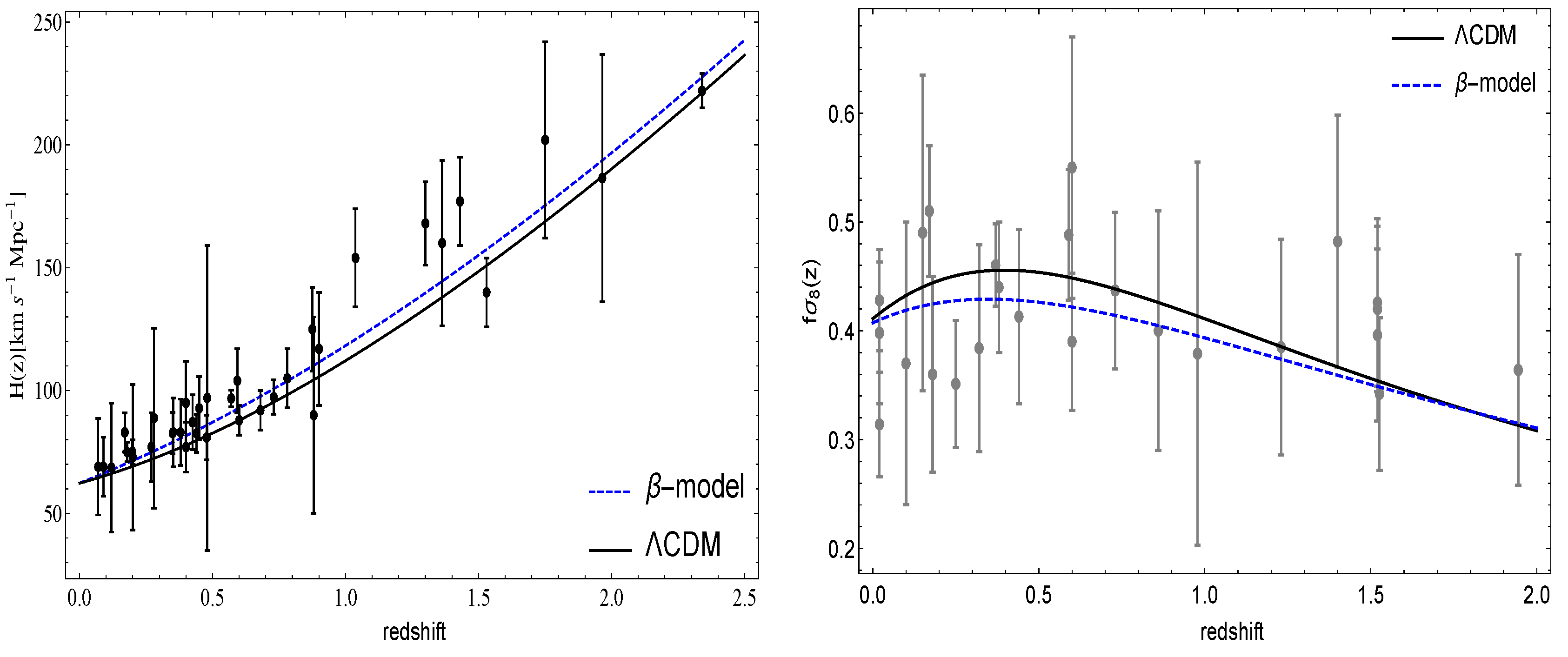
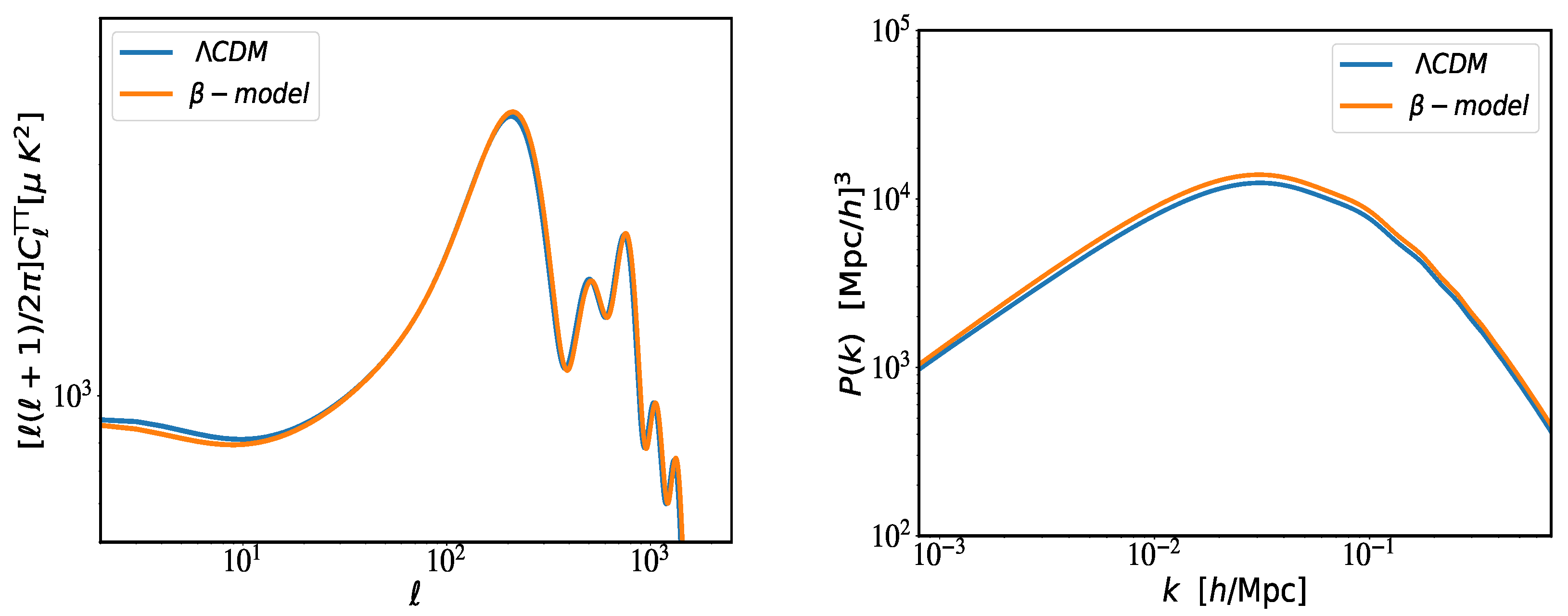
| Parameter | Priors |
|---|---|
| [0.01, 3] | |
| [0.01, 0.3] | |
| [0.01, 0.8] | |
| [0.8, 1.2] | |
| [1.61, 3.91] | |
| [0.5, 10] |
| Parameters | P18+BAO+HST | |
|---|---|---|
| CDM | -Model | |
| w | ||
| Dataset | Redshift | f | |
|---|---|---|---|
| 6dFGS+SnIa | 0.02 | 0.3 | |
| SnIa+IRAS | 0.02 | 0.3 | |
| 2MASS | 0.02 | 0.266 | |
| SDSS-veloc | 0.10 | 0.3 | |
| SDSS-MGS | 0.15 | 0.31 | |
| 2dFGRS | 0.17 | 0.3 | |
| GAMMA | 0.18 | 0.27 | |
| GAMMA | 0.38 | 0.27 | |
| SDSS-LRG-200 | 0.25 | 0.25 | |
| SDSS-LRG-200 | 0.37 | 0.25 | |
| BOSS-LOWZ | 0.32 | 0.274 | |
| SDSS-CMASS | 0.59 | 0.30711 | |
| WiggleZ | 0.44 | 0.27 | |
| WiggleZ | 0.60 | 0.27 | |
| WiggleZ | 0.73 | 0.27 | |
| Vipers PDR-2 | 0.60 | 0.3 | |
| Vipers PDR-2 | 0.86 | 0.3 | |
| FastSound | 1.40 | 0.270 | |
| BOSS-Q | 1.52 | 0.31 | |
| SDSS-IV | 1.52 | 0.26479 | |
| SDSS-IV | 1.52 | 0.31 | |
| SDSS-IV | 0.978 | 0.31 | |
| SDSS-IV | 1.23 | 0.31 | |
| SDSS-IV | 1.526 | 0.31 | |
| SDSS-IV | 1.944 | 0.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capistrano, A.J.S.; Cabral, L.A.; Coimbra-Araújo, C.H.; Marão, J.A.P.F. On Low Hubble Expansion Rate from Planck Data Anomalies. Galaxies 2022, 10, 118. https://doi.org/10.3390/galaxies10060118
Capistrano AJS, Cabral LA, Coimbra-Araújo CH, Marão JAPF. On Low Hubble Expansion Rate from Planck Data Anomalies. Galaxies. 2022; 10(6):118. https://doi.org/10.3390/galaxies10060118
Chicago/Turabian StyleCapistrano, Abraão J. S., Luís A. Cabral, Carlos H. Coimbra-Araújo, and José A. P. F. Marão. 2022. "On Low Hubble Expansion Rate from Planck Data Anomalies" Galaxies 10, no. 6: 118. https://doi.org/10.3390/galaxies10060118
APA StyleCapistrano, A. J. S., Cabral, L. A., Coimbra-Araújo, C. H., & Marão, J. A. P. F. (2022). On Low Hubble Expansion Rate from Planck Data Anomalies. Galaxies, 10(6), 118. https://doi.org/10.3390/galaxies10060118






