On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030
Abstract
1. Introduction
2. SNe Ia Cosmology
3. The Contribution of BAOs
4. Multidimensional Binned Analysis with SNe Ia and BAOs
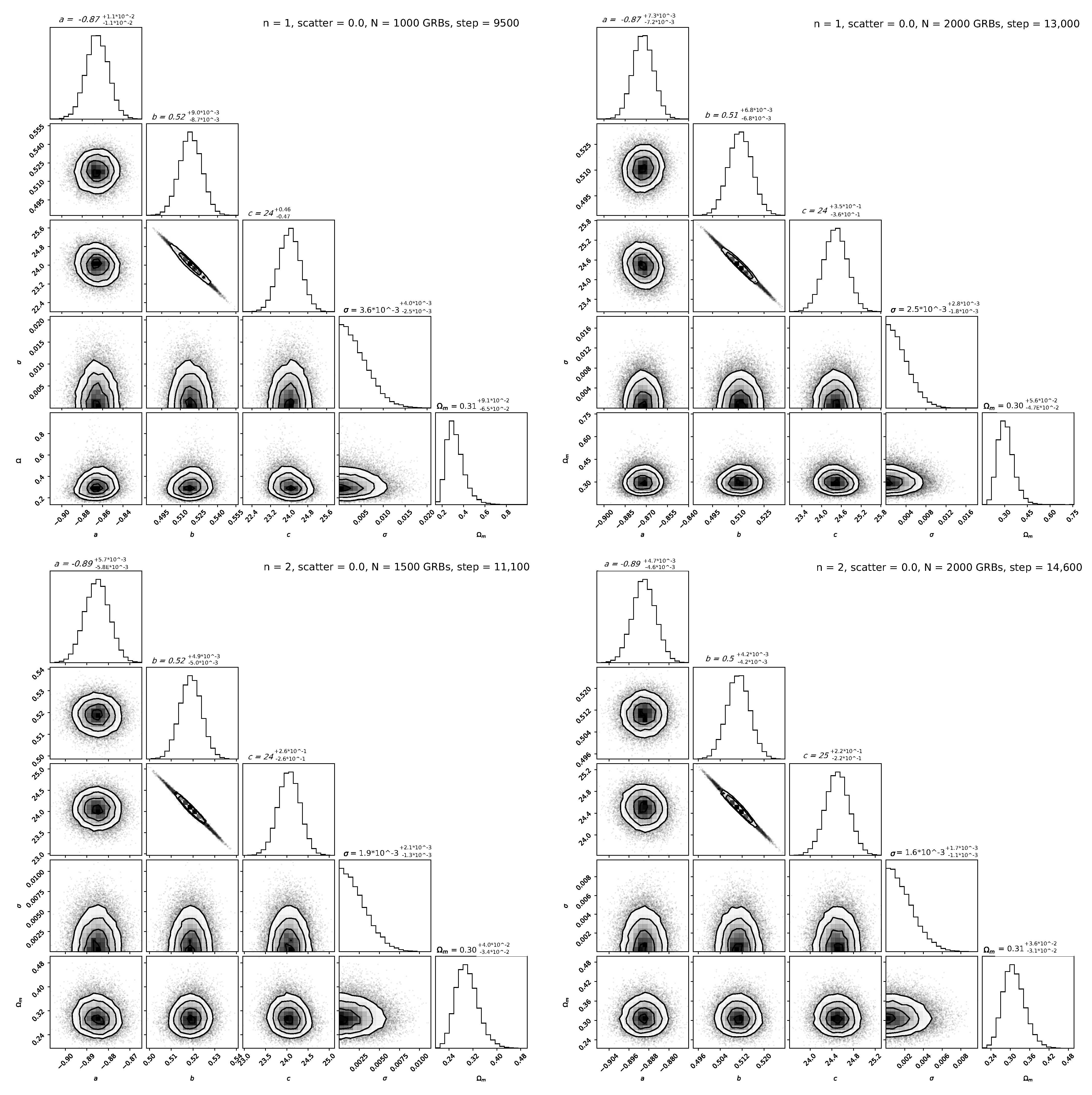
5. Perspective of the Future Contribution of GRB-Cosmology in 2030
6. Discussions on the Results
6.1. Astrophysical Effects
6.2. Theoretical Interpretations
6.2.1. The Scalar Tensor Theory of Gravity
6.2.2. Metric f(R) Gravity in the Jordan Frame
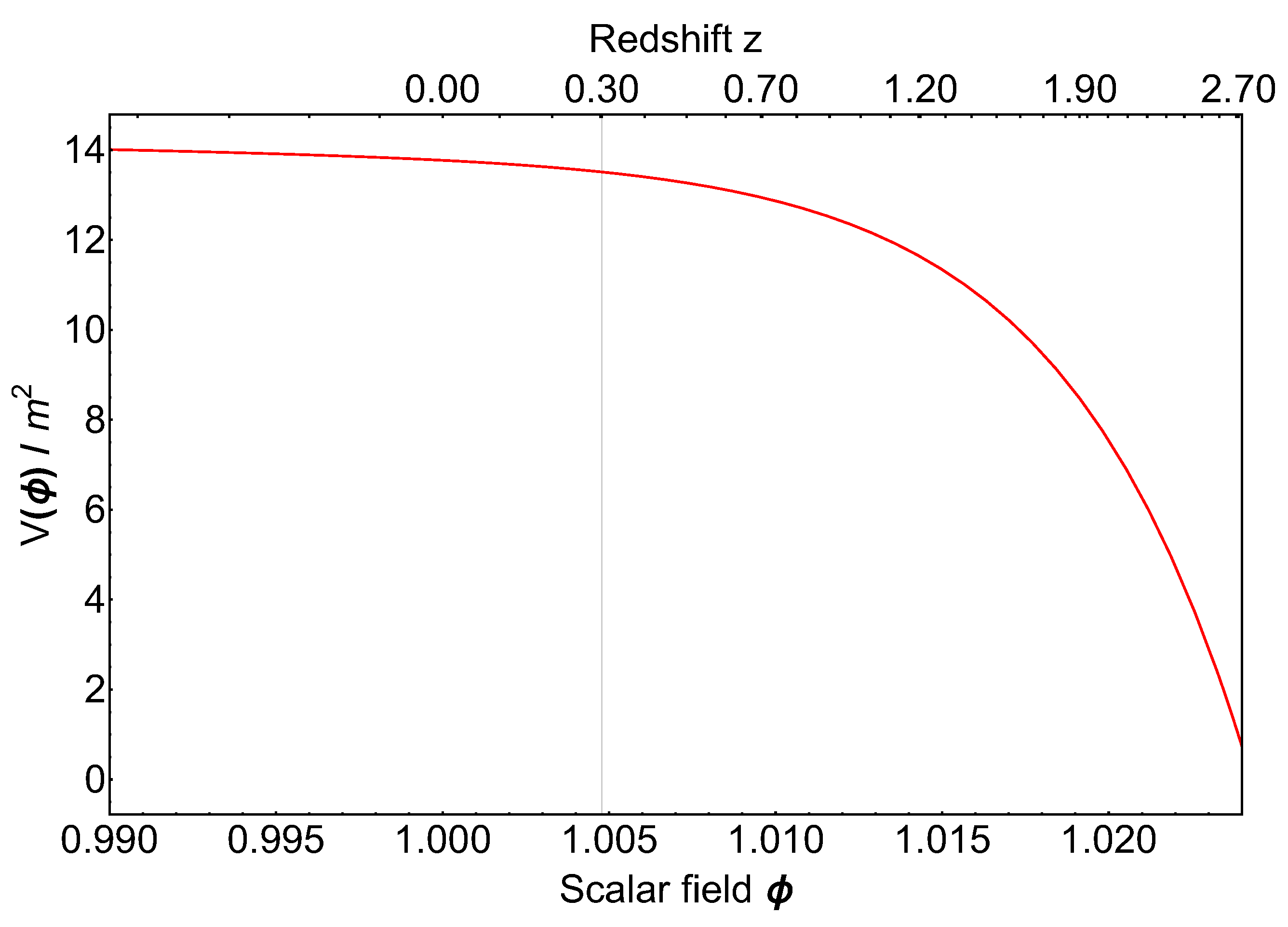
7. The Binned Analysis with Modified f(R) Gravity
Hu–Sawicki Model
8. Requirements for a Suitable f(R) Model
8.1. An Example for Low Redshifts
8.2. Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://github.com/dscolnic/Pantheon (accessed on 21 December 2020). |
| 2 | The code is available upon request. |
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Peebles, P.J.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2020, 2, 013028. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW–XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. R. Astron. Soc. 2020, 498, 1420–1439. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Amendola, L. H0 from cosmic chronometers and Type Ia supernovae, with Gaussian Processes and the novel Weighted Polynomial Regression method. J. Cosmol. Astropart. Phys. 2018, 2018, 051. [Google Scholar] [CrossRef]
- Reid, M.J.; Pesce, D.W.; Riess, A.G. An Improved Distance to NGC 4258 and Its Implications for the Hubble Constant. Astrophys. J. Lett. 2019, 886, L27. [Google Scholar] [CrossRef]
- Planck Collaboration ; Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Rodney, S.A.; Riess, A.G.; Scolnic, D.M.; Jones, D.O.; Hemmati, S.; Molino, A.; McCully, C.; Mobasher, B.; Strolger, L.G.; Graur, O.; et al. Erratum: “Two SNe Ia at redshift ∼2: Improved Classification and redshift determination with medium-band infrared imaging” (2015, AJ, 150, 156). Astron. J. 2016, 151, 47. [Google Scholar] [CrossRef]
- Cucchiara, A.; Levan, A.J.; Fox, D.B.; Tanvir, N.R.; Ukwatta, T.N.; Berger, E.; Krühler, T.; Yoldaş, A.K.; Wu, X.F.; Toma, K.; et al. A photometric redshift OFz∼ 9.4 for grb 090429B. Astrophys. J. 2011, 736, 7. [Google Scholar] [CrossRef]
- Wang, F.; Yang, J.; Fan, X.; Hennawi, J.F.; Barth, A.J.; Banados, E.; Bian, F.; Boutsia, K.; Connor, T.; Davies, F.B.; et al. A Luminous Quasar at Redshift 7.642. Astrophys. J. Lett. 2021, 907, L1. [Google Scholar] [CrossRef]
- Cardone, V.F.; Capozziello, S.; Dainotti, M.G. An updated gamma-ray bursts Hubble diagram. Mon. Not. R. Astron. Soc. 2009, 400, 775–790. [Google Scholar] [CrossRef]
- Cardone, V.F.; Dainotti, M.G.; Capozziello, S.; Willingale, R. Constraining cosmological parameters by gamma-ray burst X-ray afterglow light curves. Mon. Not. R. Astron. Soc. 2010, 408, 1181–1186. [Google Scholar] [CrossRef]
- Cardone, V.F.; Perillo, M.; Capozziello, S. Systematics in the gamma-ray burst Hubble diagram. Mon. Not. R. Astron. Soc. 2011, 417, 1672–1683. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Cardone, V.F.; Piedipalumbo, E.; Capozziello, S. Slope evolution of GRB correlations and cosmology. Mon. Not. R. Astron. Soc. 2013, 436, 82–88. [Google Scholar] [CrossRef]
- Postnikov, S.; Dainotti, M.G.; Hernandez, X.; Capozziello, S. Nonparametric Study of the Evolution of the Cosmological Equation of State with Sneia, Bao, and High-Redshift Grbs. Astrophys. J. 2014, 783, 126. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; Montanari, E.; et al. Intrinsic spectra and energetics of BeppoSAX Gamma-Ray Bursts with known redshifts. Astron. Astrophys. 2002, 390, 81–89. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Nakamura, T.; Yamazaki, R.; Inoue, A.K.; Ioka, K. Gamma-Ray Burst Formation Rate Inferred from the Spectral Peak Energy–Peak Luminosity Relation. Astrophys. J. 2004, 609, 935–951. [Google Scholar] [CrossRef]
- Ito, H.; Matsumoto, J.; Nagataki, S.; Warren, D.C.; Barkov, M.V.; Yonetoku, D. The photospheric origin of the Yonetoku relation in gamma-ray bursts. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Liang, E.; Zhang, B. Model-independent Multivariable Gamma-Ray Burst Luminosity Indicator and Its Possible Cosmological Implications. Astrophys. J. 2005, 633, 611–623. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Nava, L.; Ghisellini, G. Spectral-luminosity relation within individual Fermi gamma rays bursts. Astron. Astrophys. 2010, 511, A43. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Cardone, V.F.; Capozziello, S. A time-luminosity correlation for γ-ray bursts in the X-rays. Mon. Not. R. Astron. Soc.: Letters 2008, 391, L79–L83. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Willingale, R.; Capozziello, S.; Cardone, V.F.; Ostrowski, M. Discovery of a Tight Correlation for Gamma-Ray Burst Afterglows with “Canonical” Light Curves. Astrophys. J. Lett. 2010, 722, L215–L219. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Cardone, V.F.; Capozziello, S.; Ostrowski, M.; Willingale, R. Study of possible systematics in the L*X - Ta* correlation of Gamma Ray Bursts. Astrophys. J. 2011, 730, 135. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Petrosian, V.; Singal, J.; Ostrowski, M. Determination of the intrinsic luminosity time correlation in the X-ray afterglows of gamma-ray bursts. Astrophys. J. 2013, 774, 157. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Vecchio, R.D.; Shigehiro, N.; Capozziello, S. Selection effects in Gamma-Ray Burst Correlations: Consequences on the Ratio Between Gamma-Ray Burst And Star Formation rates. Astrophys. J. 2015, 800, 31. [Google Scholar] [CrossRef]
- Dainotti, M.; Petrosian, V.; Willingale, R.; O’Brien, P.; Ostrowski, M.; Nagataki, S. Luminosity–time and luminosity–luminosity correlations for GRB prompt and afterglow plateau emissions. Mon. Not. R. Astron. Soc. 2015, 451, 3898–3908. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Postnikov, S.; Hernandez, X.; Ostrowski, M. A fundamental Plane for Long Gamma-Ray Bursts with X-Ray plateaus. Astrophys. J. Lett. 2016, 825, L20. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Nagataki, S.; Maeda, K.; Postnikov, S.; Pian, E. A study of gamma ray bursts with afterglow plateau phases associated with supernovae. Astron. Astrophys. 2017, 600, A98. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Hernandez, X.; Postnikov, S.; Nagataki, S.; O’brien, P.; Willingale, R.; Striegel, S. A Study of the Gamma-Ray Burst Fundamental Plane. Astrophys. J. 2017, 848, 88. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Amati, L. Gamma-ray Burst Prompt Correlations: Selection and Instrumental Effects. Astrophys. J. 2018, 130, 051001. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Del Vecchio, R.; Tarnopolski, M. Gamma-Ray Burst Prompt Correlations. Adv. Astron. 2018, 2018, 1–31. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.Ł; Sarracino, G.; Nagataki, S.; Capozziello, S.; Fraija, N. The X-ray Fundamental Plane of the Platinum Sample, the Kilonovae, and the SNe Ib/c Associated with GRBs. Astrophys. J. 2020, 904, 97. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Omodei, N.; Srinivasaragavan, G.P.; Vianello, G.; Willingale, R.; O’Brien, P.; Nagataki, S.; Petrosian, V.; Nuygen, Z.; Hernandez, X.; et al. On the Existence of the Plateau Emission in High-energy Gamma-Ray Burst Light Curves Observed by Fermi-LAT. Astrophys. J. Suppl. Ser. 2021, 255, 13. [Google Scholar] [CrossRef]
- Dainotti, M.; Levine, D.; Fraija, N.; Chandra, P. Accounting for Selection Bias and Redshift Evolution in GRB Radio Afterglow Data. Galaxies 2021, 9, 95. [Google Scholar] [CrossRef]
- Vecchio, R.D.; Dainotti, M.G.; Ostrowski, M. Study of Grb Light-Curve Decay Indices in the Afterglow phase. Astrophys. J. 2016, 828, 36. [Google Scholar] [CrossRef]
- Duncan, R.C. Gamma-ray bursts from extragalactic Magnetar Flares. AIP Conf. Proc. 2001, 586, 495–500. [Google Scholar] [CrossRef]
- Dall’Osso, S.; Granot, J.; Piran, T. Magnetic field decay in neutron stars: From soft gamma repeaters to “weak-field magnetars”. Mon. Not. R. Astron. Soc. 2012, 422, 2878–2903. [Google Scholar] [CrossRef]
- Rowlinson, A.; Gompertz, B.P.; Dainotti, M.; O’Brien, P.T.; Wijers, R.A.M.J.; van der Horst, A.J. Constraining properties of GRB magnetar central engines using the observed plateau luminosity and duration correlation. Mon. Not. R. Astron. Soc. 2014, 443, 1779–1787. [Google Scholar] [CrossRef]
- Rea, N.; Gullón, M.; Pons, J.A.; Perna, R.; Dainotti, M.G.; Miralles, J.A.; Torres, D.F. Constraining The Grb-Magnetar Model By Means Of The Galactic Pulsar PopulatioN. Astrophys. J. 2015, 813, 92. [Google Scholar] [CrossRef]
- Stratta, G.; Dainotti, M.G.; Dall’Osso, S.; Hernandez, X.; Cesare, G.D. On the Magnetar Origin of the GRBs Presenting X-Ray Afterglow Plateaus. Astrophys. J. 2018, 869, 155. [Google Scholar] [CrossRef]
- Amati, L.; D’Agostino, R.; Luongo, O.; Muccino, M.; Tantalo, M. Addressing the circularity problem in the Ep-Eiso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. Lett. 2019, 486, L46–L51. [Google Scholar] [CrossRef]
- Liao, K.; Shafieloo, A.; Keeley, R.E.; Linder, E.V. A Model-independent Determination of the Hubble Constant from Lensed Quasars and Supernovae Using Gaussian Process Regression. Astrophys. J. Lett. 2019, 886, L23. [Google Scholar] [CrossRef]
- Keeley, R.E.; Shafieloo, A.; Hazra, D.K.; Souradeep, T. Inflation wars: A new hope. J. Cosmol. Astropart. Phys. 2020, 2020, 055. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. Cosmological Constraints from the Hubble Diagram of Quasars at High Redshifts. Nat. Astron. 2019, 3, 272–277. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. Astrophys. J. 2019, 882, 34. [Google Scholar] [CrossRef]
- Dutta, K.; Roy, A.; Ruchika; Sen, A.A.; Sheikh-Jabbari, M.M. Cosmology with low-redshift observations: No signal for new physics. Phys. Rev. D 2019, 100, 103501. [Google Scholar] [CrossRef]
- Yang, T.; Banerjee, A.; Ó Colgáin, E. Cosmography and flat ΛCDM tensions at high redshift. Phys. Rev. D 2020, 102, 123532. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble Constant Tension in the SNe Ia Pantheon Sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Ingram, A.; Mastroserio, G.; van der Klis, M.; Nathan, E.; Connors, R.; Dauser, T.; García, J.A.; Kara, E.; König, O.; Lucchini, M.; et al. On measuring the Hubble constant with X-ray reverberation mapping of active galactic nuclei. arXiv 2021, arXiv:2110.15651. [Google Scholar] [CrossRef]
- Agrawal, P.; Cyr-Racine, F.Y.; Pinner, D.; Randall, L. Rock ’n’ Roll Solutions to the Hubble Tension. arXiv 2019, arXiv:1904.01016. [Google Scholar]
- Arjona, R.; Espinosa-Portales, L.; García-Bellido, J.; Nesseris, S. A GREAT model comparison against the cosmological constant. arXiv 2021, arXiv:2111.13083. [Google Scholar]
- Fernandez-Martinez, E.; Pierre, M.; Pinsard, E.; Rosauro-Alcaraz, S. Inverse Seesaw, dark matter and the Hubble tension. Eur. Phys. J. C 2021, 81, 954. [Google Scholar] [CrossRef]
- Ghose, S.; Bhadra, A. Is non-particle dark matter equation of state parameter evolving with time? Eur. Phys. J. C 2021, 81, 683. [Google Scholar] [CrossRef]
- Hart, L.; Chluba, J. Varying fundamental constants principal component analysis: Additional hints about the Hubble tension. Mon. Not. R. Astron. Soc. 2021, 510, 2206–2227. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Bettoni, D.; Figueruelo, D.; Pannia, F.A.T.; Tsujikawa, S. Probing elastic interactions in the dark sector and the role of S8. Phys. Rev. D. 2021, 104, 103503. [Google Scholar] [CrossRef]
- Rezaei, M.; Peracaula, J.; Malekjani, M. Cosmographic approach to Running Vacuum dark energy models: New constraints using BAOs and Hubble diagrams at higher redshifts. Mon. Not. R. Astron. Soc. 2022, 509, 2593–2608. [Google Scholar] [CrossRef]
- Shah, P.; Lemos, P.; Lahav, O. A buyer’s guide to the Hubble constant. Astron. Astrophys. Rev. 2021, 29, 9. [Google Scholar] [CrossRef]
- Firouzjahi, H. Cosmological constant problem on the horizon. arXiv 2022, arXiv:2201.02016. [Google Scholar]
- Banihashemi, A.; Khosravi, N.; Shafieloo, A. Dark energy as a critical phenomenon: A hint from Hubble tension. J. Cosmol. Astropart. Phys. 2021, 2021, 003. [Google Scholar] [CrossRef]
- Ballardini, M.; Finelli, F.; Sapone, D. Cosmological constraints on Newton’s gravitational constant. arXiv 2021, arXiv:2111.09168. [Google Scholar]
- Corona, M.A.; Murgia, R.; Cadeddu, M.; Archidiacono, M.; Gariazzo, S.; Giunti, C.; Hannestad, S. Pseudoscalar sterile neutrino self-interactions in light of Planck, SPT and ACT data. arXiv 2021, arXiv:astro-ph.CO/2112.00037. [Google Scholar]
- Cyr-Racine, F.Y.; Ge, F.; Knox, L. A Symmetry of Cosmological Observables, and a High Hubble Constant as an Indicator of a Mirror World Dark Sector. arXiv 2021, arXiv:astro-ph.CO/2107.13000. [Google Scholar]
- Valentino, E.D.; Gariazzo, S.; Giunti, C.; Mena, O.; Pan, S.; Yang, W. Minimal dark energy: Key to sterile neutrino and Hubble constant tensions? arXiv 2021, arXiv:astro-ph.CO/2110.03990. [Google Scholar]
- Valentino, E.D.; Melchiorri, A. Neutrino Mass Bounds in the era of Tension Cosmology. arXiv 2021, arXiv:astro-ph.CO/2112.02993. [Google Scholar]
- Drees, M.; Zhao, W. U(1)Lμ-Lτ for Light Dark Matter, gμ-2, the 511 keV excess and the Hubble Tension. arXiv 2021, arXiv:hep-ph/2107.14528. [Google Scholar]
- Gu, Y.; Wu, L.; Zhu, B. Axion Dark Radiation and Late Decaying Dark Matter in Neutrino Experiment. arXiv 2021, arXiv:hep-ph/2105.07232. [Google Scholar]
- Khalifeh, A.R.; Jimenez, R. Using Neutrino Oscillations to Measure H0. arXiv 2021, arXiv:astro-ph.CO/2111.15249. [Google Scholar]
- Li, J.; Zhou, Y.; Xue, X. Spatial Curvature and Large Scale Lorentz Violation. arXiv 2021, arXiv:gr-qc/2112.02364. [Google Scholar]
- Lulli, M.; Marciano, A.; Shan, X. Stochastic Quantization of General Relativity à la Ricci-Flow. arXiv 2021, arXiv:gr-qc/2112.01490. [Google Scholar]
- Mawas, E.; Street, L.; Gass, R.; Wijewardhana, L.C.R. Interacting dark energy axions in light of the Hubble tension. arXiv 2021, arXiv:astro-ph.CO/2108.13317. [Google Scholar]
- Moreno-Pulido, C.; Peracaula, J.S. Renormalized ρvac without m4 terms. arXiv 2021, arXiv:gr-qc/2110.08070. [Google Scholar]
- Naidoo, K.; Massara, E.; Lahav, O. Cosmology and neutrino mass with the Minimum Spanning Tree. arXiv 2021, arXiv:astro-ph.CO/2111.12088. [Google Scholar]
- Niedermann, F.; Sloth, M.S. Hot New Early Dark Energy: Towards a Unified Dark Sector of Neutrinos, Dark Energy and Dark Matter. arXiv 2021, arXiv:hep-ph/2112.00759. [Google Scholar]
- Nilsson, N.A.; Park, M.I. Tests of Standard Cosmology in Horava Gravity. arXiv 2021, arXiv:hep-th/2108.07986. [Google Scholar]
- Ray, P.P.; Tarai, S.; Mishra, B.; Tripathy, S.K. Cosmological models with Big rip and Pseudo rip Scenarios in extended theory of gravity. arXiv 2021, arXiv:gr-qc/2107.04413. [Google Scholar] [CrossRef]
- Schöneberg, N.; Abellán, G.F.; Sánchez, A.P.; Witte, S.J.; Poulin, V.; Lesgourgues, J. The H0 Olympics: A fair ranking of proposed models. arXiv 2021, arXiv:astro-ph.CO/2107.10291. [Google Scholar]
- Trott, E.; Huterer, D. Challenges for the statistical gravitational-wave method to measure the Hubble constant. arXiv 2021, arXiv:astro-ph.CO/2112.00241. [Google Scholar]
- Ye, G.; Zhang, J.; Piao, Y.S. Resolving both H0 and S8 tensions with AdS early dark energy and ultralight axion. arXiv 2021, arXiv:astro-ph.CO/2107.13391. [Google Scholar]
- Zhou, Z.; Liu, G.; Xu, L. Can late dark energy restore the Cosmic concordance? arXiv 2021, arXiv:astro-ph.CO/2105.04258. [Google Scholar]
- Zhu, L.G.; Xie, L.H.; Hu, Y.M.; Liu, S.; Li, E.K.; Napolitano, N.R.; Tang, B.T.; dong Zhang, J.; Mei, J. Constraining the Hubble constant to a precision of about 1multi-band dark standard siren detections. arXiv 2021, arXiv:astro-ph.CO/2110.05224. [Google Scholar]
- Alestas, G.; Perivolaropoulos, L.; Tanidis, K. Constraining a late time transition of Geff using low-z galaxy survey data. arXiv 2022, arXiv:astro-ph.CO/2201.05846. [Google Scholar]
- Cea, P. The Ellipsoidal Universe and the Hubble tension. arXiv 2022, arXiv:astro-ph.CO/2201.04548. [Google Scholar]
- Gurzadyan, V.G.; Fimin, N.N.; Chechetkin, V.M. On the origin of cosmic web. Eur. Phys. J. Plus 2022, 137. [Google Scholar] [CrossRef]
- Rashkovetskyi, M.; Muñoz, J.; Eisenstein, D.; Dvorkin, C. Small-scale clumping at recombination and the Hubble tension. Phys. Rev. D 2021, 104, 103517. [Google Scholar] [CrossRef]
- Das, A. Self-interacting neutrinos as a solution to the Hubble tension? arXiv 2021, arXiv:2109.03263. [Google Scholar]
- Karwal, T.; Kamionkowski, M. Dark energy at early times, the Hubble parameter, and the string axiverse. Phys. Rev. D. 2016, 94, e103523. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Nunes, R.C.; Vagnozzi, S.; Mota, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. J. Cosmol. Astropart. Phys. 2018, 2018, 019. [Google Scholar] [CrossRef]
- Di Valentino, E.; Linder, E.V.; Melchiorri, A. Vacuum phase transition solves the H0 tension. Phys. Rev. D 2018, 97, 043528. [Google Scholar] [CrossRef]
- Di Valentino, E.; Ferreira, R.Z.; Visinelli, L.; Danielsson, U. Late time transitions in the quintessence field and the H0 tension. Phys. Dark Univ. 2019, 26, 100385. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Di Valentino, E.; Shafieloo, A.; Chakraborty, S. Reconciling H0 tension in a six parameter space? J. Cosmol. Astropart. Phys. 2020, 2020, 062. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Snowmass2021 - Letter of interest cosmology intertwined I: Perspectives for the next decade. Astropart. Phys. 2021, 131, 102606. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Snowmass2021—Letter of interest cosmology intertwined II: The hubble constant tension. Astropart. Phys. 2021, 131, 102605. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Cosmology Intertwined III: fσ8 and S8. Astropart. Phys. 2021, 131, 102604. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Snowmass2021—Letter of interest cosmology intertwined IV: The age of the universe and its curvature. Astropart. Phys. 2021, 131, 102607. [Google Scholar] [CrossRef]
- Di Valentino, E.; Bœhm, C.; Hivon, E.; Bouchet, F.R. Reducing the H0 and σ8 tensions with dark matter-neutrino interactions. Phys. Rev. D 2018, 97, 043513. [Google Scholar] [CrossRef]
- Di Valentino, E.; Pan, S.; Yang, W.; Anchordoqui, L.A. Touch of neutrinos on the vacuum metamorphosis: Is the H0 solution back? Phys. Rev. D 2021, 103, 123527. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Di Valentino, E.; Pan, S.; Yang, W. Dissecting the H0 and S8 tensions with Planck + BAO + supernova type Ia in multi-parameter cosmologies. J. High Energy Astrophys. 2021, 32, 28–64. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mukherjee, A.; Sen, A.A. Dark Energy with Phantom Crossing and the H0 Tension. Entropy 2021, 23, 404. [Google Scholar] [CrossRef]
- Di Valentino, E.; Linder, E.V.; Melchiorri, A. H0 ex machina: Vacuum metamorphosis and beyond H0. Phys. Dark Univ. 2020, 30, 100733. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Planck evidence for a closed Universe and a possible crisis for cosmology. Nat. Astron. 2020, 4, 196–203. [Google Scholar] [CrossRef]
- Allali, I.J.; Hertzberg, M.P.; Rompineve, F. Dark sector to restore cosmological concordance. Phys. Rev. D 2021, 104. [Google Scholar] [CrossRef]
- Anderson, R.I. Relativistic corrections for measuring Hubble’s constant to 1stellar standard candles. arXiv 2021, arXiv:astro-ph.CO/2108.09067. [Google Scholar]
- Asghari, M.; Sheykhi, A. Observational constraints of the modified cosmology through Barrow entropy. arXiv 2021, arXiv:gr-qc/2110.00059. [Google Scholar]
- Brownsberger, S.; Brout, D.; Scolnic, D.; Stubbs, C.W.; Riess, A.G. The Pantheon+ Analysis: Dependence of Cosmological Constraints on Photometric-Zeropoint Uncertainties of Supernova Surveys. arXiv 2021, arXiv:astro-ph.CO/2110.03486. [Google Scholar]
- Cyr-Racine, F.Y. Cosmic Expansion: A mini review of the Hubble-Lemaitre tension. arXiv 2021, arXiv:astro-ph.CO/2105.09409. [Google Scholar]
- Khosravi, N.; Farhang, M. Phenomenological Gravitational Phase Transition: Early and Late Modifications. arXiv 2021, arXiv:astro-ph.CO/2109.10725. [Google Scholar]
- Mantz, A.B.; Morris, R.G.; Allen, S.W.; Canning, R.E.A.; Baumont, L.; Benson, B.; Bleem, L.E.; Ehlert, S.R.; Floyd, B.; Herbonnet, R.; et al. Cosmological constraints from gas mass fractions of massive, relaxed galaxy clusters. Mon. Not. R. Astron. Soc. 2021, 510, 131–145. [Google Scholar] [CrossRef]
- Mortsell, E.; Goobar, A.; Johansson, J.; Dhawan, S. The Hubble Tension Bites the Dust: Sensitivity of the Hubble Constant Determination to Cepheid Color Calibration. arXiv 2021, arXiv:astro-ph.CO/2105.11461. [Google Scholar]
- Mortsell, E.; Goobar, A.; Johansson, J.; Dhawan, S. The Hubble Tension Revisited: Additional Local Distance Ladder Uncertainties. arXiv 2021, arXiv:astro-ph.CO/2106.09400. [Google Scholar]
- Theodoropoulos, A.; Perivolaropoulos, L. The Hubble Tension, the M Crisis of Late Time H(z) Deformation Models and the Reconstruction of Quintessence Lagrangians. Universe 2021, 7, 300. [Google Scholar] [CrossRef]
- Gómez-Valent, A. Measuring the sound horizon and absolute magnitude of SNIa by maximizing the consistency between low-redshift data sets. arXiv 2022, arXiv:astro-ph.CO/2111.15450. [Google Scholar]
- Pol, A.R.; Caprini, C.; Neronov, A.; Semikoz, D. The gravitational wave signal from primordial magnetic fields in the Pulsar Timing Array frequency band. arXiv 2022, arXiv:astro-ph.CO/2201.05630. [Google Scholar]
- Wong, J.H.W.; Shanks, T.; Metcalfe, N. The Local Hole: A galaxy under-density covering 90% of sky to 200 Mpc. arXiv 2022, arXiv:astro-ph.CO/2107.08505. [Google Scholar]
- Romaniello, M.; Riess, A.; Mancino, S.; Anderson, R.I.; Freudling, W.; Kudritzki, R.P.; Macri, L.; Mucciarelli, A.; Yuan, W. The iron and oxygen content of LMC Classical Cepheids and its implications for the Extragalactic Distance Scale and Hubble constant. arXiv 2021, arXiv:astro-ph.CO/2110.08860. [Google Scholar] [CrossRef]
- Luu, H.N. Axi-Higgs cosmology: Cosmic Microwave Background and cosmological tensions. arXiv 2021, arXiv:astro-ph.CO/2111.01347. [Google Scholar]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. w -M phantom transition at zt<0.1 as a resolution of the Hubble tension. Phys. Rev. D 2021, 103, 083517. [Google Scholar] [CrossRef]
- Sakr, Z.; Sapone, D. Can varying the gravitational constant alleviate the tensions? arXiv 2021, arXiv:astro-ph.CO/2112.14173. [Google Scholar]
- Wang, Y.Y.; Tang, S.P.; Li, X.Y.; Jin, Z.P.; Fan, Y.Z. Prospects of calibrating afterglow modeling of short GRBs with gravitational wave inclination angle measurements and resolving the Hubble constant tension with a GW/GRB association event. arXiv 2021, arXiv:astro-ph.HE/2111.02027. [Google Scholar]
- Safari, Z.; Rezazadeh, K.; Malekolkalami, B. Structure Formation in Dark Matter Particle Production Cosmology. arXiv 2022, arXiv:astro-ph.CO/2201.05195. [Google Scholar]
- Roth, M.M.; Jacoby, G.H.; Ciardullo, R.; Davis, B.D.; Chase, O.; Weilbacher, P.M. Towards Precision Cosmology With Improved PNLF Distances Using VLT-MUSE I. Methodology and Tests. Astrophys. J. 2021, 916, 21. [Google Scholar] [CrossRef]
- Gutiérrez-Luna, E.; Carvente, B.; Jaramillo, V.; Barranco, J.; Escamilla-Rivera, C.; Espinoza, C.; Mondragón, M.; Núñez, D. Scalar field dark matter with two components: Combined approach from particle physics and cosmology. arXiv 2021, arXiv:astro-ph.CO/2110.10258. [Google Scholar]
- Chang, C. Imprint of early dark energy in stochastic gravitational wave background. Phys. Rev. D 2022, 105, 023508. [Google Scholar] [CrossRef]
- Liu, S.; Zhu, L.; Hu, Y.; Zhang, J.; Ji, M. Capability for detection of GW190521-like binary black holes with TianQin. Phys. Rev. D 2022, 105, 023019. [Google Scholar] [CrossRef]
- Farrugia, C.; Sultana, J.; Mifsud, J. Spatial curvature in f(R) gravity. Phys. Rev. D 2021, 104, 123503. [Google Scholar] [CrossRef]
- Lu, W.; Qin, Y. New constraint of the Hubble constant by proper motions of radio components observed in AGN twin-jets. Res. Astron. Astrophys. 2021, 21, 261. [Google Scholar] [CrossRef]
- Greene, K.; Cyr-Racine, F. Hubble distancing: Focusing on distance measurements in cosmology. arXiv 2021, arXiv:2112.11567. [Google Scholar]
- Borghi, N.; Moresco, M.; Cimatti, A. Towards a Better Understanding of Cosmic Chronometers: A new measurement of H(z) at z∼0.7. arXiv 2021, arXiv:2110.04304. [Google Scholar]
- Asencio, E.; Banik, I.; Kroupa, P. A massive blow for ΛCDM—The high redshift, mass, and collision velocity of the interacting galaxy cluster El Gordo contradicts concordance cosmology. Mon. Not. R. Astron. Soc. 2021, 500, 5249–5267. [Google Scholar] [CrossRef]
- Javanmardi, B.; Mérand, A.; Kervella, P.; Breuval, L.; Gallenne, A.; Nardetto, N.; Gieren, W.; Pietrzyński, G.; Hocdé, V.; Borgniet, S. Inspecting the Cepheid Distance Ladder: The Hubble Space Telescope Distance to the SN Ia Host Galaxy NGC 5584. Astrophys. J. 2021, 911, 12. [Google Scholar] [CrossRef]
- Zhao, D.; Xia, J.Q. Constraining the anisotropy of the Universe with the X-ray and UV fluxes of quasars. arXiv 2021, arXiv:2105.03965. [Google Scholar] [CrossRef]
- Thakur, R.K.; Singh, M.; Gupta, S.; Nigam, R. Cosmological Analysis using Panstarrs data: Hubble Constant and Direction Dependence. arXiv 2021, arXiv:2105.14514. [Google Scholar] [CrossRef]
- Sharov, G.S.; Sinyakov, E.S. Cosmological models, observational data and tension in Hubble constant. arXiv 2020, arXiv:2002.03599. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Pacucci, F.; Loeb, A. Implications for the Hubble tension from the ages of the oldest astrophysical objects. arXiv 2021, arXiv:2105.10421. [Google Scholar]
- Staicova, D. Hints of the H0-rd tension in uncorrelated Baryon Acoustic Oscillations dataset. arXiv 2021, arXiv:astro-ph.CO/2111.07907. [Google Scholar]
- Krishnan, C.; Mohayaee, R.; Colgain, E.O.; Sheikh-Jabbari, M.M.; Yin, L. Hints of FLRW Breakdown from Supernovae. arXiv 2021, arXiv:astro-ph.CO/2106.02532. [Google Scholar]
- Li, B.; Shapiro, P.R. Precision cosmology and the stiff-amplified gravitational-wave background from inflation: NANOGrav, Advanced LIGO-Virgo and the Hubble tension. J. Cosmol. Astropart. Phys. 2021, 2021, 024. [Google Scholar] [CrossRef]
- Mozzon, S.; Ashton, G.; Nuttall, L.K.; Williamson, A.R. Does non-stationary noise in LIGO and Virgo affect the estimation of H0? arXiv 2021, arXiv:astro-ph.CO/2110.11731. [Google Scholar]
- Abbott, T.C.; Buffaz, E.; Vieira, N.; Cabero, M.; Haggard, D.; Mahabal, A.; McIver, J. GWSkyNet-Multi: A Machine Learning Multi-Class Classifier for LIGO-Virgo Public Alerts. arXiv 2021, arXiv:astro-ph.IM/2111.04015. [Google Scholar]
- Mehrabi, A.; Basilakos, S.; Tsiapi, P.; Plionis, M.; Terlevich, R.; Terlevich, E.; Moran, A.L.G.; Chavez, R.; Bresolin, F.; Arenas, D.F.; et al. Using our newest VLT-KMOS HII Galaxies and other cosmic tracers to test the ΛCDM tension. Mon. Not. R. Astron. Soc. 2021, 509, 224–231. [Google Scholar] [CrossRef]
- Li, J.X.; Wu, F.Q.; Li, Y.C.; Gong, Y.; Chen, X.L. Cosmological constraint on Brans–Dicke Model. Res. Astron. Astrophys. 2015, 15, 2151–2163. [Google Scholar] [CrossRef][Green Version]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, G.Q.; Wang, F.Y. An 8% Determination of the Hubble Constant from localized Fast Radio Bursts. arXiv 2021, arXiv:astro-ph.CO/2108.00581. [Google Scholar]
- Perivolaropoulos, L.; Skara, F. Hubble tension or a transition of the Cepheid Sn Ia calibrator parameters? arXiv 2021, arXiv:astro-ph.CO/2109.04406. [Google Scholar]
- Horstmann, N.; Pietschke, Y.; Schwarz, D.J. Inference of the cosmic rest-frame from supernovae Ia. arXiv 2021, arXiv:astro-ph.CO/2111.03055. [Google Scholar]
- Ferree, N.C.; Bunn, E.F. Constraining H0 Via Extragalactic Parallax. arXiv 2021, arXiv:astro-ph.CO/2109.07529. [Google Scholar]
- Luongo, O.; Muccino, M.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yin, L. On Larger H0 Values in the CMB Dipole Direction. arXiv 2021, arXiv:astro-ph.CO/2108.13228. [Google Scholar]
- de Souza, J.M.S.; Sturani, R.; Alcaniz, J. Cosmography with Standard Sirens from the Einstein Telescope. arXiv 2021, arXiv:gr-qc/2110.13316. [Google Scholar]
- Fang, Y.; Yang, H. Orbit Tomography of Binary Supermassive Black Holes with Very Long Baseline Interferometry. arXiv 2021, arXiv:gr-qc/2111.00368. [Google Scholar]
- Palmese, A.; Bom, C.R.; Mucesh, S.; Hartley, W.G. A standard siren measurement of the Hubble constant using gravitational wave events from the first three LIGO/Virgo observing runs and the DESI Legacy Survey. arXiv 2021, arXiv:astro-ph.CO/2111.06445. [Google Scholar]
- Yang, T.; Lee, H.M.; Cai, R.G.; gil Choi, H.; Jung, S. Space-borne Atom Interferometric Gravitational Wave Detections II: Dark Sirens and Finding the One. arXiv 2021, arXiv:gr-qc/2110.09967. [Google Scholar] [CrossRef]
- Gray, R.; Messenger, C.; Veitch, J. A Pixelated Approach to Galaxy Catalogue Incompleteness: Improving the Dark Siren Measurement of the Hubble Constant. arXiv 2021, arXiv:astro-ph.CO/2111.04629. [Google Scholar]
- Moresco, M.; Amati, L.; Amendola, L.; Birrer, S.; Blakeslee, J.P.; Cantiello, M.; Cantiello, A.; Darling, J.; Della Valle, M.; Fishbach, M.; et al. Unveiling the Universe with Emerging Cosmological Probes. arXiv 2022, arXiv:astro-ph.CO/2201.07241. [Google Scholar]
- The LIGO Scientific Collaboration; the Virgo Collaboration; the KAGRA Collaboration; Abbott, R.; Abe, H.; Acernese, F.; Ackley, K.; Adhikari, N.; Adhikari, R.X.; Adkins, V.K.; et al. Constraints on the cosmic expansion history from GWTC-3. arXiv 2021, arXiv:2111.03604. [Google Scholar]
- Nunes, R.C.; Pan, S.; Saridakis, E.N.; Abreu, E.M. New observational constraints onf(R) gravity from cosmic chronometers. J. Cosmol. Astropart. Phys. 2017, 2017, 005. [Google Scholar] [CrossRef]
- Nunes, R.C. Structure formation in f(T) gravity and a solution for H0 tension. J. Cosmol. Astropart. Phys. 2018, 2018, 052. [Google Scholar] [CrossRef]
- Benetti, M.; Capozziello, S.; Lambiase, G. Updating constraints on f(T) teleparallel cosmology and the consistency with big bang nucleosynthesis. Mon. Not. R. Astron. Soc. 2020, 500, 1795–1805. [Google Scholar] [CrossRef]
- Räsänen, S. Light propagation in statistically homogeneous and isotropic dust universes. J. Cosmol. Astropart. Phys. 2009, 2009, 011. [Google Scholar] [CrossRef]
- Räsänen, S. Light propagation in statistically homogeneous and isotropic universes with general matter content. J. Cosmol. Astropart. Phys. 2010, 2010, 018. [Google Scholar] [CrossRef]
- Sotiriou, T.P. f(R) gravity and scalar tensor theory. Class. Quantum Gravity 2006, 23, 5117–5128. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 04, 115–145. [Google Scholar] [CrossRef]
- Koksbang, S.M. Towards statistically homogeneous and isotropic perfect fluid universes with cosmic backreaction. Class. Quantum Gravity 2019, 36, 185004. [Google Scholar] [CrossRef]
- Koksbang, S. Another look at redshift drift and the backreaction conjecture. J. Cosmol. Astropart. Phys. 2019, 2019, 036. [Google Scholar] [CrossRef]
- Koksbang, S.M. Observations in statistically homogeneous, locally inhomogeneous cosmological toy-models without FLRW backgrounds. arXiv 2020, arXiv:astro-ph.CO/2008.07108. [Google Scholar]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Odderskov, I.; Koksbang, S.; Hannestad, S. The local value ofH0in an inhomogeneous universe. J. Cosmol. Astropart. Phys. 2016, 2016, 001. [Google Scholar] [CrossRef][Green Version]
- Nájera, A.; Fajardo, A. Testing f(Q,T) gravity models that have ΛCDM as a submodel. arXiv 2021, arXiv:2104.14065. [Google Scholar]
- Nájera, A.; Fajardo, A. Fitting f(Q,T) gravity models with a ΛCDM limit using H(z) and Pantheon data. Phys. Dark Univ. 2021, 34, 100889. [Google Scholar] [CrossRef]
- Nájera, A.; Fajardo, A. Cosmological Perturbation Theory in f(Q,T) Gravity. arXiv 2021, arXiv:gr-qc/2111.04205. [Google Scholar]
- Linares Cedeño, F.X.; Nucamendi, U. Revisiting cosmological diffusion models in Unimodular Gravity and the H0 tension. Phys. Dark Univ. 2021, 32, 100807. [Google Scholar] [CrossRef]
- Fung, L.W.; Li, L.; Liu, T.; Luu, H.N.; Qiu, Y.C.; Tye, S.H.H. The Hubble Constant in the Axi-Higgs Universe. arXiv 2021, arXiv:astro-ph.CO/2105.01631. [Google Scholar]
- Shokri, M.; Sadeghi, J.; Setare, M.R.; Capozziello, S. Nonminimal coupling inflation with constant slow roll. arXiv 2021, arXiv:2104.00596. [Google Scholar] [CrossRef]
- Castellano, A.; Font, A.; Herraez, A.; Ibáñez, L.E. A Gravitino Distance Conjecture. arXiv 2021, arXiv:2104.10181. [Google Scholar] [CrossRef]
- Tomita, K. Cosmological renormalization of model parameters in second-order perturbation theory. Prog. Theor. Exp. Phys. 2017, 2017, 053E01. [Google Scholar] [CrossRef]
- Tomita, K. Cosmological models with the energy density of random fluctuations and the Hubble-constant problem. Prog. Theor. Exp. Phys. 2017, 2017, 083E04. [Google Scholar] [CrossRef]
- Tomita, K. Super-horizon second-order perturbations for cosmological random fluctuations and the Hubble-constant problem. Prog. Theor. Exp. Phys. 2018, 2018, 021E01. [Google Scholar] [CrossRef]
- Tomita, K. Hubble constants and luminosity distance in the renormalized cosmological models due to general-relativistic second-order perturbations. arXiv 2019, arXiv:1906.09519. [Google Scholar]
- Tomita, K. Cosmological renormalization of model parameters in the second-order perturbation theory. Prog. Theor. Exp. Phys. 2020, 2020, 019202. [Google Scholar] [CrossRef]
- Belgacem, E.; Prokopec, T. Quantum origin of dark energy and the Hubble tension. arXiv 2021, arXiv:astro-ph.CO/2111.04803. [Google Scholar]
- Bernardo, R.C.; Grandón, D.; Said, J.L.; Cárdenas, V.H. Parametric and nonparametric methods hint dark energy evolution. arXiv 2022, arXiv:astro-ph.CO/2111.08289. [Google Scholar]
- Ambjorn, J.; Watabiki, Y. Easing the Hubble constant tension? arXiv 2021, arXiv:gr-qc/2111.05087. [Google Scholar]
- Di Bari, P.; Marfatia, D.; Zhou, Y.L. Gravitational waves from first-order phase transitions in Majoron models of neutrino mass. arXiv 2021, arXiv:2106.00025. [Google Scholar] [CrossRef]
- Duan, W.F.; Li, S.P.; Li, X.Q.; Yang, Y.D. Linking RK(*) anomalies to H0 tension via Dirac neutrino. arXiv 2021, arXiv:hep-ph/2111.05178. [Google Scholar]
- Ghosh, D. Explaining the RK and RK* anomalies. Eur. Phys. J. C 2017, 77. [Google Scholar] [CrossRef]
- Burgess, C.P.; Dineen, D.; Quevedo, F. Yoga Dark Energy: Natural Relaxation and Other Dark Implications of a Supersymmetric Gravity Sector. arXiv 2021, arXiv:hep-th/2111.07286. [Google Scholar]
- Jiang, J.Q.; Piao, Y.S. Testing AdS early dark energy with Planck, SPTpol and LSS data. arXiv 2021, arXiv:astro-ph.CO/2107.07128. [Google Scholar] [CrossRef]
- Karwal, T.; Raveri, M.; Jain, B.; Khoury, J.; Trodden, M. Chameleon Early Dark Energy and the Hubble Tension. arXiv 2021, arXiv:astro-ph.CO/2106.13290. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Sáez-Chillón Gómez, D.; Sharov, G.S. Modeling and testing the equation of state for (Early) dark energy. Phys. Dark Univ. 2021, 32, 100837. [Google Scholar] [CrossRef]
- Tian, S.X.; Zhu, Z.H. Early dark energy in k-essence. Phys. Rev. D 2021, 103, 043518. [Google Scholar] [CrossRef]
- Linares Cedeño, F.X.; Roy, N.; Ureña-López, L.A. Tracker phantom field and a cosmological constant: Dynamics of a composite dark energy model. arXiv 2021, arXiv:2105.07103. [Google Scholar]
- Hernández-Almada, A.; Leon, G.; Magaña, J.; García-Aspeitia, M.A.; Motta, V.; Saridakis, E.N.; Yesmakhanova, K. Kaniadakis holographic dark energy: Observational constraints and global dynamics. arXiv 2021, arXiv:astro-ph.CO/2111.00558. [Google Scholar]
- Hernández-Almada, A.; García-Aspeitia, M.A.; Rodríguez-Meza, M.A.; Motta, V. A hybrid model of viscous and Chaplygin gas to tackle the Universe acceleration. Eur. Phys. J. C 2021, 81, 295. [Google Scholar] [CrossRef]
- Abchouyeh, M.A.; van Putten, M.H.P.M. Late-time Universe, H0-tension, and unparticles. Phys. Rev. D 2021, 104, 083511. [Google Scholar] [CrossRef]
- Wang, D. Dark energy constraints in light of Pantheon SNe Ia, BAO, cosmic chronometers and CMB polarization and lensing data. Phys. Rev. D 2018, 97, 123507. [Google Scholar] [CrossRef]
- Ye, G.; Hu, B.; Piao, Y.S. Implication of the Hubble tension for the primordial Universe in light of recent cosmological data. Phys. Rev. D 2021, 104, 063510. [Google Scholar] [CrossRef]
- Nguyen, H. Analyzing Pantheon SNeIa data in the context of Barrow’s variable speed of light. arXiv 2020, arXiv:2010.10292. [Google Scholar]
- Barrow, J.D. Cosmologies with varying light speed. Phys. Rev. D 1999, 59, 043515. [Google Scholar] [CrossRef]
- Artymowski, M.; Ben-Dayan, I.; Kumar, U. More on Emergent Dark Energy from Unparticles. arXiv 2021. [Google Scholar]
- Yang, W.; Di Valentino, E.; Pan, S.; Shafieloo, A.; Li, X. Generalized Emergent Dark Energy Model and the Hubble Constant Tension. arXiv 2021, arXiv:2103.03815. [Google Scholar] [CrossRef]
- Adil, S.A.; Gangopadhyay, M.R.; Sami, M.; Sharma, M.K. Late time acceleration due to generic modification of gravity and Hubble tension. arXiv 2021, arXiv:2106.03093. [Google Scholar] [CrossRef]
- Vagnozzi, S. Consistency tests of ΛCDM from the early ISW effect: Implications for early-time new physics and the Hubble tension. arXiv 2021, arXiv:2105.10425. [Google Scholar]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. H0 tension, phantom dark energy, and cosmological parameter degeneracies. Phys. Rev. D 2020, 101, 123516. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Koo, H.; Nesseris, S.; Perivolaropoulos, L.; Shafieloo, A. Hints for possible low redshift oscillation around the best-fitting ΛCDM model in the expansion history of the Universe. Mon. Not. R. Astron. Soc. 2021, 501, 3421–3426. [Google Scholar] [CrossRef]
- Martín, M.S.; Rubio, C. Hubble tension and matter inhomogeneities: A theoretical perspective. arXiv 2021, arXiv:astro-ph.CO/2107.14377. [Google Scholar]
- Buchert, T. On Average Properties of Inhomogeneous Fluids in General Relativity: Dust Cosmologies. Gen. Relativ. Gravit. 2000, 32, 105–125. [Google Scholar] [CrossRef]
- Gasperini, M.; Marozzi, G.; Veneziano, G. Gauge invariant averages for the cosmological backreaction. J. Cosmol. Astropart. Phys. 2009, 2009, 011. [Google Scholar] [CrossRef]
- Gasperini, M.; Marozzi, G.; Nugier, F.; Veneziano, G. Light-cone averaging in cosmology: Formalism and applications. J. Cosmol. Astropart. Phys. 2011, 2011, 008. [Google Scholar] [CrossRef]
- Fanizza, G.; Gasperini, M.; Marozzi, G.; Veneziano, G. Generalized covariant prescriptions for averaging cosmological observables. J. Cosmol. Astropart. Phys. 2020, 2020, 017. [Google Scholar] [CrossRef]
- Ben-Dayan, I.; Gasperini, M.; Marozzi, G.; Nugier, F.; Veneziano, G. Average and dispersion of the luminosity-redshift relation in the concordance model. J. Cosmol. Astropart. Phys. 2013, 2013, 002. [Google Scholar] [CrossRef]
- Fleury, P.; Clarkson, C.; Maartens, R. How does the cosmic large-scale structure bias the Hubble diagram? J. Cosmol. Astropart. Phys. 2017, 2017, 062. [Google Scholar] [CrossRef]
- Adamek, J.; Clarkson, C.; Coates, L.; Durrer, R.; Kunz, M. Bias and scatter in the Hubble diagram from cosmological large-scale structure. Phys. Rev. D 2019, 100, 021301. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Avgoustidis, A.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Relativ. 2018, 21, 2. [Google Scholar] [CrossRef] [PubMed]
- Fanizza, G. Precision Cosmology and Hubble tension in the era of LSS survey. arXiv 2021, arXiv:astro-ph.CO/2110.15272. [Google Scholar]
- Andreoni, I.; Margutti, R.; Salafia, O.S.; Parazin, B.; Villar, V.A.; Coughlin, M.W.; Yoachim, P.; Mortensen, K.; Brethauer, D.; Smartt, S.J.; et al. Target of Opportunity Observations of Gravitational Wave Events with Vera C. Rubin Observatory. arXiv 2021, arXiv:astro-ph.HE/2111.01945. [Google Scholar]
- Ben-Dayan, I.; Durrer, R.; Marozzi, G.; Schwarz, D.J. Value of H0 in the Inhomogeneous Universe. Phys. Rev. Lett. 2014, 112, 221301. [Google Scholar] [CrossRef]
- Fanizza, G.; Fiorini, B.; Marozzi, G. Cosmic variance of H0 in light of forthcoming high-redshift surveys. Phys. Rev. D 2021, 104, 083506. [Google Scholar] [CrossRef]
- Haslbauer, M.; Banik, I.; Kroupa, P. The KBC void and Hubble tension contradict ΛCDM on a Gpc scale—Milgromian dynamics as a possible solution. Mon. Not. R. Astron. Soc. 2020, 499, 2845–2883. [Google Scholar] [CrossRef]
- Perivolaropoulos, L. Large Scale Cosmological Anomalies and Inhomogeneous Dark Energy. Galaxies 2014, 2, 22–61. [Google Scholar] [CrossRef]
- Castello, S.; Högås, M.; Mörtsell, E. A Cosmological Underdensity Does Not Solve the Hubble Tension. arXiv 2021, arXiv:astro-ph.CO/2110.04226. [Google Scholar]
- Banik, I.; Zhao, H. From galactic bars to the Hubble tension—Weighing up the astrophysical evidence for Milgromian gravity. arXiv 2021, arXiv:astro-ph.CO/2110.06936. [Google Scholar]
- Alestas, G.; Perivolaropoulos, L. Late-time approaches to the Hubble tension deforming H(z), worsen the growth tension. Mon. Not. R. Astron. Soc. 2021, 504, 3956–3962. [Google Scholar] [CrossRef]
- Normann, B.D.; Brevik, I.H. Can the Hubble tension be resolved by bulk viscosity? Mod. Phys. Lett. A 2021, 36, 2150198. [Google Scholar] [CrossRef]
- Bernal, J.L.; Verde, L.; Jimenez, R.; Kamionkowski, M.; Valcin, D.; Wandelt, B.D. Trouble beyond H0 and the new cosmic triangles. Phys. Rev. D 2021, 103, 103533. [Google Scholar] [CrossRef]
- Thiele, L.; Guan, Y.; Hill, J.C.; Kosowsky, A.; Spergel, D.N. Can small-scale baryon inhomogeneities resolve the Hubble tension? An investigation with ACT DR4. arXiv 2021, arXiv:2105.03003. [Google Scholar] [CrossRef]
- Grande, J.; Perivolaropoulos, L. Generalized Lemaître-Tolman-Bondi model with inhomogeneous isotropic dark energy: Observational constraints. Phys. Rev. D 2011, 84, 023514. [Google Scholar] [CrossRef]
- Dinda, B.R. Cosmic expansion parametrization: Implication for curvature and H0 tension. arXiv 2021, arXiv:2106.02963. [Google Scholar]
- Marra, V.; Perivolaropoulos, L. Rapid transition of Geff at zt≈0.01 as a possible solution of the Hubble and growth tensions. Phys. Rev. D 2021, 104. [Google Scholar] [CrossRef]
- Krishnan, C.; Colgáin, E.Ó.; Sen, A.A.; Sheikh-Jabbari, M.M.; Yang, T. Is there an early Universe solution to Hubble tension? Phys. Rev. D 2020, 102, 103525. [Google Scholar] [CrossRef]
- Krishnan, C.; Colgain, E.O.; Sheikh-Jabbari, M.M.; Yang, T. Running Hubble tension and a H0 diagnostic. Phys. Rev. D 2021, 103, 103509. [Google Scholar] [CrossRef]
- Krishnan, C.; Mohayaee, R.; Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Yin, L. Does Hubble Tension Signal a Breakdown in FLRW Cosmology? arXiv 2021, arXiv:2105.09790. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and World-Structure. Astrophys. J. 1935, 82, 284. [Google Scholar] [CrossRef]
- Gerardi, F.; Feeney, S.M.; Alsing, J. Unbiased likelihood-free inference of the Hubble constant from light standard sirens. arXiv 2021, arXiv:2104.02728. [Google Scholar] [CrossRef]
- Escamilla-Rivera, C.; Levi Said, J.; Mifsud, J. Performance of Non-Parametric Reconstruction Techniques in the Late-Time Universe. arXiv 2021, arXiv:2105.14332. [Google Scholar] [CrossRef]
- Sun, W.; Jiao, K.; Zhang, T.J. Influence of the Bounds of the Hyperparameters on the Reconstruction of Hubble Constant with Gaussian Process. arXiv 2021, arXiv:astro-ph.CO/2105.12618. [Google Scholar] [CrossRef]
- Renzi, F.; Silvestri, A. A look at the Hubble speed from first principles. arXiv 2020, arXiv:astro-ph.CO/2011.10559. [Google Scholar]
- Gurzadyan, V.G.; Stepanian, A. Hubble tension vs. two flows. Eur. Phys. J. Plus 2021, 136. [Google Scholar] [CrossRef]
- Geng, C.Q.; Hsu, Y.T.; Lu, J.R.; Yin, L. A Dark Energy model from Generalized Proca Theory. Phys. Dark Univ. 2021, 32, 100819. [Google Scholar] [CrossRef]
- Reyes, M.; Escamilla-Rivera, C. Improving data-driven model-independent reconstructions and updated constraints on dark energy models from Horndeski cosmology. arXiv 2021, arXiv:2104.04484. [Google Scholar] [CrossRef]
- Petronikolou, M.; Basilakos, S.; Saridakis, E.N. Alleviating H0 tension in Horndeski gravity. arXiv 2021, arXiv:gr-qc/2110.01338. [Google Scholar]
- Alestas, G.; Antoniou, I.; Perivolaropoulos, L. Hints for a Gravitational Transition in Tully–Fisher Data. Universe 2021, 7, 366. [Google Scholar] [CrossRef]
- Benisty, D.; Staicova, D. A preference for Dynamical Dark Energy? arXiv 2021, arXiv:astro-ph.CO/2107.14129. [Google Scholar]
- Ó Colgáin, E.; Sheikh-Jabbari, M.; Yin, L. Can dark energy be dynamical? Phys. Rev. D 2021, 104. [Google Scholar] [CrossRef]
- Chevallier, M.; Polarski, D. Accelerating Universes with Scaling Dark Matter. Int. J. Mod. Phys. D 2001, 10, 213–223. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the Expansion History of the Universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef]
- Aloni, D.; Berlin, A.; Joseph, M.; Schmaltz, M.; Weiner, N. A Step in Understanding the Hubble Tension. arXiv 2021, arXiv:astro-ph.CO/2111.00014. [Google Scholar]
- Ghosh, S.; Kumar, S.; Tsai, Y. Free-streaming and Coupled Dark Radiation Isocurvature Perturbations: Constraints and Application to the Hubble Tension. arXiv 2021, arXiv:astro-ph.CO/2107.09076. [Google Scholar]
- Shrivastava, P.; Khan, A.J.; Goswami, G.K.; Yadav, A.K.; Singh, J.K. The simplest parametrization of equation of state parameter in the scalar field Universe. arXiv 2021, arXiv:astro-ph.CO/2107.05044. [Google Scholar]
- Pereira, S.H. An unified cosmological model driven by a scalar field nonminimally coupled to gravity. arXiv 2021, arXiv:astro-ph.CO/2111.00029. [Google Scholar]
- Bag, S.; Sahni, V.; Shafieloo, A.; Shtanov, Y. Phantom braneworld and the Hubble tension. arXiv 2021, arXiv:astro-ph.CO/2107.03271. [Google Scholar] [CrossRef]
- Franchino-Viñas, S.A.; Mosquera, M.E. The cosmological lithium problem, varying constants and the H0 tension. arXiv 2021, arXiv:astro-ph.CO/2107.02243. [Google Scholar]
- Palle, D. Einstein–Cartan cosmology and the high-redshift Universe. arXiv 2021, arXiv:physics.gen-ph/2106.08136. [Google Scholar]
- Liu, W.; Anchordoqui, L.A.; Valentino, E.D.; Pan, S.; Wu, Y.; Yang, W. Constraints from High-Precision Measurements of the Cosmic Microwave Background: The Case of Disintegrating Dark Matter with Λ or Dynamical Dark Energy. arXiv 2021, arXiv:astro-ph.CO/2108.04188. [Google Scholar]
- Blinov, N.; Krnjaic, G.; Li, S.W. Towards a Realistic Model of Dark Atoms to Resolve the Hubble Tension. arXiv 2021, arXiv:hep-ph/2108.11386. [Google Scholar]
- Galli, S.; Pogosian, L.; Jedamzik, K.; Balkenhol, L. Consistency of Planck, ACT and SPT constraints on magnetically assisted recombination and forecasts for future experiments. arXiv 2021, arXiv:astro-ph.CO/2109.03816. [Google Scholar] [CrossRef]
- Liu, X.H.; Li, Z.H.; Qi, J.Z.; Zhang, X. Galaxy-Scale Test of General Relativity with Strong Gravitational Lensing. arXiv 2021, arXiv:astro-ph.CO/2109.02291. [Google Scholar]
- Hou, S.; Fan, X.L.; Zhu, Z.H. Constraining cosmological parameters from strong lensing with DECIGO and B-DECIGO sources. Mon. Not. R. Astron. Soc. 2021, 507, 761–771. [Google Scholar] [CrossRef]
- Sola, J. Running vacuum interacting with dark matter or with running gravitational coupling. Phenomenological implications. arXiv 2021, arXiv:gr-qc/2109.12086. [Google Scholar]
- Cuesta, A.J.; Gómez, M.E.; Illana, J.I.; Masip, M. Cosmology of an Axion-Like Majoron. arXiv 2021, arXiv:hep-ph/2109.07336. [Google Scholar]
- González-López, M. Neutrino Masses and Hubble Tension via a Majoron in MFV. arXiv 2021, arXiv:hep-ph/2110.15698. [Google Scholar]
- Prat, J.; Hogan, C.; Chang, C.; Frieman, J. Vacuum Energy Density Measured from Cosmological Data. arXiv 2021, arXiv:astro-ph.CO/2111.08151. [Google Scholar]
- Joseph, A.; Saha, R. Dark energy with oscillatory tracking potential: Observational Constraints and Perturbative effects. arXiv 2021, arXiv:astro-ph.CO/2110.00229. [Google Scholar] [CrossRef]
- Aghababaei, S.; Moradpour, H.; Vagenas, E.C. Hubble tension bounds the GUP and EUP parameters. Eur. Phys. J. Plus 2021, 136. [Google Scholar] [CrossRef]
- Bansal, S.; Kim, J.H.; Kolda, C.; Low, M.; Tsai, Y. Mirror Twin Higgs Cosmology: Constraints and a Possible Resolution to the H0 and S8 Tensions. arXiv 2021, arXiv:hep-ph/2110.04317. [Google Scholar]
- Dialektopoulos, K.; Said, J.L.; Mifsud, J.; Sultana, J.; Adami, K.Z. Neural Network Reconstruction of Late-Time Cosmology and Null Tests. arXiv 2021, arXiv:astro-ph.CO/2111.11462. [Google Scholar]
- Alestas, G.; Camarena, D.; Valentino, E.D.; Kazantzidis, L.; Marra, V.; Nesseris, S.; Perivolaropoulos, L. Late-transition vs. smooth H(z) deformation models for the resolution of the Hubble crisis. arXiv 2021, arXiv:astro-ph.CO/2110.04336. [Google Scholar]
- Parnovsky, S. Possible Modification of the Standard Cosmological Model to Resolve a Tension with Hubble Constant Values. Ukr. J. Phys. 2021, 66, 739. [Google Scholar] [CrossRef]
- Zhang, P.; D’Amico, G.; Senatore, L.; Zhao, C.; Cai, Y. BOSS Correlation Function Analysis from the Effective Field Theory of Large-Scale Structure. arXiv 2021, arXiv:astro-ph.CO/2110.07539. [Google Scholar]
- Hansen, S.H. Accelerated expansion induced by dark matter with two charges. Mon. Not. R. Astron. Soc. Lett. 2021, 508, 22–25. [Google Scholar] [CrossRef]
- Gariazzo, S.; Valentino, E.D.; Mena, O.; Nunes, R.C. Robustness of non-standard cosmologies solving the Hubble constant tension. arXiv 2021, arXiv:astro-ph.CO/2111.03152. [Google Scholar]
- Ruiz-Zapatero, J.; Stölzner, B.; Joachimi, B.; Asgari, M.; Bilicki, M.; Dvornik, A.; Giblin, B.; Heymans, C.; Hildebrandt, H.; Kannawadi, A.; et al. Geometry versus growth—Internal consistency of the flat model with KiDS-1000. Astron. Astrophys. 2021, 655, A11. [Google Scholar] [CrossRef]
- Cai, R.G.; Guo, Z.K.; Wang, S.J.; Yu, W.W.; Zhou, Y. A No-Go guide for the Hubble tension. arXiv 2021, arXiv:astro-ph.CO/2107.13286. [Google Scholar]
- Mehrabi, A.; Vazirnia, M. Non-parametric modeling of the cosmological data, base on the χ2 distribution. arXiv 2021, arXiv:astro-ph.CO/2107.11539. [Google Scholar]
- Parnovsky, S.L. Bias of the Hubble constant value caused by errors in galactic distance indicators. arXiv 2021, arXiv:astro-ph.CO/2109.09645. [Google Scholar] [CrossRef]
- Baldwin, D.; Schechter, P.L. A Malmquist-like bias in the inferred areas of diamond caustics and the resulting bias in inferred time delays for gravitationally lensed quasars. arXiv 2021, arXiv:astro-ph.CO/2110.06378. [Google Scholar]
- Huber, S.; Suyu, S.H.; Ghoshdastidar, D.; Taubenberger, S.; Bonvin, V.; Chan, J.H.H.; Kromer, M.; Noebauer, U.M.; Sim, S.A.; Leal-Taixé, L. HOLISMOKES—VII. Time-delay measurement of strongly lensed SNe Ia using machine learning. arXiv 2021, arXiv:astro-ph.CO/2108.02789. [Google Scholar]
- Mercier, C. A New Physics Would Explain What Looks Like an Irreconcilable Tension between the Values of Hubble Constants and Allows H0 to Be Calculated Theoretically Several Ways. J. Mod. Phys. 2021, 12, 1656–1707. [Google Scholar] [CrossRef]
- Ren, X.; Wong, T.H.T.; Cai, Y.F.; Saridakis, E.N. Data-driven reconstruction of the late-time cosmic acceleration with f(T) gravity. Phys. Dark Univ. 2021, 32, 100812. [Google Scholar] [CrossRef]
- Hryczuk, A.; Jodłowski, K. Self-interacting dark matter from late decays and the H0 tension. Phys. Rev. D 2020, 102. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. arXiv 2021, arXiv:2105.05208. [Google Scholar]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Vargas Moniz, P.; Capozziello, S.; Beltrán Jiménez, J.; De Laurentis, M.; Olmo, G.J.; Akrami, Y.; Bahamonde, S.; et al. Modified Gravity and Cosmology: An Update by the CANTATA Network. arXiv 2021, arXiv:2105.12582. [Google Scholar]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Guy, J.; Sullivan, M.; Conley, A.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. The Supernova Legacy Survey 3-year sample: Type Ia supernovae photometric distances and cosmological constraints. Astron. Astrophys. 2010, 523, A7. [Google Scholar] [CrossRef]
- Chotard, N.; Gangler, E.; Aldering, G.; Antilogus, P.; Aragon, C.; Bailey, S.; Baltay, C.; Bongard, S.; Buton, C.; Canto, A.; et al. The reddening law of type Ia supernovae: Separating intrinsic variability from dust using equivalent widths. Astron. Astrophys. 2011, 529, L4. [Google Scholar] [CrossRef]
- Kenworthy, W.D.; Scolnic, D.; Riess, A. The Local Perspective on the Hubble Tension: Local Structure Does Not Impact Measurement of the Hubble Constant. Astrophys. J. 2019, 875, 145. [Google Scholar] [CrossRef]
- Deng, H.K.; Wei, H. Null signal for the cosmic anisotropy in the Pantheon supernovae data. Eur. Phys. J. C 2018, 78, 755. [Google Scholar] [CrossRef]
- Akarsu, Ö.; Kumar, S.; Sharma, S.; Tedesco, L. Constraints on a Bianchi type I spacetime extension of the standard Λ CDM model. Phys. Rev. D 2019, 100, 023532. [Google Scholar] [CrossRef]
- Shafieloo, A.; L’Huillier, B.; Starobinsky, A.A. Falsifying ΛCDM: Model-independent tests of the concordance model with eBOSS DR14Q and Pantheon. Phys. Rev. D 2018, 98, 083526. [Google Scholar] [CrossRef]
- Hossienkhani, H.; Azimi, N.; Zarei, Z. Probing the anisotropy effects on the CPL parametrizations from light-curve SNIa, BAO and OHD datasets. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950177. [Google Scholar] [CrossRef]
- L’Huillier, B.; Shafieloo, A.; Linder, E.V.; Kim, A.G. Model independent expansion history from supernovae: Cosmology versus systematics. Mon. Not. R. Astron. Soc. 2019, 485, 2783–2790. [Google Scholar] [CrossRef]
- Lusso, E.; Piedipalumbo, E.; Risaliti, G.; Paolillo, M.; Bisogni, S.; Nardini, E.; Amati, L. Tension with the flat ΛCDM model from a high-redshift Hubble diagram of supernovae, quasars, and gamma-ray bursts. Astron. Astrophys. 2019, 628, L4. [Google Scholar] [CrossRef]
- Ma, Y.B.; Cao, S.; Zhang, J.; Qi, J.; Liu, T.; Liu, Y.; Geng, S. Testing Cosmic Opacity with the Combination of Strongly Lensed and Unlensed Supernova Ia. Astrophys. J. 2019, 887, 163. [Google Scholar] [CrossRef]
- Sadri, E. Observational constraints on interacting Tsallis holographic dark energy model. Eur. Phys. J. C 2019, 79, 762. [Google Scholar] [CrossRef]
- Sadri, E.; Khurshudyan, M. An interacting new holographic dark energy model: Observational constraints. Int. J. Mod. Phys. D 2019, 28, 1950152. [Google Scholar] [CrossRef]
- Wagner, J.; Meyer, S. Generalized model-independent characterization of strong gravitational lenses V: Reconstructing the lensing distance ratio by supernovae for a general Friedmann universe. Mon. Not. R. Astron. Soc. 2019, 490, 1913–1927. [Google Scholar] [CrossRef]
- Zhai, Z.; Wang, Y. Robust and model-independent cosmological constraints from distance measurements. J. Cosmol. Astropart. Phys. 2019, 2019, 005. [Google Scholar] [CrossRef]
- Zhao, D.; Zhou, Y.; Chang, Z. Anisotropy of the Universe via the Pantheon supernovae sample revisited. Mon. Not. R. Astron. Soc. 2019, 486, 5679–5689. [Google Scholar] [CrossRef]
- Abdullah, M.H.; Klypin, A.; Wilson, G. Cosmological Constraints on Ωm and σ8 from Cluster Abundances Using the GalWCat19 Optical-spectroscopic SDSS Catalog. Astrophys. J. 2020, 901, 90. [Google Scholar] [CrossRef]
- Al Mamon, A.; Saha, S. The logotropic dark fluid: Observational and thermodynamic constraints. Int. J. Mod. Phys. D 2020, 29, 2050097. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Basilakos, S.; Saridakis, E.N. Observational constraints on Barrow holographic dark energy. Eur. Phys. J. C 2020, 80, 826. [Google Scholar] [CrossRef]
- Brout, D.; Hinton, S.R.; Scolnic, D. Binning is Sinning (Supernova Version): The Impact of Self-calibration in Cosmological Analyses with Type Ia Supernovae. Astrophys. J. Lett. 2021, 912, L26. [Google Scholar] [CrossRef]
- Cai, R.G.; Ding, J.F.; Guo, Z.K.; Wang, S.J.; Yu, W.W. Do the observational data favor a local void? Phys. Rev. D 2021, 103, 123539. [Google Scholar] [CrossRef]
- Chang, Z.; Zhao, D.; Zhou, Y. Constraining the anisotropy of the Universe with the Pantheon supernovae sample. Chin. Phys. C 2019, 43, 125102. [Google Scholar] [CrossRef]
- D’Amico, G.; Senatore, L.; Zhang, P. Limits on wCDM from the EFTofLSS with the PyBird code. J. Cosmol. Astropart. Phys. 2021, 2021, 006. [Google Scholar] [CrossRef]
- Di Valentino, E.; Gariazzo, S.; Mena, O.; Vagnozzi, S. Soundness of dark energy properties. J. Cosmol. Astropart. Phys. 2020, 2020, 045. [Google Scholar] [CrossRef]
- Gao, C.; Chen, Y.; Zheng, J. Investigating the relationship between cosmic curvature and dark energy models with the latest supernova sample. Res. Astron. Astrophys. 2020, 20, 151. [Google Scholar] [CrossRef]
- Garcia-Quintero, C.; Ishak, M.; Ning, O. Current constraints on deviations from General Relativity using binning in redshift and scale. J. Cosmol. Astropart. Phys. 2020, 2020, 018. [Google Scholar] [CrossRef]
- Geng, S.; Cao, S.; Liu, T.; Biesiada, M.; Qi, J.; Liu, Y.; Zhu, Z.H. Gravitational-wave Constraints on the Cosmic Opacity at z ∼ 5: Forecast from Space Gravitational-wave Antenna DECIGO. Astrophys. J. 2020, 905, 54. [Google Scholar] [CrossRef]
- Ghaffari, S.; Sadri, E.; Ziaie, A.H. Tsallis holographic dark energy in fractal universe. Mod. Phys. Lett. A 2020, 35, 2050107. [Google Scholar] [CrossRef]
- Hu, J.P.; Wang, Y.Y.; Wang, F.Y. Testing cosmic anisotropy with Pantheon sample and quasars at high redshifts. Astron. Astrophys. 2020, 643, A93. [Google Scholar] [CrossRef]
- Huang, Z. Supernova Magnitude Evolution and PAge Approximation. Astrophys. J. Lett. 2020, 892, L28. [Google Scholar] [CrossRef]
- Çamlıbel, A.K.; Semiz, İ.; Feyizoǧlu, M.A. Pantheon update on a model-independent analysis of cosmological supernova data. Class. Quantum Gravity 2020, 37, 235001. [Google Scholar] [CrossRef]
- Liao, K.; Shafieloo, A.; Keeley, R.E.; Linder, E.V. Determining Model-independent H0 and Consistency Tests. Astrophys. J. Lett. 2020, 895, L29. [Google Scholar] [CrossRef]
- Koo, H.; Shafieloo, A.; Keeley, R.E.; L’Huillier, B. Model selection and parameter estimation using the iterative smoothing method. J. Cosmol. Astropart. Phys. 2021, 2021, 034. [Google Scholar] [CrossRef]
- Li, E.K.; Du, M.; Xu, L. General cosmography model with spatial curvature. Mon. Not. R. Astron. Soc. 2020, 491, 4960–4972. [Google Scholar] [CrossRef]
- Luković, V.V.; Haridasu, B.S.; Vittorio, N. Exploring the evidence for a large local void with supernovae Ia data. Mon. Not. R. Astron. Soc. 2020, 491, 2075–2087. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M. Kinematic constraints beyond z≃0 using calibrated GRB correlations. Astron. Astrophys. 2020, 641, A174. [Google Scholar] [CrossRef]
- Micheletti, S.M.R. Quintessence and tachyon dark energy in interaction with dark matter: Observational constraints and model selection. Int. J. Mod. Phys. D 2020, 29, 2050057. [Google Scholar] [CrossRef]
- Mishra, R.K.; Dua, H. Phase transition of cosmological model with statistical techniques. Astrophys. Space Sci. 2020, 365, 131. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Sáez-Chillón Gómez, D.; Sharov, G.S. Analyzing the H0 tension in F(R) gravity models. Nucl. Phys. B 2021, 966, 115377. [Google Scholar] [CrossRef]
- Prasad, R.; Singh, M.; Yadav, A.K.; Beesham, A. An exact solution of the observable universe in Bianchi V space-time. Int. J. Mod. Phys. A 2021, 36, 2150044. [Google Scholar] [CrossRef]
- Rezaei, M.; Pour-Ojaghi, S.; Malekjani, M. A Cosmography Approach to Dark Energy Cosmologies: New Constraints Using the Hubble Diagrams of Supernovae, Quasars, and Gamma-Ray Bursts. Astrophys. J. 2020, 900, 70. [Google Scholar] [CrossRef]
- Ringermacher, H.I.; Mead, L.R. Reaffirmation of cosmological oscillations in the scale factor from the Pantheon compilation of 1048 Type Ia supernovae. Mon. Not. R. Astron. Soc. 2020, 494, 2158–2165. [Google Scholar] [CrossRef]
- Tang, L.; Li, X.; Lin, H.N.; Liu, L. Model-independently Calibrating the Luminosity Correlations of Gamma-Ray Bursts Using Deep Learning. Astrophys. J. 2021, 907, 121. [Google Scholar] [CrossRef]
- Wang, K.; Chen, L. Constraints on Newton’s constant from cosmological observations. Eur. Phys. J. C 2020, 80, 570. [Google Scholar] [CrossRef]
- Wei, J.J.; Melia, F. Cosmology-independent Estimate of the Hubble Constant and Spatial Curvature using Time-delay Lenses and Quasars. Astrophys. J. 2020, 897, 127. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Q.G. Measuring H0 from low-z datasets. Sci. China Phys. Mech. Astron. 2020, 63, 290402. [Google Scholar] [CrossRef]
- Baxter, E.J.; Sherwin, B.D. Determining the Hubble constant without the sound horizon scale: Measurements from CMB lensing. Mon. Not. R. Astron. Soc. 2021, 501, 1823–1835. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. On the use of the local prior on the absolute magnitude of Type Ia supernovae in cosmological inference. Mon. Not. R. Astron. Soc. 2021, 504, 5164–5171. [Google Scholar] [CrossRef]
- Cao, S.; Ryan, J.; Ratra, B. Using Pantheon and DES supernova, baryon acoustic oscillation, and Hubble parameter data to constrain the Hubble constant, dark energy dynamics, and spatial curvature. Mon. Not. R. Astron. Soc. 2021, 504, 300–310. [Google Scholar] [CrossRef]
- Heisenberg, L.; Bartelmann, M.; Brandenberger, R.; Refregier, A. Model independent analysis of supernova data, dark energy, trans-Planckian censorship and the swampland. Phys. Lett. B 2021, 812, 135990. [Google Scholar] [CrossRef]
- Jesus, J.F.; Valentim, R.; Moraes, P.H.R.S.; Malheiro, M. Kinematic constraints on spatial curvature from supernovae Ia and cosmic chronometers. Mon. Not. R. Astron. Soc. 2021, 500, 2227–2235. [Google Scholar] [CrossRef]
- Lee, S. Constraints on the time variation of the speed of light using Pantheon dataset. arXiv 2021, arXiv:2101.09862. [Google Scholar]
- Montiel, A.; Cabrera, J.I.; Hidalgo, J.C. Improving sampling and calibration of gamma-ray bursts as distance indicators. Mon. Not. R. Astron. Soc. 2021, 501, 3515–3526. [Google Scholar] [CrossRef]
- Mukherjee, P.; Banerjee, N. Non-parametric reconstruction of the cosmological jerk parameter. Eur. Phys. J. C 2021, 81, 36. [Google Scholar] [CrossRef]
- Wang, G.J.; Ma, X.J.; Xia, J.Q. Machine learning the cosmic curvature in a model-independent way. Mon. Not. R. Astron. Soc. 2021, 501, 5714–5722. [Google Scholar] [CrossRef]
- Torrado, J.; Lewis, A. Cobaya: Code for Bayesian Analysis of hierarchical physical models. J. Cosmol. Astropart. Phys. 2021, 05, 057. [Google Scholar] [CrossRef]
- Sharov, G.S.; Vasiliev, V.O. How predictions of cosmological models depend on Hubble parameter data sets. Math. Model. Geom. 2018, 6. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Cuceu, A.; Farr, J.; Lemos, P.; Font-Ribera, A. Baryon Acoustic Oscillations and the Hubble constant: Past, present and future. J. Cosmol. Astropart. Phys. 2019, 2019, 044. [Google Scholar] [CrossRef]
- Aubourg, É.; Bailey, S.; Bautista, J.E.; Beutler, F.; Bhardwaj, V.; Bizyaev, D.; Blanton, M.; Blomqvist, M.; Bolton, A.S.; Bovy, J.; et al. Cosmological implications of baryon acoustic oscillation measurements. Phys. Rev. D 2015, 92, 123516. [Google Scholar] [CrossRef]
- Singal, J.; Petrosian, V.; Lawrence, A. On the Radio and Optical Luminosity Evolution of Quasars. Astrophys. J. 2011, 743, 104. [Google Scholar] [CrossRef]
- Singal, J.; Petrosian, V.; Lawrence, A. The Radio and Optical Luminosity Evolution of Quasars. II. The SDSS Sample. Astrophys. J. 2013, 764, 43. [Google Scholar] [CrossRef]
- Petrosian, V.; Kitanidis, E.; Kocevski, D. Cosmological Evolution of Long Gamma-Ray Bursts and the Star Formation Rate. Astrophys. J. 2015, 806, 44. [Google Scholar] [CrossRef]
- Lloyd, N.M.; Petrosian, V. Synchrotron Radiation as the Source of Gamma-Ray Burst Spectra. Astrophys. J. 2000, 543, 722–732. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Petrosian, V.; Bowden, L. Cosmological Evolution of the Formation Rate of Short Gamma-Ray Bursts with and without Extended Emission. Astrophys. J. 2021, 914, L40. [Google Scholar] [CrossRef]
- Atteia, J.L. Gamma-ray bursts: Towards a standard candle luminosity. Astron. Astrophys. 1997, 328, L21–L24. [Google Scholar]
- Atteia, J.L. Choosing a measure of GRB brightness that approaches a standard candle. In Gamma-Ray Bursts, 4th Hunstville Symposium; Meegan, C.A., Preece, R.D., Koshut, T.M., Eds.; American Institute of Physics Conference Series; American Institute of Physics: College Park, MD, USA, 1998; Volume 428, pp. 92–96. [Google Scholar] [CrossRef]
- Simone, B.D.; Nielson, V.; Rinaldi, E.; Dainotti, M.G. A new perspective on cosmology through Supernovae Ia and Gamma Ray Bursts. arXiv 2021, arXiv:astro-ph.CO/2110.11930. [Google Scholar]
- Cao, S.; Dainotti, M.; Ratra, B. Standardizing Platinum Dainotti-correlated gamma-ray bursts, and using them with standardized Amati-correlated gamma-ray bursts to constrain cosmological model parameters. arXiv 2022, arXiv:astro-ph.CO/2201.0524. [Google Scholar]
- Cao, S.; Khadka, N.; Ratra, B. Standardizing Dainotti-correlated gamma-ray bursts, and using them with standardized Amati-correlated gamma-ray bursts to constrain cosmological model parameters. Mon. Not. R. Astron. Soc. 2022, 510, 2928–2947. [Google Scholar] [CrossRef]
- Efron, B.; Petrosian, V. A simple test of independence for truncated data with applications to redshift surveys. Astrophys. J. 1992, 399, 345–352. [Google Scholar] [CrossRef]
- D’Agostini, G. A multidimensional unfolding method based on Bayes’ theorem. Nucl. Instrum. Methods Phys. Res. A 1995, 362, 487–498. [Google Scholar] [CrossRef]
- Conley, A.; Guy, J.; Sullivan, M.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. Supernova constraints and systematic uncertainties from the first three years of the supernova legacy survey. Astrophys. J. Suppl. Ser. 2010, 192, 1. [Google Scholar] [CrossRef]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Bargiacchi, G.; Benetti, M.; Capozziello, S.; Lusso, E.; Risaliti, G.; Signorini, M. Quasar cosmology: Dark energy evolution and spatial curvature. arXiv 2021, arXiv:2111.02420. [Google Scholar]
- Bargiacchi, G.; Risaliti, G.; Benetti, M.; Capozziello, S.; Lusso, E.; Saccardi, A.; Signorini, M. Cosmography by orthogonalized logarithmic polynomials. Astron. Astrophys. 2021, 649, A65. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Bogdan, M.; Narendra, A.; Gibson, S.J.; Miasojedow, B.; Liodakis, I.; Pollo, A.; Nelson, T.; Wozniak, K.; Nguyen, Z.; et al. Predicting the Redshift of γ-Ray-loud AGNs Using Supervised Machine Learning. Astrophys. J. 2021, 920, 118. [Google Scholar] [CrossRef]
- Dainotti, M.; Petrosian, V.; Bogdan, M.; Miasojedow, B.; Nagataki, S.; Hastie, T.; Nuyngen, Z.; Gilda, S.; Hernández, X.; Krol, D. Gamma-ray Bursts as distance indicators through a machine learning approach. arXiv 2019, arXiv:1907.05074. [Google Scholar]
- Childress, M.; Aldering, G.; Antilogus, P.; Aragon, C.; Bailey, S.; Baltay, C.; Bongard, S.; Buton, C.; Canto, A.; Cellier-Holzem, F.; et al. Host Galaxies of Type Ia Supernovae from the Nearby Supernova Factory. Astrophys. J. 2013, 770, 107. [Google Scholar] [CrossRef]
- Nicolas, N.; Rigault, M.; Copin, Y.; Graziani, R.; Aldering, G.; Briday, M.; Kim, Y.L.; Nordin, J.; Perlmutter, S.; Smith, M. Redshift evolution of the underlying type Ia supernova stretch distribution. Astron. Astrophys. 2021, 649, A74. [Google Scholar] [CrossRef]
- Brout, D.; Taylor, G.; Scolnic, D.; Wood, C.M.; Rose, B.M.; Vincenzi, M.; Dwomoh, A.; Lidman, C.; Riess, A.; Ali, N.; et al. The Pantheon+ Analysis: SuperCal-Fragilistic Cross Calibration, Retrained SALT2 Light Curve Model, and Calibration Systematic Uncertainty. arXiv 2021, arXiv:astro-ph.CO/2112.03864. [Google Scholar]
- Carr, A.; Davis, T.M.; Scolnic, D.; Said, K.; Brout, D.; Peterson, E.R.; Kessler, R. The Pantheon+ Analysis: Improving the Redshifts and Peculiar Velocities of Type Ia Supernovae Used in Cosmological Analyses. arXiv 2021, arXiv:astro-ph.CO/2112.01471. [Google Scholar]
- Popovic, B.; Brout, D.; Kessler, R.; Scolnic, D. The Pantheon+ Analysis: Forward-Modeling the Dust and Intrinsic Colour Distributions of Type Ia Supernovae, and Quantifying their Impact on Cosmological Inferences. arXiv 2021, arXiv:astro-ph.CO/2112.04456. [Google Scholar]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Type Ia Supernova Sample: The Full Dataset and Light-Curve Release. arXiv 2021, arXiv:astro-ph.CO/2112.03863. [Google Scholar]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Breuval, L.; Brink, T.G.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. arXiv 2022, arXiv:astro-ph.CO/2112.04510. [Google Scholar]
- Damour, T.; Nordtvedt, K. Tensor-scalar cosmological models and their relaxation toward general relativity. Phys. Rev. D 1993, 48, 3436–3450. [Google Scholar] [CrossRef]
- Damour, T.; Polyakov, A.M. The string dilation and a least coupling principle. Nucl. Phys. B 1994, 423, 532–558. [Google Scholar] [CrossRef]
- Damour, T. Gravitation, experiment and cosmology. Les Houches Summer School on Gravitation and Quantizations, Session 57. arXiv 1996, arXiv:gr-qc/gr-qc/9606079. [Google Scholar]
- Boisseau, B.; Esposito-Farèse, G.; Polarski, D.; Starobinsky, A.A. Reconstruction of a Scalar-Tensor Theory of Gravity in an Accelerating Universe. Phys. Rev. Lett. 2000, 85, 2236–2239. [Google Scholar] [CrossRef] [PubMed]
- Esposito-Farèse, G.; Polarski, D. Scalar-tensor gravity in an accelerating universe. Phys. Rev. D 2001, 63, 063504. [Google Scholar] [CrossRef]
- Jordan, P. Schwerkraft und Weltall: Grundlagen der theoretischen Kosmologie; Die Wissenschaft: Braunschweig, Germany, 1955. [Google Scholar]
- Fierz, M. On the physical interpretation of P. Jordan’s extended theory of gravitation. Helv. Phys. Acta 1956, 29, 128–134. [Google Scholar]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Singh, C.P.; Peracaula, J.S. Friedmann cosmology with decaying vacuum density in Brans–Dicke theory. arXiv 2021, arXiv:gr-qc/2110.12411. [Google Scholar] [CrossRef]
- Catena, R.; Fornengo, N.; Masiero, A.; Pietroni, M.; Rosati, F. Dark matter relic abundance and scalar-tensor dark energy. Phys. Rev. D 2004, 70, 063519. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Hints of a local matter underdensity or modified gravity in the low z Pantheon data. Phys. Rev. D 2020, 102, 023520. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f(R) cosmic acceleration that evade solar system tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f( R) gravity. Sov. J. Exp. Theor. Phys. Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75, 083504. [Google Scholar] [CrossRef]
- Tsujikawa, S. Observational signatures of f(R) dark energy models that satisfy cosmological and local gravity constraints. Phys. Rev. D 2008, 77, 023507. [Google Scholar] [CrossRef]
- Martinelli, M.; Melchiorri, A.; Amendola, L. Cosmological constraints on the Hu-Sawicki modified gravity scenario. Phys. Rev. D 2009, 79, 123516. [Google Scholar] [CrossRef]
- Burrage, C.; Sakstein, J. Tests of chameleon gravity. Living Rev. Relativ. 2018, 21, 1. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Zhang, X.; Zhao, W. Constraining f(R) gravity in solar system, cosmology and binary pulsar systems. Phys. Lett. B 2018, 777, 286–293. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Riotto, A. Inflation and the Theory of Cosmological Perturbations. ICTP Lect. Notes Ser. 2003, 14, 317–413. [Google Scholar]
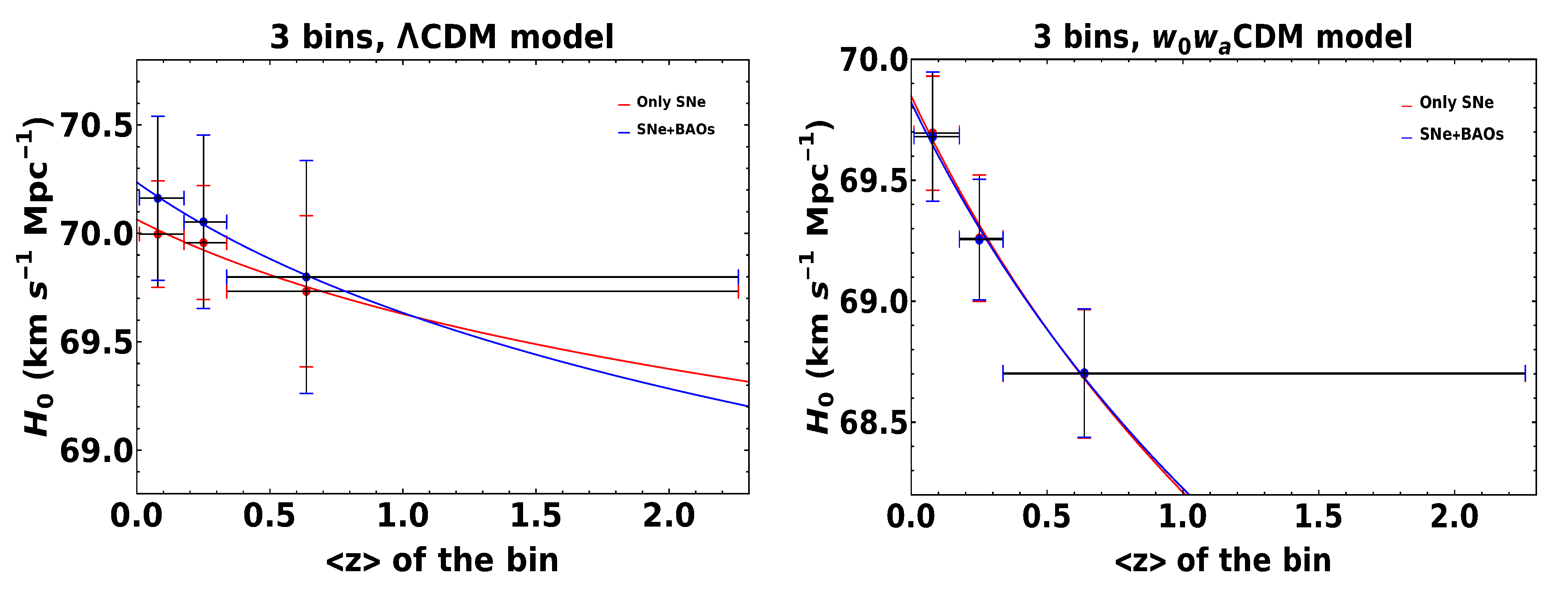
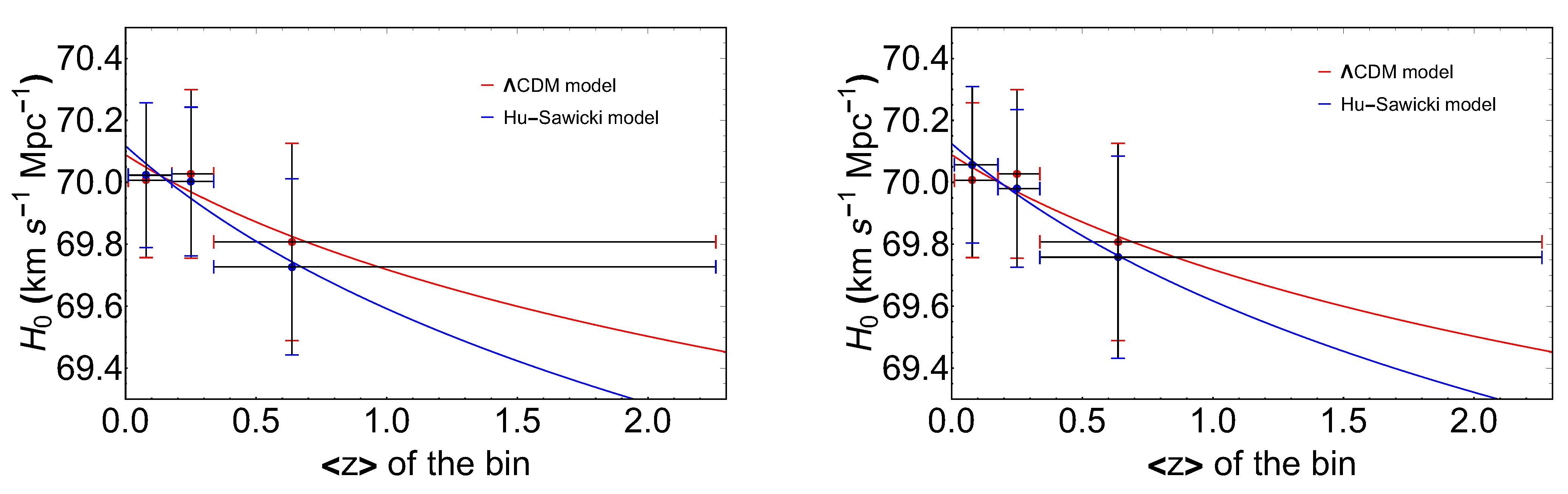
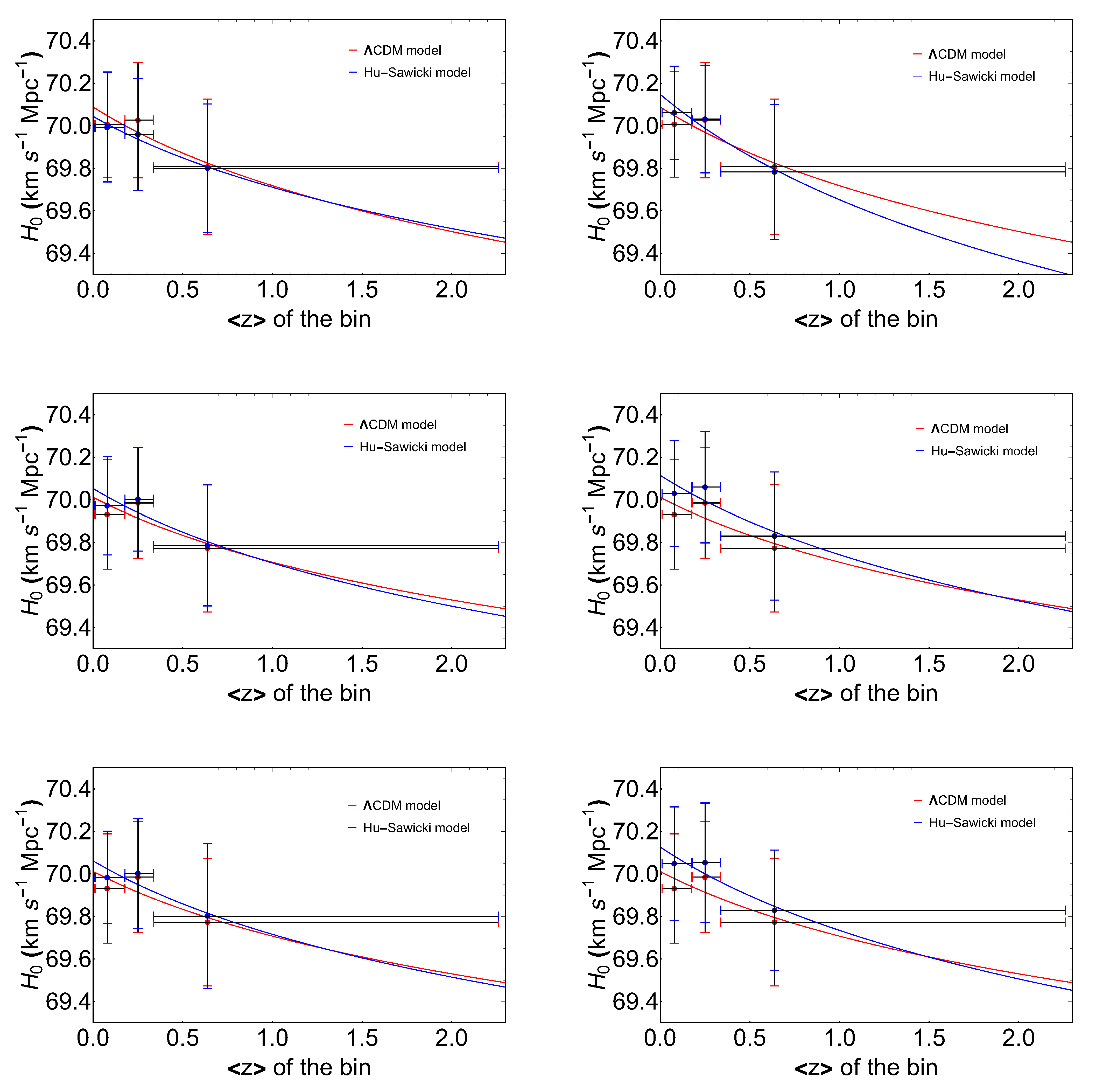
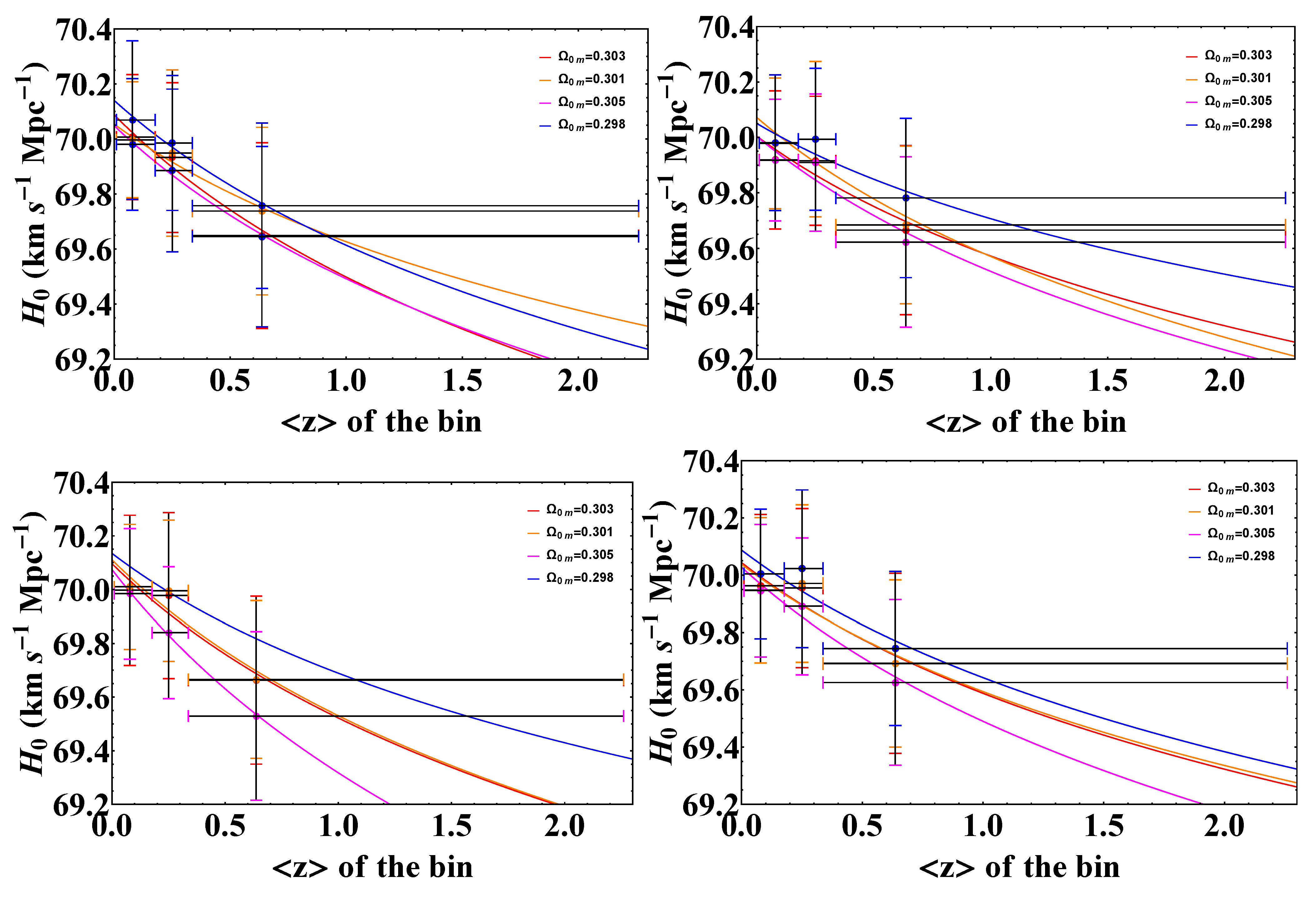
| Flat CDM model, without BAOs, varying and | |||
| Bins | |||
| 3 | |||
| Flat CDM model, including BAOs, varying and | |||
| Bins | |||
| 3 | |||
| Flat CDM model, without BAOs, varying and | |||
| Bins | |||
| 3 | |||
| Flat CDM model, including BAOs, varying and | |||
| Bins | |||
| 3 | |||
| Hu–Sawicki Model, Results of the Redshift Binned Analysis | |||||
|---|---|---|---|---|---|
| Bins | Sample | ||||
| 3 | SNe | ||||
| 3 | SNe + BAOs | ||||
| 3 | SNe | ||||
| 3 | SNe + BAOs | ||||
| 3 | SNe | ||||
| 3 | SNe + BAOs | ||||
| 3 | SNe | ||||
| 3 | SNe + BAOs | ||||
| Hu–Sawicki Model, Results of the 3 Bins Analysis | |||||
|---|---|---|---|---|---|
| Sample | |||||
| 0.298 | SNe | ||||
| 0.298 | SNe + BAOs | ||||
| 0.303 | SNe | ||||
| 0.303 | SNe + BAOs | ||||
| 0.301 | SNe | ||||
| 0.301 | SNe + BAOs | ||||
| 0.305 | SNe | ||||
| 0.305 | SNe + BAOs | ||||
| 0.298 | SNe | ||||
| 0.298 | SNe + BAOs | ||||
| 0.303 | SNe | ||||
| 0.303 | SNe + BAOs | ||||
| 0.301 | SNe | ||||
| 0.301 | SNe + BAOs | ||||
| 0.305 | SNe | ||||
| 0.305 | SNe + BAOs | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G.; Bogdan, M.; Ugale, S. On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies 2022, 10, 24. https://doi.org/10.3390/galaxies10010024
Dainotti MG, De Simone B, Schiavone T, Montani G, Rinaldi E, Lambiase G, Bogdan M, Ugale S. On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies. 2022; 10(1):24. https://doi.org/10.3390/galaxies10010024
Chicago/Turabian StyleDainotti, Maria Giovanna, Biagio De Simone, Tiziano Schiavone, Giovanni Montani, Enrico Rinaldi, Gaetano Lambiase, Malgorzata Bogdan, and Sahil Ugale. 2022. "On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030" Galaxies 10, no. 1: 24. https://doi.org/10.3390/galaxies10010024
APA StyleDainotti, M. G., De Simone, B., Schiavone, T., Montani, G., Rinaldi, E., Lambiase, G., Bogdan, M., & Ugale, S. (2022). On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies, 10(1), 24. https://doi.org/10.3390/galaxies10010024







