Optimization of Design Parameters for Gravitational Wave Detector DECIGO Including Fundamental Noises
Abstract
:1. Introduction
2. GWs from DWDs
3. Thermal Noise
3.1. Thermal Noise in a Residual Gas
3.2. Internal Thermal Noise
3.3. Other Sources of Thermal Noise
4. Method of Optimization
- One cluster consists of three interferometers.
- There are differential Fabry-Perot (FP) interferometers with 60° between each arm.
- Each interferometer shares each arm with two other interferometers.
4.1. Treatment of Each Noise in the Simulation
4.2. Method of Calculation
5. Result
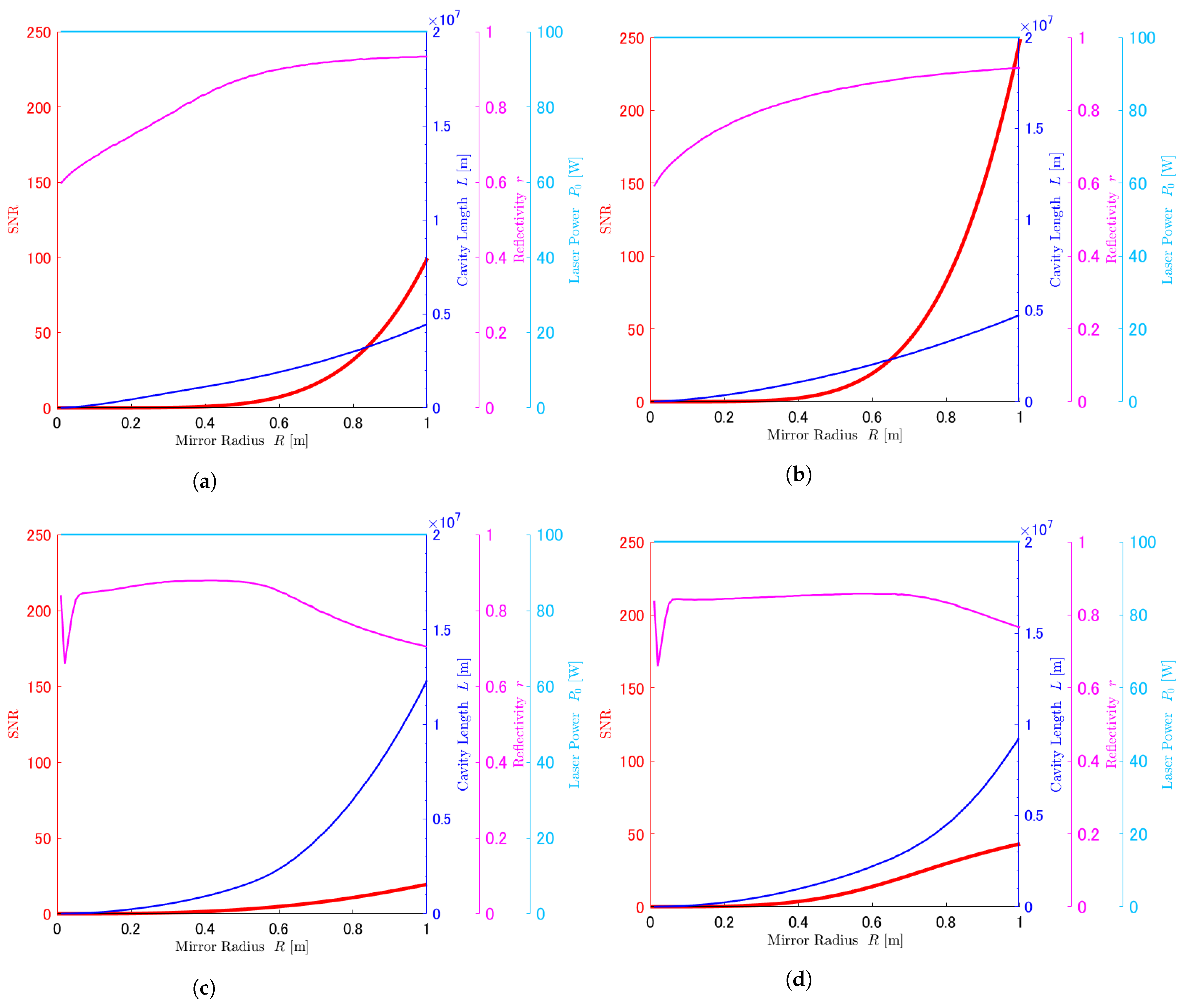
5.1. Optimization of SNR and Parameters
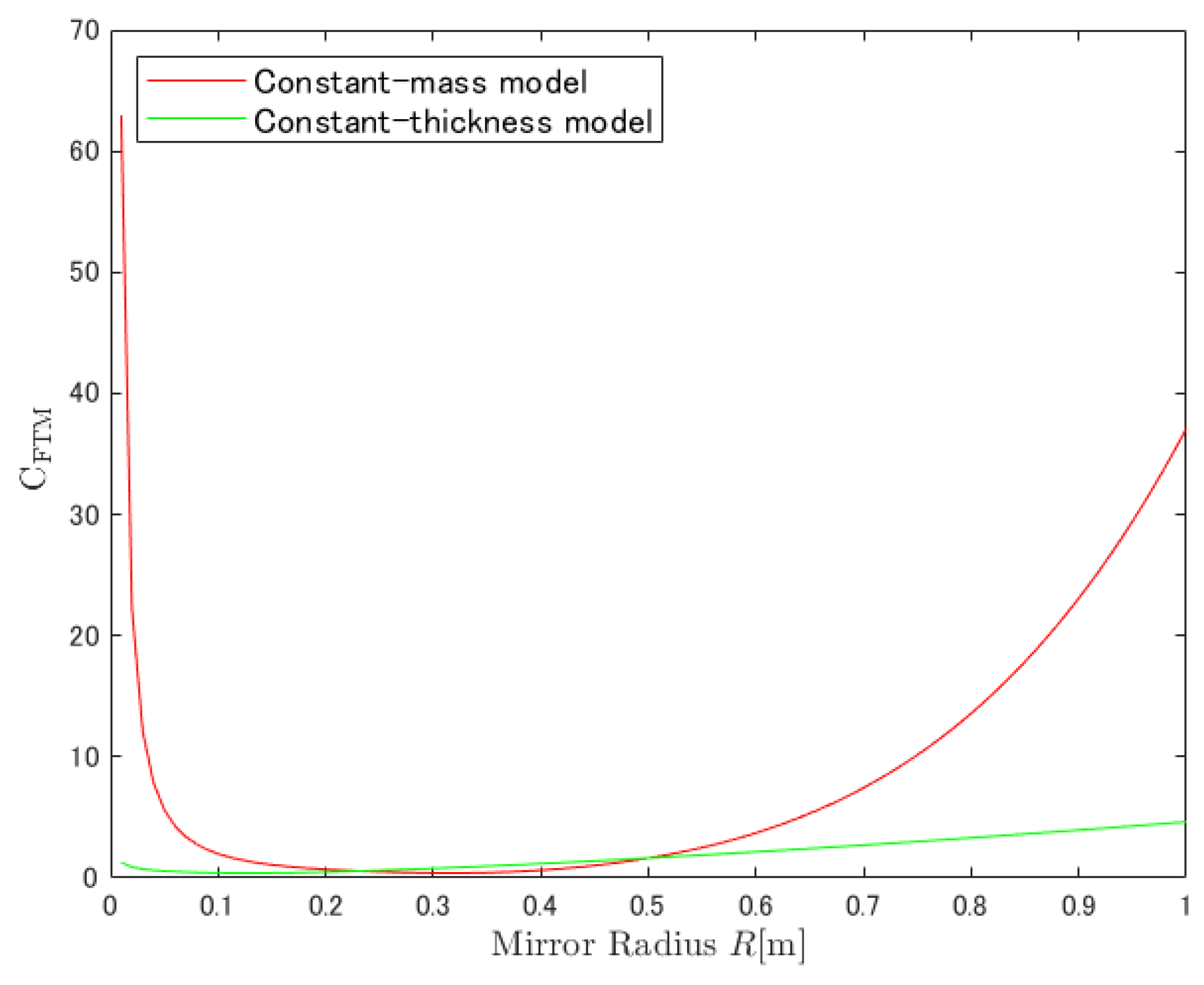
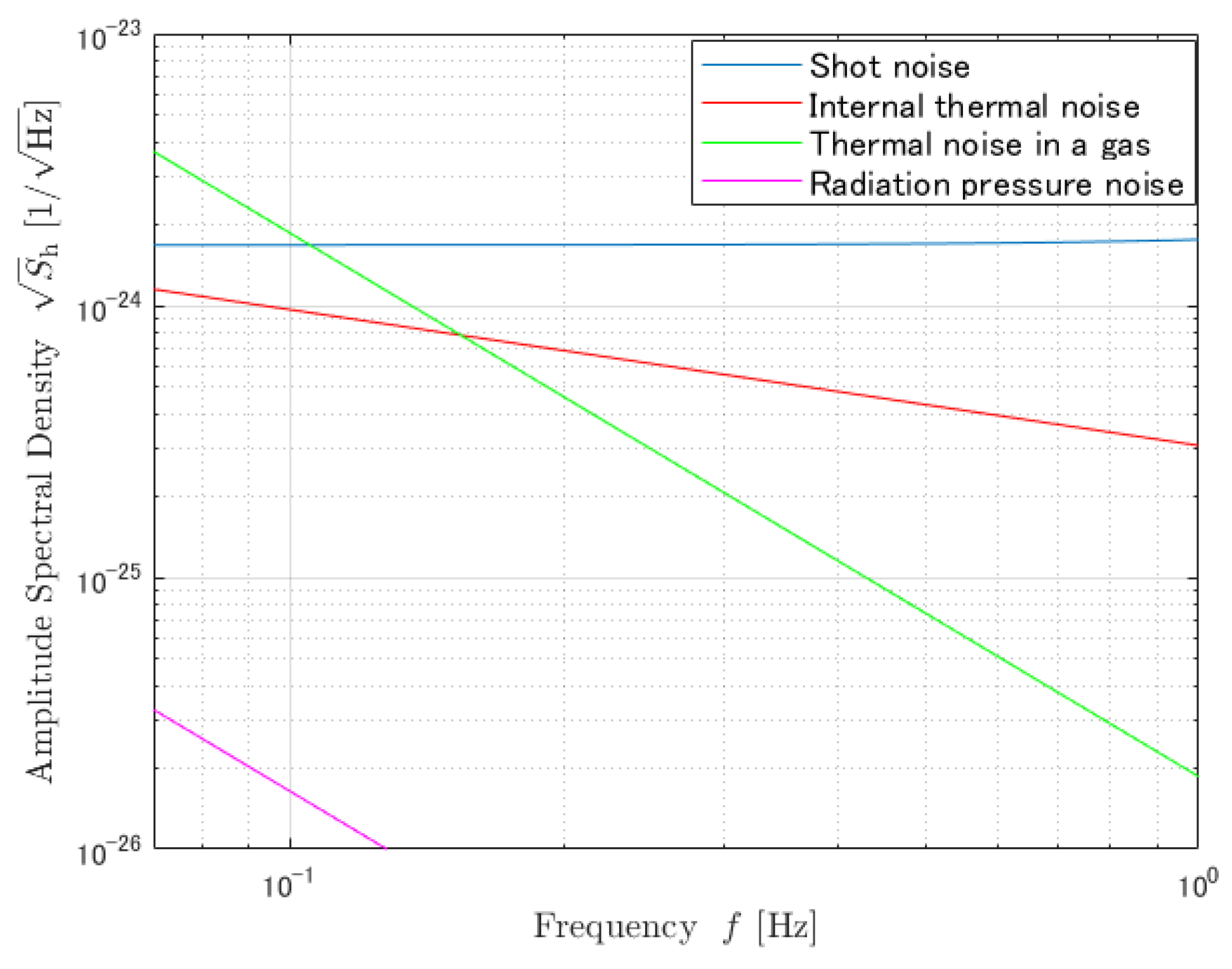
5.2. Comparison of the Estimated Strain Sensitivities, Especially at Large R
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Factor b
Appendix B. Effect of Diffraction Loss
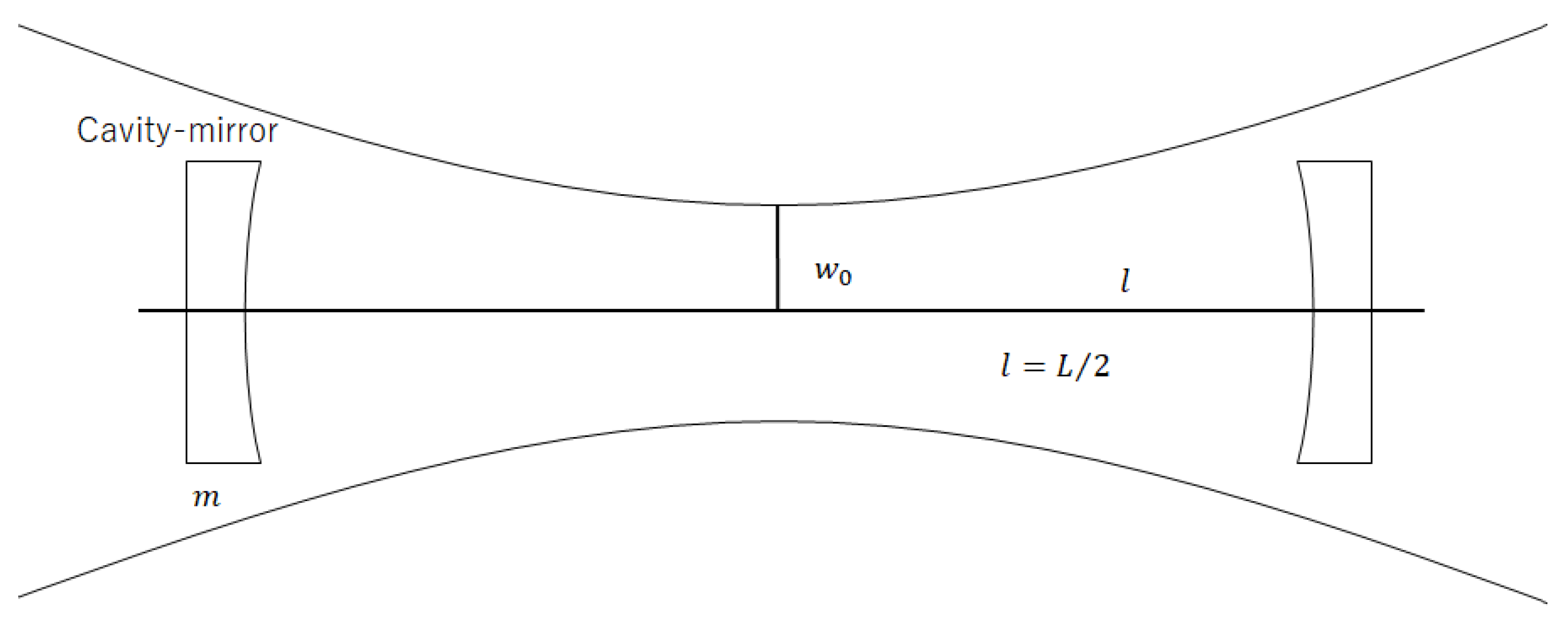
Appendix C. Derivation of Factor CFTM
References
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of Direct Measurement of the Acceleration of the Universe Using 0.1 Hz Band Laser Interferometer Gravitational Wave Antenna in Space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef] [PubMed]
- Kawamura, S.; Nakamura, T.; Ando, M.; Seto, N.; Akutsu, T.; Funaki, I.; Ioka, K.; Kanda, N.; Kawano, I.; Musha, M.; et al. Space gravitational-wave antennas DECIGO and B-DECIGO. Int. J. Mod. Phys. D 2019, 28, 1845001. [Google Scholar] [CrossRef]
- Kinugawa, T.; Takeda, H.; Yamaguchi, H. Probe for Type Ia supernova progenitor in decihertz gravitational wave astronomy. arXiv 2019, arXiv:1910.01063. [Google Scholar]
- Kawamura, S.; Nakamura, T.; Ando, M.; Seto, N.; Tsubono, K.; Numata, K.; Takahashi, R.; Nagano, S.; Ishikawa, T.; Musha, M.; et al. The Japanese space gravitational wave antenna: DECIGO. Class. Quantum Grav. 2011, 28, 094011. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef] [Green Version]
- BICEP/Keck Collaboration. BICEP/Keck XIII. Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season. Phys. Rev. Lett. 2021, 127, 15130. [Google Scholar]
- Kuroyanagi, S. Implications of the B-mode Polarization Measurement for Direct Detection of Inflationary Gravitational Waves. Phys. Rev. D 2014, 90, 063513. [Google Scholar] [CrossRef] [Green Version]
- Ishikawa, T.; Iwaguchi, S.; Michimura, Y.; Ando, M.; Yamada, R.; Watanabe, I.; Nagano, K.; Akutsu, T.; Komori, K.; Musha, M.; et al. Improvement of the target sensitivity in DECIGO by optimizing its parameters for quantum noise including the effect of diffraction loss. Galaxies 2021, 9, 14. [Google Scholar] [CrossRef]
- Iwaguchi, S.; Ishikawa, T.; Ando, M.; Michimura, Y.; Komori, K.; Nagano, K.; Akutsu, T.; Musha, M.; Yamada, R.; Watanabe, I.; et al. Quantum Noise in a Fabry-Perot Interferometer Including the Influence of Diffraction Loss of Light. Galaxies 2021, 9, 9. [Google Scholar] [CrossRef]
- Farmer, A.J.; Phinney, E.S. The Gravitational Wave Background from Cosmological Compact Binaries. Mon. Not. R. Astron. Soc. 2003, 346, 1197–1214. [Google Scholar] [CrossRef] [Green Version]
- Boileau, G.; Lamberts, A.; Christensen, N.; Cornish, N.J.; Meyer, R. Spectral separation of the stochastic gravitational-wave background for LISA in the context of a modulated Galactic foreground. arXiv 2021, arXiv:2105.04283. [Google Scholar]
- Callen, H.B.; Welton, T.A. Irreversibility and Generalized Noise. Phys. Rev. 1951, 83, 34. [Google Scholar] [CrossRef]
- Saulson, P.R. Fundamentals of Interferometric Gravitational Wave Detectors; World Scientific: Singapore, 1994; pp. 107–116. [Google Scholar]
- Levin, Y. Internal thermal noise in the LIGO test masses: A Direct approach. Phys. Rev. D 1998, 57, 659. [Google Scholar] [CrossRef] [Green Version]
- Braginsky, V.B.; Gorodetsky, M.L.; Vyatchanin, S.P. Thermodynamical fluctuations and photo-thermal shot noise in gravitational wave antennae. Phys. Lett. A 1999, 264, 1. [Google Scholar] [CrossRef] [Green Version]
- Nakagawa, N.; Gretarsson, A.M.; Gustafson, E.K.; Fejer, M.M. Thermal noise in half-infinite mirrors with nonuniform loss: A slab of excess loss in a half-infinite mirror. Phys. Rev. D 2002, 65, 102001. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.T.; Thorne, T.S. Thermoelastic noise and homogeneous thermal noise in finite sized gravitational-wave test masses. Phys. Rev. D 2000, 62, 122002. [Google Scholar] [CrossRef] [Green Version]
- Somiya, K.; Yamamoto, K. Coating thermal noise of a finite-size cylindrical mirror. Phys. Rev. D 2009, 79, 102004. [Google Scholar] [CrossRef] [Green Version]
- Numata, K.; Kemery, A.; Jordan, C. Thermal-Noise Limit in the Frequency Stabilization of Lasers with Rigid Cavities. Phys. Rev. Lett. 2004, 93, 250602. [Google Scholar] [CrossRef] [PubMed]
- Prince, T.A.; Tinto, M.; Larson, S.L.; Armstrong, J.W. LISA optimal sensitivity. Phys. Rev. D 2002, 66, 122002. [Google Scholar] [CrossRef] [Green Version]




| Symbol | Meaning |
|---|---|
| Boltzmann constant | |
| T (=300 K) | Mirror temperature |
| m | Mirror mass |
| R | Mirror radius |
| S | Mirror cross section |
| h | Mirror thickness |
| d | Coating thickness |
| L | Cavity length |
| (=7.4 × 10 | Young’s modulus |
| (=0.17) | Poisson’s modulus |
| Thermal expansion rate | |
| C | Specific heat per volume |
| Diffusivity of the mirror | |
| Beam radius | |
| P | Pressure in the satellite |
| Mass of a gas molecule in the satellite |
| Symbol | Meaning |
|---|---|
| L | Cavity length |
| m | Mirror mass |
| Laser power entering beam splitter | |
| (=515 × | Laser wavelength |
| r | Mirror reflectivity |
| t | Mirror transmissivity |
| D | Effect of diffraction loss |
| Effective mirror reflectivity | |
| Effective mirror transmissivity | |
| c (=2.9979 × | Light speed |
| ℏ (=1.0546 × | Planck constant |
| (=70/3.086 × | Hubble constant |
| Finesse | |
| Cavity pole frequency | |
| Effective finesse |
| Symbol | Range |
|---|---|
| R | 0 to 1 m |
| r | 0 to 1 |
| 0 to 100 W | |
| L | No limit |
| Parameter | Value in Each Model |
|---|---|
| Cutoff frequency | 0.07 Hz/0.1 Hz |
| Pressure in the satellite | Pa/ Pa |
| Mirror mass | Constant (100 kg)/Proportional to the square of R. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawasaki, Y.; Shimizu, R.; Ishikawa, T.; Nagano, K.; Iwaguchi, S.; Watanabe, I.; Wu, B.; Yokoyama, S.; Kawamura, S. Optimization of Design Parameters for Gravitational Wave Detector DECIGO Including Fundamental Noises. Galaxies 2022, 10, 25. https://doi.org/10.3390/galaxies10010025
Kawasaki Y, Shimizu R, Ishikawa T, Nagano K, Iwaguchi S, Watanabe I, Wu B, Yokoyama S, Kawamura S. Optimization of Design Parameters for Gravitational Wave Detector DECIGO Including Fundamental Noises. Galaxies. 2022; 10(1):25. https://doi.org/10.3390/galaxies10010025
Chicago/Turabian StyleKawasaki, Yuki, Ryuma Shimizu, Tomohiro Ishikawa, Koji Nagano, Shoki Iwaguchi, Izumi Watanabe, Bin Wu, Shuichiro Yokoyama, and Seiji Kawamura. 2022. "Optimization of Design Parameters for Gravitational Wave Detector DECIGO Including Fundamental Noises" Galaxies 10, no. 1: 25. https://doi.org/10.3390/galaxies10010025
APA StyleKawasaki, Y., Shimizu, R., Ishikawa, T., Nagano, K., Iwaguchi, S., Watanabe, I., Wu, B., Yokoyama, S., & Kawamura, S. (2022). Optimization of Design Parameters for Gravitational Wave Detector DECIGO Including Fundamental Noises. Galaxies, 10(1), 25. https://doi.org/10.3390/galaxies10010025






