The GRB Prompt Emission: An Unsolved Puzzle
Abstract
1. Introduction
2. Prompt GRB Emission: Key Observational Properties
2.1. Spectral Properties: Sub-MeV Emission
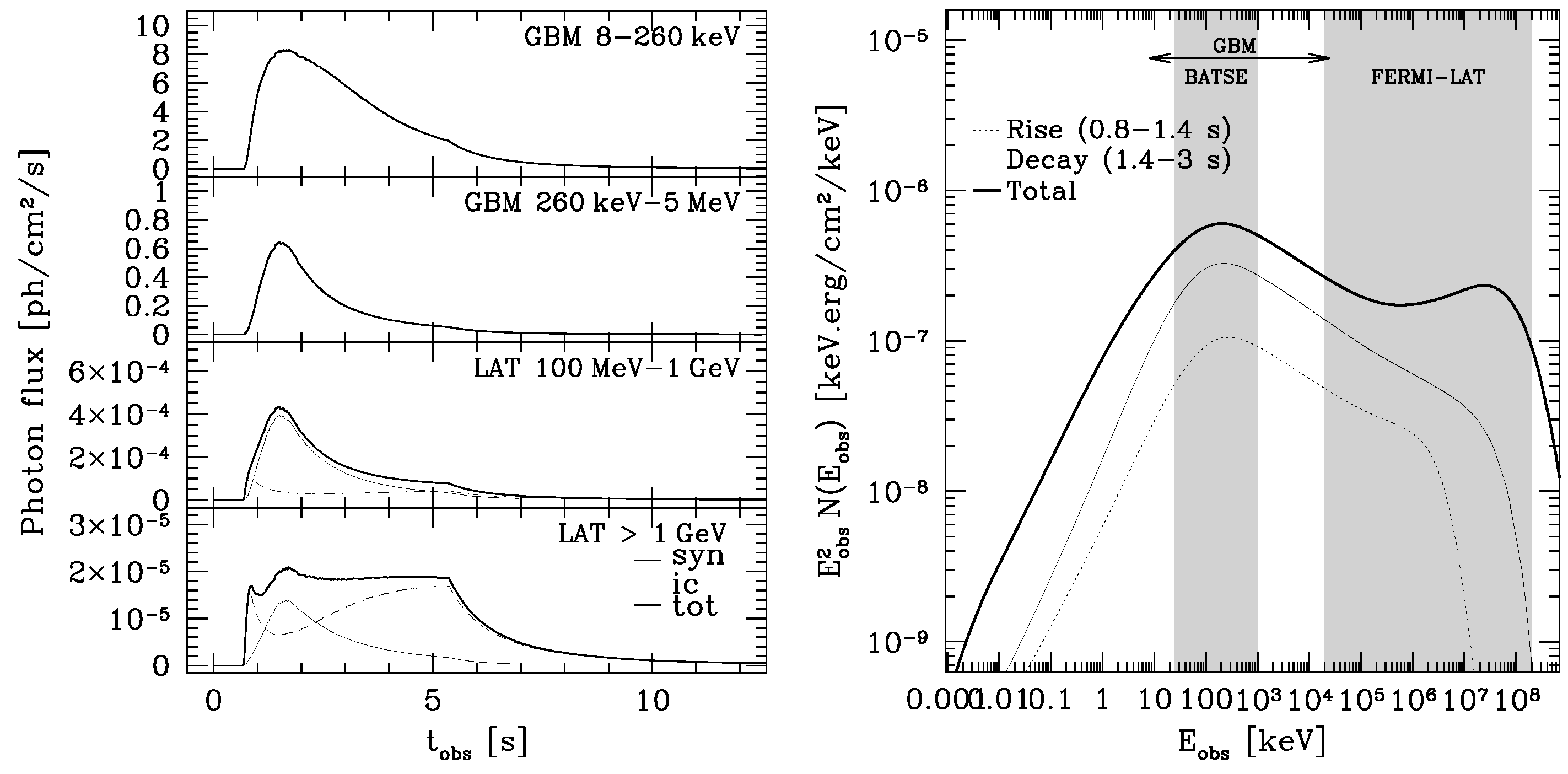
High Energy Emission
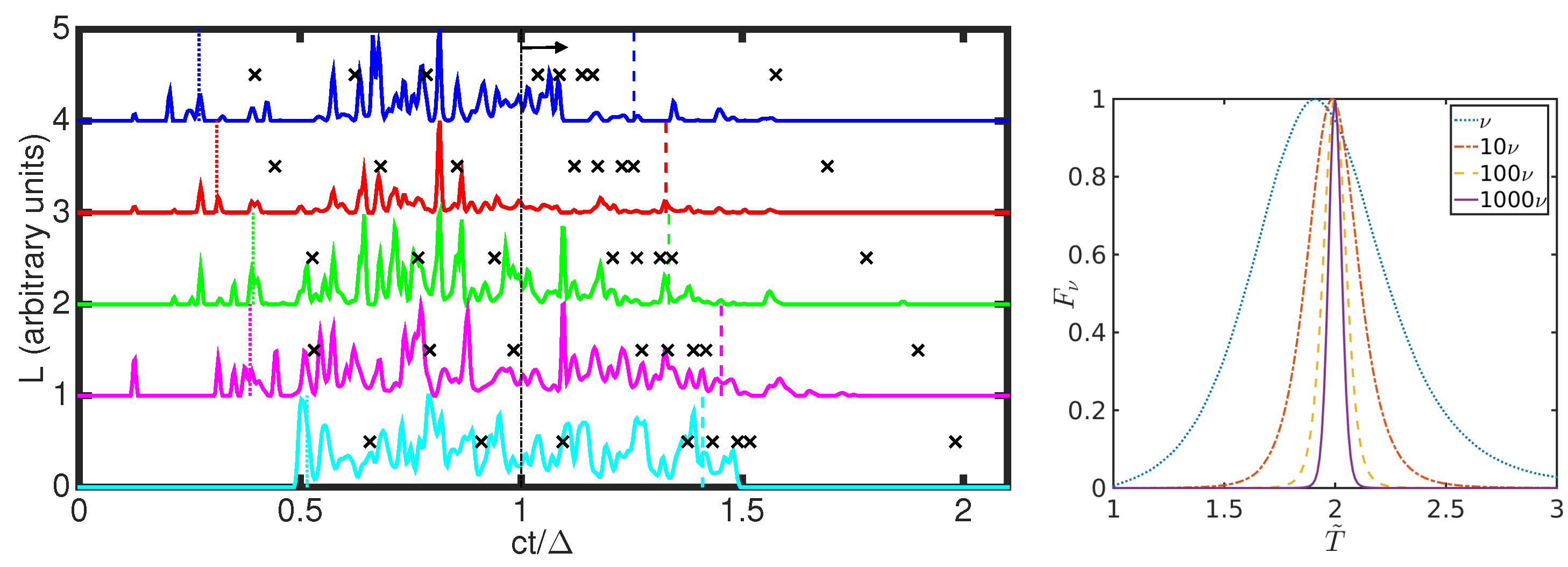
2.2. Light Curve Properties
2.3. Polarization
3. Theories of GRB Prompt Emission
3.1. Hot Fireball Model
3.2. Particle Acceleration
3.3. Internal Shock Model
3.4. The Role of Neutrons in the GRB Jet
3.5. Magnetically Dominated Jet
3.6. Radiative Processes
3.6.1. Synchrotron Emission and Inverse Compton Scatterings
3.6.2. Comptonized Thermal Radiation
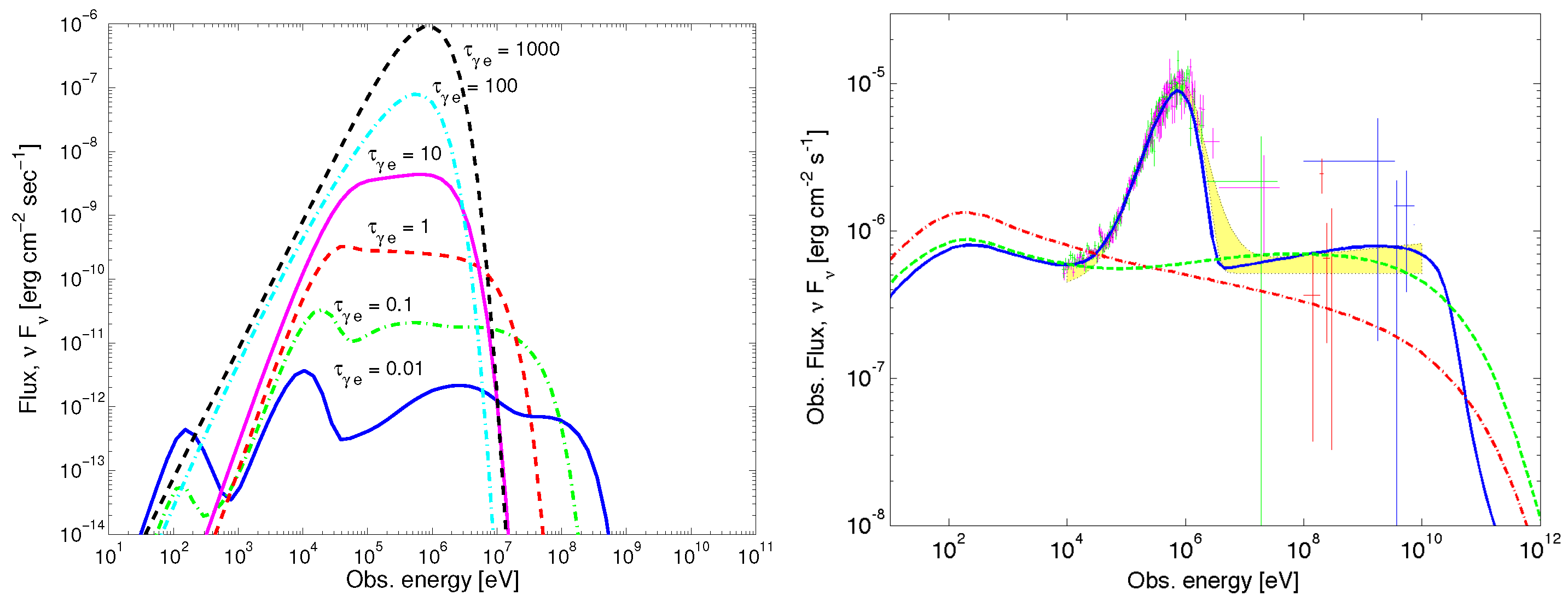
3.6.3. Hadronic Processes
4. Discussion: A Look into the Future
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Kasliwal, M.M.; Nakar, E.; Singer, L.P.; Kaplan, D.L.; Cook, D.O.; Van Sistine, A.; Lau, R.M.; Fremling, C.; Gottlieb, O.; Jencson, J.E.; et al. Illuminating gravitational waves: A concordant picture of photons from a neutron star merger. Science 2017, 358, 1559–1565. [Google Scholar] [CrossRef]
- Kasen, D.; Metzger, B.; Barnes, J.; Quataert, E.; Ramirez-Ruiz, E. Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature 2017, 551, 80–84. [Google Scholar] [CrossRef]
- Smartt, S.J.; Chen, T.W.; Jerkstrand, A.; Coughlin, M.; Kankare, E.; Sim, S.A.; Fraser, M.; Inserra, C.; Maguire, K.; Chambers, K.C.; et al. A kilonova as the electromagnetic counterpart to a gravitational-wave source. Nature 2017, 551, 75–79. [Google Scholar] [CrossRef]
- MAGIC Collaboration; Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; et al. Teraelectronvolt emission from the γ-ray burst GRB 190114C. Nature 2019, 575, 455–458. [Google Scholar] [CrossRef]
- Abdalla, H.; Adam, R.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arakawa, M.; Arcaro, C.; Armand, C.; Ashkar, H.; Backes, M.; et al. A very-high-energy component deep in the γ-ray burst afterglow. Nature 2019, 575, 464–467. [Google Scholar] [CrossRef]
- Deoskar, K.; Coppin, P.; Friedman, E. Searches for Neutrinos from Precursors and Afterglows of Gamma-ray Bursts using the IceCube Neutrino Observatory. arXiv 2021, arXiv:2107.08870. [Google Scholar]
- Klebesadel, R.W.; Strong, I.B.; Olson, R.A. Observations of Gamma-Ray Bursts of Cosmic Origin. Astrophys. J. 1973, 182, L85. [Google Scholar] [CrossRef]
- Meegan, C.A.; Fishman, G.J.; Wilson, R.B.; Paciesas, W.S.; Pendleton, G.N.; Horack, J.M.; Brock, M.N.; Kouveliotou, C. Spatial distribution of γ-ray bursts observed by BATSE. Nature 1992, 355, 143–145. [Google Scholar] [CrossRef]
- Band, D.; Matteson, J.; Ford, L.; Schaefer, B.; Palmer, D.; Teegarden, B.; Cline, T.; Briggs, M.; Paciesas, W.; Pendleton, G.; et al. BATSE Observations of Gamma-Ray Burst Spectra. I. Spectral Diversity. Astrophys. J. 1993, 413, 281. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Arimoto, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. Fermi Observations of High-Energy Gamma-Ray Emission from GRB 080916C. Science 2009, 323, 1688–1693. [Google Scholar] [CrossRef]
- Zhang, B. Gamma-Ray Burst Prompt Emission. Int. J. Mod. Phys. D 2014, 23, 30002. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts and relativistic jets. Phys. Rep. 2015, 561, 1–109. [Google Scholar] [CrossRef]
- Pe’er, A. Physics of Gamma-Ray Bursts Prompt Emission. Adv. Astron. 2015, 2015, 907321. [Google Scholar] [CrossRef]
- Dai, Z.; Daigne, F.; Mészáros, P. The Theory of Gamma-Ray Bursts. Space Sci. Rev. 2017, 212, 409–427. [Google Scholar] [CrossRef]
- Beloborodov, A.M.; Mészáros, P. Photospheric Emission of Gamma-Ray Bursts. Space Sci. Rev. 2017, 207, 87–110. [Google Scholar] [CrossRef]
- Meegan, C.; Lichti, G.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Connaughton, V.; Diehl, R.; Fishman, G.; Greiner, J.; Hoover, A.S.; et al. The Fermi Gamma-ray Burst Monitor. Astrophys. J. 2009, 702, 791–804. [Google Scholar] [CrossRef]
- Poolakkil, S.; Preece, R.; Fletcher, C.; Goldstein, A.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Burns, E.; Cleveland, W.H.; Giles, M.M.; et al. The Fermi GBM Gamma-Ray Burst Spectral Catalog: 10 Years of Data. arXiv 2021, arXiv:2103.13528. [Google Scholar] [CrossRef]
- Goldstein, A.; Burgess, J.M.; Preece, R.D.; Briggs, M.S.; Guiriec, S.; van der Horst, A.e.J.; Connaughton, V.; Wilson-Hodge, C.A.; Paciesas, W.S.; Meegan, C.A.; et al. The Fermi GBM Gamma-Ray Burst Spectral Catalog: The First Two Years. Astrophys. J. Suppl. Ser. 2012, 199, 19. [Google Scholar] [CrossRef]
- Gruber, D.; Goldstein, A.; Weller von Ahlefeld, V.; Narayana Bhat, P.; Bissaldi, E.; Briggs, M.S.; Byrne, D.; Cleveland, W.H.; Connaughton, V.; Diehl, R.; et al. The Fermi GBM Gamma-Ray Burst Spectral Catalog: Four Years of Data. Astrophys. J. Suppl. Ser. 2014, 211, 12. [Google Scholar] [CrossRef]
- Yu, H.F.; Preece, R.D.; Greiner, J.; Narayana Bhat, P.; Bissaldi, E.; Briggs, M.S.; Cleveland, W.H.; Connaughton, V.; Goldstein, A.; von Kienlin, A.; et al. The Fermi GBM gamma-ray burst time-resolved spectral catalog: Brightest bursts in the first four years. Astron. Astrophys. 2016, 588, A135. [Google Scholar] [CrossRef]
- Oganesyan, G.; Nava, L.; Ghirlanda, G.; Celotti, A. Characterization of gamma-ray burst prompt emission spectra down to soft X-rays. Astron. Astrophys. 2018, 616, A138. [Google Scholar] [CrossRef]
- Toffano, M.; Ghirlanda, G.; Nava, L.; Ghisellini, G.; Ravasio, M.E.; Oganesyan, G. The slope of the low-energy spectrum of prompt gamma-ray burst emission. Astron. Astrophys. 2021, 652, A123. [Google Scholar] [CrossRef]
- Yu, H.F.; van Eerten, H.J.; Greiner, J.; Sari, R.; Narayana Bhat, P.; von Kienlin, A.; Paciesas, W.S.; Preece, R.D. The sharpness of gamma-ray burst prompt emission spectra. Astron. Astrophys. 2015, 583, A129. [Google Scholar] [CrossRef][Green Version]
- Acuner, Z.; Ryde, F.; Pe’er, A.; Mortlock, D.; Ahlgren, B. The Fraction of Gamma-Ray Bursts with an Observed Photospheric Emission Episode. Astrophys. J. 2020, 893, 128. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. The expected thermal precursors of gamma-ray bursts in the internal shock model. Mon. Not. R. Astron. Soc. 2002, 336, 1271–1280. [Google Scholar] [CrossRef]
- Hascoët, R.; Daigne, F.; Mochkovitch, R. Prompt thermal emission in gamma-ray bursts. Astron. Astrophys. 2013, 551, A124. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Celotti, A.; Ghisellini, G. Extremely hard GRB spectra prune down the forest of emission models. Astron. Astrophys. 2003, 406, 879–892. [Google Scholar] [CrossRef]
- Acuner, Z.; Ryde, F.; Yu, H.F. Non-dissipative photospheres in GRBs: Spectral appearance in the Fermi/GBM catalogue. Mon. Not. R. Astron. Soc. 2019, 487, 5508–5519. [Google Scholar] [CrossRef]
- Bosnjak, Z.; Celotti, A.; Ghirlanda, G. GRB 990413: Insight into the thermal phase evolution. Mon. Not. R. Astron. Soc. 2006, 370, L33–L37. [Google Scholar] [CrossRef]
- Ryde, F.; Pe’er, A. Quasi-blackbody Component and Radiative Efficiency of the Prompt Emission of Gamma-ray Bursts. Astrophys. J. 2009, 702, 1211–1229. [Google Scholar] [CrossRef]
- Ryde, F.; Pe’er, A.; Nymark, T.; Axelsson, M.; Moretti, E.; Lundman, C.; Battelino, M.; Bissaldi, E.; Chiang, J.; Jackson, M.S.; et al. Observational evidence of dissipative photospheres in gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 415, 3693–3705. [Google Scholar] [CrossRef]
- Guiriec, S.; Mochkovitch, R.; Piran, T.; Daigne, F.; Kouveliotou, C.; Racusin, J.; Gehrels, N.; McEnery, J. GRB 131014A: A Laboratory for Studying the Thermal-like and Non-thermal Emissions in Gamma-Ray Bursts, and the New LnThi-EnTh,restpeak,i Relation. Astrophys. J. 2015, 814, 10. [Google Scholar] [CrossRef]
- Guiriec, S.; Gehrels, N.; McEnery, J.; Kouveliotou, C.; Hartmann, D.H. Photospheric Emission in the Joint GBM and Konus Prompt Spectra of GRB 120323A. Astrophys. J. 2017, 846, 138. [Google Scholar] [CrossRef]
- Li, L. Thermal Components in Gamma-Ray Bursts. I. How Do They Affect Nonthermal Spectral Parameters? Astrophys. J. Suppl. Ser. 2019, 245, 7. [Google Scholar] [CrossRef]
- Li, L.; Ryde, F.; Pe’er, A.; Yu, H.F.; Acuner, Z. Bayesian Time-resolved Spectroscopy of Multipulse GRBs: Variations of Emission Properties among Pulses. Astrophys. J. Suppl. Ser. 2021, 254, 35. [Google Scholar] [CrossRef]
- Kanbach, G.; Bertsch, D.L.; Fichtel, C.E.; Hartman, R.C.; Hunter, S.D.; Kniffen, D.A.; Hughlock, B.W.; Favale, A.; Hofstadter, R.; Hughes, E.B. The project EGRET (energetic gamma-ray experiment telescope) on NASA’s Gamma-Ray Observatory GRO. Space Sci. Rev. 1989, 49, 69–84. [Google Scholar] [CrossRef]
- Schneid, E.J.; Bertsch, D.L.; Fichtel, C.E.; Hartman, R.C.; Hunter, S.D.; Kanbach, G.; Kniffen, D.A.; Kwok, P.W.; Lin, Y.C.; Mattox, J.R.; et al. EGRET detection of high energy gamma rays from the gamma-ray burst of 3 May 1991. Astron. Astrophys. 1992, 255, L13. [Google Scholar]
- Sommer, M.; Bertsch, D.L.; Dingus, B.L.; Fichtel, C.E.; Fishman, G.J.; Harding, A.K.; Hartman, R.C.; Hunter, S.D.; Hurley, K.; Kanbach, G.; et al. High-Energy Gamma Rays from the Intense 1993 January 31 Gamma-Ray Burst. Astrophys. J. 1994, 422, L63. [Google Scholar] [CrossRef]
- Hurley, K.; Dingus, B.L.; Mukherjee, R.; Sreekumar, P.; Kouveliotou, C.; Meegan, C.; Fishman, G.J.; Band, D.; Ford, L.; Bertsch, D.; et al. Detection of a γ-ray burst of very long duration and very high energy. Nature 1994, 372, 652–654. [Google Scholar] [CrossRef]
- González, M.M.; Dingus, B.L.; Kaneko, Y.; Preece, R.D.; Dermer, C.D.; Briggs, M.S. A γ-ray burst with a high-energy spectral component inconsistent with the synchrotron shock model. Nature 2003, 424, 749–751. [Google Scholar] [CrossRef] [PubMed]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The Large Area Telescope on the Fermi Gamma-Ray Space Telescope Mission. Astrophys. J. 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
- Ajello, M.; Arimoto, M.; Axelsson, M.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bhat, P.N.; Bissaldi, E.; Blandford, R.D.; et al. A Decade of Gamma-Ray Bursts Observed by Fermi-LAT: The Second GRB Catalog. Astrophys. J. 2019, 878, 52. [Google Scholar] [CrossRef]
- MAGIC Collaboration; Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Engels, A.A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; et al. Observation of inverse Compton emission from a long γ-ray burst. Nature 2019, 575, 459–463. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Variability in Gamma-Ray Bursts: A Clue. Astrophys. J. 1997, 485, 270–273. [Google Scholar] [CrossRef]
- Narayan, R.; Kumar, P. A turbulent model of gamma-ray burst variability. Mon. Not. R. Astron. Soc. 2009, 394, L117–L120. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of two classes of gamma-ray bursts. Astrophys. J. 1993, 413, L101–L104. [Google Scholar] [CrossRef]
- Bromberg, O.; Nakar, E.; Piran, T.; Sari, R. Short versus Long and Collapsars versus Non-collapsars: A Quantitative Classification of Gamma-Ray Bursts. Astrophys. J. 2013, 764, 179. [Google Scholar] [CrossRef]
- Ahumada, T.; Singer, L.P.; Anand, S.; Coughlin, M.W.; Kasliwal, M.M.; Ryan, G.; Andreoni, I.; Cenko, S.B.; Fremling, C.; Kumar, H.; et al. Discovery and confirmation of the shortest gamma-ray burst from a collapsar. Nat. Astron. 2021, 5, 917–927. [Google Scholar] [CrossRef]
- Woosley, S.E. Gamma-ray bursts from stellar mass accretion disks around black holes. Astrophys. J. 1993, 405, 273–277. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E. Collapsars: Gamma-Ray Bursts and Explosions in “Failed Supernovae”. Astrophys. J. 1999, 524, 262–289. [Google Scholar] [CrossRef]
- Hjorth, J.; Sollerman, J.; Møller, P.; Fynbo, J.P.U.; Woosley, S.E.; Kouveliotou, C.; Tanvir, N.R.; Greiner, J.; Andersen, M.I.; Castro-Tirado, A.J.; et al. A very energetic supernova associated with the γ-ray burst of 29 March 2003. Nature 2003, 423, 847–850. [Google Scholar] [CrossRef]
- Campana, S.; Mangano, V.; Blustin, A.J.; Brown, P.; Burrows, D.N.; Chincarini, G.; Cummings, J.R.; Cusumano, G.; Della Valle, M.; Malesani, D.; et al. The association of GRB 060218 with a supernova and the evolution of the shock wave. Nature 2006, 442, 1008–1010. [Google Scholar] [CrossRef] [PubMed]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and gamma-rays from coalescing neutron stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Norris, J.P.; Bonnell, J.T. Short Gamma-Ray Bursts with Extended Emission. Astrophys. J. 2006, 643, 266–275. [Google Scholar] [CrossRef]
- Genet, F.; Butler, N.R.; Granot, J. The long rapid decay phase of the extended emission from the short GRB 080503. Mon. Not. R. Astron. Soc. 2010, 405, 695–700. [Google Scholar] [CrossRef][Green Version]
- Perley, D.A.; Metzger, B.D.; Granot, J.; Butler, N.R.; Sakamoto, T.; Ramirez-Ruiz, E.; Levan, A.J.; Bloom, J.S.; Miller, A.A.; Bunker, A.; et al. GRB 080503: Implications of a Naked Short Gamma-Ray Burst Dominated by Extended Emission. Astrophys. J. 2009, 696, 1871–1885. [Google Scholar] [CrossRef]
- Bhat, P.N.; Fishman, G.J.; Meegan, C.A.; Wilson, R.B.; Brock, M.N.; Paciesas, W.S. Evidence for sub-millisecond structure in a γ-ray burst. Nature 1992, 359, 217–218. [Google Scholar] [CrossRef]
- Walker, K.C.; Schaefer, B.E.; Fenimore, E.E. Gamma-Ray Bursts Have Millisecond Variability. Astrophys. J. 2000, 537, 264–269. [Google Scholar] [CrossRef]
- Piran, T. Gamma-ray bursts and the fireball model. Phys. Rep. 1999, 314, 575–667. [Google Scholar] [CrossRef]
- Tang, Q.W.; Wang, X.Y.; Liu, R.Y. Evidence of an Internal Dissipation Origin for the High-energy Prompt Emission of GRB 170214A. Astrophys. J. 2017, 844, 56. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; Wiley-Interscience: New York, NY, USA, 1979; p. 393. [Google Scholar]
- Covino, S.; Lazzati, D.; Ghisellini, G.; Saracco, P.; Campana, S.; Chincarini, G.; di Serego, S.; Cimatti, A.; Vanzi, L.; Pasquini, L.; et al. GRB 990510: Linearly polarized radiation from a fireball. Astron. Astrophys. 1999, 348, L1–L4. [Google Scholar]
- Wijers, R.A.M.J.; Vreeswijk, P.M.; Galama, T.J.; Rol, E.; van Paradijs, J.; Kouveliotou, C.; Giblin, T.; Masetti, N.; Palazzi, E.; Pian, E.; et al. Detection of Polarization in the Afterglow of GRB 990510 with the ESO Very Large Telescope. Astrophys. J. 1999, 523, L33–L36. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J.; Kumar, P. Linear polarization in gamma-ray burst prompt emission. MNRAS 2020, 491, 3343–3373. [Google Scholar] [CrossRef]
- Coburn, W.; Boggs, S.E. Polarization of the prompt γ-ray emission from the γ-ray burst of 6 December 2002. Nature 2003, 423, 415–417. [Google Scholar] [CrossRef]
- Willis, D.R.; Barlow, E.J.; Bird, A.J.; Clark, D.J.; Dean, A.J.; McConnell, M.L.; Moran, L.; Shaw, S.E.; Sguera, V. Evidence of polarisation in the prompt gamma-ray emission from GRB 930131 and GRB 960924. Astron. Astrophys. 2005, 439, 245–253. [Google Scholar] [CrossRef]
- Kalemci, E.; Boggs, S.E.; Kouveliotou, C.; Finger, M.; Baring, M.G. Search for Polarization from the Prompt Gamma-Ray Emission of GRB 041219a with SPI on INTEGRAL. Astrophys. J. Suppl. Ser. 2007, 169, 75–82. [Google Scholar] [CrossRef]
- McGlynn, S.; Clark, D.J.; Dean, A.J.; Hanlon, L.; McBreen, S.; Willis, D.R.; McBreen, B.; Bird, A.J.; Foley, S. Polarisation studies of the prompt gamma-ray emission from GRB 041219a using the spectrometer aboard INTEGRAL. Astron. Astrophys. 2007, 466, 895–904. [Google Scholar] [CrossRef]
- Götz, D.; Laurent, P.; Lebrun, F.; Daigne, F.; Bošnjak, Ž. Variable Polarization Measured in the Prompt Emission of GRB 041219A Using IBIS on Board INTEGRAL. Astrophys. J. 2009, 695, L208–L212. [Google Scholar] [CrossRef]
- Götz, D.; Covino, S.; Fernández-Soto, A.; Laurent, P.; Bošnjak, Ž. The polarized gamma-ray burst GRB 061122. Mon. Not. R. Astron. Soc. 2013, 431, 3550–3556. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Gunji, S.; Mihara, T.; Toma, K.; Sakashita, T.; Morihara, Y.; Takahashi, T.; Toukairin, N.; Fujimoto, H.; et al. Detection of Gamma-Ray Polarization in Prompt Emission of GRB 100826A. Astrophys. J. 2011, 743, L30. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Gunji, S.; Mihara, T.; Toma, K.; Morihara, Y.; Takahashi, T.; Wakashima, Y.; Yonemochi, H.; Sakashita, T.; et al. Magnetic Structures in Gamma-Ray Burst Jets Probed by Gamma-Ray Polarization. Astrophys. J. 2012, 758, L1. [Google Scholar] [CrossRef]
- Rao, A.R.; Chand, V.; Hingar, M.K.; Iyyani, S.; Khanna, R.; Kutty, A.P.K.; Malkar, J.P.; Paul, D.; Bhalerao, V.B.; Bhattacharya, D.; et al. AstroSat CZT Imager Observations of GRB 151006A: Timing, Spectroscopy, and Polarization Study. Astrophys. J. 2016, 833, 86. [Google Scholar] [CrossRef]
- Chand, V.; Chattopadhyay, T.; Oganesyan, G.; Rao, A.R.; Vadawale, S.V.; Bhattacharya, D.; Bhalerao, V.B.; Misra, K. AstroSat-CZTI Detection of Variable Prompt Emission Polarization in GRB 171010A. Astrophys. J. 2019, 874, 70. [Google Scholar] [CrossRef]
- Sharma, V.; Iyyani, S.; Bhattacharya, D.; Chattopadhyay, T.; Rao, A.R.; Aarthy, E.; Vadawale, S.V.; Mithun, N.P.S.; Bhalerao, V.B.; Ryde, F.; et al. Time-varying Polarized Gamma-Rays from GRB 160821A: Evidence for Ordered Magnetic Fields. Astrophys. J. 2019, 882, L10. [Google Scholar] [CrossRef]
- Kole, M.; De Angelis, N.; Berlato, F.; Burgess, J.M.; Gauvin, N.; Greiner, J.; Hajdas, W.; Li, H.C.; Li, Z.H.; Produit, N.; et al. The POLAR Gamma-Ray Burst Polarization Catalog. arXiv 2020, arXiv:2009.04871. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J.; Papathanassiou, H. Spectral properties of blast-wave models of gamma-ray burst sources. Astrophys. J. 1994, 432, 181–193. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. The physics of pulses in gamma-ray bursts: Emission processes, temporal profiles and time-lags. Mon. Not. R. Astron. Soc. 2003, 342, 587–592. [Google Scholar] [CrossRef]
- Thompson, C. A Model of Gamma-Ray Bursts. Mon. Not. R. Astron. Soc. 1994, 270, 480–498. [Google Scholar] [CrossRef]
- Rees, M.J.; Mészáros, P. Dissipative Photosphere Models of Gamma-Ray Bursts and X-Ray Flashes. Astrophys. J. 2005, 628, 847–852. [Google Scholar] [CrossRef]
- Pe’er, A. Temporal Evolution of Thermal Emission from Relativistically Expanding Plasma. Astrophys. J. 2008, 682, 463–473. [Google Scholar] [CrossRef]
- Toma, K.; Wu, X.F.; Mészáros, P. Photosphere-internal shock model of gamma-ray bursts: Case studies of Fermi/LAT bursts. Mon. Not. R. Astron. Soc. 2011, 415, 1663–1680. [Google Scholar] [CrossRef]
- Cavallo, G.; Rees, M.J. A qualitative study of cosmic fireballs and γ-ray bursts. Mon. Not. R. Astron. Soc. 1978, 183, 359–365. [Google Scholar] [CrossRef]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. 1986, 308, L43–L46. [Google Scholar] [CrossRef]
- Goodman, J. Are gamma-ray bursts optically thick? Astrophys. J. 1986, 308, L47–L50. [Google Scholar] [CrossRef]
- Shemi, A.; Piran, T. The Appearance of Cosmic Fireballs. Astrophys. J. 1990, 365, L55. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J. Relativistic fireballs and their impact on external matter—Models for cosmological gamma-ray bursts. Astrophys. J. 1993, 405, 278–284. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Steep Slopes and Preferred Breaks in Gamma-Ray Burst Spectra: TheRole of Photospheres and Comptonization. Astrophys. J. 2000, 530, 292–298. [Google Scholar] [CrossRef]
- Mészáros, P.; Ramirez-Ruiz, E.; Rees, M.J.; Zhang, B. X-Ray-rich Gamma-Ray Bursts, Photospheres, and Variability. Astrophys. J. 2002, 578, 812–817. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Collisional mechanism for gamma-ray burst emission. Mon. Not. R. Astron. Soc. 2010, 407, 1033–1047. [Google Scholar] [CrossRef]
- Pe’er, A.; Ryde, F. A Theory of Multicolor Blackbody Emission from Relativistically Expanding Plasmas. Astrophys. J. 2011, 732, 49. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, B. Low Energy Spectral Index and Ep Evolution of Quasi-thermal Photosphere Emission of Gamma-Ray Bursts. Astrophys. J. 2014, 785, 112. [Google Scholar] [CrossRef]
- Lundman, C.; Pe’er, A.; Ryde, F. A theory of photospheric emission from relativistic, collimated outflows. Mon. Not. R. Astron. Soc. 2013, 428, 2430–2442. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; et al. Fermi Observations of GRB 090902B: A Distinct Spectral Component in the Prompt and Delayed Emission. Astrophys. J. 2009, 706, L138–L144. [Google Scholar] [CrossRef]
- Zhang, B.; Pe’er, A. Evidence of an Initially Magnetically Dominated Outflow in GRB 080916C. Astrophys. J. 2009, 700, L65–L68. [Google Scholar] [CrossRef]
- Wijers, R.A.M.J.; Rees, M.J.; Meszaros, P. Shocked by GRB 970228: The afterglow of a cosmological fireball. Mon. Not. R. Astron. Soc. 1997, 288, L51–L56. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. 1998, 497, L17–L20. [Google Scholar] [CrossRef]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Fermi, E. Galactic Magnetic Fields and the Origin of Cosmic Radiation. Astrophys. J. 1954, 119, 1. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts. I. Mon. Not. R. Astron. Soc. 1978, 182, 147–156. [Google Scholar] [CrossRef]
- Blandford, R.D.; Ostriker, J.P. Particle acceleration by astrophysical shocks. Astrophys. J. 1978, 221, L29–L32. [Google Scholar] [CrossRef]
- Blandford, R.; Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 1987, 154, 1–75. [Google Scholar] [CrossRef]
- Jones, F.C.; Ellison, D.C. The plasma physics of shock acceleration. Space Sci. Rev. 1991, 58, 259–346. [Google Scholar] [CrossRef]
- Silva, L.O.; Fonseca, R.A.; Tonge, J.W.; Dawson, J.M.; Mori, W.B.; Medvedev, M.V. Interpenetrating Plasma Shells: Near-equipartition Magnetic Field Generation and Nonthermal Particle Acceleration. Astrophys. J. 2003, 596, L121–L124. [Google Scholar] [CrossRef]
- Nishikawa, K.I.; Hardee, P.; Richardson, G.; Preece, R.; Sol, H.; Fishman, G.J. Particle Acceleration in Relativistic Jets Due to Weibel Instability. Astrophys. J. 2003, 595, 555–563. [Google Scholar] [CrossRef]
- Spitkovsky, A. Particle Acceleration in Relativistic Collisionless Shocks: Fermi Process at Last? Astrophys. J. 2008, 682, L5. [Google Scholar] [CrossRef]
- Haugbølle, T. Three-dimensional Modeling of Relativistic Collisionless Ion-electron Shocks. Astrophys. J. 2011, 739, L42. [Google Scholar] [CrossRef][Green Version]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Pair Shocks: Dependence of Shock Acceleration on Magnetic Obliquity. Astrophys. J. 2009, 698, 1523–1549. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Electron-Ion Shocks. Astrophys. J. 2011, 726, 75. [Google Scholar] [CrossRef]
- Summerlin, E.J.; Baring, M.G. Diffusive Acceleration of Particles at Oblique, Relativistic, Magnetohydrodynamic Shocks. Astrophys. J. 2012, 745, 63. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Relativistic Reconnection: An Efficient Source of Non-thermal Particles. Astrophys. J. 2014, 783, L21. [Google Scholar] [CrossRef]
- Lemoine, M.; Vanthieghem, A.; Pelletier, G.; Gremillet, L. Physics of relativistic collisionless shocks. II. Dynamics of the background plasma. Phys. Rev. E 2019, 100, 033209. [Google Scholar] [CrossRef] [PubMed]
- Nagar, Y.; Keshet, U. Diffusive acceleration in relativistic shocks: Particle feedback. Mon. Not. R. Astron. Soc. 2021, 501, 329–336. [Google Scholar] [CrossRef]
- Kundu, S.; Vaidya, B.; Mignone, A. Numerical Modeling and Physical Interplay of Stochastic Turbulent Acceleration for Nonthermal Emission Processes. Astrophys. J. 2021, 921, 74. [Google Scholar] [CrossRef]
- Sironi, L.; Petropoulou, M.; Giannios, D. Relativistic jets shine through shocks or magnetic reconnection? Mon. Not. R. Astron. Soc. 2015, 450, 183–191. [Google Scholar] [CrossRef]
- Zenitani, S.; Hoshino, M. The Generation of Nonthermal Particles in the Relativistic Magnetic Reconnection of Pair Plasmas. Astrophys. J. 2001, 562, L63–L66. [Google Scholar] [CrossRef]
- Zenitani, S.; Hoshino, M. Particle Acceleration and Magnetic Dissipation in Relativistic Current Sheet of Pair Plasmas. Astrophys. J. 2007, 670, 702–726. [Google Scholar] [CrossRef]
- McKinney, J.C.; Uzdensky, D.A. A reconnection switch to trigger gamma-ray burst jet dissipation. Mon. Not. R. Astron. Soc. 2012, 419, 573–607. [Google Scholar] [CrossRef]
- Guo, F.; Li, H.; Daughton, W.; Liu, Y.H. Formation of Hard Power Laws in the Energetic Particle Spectra Resulting from Relativistic Magnetic Reconnection. Phys. Rev. Lett. 2014, 113, 155005. [Google Scholar] [CrossRef]
- Guo, F.; Liu, Y.H.; Daughton, W.; Li, H. Particle Acceleration and Plasma Dynamics during Magnetic Reconnection in the Magnetically Dominated Regime. Astrophys. J. 2015, 806, 167. [Google Scholar] [CrossRef]
- Sironi, L.; Giannios, D.; Petropoulou, M. Plasmoids in relativistic reconnection, from birth to adulthood: First they grow, then they go. Mon. Not. R. Astron. Soc. 2016, 462, 48–74. [Google Scholar] [CrossRef]
- Werner, G.R.; Uzdensky, D.A. Nonthermal Particle Acceleration in 3D Relativistic Magnetic Reconnection in Pair Plasma. Astrophys. J. 2017, 843, L27. [Google Scholar] [CrossRef]
- Kagan, D.; Nakar, E.; Piran, T. Physics of the saturation of particle acceleration in relativistic magnetic reconnection. Mon. Not. R. Astron. Soc. 2018, 476, 3902–3912. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Unsteady outflow models for cosmological gamma-ray bursts. Astrophys. J. 1994, 430, L93–L96. [Google Scholar] [CrossRef]
- Paczynski, B.; Xu, G. Neutrino bursts from gamma-ray bursts. Astrophys. J. 1994, 427, 708–713. [Google Scholar] [CrossRef]
- Kobayashi, S.; Piran, T.; Sari, R. Can Internal Shocks Produce the Variability in Gamma-Ray Bursts? Astrophys. J. 1997, 490, 92. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. Gamma-ray bursts from internal shocks in a relativistic wind: Temporal and spectral properties. Mon. Not. R. Astron. Soc. 1998, 296, 275–286. [Google Scholar] [CrossRef]
- Kumar, P.; McMahon, E. A general scheme for modelling γ-ray burst prompt emission. Mon. Not. R. Astron. Soc. 2008, 384, 33–63. [Google Scholar] [CrossRef]
- Bošnjak, Ž.; Daigne, F.; Dubus, G. Prompt high-energy emission from γ-ray bursts in the internal shock model. Astron. Astrophys. 2009, 498, 677–703. [Google Scholar] [CrossRef]
- Bošnjak, Ž.; Daigne, F. Spectral evolution in gamma-ray bursts: Predictions of the internal shock model and comparison to observations. Astron. Astrophys. 2014, 568, A45. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. Gamma-ray bursts from internal shocks in a relativistic wind: A hydrodynamical study. Astron. Astrophys. 2000, 358, 1157–1166. [Google Scholar]
- Mimica, P.; Aloy, M.A.; Müller, E. Internal shocks in relativistic outflows: Collisions of magnetized shells. Astron. Astrophys. 2007, 466, 93–106. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Cosmological gamma-ray bursts: Internal versus external shocks. Mon. Not. R. Astron. Soc. 1997, 287, 110–116. [Google Scholar] [CrossRef]
- Kumar, P. Gamma-Ray Burst Energetics. Astrophys. J. 1999, 523, L113–L116. [Google Scholar] [CrossRef]
- Spada, M.; Panaitescu, A.; Mészáros, P. Analysis of Temporal Features of Gamma-Ray Bursts in the Internal Shock Model. Astrophys. J. 2000, 537, 824–832. [Google Scholar] [CrossRef]
- Lloyd, N.M.; Petrosian, V. Synchrotron Radiation as the Source of Gamma-Ray Burst Spectra. Astrophys. J. 2000, 543, 722–732. [Google Scholar] [CrossRef]
- Bykov, A.M.; Meszaros, P. Electron Acceleration and Efficiency in Nonthermal Gamma-Ray Sources. Astrophys. J. 1996, 461, L37. [Google Scholar] [CrossRef]
- Spruit, H.C.; Daigne, F.; Drenkhahn, G. Large scale magnetic fields and their dissipation in GRB fireballs. Astron. Astrophys. 2001, 369, 694–705. [Google Scholar] [CrossRef]
- Gruzinov, A.; Mészáros, P. Photon Acceleration in Variable Ultrarelativistic Outflows and High-Energy Spectra of Gamma-Ray Bursts. Astrophys. J. 2000, 539, L21–L24. [Google Scholar] [CrossRef]
- Kumar, P.; Narayan, R. GRB 080319B: Evidence for relativistic turbulence, not internal shocks. Mon. Not. R. Astron. Soc. 2009, 395, 472–489. [Google Scholar] [CrossRef]
- Zou, Y.C.; Piran, T.; Sari, R. Clues from the Prompt Emission of GRB 080319B. Astrophys. J. 2009, 692, L92–L95. [Google Scholar] [CrossRef]
- Derishev, E.V.; Kocharovsky, V.V.; Kocharovsky, V.V. The Neutron Component in Fireballs of Gamma-Ray Bursts: Dynamics and Observable Imprints. Astrophys. J. 1999, 521, 640–649. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Multi-GEV Neutrinos from Internal Dissipation in Gamma-Ray Burst Fireballs. Astrophys. J. 2000, 541, L5–L8. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Nuclear Composition of Gamma-Ray Burst Fireballs. Astrophys. J. 2003, 588, 931–944. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Hyper-accreting black holes. In Cool Discs, Hot Flows: The Varying Faces of Accreting Compact Objects; Axelsson, M., Ed.; American Institute of Physics Conference Series; 2008; Volume 1054, pp. 51–70. Available online: https://ui.adsabs.harvard.edu/abs/2008AIPC.1054...51B (accessed on 1 December 2021).
- Vurm, I.; Beloborodov, A.M.; Poutanen, J. Gamma-Ray Bursts from Magnetized Collisionally Heated Jets. Astrophys. J. 2011, 738, 77. [Google Scholar] [CrossRef]
- Usov, V.V. Millisecond pulsars with extremely strong magnetic fields as a cosmological source of γ-ray bursts. Nature 1992, 357, 472–474. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Poynting Jets from Black Holes and Cosmological Gamma-Ray Bursts. Astrophys. J. 1997, 482, L29–L32. [Google Scholar] [CrossRef]
- Spruit, H.C. Gamma-ray bursts from X-ray binaries. Astron. Astrophys. 1999, 341, L1–L4. [Google Scholar]
- Lyutikov, M.; Blandford, R. Gamma Ray Bursts as Electromagnetic Outflows. arXiv 2003, arXiv:astro–ph/0312347. [Google Scholar]
- Narayan, R.; Kumar, P.; Tchekhovskoy, A. Constraints on cold magnetized shocks in gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 416, 2193–2201. [Google Scholar] [CrossRef][Green Version]
- Kumar, P.; Crumley, P. Radiation from a relativistic Poynting jet: Some general considerations. Mon. Not. R. Astron. Soc. 2015, 453, 1820–1828. [Google Scholar] [CrossRef]
- Drenkhahn, G. Acceleration of GRB outflows by Poynting flux dissipation. Astron. Astrophys. 2002, 387, 714–724. [Google Scholar] [CrossRef]
- Drenkhahn, G.; Spruit, H.C. Efficient acceleration and radiation in Poynting flux powered GRB outflows. Astron. Astrophys. 2002, 391, 1141–1153. [Google Scholar] [CrossRef]
- Giannios, D.; Spruit, H.C. Spectra of Poynting-flux powered GRB outflows. Astron. Astrophys. 2005, 430, 1–7. [Google Scholar] [CrossRef]
- Giannios, D. Prompt GRB emission from gradual energy dissipation. Astron. Astrophys. 2008, 480, 305–312. [Google Scholar] [CrossRef]
- Bégué, D.; Pe’er, A.; Lyubarsky, Y. Radiative striped wind model for gamma-ray bursts. Mon. Not. R. Astron. Soc. 2017, 467, 2594–2611. [Google Scholar] [CrossRef]
- Giannios, D.; Uzdensky, D.A. GRB and blazar jets shining through their stripes. Mon. Not. R. Astron. Soc. 2019, 484, 1378–1389. [Google Scholar] [CrossRef]
- Giannios, D. Prompt emission spectra from the photosphere of a GRB. Astron. Astrophys. 2006, 457, 763–770. [Google Scholar] [CrossRef]
- Giannios, D. The peak energy of dissipative gamma-ray burst photospheres. Mon. Not. R. Astron. Soc. 2012, 422, 3092–3098. [Google Scholar] [CrossRef]
- Beniamini, P.; Giannios, D. Prompt gamma-ray burst emission from gradual magnetic dissipation. MNRAS 2017, 468, 3202–3211. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J.; Beniamini, P. GRB spectrum from gradual dissipation in a magnetized outflow. Mon. Not. R. Astron. Soc. 2020, 499, 1356–1372. [Google Scholar] [CrossRef]
- Contopoulos, J. A Simple Type of Magnetically Driven Jets: An Astrophysical Plasma Gun. Astrophys. J. 1995, 450, 616. [Google Scholar] [CrossRef]
- Granot, J.; Komissarov, S.S.; Spitkovsky, A. Impulsive acceleration of strongly magnetized relativistic flows. Mon. Not. R. Astron. Soc. 2011, 411, 1323–1353. [Google Scholar] [CrossRef]
- Granot, J. The effects of sub-shells in highly magnetized relativistic flows. Mon. Not. R. Astron. Soc. 2012, 421, 2467–2477. [Google Scholar] [CrossRef][Green Version]
- Komissarov, S.S. Shock dissipation in magnetically dominated impulsive flows. Mon. Not. R. Astron. Soc. 2012, 422, 326–346. [Google Scholar] [CrossRef]
- Lazar, A.; Nakar, E.; Piran, T. Gamma-Ray Burst Light Curves in the Relativistic Turbulence and Relativistic Subjet Models. Astrophys. J. 2009, 695, L10–L14. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, H. The Internal-collision-induced Magnetic Reconnection and Turbulence (ICMART) Model of Gamma-ray Bursts. Astrophys. J. 2011, 726, 90. [Google Scholar] [CrossRef]
- Beniamini, P.; Granot, J. Properties of GRB light curves from magnetic reconnection. Mon. Not. R. Astron. Soc. 2016, 459, 3635–3658. [Google Scholar] [CrossRef]
- Barniol Duran, R.; Leng, M.; Giannios, D. An anisotropic minijets model for the GRB prompt emission. Mon. Not. R. Astron. Soc. 2016, 455, L6–L10. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Asano, K.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. The First Fermi-LAT Gamma-Ray Burst Catalog. Astrophys. J. Suppl. Ser. 2013, 209, 11. [Google Scholar] [CrossRef]
- Rees, M.J.; Mészáros, P. Relativistic fireballs: Energy conversion and time-scales. Mon. Not. R. Astron. Soc. 1992, 258, 41P–43P. [Google Scholar] [CrossRef]
- Meszaros, P.; Laguna, P.; Rees, M.J. Gasdynamics of relativistically expanding gamma-ray burst sources—Kinematics, energetics, magnetic fields, and efficiency. Astrophys. J. 1993, 415, 181–190. [Google Scholar] [CrossRef]
- Papathanassiou, H.; Meszaros, P. Spectra of Unsteady Wind Models of Gamma-Ray Bursts. Astrophys. J. 1996, 471, L91. [Google Scholar] [CrossRef]
- Beniamini, P.; Piran, T. Constraints on the Synchrotron Emission Mechanism in Gamma-Ray Bursts. Astrophys. J. 2013, 769, 69. [Google Scholar] [CrossRef]
- Beniamini, P.; Piran, T. The emission mechanism in magnetically dominated gamma-ray burst outflows. Mon. Not. R. Astron. Soc. 2014, 445, 3892–3907. [Google Scholar] [CrossRef]
- Katz, J.I. Low-frequency spectra of gamma-ray bursts. Astrophys. J. 1994, 432, L107–L109. [Google Scholar] [CrossRef]
- Pe’er, A.; Zhang, B. Synchrotron Emission in Small-Scale Magnetic Fields as a Possible Explanation for Prompt Emission Spectra of Gamma-Ray Bursts. Astrophys. J. 2006, 653, 454–461. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z.; Liu, X.; Zhang, B.b.; Bai, J.; Mészáros, P. Gamma-Ray Burst Spectrum with Decaying Magnetic Field. Astrophys. J. 2014, 780, 12. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Kumar, P. On explaining prompt emission from GRB central engines with photospheric emission model. arXiv 2021, arXiv:2110.14792. [Google Scholar]
- Derishev, E.V. Synchrotron emission in the fast cooling regime: Which spectra can be explained? Astrophys. Space Sci. 2007, 309, 157–161. [Google Scholar] [CrossRef]
- Nakar, E.; Ando, S.; Sari, R. Klein-Nishina Effects on Optically Thin Synchrotron and Synchrotron Self-Compton Spectrum. Astrophys. J. 2009, 703, 675–691. [Google Scholar] [CrossRef]
- Daigne, F.; Bošnjak, Ž.; Dubus, G. Reconciling observed gamma-ray burst prompt spectra with synchrotron radiation? Astron. Astrophys. 2011, 526, A110. [Google Scholar] [CrossRef]
- Barniol Duran, R.; Bošnjak, Ž.; Kumar, P. Inverse-Compton cooling in Klein-Nishina regime and gamma-ray burst prompt spectrum. Mon. Not. R. Astron. Soc. 2012, 424, 3192–3200. [Google Scholar] [CrossRef][Green Version]
- Beniamini, P.; Barniol Duran, R.; Giannios, D. Marginally fast cooling synchrotron models for prompt GRBs. Mon. Not. R. Astron. Soc. 2018, 476, 1785–1795. [Google Scholar] [CrossRef]
- Piran, T.; Sari, R.; Zou, Y.C. Observational limits on inverse Compton processes in gamma-ray bursts. Mon. Not. R. Astron. Soc. 2009, 393, 1107–1113. [Google Scholar] [CrossRef]
- Paczynski, B. Super-Eddington winds from neutron stars. Astrophys. J. 1990, 363, 218–226. [Google Scholar] [CrossRef]
- Preece, R.D.; Briggs, M.S.; Mallozzi, R.S.; Pendleton, G.N.; Paciesas, W.S.; Band, D.L. The Synchrotron Shock Model Confronts a “Line of Death” in the BATSE Gamma-Ray Burst Data. Astrophys. J. 1998, 506, L23–L26. [Google Scholar] [CrossRef]
- Eichler, D.; Levinson, A. A Compact Fireball Model of Gamma-Ray Bursts. Astrophys. J. 2000, 529, 146–150. [Google Scholar] [CrossRef]
- Pe’er, A.; Waxman, E. Prompt Gamma-Ray Burst Spectra: Detailed Calculations and the Effect of Pair Production. Astrophys. J. 2004, 613, 448–459. [Google Scholar] [CrossRef]
- Pe’er, A.; Mészáros, P.; Rees, M.J. Peak Energy Clustering and Efficiency in Compact Objects. Astrophys. J. 2005, 635, 476–480. [Google Scholar] [CrossRef]
- Pe’er, A.; Mészáros, P.; Rees, M.J. The Observable Effects of a Photospheric Component on GRB and XRF Prompt Emission Spectrum. Astrophys. J. 2006, 642, 995–1003. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Radiative Transfer in Ultrarelativistic Outflows. Astrophys. J. 2011, 737, 68. [Google Scholar] [CrossRef]
- Vereshchagin, G.V. Physics of Nondissipative Ultrarelativistic Photospheres. Int. J. Mod. Phys. D 2014, 23, 30003. [Google Scholar] [CrossRef]
- Ito, H.; Nagataki, S.; Ono, M.; Lee, S.H.; Mao, J.; Yamada, S.; Pe’er, A.; Mizuta, A.; Harikae, S. Photospheric Emission from Stratified Jets. Astrophys. J. 2013, 777, 62. [Google Scholar] [CrossRef]
- Lundman, C.; Pe’er, A.; Ryde, F. Polarization properties of photospheric emission from relativistic, collimated outflows. Mon. Not. R. Astron. Soc. 2014, 440, 3292–3308. [Google Scholar] [CrossRef]
- Meng, Y.Z.; Liu, L.D.; Wei, J.J.; Wu, X.F.; Zhang, B.B. The Time-resolved Spectra of Photospheric Emission from a Structured Jet for Gamma-Ray Bursts. Astrophys. J. 2019, 882, 26. [Google Scholar] [CrossRef]
- Parsotan, T.; Lazzati, D. Monte Carlo Simulations of Photospheric Emission in Gamma Ray Bursts. arXiv 2021, arXiv:2110.13038. [Google Scholar]
- Eichler, D.; Manis, H. Spectral Lags Explained as Scattering from Accelerated Scatterers. Astrophys. J. 2008, 689, L85. [Google Scholar] [CrossRef]
- Eichler, D. Cloaked Gamma-Ray Bursts. Astrophys. J. 2014, 787, L32. [Google Scholar] [CrossRef]
- Vyas, M.K.; Pe’er, A.; Eichler, D. A Backscattering-dominated Prompt Emission Model for the Prompt Phase of Gamma-Ray Bursts. Astrophys. J. 2021, 908, 9. [Google Scholar] [CrossRef]
- Vyas, M.K.; Pe’er, A.; Eichler, D. Predicting Spectral Parameters in the Backscattering-dominated Model for the Prompt Phase of GRBs. Astrophys. J. 2021, 918, L12. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; in’t Zand, J.J.M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; et al. Intrinsic spectra and energetics of BeppoSAX Gamma-Ray Bursts with known redshifts. Astron. Astrophys. 2002, 390, 81–89. [Google Scholar] [CrossRef]
- Pe’er, A.; Zhang, B.B.; Ryde, F.; McGlynn, S.; Zhang, B.; Preece, R.D.; Kouveliotou, C. The connection between thermal and non-thermal emission in gamma-ray bursts: General considerations and GRB 090902B as a case study. Mon. Not. R. Astron. Soc. 2012, 420, 468–482. [Google Scholar] [CrossRef]
- Gupta, N.; Zhang, B. Prompt emission of high-energy photons from gamma ray bursts. Mon. Not. R. Astron. Soc. 2007, 380, 78–92. [Google Scholar] [CrossRef]
- Fan, Y.Z.; Piran, T. High-energy γ-ray emission from gamma-ray bursts—Before GLAST. Front. Phys. China 2008, 3, 306–330. [Google Scholar] [CrossRef][Green Version]
- Asano, K.; Inoue, S.; Mészáros, P. Prompt High-Energy Emission from Proton-Dominated Gamma-Ray Bursts. Astrophys. J. 2009, 699, 953–957. [Google Scholar] [CrossRef]
- Wang, X.Y.; Li, Z.; Dai, Z.G.; Mészáros, P. GRB 080916C: On the Radiation Origin of the Prompt Emission from keV/MeV TO GeV. Astrophys. J. 2009, 698, L98–L102. [Google Scholar] [CrossRef][Green Version]
- Razzaque, S.; Dermer, C.D.; Finke, J.D. Synchrotron Radiation from Ultra-High Energy Protons and the Fermi Observations of GRB 080916C. Open Astron. J. 2010, 3, 150–155. [Google Scholar] [CrossRef]
- Asano, K.; Mészáros, P. Delayed Onset of High-energy Emissions in Leptonic and Hadronic Models of Gamma-Ray Bursts. Astrophys. J. 2012, 757, 115. [Google Scholar] [CrossRef]
- Crumley, P.; Kumar, P. Hadronic models for Large Area Telescope prompt emission observed in Fermi gamma-ray bursts. Mon. Not. R. Astron. Soc. 2013, 429, 3238–3251. [Google Scholar] [CrossRef]
- Ghisellini, G.; Ghirlanda, G.; Oganesyan, G.; Ascenzi, S.; Nava, L.; Celotti, A.; Salafia, O.S.; Ravasio, M.E.; Ronchi, M. Proton-synchrotron as the radiation mechanism of the prompt emission of gamma-ray bursts? Astron. Astrophys. 2020, 636, A82. [Google Scholar] [CrossRef]
- Schüssler, F. The Transient program of the Cherenkov Telescope Array. arXiv 2019, arXiv:1907.07567. [Google Scholar]
- Fioretti, V.; Ribeiro, D.; Humensky, T.B.; Bulgarelli, A.; Maier, G.; Moralejo, A.; Nigro, C. The Cherenkov Telescope Array sensitivity to the transient sky. arXiv 2019, arXiv:1907.08018. [Google Scholar]
- Inoue, S.; Granot, J.; O’Brien, P.T.; Asano, K.; Bouvier, A.; Carosi, A.; Connaughton, V.; Garczarczyk, M.; Gilmore, R.; Hinton, J.; et al. Gamma-ray burst science in the era of the Cherenkov Telescope Array. Astropart. Phys. 2013, 43, 252–275. [Google Scholar] [CrossRef]
- Kakuwa, J.; Murase, K.; Toma, K.; Inoue, S.; Yamazaki, R.; Ioka, K. Prospects for detecting gamma-ray bursts at very high energies with the Cherenkov Telescope Array. Mon. Not. R. Astron. Soc. 2012, 425, 514–526. [Google Scholar] [CrossRef]
- Wei, J.; Cordier, B.; Antier, S.; Antilogus, P.; Atteia, J.L.; Bajat, A.; Basa, S.; Beckmann, V.; Bernardini, M.G.; Boissier, S.; et al. The Deep and Transient Universe in the SVOM Era: New Challenges and Opportunities—Scientific prospects of the SVOM mission. arXiv 2016, arXiv:1610.06892. [Google Scholar]
- Rudolph, A.; Bošnjak, Ž.; Palladino, A.; Sadeh, I.; Winter, W. Multi-wavelength radiation models for low-luminosity GRBs, and the implications for UHECRs. arXiv 2021, arXiv:2107.04612. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quantum Gravity 2010, 27, 194002. [Google Scholar] [CrossRef]
- Clark, B.A.; IceCube-Gen2 collaboration. The IceCube-Gen2 Neutrino Observatory. J. Instrum. 2021, 16, C10007. [Google Scholar] [CrossRef]
- Piro, L.; Ahlers, M.; Coleiro, A.; Colpi, M.; de Oña Wilhelmi, E.; Guainazzi, M.; Jonker, P.G.; Mc Namara, P.; Nichols, D.A.; O’Brien, P.; et al. Multi-messenger-Athena Synergy White Paper. arXiv 2021, arXiv:2110.15677. [Google Scholar]
- Pitik, T.; Tamborra, I.; Petropoulou, M. Neutrino signal dependence on gamma-ray burst emission mechanism. J. Cosmol. Astropart. Phys. 2021, 2021, 034. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bošnjak, Ž.; Barniol Duran, R.; Pe’er, A. The GRB Prompt Emission: An Unsolved Puzzle. Galaxies 2022, 10, 38. https://doi.org/10.3390/galaxies10020038
Bošnjak Ž, Barniol Duran R, Pe’er A. The GRB Prompt Emission: An Unsolved Puzzle. Galaxies. 2022; 10(2):38. https://doi.org/10.3390/galaxies10020038
Chicago/Turabian StyleBošnjak, Željka, Rodolfo Barniol Duran, and Asaf Pe’er. 2022. "The GRB Prompt Emission: An Unsolved Puzzle" Galaxies 10, no. 2: 38. https://doi.org/10.3390/galaxies10020038
APA StyleBošnjak, Ž., Barniol Duran, R., & Pe’er, A. (2022). The GRB Prompt Emission: An Unsolved Puzzle. Galaxies, 10(2), 38. https://doi.org/10.3390/galaxies10020038






