From Vesicles to Protocells: The Roles of Amphiphilic Molecules
Abstract
:1. Introduction: A Scenario from Molecular Assembly to Protocell
1.1. Formation of Vesicle
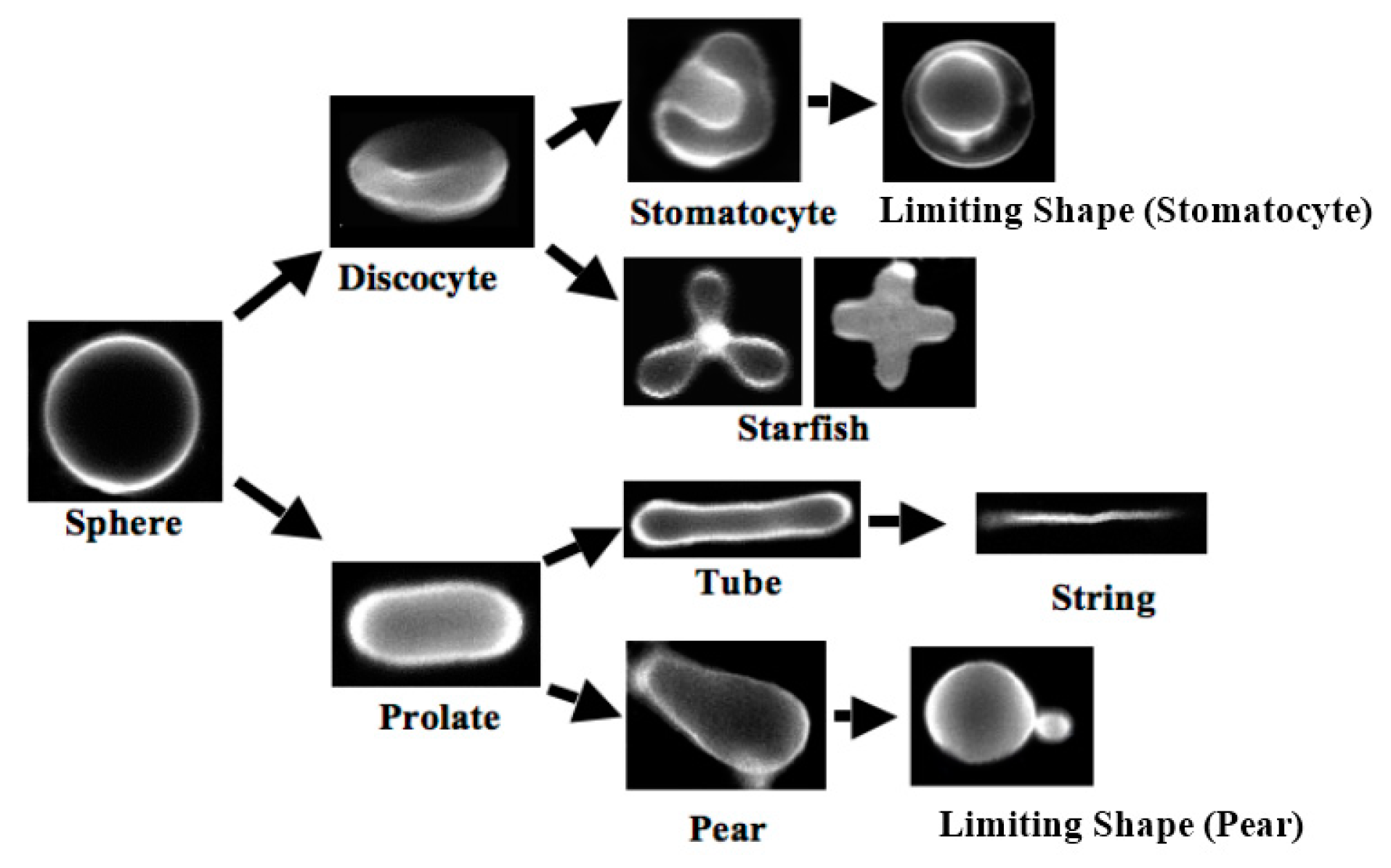
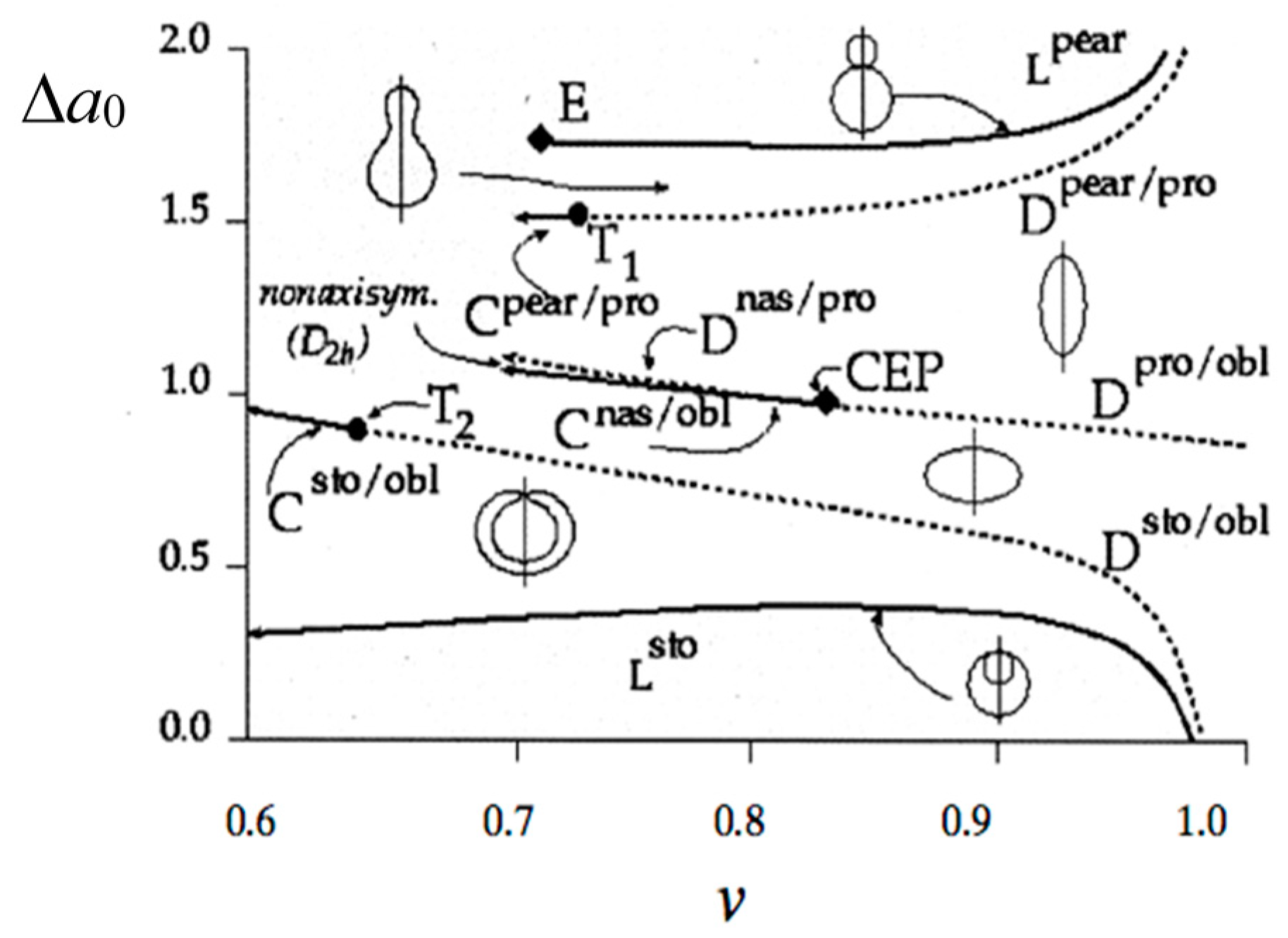
1.2. From Vesicle to Protocell
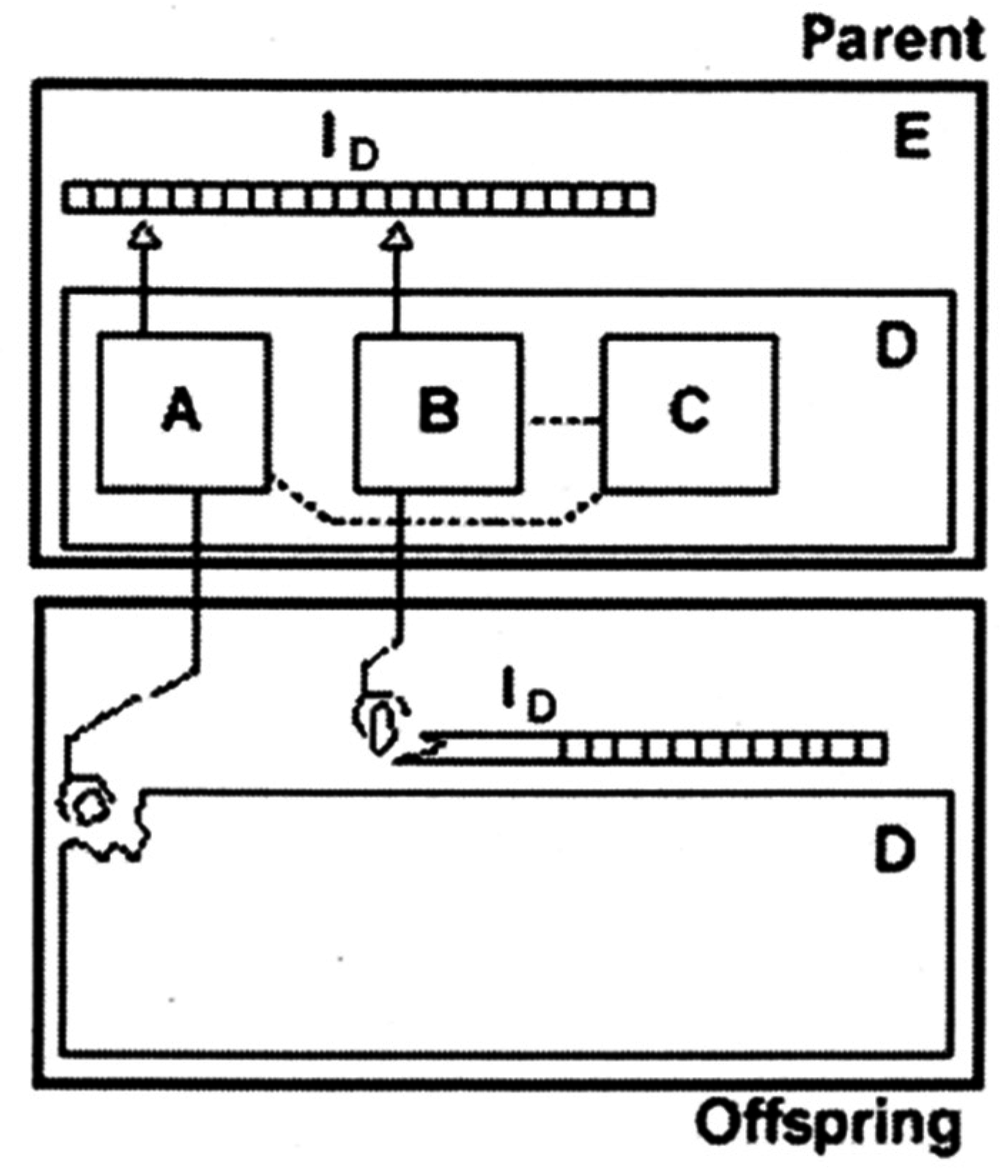
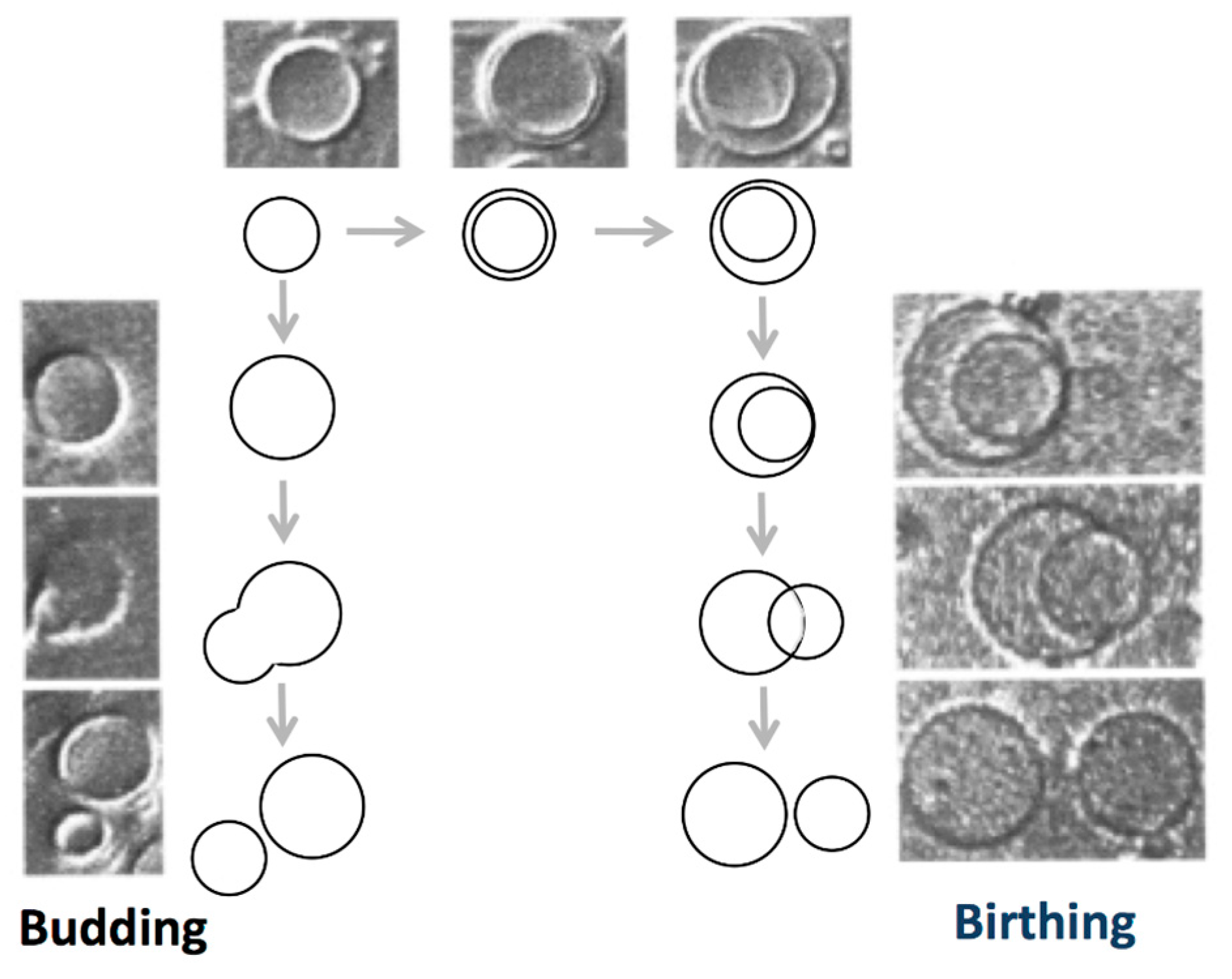
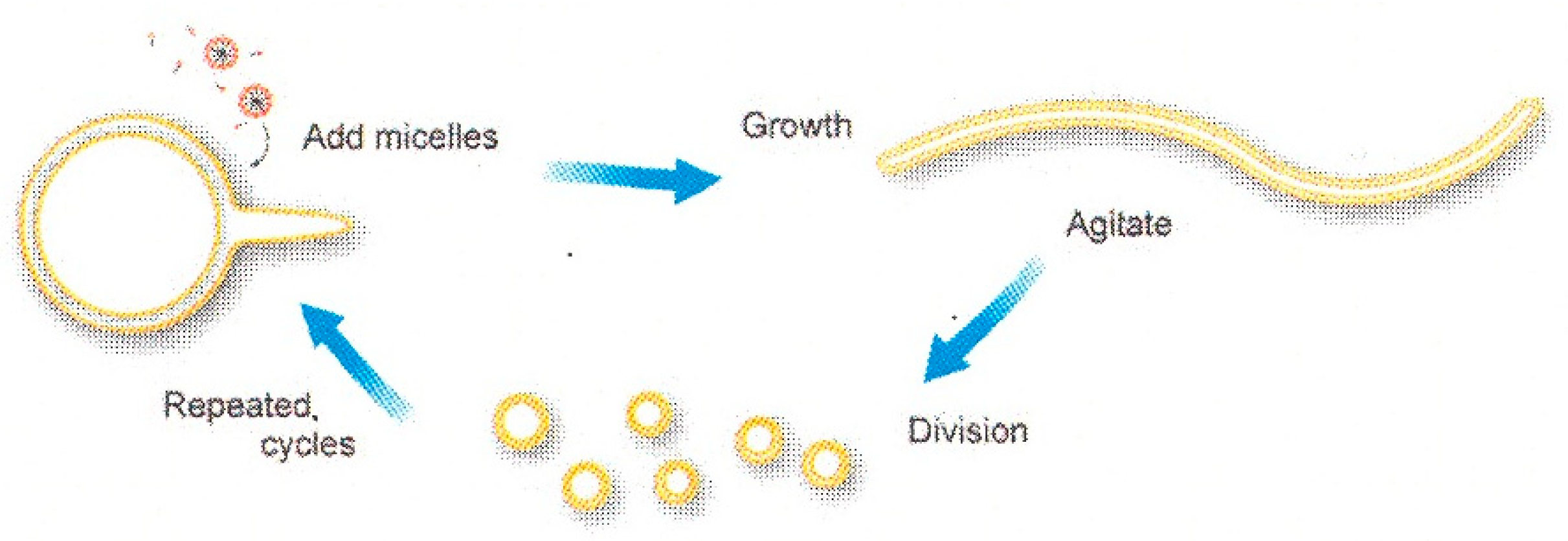

2. Amphiphilic Molecules
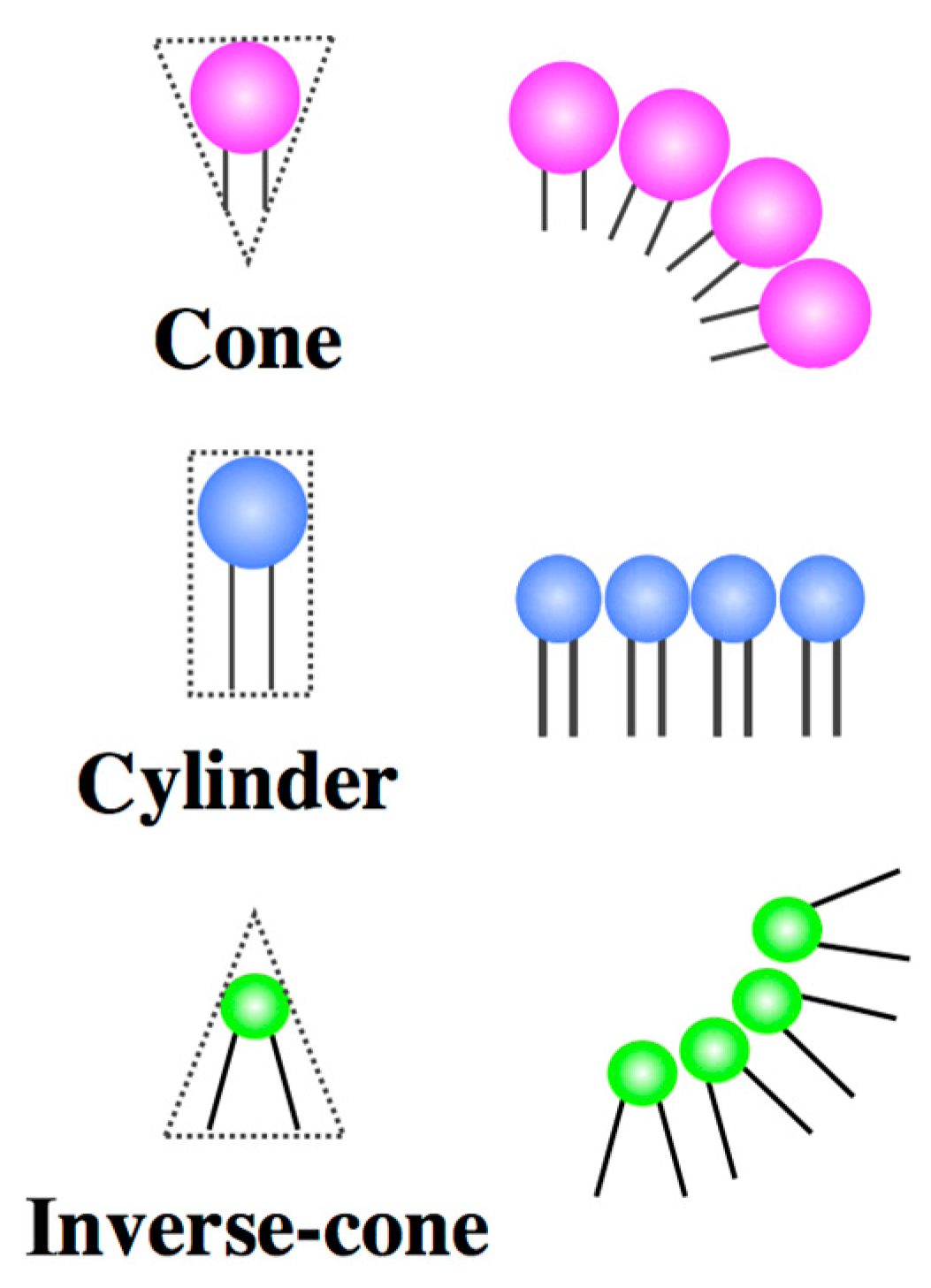
2.1. Architecture of Amphiphilic Molecules
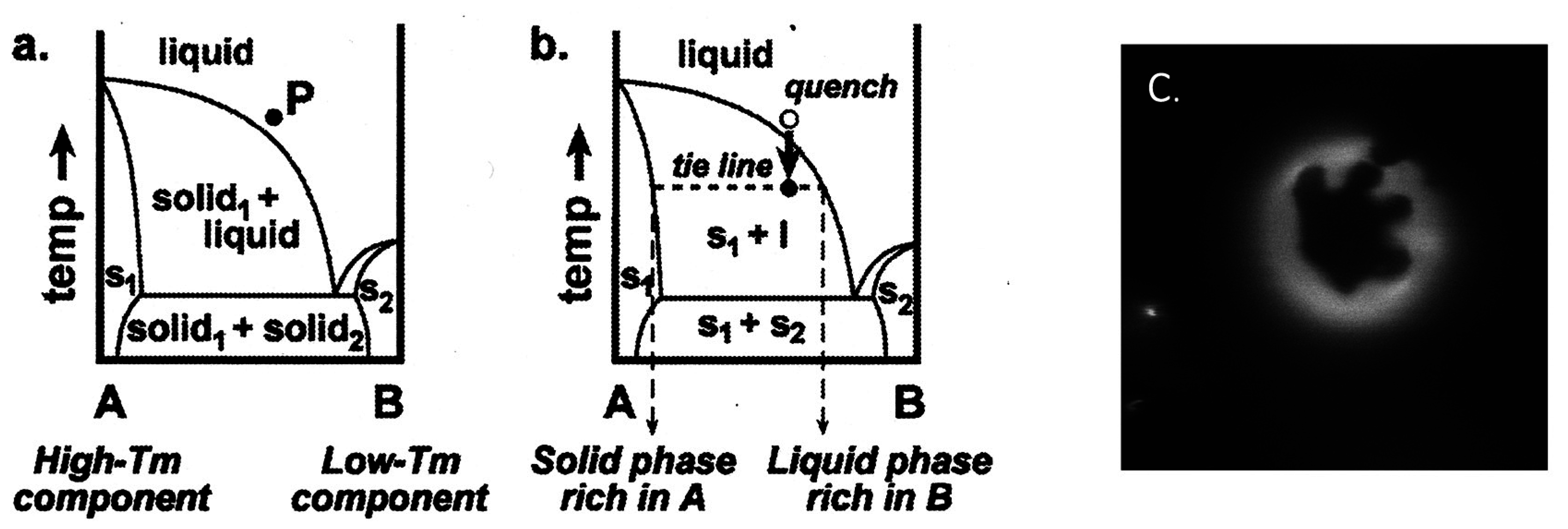
2.2. Binary Vesicle
3. Functions of the Protocell Reproduced by Binary Vesicles
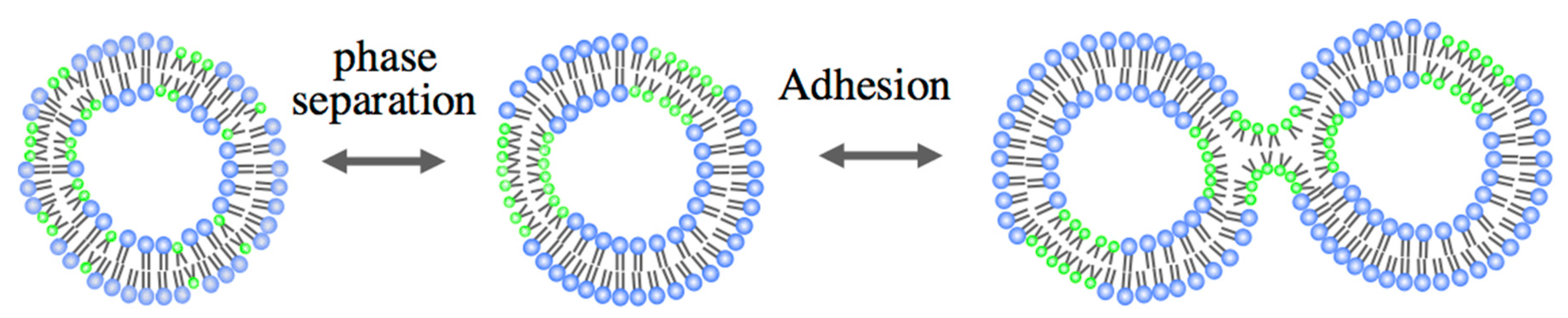
3.1. Adhesion
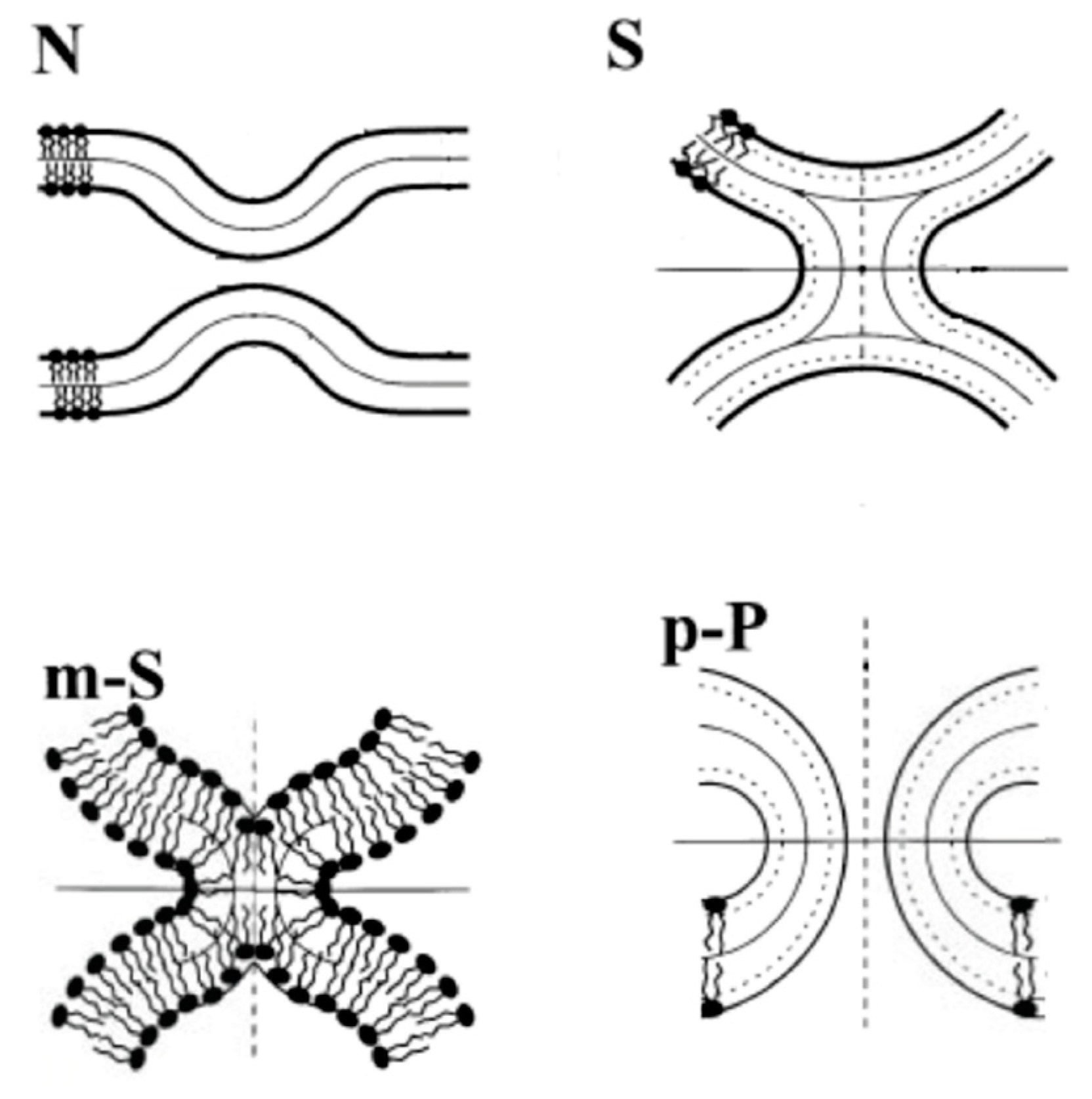
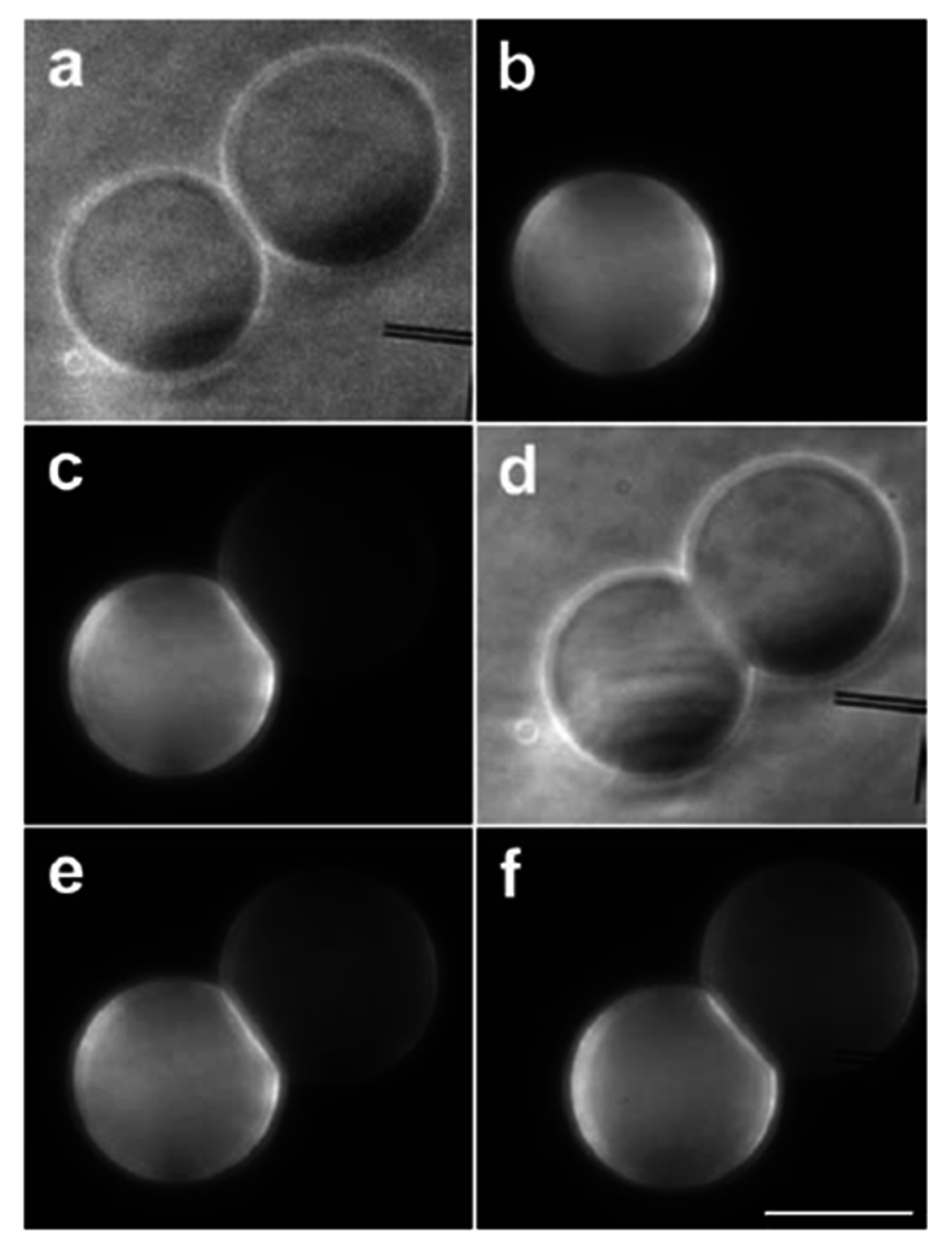

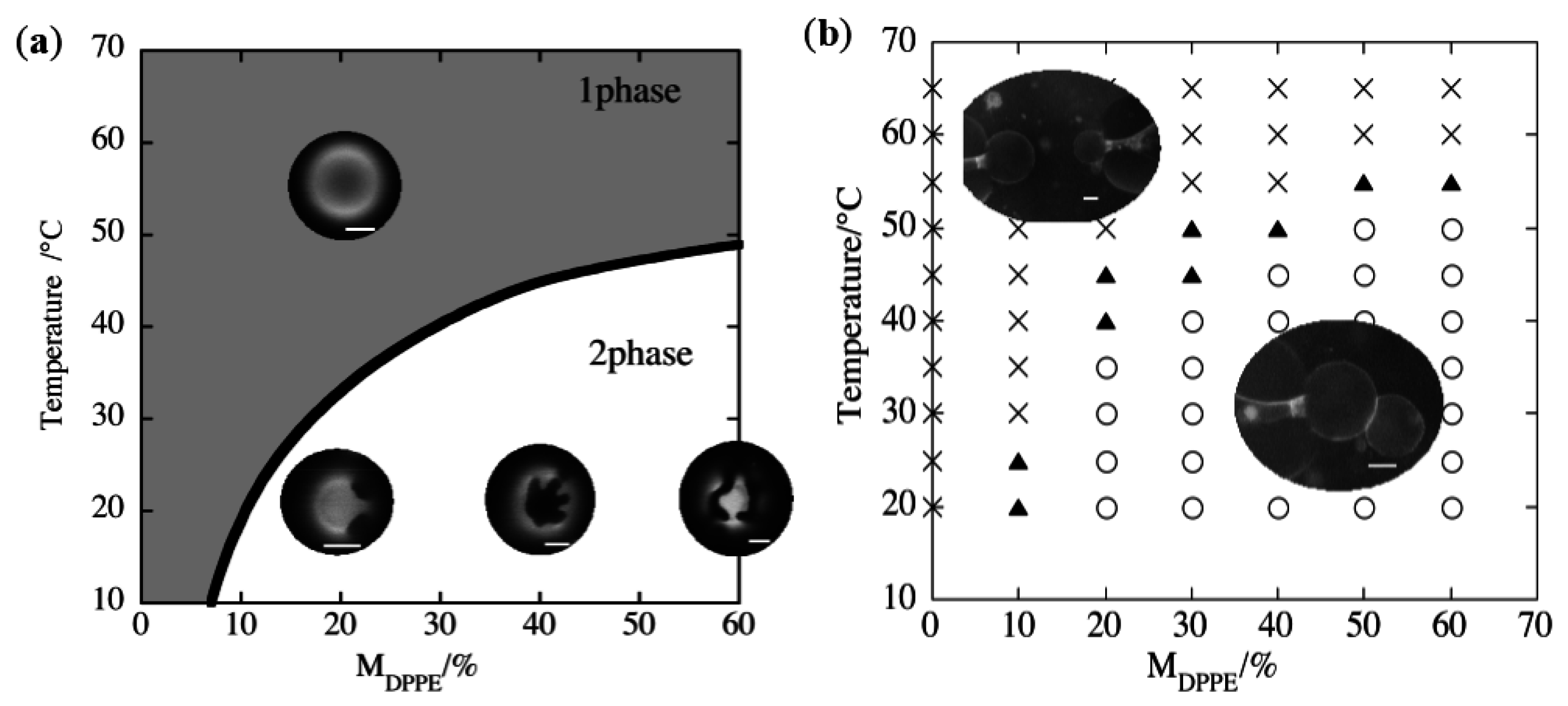


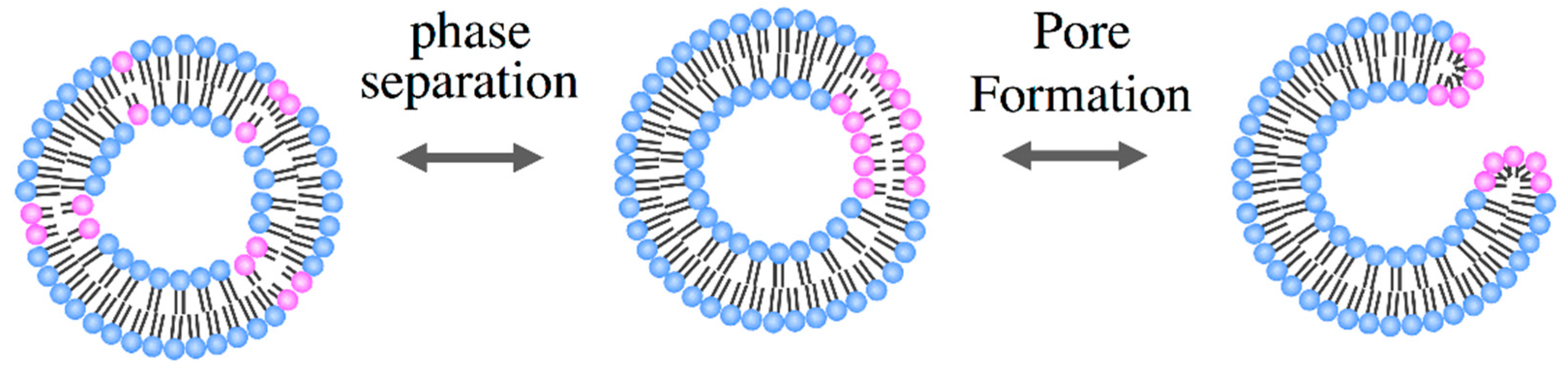
3.2. Pore Formation


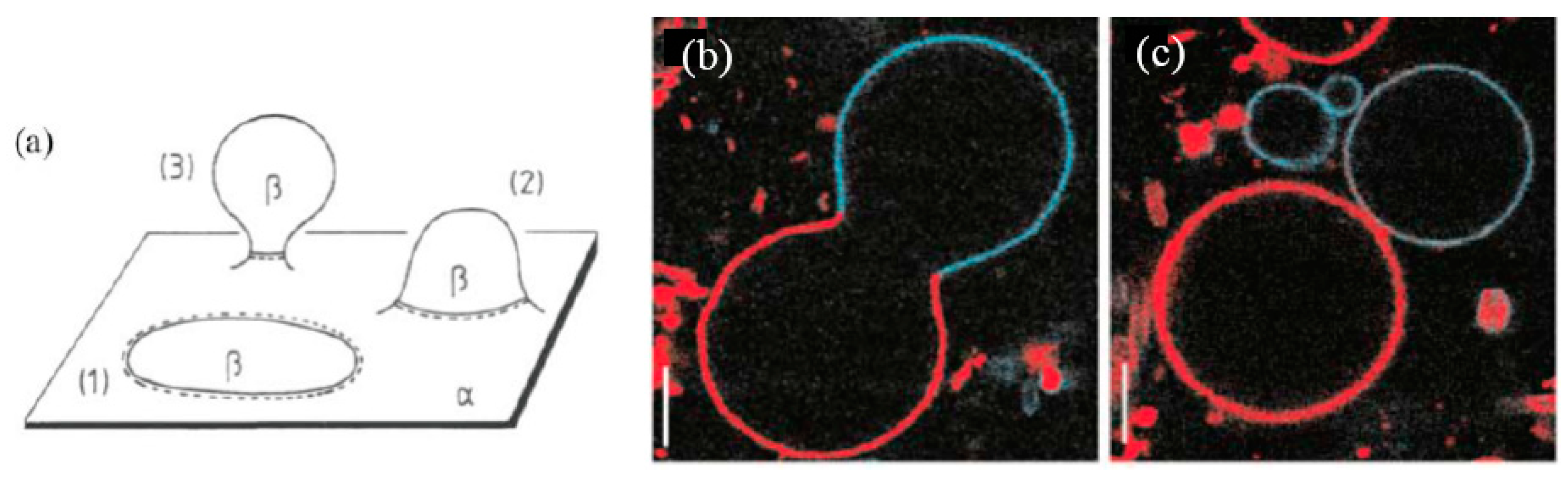
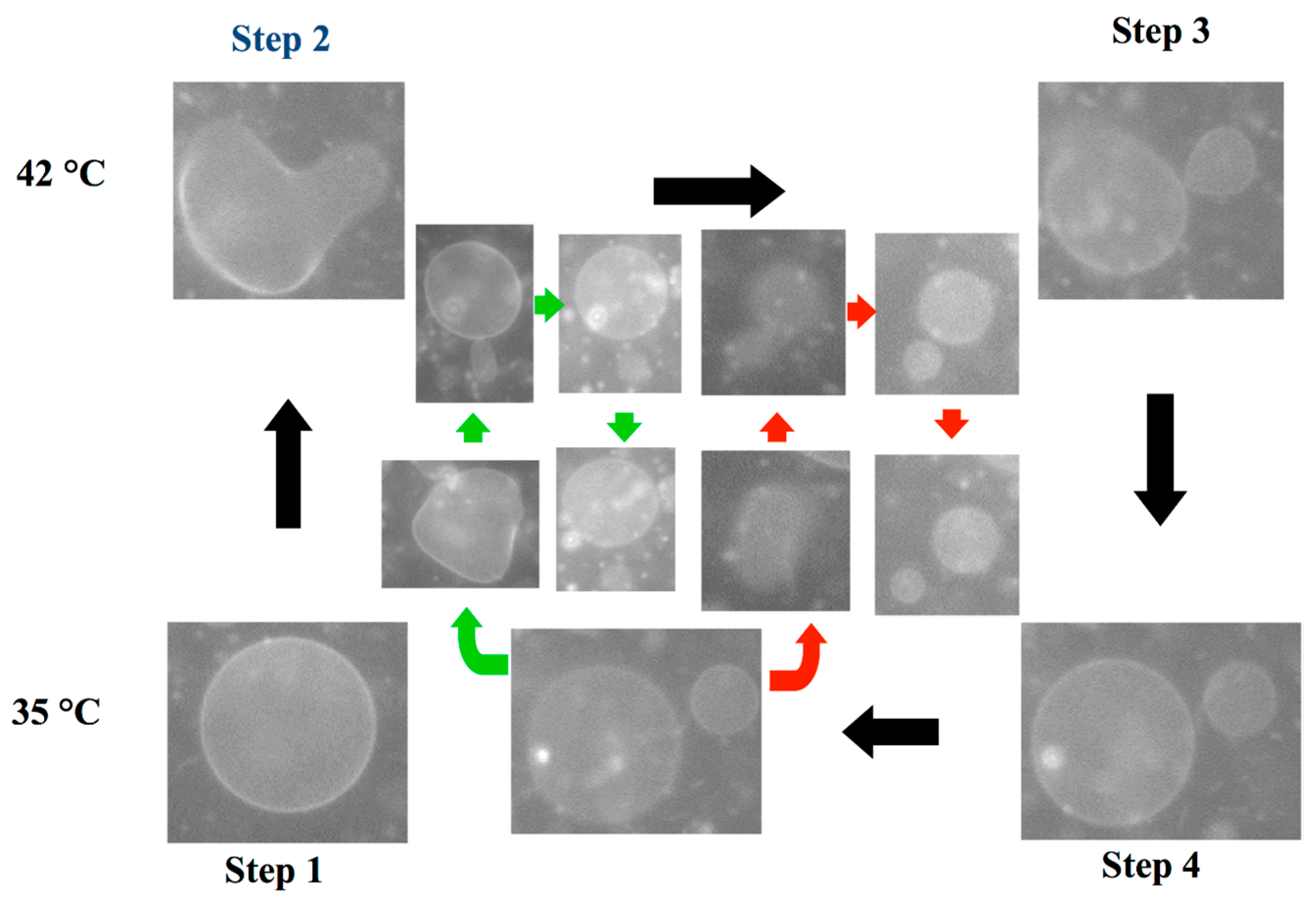
3.3. Self-Reproduction of Vesicle

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deamer, D.W.; Dworkin, J.P. Chemistry and Physics of Primitive Membranes. Top. Curr. Chem. 2005, 259, 1–27. [Google Scholar]
- Walde, P. Surfactant Assemblies and their various possible roles for the origin(s) of life. Orig. Life Evol. Biosph. 2006, 36, 109–150. [Google Scholar] [CrossRef] [PubMed]
- Israelachvli, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: London, UK, 1992. [Google Scholar]
- Safran, S.A. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes; Addison-Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Monnard, P.-A.; Deamer, D.W. Preparation of vesicles from nonphospholipid amphiphiles. Methods Enzymol. 2003, 372, 133–151. [Google Scholar] [PubMed]
- Smith, R.; Tanford, C. The critical micelle concentration of l-α-dipalmitoylphoshatidylcholine in water and in water/methanol solutions. J. Mol. Biol. 1972, 67, 75–83. [Google Scholar] [CrossRef] [PubMed]
- Hotani, H. Transformation pathways of liposomes. J. Mol. Biol. 1984, 178, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Yanagisawa, M.; Imai, M.; Taniguchi, T. Shape deformation of ternary vesicles coupled with phase separation. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef]
- Taniguchi, T.; Kawasaki, K.; Andelman, D.; Kawakatsu, T. Phase transitions and shapes of two component membranes and vesicles II: Weak segregation limit. J. Phys. II 1994, 4, 1333–1362. [Google Scholar]
- Heinrich, V.; Svetina, S.; Žekš, B. Nonaxisymmetric vesicle shapes in a generalized bilayer-couple model and the transition between oblate and prolate axisymmetric shapes. Phys. Rev. E 1993, 48, 3112–3123. [Google Scholar] [CrossRef]
- Miao, L.; Seifert, U.; Wortis, M.; Döbereiner, H.-G. Budding transitions of fluid-bilayer vesicles: The effect of area-difference elasticity. Phys. Rev. E 1994, 49, 5389–5407. [Google Scholar] [CrossRef]
- Seifert, U. Configurations of fluid membranes and vesicles. Adv. Phys. 1997, 46, 13–137. [Google Scholar] [CrossRef]
- Jarić, M.; Seifert, U.; Wintz, W.; Wortis, M. Vesicular instabilities: The prolate-to-oblate transition and other shape instabilities of fluid bilayer membranes. Phys. Rev. E 1995, 52, 6623–6634. [Google Scholar] [CrossRef]
- Döbereiner, H.-G.; Evans, E.; Kraus, M.; Seifert, U.; Wortis, M. Mapping vesicle shapes into the phase diagram: A comparison of experiment and theory. Phys. Rev. E 1997, 55, 4458–4474. [Google Scholar] [CrossRef]
- Sakashita, A.; Urakami, N.; Ziherl, P.; Imai, M. Three-dimensional analysis of lipid vesicle transformations. Soft Matter 2012, 8, 8569–8581. [Google Scholar] [CrossRef]
- Deamer, D.W. Boundary structures are formed by organic components of the Murchison carbonaceous chondrites. Nature 1985, 317, 792–794. [Google Scholar] [CrossRef]
- Deamer, D.W.; Pashley, R.M. Amphiphilic components of the Murchison carbonaceous chondrite: Surface properties and membrane formation. Orig. Life Evol. Biosph. 1989, 19, 21–38. [Google Scholar] [CrossRef] [PubMed]
- Luisi, P.L. The Emergence of Life: From Chemical Origins to Synthetic Biology; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Rasmussen, S.; Bedau, M.A.; Chen, L.; Deamer, D.; Krakauer, D.C.; Packard, N.H.; Stadler, P.F. (Eds.) Protocells: Bridging Nonliving and Living Matter; The MIT Press: Cambridge, UK, 2009.
- Deamer, D.; Szostak, J.W. (Eds.) The Origins of Life; Cold Spring Harbor Laboratory Press: New York, NY, USA, 2010.
- Luisi, P.L.; Stano, P. (Eds.) The Minimal Cell: The Biophysics of Cell Compartment and the Origin of Cell Functionality; Springer: Dordrecht, The Netherlands, 2011.
- Deamer, D. First Life: Discovering the Connections between Stars, Cells, and How Life Began; University of California Press: Los Angeles, CA, USA, 2011. [Google Scholar]
- Szostak, J.W.; Bartel, D.P.; Luisi, P.L. Synthesizing life. Nature 2001, 409, 387–390. [Google Scholar] [CrossRef] [PubMed]
- Von Neumann, J. The general and logical theory of automata. In Cerebral Mechanisms in Behavior: The Hixon Symposium; Jeffress, L.A., Ed.; Wiley: New York, NY, USA, 1951. [Google Scholar]
- Noireauxa, V.; Maeda, Y.T.; Libchaberb, A. Development of an artificial cell, from self-organization to computation and self-reproduction. Proc. Natl. Acad. Sci. USA 2011, 108, 3473–3480. [Google Scholar] [CrossRef] [PubMed]
- Morigami, K.; Walde, P. Fatty acid vesicles. Curr. Opin. Colloid Interface Sci. 2007, 12, 75–80. [Google Scholar] [CrossRef]
- Stano, P.; Luisi, P.L. Achievements and open questions in the self-reproduction of vesicles and synthetic minimal cells. Chem. Commun. 2010, 46, 3639–3653. [Google Scholar] [CrossRef]
- Chen, I.A.; Walde, P. From self-assembled vesicles to protocells. Cold Spring Harb. Perspect. Biol. 2010, 2. [Google Scholar] [CrossRef]
- Svetina, S. Cellular life could have emerged from properties of vesicles. Orig. Life Evol. Biosph. 2012, 42, 483–486. [Google Scholar] [CrossRef] [PubMed]
- Murtas, G. Early self-reproduction, the emergence of division mechanisms in protocells. Mol. BioSyst. 2013, 9, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Walde, P.; Wick, R.; Fresta, M.; Annarosa Mangone, A.; Luisi, P.L. Autopoietic Self-Reproduction of Fatty Acid Vesicles. J. Am. Chem. Soc. 1994, 116, 11649–11654. [Google Scholar] [CrossRef]
- Wick, R.; Walde, P.; Luisi, P.L. Light Microscopic Investigations of the autocatalytic self-reproduction of giant vesicles. J. Am. Chem. Soc. 1995, 117, 1435–1436. [Google Scholar] [CrossRef]
- Cistola, D.P.; Hamilton, J.A.; Jackson, D.; Small, D.M. Ionization and phase behavior of fatty acids in water: Application of the Gibbs phase rule. Biochemistry 1988, 27, 1881–1888. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.F.; Szostak, J.W. Coupled Growth and Division of Model Protocell Membranes. J. Am. Chem. Soc. 2009, 131, 5705–5713. [Google Scholar] [CrossRef] [PubMed]
- Budin, I.; Debnath, A.; Szostak, J.W. Concentration-Driven Growth of Model Protocell Membranes. J. Am. Chem. Soc. 2012, 134, 20812–20819. [Google Scholar] [CrossRef] [PubMed]
- Takakura, K.; Sugawara, T. Membrane Dynamics of a Myelin-like Giant Multilamellar Vesicle Applicable to a Self-Reproducing System. Langmuir 2004, 20, 3832–3834. [Google Scholar] [CrossRef] [PubMed]
- Toyota, T.; Takakura, K.; Kageyama, Y.; Kurihara, K.; Maru, N.; Ohnuma, K.; Kaneko, K.; Sugawara, T. Population Study of Sizes and Components of Self-Reproducing Giant Multilamellar Vesicles. Langmuir 2008, 24, 3037–3044. [Google Scholar] [CrossRef] [PubMed]
- Kurihara, K.; Tamura, M.; Shoda, K.; Toyota, T.; Suzuki, K.; Sugawara, T. Self-reproduction of supramolecular giant vesicles combined with the amplification of encapsulated DNA. Nat. Chem. 2011, 3, 775–781. [Google Scholar] [CrossRef] [PubMed]
- Božič, B.; Svetina, S. A relationship between membrane properties forms the basis of a selectivity mechanism for vesicle self-reproduction. Eur. Biophys. J. 2004, 33, 565–571. [Google Scholar] [CrossRef] [PubMed]
- Božič, B.; Svetina, S. Vesicle self-reproduction: The involvement of membrane hydraulic and solute permeabilities. Eur. Phys. J. E 2007, 24, 79–90. [Google Scholar] [CrossRef] [PubMed]
- Käs, J.; Sackmann, E.; Podgornik, R.; Svetina, S.; Žekš, B. Thermally induced budding of phospholipid vesicles—A discontinuous process. J. Phys. II 1993, 3, 631–645. [Google Scholar]
- Kauffman, S. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S. Approaches to the Origin of Life on Earth. Life 2011, 1, 34–48. [Google Scholar] [CrossRef] [PubMed]
- Zimmerberg, J.; Kozlov, M.M. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 2006, 7, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Nagle, J.F.; Nagle, S.T. Structure of lipid bilayer. Biochim. Biophys. Acta 2000, 1469, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Veatch, S.L.; Keller, S.L. Seeing spots: Complex phase behavior in simple membrane. Biochim. Biophys. Acta 2005, 1746, 172–185. [Google Scholar] [CrossRef] [PubMed]
- Witen, T.A.; Sander, L.M. Diffusion-Limited Aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 1981, 47, 1400–1403. [Google Scholar] [CrossRef]
- Sakuma, Y.; Imai, M.; Yanagisawa, M.; Komura, S. Adhesion of Binary Giant Vesicles Containing Negative Spontaneous Curvature Lipids Induced by Phase Separation. Eur. Phys. J. E 2008, 25, 403–413. [Google Scholar] [CrossRef] [PubMed]
- Sakuma, Y.; Taniguchi, T.; Imai, M. Pore Formation in a Binary Giant Vesicle Induced by Cone-Shaped Lipids. Biophys. J. 2010, 99, 472–479. [Google Scholar] [CrossRef] [PubMed]
- Sakuma, Y.; Imai, M. Model System of Self-Reproducing Vesicles. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef] [PubMed]
- Alberts, B.; Bray, D.; Lewis, J.; Raff, M.; Roberts, K.; Watson, J.D. Molecular Biology of the Cell, 3rd ed.; Garland: New York, NY, USA, 1994. [Google Scholar]
- Simson, R.; Sackmann, E. Mimicking physics of cell adhesion. In Physical Chemistry of Biological Interfaces; Baszkin, A., Norde, W., Eds.; Marcel Dekker Inc.: New York, NY, USA, 2000. [Google Scholar]
- Weikl, T.R.; Lipowsky, R. Membrane Adhesion and Domain Formation. In Advance in Planar Lipid Bilayers and Liposomes; Liu, A.L., Ed.; Elsevier: Amsterdam, The Netherland, 2007; Volume 5, pp. 63–131. [Google Scholar]
- Kuzmin, P.I.; Zimmerberg, J.; Chizmadzhev, Y.A.; Cohen, F.S. A quantitative model for membrane fusion based on low-energy intermediates. Proc. Natl. Acad. Sci. USA 2001, 98, 7235–7240. [Google Scholar] [CrossRef] [PubMed]
- Gingell, D.; Ginsberg, I. Problems in the physical interpretation of membrane interaction and fusion. In Membrane Fusion; Post, G., Nicholson, G.L., Eds.; Elsevier: Amsterdam, The Netherland, 1978; pp. 791–833. [Google Scholar]
- Heuvingh, J.; Pincet, F.; Cribier, S. Hemifusion and fusion of giant vesicles induced by reduction of inter-membrane distance. Eur. Phys. J. E 2004, 14, 269–276. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Huang, H.W. Observation of a membrane fusion intermediate structure. Science 2002, 297, 1877–1879. [Google Scholar] [CrossRef] [PubMed]
- Mansy, S.S. Membrane Transport in Primitive Cells. In The Origins of Life; Deamer, D., Szostak, J.W., Eds.; Cold Spring Harbor Laboratory Press: New York, NY, USA, 2010. [Google Scholar]
- Iacovache, I.; Gisou van der Goot, F.; Pernot, L. Pore formation: An ancient yet complex form of attack. Biochim. Biophys. Acta 2008, 1778, 1611–1623. [Google Scholar] [CrossRef] [PubMed]
- Dempsey, C.E. The action of melittin on membranes. Biochim. Biophys. Acta 1990, 1031, 143–161. [Google Scholar] [CrossRef] [PubMed]
- Sandre, O.; Moreaux, L.; Brochard-Wyart, F. Dynamics of transient pores in stretched vesicles. Proc. Natl. Acad. Sci. USA 1999, 96, 10591–10596. [Google Scholar] [CrossRef] [PubMed]
- Nomura, F.; Nagata, M.; Inaba, T.; Hiramatsu, H.; Hotani, H.; Takiguchi, K. Capabilities of liposomes for topological transformation. Proc. Natl. Acad. Sci. USA 2001, 98, 2340–2345. [Google Scholar] [CrossRef] [PubMed]
- Karatekin, E.; Sandre, O.; Guitouni, H.; Borghi, N.; Puech, P.-H.; Brochard-Wyart, F. Cascades of transient pores in giant vesicles: Line tension and transport. Biophys. J. 2003, 84, 1734–1749. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, N.; Cribier, S.; Pincet, F. Transition from long- to short-lived transient pores in giant vesicles in an aqueous medium. Phys. Rev. E 2006, 74, 061902. [Google Scholar] [CrossRef]
- Lipfert, J.; Columbus, L.; Chu, V.B.; Lesley, S.A.; Doniach, S. Size and shape of detergent micelles determined by small-angle-X-ray scattering. J. Phys. Chem. B 2007, 111, 12427–12438. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, R. Budding of membranes induced by intramembrane domains. J. Phys. II 1992, 2, 1825–1840. [Google Scholar]
- Döbereiner, H.-G.; Käs, J.; Noppl, D.; Sprenger, I.; Sackmann, E. Budding and Fission of Vesicles. Biophys. J. 1993, 65, 1396–1403. [Google Scholar] [CrossRef] [PubMed]
- Baumgart, T.; Hess, S.T.; Webb, W.W. Imaging coexcisting fluid domains in biomembrane models cupling curvature and line tension. Nature 2003, 425, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Emoto, K.; Kobayashi, T.; Yamaji, A.; Aizawa, H.; Tahara, I.; Inoue, K.; Umeda, M. Redistribution of phosphatidylethanolamine at the cleavage furrow of dividing cells during cytokinesis. Proc. Natl. Acad. Sci. USA 1996, 93, 12867–12872. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.P.; Kozlov, M.M. The Gaussian curvature elastic modulus of N-monomethylated dioleoylphosphatidylethanolamine: Relevance to membrane fusion and lipid phase behavior. Biophys. J. 2004, 87, 366–374. [Google Scholar] [CrossRef] [PubMed]
- Kamal, M.M.; Mills, D.; Grzybek, M.; Howard, J. Measurement of the membrane curvature preference of phospholipids reveals only weak coupling between lipid shape and leaflet curvature. Proc. Natl. Acad. Sci. USA 2009, 106, 22245–22250. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-M.; Higgs, P.G.; MacKintosh, F.C. Theory of fission for two-component lipid vesicles. Phys. Rev. Lett. 1997, 79, 1579–1582. [Google Scholar] [CrossRef]
- Bar-Ziv, R.; Moses, E.; Nelson, P. Dynamic Excitations in Membranes Induced by Optical Tweezers. Biophys. J. 1998, 75, 294–320. [Google Scholar] [CrossRef] [PubMed]
- Khalifat, N.; Puff, N.; Bonneau, B.; Fournier, J.B.; Angelova, M.I. Membrane Deformation under Local pH Gradient: Mimicking Mitochondrial Cristae Dynamics. Biophys. J. 2008, 95, 4924–4933. [Google Scholar] [CrossRef] [PubMed]
- Bitbol, A.-F.; Puff, N.; Sakuma, Y.; Imai, M.; Fournier, J.B.; Angelova, M.I. Lipid membrane deformation in response to a local pH modification: Theory and experiments. Soft Matter 2012, 8, 6073–6082. [Google Scholar] [CrossRef]
- McMahon, H.T.; Gallop, J.L. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature 2005, 438, 590–596. [Google Scholar] [CrossRef] [PubMed]
- Sorre, B.; Callan-Jones, A.; Manneville, J.-M.; Nassoy, P.; Joanny, J.-F.; Prost, J.; Goud, B.; Bassereau, P. Curvature-driven lipid sorting needs proximity to a demixing point and is aided by proteins. Proc. Natl. Acad. Sci. USA 2009, 106, 5622–5626. [Google Scholar] [CrossRef] [PubMed]
- Tian, A.; Baumgart, T. Sorting of lipids and proteins in membrane curvature gradients. Biophys. J. 2009, 96, 2676–2688. [Google Scholar] [CrossRef] [PubMed]
- Sakuma, Y.; Urakami, N.; Taniguchi, T.; Imai, M. Asymmetric distribution of cone-shaped lipids in a highly curved bilayer revealed by a small angle neutron scattering technique. J. Phys. Condens. Matter 2011, 23. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakuma, Y.; Imai, M. From Vesicles to Protocells: The Roles of Amphiphilic Molecules. Life 2015, 5, 651-675. https://doi.org/10.3390/life5010651
Sakuma Y, Imai M. From Vesicles to Protocells: The Roles of Amphiphilic Molecules. Life. 2015; 5(1):651-675. https://doi.org/10.3390/life5010651
Chicago/Turabian StyleSakuma, Yuka, and Masayuki Imai. 2015. "From Vesicles to Protocells: The Roles of Amphiphilic Molecules" Life 5, no. 1: 651-675. https://doi.org/10.3390/life5010651
APA StyleSakuma, Y., & Imai, M. (2015). From Vesicles to Protocells: The Roles of Amphiphilic Molecules. Life, 5(1), 651-675. https://doi.org/10.3390/life5010651





