Effects of Different Hard Finishing Processes on Gear Excitation
Abstract
:1. Introduction
1.1. Motivation
1.2. Objective and Approach
1.3. State of the Art
2. Materials and Methods
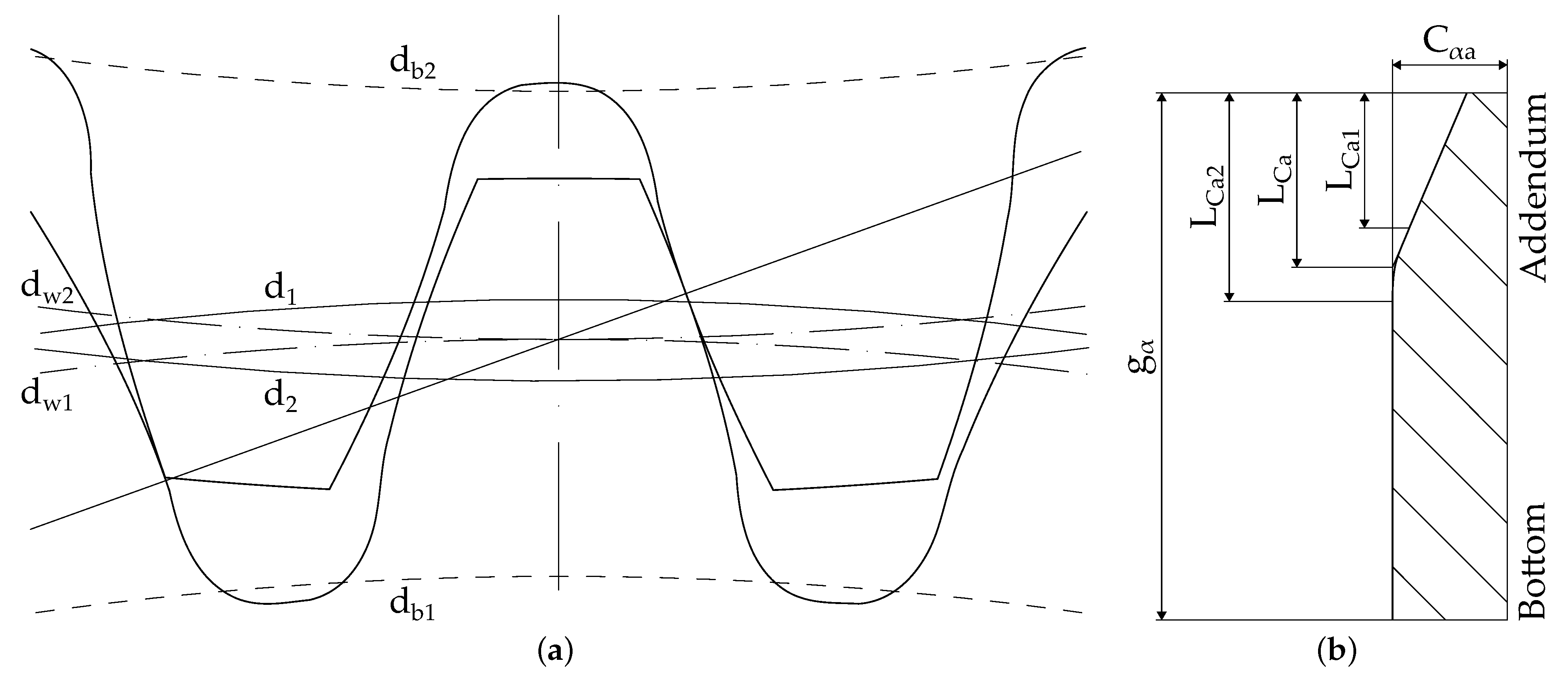
2.1. Gear Design Used in the Experiment
2.2. Manufacturing of the Test Gears
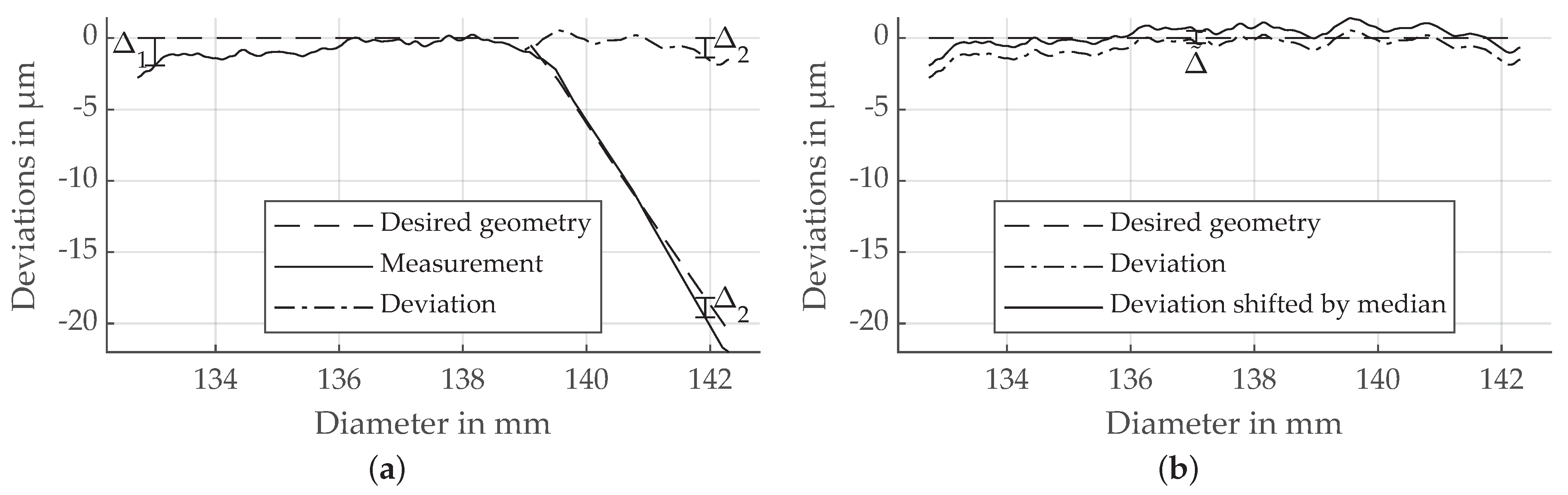
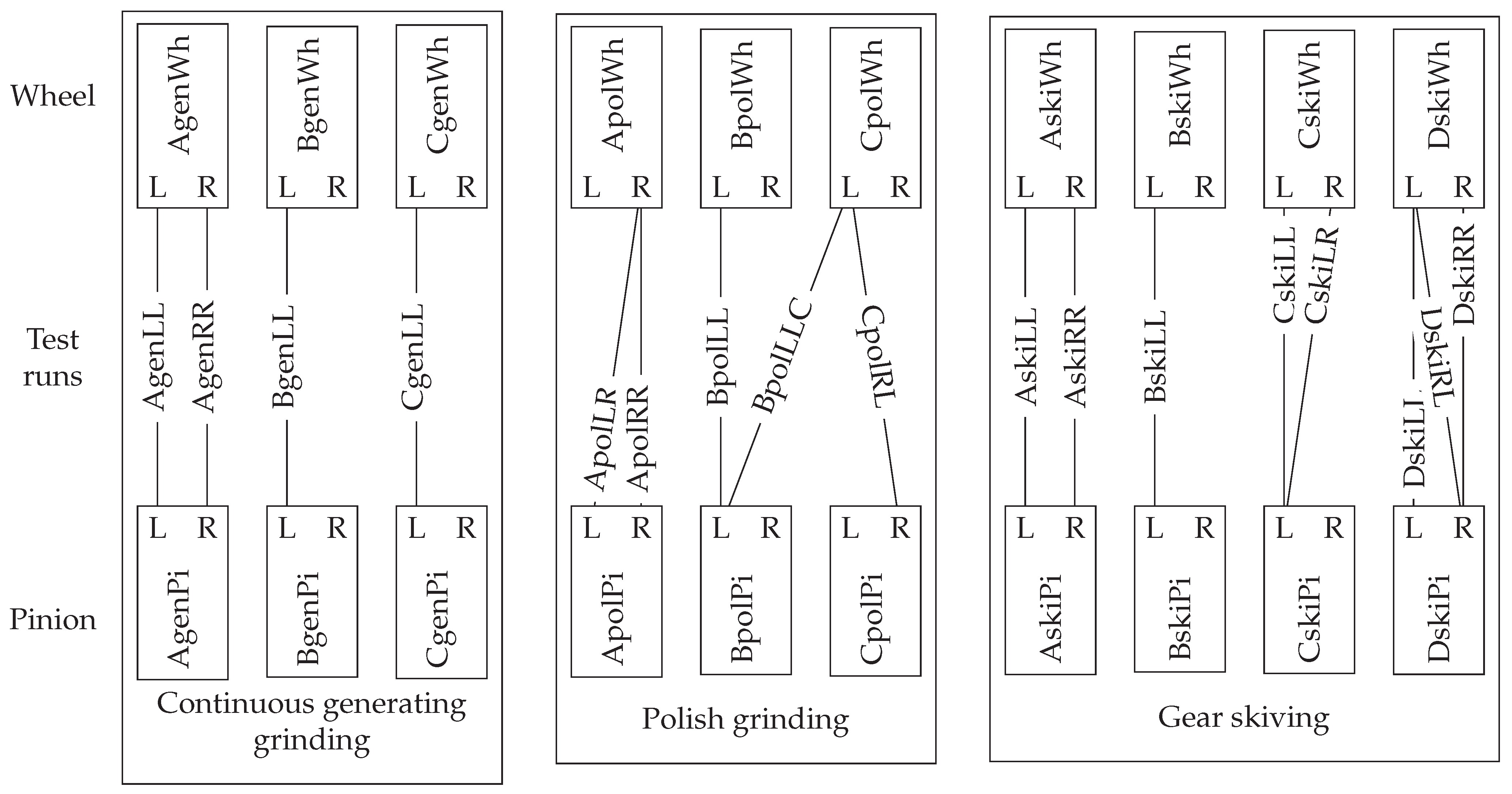
2.3. Documentation of the Test Gears
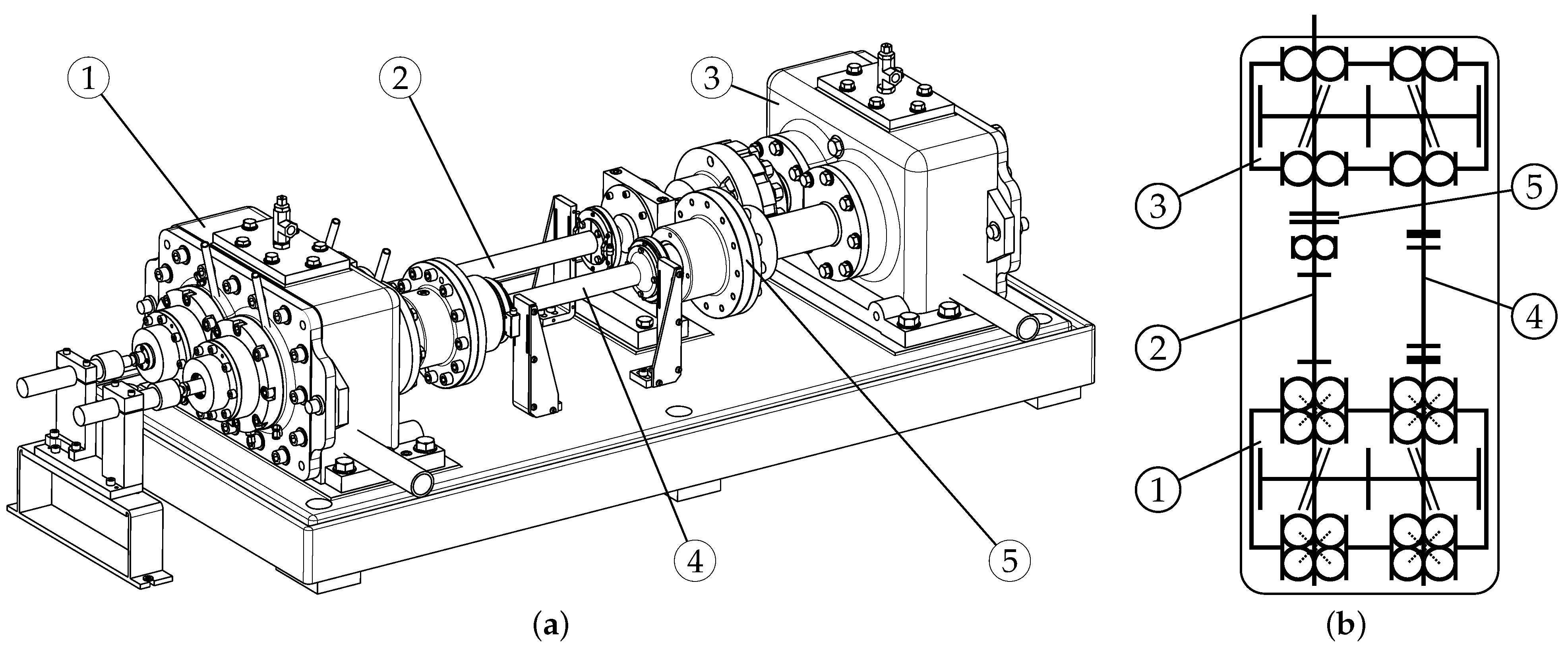
2.4. Design and Sensors of the Dynamic Test Rig
2.5. Test Procedure and Evaluation
2.6. Experimental Program
3. Results
3.1. Flank Roughness
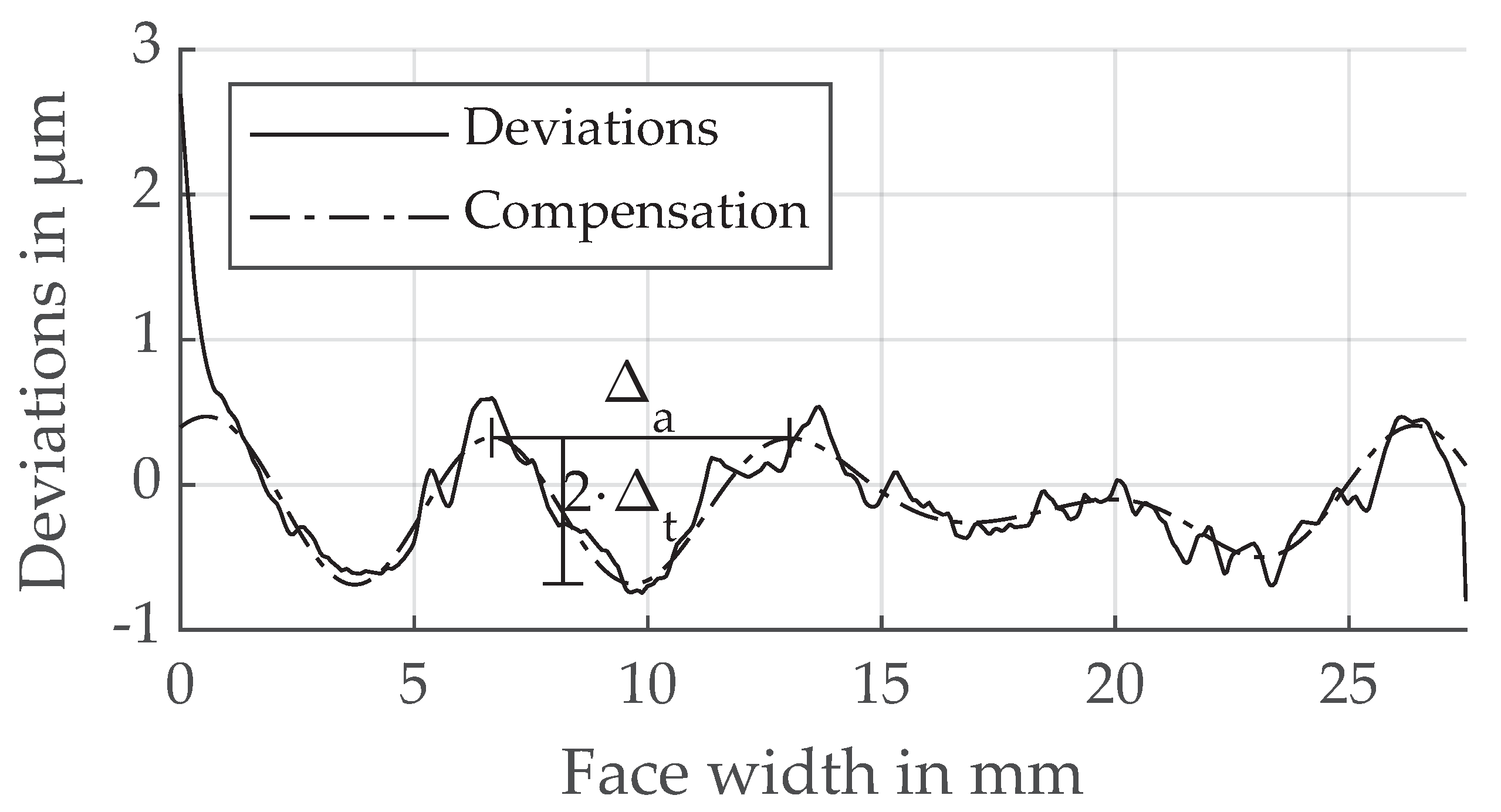
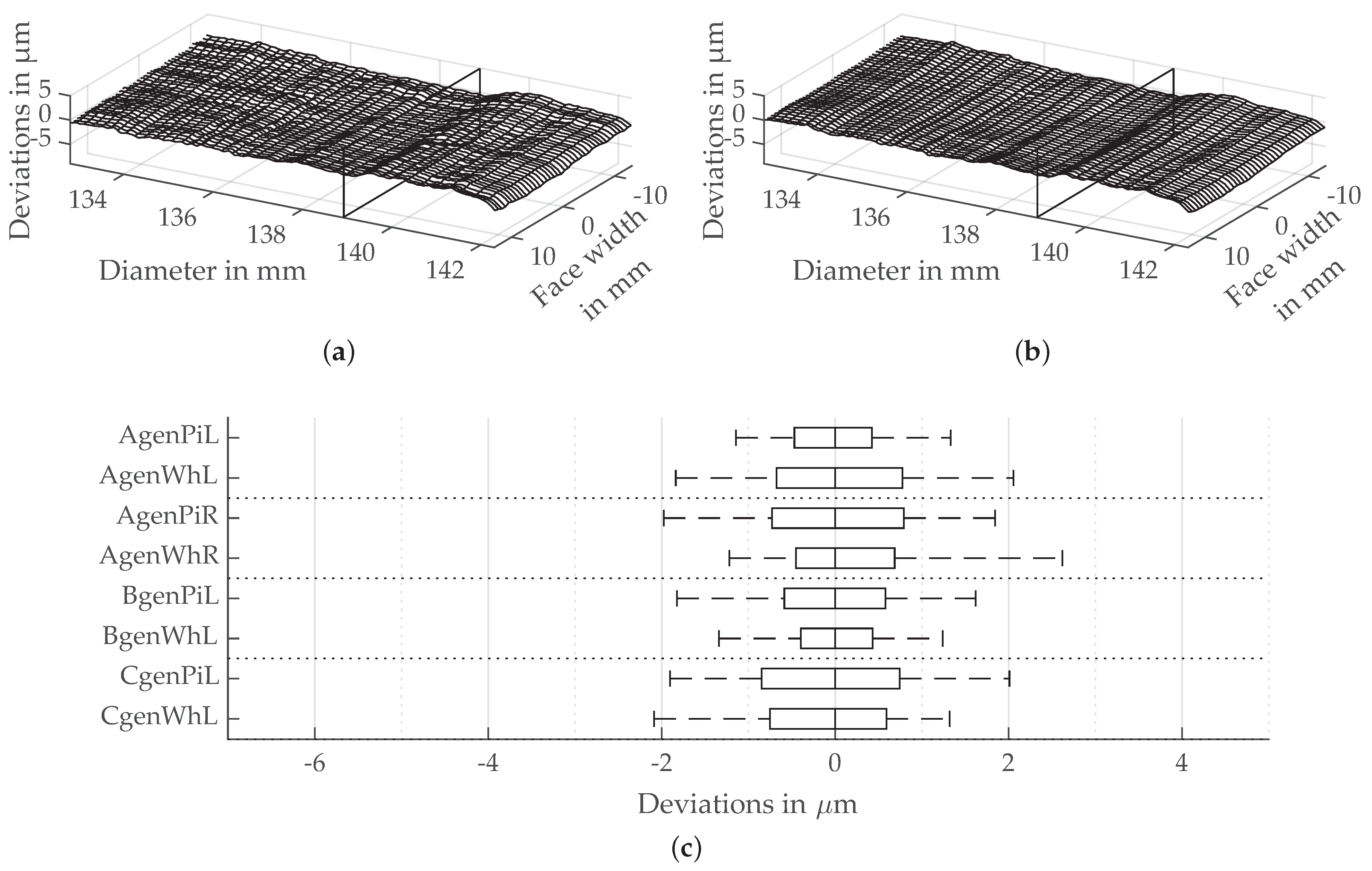
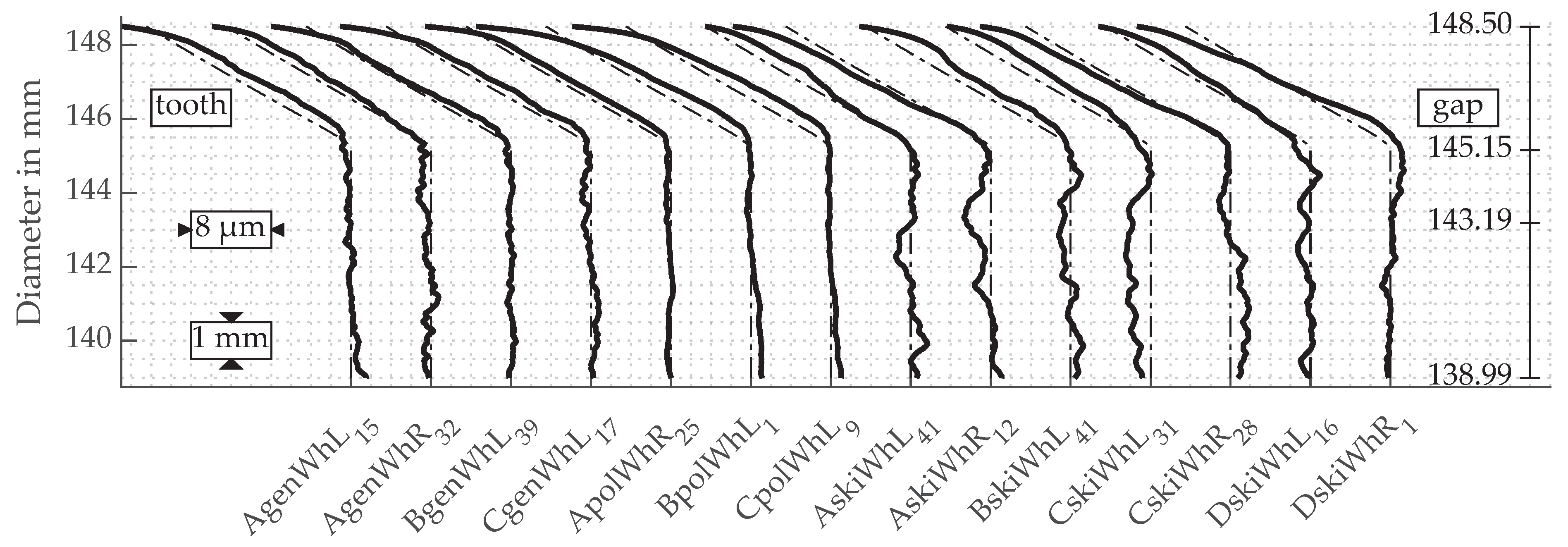
3.2. Flank Surface Structure Resulting from Continuous Generating Grinding
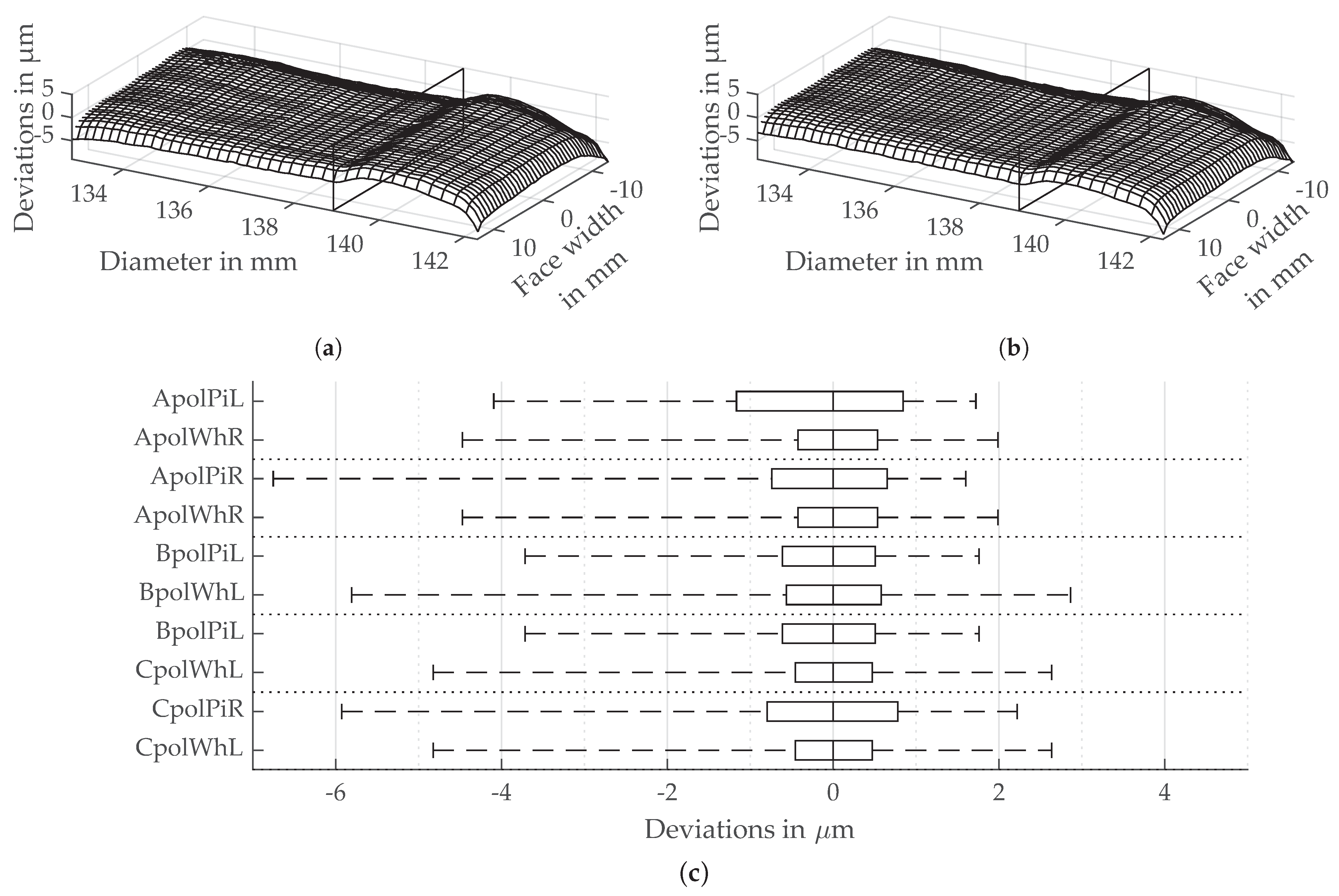
3.3. Flank Surface Structure Resulting from Polish Grinding
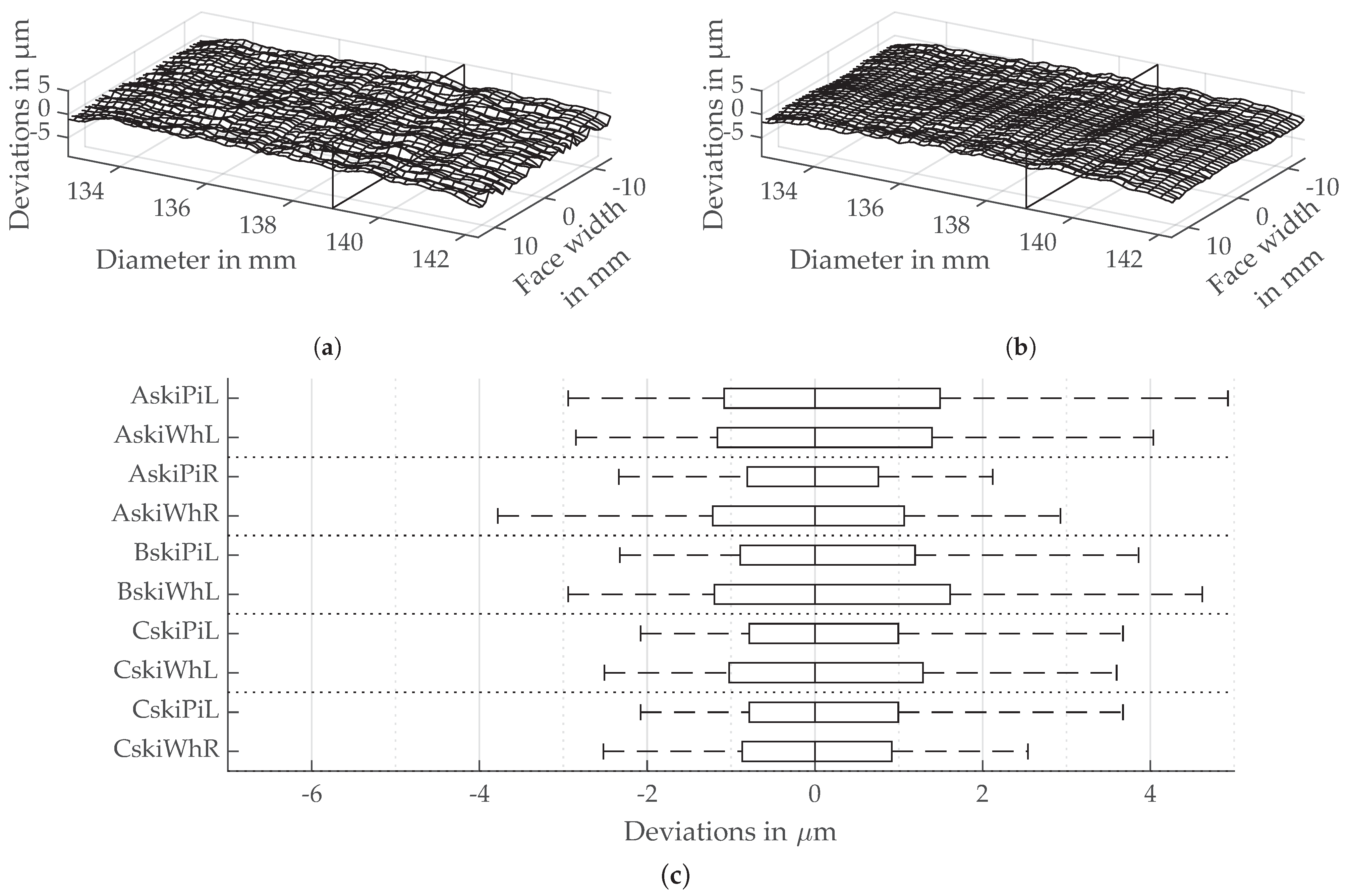
3.4. Flank Surface Structure Resulting from Gear Skiving
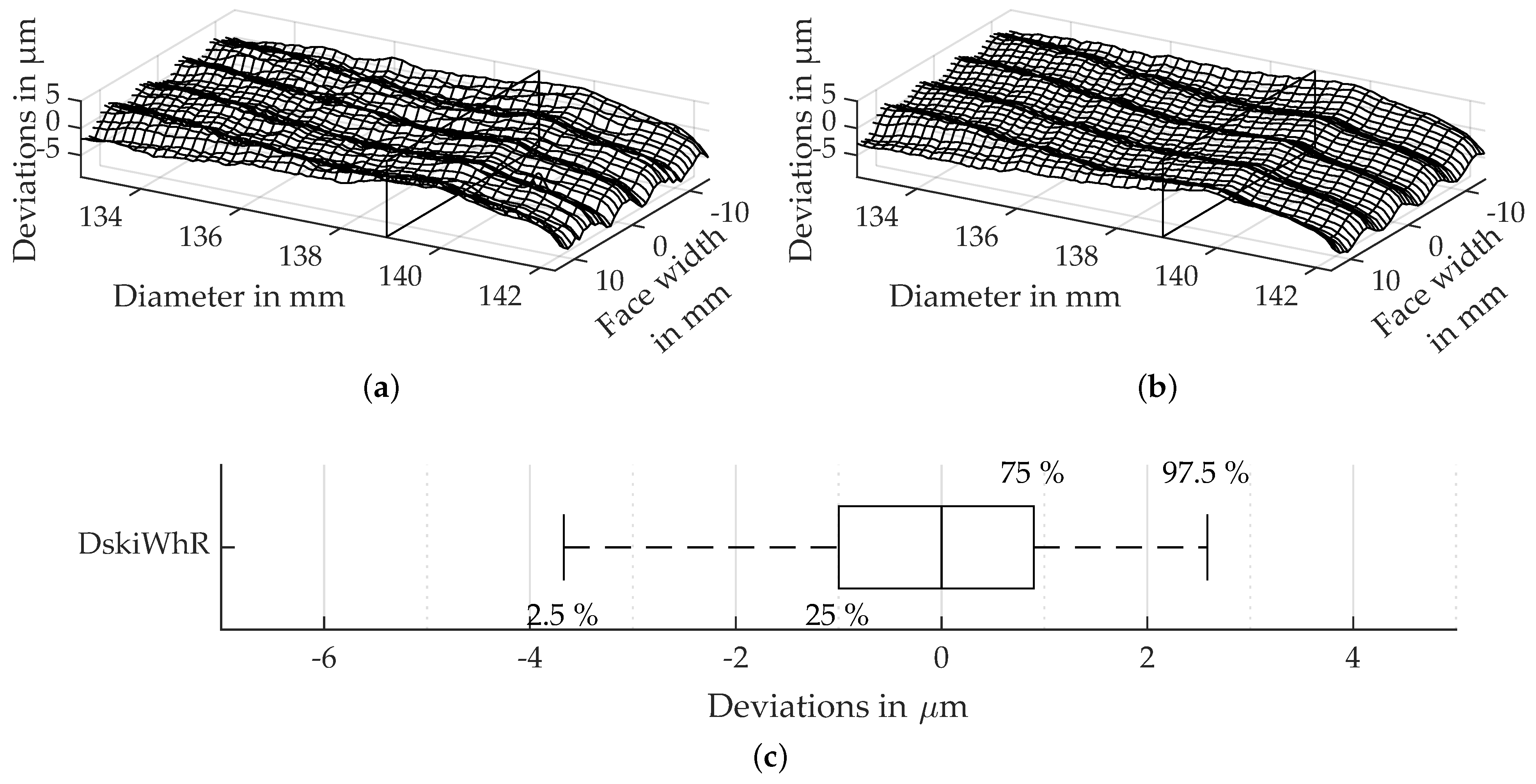
3.5. Flank Surface Structure Resulting from Gear Skiving-Half Axial Feed
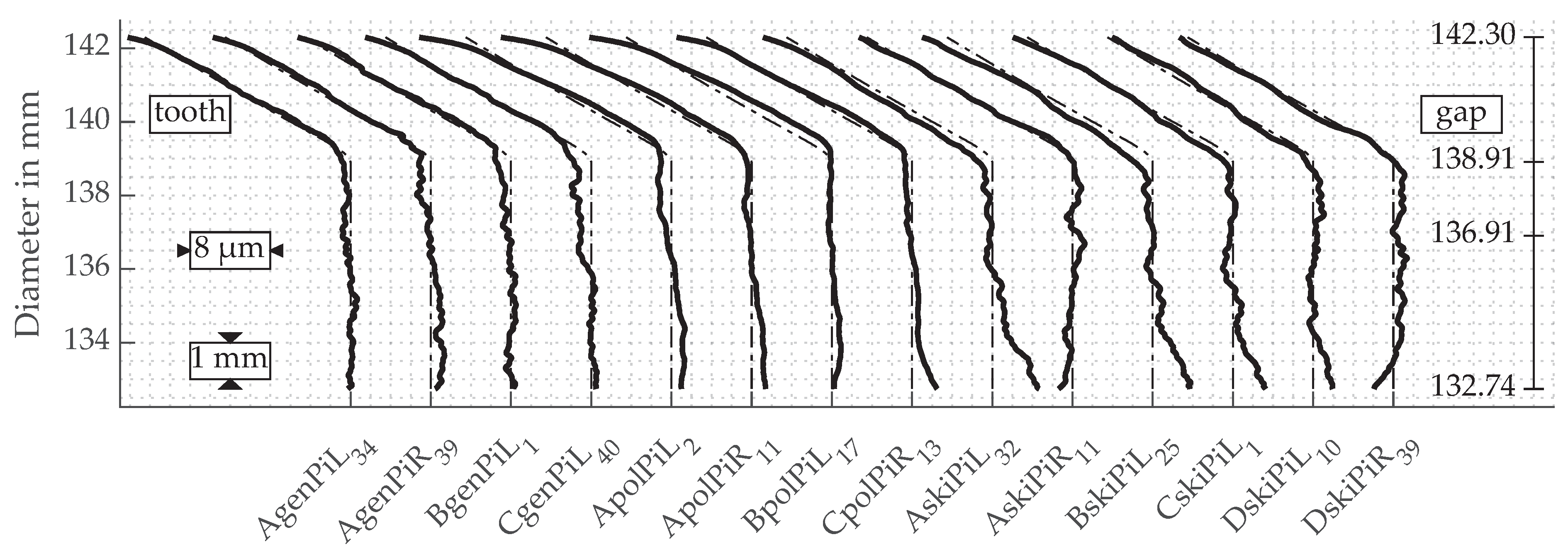
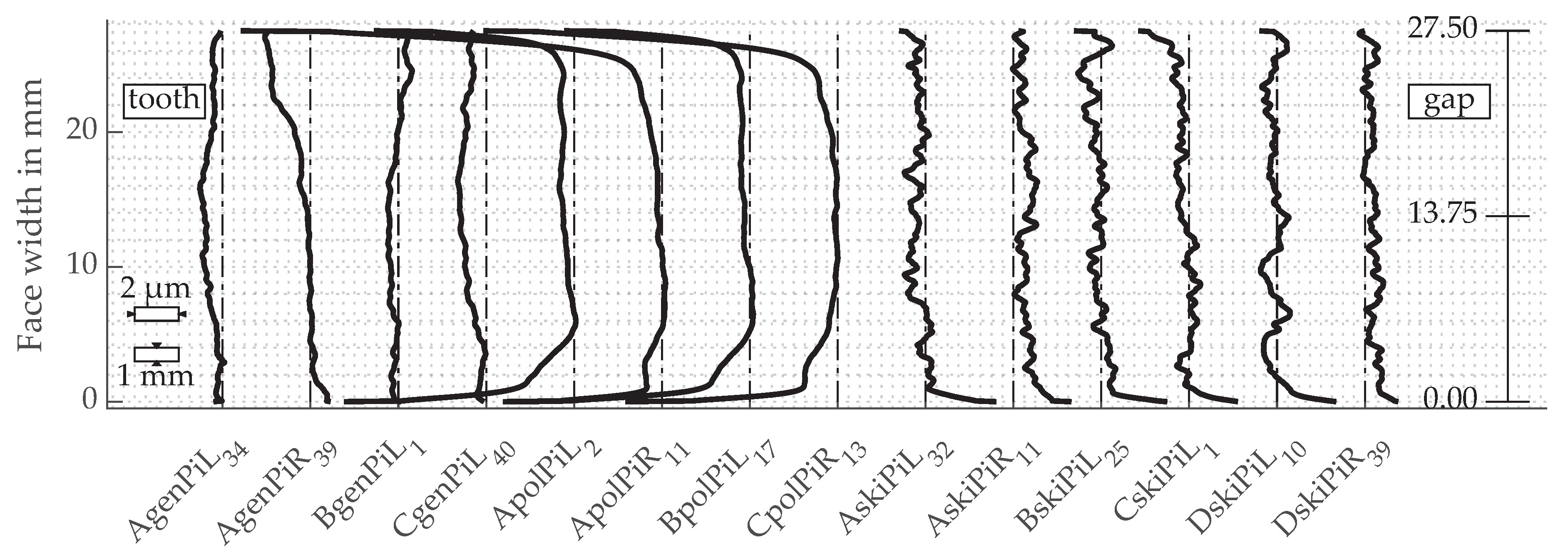
3.6. Profile and Lead Lines
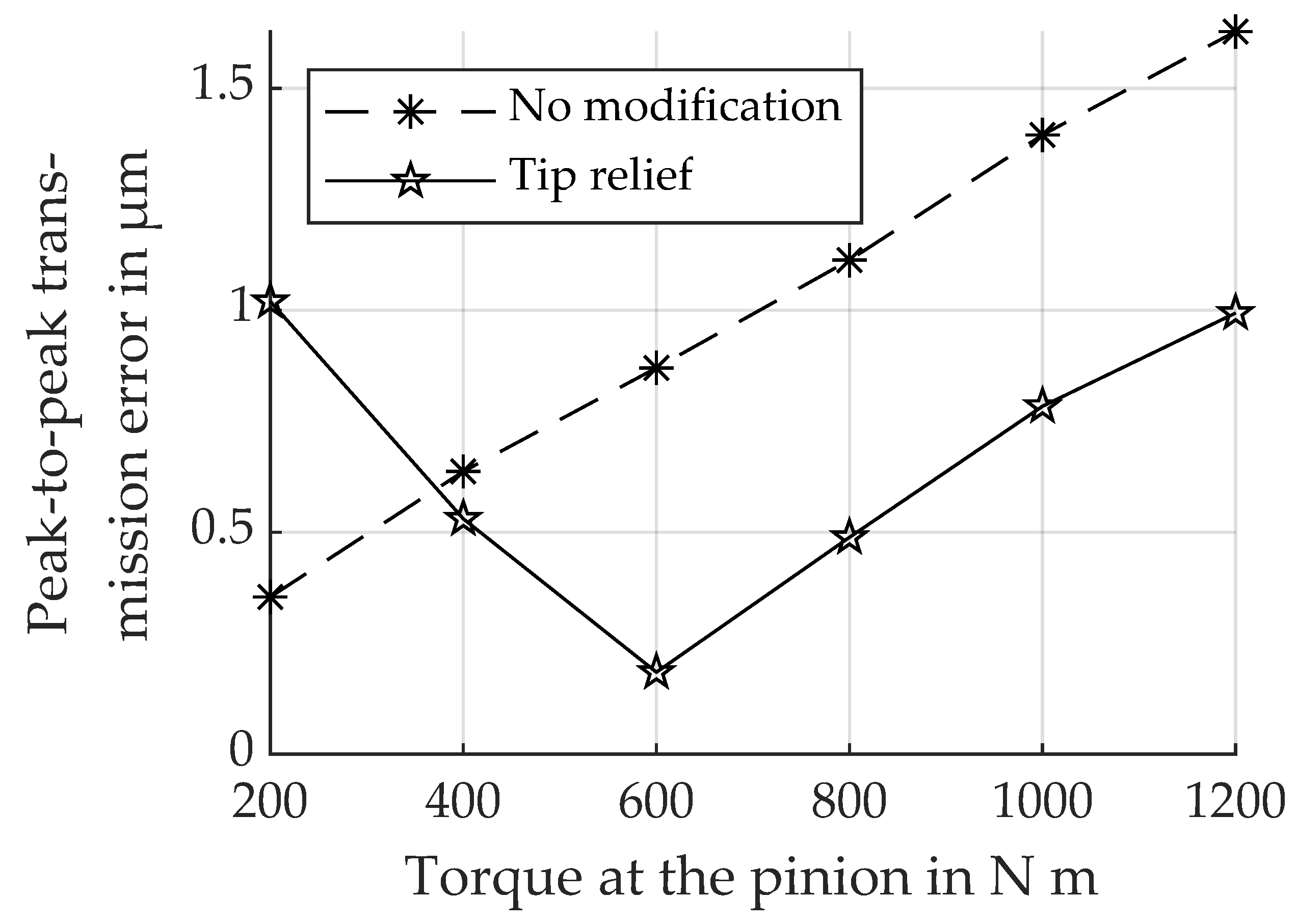
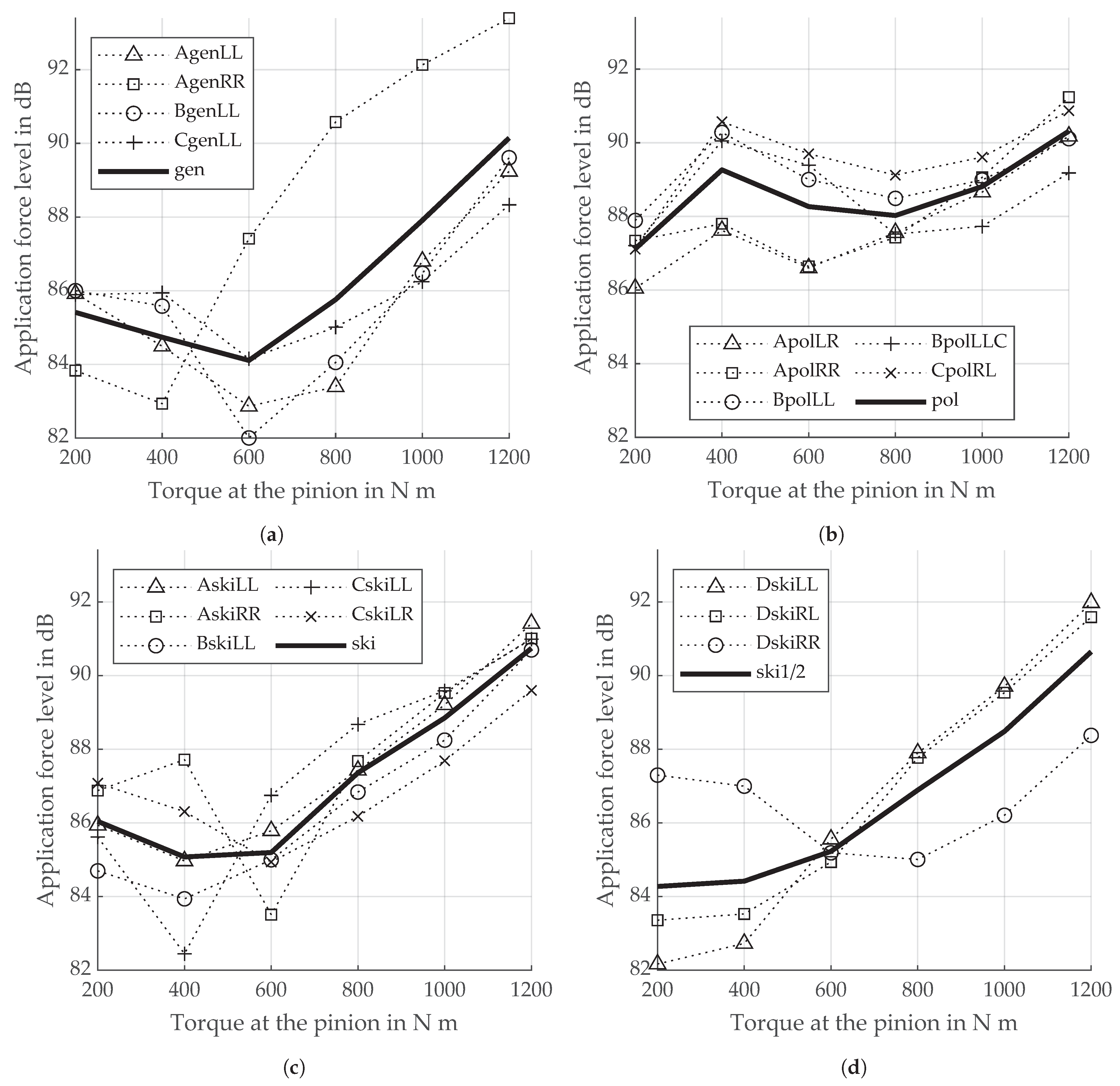
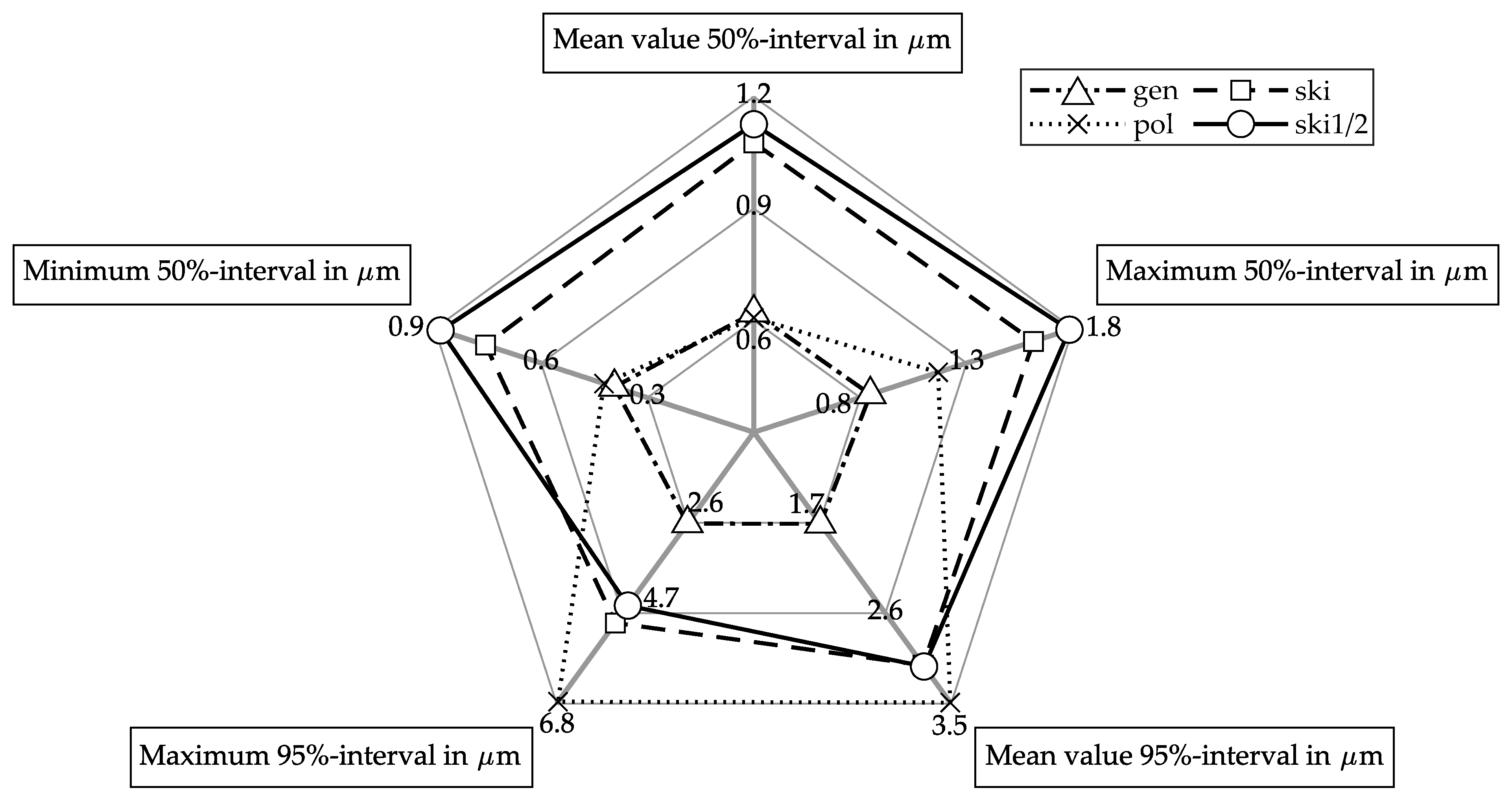
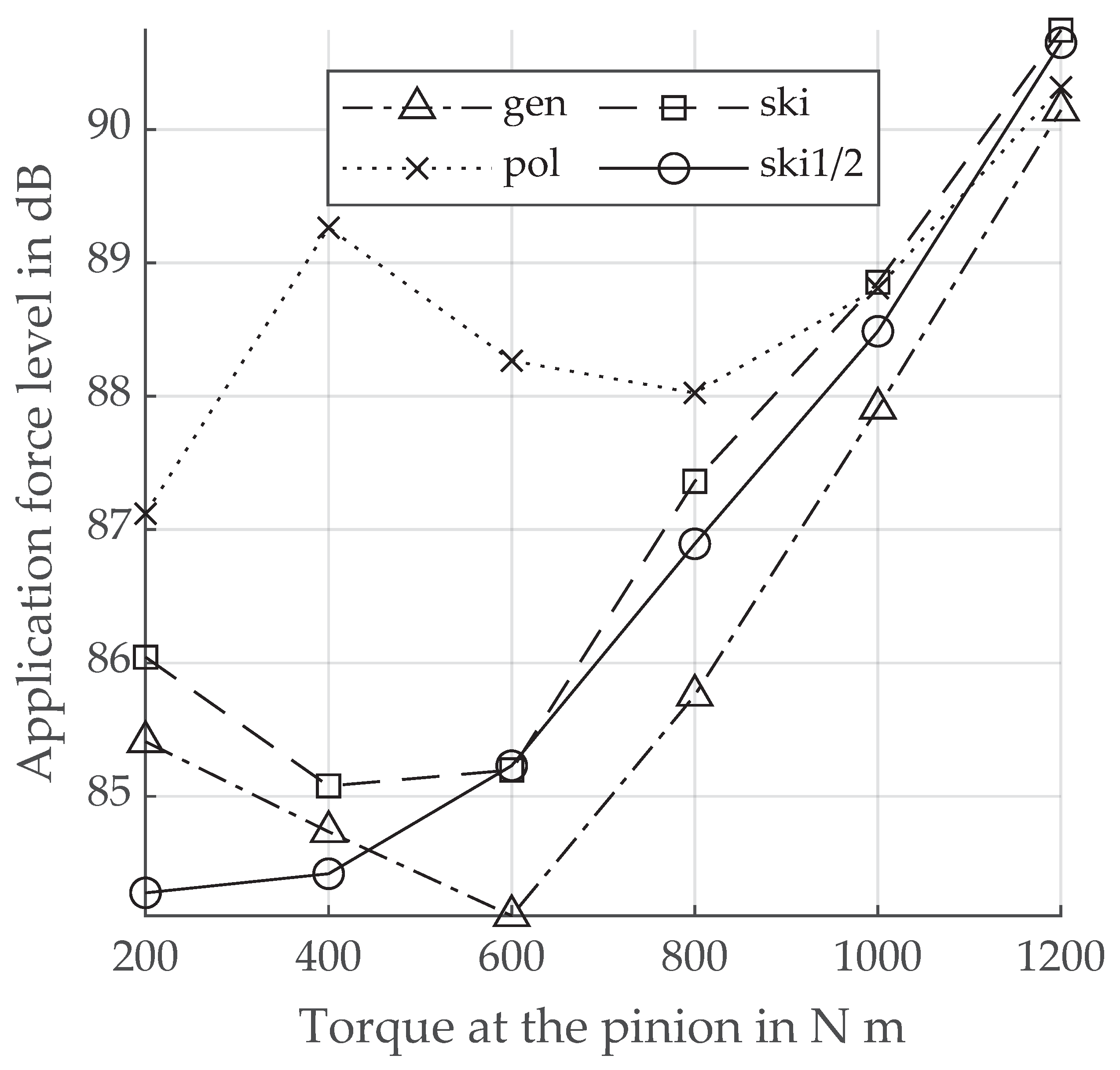
3.7. Application Force Level
4. Discussion
4.1. Flank Roughness, Surface as Well as Profile and Lead Line
4.2. Excitation Behavior
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FZG | Gear Research Centre |
| NVH | noise, vibration and harshness |
| FVA | Research Association for Drive Technology |
| DZP | Dynamic Tooth Force Program |
| gen | Label for test gears manufactured by continuous generating grinding |
| pol | Label for test gears manufactured by polish grinding |
| ski | Label for test gears manufactured by gear skiving |
| Pi | Label for pinion used in experiment |
| Wh | Label for wheel used in experiment |
| L | Label for left flank |
| R | Label for right flank |
References
- Aminbi, N. Surface Machining for Noise Suppression. Ph.D. Thesis, Chalmers University of Technology Goteburg, Gothenburg, Sweden, 1991. [Google Scholar]
- Jia, K.; Zheng, S.; Guo, J.; Hong, J. A surface enveloping-assisted approach on cutting edge calculation and machining process simulation for skiving. Int. J. Adv. Manuf. Technol. 2019, 100, 1635–1645. [Google Scholar] [CrossRef]
- Heider, M. Schwingungsverhalten von Zahnradgetrieben: Beurteilung und Optimierung des Schwingungsverhaltens von Stirnrad- und Planetengetrieben. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2012. [Google Scholar]
- Graf, W. Polish Grinding of Gears for Higher Transmission Efficiency. In American Gear Manufacturers Association Fall Technical Meeting; American Gear Manufacturers Association (AGMA): Detroit, MI, USA, 2015; pp. 265–277. [Google Scholar]
- Klocke, F.; Brecher, C. Zahnrad- und Getriebetechnik: Auslegung-Herstellung-Untersuchung-Simulation, 1st ed.; Carl Hanser Verlag: Munich, Germany, 2017. [Google Scholar]
- Klocke, F.; Koellner, T. Hard gear finishing with a geometrically defined cutting edge. Gear Technol. 1999, 16, 24–29. [Google Scholar]
- Hühsam, A. Modellbildung und Experimentelle Untersuchung des Wälzschälprozesses. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2002. [Google Scholar]
- Trübswetter, M.; Otto, M.; Stahl, K. Evaluation of Gear Flank Surface Structure Produced by Skiving. Forsch. Ingenieurwesen 2019, 83, 719–726. [Google Scholar] [CrossRef]
- Utakapan, T.; Kohn, B.; Fromberger, M.; Heider, M.; Otto, M.; Stahl, K. Measurement of gear noise behaviour for different microgeometries. Internoise 2016, 253, 3964–3974. [Google Scholar]
- Winter, H.; Seifried, A.; Ill, M. Einfluß von Verzahnungsgenauigkeit und Oberflächenstruktur der Zahnflanken auf das Geräuschverhalten von Stirnrädern. VDI Z. 1965, 107, 245–320. [Google Scholar]
- Gravel, G. Simulation of Deviations in Hobbing and Generation Grinding. In Proceedings of the International Conference on Gears, Garching, Germany, 7–9 October 2013. [Google Scholar]
- Gravel, G. Analysis of Ripple on Noisy Gears. In American Gear Manufacturers Association Fall Technical Meeting; American Gear Manufacturers Association (AGMA): Dearborn, MI, USA, 2012. [Google Scholar]
- Kohn, B.; Utakapan, T.; Fromberger, M.; Otto, M.; Stahl, K. Flank modifications for optimal excitation behaviour. Forsch. Ingenieurwesen 2017, 81, 65–71. [Google Scholar] [CrossRef]
- Kohn, B. Topologische Flankenkorrektur zur Anregungsoptimierung von Stirnradgetrieben: Entwicklung und Überprüfung von Auslegungsmethoden zur Ableitung Anregungsoptimierter Flankenkorrekturen von Stirnradgetrieben unter Berücksichtigung der Fertigbarkeit und Flankentragfähigkeit. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2019. [Google Scholar]
- Reishauer AG. Gear Grinding Machines—RZ 260; Reishauer AG: Wallisellen, Switzerland, 2018. [Google Scholar]
- Reishauer AG. Threaded Grinding Wheels—Reishauer Threaded Wheels; Reishauer AG: Wallisellen, Switzerland, 2018. [Google Scholar]
- Klingelnberg GmbH Präzisionsmesszentren P26|P40; Klingelnberg GmbH: Hückeswagen, Germany, 2020.
- Jenoptik Industrial Metrology Germany GmbH Waveline Rauheits- und Konturenmesstechnik; Jenoptik Industrial Metrology Germany GmbH: Schwenningen, Germany, 2015.
- ISO International Organization for Standardization. Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Metrological Characteristics of Phase Correct Filters; ISO 11562; ISO International Organization for Standardization: Geneva, Switzerland, 1996. [Google Scholar]
- Müller, R. Schwingungs- und Geräuschanregung bei Stirnradgetrieben. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 1991. [Google Scholar]
- Gwinner, P. Schwingungsarme Achsgetriebe Elektromechanischer Antriebsstränge. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2017. [Google Scholar]
- MT-8/A Instruction Manual. Available online: https://www.magtrol.com/wp-content/uploads/mt8manual.pdf (accessed on 29 July 2021).
- Heider, M.; Ingeli, J. FVA-Forschungsvorhaben 487 III: Neue Kennwerte zur rechnerischen Beurteilung des Anregungsverhaltens von Verzahnungen. In FVA-Heft 983; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt, Germany, 2011. [Google Scholar]
- Utakapan, T.; Ingeli, J. FVA-Forschungsvorhaben 487 IV: Neue Kennwerte zur rechnerischen Beurteilung des Anregungsverhaltens von Verzahnungen. In FVA-Heft 1101; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt, Germany, 2014. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. Oberflächenrauheit von Zahnflanken: Rauheitskenngrößen, Oberflächenklassen; DIN 3969-1; Beuth Verlag GmbH: Berlin, Germany, 1991. [Google Scholar]
- Radzevich, S.P.; Dudley, D.W. Dudley’s Handbook of Practical Gear Design and Manufacture, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Weck, M. Moderne Leistungsgetriebe: Verzahnungsauslegung und Betriebsverhalten; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Opitz, H.; Timmers, J.; Bosch, M.; Rademacher, J. Möglichkeiten zur Verbesserung des Geräuschverhaltens von Zahnradgetrieben. In Forschungsberichte des Landes Nordrhein-Westfalen; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 1967. [Google Scholar]




| Description | Unit | Pinion | Wheel | |
|---|---|---|---|---|
| Normal pressure angle | ° | |||
| Helix angle | ° | |||
| Number of teeth | z | 43 | 45 | |
| Centre distance | a | |||
| Normal module | ||||
| Profile shift coefficient | x | |||
| Face width | b | |||
| Transverse contact ratio | ||||
| Overlap ratio | ||||
| Total contact ratio | ||||
| Tip diameter | ||||
| Start of active profile diameter | ||||
| Tip Relief | Value | Rounding | Value | |||
|---|---|---|---|---|---|---|
| Amount | Start | 23% | ||||
| Roll length | (28%) | End | 30% | |||
| Continuous Generating Grinding | Polish Grinding | Gear Skiving | Gear Skiving Half Axial Feed | ||||
|---|---|---|---|---|---|---|---|
| Pinion | Wheel | Pinion | Wheel | Pinion | Wheel | Pinion | Wheel |
| AgenPi | AgenWh | ApolPi | ApolWh | AskiPi | AskiWh | DskiPi | DskiWh |
| BgenPi | BgenWh | BpolPi | BpolWh | BskiPi | BskiWh | ||
| CgenPi | CgenWh | CpolPi | CpolWh | CskiPi | CskiWh | ||
| Load Stages | Load in N m | Revolutions Ramp-Up |
|---|---|---|
| 1 | 200 | 450 … 5050 min−1 (, duration: 90 ) via main drive |
| 2 | 400 | |
| 3 | 600 | |
| 4 | 800 | |
| 5 | 1000 | |
| 6 | 1200 |
| Parameter | Symbol | Minimum | Maximum |
|---|---|---|---|
| Speed | 1000 min−1 | 4800 min−1 | |
| Frequency | 0 | 10,000 Hz | |
| Order |
| Manufacturing Method | Gear | |
|---|---|---|
| Continuous generating grinding | AgenWhL | |
| Polish grinding | CpolWhL | |
| Gear skiving | AskiWhL | |
| Gear skiving half axial feed | DskiWhL |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trübswetter, M.; Götz, J.; Kohn, B.; Otto, M.; Stahl, K. Effects of Different Hard Finishing Processes on Gear Excitation. Machines 2021, 9, 169. https://doi.org/10.3390/machines9080169
Trübswetter M, Götz J, Kohn B, Otto M, Stahl K. Effects of Different Hard Finishing Processes on Gear Excitation. Machines. 2021; 9(8):169. https://doi.org/10.3390/machines9080169
Chicago/Turabian StyleTrübswetter, Maximilian, Joshua Götz, Bernhard Kohn, Michael Otto, and Karsten Stahl. 2021. "Effects of Different Hard Finishing Processes on Gear Excitation" Machines 9, no. 8: 169. https://doi.org/10.3390/machines9080169
APA StyleTrübswetter, M., Götz, J., Kohn, B., Otto, M., & Stahl, K. (2021). Effects of Different Hard Finishing Processes on Gear Excitation. Machines, 9(8), 169. https://doi.org/10.3390/machines9080169







