A Simple Soft Computing Structure for Modeling and Control
Abstract
:1. Introduction
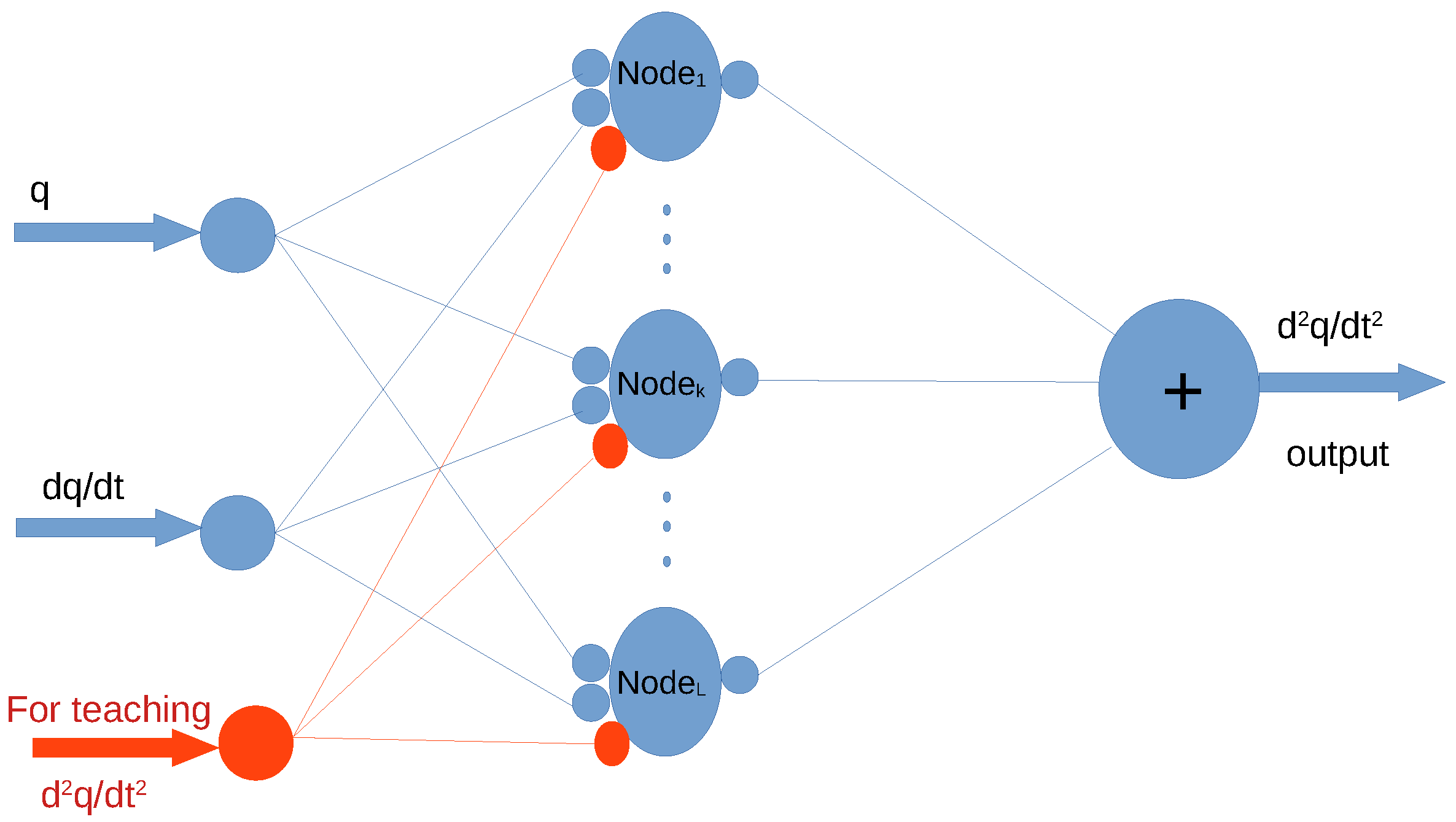
2. The Model Structure, the Activation Function and the Teaching Process
- Each neuron investigates if the input belongs to its range of competence. If then the given neuron (number i) is competent to make operation. In this case, in the learning phase, it
- associates the appropriate input value with the given grid element;
- augments the vector into , into in which and are the “dummy components” that guarantee the common norm ;
- calculates the unit vectors , and the angle of abstract rotation, , and finally
- if the place of the appropriate node is still empty, simply stores the computed data in the hyper-matrix as , , and where the subscripts and now denote the number of the given cell/node.
- If the node already is filled in, it either does nothing (simple skips the operation), or applies “incremental learning”.
- 1.
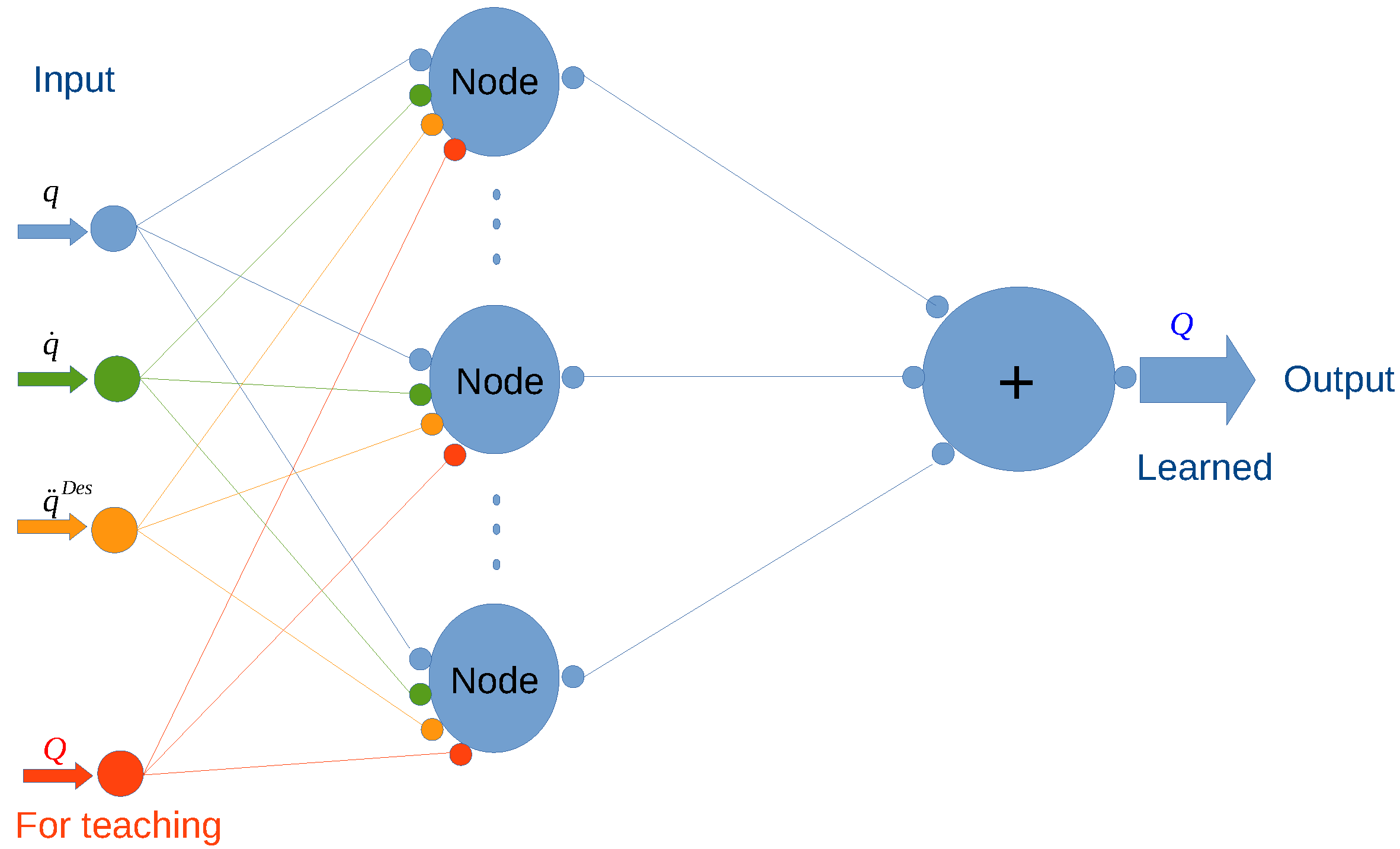
- For a given pair each neuron determines whether the input belongs to the box associated with its “competence of operation”: if not, the output value will be zero, otherwise it completes the following calculations:
- 2.
- the neuron retrieves the parameters of the activation function as , , and ,
- 3.
- computes the orthogonal matrix O in (4);
- 4.
- augments the vector into , where d is the physically not interpreted “dummy component”;
- 5.
- computes the rotated vector , and uses its first component as obtained from this special model, and
- 6.
- optionally it can refresh the cell content via “incremental learning”.
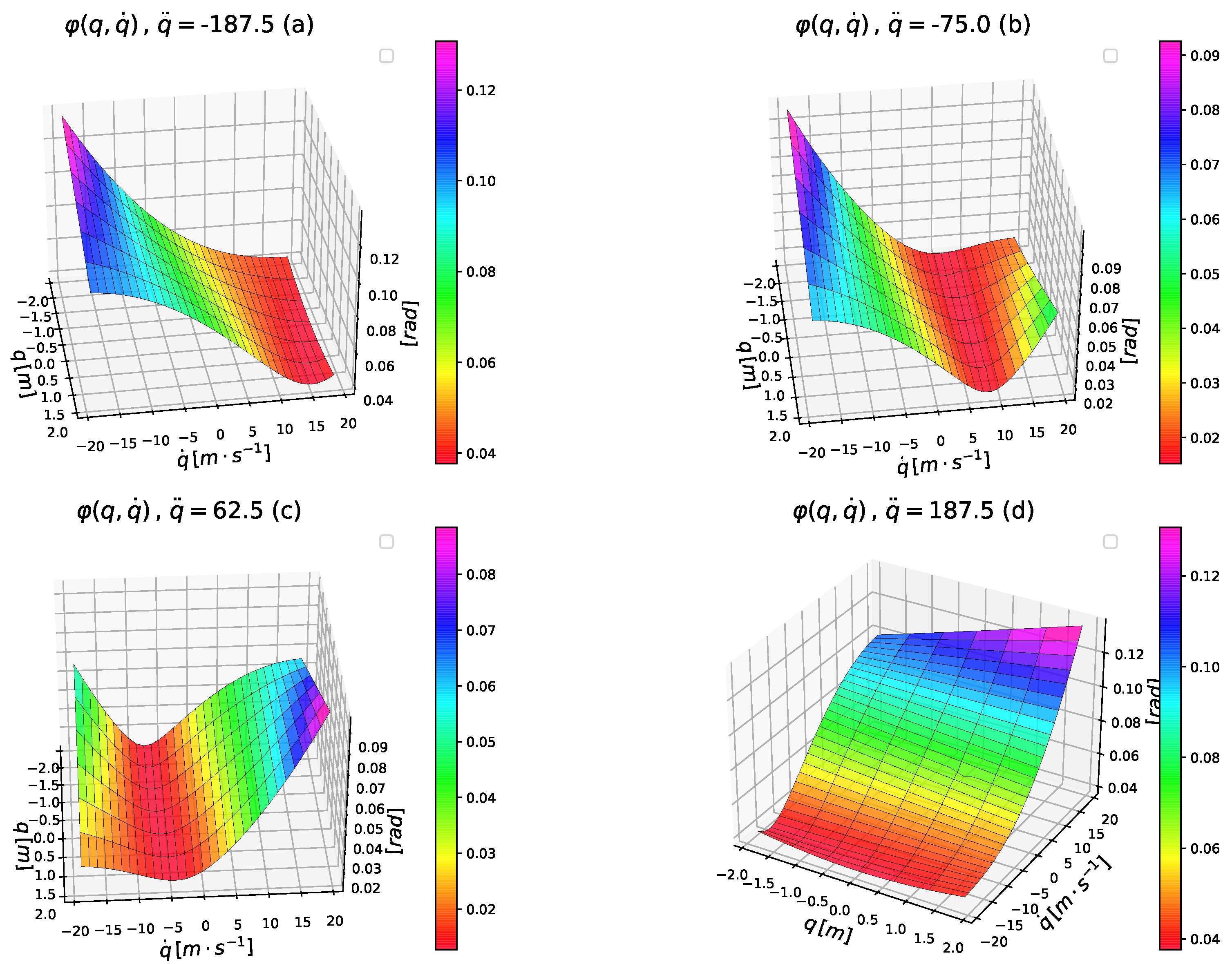
3. Teaching Example: The Free Motion of the van der Pol Oscillator
4. Controlled Motion of the van der Pol Oscillator Using the Novel Neural Model
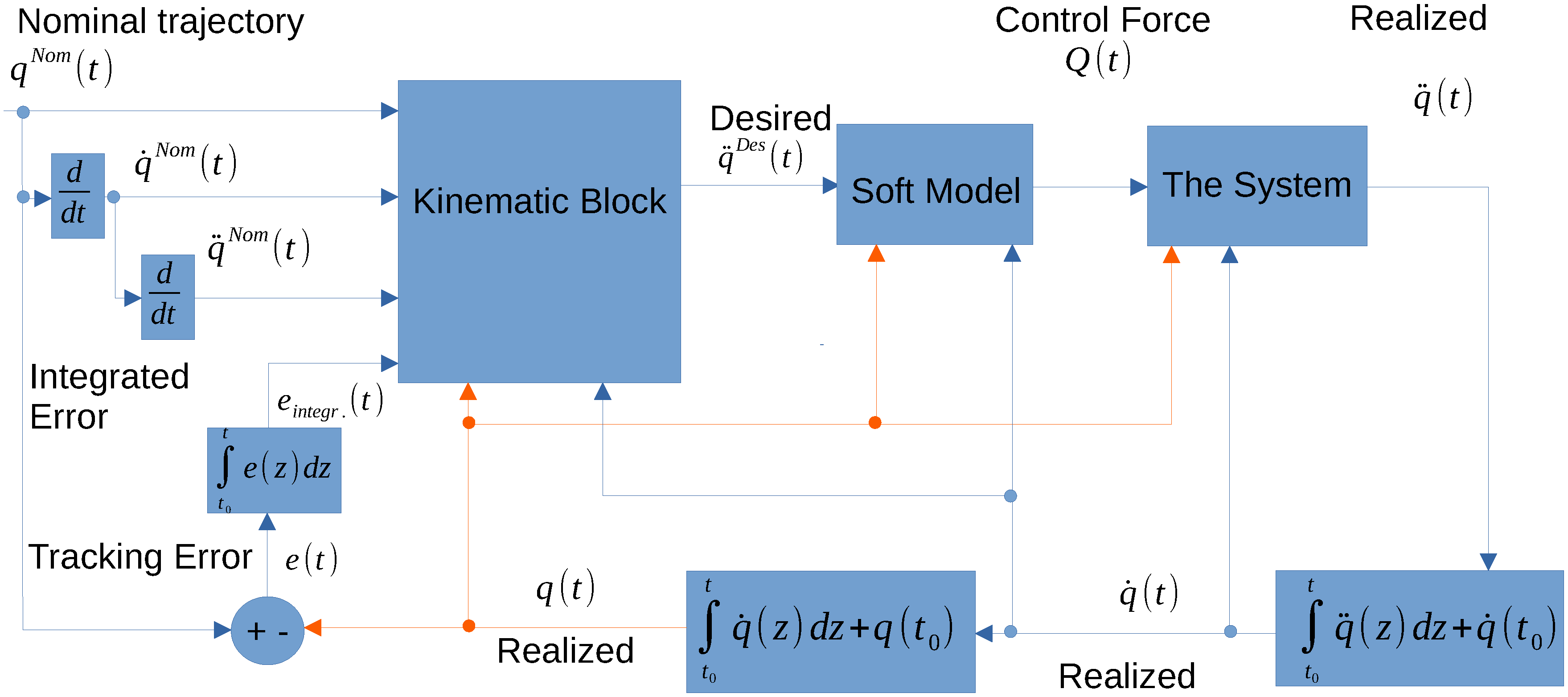
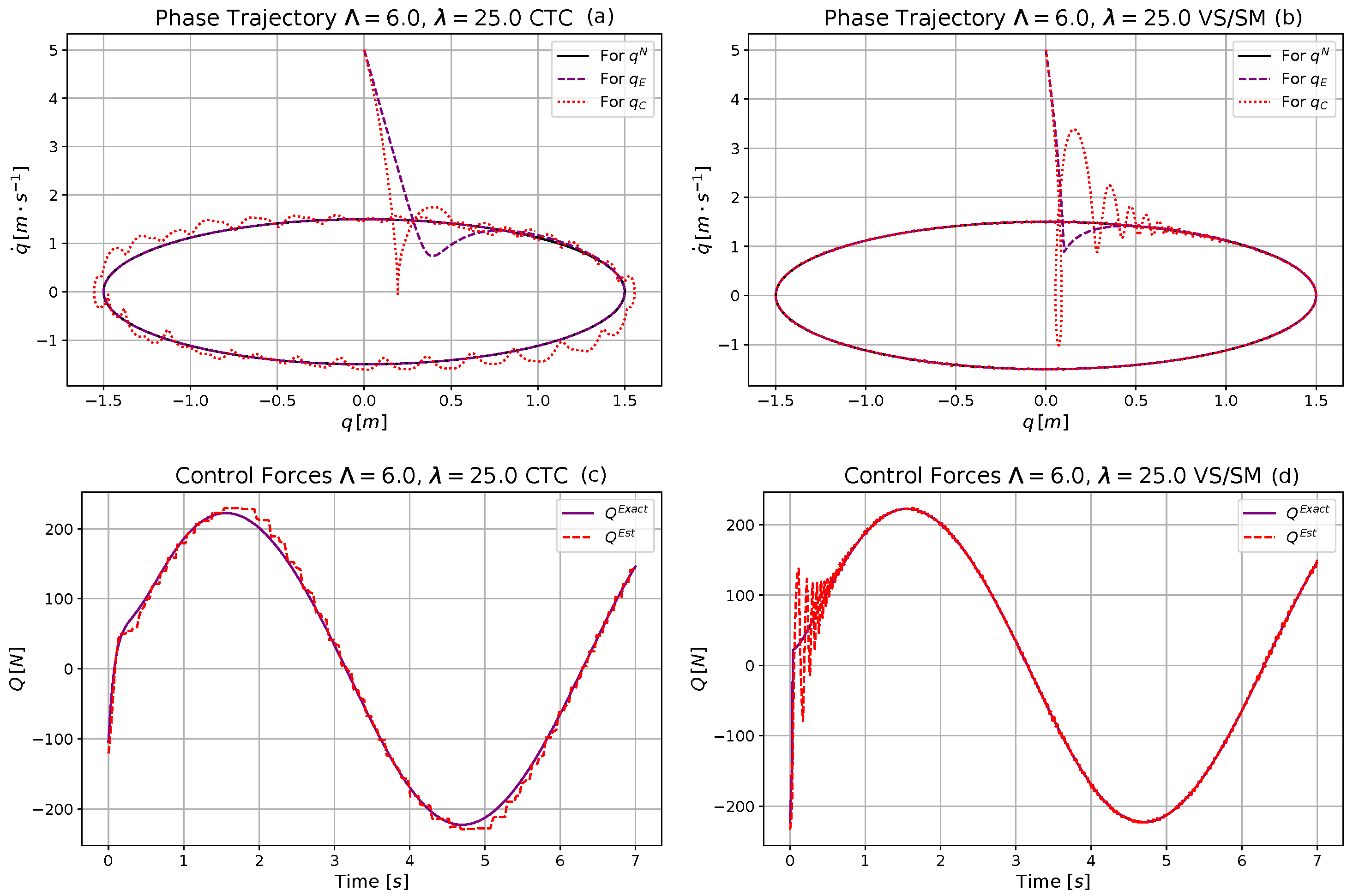
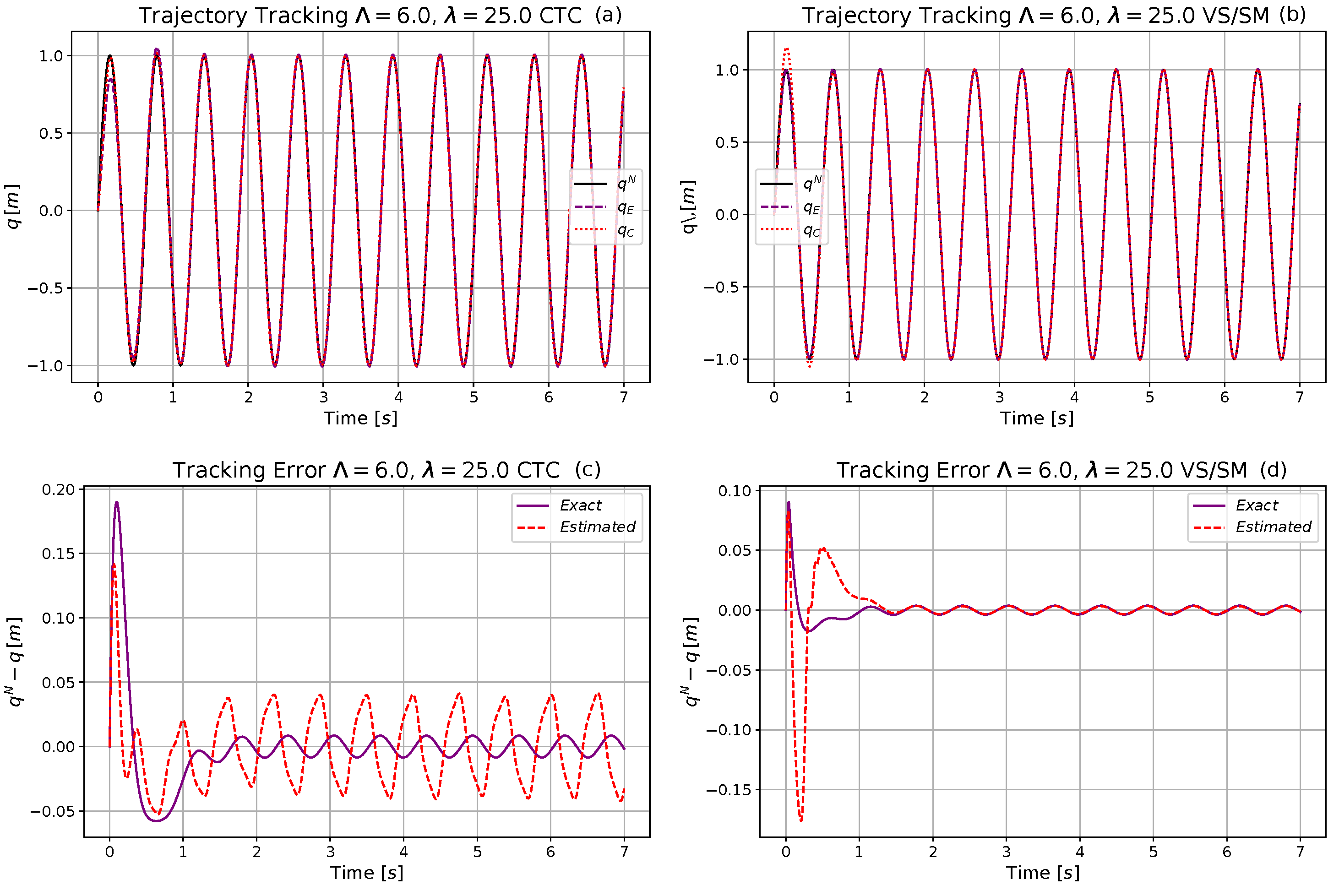
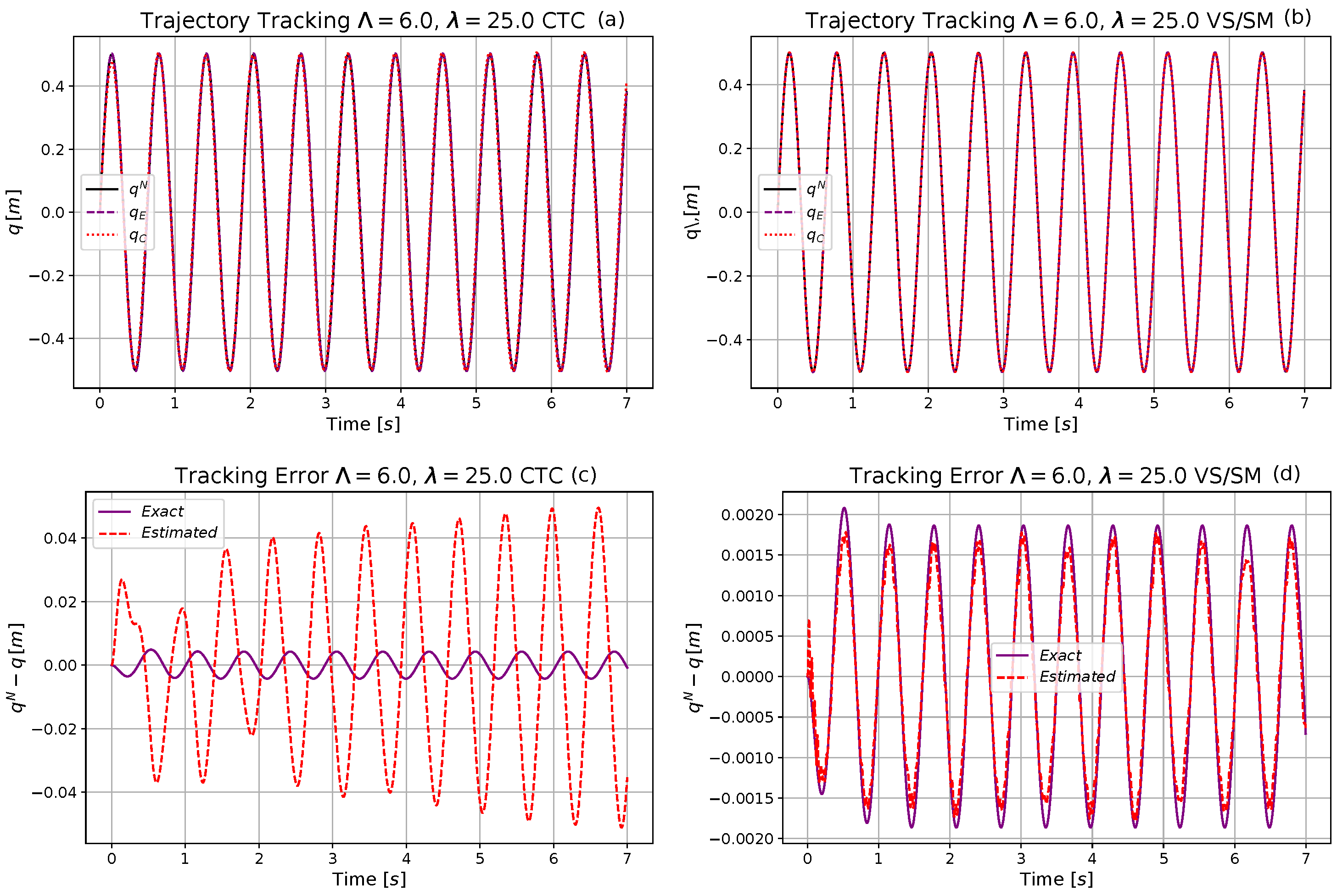
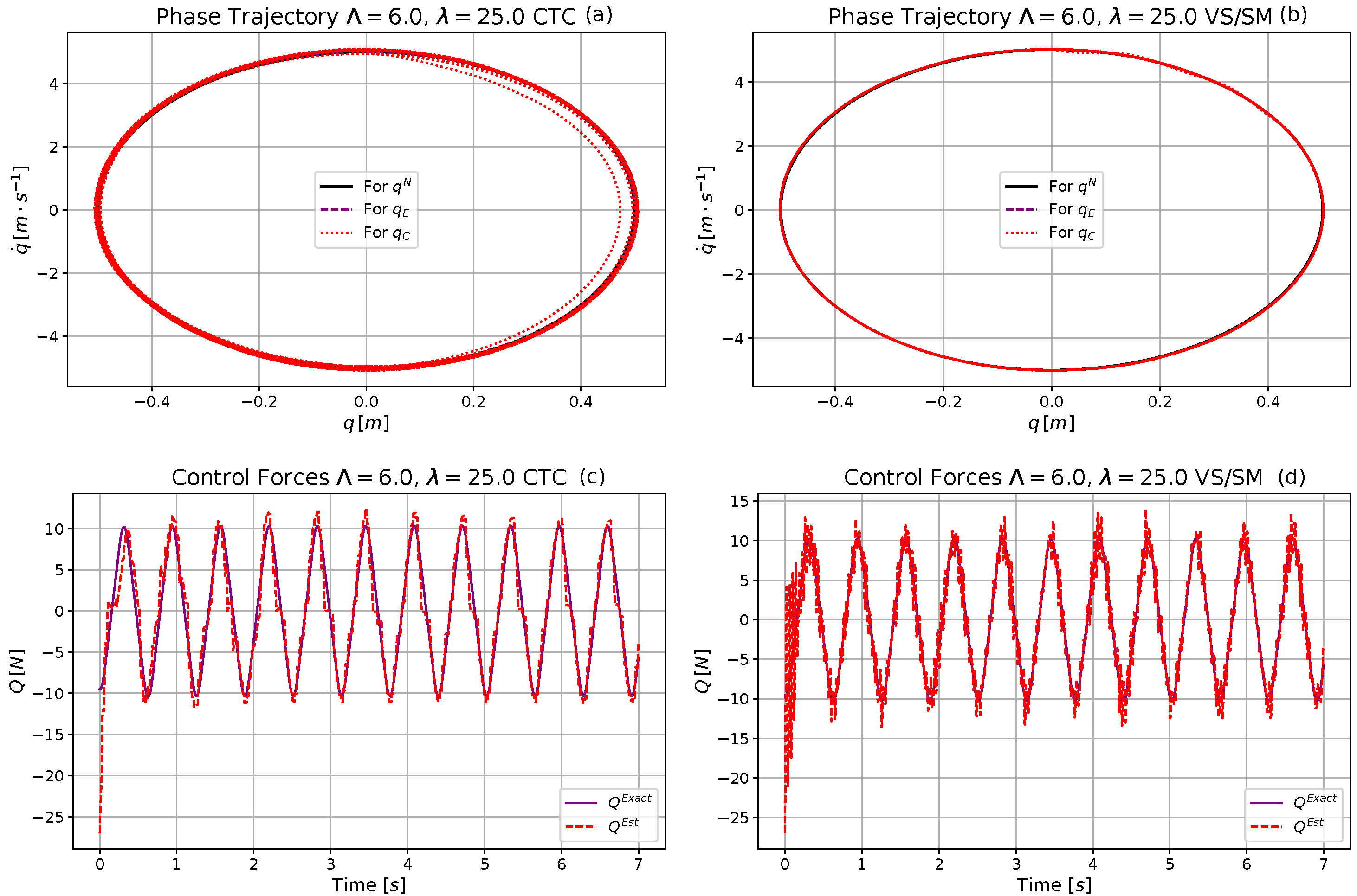
4.1. The Computed Torque Control and the Robust VS/SM Schemata
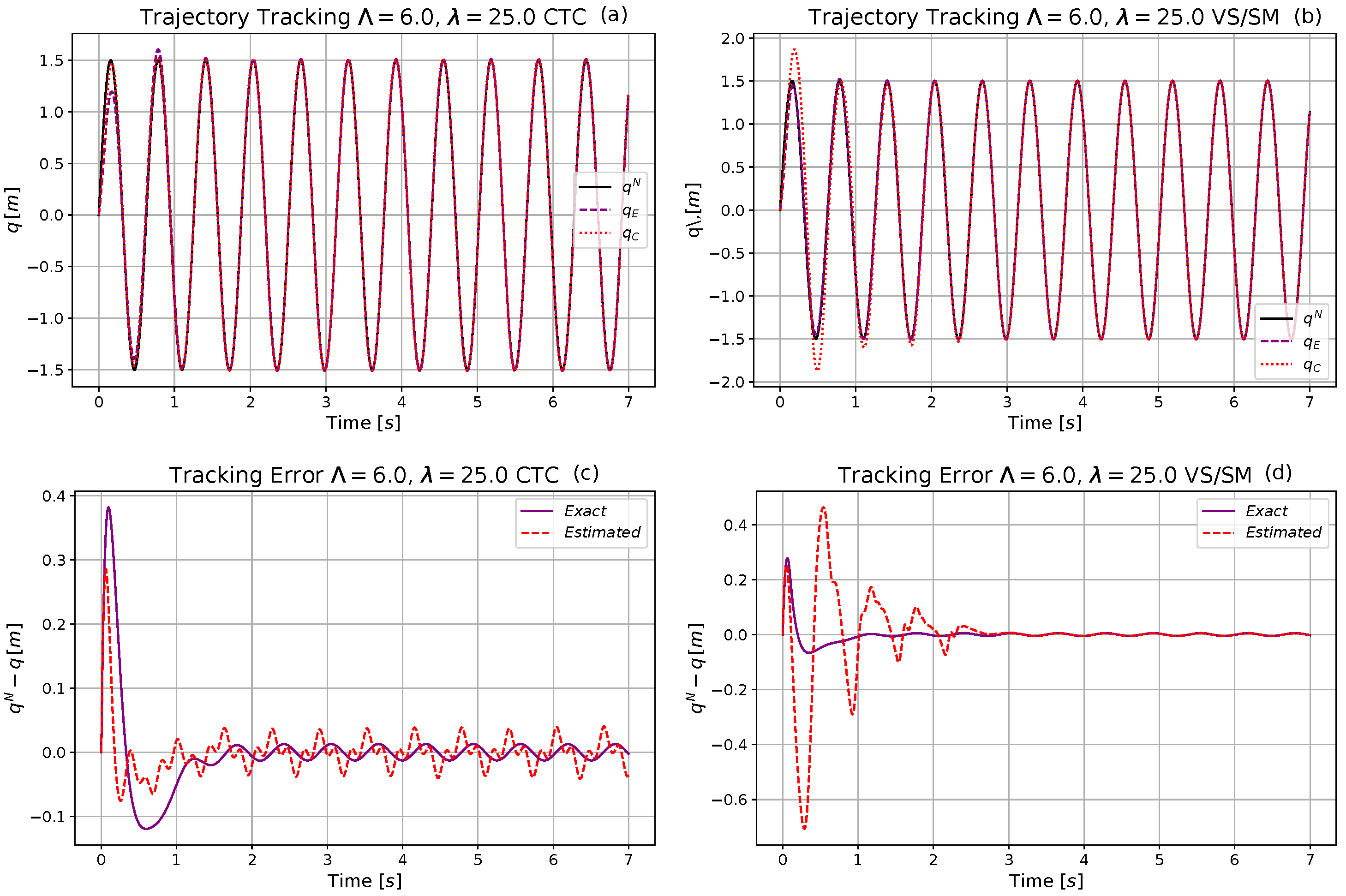
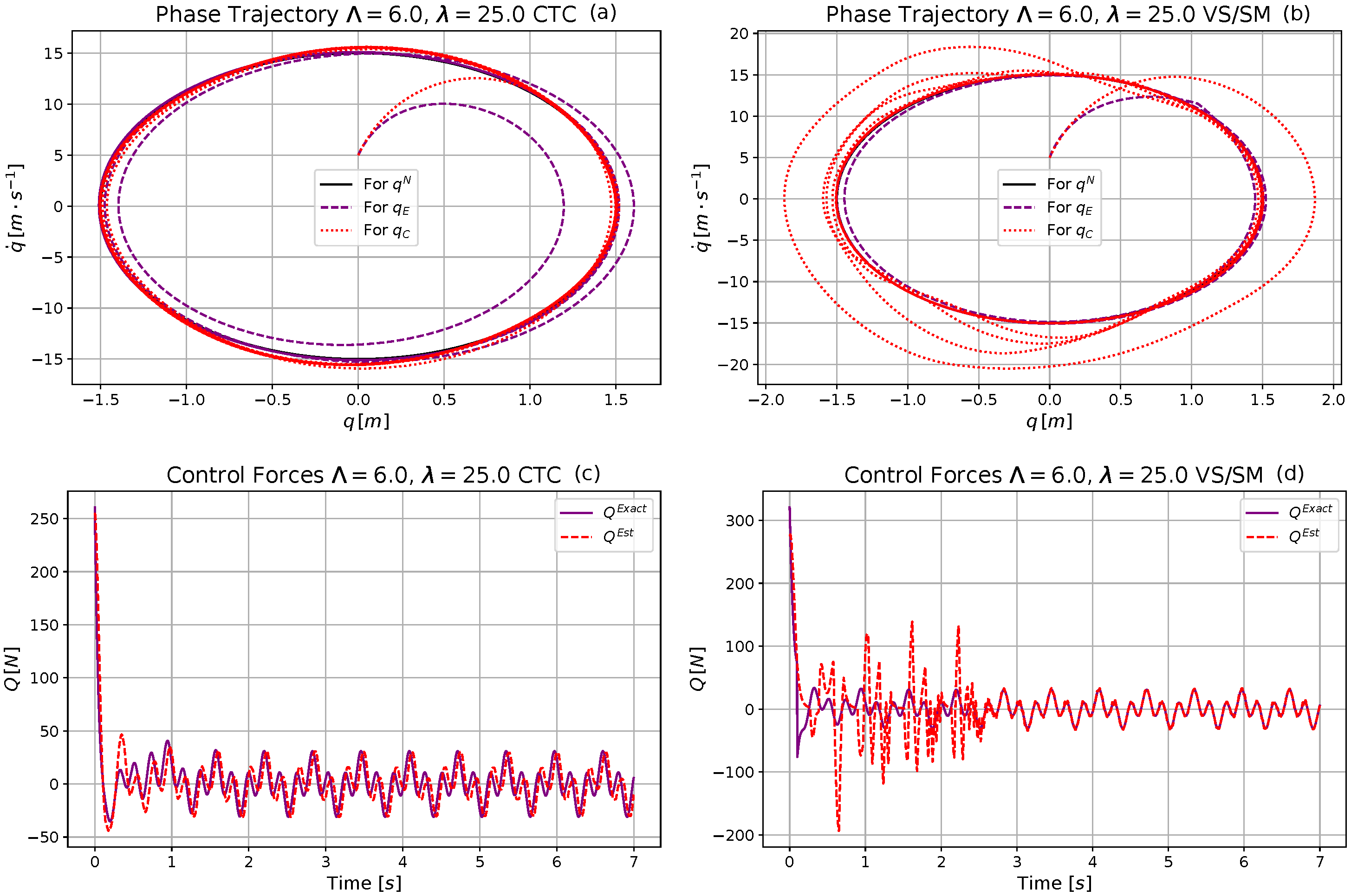
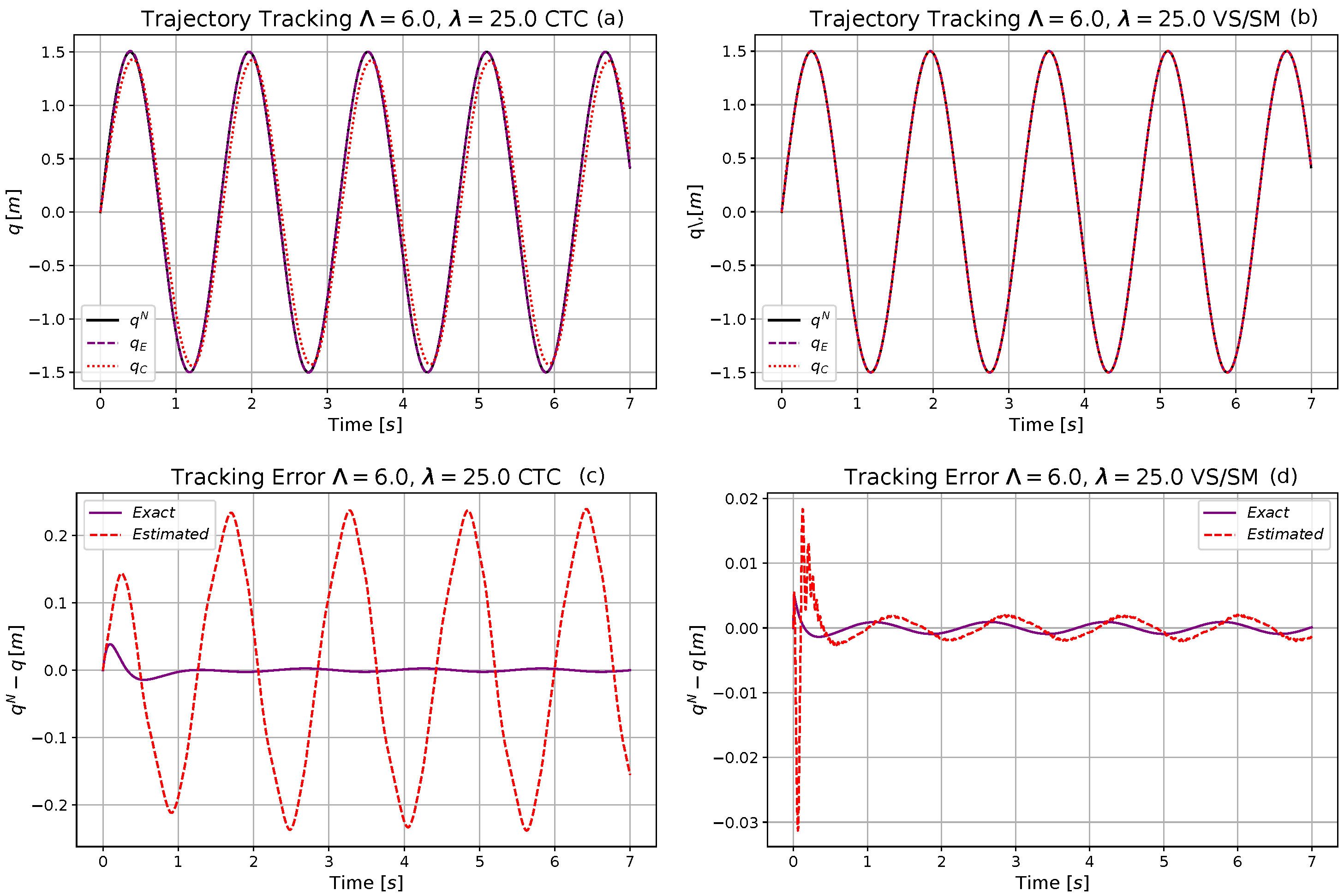
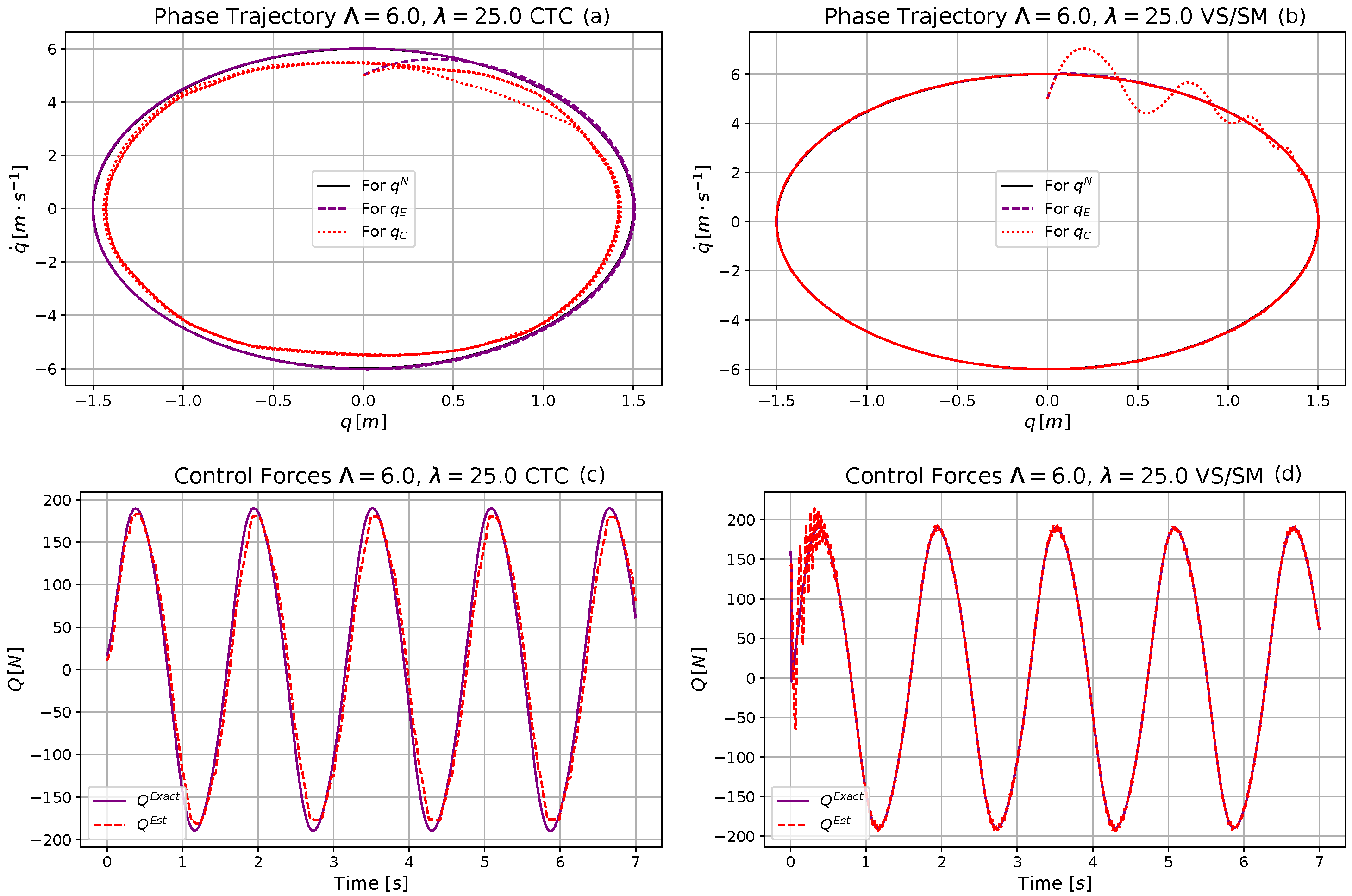
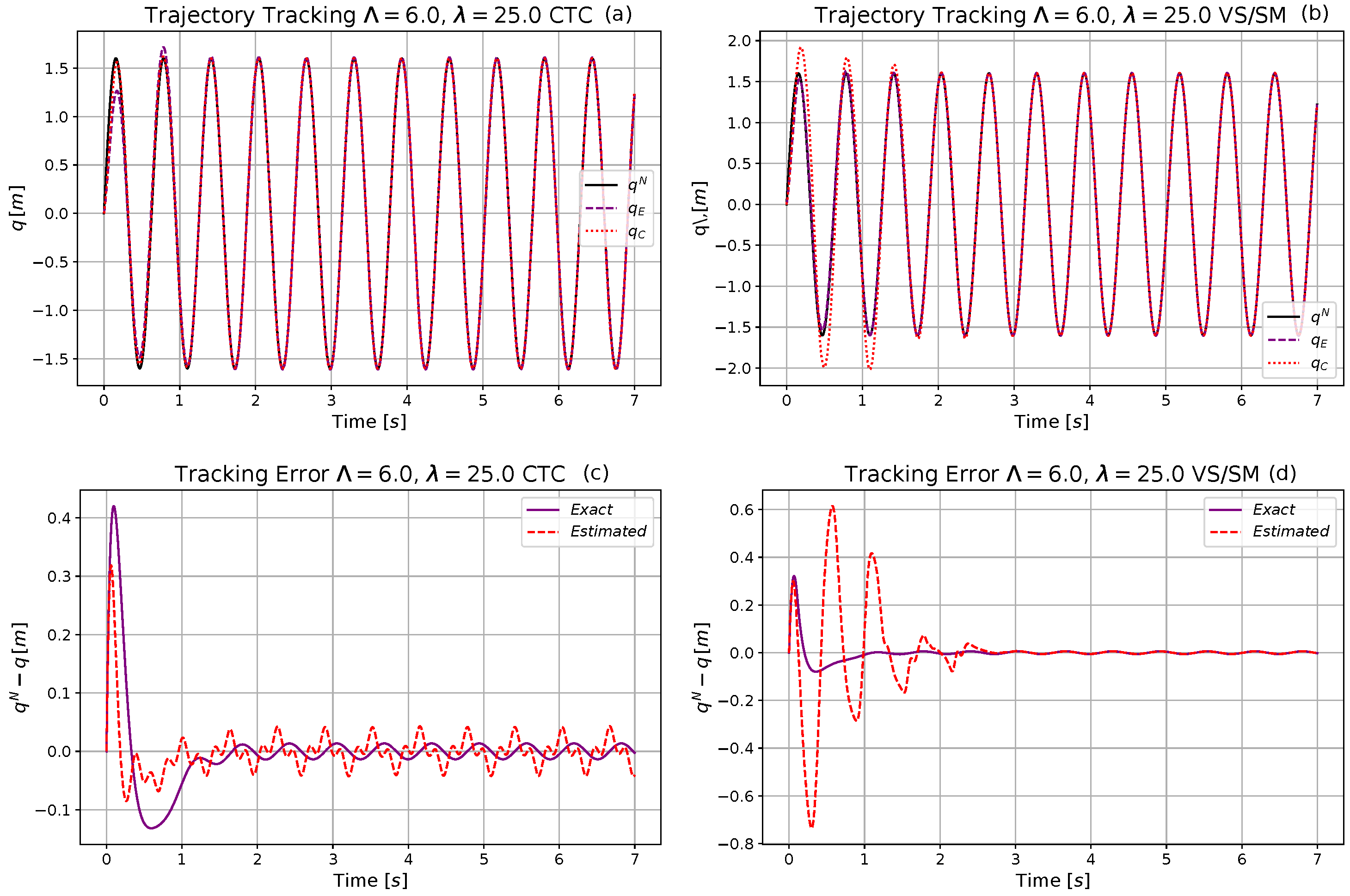
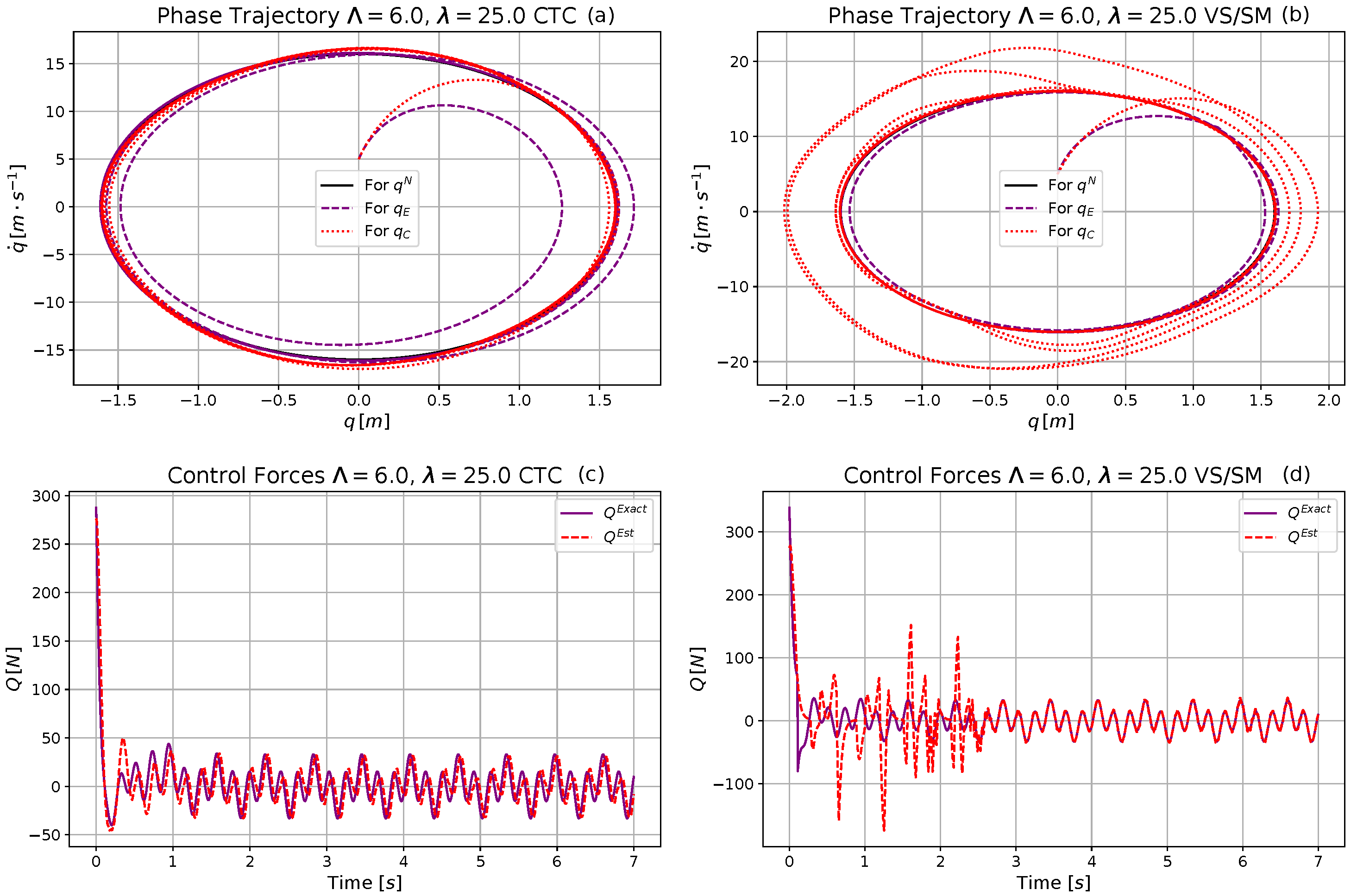
4.2. Simulation Investigations
5. Conclusions
- Its activation function’s operation has simple geometric interpretation: it executes abstract rotations in higher-dimensional Euclidean spaces;
- The parameters of this function are encoded in two orthogonal unit vectors and in the angle of the abstract rotation that is executed by this function;
- The “extrapolation ability” of this function originates from the fact that with this rotation operator an array has to be transformed that conveys information on the “absolute value” of the modeled state;
- As with the polytopic models, the system model is so coded that each cell in a grid has its own activation function with its parameters;
- In contrast to the multilayer perceptrons or recurrent neural networks, no complicated “connecting wire structure” must be realized in its implementation;
- In contrast to the teaching phase of a multilayer perceptron, in which the error backpropagation requires the modification of the parameters of each function and the weight parameters in a massively parallel process, in this system only one neuron is active in a given time instant that is responsible for the necessary rotation. The other cells only must determine whether they must make any computation;
- In a similar manner, in the operating phase, when the model is in use, only one neuron executes the necessary transformation in a given time; the other ones only must check their competence. In contrast to that, the fuzzy inference systems must make massive distributed operations by executing the necessary “AND” and “OR” operations, fuzzification of the input and defuzzification of the output. Additionally, in the case of a multilayer perceptron, each neuron has to essentially take part in the computation of the final result that can be obtained by collecting the output of each neuron of a given layer, and forwarding their output to the neurons of the next layer;
- Due to the fact that the parameters of the functions are interpreted as orthogonal unit vectors, incremental adaptive improvement or “further teaching” of this model during its operation is possible by the use of a simple approximate “aggregation technique” that was elaborated for unit vectors.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Yan, H. Reconstruction Designs of Lost Ancient Chinese Machinery; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Rossi, C.; Russo, F. Automata (Towards Automation and Robots), Ancient Engineers’ Inventions; Springer: Dordrecht, The Netherlands, 2017; pp. 353–380. [Google Scholar]
- Hills, R. Power from the Wind; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Maxwell, J. On Governors. Proc. R. Soc. 1868, 16, 270–283. [Google Scholar]
- Lyapunov, A. A General Task about the Stability of Motion. Ph.D. Thesis, University of Kazan, Tatarstan, Russia, 1892. (In Russian). [Google Scholar]
- Lyapunov, A. Stability of Motion; Academic Press: New York, NY, USA; London, UK, 1966. [Google Scholar]
- Lagrange, J.; Binet, J.; Garnier, J. Mécanique Analytique (Analytical Mechanics); Binet, J.P.M., Garnier, J.G., Eds.; Ve Courcier: Paris, France, 1811. [Google Scholar]
- Canudas de Wit, C.; Olsson, H.; Åström, K.; Linschinsky, P. Dynamic friction models and control design. In Proceedings of the 1993 American Control Conference, San Francisco, CA, USA, 2–4 June 1993; Volume 40, pp. 1920–1926. [Google Scholar]
- Márton, L.; Lantos, B. Identification and Model-based Compensation of Striebeck Friction. Acta Polytech. Hung. 2006, 3, 45–58. [Google Scholar]
- Armstrong, B.; Khatib, O.; Burdick, J. The Explicit Dynamic Model and Internal Parameters of the PUMA 560 Arm. In Proceedings of the 1986 IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 7–10 April 1986; pp. 510–518. [Google Scholar]
- Corke, P.; Armstrong-Helouvry, B. A Search for Consensus Among Model Parameters Reported for the PUMA 560 Robot. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 1608–1613. [Google Scholar]
- Bergman, R.; Ider, Y.; Bowden, C.; Cobelli, C. Quantitative estimation of insulin sensitivity. Am. J. Physiol. Endocrinol. Metab. 1979, 236, E667–E677. [Google Scholar] [CrossRef] [PubMed]
- Sörensen, J. A Physiologic Model of Glucose Metabolism in Man and Its use to Design and Assess Improved Insulin Therapies for Diabetes. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1985. [Google Scholar]
- Man, C.D.; Rizza, R.; Cobelli, C. Meal simulation model of glucose-insulin system. IEEE Trans. Biomed. Eng. 2007, 54, 1740–1749. [Google Scholar] [PubMed]
- Man, C.D.; Micheletto, F.; Lv, D.; Breton, M.; Kovatchev, B.; Cobelli, C. The UVA/PADOVA Type 1 Diabetes Simulator: New Features. J. Diabetes Sci. Technol. 2014, 8, 26–34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eigner, G.; Tar, J.; Rudas, I.; Kovács, L. LPV-based quality interpretations on modeling and control of diabetes. Acta Polytech. Hung. 2016, 13, 171–190. [Google Scholar]
- Andoga, R.; Főző, L. Near Magnetic Field of a Small Turbojet Engine. Acta Phys. Pol. 2017, 131, 1117–1119. [Google Scholar] [CrossRef]
- Andoga, R.; Főző, L.; Schrötter, M.; Češkovič, M.; Szabo, S.; Bréda, R.; Schreiner, M. Intelligent Thermal Imaging-Based Diagnostics of Turbojet Engines. Appl. Sci. 2019, 9, 2253. [Google Scholar] [CrossRef] [Green Version]
- Andoga, R.; Főző, L.; Judičák, J.; Bréda, R.; Szabo, S.; Rozenberg, R.; Džunda, M. Intelligent Situational Control of Small Turbojet Engines. Int. J. Aerosp. Eng. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Andoga, R.; Főző, L.; Kovács, R.; Beneda, K.; Moravec, T.; Schreiner, M. Robust Control of Small Turbojet Engines. Machines 2019, 7, 3. [Google Scholar] [CrossRef] [Green Version]
- Főző, L.; Andoga, R.; Kovács, L.; Schreiner, M.; Beneda, K.; Savka, J.; Soušek, R. Virtual Design of Advanced Control Algorithms for Small Turbojet Engines. Acta Polytech. Hung. 2019, 16, 101–117. [Google Scholar] [CrossRef]
- Emelyanov, S.; Korovin, S.; Levantovsky, L. Higher Order Sliding Regimes in the Binary Control Systems. Sov. Phys. 1986, 31, 291–293. [Google Scholar]
- Levant, A. Arbitrary-order Sliding Modes with Finite Time Convergence. In Proceedings of the the 6th IEEE Mediterranean Conference on Control and Systems, Alghero, Sardinia, Italy, 9–11 June 1998. [Google Scholar]
- Utkin, V. Sliding Modes in Optimization and Control Problems; Springer: New York, NY, USA, 1992. [Google Scholar]
- Tar, J.; Bitó, J.; Nádai, L.; Tenreiro Machado, J. Robust Fixed Point Transformations in Adaptive Control Using Local Basin of Attraction. Acta Polytech. Hung. 2009, 6, 21–37. [Google Scholar]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (About the Operations in the Abstract Sets and Their Application to Integral Equations). Fund. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Tar, J.; Rudas, I.; Dineva, A.; Várkonyi-Kóczy, A. Stabilization of a Modified Slotine-Li Adaptive Robot Controller by Robust Fixed Point Transformations. In Proceedings of the Recent Advances in Intelligent Control, Modelling and Simulation, Cambridge, MA, USA, 29–31 January 2014; pp. 35–40. [Google Scholar]
- Dineva, A.; Várkonyi-Kóczy, A.; Tar, J. Combination of RFPT-based Adaptive Control and Classical Model Identification. In Proceedings of the 2014 IEEE 12th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 23–25 January 2014; pp. 35–40. [Google Scholar]
- Csanádi, B.; Galambos, P.; Tar, J.; Györök, G.; Serester, A. Revisiting Lyapunov’s Technique in the Fixed Point Transformation-based Adaptive Control. In Proceedings of the 2018 IEEE 22nd International Conference on Intelligent Engineering Systems (INES), Las Palmas de Gran Canaria, Spain, 21–23 June 2018; pp. 329–334. [Google Scholar] [CrossRef]
- Weierstraß, K. Über die analytische Darstellbarkeit sogenannter willkürlicher Functionen einer reellen Veränderlichen (About the analytical representability of so-called arbitrary functions of a real variable). Sitzungsberichte Akad. Berl. (Inaug. Lect. Acad. Berl.) 1885, 2, 789–805. [Google Scholar]
- Stone, M. A generalized Weierstrass approximation theorem. Math. Mag. 1948, 21, 237–254. [Google Scholar] [CrossRef]
- Wang, L.X.; Mendel, J. Fuzzy Basis Functions, Universal Approximation and Orthogonal Least Squares Learning. IEEE Trans. Neural Netw. 1992, 3, 807–814. [Google Scholar] [CrossRef] [Green Version]
- Hilbert, D. Mathematical Problems. Bull. Am. Math. Soc. 1902, 8, 437–479. [Google Scholar] [CrossRef] [Green Version]
- Kolmogorov, A. On the representation of continuous functions of many variables by superposition of continuous functions of one variable and addition (in Russian). Dokl. Akad. Nauk. SSSR 1957, 114, 953–956. [Google Scholar]
- Sprecher, D. On the Structure of Continuous Functions of Several Variables. Trans. Am. Math. Soc. 1965, 115, 340–355. [Google Scholar] [CrossRef]
- Lorentz, G. Approximation of Functions; Holt, Reinhard and Winston: New York, NY, USA, 1965. [Google Scholar]
- Volterra, V. Theory of Functionals and of Integrals and Integro-Differential Equations (Reprinted Translation of the Original Work in Spanish Issued in Madrid in 1927); Dover Publications: New York, NY, USA, 1959. [Google Scholar]
- Kůrková, V. Kolmogorov’s Theorem and Multilayer Neural Networks. Neural Netw. 1992, 5, 501–506. [Google Scholar] [CrossRef]
- Miyanawala, T.P.; Jaiman, R.K. An Efficient Deep Learning Technique for the Navier-Stokes Equations: Application to Unsteady Wake Flow Dynamics. arXiv 2018, arXiv:1710.09099v3. [Google Scholar]
- Hopfield, J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [Green Version]
- Elman, J. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Kosko, B. Fuzzy Systems as Universal Approximators. In Proceedings of the IEEE International Conference on Fuzzy Systems, San Diego, CA, USA, 8–12 March 1992; pp. 1153–1162. [Google Scholar]
- Castro, J. Fuzzy Logic Controllers are Universal Approximators. IEEE Trans. SMC 1995, 25, 629–635. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organized Formation of Topologically Correct Feature Maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Sekaj, I.; Veselý, V. Robust Output Feedback Controller Design: Genetic Algorithm Approach. IMA J. Math. Control Inf. 2005, 22, 257–265. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Kinnenbrock, W. Accelerating the Standard Backpropagation Method Using a Genetic Approach. Neurocomputing 1994, 6, 583–588. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Dantzig, G. Origins of the Simplex Method (TECHNICAL REPORT SOL 87-5); Systems Optimization Laboratory, Department of Operations Research, Stanford University: Stanford, CA, USA, 1987. [Google Scholar]
- Nelder, J.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Lagarias, J.; Reeds, J.; Wright, M.; Wright, P. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef] [Green Version]
- Galántai, A. A convergence analysis of the Nelder-Mead simplex method. Acta Polytech. Hung. 2021, 18, 93–105. [Google Scholar] [CrossRef]
- Potter, M.; Jong, K. A cooperative coevolutionary approach to function optimization. In Proceedings of the International Conference on Evolutionary Computati on the Third Conference on Parallel Problem Solving from Nature—PPSN III, Jerusalem, Israel, 9–14 October 1994. [Google Scholar]
- Nishida, K.; Yamauchi, K. Detecting concept drift using statistical testing. In Proceedings of the 10th International Conference, (DS’07), Sendai, Japan, 1–4 October 2007; Volume 4755, pp. 264–269. [Google Scholar]
- Barros, R.; Santos, S. A large-scale comparison of concept drift detectors. Inf. Sci. 2018, 451–452, 348–370. [Google Scholar] [CrossRef]
- Baranyi, P.; Szeidl, L.; Várlaki, P.; Yam, Y. Definition of the HOSVD-based canonical form of polytopic dynamic models. In Proceedings of the 3rd International Conference on Mechatronics (ICM 2006), Budapest, Hungary, 3–5 July 2006; pp. 660–665. [Google Scholar]
- Baranyi, P.; Szeidl, L.; Várlaki, P.; Yam, Y. Numerical reconstruction of the HOSVD-based canonical form of polytopic dynamic models. In Proceedings of the 10th International Conference on Intelligent Engineering Systems, London, UK, 26–28 June 2006; pp. 196–201. [Google Scholar]
- Golub, G.; Kahan, W. Calculating the singular values and pseudoinverse of a matrix. SIAM J. Numer. Anal. 1965, 2, 205–224. [Google Scholar]
- Lathauwer, L.; Moor, B.; Vandewalle, J. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef] [Green Version]
- Colaneri, P. Analysis and Control of Linear Switched Systems (Lecture Notes); Politecnico di Milano: Milan, Italy, 2009. [Google Scholar]
- Horváth, Z.; Edelmayer, A. Robust Model-Based Detection of Faults in the Air Path of Diesel Engines. Acta Univ. Sapientiae Electr. Mech. Eng. 2015, 7, 5–22. [Google Scholar]
- Eigner, G. Novel LPV-based Control Approach for Nonlinear Physiological Systems. Acta Polytech. Hung. 2017, 14, 45–61. [Google Scholar]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Lapicque, L. Recherches quantitatives sur l’excitation électrique des nerfs traitée comme une polarisation (Quantitative Research on the Electric Excitation of Nerves by Polarisation). J. Physiol. Pathol. 1907, 9, 620–635. [Google Scholar]
- Hodgkin, A.; Huxley, A. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Zhabotinsky, A. Periodic processes of malonic acid oxidation in a liquid phase. Biophysika 1964, 9, 306–311. [Google Scholar]
- Field, R.; Koros, E.; Noyes, R. Oscillations in Chemical Systems. II. Thorough Analysis of Temporal Oscillation in the Bromate-Cerium-Malonic Acid System. J. Am. Chem. Soc. 1972, 94, 8649–8664. [Google Scholar] [CrossRef]
- Tyson, J. The Belousov-Zhabotinskii Reaction—Lecture Notes in Biomathematics 10; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics; John Wiley & Sons: Chichester, UK, 1998. [Google Scholar]
- Matsumoto, T. A Chaotic Attractor from Chua’s Circuit. IEEE Trans. Circuits Syst. 1984, CAS-31, 1055–1058. [Google Scholar] [CrossRef]
- Lorenz, E. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Mickens, R. Mathematical and numerical study of the Duffing-harmonic oscillator. J. Sound Vib. 2001, 244, 563–567. [Google Scholar] [CrossRef]
- van der Pol, B. Forced oscillations in a circuit with non-linear resistance (reception with reactive triode). Lond. Edinb. Dublin Philos. Mag. J. Sci. 1927, 7, 65–80. [Google Scholar] [CrossRef]
- Csanádi, B.; Galambos, P.; Tar, J.; Györök, G.; Serester, A. A Novel, Abstract Rotation-based Fixed Point Transformation in Adaptive Control. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC2018), Miyazaki, Japan, 7–10 October 2018; pp. 2577–2582. [Google Scholar]
- Rodrigues, O. Des lois géometriques qui regissent les déplacements d’ un systéme solide dans l’ espace, et de la variation des coordonnées provenant de ces déplacement considérées indépendent des causes qui peuvent les produire (Geometric laws which govern the displacements of a solid system in space: And the variation of the coordinates coming from these displacements considered independently of the causes which can produce them). J. Math. Pures Appl. 1840, 5, 380–440. [Google Scholar]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V. Julia. Available online: https://julialang.org (accessed on 5 May 2019).
- Lantos, B.; Bodó, Z. High Level Kinematic and Low Level Nonlinear Dynamic Control of Unmanned Ground Vehicles. Acta Polytech. Hung. 2019, 16, 97–117. [Google Scholar]
- Weierstraß, K. Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen, (On single variable continuous functions that nowhere are differentiable). In Königlich Preussichen Akademie der Wissenschaften, Mathematische Werke von Karl Weierstrass; Mayer & Mueller: Berlin, Germany, 1895; Volume 2, pp. 71–74. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Redjimi, H.; Tar, J.K. A Simple Soft Computing Structure for Modeling and Control. Machines 2021, 9, 168. https://doi.org/10.3390/machines9080168
Redjimi H, Tar JK. A Simple Soft Computing Structure for Modeling and Control. Machines. 2021; 9(8):168. https://doi.org/10.3390/machines9080168
Chicago/Turabian StyleRedjimi, Hemza, and József Kázmér Tar. 2021. "A Simple Soft Computing Structure for Modeling and Control" Machines 9, no. 8: 168. https://doi.org/10.3390/machines9080168
APA StyleRedjimi, H., & Tar, J. K. (2021). A Simple Soft Computing Structure for Modeling and Control. Machines, 9(8), 168. https://doi.org/10.3390/machines9080168





