Abstract
This paper presents a framework for the motion planning and control of redundant manipulators with the added task of collision avoidance. The algorithms that were previously studied and tested by the authors for planar cases are here extended to full mobility redundant manipulators operating in a three-dimensional workspace. The control strategy consists of a combination of off-line path planning algorithms with on-line motion control. The path planning algorithm is used to generate trajectories able to avoid fixed obstacles detected before the robot starts to move; this is based on the potential fields method combined with a smoothing interpolation that exploits Bézier curves. The on-line motion control is designed to compensate for the motion of the obstacles and to avoid collisions along the kinematic chain of the manipulator; this is realized using a velocity control law based on the null space method for redundancy control. Furthermore, an additional term of the control law is introduced which takes into account the speed of the obstacles, as well as their position. In order to test the algorithms, a set of simulations are presented: the redundant collaborative robot KUKA LBR iiwa is controlled in different cases, where fixed or dynamic obstacles interfere with its motion. The simulated data show that the proposed method for the smoothing of the trajectory can give a reduction of the angular accelerations of the motors of the order of , with an increase of less than of the calculation time. Furthermore, the dependence of the on-line control law on the speed of the obstacle can lead to reductions in the maximum speed and acceleration of the joints of approximately and , respectively, without significantly increasing the computational effort that is compatible for transferability to a real system.
1. Introduction
Nowadays, robots are increasingly asked to work in unstructured environments. In many cases, they are supported by sensor-based safety systems, avoiding fences that typically isolate the cell workspace within the workshop. Moreover, the trend toward collaborative robotics portends to a workshop layout where robots and humans share the workspace and collaborate in many operations, in a dynamical and unforeseeable scenario. In addition to dedicated hardware and design principles, collaborative robotics implies specific control strategies to ensure safety [1,2]. In this sense, collision avoidance control techniques represent a powerful means of improving the safety and flexibility of robots. A number of papers are available in the literature on path planning and obstacle avoidance for mobile robots [3], which is a very common problem. A more complex problem is the collision avoidance for industrial manipulators, which suffer from the limitations of the workspace and problems of singularity. In this case, redundant manipulators offer greater dexterity than traditional manipulators, which aids in the development of task-oriented control strategies taking advantage of the additional degrees of freedom. Thus, redundant manipulators are the best candidates for high dexterity tasks with collision avoidance capability [4,5]. Moreover, redundancy can also be exploited with standard manipulators if some of the degrees of freedom of the end-effector, e.g., the orientation angles, can be kept free during motion.
Thus, an overall control strategy for a manipulator working in a dynamic environment can be conceived as the combination of:
- An off-line path planning algorithm, which plans the trajectory of the robot’s end-effector taking into account the possible presence of disturbing obstacles, modifying the path based on the positions of the obstacles before the motion starts;
- An on-line motion control algorithm, which controls in real-time the robot compensating for obstacles that are moving, or new obstacles entering the workspace;
- A redundancy control strategy that exploits the dexterity of the manipulator to avoid collisions between obstacles and the kinematic chain of the manipulator;
- A robust technique for the avoidance of singular configurations during motion.
Dealing with motion planning for obstacle avoidance, several methods are available in the literature [6], such as Rapidly-exploring Random Trees (RRT) [7,8], grid-based algorithms [9,10] or Batch Informed Trees (BIT) and Model Predictive Control (MPC) [11]. A very common approach consists in defining artificial potential fields, which drive the robot to the target inside the workspace [12,13,14]. The result of the potential fields is a set of forces, attractive toward the goal and repulsive from the obstacle regions. Typically, such forces are associated with velocities applied to the end-effector of the manipulator; then, the trajectory can be obtained by numerical integration.
A further problem in optimal path planning for automation and robotics is the generation of smooth trajectories: an optimal algorithm for trajectory generation must guarantee smoothness in terms of position and velocity to be implemented in the controller of a real system. The use of smooth curves, e.g., the Bézier curves, can help solve this problem, as proposed by the authors in [15]: several examples of applications can be found in different fields, such as automated vehicle guidance [16,17], aerial autonomous vehicles [18] or spherical parallel manipulators [19,20].
The same principle of repulsive velocities generated by obstacles can be used to avoid collisions between obstacles and control points along the kinematic chain of the manipulator: in addition to the motion imposed to end-effector, a repulsive velocity vector can be applied to the point of the robot that is closer to one of the obstacles, adding a task to the control system [21,22]. Such an approach is typically applied to redundant manipulators [23,24], where additional tasks can be assigned maintaining the trajectory of the end-effector. Furthermore, the entity of the repulsive velocity can be thought in general as a function of several parameters besides obstacle/robot positions, e.g., the relative speed [25] or other energetic criteria [26].
The authors studied this kind of approach in [15] for a planar case; in addition to the standard method, a modified repulsive velocity was introduced, improving the capability of the algorithm to compensate for dynamic obstacles.
Inspired by the background described above and using of previous research conducted by the authors for the planar case, this study presents an extension of the proposed algorithms to a three-dimensional workspace and redundant manipulators with full mobility. In addition, a strategy based on the least-square damped method for the inversion of the Jacobian matrices is introduced in order to avoid passages through points which are too close to singular configurations. Finally, once the validity of algorithms is verified, an estimation of the computational time required to execute the path planning and motion control loop is given, proving that the proposed control technique is able to be implemented in a real system.
The rest of the paper is organized as follows: the algorithms for off-line path planning and on-line motion control are described in Section 2 and Section 3, respectively; results obtained by a series of simulations are described in Section 4; a discussion on the computational effort required on the issues related to transferability of the control law to a real system is presented in Section 5, whereas conclusions are drawn in Section 6.
In summary, this paper presents a general framework for path planning and motion control with collision avoidance for a redundant 7-DOF manipulator in a dynamically varying workspace. The algorithms are fine-tuned and verified by means of simulations, which also provide insight into the computational effort required, in line with the requirements of industrial robot controllers.
2. Off-Line Path Planning
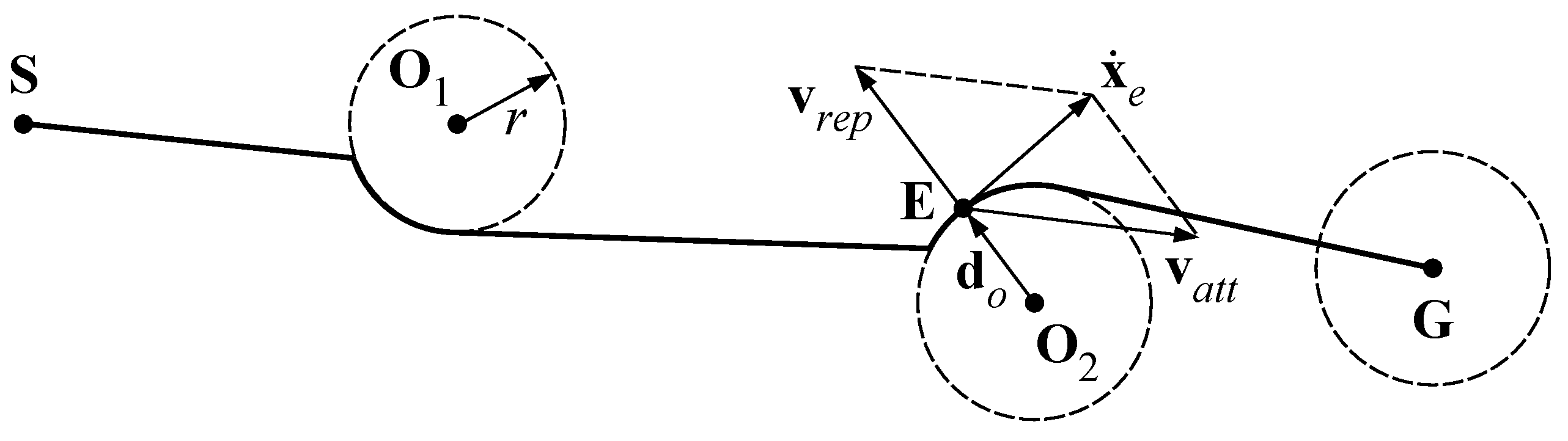
The trajectory planning algorithm used to define the motion of the end-effector, proposed by the authors in [15,27], is extended in the present paper to the 3D case. The generated path allows to reach the target position and to avoid the obstacles that are inside the workspace before the motion of the robot starts. The algorithm is based on the definition of potential fields that generate repulsive and attractive velocity components, defined and , respectively, which drive the end-effector following the minimum potential path towards the goal. As shown in Figure 1, is the initial position of the end-effector, is the goal and are the obstacles, with their region of influence outlined by their radius . Moreover: and . Based on [28], Equation (1) defines attractive and repulsive velocities as:
where the symbol ∇ indicates the gradient operator. Norms of velocities must be set based on the type of application; as an example, values used in the simulations presented in the following of this paper are and .
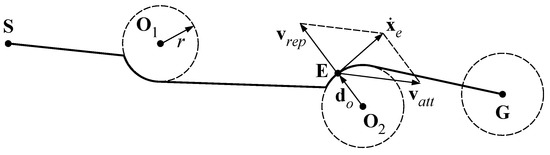
Figure 1.
Potential fields for trajectory planning.
The end-effector trajectory can be found by numerical integration of the resulting velocity:
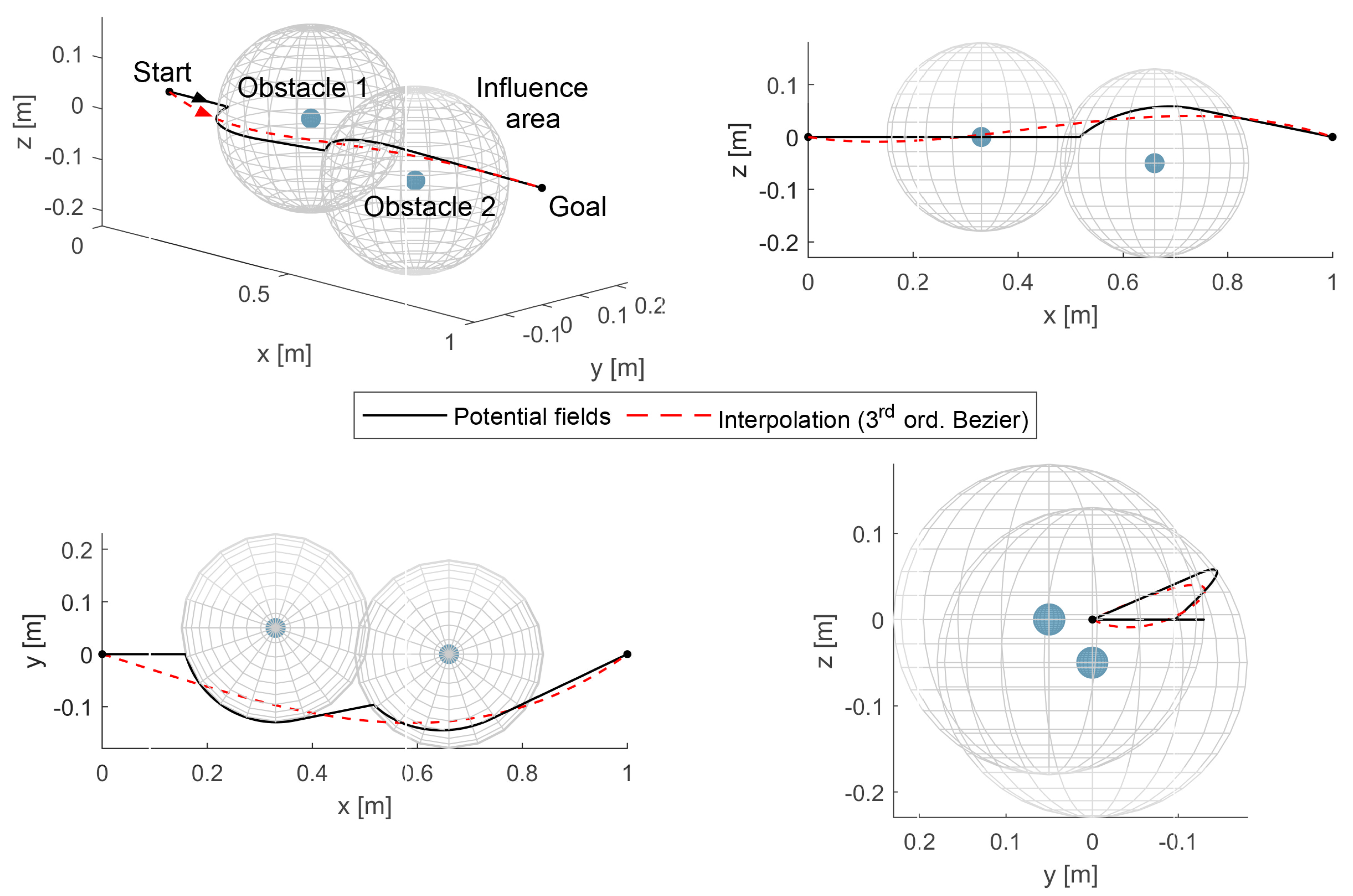
As a consequence, the end-effector position is iteratively updated by Equation (2) in accordance with the velocity imposed at each time step. The procedure ends when the distance between the end-effector and the target is lower than a predefined threshold, which is set at for the examples shown in this paper. Then, an interpolation with a fifth order polynomial law is used to generate a timed motion law over the path previously found. Nevertheless, the trajectory resulting from Equations (1) and (2) is typically characterized by short-radius curves and sharp corners that may originate high accelerations and vibration problems, as shown in the example of Figure 2: here, two obstacles are interposed between the start and goal points preventing the motion over the ideal linear trajectory; the planning algorithm generates the black curve that remains outside the region of influence of the obstacles in all its points, but presents fast changes of directions in two points, i.e., where the trajectory meets the influence spheres of the obstacles. An interpolation procedure that exploits a smoother type of curve, e.g., a Bézier curve, can be used to solve the problem. In more detail, given points , where n is the power of the Bézier curve, the latter is defined as a parametric function of the variable s as:
without any loss of generality, let’s consider a third order Bézier curve:
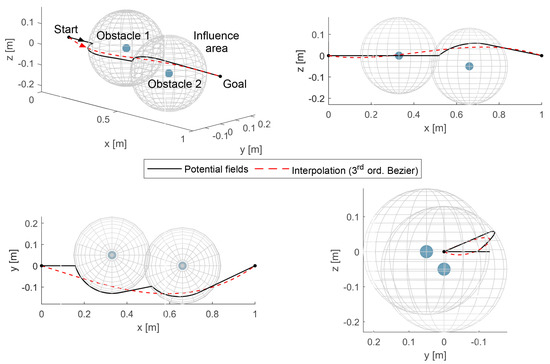
Figure 2.
Example of path planning in 3D space with two obstacles.
The points and being coincident with the starting and goal points, respectively, the fitting procedure seeks for points and generating the curve that best approximates the original one with a least-square metric. Thus, an optimization problem must be solved in order to find the six variables defining points and which minimize the quadratic error between the original path and the Bézier curve. A closed-form solution to the problem can be found manipulating Equation (4) as follows:
If the curvilinear abscissa s is discretized in m samples, the trajectory becomes a set of m points. Thus, Equation (6) can be written m times for the points , assuming the form:
where:
A closed-form solution for the optimal set of coefficients can be easily found manipulating Equation (7) and substituting the matrix with the analogous matrix that is built with the points belonging to the trajectory found with the potential field algorithm:
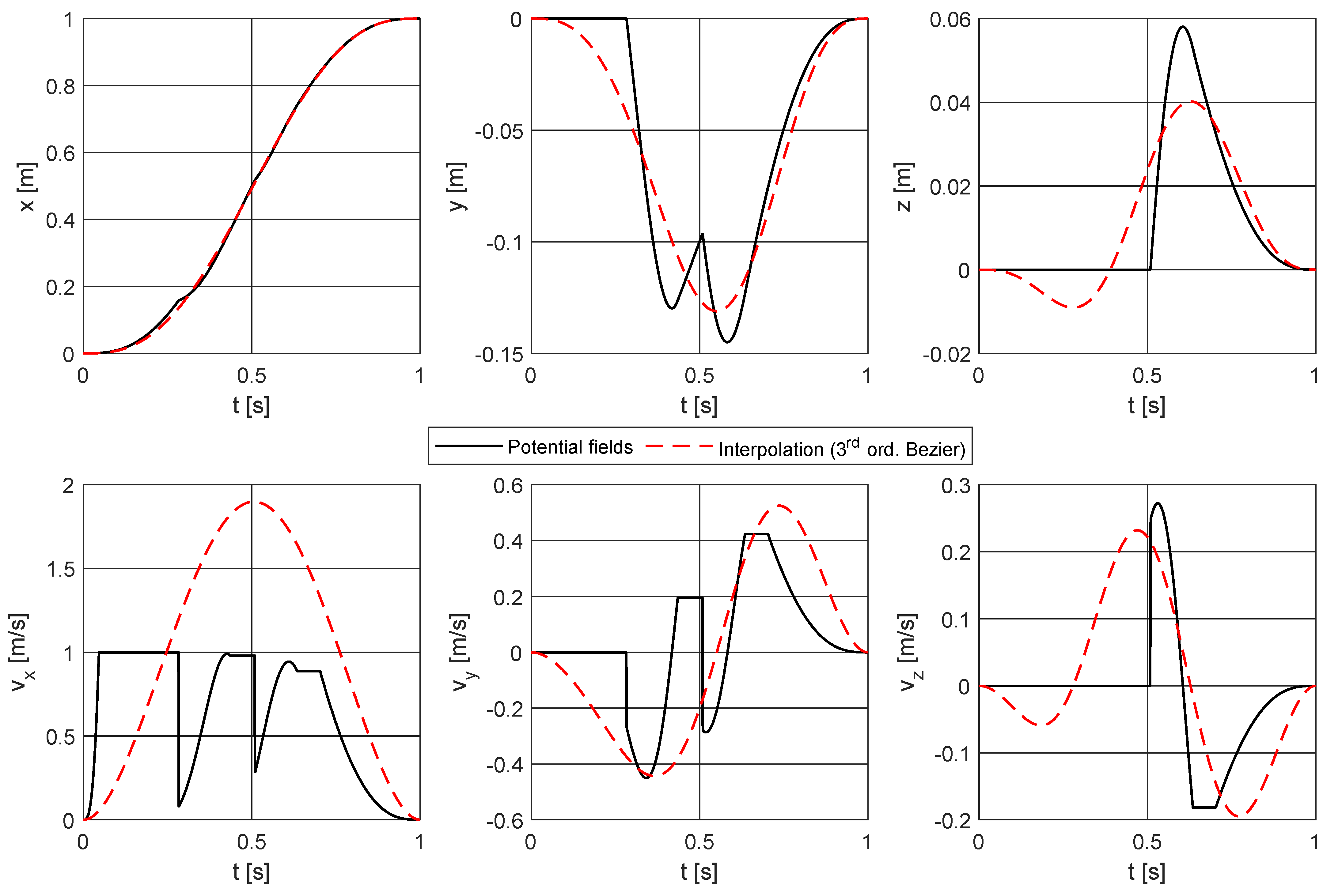
where † represents the pseudo-inverse operator according to the Moore-Penrose definition, which intrinsically provides the coefficients of the curve that best fits the original trajectory by minimizing the least squares error. An example is given in Figure 2 in order to show the effect of the smoothing procedure: given the start and goal points and two obstacles preventing from the linear trajectory, the potential fields method described by Equations (1) and (2) gives the path plotted in black, whereas the interpolation procedure described by Equations (3)–(10) returns the Bézier curve plotted in red. A deeper comparison is given by Figure 3, where the Cartesian components of position and velocity of the end-effector are plotted versus time: the path directly obtained by the potential fields algorithm (black plot) presents cusps and discontinuities in the position and velocity profiles, respectively, whereas the trajectory related to the Bézier curve (red plot) is smooth both in position and velocity; thus, it is feasible for it to be assigned to a real manipulator. Bézier curves of higher order have been also tested, but they suffer from too sharp curvatures and high computational times; thus, they are not suitable for the purpose.
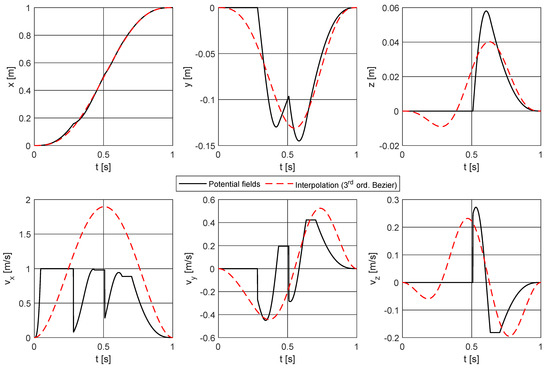
Figure 3.
Comparison between position and velocity profiles of potential fields trajectory and smoothed trajectory related to the example of Figure 2.
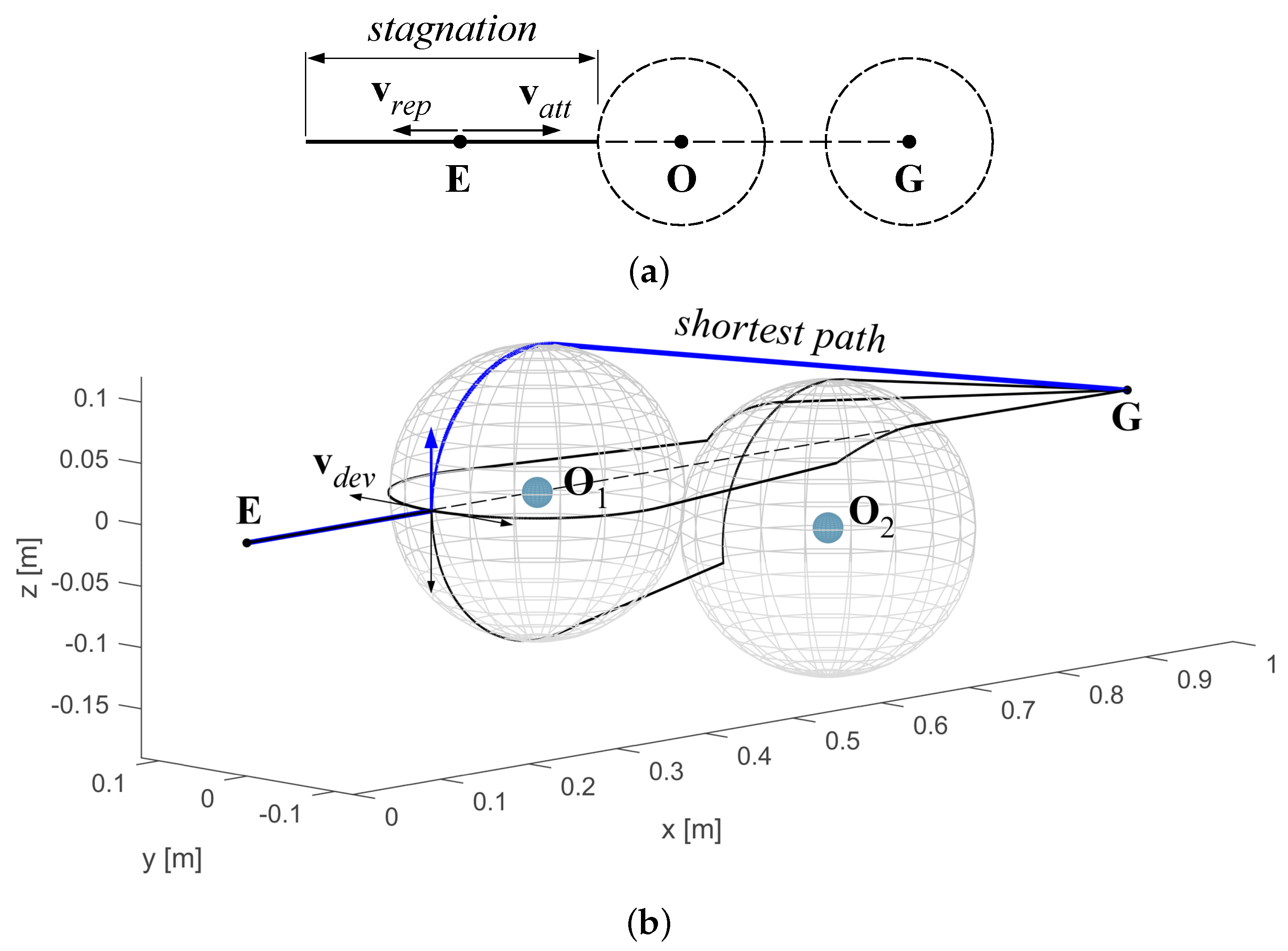
When the potential fields approach is used in path planning a particular condition must be taken into account: as shown in Figure 4a in a simplified planar scheme, when an obstacle lies exactly on the segment joining the end-effector to the goal point, the attractive and repulsive velocities act in contrast to each other and the end-effector rebounds from the obstacle along such segment, without accomplishing the task. The proposed algorithm overcomes the problem as follows: when the aligning condition between , and is verified, an infinitesimal component of velocity orthogonal to is added in order to force the trajectory to exit from the stagnation; among infinite directions that can be assigned to orthogonal to , a subset of four of them is selected (aligned with Cartesian axes, with positive or negative directions), whereas its magnitude is constant and predefined. The effect of the deviatoric velocity is to bring the end-effector out of the stagnation line. Obviously, for each one of the selected directions the resulting path is different. Thus, the shortest one is considered for further steps. The example shown in Figure 4b gives a three-dimensional representation of the problem and shows the trajectories obtained with each one of the four different directions assigned to ; among them the shorted one (blue curve) is chosen.
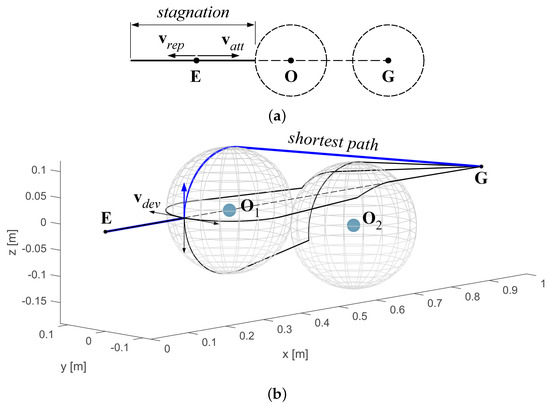
Figure 4.
(a) Alignment condition between end-effector, obstacle and goal in a simplified 2D representation; (b) example of trajectories generated by different directions of in the 3D space.
All the issues discussed above in this section concerned the planning of the Cartesian position of the end-effector of the manipulator, that is, the generation of the motion laws . A different strategy must be defined to generate a smooth transition between the initial and final orientation of the end-effector: if the orientation at the target point is different from the initial one, a linear transition with the same timing law used for the position is defined for the three parameters used for the representation, e.g., the Euler angles.
3. On-Line Motion Control
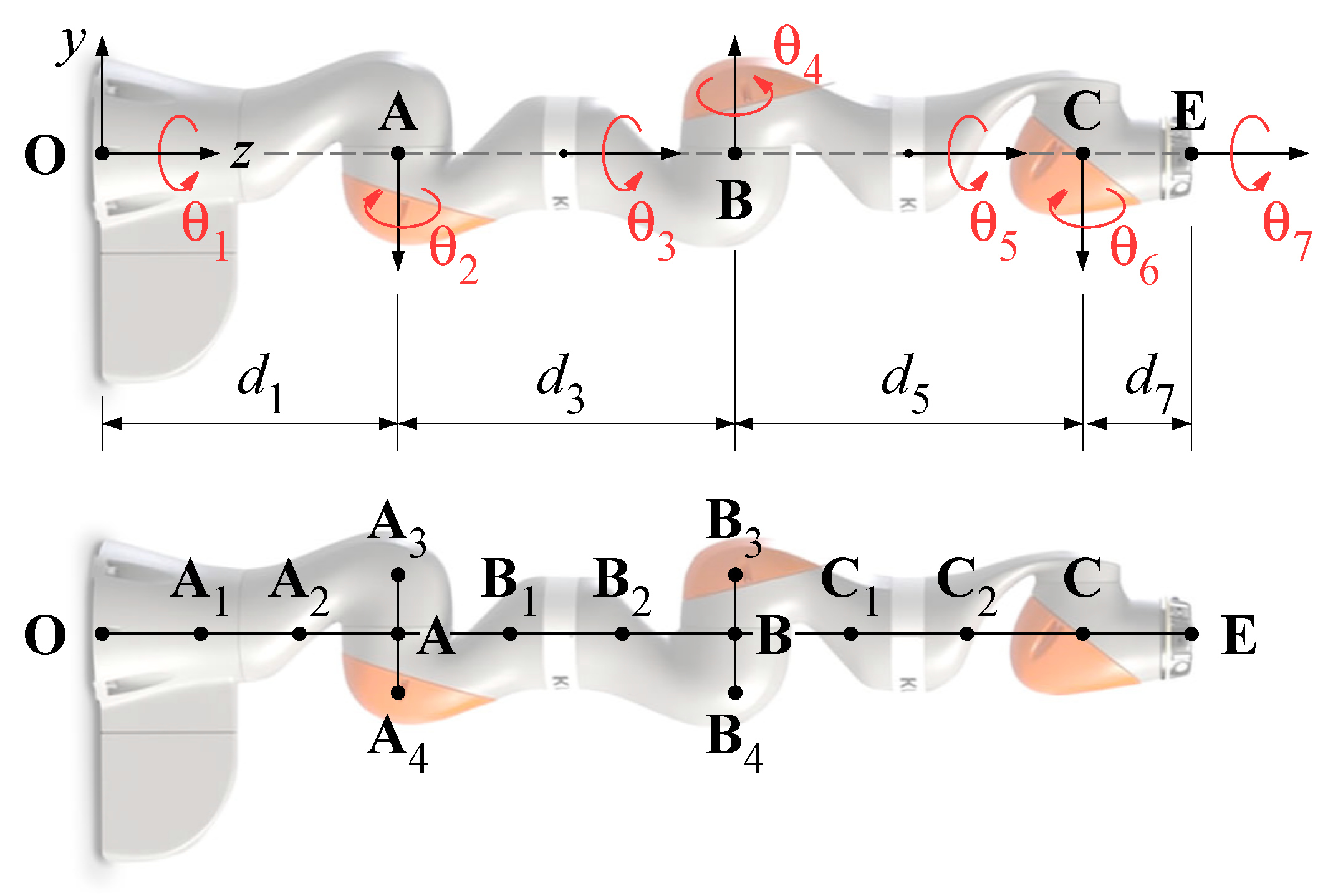
Starting from the results obtained by the authors in [15], the mentioned algorithms are implemented in the present work for a redundant manipulator with full mobility, i.e., the KUKA LBR iiwa 14 R820 robot. The kinematic scheme of the manipulator is shown in Figure 5. The pose of the end-effector in the Cartesian space is defined by the vector , where the last three components are the Euler angles according to the convention. The seven rotations related to the revolute joints of the serial kinematic chain form the joint space position vector, defined as . Thus, the kinematic chain of the manipulator has a redundant degree of freedom with respect to the task. Besides the end-effector , a total of 13 control points () belonging to the kinematic chain characterizes the manipulator, as shown in the bottom picture of Figure 5.
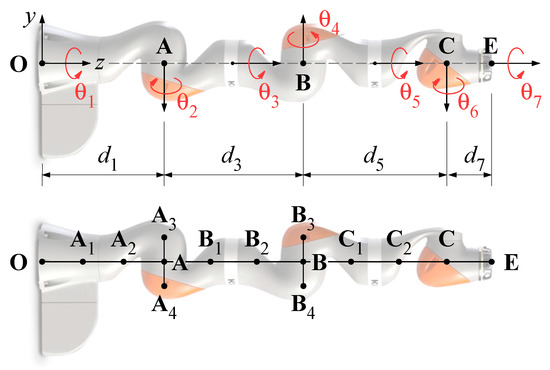
Figure 5.
Kinematic chain (top) and control points (bottom) for the KUKA LBR iiwa robot.
The forward kinematics of the manipulator can be described by:
In the previous equations represents the expression of the position forward kinematics and is the analytic Jacobian composed by the position and orientation Jacobian matrices and , each one of dimensions ; the velocity vector is composed by the linear velocity and the angular velocity , whose expressions, accordingly to the Euler angles representation, are given by:
Due to redundancy, the inverse position kinematics problem is not uniquely defined, but it can be workedout by the following differential formulation:
The terms of Equation (14) are defined as follows: is the joint null space velocity, whose effect is to generate internal motions leaving the pose of end-effector unchanged; = is the pseudoinverse of the Jacobian matrix ; = is the orthogonal projection into the null space of .
The inverse kinematic problem formulated in Equation (14) suffers from numerical problems due to the inversion of the Jacobian matrix when the manipulator is near to a singular configuration, i.e., when the singular values of tend to zero. In order to avoid singularity problems, the use of the well known damped least-square method was applied [29]. Such a method consists in the substitution of the pseudoinverse of the Jacobian by:
where represents a damping factor that confers a better numerical conditioning to the inversion problem. The value of should be a compromise between accuracy (low value) and numerical robustness (high value). An efficient way to determine is to define it as a function of the smallest singular value of :
In this way the effect of the approximation vanishes when the smallest singular valuer is greater than a threshold , where when , being and tunable parameters of the algorithm. This kind of approximation introduces a position error that must be subsequently recovered by a proportional term in the control law, as typically done in Closed-Loop Inverse Kinematics (CLIK) control laws [30].
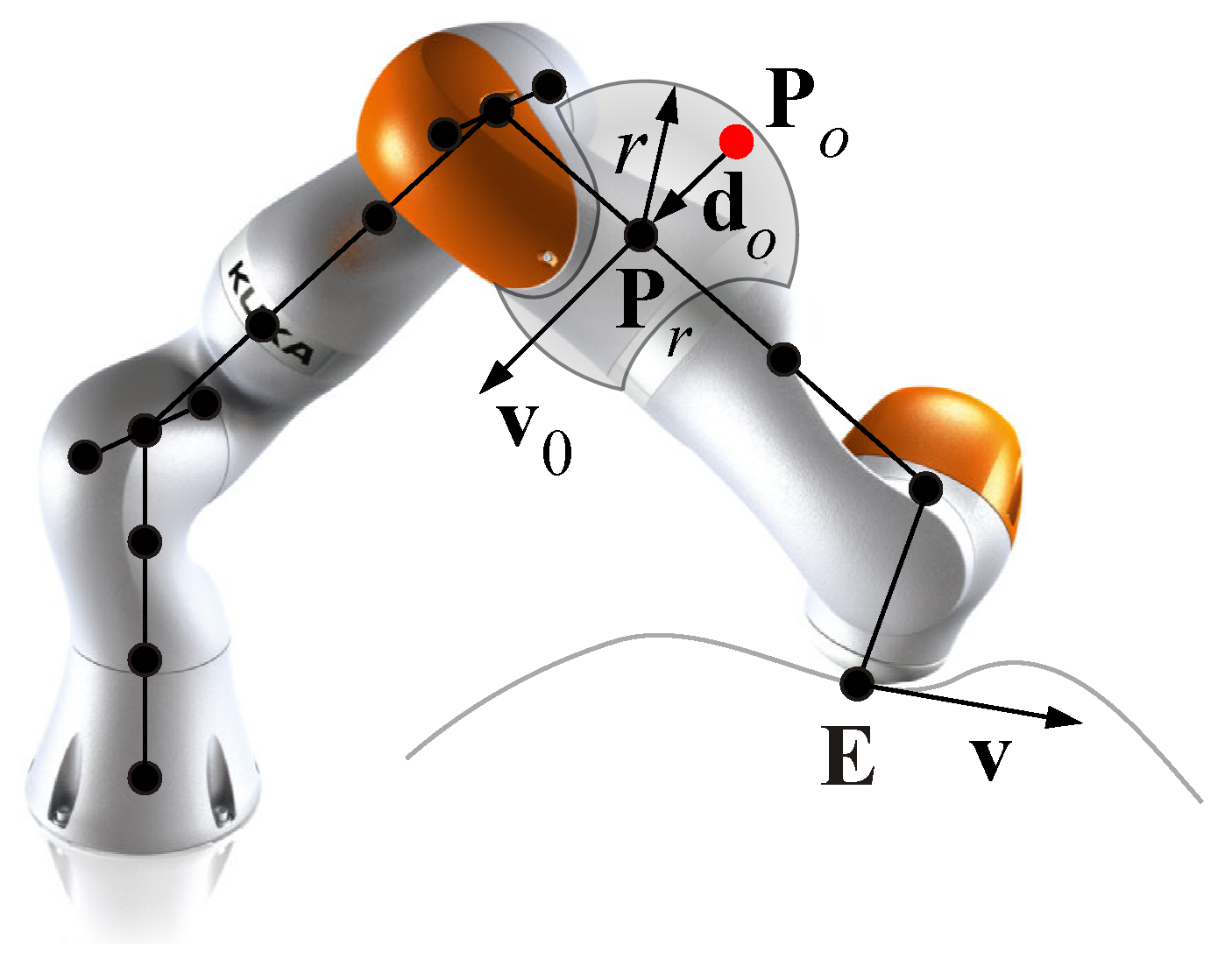
In addition to the basic control law, an obstacle avoidance strategy is introduced: inspired by the null space methods for the control of redundant manipulators [21], an additional velocity vector is assigned to the control point of the robot which is the closest to one of the obstacles within the workspace, so that the control point can move away form the obstacle, while the motion of the end-effector is not affected. In more detail, referring to the Figure 6, the couple of points and at the minimum distance is identified at each time step. The region of influence of each control point is delimited by the radius r. If at a certain time step during the motion the condition is verified, a repulsive velocity is imposed to the relative control point along the direction of . Being the manipulator characterized by one redundant DOF, only one repulsive velocity vector can be assigned at each time step, thus the point to which it is assigned may change over time with the criterion of minimum distance from one of the obstacles. Such a point can be also the end-effector: besides the velocity vector assigned by the off-line path planning in order to describe the desired trajectory, the repulsive velocity vector can be applied to , modifying its trajectory, if the position of an obstacle changes from its initial state or a new obstacle enters the workspace, interfering with the motion of . In this case, the position of the end-effector drifts from the originally planned trajectory, originating a position error analogous to the one related to the damped least-square approximation for the inversion of the Jacobian matrix. Nevertheless, the CLIK control law can be exploited to recover the error.
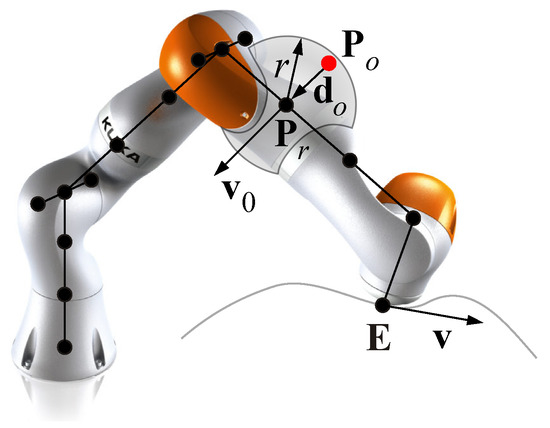
Figure 6.
Linear velocity of the end-effector and of the control point closest to the obstacle .
In terms of equations, the following expressions (18) and (19) must be imposed in order to assign the two velocity tasks above described:
where represents the upper part of the Jacobian matrix associated to the velocity of the point .
Thus, Equation (14) can be modified in [31,32]:
where , is the corrected end-effector velocity, a positive-defined gain matrix (for simplicity defined as ) and is the position error between the desired position and the actual position . The error can be represented by [29]:
where the translation error is given by the vector and the orientation error is given by the vector . The end-effector position is expressed by the position vector , whereas its orientation by the rotation matrix , with being the unit vectors of the end-effector frame.
The first term of Equation (20) guarantees the exact velocity of the end effector with minimum joints speed. The second term drives the motion of the point of the robot, satisfying the collision avoidance additional task. The choice of is a critical point of the algorithm. The proposed strategy is to change according to the distance from the obstacle. To avoid a discontinuity and give smoothness to the motion, two weighting coefficients, and , are introduced:
Thus, a nominal repulsive velocity is modulated by as a function of the distance , whereas acts with a weight that balances the effect of the homogeneous solution (related to the collision avoidance) with respect to the total.
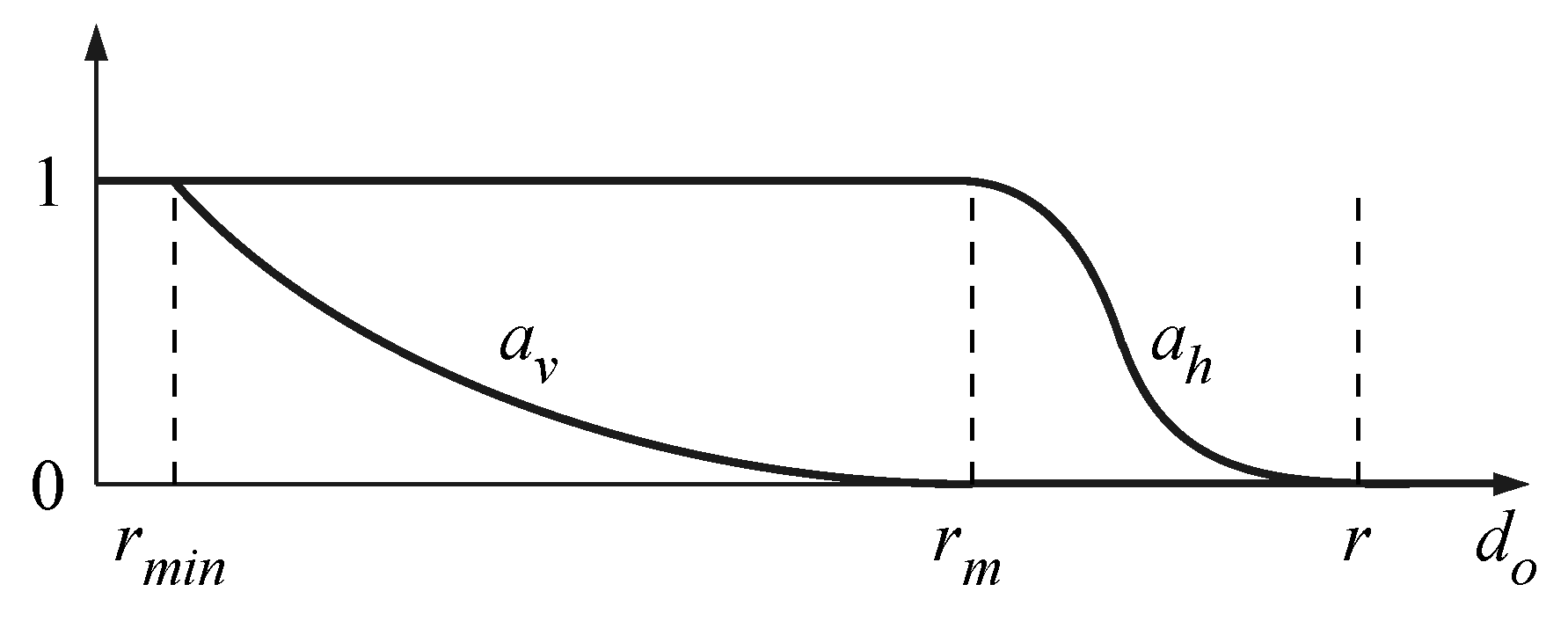
In more detail, let r be the control distance that defines the region of influence of a control point, the distance under which no action is possible, and an intermediate critical distance between and r. No influence of the obstacle is desired if , whereas the algorithm fails (the robot stops) if . Between these limits the weighting coefficients vary continuously from 0 to 1, as shown in Figure 7, accordingly to the following expressions [4]:
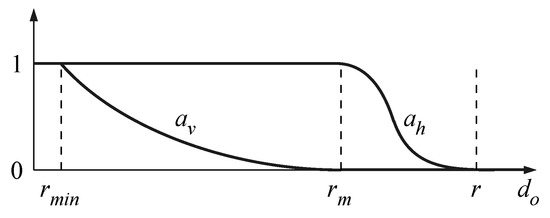
Figure 7.
Weighting coefficients and as functions of the distance .
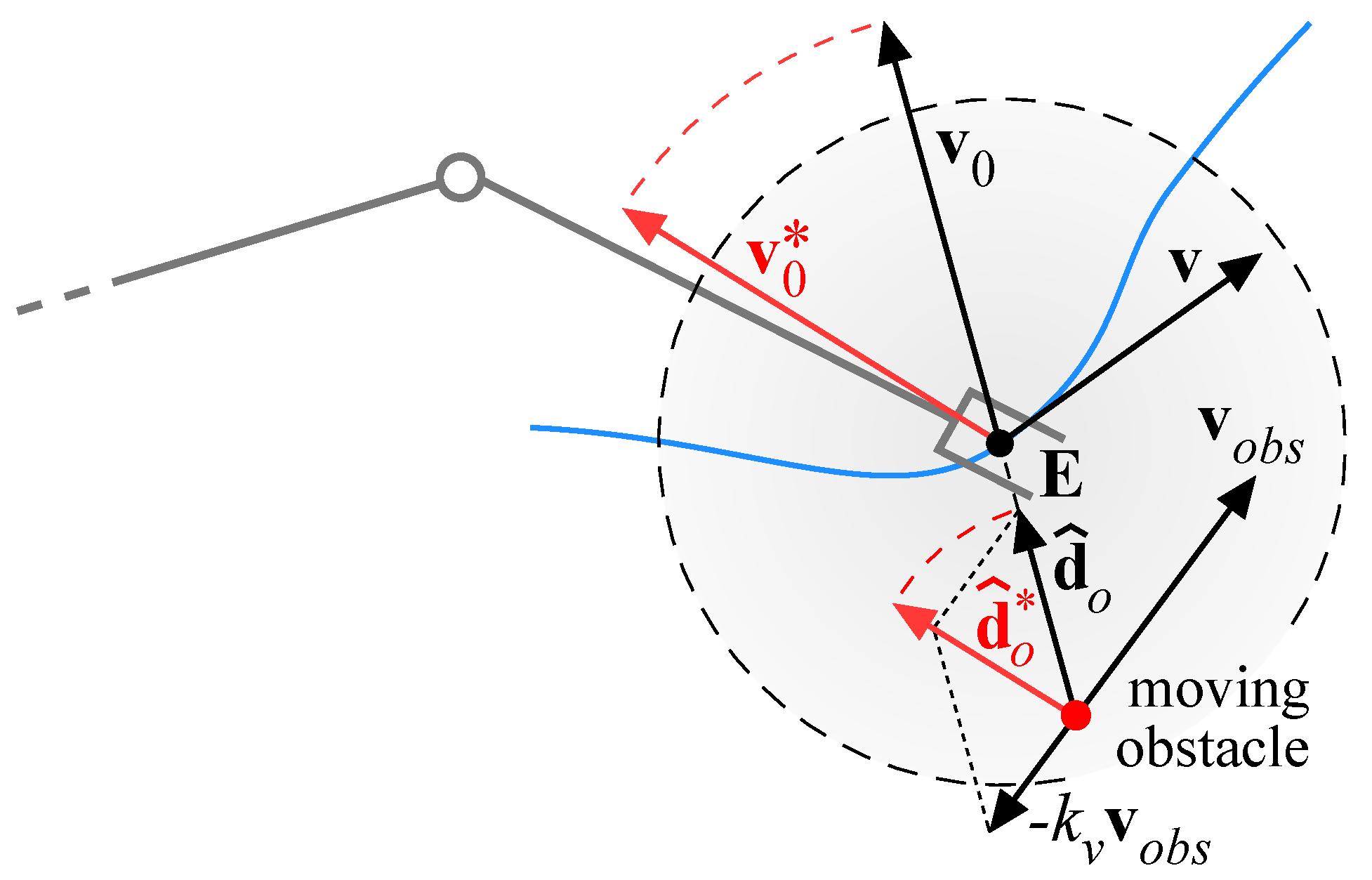
In order to improve the ability of the algorithm to avoid moving obstacles, a modification of the control law expressed by Equation (23) can be introduced changing the definition of the repulsive velocity [15]: it is reasonable that not only the position, but also the velocity of an obstacle should influence the control of the robot. As an example, if the end-effector moves toward an obstacle having an orthogonal velocity, it is preferable to modify the trajectory of the end-effector pushing it in the direction opposite to the obstacle velocity. Thus, if the end-effector is the control point closest to the obstacle, the repulsive velocity vector is modified as follows:
where, as described in Figure 8, is the obstacle velocity, is the repulsive velocity along the direction of , is a gain term and is the modified repulsive velocity applied to the end-effector in combination with the planned velocity . As a consequence, the direction of the repulsive velocity is modified, whereas its magnitude does not change; furthermore, for , the effect vanishes.
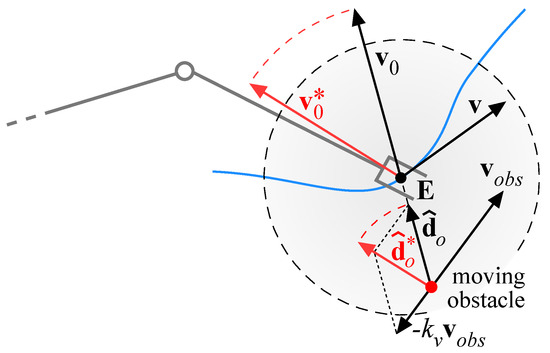
Figure 8.
Modified repulsive velocity.
4. Results
The algorithms presented in the previous sections were tested by Matlab simulations over a wide range of conditions. In this section, five different examples are shown. The first three examples help to understand the behavior of the control law in different conditions, with fixed or moving obstacles interfering with the manipulator in different points of the kinematic chain; a common set of parameters is used (Table 1) and a threshold is imposed for the angular velocity of all joints. Thus, if the control asks for a joint speed higher than , the velocity saturates avoiding dangerous situations, whereas the consequent positioning error is recovered by means of the corrective proportional term during the following part of the motion.

Table 1.
Parameters values used for simulations.
Two other examples are then discussed to demonstrate the effectiveness of the contributions introduced by the authors with respect to standard methods: Section 4.4 shows the advantages of trajectory interpolation using Bézier curves, while Section 4.5 shows how the modified repulsive velocity described in Section 3 is able to improve the response of the control in case of moving obstacles.
4.1. Example 1
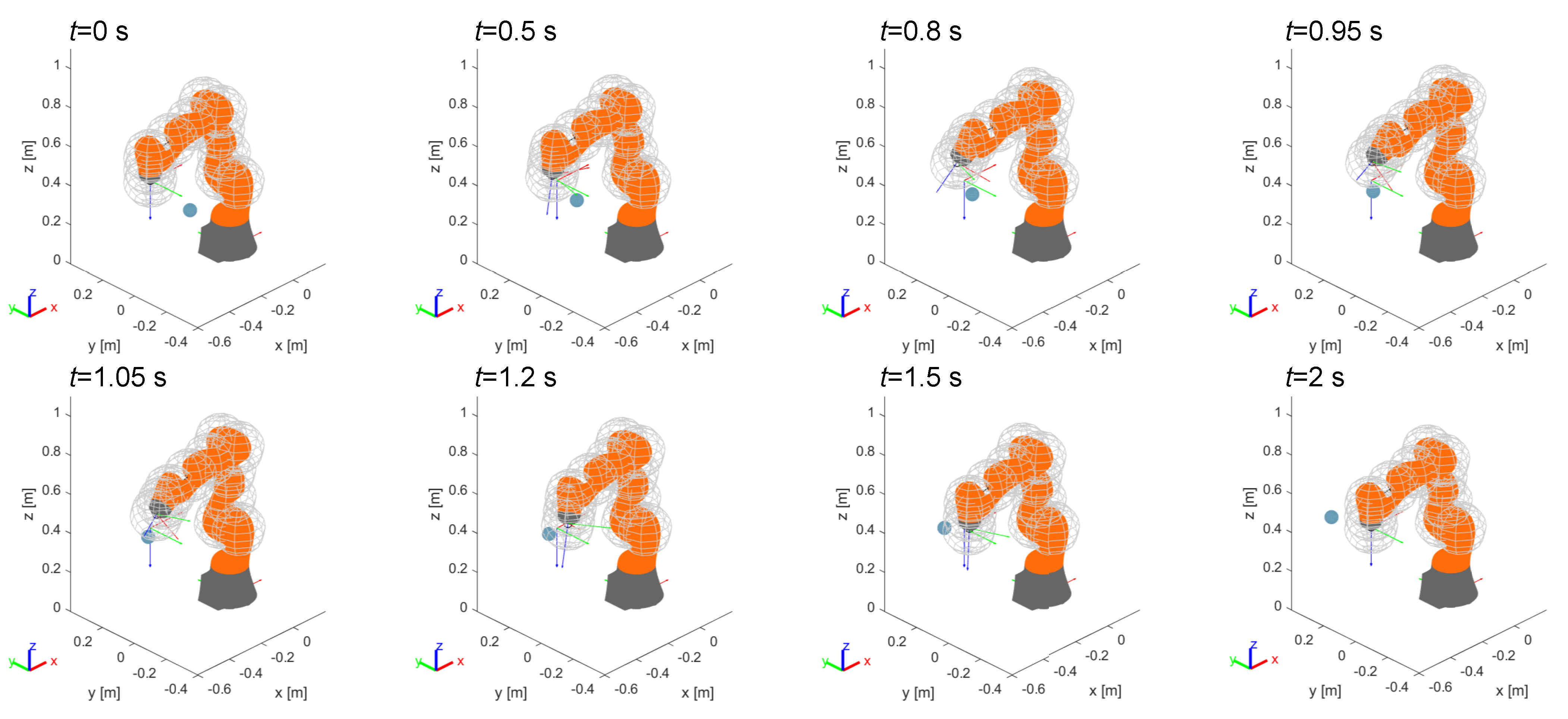
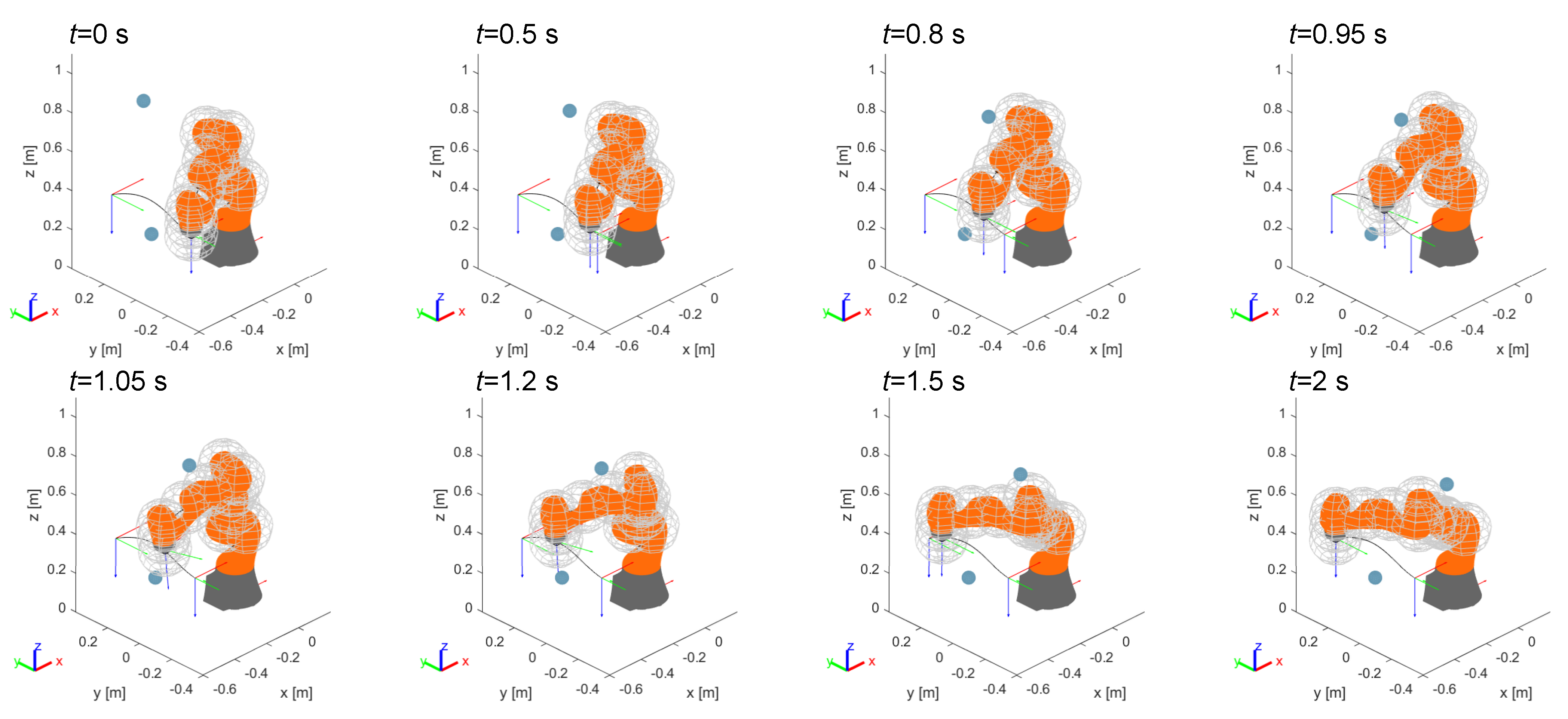
In the first example the robot is fixed while a dynamic obstacle is interfering with the end-effector. The obstacle moves linearly in the horizontal plane along y direction, with a speed of . Figure 9 shows eight steps of the motion: when the obstacle reaches the region of influence of the end-effector point of the robot the control reacts keeping the obstacle outside from the safety sphere with radius . Then, the positioning and orientation error generated by the control is suddenly recovered once the obstacle overcomes the region of influence.
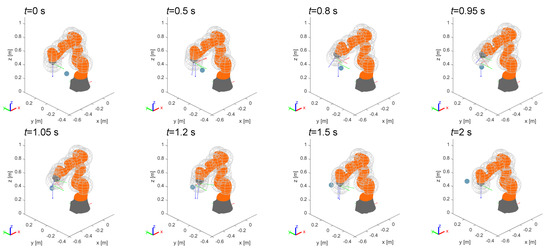
Figure 9.
Example 1: avoidance of a dynamic obstacle interfering with the end-effector in a fixed position.
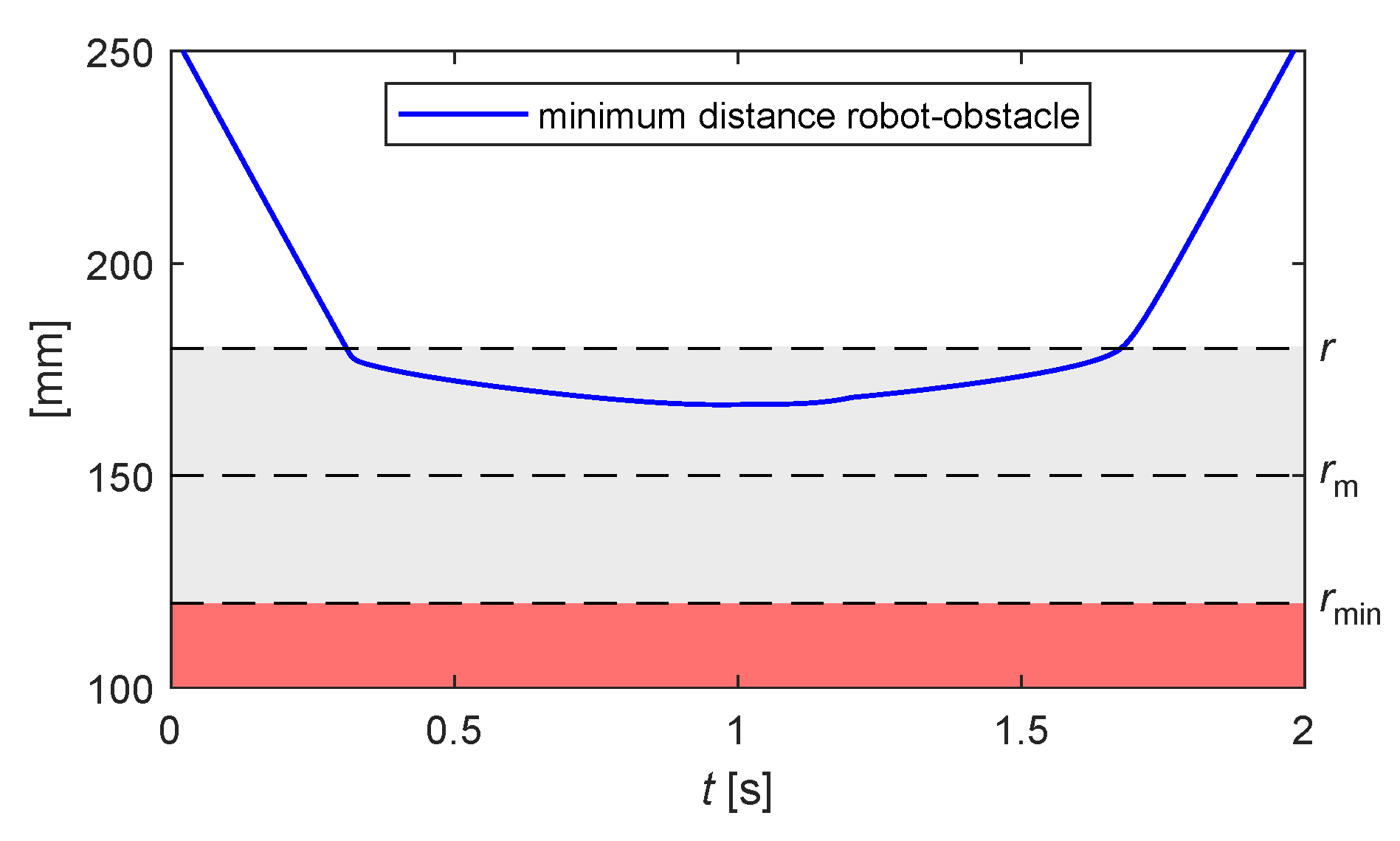
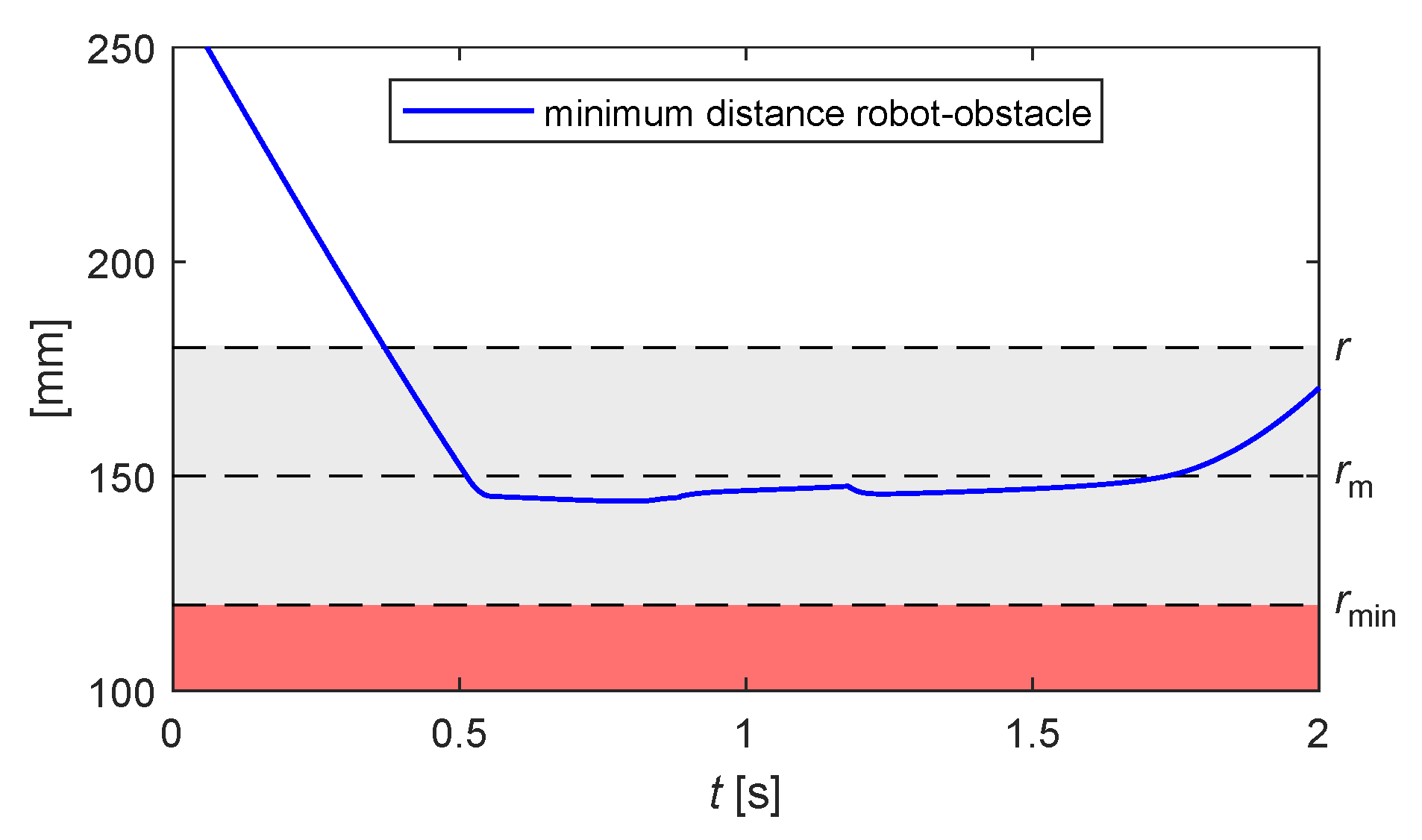
Figure 10 traces the trend over time of the minimum distance between the obstacle and the robot: it is visible how the anti-collision control is activated once the distance becomes lower than the threshold r that delimits the region of influence around the robot control point.
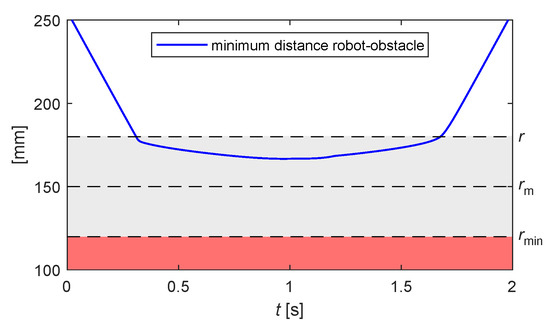
Figure 10.
Example 1: minimum distance robot-obstacle for the motion shown in Figure 9.
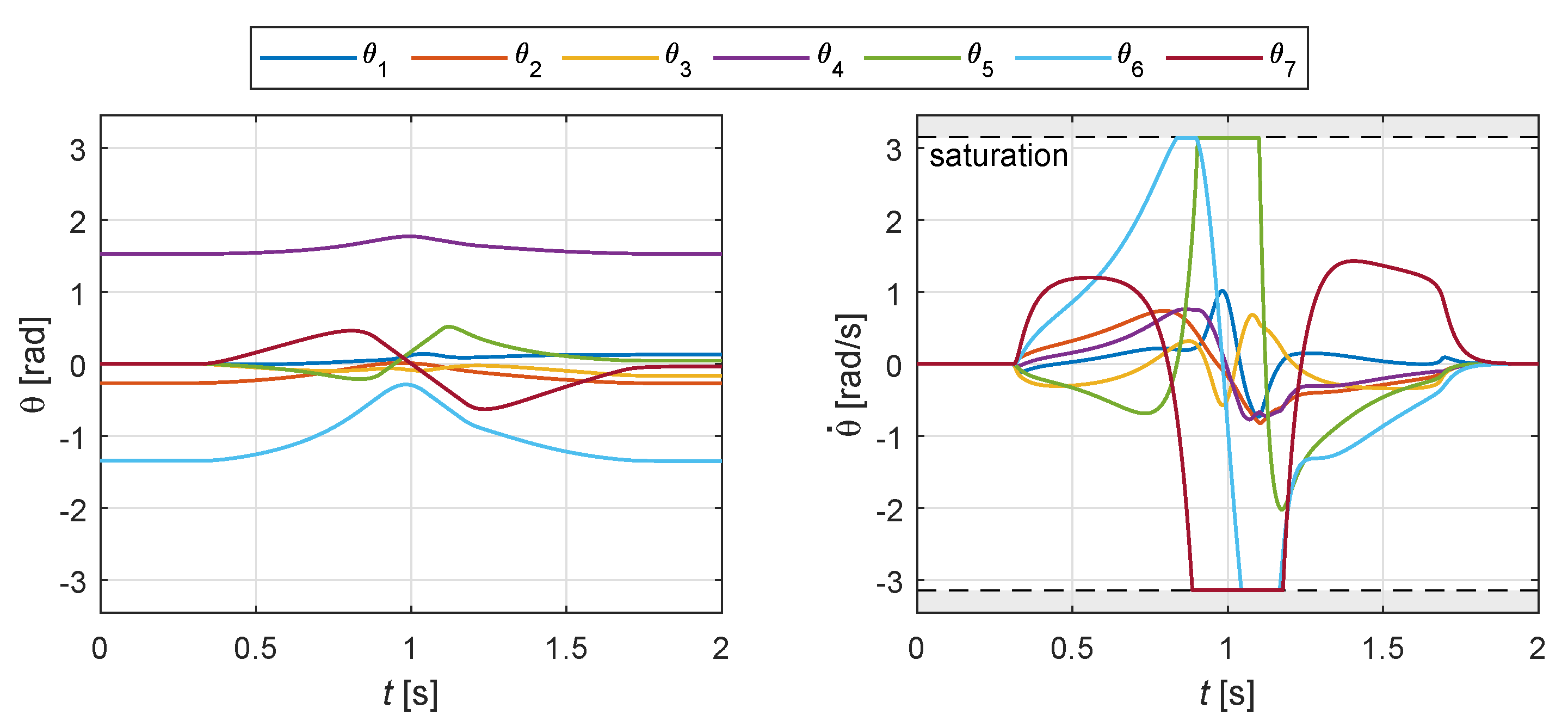
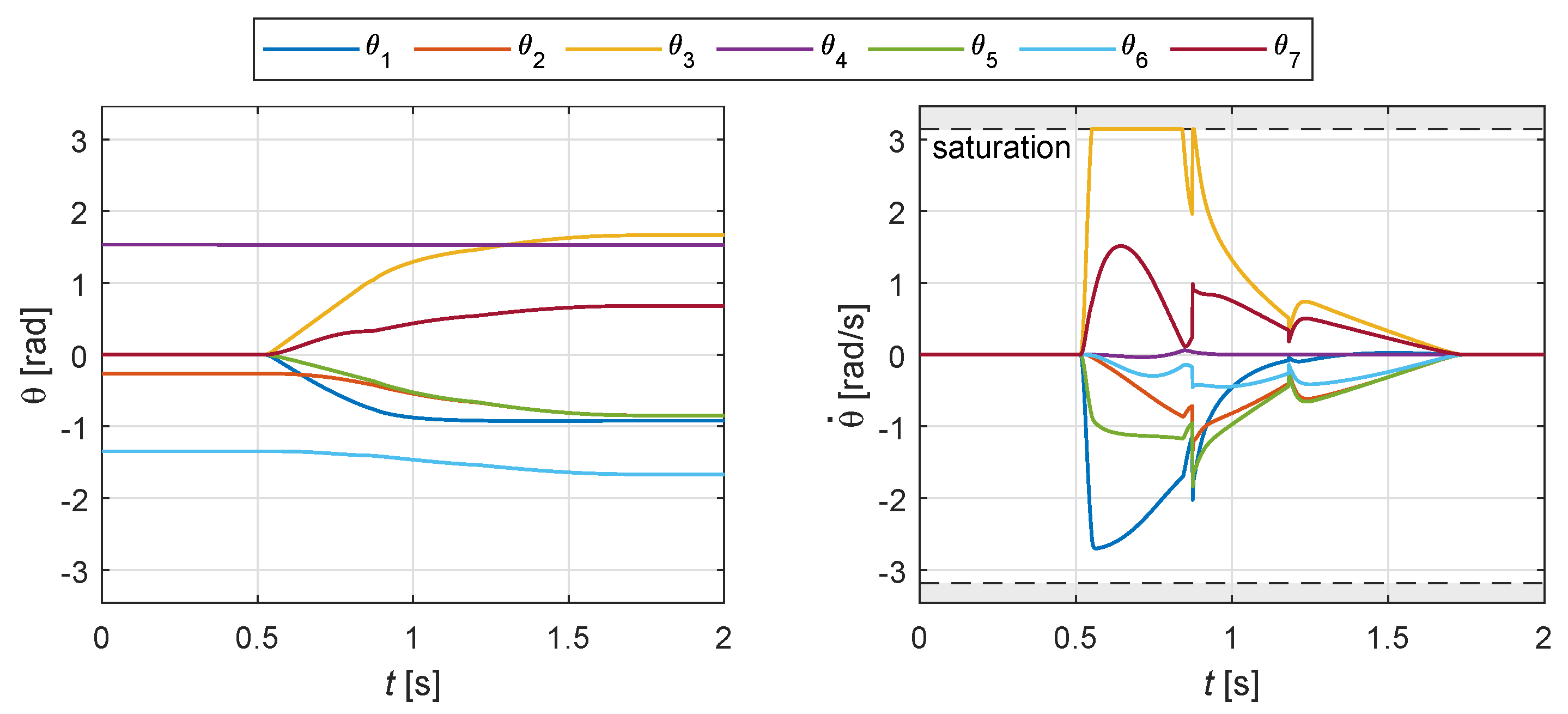
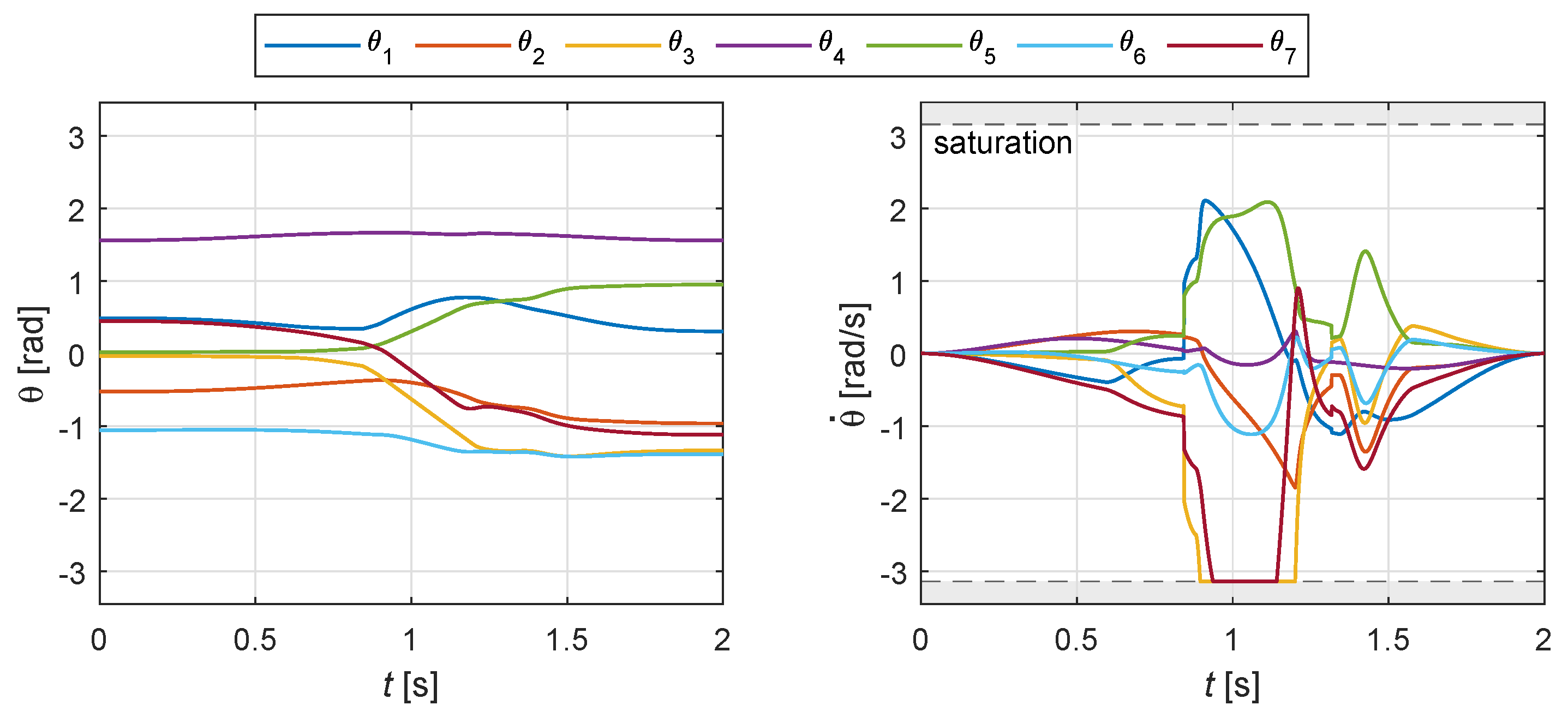
The corresponding profiles of joint rotations and speeds are shown in Figure 11: the effect of the obstacle is visible at , where the joint speed curves suddenly increase their magnitude, reaching in some case the saturation in the middle part of the motion. The effect of the redundancy of the kinematics is clearly visible looking at the final values of joint angles, which are different from the initial ones, despite the Cartesian pose of the manipulator is the same.
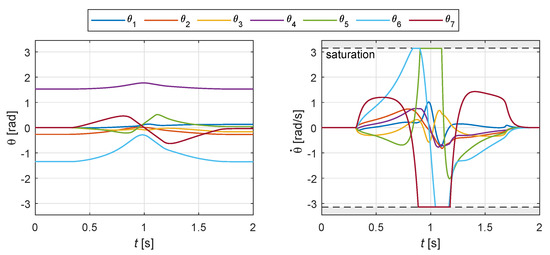
Figure 11.
Example 1: joint rotations and speeds for the motion shown in Figure 9.
4.2. Example 2
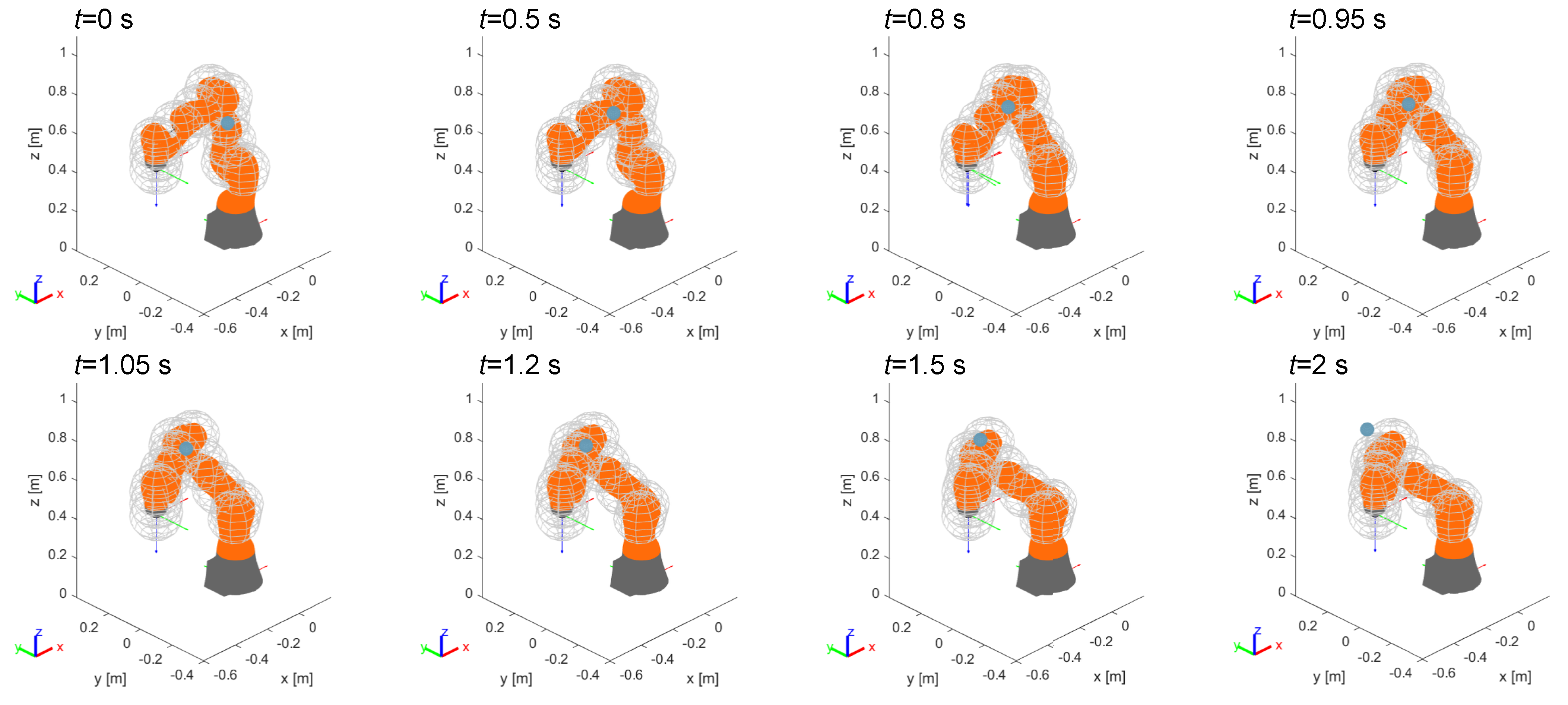
In this example the obstacle moves again linearly in the horizontal plane along y direction, with a speed of , but, differently from the previous case, the end-effector position is not altered by the obstacle. As shown in Figure 12, the risk of collision occurs in a point of the robot belonging to an intermediate link of the manipulator. Thanks to the redundancy of the kinematic chain, the control is able to reconfigure the manipulator without changing the pose of the end-effector.
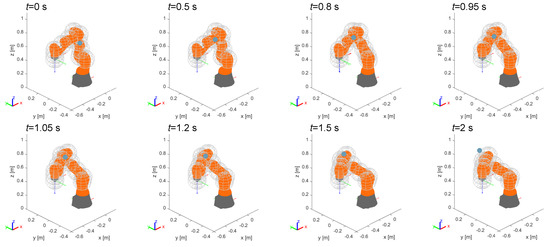
Figure 12.
Example 2: avoidance of a dynamic obstacle interfering with an internal point of the manipulator.
In this case, the plot of Figure 13 regards the distance between the obstacle and control points belonging to the 4th and 5th links of the kinematic chain of the manipulator, whereas the end-effector position does not influence the control.
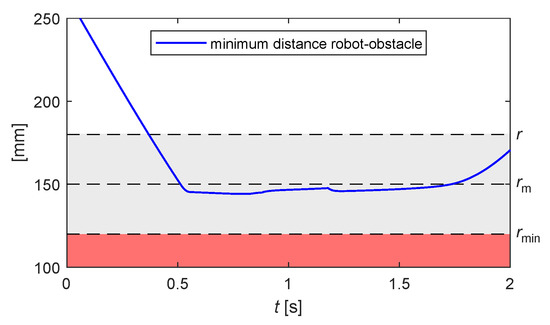
Figure 13.
Example 2: minimum distance robot-obstacle for the motion shown in Figure 12.
Due to the saturation of the speed of the third joint (Figure 14), a small motion of the end-effector can be noticed (), which however is quickly recovered by the control. In a similar case, where the task could be performed without speed saturation, the absence of motion of the end-effector would be guaranteed.
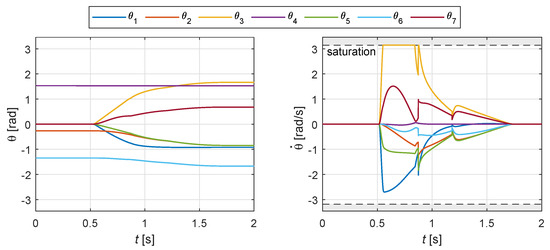
Figure 14.
Example 2: joint rotations and speeds for the motion shown in Figure 12.
4.3. Example 3
The third example, more complex, presents two obstacles (Figure 15). The first, fixed, is located under the linear path of the robot. Since its proximity to the path is less than the radius r of the end-effector’s region of influence, the off-line trajectory planner generates a Bézier curve that avoids the obstacle by passing over it. Once the trajectory is assigned and the motion of the manipulator starts, a second obstacle, dynamic, moves linearly at the speed of along a path that intersects the kinematic chain of the robot.
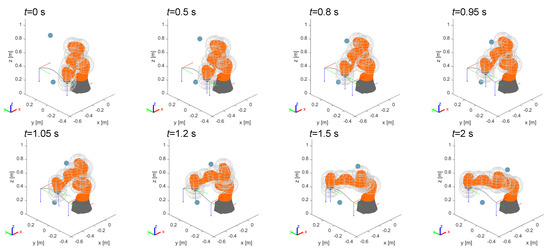
Figure 15.
Example 3: avoidance of two obstacles.
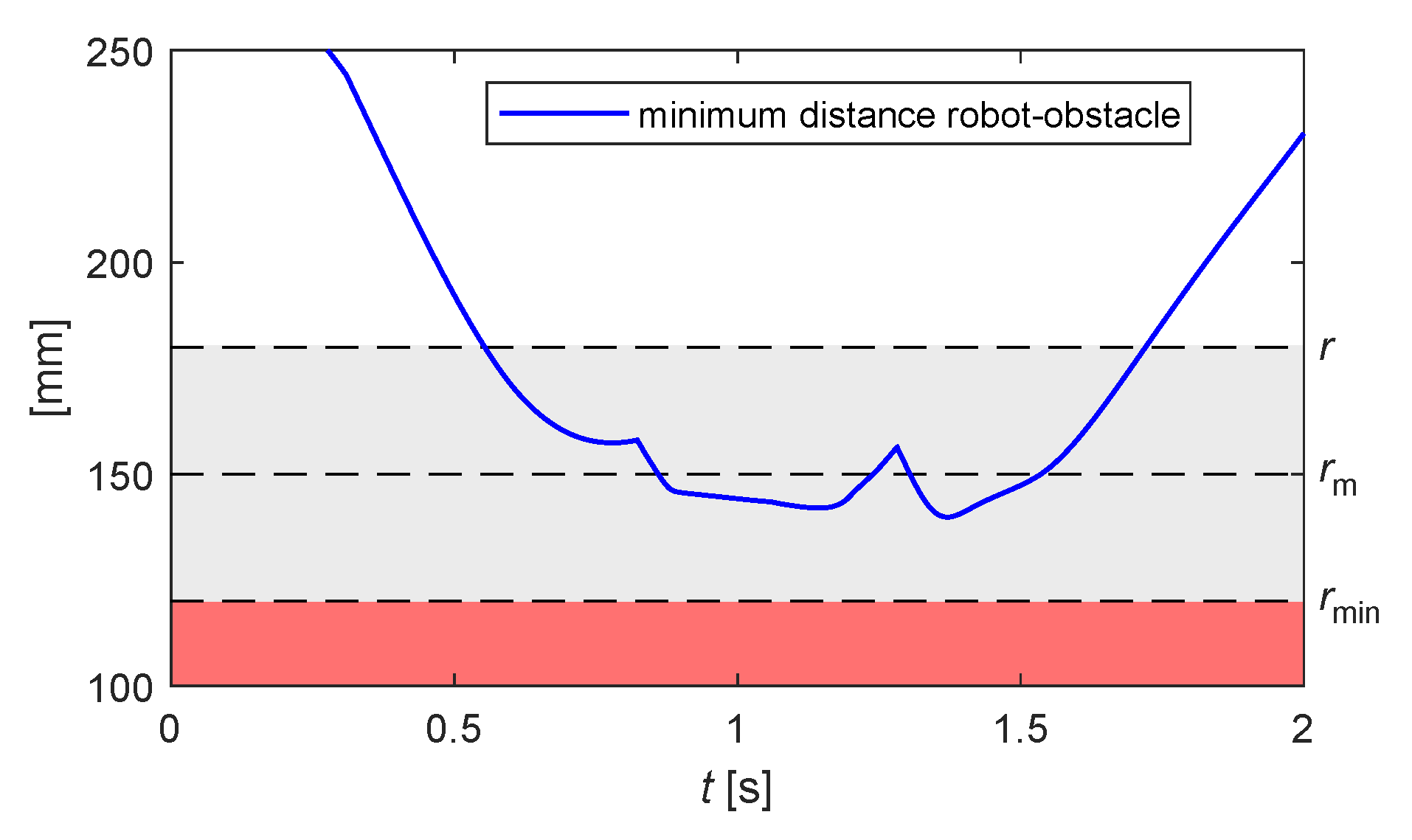
The effect of the second obstacle is visible in Figure 16 at approximately , when the distance rapidly decreases before the control readily flattens the curve. Such effect is clearly visible also in Figure 17, where a sudden change of the velocity profiles is visible at the same instant. Despite the interference of the two obstacles and the speed saturation for some joints, the control is able to execute the task.
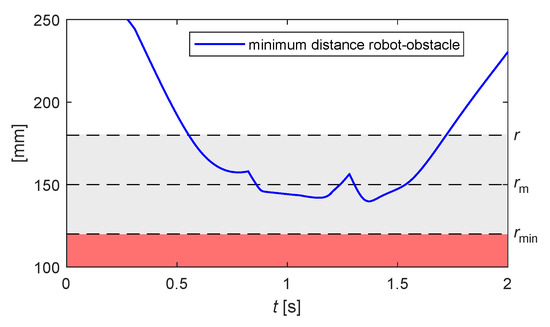
Figure 16.
Example 3: minimum distance robot-obstacle for the motion shown in Figure 15.
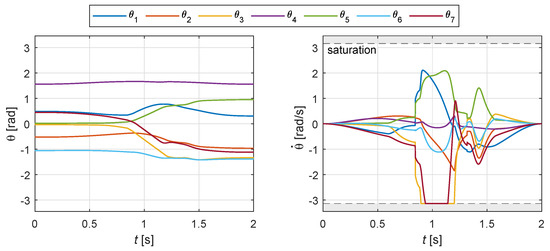
Figure 17.
Example 3: joint rotations and speeds for the motion shown in Figure 15.
4.4. Example 4
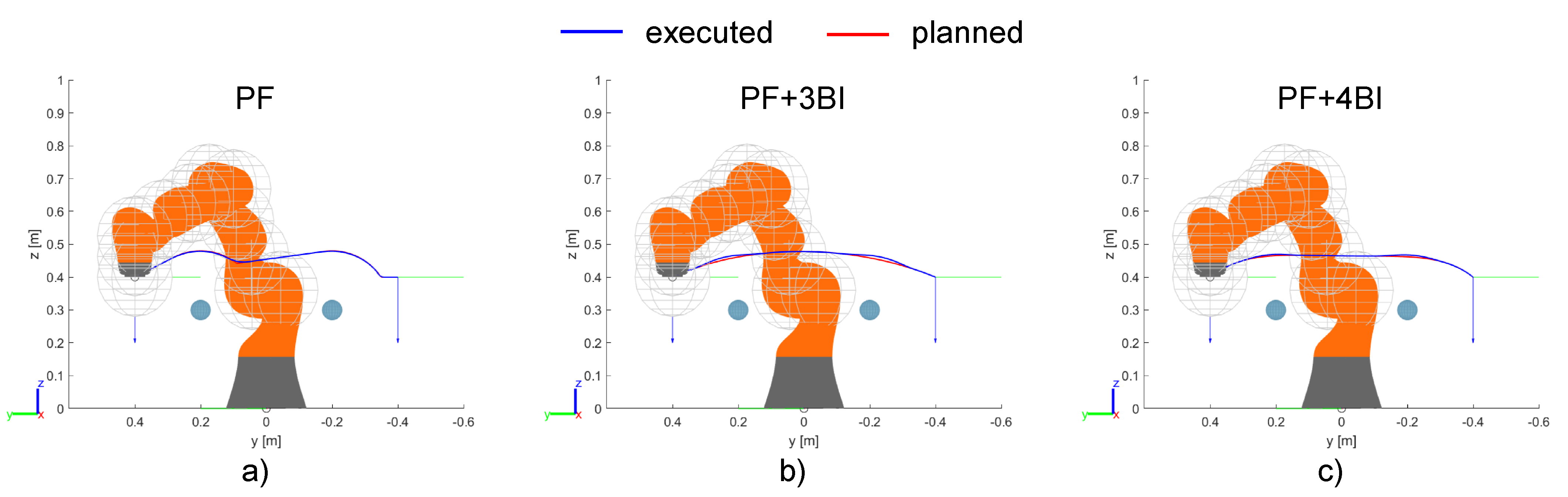
This example presents three simulations showing the differences resulting from different path generation methods. As shown in Figure 18, the robot is asked to move on a linear path, but two fixed obstacles prevent this trajectory by violating the safety distance. Therefore, an alternative path is required. Starting from the standard method of Potential Fields (PF, Figure 18a), two other strategies are adopted, i.e., an interpolation with a third (PF + 3BI, Figure 18b) and fourth (PF + 4BI, Figure 18c) order Bézier curve, respectively, according to the method described in Section 2.

Figure 18.
Example 4: comparison between different methods for path generation; (a) Potential Fields, (b) Potential Fields with 3rd order Bézier Interpolation, (c) Potential Fields with 4th order Bézier Interpolation.
The trajectory plots show that the first method is able to respect the safety region, so that the trajectory executed by the robot coincides with the planned one. On the other hand, the trajectory has two very sharp curves, which result in high accelerations. The second method allows for smoother curves, reducing accelerations. Furthermore, even if the predicted trajectory slightly violates the safety zone of the obstacles, the on-line anti-collision control is able to correct the motion with a small deviation. When a fourth order Bézier curve is used, the deviation between planned and executed trajectories is smaller, which means that anti-collision control is almost unnecessary; however, the curves are sharper than in the 3rd order case.
In order to compare the effort required of the motors in the three different cases, the norm of the joints angular velocity vector and the norm of the joints angular acceleration vector are analyzed, and their maximum values assumed during the motion, and , respectively, are used as indexes. Table 2 confirms the aforementioned considerations. With the same motion time T, the PF method gives a path length L larger than PF + 3BI and PF + 4BI, which give a reduction in the order of 3%. Dealing with the angular velocity, the three methods result in quite similar maximum values (differences in the order of 3%), but the advantage of interpolation is much evident in terms of acceleration: peaks of angular acceleration are in this case reduced of about 90% with respect to the potential fields method without interpolation, which results in much less torque and power by the motors. This important advantage is not affected by a longer computational time, which is only marginally higher in the PF + 3BI (+11.1%) and PF+4BI (+14.8%) cases.

Table 2.
Results from simulations of Example 4.
4.5. Example 5
The last example of this section is aimed at highlighting the effect of the repulsive speed in its traditional definition compared with the one introduced by the authors, which takes into account the velocity of the moving obstacle according to Equation (26).
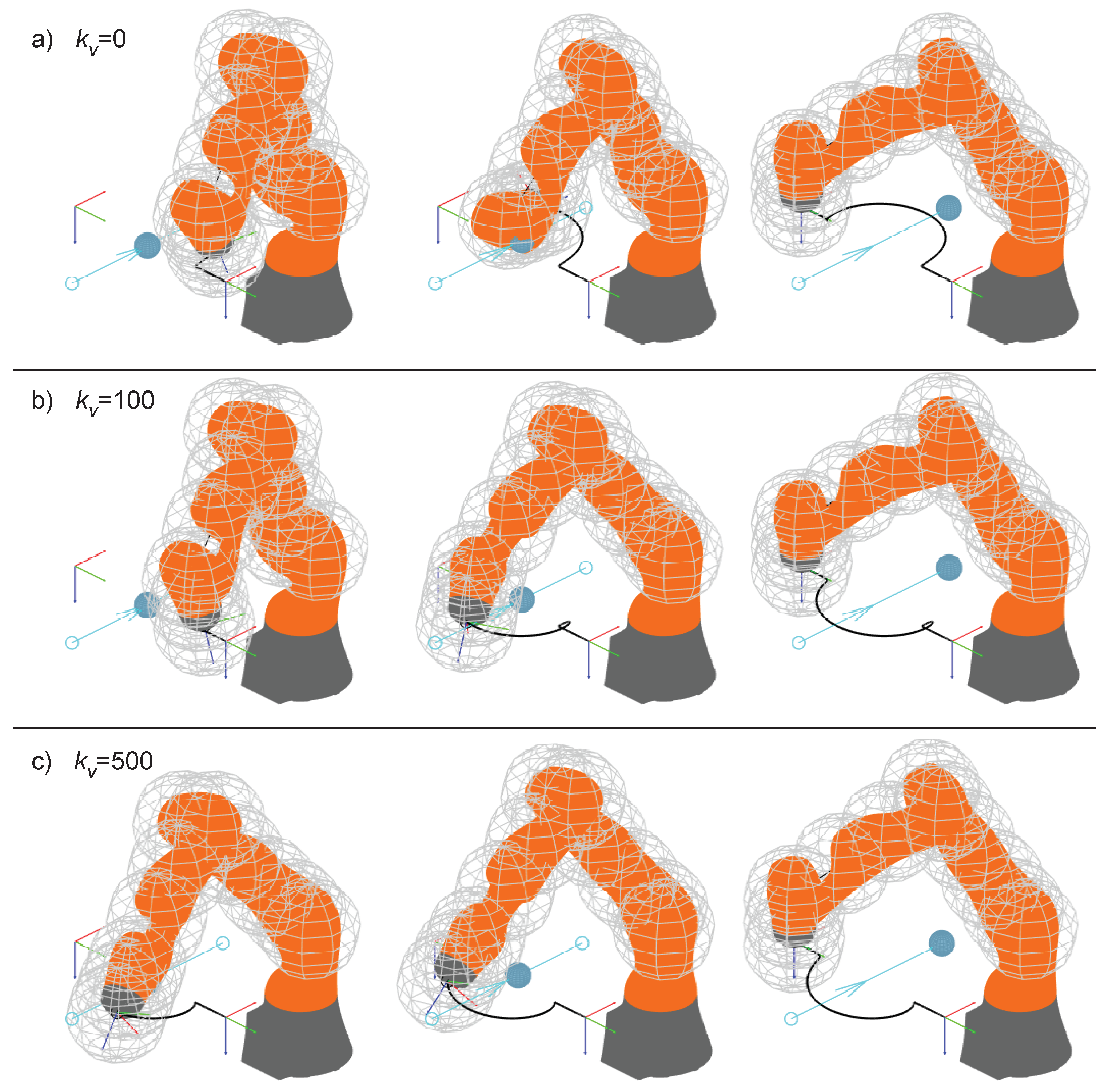
Figure 19 shows the test case: the robot is moving linearly on the horizontal plane while an obstacle is moving on the same plane in the orthogonal direction, intersecting the robot planned trajectory in the midpoint. As a consequence, the on-line control acts once the obstacle enters the safety region of the end-effector. The response of the control is different in the three cases presented: the gain term , introduced in Equation (26), is set to 0 in Figure 19a, whereas Figure 19b,c refers to and , respectively. In other words, in the first case the repulsive speed is defined solely on the basis of the position of the obstacle, while the speed of the obstacle is considered with increasing influence in the two following cases.
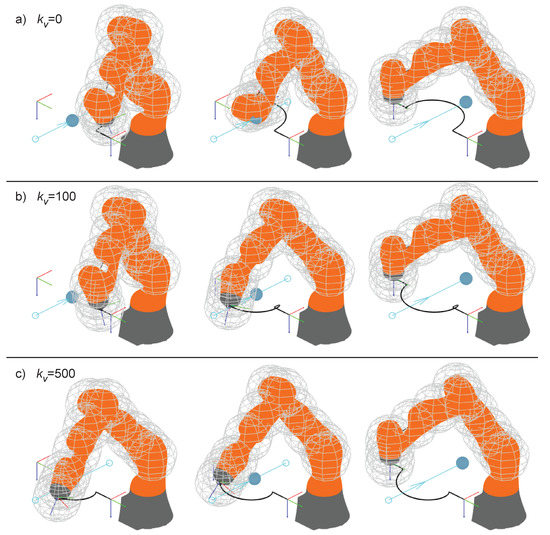
Figure 19.
Example 5: response of the control law to a moving obstacle with different values of .
When , the robot tries to avoid the collision by deviating its trajectory in the same direction as the speed of the obstacle; the effect is that the obstacle pushes the end-effector further and further away from its planned path, until the term proportional to the positioning error is able to recover the drift. Furthermore, looking at the second frame of the motion in Figure 19a, the control is not able to avoid the collision, which means that in a real implementation the robot should be stopped at this stage, or more precisely at the first moment when the safety limit is crossed. In the case of the end-effector initially tries to avoid the obstacle by deviating along its speed, but after a while the direction of the end-effector is reversed and the obstacle is successfully avoided on the upstream side. The effect is even more evident with , when the control is able to deviate the end-effector to the upstream side of the obstacle since the first instant of the interaction.
A more detailed comparison can be done based on the data collected in Table 3: as expected, the case with is the worst one in terms of length of the path, maximum joints speed, and most of all in terms of maximum angular acceleration of joints. Increasing the gain all the indexes reduce, especially the one related to the acceleration. The best performance is found for , whereby the minimum path length is obtained with, at the same time, a reduction of about 80% of the maximum acceleration of the joints and a reduction of about 49% of the maximum speed of the joints. On the other hand, the computation time required to perform an iteration of the control loop is substantially equivalent; for the fourth case with there is only a slight increase of about 5%. It is worth pointing out that high values of may not lead to more beneficial motions. In fact, looking at the fourth row of Table 3 referring to , an improvement is obtained compared to the case with , but it is a worse result than the case with . Therefore, the optimal value of must be found case by case, according to the expected speed of the potential obstacles, the speed of the manipulator itself and other variables related to the working conditions.

Table 3.
Results from simulations of Example 5.
5. Discussion
The simulations presented in the previous section are intended to verify the correctness of the method and to investigate the computational effort needed to implement the related algorithms in a real system. As a matter of fact, the final objective of this research is to transfer the control framework to a real system, now under construction in laboratory, where the robot will be equipped with a vision system composed by three depth cameras (Intel RealSense D455), able to acquire the surrounding environment and extrapolate the position of objects and humans within the workspace. Fixed obstacles simulated in this study can be thought of as fixed objects inadvertently left inside the workspace, such as furniture elements or mechanical tools, whereas dynamic obstacles may represent humans operating in the shared workspace.
What is expected as a critical issue in the implementation on the real system is the speed of execution of the control loop. Based on the results presented in this paper, referring in particular to the most demanding case of example 3, it can be summarized that for the execution of the off-line path planning algorithm the average computational time is approximately , whereas the on-line motion control is able to run with a cycle time of approximately , comparable with rates typically used in the communication between external controllers and main controllers of robots. Furthermore, a standard laptop (i7 CPU @1.8 GHz, 16 GB RAM) was used for simulations; thus, a reduction of computational times can be expected if a more performing hardware is used.
6. Conclusions
In this paper, an obstacle avoidance strategy for robots moving in dynamically varying environments is presented and verified by simulation. Two main aspects characterize the proposed algorithms: first, the trajectory planned by the potential fields method is smoothed using a best-fit interpolation with Bézier curves; second, a modified repulsive velocity for the end-effector is introduced in order to consider also the velocity of the obstacles, improving the avoidance ability in dynamic environments. The algorithms previously tested for simplified planar cases are extended to a full mobility redundant manipulator operating in a spatial workspace. In addition to confirming the effectiveness of the control strategy, simulations give an estimation of the computational effort required to execute the algorithms, which is in line with typical requirements of robot controllers and can be improved by using higher performing hardware.
Future work will be directed on the one hand to improving the algorithms and on the other hand to transferring the control to a real system, now being installed. Some changes can be envisaged to the definition of the safety zone around obstacles/control points, which could be defined based on the relative speed between robot and obstacles, increasing for high speeds to ensure greater safety and vice versa to ensure greater mobility in case of static or quasi-static obstacles. Furthermore, the limitations imposed on the motor speeds could be exploited to estimate an overall parameter, such as the maximum speed allowed for obstacles, which can be used to verify a priori the ability to avoid an obstacle once its speed is perceived by the sensors of the system.
Author Contributions
Conceptualization, G.P. and C.S.; investigation, G.P. and C.S.; writing—original draft preparation, C.S.; writing—review and editing, G.P.; supervision, G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partly funded by the project URRA’ “usability of robots and reconfigurability of processes: enabling technologies and use cases”, on the topics of User-Centered Manufacturing and Industry 4.0, which is part of the project EU ERDF, POR MARCHE Region FESR 2014/2020–AXIS 1–Specific Objective 2–ACTION 2.1,“HD3Flab-Human Digital Flexible Factory of the Future Laboratory”, coordinated by the Polytechnic University of Marche.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pedrocchi, N.; Vicentini, F.; Matteo, M.; Tosatti, L.M. Safe human–robot Cooperation in an Industrial Environment. Int. J. Adv. Robot. Syst. 2013, 10, 27. [Google Scholar] [CrossRef]
- Vicentini, F. Collaborative Robotics: A Survey. J. Mech. Des. 2020, 143, 040802. [Google Scholar] [CrossRef]
- Tang, S.H.; Kamil, F.; Khaksar, W.; Zulkifli, N.; Ahmad, S.A. Robotic motion planning in unknown dynamic environments: Existing approaches and challenges. In Proceedings of the 2015 IEEE International Symposium on Robotics and Intelligent Sensors (IRIS), Langkawi, Malaysia, 18–20 October 2015; pp. 288–294. [Google Scholar]
- Zlajpah, L.; Nemec, B. Kinematic control algorithms for on-line obstacle avoidance for redundant manipulators. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, Lausanne, Switzerland, 30 September–4 October 2002; pp. 1898–1903. [Google Scholar]
- Bottin, M.; Rosati, G. Trajectory Optimization of a Redundant Serial Robot Using Cartesian via Points and Kinematic Decoupling. Robotics 2019, 8, 101. [Google Scholar] [CrossRef]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Path planning and trajectory planning algorithms: A general overview. In Motion and Operation Planning of Robotic Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 3–27. [Google Scholar]
- Han, B.; Luo, X.; Luo, Q.; Zhao, Y.; Lin, B. Research on Obstacle Avoidance Motion Planning Technology of 6-DOF Manipulator. In International Conference on Geometry and Graphics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 604–614. [Google Scholar]
- Wang, J.; Liu, S.; Zhang, B.; Yu, C. Manipulation Planning with Soft Constraints by Randomized Exploration of the Composite Configuration Space. Int. J. Control. Autom. Syst. 2021, 19, 1340–1351. [Google Scholar] [CrossRef]
- Willms, A.R.; Yang, S.X. Real-time robot path planning via a distance-propagating dynamic system with obstacle clearance. IEEE Trans. Syst. Man, Cybern. Part B 2008, 38, 884–893. [Google Scholar] [CrossRef]
- Jung, J.H.; Kim, D.H. Local Path Planning of a Mobile Robot Using a Novel Grid-Based Potential Method. Int. J. Fuzzy Log. Intell. Syst. 2020, 20, 26–34. [Google Scholar] [CrossRef]
- Xu, P.; Wang, N.; Dai, S.L.; Zuo, L. Motion Planning for Mobile Robot with Modified BIT* and MPC. Appl. Sci. 2021, 11, 426. [Google Scholar] [CrossRef]
- Xu, X.; Hu, Y.; Zhai, J.; Li, L.; Guo, P. A novel non-collision trajectory planning algorithm based on velocity potential field for robotic manipulator. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418787075. [Google Scholar] [CrossRef]
- Lee, K.; Choi, D.; Kim, D. Potential Fields-Aided Motion Planning for Quadcopters in Three-Dimensional Dynamic Environments. In Proceedings of the AIAA Scitech 2021 Forum, 11–15 January 2021; p. 1410. [Google Scholar]
- Abhishek, T.S.; Schilberg, D.; Doss, A.S.A. Obstacle Avoidance Algorithms: A Review. IOP Conf. Series: Mater. Sci. Eng. 2021, 1012, 012052. [Google Scholar] [CrossRef]
- Scoccia, C.; Palmieri, G.; Palpacelli, M.C.; Callegari, M. A Collision Avoidance Strategy for Redundant Manipulators in Dynamically Variable Environments: On-Line Perturbations of Off-Line Generated Trajectories. Machines 2021, 9, 30. [Google Scholar] [CrossRef]
- Chen, L.; Qin, D.; Xu, X.; Cai, Y.; Xie, J. A path and velocity planning method for lane changing collision avoidance of intelligent vehicle based on cubic 3-D Bezier curve. Adv. Eng. Softw. 2019, 132, 65–73. [Google Scholar] [CrossRef]
- Kawabata, K.; Ma, L.; Xue, J.; Zhu, C.; Zheng, N. A path generation for automated vehicle based on Bezier curve and via-points. Robot. Auton. Syst. 2015, 74, 243–252. [Google Scholar] [CrossRef]
- Yu, X.; Zhu, W.; Xu, L. Real-time Motion Planning and Trajectory Tracking in Complex Environments based on Bézier Curves and Nonlinear MPC Controller. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), IEEE, Hefei, China, 22–24 August 2020; pp. 1540–1546. [Google Scholar]
- Corinaldi, D.; Carbonari, L.; Callegari, M. Optimal Motion Planning for Fast Pointing Tasks With Spherical Parallel Manipulators. IEEE Robot. Autom. Lett. 2018, 3, 735–741. [Google Scholar] [CrossRef]
- Corinaldi, D.; Callegari, M.; Angeles, J. Singularity-free path-planning of dexterous pointing tasks for a class of spherical parallel mechanisms. Mech. Mach. Theory 2018, 128, 47–57. [Google Scholar] [CrossRef]
- Maciejewski, A.A.; Klein, C.A. Obstacle avoidance for kinematically redundant manipulators in dynamically varying environments. Int. J. Robot. Res. 1985, 4, 109–117. [Google Scholar] [CrossRef]
- Scimmi, L.S.; Melchiorre, M.; Troise, M.; Mauro, S.; Pastorelli, S. A Practical and Effective Layout for a Safe human–robot Collaborative Assembly Task. Appl. Sci. 2021, 11, 1763. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, M.; Wang, X.; He, S.; He, J.; Xu, Z. An improved artificial potential field method of trajectory planning and obstacle avoidance for redundant manipulators. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Safeea, M.; Béarée, R.; Neto, P. Collision Avoidance of Redundant Robotic Manipulators Using Newton’s Method. J. Intell. Robot. Syst. 2020, 99, 673–681. [Google Scholar] [CrossRef]
- Safeea, M.; Neto, P.; Bearee, R. On-line collision avoidance for collaborative robot manipulators by adjusting off-line generated paths: An industrial use case. Robot. Auton. Syst. 2019, 119, 278–288. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, H.; Liu, Z.; Liu, Y.; Zhu, Y.; Zhao, J. Real-time kinematic control for redundant manipulators in a time-varying environment: Multiple-dynamic obstacle avoidance and fast tracking of a moving object. IEEE Trans. Ind. Inform. 2019, 16, 28–41. [Google Scholar] [CrossRef]
- Scoccia, C.; Palmieri, G.; Palpacelli, M.C.; Callegari, M. Real-Time Strategy for Obstacle Avoidance in Redundant Manipulators. In Proceedings of the International Conference of IFToMM ITALY; Springer: Berlin/Heidelberg, Germany, 2020; pp. 278–285. [Google Scholar]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Chiaverini, S.; Siciliano, B.; Egeland, O. Review of the damped least-squares inverse kinematics with experiments on an industrial robot manipulator. IEEE Trans. Control Syst. Technol. 1994, 2, 123–134. [Google Scholar] [CrossRef]
- Melchiorre, M.; Scimmi, L.S.; Pastorelli, S.P.; Mauro, S. Collison Avoidance using Point Cloud Data Fusion from Multiple Depth Sensors: A Practical Approach. In Proceedings of the 23rd International Conference on Mechatronics Technology (ICMT), IEEE, Salerno, Italy, 23–26 October 2019; pp. 1–6. [Google Scholar]
- Cefalo, M.; Magrini, E.; Oriolo, G. Sensor-based task-constrained motion planning using model predictive control. IFAC-PapersOnLine 2018, 51, 220–225. [Google Scholar] [CrossRef]
- Lee, K.K.; Buss, M. Obstacle avoidance for redundant robots using Jacobian transpose method. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, San Diego, CA, USA, 29 October–2 November 2007; pp. 3509–3514. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).