Numerical and Experimental Investigation of the Temperature Rise of Cutting Tools Caused by the Tool Deflection Energy
Abstract
:1. Introduction
2. The Mechanism of Heat Generation
2.1. Tool Deflection Energy
2.1.1. Theory of Tool Bending and Torsional Deflection
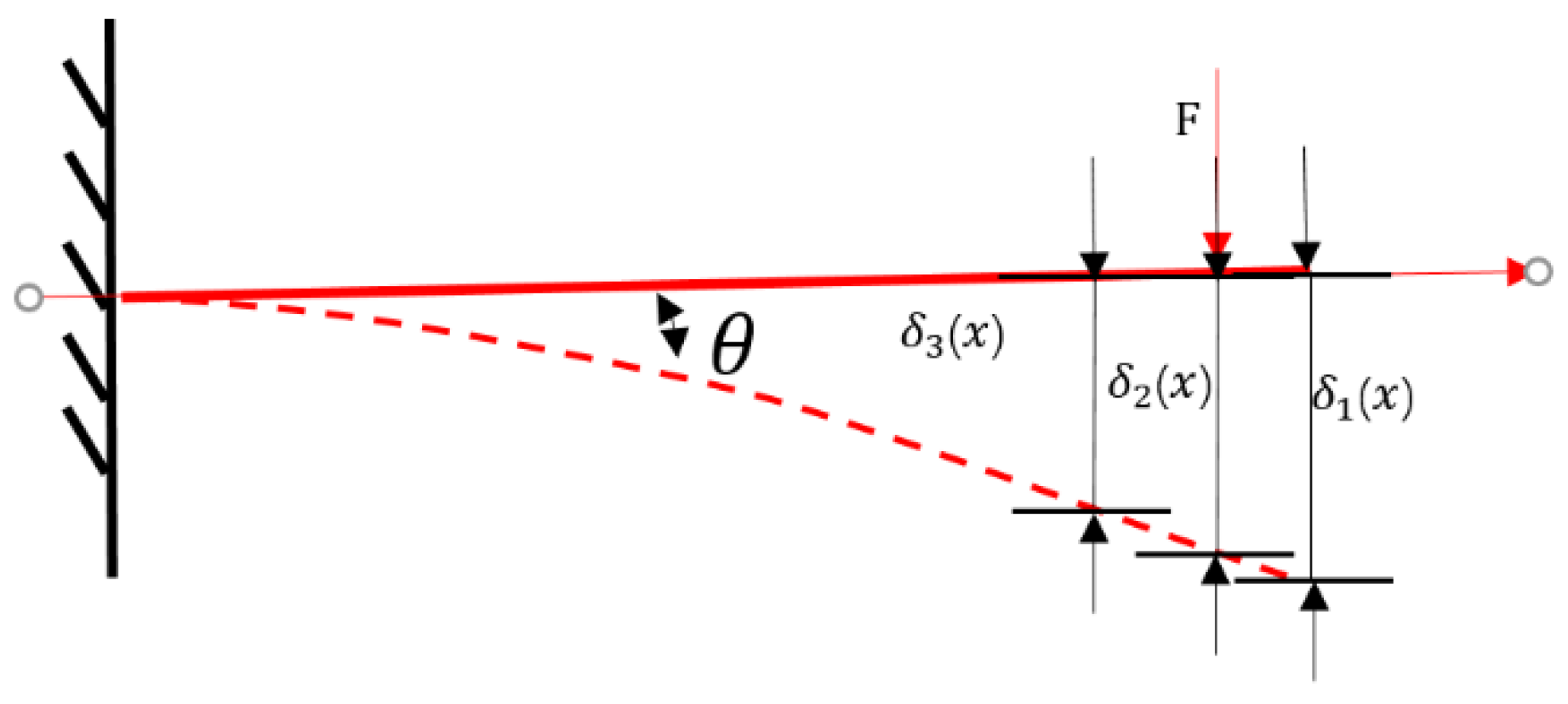
2.1.2. Tool Potential Energy
- Cutting force
- 2.
- Tool deflection
- 3.
- Calculation of tool potential energy
- (1)
- Potential energy under a milling force
- (2)
- Calculation of potential energy by deflection
- (3)
- Potential energy analysis
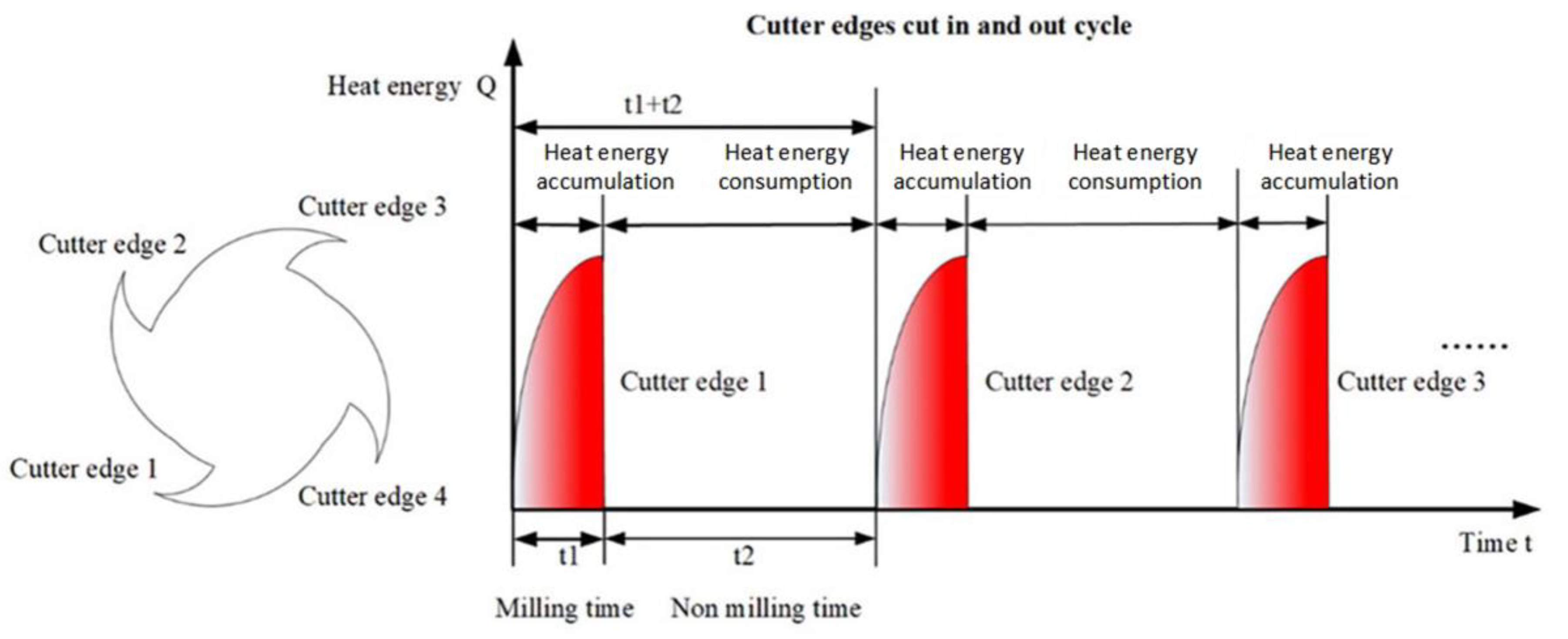
2.2. Heat Generation
- Cutter edge cutting-in stage
- 2.
- Cutter edge cutting-out stage
- 3.
- Cutter edge energy absorption process
3. Tool Temperature Modeling
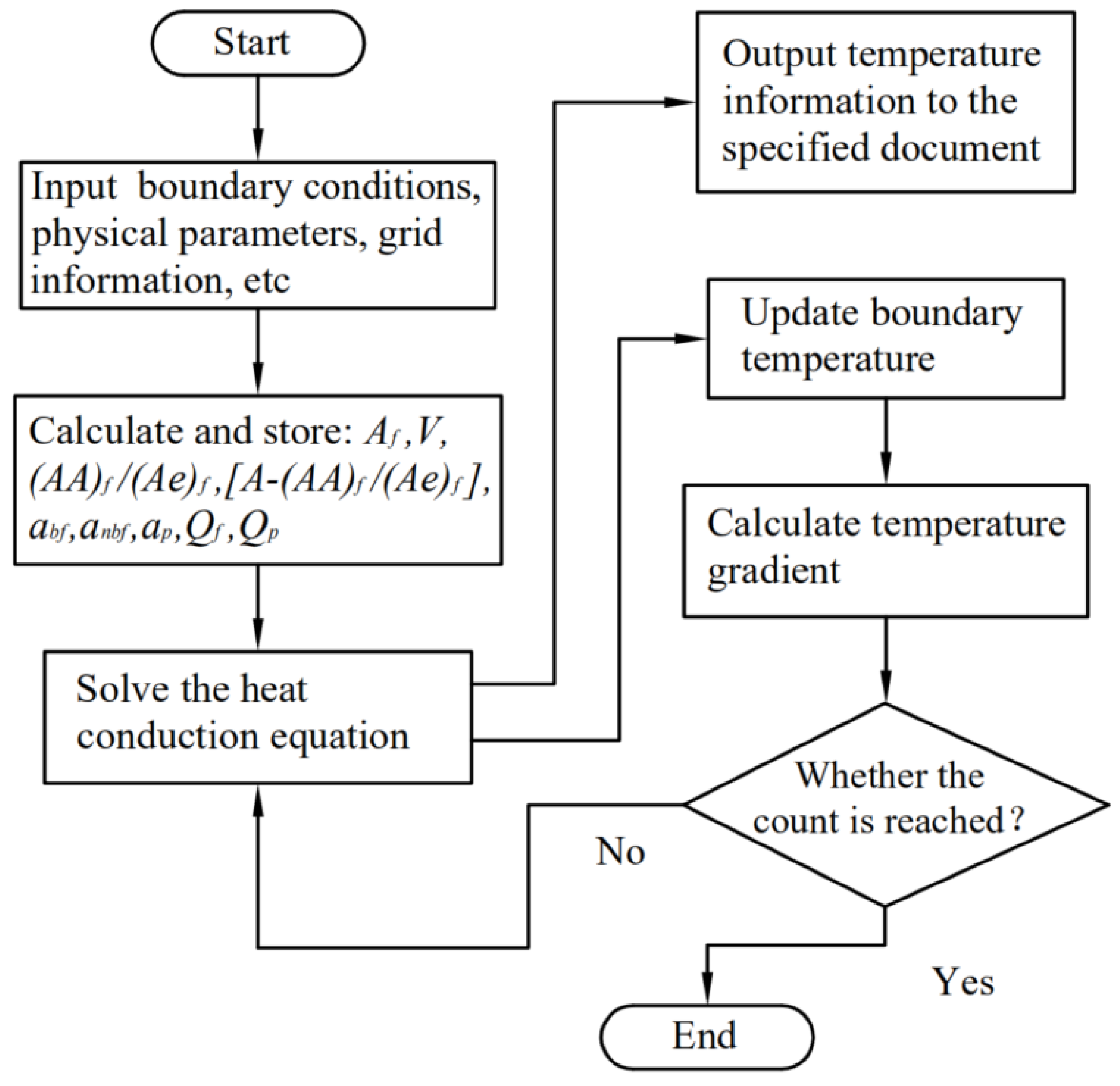
3.1. Numerical Methodology
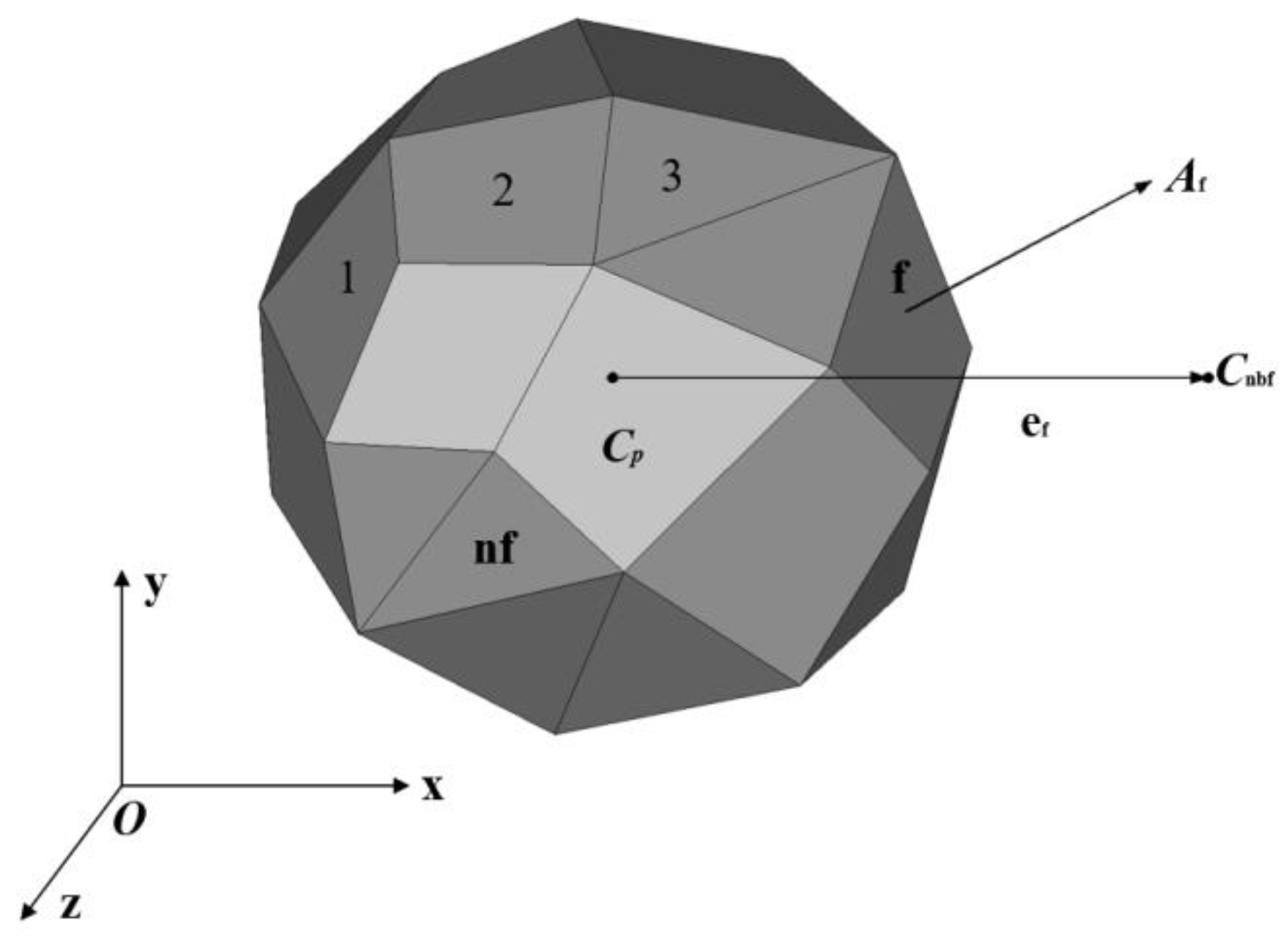
3.2. Heat Conduction Equation
3.3. Numerical Discretization and Boundary Conditions
3.3.1. Numerical Discretization
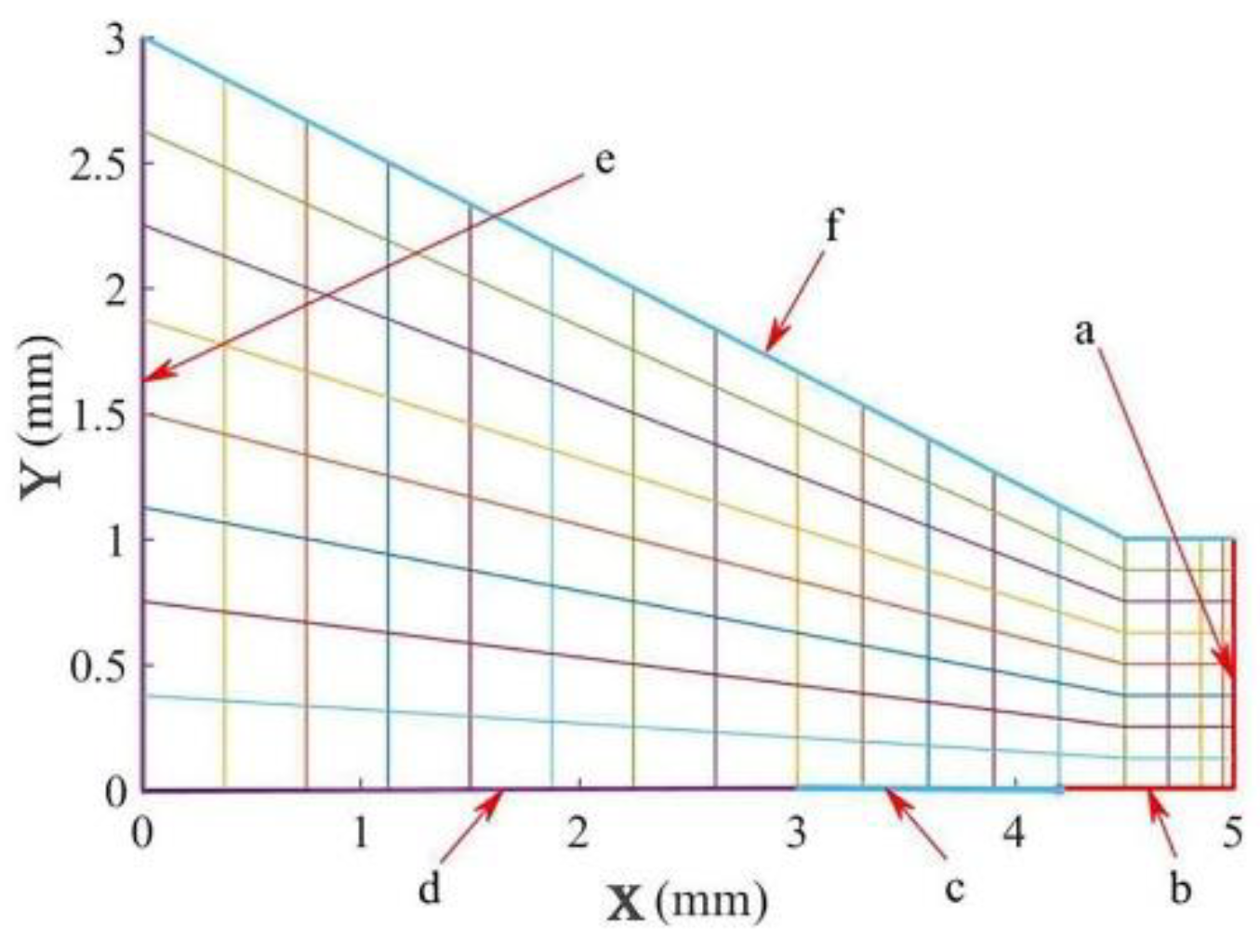
3.3.2. Boundary Condition Analysis
- Boundaries a and b: a is the front face and b is the back face of the milling cutter edge. In the range 0–3 mm in the Z direction of the cutter, boundaries a and b are endothermic during cutting and exothermic during non-cutting. The range 3–12 mm in the Z direction of the cutter does not participate in cutting, and is always exothermic.
- Boundaries c and f: During cutting, these are always in an exothermic state.
- Boundaries d and e: Since edge d is in contact with edge e, and far away from the tool nose, there is only a small amount of heat. Similarly, edge e sees only a small amount of heat. The heat and the emission are equal, so it is assumed that the boundary is adiabatic.
3.4. Heat Distribution
4. Numerical Simulation
4.1. Simulation Parameters and Programming Flow
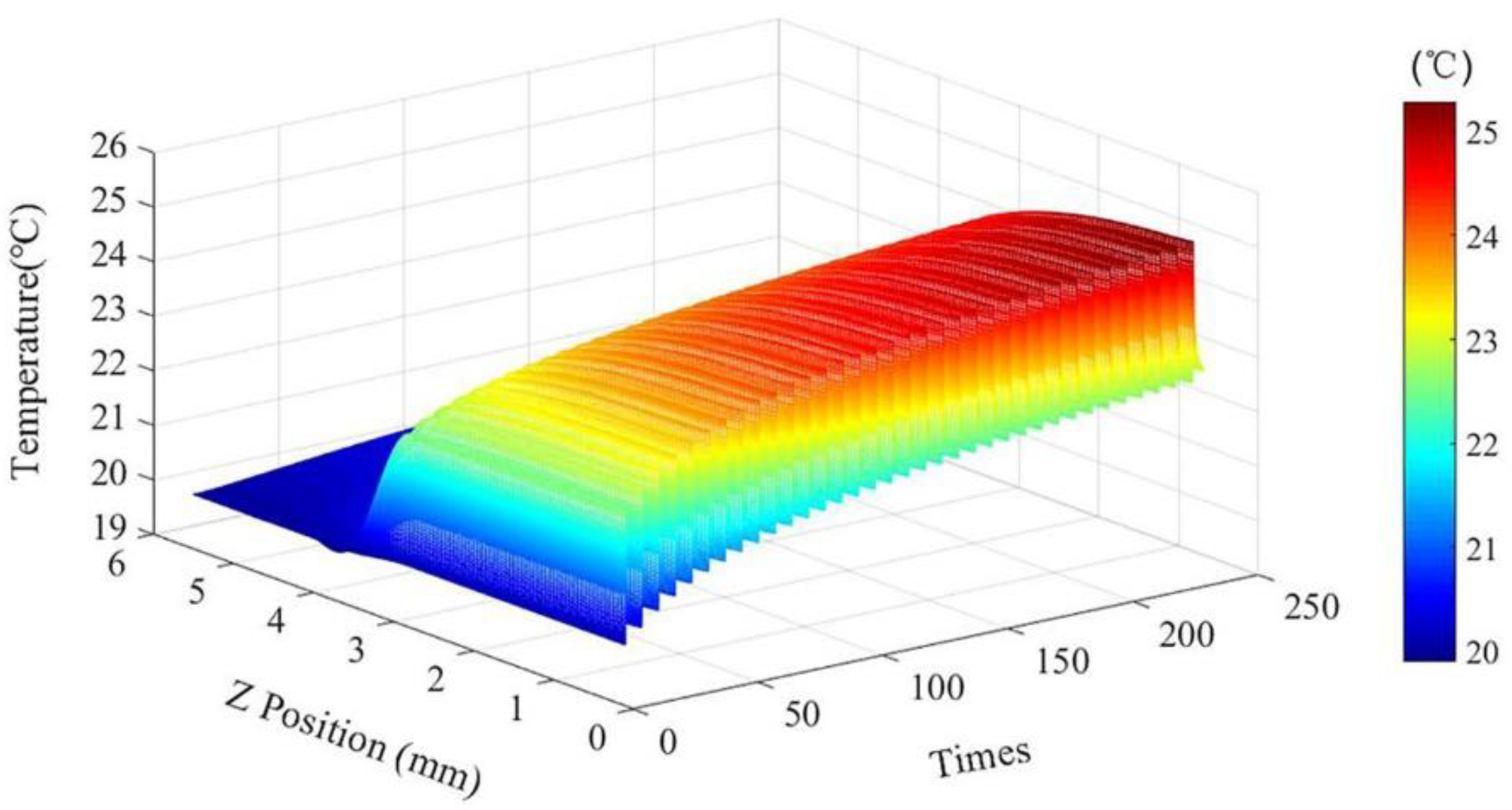
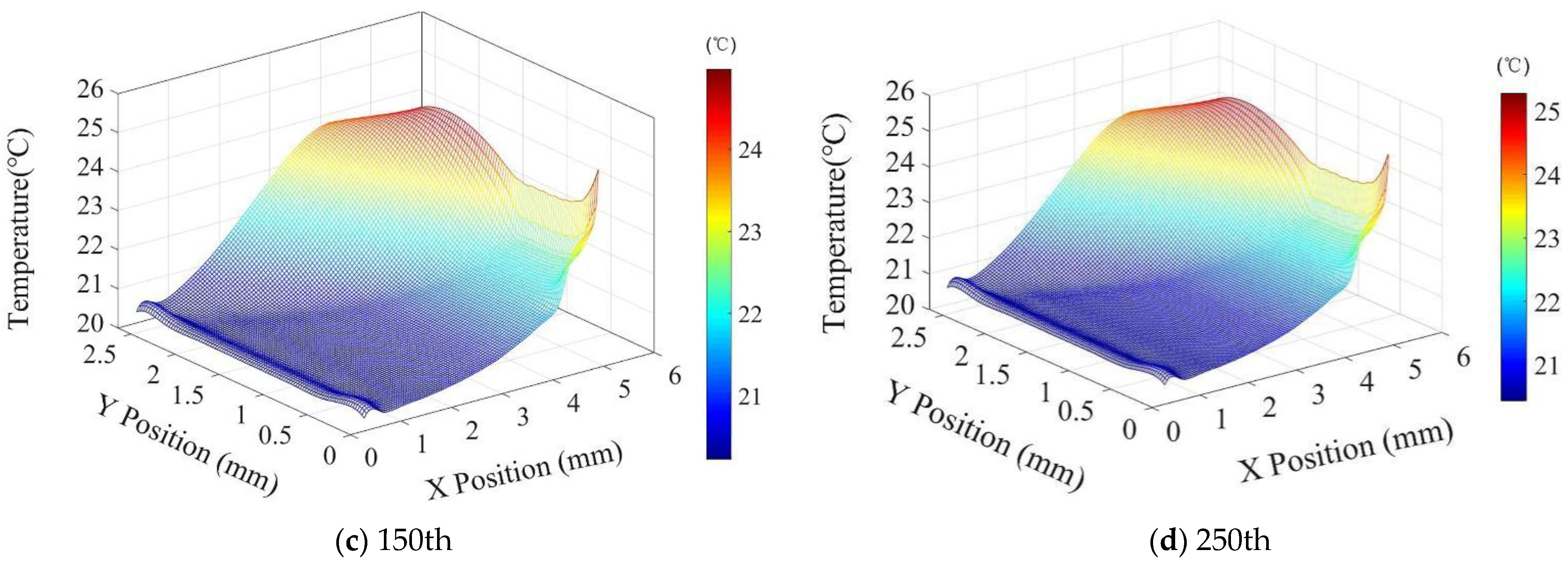
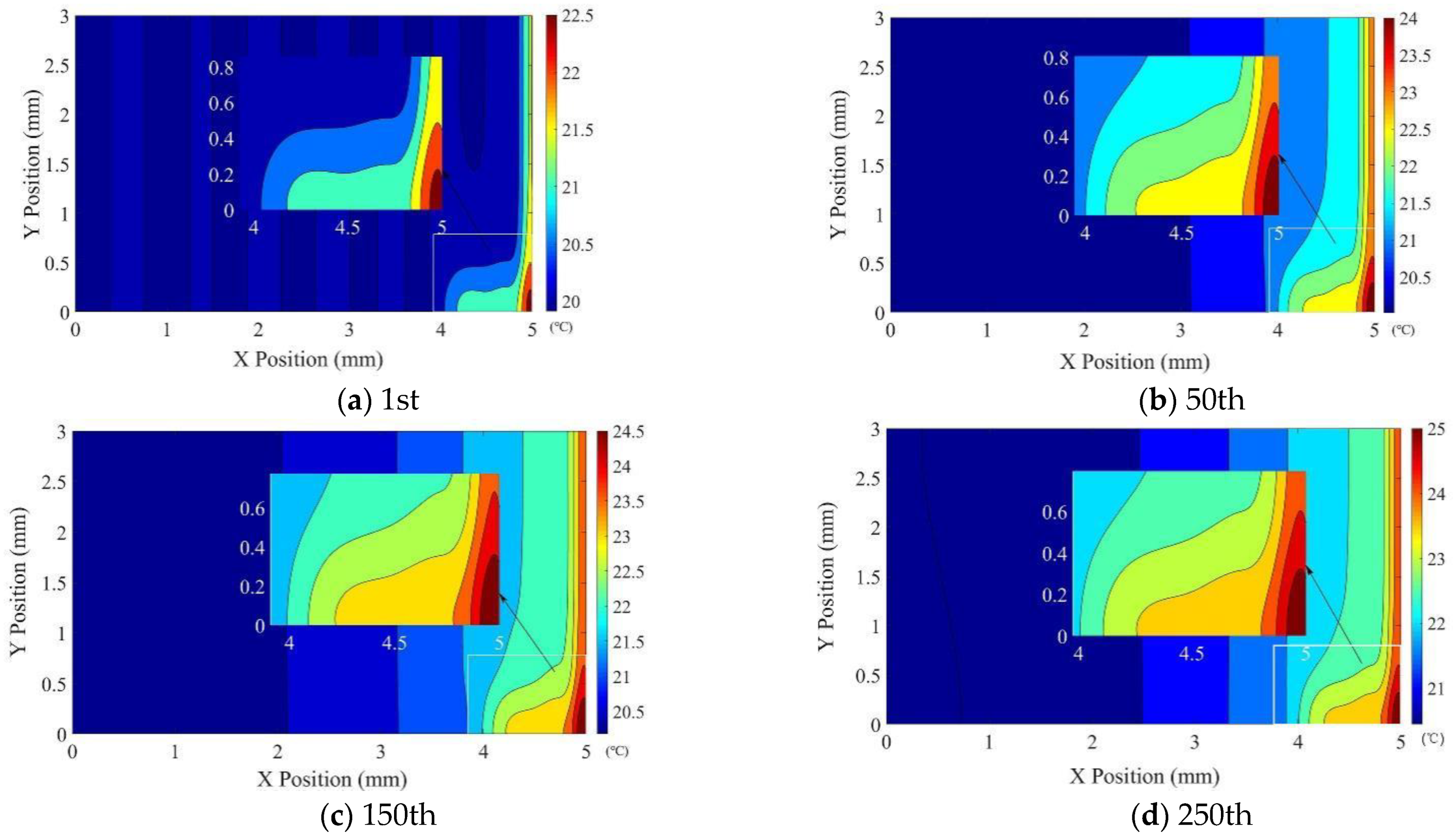
4.2. Numerical Analysis
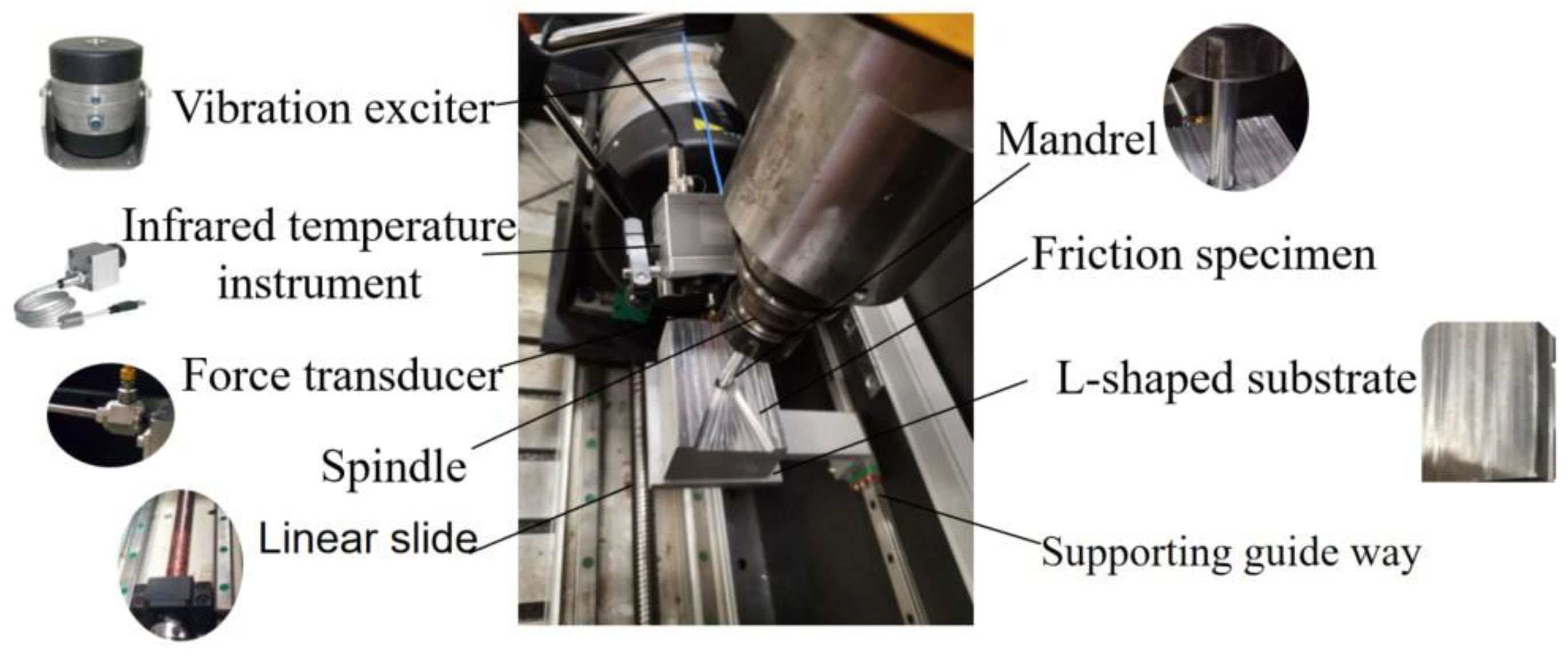
5. Experiments
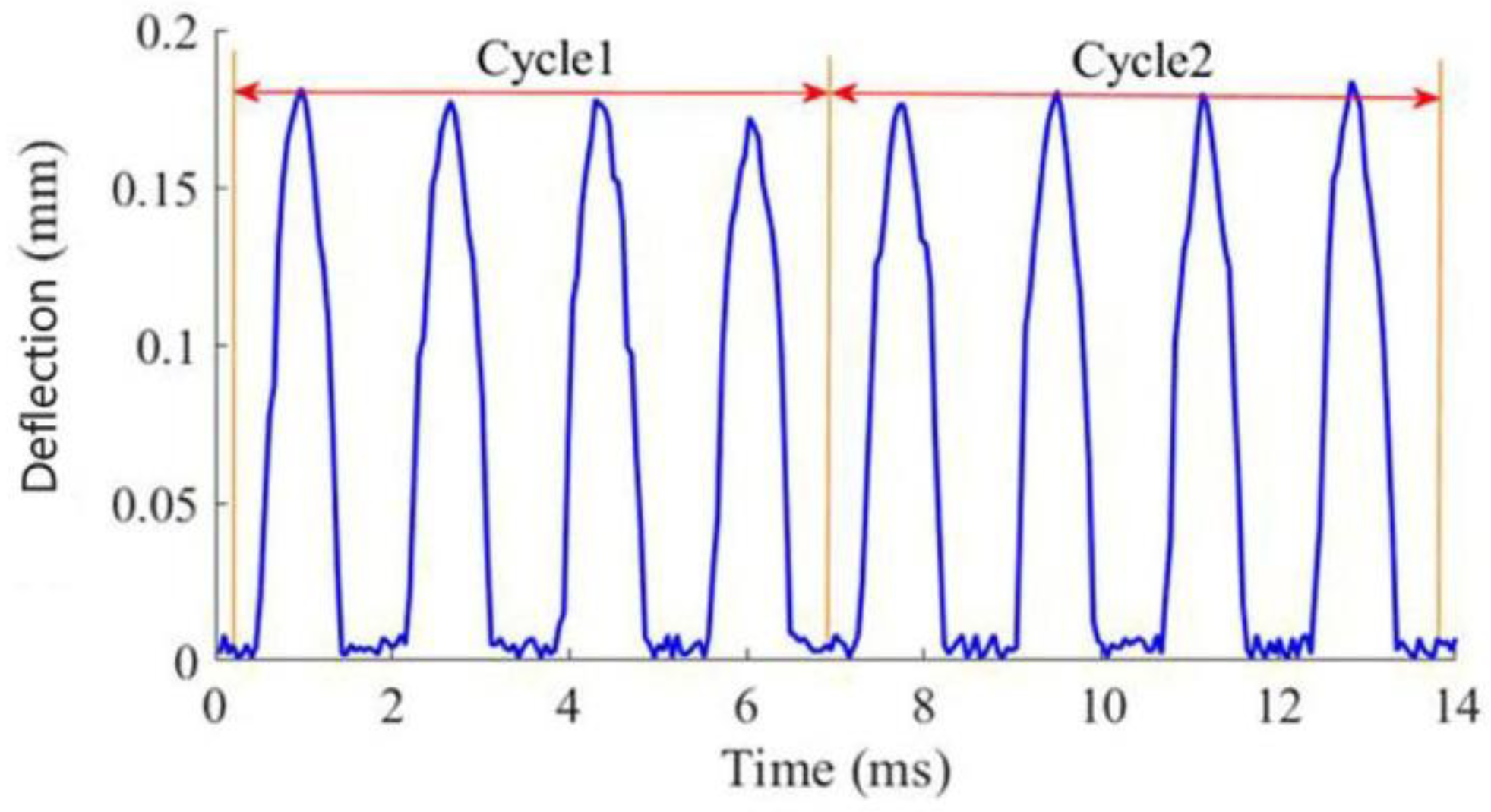
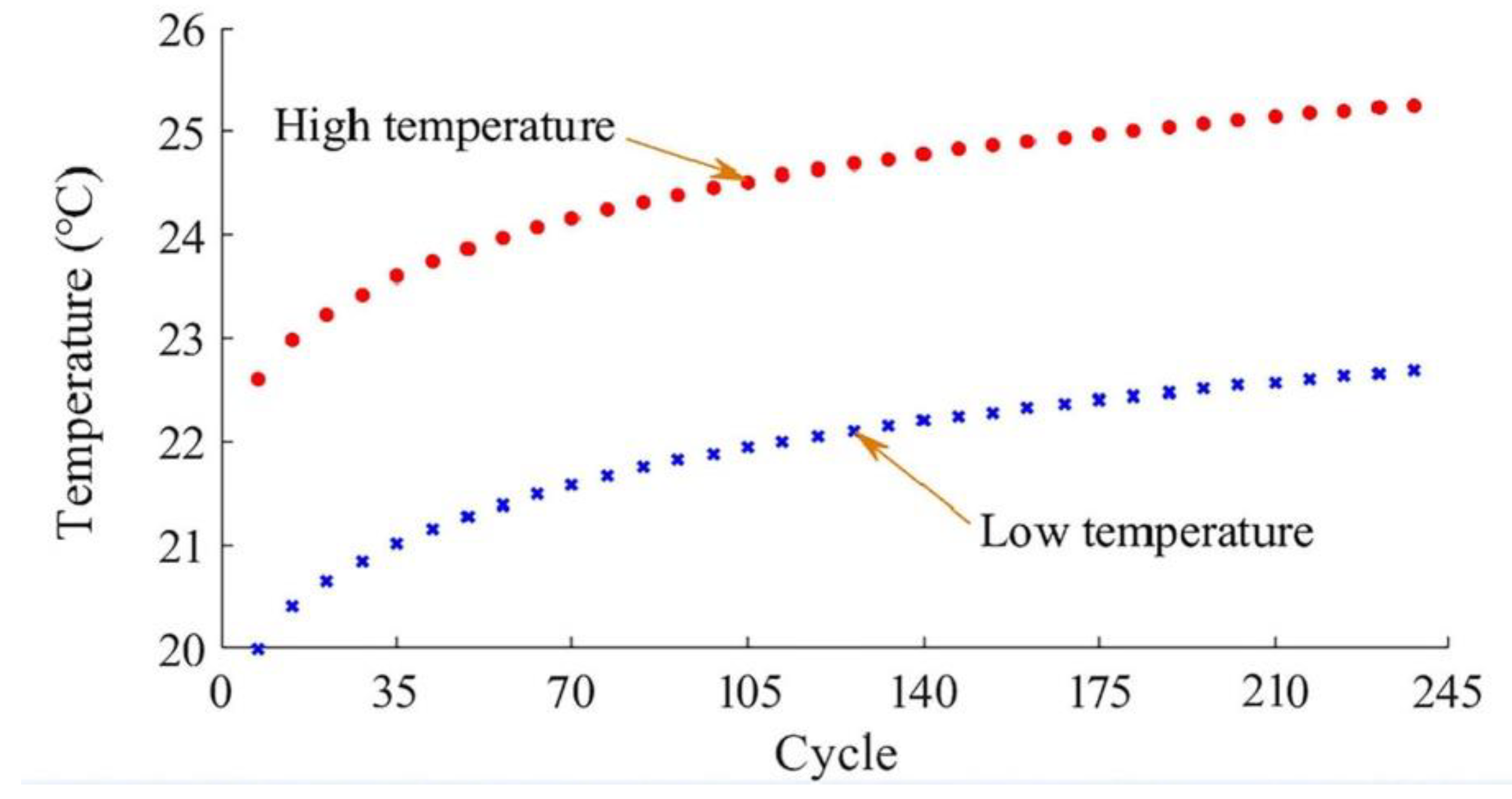
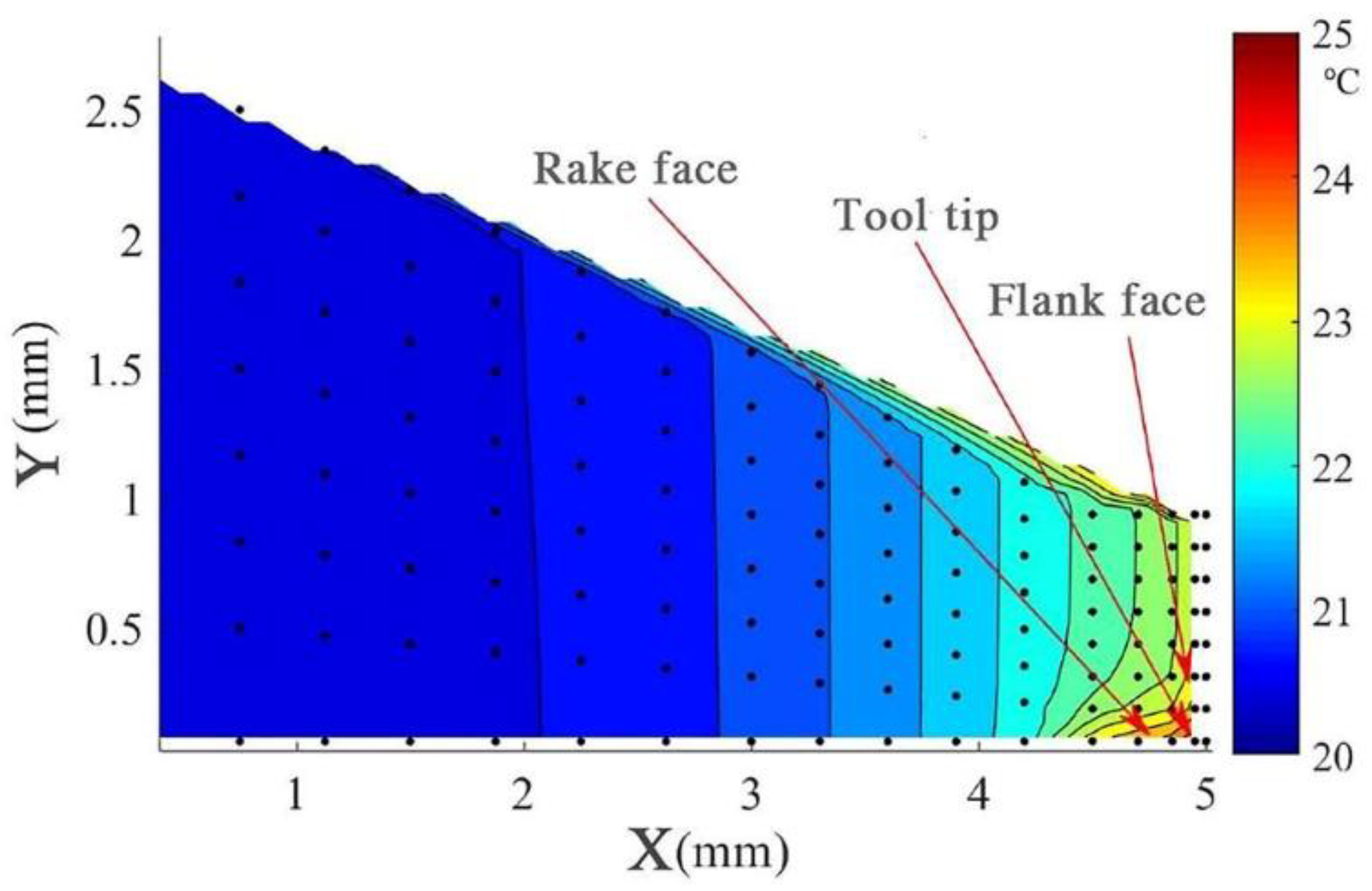
5.1. Total Temperature Rise of the Cutting Tool
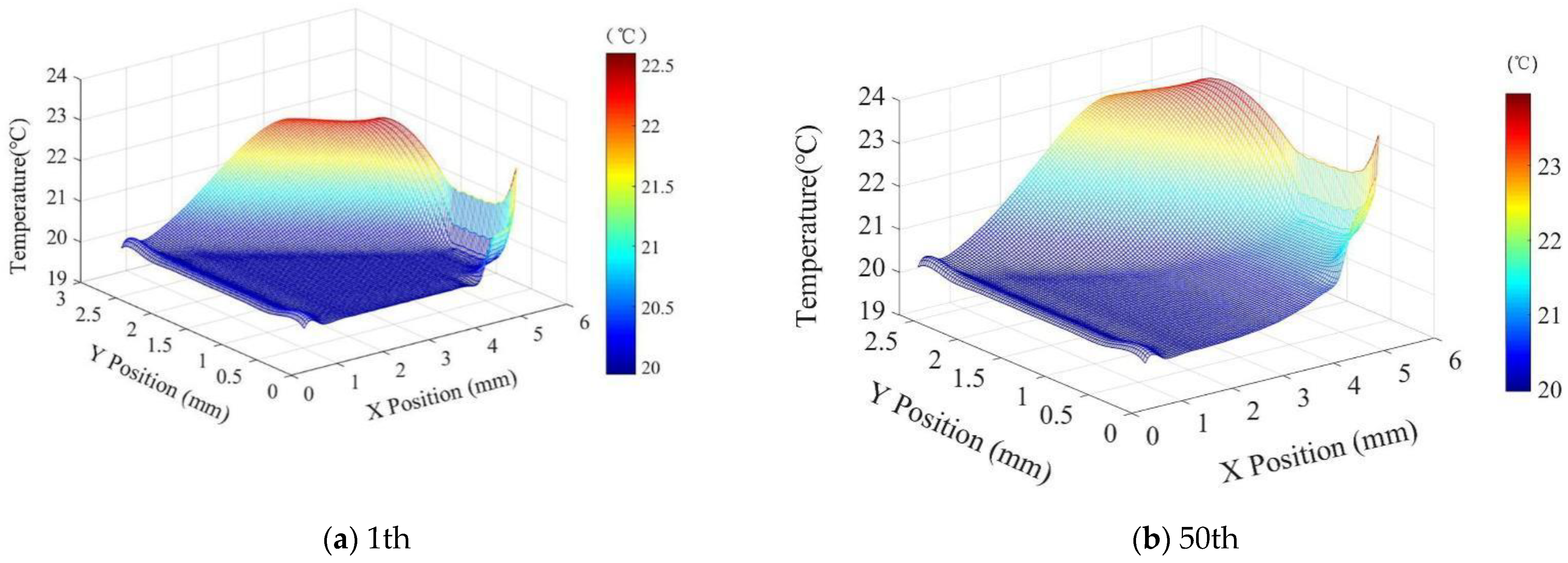
5.2. Temperature Rise Due to Tool Friction Alone
5.3. Temperature Rise Due to Tool Deflection and Friction
5.4. Results and Discussion
6. Conclusions
- (1)
- A heat generation mechanism is proposed. In precision or micro milling, heat has a great influence on a tool with small diameter and large cantilever elongation.
- (2)
- For the cutting parameters used, the change rule in the cutting force and cutter deflection is consistent with the change in the tool potential energy. The torsional potential energy of the tool is much less than its bending potential energy. Compared with the two-dimensional simulation, the boundary conditions for tool heat conduction can be set more accurately using the finite volume method. Moreover, the numerical discretization is more reasonable, and the calculation results are more realistic.
- (3)
- A numerical calculation based on the working conditions used shows that the high-temperature region is mainly concentrated in the range near the tool nose, and the highest temperature is on the back face.
- (4)
- A test platform to measure the tool temperature rise caused by the tool deflection was designed. The relative difference between the temperature calculated and the measured temperature was less than 5%. In addition, the temperature rise due to the tool deflection potential energy was consistent with the temperature rise during cutting, and was up to 6.57% of the total temperature rise of the cutting tool.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Density, (kg/m3) | |
| C | Specific heat, J/(kg·K) |
| K | Thermal conductivity, W/(m·K) |
| Heat flux, W/mm2 | |
| Current element, mm3 | |
| The f-th adjacent element, mm3 | |
| Temperature at the center ofthe current element , °C | |
| Temperature at the center ofthe adjacent element , °C | |
| A | Area vector of the elementSurface , mm2 |
| e | Distance vector across thefaces between elements, mm |
| Time step | |
| Current time, s | |
| Previous time, s | |
| the number of inner face elements | |
| Temperature on boundary, °C | |
| Normal heat flux on boundary, W/mm2 | |
| Thermal conductivity on boundary , W/(m K) | |
| Component of the external normal unit vector n perpendicular to interface S | |
| the number of element faces of the second type on boundary | |
| the number of element faces of the third type on boundary |
Appendix A
- 1
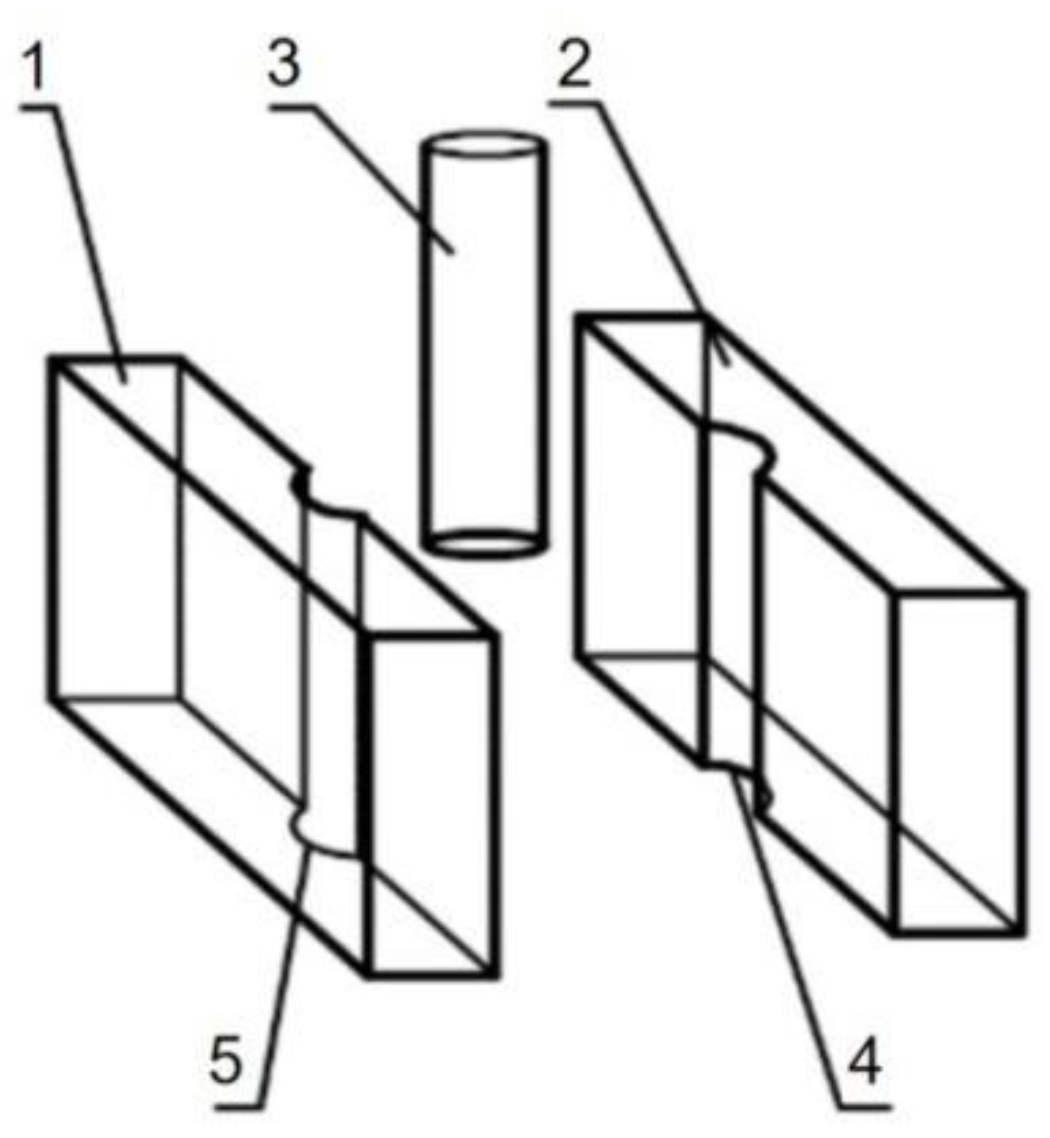
- To ensure that the experimental data were true and practical, a special customized cutting tool was used. A ring with a radius of 15 mm was placed around the tool 15 mm away from the tip and welded in place. The tool and the ring were concentric. The customized tool had two functions: First, it prevented interference between the two eddy current displacement sensors. Second, the cross-sections of the blade and the tip were the same, so that the displacement of the blade truly reflected the displacement of the tip.
- 2
- In order to minimize the impact of other factors, we had to limit the experimental conditions when measuring displacement:
- (1)
- The experiment was executed under cold machine conditions in order to diminish the influence of thermal error of machine tool.
- (2)
- In the experiment, it was necessary to monitor the vibration signal, reduce the vibration, and ensure the stability of milling.
- (3)
- The displacement information of no-load and load cutting should be measured simultaneously under the same conditions.
- 3
- In the manuscript, the cell-centered finite volume method was used. The control volume was usually a mesh element discretion from the computational domain, and the dependent variables were stored in the center of the cell. Any unstructured mesh was used to divide the computational domain, and the mesh element was used as the control equation of heat dissipation.
References
- Bi, Y.B.; Fang, Q.; Dong, Y.H.; Ke, Y.L. Research on 3D numerical simulation and experiment of cutting temperature for high speed milling of aerospace aluminum alloy. Chin. J. Mech. Eng. 2010, 46, 160–165. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.H. Systematic study on cutting force modelling methods for peripherailling. Int. J. Mach. Tool Manuf. 2009, 49, 424–432. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y. Modeling and avoidance of static form errors in peripheral milling of plates. Int. J. Mach. Tool Manuf. 1995, 35, 459–476. [Google Scholar] [CrossRef]
- Dotcheva, M.; Millward, H.; Lewis, A. The evaluation of cutting-force coefficients using surface error measurements. J. Mater. Process. Technol. 2008, 196, 42–51. [Google Scholar] [CrossRef]
- Colpani, A.; Fiorentino, A.; Ceretti, E.; Attanasio, A. Tool wear analysis in micromilling of titanium alloy. Precis. Eng. 2019, 57, 83–94. [Google Scholar] [CrossRef]
- Shaw, M.C. Metal Cutting Principles, 2nd ed.; Oxford University Press: Oxford, UK, 2005; pp. 9–12. [Google Scholar]
- Levin, P. A general solutions of 3-D quasi-steady-state problem of a moving heat source on a semi-infinite solid. Mech. Res. Commun. 2008, 353, 151–157. [Google Scholar] [CrossRef]
- Xu, H.; Chen, W.W.; Zhou, K.; Huang, Y.; Wang, Q.J. Temperature field computation for a rotating cylindrical workpiece under laser quenching. Int. J. Adv. Manuf. Tech. 2010, 47, 679–686. [Google Scholar] [CrossRef]
- Wang, Z. Study on the Temperature Field Modelling and the Real-Time Online Temperature Measuring Technique for the High Speed End Mill. Ph.D. Thesis, Harbin University of Science and Technology, Harbin, China, 2015. [Google Scholar]
- Putz, M.; Schmidt, G.; Semmler, U.; Dix, M.; Bräunig, M.; Brockmann, M.; Gierlings, S. Heat Flux in Cutting: Importance, Simulation and Validation. Procedia CIRP 2015, 31, 334–339. [Google Scholar] [CrossRef]
- Wu, B.H.; Cui, D.; He, X.D.; Zhang, D.H.; Kai, K. Cutting tool temperature prediction method using analytical model for end milling. Chin. J. Aeronaut. 2016, 29, 1788–1794. [Google Scholar]
- Wu, X.; Li, J.; Jin, Y.; Zheng, S. Temperature calculation of the tool and chip in slicing process with equal-rake angle arc-tooth slice tool. Mech. Syst. Signal Process. 2020, 143, 106793. [Google Scholar] [CrossRef]
- Islam, C.; Altintas, Y. A two-dimensional transient thermal model for coated cutting tools. Trans. ASME J. Manuf. Sci. Eng. 2019, 141, 071003–071014. [Google Scholar] [CrossRef]
- Shan, C.; Zhang, X.; Shen, B.; Zhang, D. An improved analytical model of cutting temperature in orthogonal cutting of Ti6Al4V. Chin. J. Aeronaut. 2019, 32, 759–769. [Google Scholar] [CrossRef]
- Reznikov, A.N. Thermophysical aspects of metal cutting processes. Mashinostroenie Mosc. 1981, 212. [Google Scholar]
- Kato, T.; Fujii, H. Temperature measurement of workpieces in converntional surface grinding. J. Manuf. Sci. 1998, 122, 297–303. [Google Scholar] [CrossRef]
- Rech, J.; Arrazola, P.J.; Claudin, C.; Courbon, C.; Pusavec, F.; Kopac, J. Characterisation of friction and heat partition coefficients at the tool-work material interface in cutting. CIRP Ann. 2013, 62, 79–82. [Google Scholar] [CrossRef]
- Gecim, B.; Winer, W.O. Transient temperatures in the vicinity of an asperity contact. ASME J. Tribol. 1985, 107, 333–342. [Google Scholar] [CrossRef]
- Zhao, J.F.; Liu, Z.Q. Modelling for prediction of time-varying heat partition coefficient at coated tool-chip interface in continuous turning and interrupted milling. Int. J. Mach. Tool Manuf. 2019, 147, 103467. [Google Scholar] [CrossRef]
- Liu, H.W. Mechanics of Materials. I, 4th ed.; Higher Education Press: Beijing, China, 2011; pp. 175–189. [Google Scholar]
- Liu, H.W. Mechanics of Materials. II, 4th ed.; Higher Education Press: Beijing, China, 2011; pp. 28–34. [Google Scholar]
- Chen, M.; An, Q.L.; Liu, Z.Q. Fundamentals and Applications of High Speed Cutting, 1st ed.; Shanghai Science and Technology Press: Shanghai, China, 2012. [Google Scholar]
- Zener, C. Elasticity and Anelasticity of the Metals; Science Press: Beijing, China, 1965. [Google Scholar]
- Jiang, F.L. Investigation of Transient Cutting Temperature of Workpiece and Cutting Tool in High Speed Intermittent Machining Process. Ph.D. Thesis, Shandong University, China, 2011. [Google Scholar]
- Casto, S.L.; Valvo, E.L.; Micari, F. Measurement of temperature distribution within tool in metal cutting experimental tests and numerical analysis. J. Mech. Sci. Technol. 1989, 20, 35–46. [Google Scholar] [CrossRef]
- Abukhshim, N.A.; Mativenga, P.T.; Sheikh, M.A. Investigation of heat partition in high speed turning of high strength alloy steel. Int. J. Mach. Tool Manuf. 2005, 45, 1687–1695. [Google Scholar] [CrossRef]
- Mabrouki, T.; Rigal, J.F. A contribution to a qualitative understanding of thermo-mechanical effects during chip formation in hard turning. J. Mater. Process. Technol. 2006, 176, 214–221. [Google Scholar] [CrossRef]
- Zhang, H.C. Ansys14.0 Theory Analysis and Engineering Application Example, 1st ed.; Machinery Industry Press: Beijing, China, 2012; p. 282. [Google Scholar]
- Sato, M.; Tamura, N.; Tanaka, H. Temperature Variation in the Cutting Tool in End Milling. ASME. J. Manuf. Sci. Eng. 2011, 133, 021005. [Google Scholar] [CrossRef]
- Shimanuki, K.J.; Hosokawa, A.; Koyano, T.; Furumoto, T.; Hashimoto, Y. Studies on high-efficiency and high-precision orthogonal turn-milling-The effects of relative cutting speed and tool axis offset on tool flank temperature. Precis Eng. 2020, 66, 180–187. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Diameter (mm) | 10 |
| Length (mm) | 70 |
| Blade length (mm) | 40 |
| Helix angle (°) | 35 |
| Number of teeth | 4 |
| Density (kg/cm3) | 14.8 |
| Young’s modulus (GPa) | 600 |
| Thermal conductivity (W/(m·K)) | 79.5 |
| Coefficient of thermal expansion (m/°C) | 5.2 |
| Specific heat (J/(kg·K)) | 209.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Ye, W.; Xu, X. Numerical and Experimental Investigation of the Temperature Rise of Cutting Tools Caused by the Tool Deflection Energy. Machines 2021, 9, 122. https://doi.org/10.3390/machines9060122
Guo Y, Ye W, Xu X. Numerical and Experimental Investigation of the Temperature Rise of Cutting Tools Caused by the Tool Deflection Energy. Machines. 2021; 9(6):122. https://doi.org/10.3390/machines9060122
Chicago/Turabian StyleGuo, Yunxia, Wenhua Ye, and Xiang Xu. 2021. "Numerical and Experimental Investigation of the Temperature Rise of Cutting Tools Caused by the Tool Deflection Energy" Machines 9, no. 6: 122. https://doi.org/10.3390/machines9060122
APA StyleGuo, Y., Ye, W., & Xu, X. (2021). Numerical and Experimental Investigation of the Temperature Rise of Cutting Tools Caused by the Tool Deflection Energy. Machines, 9(6), 122. https://doi.org/10.3390/machines9060122





