Abstract
This review is dedicated to balancing methods that are used to solve the rotor-balancing problem. To ensure a stable operation over an operating speed range, it is necessary to balance a rotor. The traditional methods, including the influence coefficient method (ICM) and the modal balancing method (MBM) are introduced, and the research progress, operation steps, advantages and disadvantages of these methods are elaborated. The classification of new balancing methods is reviewed. Readers are expected to obtain an overview of the research progress of existing balancing methods and the directions for future studies.
1. Introduction
Rotor unbalance is one of the main reasons for the vibration of rotating machinery [1]. A rotor unbalance can be induced by defective materials, errors during processing and assembling, an asymmetric structure, rotor wearing, temperature changes during operation, and so on [2]. The unbalance of a rotor is inherent that the rotor’s rotation axis is not coincident with the geometric axis, resulting in rotational inertial force motivated when rotating (shown in Figure 1). The unbalance can be eliminated by making the inertia principal axis coincide with the rotor’s rotational axis using redistribution. However, the ideal balance is hard to achieve in practice. Generally, the rotor balance is considered to have been reached in engineering if a rotor is operating steadily, namely, when the vibration amplitude of a rotor is reduced to an allowable range [3].
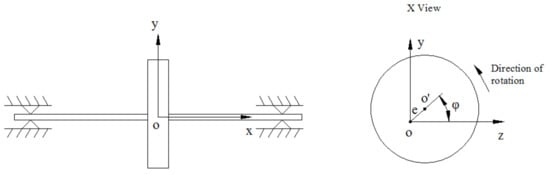
Figure 1.
A rotating rotor whose axis is not coincident with the geometric axis. (x-the rotor’s rotation axis, o-the disk’s rotation center, o’-the disk’s geometric center, e-the disk’s eccentric distance, φ-the disk’s rotation phase angle.)
In the early 1930s, researchers began to study rotor-balancing methods, including the ICM, the MBM, and other methods. Currently, the demand for precision balancing methods is increasing, particular for heavy-load and high-speed rotating machinery. Since the existing balancing methods still have significant limitations, more research is needed to improve these methods or develop new methods [4].
In 1991, Parkinson [5] gave a review of rotating machinery. Balancing procedures for both rigid and flexible shafts were discussed, but emphasis was on balancing flexible shafts that run in high speed. Foiles [6] surveyed the methods in balancing rotating machinery including ones that use influence coefficient, modal, unified, no phase, and no amplitude to balance. Computational algorithms and physical concepts in rotor balancing were involved. Zhou [4] presented the research work on dynamic modeling and analysis techniques of rotor systems and reviewed the research work performed in real-time active balancing and active vibration control for rotating machinery as well.
This review is dedicated to balancing methods, and it is organized as follows. With regard to the development process, operation steps, advantages and disadvantages, Section 2 and Section 3 deal with the ICM and the MBM, respectively. Section 4 emphasizes the classification of new balancing methods. Nonlinear rotor-balancing methods, transient rotor-balancing methods, homologous information fusion rotor-balancing methods and balancing methods for specific rotors are discussed emphatically in this section. In Section 5, future research directions regarding new rotor-balancing methods are proposed.
2. Review of the ICM
2.1. Development of the ICM
As mentioned previously, rotor unbalance is widely produced in manufacturing and servicing. Generally, the unbalance is randomly distributed along the axis of rotation and difficult to obtain completely. These unbalances cause inertial force to excite the rotor vibration when running. Actually, it is not necessary to know the unbalance distribution in the rotor completely. As long as the inertial force caused by using a set of correction weights counteract the vibration caused by the original unbalance of the rotor, the rotor will be balanced. An influence coefficient matrix is needed to calculate the correction weights.
The influence coefficient matrix and the correction weights can be identified by measuring the initial vibration of the different balancing planes and the vibration after installing the trial weights. This treatment, called the ICM, was initially used to balance a rigid rotor. For a rigid rotor, this purpose can be achieved by choosing two balancing planes at a balancing speed. American scholar Thearle [7] first proposed this method based on an experiment. Since this method can only be applied to a rigid rotor, Baker [8] improved upon the method, but the experimental result was not satisfactory.
After the 1950s, rotors became more flexible and the rotor unbalancing became more prominent, so there was an urgent need for an improved balancing method. The bend of a flexible rotor is related to its speed. There is no guarantee that a rotor will reach balance within an operating speed range even when choosing a balancing speed, which is different from the behavior of a rigid rotor. In order to guarantee a smooth pass through all the bending critical speeds, multiple balance speeds and multiple balance planes should be chosen. In other words, the ICM for a flexible rotor should use multiple planes and multiple speeds.
Goodman [9] published a well-known paper on using the least squares method to compute balance corrections and verified it by experiments. The paper elaborated on the theoretical foundation of the ICM and applied the principle of the least squares method to the ICM. The key to this application was the reduction of the amount of residual vibrations of the measuring points. This method solves the contradiction between the number of measure points and balance planes. The number of measure points is not restricted, and this number can be far higher than the number of balance planes. This method satisfies the demands of balancing the flexible rotors and the shaft system with multiple planes and multiple speeds. Since the use of this method began, the rotor-balancing process has been programmed so that the ICM has a practical meaning.
Anderson et al. [10] used the improved ICM to calculate the balance correction. The experiments verified that the adoption of the balancing method is effective in reducing the vibration of large rotors. The experimental speed passes through three critical speeds: two rigid critical speeds and one bending critical speed. As the sliding bearing is located near the node of the rotating shaft, the damping at the bending critical speed is very small, which causes significant vibration at the bending critical speed. The researchers also discovered that the balancing results also depend on the accuracy of experimental instruments and the experience of the operators. If the dynamic response of the unbalanced rotor is known, the accuracy of balance process can be greatly improved.
Since 1971, American scholars have paid more attention to the balance theory and experiment of flexible rotors. As a typical example, Tessarzik [11] investigated four distinct practical aspects of the flexible rotor balancing: (1) the balance of rotors operating through multiple bending critical speeds; (2) the balance of rotors supported by both rigid and flexible bearings, where the latter had significantly different stiffness in the horizontal and vertical directions causing severe ellipticity in vibration orbits; (3) the balance of rotors with various amounts of measured vibration response information (e.g., numbers of vibration data sets and numbers and types of vibration sensors) and with different numbers of correction planes; (4) the balance of rotors with different (though arbitrary) initial unbalanced configurations. The balancing method was in every instance effective, practical, and economical and it permitted safe rotor operation over the full-speed range.
Gu [12] and Zhong et al. [13] described the ICM for flexible rotors and a method that combined the least squares method with the ICM. Then Deng [14] proposed a high-speed rotor-balancing method with multiple speeds, multiple balance planes and multiple balance steps. Bin et al. [15] established a finite element model of rotor and calculated the influence coefficients through added trial weights. However, due to nonlinearity, the stiffness and damping could not be estimated accurately, and thus the results had inevitable errors.
2.2. Operational Steps of the ICM
- Choose appropriate balance planes and experimental speeds. In general, the positions of balance planes are determined by engineers when designing rotors. The number of the balance planes should not be less than the modal modes within the maximum working speed. The experimental speeds should be chosen in different working conditions and the sensors should be set up on the specific axial positions (e.g., on the bearing support) as measurement points.
- Measure the initial vibration. Start the rotor and measure the vibrations (including the amplitude and the phase angle) at different measurement points and at different speeds.
- Measure the vibration after installing trial weights on the rotor. Install the trial weight whose mass is known on the first balance plane and record its position (including the radius and the phase angle). Start the rotor again and measure the vibrations at different measurement points and at different speeds. Repeat these operations in other balance planes.
- Calculate the influence coefficients and the balance corrections. When the rotor rotates at , the influence coefficients can be calculated using:where denotes the influence coefficient, is the vibration amplitude at the ith measurement points and jth balance plane, is the initial vibration amplitude, denotes the mass of the trial weights, the radius and the phase angle are used to locate the trial weight, and .
The influence coefficient matrix is:
where is the number of measurement points, is the number of speeds and is the number of balance planes.
Therefore, the balance corrections are defined by:
where , , , denote the balance corrections.
Three possibilities exist when solving the matrix equations:
(i) .
In this case, the number of balance planes is greater than the number of balance conditions. In theory, the total vibration can be decreased by choosing random balance planes. However, the question is which combinations will result in the best balancing result. To answer this question, the balancing problem becomes a mathematical issue regarding the choice of the best combination of the balance planes. This issue can be solved by adding some restrictions.
(ii)
The number of balance planes for this case is equal to the number of balance conditions. According to Equation (3), the inertial forces generated by adding correction weights on q balance planes counteract the vibration caused by the inherent unbalance of the rotor. One can obtain the following equation:
This equation has unique solution. As a result:
where is the balance correction (mass-radius product) installed on the jth balance plane and is the phase angle of the balance correction on the rotor.
(iii) .
The number of balance planes is less than the number of balance conditions. In this case, Equation (3) becomes incompatible. This is a common problem in the practical balancing process, and it can be solved using the least square method.
- 5.
- Balancing the rotor according to the calculated results. Due to the inevitable errors in the principle, measurement and operation, it is necessary to repeat the balancing process until the required precision is reached.
2.3. Advantages and Disadvantages of the ICM
The main advantages of the ICM in relation to the development and balance processes are as follows:
- As each element is measured by experiment, these coefficients can reflect the influences of the vibration mode, the support stiffness, and other factors.
- There is no need to know the dynamic response in advance. Enough sensitive information can be achieved at all critical speeds if the rotor operates safely within the normal speed range.
- The ICM is readily computerized and automated.
- Data manipulation techniques can be used to compensate for measurement errors.
- The ICM is an entirely empirical procedure, which requires minimal foreknowledge of rotor dynamics.
The main disadvantages of the ICM are as follows:
- As each influence coefficient is measured by experiment, some measurement error is inevitable.
- A significant number of revolutions are required to obtain sensitivity data at the highest balancing speed.
- The use of the least square method can affect the previously balanced modes, unless these modes are heavily weighted, and the other modes may receive insufficient emphasis.
- The misuse of the non-independent balance planes often results in impractical (and generally inappropriate) results, and the balance process thus becomes invalid.
3. Review of the MBM
3.1. Development of the MBM
The MBM operates by separating the principal mode of vibration and balancing each mode independently to achieve balance [12]. This method is based on the rules of flexural deformation for an unbalanced rotor. The unbalance can be expressed in the form of each vibration mode, and the rotor deflection of each mode can be stimulated by the corresponding vibration unbalance. When the rotor operates near the critical speed, the deflection can be approximately considered as a vibration mode, and then the deflection is determined by the modal unbalance and the damping of the rotor-bearing system. When using several concentrated balance corrections to reduce the unbalance of each vibration mode, the corresponding deflection will be reduced. Thus, the balance can be achieved so that the rotor can run smoothly.
In order to obtain the balanced mode of the rotor, appropriate modal analysis methods should be used. Urbikain et al. [16,17] presented vibration and oscillation equations in turning. New ways of solving the equations were raised such as Chebyshev method and the ode23 algorithm. Experiments show that these methods are effective to obtain the vibration modes of machine tools, and useful in machine tool designing and tool machining.
Grobel [18] proposed a balancing method for the turbine rotor that was related to the earliest MBM. Kellenberger et al. [19,20] undertook an in-depth study of the MBM, where the N and (N+2) plane balancing methods for the flexible rotor were proposed. An experiment on a 650-MW turbo-alternator was performed by N and (N+2) plane balancing methods. The results show that the N+2 method was able to achieve better accuracy but needed additional effort and time compared with N method.
Palazzolo et al. [21] developed a method for determining the unbalance distribution of a flexible rotor without trial weights and verified it by experiments. By knowing the rotor modal mass and the mode shape, a modal balancing distribution can be calculated. This relationship provides a quick procedure to estimate the first mode balance correction weight for both the magnitude and the angular location. However, there are several limitations to this procedure. The rotor should be capable of operating through the critical speed region, and also the rotor should be lightly damped.
Meacham [22] presented a balancing procedure utilizing the Complex Modal Method for a linear flexible rotor having a residual bow. The method does not require trial runs. However, a valid mathematical model is required to obtain the rotor’s modal parameters, which are used to relate the balance corrections to the measured responses. Several balancing strategies based on the extension of previous work were suggested for single-speed balancing. Two applications were presented, a gas turbine system and an operating steam turbine-generator system.
In the 21st century, the MBM has been improved both in theory and by experiment. Bucher [23] summarized the differences between the mathematical models used for the dynamic analysis of nonrotating and rotating structures and verified it by experiments. Different types of rotating structures should use different models. The paper made a classification of different models and pointed out their preconditions and characteristics. Then relevant modal experiments were carried out to validate the proposed theory.
3.2. Operational Steps of the MBM
(a) The initial vibration should be measured firstly. Install the rotor on the dynamic balancing machine or the bearing support. Drive the rotor close to its first critical speed, usually at 90%, and then the unbalanced vibration of the rotor or the bearing support can be measured and recorded.
(b) Measure the vibration after installing the trial weights. Install a trial weight on the balance plane near the middle of the rotor (near the peak of the vibration mode, as shown in Figure 2). In order to simplify the calculation, the position of the trial weight is similar to the radius of the balance correction, and the phase angle can be chosen freely. Then drive the rotor to the same speed as in step (a), and measure and record the unbalance vibration of the rotor or the bearing support.
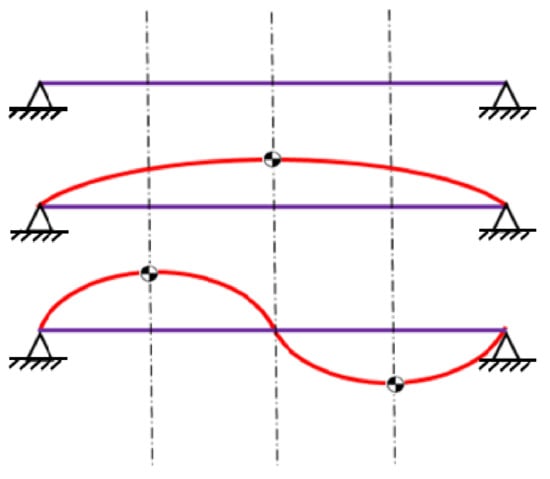
Figure 2.
Modal shapes of simply supported rotors.
(c) Calculate the balance correction and balance the first mode shape. The balance correction is given by:
where is the initial unbalance vibration vector, and its phase angle is determined by the arbitrary set phase angle baseline, is the vibration vector after installing the trial weight, reflects the trial weight effect (as shown in Figure 3), is the mass of the balance correction, is the radius of the position where the balance correction is installed, is the mass of the trial weight, the radius is used to locate the trial weight, usually the value of is equal to .
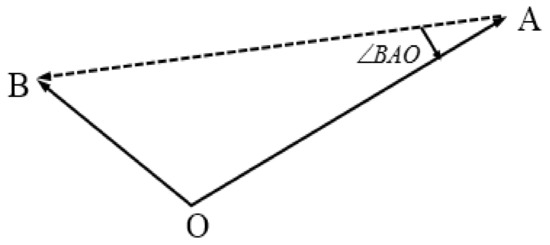
Figure 3.
Vibration vector diagram.
From the phase angle position of the trial weight turns, is the position of the balance correction.
According to the calculation results, the first mode shape can be balanced. In order to reduce the unbalanced vibration to an allowable value, the steps must be repeated.
(d) Repeat the aforementioned operations and balance other vibration modes within the working speed range.
3.3. Advantages and Disadvantages of the MBM
The main advantages of the MBM in terms of its development and balance process are as follows.
- The number of start–stop times required at the highest balancing speed is minimized.
- Good sensitivity at the highest balancing speed can always be achieved.
- Balancing a specific mode is permitted, and this balancing does not affect the previously balanced (usually, lower) modes.
- The MBM can be an entirely empirical procedure that requires only an understanding of the modal character of the unbalance. Nevertheless, it is in practice most often used in conjunction with analytically determined mode shapes rather than in an empirical manner.
By contrast, the main disadvantages of the MBM are:
- The planar mode assumption can be invalid for systems with substantial damping or bearing cross-coupling effects.
- In theory, balance planes can be set at an arbitrary axial location, but for sensitivity purposes, they are usually set at peaks and troughs of the rotor’s vibration mode. Therefore, in order to determine the test speeds and balance planes, the critical speed and its vibration mode within the operating speed range should be understood before experimenting.
- Balancing results are generally based on the vibration measured by only one or two sensors for a specific mode, which cannot result in a uniformly well-balanced rotor.
- Modal balancing is not usually automated and it does not easily lend itself to production applications.
- The trimming of lower modes while balancing higher modes is liable to affect the higher modes (although, in theory, this can be avoided with the addition of extra balancing planes).
4. New Balancing Methods
After the ICM and MBM were proposed, they were gradually improved [24], and subsequently, many new methods have been developed.
For example, in order to take advantage of the ICM and MBM, Darlow et al. [25] proposed a unified balancing approach (UBA) and verified its effectiveness through a series of experiments. More specifically, the experimental results confirmed the superiority of this method for a supercritical shaft and for multiple-mode balancing in particular. Afterwards, Darlow [26] detailed the three principal flexible rotor balancing methods: the MBM, the ICM and the UBA, in terms of a theoretical basis and specific implementation procedures. The methods have been compared from a procedural standpoint and results from a series of comparative tests are presented. The test results indicate the superiority of the UBA.
Beyond these methods, scholars have improved the classical methods and proposed many new balancing methods from different angles, including the nonlinear rotor-balancing methods, transient rotor balancing methods, balancing methods based on homologous information fusion technology, balancing methods for specific rotors, and so on. Each new method highlights different factors.
4.1. Nonlinear Rotor-Balancing Methods
The classical balancing methods are based on a linear assumption, and thus the unbalance excitation has a linear relationship with the response. By installing trial weights, the linear relationship between the excitation and the response can be identified so that the balancing process can be completed. For a nonlinear rotor system, however, the unbalance excitation has a nonlinear relationship with the response, and therefore if one uses linear assumption, the results cannot reflect the real case. As a result, the nonlinear dynamic theory should be employed to reveal the various nonlinear dynamics [27] and nonlinear rotor balancing methods should be developed.
Luo et al. [28] established a dynamic model with nonlinear stiffness for an elastic shaft. They studied the periodic response of the unbalanced system and the nonlinear dynamic behavior, including bifurcation and chaos, by using numerical integration and Poincare mapping. The result shows that both the eccentricity and the nonlinear coefficient were the reasons for chaotic motion. The chaotic motion can cause instability, and thus it is necessary to consider the influence of nonlinearities in designing a rotor and in the process of rotor balancing.
Guskov [29] presented a generalized version of harmonic balance coupled with arc-length continuation, which was carried out in order to study the nonlinear responses of a modified Jeffcott rotor system with piece-wise radial stiffness that was subject to multiple unbalances. Numerically, the nonlinear terms were taken into account via an alternating frequency-time domain procedure (AFT), which is involved in a multidimensional FFT. An improvement to the AFT approach was proposed.
Turpin et al. [30] considered the nonlinearity of bearings and built an equivalent linear system modal using the ICM and the Lagrange equation, and they achieved an accurate correction of the nonlinear system.
Cao et al. [31] proposed a nonlinear transfer function method for balancing rotors by incorporating the oil slick nonlinearity of a sliding bearing. This method further improved the balancing accuracy.
Nauclér et al. [32] considered the problem of unbalance estimation. They transformed the nonlinear problem into a linear problem. Two procedures were compared, and the statistical accuracy was analyzed. Through the example of the unbalance estimation of a separator, the nonlinear approach was shown to give superior performance.
Green et al. [33] presented a nonlinear bifurcation analysis of the dynamics of an automatic dynamic balancing mechanism for rotating machines. The results revealed the broad trends on the existence of a stable, dynamically balanced steady-state solution for specific rotation speeds and eccentricities. However, the analysis also revealed other potentially attracting states: nontrivial steady states, limit cycles, and chaotic motion, which were not in balance.
4.2. Transient Rotor-Balancing Methods
It can be observed that traditional rotor-balancing methods are used at the steady speeds. With regard to the problems of flexible rotors with excessive vibration and phase angles that are unstable at critical speeds, transient rotor-balancing methods should be developed.
Yang et al. [34] proposed that the transient dynamic characteristics should be further studied after reviewing the rotor dynamics from 2000 to 2010. In 1998, Chen et al. [35] developed the transient balancing method with the use of the ICM to balance a flexible rotor. In order to obtain the transient responses, a transfer matrix method was combined with the Wilson-method. The results verify that the transient balance method is feasible.
Zheng et al. [36], Fu et al. [37], Huang et al. [38] and Huang [39] all adopted the transient balancing method to balance the rotor system. Among these authors, Fu et al. [37] considered the uncertainty of the rotor during the balancing process, and Huang [39] discussed the transient responses of a dual-rotor system.
4.3. Balancing Methods Using Homologous Information Fusion Technology
Rotating machinery is a multisource information system, including the information sources of the vibration, pressure, flow, and temperature, this system has a common time and space reference system. Compared to a single-source information signal test system, the multisource information fusion method can cover a signal more comprehensively and improve the precision of a signal test effectively. However, the balance results of traditional balancing methods largely depend on whether a signal can be accurately measured. Therefore, a single measuring point cannot reflect the real vibration signals. In order to fix this issue, balancing methods based on homologous information fusion technology should be developed.
Among the type of homologous information fusion technologies, there are three mature technologies: the full spectrum technology of the Bently Nevada Corporation [40], the Holospectrum technology of the team of academician Qu et al. [41,42] and the full vector spectrum technology of Han [43,44].
The first technology is the full spectrum technology of the Bently Nevada Corporation [40]. One advantage of this technology is high resolution, and another advantage is that the procession direction is easy to identify. The disadvantages are the difficulties in accurately expressing the vibration intensity and in analyzing the vibration.
Then the team of academician Qu [41,42] developed the Holospectrum technology. The advantage of this technology is that the whirling motion intensity in each harmonic frequency and phase can be reflected directly, and thus, the operators can understand the working conditions. Its disadvantages are the difficulties in analyzing the vibration energy and in the mixture of the test track due to the low resolution.
Later on, Han [43,44] developed the full vector spectrum technology. One advantage of this technology is reflected in the high resolution, and another advantage is that it is easy to combine with the intelligent diagnosis method. However, this method pays less attention to the phase information and the multisource information fusion.
Based on the three technologies discussed above, several scholars have conducted further research. Xu and Qu [45] and Lang et al. [46] conducted a comprehensive test on the rotor unbalance, but this method complicated the balancing process. In addition, Xu et al. [47] developed a new rotor balancing method by using the balancing objective of the ICM and the initial phase point of Holospectrum technology. A simple flexible rotor with continuous mass distribution, as shown in Figure 4, was chosen as the numerical example. The theoretical model of the rotor is shown in Figure 5. Both the simulation and experimental results show that this method can reduce the residual vibrations effectively.
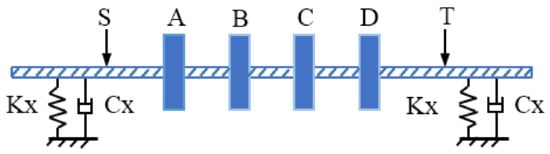
Figure 4.
Configuration of the numerical example [47]. (A,B,C,D-four disks on the shaft, Kx- stiffness of bearing, Cx- damping of bearing, S,T- measuring plane locations.)
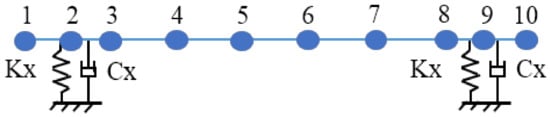
Figure 5.
Theoretical model of the numerical example [47]. (1-10-ten lumped masses, Kx-stiffness of bearing, Cx-damping of bearing.)
4.4. Balancing Methods for Specific Rotors
The stability requirement for modern rotating machinery has increasingly risen. Apart from the increased accuracy in selecting suitable material, processing, assembling, and so on, rotor balancing is one of the indispensable steps before putting a rotor into operation. Using different methods to balance different types of rotors can greatly improve the effect of the balance. In order to balance the specific rotors, such as dual-rotor system, bending rotors, asymmetric rotors, and overhung rotors, specific methods should be developed.
4.4.1. Balancing Methods for Asymmetric Rotors and Overhung Rotors
The rotor system includes the rotating disks, shafts, blades, bearing, seal and housing. Both rotor and stator parts may be anisotropic. Han [48] studied the phenomenon of multiple harmonics in the unbalance response of anisotropic rotors and found that each harmonic is combined with multiple modal parameters and proposed the concept of dominant balancing mode. Kang et al. [49] derived the influence coefficient matrix for anisotropic rotors. The results show that two trial operations are required for one balancing plane. A modified influence coefficient method was proposed by using forward precessions to calculate the influence coefficients and imbalance distribution. Later Kang et al. [50] further improved on this rotor balancing method. Yu et al. [51] and Zhang [52] studied the vibration response and balancing methods of the overhung rotors.
4.4.2. Balancing Methods for a Dual-Rotor System
For a dual-rotor system, the vibrations of the inner and outer rotors are highly coupled because of the influence of the intershaft bearing. It is well known that this bearing is both a key and weak component. Liao et al. [53] analyzed the vibrations of a dual-rotor system that had intershaft bearings. The results of this analysis show that the anisotropy of the intershaft bearings stiffness can cause gravity critical phenomena. In addition, a beat vibration can occur when the two rotors are operating at approximate speeds. Han et al. [54] studied the beat vibration, and they found that the beat vibration was related to the speed differences and the phase of the unbalance. Therefore, the unbalance response becomes more complicated.
However, few studies on the balance of dual-rotor system have been performed. The main difficulties of these studies involve identifying the unbalance response of the two rotors from the complex vibration signal and accounting for the interaction of the unbalance vibrations between the two rotors.
Zhang et al. [55] proposed the use eight ICM to achieve a balance of the dual-rotor system with a very small speed difference. The theoretical analysis and the experimental study showed that the vibrations of the inner and outer rotors had little effect on each other. Thus, the eight ICM could balance the dual-rotor system quickly and efficiently.
Yang et al. [56] proposed a new method for separating the vibration signals of a dual-rotor system with a small speed difference. The magnitude and phase values of the unbalanced weights were obtained directly by sampling the vibration signal synchronized with a reference signal. The balance process was accomplished using an ICM. This method was successfully applied to balance the dual-rotor systems such as centrifuges.
In practice, when balancing a dual-rotor system in an aeroengine, a suitable treatment is still to balance the two rotors separately. However, due to the coupling effect of the intershaft bearing, the clearance of the bearings and the nonlinear interaction of the rotors, the system unbalance can occur even when the single rotor has been well balanced individually. Thus, the balancing methods for a dual-rotor system are worthy of further research.
4.4.3. Balancing Methods for Bending Rotors
Unbalancing and bending are considered to be the main causes of vibration for rotating machinery [57]. The balancing methodology is explained in Figure 6. Two classifications exist for the bending faults: (a) according to the causes of bending, there is initial bending, general thermal bending, and thermal bending due to rub [58] and (b) in accordance with the properties of bending, there are temporary and permanent bendings [59]. Temporary bending is due to the external experimental changes or external force applied to the rotor when the rotor does not need balancing. However, once the force exceeds a certain limit, permanent bending can occur, and the rotor would have significant vibrations.

Figure 6.
Flow chart of the balancing methodology [57].
Nicholas et al. [60,61] presented three methods for balancing a rotor with residual shaft bending. The first method balanced the total shaft amplitude to zero at the balance speed. The second method balanced the elastic deflection to zero at the balance speed, leaving the residual bow amplitude. The third method balanced the total shaft amplitude to zero at the critical speed without actually operating the rotor at the critical speed.
Deepthikumar et al. [62] considered the synchronous response of rotors as a function of influence coefficients. The coefficients were analytically derived by using the transfer matrix method for a rotor-bearing system having both mass unbalance and a bow. This method is helpful for estimating the correction mass in a single trial run and a single balancing plane, and thus, reducing the cycle time for balancing flexible rotors.
Liu et al. [63] researched the overhung thermal bending rotors, Jeffcott rotors and simply supported rotors. They studied the vibrations and presented a general program that was helpful for modal balancing theory. In addition, scholars such as Parkinson et al. [64], Rao et al. [65] and He et al. [66] conducted correlational studies for bending rotors.
4.5. Other Rotor Balancing Methods
In addition to the aforementioned methods, the following list presents some other methods:
- Transfer function method. Cao et al. [67] examined the selection of a balance plane in high-speed balancing methods and proposed the transfer function method for high-speed flexible rotors. Tiwari et al. [68] applied a similar ideology, identifying the unbalance using a numerical simulation. Khulief et al. [69] generalized this method to field balancing.
- The balancing method without trial weights. For the cases of installing trial weights and multiple start–stop actions of rotors, Wang et al. [70] proposed a balancing method without trial weights for high speed flexible rotors. By using the finite element method to simulate the dynamic characteristics of the rotor, in this way, the vibration mode function can be obtained. Li et al. [71] carried out a series of tests without the trial weights on a high-speed flexible simulated rotor tester. They found that the vibration amplitude was reduced by more than 70% after one balance. The results verified that this method could obtain the unbalance magnitude and direction accurately and quickly. However, because of the limitation of the rotor tester, this method can only balance the first mode shape. Liu et al. [72] used a similar method, but it had the disadvantage of the dependence of the balance accuracy on the finite element calculation.
- The local balancing method, including the vector analytical method and the three-shooting method [73]. These methods have been used in practice [74,75]. However, the disadvantage of these methods is that they require multiple start–stop actions [76,77], which can cost a lot of money and time.
- Online balancing method. Zhang [78] reviewed the online balancing research achievement, proposed a new type of pure mechanical balancing head and achieved online balancing. Wang et al. [79] presented the electromagnetic online automatic balancing system and discussed its principle, structure and balancing method.
- Balancing method by using a specific device. For aeroengines, engineers often used the Multiplane/Multispeed Balancing Method or the Exact Point-Speed ICM. This method is based on the ICM and it is generally carried out on a special balancing device. For this method, multiple planes and multiple speeds are needed to obtain enough influence coefficients. For a slender shaft, it is usually necessary to attach a precision collar. By using this method, NASA had successfully balanced the engines of a T700 [80,81], T53/T55 [82,83], and so on. In China, Deng et al. [84] adopted a similar method to balance engines.
- Using slow-speed data to balance high-speed rotors. Tresser et al. [85] proposed that by using slow-speed data via parametric excitation can achieve balance for super-critical rotating structures. Analytical, numerical and experimental results were shown to validate this method.
- New methods that combine emerging technologies with traditional balancing methods. Untaroiu et al. [86] combined the convex optimization technology with the ICM to balance flexible rotors. Mohammadi et al. [87] combined the Imperialist Competitive Algorithm with the ICM to balance flexible rotors. Saldarriaga et al. [88] used an inverse problem approach to balance flexible rotating machines.
5. Conclusions
This paper provided a detailed discussion of the rotor-balancing methods, including traditional methods and some new methods. Based on the discussion, future research directions are proposed as follows.
- The nonlinearity cannot be ignored for the system containing non-smooth factors such as collision, shock and dry friction. Therefore, the conventional balancing method based on linear assumption should be modified using nonlinear theory.
- For high-speed rotor systems, such as aeroengine rotor systems and large thermal power-generation unit rotor systems, it is harmful if starting and stopping the rotor multiple times. Therefore, further research needs to be done in order to improve the balancing efficiency. The transient rotor balancing method and the method of using slow-speed data to balance the high-speed rotor system may solve this problem.
- Balancing methods should be improved by use of the multisource information fusion technologies. The signals of the unbalanced vibration of the rotor are not only determined by the dynamics of the rotor, but also closely related to test and analysis technology. Multi-information fusion and integration technologies will play a certain role in improving the accuracy and speed of rotor dynamic balance.
- For special rotor systems, different kinds of methods should be applied. For example, when balancing the dual-rotor system of an aeroengine, if balancing the inner and outer rotors separately, the system unbalance would occur even if a single rotor has been balanced. Therefore, a specific balancing method should be developed for dual-rotor systems.
- More and more methods such as transfer function method, no trial weights methods, online balancing methods will be developed to make rotor dynamic balance more convenient, more accurate, more energy saving and faster.
Author Contributions
The author contributions are as follows: S.C. was in charge of the whole trial; L.L. wrote the manuscript; J.L., R.N. and L.H. assisted with consulting literature. All authors have read and agreed to the published version of the manuscript.
Funding
Supported by National Natural Science Foundation of China (Grant No. 11872045).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects.
Data Availability Statement
Not applicable.
Acknowledgments
The authors sincerely thank Shiyu Wang of Tianjin University for his critical discussion and reading during manuscript preparation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, M.; Marangoni, R.D. Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance, part i: Theoretical model and analysis. J. Sound Vib. 1994, 176, 663–679. [Google Scholar] [CrossRef]
- Wang, H.Y.; Zhang, Z.S.; Xu, X.L. Rotor Balancing Technology and Balancing Machine, 1st ed.; China Machine Press: Beijing, China, 1988. (In Chinese) [Google Scholar]
- Deng, W.Q.; Tang, G.; Gao, D.P. Research summary of rotor dynamic characteristics and dynamic balance. Gas Turbine Exp. Res. 2008, 21, 57–62. (In Chinese) [Google Scholar]
- Zhou, S.; Shi, J. Active Balancing and Vibration Control of Rotating Machinery: A Survey. Shock Vib. Dig. 2001, 33, 361–371. [Google Scholar] [CrossRef]
- Parkinson, A.G. Balancing of Rotating Machinery. Proc. Inst. Mech. Eng. Part C Mech. Eng. Sci. 1991, 205, 53–66. [Google Scholar] [CrossRef]
- Foiles, W.C.; Allaire, P.E.; Gunter, E.J. Rotor balancing. Shock Vib. 1998, 5, 325–336. [Google Scholar] [CrossRef]
- Thearle, E. Dynamic balancing of rotating machinery in the field. Trans. ASME 1934, 56, 745–753. [Google Scholar]
- Baker, J. Methods of rotor-unbalance determination. ASME J. Appl. Mech. 1939, 61, A1–A6. [Google Scholar] [CrossRef]
- Goodman, T.P. A least-squares method for computing balance corrections. J. Manuf. Sci. Eng. 1964, 83, 273–277. [Google Scholar] [CrossRef]
- Tessarzik, J.M.; Badgley, R.H.; Anderson, W.J. Flexible rotor balancing by the exact point- speed influence coefficient method. J. Eng. Ind. 1972, 94, 148–158. [Google Scholar] [CrossRef]
- Tessarzik, J.M. Flexible Rotor Balancing by the Influence Coefficient Method: Multiple Critical Speeds with Rigid or Flexible Supports; National Aeronautics and Space Administration: Washinghton, DC, USA, 1975. [Google Scholar]
- Gu, J.L. Rotor Dynamics; National Defense Industry Press: Beijing, China, 1985. (In Chinese) [Google Scholar]
- Zhong, Y.E.; He, Y.Z.; Wang, Z. Rotor Dynamics; Tsinghua University Press: Beijing, China, 1987. (In Chinese) [Google Scholar]
- Deng, W.Q. Experiment Investigation of Dynamic Characteristics and High Speed Dynamic Balance of a Aeroengine Flexible rotor. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2006. (In Chinese). [Google Scholar]
- Bin, G.; Yao, J.; Jiang, Z.; Gao, J. Solving method of influence coefficient for rotor dynamic balance based on finite element model. J. Vib. Meas. Diagn. 2013, 33, 998–1002. (In Chinese) [Google Scholar]
- Urbikain, G.; Olvera, D.; López de Lacalle, L.N.; Elías-Zúñiga, A. Stability and vibrational behaviour in turning processes with low rotational speeds. Int. J. Adv. Manuf. Technol. 2015, 80, 871–885. [Google Scholar] [CrossRef]
- Urbikain, G.; Alvarez, A.; López de Lacalle, L.N.; Arsuaga, M.; Alonso, M.A.; Veiga, F. A Reliable Turning Process by the Early Use of a Deep Simulation Model at Several Manufacturing Stages. Machines 2017, 5, 15. [Google Scholar] [CrossRef]
- Grobel, L.P. Balancing turbine-generator rotors. Nav. Eng. J. 2010, 65, 868–874. [Google Scholar]
- Kellenberger, W. Balancing flexible rotors on two generally flexible bearings. Brown Boveri Rev. 1967, 54, 603–617. [Google Scholar]
- Kellenberger, W. Should a Flexible Rotor Be Balanced in N or (N + 2) Planes? Trans. ASME 1972, 548–588. [Google Scholar] [CrossRef]
- Palazzolo, A.B.; Gunter, E.J. Modal balancing of a multi-mass flexible rotor without trial weights. In Proceedings of the ASME 1982 International Gas Turbine Conference and Exhibit 1982, London, UK, 18–22 April 1982; ASME: New York, NY, USA, 1982; pp. 1–11. [Google Scholar]
- Meacham, W.L.; Talbert, P.B.; Nelson, H.D.; Cooperrider, N.K. Complex modal balancing of flexible rotors including residual bow. J. Propuls. Power 1988, 4, 245–251. [Google Scholar] [CrossRef]
- Bucher, I.; Ewins, D.J. Modal analysis and testing of rotating structures. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2001, 359, 61–96. [Google Scholar] [CrossRef]
- Sharp, R.S. Flexible rotor balancing: A review of principles and practices. Tribol. Int. 1980, 13, 211–217. [Google Scholar] [CrossRef]
- Darlow, M.S.; Smalley, A.J.; Parkinson, A.G. Demonstration of a unified approach to the balancing of flexible rotors. J. Eng. Power 1981, 103, 101–107. [Google Scholar] [CrossRef]
- Darlow, M.S. Balancing of high-speed machinery: Theory, methods and experimental results. Mech. Syst. Signal Process. 1987, 1, 105–134. [Google Scholar] [CrossRef]
- Huang, W.H.; Wu, X.H.; Jiao, Y.H.; Xia, S.B.; Chen, Z.B. Review of nonlinear rotor dynamics. J. Vib. Eng. 2000, 13, 5–17. (In Chinese) [Google Scholar]
- Luo, Y.G.; Bao, W.B.; Jin, Z.H.; Wen, B.C. Study on dynamic behavior of nonlinear rigid unbalanced rotor system. J. Vib. Shock 2002, 21, 84–86. (In Chinese) [Google Scholar]
- Guskov, M.; Sinou, J.J.; Thouverez, F. Multi-dimensional harmonic balance applied to rotor dynamics. Mech. Res. Commun. 2007, 35, 537–545. [Google Scholar] [CrossRef]
- Turpin, A.; Sharan, A.M. Balancing of rotors supported on bearings having nonlinear stiffness characteristics. J. Eng. Gas Turbines Power 1994, 116, 718–726. [Google Scholar] [CrossRef]
- Cao, S.Q.; Chen, Y.S.; Ding, Q.; Lang, Z.G.; Zhang, Y.A. Nonlinear transfer function method of high-speed dynamic balance of rotor. In Proceedings of the 2003 Large Generator Set Vibration and Rotor Dynamics Academic Conference, Jiaozuo, China; 2003; pp. 300–304. (In Chinese). [Google Scholar]
- Nauclér, P.; Söderström, T. Unbalance estimation using linear and nonlinear regression. Automatica 2010, 46, 1752–1761. [Google Scholar] [CrossRef]
- Green, K.; Champneys, A.R.; Lieven, N.J. Bifurcation analysis of an automatic dynamic balancing mechanism for eccentric rotors. J. Sound Vib. 2006, 291, 861–881. [Google Scholar] [CrossRef]
- Yang, Y.F.; Ren, X.M.; Xu, B. Review of international researches on rotor dynamics. Mech. Sci. Technol. Aerosp. Eng. 2011, 30, 1775–1780. (In Chinese) [Google Scholar]
- Chen, P.; Liao, M.F. Research on transient equilibrium method of flexible rotor. In Proceedings of the Chinese Society of Aeronautics and Astronautics Aeronautical Society Aviation Engine Structural Strength Vibration Academic Conference, Wuyishan, China; 1998; pp. 280–284. (In Chinese). [Google Scholar]
- Zheng, L.X.; Gao, X.G.; Li, X.F. Transient field balancing technique for a micro turbo-jet engine. Meas. Diagn. 2008, 28, 282–285. (In Chinese) [Google Scholar]
- Fu, C.; Ren, X.M.; Yang, Y.F.; Deng, W.Q. Transient dynamic balancing of rotor system with parameter uncertainties. J. Dyn. Control 2017, 15, 453–458. (In Chinese) [Google Scholar]
- Huang, X.; Zhou, J.P.; Wen, G.R.; Jiang, H.; Tan, Y. Balancing under all working conditions of rotor based on parameterized time-frequency analysis. J. Vib. Meas. Diagn. 2017, 37, 134–139. (In Chinese) [Google Scholar]
- Huang, J.P. Study on the Transient Balancing Method of Rotors. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2006. (In Chinese). [Google Scholar]
- Goldman, P.; Muszynska, A. Application of full spectrum to rotating machinery diagnostics. Orbit 1999, 20, 17–21. [Google Scholar]
- Qu, L.S.; Liu, X.; Peyronne, G.; Chen, Y.D. The holospectrum: A new method for rotor surveillance and diagnosis. Mech. Syst. Signal Process. 2003, 3, 255–267. [Google Scholar] [CrossRef]
- Qu, L.S.; Qiu, H. Rotor balancing based on holospectrum analysis: Principle and practice. Chin. Mech. Eng. 1998, 9, 60–63. (In Chinese) [Google Scholar]
- Han, J.; Guan, H.L.; Liang, C. Vector spectrum: A practical analysis method of the rotary machine fault diagnosis. J. Mech. Strength 1998, 20, 212–215. [Google Scholar]
- Han, J. Research on the Application of Full Vector Spectrum Technology and Equipment Fault Diagnosis. Ph.D. Thesis, Tongji University, Shanghai, China, 2005. (In Chinese). [Google Scholar]
- Xu, B.G.; Qu, L.S. Holobalancing of asymmetric rotors. J. Xi’an Jiaotong Univ. 2000, 34, 60–65. (In Chinese) [Google Scholar]
- Lang, G.F.; Lin, J.; Liao, Y.H. Phase compensation method of holobalancing. J. Mech. Eng. 2014, 50, 16–21. (In Chinese) [Google Scholar] [CrossRef]
- Xu, B.; Qu, L.; Sun, R. The optimization technique-based balancing of flexible rotors without test runs. J. Sound Vib. 2000, 238, 877–892. [Google Scholar] [CrossRef]
- Han, D.J. Generalized modal balancing for non-isotropic rotor systems. Mech. Syst. Signal Process. 2007, 21, 2137–2160. [Google Scholar] [CrossRef]
- Kang, Y.; Liu, C.P.; Sheen, G.J. A modified influence coefficient method for balancing unsymmetrical rotor-bearing systems. J. Sound Vib. 1996, 194, 199–218. [Google Scholar] [CrossRef]
- Kang, Y.; Sheen, G.J.; Wang, S.M. Development and modification of a unified balancing method for unsymmetrical rotor-bearing systems. J. Sound Vib. 1997, 199, 349–369. [Google Scholar] [CrossRef]
- Yu, T.; Han, Q.K.; Li, S.D.; Wen, B.; Zhang, Z.S. Study on dynamic characteristics and imbalance response of double-over-hung rotor system. J. Vib. Meas. Diagn. 2007, 27, 186–189. (In Chinese) [Google Scholar]
- Zhang, J.Q. Investigation of Pure Mechanical On-Line Balancing System. Master’s Thesis, Zhejiang University, Hangzhou, China, 2006. (In Chinese). [Google Scholar]
- Liao, M.F.; Liu, Y.Q.; Wang, S.J.; Wang, Y.; Pin, L. The vibration features of a twin spool rotor system with an inter-bearing. Mech. Sci. Technol. Aerosp. Eng. 2013, 32, 641–646. (In Chinese) [Google Scholar]
- Han, J.; Gao, D.P.; Hu, X.; Chen, G. Research on beat vibration of dual-rotor for aero-engine. Acta Aeronaut. Et Astronaut. Sin. 2007, 28, 1369–1373. (In Chinese) [Google Scholar]
- Zhang, Z.X.; Jin, Z.J.; He, S.Z. Study on whole machine balancing method for coaxial dual-rotor system with little rotating speed difference. Chin. J. Mech. Eng. 2004, 40, 40–44. (In Chinese) [Google Scholar] [CrossRef]
- Yang, J.; He, S.Z.; Wang, L.Q. Dynamic balancing of a centrifuge: Application to a dual-rotor system with very little speed difference. J. Vib. Contro 2004, 10, 1029–1040. [Google Scholar] [CrossRef]
- Deepthikumar, M.B.; Sekhar, A.S.; Srikanthan, M.R. Modal balancing of flexible rotors with bow and distributed unbalance. J. Sound Vib. 2013, 332, 6216–6233. [Google Scholar] [CrossRef]
- Wu, X.H.; Liu, Z.S.; Zhang, X.Y. Characteristic analysis of bending faults of shaft. J. Vib. Eng. 1990, 3, 95–102. (In Chinese) [Google Scholar]
- Xia, Y.L. Study on Vibration Characteristics and Reduction Technology of Rotating Machinery with Bend Rotor. Master’s Thesis, Southeast University, Nanjing, China, 2017. (In Chinese). [Google Scholar]
- Nicholas, J.C.; Gunter, E.J.; Allaire, P.E. Effect of residual shaft bow on unbalance response and balancing of a single mass flexible rotor: Part l: Balancing. J. Eng. Gas Turbines Power 1976, 98, 182–187. [Google Scholar] [CrossRef]
- Nicholas, J.C.; Gunter, E.J.; Allaire, P.E. Effect of residual shaft bow on unbalance response and balancing of a single mass flexible rotor—part II: Balancing. J. Eng. Gas Turbines Power 1976, 98, 171–181. [Google Scholar] [CrossRef]
- Deepthikumar, M.B.; Sekhar, A.S.; Srikanthan, M.R. Balancing of flexible rotor with bow using transfer matrix method. J. Vib. Control 2014, 20, 225–240. [Google Scholar] [CrossRef]
- Liu, J.Y.; Ren, P.Z.; Liao, M.F.; Zhao, M.Y.; Yang, H.Y. A study on the vibration of flexible rotor due to its initial bending and unbalance. J. Vib. 1998, 18, 282–286. (In Chinese) [Google Scholar]
- Parkinson, A.G.; Darlow, M.S.; Smalley, A.J. Balancing flexible rotating shafts with an initial bend. Aiaa J. 1984, 22, 683–689. [Google Scholar] [CrossRef]
- Rao, J.S. A note on jeffcott warped rotor. Mech. Mach. Theory 2001, 36, 563–575. [Google Scholar] [CrossRef]
- He, G.A.; Zhang, S.J.; Zhang, X.Y. Dynamic balance research on progressive bending rotor faults of large turbo-generator units. Turbine Technol. 2014, 56, 439–442. (In Chinese) [Google Scholar]
- Cao, S.Q.; Chen, Y.S.; Ding, Q.; Zhang, Y.A.; Lang, Z.G. Transfer function technique of dynamic balancing for high-speed rotors. J. Mech. Strength 2002, 24, 500–504. (In Chinese) [Google Scholar]
- Tiwari, R.; Chakravarthy, V. Simultaneous identification of residual unbalances and bearing dynamic parameters from impulse responses of rotor–bearing systems. Mech. Syst. Signal Process. 2006, 20, 1590–1614. [Google Scholar] [CrossRef]
- Khulief, Y.A.; Mohiuddin, M.A.; El-Gebeily, M. A new method for field-balancing of high-speed flexible rotors without trial weights. Int. J. Rotating Mach. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Wang, W.M.; Gao, J.J.; Jiang, Z.N.; Yan, L.I. Principle and application of no trial weight field balancing for a rotating machinery. Zhendong Yu Chongji/J. Vib. Shock 2010, 29, 212–215. (In Chinese) [Google Scholar]
- Xi, X.F.; Zheng, L.X.; Liu, Z.X. Theoretical and experimental research on balancing of flexible rotors without trial weights. J. Vib. Meas. Diagn. 2013, 33, 565–570. (In Chinese) [Google Scholar]
- Liu, G.Q.; Zheng, L.X.; Mei, Q.; Huang, J.J. Balancing method of flexible rotor across second order without trial weights. Acta Aeronaut. Et Astronaut. Sin. 2014, 35, 1019–1025. (In Chinese) [Google Scholar]
- Yan, L.T.; Xiao, G. CFM56-3 Aeroengine local balancing technology. Int. Aviat. 1989, 32–34. (In Chinese) [Google Scholar]
- Jiang, G.Y.; Wang, D.Y.; Jiao, Y.Q. Experimentd investigation of local balanced technique for large aeroengine rotor. Aeroengine 2008, 34, 19–22. (In Chinese) [Google Scholar]
- Chen, X.; Liao, M.F.; Zhang, X.M.; Wang, S.J. Field balancing technology for low pressure rotors of high bypass ratio turbofan engines. Hangkong Dongli Xuebao/J. Aerosp. Power 2017, 32, 808–819. (In Chinese) [Google Scholar]
- Chen, B.Y. Balance technology for aeroengine. Aeronaut. Sci. Technol. 1996, 7–11. (In Chinese) [Google Scholar]
- Chen, B.Y. Development of balance technology for aeroengines. J. Propuls. Technol. 1998, 19, 105–109. (In Chinese) [Google Scholar]
- Zhang, M. Study on Transient Dynamic Balance Method and its Influencing Factors of Single-Disc Overhung Rotor. Master’s Thesis, Northwestern Polytechnical University, Xi’an, China, 2017. (In Chinese). [Google Scholar]
- Wang, X.X.; Zeng, S. Study of an on-line automatic dynamic balancing system and its dynamic balancing method when used on a flexible rotor. Therm. Energy Power Eng. 2003, 18, 53–57. (In Chinese) [Google Scholar]
- Burgess, G.; Rio, R. T700 Power Turbine Rotor Multiplane/Multispeed Balancing Demonstration; Technical Information Service: Springfield, VA, USA, 1979. [Google Scholar]
- Walton, J.; Lee, C.; Martin, M. High Speed Balancing Applied to the t700 Engine; Mechanical Technology Inc.: Latham, NY, USA, 1989. [Google Scholar]
- Martin, M.A. T55 Power Turbine Rotor Multiplane/Multispeed Balancing Study; Mechanical Technology Inc.: Latham, NY, USA, 1982. [Google Scholar]
- Martin, M.R. Development of a Multiplane/Multispeed Balancing System for Turbine Engines; Mechanical Technology Inc.: Latham, NY, USA, 1984. [Google Scholar]
- Deng, W.Q.; Gao, D.Q. High speed dynamic balance technique applied to flexible rotors of a small-sized engine. Gas Turbine Exp. Res. 2003, 16, 30–33. (In Chinese) [Google Scholar]
- Tresser, S.; Dolev, A.; Bucher, I. Dynamic balancing of super-critical rotating structures using slow-speed data via parametric excitation. J. Sound Vib. 2018, 415, 59–77. [Google Scholar] [CrossRef]
- Untaroiu, C.D.; Allaire, P.E.; Foiles, W.C. Balancing of flexible rotors using convex optimization techniques: Optimum min-max lmi influence coefficient balancing. J. Vib. Acoust. 2008, 130, 111–120. [Google Scholar] [CrossRef]
- Mohammadi, N.; Mohammadzadeh, A. Balancing of the flexible rotors with ica methods. Int. J. Res. Rev. Appl. Sci. 2015, 23, 54–64. [Google Scholar]
- Saldarriaga, M.V.; Steffen, V.; Der Hagopian, J.; Mahfoud, J. On the balancing of flexible rotating machines by using an inverse problem approach. J. Vib. Control 2011, 17, 1021–1033. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).