An Investigation on the Grasping Position Optimization-Based Control for Industrial Soft Robot Manipulator

Abstract

Mitigating fatigue damage and improving grasping performance are the two main challenging tasks of applying the soft manipulator into industrial production. In this paper, the grasping position optimization-based control strategy is proposed for the soft manipulator and the corresponding characteristics are studied theoretically and experimentally. Specifically, based on the simulation, the resultant stress of step-function-type channels at the same pressure condition that was smallest compared with those of sine-function- and ramp-function-type channels, hence, a pneumatic network with step-function-type channels was selected for the proposed soft manipulator. Furthermore, in order to improve the grasping performance, the kinematics, mechanical, and grasping modeling for the soft manipulator were established, and a control strategy considering the genetic algorithm is introduced to detect the optimal position of the soft manipulator. The corresponding fabrication process and experiments were conducted to cross verify the results of the modeling and the control strategy. It is demonstrated that the internal pressure of the soft manipulator was reduced by 13.05% at the optimal position, which effectively helped mitigate the fatigue damage of the soft manipulator and prolonged the lifespan.

1. Introduction

With the development of robotic technology, there are many kinds of robots that have been applied to industrial applications such as carrying robots and assembling robots [1,2]. But owing to their self-defects with high rigidity, the mechanical manipulator of traditional industrial robots is not suitable for complex and unstructured environments. In recent years, research on soft robots that can adapt themselves with bending and deforming has developed rapidly [3,4,5,6]. Due to the advantages of soft robots, the risk of injury to itself and the products from collision is reduced in process of grasping. In the field of soft robots, the soft manipulator is a key components of the robot terminal grasping device. Due to the requirements of industrial automation, an industrial soft robot manipulator is increasingly used in machinery manufacturing, metallurgy, and other fields [7]. It has a certain degree of automaticity, which can rely on power energy and control ability to achieve various industrial processing and manufacturing functions. In addition industrial soft robot manipulators can also be applied in electronics, logistics, the chemical industry, and other industrial fields.

In the recent years, researcher have studied the material, structure, control, and other aspects of the soft manipulator. Considering the materials utilized in the soft robot, the main body of a soft robot is usually a rubber material. With regard to the characteristics of rubber, it can be composed of complex morphologies of soft robot [8]. Liu et al. [9] proposed a random forest machine learning method and established a nonlinear cumulative damage model to calculate the fatigue life of rubber under variable amplitude stress. The amplitude stress fatigue life data of rubber under variable amplitude stress can be calculated according to constant. Peng et al. [10] studied the distribution of crack energy density (CED) under finite deformation and the rule of estimating rubber fatigue life by CED criterion. The effects of crack azimuth and main tensile ratio on the relationship between strain energy density and variable energy density were obtained.

Different from the traditional industrial robot, where the joint parts of the manipulator need a certain torsional stiffness to complete grasping work, and to identify the torsional stiffness of the joint [11], in the field of soft robots, evolutionary algorithms are widely utilized to optimize the structure [12,13]. Sung et al. [14] attached the joint part of the soft manipulator to the photo-responsive polymers and designed an anti-obstructing motion based on the nonlinear co-rotation finite element model, enabling the soft manipulator to grasp objects in the directly direction and avoid obstacles through multiscale simulations and structural designs. Trivedi et al. [15], based on the cosine theory of geometry and the reinforced model of air control, proposed a new method for soft robot manipulator with nonlinear material and distributed weight and payload effects. The result showed that the average error of manipulator was less than 5% under a wide range of pressure.

In the aspect of control, the study of manipulator control for soft robots has achieved lots of attention. Due to the controllability of pressure control, the manipulator can accommodate different grasping working conditions [16,17,18]. Most researchers mainly studied the fluid hydraulic actuation [19,20,21,22,23,24] and pneumatic actuation [25,26,27,28] in the field of soft robot. Zhang et al. [29] proposed a soft hydraulic robot that showed excellent actuating performance through combining dielectric elastomer with hydrogel. Tolley et al. [30] studied a kind of soft robot which can bear more pressure through pneumatically powered. Mosadegh et al. [31] designed a new pneumatic network chamber combining high actuate rate and high reliability of the actuator, which reduced the amount of pneumato needed to inject and improved the moving speed of the soft robot. Li et al. [32] proposed a new passive particle jamming principle that did not require vacuum power or other control means. By applying pressure to particles to increase finger stiffness, the controllability of manipulator stiffness can be realized, and the grasping ability of soft robot manipulator can be enhanced to perform more forms of grasping. However, in the process of repetitive grasping, the soft manipulator surface suffers tissue fatigue damage phenomenon occurring with excessive internal pressure. In order to apply the soft robot into industrial applications, a study on the improvement of the grasping performance and mitigating fatigue damage of the soft manipulator is needed desperately. Therefore, how to detect the optimal grasping position of soft robot to improve grasping performance and mitigate fatigue damage remains to be further studied.

The key action of the soft robot is the grasping an object. If the command “Grasp the object” is received, it will executive the command to grasp object. In the process of grasping, the position of grasping must be determined firstly. For the purpose of determining a grasping position, it is necessary to recognize the shape of the object and detect position, which are optimal for grasp [33]. A genetic algorithm [34] is introduced to solve this point by detecting the pressure required at different positions. In the industrial applications, when the soft manipulator is engaged in the repetitive grasping work, it is of great significance to study the fatigue damage effects, extension of the service life, and improvement the grasping performance of the soft manipulator through controlling the grasping position.

In this paper, a grasping position optimization-based control strategy was proposed for the soft manipulator, and the corresponding characteristics were studied theoretically and experimentally. The simulation work was conducted and a pneumatic network with step-function-type channels were selected for the proposed soft manipulator. The kinematics model of the soft manipulator and the mechanical model of grasping target were established. The control strategy considering the genetic algorithm was introduced to detect the optimal position of the soft manipulator. The experimental results show that the minimum ventilation pressure of the grasping objects with the same weight was reduced approximately 13.05% while working at the optimal grasping position. Benefiting from the reduction in the ventilation pressure by optimizing the grasping position of soft manipulator, the grasping performance could be effectively improved, and the resultant fatigue damage could be mitigated; meanwhile, the maintenance cost of the soft manipulator will be reduced.

2. Modeling

2.1. Design

In industrial production, spherical contour products are widely found in the production process, it is helpful by introducing the soft manipulator to carry and assemble the products for nondestructive purpose; hence, a sphere was selected as the grasped target in this paper. A four-finger soft manipulator was proposed and is shown in Figure 1a. The design of the soft manipulator was divided into an external structure and an internal cavity as shown in Figure 1b,c. The external structure design of the manipulator took the certain contour as the prototype, and the internal part of the protruding module is the internal cavity part. In this paper, in order to study the influence of the different channels’ structures on the grasping performance of the soft manipulator, three different kinds of channels for the soft manipulator were studied, namely, step-function-type, sine-function-type, and ramp-function-type channels [35,36]. The manipulator consisted of two parts, namely, the top layer with large deformation and the bottom layer with small deformation. The top layer was made of silicone rubber material with low stiffness, and the bottom layer was made of silicone rubber material with high stiffness. When the pressure was applied to the internal cavity of the soft manipulator, the internal cavity pressure of the soft manipulator would be larger than that of the external pressure, and the internal and external pressure difference is formed; hence, the deformation for the finger of the soft manipulator with concave and convex layers would generate. 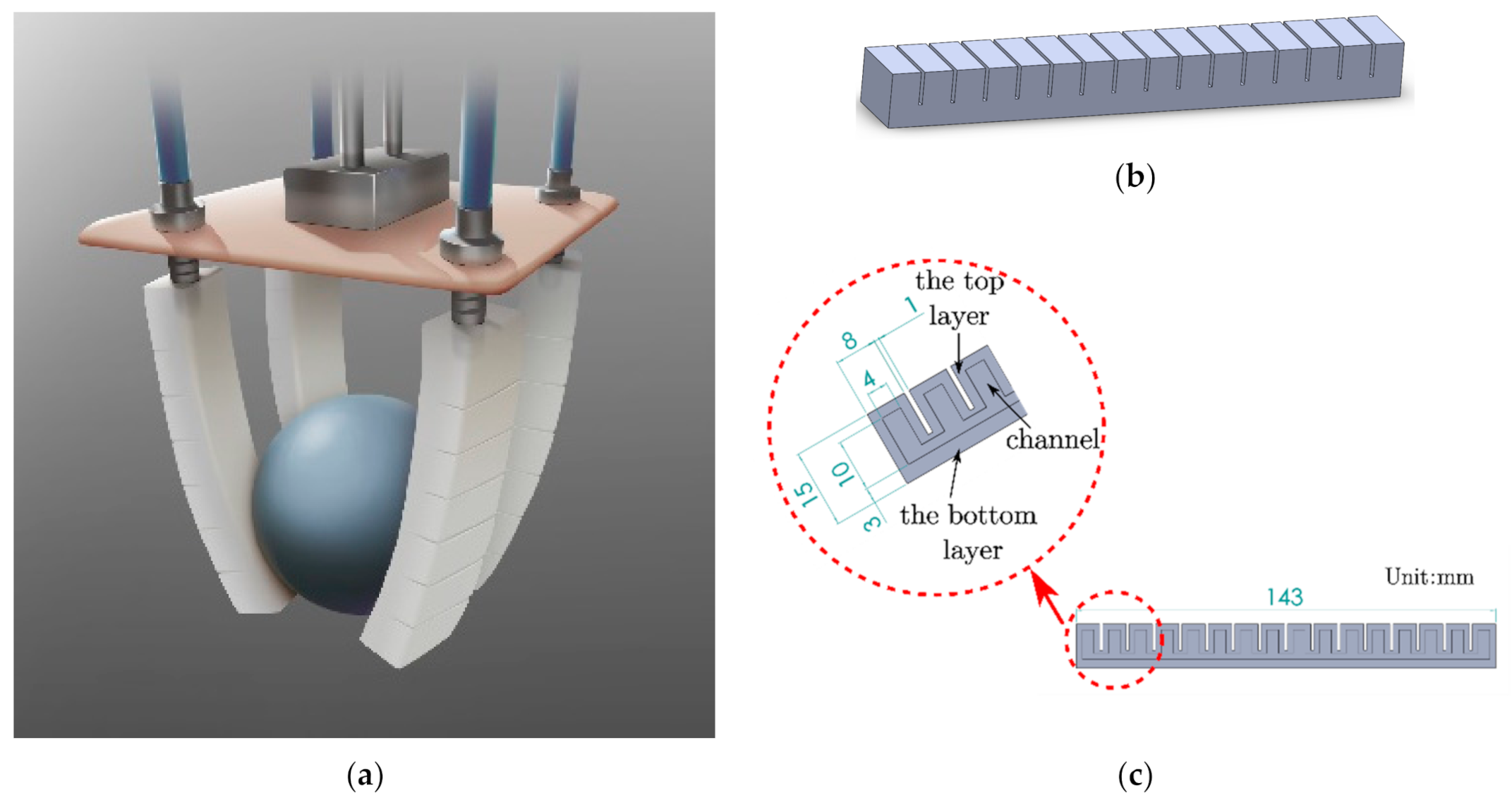Since the deformation of the top layer was larger than that of the bottom layer, the soft manipulator would perform a downward bending grasping action.

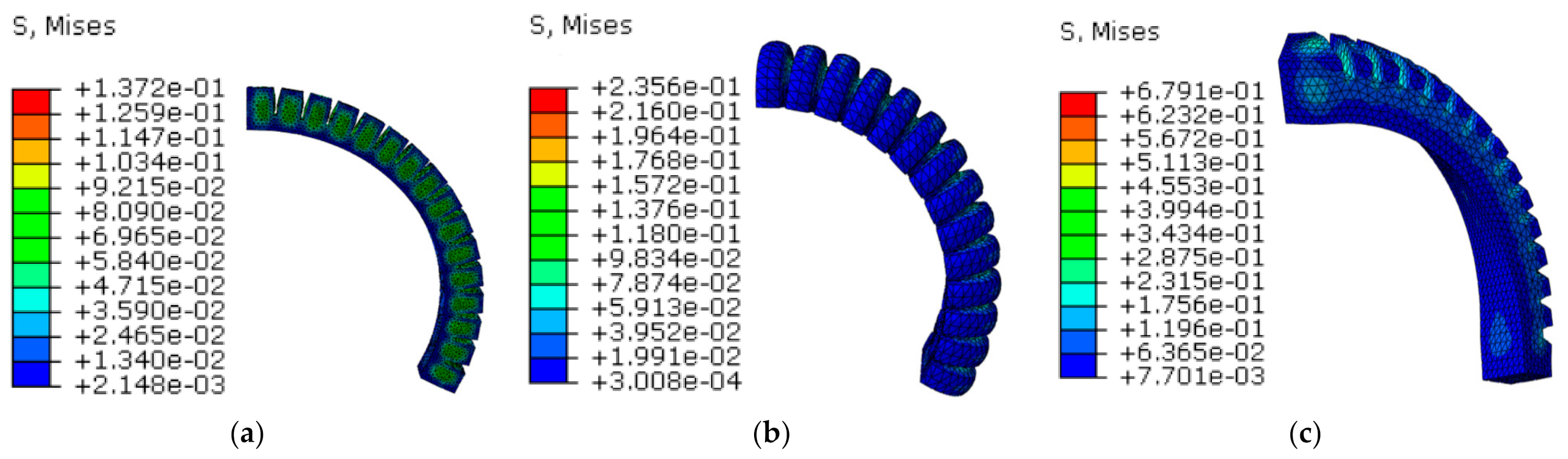
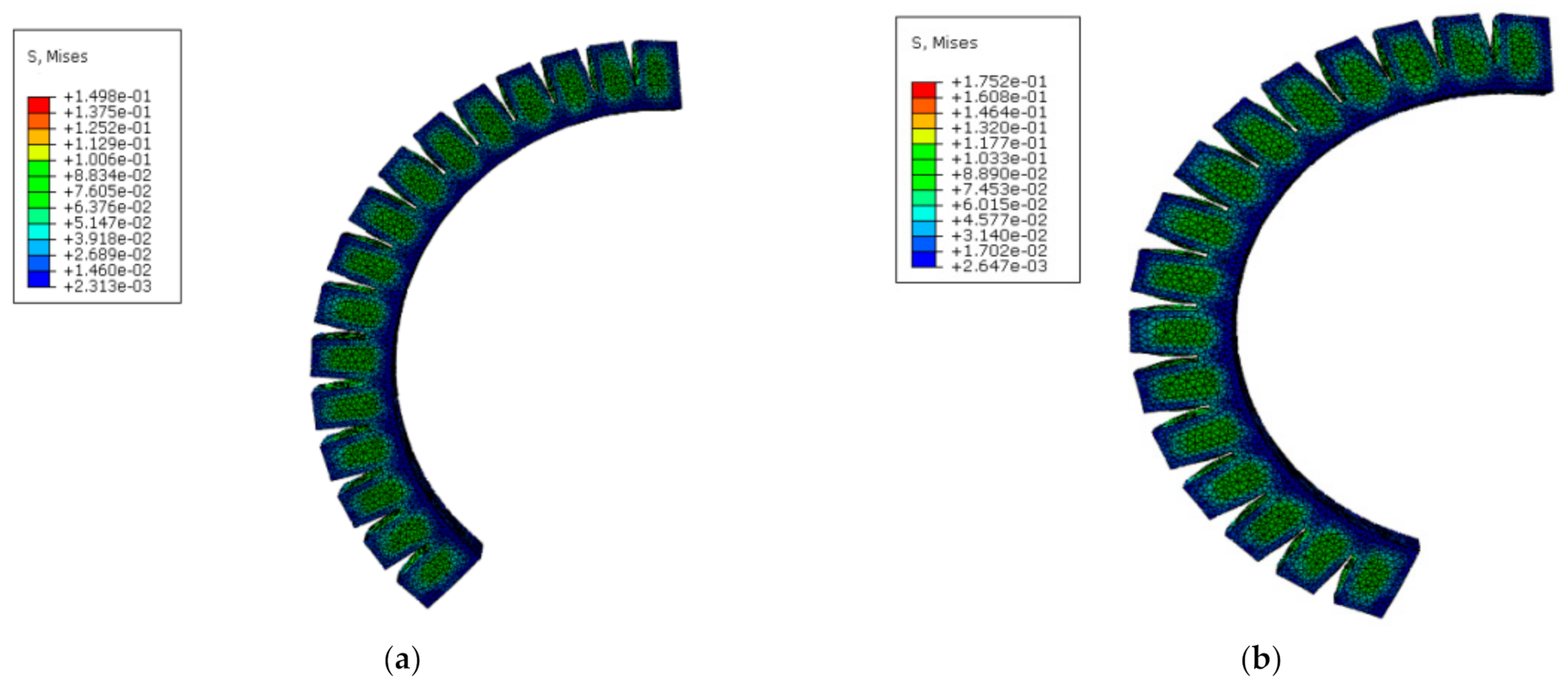
2.2. Simulation

To describe the bending and stress state of the designed three kinds of soft manipulator models, a finite element simulation analysis of the soft manipulator design model was performed based on the Yeoh model. Yeoh models have the advantages of simple form and high precision. It can well simulate the properties of rubber materials under large strain and can be used to simulate the mechanical behavior of other deformations with simple uniaxial tensile experiment data. Moreover, the material parameters of the Yeoh model can be determined by a uniaxial compression experiment.

The definition of the strain energy function of the Yeoh model is:

$$\mathrm{W}=W(I_1,I_2,I_3)$$

(1)

where $I_{\mathrm{i}}$ represents strain tensor in three directions, $I_{\mathrm{i}}$ satisfies the following relation:

$$\left\{\begin{array}{l}{I}_1={\lambda }_1{}^2+{\lambda }_2{}^2+{\lambda }_3{}^2\\ I_2={\lambda }_1{}^2{\lambda }_2{}^2+{\lambda }_2{}^2{\lambda }_3{}^2+{\lambda }_3{}^2{\lambda }_1{}^2\\ I_3={\lambda }_1{}^2{\lambda }_2{}^2{\lambda }_3{}^2\\ {\lambda }_i=1+{\epsilon }_i\end{array}\right.$$

(2)

where ${\lambda }_i$ represents main elongation ratio in three directions, ${\epsilon }_i$ represents principal strains in three directions.

The second-order form of strain energy function can be expressed as:

$$W=C_{10}(I_1-3)+C_{20}{(I_2-3)}^2$$

(3)

According to the literature [37], the Yeoh model parameters—$C_{10}$ and $C_{20}$—are set to 0.11 and 0.02. The density $\rho$ of this material is set to 1130 kg/m³.

As the material of the top layer and the bottom layer of the soft manipulator are different, it is necessary to use the linear elastic model to describe the material model in the simulation. The material parameters of the bottom layer are listed in

Table 1. Material parameters of the bottom layer.

Elasticity Modulus/GPa	Poisson’s Ratio	Density/kg·m−3
6.5	0.2	750

.

To study the influence of bending performance with different structures, the soft manipulator model was imported into the simulation software (Abaqus), the ventilation pressure for the different structures of the soft manipulator model stayed the same. The resultant stress and bending angle in bending deformation were studied. The angle between the position after ventilation and the initial position is the bending angle.

Pressures with the values of 25, 45, 65, 75, and 80 kPa were applied to the three different structures of the soft manipulator model, respectively, the bending changes and stress changes were shown in Figure 2.

Comparing the resultant stress of three kinds of soft manipulators as shown in Figure 3a. it can be seen that the resultant stress of the step-function- and sine-function-type soft manipulators were related to the ventilation pressure and the resultant stress of the soft manipulator with the step-function type was smallest, while the surface stress of the ramp-function-type soft manipulator increased sharply when the ventilation pressure increased from 45 to 65 kPa. It is easily understood that the surface stress increased by the torsion of the ramp-function soft manipulator after the bending deformation. It can be seen from Figure 3b that the bending angle of the step-function soft manipulator was obviously larger than the others under the same ventilation pressure. Therefore, the step-function soft manipulator performed the best bending deformation simulation effect.

In order to study the resultant stress of three kinds of soft manipulators when grasping the sphere with same weight and volume, a simulation was conducted. When the soft manipulator grasps the sphere, it is equivalent to applying corresponding force to the soft manipulator. When the ventilation pressure is 25 kPa, in order to simulate the performance of sphere grasping of the proposed soft manipulators with different types of channels, the equivalent force 1 N is applied to the grasping surface, respectively. Based on the results of the simulation, the resultant stress of the step-function-type soft manipulator was the smallest compared with those of sine-function-type and ramp-function-type soft manipulators as shown in Figure 4. Therefore, the step-function soft manipulator was selected as the research object in this paper.

When the soft manipulator is filled with the same ventilation pressure, the bending angle of one cavity is larger than those of other cavities, and it is softer. The phenomenon of the stress of a rubber material stretched to a certain strain again that is less than the stress at the initial stretch to that strain is called the Mullins effect [38], and it is mainly manifested by the phenomenon of the stress softening of silicone rubber materials during experiment. In this paper, Abaqus simulation software was used to study the Mullins effect of the soft manipulator. The Mullins effect simulation parameters were selected as the parameter value of Mullins effect of silicone rubber material. When the ventilation pressure was 30 kPa, the simulation results are shown in Figure 5. It can be seen that the maximum stress of the soft manipulator without Mullins effect was 0.1498 MPa, and the soft manipulator with Mullins effect was 0.1752 MPa. The Mullins effect increased the maximum stress of the soft manipulator. Besides, it can be seen that the bending angle of Mullins effect soft manipulator was significantly larger than the original. In practical applications, fatigue damage and the Mullins effect of rubber soft manipulators are unavoidable, badly affecting the grasping performance and reducing the service life of soft manipulators. In this paper, the ventilation pressure of a soft manipulator was reduced by controlling the grasping position of soft manipulators to mitigate the fatigue damage.

2.3. Study on the Soft Manipulator Optimal Grasping Position

The fatigue damage of from soft manipulator is caused by high ventilation pressure, which affects its grasping performance. In this paper, the kinematics, mechanical and grasping modeling for the manipulator are established, the control strategy considering the genetic algorithm is introduced to detect the optimal grasping position of soft robot manipulator.

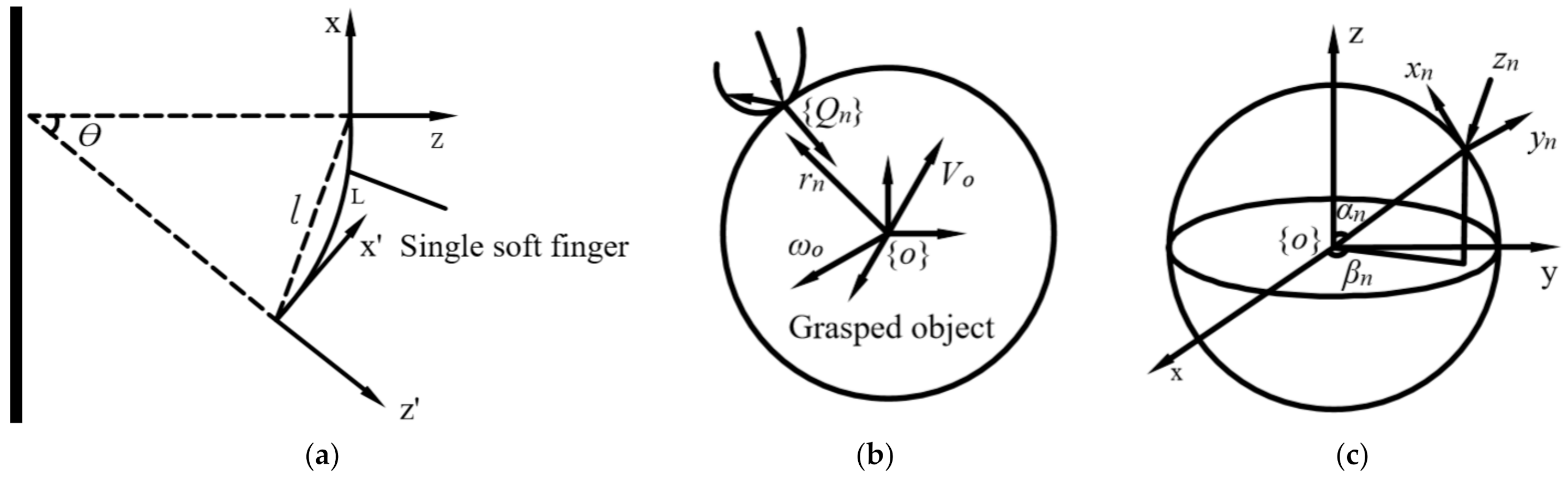
2.3.1. Kinematics Modeling of Soft Manipulator

The single soft finger is simplified into a circular arc with equal curvature without considering the influence of its own gravity on grasping performance. The kinematics model of the single soft finger based on the model of constant curvature beam as shown in Figure 6a. The coordinate system is set-up at both ends of the single soft finger. The direction tangent to the arc part is $x$-axis, the direction perpendicular to the arc is $y$-axis, and the direction pointing to the center of the circle is the $z$-axis.

In the simplified kinematics model of the single soft finger, the bending angle of single soft finger is $\theta$, the length of arc corresponding to the length of single soft finger is $L$, the chord length of arc is $l$, and the curvature of arc is $k$.

According to the geometric relation in the simplified model, the following formulas can be obtained:

$$\left\{\begin{array}{l}\theta =L\cdot k\\ l=\frac{2}{k}\sin \frac{L\cdot k}{2}\end{array}\right.$$

(4)

The position of the grasping coordinate system relative to another coordinate system is shown as follows:

$$\left\{\begin{array}{l}{x}^{\prime }=-\frac{2}{k}\cdot \sin \frac{L\cdot k}{2}\cos \frac{L\cdot k}{2}\\ y^{\prime }=0\\ z^{\prime }=\frac{2}{k}{\sin }^2\frac{L\cdot k}{2}\end{array}\right.$$

(5)

Matrix transformation is used to describe the relationship between the two coordinate systems, the expression of the transformation matrix as:

$$T=\left[\begin{array}{cccc}\cos (L\cdot k)& 0& \sin (L\cdot k)& -\frac{2}{k}\sin \frac{L\cdot k}{2}\cos \frac{L\cdot k}{2}\\ 0& 1& 0& 0\\ -\sin (L\cdot k)& 0& \cos (L\cdot k)& \frac{2}{k}{\sin }^2(\frac{L\cdot k}{2})\\ 0& 0& 0& 1\end{array}\right]$$

(6)

2.3.2. Mechanical Modeling of Grasping Object

The mechanical analysis modeling of the grasped object is established. The reference coordinate system of the grasped object is shown in Figure 6b. The coordinate system of the grasped object $\left\{O\right\}$ locates at the center of the sphere container.

Supposing that the finger index of the soft manipulator is $n$, let the vector of the contact point between the single finger of the nth soft manipulator and the grasped object in the reference coordinate system is $r_n=(x_n,y_n,z_n{)}^T$, a point on the surface of the grasped sphere is selected as the contact point of the soft manipulator. The contact coordinate system of the nth contact point is $\left\{Q_n\right\}$. The origin of the coordinate system is the contact point between single soft finger and the grasped object.

Supposing that the number of contact points between the soft manipulator and the grasped object is $a$, and the positions of these contact points relative to the reference coordinate system of the grasped object can be represented by a grasping matrix $G$ as:

$$G=\left[\begin{array}{ccc}I& \dots & I\\ R_1& \dots & R_a\end{array}\right]$$

(7)

$I$ represents the identity matrix, and the expression of $R_a$ is:

$$R_a=\left[\begin{array}{ccc}0& -z_a& y_a\\ z_a& 0& -x_a\\ y_a& x_a& 0\end{array}\right]$$

(8)

There is a resultant of all the external force $F$ and a resultant of all the external torque $M$ at the contact point between the object and the soft manipulator, which are expressed as:

$$\left\{\begin{array}{l}F=(F_x,F_y,F_z{)}^T\\ M={(M_x,M_y,M_z)}^T\end{array}\right.$$

(9)

The combination of external force and external torque is the combination of external force spiral, and the expression of external force spiral $F_h$ is:

$$F_h={(F_x,F_y,F_z,M_x,M_y,M_z)}^T$$

(10)

There is an interaction force between the soft manipulator and the object in the process of grasping. Supposing that the interaction force generated by the nth contact point is $F_{jn}$, then the expression of $F_{jn}$ is:

$$F_{jn}={(F_{jnx},F_{jny},F_{jnz})}^T$$

(11)

$F_{jnx}$ and $F_{jny}$ represent the tangential components of the force, $F_{jn\mathrm{z}}$ is the normal component of the force.

After the object was grasped by the soft manipulator, the interaction force $F_{jn}$ and the combined external force spiral $F_h$ satisfy the static equilibrium equation as:

$$F_h=G\cdot F_{jn}\cdot {}_{\mathrm{c}}{}^{0}T$$

(12)

where ${}_{\mathrm{c}}{}^{0}T$ is the direction matrix of the coordinate system of the nth contact point, the expression is:

$${}_{\mathrm{c}}{}^{0}T=\left(\begin{array}{cccc}{}_{\mathrm{c}1}{}^{0}T& {}_{\mathrm{c}2}{}^{0}T& \dots & {}_{\mathrm{cn}}{}^{0}T\end{array}\right)$$

(13)

Owing to the soft manipulator having only pressure force on the grasped object, $F_{jn\mathrm{z}}\ge 0$. In order to ensure that there is no relative sliding between the single soft finger and the grasped object, each contact point must satisfy the friction constraint condition, and the equation for the friction constraint is:

$$\sqrt{F^2{}_{jnx}+F^2{}_{jny}}\le \mu F_{jnz}\hspace{1em}\hspace{1em}\hspace{1em}n=(1,\cdots ,n)$$

(14)

$\mu$ is the static friction coefficient of the contact point between single soft finger and grasped object.

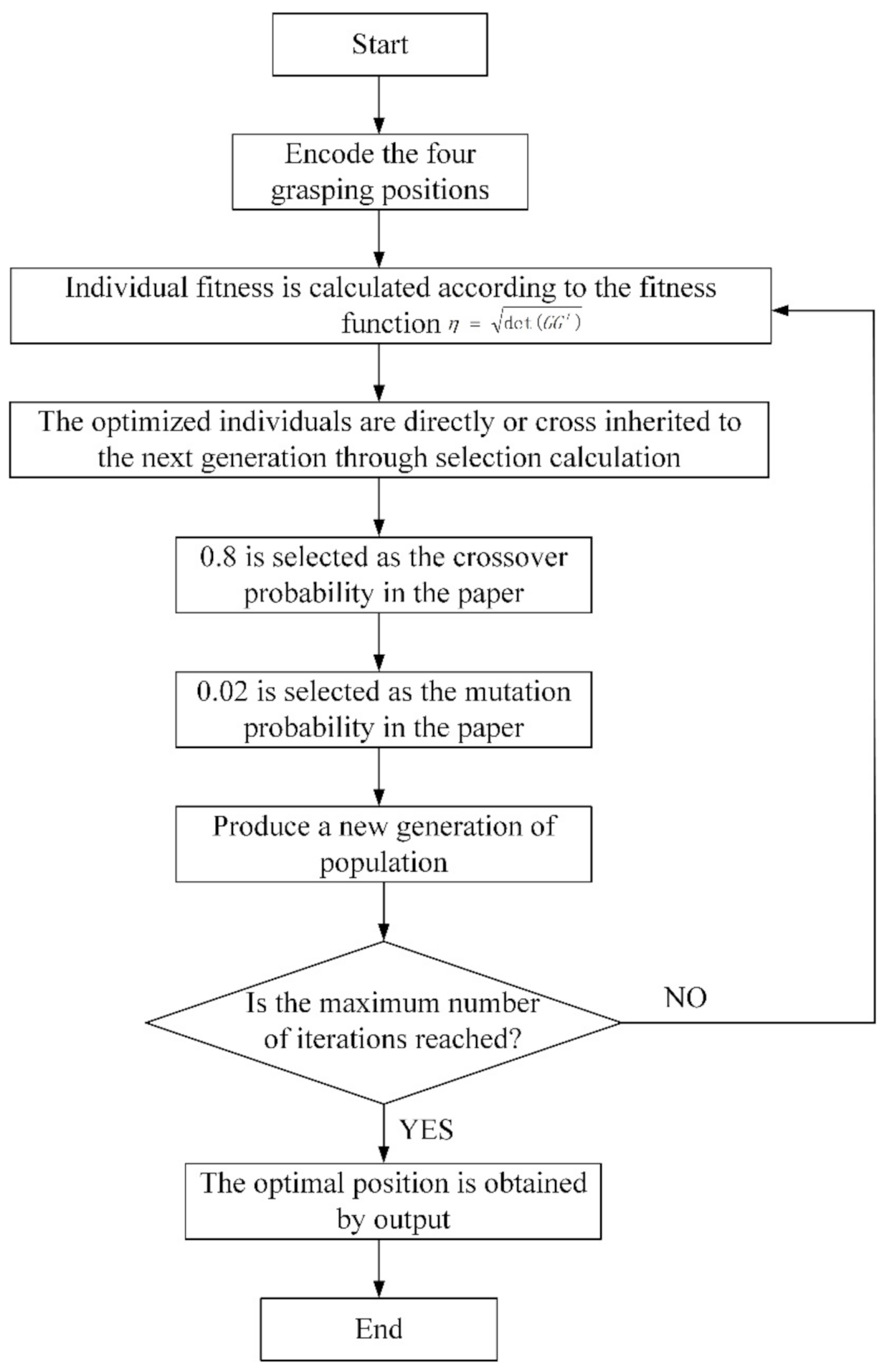
2.3.3. Grasping Position Modeling

The coefficient $\eta$ is introduced as the stability coefficient of the multi-finger soft manipulator. The stability coefficient is related to the shape characteristics and the position of the grasped object, which is related to the grasping matrix $G$. The grasping stability coefficient $\eta$ and the grasping matrix $G$ are taken as the research targets to reflect the requirements of grasping position for the grasping performance of soft manipulator. Therefore, the grasping matrix $G$ is taken as the optimization objective. The larger the stability coefficient $\eta$ is, the better the position is.

The grasping stability coefficient is used to represent the grasping stability of the soft manipulator. $\eta$ is only related to the grasping matrix $G$, and the range of the stability coefficient is $0\le \eta \le 1$. The larger the value of the stability coefficient $\eta$, it means that the grasping position in this state is the optimal grasping position of the soft manipulator. The expression of $\eta$ is:

$$\eta =\sqrt{\det (G{G}^T)}$$

(15)

det(x)—solution function of matrix determinant.

This section is about the stability analysis of the four-finger soft manipulator. There are four fingers in the four-finger soft manipulator, there are four contact points between the soft manipulator and the grasped object. The grasping model of the grasped object is shown in Figure 6c. The central coordinate system is $\left\{o\right\}$, and the coordinate system of the nth grasping contact point is $\left\{Q_n\right\}$.

The coordinates of the nth grasping contact point can be expressed as follows:

$$\left\{\begin{array}{l}{x}_n=A\sin {\alpha }_n\cos {\beta }_n\\ y_n=A\sin {\alpha }_n\sin {\beta }_n\\ z_n=A\cos {\alpha }_n\end{array}\right.$$

(16)

$A$ is the radius of the sphere. According to Equation (7), the expression of the grasping matrix of the soft manipulator as:

$$G=\left[\begin{array}{cccc}I& I& I& I\\ R_1& R_2& R_3& R_4\end{array}\right]$$

(17)

From Equation (8), get the expression of $R_n$ as:

$$R_n=\left[\begin{array}{ccc}0& -A\cos {\alpha }_n& A\sin {\alpha }_n\sin {\beta }_n\\ A\cos {\alpha }_n& 0& -A\sin {\alpha }_n\cos {\beta }_n\\ A\sin {\alpha }_n\sin {\beta }_n& A\sin {\alpha }_n\cos {\beta }_n& 0\end{array}\right]n=(1,2,3,4)$$

(18)

From the above, obtain the grasping position function formula of soft manipulator as:

$$\left\{\begin{array}{l}\min \to -\eta =-\sqrt{\det (G{G}^T)}\\ G\cdot F_{jn}\cdot {}_c{}^o\mathrm{T}-F_{\mathrm{h}}=0\\ -F_{jnz}\le 0\\ \sqrt{F^2{}_{jnx}+F^2{}_{jny}}-\mu F_{jnz}\le 0\end{array}\right.$$

(19)

By utilizing the established model, the four-finger soft manipulator was used in the experiment, but the model is also suitable for two-finger soft manipulator, three-finger soft manipulator, and multi-finger soft manipulator. The model has the same applicability to study the optimal grasping position of the multi-finger soft manipulator.

2.3.4. The Results of Solution

Genetic algorithm was introduced to solve the results of the optimal grasping position. It was introduced in this paper to determine the optimal solution in the search area by simulating the process of natural selection mathematically. In the process of solving using genetic algorithm, firstly, the genetic algorithm generates the first generation population randomly for coding, then the genetic algorithm selects according to the fitness function and generates a new population through the crossover and mutation of different individual genes. A single-point crossover operator was used, integer and decimal places corresponded to crossover, crossover probability was 0.8. Base place mutation was used, and integer place mutation randomly within the search interval with a probability of 0.02. After the process was iterated, the new population had higher fitness than the previous, and the best solution was the one with the highest fitness. The flow chart of genetic algorithm for detecting the optimal grasping position of the soft manipulator is shown in Figure 7.

Combining the genetic algorithm with the optimal grasping position of soft manipulator, the genetic algorithm for detecting the optimal grasping position of the soft manipulator was compiled. The genetic algorithm for detecting the optimal grasping position was used to predict different grasping contact points, and the results were verified by experiments.

3. Experimental Setup

3.1. Fabrication Process

On the basis of the design and simulation, the forming principle of fabricating a single soft finger is shown in Figure 8a. The fabrication method of the single soft finger was a silica gel pouring method. The particles on the surface of the 3D-printed mold were polished to improve the sealing performance and surface smoothness as shown in Figure 8b. The evenly stirred ecoflex00-30 mixed liquid was poured into a treated mold as shown in Figure 8c. After the mold was sealed, the mold was left for 6–8 h, and the real part of the single soft finger was obtained as shown in Figure 8d.

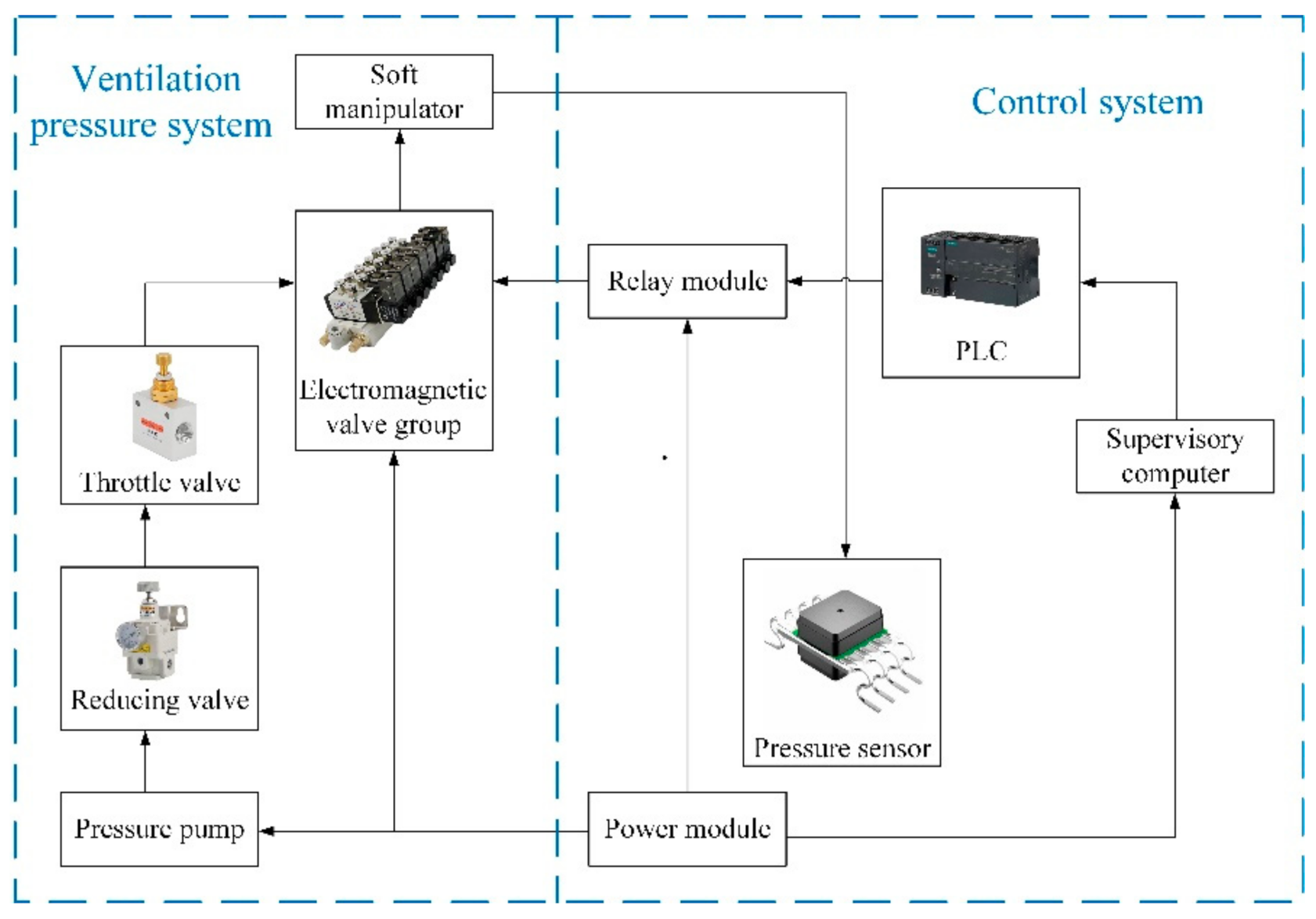
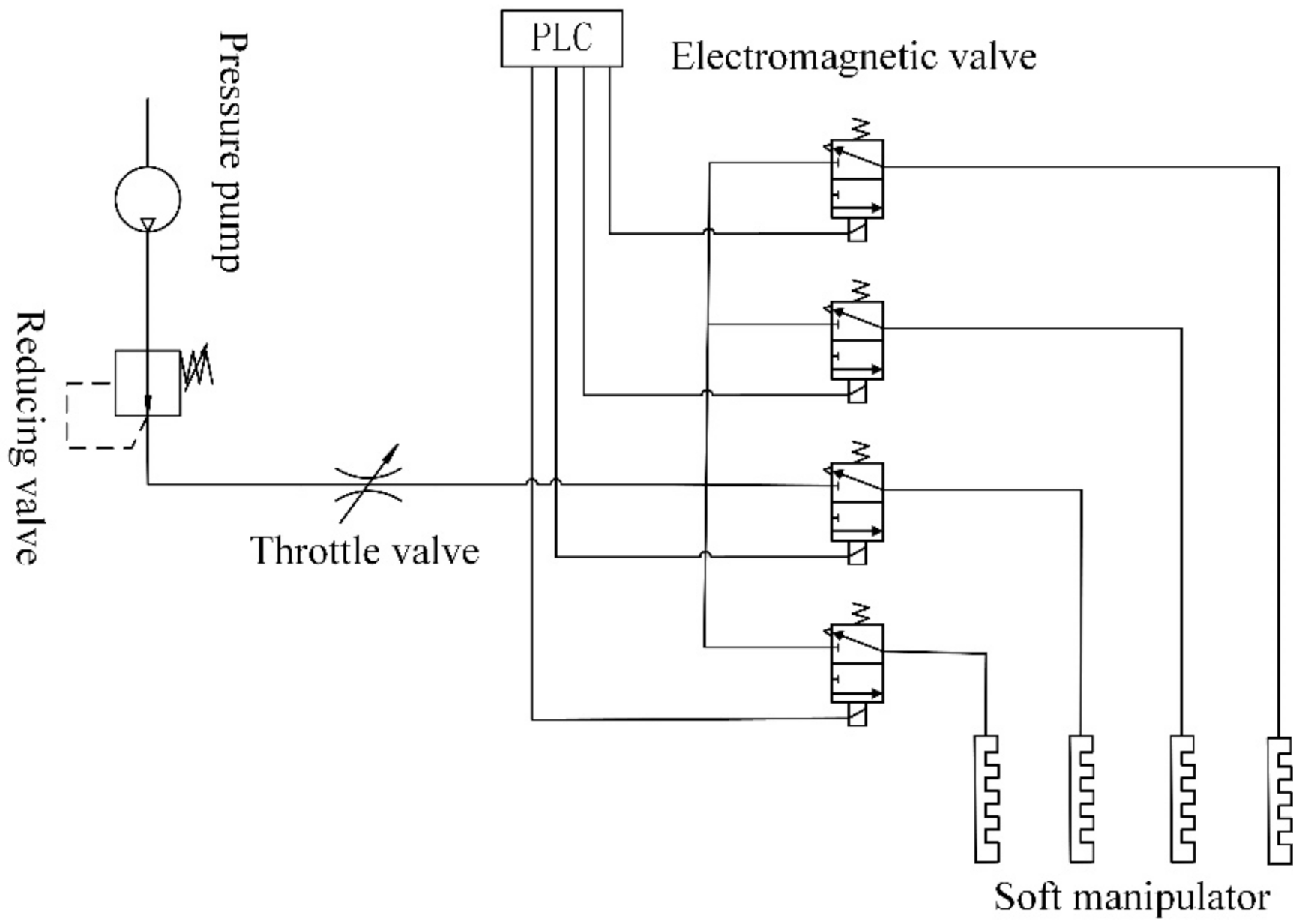
3.2. Experimental Control System

The soft manipulator experimental system consisted of a supervisory computer, PLC, and several components as shown in Figure 9. It included a control system and ventilation pressure system. The supervisory computer sent instructions to the PLC module, the PLC module received the instructions according to the content that would be transmitted to the relay module, and the relay module controlled the electromagnetic valve group according to the designed program, and then to control the soft manipulator. During the grasping experiment, the pressure of the soft manipulator as measured by the pressure sensor.

3.3. Experimental Ventilation Pressure System

The experimental ventilation pressure system in this paper included a pressure pump to provide a pressure source as shown in Figure 10. To reduce the pressure, pressure pump, and throttle valve and reducing valve series. Each finger needed to be connected with the electromagnetic valve and a pressure sensor to measure the pressure of the soft manipulator, so as to complete the experiment for the multi-finger soft manipulator.

According to the designed system, a multi-finger soft manipulator experimental platform was built as shown in Figure 11a. Assembling the newly made soft manipulator on the experimental platform as shown in Figure 11b.

4. Results and Discussion

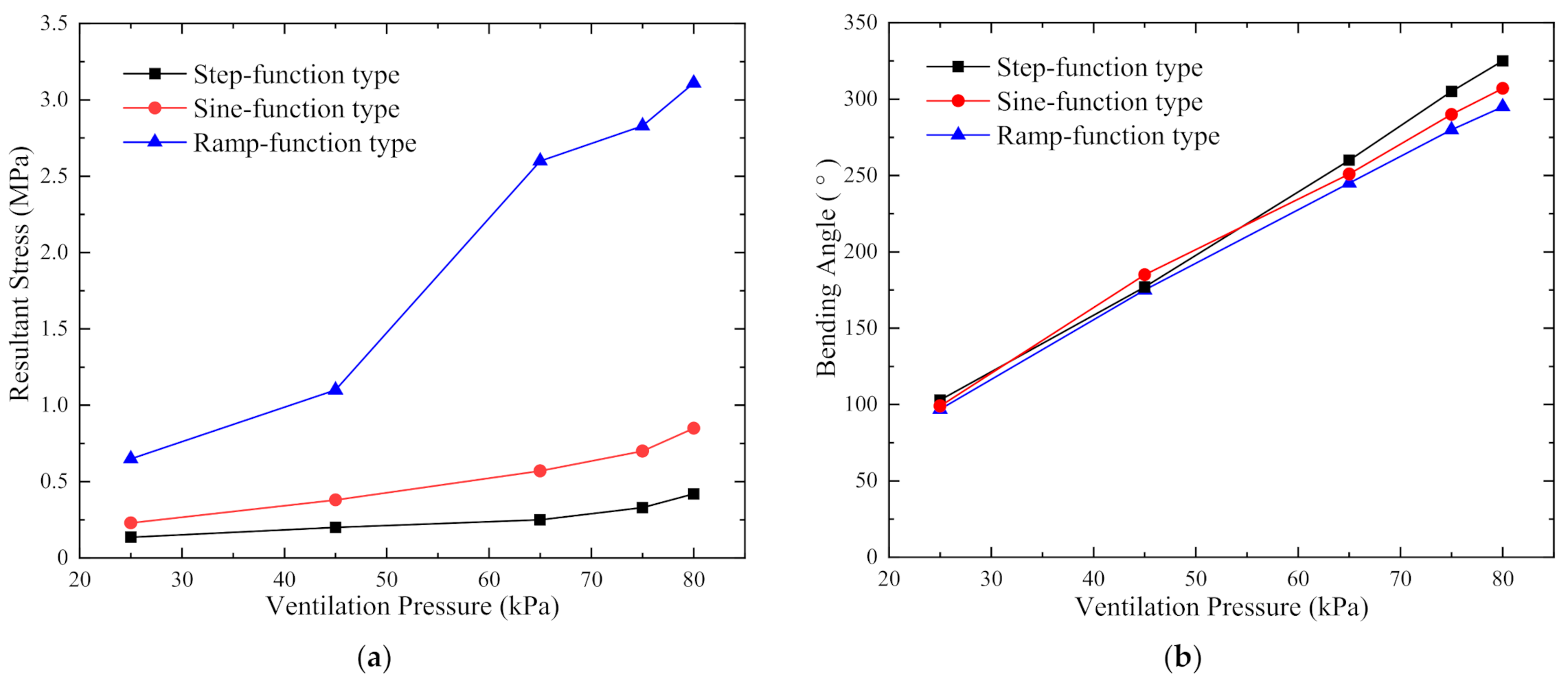
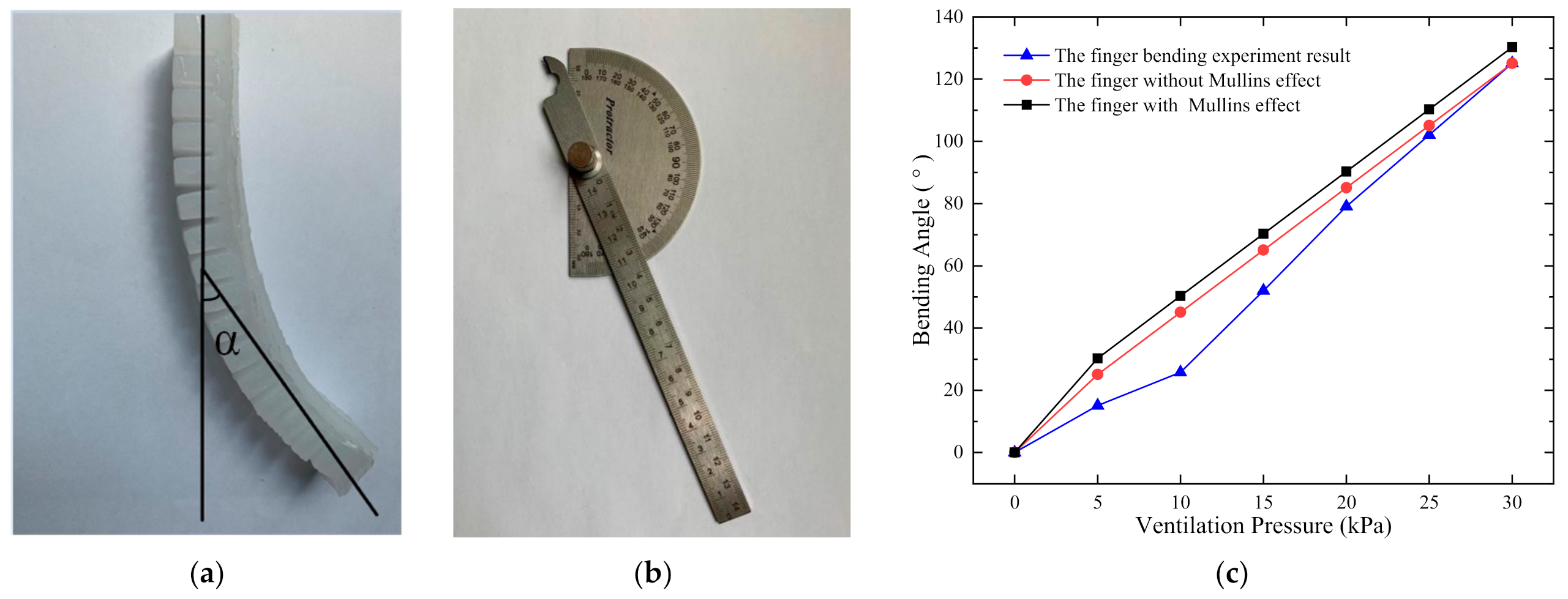
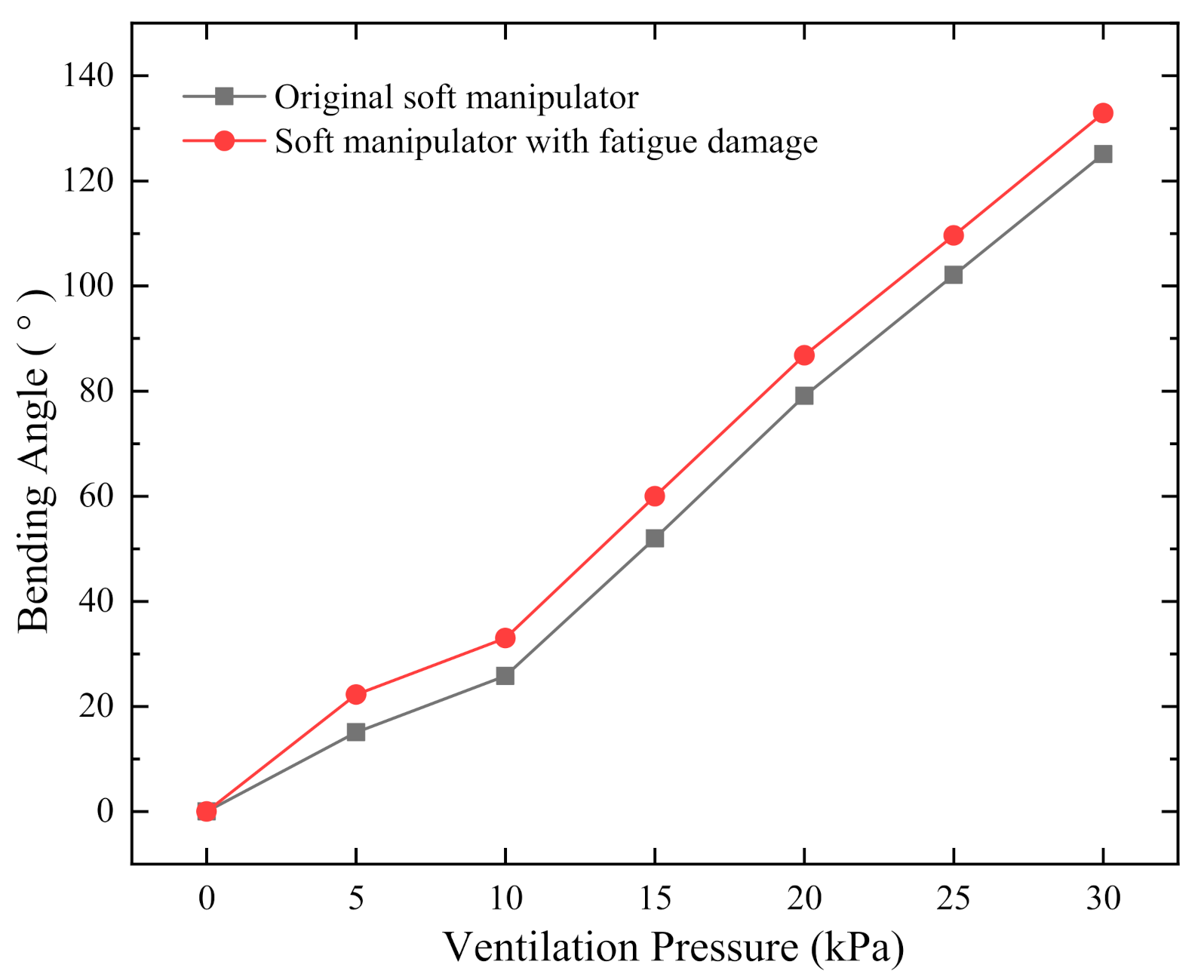
4.1. Study on Bending Angle

The relationship between the angle of bending deformation and ventilation pressure determines the performance of the soft manipulator. The definition of the single soft finger bending angle of the soft manipulator is shown in Figure 12a; the angle between the position after ventilation and the initial position is the bending angle. The tool for measuring the bending angle of the soft manipulator is an angle measuring ruler as shown in Figure 12b.

The soft manipulator bended and deform when pressure was applied, and the bending angle of the soft manipulator was recorded. The simulation results of the soft manipulator with or without the Mullins effect were compared with the experimental results, as shown in Figure 12c. The bending deformation of the soft manipulator had a similar trend to the simulation results. The bending angle of the soft manipulator was positively correlated with the ventilation pressure. The main reason for the difference between the experimental results and the simulation results may have some influencing factors in the process of the soft manipulator fabrication, including the mold accuracy of 3D printing, the tiny damage to the soft manipulator during demoulding, and the human error during the experimental measurement, all of which have certain influences on the experimental bending–deformation results.

Then, the soft manipulator with the same material and the same manufacturing under the same ventilation pressure, fatigue damage of the soft manipulator bending–deformation angles larger than the original, indicating that fatigue damage of the soft manipulator bending performance changed as shown in Figure 13. Therefore, the fatigue damage of the soft manipulator should be mitigated, and the bending performance of the soft manipulator should be improved.

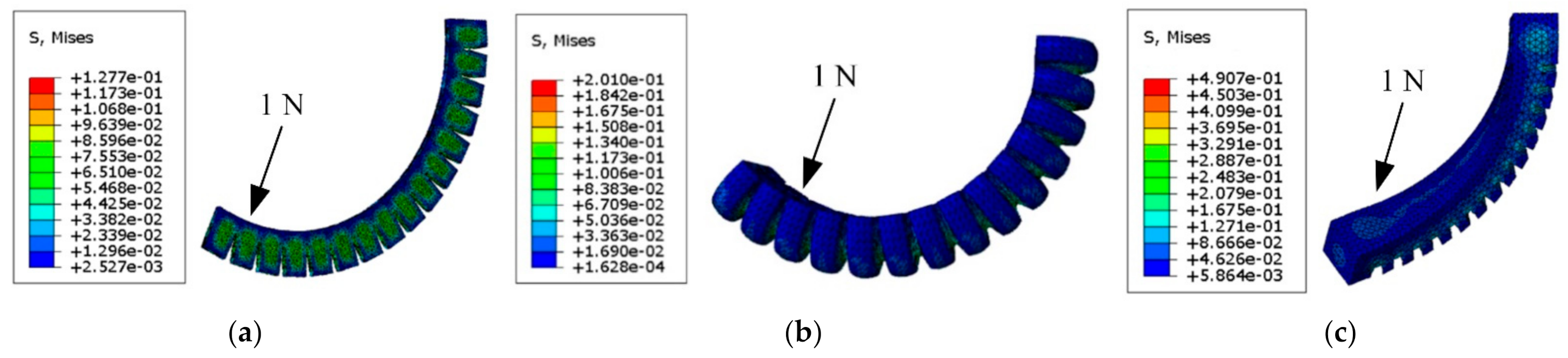
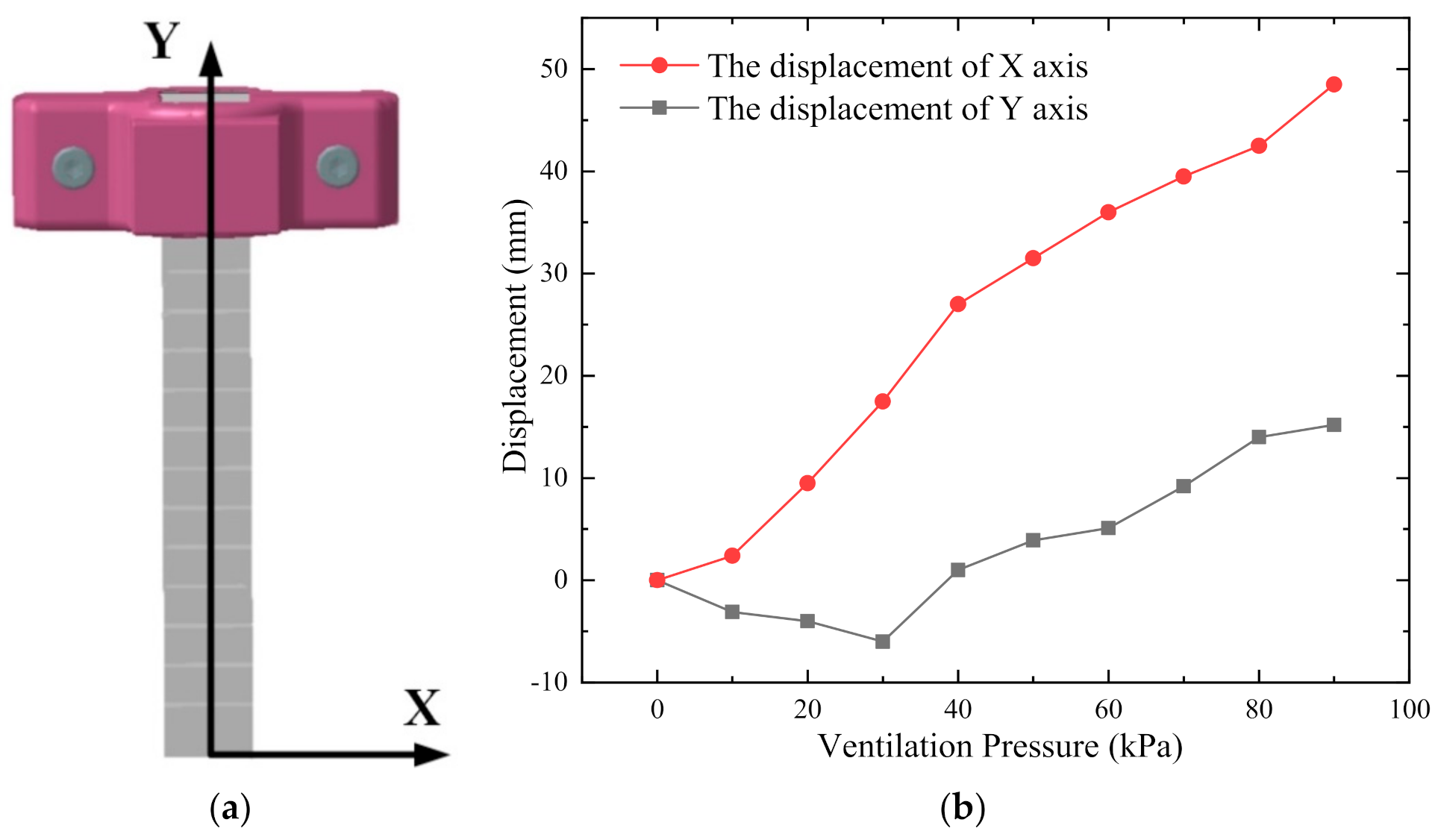
4.2. The end Displacement of the Soft Manipulator

In this experiment, the end displacement of the single soft finger after ventilation was studied. Supposing that all parts of the single soft finger had equal stress deformation, the end position was defined as the research target. Taking the end position as the origin coordinate, the x-axis and y-axis are taken along the direction and vertical direction of the single soft finger, respectively as shown in Figure 14a. The motion trajectory of the end position in the coordinate system is the displacement of the end position.

Figure 14b shows the displacement of the single soft finger on the x-axis and y-axis. It can be seen that the displacement in the coordinate of the y-axis is obviously smaller than the x-axis, which proves that the bottom layer can effectively limit the deformation ability. A negative value appeared in the y-axis direction at the beginning of ventilation, indicating that single soft finger would expand and extend in the negative direction of y-axis under the action of ventilation pressure.

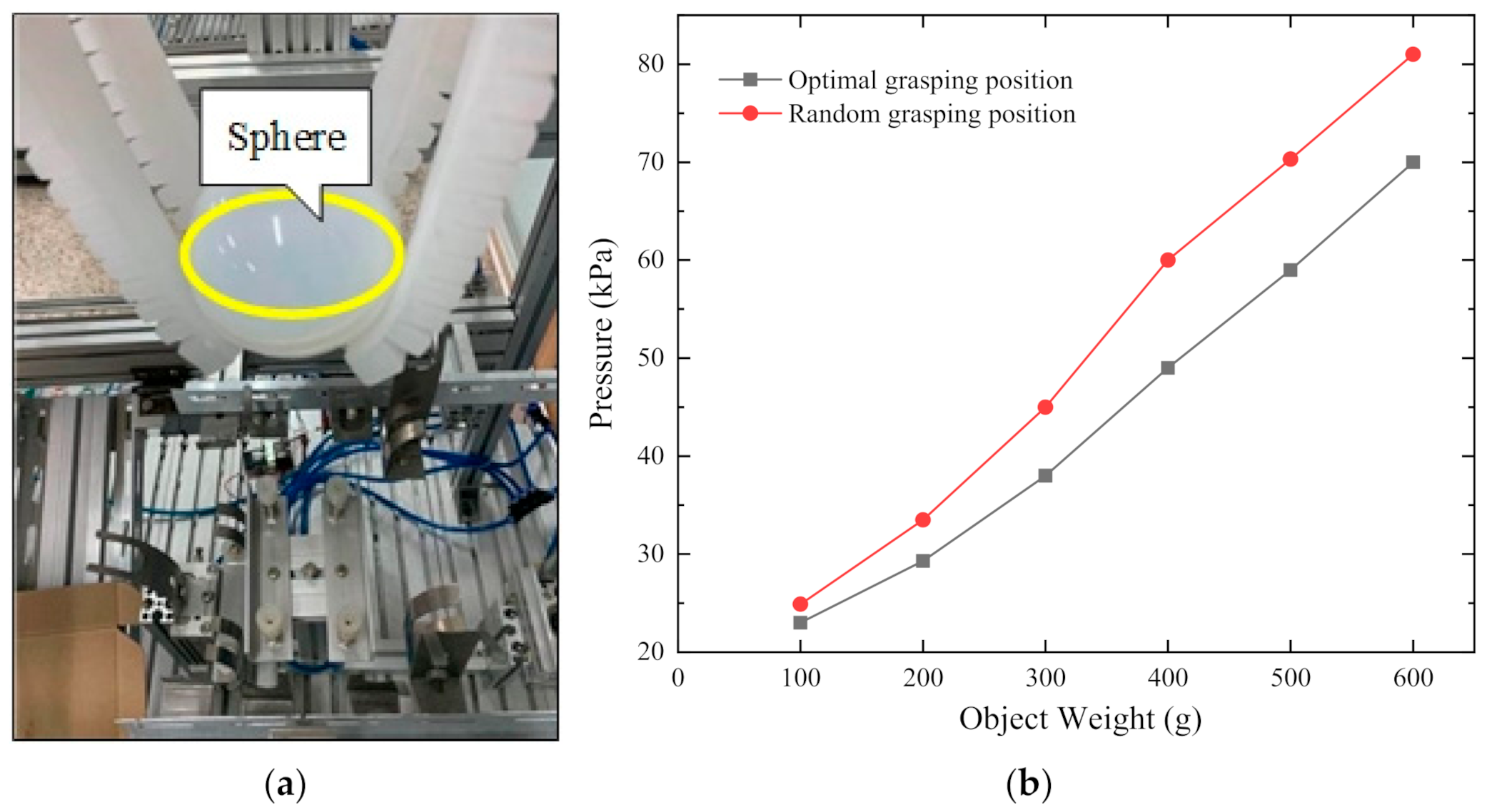
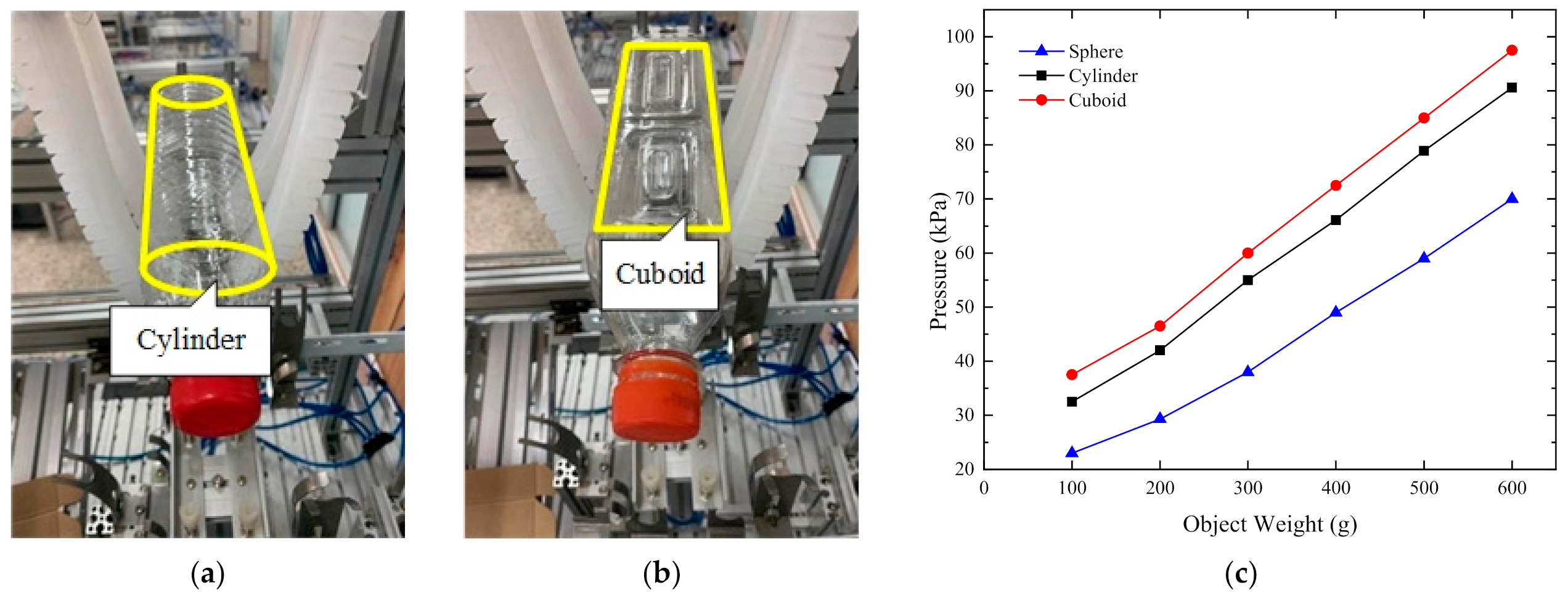
4.3. Pressure Compared between Optimal Position and Random Position

If the grasped object is a sphere with a radius of 45 mm, put A = 54 mm into Equation (18) and solve Equation (19). After the calculation of the above optimization algorithm, it can be found that the results of the optimal grasping position of the soft manipulator are shown in

Table 2. Solution results of optimal grasping position.

	${\mathit{\alpha }}_1$	${\mathit{\beta }}_1$	${\mathit{\alpha }}_2$	${\mathit{\beta }}_2$	${\mathit{\alpha }}_3$	${\mathit{\beta }}_3$	${\mathit{\alpha }}_4$	${\mathit{\beta }}_4$
Angle (°)	91.65	47.34	91.65	136.82	91.65	227.09	91.65	318.71

.

The four points represent the optimal grasping position of the soft manipulator. It can be found that the distribution of the optimal solution of the grasping position presents the following rulers:

• The four contact points of the optimal solution are distributed near the xoy plane;
• The distance between the four contact points is about 90 degrees.

To verify the optimal grasping position of the soft manipulator, experiments were carried out on the experimental platform, and the grasped object of the experiment was a spherical container that can change its mass through inject water.

The experimental steps are as follows:

• Ventilate each finger of the soft manipulator;
• The four-finger soft manipulator is moved to the optimal position to grasp;
• The four-finger soft manipulator is moved to random position to grasp;
• By injecting water into the spherical container to change the weight, then measure the ventilation pressure.

The soft manipulator was tested to grasp a 100, 200, 300, 400, 500, and 600 g sphere as shown in Figure 15a. The optimal grasping position and random grasping position were tested 100 times, and the average value was obtained. The ventilation pressure of the soft manipulator at the optimal grasping position and random grasping position was compared as shown in Figure 15b.

It can be seen that the ventilation pressure of the soft manipulator at the optimal grasping position was significantly less than the random grasping position when grasp the same weight object. The ventilation pressure of the optimal grasping position was 13.05% lower than the random grasping position, which can satisfy the requirements of grasping objects with the minimum ventilation pressure. Therefore, the purpose of mitigating the fatigue damage of the soft manipulator was achieved.

The four-finger soft manipulator grasps cylinder container, cuboid container, and sphere container is shown in Figure 15a, and Figure 16a,b, respectively. Injecting water into the three containers to change the object weight, analyzing the grasping performance. When grasping cuboids, cylinders, and spheres of the same weight and volume at the optimal position, the ventilation pressure of the grasping sphere was minimum as shown Figure 16c. Under the same weight and volume of the three containers, the four-finger soft manipulator easily grasped the spherical container and the ventilation pressure was the lowest, indicating that the spherical object was easier to grasp.

5. Conclusions

In the paper, the grasping performance of a four-finger soft manipulator and the bending deformation of single soft finger were analyzed for a step-function-type soft manipulator, and the grasping position optimization-based control strategy was proposed and studied by introducing the genetic algorithm.

The contributions are summarized in the following points. Firstly, through simulation analysis, the resultant stress of step-function-type channel soft manipulators at same pressure condition that are smallest compared with those of sine-function- and ramp-function-type channels. Secondly, the experimental results showed that the bending angle of the soft manipulator with fatigue damage and Mullins effect was larger than the original condition, indicating that the bending performance and grasping performance of the soft manipulator with fatigue damage and Mullins effect were changing while working. The end displacement of the single soft finger is studied and the displacement in the coordinate of the y-axis is obviously smaller than the x-axis, which proves that the bottom layer can effectively limit the deformation ability. Thirdly, the grasping modeling of soft manipulator is modeled, and the kinematics model of the soft manipulator and the mechanical modeling of grasping object were established, and the control strategy considering the genetic algorithm was introduced to detect the optimal grasping position of soft robot manipulator. Finally, experimental results showed that the ventilation pressure of the optimal grasping position was lower than that of the random grasping position, and the ventilation pressure of the optimal grasping position was 13.05% lower than that of the random grasping position on average. The results are also of great significance to help reduce the fatigue damage of soft manipulator a hydraulic system.

For the future study of soft manipulators, an important consideration is how to mitigate fatigue damage to obtain the expected lifespan through optimized control strategy in industrial production. In addition, the current control methods of soft manipulators mainly depend on the external, and it is necessary to further study the control ability of existing systems.