Investigation on Unsteady Cavitation Flow and Excited Pressure Fluctuations in Regulating Valve
Abstract
:1. Introduction
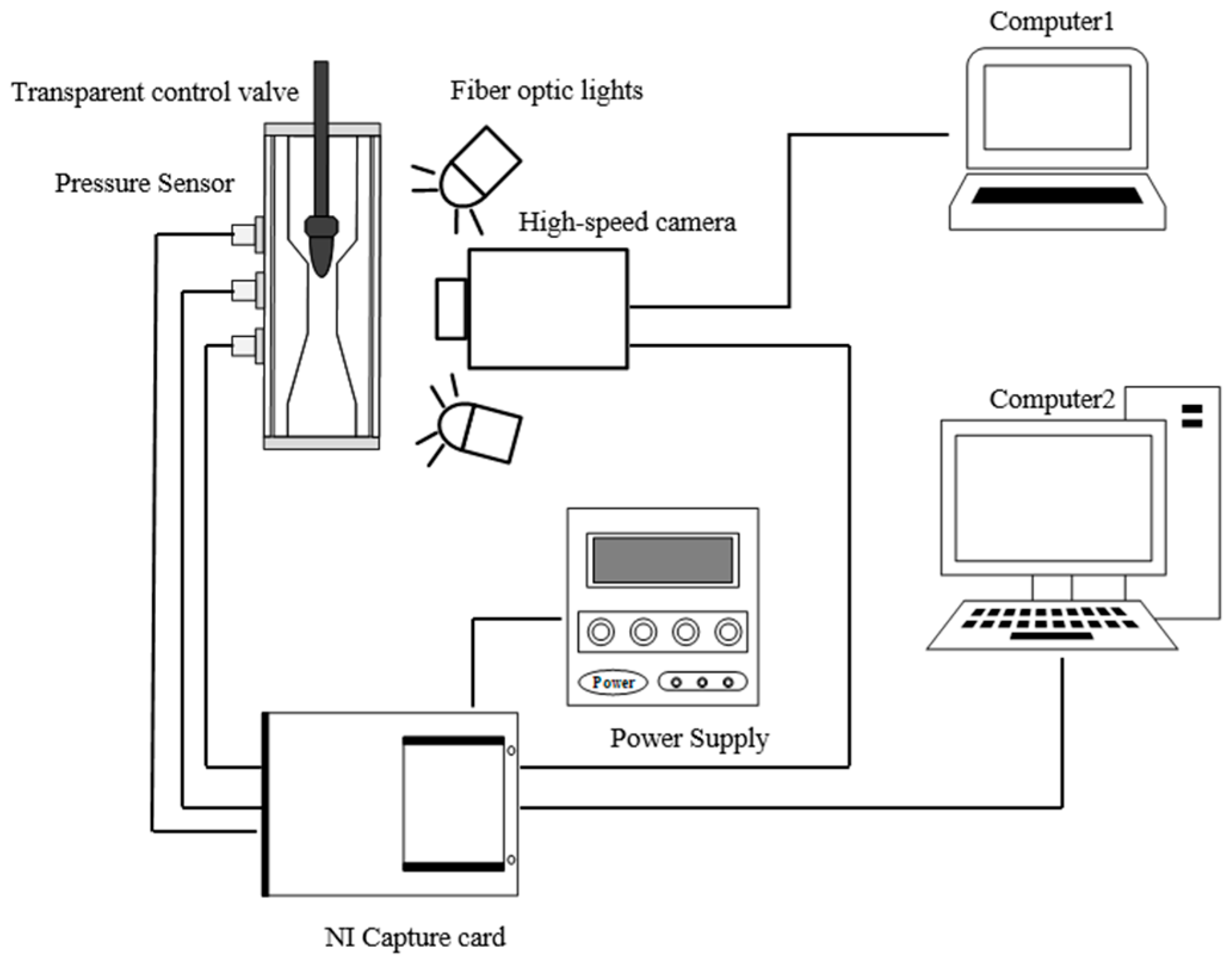
2. Experimental Setup
2.1. Hydraulic System
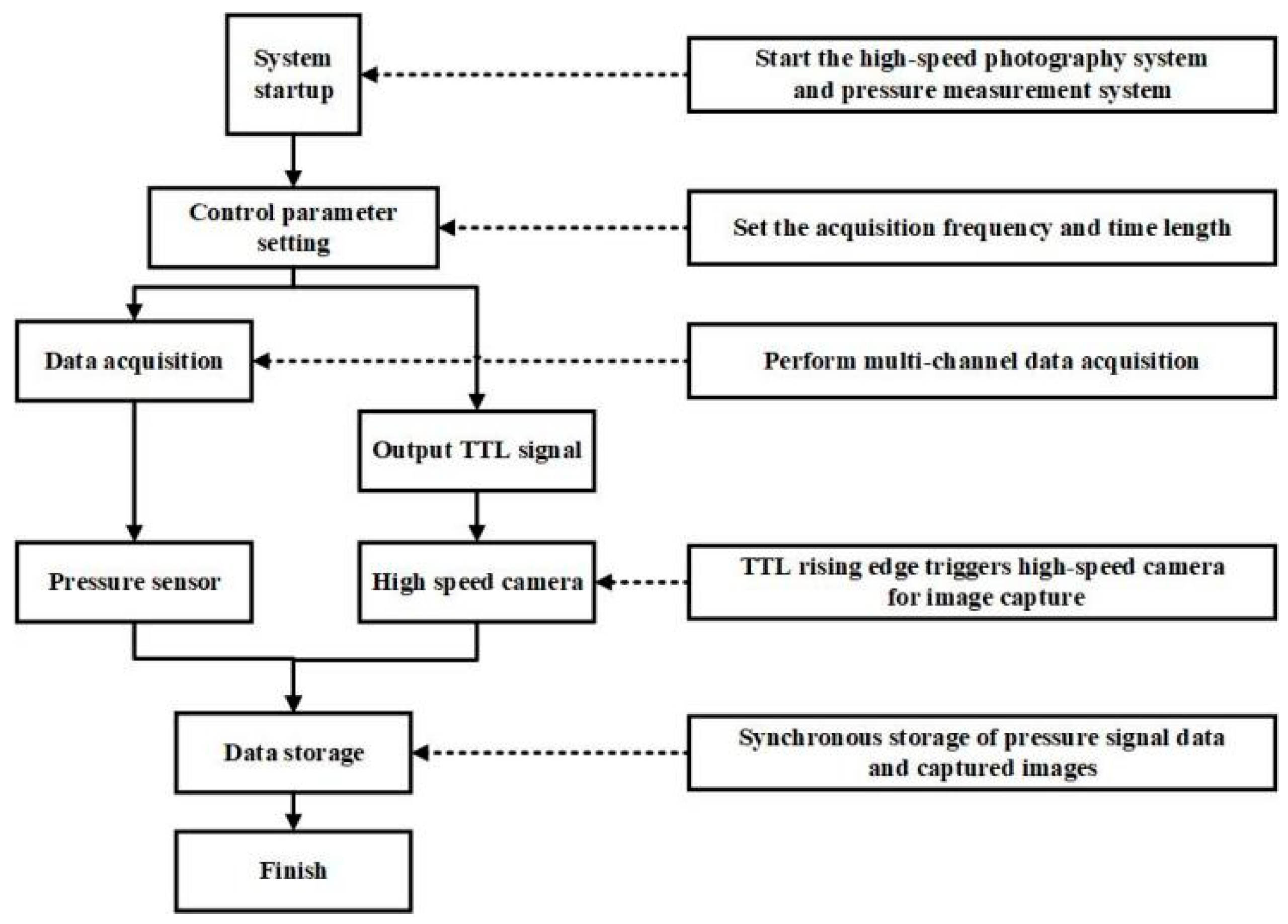
2.2. A Synchronous Measurement System
2.3. Typical Results
3. Results and Discussion
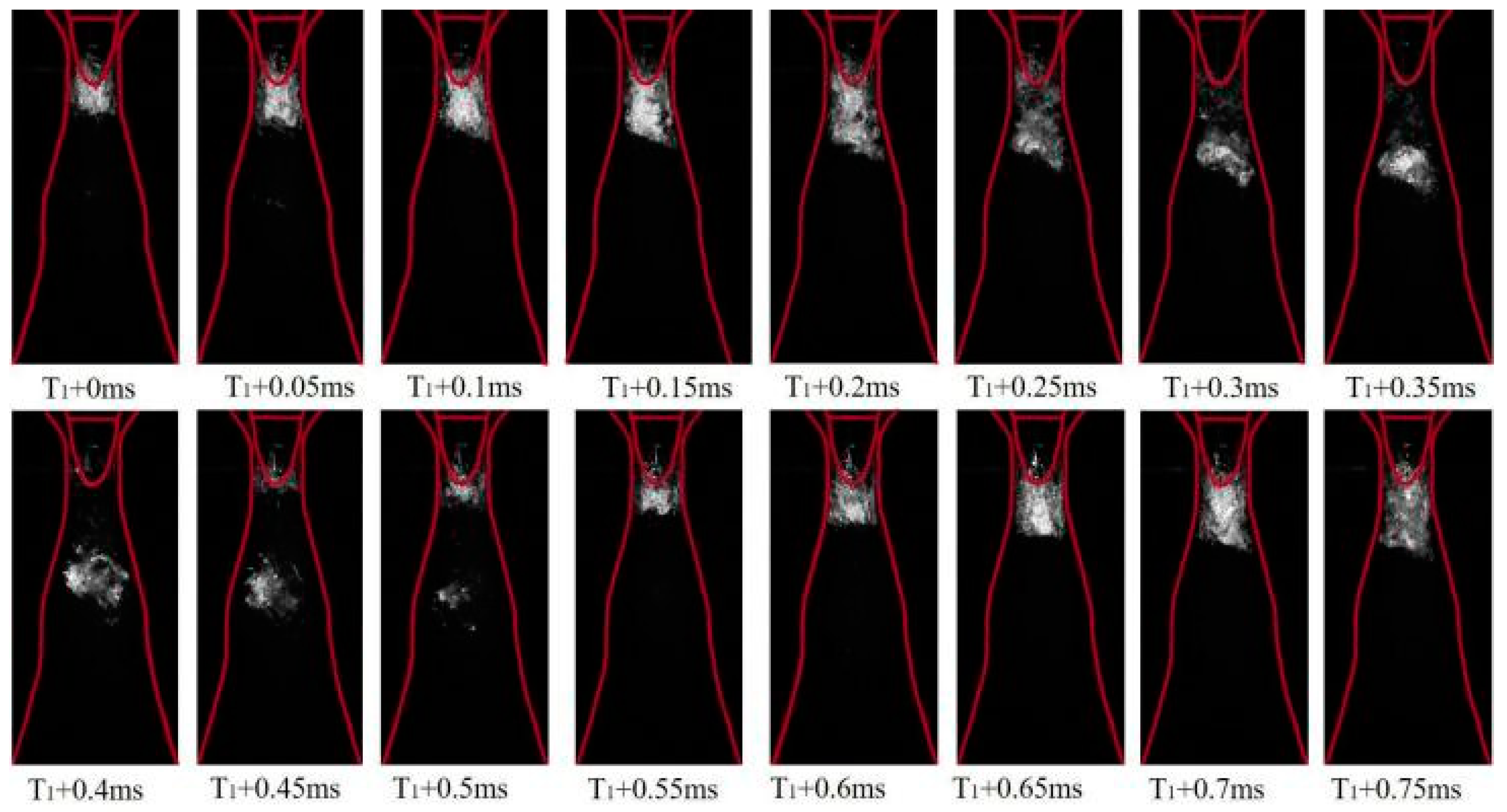
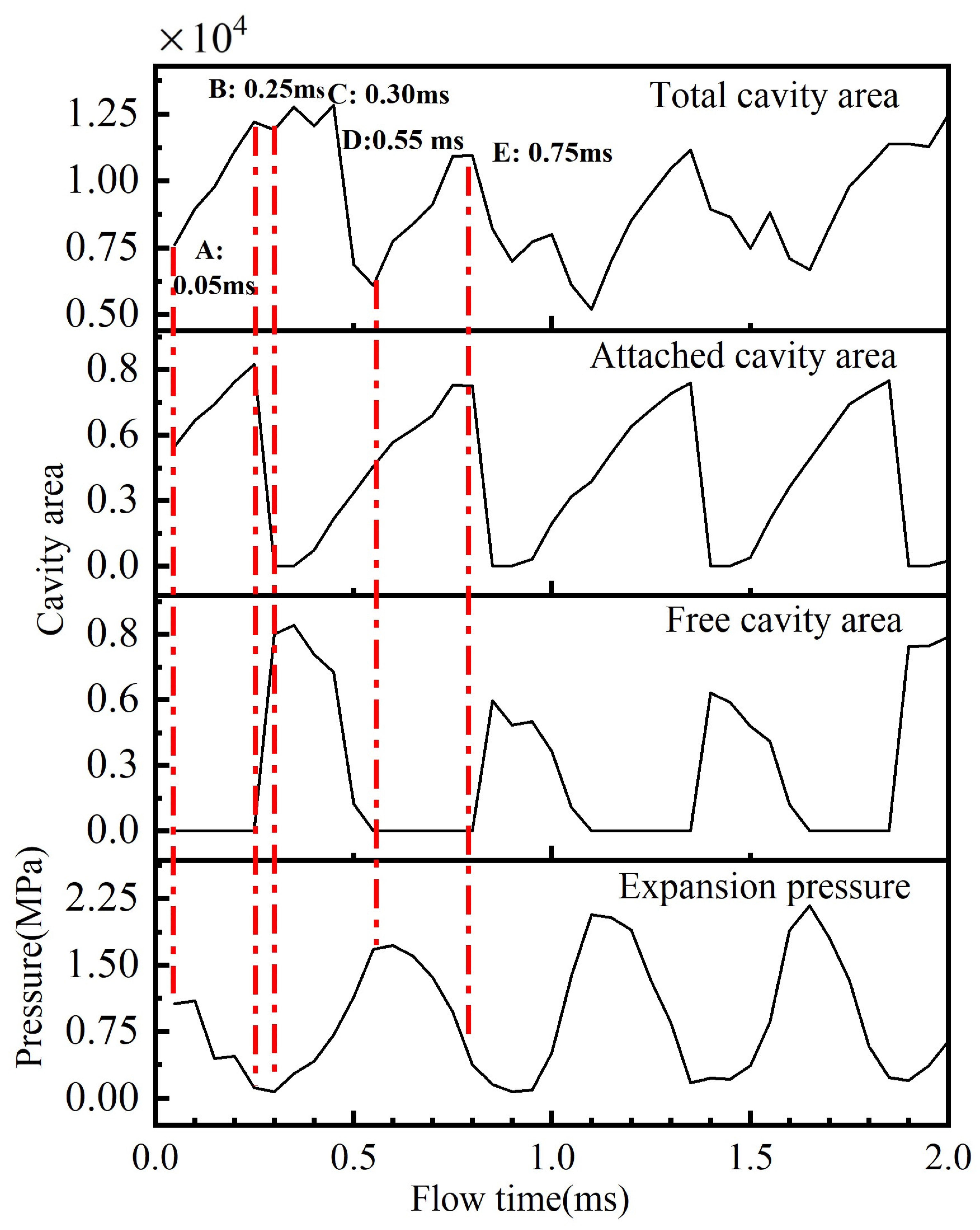
3.1. Time Evolution of Cavitation Behaviors and Its Excited Pressure Fluctuation
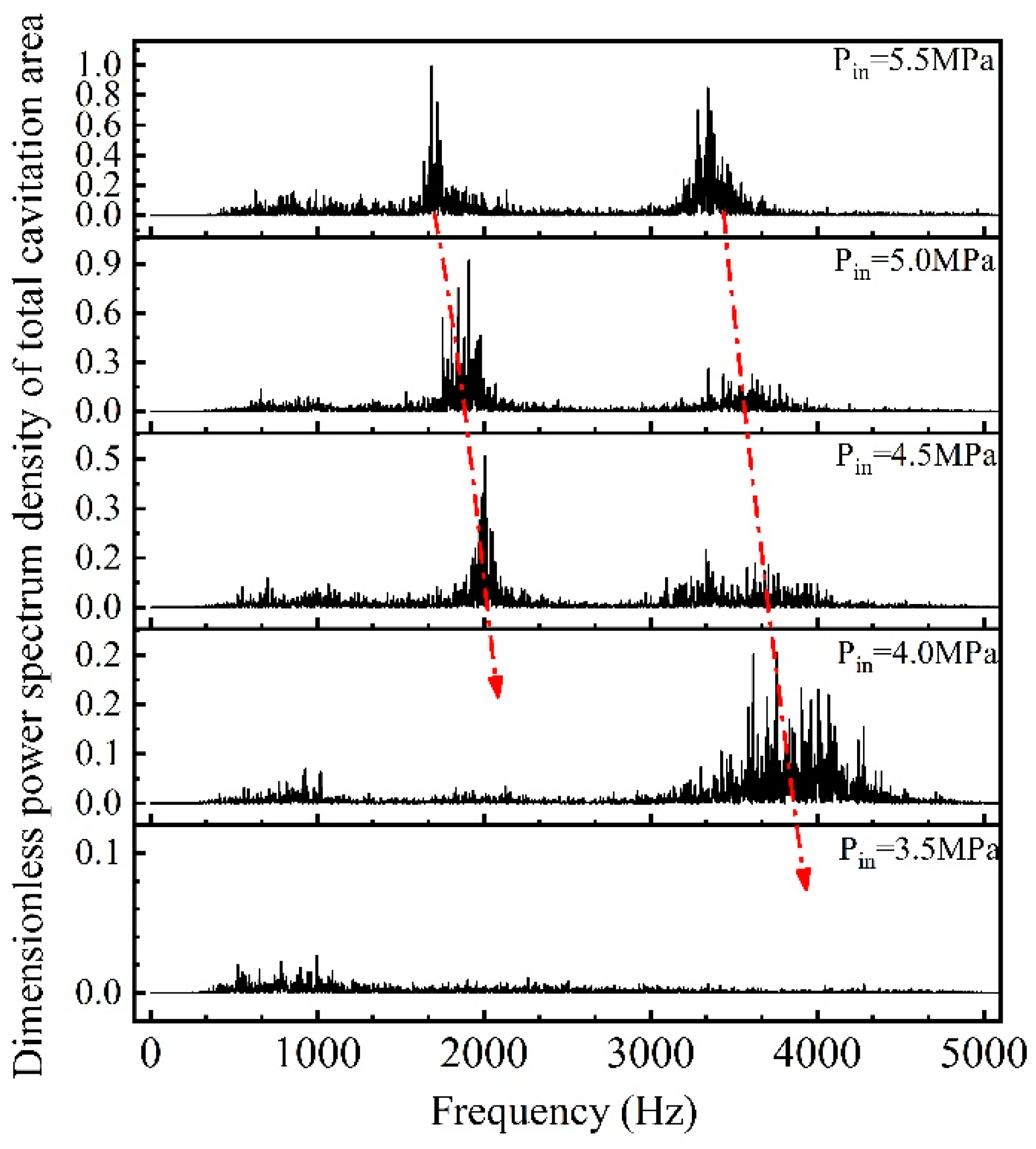
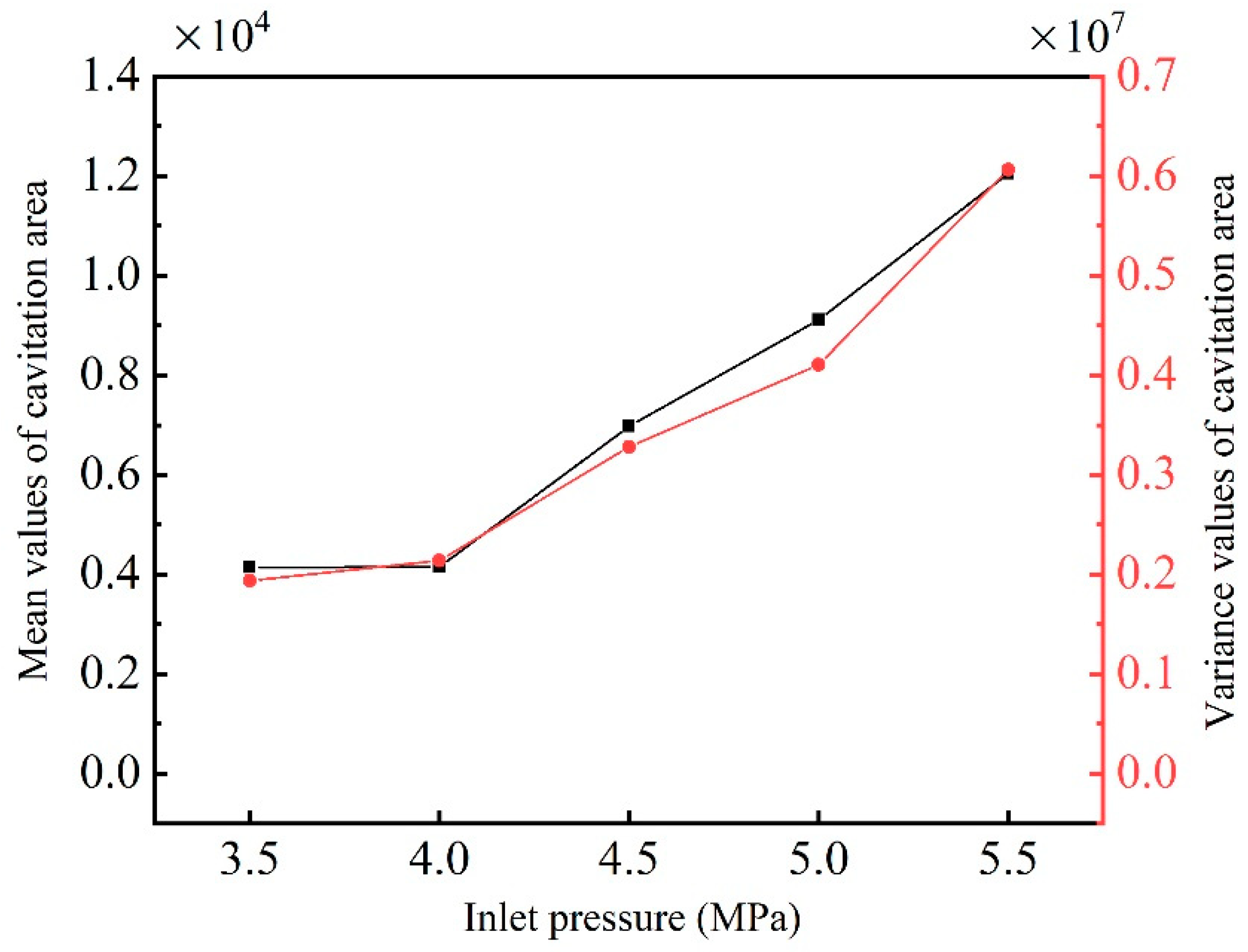
3.2. Influence of Inlet Pressure on Cavity Area
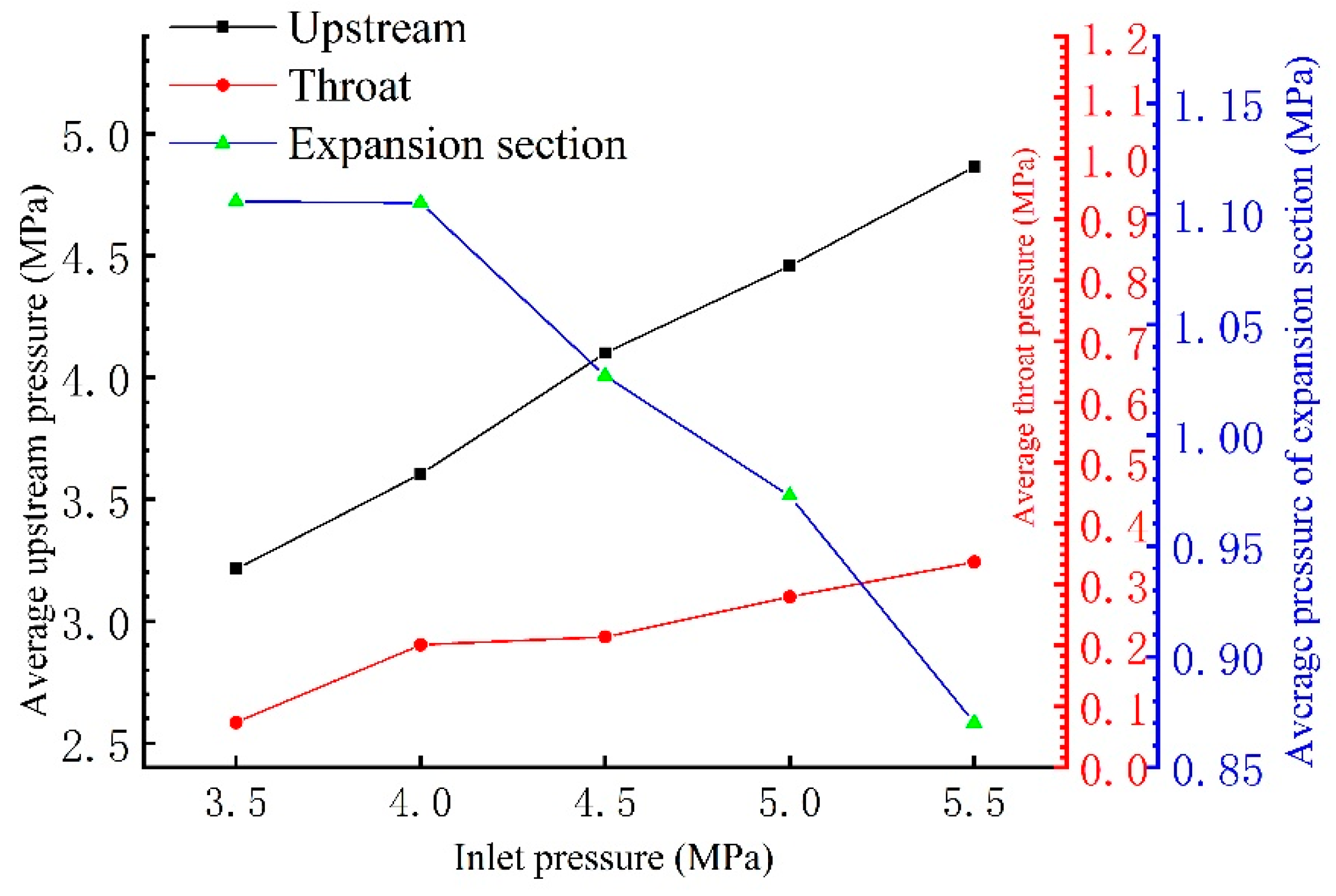
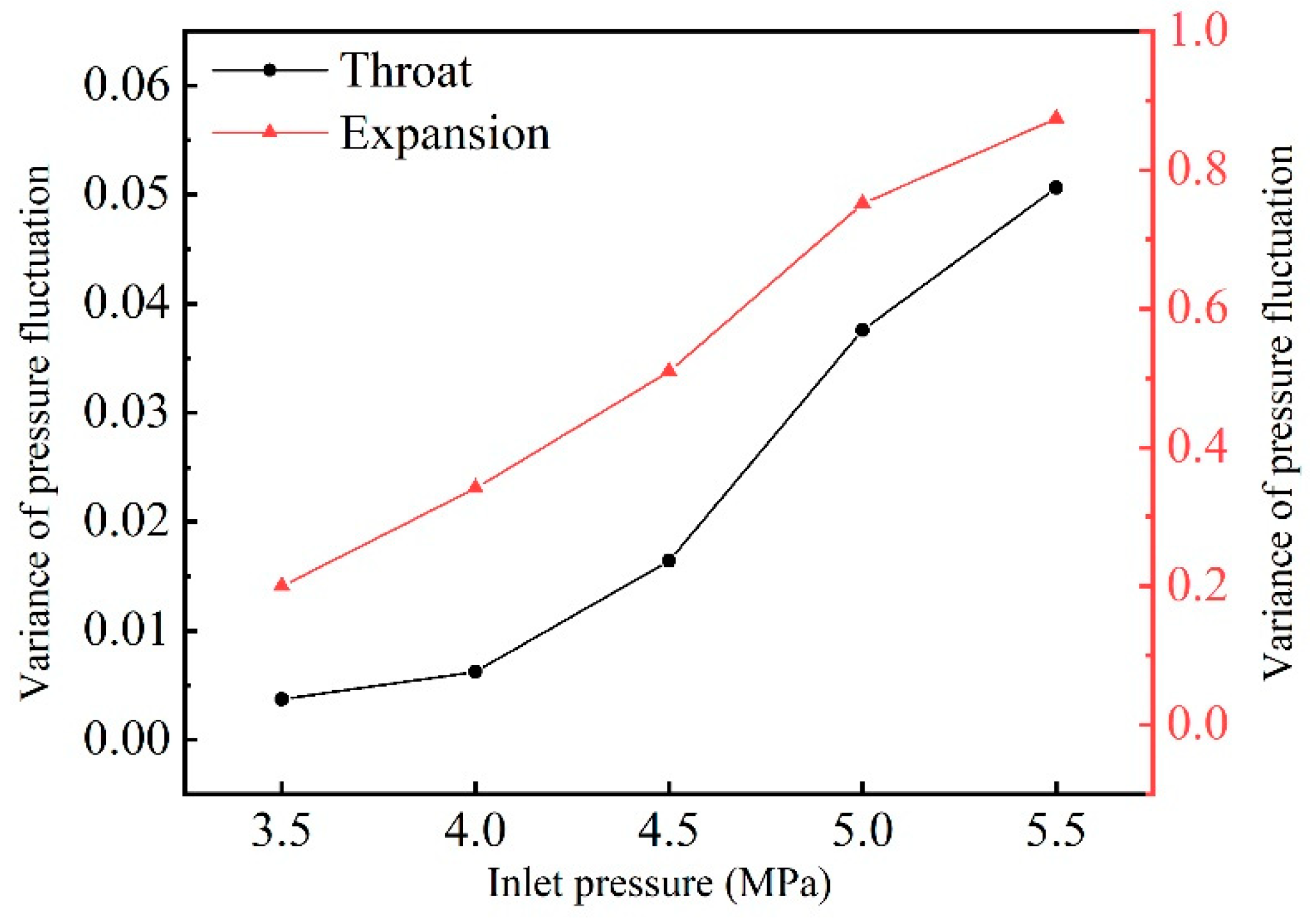
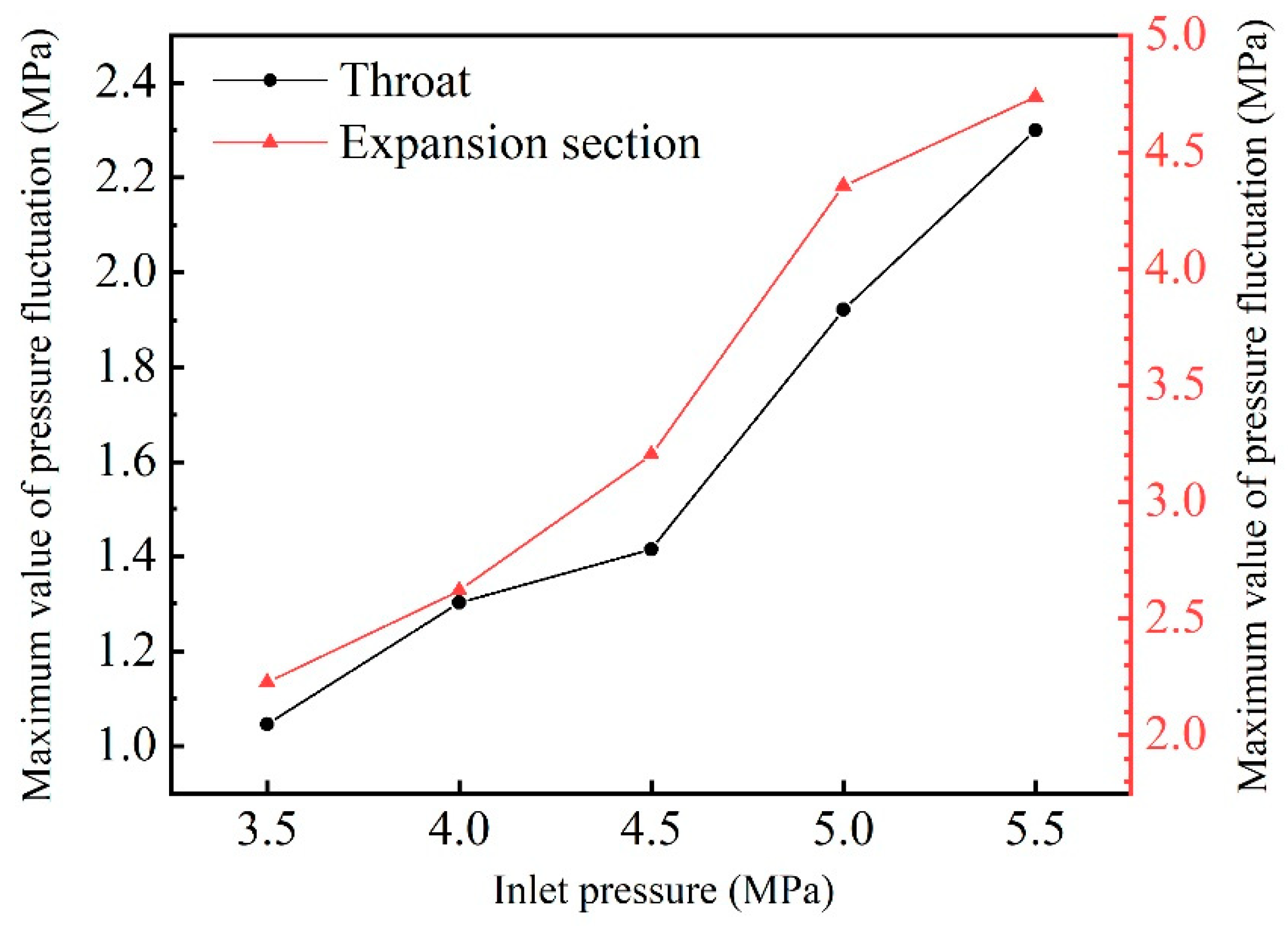
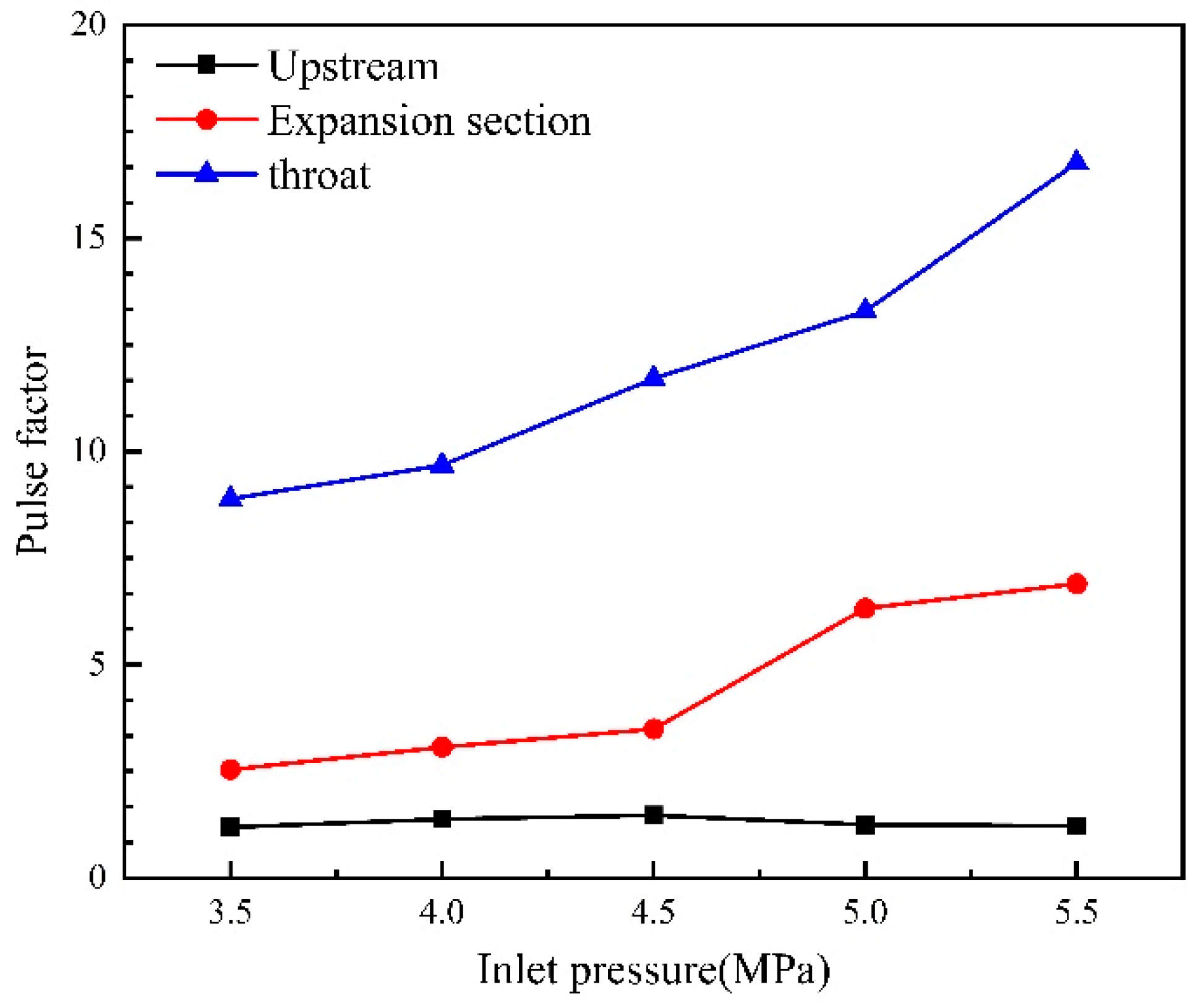
3.3. Influence of Inlet Pressure on Pressure Pulsation
4. Conclusions
- (1)
- The cavitation flow in the regulating valve is a quasi-periodic process with a period about 0.5 ms. A typical unsteady cavitation development process could be divided into three processes: the growth of the attached cavity, the fracture and shedding of the attached cavity and the growth and collapse of the free cavity.
- (2)
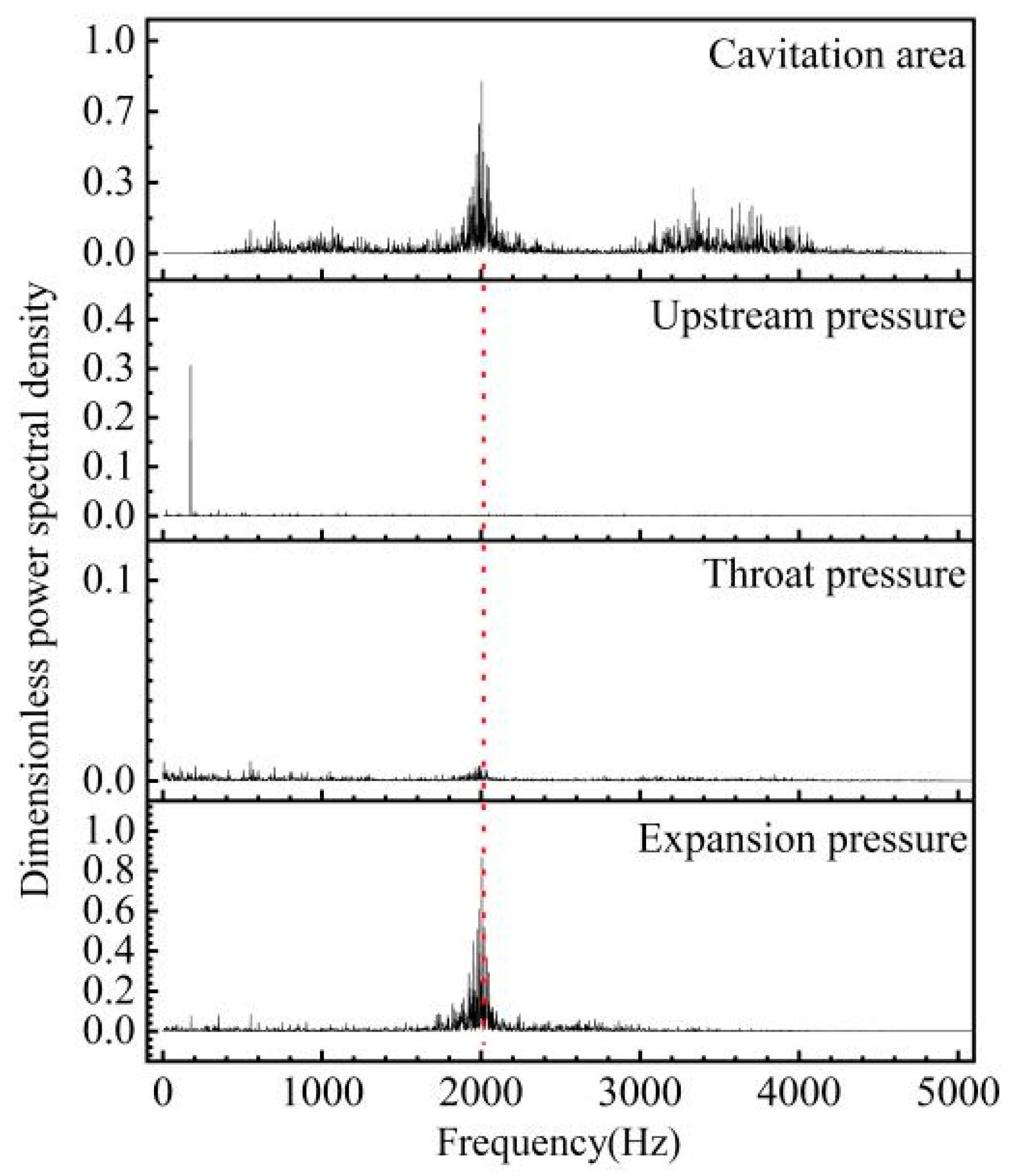
- The time evolution of the cavitation flow is highly related with excited pressure fluctuations. The dominant frequency of pressure and the cavity area is almost the same, about 2000 Hz. The characteristics of pressure pulsation at the three measuring points are different. The pressure pulsation at the upstream section is mainly affected by the pressure pulsation of the pump. The power spectral density of dominant frequency at the expansion section is much higher than that at the throat. With the increase in inlet pressure, the frequency of cavity area gradually decreases, and the mean value of cavity area and the variance value of cavitation area gradually increase.
- (3)
- The change of cavity area is also an important reason for the excited pressure pulsation. With the increase in inlet pressure, the attached cavity at the throat section began to fall off and break into free cavity, and the mean value of pressure pulsation gradually increased. At the expansion section, the pressure decreases due to continuous coverage of free cavity. In addition, with the increase in inlet pressure, the pressure fluctuation at each measuring point becomes more intense, and the variance value of pressure fluctuation and the maximum pressure value also increase gradually.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; He, J.; Li, B.; Zhang, C.; Xu, H.; Li, W.; Xie, F. Study on Unsteady Cavitation Flow and Pressure Pulsation Characteristics in the Regulating Valve. Shock. Vib. 2021, 2021, 6620087. [Google Scholar] [CrossRef]
- Jin, H.Z.; Zheng, Z.J.; Ou, G.F.; Zhang, L.T.; Rao, J.; Shu, G.P.; Wang, C. Failure analysis of a high pressure differential regulating valve in coal liquefaction. Eng. Fail. Anal. 2015, 55, 115–130. [Google Scholar] [CrossRef]
- Zheng, K.X.; Hu, H.X.; Chen, F.G.; Zheng, Y.G. Failure analysis of the blackwater regulating valve in the coal chemical industry. Eng. Fail. Anal. 2021, 125, 105442. [Google Scholar] [CrossRef]
- Min, W.; Wang, H.Y.; Zheng, Z.; Wang, D.; Ji, H.; Wang, Y.B. Visual experimental investigation on the stability of pressure regulating poppet valve. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 2329–2348. [Google Scholar] [CrossRef]
- Oshima, S.; Leino, T.; Linjama, M.; Koskinen, K.T.; Vilenius, M.J. Effect of Cavitation in Water Hydraulic Poppet Valves. Int. J. Fluid Power 2001, 2, 5–13. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W.; Chen, J.; Qiu, L.; Sun, D. Validation of dynamic cavitation model for unsteady cavitating flow on NACA66. Sci. China Technol. Sci. 2014, 57, 819–827. [Google Scholar] [CrossRef]
- Jazi, A.M.; Rahimzadeh, H. Detecting cavitation in globe valves by two methods: Characteristic diagrams and acoustic analysis. Appl. Acoust. 2009, 70, 1440–1445. [Google Scholar] [CrossRef]
- Liang, J.; Luo, X.; Liu, Y.; Li, X.; Shi, T. A numerical investigation in effects of inlet pressure fluctuations on the flow and cavitation characteristics inside water hydraulic poppet valves. Int. J. Heat Mass Transf. 2016, 103, 684–700. [Google Scholar] [CrossRef]
- Domnick, C.B.; Benra, F.-K.; Brillert, D.; Dohmen, H.J.; Musch, C. Numerical Investigation on the Time-Variant Flow Field and Dynamic Forces Acting in Steam Turbine Inlet Valves. J. Eng. Gas Turbines Power-Trans. ASME 2015, 137, 081601. [Google Scholar] [CrossRef]
- Stutz, B.; Legoupil, S. X-ray measurements within unsteady cavitation. Exp. Fluids 2003, 35, 130–138. [Google Scholar] [CrossRef]
- Dular, M.; Bachert, B.; Stoffel, B.; Sirok, B. Relationship between cavitation structures and cavitation damage. Wear 2004, 257, 1176–1184. [Google Scholar] [CrossRef]
- Kan, X.-Y.; Yan, J.-L.; Li, S.; Zhang, A.M. Rupture of a rubber sheet by a cavitation bubble: An experimental study. Acta Mech. Sin. 2021, 37, 1489–1497. [Google Scholar] [CrossRef]
- Petkovsek, M.; Hocevar, M.; Dular, M. Visualization and measurements of shock waves in cavitating flow. Exp. Therm. Fluid Sci. 2020, 119, 10. [Google Scholar] [CrossRef]
- Choi, M.J.; Kwon, O. Temporal and spectral characteristics of the impulsive waves produced by a clinical ballistic shock wave therapy device. Ultrasonics 2021, 110, 106238. [Google Scholar] [CrossRef]
- Brinkhorst, S.; von Lavante, E.; Wendt, G. Experimental and numerical investigation of the cavitation-induced choked flow in a herschel venturi-tube. Flow Meas. Instrum. 2017, 54, 56–67. [Google Scholar] [CrossRef]
- Chen, G.; Wang, G.; Hu, C.; Huang, B.; Gao, Y.; Zhang, M. Combined experimental and computational investigation of cavitation evolution and excited pressure fluctuation in a convergent-divergent channel. Int. J. Multiph. Flow 2015, 72, 133–140. [Google Scholar] [CrossRef]
- Reuter, F.; Gonzalez-Avila, S.R.; Mettin, R.; Ohl, C.-D. Flow fields and vortex dynamics of bubbles collapsing near a solid boundary. Phys. Rev. Fluids 2017, 2, 064202. [Google Scholar] [CrossRef]
- Leroux, J.B.; Coutier-Delgosha, O.; Astolfi, J.A. A joint experimental and numerical study of mechanisms associated to instability of partial cavitation on two-dimensional hydrofoil. Phys. Fluids 2005, 17, 20. [Google Scholar] [CrossRef] [Green Version]
- Stanley, C.; Barber, T.; Rosengarten, G. Re-entrant jet mechanism for periodic cavitation shedding in a cylindrical orifice. Int. J. Heat Fluid Flow 2014, 50, 169–176. [Google Scholar] [CrossRef]
- Foeth, E.-J.; van Terwisga, T.; van Doorne, C. On the collapse structure of an attached cavity on a three-dimensional hydrofoil. J. Fluids Eng.-Trans. ASME 2008, 130, 071303. [Google Scholar] [CrossRef] [Green Version]
- Smith, S.M.; Venning, J.A.; Pearce, B.W.; Young, Y.L.; Brandner, P.A. The influence of fluid-structure interaction on cloud cavitation about a stiff hydrofoil. Part 1. J. Fluid Mech. 2020, 896, A1. [Google Scholar] [CrossRef]
- Ganesh, H.; Makiharju, S.A.; Ceccio, S.L. Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities. J. Fluid Mech. 2016, 802, 37–78. [Google Scholar] [CrossRef] [Green Version]
- Kambayashi, I.; Kang, D.; Nishimura, N. Theoretical, Numerical, and Experimental Study on an Unsteady Venturi Flowmeter for Incompressible Flows. J. Fluids Eng. 2021, 143, 021308. [Google Scholar] [CrossRef]
- Long, Y.; Long, X.; Ji, B. LES investigation of cavitating flows around a sphere with special emphasis on the cavitation-vortex interactions. Acta Mech. Sin. 2020, 36, 1238–1257. [Google Scholar] [CrossRef]
- Sayyaadi, H. Instability of the cavitating flow in a venturi reactor. Fluid Dyn. Res. 2010, 42, 055503. [Google Scholar] [CrossRef]
- Liu, X.M.; Wu, Z.H.; Li, B.B.; Zhao, J.Y.; He, J.; Li, W.; Zhang, C.; Xie, F.W. Influence of inlet pressure on cavitation characteristics in regulating valve. Eng. Appl. Comput. Fluid Mech. 2020, 14, 299–310. [Google Scholar] [CrossRef]
- Han, M.; Liu, Y.; Wu, D.; Zhao, X.; Tan, H. A numerical investigation in characteristics of flow force under cavitation state inside the water hydraulic poppet valves. Int. J. Heat Mass Transf. 2017, 111, 1–16. [Google Scholar] [CrossRef]
- Ou, G.-F.; Rao, J.; Zhang, L.-T.; Zheng, Z.-J.; Ye, J. Numerical investigation of cavitation erosion/solid particle erosion in high differential pressure control valves in coal liquefaction. Mocaxue Xuebao/Tribol. 2013, 33, 155–161. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; He, J.; Xie, Y.; Li, B.; Zhang, Y.; Chen, J.; Liu, Q. Investigation on Unsteady Cavitation Flow and Excited Pressure Fluctuations in Regulating Valve. Machines 2022, 10, 32. https://doi.org/10.3390/machines10010032
Liu X, He J, Xie Y, Li B, Zhang Y, Chen J, Liu Q. Investigation on Unsteady Cavitation Flow and Excited Pressure Fluctuations in Regulating Valve. Machines. 2022; 10(1):32. https://doi.org/10.3390/machines10010032
Chicago/Turabian StyleLiu, Xiumei, Jie He, Yongwei Xie, Beibei Li, Yujia Zhang, Jinsong Chen, and Qihang Liu. 2022. "Investigation on Unsteady Cavitation Flow and Excited Pressure Fluctuations in Regulating Valve" Machines 10, no. 1: 32. https://doi.org/10.3390/machines10010032
APA StyleLiu, X., He, J., Xie, Y., Li, B., Zhang, Y., Chen, J., & Liu, Q. (2022). Investigation on Unsteady Cavitation Flow and Excited Pressure Fluctuations in Regulating Valve. Machines, 10(1), 32. https://doi.org/10.3390/machines10010032






