Research and Experimental Verification on Topology-Optimization Design Method of Space Mirror Based on Additive-Manufacturing Technology
Abstract
:1. Introduction
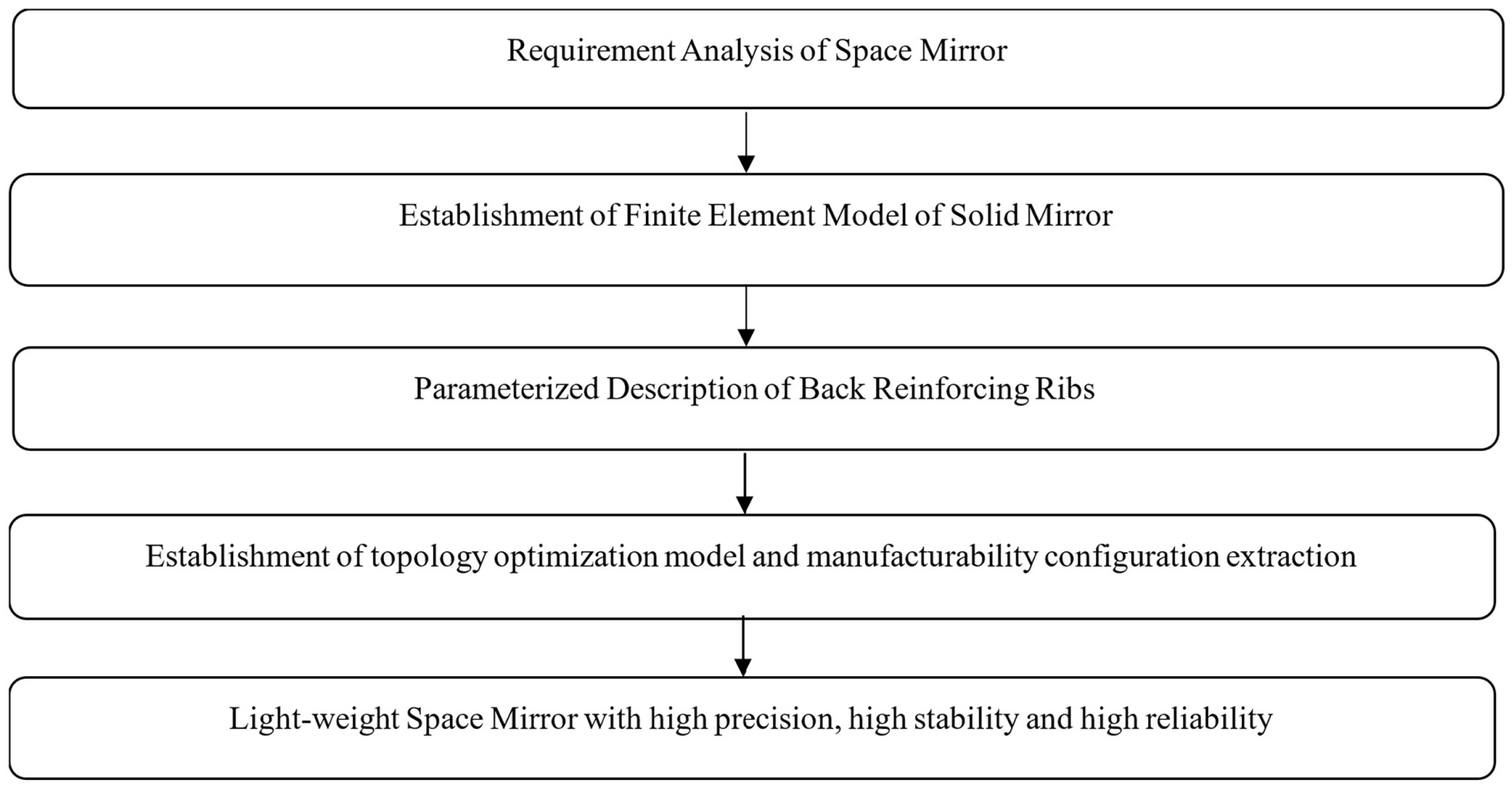
2. Three-Dimensional Solid Mirror Topology Optimization Design Method
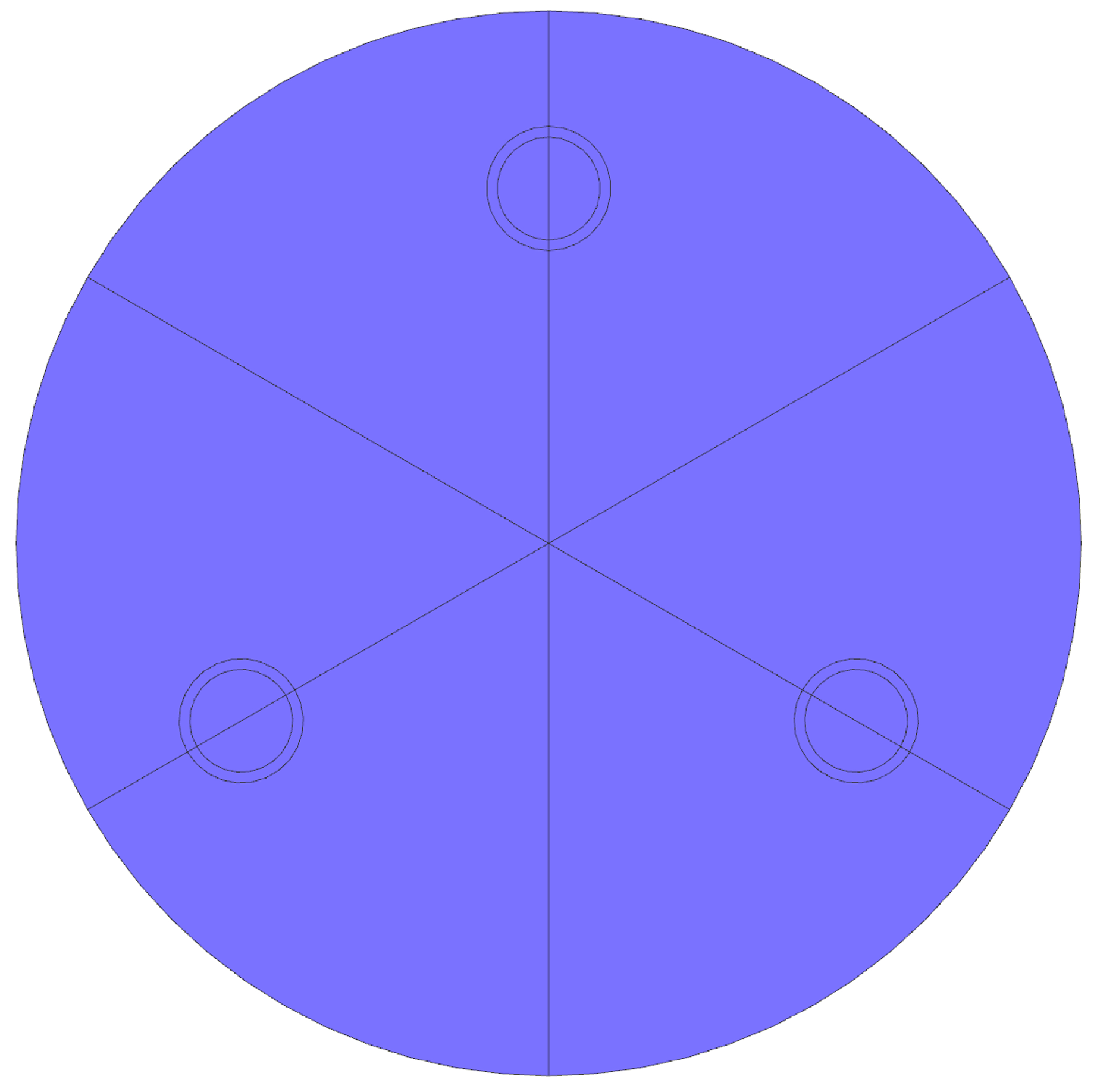
2.1. Analysis Method for Surface Accuracy of Space Mirrors
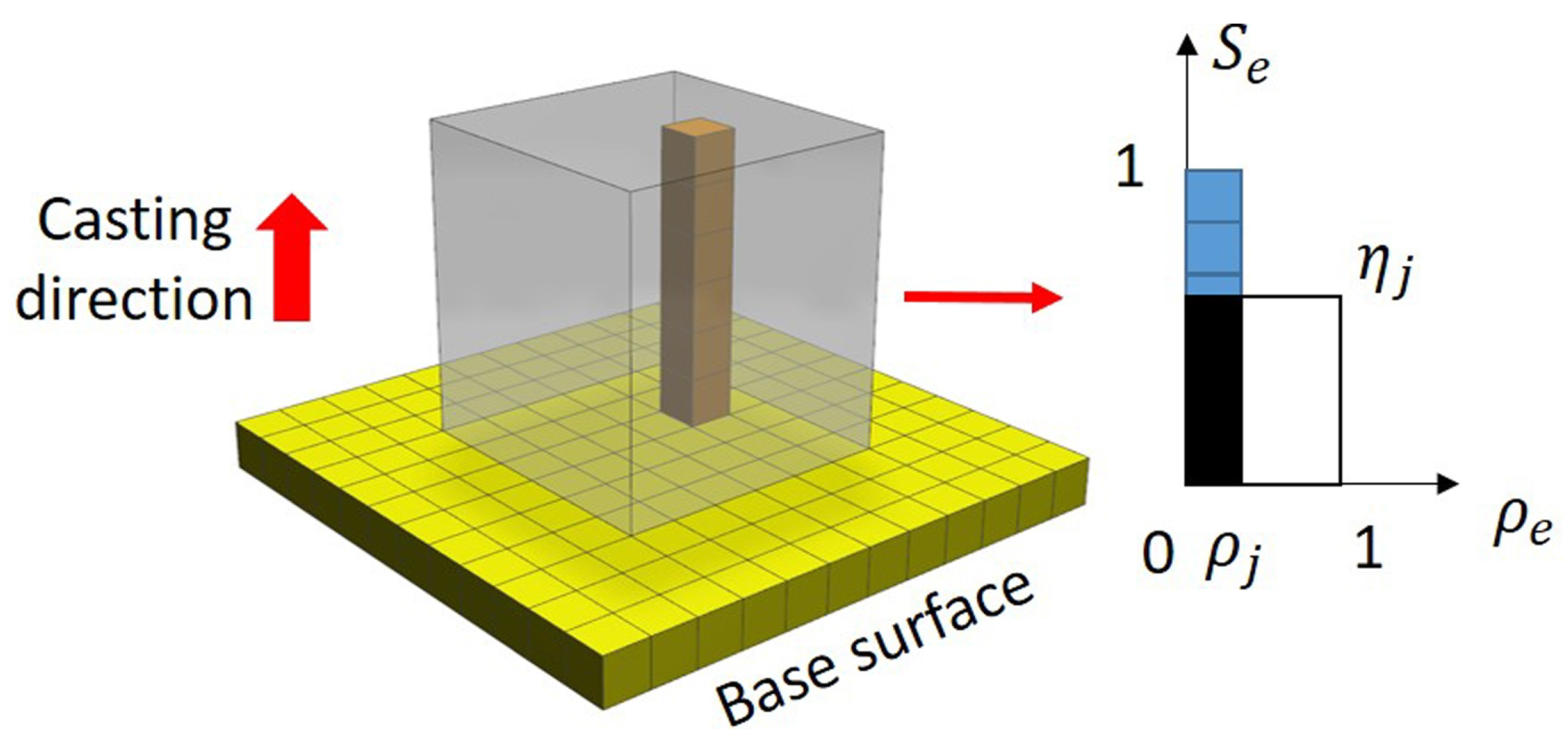
2.2. Description of the Back Ribs Layout and Height-Constraint Design Method of Space Mirror
2.3. Mathematical Modeling of the Topology Optimization for the Back-Solid Mirror
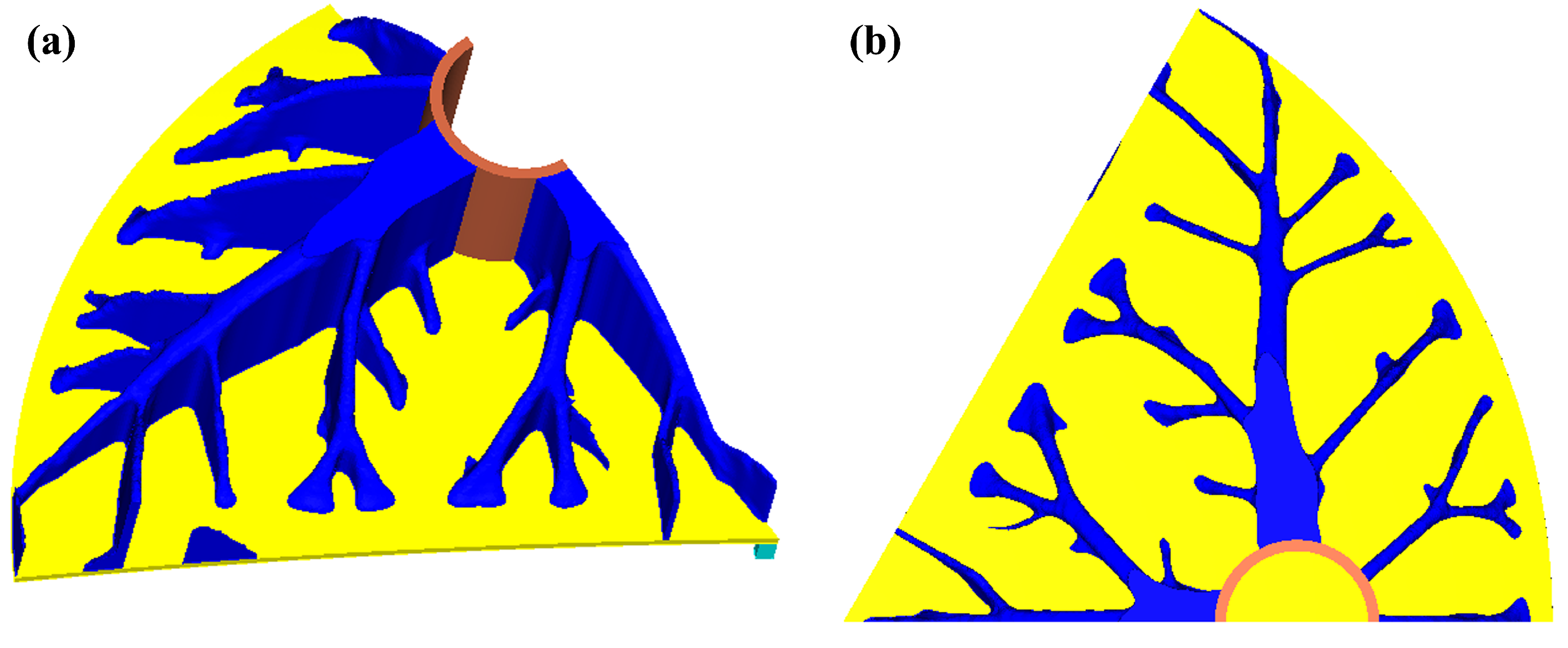
2.4. Optimized Configuration Extraction Method and Detailed Design
3. Topology-Optimization-Design Results of Additive-Manufacturing Space Mirror
4. Mirror Preparation and Performance Verification
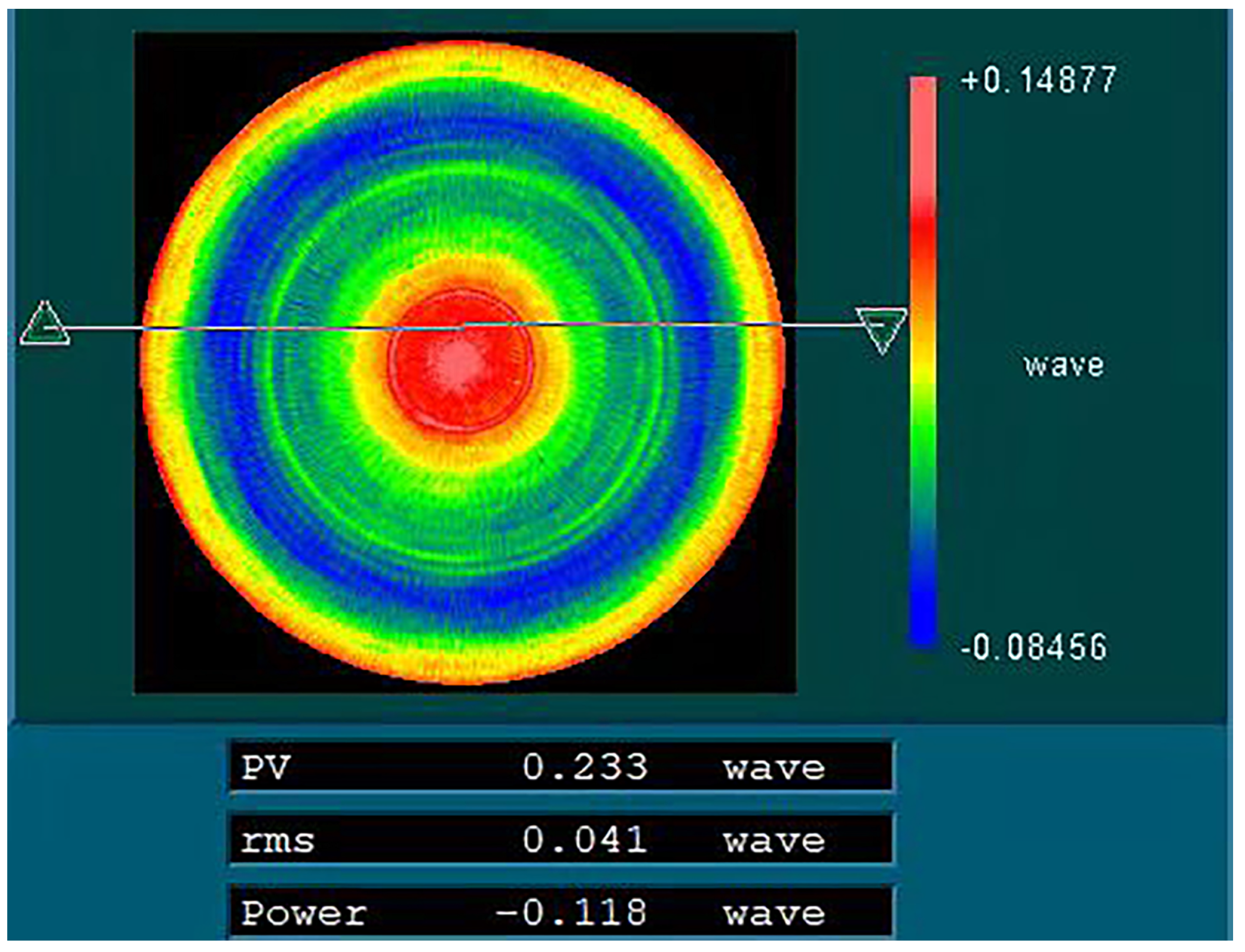
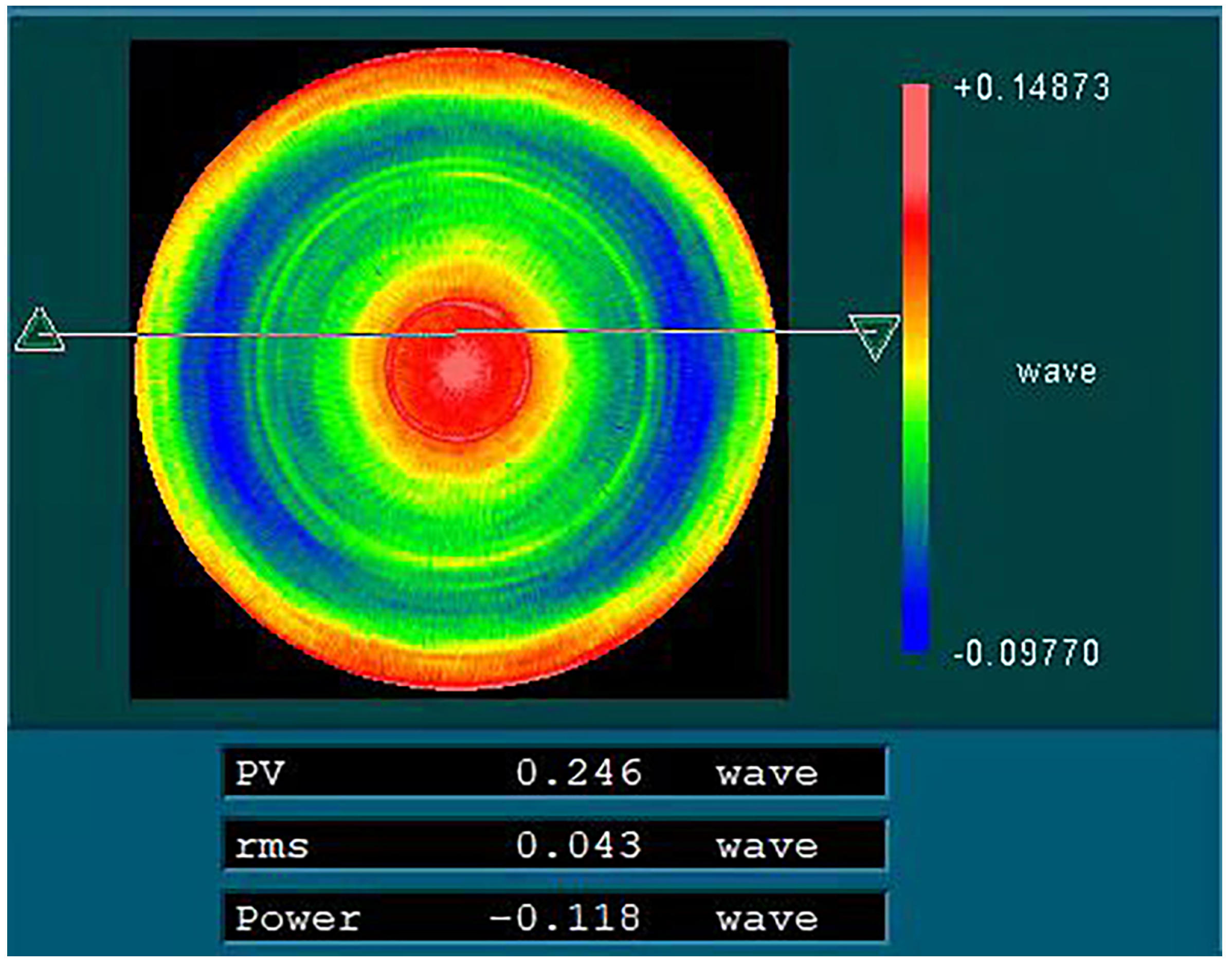
4.1. Mirror Preparation Verification
4.2. Mechanical Performance Verification
4.3. Machinability Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Talapatra, D.C. On the Self-weight Sag of Arch-like Structures in the Context of Light-weight Mirror Design. Opt. Acta Int. J. Opt. 1975, 22, 745–759. [Google Scholar]
- Valente, T.M.; Vukobratovich, D. A Comparison of the Merits of Open-Back, Symmetric Sandwich, and Contoured Back Mirrors as Light-Weighted Optics. In Proceedings of the Precision Engineering and Optomechanics, San Diego, CA, USA, 7–11 August 1989; Volume 1167, pp. 20–36. [Google Scholar]
- Fan, Y.C.; Chai, F.M.; Li, Z.L.; Yang, H.S. Lightweight Design of Primary Mirror with Large Aperture for Optical Remote Sensor. Opto-Electron. Eng. 2012, 39, 123–128. [Google Scholar]
- Bendsoe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Guest, J.K.; Prévost, J.H.; Belytschko, T. Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int. J. Numer. Methods Eng. 2004, 61, 238–254. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X.M.; Guo, D.M. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Park, K.S.; Chang, S.Y.; Youn, S.K. Topology optimization of the primary mirror of a multi-spectral camera. Struct. Multidiscip. Optim. 2003, 25, 46–53. [Google Scholar] [CrossRef]
- Lee, D.C.; Lee, J.I. Structural optimization design for large mirror. Opt. Lasers Eng. 2004, 42, 109–117. [Google Scholar] [CrossRef]
- Liu, L.; Gao, M.H.; Li, L.F.; Tan, Z.A. Primary mirror topological optimum design of space camera. Infrared Laser Eng. 2010, 39, 1066–1069. [Google Scholar]
- Li, Y.W.; Yang, H.B.; Geng, Q.X.; Liu, X.B.; Lei, C.H. Large-aperture lightweight primary mirror design method using topology optimization. Opt. Tech. 2008, 34, 236–238. [Google Scholar]
- Wang, X.; Wang, W. A new primary mirror based on topology optimization. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013: Imaging Sensors and Applications, Beijing, China, 25–27 June 2013; Volume 8908, pp. 165–189. [Google Scholar]
- Brackett, D.; Ashcroft, I.; Hague, R. Topology optimization for additive manufacturing. In Proceedings of the 24th Solid Freeform Fabrication Symposium, Austin, TX, USA, 17 August 2011; pp. 6–8. [Google Scholar]
- Woodard, K.S.; Myrick, B.H. Progress on high-performance rapid prototype aluminum mirrors. In Proceedings of the Advanced Optics for Defense Applications: UV through LWIR II, Anaheim, CA, USA, 9–13 April 2017; Volume 10181, p. 101810T. [Google Scholar]
- Woodard, K.S.; Comstock, L.E.; Wamboldt, L.; Sutherland, J.S. Optimum selection of high performance mirror substrates for diamond finishing. In Proceedings of the Advanced Optics for Defense Applications: UV through LWIR, Baltimore, MD, USA, 17–21 April 2016; Volume 9822, p. 98220C. [Google Scholar]
- Hilpert, E.; Hartung, J.; Risse, S.; Eberhardt, R.; Tünnermann, A. Precision manufacturing of a lightweight mirror body made by selective laser melting. Precis. Eng. 2018, 53, 310–317. [Google Scholar] [CrossRef] [Green Version]
- Tan, S.; Ding, Y.; Xu, Y.; Shi, L. Design and fabrication of additively manufactured aluminum mirrors. Opt. Eng. 2020, 59, 013103. [Google Scholar] [CrossRef]
- Long, K.; Chen, Z.; Zhang, C.; Yang, X.; Saeed, N. An Aggregation-Free Local Volume Fraction Formulation for Topological Design of Porous Structure. Materials 2021, 14, 5726. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, V.N. Circle Polynomials and Optical Aberrations of Systems with Circular Pupils. Appl. Opt. 1994, 33, 8121–8124. [Google Scholar] [CrossRef] [PubMed]
- Doyle, K.B.; Genberg, V.L.; Michels, G.J. Integrated Optomechanical Analysis, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2012; p. 31. [Google Scholar]
- Vukobratovich, D.; Schaefer, J.P. Large stable aluminum optics for aerospace applications. In Proceedings of the Optomechanics 2011: Innovations and Solutions, San Diego, CA, USA, 21–25 August 2011; Volune 8125, p. 81250T. [Google Scholar]








| Character | Value |
|---|---|
| Aperture | 260 mm |
| Support hole diameter | 30 mm |
| Vertex radius | 1500 mm |
| Character | Value |
|---|---|
| Surface thickness | ≥5 mm |
| Minimum structure size | ≥3 mm |
| Support hole wall thickness | 6 mm |
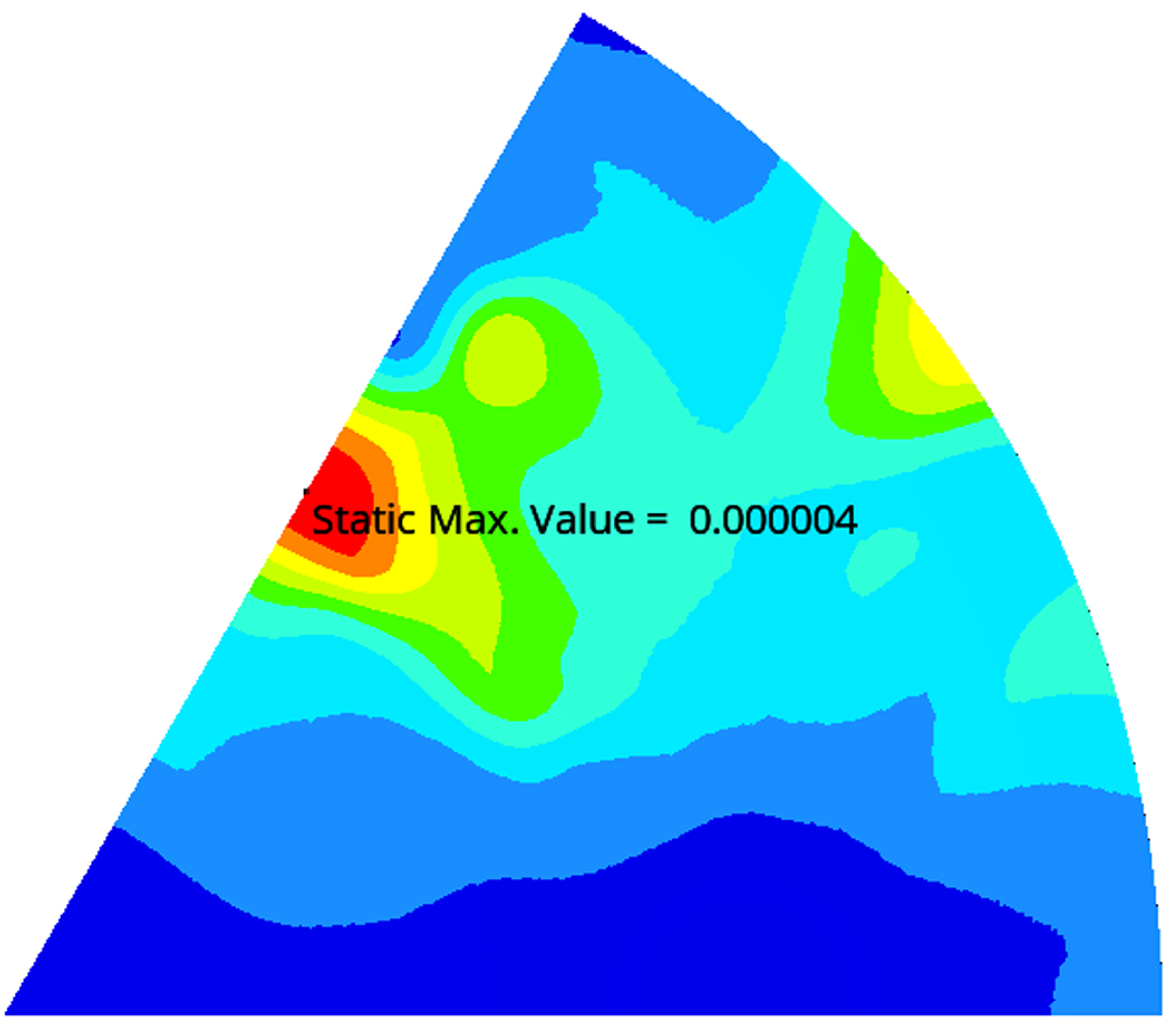
| Mirror surface deformation under self-weight | ≤/20 ( = 632 nm) |
| Area density | ≤30 kg/m |
| Lightweight rate | ≥80% |
| Basic Parameter | Mass (kg) |
|---|---|
| Simulated CAD model | 1.09 |
| Printed part | 1.11 |
| Relative variation | 1.9% |
| Character | Value |
|---|---|
| Equipment name | Inherent frequency test system |
| Specification/model | LMS SCADAS SCM2E01 |
| Equipment number | Z-L-085 |
| Equipment manufacturers | Siemens |
| Scope of use | 3.15 Hz–20 KHz, 17 dB–138 dB |
| Equipment accuracy | 50 mv/Pa |
| Modal Order | Test Results | Analysis Results | Relative Error |
|---|---|---|---|
| First order | 666 Hz | 664 Hz | 0.3% |
| Second order | 868 Hz | 878 Hz | −1.2% |
| Third order | 1021 Hz | 1037 Hz | −1.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Dong, D.; Li, C.; Sun, Y.; Zhang, Z.; Wu, F.; Yang, L.; Li, Q.; Guan, Y. Research and Experimental Verification on Topology-Optimization Design Method of Space Mirror Based on Additive-Manufacturing Technology. Machines 2021, 9, 354. https://doi.org/10.3390/machines9120354
Fan Y, Dong D, Li C, Sun Y, Zhang Z, Wu F, Yang L, Li Q, Guan Y. Research and Experimental Verification on Topology-Optimization Design Method of Space Mirror Based on Additive-Manufacturing Technology. Machines. 2021; 9(12):354. https://doi.org/10.3390/machines9120354
Chicago/Turabian StyleFan, Yanchao, Deyi Dong, Chao Li, Yuxin Sun, Zhiyu Zhang, Fanlu Wu, Liwei Yang, Quhao Li, and Yingjun Guan. 2021. "Research and Experimental Verification on Topology-Optimization Design Method of Space Mirror Based on Additive-Manufacturing Technology" Machines 9, no. 12: 354. https://doi.org/10.3390/machines9120354
APA StyleFan, Y., Dong, D., Li, C., Sun, Y., Zhang, Z., Wu, F., Yang, L., Li, Q., & Guan, Y. (2021). Research and Experimental Verification on Topology-Optimization Design Method of Space Mirror Based on Additive-Manufacturing Technology. Machines, 9(12), 354. https://doi.org/10.3390/machines9120354








