Abstract
A switched reluctance motor has a very simple structure which becomes its key signature and leads to various advantages. However, because of its double saliency and switching principle, the motor is also known to have a relatively high torque ripple, and this hinders its use as a high-performance drive. In this paper, a method to reduce torque ripple while maintaining average torque is introduced. Two elements are used to achieve this, namely, a non-uniform air-gap on the rotor-pole face and one hole in each non-uniform region, which maintains the saturation level of the air-gap. This approach preserves the mechanical simplicity of the motor and is easy to implement. Simulations and experiments were performed to verify the effectiveness of the proposed design.
1. Introduction
A switched reluctance motor (SRM) is known for its simple and robust mechanical structure. The motor consists only of stator and rotor steel laminations and its windings are wound around the stator pole in a concentrated manner. The simplicity of SRM is its main point of attraction, making it a promising candidate for a wide range of applications ranging from household appliances to automotives, including heavy industrial use [,,]. Moreover, with the absence of permanent magnets in general, SRM is also gaining popularity as a potential alternative to permanent magnet machines [].
As a doubly salient, singly-excited machine with non-linear magnetic characteristics, SRM inherently produces a relatively high torque ripple, compared to other AC machines with rounded cores [,]. Extensive research has been performed over the years to solve this problem. Generally, the effort to reduce the torque ripple in SRM can be divided into two approaches, which are the design and control approaches. The study in [] briefly summarizes some torque ripple minimization strategies that can be adopted. One of the most popular approaches is to use a torque sharing function where the phase torques can be controlled independently to follow a certain shape. Even simply changing the turn of on and off angles can reduce torque ripple []. This is because SRM generates only an electromagnetic torque which depends on the excitation angle according to rotor position. However, control methods can only go so far as to compensate the torque ripple which is mainly caused by the design.
From the design perspective, various geometries of stator and rotor cores have been developed to solve the problem. A study in [] compared stacked core SRMs with conventional ones. Winding configuration, converter topologies, and some control strategies are also discussed. It has been reported that a multi-stack structure produces lower torque ripple [,]. Its concept is to create a more circular air-gap, which is why it is effective to reduce the torque ripple. Other methods that use a similar concept are to implement a wide pole arc to increase the positive torque area, as presented in [], and skewed poles to provide continuous rotor pull as found in []. Creating a notch or a cut to the side of the rotor pole is also reported to reduce the torque ripple []. A flux barrier can also be used in the rotor since it alters the way the flux crosses the air-gap []. By modifying the way the flux flows in the motor, the torque can be shaped accordingly. As the name suggests, the flux barrier disturbs the flow of the flux by creating a cavity in each rotor pole-like a wall through which the flux cannot pass. A simpler version is the air-gap window, in which a rectangular hole is cut in each rotor pole as introduced in []. It is stated that the height of the window does not have a strong influence on torque, compared to the width. The reason is apparent, by blocking the flux path through use of the hole, the flux is forced to go around it, and passes only the solid core part which can reshape the torque profile. Furthermore, optimization algorithms can be added to find the best shape and placement of the holes as done in [] using computer-aided design and finite element method (FEM) programs.
The most popular method to reduce torque ripple in SRM, however, is using the non-uniform air-gap to affect the flux crossing the air-gap. In [], the rotor tips on the sides are chamfered to create a smooth torque profile, instead of a sudden increase when the stator starts to overlap with the rotor pole. Other methods include a sloping rotor pole with a face and jagged-tooth tip. In [], a stepped rotor is used for a 2-phase SRM, dividing the rotor pole area into two with different air-gap lengths. In [], a much smoother approach is adopted by using a slope that changes the air-gap length gradually. The non-uniform air-gap can then be combined with other design topologies such as in [], where the stator pole face is cut with a curve shape and pole shoes are added to the rotor pole.
Torque production in SRM can be described by using the mathematical formula below. is the electromagnetic torque produced at each phase excitation, is the excited phase current, and are phase inductance and rotor position. It is clear that torque generation depends on the current magnitude, regardless of direction, and the change of inductance according to rotor position.
Figure 1 shows the torque generation principle of SRM, corresponding to (1). A static analysis refers to the condition where the direct current flows to each phase, as presented in Figure 1a. On the other hand, the phases are switched on and off in the dynamic analysis, similar to the actual operation. Figure 1b shows this excitation and the related angle parameters. In a static analysis, the switching operation and current rising/falling time are not considered. Moreover, the rectangular shape can only be achieved by implementing a hysteresis current control that limits the maximum value. Unless the motor is designed to operate at its rated condition with hysteresis control, analyzing the electromagnetic characteristic from the dynamic perspective will produce more accurate results.
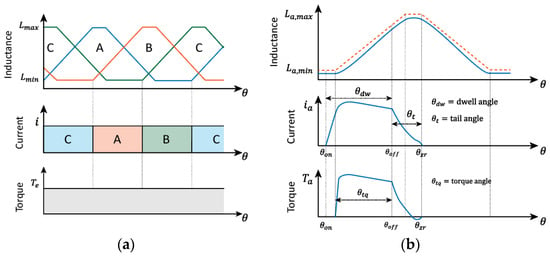
Figure 1.
Ideal SRM torque characteristics: (a) Static; (b) Dynamic.
In this paper, the non-uniform air-gap on the rotor side is combined with the hole-windowing approach to reduce the torque ripple of a 3-phase 12/8 SRM. A similar method was introduced in [], where two holes are cut into each rotor pole to make up for the lower saturation level due to the larger air-gap. The rough positioning of the holes is mentioned in [], but the effect of each hole parameter such as hole diameter, the position from the pole face and side, are not explained. Furthermore, only a static analysis was performed, in which the current was assumed to be constant. Instead of using two holes, the proposed design in this paper uses only one, which simplifies the design process. Each hole parameter is carefully observed to find the optimum placement. This paper focuses on the dynamic analysis to obtain a more precise torque-ripple characteristic. Skewed and multi-stack methods are effective, but they increase mechanical complexity significantly.
The main contribution of this paper is as follows. First, the study offers a method to reduce torque ripple while maintaining average torque, a very simple approach that can be performed by future researchers as a base to further improve the performance of SRM. Second, the study presents an analysis on how the combination of a non-uniform air-gap and the hole works, so that the design principle in this paper can be applied to other designs as well. Finally, a dynamic analysis whereby the phase switching is performed is preferred in this paper instead of the static analysis. Torque ripple is caused by excitation and thus dynamic torque profiles have to be considered for a more accurate result. The key strategy is to keep the design simple, which comprises the most important aspect of SRM since it affects the manufacturing cost.
2. Conventional and Non-Uniform Air-Gap Rotors
2.1. Conventional Rotor
The structure of a conventional 3-phase 12/8 SRM is shown in Figure 2. The circumference of the stator and rotor pole faces are both uniform and thus the air-gap length between them is constant during alignment. This feature is usually preserved to ensure the bidirectional rotating capability of the motor. denotes the rotor pole arc. It is customary to set to be wider than that of the stator or vice versa to obtain a sufficient torque, but this varies depending on application. Overall, the structure of SRM is very simple since the components involved are only a concentrated type of winding wound around each stator pole, one stator core, and one rotor core, as can be seen in the figure.
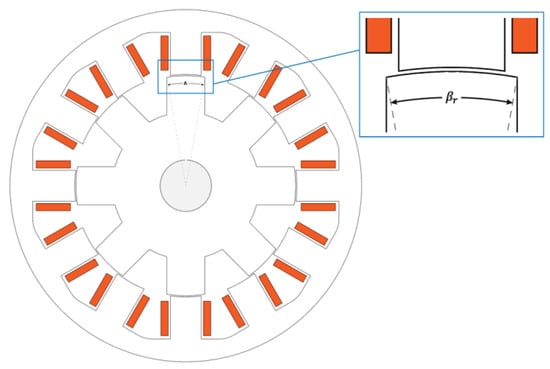
Figure 2.
Conventional 12/8 SRM.
The SRM used in this paper was initially designed to act as an actuator of a shift-by-wire or for the automatic transmission in vehicles. The specifications are presented below in Table 1.

Table 1.
Design Specifications.
The electromagnetic profile of this conventional model is shown in Figure 3. The switching angles have been adjusted to satisfy the required output. The actual phase current is not a constant DC value, and thus the torque is also not constant. The average torque is calculated to be 0.24 Nm and the torque ripple is 114.4%. The calculation for torque ripple is as follows,
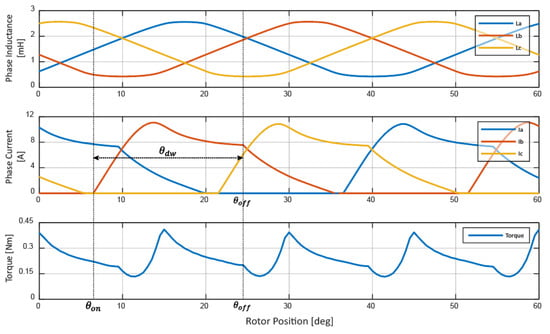
Figure 3.
Characteristics of a conventional 12/8 SRM.
The next thing that can be observed is the flux distribution of the motor. Figure 4 shows the flux density of the conventional 12/8 SRM. Only one pole set is analyzed since the others will follow a similar fashion. The arrow on Figure 4a marks the rotating direction and the circles, which show the point of interest where the stator and rotor pole start to overlap, as presented in Figure 4b. This is also the point at which the torque reaches its maximum value. In Figure 4c the phase current is shown to be turned off. Unless there is a slightly higher flux density at the tip edges, the rest of the overlapping faces have a uniform density level, because the air-gap length at that region is constant. The scale is set to 0 to 1.8 T since the saturated level of the core is 1.8 T based on the material datasheet. Since the phase self-inductance profile is symmetrical, rotation in the reversed direction will also show identical characteristics.
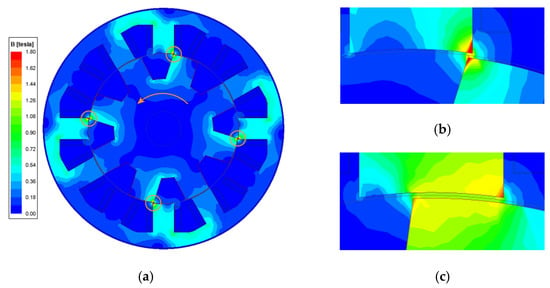
Figure 4.
Flux density of conventional 12/8 SRM: (a) Overall motor; (b) Start of overlap re-gion; (c) Turn-off point.
2.2. Non-Uniform Air-Gap
It is well-known that energy conversion occurs in the air-gap. Therefore, to modify the torque through design, changing the pole-tip shape is a commonly used method, especially in SRMs. Creating a non-uniform air-gap by cutting either the stator or rotor pole edges is a popular design method. In this paper, a smooth arc-shaped cutting for the rotor pole is selected. To preserve the bidirectional rotating capability, as this is a requirement of SBW application, the non-uniform part is mirrored for each pole pair, as shown in Figure 5 below. and are non-uniform and uniform arcs of the rotor pole. and are air-gap lengths of the uniform and non-uniform parts. Additionally, is measured from the rotor pole face based on and therefore the total length for non-uniform region becomes . There are four rotor pole pairs in a 12/8 SRM. Therefore, there are each four cuts in the same direction according to the rotating direction of the motor. More details on this approach are available in [].
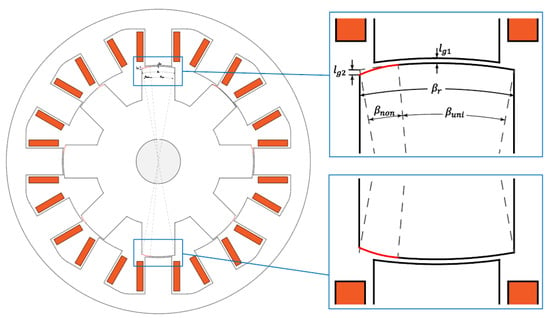
Figure 5.
Non-uniform air-gap, mirrored rotor cut.
FEA simulation is performed to observe the torque characteristics of each model. The result are shown in Figure 6. The static analysis is presented in detail in []. Taking only one dynamic torque waveform, it can be observed that instead of a ‘sudden’ increase of torque as such in the case of the conventional one, due to a sudden change of air-gap when the rotor aligns with the stator, a much smoother waveform can be observed in non-uniform types which reduces the peak torque. It would seem that the average torque should be lower, but a wider positive torque area can be obtained, resulting in a higher output torque. The numerical comparison is presented in Table 2 in unit ratio to the conventional model. The value of 0.15 mm is selected in this study in accordance with [].
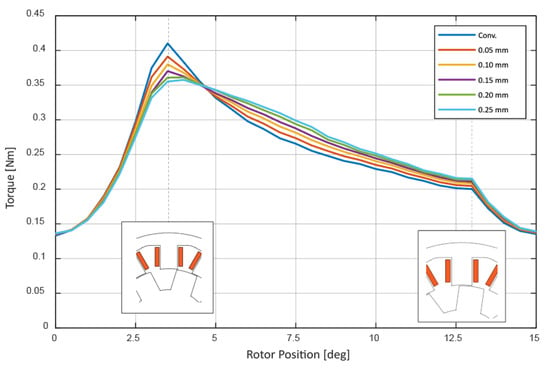
Figure 6.
Torque characteristics of conventional and non-uniform models.

Table 2.
Comparison of Torque Parameters.
Figure 7 shows the flux density of the non-uniform model. For one pole pair, the non-uniform part is mirrored. Thus, if one side meets the stator with a larger air-gap, the other side is aligned, starting from the smaller one. This in turn preserves the bidirectional nature of the motor. However, as the main point of this study, Figure 7b,c only highlight the effect of non-uniformity of the air-gap. Comparing Figure 4b and Figure 7b, the saturation level at the pole tips is found to be much lower in the non-uniform model. The same result can be obtained when comparing Figure 4c and Figure 7c. The non-uniform region generates a lower flux density in the air-gap, but allows more fringing flux in the surrounding area, which explains the wider torque area and the increase in average torque output, since torque can be measured by the extent to which the flux crosses the air-gap to reach the other side of the pole.
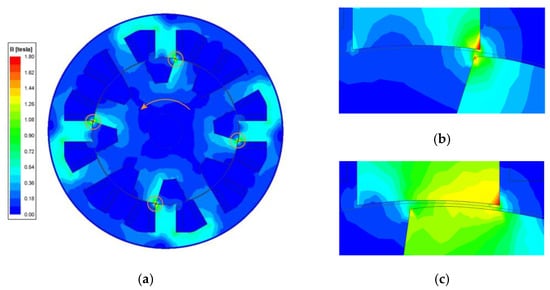
Figure 7.
Flux density of non-uniform rotor 12/8 SRM (): (a) Overall motor; (b) Start of overlap region; (c) Turn-off point.
3. Proposed Rotor with Non-Uniform Air-Gap and One-Hole
3.1. Design of Proposed Rotor
Due to the absence of permanent magnets in SRM, the motor completely relies on electromagnetic torque production. Therefore, the air-gap length plays an important role in determining the density of flux transfer between stator and rotor. However, as shown in the previous section, the flux density at the non-uniform region is lower than that of the conventional type. To compensate for the reduced density, it is necessary to increase the saturation for the non-uniform area. In this paper, a simple hole, drilled in the rotor, is proposed to redirect and focus the flux to create higher saturation and thereby increase torque. Figure 8 shows the proposed structure and the corresponding parameters. There are three design parameters corresponding to the hole. First is , which is the depth calculated from the non-uniform tip to the top edge of the hole. The next is , which represents the hole position along the non-uniform arc, calculated from the center of to the hole center. Finally, denotes the hole radius. In this section, iteration simulation is performed to find the effect of these three parameters. The location of the hole is also mirrored for each pole pair, according to the non-uniform area side.
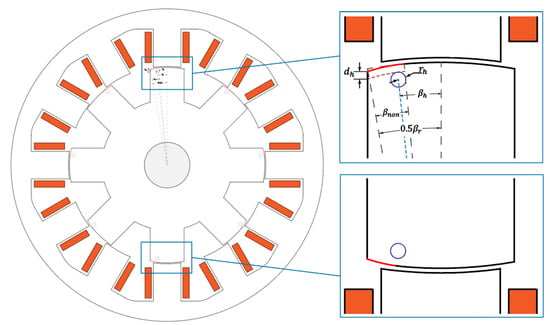
Figure 8.
Proposed rotor with one-hole in the non-uniform area.
3.2. Simulation Results of Proposed Rotor
The results of iteration are shown in Figure 9 and Figure 10 below. Specifically, Figure 9 focuses on the torque characteristic whereas Figure 10 focuses on the effect on magnetic saturation and the resulting core loss of the rotor only. Figure 9a,c,e present the average torque output when is set to 0.05, 0.30, and 0.55 mm, respectively, while Figure 9b,d,f present the corresponding torque ripple. The scale for the same figure category is the same, and thus the trend can be roughly observed from just the color gradient.
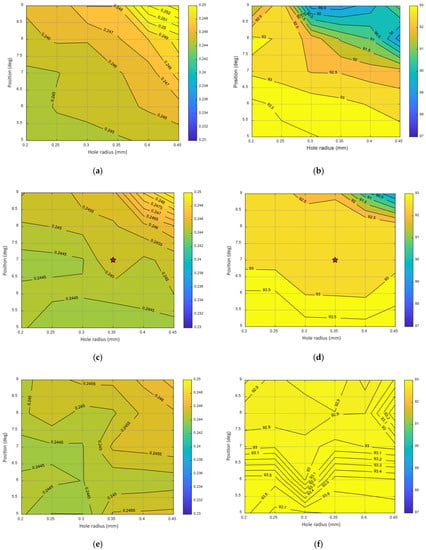
Figure 9.
Torque characteristic with varying , and : (a) Average torque ; (b) Torque ripple ; (c) Average torque ; (d) Torque ripple ; (e) Average torque ; (f) Torque ripple .
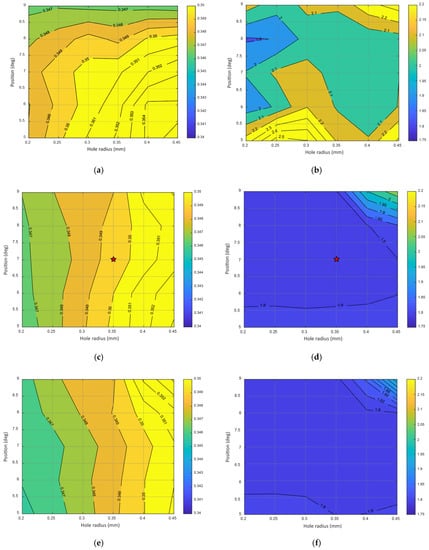
Figure 10.
Magnetic characteristic with varying , and : (a) Rotor core loss ; (b) Rotor saturation ; (c) Rotor core loss ; (d) Rotor saturation ; (e) Rotor core loss ; (f) Rotor saturation.
By analyzing the result in Figure 9, the effect of placing the hole in the non-uniform area of torque can be observed, and is as follows:
- When the hole is located too deep (large ) from the rotor-pole face, it has little effect. The change in the other two parameters at this point is unnoticeable.
- The same is applicable for . A greater value of produces a more noticeable change. However, this still depends on
- As for , the effect is more noticeable when it is closer to the side tip (larger ), this too depends on .
- It can be supposed that the hole does not affect the average torque by a wide range. The variance of maximum and minimum values from the three sets of figures is less than 3% of the rated torque of 0.24 Nm.
- Torque ripple, however, shows a slightly higher variance of 4.2%.
Figure 10 consists of the same structure as Figure 9, in which Figure 10a,c,e represent the rotor core loss when is set to 0.05, 0.30, and 0.55 mm, respectively, and Figure 10b,d,f are the corresponding maximum magnetic saturations, obtained at the turn off point.
For the same switching frequency, a higher average flux density will generate a higher loss. Therefore, the core loss here can also represent the average flux density. Again, is the most determinant factor. For the same and , increasing leads to a higher loss, although the variance is very slight. As explained before, the saturation point of the core material is 1.8 T, and thus, choosing a design value of below and/or close to 1.8 T is preferred. Thus, although a small affects the torque to a greater degree, the core is over-saturated. Moreover, the mechanical structure at this position will be much weaker and may lead to breakage during operation, which is dangerous.
As a summary, the hole parameter selection is mainly based on torque ripple. Average torque is observed to make sure that it is not reduced significantly. Conditions for the hole location is that it must not create over-saturation, which can occur if the hole is too close to the pole tip or surface, or if the radius is too large. Furthermore, it has to be inside the non-uniform section, since its role is to compensate for the reduced saturation as a result of the larger air gap. Based on these considerations, the selected values for , and are 0.30 mm, 7 degrees, and 0.35 mm, as marked with red stars in both Figure 9 and Figure 10.
The numerical comparison for torque is shown below in Table 3. Graphically, the torque comparison is shown in Figure 11. The non-uniform air-gap is responsible for a reduction in the peak torque and provides a smoother change of torque during rising and falling, based on the peak value. The peak is reduced, but the positive torque area after this point increases, which results in a slightly higher torque output. Then, by adding the hole, the average torque remains the same, but the torque ripple is reduced. This is caused by a reduced peak but also a slightly steeper slope during rising as well as a slower decrease.

Table 3.
Comparison of Torque Parameters.
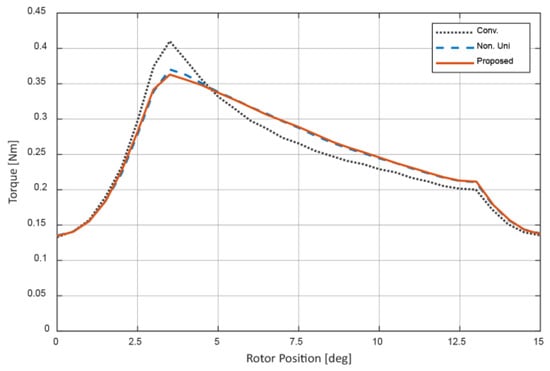
Figure 11.
Final torque comparison.
The flux density of the proposed structure is shown in Figure 12. Compared to the non-uniform model in Figure 7, the non-uniform area has a higher density in the proposed SRM. However, when the hole area already fully overlaps the stator pole, it can be seen that the top area immediately above the hole to the pole face has a slightly reduced density. This is because flux has to travel around the hole to cross the air-gap. A solution to this problem, so as to optimize the core area so that uniform density can be eliminated, is optimizing the shape of the hole. However, it is not in the scope of this paper.
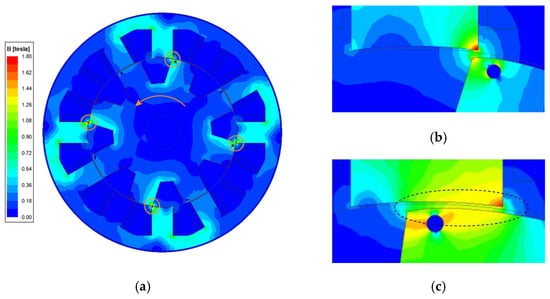
Figure 12.
Flux density of proposed 12/8 SRM: (a) Overall motor; (b) Start of overlap region; (c) Turn-off point.
4. Experimental Results
The 12/8 SRM was manufactured to verify the effectiveness of the proposed design. Since a comparison between conventional and the non-uniform rotors, combined with two holes, is already presented in [], in this paper, the hole effect is solely observed. Two rotors were manufactured, the non-uniform without holes and the proposed model (with hole). Figure 13 shows the prototype stator and rotors.
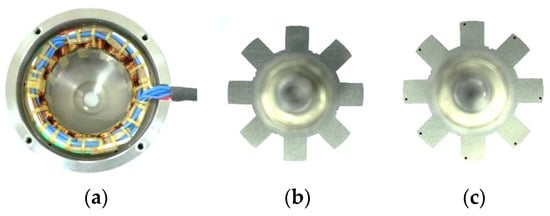
Figure 13.
Manufactured motor: (a) Stator; (b) Non-uniform rotor; (c) Proposed rotor.
Figure 14 shows the experimental setup. An electronic clutch was used to provide the load to the motor. The torque sensor was connected to a torque indicator that displays the load torque. However, the value that can be obtained from the sensor is only the mean torque level and the sensor itself is insufficient to obtain an accurate waveform. Therefore, the experimental torque ripple is predicted using the resulting current waveform.

Figure 14.
Experimental setup.
Figure 15 shows the experimental result at the rated condition at 1800 RPM and 0.24 Nm. Considering the SBW application of the motor, the control used here is a simple single-pulse method. This means there is no need to control the PWM for the power switches since they simply turn on and off at the set angles. First, it can be observed that the peak current of the proposed model is lower by around 2 A. However, since the peak is lower, the dwell angle, as was previously illustrated in Figure 1, must be widened to obtain the same current RMS value. The turn on and off angles were adjusted to achieve the speed requirement of 1800 RPM. Because of single pulse control, the phase current at the rated condition was not a constant DC value, which means dynamic electromagnetic analysis is more beneficial compared to the static analysis.
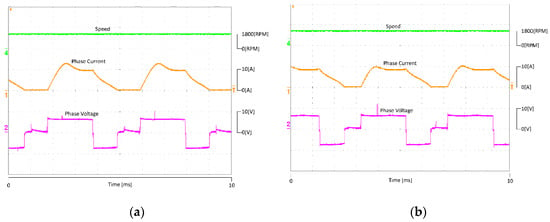
Figure 15.
Experimental result at rated condition: (a) Non-uniform rotor; (b) Proposed.
To verify the torque ripple of the proposed motor, simulations were performed based on the experimental result. The current and torque were reconstructed in the software to match the actual values, using the motor models from the previous sections’ analysis. The result is shown in Figure 16, and it is in conformity with the simulation. The peak torque of the proposed motor is slightly lower. The calculated torque ripple for the non-uniform and proposed models is 94.9% and 93.2% which means the proposed model produces less torque ripple by 1.7%, whereas the simulation result shows a reduction of 2%.
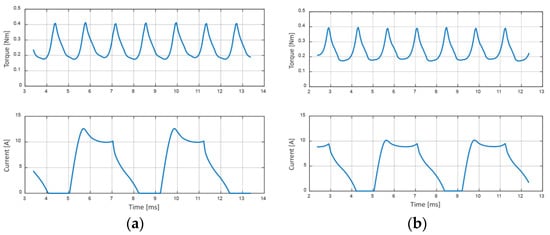
Figure 16.
Torque reconstruction based on experimental result: (a) Non-uniform rotor; (b) Proposed.
5. Discussions
This paper concerns torque-ripple reduction of SRM by adding a hole in each non-uniform region in the rotor. The non-uniform arc and hole location is mirrored for each pole pair, to maintain the symmetric property of the torque profile for bidirectional rotation. The key element here is to have a very simple, yet effective, design to lower the torque ripple. As presented above, the non-uniform air-gap plays the greatest role in reducing torque ripple. However, further reductions can be achieved by adding a hole to increase the reduced saturation level at the pole surface of the non-uniform section. A simple iteration method was performed to find the appropriate hole size and position. Intelligent optimization algorithms can be used, but they are very time-consuming and were deemed unnecessary in this study since only three parameters were considered. Furthermore, the study focuses more on the investigation of each parameter in acting as the base principle for further studies. Therefore, the proposed hole parameters were found to be appropriate in the scope of this study.
The target application is the shift-by-wire actuator. The motor drives the parking mechanism in automatic vehicles. The application requires that the actuator must shift comfortably, which is why torque ripple is considered to be one of the important performance parameters. As shown in Table 1, the size of the motor is small. The behavior of the flux and torque of SRM is the same regardless of size. However, whether the result of this study is scalable (for larger applications) or not requires further investigation. Core saturation levels may differ for each motor, according to the target application and the proposed idea cannot be applied to SRMs operating in unsaturated regions. Small to medium size SRMs might benefit from this study (most SRMs in home appliances or small automotive parts), but large-size motors (in vehicle or aircraft engines) need to be studied further.
The hole shape was chosen to be circular to ensure the simplicity of the design. Other hole shapes can be considered in future, according to the design goals. Adding the holes to the rotor requires one additional step in the manufacturing process, which is the punching process. Holes are punched into each lamination using a machine. Simple, small, circular holes are easy to punch in. A cost difference was not observed for the prototypes either with or without holes. However, there could be a slight price difference in mass production because of the extra manufacturing step. Nevertheless, the overall cost is still expected to be lower than for complicated designs such as skewed cores.
6. Conclusions
In this paper, a rotor structure of a 12/8 SRM, that adopts a non-uniform air-gap and one hole near the tip for each pole, is presented. The analysis of motor characteristics is based on the dynamic steady-state condition, in which the switching operation of SRM is simulated. The non-uniform air-gap is shown to reduce the value of peak torque and extend the positive torque area, leading to a slightly higher average torque value. Furthermore, the hole was placed in the non-uniform section to compensate for the reduced flux. Each design parameter, beginning with the non-uniform air-gap length, to the three hole parameters, namely, depth, arc position, and radius are observed. Among these parameters, the depth is of the utmost importance. Using the proposed structure, the simulation results show that the average torque increases by 4% while torque ripple is reduced by 21.4% compared to the conventional model. Experiments were performed to verify the proposed structure. Compared to the non-uniform model, the proposed rotor topology generates a slightly lower torque ripple of 93.2%. Nevertheless, the aim of this paper is to present a method by which the flux that flows through the air-gap can be manipulated using a non-uniform pole face with the addition of just one hole to reduce the torque ripple. The method is simple and easy to implement. In the future, the hole shape can be optimized to maximize the flux flow crossing the air-gap and to eliminate the reduced density area near the hole.
Author Contributions
Conceptualization, G.F.L. and J.-W.A.; formal analysis, G.F.L.; investigation, G.F.L.; methodology, G.F.L.; software, G.F.L.; validation, G.F.L. and J.-W.A.; visualization, G.F.L.; writing—original draft preparation, G.F.L.; writing—review and editing, G.F.L. and J.-W.A.; supervision, J.-W.A.; project administration, J.-W.A.; resources, J.-W.A.; funding acquisition, J.-W.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education (2018R1D1A1B0704373514) and Kyungsung University Research Grants in 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, C.; Wang, G.; Li, Y.; Xu, A. Robust Adaptive Neural Network Control for Switched Reluctance Motor Drives. Automatika 2018, 59, 24–34. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, C.; Yue, Y.; Wei, W.; Zhao, C. Design and Optimisation of an In-Wheel Switched Reluctance Motor for Electric Vehicles. IET Intell. Transp. Syst. 2018, 13, 175–182. [Google Scholar] [CrossRef]
- Elhomdy, E.; Li, G.; Liu, J.; Bukhari, S.A.; Cao, W.-P. Design and Experimental Verification of a 72/48 Switched Reluctance Motor for Low-Speed Direct-Drive Mining Applications. Energies 2018, 11, 192. [Google Scholar] [CrossRef] [Green Version]
- Boynov, K.; Paulides, J.J.H.; Lomonova, E.A. Comparative Analysis of the SRM as an Alternative to the PM Motor for Automotive Applications. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2014, 33, 1599–1612. [Google Scholar] [CrossRef]
- Xu, A.-d.; Zhao, X.; He, K.; Cao, Y. Torque-Ripple Reduction of SRM Using Optimised Voltage Vector in DTC. IET Electr. Syst. Transp. 2018, 8, 35–43. [Google Scholar] [CrossRef]
- Gan, C.; Wu, J.; Sun, Q.; Kong, W.; Li, H.; Hu, Y. A Review on Machine Topologies and Control Techniques for Low-Noise Switched Reluctance Motors in Electric Vehicle Applications. IEEE Access 2018, 6, 31430–31443. [Google Scholar] [CrossRef]
- Abdel-Fadil, R.; Al-Amyal, F.; Számel, L. Torque Ripples Minimization Strategies of Switched Reluctance Motor—A Review. In Proceedings of the 2019 International IEEE Conference and Workshop in Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 20–21 November 2019; pp. 41–46. [Google Scholar] [CrossRef]
- Shahabi, A.; Rashidi, A.; Nejad, S. Commutation Angles Adjustment in SRM Drives to Reduce Torque Ripple below the Motor Base Speed. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 669–682. [Google Scholar] [CrossRef]
- Lan, Y.; Benomar, Y.; Deepak, K.; Aksoz, A.; Baghdadi, M.E.; Bostanci, E.; Hegazy, O. Switched Reluctance Motors and Drive Systems for Electric Vehicle Powertrains: State of the Art Analysis and Future Trends. Energies 2021, 14, 2079. [Google Scholar] [CrossRef]
- Seshadri, A.; Lenin, N.C. Review Based on Losses, Torque Ripple, Vibration and Noise in Switched Reluctance Motor. IET Electr. Power Appl. 2020, 14, 1311–1326. [Google Scholar] [CrossRef]
- Ding, W.; Yin, Z.; Liu, L.; Lou, J.; Hu, Y.; Liu, Y. Magnetic Circuit Model and Finite-Element Analysis of a Modular Switched Reluctance Machine with E-Core Stators and Multi-Layer Common Rotors. IET Electr. Power Appl. 2014, 8, 296–309. [Google Scholar] [CrossRef]
- Lee, D.-H.; Ahn, J.-W. Performance of High-Speed 4/2 Switched Reluctance Motor. J. Electr. Eng. Technol. 2011, 6, 640–646. [Google Scholar] [CrossRef] [Green Version]
- Marcsa, D.; Kuczmann, M. Design and Control for Torque Ripple Reduction of a 3-Phase Switched Reluctance Motor. Comput. Math. Appl. 2017, 74, 89–95. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, H.S.; Kwon, B.I.; Kim, B.T. New Rotor Shape Design for Minimum Torque Ripple of SRM Using FEM. IEEE Trans. Magn. 2004, 40, 754–757. [Google Scholar] [CrossRef]
- Hur, J.; Kang, G.H.; Lee, J.Y.; Hong, J.P.; Lee, B.K. Design and Optimization of High Torque, Low Ripple Switched Reluctance Motor with Flux Barrier for Direct Drive. In Proceedings of the Conference Record of the 2004 IEEE Industry Applications Conference, 2004. 39th IAS Annual Meeting, Seattle, WA, USA, 3–7 October 2004; p. 407. [Google Scholar] [CrossRef]
- Sanada, M.; Morimoto, S.; Takeda, Y.; Matsui, N. Novel Rotor Pole Design of Switched Reluctance Motors to Reduce the Acoustic Noise. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference. Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy (Cat. No.00CH37129), Rome, Italy, 8–12 October 2000; pp. 107–113. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, S. Topology Optimization of Rotor Pole in Switched Reluctance Motor for Minimum Torque Ripple. Electr. Power Compon. Syst. 2017, 45, 905–911. [Google Scholar] [CrossRef]
- Moallem, M.; Ong, C.M.; Unnewehr, L.E. Effect of Rotor Profiles on the Torque of a Switched Reluctance Motor. In Proceedings of the Conference Record of the 1990 IEEE Industry Applications Society Annual Meeting, Seattle, WA, USA, 7–12 October 1990; pp. 247–253. [Google Scholar] [CrossRef]
- Nabeta, S.I.; Chabu, I.E.; Lebensztajn, L.; Correa, D.A.P.; da Silva, W.M.; Hameyer, K. Mitigation of the Torque Ripple of a Switched Reluctance Motor through a Multiobjective Optimization. IEEE Trans. Magn. 2008, 44, 1018–1021. [Google Scholar] [CrossRef]
- Hieu, P.T.; Lee, D.-H.; Ahn, J.-W. High Speed Segmental Stator Type 4/3 SRM: Design, Analysis, and Experimental Verification. J. Electr. Eng. Technol. 2017, 12, 1864–1871. [Google Scholar] [CrossRef]
- Choi, Y.K.; Yoon, H.S.; Koh, C.S. Pole-Shape Optimization of a Switched-Reluctance Motor for Torque Ripple Reduction. IEEE Trans. Magn. 2007, 43, 1797–1800. [Google Scholar] [CrossRef]
- Lukman, G.F.; Nguyen, X.S.; Ahn, J.-W. Design of a Low Torque Ripple Three-Phase SRM for Automotive Shift-by-Wire Actuator. Energies 2020, 13, 2329. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).