Modeling, Design, and Implementation of an Underactuated Gripper with Capability of Grasping Thin Objects

Abstract

Underactuated robotic grippers have the advantage of lower cost, simpler control, and higher safety over the fully actuated grippers. In this study, an underactuated robotic finger is presented. The design issues that should be considered for stable grasping are discussed in detail. This robotic finger is applied to design a two-fingered underactuated gripper. Firstly, a new three-DOF linkage-driven robotic finger that combines a five-bar mechanism and a double parallelogram is presented. This special architecture allows us to put all of the required actuators into the palm. By adding a torsion spring and a mechanical stopper at a passive joint, this underactuated finger mechanism can be used to perform parallel grasping, shape-adaptive grasping, and environmental contact-based grasp. Secondly, the dynamic model of this robotic finger is developed to investigate how to select an appropriate torsion spring. The dynamic simulation is performed with a multi-body dynamic simulator to verify our proposed approach. Moreover, static grasp models of both two-point and three-point contact grasps are investigated. Finally, different types of grasping modes are verified experimentally with a two-fingered underactuated robotic gripper.

1. Introduction

Till now, different types of robotic hands have been developed for the purpose of grasping and manipulating daily objects. Among them, anthropomorphic hands were developed to mimic the dexterity of the human hand. Well-known designs include the Utah-MIT Hand [1], the DLR Hand [2], the Shadow Hand [3], and the Robonaut 2 Hand [4]. Most of these dexterous robotic hands are complicated in either mechanical structure or control architecture. In general, their maintenance is complicated and their manufacturing costs are high. Hence, most of them are only applied to the research community and are still far from practical applications, as reported in [5]. Thus, a lot of effort has been put into the design of low-cost, simple-maintenance, and easy-operation robotic hands which could be widely applied to practical applications such as the automation industry and medical rehabilitation. To this end, particular attention has been paid to designing non-anthropomorphic robotic hands/grippers with an underactuated structures which could reduce the number of actuators and require simple control systems for a given task [6,7,8,9]. Compared with fully actuated robotic hands, underactuated robotic hands reduce the number of actuators while relatively preserving the ability of dexterous grasping [10]. Moreover, underactuation design also provides safety and robustness against environmental uncertainties during grasping [11,12].

Based on mechanical elements used in the power transmission system, underactuated robotic hands/grippers can be classified into three main types as follows: the wire-driven type [13,14,15,16,17,18,19,20,21,22], the linkage-driven type [23,24,25,26,27,28,29,30,31,32,33,34], the gear-driven type [35,36,37,38,39], and some combinations [40,41,42]. The wire-driven type has advantages of compact size, light weight, and good shape-adaptive properties when encompassing the object to be grasped. However, it has disadvantages such as wire slack, complicated maintenance, and a small grasping force that is constrained by the cable strength and pretension force. Comparatively, the linkage-driven type has the advantage of high safety because the rigid linkages can be used to transmit large force. However, due to the link interference, its workspace, in general, is smaller than that of the wire-driven or gear-driven type. Moreover, for a multi-degree-of-freedom (DOF) linkage-driven finger mechanism, it is difficult to mount all of the actuators on the base (palm).

In general, elastic elements such as springs and compliant joints are required and combined with mechanical stoppers for the purpose of avoiding undesired motion and achieving multiple grasp modes stably. To prevent undesired motion during underactuated grasping, elastic elements (springs and compliant joints) and mechanical stoppers generally are required to provide passive control. These passive elements are also referred to as “passive actuators”. During the open-close motion of the finger, the stiffness of the spring should be large enough to prevent undesired motion due to gravity and inertia terms. Once contact with an object is established at the proximal phalanx, the actuator has to increase the actuation torque (to withstand preloading and deformation of the spring) to continue the close motion until a static equilibrium is achieved. This variation is generally significant. For a certain range of input torque and object sizes, a balance of design stiffness and preloading of the torsion spring should be considered to maximize the stable power-grasping region [43]. In our previous study [27], a functional robotic finger prototype was designed intuitively without investigating the grasping behavior of the final design. The development of this finger prototype is primarily based on a specific CAD-aided simulation and lacks a systematic framework for its designing and analysis. For bin-picking applications, a gripper that combines vacuum suction grasping [44] and two independently controlled mechanical fingers has been built using a similar approach, i.e., intuitive design based on a specific CAD-aided simulation. In this paper, the authors tried to provide an approach that combines the dynamics and statics of the underactuated robotic finger to select the appropriate stiffness and preloading of the spring.

In this paper, we present the design issues and applications of a 3-DOF underactuated robotic finger. Architecture description and grasping modes analysis are presented in Section 1. Section 3 presents the dynamic modeling of this robotic finger and an approach to selecting the torsional spring. In Section 4, static modeling of this finger mechanism is presented. In Section 5, a two-fingered underactuated robotic gripper is developed. Finally, multiple grasping modes of this robotic finger are verified experimentally.

2. Architecture of the Robotic Finger Mechanism

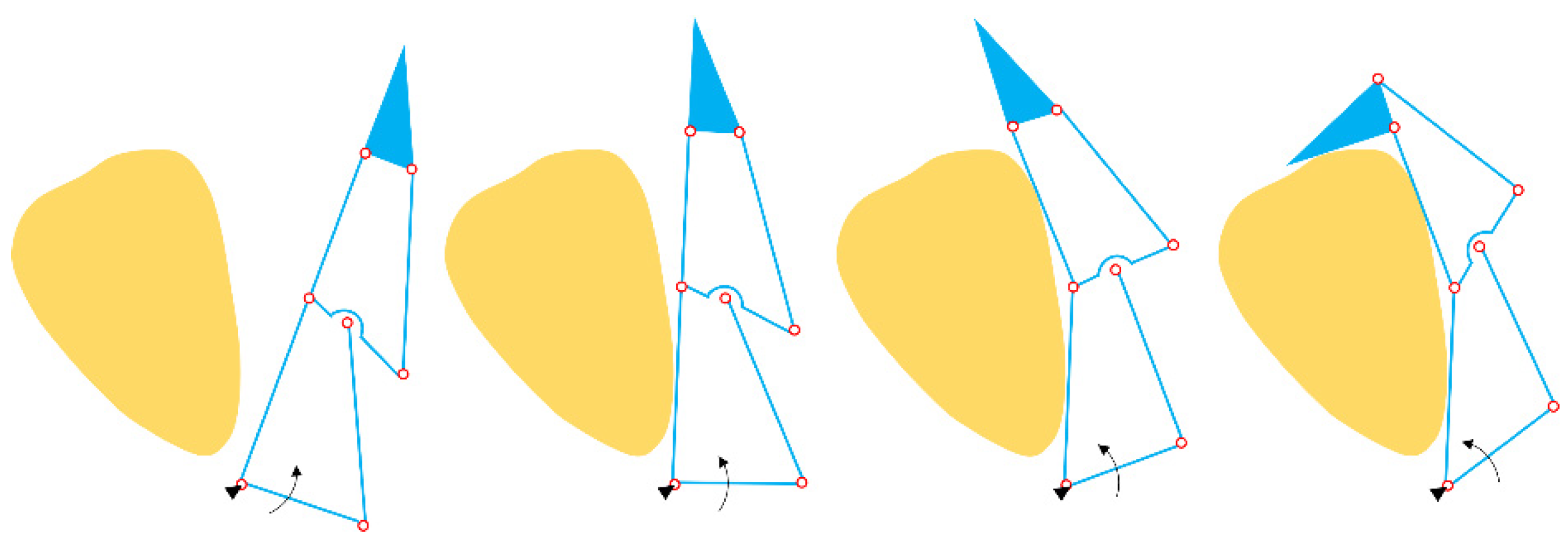
The grasping sequence of a general three-phalanx underactuated robotic finger is shown in Figure 1. By adding passive elements (springs and mechanical stoppers) at the pivot joint between adjacent phalanxes and activating the lower link (indicated by the arrow), the proximal, intermediate, and distal phalanx will make a contact with the object in sequence once the lower link (indicated by the arrow) is actuated. This finger can only be used to perform shape-adaptive grasping. However, in a real-world scenario, users expect the robotic finger to perform multiple grasping tasks such as parallel grasping and shape-adaptive grasping. In this case, special design architecture is required. The well-known three-phalanx adaptive gripper from the Robotiq company (licensed from [45]) is developed by modifying the robotic finger shown in Figure 1.

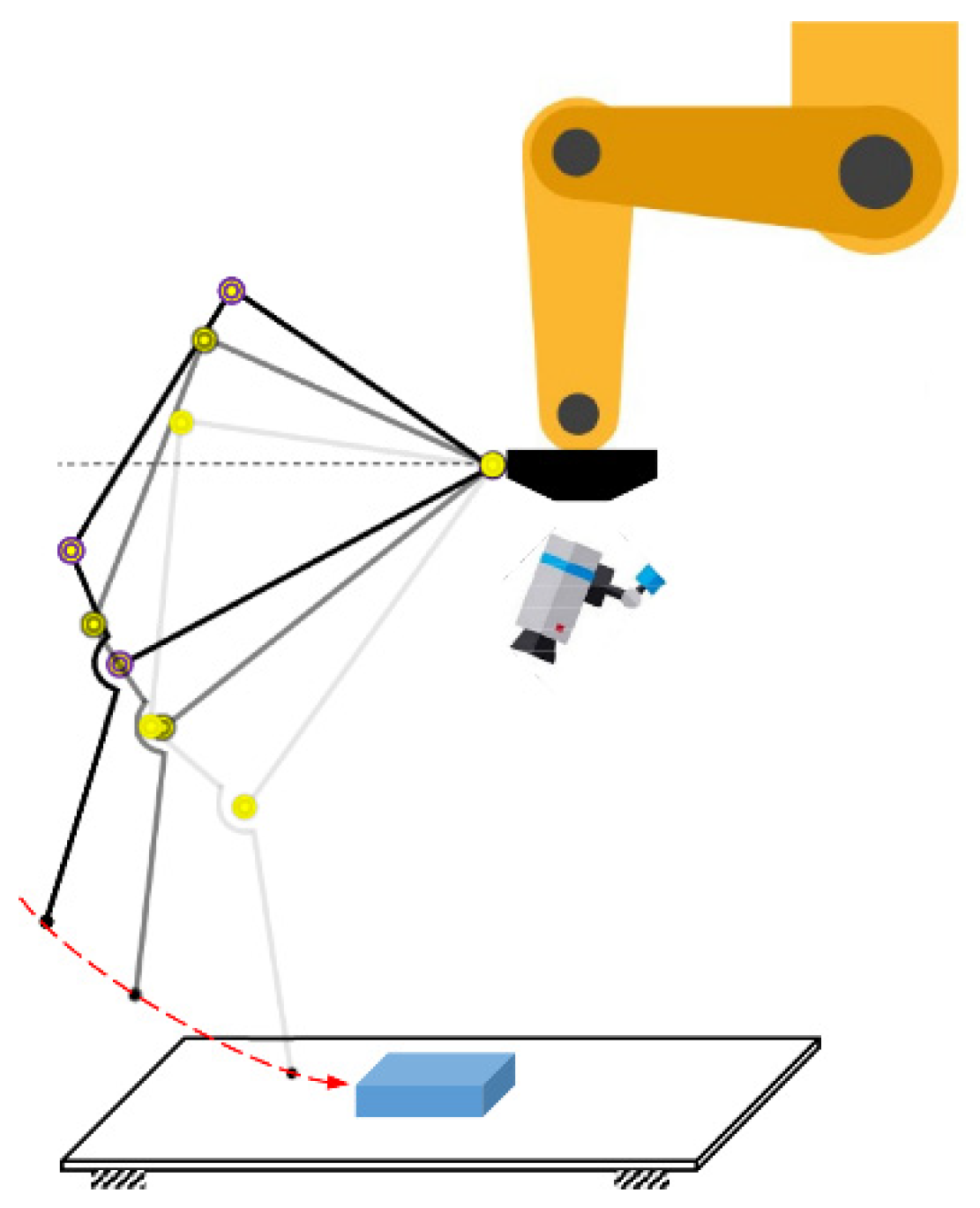
The motivation of this research is to develop a new robotic gripper for grasping a wide range of household objects. According to this grasping scenario, the robotic gripper is expected to provide the following functions: fingertip parallel grasping; shape-adaptive grasping; and the ability to stably grasp objects with low heights, such as a coin, pill, pen, toothbrush, phone, etc., lying on a flat surface. Except for the simple parallel-jaw gripper, most of the other grippers are rotational grippers, i.e., the whole finger open-close motion is controlled by a rotational joint as illustrated in Figure 2, from which we can find that the trajectory of the fingertip point is an arc (swing trajectory indicated by red dashed line). Obviously, the vertical distance from the fingertip to the palm (usually fixed to the end-effector of an industrial robot) will be changed during the grasping. If the industrial robot is fixed during this process, the vertical distance from the fingertip to the supporting surface also keeps changing. In this case, the industrial robot generally has to be controlled by using certain robot-vison algorithms to adjust the position of the fingertip in order to make contact with the object to be grasped. For those objects with low heights, a good calibration algorithm and a highly accurate robot-vision system are generally required for avoiding making contact with the supporting surface. As visual localization errors always exist, coordinate control errors of industrial robot and robotic gripper, and uncertainties of the grasping environment, the fingertip makes contact with the environment frequently while grasping household objects that have varied shapes and sizes. For many of the previous underactuated grippers, the fingertips are passively coupled with other phalanxes and the directions of the fingertips will be changed passively and become not parallel to each other while making contact with the supporting surface. Such non-parallel fingertips may cause unstable contact-based pinching grasping. A stable contact-based pinching grasping requires that the fingertip is not passively coupled with other phalanxes, i.e., after contact with the supporting surface, the direction of the fingertip will not be changed passively. This design concept is shown in Figure 3.

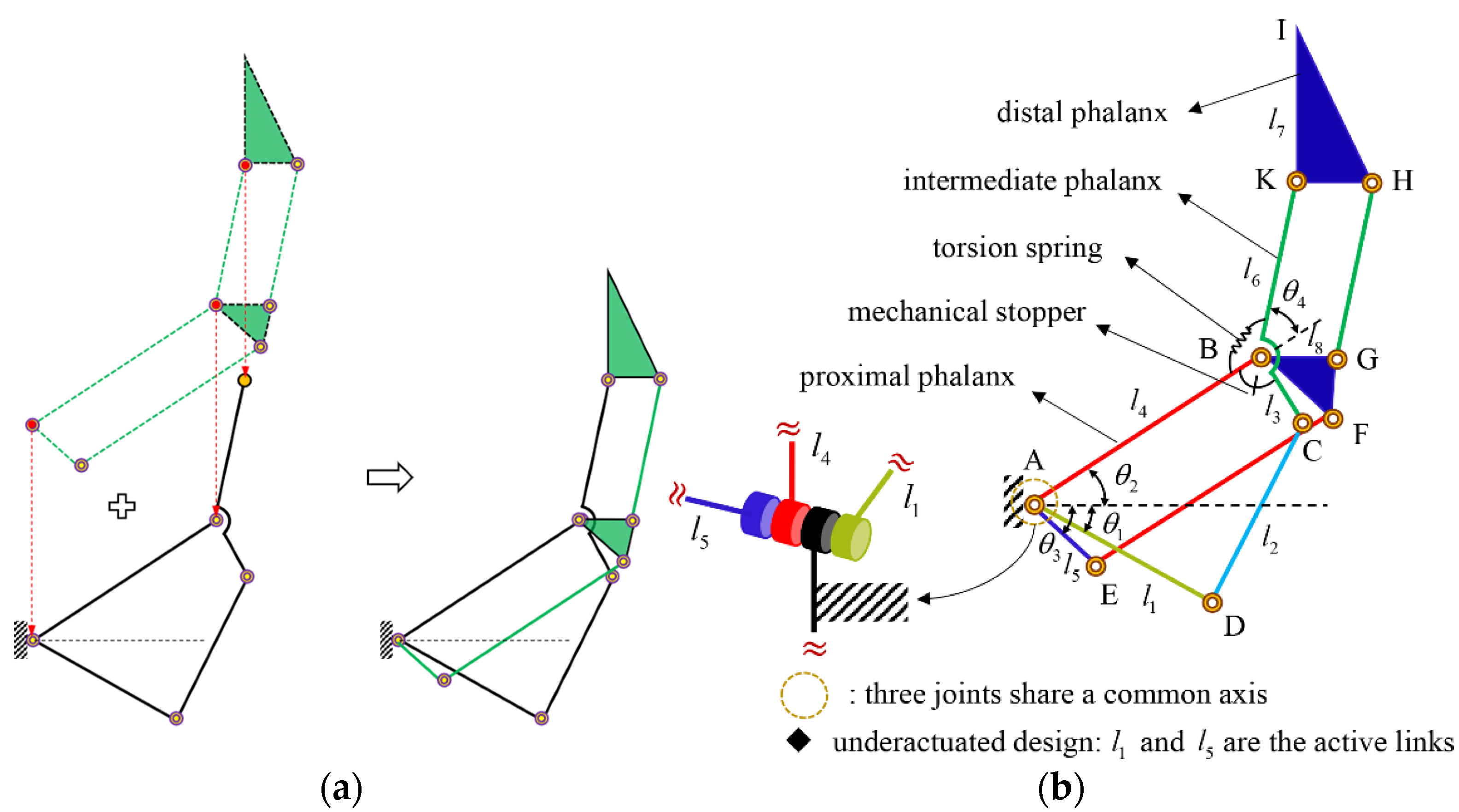
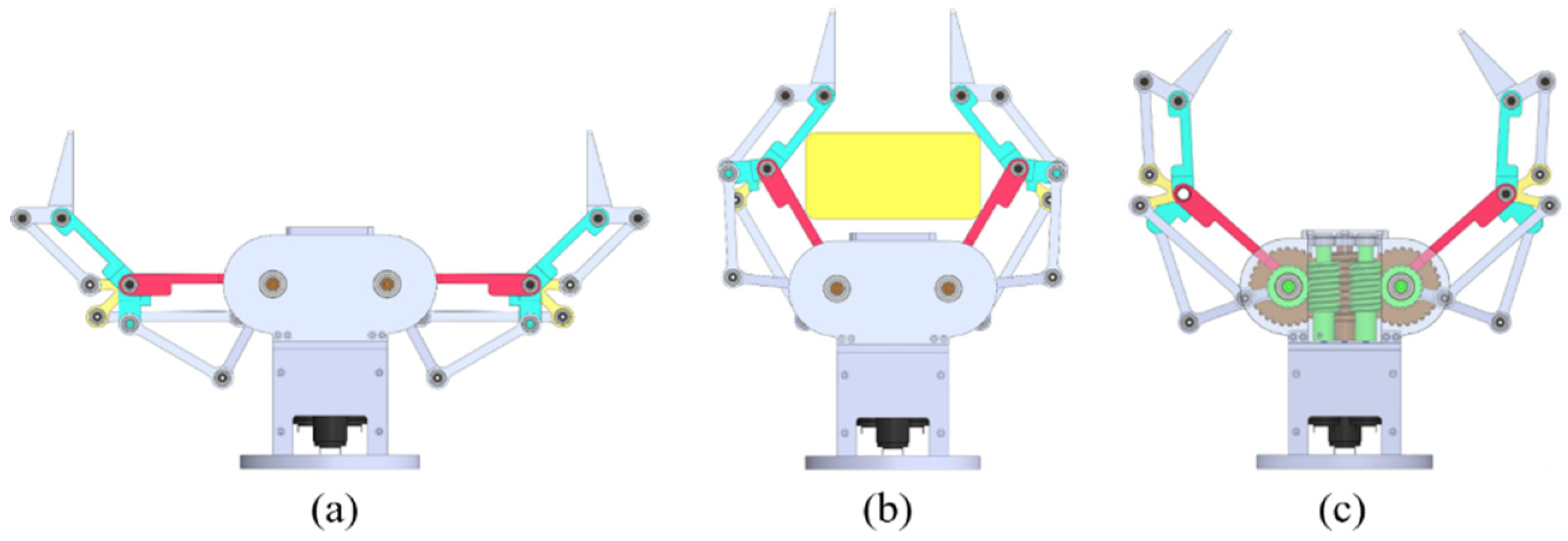
Based on the above analysis, a three-phalanx linkage-driven robotic finger is proposed as shown in Figure 4a. The proposed finger mechanism was constructed by stacking one four-bar mechanism (underactuated 2-DOF finger) over one double parallelogram mechanism. Referring to Figure 4b, this finger has three DOFs, which can be fully controlled by activating the three independent links ($l_1$, $l_4$, and $l_5$). It is noted that the three independent links are pivoted at the same joint axis and that all the actuators can be mounted on the base. In this work, we focus on the underactuated design that can be achieved by only activating the links $l_1$ and $l_5$ as shown in Figure 4b. The link $l_4$ is designed as a passive link to adapt to different shapes of objects. One torsion spring is used to prevent the counterclockwise rotation (caused by gravity and inertia effects) between the proximal and intermediate phalanxes. One mechanical stopper is used to prevent hyperextension rotation in the clockwise direction. Moreover, ball bearings are placed at each joint to reduce friction and backlash. It is noted that the link $l_5$ is used to control the orientation of the distal phalanx independently. Independent fingertip control not only provides stable contact-based grasping, but also reduces the control complexity in other grasping tasks.

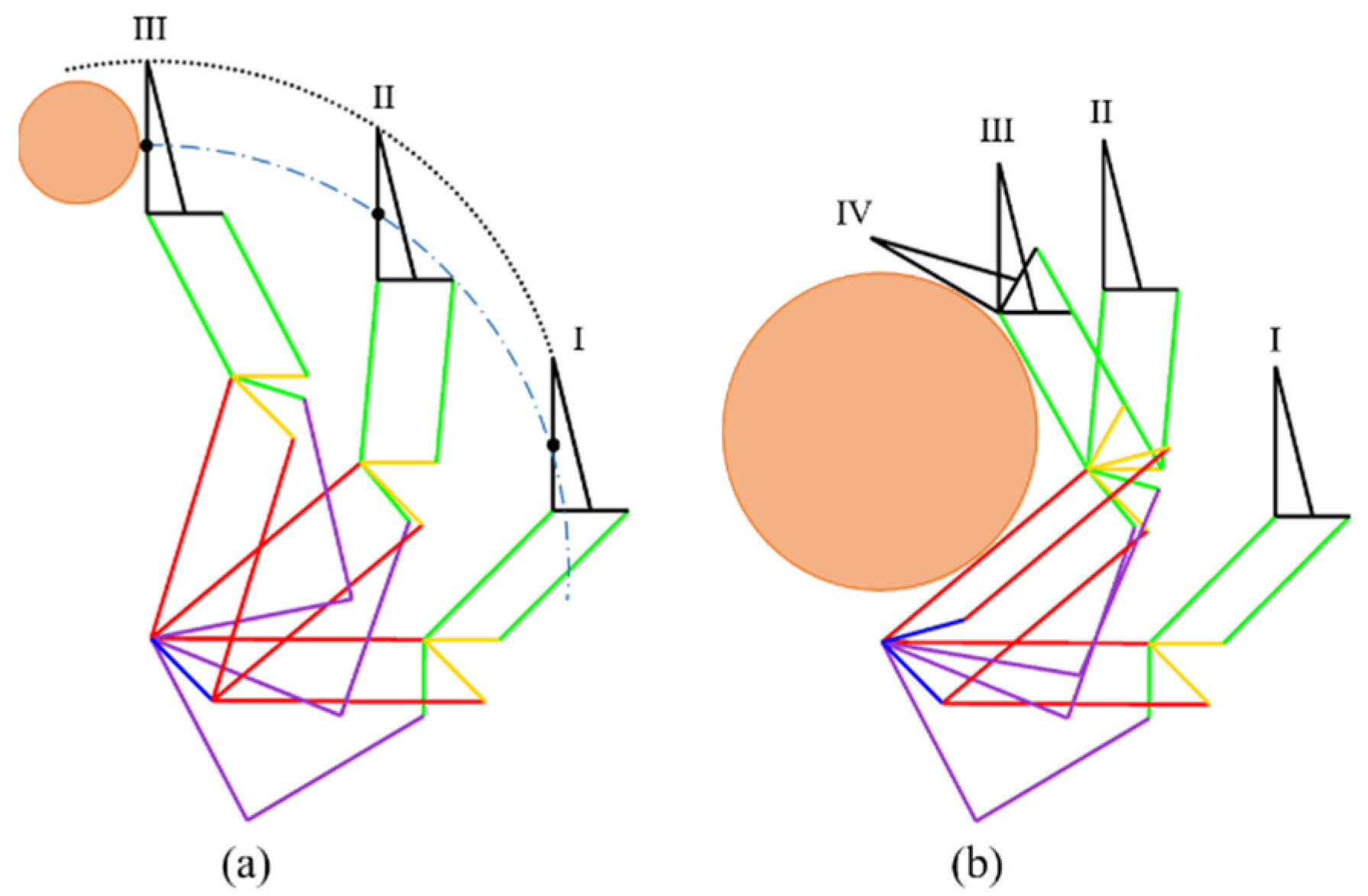
A comparison of the Robotiq three-phalanx gripper (licensed from Sarah hand [45]) is shown in Figure 5. We can find that both of these two grippers can achieve parallel precision and power grasping. We note that even though these two finger mechanisms have similar appearances, a detailed investigation revealed that their mechanical structures and working principles are completely different from each other and our proposed finger mechanism has a simpler architecture. For the proposed finger mechanism shown in Figure 5a–c, the direction of its fingertip is decoupled from the movements of the proximal and intermediate phalanxes. To perform some challenging grasping tasks, the fingertip is designed to be actively controlled. The Sarah finger mechanism shown in Figure 5d–f was constructed by stacking one double parallelogram over a general three-phalanx adaptive finger that consists of two four-bar mechanisms. Mechanical stoppers and springs are installed at both the top and bottom ends of the finger. The clever idea behind Sarah finger is that the intermediate phalanx is passively coupled with the proximal phalanx and the fingertip (the distal phalanx) is passively coupled with the intermediate phalanx.

As shown in Figure 6, both parallel and shape-adaptive grasping can be achieved by using this underactuated finger mechanism. Through activating the link $l_1$ shown in Figure 4b, the parallel grasping can be achieved if no external contact occurs at the proximal phalanx. A torsion spring and mechanical stopper are used to provide passive control so that the proximal and intermediate phalanxes can move together as shown in Figure 6a. If the proximal phalanx makes physical contact with the object firstly during activating the link $l_1$, the shape-adaptive grasping will start as shown in Figure 6b. In this case, the intermediate phalanx continues to move, and the actuator has to increase the torque significantly to withstand the twisting of the torsion spring. From phase III to phase IV, the orientation of the distal phalanx is adjusted to provide one more contact with the object by activating the link $l_5$.

3. Dynamic Modeling of the Robotic Finger

The dynamic model provides the relationship between the input actuation torque and output motion of the robotic finger, and thus it is important for the design and control of a robotic finger systematically. For example, in a piece-picking challenge, the users might expect high-speed open-close motion of a gripper. For a target open-close speed, the dynamic model can be used to evaluate how much torque the actuator should provide to generate such a high-speed open-close motion. Then the appropriate actuator size can be determined and vice versa. As far as our underactuated finger is considered, a torsion spring is used to provide passive control. For the parallel grasping shown in Figure 3, preloading of the torsion spring should be large enough to prevent counterclockwise rotation (between the proximal and intermediate phalanxes) due to gravity and inertia effects. In this paper, the authors attempted to analytically investigate how much preloading the spring should be designed with. The dynamics and statics of this robotic finger are combined to provide guidance for selecting appropriate torsion springs.

3.1. Dynamic Model

For the underactuated design shown in Figure 4b, the joint ${\theta }_1$ and ${\theta }_3$ are selected as the active joints while the joint ${\theta }_4$ is a passive joint. A torsion spring and a mechanical stopper, instead, are mounted on the joint ${\theta }_4$ to provide passive control. As discussed above, the preloading of the torsion spring should be bigger than the negative (clockwise direction) torque required at the joint ${\theta }_4$ for stable parallel grasping. To determine how much preloading of the torsion spring should be designed, we assume that the joint ${\theta }_4$ is a virtual active joint and there exists no torsion spring or mechanical stopper installed at this joint. Hence, we select the joints ${\theta }_1$, ${\theta }_3$, and ${\theta }_4$ as the three independent joint variables to build the finger dynamic model.

The Lagrangian of this robotic finger is defined as

$$L=K+P$$

(1)

where $K$ denotes the kinetic energy and $P$ denotes the potential energy.

The kinetic energy can be found as

$$K=\frac{1}{2}{\dot{\mathit{q}}}^{T}D\left(q\right)\dot{\mathit{q}}$$

(2)

where $q={\left[{\theta }_1 {\theta }_3 {\theta }_4\right]}^T$,

$$D\left(q\right)=\left[{\displaystyle \sum _{i=1}^m\left\{\begin{array}{l}{m}_i{J}_v^i{\left(q\right)}^T{J}_v^i\left(q\right)\\ +J_w^i{\left(q\right)}^T{R}_i\left(q\right)I_i{R}_i{\left(q\right)}^T{J}_w^i\left(q\right)\end{array}\right\}}\right].$$

(3)

Here, $R_i$ and $I_i$ represent the rotation matrix and inertia matrix of link $i$, respectively. $J_v^i\left(q\right)$ and $J_w^i\left(q\right)$ represent the linear and angular velocity Jacobians of link $i$, respectively. They can be described as

$$J_v^i=\left[J_{v1}^i\dots J_{vi}^{i}0\dots 0\right], J_w^i=\left[J_{w1}^i\dots J_{wi}^{i}0\dots 0\right]$$

(4)

where $J_{vj}^i=z_j\times \left(p_{li}-p_j\right)$, $J_{wj}^i=z_j$, and $z_j$ represents a unit vector along the direction of the joint $j$ in a serial open chain used for calculating the linear and angular velocity Jacobians of link $i$.

The potential energy can be written as

$$P={\displaystyle \sum _{i=1}^m{m}_i}{g}^T{p}_{li}$$

(5)

where $g$ is the gravitational vector and $p_{li}$ is the position vector of the mass center of the link $i$. The equations of motion for this robotic finger can be found as

$$\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{\mathit{q}}}_i}\right)-\frac{\partial L}{\partial q_i}={\tau }_i.$$

(6)

For the parallel grasping, the joint ${\theta }_4$ keeps being constant. Thus, we have

$${\dot{\theta }}_4=0, {\ddot{\theta }}_4=0.$$

(7)

Once a joint trajectory is defined ($q$, $\dot{\mathit{q}}$, and $\ddot{\mathit{q}}$ are knowns) for the parallel grasping, the actuation torque required at the joint ${\theta }_4$ can be obtained by using Equation (6). However, in areal situation, joint ${\theta }_4$ is a passive joint and its motion is passively controlled by the torsion spring and mechanical stopper. It is noted that the mechanical stopper is used to constrain the relative rotation (between the proximal and intermediate phalanxes) in the clockwise direction while the torsion spring is used to constrain the relative rotation in the counterclockwise direction. To make sure that the joint angle ${\theta }_4$ is constant during parallel grasping, the preloading of the torsional spring should be bigger than the torque required in the clockwise direction. The stopper provides a rigid constraint in the clockwise direction. Thus, any motion trend in the clockwise direction is prohibited by the stopper. Comparatively, any motion in the counterclockwise direction is allowed, but constrained by the torsion spring.

3.2. Dynamic Simulations and Selection of the Torsion Spring

In order to precisely select a torsion spring for a target grasping application, we need to consider different velocities, accelerations, and decelerations during dynamic simulations. However, we cannot take all the real scenarios into consideration actually. Instead, we could approximately evaluate the minimum preloading of the torsion spring and provide dynamic guidance to select the torsion spring by considering several bad-case scenarios. An exemplary joint trajectory is defined as

$$\begin{array}{l}{\theta }_3\left(t\right)=-\frac{\pi }{4}, {\dot{\theta }}_3\left(t\right)=0, {\ddot{\theta }}_3\left(t\right)=0;\\ {\theta }_4\left(t\right)=\frac{\pi }{4}, {\dot{\theta }}_4\left(t\right)=0, {\ddot{\theta }}_4\left(t\right)=0;\\ {\theta }_1\left(0\right)=-\frac{\pi }{3}, {\theta }_1\left(2\right)=-\frac{\pi }{3}+\frac{70}{180}\pi , {\theta }_1\left(4\right)=0;\end{array}$$

(8)

where $t\in \left(0 s,4 s\right)$. Additionally, for the joint ${\theta }_1$, two fifth-order polynomials are used during $t\in \left(0 s,2 s\right)$ and $t\in \left(2 s,4 s\right)$, respectively. This trajectory implies that the finger finished closing or opening of 70 degrees (almost from the fully opened to closed) in two seconds, which is fast enough for our application.

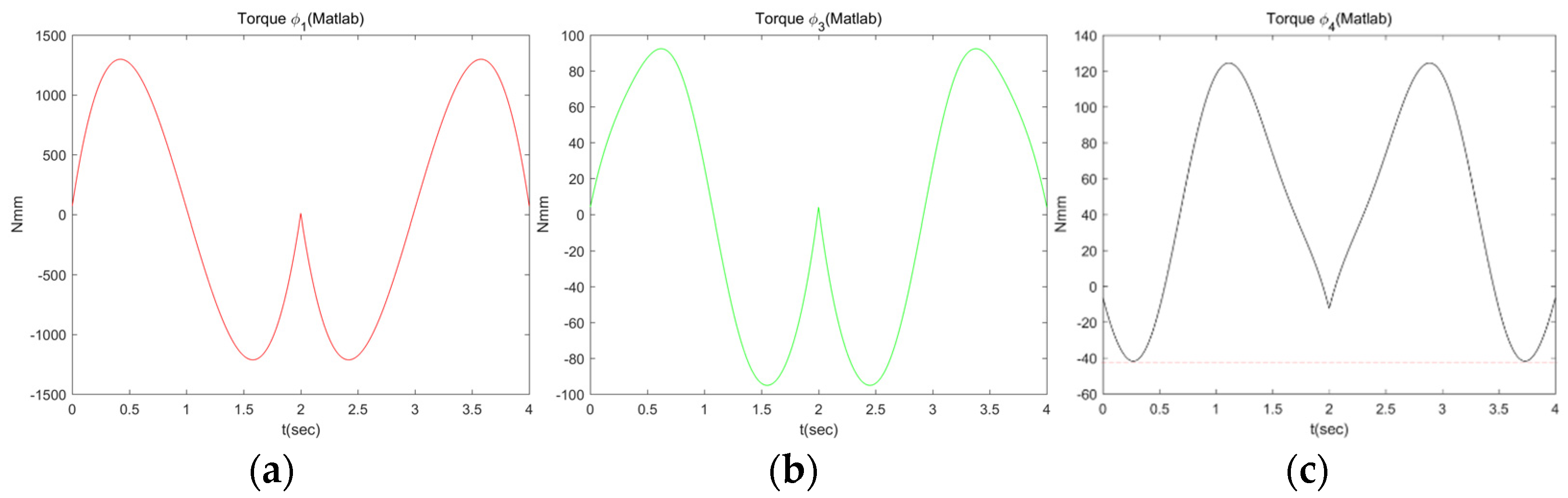
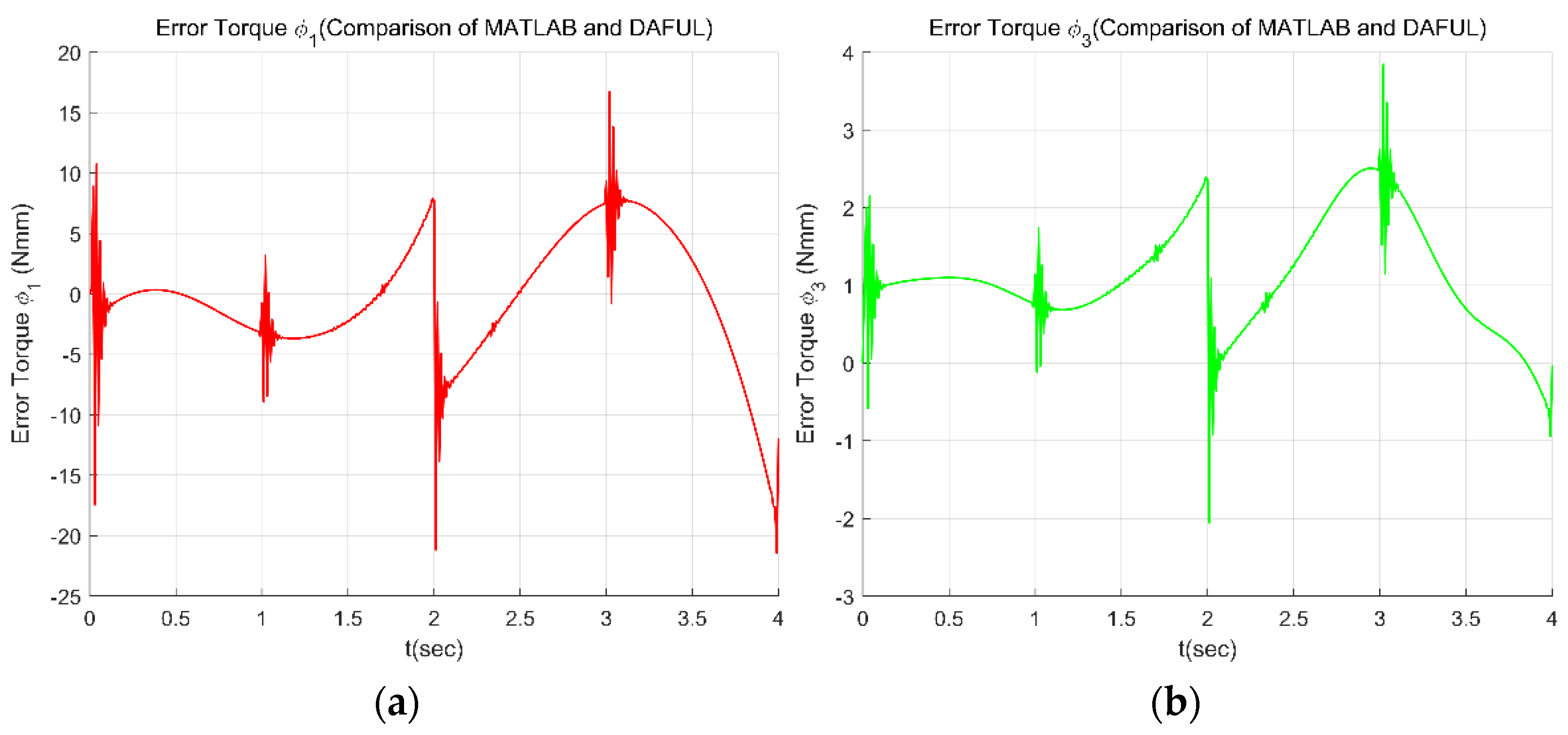
We performed the dynamic simulations in MATLAB and verified the analytical model in a commercialized multi-body dynamic simulator called “DAFUL”, which has now been sold and merged into the ANSYS environment with a new name called “ANSYS Motion” [46]. The MATLAB simulation result is shown in Figure 7. A comparison with the DAFUL simulation result is shown in Figure 8. Referring to Figure 8, we can find that the difference between our analytical dynamic model and the multi-body dynamic simulation result is quite small (the very small difference might come from the non-perfect dynamic parameters that we got from the 3D software). From Figure 7c, we can find the negative (clockwise direction) torque required at the joint ${\theta }_4$ during the trajectory. In a real situation, this torque should be provided by the torsion spring to ensure that the parallel grasping is stable. Hence, the preloading of the torsion spring should be bigger than the maximum torque (around −40 Nmm) required in the clockwise direction.

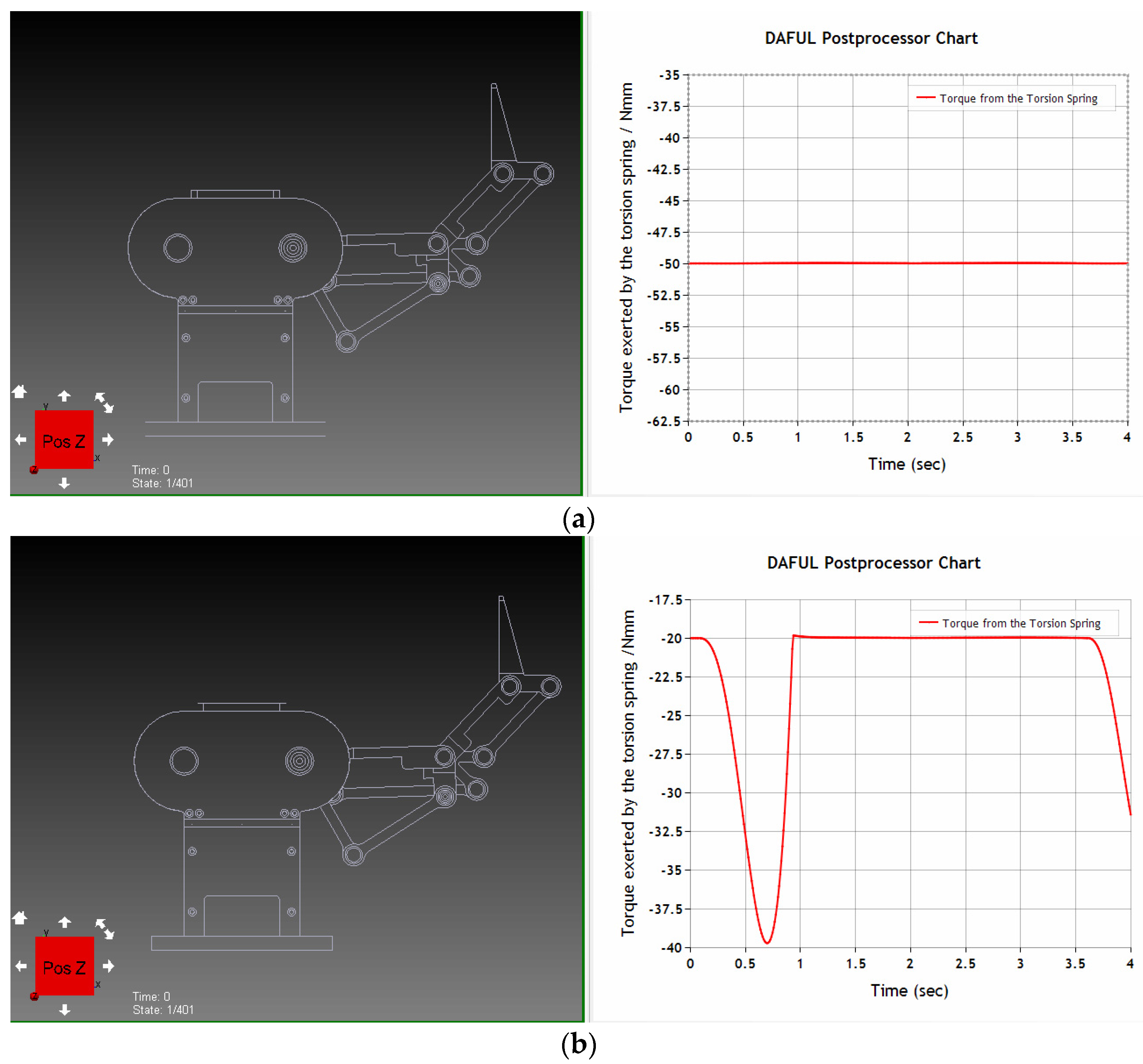
To verify the above-mentioned hypothesis, we have performed another DAFUL simulation where the joint ${\theta }_4$ is defined as a passive joint and the torsion spring and mechanical stopper are added instead. Two different preloadings (50 Nmm and 20 Nmm) of the torsion spring have been tested in the DAFUL simulation. Variations of the resistance torque of the torsion spring with preloadings of 50 Nmm and 20 Nmm during the trajectory are shown in Figure 9a,b, respectively. In each subfigure, the left panel shows the initial and final state of the finger in the dynamic simulator, whilethe right panel shows the variation of the torque exerted by the torsion spring during the dynamic simulation. From Figure 9a, we can find that the torque of the torsion spring keeps being constant (the same as the preloading of 50 Nmm), which implies that the joint ${\theta }_4$ keeps being constant, and there exists no passive motion between the proximal and intermediate phalanxes during the trajectory. On the other hand, it can be found from Figure 9b that the torque of the torsion spring varies due to inertia and gravity effects. This implies that the joint ${\theta }_4$ has a small undesired variation that may cause unstable parallel grasping. Other joint trajectories with higher joint acceleration or deceleration could be performed in MATLAB. Ultimately, by investigating the maximum torque that appeared in the clockwise direction and considering a certain safety threshold, an appropriate torsion spring can be selected. It is noted that the approach presented here can be generalized and applied to design other underactuated robotic hands.

4. Static Grasp Model

The quasi-static grasp model provides the relationship between the input actuation torque and the contact forces exerted on the object. Expanded details of the following derivation can be found in Appendix A and Appendix B. The four-bar linkages ABCD shown in Figure 4b have two DOFs, from which all the joint angles of the linkages can be determined. We write the closed-loop kinematic equations and express the matrix $C$, which relates dependent joint variables to independent joint variables. For our model, those variables are defined as

$${\theta }_{ind2}={\left[{\theta }_1 {\theta }_2\right]}^T, {\theta }_{dep}={\left[\angle ADC \angle BCD\right]}^T.$$

(9)

Such that

$${\dot{\mathit{\theta }}}_{dep}=C{\dot{\mathit{\theta }}}_{ind2}.$$

(10)

By considering the different number of contact points, two types of static grasp models are developed, respectively.

4.1. Two-Point Contact Model

By activating the joint ${\theta }_1$ at link AD, a shape-adaptive two-point contact can happen as shown in Figure 10a. Expanded details of the following derivation of this section can be found in Appendix A. Through analyzing the four-bar linkages ABCD, we define the matrix $J_t$ that relates dependent joint ${\theta }_4$ to ${\theta }_{ind2}$, and the matrix $J_{a1}$ that relates the actuated joint angle ${\theta }_1$ to ${\theta }_{ind2}$, such that

$${\dot{\theta }}_4=J_t{\dot{\mathit{\theta }}}_{ind2}$$

(11)

$${\dot{\theta }}_1=J_{a1}{\dot{\mathit{\theta }}}_{ind2}.$$

(12)

Then we define two matrices $J_{c1}$ and $J_{c2}$ that relate the motion of the two contact points, $P_1$ and $P_2$, to ${\dot{\mathit{\theta }}}_{ind2}$, such that

$$\left[\begin{array}{c}{\dot{\mathit{p}}}_1\\ {\dot{\mathit{p}}}_2\end{array}\right]={\left[\begin{array}{c}{J}_{p1}\\ J_{p2}\end{array}\right]}_{4\times 2}{\dot{\mathit{\theta }}}_{ind2}=J_{2c}{\dot{\mathit{\theta }}}_{ind2}.$$

(13)

In order to obtain the simple and general results that can characterize the finger itself, only the normal force at the contact point is considered. Obviously, the omitted local properties such as friction coefficients at the contact surface can have an impact on the grasp stability but exceed the scope of this paper. Our primary goal is to investigate the capability of the robotic finger (and only the finger) to exert a wrench onto a fixed object. We are, therefore, not interested in the local properties of the contact, such as friction or geometry of the contact. By defining a selection matrix, $T_{2normal}$, we can reformulate the Jacobian of $J_{2c}$ in Equation (13) to remove tangential components, and the final result is given as

$$\left[\begin{array}{c}{\dot{p}}_{1normal}\\ {\dot{p}}_{2normal}\end{array}\right]=T_{2normal}{J}_{2c}{\dot{\mathit{\theta }}}_{ind2}=J_{2cn}{\dot{\mathit{\theta }}}_{ind2}.$$

(14)

By using the virtual work principle, the static equilibrium of the two-point contact can be achieved if the following effective torque relationship with respect to the independent input holds

$$J_{a1}{}^T{\tau }_{a1}+J_{2cn}{}^T{f}_{2cn}+J_t{}^T{\tau }_t=0$$

(15)

where ${\tau }_{a1}$ is the actuation torque, and $f_{2cn}$ is the vector composed of normal contact forces at proximal and intermediate phalanxes. ${\tau }_t=-\left(k_t\left({\theta }_{t0}-\left(\pi -{\theta }_4\right)\right)+{\tau }_{t0}\right)$ is the twisted torque of the torsion spring; ${\tau }_{t0}$ denoted the preloading of the torsion spring before the adaptive grasping happens, and the constant value ${\theta }_{t0}$ is assumed to be the same as the initial angle of $\angle ABK$ that is designed as 135° here.

Finally, the two contact forces, $f_1$ and $f_2$, can be solved as

$$f_{2cn}=-{\left(J_{2cn}{}^T\right)}^{-1}\left(J_{a1}{}^T{\tau }_{a1}+J_t{}^T{\tau }_t\right)$$

(16)

where $f_{2cn}={\left[f_1 f_2\right]}^T$.

4.2. Three-Point Contact Model

As shown in Figure 10b, the distal phalanx of this robotic finger can be independently controlled by the active joint ${\theta }_3$ to add one more contact with the object. Expanded details of the following derivation of this section can be found in Appendix B. In this model, the independent joint variables are defined as

$${\theta }_{ind3}={\left[{\theta }_1 {\theta }_2 {\theta }_3\right]}^T.$$

(17)

Firstly, the active joints ${\theta }_1$ and ${\theta }_3$ can be expressed as

$$\left[\begin{array}{c}{\dot{\theta }}_1\\ {\dot{\theta }}_3\end{array}\right]=\left[\begin{array}{c}{J}_{a1}\\ J_{a3}\end{array}\right]{\dot{\mathit{\theta }}}_{ind3}=J_a{\dot{\mathit{\theta }}}_{ind3}$$

(18)

where $J_{a1}=\left[1 0 0\right]$, $J_{a3}=\left[0 0 1\right]$.

Similar to the two-point contact model, the motion of the three contact points can be obtained as

$$\left[\begin{array}{c}{\dot{\mathit{p}}}_1\\ {\dot{\mathit{p}}}_2\\ {\dot{\mathit{p}}}_3\end{array}\right]={\left[\begin{array}{c}{J}_{p1}\\ J_{p2}\\ J_{p3}\end{array}\right]}_{6\times 3}{\dot{\mathit{\theta }}}_{ind3}=J_{3c}{\dot{\mathit{\theta }}}_{ind3}.$$

(19)

By defining a selection matrix, $T_{3normal}$, we can take the normal components of the motion at the three contact points as

$$\left[\begin{array}{c}{\dot{p}}_{1normal}\\ {\dot{p}}_{2normal}\\ {\dot{p}}_{3normal}\end{array}\right]=T_{3normal}{\left[\begin{array}{c}{J}_{p1}\\ J_{p2}\\ J_{p3}\end{array}\right]}_{6\times 3}{\dot{\mathit{\theta }}}_{ind3}=J_{3cn}{\dot{\mathit{\theta }}}_{ind3}.$$

(20)

By using the virtual work principle, the conditions for static equilibrium of the three-point contact can be obtained as

$$J_a{}^T{\tau }_a+J_{3cn}{}^T{f}_{3cn}+J_t{}^T{\tau }_t=0.$$

(21)

Finally, the three contact forces, $f_1$, $f_2$, and $f_3$, can be obtained as

$$f_{3cn}=-{\left(J_{3cn}{}^T\right)}^{-1}\left(J_a{}^T{\tau }_a+J_t{}^T{\tau }_t\right)$$

(22)

where $f_{3cn}={\left[f_1 f_2 f_3\right]}^T$.

4.3. Simulation of the Grasping Motion

A cylindrical object is used as a typical example in developing the contact model. As far as the configuration of the object is given, the configuration of the robotic finger can be completely defined by considering the contact constraints shown in Figure 10. Then the normal contact forces can be calculated for a given object and actuation torque. A shape-adaptive two-point contact shown in Figure 10a is selected as an example to investigate the relationship among the contact forces, the stiffness and preloading of the torsion spring, and the actuation torque. In Figure 10, the reference coordinate is located at the point $A$; $Q_x$ and $Q_y$ denote the coordinates of the center of the circle.

Firstly, given the position of the center (denoted by $Q$) of the cylindrical object, the angle ${\theta }_2$ can be found as

$${\theta }_2=\angle QAO-\angle QA{P}_1$$

(23)

where $\angle QAO=atan2\left(\frac{Q_y}{QA}, \frac{Q_y}{QA}\right)$, $\angle QA{P}_1=atan2\left(\frac{r_c}{QA}, \frac{A{P}_1}{QA}\right)$.

Then the angle ${\theta }_4$ can be found as

$${\theta }_4=\pi -\angle ABK=\pi -2\angle QBP$$

(24)

where $\angle QB{P}_1=atan2\left(\frac{r_c}{QB},\frac{B{P}_1}{QB}\right)$.

Finally, by analyzing the four-bar linkage ABCD, we can obtain the angle ${\theta }_1$, and the contact forces can be found by using Equation (16).

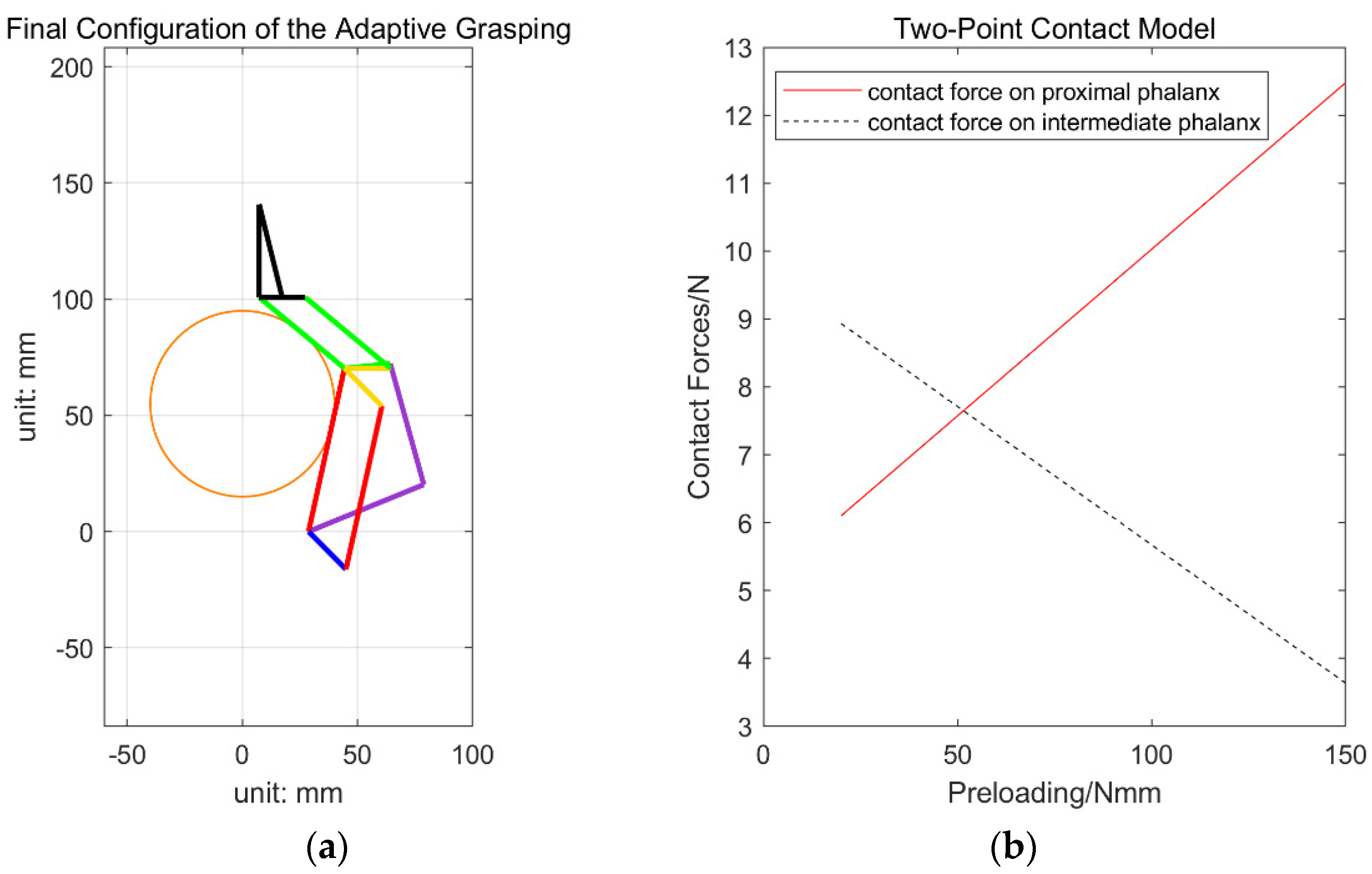
For shape-adaptive grasping, stiffness and preloading of the torsion spring are useful for holding the object. During the grasping process toward the static equilibrium, the second contact will be retained with the intermediate phalanx by sliding against the object. If the preloading and stiffness of the torsion spring are too low, closing ejection might happen, which implies that the proximal phalanx will lose contact with the object. For one example of the input torque ${\tau }_{a1}=800 \mathrm{Nmm}$, the relationship between the two contact forces exerted on the proximal and intermediate phalanxes and the preloading of the torsion spring is shown in Figure 11b. It is noted that the spring stiffness used in this simulation is 3 Nmm/deg. It can be found that after increasing the preloading of the spring, the contact force at the proximal phalanx will increase while the contact force at the intermediate phalanx will decrease. For a stable two-point contact grasp, both of the two contact forces exerted on the proximal and intermediate phalanxes should be positive to avoid losing contact with the object. For a certain range of input torque and object sizes, a balance of design stiffness and preloading of the torsion spring should be considered to maximize the stable grasping region. We note that the crossing point of red and black lines shown in Figure 11b is not directly used to decide the stable grasp region. In this paper, a stable grasp refers to a contact situation that no contact force exerted on a phalanx is negative, and this paper tries to analyze the capability of the finger itself (from input torque to the output contact force) independently from the object to be grasped. The dynamic simulation result shown in Figure 7c shows that a preloading of the torsion spring around 40 Nmm is quite enough to provide the passive control in our application. Figure 11b shows that preloading of 40 Nmm can also generate a relatively uniform contact force distribution that we prefer. Hence, the actual preloading of the torsion spring is selected around 40 Nmm.

5. Design, Analysis, and Experimental Evaluation

5.1. Design of a Two-Fingered Underactuated Gripper

The first prototype of an underactuated gripper having two fingers is developed as shown in Figure 12. As mentioned above, the linkage of each finger has three DOFs. To fully actuate this two-finger gripper, six actuators are required in total. For the underactuated design presented in this paper, we use only three actuators to control the grasping motion and fingertip orientation. One powerful actuator fixed to the orange worm is used to control the open-close (grasping) motion of the two fingers synchronously. The other two less powerful actuators fixed to the green worms are used to control the orientations of the distal phalanxes of the two fingers, respectively. After installing the torsion spring at the passive joint, the actual preloading of the torsion spring is around 40 Nmm, which is quite enough to provide passive control in our application. Many types of grasping modes, such as parallel grasping, shape-adaptive grasping, and environmental contact-based grasping can be successfully achieved. The kinematic parameters of the underactuated gripper are listed in

Table 1. Kinematic parameters ¹ of the robotic finger.

Length (mm)	Length (mm)	Angle (Deg)
$L_{\mathrm{AE}}=23.0$	$L_{\mathrm{BF}}=23.0$
$L_{\mathrm{AD}}=54.0$	$L_{\mathrm{BG}}=20.0$	${\varphi }_{\mathrm{KBC}}=135$
$L_{\mathrm{AB}}=72.0$	$L_{\mathrm{BK}}=48.0$	${\varphi }_{\mathrm{FBG}}=45$
$L_{\mathrm{BC}}=20.0$	$L_{\mathrm{GH}}=48.0$	${\varphi }_{\mathrm{KBA}}\le 135$
$L_{\mathrm{CD}}=54.0$	$L_{\mathrm{KH}}=20.0$	(${\varphi }_{\mathrm{KBA}}$ is Constrained by the mechanical stopper)
$L_{\mathrm{EF}}=72.0$	$L_{\mathrm{KI}}=40.0$

¹ Referring to Figure 4b.

. And the specifications of the actuation system are listed in

Table 2. Specifications of the actuation system.

FAULHABER	Motor 1 1	Motor 2 2	Motor 3 2
Motor type	1724T012SR	1717T012SR	1717T012SR
Rated torque	4.5 Nmm	2.1 Nmm	2.1 Nmm
Controller type	MCDC 3006 S	MCDC 3006 S	MCDC 3006 S

¹ Denote the powerful motor fixed to the orange worm in Figure 12. ² Denote the two less powerful motors fixed to the two green worms in Figure 12.

.

Parallel grasping is demonstrated in Figure 13a. It can be found that the workspace of the gripper is very big and the maximum span of the gripper is around 260 mm. The payload for parallel grasping is around 2.5 kg. Figure 13b demonstrates the shape-adaptive grasping. Moreover, the orientation of the distal phalanx is decoupled from the open-close motion and can be actively adjusted as shown in Figure 13c. Thus, the orientation of the distal phalanx can be maintained at a desired angle during grasping, even when the distal phalanx makes a contact with the supported environment accidentally as shown in Figure 14. Hence, parallel grasping can be continued and we call this grasping mode ‘environmental contact-based grasping’. This grasping mode is very useful for grasping thin objects lying on flat surfaces. For many other grippers, instead, a combination of some new grasping strategy and special designs is required for picking up small objects lying on flat surfaces [39,47].

5.2. Analysis of the Environmental Contact-Based Grasping

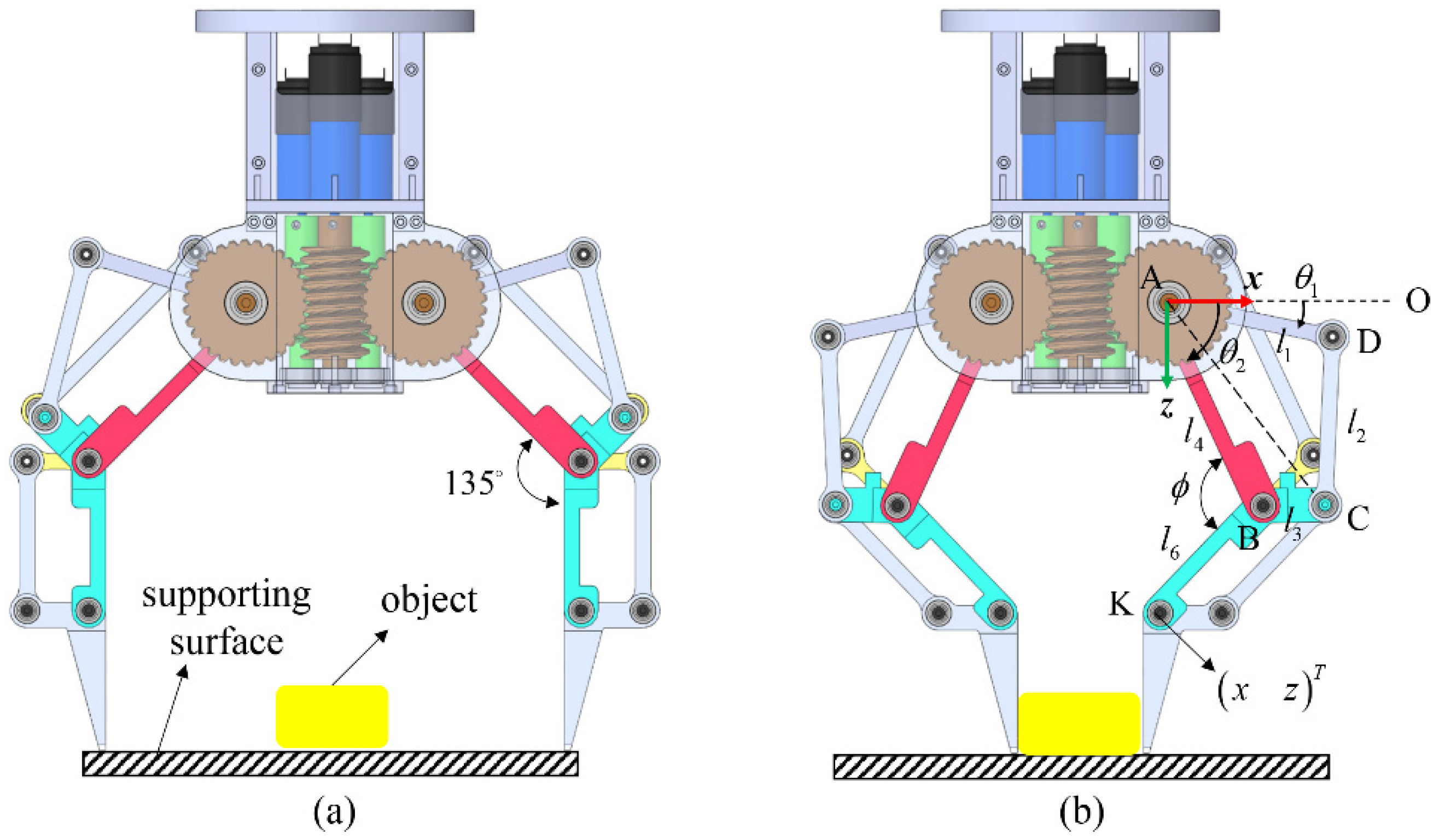
The aforementioned contact-based grasping is very useful for picking up thin and small objects lying on flat surfaces. To ensure that the grasping is stable, a simple control algorithm might be required. As shown in Figure 14b, the torsion spring will be twisted during the fingertip-surface-contact process. The angle between proximal and intermediate phalanxes will be continuously decreasing ($\varphi \le 135°$) until the fingertip makes contact with the object to be grasped. When the gripper finished contact-based grasping, an industrial robot will be controlled to lift up the gripper and object. During this lifting up process and before the fingertip totally leaves the supporting surface, the resistance torque of the torsion spring will try to force the proximal and intermediate phalanxes to move back to their home position, where the angle between them is designed as 135° ($\varphi =135°$). Thus, during the lifting up process, the distance between the two fingertips might increase or decrease, which depends on the finger structure and grasping state. If the distance between the two fingertips is trying to decrease, the resistance torque of the torsion spring will force the fingertip to grasp the object and the grasping is stable, i.e., the object will not fall down. However, if the distance between the two fingertips is trying to increase, the object might fall down if no gripper control is applied. Several hardware-based approaches could be used to solve this problem. For example, during the lifting up process, we can use a magnetic brake to lock the relative position between proximal and intermediate phalanxes. Installing an anti-moving back mechanism at the pivot joint where the torsion spring is installed is another approach [11]. In this work, a simple control algorithm is used to ensure that the grasping is stable.

As the gripper is attached to a robot arm, we can control the lifting up motion of the robot arm and the closing motion of the gripper during lifting up process to make sure that the contact-based grasping is stable.

Figure 14b shows a reference state when the gripper moves upward with the robot arm but still in contact with the supporting surface. Taking the coordinates (x, z) of the point $K$ into consideration, the problem can be stated as: when the coordinate z increases (lifted by the robot arm), find out how much the angle ${\theta }_1$ should increase (controlled by the gripper) to ensure that the coordinate x is not increasing to maintain the grasping. The key here is to build the relationship between $\dot{z}$ and ${\dot{\theta }}_1$. Referring to Figure 14b, we have

$$\left[\begin{array}{c}x\\ z\end{array}\right]=\left[\begin{array}{c}{l}_4\cos {\theta }_2+l_6\cos \left({\theta }_2+180°-\varphi \right)\\ l_4\sin {\theta }_2+l_6\sin \left({\theta }_2+180°-\varphi \right)\end{array}\right].$$

(25)

The goal is to make the coordinate $x$ keep constant. Differentiating the two terms in Equation (25) with respect to time, we have

$$\begin{array}{l}\dot{x}=0=-l_4\sin {\theta }_2{\dot{\theta }}_2+l_6\sin \left({\theta }_2-\varphi \right){\dot{\theta }}_2-l_6\sin \left({\theta }_2-\varphi \right)\dot{\varphi }\\ \dot{z}=l_4\cos {\theta }_2{\dot{\theta }}_2-l_6\cos \left({\theta }_2-\varphi \right){\dot{\theta }}_2+l_6\cos \left({\theta }_2-\varphi \right)\dot{\varphi }\end{array}$$

(26)

From the first term of Equation (26), we have

$${\dot{\theta }}_2=\frac{l_6\sin \left({\theta }_2-\varphi \right)}{l_6\sin \left({\theta }_2-\varphi \right)-l_4\sin {\theta }_2}\dot{\varphi }.$$

(27)

Substituting Equation (27) into the second term of Equation (26), we can obtain

$$\dot{\varphi }=m_1\dot{z}$$

(28)

where

$$m_1=\frac{l_4\sin {\theta }_2+l_6\sin \left({\theta }_2+180°-\varphi \right)}{l_4{l}_6\sin \varphi }.$$

(29)

Referring to Figure 11b, we know

$${\theta }_1={\theta }_2-\angle BAD, \angle BAD=\angle BAC+\angle CAD.$$

(30)

Differentiating Equation (30) with respect to time, we obtain

$${\dot{\theta }}_1={\dot{\theta }}_2-\stackrel{·}{\angle BAD}, \stackrel{·}{\angle BAD}=\stackrel{·}{\angle BAC}+\stackrel{·}{\angle CAD}.$$

(31)

In this design, $\angle KBC=135°$, then $l_{AC}$ can be expressed as

$$l_{AC}^2=l_3^2+l_4^2-2l_3{l}_4\cos \left(360°-135°-\varphi \right).$$

(32)

Similarly, $l_3$ and $l_2$ can be expressed as

$$\begin{array}{l}{l}_3^2=l_4^2+l_{AC}^2-2l_4{l}_{AC}\cos \angle BAC\\ l_2^2=l_1^2+l_{AC}^2-2l_1{l}_{AC}\cos \angle CAD\end{array}$$

(33)

Substituting Equation (32) into the two terms of Equation (33) and differentiating them with respect to time yields

$$\begin{array}{l}{l}_3\sin \left(225°-\varphi \right)\dot{\varphi }=\left(l_{AC}\sin \angle BAC\right)\stackrel{·}{\angle BAC}\\ l_4{l}_3\sin \left(225°-\varphi \right)\dot{\varphi }=\left(l_{AC}{l}_1\sin \angle CAD\right)\stackrel{·}{\angle CAD}\end{array}$$

(34)

From Equation (34), we have

$$\stackrel{·}{\angle BAC}+\stackrel{·}{\angle CAD}=\left(\frac{l_3\sin \left(225°-\varphi \right)}{l_{AC}\sin \angle BAC}+\frac{l_4{l}_3\sin \left(225°-\varphi \right)}{l_{AC}{l}_1\sin \angle CAD}\right)\dot{\varphi }.$$

(35)

Substituting Equation (35) into Equation (31) and combining with Equation (27) results in

$${\dot{\theta }}_1=m_2\dot{\varphi }$$

(36)

where

$$m_2=\frac{l_6\sin \left({\theta }_2-\varphi \right)}{l_6\sin \left({\theta }_2-\varphi \right)-l_4\sin {\theta }_2}-\frac{l_3\sin \left(225°-\varphi \right)}{l_{AC}\sin \angle BAC}-\frac{l_4{l}_3\sin \left(225°-\varphi \right)}{l_{AC}{l}_1\sin \angle CAD}.$$

Combining Equations (28) and (36), we can obtain

$${\dot{\theta }}_1=m_1{m}_2\dot{z}.$$

(37)

Thus, to ensure that the parallel grasping is maintained during lifting, the closing speed of the gripper should be controlled to be larger than $m_1{m}_2\dot{z}$. where $\dot{z}$ represents the lifting speed of the robot arm.

5.3. Experimental Evaluation

Figure 15 shows three examples of fingertip parallel grasping. A wide span allows this gripper to grasp a large variety of objects with different sizes. Figure 16 demonstrates two examples of shape-adaptive grasping. As mentioned above, the orientation of the distal phalanx can be actively adjusted, which allows users to use pinch motion to grasp objects with irregular shape as shown in Figure 17. For objects shown in Figure 17b,c, there exists spare space between the object and the supported base. Actively controlled distal phalanx allows the gripper to scoop the object up from the bottom side. Figure 17d demonstrates that by closing the distal phalanx, objects with lifting ears can be grasped similar to a caging grasp.

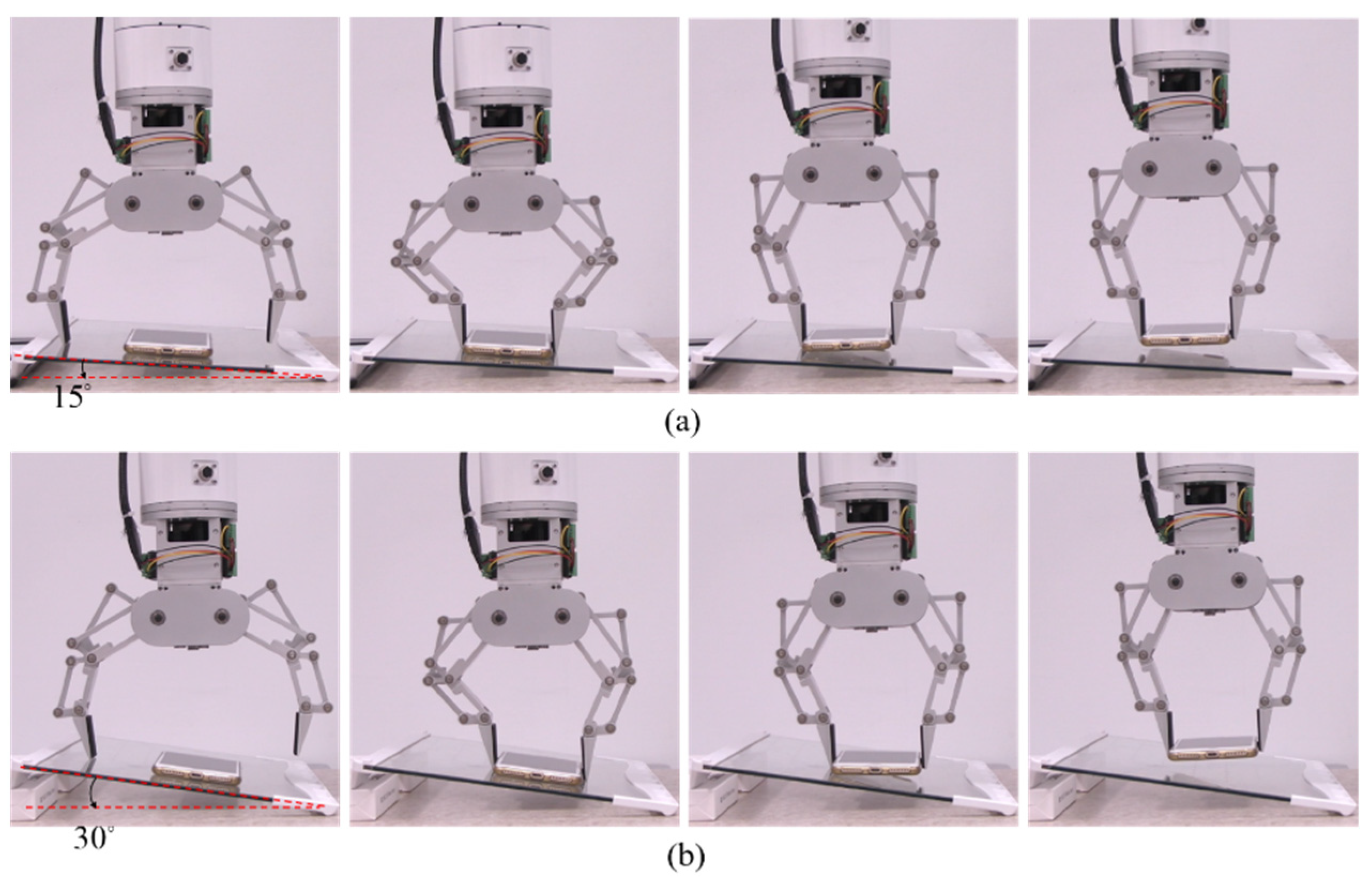
Figure 18 shows the grasping sequence while making contact with the supported base. Even in the scenario that the supported base is inclined, parallel grasping can still be achieved successfully as shown in Figure 19. This is because each finger deflects upon contact with the base independently due to torsional spring and that the orientation of the distal phalanx can be independently controlled to maintain parallel grasping. Compared to other grippers, we found that it is also quite simple to use this gripper to pick up thin objects lying on a flat surface as shown in Figure 20. Many other grippers/hands might fail to grasp objects in such a simple manner because once contact was established with the supporting base, the orientation of the distal phalanx generally will be changed passively. Continuing closing the finger will result in unstable grasping of thin objects. One example of failure of contact-based grasp using a Robotiq 2-finger gripper is shown in Figure 21a–c. Figure 21d–f shows the success of grasping such a nail using the proposed gripper. Hence, to grasp such objects without making any contact with the supported base, a highly accurate calibration algorithm and vision system are generally required. For more details about the experiment, please refer to the video uploaded along with this manuscript.

6. Discussion

Different from many previous studies that use intuitive design and specific CAD-aided simulation to build robotic grippers, this paper presents an effort to establish a systematic approach that combines the dynamics and statics model of the robotic finger for the purpose of providing an analytical guidance for users to select appropriate torsion spring and finally come up with a suitable design.

While developing the quasi-static model of the robotic finger, friction terms at contact surfaces are ignored. Our primary goal is to investigate the capability of the robotic finger (and only the finger) to exert a wrench onto a fixed object. We are, therefore, not interested in the local properties of the contact, such as friction or geometry of the contact. In order to obtain simple and general results that can characterize the finger itself and not the system formed by the finger and the object, pure normal contact forces should be considered. These normal contact forces depend on the locations of contact points, actuation torque, and resistance torque exerted by the torsion spring. To determine them, we proceed with a quasi-static modelling of the finger by ignoring the friction term and fixing the object. Obviously, the friction coefficient at the contact surface can have an impact in terms of the grasp stability. In future studies, we will especially focus on the whole grasping system formed by the gripper and the object to investigate the influence of the friction in grasping.

As far as the grasping experiment is concerned, we note that only the open-loop control method was used to detect the object to be grasped and we did not apply the camera information into the controller. This is because we only want to demonstrate the performance of the gripper itself and the open-loop control method could greatly simplify the experiment. Object recognition definitely is another important research issue in robotic grasping and the conventional technique route is combining RGB-D camera (according to the relative configuration between the camera and robot, two approaches: eye to hand or eye in hand) with certain vision algorithms (especially the machine-learning-based approach) for detecting object postures. But it exceeds the scope of this paper which focuses on the modelling and design.

As far as the grasping force control is concerned, usually force sensors (e.g., tactile sensor attached to the finger pad) are required for providing high-accuracy grasping force control, also possible for detecting and avoiding object sliding during grasping. However, in the current design, we did not use any external force/tactile sensor to detect the grasping force. We are using the motor current as the feedback to control the velocity. For a certain object, we can approximately apply a certain grasping force by setting a certain motor current value as the feedback in the velocity controller. This is because the controller hardware (from the Faulhaber company, MCDC series) used in our gripper can only provide position and velocity control functions (but could provide the actual position, velocity, and current feedback value from the motor encoder). To be honest, this approach has low accuracy and much noise that might be caused by the friction of the power transmission system. As the example objects used in our experiment are relatively rigid, this approach works and did not break the object to be grasped. However, to grasp some soft and fragile object, we suggest using force/tactile sensors to avoid breaking the object to be grasped.

7. Conclusions

In this paper, we have presented a three-DOF linkage-driven robotic finger and developed a two-fingered underactuated gripper. The main theoretical contribution of this paper includes providing an analytical guidance for users to select appropriate parameters for the torsion spring at the passive joint by combining the dynamic and static grasp model of the underactuated finger and investigating the control strategy of environmental contact-based grasping.

Through multiple experiments, it is demonstrated that the first prototype of the two-finger underactuated gripper can be used to perform fingertip parallel grasping and shape-adaptive grasping successfully. During grasping household objects, especially those objects with low heights, a good calibration algorithm and highly accurate robot-vision system are generally required for avoiding making contact with the supporting surface. However, because visual localization errors, coordinate control errors of the industrial robot and robotic gripper, and uncertainties of the grasping environment always exist, the fingertip makes contact with the supporting surface frequently while grasping household objects that have varied shapes and sizes. Independent fingertip control and passive compliance caused by the underactuation design allow us to perform environmental contact-based grasping simply and robustly. Environmental-contact based grasping can be used to grasp low-height objects lying on a flat surface simply and efficiently. Comparatively, using most of other grippers to fulfill such tasks required high-precision calibration and control algorithms for avoiding collisions with the supporting surface. Future work includes using tactile sensors instead of motor current feedback for accurate grasping force control.