Development of an Automatic Elastic Torque Control System Based on a Two-Mass Electric Drive Coordinate Observer

Abstract

Development of control system based on digital twins of physical processes is a promising area of research in the rolling industry. Closed-loop control systems are developed to control the coordinates of two-mass electromechanical systems in order to limit the dynamic loads on the equipment of main rolling lines. These control systems are based on observers (digital shadows) that indirectly detect (reconstruct) the roll speed and the elastic torque of the shaft (spindle) in real time. Notably, observers are required to work fast in order to reconstruct transients attributable to shock (impact) loads. Literature review shows that the known observers, which use complex algorithms to compute coordinates, do not respond fast enough. The paper analyzes the kinematic diagram of Mill 5000, a plate rolling mill. It presents oscillograms that prove that the elastic torque does oscillate as the rolls grip the strip dynamically. The authors hereof have developed an observer that reconstructs the coordinates of the uncontrolled mass (the shaft) and the spindle torque from the parameters of the controlled mass, namely the torque and speed of the motor. The paper further rationalizes an approach that consists of simulating the processes on a model to further directly configure them on the object. The authors analyze the transients of the reconstructed two-mass system coordinates, which are associated with the rolls gripping the strip. The paper compares data against oscillograms recorded on the mill itself. The accuracy is satisfactory. The proposed observer has been used to developed a three-loop automatic speed control system for the uncontrolled mass. Controller configurations are substantiated. The paper shows coordinates obtained by simulation modeling as functions of time. It further presents experiments run on Mill 5000; the conclusions are that the amplitude and oscillations of the elastic torque drop significantly. The paper concludes with recommendations on industrial adoption of the observer and the novel electric drive coordinate control system. Study presented herein substantiates and implements a concept of developing algorithms that solve specific problems and are readily implementable on the existing equipment without need for additional computing devices. The contribution of the paper consists of stating and solving the problem of developing and testing an automatic elastic torque control system for the shaft of a heavy-duty rolling mill. This system has been implemented in the form of algorithms that run in the software of the existing industrial controllers (PLCs). It is simple and performs well. It does not need additional sensors or computers to be implemented, nor does it rely on complex computational algorithms. Such algorithms are based on computational tables that require a priori data on numerous process parameters. In our literature review, we have not come across any industrial implementation of such algorithms on hot-rolling mills.

1. Introduction

Kalachev Yu. N. [1] defined a state observer as a model that is connected in parallel with the controlled object and continually retrieves data on change in the control action and in the controlled coordinate. This definition falls within the concept of digital shadow, which has been named a special case of a digital twin in the papers [2,3]. When using an observer, the system acquires no new information channel; rather, the controller is retrofitted with an adjuster. This effectively creates a new controller that works in a conventional closed system.

Developing an observer to control the elastic torque of a two-mass electromechanical system and designing an automatic coordinate control system based on such an observer is not a novel approach. Control of a two-mass system was originally stated as a problem for electric drives of rolling mills [4,5,6]. However, the problem is far from being solved. For instance, as plate rolling technology progressed, there emerged problems pertaining to the understudied nature of oscillatory processes in the two-mass systems of main lines of stands equipped with high-power individual motors. The key distinctive features are as follows:

• shock (impact) loads that result in fatigue destruction of mechanical equipment;
• vibrations that occur in the shaft lines of stands and in the electromechanical systems that are resiliently connected by the strip;
• instability of control systems due to torque limitations being applied to the electric drives.

Developing a parameter observer for two-mass and three-mass electromechanical systems that would be capable of reconstructing shaft torque and nondriven mass speed from the electric drive parameters is a relevant problem. In Russia, it is mainly researched by the Ivanovo State Energy University [7,8,9,10]. The problem is also covered in [11,12,13,14,15]. Dynamic stability improvement and reducing the influence of interference are the problems covered in [16,17,18,19,20].

Wang Junxiao and Yu Li have contributed significantly to the theory and practice of automatic control systems (ACS) based on observer-enabled computational algorithms. Their papers [21,22] discuss control systems with improved disturbance attenuation and contribute substantially to the advancement of the moving object control theory. To control the position of the magnetic levitation system, there has been developed and tested an adaptive algorithm for nonsingular terminal sliding mode control (NTSMC). To reduce chattering, time-varying disturbance compensation and estimation is integrated in the NTSMC controller using a generalized proportional integral observer. Simulations and experiments prove the closed loop to have satisfactory performance with regard to dynamic response and disturbance attenuation. This is the advantage of the proposed control system.

Paper [23] describes using a universal proportional integral observer for induction machines to test a robust encoderless FCS-PCC (finite control set–predictive current control) control scheme. Experimental results show that this system is highly dynamic, demonstrates good stable accuracy at low speeds, and is reliable.

Paper [24] proposes an extended state observer for a stepdown DC converter. The observer is there to monitor system status and general disturbances including deviations in load resistance and changes in the input voltage. A novel event-triggered sliding mode controller has been developed on the basis of this observer to avoid unnecessary computations. A similar problem is addressed in [25]. A sliding mode control is presented there that is based on a generalized proportional integral (GPI) observer. It accurately tracks the output voltage.

Wang Junxiao and Yu Li have undoubtedly carried out excellent research and made important findings. However, their findings do not apply to the existing rolling mills without more research and adaptation of the algorithms. This is due to the complexity of the rolling process. A priori data on numerous process parameters, which are subject to change, would be required to implement the proposed control algorithms.

Synthesizing the controllers and ensuring high ACS performance are important steps of observer R&D. Synthesizing a controller for a two-mass system where only one mass is controlled is not a trivial problem. Several papers including [26,27,28] make use of genetic algorithms with Kalman filters.

Systems based on state controllers have been considered in the papers [6,7,8,9]. Szabat K. [6] noted the control problem becomes especially challenging when some variables of the system are not measurable. This is often the case in industrial applications, including rolling mills. The paper presents a synthesized control structure featuring a proportional integral controller supported by various additional feedbacks; a system with two additional feedbacks is investigated.

Szabat K. et al. [29] have proposed using feedback on one of the two variables that describe the mechanical state. Their proposal consists of improving the classical control structure by using an additional circuit with a proportional integral (PI) controller.

The additional feedback allows setting the desired damping factor; however, it cannot simultaneously guarantee the required resonant frequency [15]. According to the literature, use of two-mass system shaft torque as feedback is a common solution.

Hidehiro I. [30] covered the development of a controller that uses a fuzzy algorithm to suppress vibrations in a multi-mass resonant system. It investigates two-mass and three-mass systems with elastic coupling. The authors developed a control system comprised of a fuzzy speed controller and a PI current controller for precise speed and torque control. Lozynskyy A. et al. [31] also analyzed the effectiveness of using fuzzy controllers in two-systems to control the variable moment of inertia of the second mass. All described research shows the results of mathematical modeling and experimental tests run on special laboratory benches. These control algorithms are of scientific interest; however, their implementation in control of industrial electromechanical systems that sustain shock (impact) loads is very complex.

However, the authors have not come across any reports on the industrial implementation or testing of known algorithms on existing hot-rolling mills. This is another proof of the practicality and prospects of industrial use of the authors’ solutions.

Newly developed solutions should not use complex mathematics to process signals in real time; besides, they should be able to be implemented in the software of controllers already installed on industrial units.

2. Problem Formulation

Many researchers, including those of South Ural State University and Magnitogorsk Iron and Steel Works (MMK PJSC), have studied the issues of limiting the dynamic loads associated with rolls gripping the metal strip [32,33,34]. These works present newly developed methods for reducing the spindle torque by optimizing stand drive speeds (tachograms). The result is attained by pre-closing the angular gaps in spindle joints. Limiting the elastic torque of the shaft by implementing short intensive braking after gripping has been additionally proposed in [35,36]. This was experimentally proven to improve dynamic readings.

However, the stated problem cannot be considered solved because the existing systems do not monitor or automatically control the spindle torque. An alternative is to directly control the elastic torque of the shaft. Systems within this concept are highly precise; however, they require direct measurement of the elastic torque. The need to install precision sensors on rotating equipment is what makes this approach particularly challenging [37,38,39].

This paper presents an elastic torque observer and a dynamic load limiter based on it; the case study under consideration involves the electromechanical systems of the reversing stand at MMK PJSC’s Mill 5000. Figure 1 and Figure 2 show the kinematic diagram of the stand and a picture of the upper roll spindle, respectively. A stand is a complex mechatronic system (Figure 1) equipped with electric and hydraulic drives. In rolling, they are elastically coupled by the metal strip.

The lines of the main electric drives (the main lines) of the rolls are two-mass electromechanical systems that have elastic couplings and angular gaps in spindle joints [36]. In Figure 2, the spindle (2) joins the work roll and the motor rotor by specially designed heads (4).

If a long shaft is present, motors and rolls in high inertia create an elastic system. In nonsteady state, the first mass and the second mass have different speeds, and the shaft sustains significant torque. This can be seen in the oscillograms in Figure 3. They were sampled by the torque monitoring system developed by SMS Group (Germany) and installed on the mill [40]. Figure 2 shows the sensor (1) and the telemetry slip ring (3) of the system.

Figure 3 shows the oscillograms of the torques M_M and M_S, the reference speed n_ref and the actual speeds n_UMD, n_LMD of the upper roll drive (UMD) and lower roll drive (LMD), respectively. Before nipping, no-load motor speeds are controlled within the range 3–3.5 mps. Rolls grip the strip as the drives are decelerating, whereby the angular gaps are fully open. Motor torques enter the domain limited at M_Mmax, which is set equal to 4200 kN·m. Torque fluctuations attenuate due to dissipative forces. However, the damping effects of the motor are mitigated by the short loss of drive control. Shaft torques have a ratio k_Sm = 2.2. This is the ratio of the maximum dynamic torque to the running torque (steady-state torque) (M_Smax = 6500 kN∙m, M_st = 3000 kN∙m).

Dynamic loads and elastic oscillations in the spindles mainly occur due to shock (impact) loads the spindles sustains as the rolls grip the strip. Torsional oscillations superimposed on the sinewave attributable to roll rotation have a significant amplitude that depends on the elastic properties of the shaft line, whereas the attenuation degree depends on the dissipative forces (friction, heating, etc.).

Rolls have individual variable-frequency electric drives based on synchronous motors. Figure 4 shows a simplified block diagram of the speed control system [41]. Apparently, deriving the elastic torque from electrical parameters will not allow us to find the peak dynamic loads at the eigenfrequencies of the mechanical system (10–25 Hz). Besides, this method does not provide sufficient accuracy in case of variable frequency drives. This is the reason to directly measure elastic oscillations, and corresponding sensors are installed directly on the spindles. In addition to the torque, they register motor parameters (rotation speed and current) as well as the rolling force. They are measured by sensors that are part of the frequency converters and of the process control system.

However, direct instrumentation is not reliable. Heavy-duty operation and relatively frequent scheduled spindle replacements, which require rather difficult sensor reinstallation, shorten the lifespan of the system components.

One of the promising solutions lies in the development of closed ACS’s featuring coordinate observers for the uncontrolled mass. In this case, these coordinates are the roll speed and the elastic torque of the spindle. Rotor of the motor constitutes the first mass. Observers have one important advantage: observer-based control systems do not need additional instrumentation (sensors, signal communication channels, etc.).

Review of literature on the observers and observer-based ACS highlighted two crucial shortcomings:

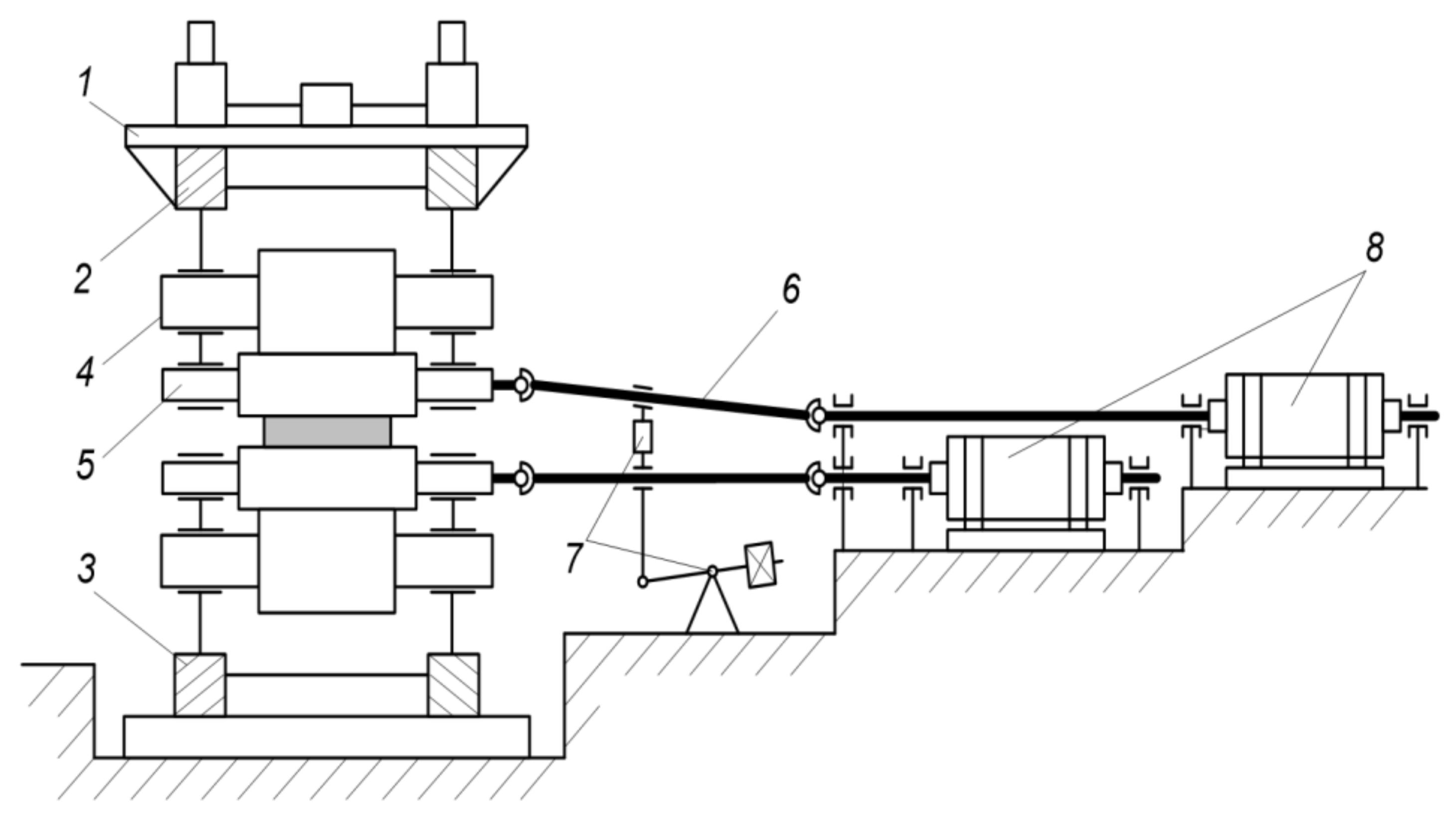
• Earlier papers present research into electromechanical systems with two electric machines installed on the ends of an elastic shaft [42,43]. This enables control over the coordinates of both electric machines. These parameters include speeds and currents, which are used to calculate the torques of these machines as well as the elastic shaft torques. These coordinates are used in control algorithms.

However, such an approach cannot be applied to industrial rolling mills because its second mass is a roll. Roll rotation speed cannot be measured because the roll is rolling hot metal whose temperature exceeds 1100 °C. This mass (the roll) is uncontrollable. Therefore, such developments made on laboratory benches do not apply to industrial units. In this regard, the present paper dwells upon the problem of developing a simple, stable system for automatic control of the elastic torque of the shaft in an industrial rolling mill.

2.

Known control systems based on uncontrolled mass coordinate observers are complex and require synthesis of multidimensional controllers, which effectively compute the coordinates [44,45,46,47]. These systems have a major flaw: they do not respond fast enough to a shock (impact) load.

The rolling mill under consideration, similarly to other such mills, sustains shock loads over 50 to 100 ms. Listed papers dwell upon fairly slow systems. They are not fast enough to respond to this dynamic process. This is confirmed by simulating the known computational algorithms. Simulations reveal slow response to the speed of the shock load that is the case of the system under consideration. Other authors make the same conclusion.

Thus, the idea was to develop a relatively simple observer that would monitor the elastic torque of the main stand line in a rolling mill, and to create a closed automatic coordinate control system based on the observer. Analysis of the scientific literature helped us to list and substantiate the following requirements to an ‘industrial’ coordinate observer for the electromechanical system of a rolling mill:

• Dynamic processes should be presented in the form of continuously measured physical parameters yet require minimum computing.
• Controllable coordinates are motor speed and torque as well as the applied load torque. The output coordinates are the roll speed and the elastic torque of the spindle.
• The developed solutions should not require complex mathematics (computing) and should be implementable in the controllers already used by the rolling mill APCS (automatic process control system).

The control system should be relatively simple and feasibly implementable as part of an industrial electric drive. This paper presents a three-loop coordinate control system for the uncontrolled mass. Such systems are well-researched, but not in the context of high-power electric drives that sustain abruptly varying loads. For a preliminary discussion, the paper analyzes the two-mass electromechanical system of a stand in Mill 5000. Notably, it is not fundamentally different from similar systems in other rolling mills.

3. Materials and Methods

Figure 5a shows the kinematic diagram of the two-mass system. System under research, electric drive and roll, can be presented as a closed dual-loop structure as shown in Figure 5b. Blocks 3, 5 to 7 are standard two-mass system model blocks [48]. They define the quality of transients in the mechanical part, including the natural attenuation of oscillations (Block 7). Block 5 simulates gaps in transmissions. Speed feedback is simulated by Block 9 that uses the factor k_S1. Block 2 represents the closed torque control loop.

For the methods and the parameters of the blocks of the model as derived from the equipment specifications and experimental oscillograms, see [49].

Table 1. Parameter of the two-mass system model, Mill 5000.

Parameter	Symbol	Dimensions	Value
Moment of inertia of the first moving mass (the motor)	J1	kg∙m2	125,000
Moment of inertia of the second moving mass (the roll)	J2	kg∙m2	114,571
Elastic coupling rigidity	c12	N∙m/rad	5,934,842
Eigenfrequency of elastic oscillations	ω12	rad/s	9.96
Electric drive acceleration	ε0	rad/s2	1–3
Transmission gap	δ	rad	0.017–0.051 (1–3°)
Mean elastic torque	M12	MN∙m	1.9
Damping ratio	β	-	2.817
Attenuation decrement	ξ	-	0.172
Speed controller gain	ksc	-	19.5
Speed controller time constant	Tsc	s	0.0041

shows the model parameters.

When developing the observer, Block 1 and the nonlinear gap-simulating Block 5 were removed from the structure. Below is the system of differential Equation (3) made with these modifications in mind. Figure 6a shows the resulting block diagram.

Matrix structure in Figure 6b corresponds to the state space equation:

$$\frac{d}{dt}\left[\begin{array}{c}{M}_{\mathrm{M}}\\ {\omega }_1\\ M_{12}\\ {\omega }_2\end{array}\right]=\left[\begin{array}{cccc}-\frac{1}{T_m}& 0& 0& 0\\ \frac{1}{J_1}& 0& -\frac{1}{J_1}& 0\\ \frac{\beta }{J_1}& C_{12}& -\beta \frac{J_1+J_2}{J_1\ast J_2}& -C_{12}\\ 0& 0& \frac{1}{J_2}& 0\end{array}\right]\ast \left[\begin{array}{c}{M}_M\\ {\omega }_1\\ M_{12}\\ {\omega }_2\end{array}\right]+\left[\begin{array}{cc}\frac{1}{T_m{k}_{fT}}& 0\\ 0& 0\\ 0& \frac{\beta }{J_2}\\ 0& -\frac{1}{J_2}\end{array}\right]\ast \left[\begin{array}{c}{M}_{1ref}\\ M_{ST}\end{array}\right],$$

(1)

where T_m is the electromechanical time constant of the motor.

For the structure, one can write the state vector X = ($M_M$,${\omega }_1$,$M_{12}$,${\omega }_2$) and the matrices:

$$A=\left[\begin{array}{cccc}-\frac{1}{T_m}& 0& 0& 0\\ \frac{1}{J_1}& 0& -\frac{1}{J_1}& 0\\ \frac{\beta }{J_1}& C_{12}& -\beta \frac{J_1+J_2}{J_1{\ast J}_2}& -C_{12}\\ 0& 0& \frac{1}{J_2}& 0\end{array}\right]; B=\left[\begin{array}{cc}\frac{1}{T_m{k}_{\mathrm{fT}}}& 0\\ 0& 0\\ 0& \frac{\beta }{J_2}\\ 0& -\frac{1}{J_2}\end{array}\right]; C=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

(2)

Thus, the system of differential equations holds true:

$$\begin{array}{cc}\hfill \frac{d{M}_M}{dt}& =-\frac{1}{T_m}{M}_1+\frac{1}{T_m{k}_{fT}}{M}_{RT}\hfill \\ \hfill \frac{d{\omega }_1}{dt}& =\frac{1}{J_1}{M}_M-\frac{1}{J_1}{M}_{12}\hfill \\ \hfill \frac{d{M}_{12}}{dt}& =C_{12}{\omega }_1-C_{12}{\omega }_2+\frac{\beta }{J_1}{M}_1-\beta \frac{J_1+J_2}{J_1\ast J_2}{M}_{12}+\frac{\beta }{J_2}{M}_{ST}\hfill \\ \hfill \frac{d{\omega }_2}{dt}& =\frac{1}{J_2}{M}_{12}-\frac{1}{J_2}{M}_{ST} \hfill \end{array}$$

(3)

This system was further used to develop an observer of the elastic torque, second mass speed and load torque; see Figure 7 for the block diagram presentation. The structure was implemented in Matlab Simulink for research purposes.

Pursuant to the block diagram in Figure 6a, the speed ω₂ must be reconstructible from the reference torque M_RT. Motor torque M_M and first mass speed ω₁ are directly measurable, whereas the load torque M_ST functions as the disturbance. Configuring the model is difficult because the observer must be able to reconstruct transients when the static torque M_ST increases abruptly. In a closed uncontrolled mass coordinate control system, such an operation could not be implemented without overshooting and oscillations unless high controller gain (measured in thousands of units) was applied, which would be impractical at best.

Therefore, an original approach was proposed when developing the observer. The idea was to feed actual real-time motor torque and speed signals to the model based on the equations above. Thus, the model parameters could be synthesized from the actual data on torque increase, and the torque would increase at a far lower rate compared to the idealized ‘abrupt’ change. Figure 8 shows the oscillograms that prove that. It shows actual signals of the load torque M_M(PDA) and motor speed n_M as acquired from the process data acquisition (PDA) system the mill is equipped with. Using the observer (digital twin), transients of the elastic torque M_R(DT) and roll speed n_R were reconstructed from this data. The figure also shows actual curves of the elastic torque M_R(PDA) as acquired from the mill sensors. They demonstrate that the static torque signal increases over the time Δt ≈ 0.07 s. This facilitates configuring the observer in development.

In Figure 8, the transients of the elastic torques M_R(DT) and M_R(PDA) match in quality and amplitude alike. The error does not exceed 5%. Speed curves were only verified by modeling because the mill does not measure roll speeds. These dependencies were derived for the case of pre-closed angular gaps in the spindle joints. Thus, the dynamic shock (impact) caused by closing the gaps when gripping the strip was not there and would not induce errors in reconstructed torque. As shown below, the actual object has arrangements in place to ensure that the gaps be closed at the moment of gripping. Because the transients under consideration coincide, the conclusion is that the model and the object are adequate.

In essence, these curves over time demonstrate an approach to configuring digital twins, which is used when control systems are commissioned virtually [50]. Under this approach, the control algorithms (in this case the observed signal reconstruction algorithm) are debugged in Matlab Simulink. This enables debugging the observer using signals from the virtual model of the mill (a digital twin of the drive system) rather than from the APCS.

Debugged models are then ‘transferred’ to the Tier 2 controllers of the APCS. Figure 8b shows the results of observer verification with actual signals. A comparison of the dependencies in Figure 8a,b demonstrates their identity. The adopted approach, in which the observer is debugged by modeling and then connected to the actual systems of the mill, did simplify the configuration and commissioning process.

4. Implementation

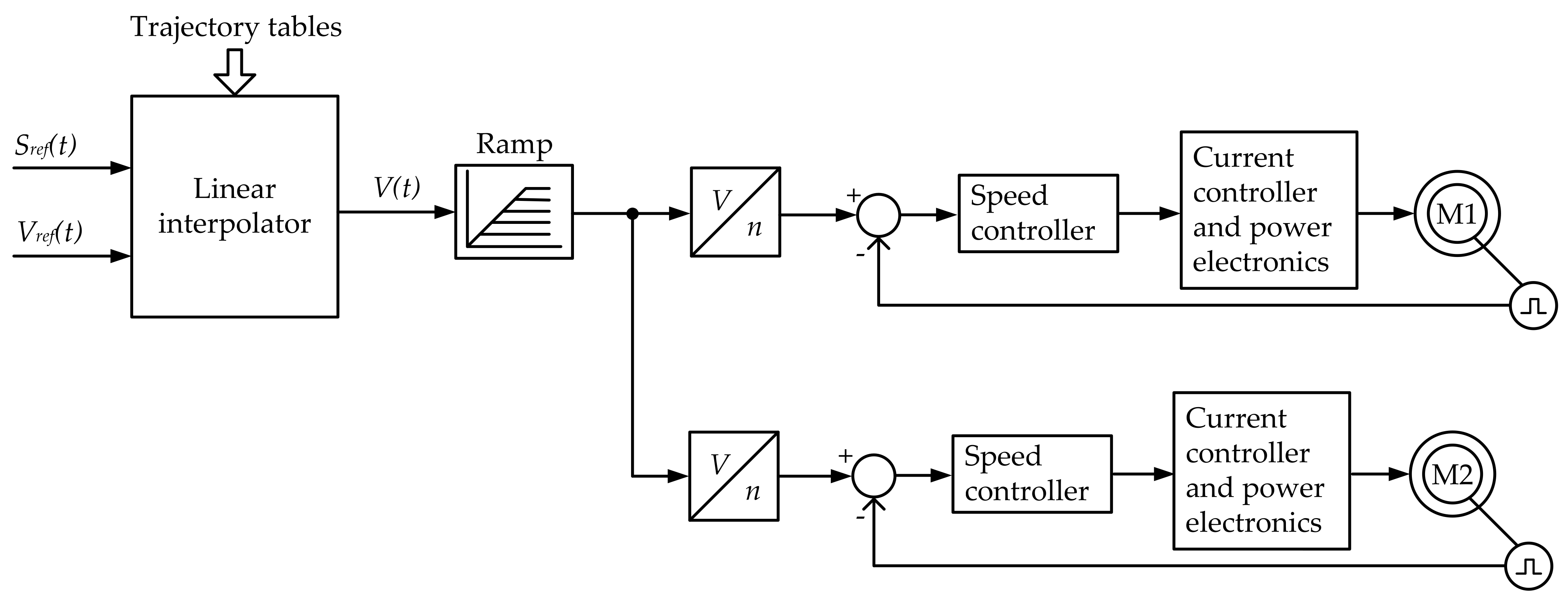
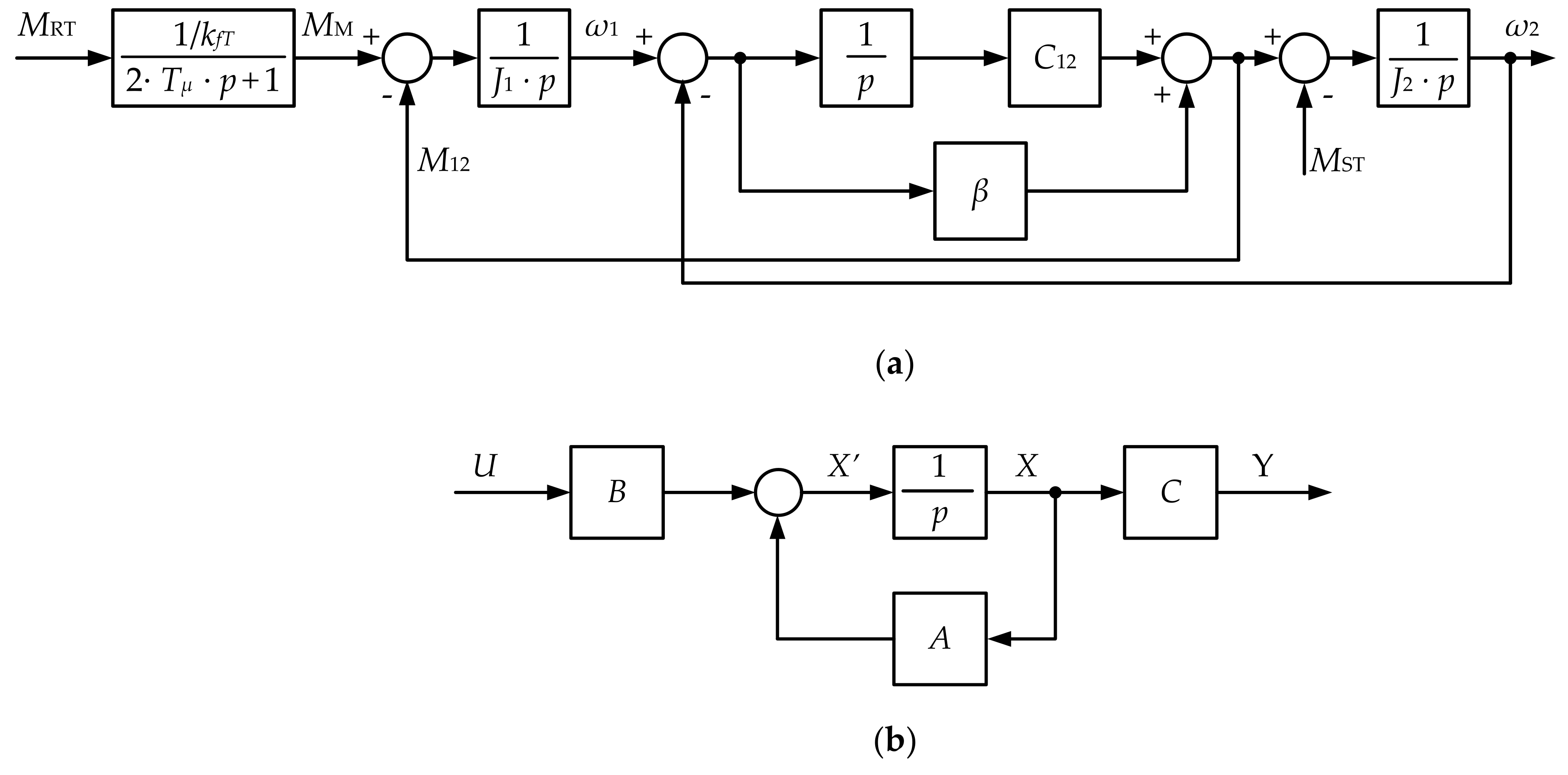
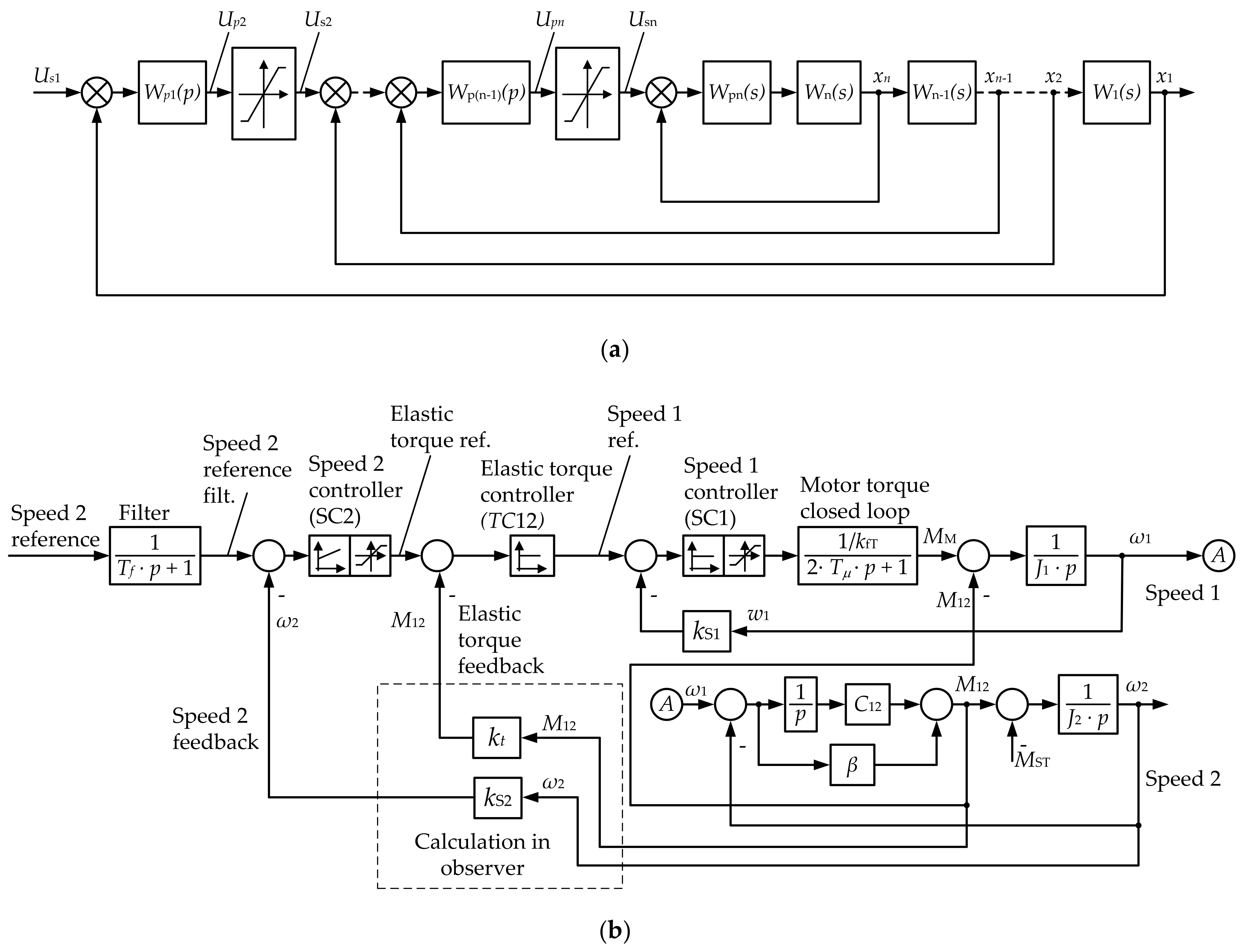
4.1. Development of the Closed Coordinate Control System for the Uncontrolled Mass

The automatic control system was based on the structure of the controlled object as shown in Figure 5. The development relied on the theory of closed systems that limit torque in mechanical transmissions; see the monograph [7] for detailed substantiation. Figure 9a shows the structure of a system that limits the input signals of internal loop controllers. Nonlinear saturated blocks are used to enable such limiting.

Based on that principle, we developed the system, see Figure 9b for the block diagram. It is a closed three-loop second mass speed ACS with the elastic torque, motor torque and speed loops as slaves. This structure can limit not only the reference value sent to the motor torque loop, but also the one sent to the elastic torque control loop.

The figure shows external controller (SC2) of the second mass speed J₂; elastic torque controller TC₁₂; external controller (SC1) of the first mass speed J₁, whose output is the desired motor torque. Gear ratios of the controllers were synthesized from the configuration rules of the slave coordinate control loops [51].

Figure 10a shows a block diagram of closed-loop elastic torque control. The utilized motor speed controller is a proportional one with the transfer function

$$W_{SC1}(p)=\frac{1}{2T_{\mu }p}\cdot \frac{1}{W_{SO1}\left(p\right)}=\frac{k_{fT}\cdot J_1}{2T_{\mu }\cdot k_{S1}}$$

(4)

where $W_{SO1}(p)=\frac{k_{S1}}{J_1\cdot p}\cdot \frac{1}{k_{fT}}$ is the feedback transfer function. With this in mind, the internal closed speed control loop for the first mass (Block 2 in Figure 10a) is represented by an aperiodic first-order element.

Transfer function of the elastic torque controller is generally written as follows:

$$W_{TC12}(p)=\frac{1}{4T_{\mu }p}\cdot \frac{1}{W_{TO}\left(p\right)}$$

(5)

where $W_{TO}(p)=\frac{c_{12}+\beta p}{p}\cdot \frac{k_{oT}}{k_{o1}}$ is the elastic torque feedback transfer function.

The utilized controller is a proportional one with the transfer function

$$W_{TC12}(p)=\frac{1}{4T_{\mu }}\cdot \frac{k_{S2}}{k_{fT}}\cdot \frac{1}{c_{12}\left(\frac{\beta }{c_{12}}p+1\right)}$$

(6)

Disregarding the attenuation ratio β, it becomes proportional:

$$W_{TC12}(p)=\frac{k_{S2}}{4T_{\mu }\cdot k_{fT}\cdot c_{12}}$$

(7)

This representation allows representing the closed elastic torque control loop 2 as an aperiodic element, see Figure 10b.

Similar reasoning produced the transfer function of the second mass speed controller ω₂:

$$W_{SC2}(p)=\frac{k_{fT}\cdot J_2}{8T_{\mu }\cdot k_{S2}}$$

(8)

A correction element (filter F) with the time constant T_f is connected in series with it to ensure astatism, see Figure 10b. This eliminates static disturbance error.

Apparently, simulation-based testing must precede industrial adoption. Of greatest interest would be to analyze transients that occur due to the limited elastic torque when opening the motor speed control loop.

4.2. Simulation Results

Figure 11a shows the simulation output with the elastic torque limited to 120% and the motor torque limited to 240%. The latter value corresponds to the existing motor speed controller configuration. Figure 11b shows equivalent processes where no limitations are applied to the controllers. Rolls grip the metal strip at the time t₁ in the motor acceleration section with the angular gaps closed.

Either way, motor torque does not reach the limit. In the first figure, spindle shaft torque (M_S) reaches 120% at time instant t₂ and is kept there by the control system. This effectively limits the elastic torque of the spindle. As a result, the second mass speed control loop is open within the interval t₂–t₃. Therefore, the transient of the motor torque M_M becomes complex, and the torque varies within the range from (−60%) to (+130%). In the second figure, the second mass speed control loop does not open. Transients of the first mass speed and second mass speed (n_MT, n_S) last about the same (t₁–t₄) in either case. Dynamic speed deviations also fall within identical ranges: 19–35 rpm at the gripping speed of 30 rpm; therefore, speed deviations from the target vary from (−37%) to (+17%).

These curves over time show that the first and second mass speeds in either case only differ (i.e., control error occurs) during transients, i.e., for 0.5 to 0.7 s after the load is applied. This is when the two-mass system shows its elastic properties. In general, the system enables astatic control over both speeds, responds satisfactorily fast, and limits the elastic torque adequately.

The next step was to test the feasibility of improving the performance of first and second mass speed control loops. To that end, second mass speed control loop (SC2) had its gain doubled, and both torques were limited to 240%. Figure 12 shows curves over time. In this case, the motor torque M_M does reach the limit. Elastic torque of the shaft M_S changes similarly to the curve in Figure 11b and increases without overshooting. Speed transients in these figures differ; however, both last ~0.5 s.

Comparison of the curves plotted in Figure 11b and Figure 12 shows that how fast the second mass speed control loop responds does not significantly affect the performance of two-mass system shaft torque control.

In order to generalize the dynamic properties, Figure 13a shows Bode plots for the conventional two-loop speed ACS with a PI controller (BP 1) and for the proposed three-loop system disregarding nonlinearities stemming from signal limitations (BP 2). To plot them, desired speed was used as the input and the second mass speed was used as the controlled signal. That means that for the second mass speed, the system enables greater bandwidth and is therefore less oscillatory.

Figure 13b shows Bode magnitude and phase plots made with an open external loop. Analysis of the plots leads to a conclusion that

• the amplitude margin is 10 dB, which is sufficient per Nyquist criterion;
• the phase plot is beak-shaped, no crossing through −180° to the left of the cutoff frequency; the phase margin is about 50°, which is also sufficient.

Analysis of the plots shows that increasing the gain did not significantly affect the resonant frequency and the oscillation amplitude of the first mass. This allows for an assertion that the developed system is able to stably control the elastic torque in a two-mass system.

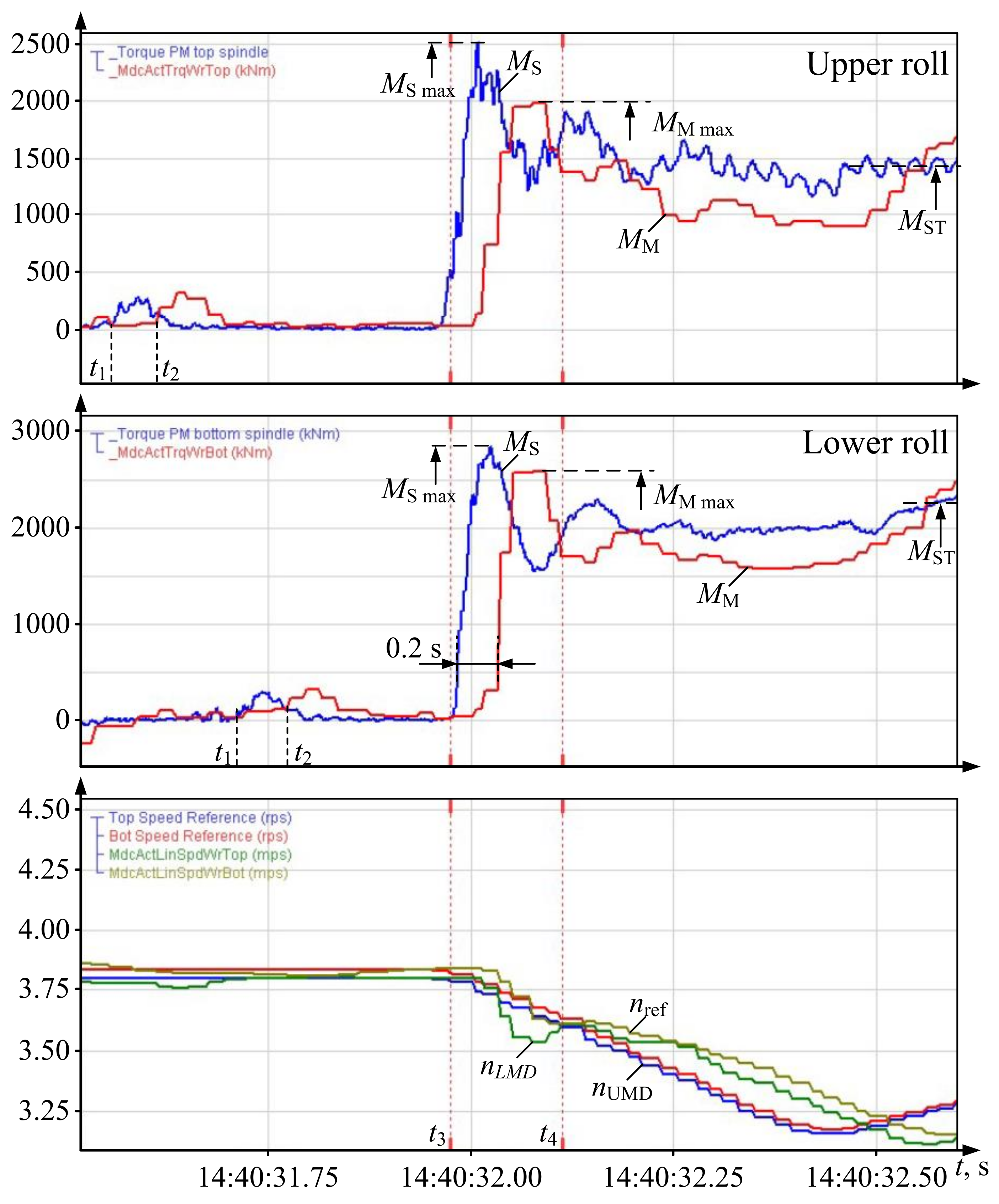
5. Experimental Results

The system has been implemented in VME BUS and LogoCAD. Cycle time to calculate the stand motor signals is 5 ms and can be reduced to 1 ms. The system was developed and configured using a method covered in paper [50] by the authors. Using the method, we sampled data on an industrial unit using signals from the stand motor control system (i.e., the PDA system). In pilot tests, we used signals from the torque meter, whose sensor is shown in Figure 2, for accuracy testing. Figure 3, Figure 8 and Figure 14 show the oscillograms of these signals. The signals were recorded by the IBA PDA system. Then they were exported to MatLab for analysis and observer modeling. Debugged MatLab models were used to write a program to execute the developed algorithms in the real-time computing system based on VME BUS and running VxWorks.

When configuring the observer and the automatic control system based thereon, the parameters of the two-mass system were assumed to be constant. Change in such parameters in the rolling process was not consideration. These assumptions are valid due to the following properties of the system.

• The system under consideration is a two-mass system where the first mass (the motor’s rotor) does not change its inertia.
• The stiffness of the elastic shaft (spindle) does not change either. This parameter depends on the length, diameter, and the properties of the metal that the shaft is made of. These parameters do not change even when the spindle is replaced.
• Second mass inertia depends on the mass of work and backup rolls, which is constant as well. The inertia of the rolled bar is 5% to 15% of the total second mass inertia. For configuration, use the mean bar inertia that deviates by 1.7% to 5%. Such deviations are commensurate with the error of the instrumentation sensors. Thus, they do not cause significant error in the configuration of the control algorithms.

Paper [40] presents an estimate of the system parameters. Successful testing and operation of this newly designed automatic elastic torque control system on an existing rolling mill is what proves the stability and reliability of the results.

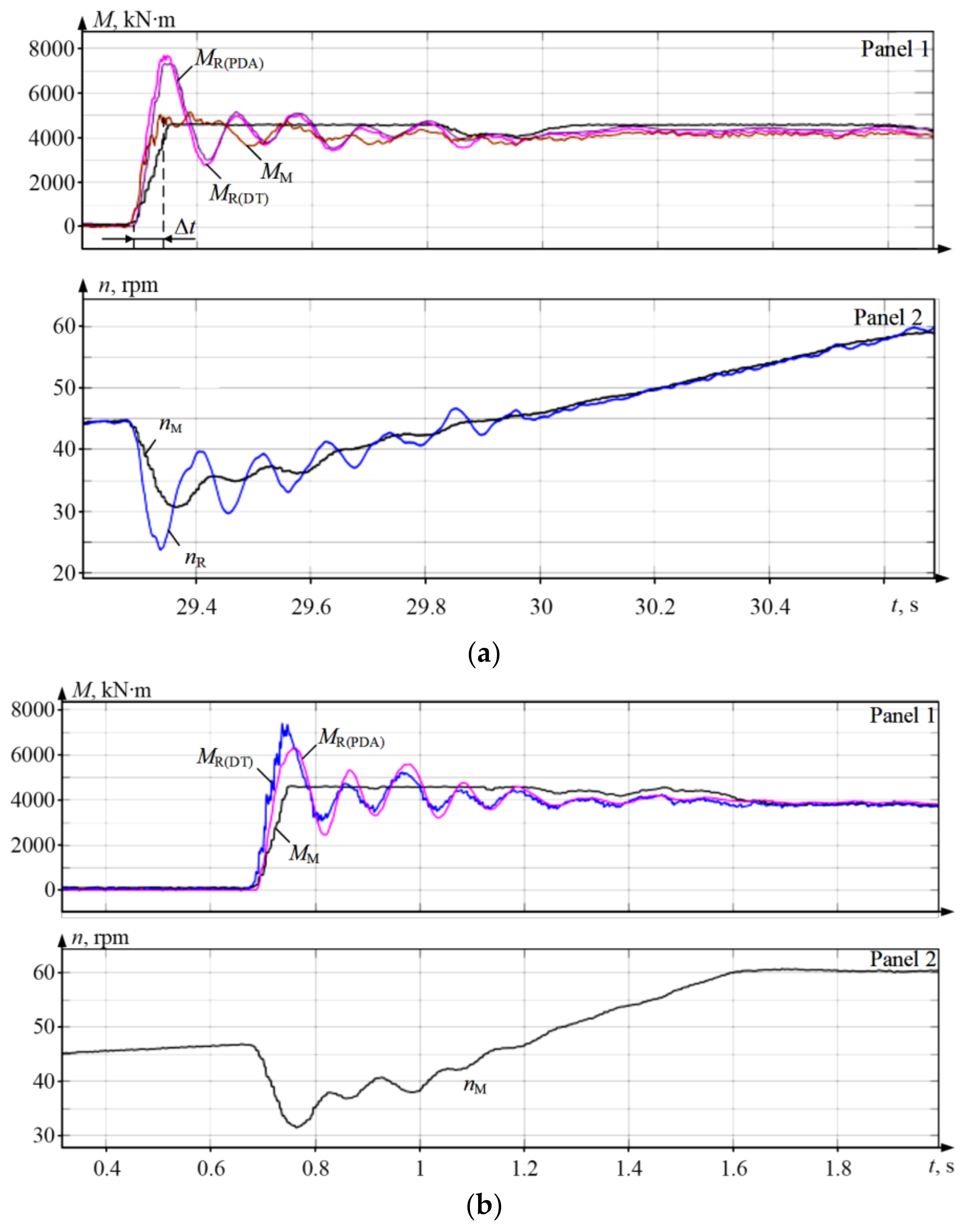
5.1. Accuracy of Reconstructed Two-Mass Coordinates

The algorithm of the developed elastic spindle torque and roll speed observer was implemented in the software of the industrial controller installed in the reversing stand of Mill 5000. Experiments produced multiple strip-gripping oscillograms with the angular gaps in spindle joints fully open. They are equivalent to those shown in Figure 8b. In this case, the dynamic torque gains a secondary component due to the shock (impact) associated with closing the gap. As a result, the elastic torque signal M_R(PDA) from the sensor is amplified, whereas the reconstructed torque M_R(DT) remains unchanged. This increases the error of reconstruction to 8–10%. The reconstructed torque has a greater amplitude than what is shown in the actual oscillogram.

Experiments carried out by rolling billets of the same grade in identical passages showed that closing the gaps would affect the dynamic spindle torque. Thus, closing the angular gaps in the spindle before feeding the strip to the stand was found to be necessary for the coordinate control systems based on the developed observer to be effective.

Figure 15 shows the generalized results of analyzing the reconstructed curves and experimental oscillograms of elastic torque for feeds of different gauge. It shows charts of spindle torque amplitude sampled with gapped and gapless joints. Gap preclosure was enabled by gripping while accelerating the electric drive. For details on how it works, see [41,52,53]. Open-gap gripping was enabled by decelerating the electric drive; see characteristic oscillograms in Figure 3 above. Figure 15 also shows charts plotted from observer-reconstructed oscillograms.

Table 2. Calculated gripping torque amplitudes.

Gauge	Measured Values				Observer Values
	Mmax (Gapped)	Mmax (Gapless)	ΔMmax (Gap/Gapl.)		Mmax(Obs.)	|ΔMmax| (Obs./Gap)		|ΔMmax| (Obs./Gapl.)
mm	p.u.	p.u.	p.u.	%	p.u.	p.u.	%	p.u.	%
9	1.55	1.45	0.1	6.9	1.35	0.2	13.8	0.1	6.9
12	1.65	1.54	0.11	7.1	1.43	0.22	14.3	0.11	7.1
18	1.92	1.77	0.15	8.5	1.67	0.25	14.1	0.1	5.6
24	2.15	2	0.15	7.5	1.89	0.26	12.1	0.11	5.5
30	2.4	2.21	0.19	8.6	2.12	0.28	11.7	0.09	4.1

generalizes experimental data.

Analysis of the results shown in the figures and in the table concludes the following:

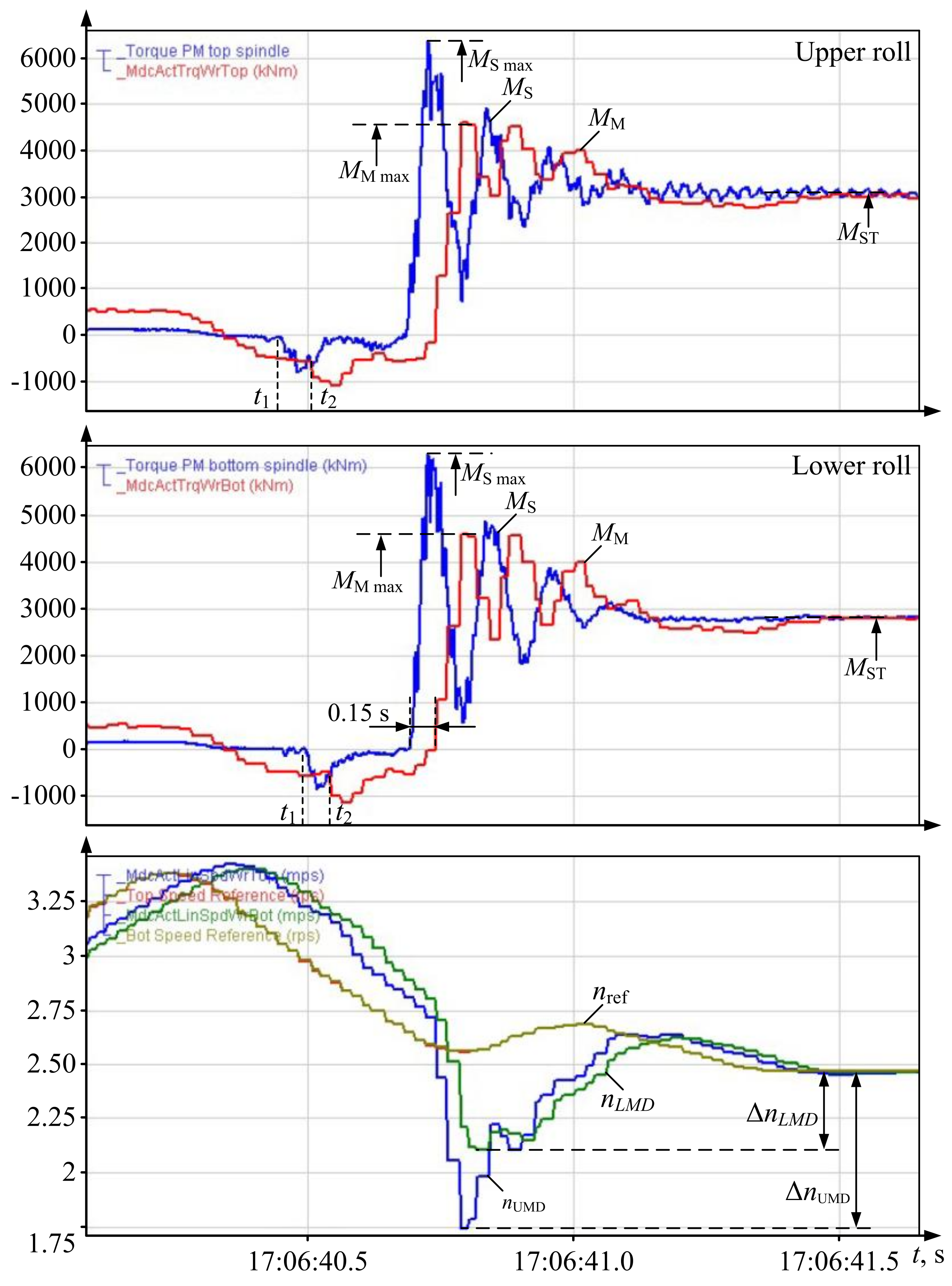
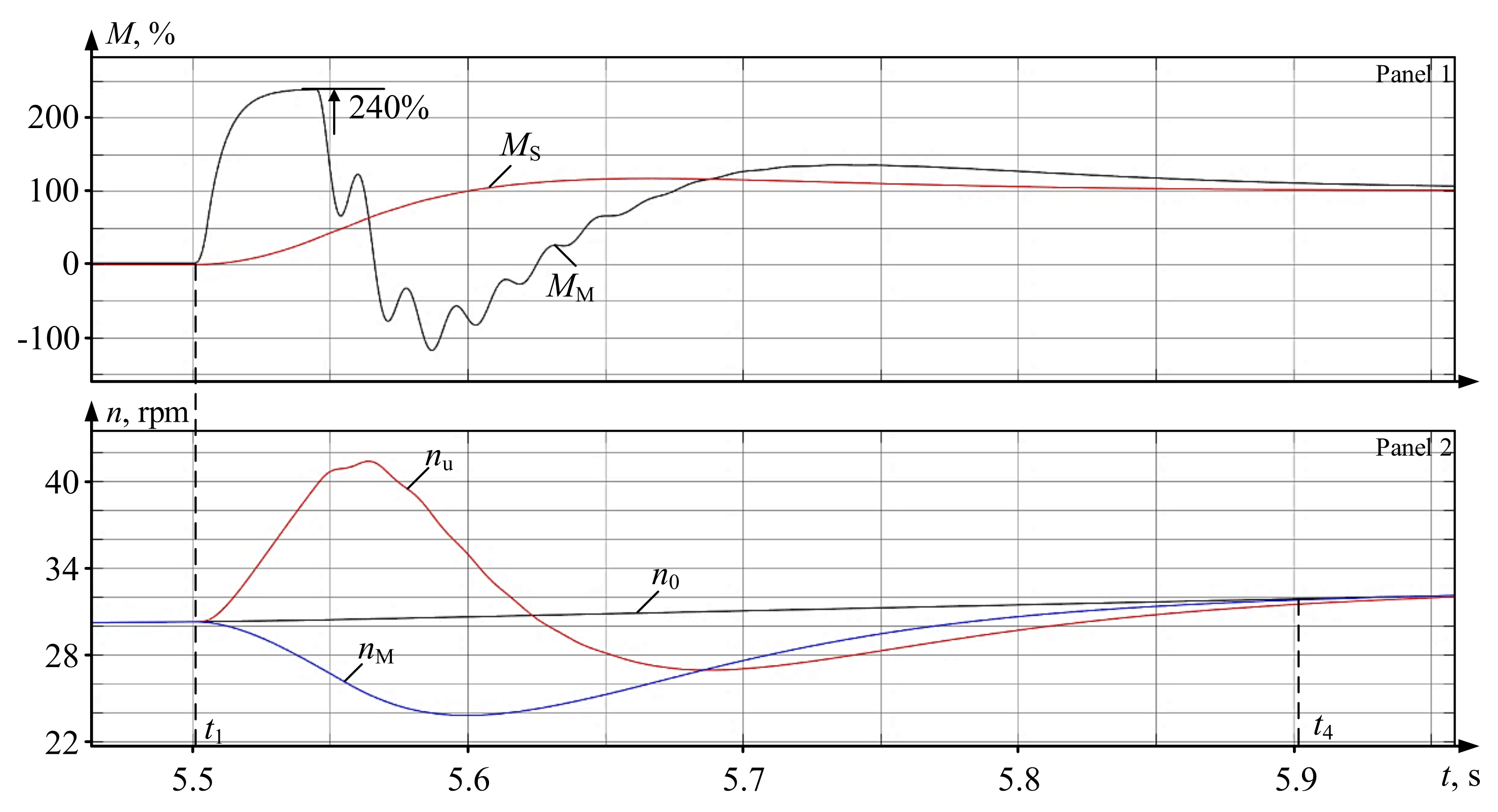
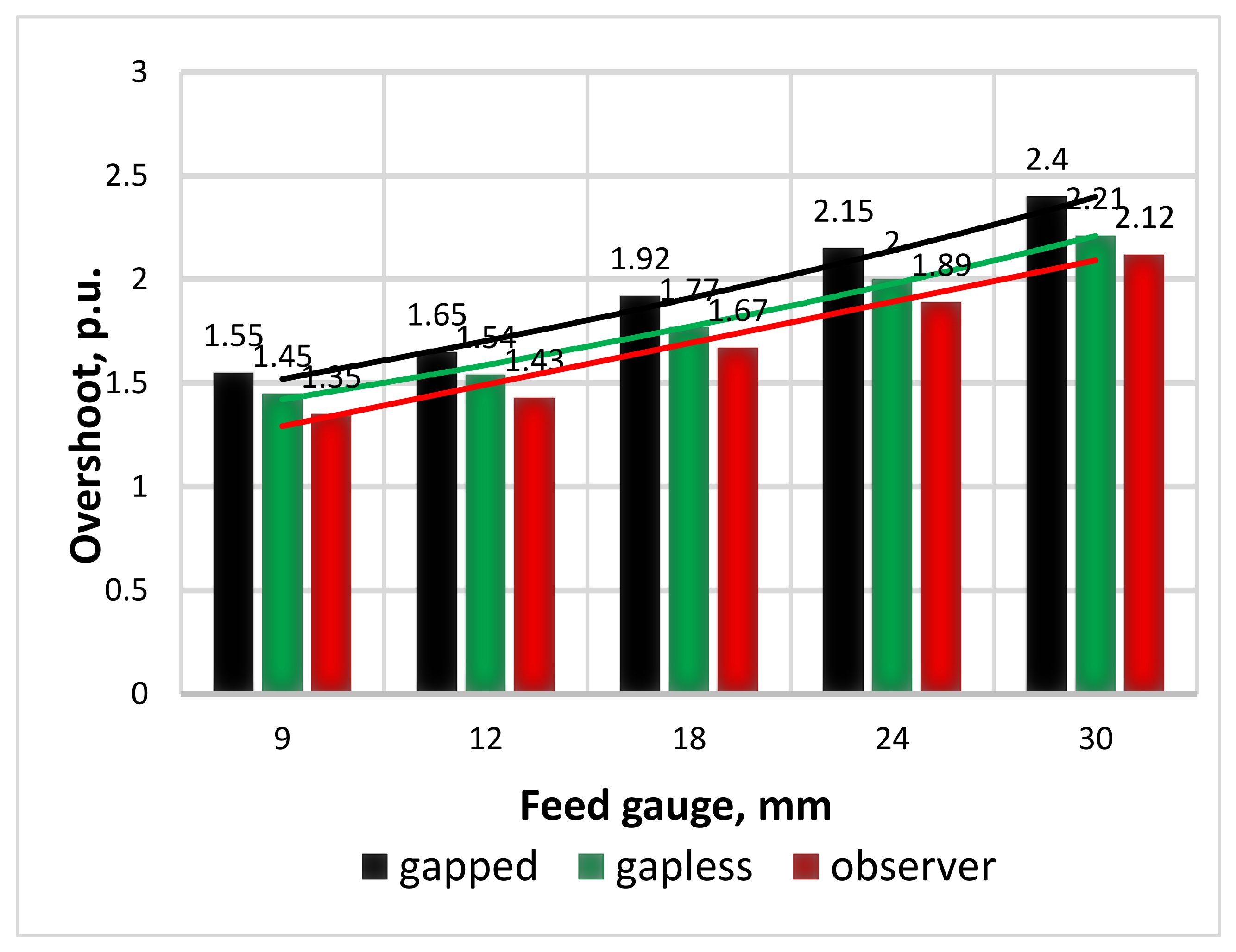
• Greater gauge is associated with greater overshoot. Thus, at 9 mm, i.e., in the later passages, the ‘gapless’ amplitude is 35%, and the ‘gapped’ amplitude is 45%. In case of 30 mm gauge (the earlier passages), it is 240% and 212%, respectively.
• The torque component that stems directly from the gap-closing shock (impact) is relatively insignificant at 6.9% at 9 mm (1.55 and 1.45 p.u. of difference in amplitudes), 8.6% at 30 mm (2.4 and 2.21 p.u., respectively). This indirectly confirms that the ‘elastic’ torque component has the maximum impact on torque overshoot [54].
• Relative difference between actual and reconstructed values decreases as the gauge increases: 6.9% at 9 mm, 5.6% at 18 mm, and 4.1% at 30 mm.

Thus, the developed observer is capable of sufficiently accurate reconstructions of the roll speed and elastic torque coordinates. This effectively allows us to proceed to industrial testing of the developed closed automatic speed control system for the second mass with limited spindle torque.

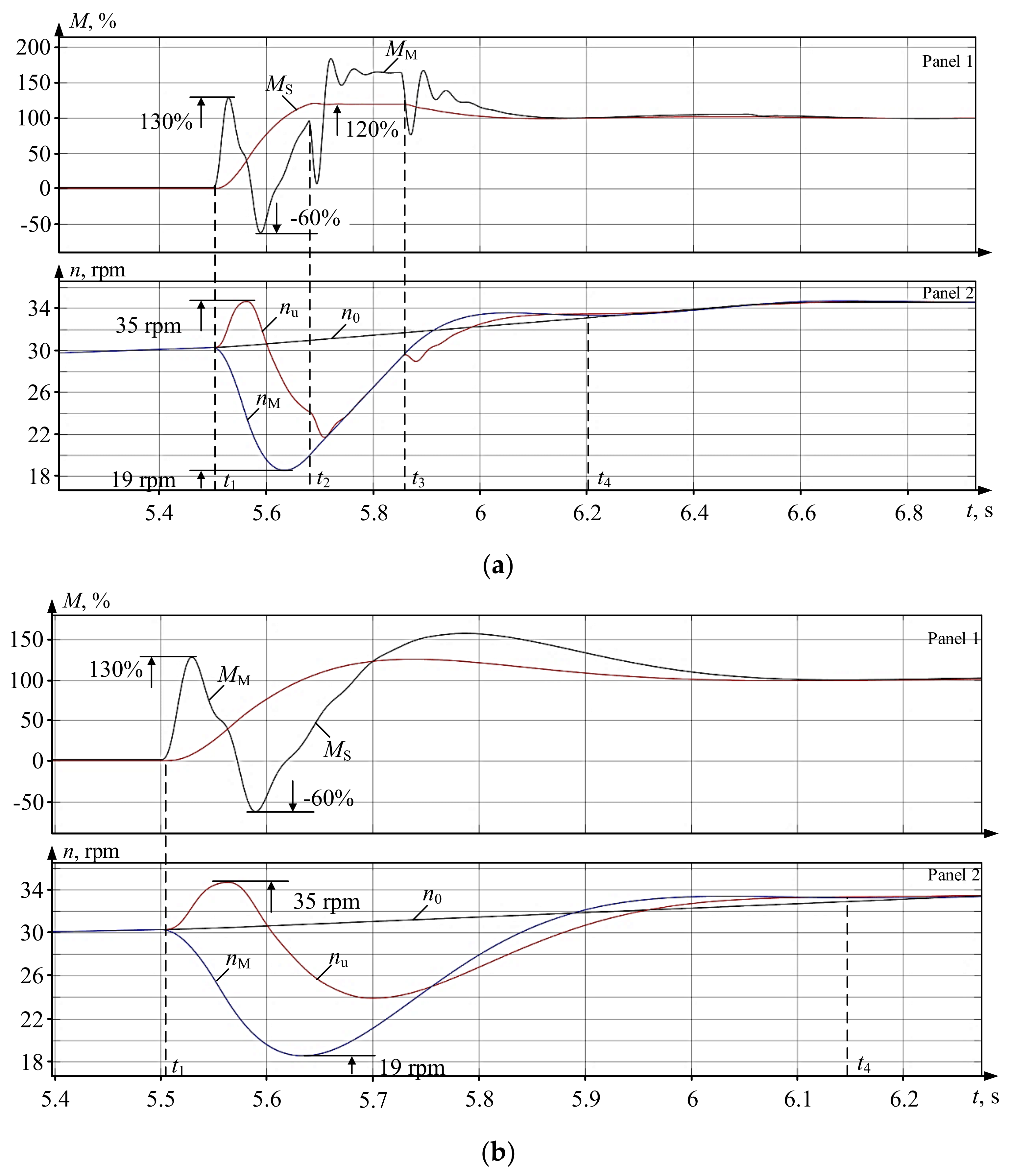
5.2. Testing the Electric Drive Coordinates in the Developed Three-Loop System

Figure 14 shows oscillograms of linear speeds and torques of upper and lower roll motors, as well as elastic torque oscillograms of shaft lines equivalent to curves in Figure 3. The difference is that the lower roll drive ACS now features the developed elastic torque limiter shown in Figure 9b. Upper roll drive was not reconfigured. This enabled comparing the oscillograms of the known system against those sampled with the developed algorithm in place.

The oscillograms were made in gripping mode with the internal loops of the speed ACS having identical configurations, i.e., the initial conditions were the same. Running rolling torques M_ST differed due to the difference in electric drive loads, which in turn were due to different pressures on the upper and lower rolls. Metal strip was gripped with the gaps closed. This can be seen from the ‘upsurge’ in the oscillograms of M_S and M_M that occurred at the times t₁ and t₂ as the gaps were closed by pre-accelerating the electric drives. The algorithm forces the electric drive to decelerate between t₃ and t₄ after gripping.

At the time t₃, static load M_ST equal to 2500 kN∙m is applied. This load is close to nominal; therefore the motor torques rise significantly. Load is applied at steady-state speed. Thus, technological factors cause a speed drop from 3.75 to 3.25 m/s. This deceleration takes almost 1 s, i.e., the deceleration rate is about 0.5 m/s². The resulting dynamic torque is negligible in comparison with the load torque. Thus, change in the motor torques over the timeframe t > t₄ is insignificant, making it barely visible on the oscillograms.

Table 3. Experimental dynamic torque deviations.

Parameter	Oscillogram Value
	UMD			LMD
Shaft torque	Mst	MSmax	kSm	Mst	MSmax	kSm
	kN∙m		-	kN∙m		-
	1400	2500	1.8	2250	2700	1.2
Motor torque	Mst	MSmax	kSm	Mst	MSmax	kSm
	kN∙m		-	kN∙m		-
	1400	2000	1.4	2250	2550	1.12

shows the dynamic deviations in the elastic torques of the shaft and electromagnetic torques of the upper roll drive (UMD) and lower roll drive (LMD). Their amplitudes are described by the ratios K_Sm and K_MTm. They are found as the ratio of the maximum torque M_Smax or M_Mmax to the running torque M_ST.

Analysis of the oscillograms and table data concluded the following:

• k_Sm was 1.8 with the initial configuration, changed to k_Sm = 1.2 after implementing the new algorithm. Thus, the algorithm reduced the torque amplitude by a factor of 1.5.
• k_Sm was 1.4 for the UMD torque M_MT, 1.12 for LMD, i.e., reduced by a factor of 1.25.
• Elastic oscillations attenuated at least twice as fast. k_Sm was 1.4 for the UMD torque Mmt, 1.12 for LMD, i.e., reduced by a factor of 1.25.

Thus, adopting the algorithm does reduce the dynamic loads in the main drive lines of the reversing stand.

6. Discussion of the Results

Curves over time shown in Figure 11a demonstrate the motor torque transient in the developed three-loop system to be of complex nature and to vary from (−60%) to (+130%). It deteriorates compared to the monotonically increasing shaft torque transient. However, oscillations in this range will not compromise a synchronous motor. The conclusion for now is that the motor and spindle torque transients are satisfactory.

The external loop is connected in order to prevent elastic torque oscillation and to limit such torque to a reasonable level. In this case, the shaft torque transient nearly matches the configured absolute optimum. It is therefore safe to say the control system functions as intended.

The strengths of the proposed observer lie in the ease of configuration and accurate reconstruction of transients. Processing over 200 oscillograms equivalent to those in Figure 8b led to the following summarizing conclusions:

• in case of gripping with pre-closed angular gaps in spindle joints, difference in the amplitudes of the measured vs reconstructed torque averages at 5 to 7%;
• equivalent difference in case of open gaps hits 10%.

This confirms an earlier conclusion that the dynamic torque component that stems from the shock (impact) associated with closing the angular gap is not significant. Radionov A.A. et al. [52] demonstrated the dynamic torque amplitude in case elastic shock (impact) (the first component) does not depend strongly on the angular gap magnitude. At a nominal torque of 1.9 MN∙m and an angular gap of 1.5°, it equals 2.7%. On the other hand, the component that stems from the elastic properties of the spindle is 10 to 15 times higher than the amplitude of the first component, thus having a greater effect on the dynamic torque in gripping.

The proposed observer lays the foundations for the development of closed coordinate control systems for nondriven masses of rolling mills. Beside the three-loop system under consideration, these include the state controller-based two-loop roll speed and elastic spindle torque ACS [7,9,55]. It provides the best performance in systems with nonrigid mechanics. The shortcoming is that configuring the computing of controlled coordinates can be tricky.

The proposed observer configuration algorithm is a specific case of using digital twins to virtualize the commissioning of electric drive control systems. This area of focus is detailed in [50], where the authors call it a promising application for the creation and improvement of electrical and mechatronic systems in rolling mills.

Digital twins made for virtual commissioning should solve the controlled object’s equations accurately and in real time. The developed two-mass coordinate observer meets this requirement.

7. Conclusions

Experimental research of grip-related transients confirmed substantial dynamic loads of oscillatory nature. This proved relevant the effort to develop control methods that could limit motor and spindle torque in such an operation.

The paper shows that known developments use computational algorithms based on computational tables. Use of such algorithms requires a priori data on numerous rolling process parameters. However, these parameters tend to change in real-world industrial settings. Changes may occur when switching to rolling a different set of products or even between passes (compressive parameters, metal stiffness, rolling speed, temperature, etc. are all subject to change). Under the proposed concept, all the required readings are sampled from the sensors of electrical parameters, which are part of the frequency converters. The algorithms have been fully implemented in the PLCs already installed on the mill. This is an undisputable advantage of the solution.

The authors developed an observer that continuously monitors the coordinates of the two-mass electromechanical system of the rolling mill stand. Experiments confirmed satisfactory accuracy of reconstructing the elastic torque of the shaft and the speed of the uncontrolled mass.

It further proves the feasibility of taking measures to guarantee the closure of angular gaps before gripping. The most feasible solution is to pre-accelerate the electric drive.

Based on the proposed observer, the research team developed a three-loop system that directly controls the speed of the uncontrolled mass and thus limits the elastic torque when shock (impact) load is applied. The system is based on a multi-loop coordinate control system that limits the inputs of slave loops.

The following controllers are justifiably connected:

• proportional speed controller for the first mass, whose output is the target motor torque;
• proportional controller of elastic torque. This configuration is optimal because the object structure contains an integrator, and this controller provides high performance;
• proportional speed controller for the second mass, which features a corrective proportional integral element at the input. This element increases the slope of the Bode magnitude plot in the low-frequency domain and enables astatic control over the second mass speed.

Analysis of mathematically modeled and experimentally derived transients confirmed a reduced amplitude of the elastic spindle torque as well as satisfactory quality of motor speed and torque transients. Similar conclusions were drawn by plotting the Bode magnitude and phase plots of the system.

The advantages of the developed solution include ease of implementation and the ability to be implemented on existing rolling mills without using additional computing devices or sensors. The solution has been pilot tested on a state-of-the-art plate mill, Mill 5000, designed and constructed with assistance from SMS Group.

The developments presented herein are recommendable for adoption in other units where electric drives sustain shock (impact) loads. In metallurgy, these include plate and broad-strip hot-rolling mills as well as roughing stands of bar mills.