GPS Path Tracking Control of Military Unmanned Vehicle Based on Preview Variable Universe Fuzzy Sliding Mode Control
Abstract
:1. Introduction
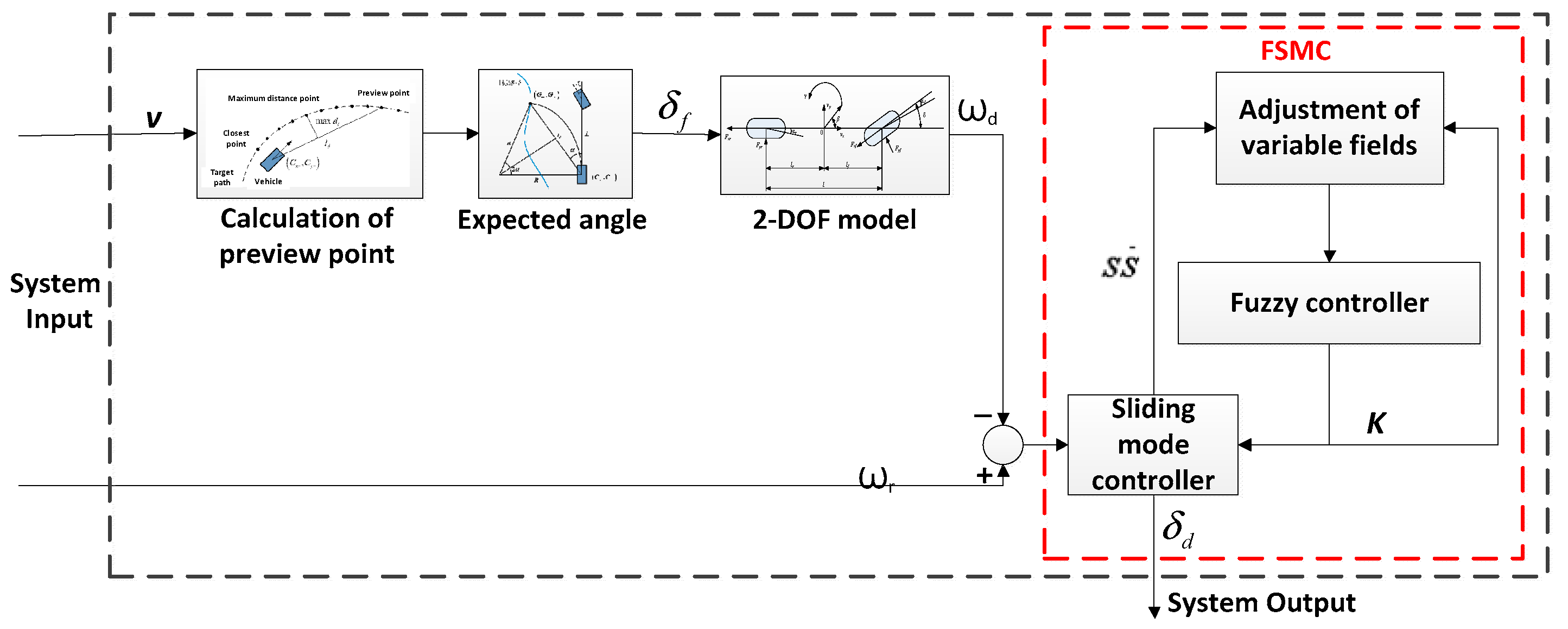
2. Acquisition of Path and Preview Information
2.1. GPS Information Processing
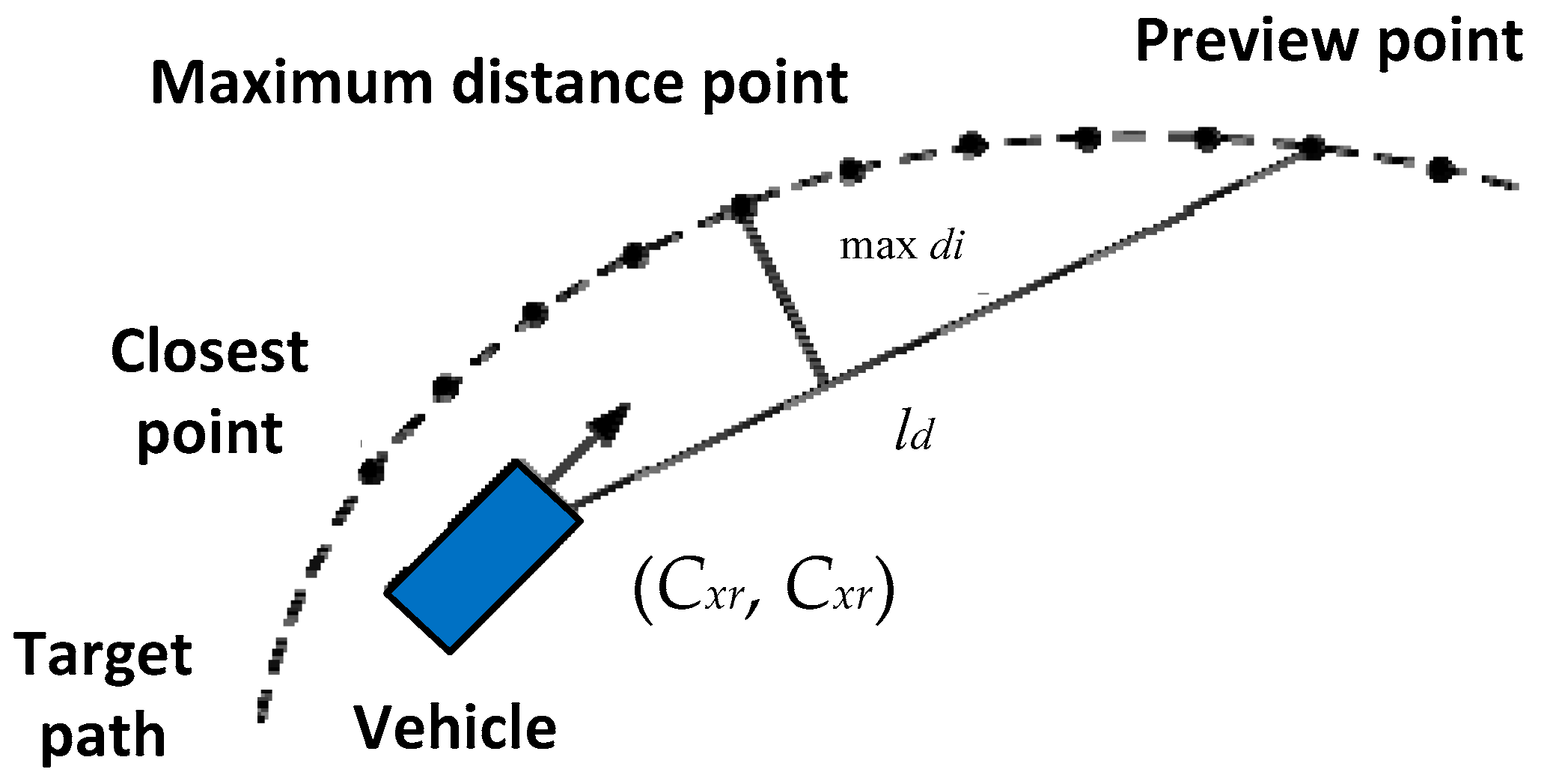
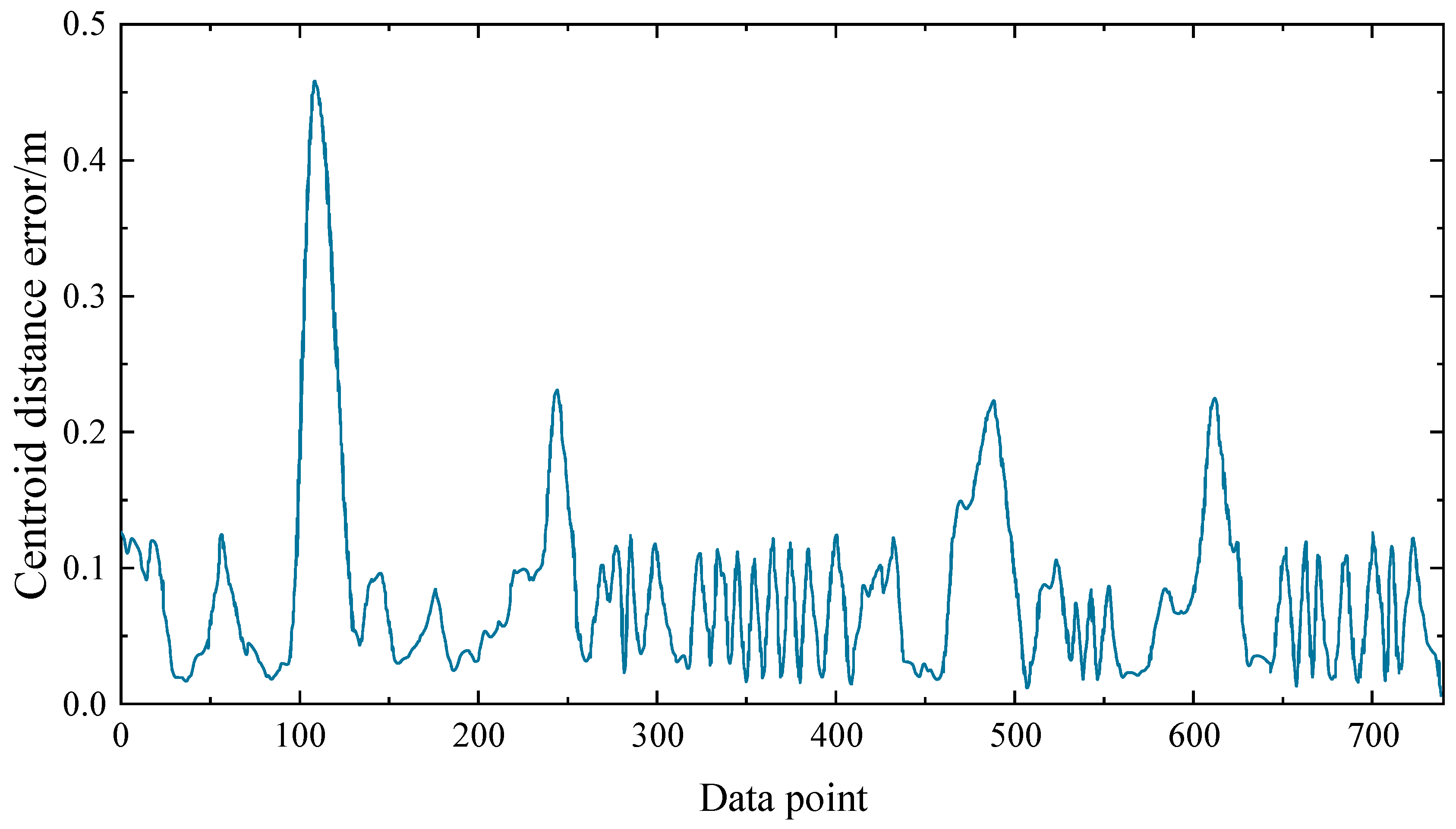
2.2. Calculation of Preview Point
- (1)
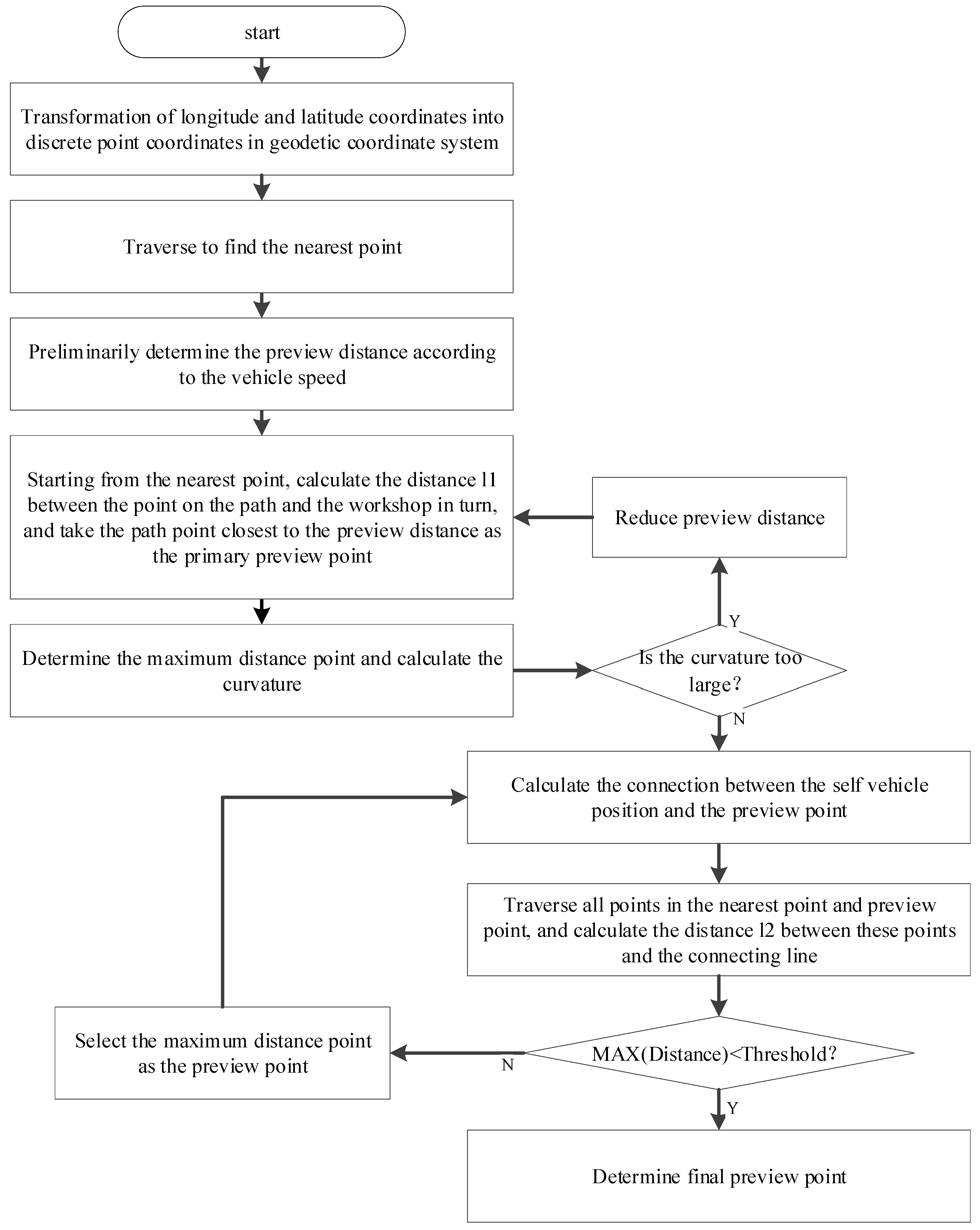
- According to the GPS information of the path, the nearest point of the vehicle position at the current moment is determined after coordinate transformation. According to Formula (1), the following formula is obtained after simplification and operation processing, and the nearest point is found by traversing the following formula:
- (2)
- The preview distance is determined according to the following formula:
- (3)
- Find the coordinates of the nearest point according to the method described in step 1, calculate the distance between the point on the path and the vehicle from the nearest point, take the path point closest to the preview distance as the preview point, return the coordinates of that point, and then obtain the pre-selected preview point.
- (4)
- After the preview point is determined, the line between the current vehicle position (Cxr, Cxr) and the preview point is calculated.
- (5)
- Traverse all the points in the nearest point and preview point, calculate the distance between these points and the line in step 4, and then determine the maximum distance point.
- (6)
- Determine whether the distance maxdi between the maximum distance point and the line in step 4 exceeds the threshold, and then judge whether the preselected preview point is reasonable. The curvature value does not need to be calculated specifically, and the curvature can be reflected by judging the distance between the maximum distance point and the line in step 1.
- (7)
- If step 3 determines that the threshold value is exceeded, the current maximum distance point is selected as the preselected preview point, and steps 1–3 are repeated until the requirements are met, and the preselected preview point is output as the preview point.
3. Lateral Motion Control Based on Variable Universe Fuzzy Sliding Mode
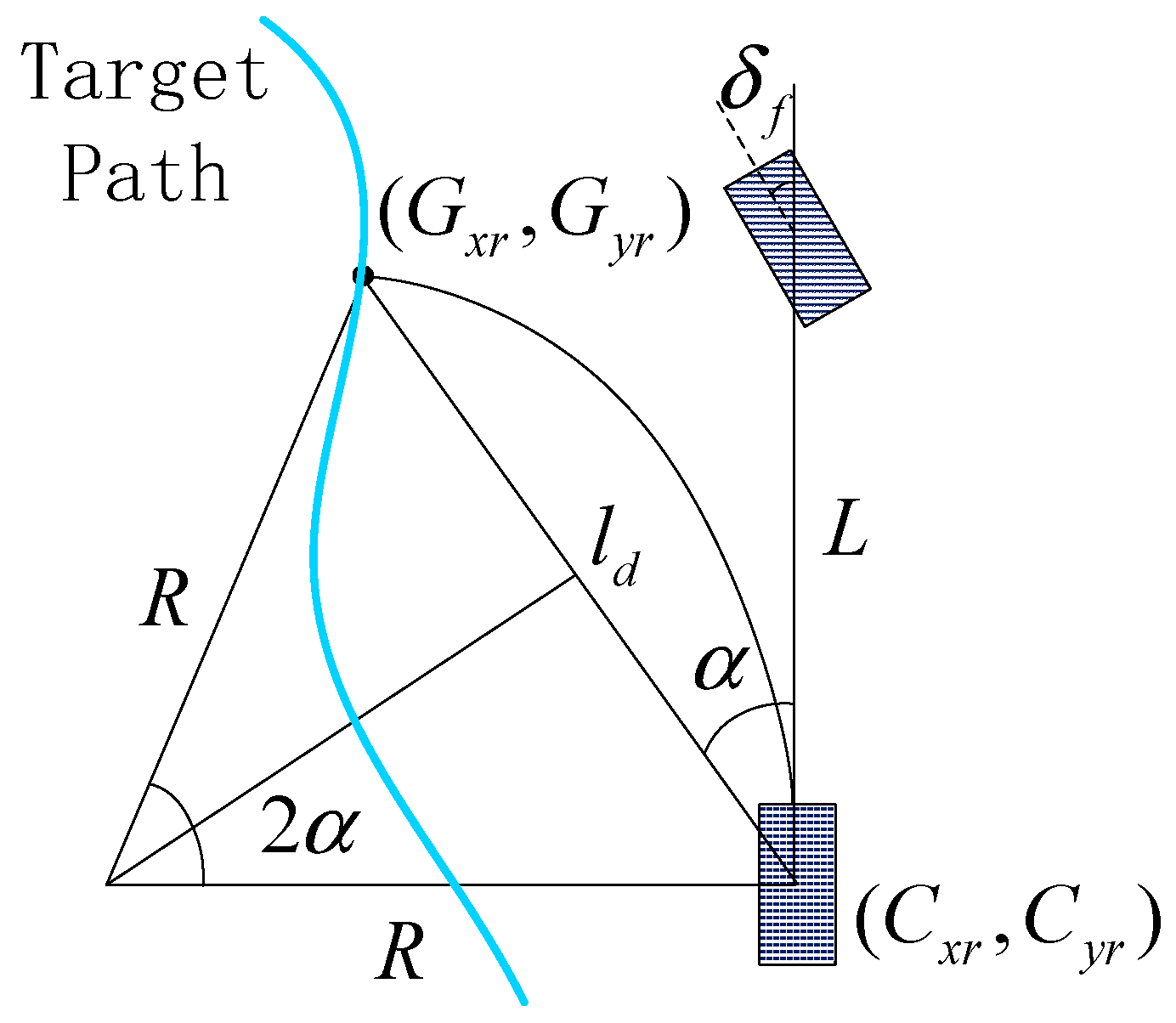
3.1. Calculation of Expected Steering Angle Based on Pure Tracking Algorithm
3.2. Design of Sliding Mode Controller
3.3. Design of Fuzzy Sliding Mode Controller
3.4. Design of Variable Universe Fuzzy Sliding Mode Controller
4. Simulation Analysis
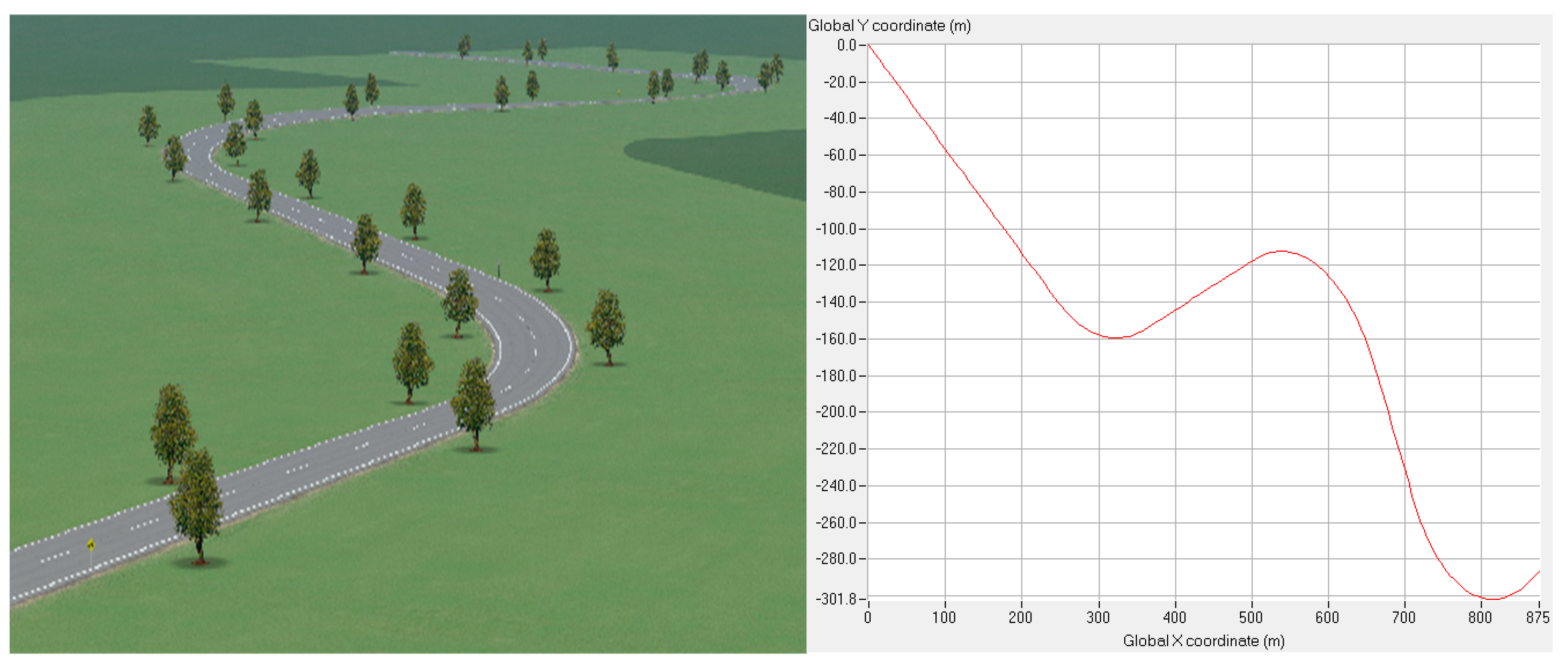
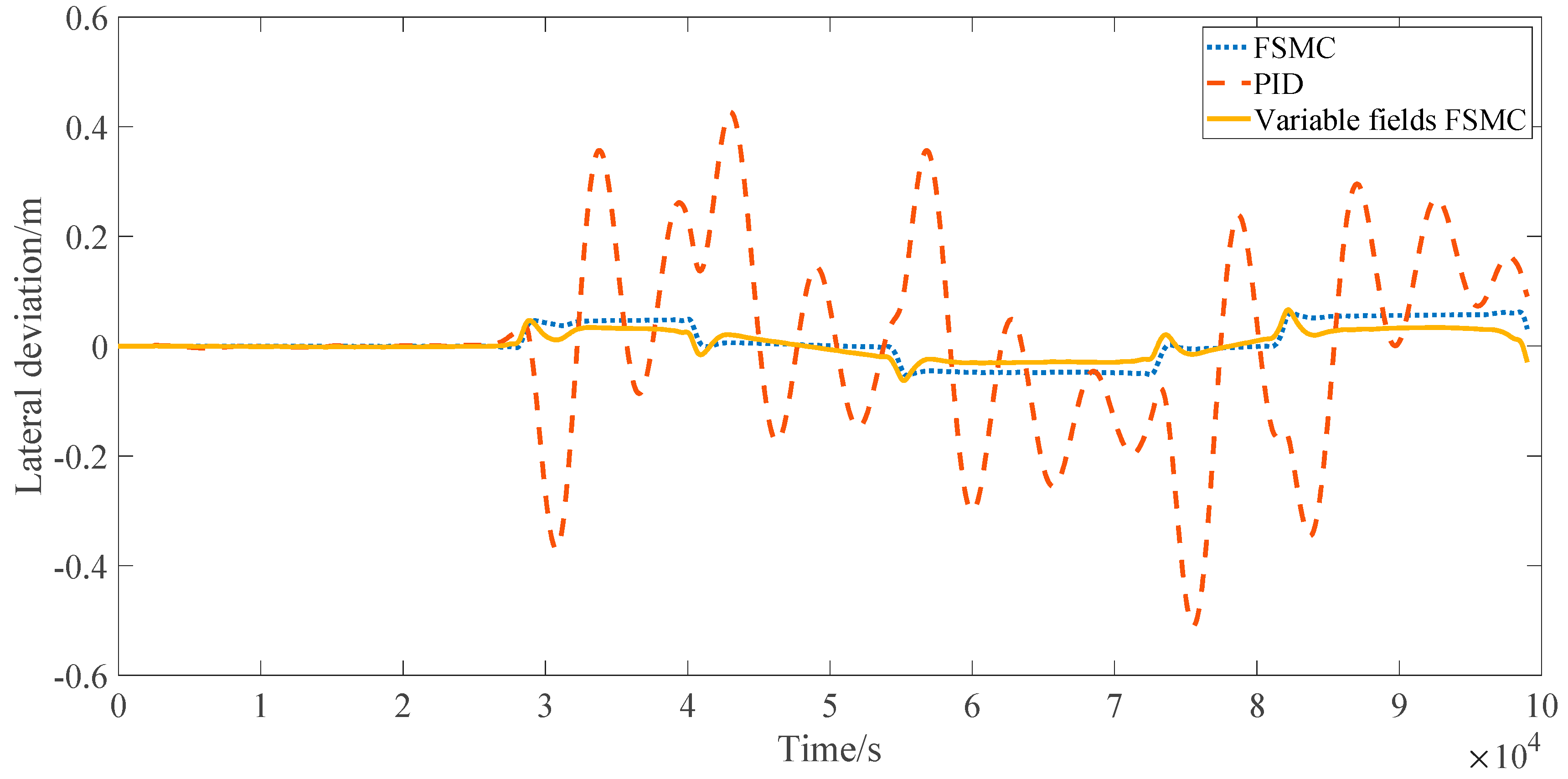
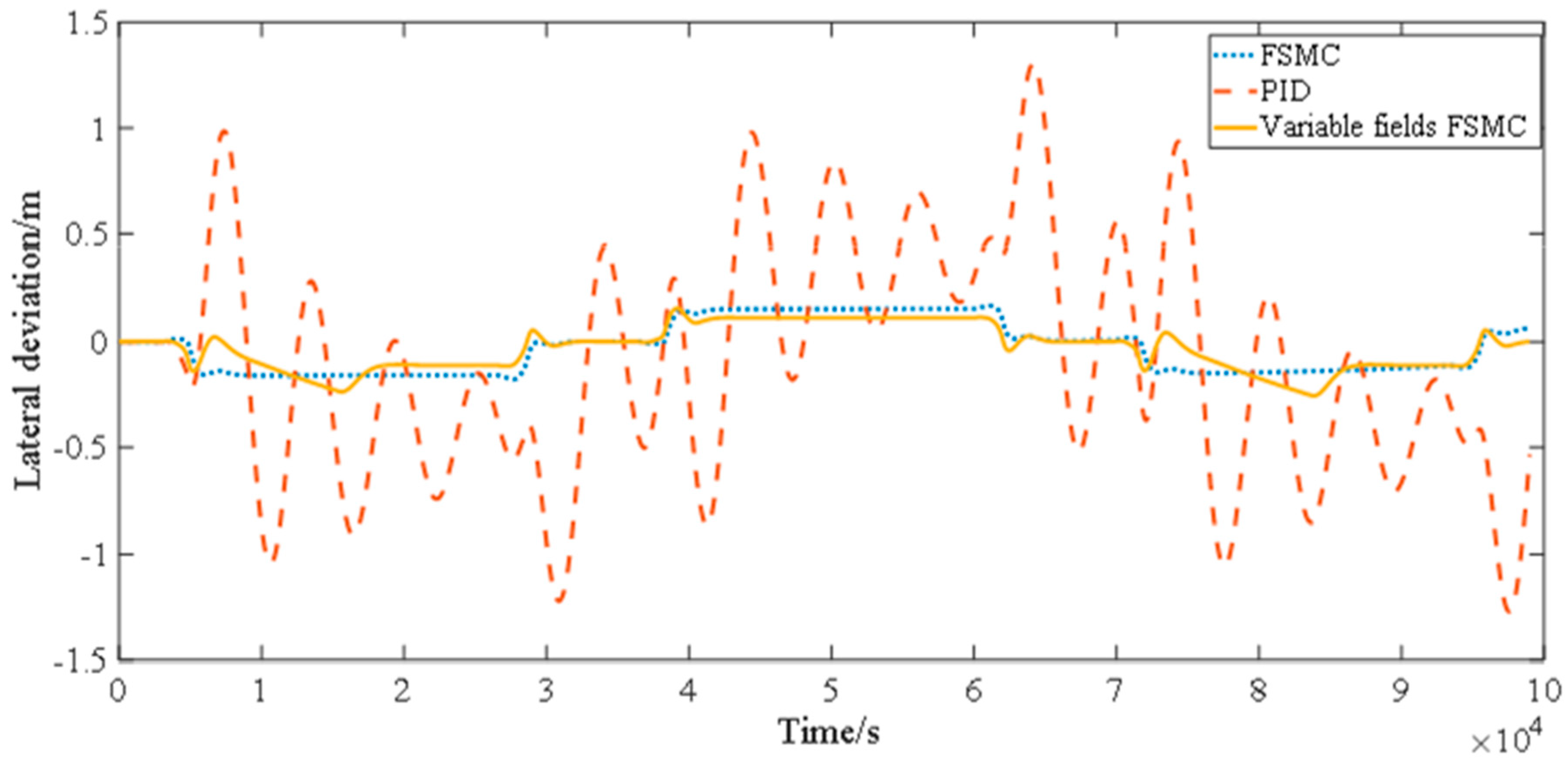
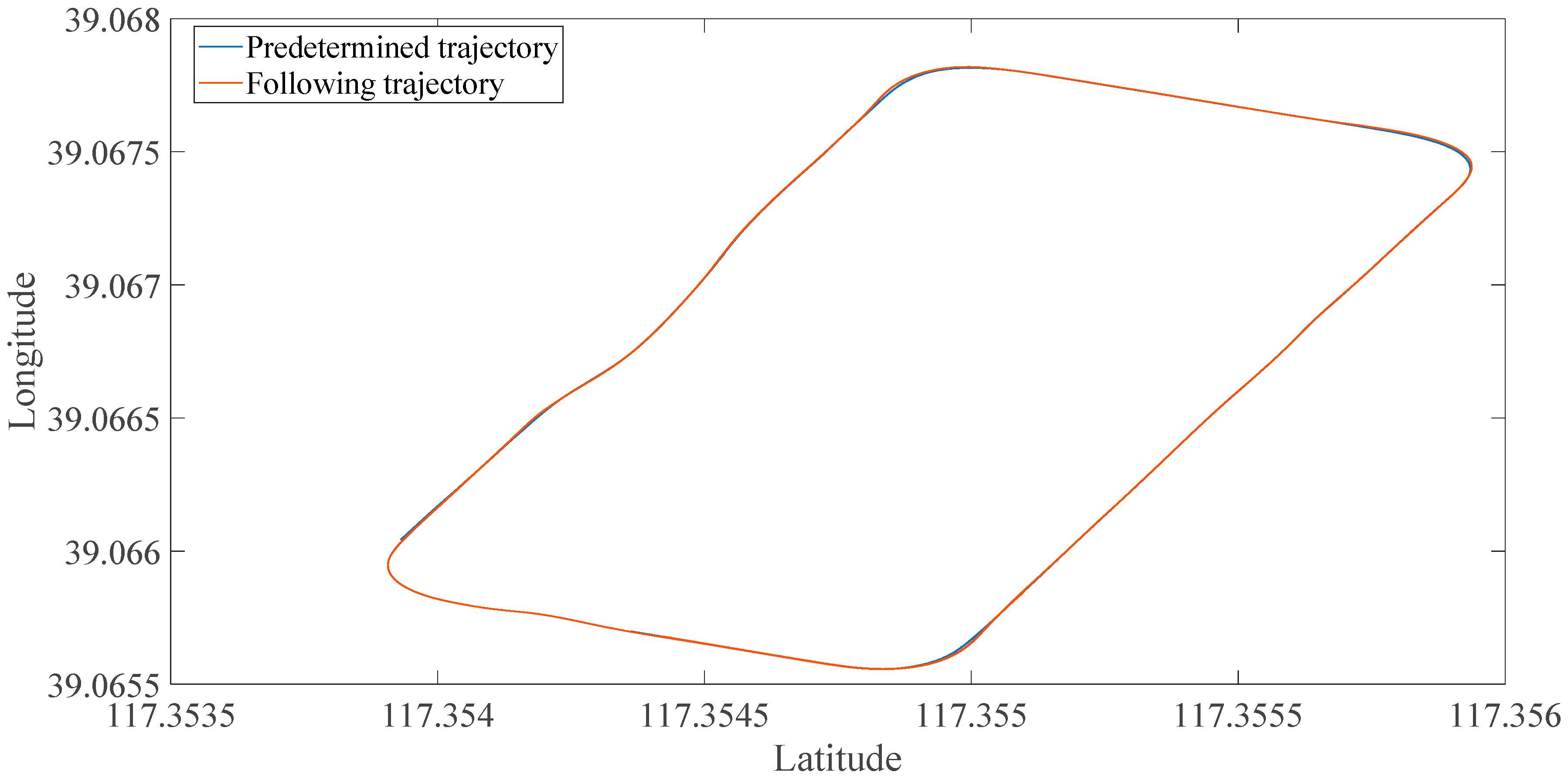
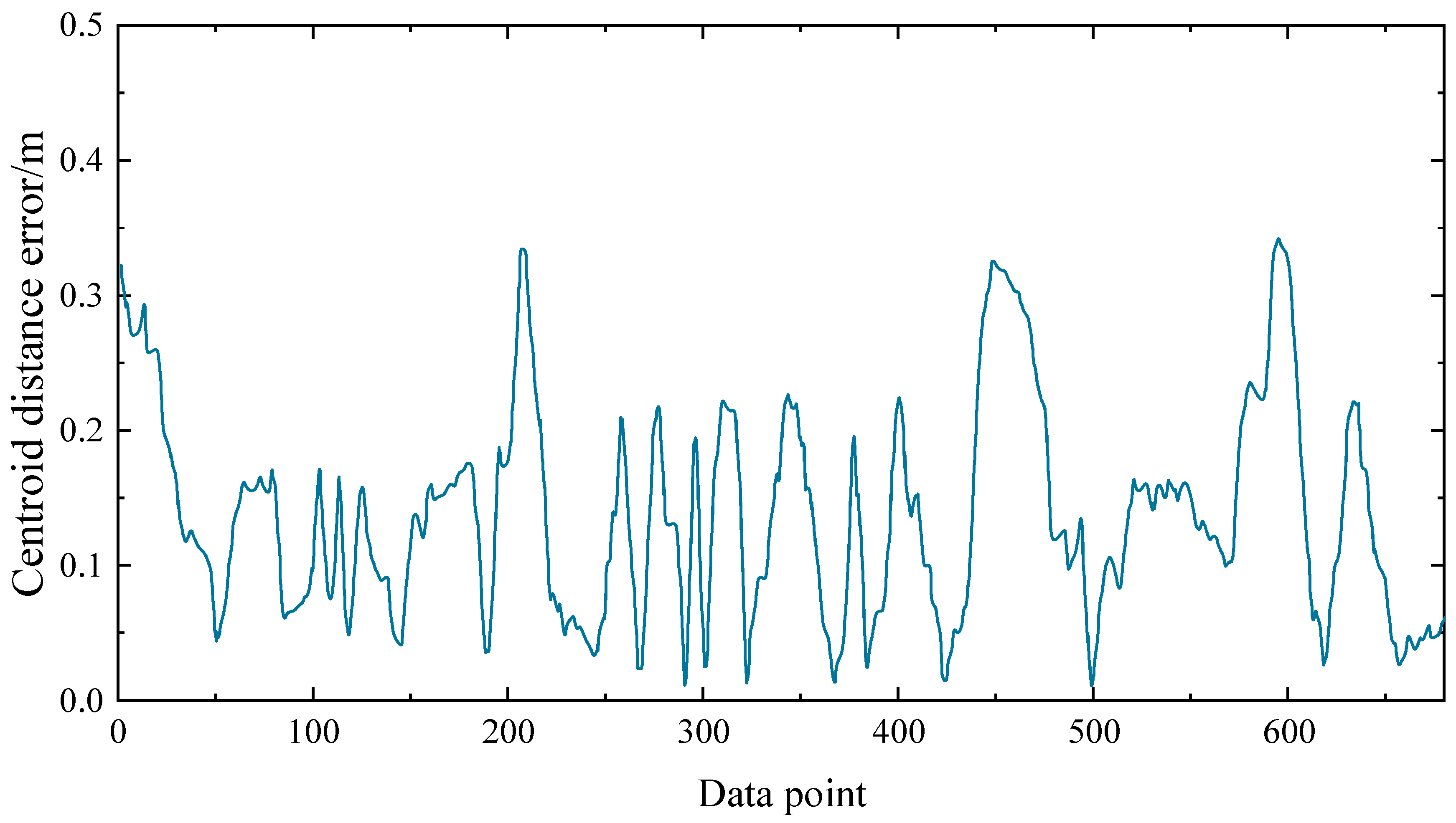
4.1. Oval Lane Test
4.2. FHWA Lane Test
4.3. “8” Lane Test
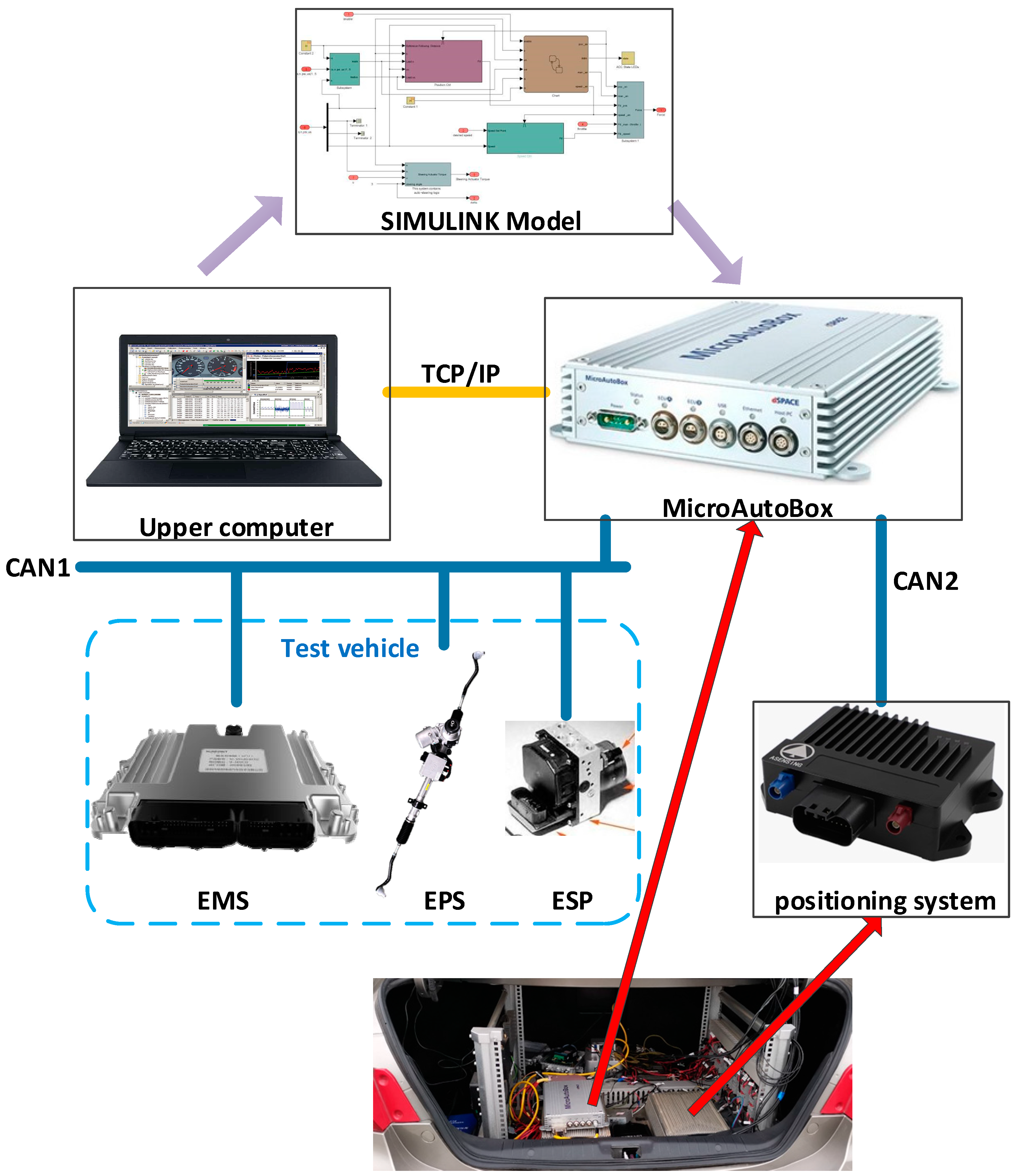
4.4. Real Vehicle Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Lu, W.; Dong, J.; Zhang, P. Research on vision enhancement system of military vehicle driver based on uncooled infrared detection technology. Appl. Opt. 2019, 40, 1033–1038. [Google Scholar]
- Xia, X.; Wang, H.; Li, X. Research on high precision automatic leveling control system of a military radar vehicle. Mech. Des. Manuf. 2019, 9, 158–160. [Google Scholar]
- Lu, H.; Xing, Y.; Zhuo, G. Review on Motion Control of Autonomous Vehicles. Available online: http://kns.cnki.net/kcms/detail/11.2187.th.20200416.1728.010.html (accessed on 6 June 2021). [CrossRef]
- Ding, N.; Ran, X.; Zhang, H. Driver model for single track vehicle based on single point preview optimal curvature model. J. Mech. Eng. 2008, 44, 220–223, 228. [Google Scholar] [CrossRef]
- Dong, T. Lane keeping system based on improved preview driver model. Pract. Automob. Technol. 2019, 24, 143–145. [Google Scholar]
- Ren, D.; Cui, S.; Wu, H. Preview control of lane keeping and its steady state error analysis. Automot. Eng. 2016, 38, 192–199. [Google Scholar]
- Xu, S.; Peng, H. Design, analysis, and experiments of preview path tracking control for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 21, 48–58. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, H. A study on lateral control method for the path tracking of intelligent vehicles. Automot. Eng. 2011, 33, 382–387. [Google Scholar]
- Pan, Z. Research on Motion Control Approaches of Autonomous Vehicle in Urban Environments; University of Science and Technology of China: Hefei, China, 2012. [Google Scholar]
- Marino, R.; Scalzi, S.; Netto, M. Nested PID steering control for lane keeping in autonomous vehicles. Control. Eng. Pract. 2011, 19, 1459–1467. [Google Scholar] [CrossRef]
- Silva, M.; Garrote, L.; Moita, F. Autonomous electric vehicle: Steering and path-following control systems. In 2012 16th IEEE Mediterranean Electrotechnical Conference; IEEE: Manhattan, NY, USA, 2012; pp. 442–445. [Google Scholar]
- Guo, J.; Luo, Y.; Li, K. An Adaptive Hierarchical Trajectory Following Control Approach of Autonomous Four-Wheel Independent Drive Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2482–2492. [Google Scholar] [CrossRef]
- Ackermann, J.; Guldner, J.; Sienel, W. Linear and nonlinear controller design for robust automatic steering. IEEE Trans. Control. Syst. Technol. 1995, 3, 132–143. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, X.; Xiong, L. Dynamic Control for Unmanned Skid-steering Vehicle with Conditional Integartors. J. Mech. Eng. 2017, 53, 29–38. [Google Scholar] [CrossRef]
- Tagne, G.; Talj, R.; Charara, A. Higher-order sliding mode control for lateral dynamics of autonomous vehicles, with experimental validation. In 2013 IEEE Intelligent Vehicles Symposium (IV); IEEE: Manhattan, NY, USA, 2013; pp. 678–683. [Google Scholar]
- Ji, X.; He, X.; Lv, C. Adaptive-neural-network-based robust lateral motion control for autonomous vehicle at driving limits. Control. Eng. Pract. 2018, 76, 41–53. [Google Scholar] [CrossRef]
- Falcone, P.; Borrelli, F.; Asgari, J.; Tseng, H.E.; Hrovat, D. Predictive Active Steering Control for Autonomous Vehicle Systems. IEEE Trans. Control. Syst. Technol. 2007, 15, 566–580. [Google Scholar] [CrossRef]
- Falcone, P.; Borrelli, F.; Tseng, H.E.; Asgari, J.; Hrovat, D. Linear time-varying model predictive control and its application to active steering systems: Stability analysis and experimental validation. Int. J. Robust Nonlinear Control. 2008, 18, 862–875. [Google Scholar] [CrossRef]
- Falcone, P.; Tseng, H.E.; Borrelli, F.; Asgari, J.; Hrovat, D. MPC-based yaw and lateral stabilisation via active front steering and braking. Veh. Syst. Dyn. 2008, 46, 611–628. [Google Scholar] [CrossRef]
- Gong, J.; Jiang, Y.; Xu, W. Model Predictive Control of Unmanned Vehicles; Beijing University of Technology Press: Beijing, China, 2014. [Google Scholar]
- Guo, H.; Liu, J.; Cao, D.; Chen, H.; Yu, R.; Lv, C. Dual-envelop-oriented moving horizon path tracking control for fully automated vehicles. Mechatronics 2018, 50, 422–433. [Google Scholar] [CrossRef] [Green Version]
- Kim, E.; Kim, J.; Sunwoo, M. Model predictive control strategy for smooth path tracking of autonomous vehicles with steering actuator dynamics. Int. J. Automot. Technol. 2014, 15, 1155–1164. [Google Scholar] [CrossRef]
- Nam, H.; Choi, W.; Ahn, C. Model predictive control for evasive steering of an autonomous vehicle. Int. J. Automot. Technol. 2019, 20, 1033–1042. [Google Scholar] [CrossRef]
- Ge, S.S.; Lee, T.H.; Hang, C.C.; Zhang, T. Stable Adaptive Neural Network Control; Kluwer Academic Publishers: New York, NY, USA, 2001. [Google Scholar]
- Wai, R.-J.; Lin, C.-M.; Hsu, C.-F. Adaptive fuzzy sliding-mode control for electrical servo drive. Fuzzy Sets Syst. 2004, 143, 295–310. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Liang, J.; Jiang, H.; Cai, Y.; Xu, X. Stability Research of Distributed Drive Electric Vehicle by Adaptive Direct Yaw Moment Control. IEEE Access 2019, 7, 2169–3536. [Google Scholar] [CrossRef]

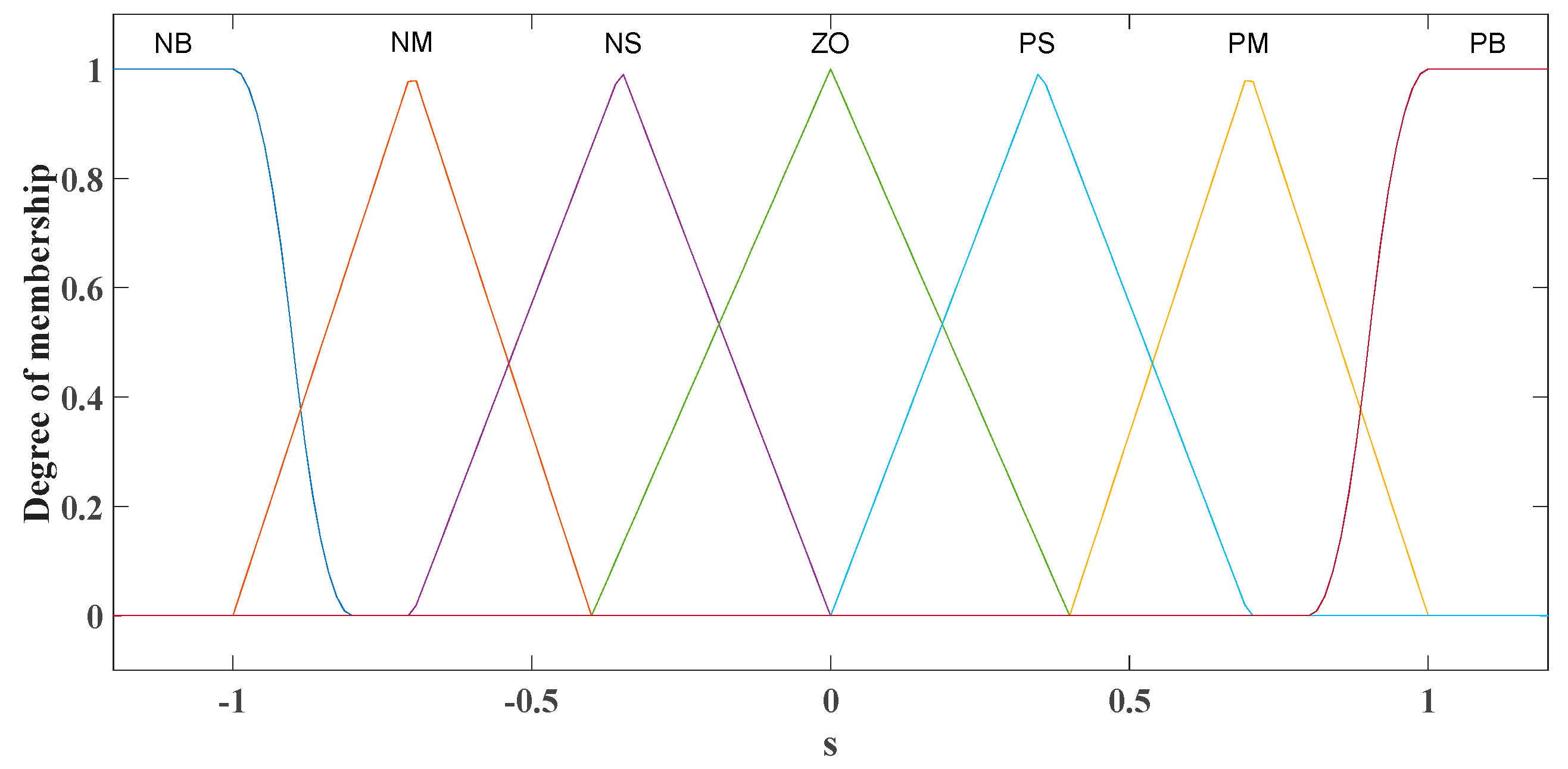
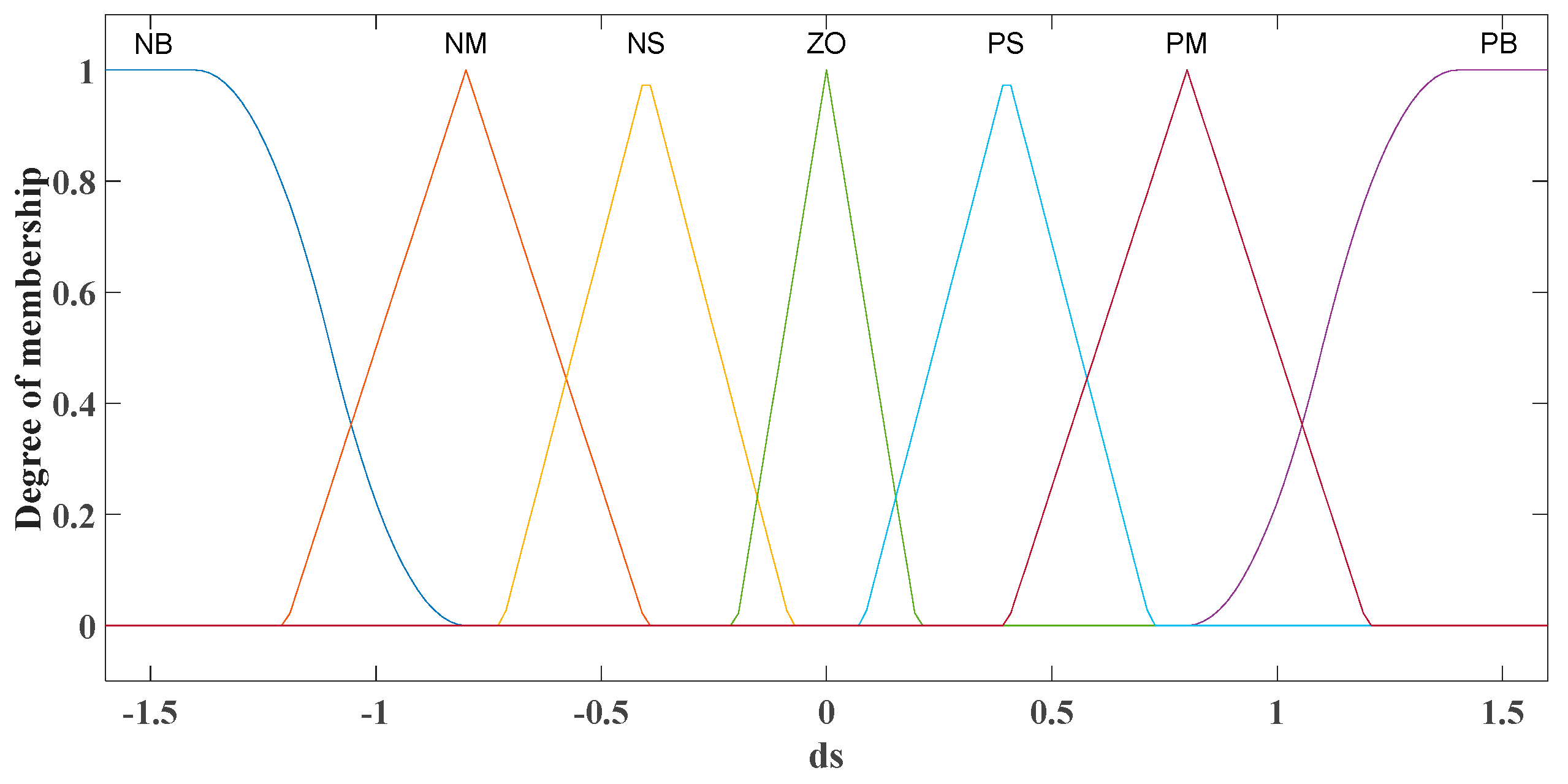
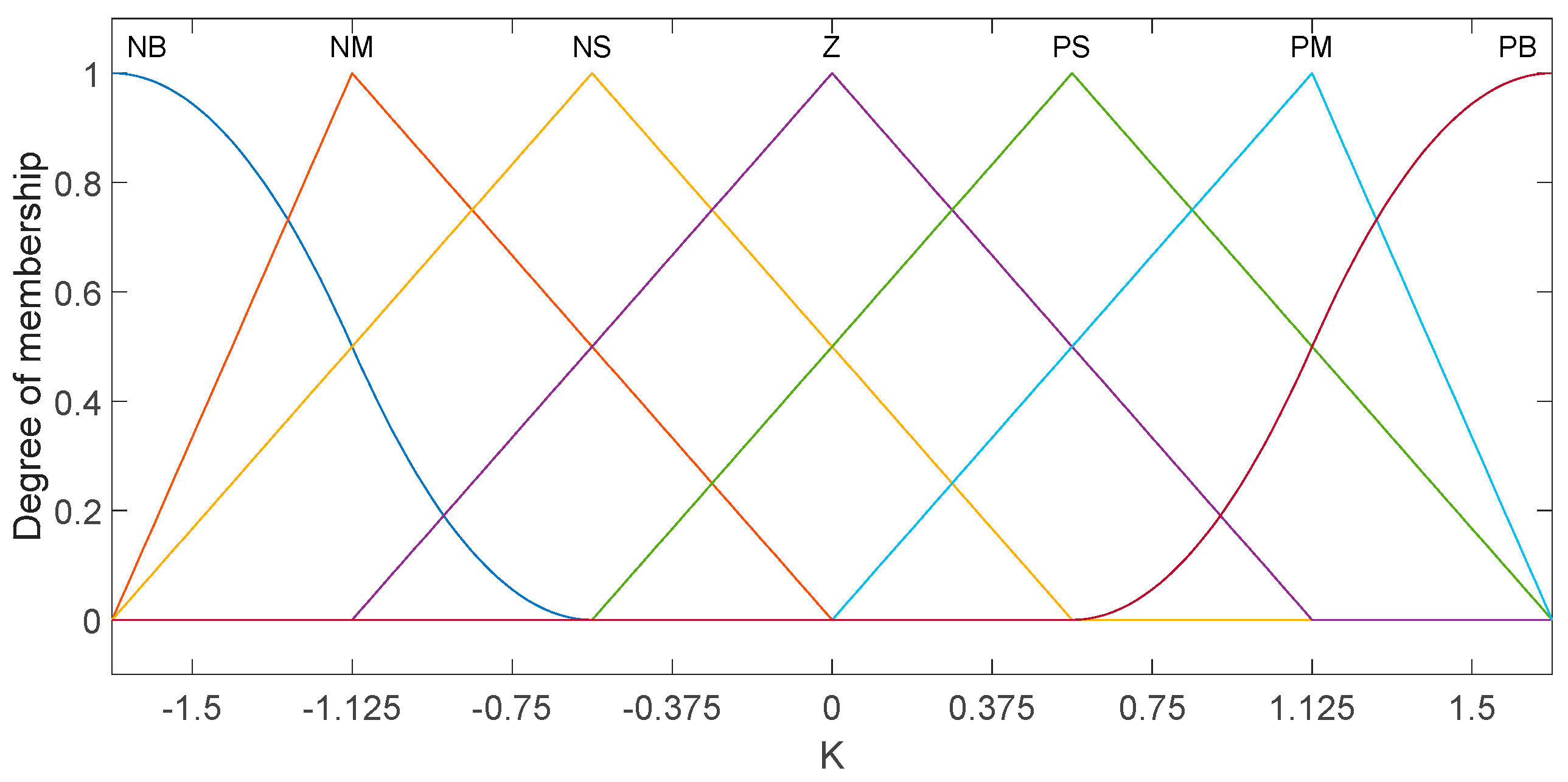





| NB | NM | NS | ZO | PS | PM | PB | |||
|---|---|---|---|---|---|---|---|---|---|
| k | |||||||||
| s | |||||||||
| NB | NB | NB | NM | ZO | PM | PB | PB | ||
| NM | NB | NM | NS | ZO | PS | PM | PB | ||
| NS | NM | NS | NS | ZO | PS | PS | PM | ||
| ZO | ZO | ZO | ZO | ZO | ZO | ZO | ZO | ||
| PS | PM | PS | PS | ZO | NS | NS | NM | ||
| PM | PB | PM | PS | ZO | NS | NM | NB | ||
| PB | PB | PB | PM | ZO | NM | NB | NB | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yang, X.; Liang, J.; Xu, X.; Sun, X. GPS Path Tracking Control of Military Unmanned Vehicle Based on Preview Variable Universe Fuzzy Sliding Mode Control. Machines 2021, 9, 304. https://doi.org/10.3390/machines9120304
Zhang H, Yang X, Liang J, Xu X, Sun X. GPS Path Tracking Control of Military Unmanned Vehicle Based on Preview Variable Universe Fuzzy Sliding Mode Control. Machines. 2021; 9(12):304. https://doi.org/10.3390/machines9120304
Chicago/Turabian StyleZhang, Houzhong, Xiangtian Yang, Jiasheng Liang, Xing Xu, and Xiaoqiang Sun. 2021. "GPS Path Tracking Control of Military Unmanned Vehicle Based on Preview Variable Universe Fuzzy Sliding Mode Control" Machines 9, no. 12: 304. https://doi.org/10.3390/machines9120304
APA StyleZhang, H., Yang, X., Liang, J., Xu, X., & Sun, X. (2021). GPS Path Tracking Control of Military Unmanned Vehicle Based on Preview Variable Universe Fuzzy Sliding Mode Control. Machines, 9(12), 304. https://doi.org/10.3390/machines9120304





