Abstract
Nowadays, traffic congestion has become a significant challenge in urban areas and densely populated cities. Real-time traffic signal control is an effective method to reduce traffic jams. This paper proposes a particle swarm optimisation with linearly decreasing weight (LDW-PSO) to tackle the signal intersection control problem, where a finite-interval model and an objective function are built to minimise spoilage time. The performance was evaluated in real-time simulation imitating a crowded intersection in Dalian city (in China) via the SUMO traffic simulator. The simulation results showed that the LDW-PSO outperformed the classical algorithms in this research, where queue length can be reduced by up to 20.4% and average waiting time can be reduced by up to 17.9%.
1. Introduction
Nowadays, with the industrialization of the world, the population in cities has grown exponentially. The urban areas will accommodate about 68% of the world’s population by 2050, according to a forecast of the world urbanisation, undertaken by the United Nations (U.N.) in 2018 [1]. This increasing population has brought many problems to the developing cities, such as traffic congestions, environmental pollution, safety, and fuel wastage [2,3,4]. According to [5], in 2014, congestion cost North Americans approximately an extra 6.9 billion hours to travel, consuming around 3.1 billion litres of additional fuel, resulting in a waste of 160 billion dollars.
Developing strategies to control or reduce vehicular traffic problems mainly involves solutions in two areas: infrastructure reconstruction and city topology optimisation. But in many cases, this is infeasible and always expensive. Hence, researchers have proposed other strategies to deal with these problems. One of these is traffic signal control. It is possible to divide the exiting traffic signal systems into two subgroups: fixed-cycle or adaptive signal control systems [6]. To a significant extent, the inefficiency of today’s traffic signal systems, which primarily use fixed-cycle signal control systems, leads to traffic congestion. All control parameters in the fixed-cycle signal control system, including cycle length, phase duration, and sequence, are preset offline according to historical traffic flow information, regardless of the number of vehicles. Although it has an excellent performance in traffic regimes with constant traffic flow or small fluctuations [7], the adaptability of this control method to traffic fluctuations is limited. Thus, it is impossible to treat with sudden changes in traffic flow [8]. Fixed-cycle methods’ major disadvantage is open-loop control since they can not adapt to real-time traffic fluctuations. And when the traffic condition changes, fixed-cycle approaches may aggravate the congestion. Therefore, the fixed-cycle signal control system is highly sub-optimal and needs to be replaced by better closed-loop methods.
Recently, an adaptive signal control system, which is still widely used commercially, has been proposed. The traffic regimes obtained from loop detectors or other traffic sensors can change the cycle length, phase splits, and sequence reasonably. The fluctuations of these changes are limited to a predetermined fixed range. Current research efforts in the field of adaptive traffic signal control are directed to two main initiatives. On the one hand, the automatic model of adaptive signal control is designed to change the control strategy when traffic regimes change. It depends on the use of traffic sensors and the real-time calculation of traffic flow. Although these tools have been operated successfully in several cities worldwide, the actual management of the traffic network usually causes a high operational cost. Besides, traffic flow in the real world tends to repeat traffic patterns, such as rush hour and holidays.
On the other hand, modern simulators [9] have great significance in traffic management since they can provide researchers with immediate traffic flow information and reliable solutions. Many studies in traffic flow simulation have been performed representing both macroscopic [2] and microscopic [10] traffic flow. Over the past few years, efforts have concentrated on combing accurate microscopic modelling of traffic flow with heuristic algorithms. Bio-inspired computation has been proven to solve complex problems with a non-polynomial computational complexity in real-world applications, especially in programming traffic signal cycles; see [11,12,13,14,15].
Several features led us to use PSO instead of other optimisation methods. First, PSO is a well-known algorithm that performs fast convergence to optimal solutions [16]. It is a highly desirable property for an optimal traffic signal cycle program, where new traffic signal schedules must be updated immediately when traffic regimes change. Second, the canonical PSO is easy to implement and adjust because of the few required parameters [17]. Third, in recent years, many researchers have demonstrated that the PSO algorithms and variants of PSO have successful applications in traffic signal optimisation [4].
The main contributions of this paper are as follows:
- Combing SUMO and LDW-PSO, a new model is proposed to reduce queue length and average waiting time in an isolated intersection with hundreds of vehicles. Besides, the objective function’s property is evaluated by this paper.
- Our experiment with traffic data is analysed under three conditions: under saturated, saturated, and oversaturated, compared with previous works only considering one specific scenario. Besides, more than 900 vehicles are simulated in oversaturated conditions to represent the high load state, which is a big challenge.
- Further comparisons against B.A., standard PSO optimisation method justify the property of the LDW-PSO. In this paper, the results obtained by LDW-PSO are compared with B.A., which is rarely compared by previous studies.
The rest of this paper is organised as follows: after the introduction, Section 2 presents the related work. Section 3 presents the microscopic simulator SUMO and the algorithms compared. Section 4 describes the objective function of the simulation model used to optimise real-time traffic signals. The experimental setup and the results of the simulation are presented in Section 5. Lastly, concluding remarks and future works are given in Section 6.
2. Related Work
Traditional metaheuristic algorithms have become very popular for solving traffic signal control problems related to biologically inspired techniques. In [18], a bi-level model based on the Stackelberg game was used to solve traffic signal optimisation problems. Bat algorithm was compared with ant colony optimisation, genetic algorithm, and hybrid algorithm in different node conditions. The article indicated that B.A. explored a wide range of solutions, although it did not get the best average wait time. An ant colony algorithm (ACA) [19] has been proposed for traffic light timing. The uncertainty and convergence of ACA were analysed numerically, although in the scope of one simple traffic intersection with a 2-phase lighting system. Focusing on two large and heterogeneous urban scenarios located in Malaga and Seville, Olivera et al. [15] experimented with hundreds of traffic lights to optimise the traffic lights timing programs through particle swarm optimisation (PSO). They used a mono-objective function based on the traffic emission model to reduce fuel consumption and gas emissions, although they did not consider the vehicular flow for sections for heavy traffic.
Besides traditional algorithms, some new optimisation algorithms are also applied in traffic signal control problems successfully. Celtek et al. [20] used social learning-particle swarm optimisation (SL-PSO) to optimise the traffic control problem in Kilis city of Turkey. In the cases of different particles and iterations, the performance of SL-PSO was tested compared to PSO. The improvement in average travel time had proven the success of SL-PSO for traffic control problems. In [21], the micro artificial system (MAIS) was developed to reduce pollution rates for a specific region of Mexico City by optimising vehicular flow. After the optimisation process, the vehicle’s waiting time was decreased and the speed was increased, leading to a decrease in fuel consumption and environmental pollution. Besides, the reason for the improved performance of the MAIS was analysed. Refs. [20,21] applied new meta-heuristic algorithms to the traffic control problem and achieved significant results. And this is the first of SL-PSO and MAIS to be used as a traffic signal optimiser.
Some efforts have concentrated on using multi-objective evolutionary methods to deal with this problem. Perez et al. [22] used a specific methodology combing simulation and multi-objective evolutionary methods to optimise the traffic signal control problem in the city of Montevideo in Uruguay. Significant improvements in travel times and pollution had been achieved because the specific methodology allowed exploring the whole search space of possible configurations. A similar task was done by Damay [23], who used a multi-objective genetic algorithm and SUMO optimising durations of the green light phases to reduce emissions and improve vehicular flow in the city of Route in France.
3. Background
3.1. Simulaiton of Urban Mobility
Many algorithms applied in Traffic Signal Control System (TSCS) have been proposed and developed in recent years. So, the real fields or simulator platforms are required to test and evaluate them. If doing this in real fields, it will be sophisticated and time-consuming work. Thus, traffic simulators are widely used for designing and evaluating in TSCS. SUMO is an open-source microscopic multi-modal traffic simulator that can simulate different types of traffic flow and provide output for future tests and analysis. One of its features is the modeling of traffic systems, specifically public transport, road vehicles, and pedestrians. Each vehicle is modelled explicitly, has its own route, and moves individually, so SUMO is purely microscopic. The simulation created using SUMO needs three main components: road network (.net.xml), route (.rou.xml) and configuration (.sumocfg) flies. The road network file contains objective road information such as road and lane details, traffic signal and phase information. It supports importing a digital map of a road network from an original map view (see Figure 1a) and the SUMO network (see Figure 1b). The routes of vehicle flow on the road network are defined by the route file, which can be created using existing origin-destination matrices or manually. All the characteristics of the vehicles are included, such as their speed, length, acceleration. The configuration file is used to combine the road network and route file as well as some additional files. One of the main advantages of SUMO is that many details of each vehicle, such as waiting time, position, and average speed can be obtained. Thus, it is possible to implement any algorithm to determine the programming of the traffic signal.
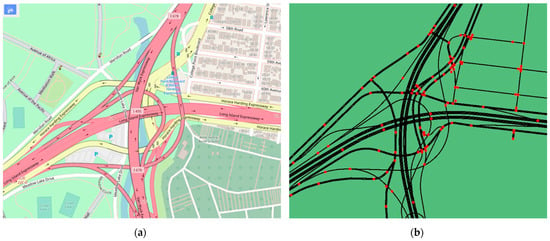
Figure 1.
Example of converting a map in OpenStreetMap. (a) Original map view of OpenStreetMap. (b) Network imported into SUMO.
3.2. Optimization Algorithms
Compared with [24], the optimisation strategy of this paper is carried out by LDW-PSO, which aims to find the optimal or “almost optimal” traffic signal cycle program. This section explains the definitions and general frameworks of B.A., standard PSO, and LDW-PSO.
Inspired by the behaviours and characteristics of micro-bats, Yang [25] proposed the standard B.A. in 2010. For each bat (), its position () and velocity (vi) in a d-dimensional search space should be defined initially, which are subsequently updated during the iterations. The general framework of B.A. is shown in Algorithm 1.
| Algorithm 1. B.A.—Bat Algorithm. | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. | |
| 11. | |
| 12. | end if |
| 13. | |
| 14. | |
| 15. | if (bfnew < bf&uniform(0,1) < A) do |
| 16. | |
| 17. | |
| 18. | end if |
| 19. | end while |
| 20. | |
| 21. | end while |
Eberhart and Kennedy developed standard PSO, a population-based metaheuristic optimisation technique [26], in 1995. Inspired by birds, standard PSO assumed that each particle () can use global and local best values to update its position () and velocity (). The definition of position and velocity for a standard PSO are as follows:
where:
- is the local best solution of particle
- is the global best solution of all particles
- and refer to the position of particle in iteration and
- and represents the velocity of particle in iteration and
In Equation (1), the is called the inertia weight of the particle. Inertia weight indicates how much of the previous speed is taken from the previous time step. Shortly, inertia weight is used to balance the global and local search capability of the PSO. Large inertia weight makes the global search easier while small weight makes the local search easier. Usually in standard PSO, . The linearly decreasing weight is used in this paper because with PSO it is easy to be precocious and oscillate near the global optimal solution in the later stage. The inertia weight decreases linearly through the optimisation process by using the following equation:
where:
- is the initial weight
- is the maximum weight
- refers to the total iterations
- refers to the current iteration
The general framework of LDW-PSO is shown in Algorithm 2.
| Algorithm 2. LDW-PSO—Particle Swarm Optimization with Linearly Decreasing Weight. | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. | |
| 11. | |
| 12. | |
| 13. | |
| 14. | |
| 15. | end if |
| 16. | end while |
| 17. | |
| 18. | end while |
4. Objective Function of the Simulation Model
This section explains the objective function, which is a minimisation function. We take the fitness function designed by Jintamuttha et al. (see [24]), but with some changes for our simulation model. We change the reward part of the number of vehicles passing through the intersection, related to Equations (11)–(13). The main task is to determine the proper phase duration of the traffic signal, which can minimise queue length and average waiting time to maintain efficient traffic flow on the intersection. In this study, the programming of phase duration is represented by a solution vector, which SUMO supports. Each element of the solution vector represents a phase duration of a state at an intersection.
In this study, each particle of LDW-PSO represents one solution vector. The following fitness equation evaluates each solution vector containing the optimal cycle values. The objective function is to minimise spoilage time at an isolated intersection for a phase duration, which is regarded as a solution vector.
The spoilage time is defined as three components’ discrete-time summation (): waiting time (), loss of start-stop time (), and time reward (), as shown in (5).
where:
- refers to the index of all phases in a traffic cycle.
- represents the duration of the green time on phase .
- is the index of discretised green time duration of phase .
Since the maximum range of cycle time is suggested to take between 60 s and 120 s, the effective green time of each phase should be limited between lower boundary () and upper boundary (), as shown in (6).
Before introducing three components of the spoilage time, two concepts should be explained with Figure 2: vehicular route and traffic road. Figure 2 shows an isolated intersection that is in a specific phase. The isolated intersection is combined with four roads; each of them has 2 incoming and 2 outcoming lanes. In this phase, the vehicular routes that allow vehicles to cross the intersection are indicated by green lines. A vehicular route from road heading to road is represented by relying on the schematic table that assigns route authority in phase . For example, assume in this phase, the route that allows vehicles from road 1 head to road 3 is represented by . Besides, the term is introduced as the traffic road of route . For example, in Figure 1, road 1 has two lanes where the lane1_1 has 2 possible outgoing routes (road and 3), and the lane1_2 has 1 provided route going to road . Given that all possible routes have equal traffic load, then , .
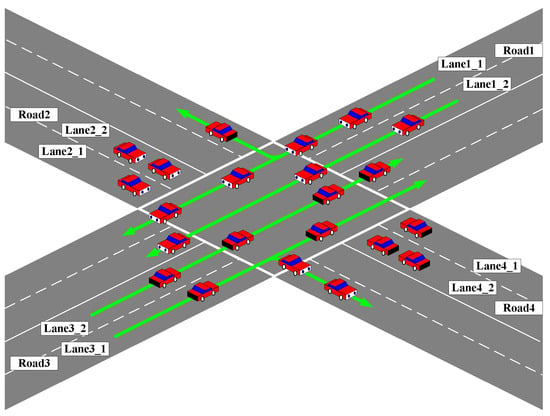
Figure 2.
An illustrative diagram of an isolated intersection.
The following Equation (7) is used to define the waiting time () at discretised time of phase .
where:
- represents all vehicular routes that allow vehicles to pass in phase .
- is the vehicle number of halting vehicles on route on time of phase , and a halting vehicle is defined as its speed below 0.1 m/s.
- refers to the waiting time of vehicle on time of phase . Specifically, the vehicle’s waiting time is accumulated over a specific time interval, rather than the time spent with a speed below 0.1 m/s since the last time it was faster than 0.1 m/s.
- is the previously defined traffic load from road heading to road .
The Equation (7) has the following limitation (8).
The term, loss of start-stop time (), reflects the time influenced by queue length. It is illustrated in (9):
where is the linear function represents the start-stop delay relying on the queue length. According to the observation of the simulation experiment, each vehicle in the queue has a 1-s delay. and play a similar role as defined in (7).
The number of halting vehicles on the route is limited by the capacity of road . Assume that is the maximum capacity of road , then the constraint of Equation (9) is shown as (10).
The last term represents the reward that the number of vehicles that can cross the intersection in phase . It is shown in (11).
where is the number of vehicles that can pass through the intersection in phase , it relies on that plays a similar role as defined in (7). In Equation (11), the value of is defined by (12).
where:
- is the total number of vehicles from heading to road , including halting vehicles and moving vehicles.
- represents the number of vehicles that can cross the intersection through the remaining time of phase .
- refers to the remaining capacity of road that can be changed over time but limited by the maximum capacity of the outgoing road as defined in (13).
5. Simulation and Results
5.1. Design of Experiment on SUMO
In this section, using LDW-PSO, the simulation is set to verify the model design and obtain some insightful information from the benchmark with B.A. [24] and standard PSO. First, the hardware and software condition used in this study is explained. Then the parameters used in the application and simulation are given.
In this study, LDW-PSO was used as an optimisation algorithm. Besides, B.A. and standard PSO were selected to compare with LDW-PSO to justify the property of the LDW-PSO. We chose B.A. as a comparison algorithm because it was rarely used in the traffic signal control problem. In [24], it was used in an isolated intersection scenario and obtained significant achievements. Thus, we wanted to make some improvements. As for standard PSO, acceleration coefficients and were set to 1.49445, and inertia weight was set to 0.729 as recommended in [26].
The simulation and three algorithms were applied on Python platform. SUMO traffic simulator was used in the Windows operation system for simulation. The simulation was performed using an Inter (R) Core (T.M.) i7-9750H CPU @ 2.6 GHz processor and 16.00 GB RAM. The Traci API of SUMO was used to retrieve simulated objects’ values and manipulate their behaviours instantly via the programmed optimisation algorithms. The process will ultimately achieve the satisficing of the real-time traffic signal control as designed. The theory of simulation using the SUMO traffic simulator is shown in Figure 3.
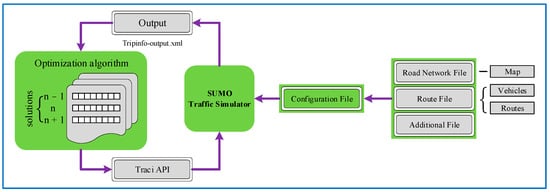
Figure 3.
Theory of simulation using SUMO traffic simulator.
The simulation was conducted based on the simulated traffic environment from a crowded intersection in Dalian city in China. Four ways are gathered to the intersection whose information is shown in Table 1. The managed 4-phase authority is shown in Figure 4.

Table 1.
Information of intersection.
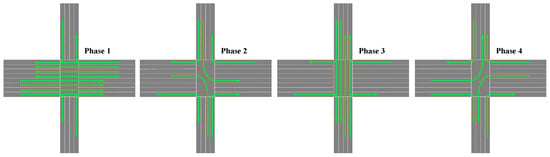
Figure 4.
Route authority of the intersection.
Because of the nature of the intersection where East and West are the main streams of the whole traffic, most of the vehicles from East and West will keep straight, and most of the vehicles from North and South will turn left and right. The specific percentage of outgoing flow from each arriving path is shown in Table 2.

Table 2.
Percentage of outgoing flow.
When the traffic regime changes, the efficiency of existing control goes down. Thus, this paper’s traffic data used for testing contains three conditions: under saturated, saturated, and oversaturated. As shown in Table 3, the model’s performance and algorithm can be better evaluated through these three conditions.

Table 3.
Proportion of simulation type.
We assumed that the distribution pattern of all vehicles arriving at the intersection from every path follows the Poisson function for the simulation. With arrival rate , Type One is under saturated condition, where vehicles from West and East are almost equal to those from North and South. With arrival rate , Type Two represents the saturated condition, where West and East have 3 times the arrivals as North and South. With arrival rate , Type Three represents the oversaturated condition where the number of vehicles from narrower paths (North and South) has increased.
The number of vehicles that can pass through the intersection will be limited by the remaining capacity . The dynamicity of an outgoing route’s available capacity is defined by the Poisson distribution with for Type One, for Type Two and for Type Three.
Table 4 summarises the totality of the vehicle, B.A., standard PSO, and LDW-PSO simulations considered. In this paper, the experiment simulation was executed for a finite period of 10 cycles per run because we wanted to simulate an infinite cycle to ensure effective traffic signal control.

Table 4.
Simulation, Vehicle, B.A., standard PSO, and LDW-PSO.
5.2. Results and Discussions
The results and the analyses are presented in this section from several viewpoints. As stated in the introduction, we mainly focus on queue length and average waiting time in this work. These two factors are the most common embodiment of congestion at an isolated intersection. To study the improvement of our proposal, we focus on the comparisons between the two algorithms. And all the results and distributions of three different conditions are based on the 8 selected runs (out of 12).
To show a first explanation view of the internal behaviours of LDW-PSO, Figure 5 plots the trace progress of the 8 independent runs of our technique when dealing with the three conditions. In these plots, we can observe that the computed solutions are close in quality, but there are some differences. As for Type One, the range of the final solutions of best fitness is around 1900. Similar behaviors can be observed for Type Two and Type Three, where the best fitness range of the solution is around 3500 and 35,000.
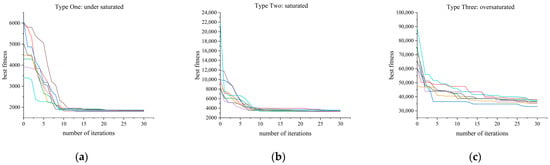
Figure 5.
Trace progress of the best fitness values in 8 independent runs of LDW-PSO. (a) Type One; (b) Type Two; (c) Type Three.
The comparison of distribution fitness and computational time can be obtained from Figure 6, where Figure 6a represents the boxplot of the distribution fitness, and Figure 6b represents the boxplot of the distribution computational time of the complete optimisation process. As expected, we can observe that both the mean fitness value and the mean computational time obtained by the three algorithms increase with the number of vehicles from Type One to Type Three. From a graphical point of view, the data distribution of LDW-PSO in Figure 6a shows better lower quartiles, medians, means and upper quartiles than B.A. and standard PSO. Figure 6b shows that the computational time obtained by LDW-PSO in Type Two is lower than that obtained by B.A. and standard PSO, but Type One and Type Three’s results are the opposite. However, the mean value of computational times of these two types for the standard PSO and LDW-PSO algorithms is not much different, and the range is in 5~8%, while the improvement of Type Two is 14.6%. We notice that in Type One, the computational time of B.A. is significantly lower, and the reason is that the solutions obtained by B.A. are trapped in the lower boundary because the lower boundary is a local optimal solution.
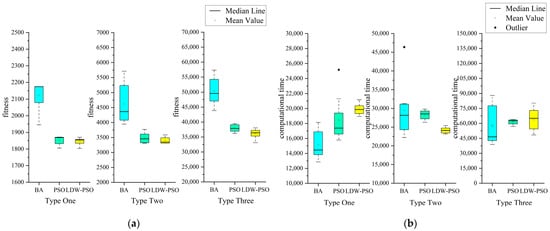
Figure 6.
Boxplot representation of distribution results. (a) fitness; (b) computational time.
Figure 7 shows the comparison of average phase durations and their error bars obtained by the three algorithms. In Figure 7, it is obverted that the total phase durations increase with the number of vehicles. Besides, except for Type One, the error bars of phase durations obtained by standard PSO and LDW-PSO are consistently lower than those obtained by B.A., representing the convergences and stabilities of standard PSO and LDW-PSO are better. For Type One, B.A. acquires shorter error bars because its results are trapped in the lower boundary. Thus, B.A. lacks the exploration of the optimal solution.

Figure 7.
Histogram representation of distribution results of the average phase durations and their error bars. (a) Type One; (b) Type Two; (c) Type Three.
In this paper, for each iteration step of three algorithms and individuals in the population, the information obtained from each simulation about both queue length and average waiting time had been saved. In this way, the progressive improvement from the initial solutions to the final ones in the traffic flow can be distinguished throughout the complete optimisation procedure. Figure 8 concerns the progressive reduction of queue length and average waiting time throughout the optimisation procedure of LDW-PSO. The mean values of B.A.’s and standard PSO’s best solutions are represented with dotted lines. In the initial stages of the optimisation process, we can clearly see that generated optimisation programs (by LDW-PSO) returned a high level of queue length and average waiting time for the three conditions. However, as the optimisation process reached the middle stages, they became lower, to stabilise in the final stages.
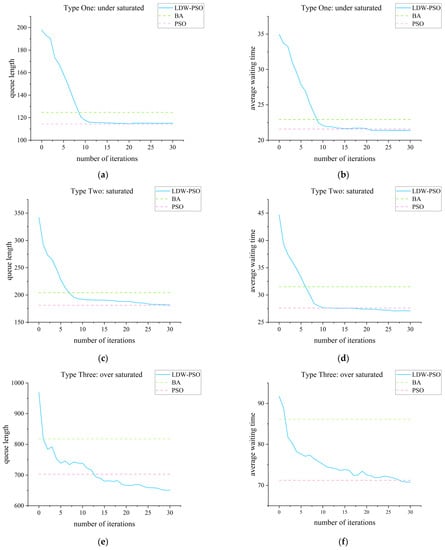
Figure 8.
Mean queue length and average waiting time of LDW-PSO solutions each iteration step. The mean values of B.A.’s and standard PSO’s best solutions are represented with dotted lines. (a) Type One’s mean queue length; (b) Type One’s mean average waiting time; (c) Type Two’s mean queue length; (d) Type Two’s mean average waiting time; (e) Type Three’s mean queue length; (f) Type Three’s mean average waiting time.
In three conditions, LDW-PSO always obtains better values than B.A. For Type One, the reduction obtained by LDW-PSO (compared to B.A.) is 7.7% for queue length and 6.7% for average waiting time. The reduction is 11.0% for queue length and 14.0% for average waiting time for Type Two. And for Type Three, the two values of reduction are 20.4% and 17.9%. Compared with standard PSO, the results obtained by LDW-PSO have a slight improvement. For Type One, the reduction obtained by LDW-PSO (compared to standard PSO) is −0.7% for queue length and 0.9% for average waiting time, which means standard PSO has a better optimisation effect than LDW-PSO for queue length. But our objective function is to minimise the weighted sum of queue length and average waiting time, so in terms of overall optimisation, LDW-PSO has a better effect. The reduction is −0.3% for queue length and 1.8% for average waiting time for Type Two. ForType Three, the two values of reduction are 7.4% and 0.7%. It is worth mentioning that the improvement reached by LDW-PSO (compared to B.A. and standard PSO) is higher in Type Three than in Type One and Type Two. It means LDW-PSO has a stronger ability to deal with complex situations with more vehicles.
To better show the micro-optimisation, the best optimisation process of LDW-PSO and B.A. for three conditions is shown in Figure 9. The mean values of queue length and average waiting time obtained by LDW-PSO and B.A. are also represented with dotted lines. Obviously, with the increase in the number of vehicles, the value of queue length and average waiting time is gradually increasing. It is unavoidable because the heavy traffic flow is a big challenge for the optimisation procedure. However, in most cases, solutions generated by LDW-PSO are lower than those generated by B.A. Thus, the improvement is noticeable.
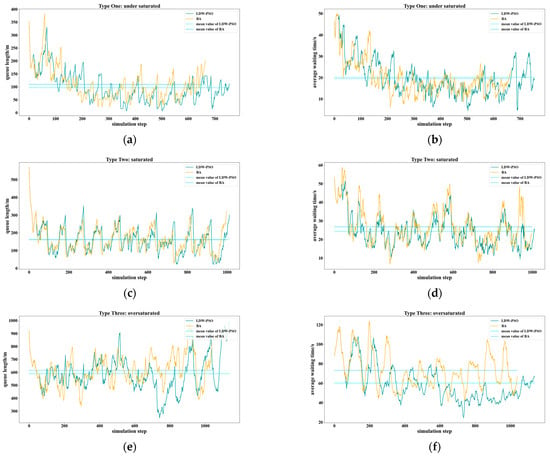
Figure 9.
Three conditions’ best optimisation process of queue length and average waiting time. Their mean values are represented with dotted lines. (a) Type One’s best optimisation process of queue length; (b) Type One’s best optimisation process of average waiting time; (c) Type Two’s best optimisation process of queue length; (d) Type Two’s best optimisation process of average waiting time; (e) Type Three’s best optimisation process of queue length; (f) Type Three’s best optimisation process of average waiting time.
Therefore, we can claim that the combination of the optimisation model and LDW-PSO can reduce queue length and average waiting time in an isolated intersection.
6. Conclusions and Future Works
In this work, an optimisation strategy of real-time traffic signal control has been proposed to reduce queue length and average waiting time. A series of experiments and analyses have been carried out from several points of view, including the internal behaviors of this optimisation strategy, the improvement of fitness value, and the quality of solutions regarding three different conditions.
The following conclusions can be drawn: Firstly, our optimisation strategy shows a successful performance in the isolated intersection with hundreds of vehicles. Our method, which practically converged after the first 10 iterations, performed a fast convergence for the three different conditions. And this suggests that the use of our proposal for real-time traffic signal control is advantageous. Secondly, the boxplot representation of distribution results shows that LDW-PSO obtained better medians and means compared to B.A. and standard PSO. Besides, histogram representation of distribution results shows that the error bars of phase durations obtained by standard PSO and LDW-PSO are consistently lower than those obtained by B.A. in most cases. It means that standard PSO and LDW-PSO have better convergences and stabilities compared to B.A. Lastly, the phase duration obtained by LDW-PSO can reduce the queue length and average waiting time for the three conditions. Compared to B.A., LDW-PSO can remarkably reduce the queue length by 20.4% and the average waiting time by 17.9% regarding Type Three. And compared to standard PSO, LDW-PSO also achieves better results in three conditions. It means LDW-PSO has a stronger ability to deal with all these scenarios, especially complex situations with more vehicles.
This paper has confirmed that our optimisation strategy has a successful performance in an isolated intersection. In fact, we are interested in larger dimension scenarios, such as large urban areas with hundreds of traffic signals. So, in the future, we will use a larger scene to carry out the experiment.
Author Contributions
Conceptualisation, Y.S.; methodology, Y.Q.; software, Y.Q.; investigation, Y.S.; data curation, L.L.; writing—original draft preparation, Y.Q.; writing—review and editing, L.L. and D.L.; visualisation, Y.Q.; supervision, L.L.; project administration, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by China National Key Research and Development Program, grant number: NO.2018YFE0197700.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Glossary
| Optimisation Algorithm: Bat Algorithm | |
| i | Each bat in the bat population |
| xi | Position of bat i |
| vi | Velocity of bat i |
| xbest | Global optimal solution of the bat algorithm |
| t | Current generation |
| Q | Frequency |
| LBb | Lower boundary of position |
| UBb | Upper boundary of position |
| A | Loudness |
| r | Pulse |
| bf | Fitness of bat |
| Optimisation Algorithm: Particle Swarm Optimization with Linearly Decreasing Weight | |
| j | Each particle in the particle swarm |
| xj | Position of particle j |
| vj | Velocity of particle j |
| pbest | Local best solution of each generation |
| gbest | Global best solution of the LDW-PSO |
| c1 | Self-learning factor |
| c2 | Global learning factor |
| ω | Inertia weight of particle |
| Ngen | Max generation |
| g | Current generation |
| Npop | Max population |
| LBP | Lower boundary of position |
| UBP | Upper boundary of position |
| LBv | Lower boundary of velocity |
| UBv | Upper boundary of velocity |
| pf | Fitness of particle |
| Objective Function of The Simulation Model | |
| n | Index of all phases in a traffic cycle |
| GTn | Duration of the green time on phase n |
| d | Index of discretised green time duration of phase n |
| S | Summation of three parts |
| Tw | Waiting time |
| Tq | Loss of start-stop time |
| Tp | Time reward |
| LB | Lower boundary of effective green time of each phase |
| UB | Upper boundary of effective green time of each phase |
| (v,w) | Vehicular route from road v heading to road w |
| L | Traffic load |
| R | All vehicular routes that allow vehicles to pass |
| VN | Vehicle number of halting vehicles |
| WT | Waiting time |
| θT | Linear function represents the start-stop delay |
| MC | Maximum capacity |
| PV | Number of vehicles that can pass through the intersection |
| TN | Total number o vehicles, including halting and moving vehicles |
| RT | Number of vehicles that can cross the intersection through the remaining time |
| RC | Remaining capacity |
References
- United Nations. World Urbanization Prospects: The 2018 Revision; Economic & Social Affairs: New York, NY, USA, 2018; pp. 1–2. [Google Scholar]
- McCrea, J.; Moutari, S. A hybrid macroscopic-based model for traffic flow in road networks. Eur. J. Oper. Res. 2010, 207, 676–684. [Google Scholar] [CrossRef]
- Ye, B.L.; Wu, W.M.; Gao, H.M.; Lu, Y.X.; Cao, Q.Q.; Zhu, L.J. Stochastic Model Predictive Control for Urban Traffic Networks. Appl. Sci. 2017, 7, 588. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Wang, H.; Yan, L.; Du, B. A swarm intelligent method for traffic light scheduling: Application to real urban traffic networks. Appl. Intell. 2016, 44, 208–231. [Google Scholar] [CrossRef]
- de Oliveira, L.F.P.; Manera, L.T.; da Luz, P.D.G. Development of a Smart Traffic Light Control System with Real-Time Monitoring. IEEE Internet Things J. 2021, 8, 3384–3393. [Google Scholar] [CrossRef]
- Hu, W.B.; Wang, H.; Min, Z.Y. A storage allocation algorithm for outbound containers based on the outer-inner cellular automaton. Inf. Sci. 2014, 281, 147–171. [Google Scholar] [CrossRef]
- Gartner, N.H.; Pooran, F.J.; Andrews, C.M. Optimised policies for adaptive control strategy in real-time traffic adaptive control systems—Implementation and field testing. Transp. Res. Rec. J. Transp. Res. Board 2002, 1811, 148–156. [Google Scholar] [CrossRef]
- Zhou, P.; Fang, Z.; Dong, H.; Liu, J.; Pan, S. Data Analysis with Multi-objective Optimisation Algorithm: A Study in Smart Traffic Signal System. In Proceedings of the 2017 IEEE/Acis 15th International Conference on Software Engineering Research, Management and Applications, London, UK, 7–9 June 2017; pp. 307–310. [Google Scholar]
- Karakuzu, C.; Demirci, O. Fuzzy logic based smart traffic light simulator design and hardware implementation. Appl. Soft. Comput. 2010, 10, 66–73. [Google Scholar] [CrossRef]
- Sanchez, J.; Galan, M.; Rubio, E. Applying a traffic lights evolutionary optimisation technique to a real case: “Las Ramblas” area in Santa Cruz de Tenerife. IEEE Trans. Evol. Comput. 2008, 12, 25–40. [Google Scholar] [CrossRef]
- Chou, L.D.; Shen, T.Y.; Tseng, C.W.; Chang, Y.J.; Kuo, Y.W. Green wave-based virtual traffic light management scheme with VANETs. Int. J. Ad Hoc Ubiquitous Comput. 2017, 24, 22–32. [Google Scholar] [CrossRef]
- Phuong Thi Mai, N.; Passow, B.N.; Yang, Y. Improving Anytime Behavior for Traffic Signal Control Optimization Based on NSGA-II and Local Search. In Proceedings of the 2016 International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 4611–4618. [Google Scholar]
- Ardiyanto, I.; Sulistyo, S. A Study on Metaheuristics for Urban Traffic Light Scheduling Problems. In Proceedings of the 2018 the 10th International Conference on Information Technology and Electrical Engineering, Bali, Indonesia, 24–26 July 2018; pp. 545–550. [Google Scholar]
- Garcia-Nieto, J.; Alba, E.; Olivera, A.C. Swarm intelligence for traffic light scheduling: Application to real urban areas. Eng. Appl. Artif. Intell. 2012, 25, 274–283. [Google Scholar] [CrossRef]
- Olivera, A.C.; Garcia-Nieto, J.M.; Alba, E. Reducing vehicle emissions and fuel consumption in the city by using particle swarm optimisation. Appl. Intell. 2015, 42, 389–405. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, H.C.; Gao, L.; Zhang, G.H. Cellular particle swarm optimisation. Inf. Sci. 2011, 181, 4460–4493. [Google Scholar] [CrossRef]
- Montes de Oca, M.A.; Stutzle, T.; Birattari, M.; Dorigo, M. Frankenstein’s PSO: A Composite Particle Swarm Optimization Algorithm. IEEE Trans. Evol. Comput. 2009, 13, 1120–1132. [Google Scholar] [CrossRef]
- Srivastava, S.; Sahana, S.K. Bat Algorithm-Based Traffic Signal Optimization Problem. In Soft Computing for Problem Solving, Socpros 2017; Springer: Singapore, 2019; Volume 1, pp. 927–936. [Google Scholar]
- He, J.J.; Hou, Z.E. Ant colony algorithm for traffic signal timing optimisation. Adv. Eng. Softw. 2012, 43, 14–18. [Google Scholar] [CrossRef]
- Celtek, S.A.; Durdu, A.; Ali, M.E.M. Real-time traffic signal control with swarm optimisation methods. Measurement 2020, 166, 7. [Google Scholar] [CrossRef]
- Galvan-Correa, R.; Olguin-Carbajal, M.; Herrera-Lozada, J.C.; Sandoval-Gutierrez, J.; Serrano-Talamantes, J.F.; Cadena-Martinez, R.; Aquino-Ruiz, C. Micro Artificial Immune System for Traffic Light Control. Appl. Sci. 2020, 10, 7933. [Google Scholar] [CrossRef]
- Peres, M.; Ruiz, G.; Nesmachnow, S.; Olivera, A.C. Multi-objective evolutionary optimisation of traffic flow and pollution in Montevideo, Uruguay. Appl. Soft. Comput. 2018, 70, 472–485. [Google Scholar] [CrossRef]
- Damay, N. Multiple-Objective Optimisation of Traffic Lights Using a Genetic Algorithm and a Microscopic Traffic Simulator. 2015. Available online: http://www.diva-portal.org/smash/get/diva2:816306/FULLTEXT01.pdf (accessed on 10 November 2021).
- Jintamuttha, K.; Watanapa, B.; Charoenkitkarn, N. Dynamic Traffic Light Timing Optimization Model Using Bat Algorithm. In Proceedings of the 2016 2nd International Conference on Control Science and Systems Engineering, Singapore, 27–29 July 2016; pp. 181–185. [Google Scholar]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization; Springer: Berlin, Germany, 2010; pp. 65–74. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimiser using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (Cat. No. 95TH8079) MHS’95, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).