Performance of Relative Clearance Ratio of Floating Ring Bearing for Turbocharger-Rotor System Stability
Abstract
:1. Introduction
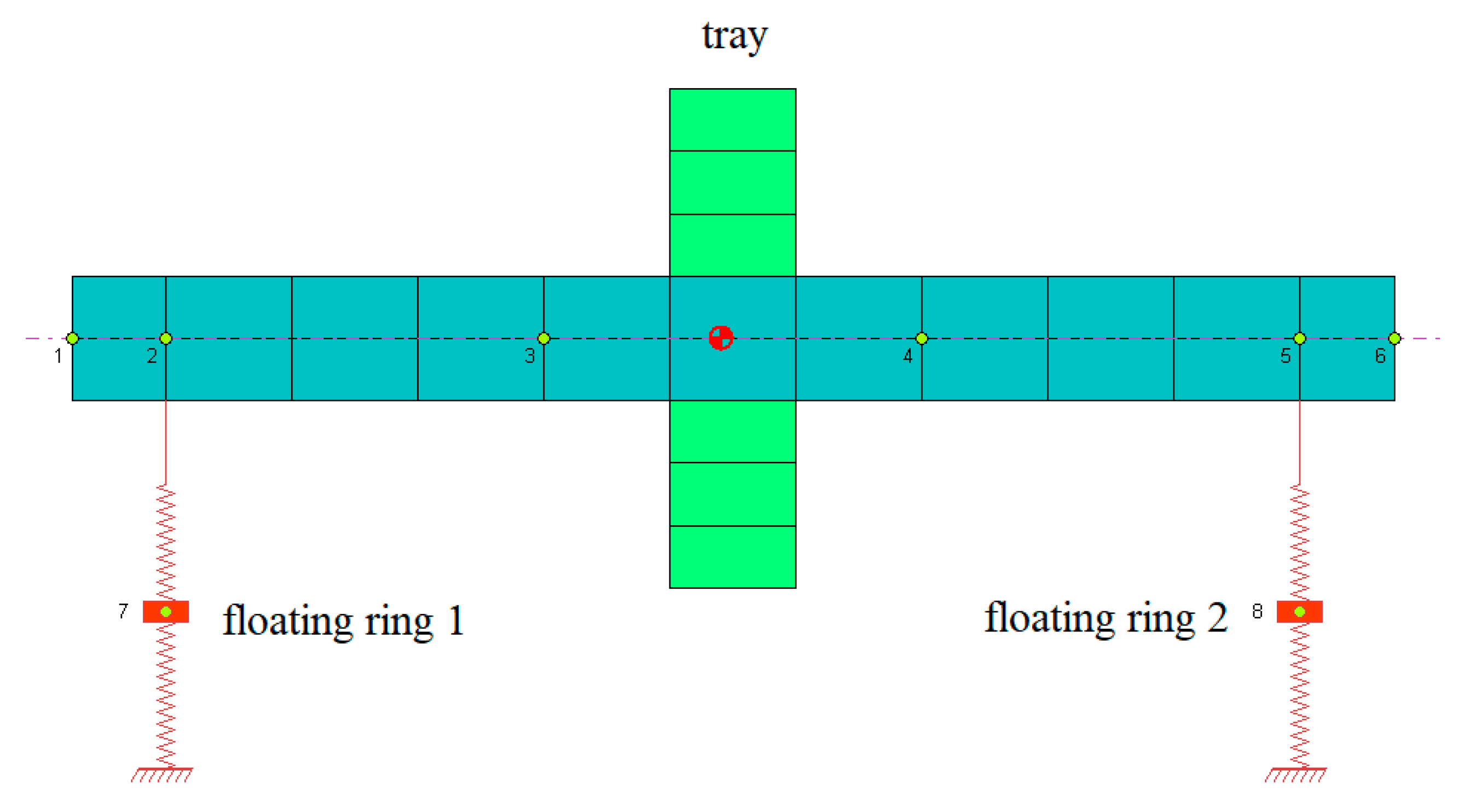
2. Dynamic Model of Floating Ring Bearing-Rotor System
2.1. Rotor Dynamics Model of Floating Ring Bearing
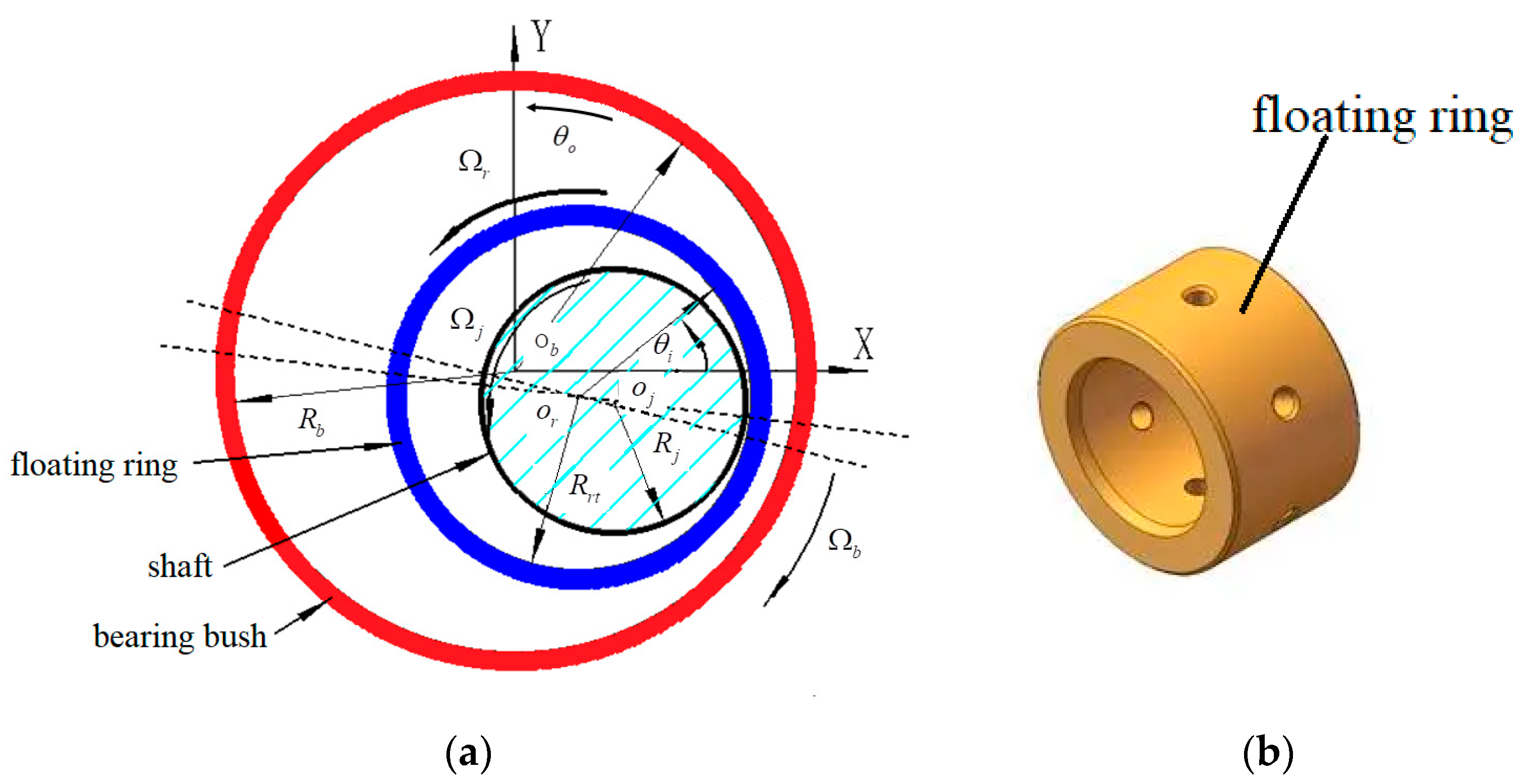
2.2. Inner and Outer Oil-Film Force Model of FRB
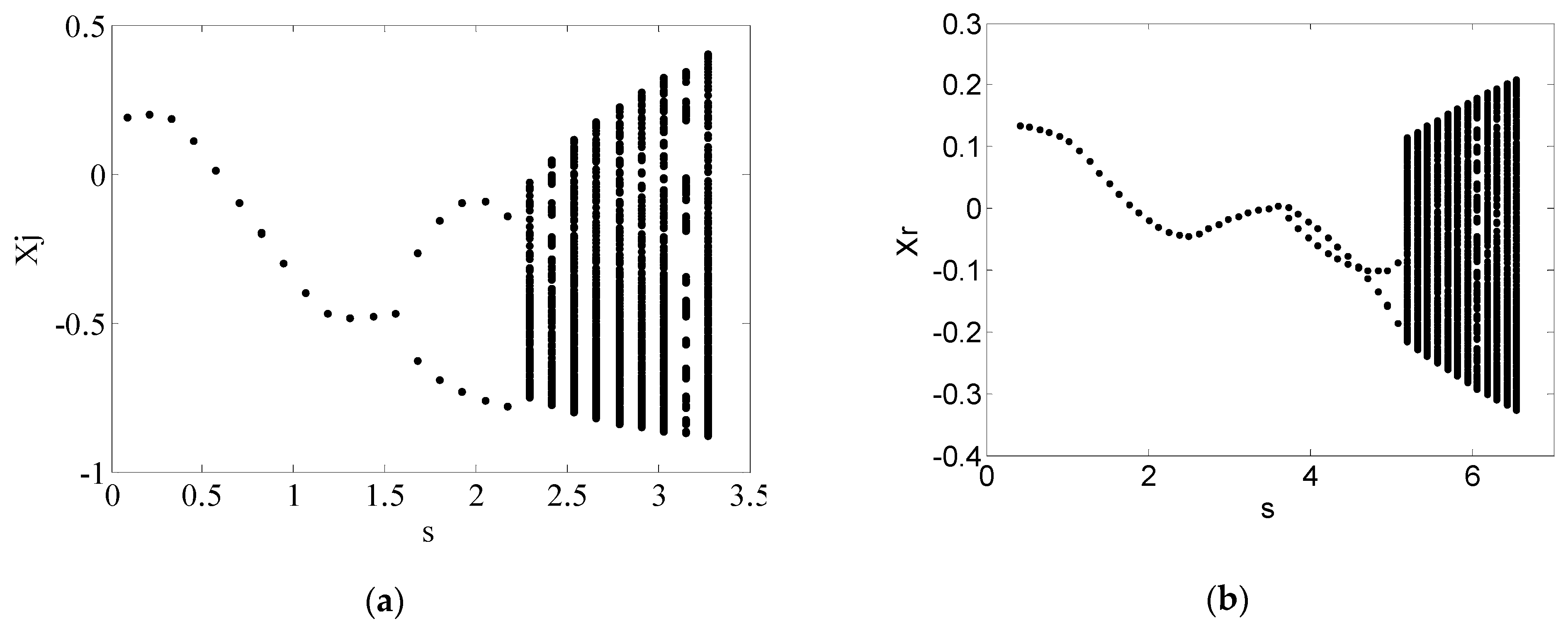
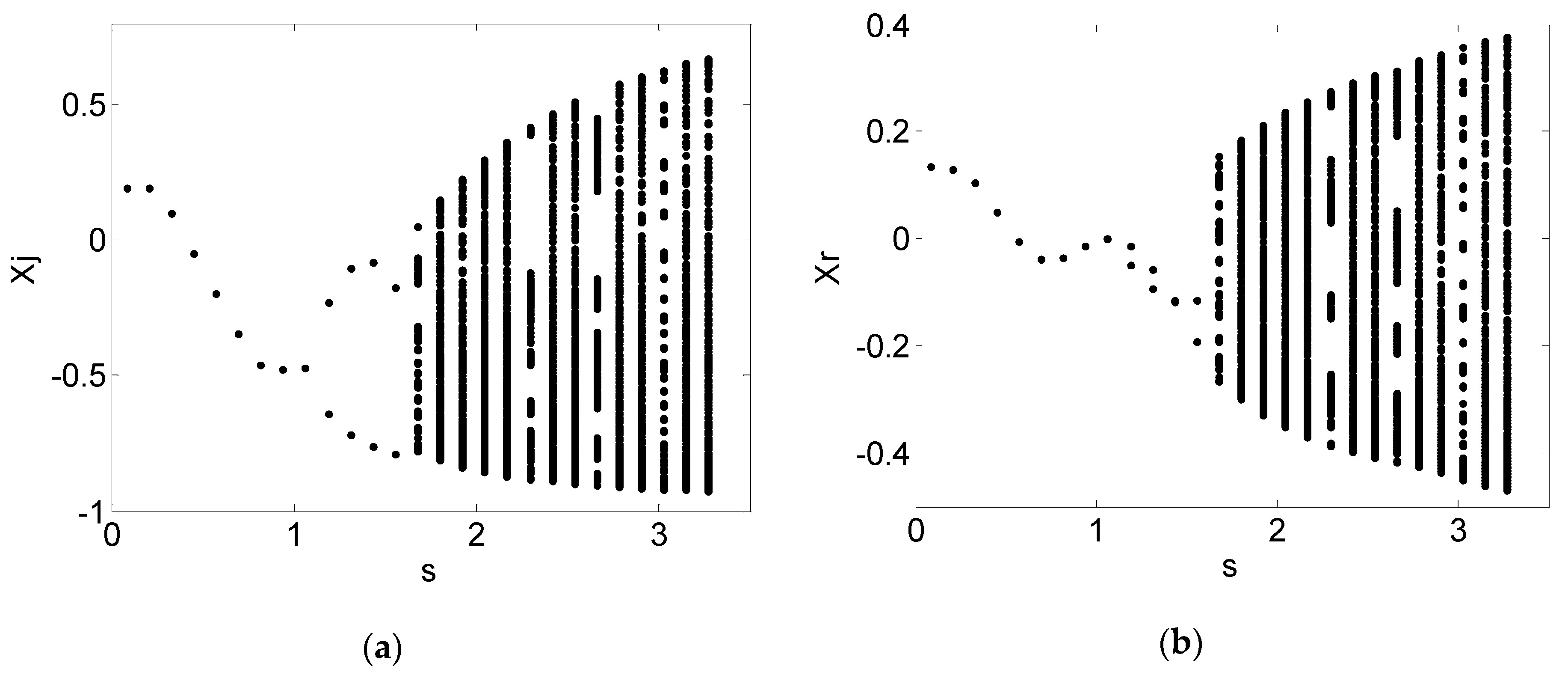
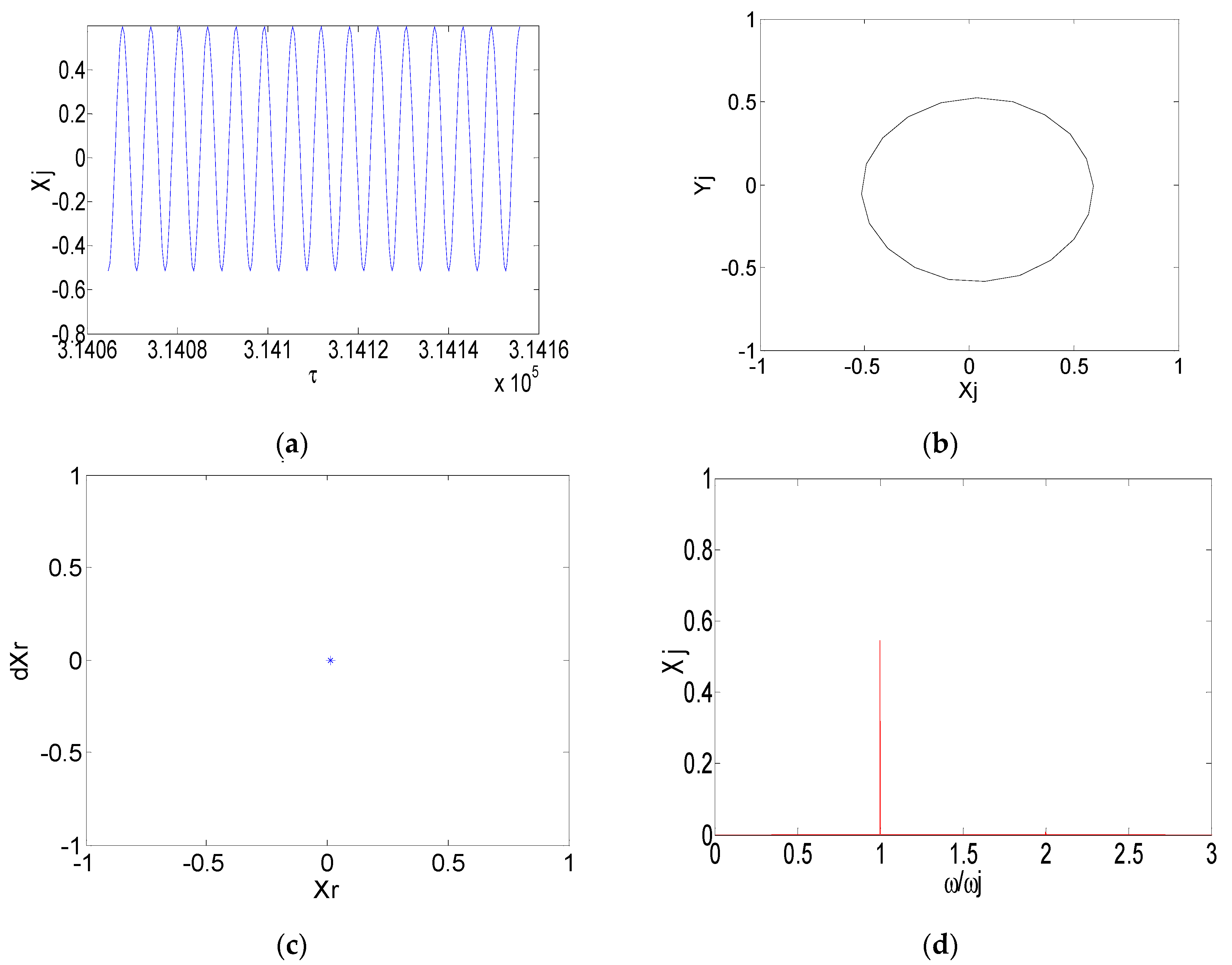
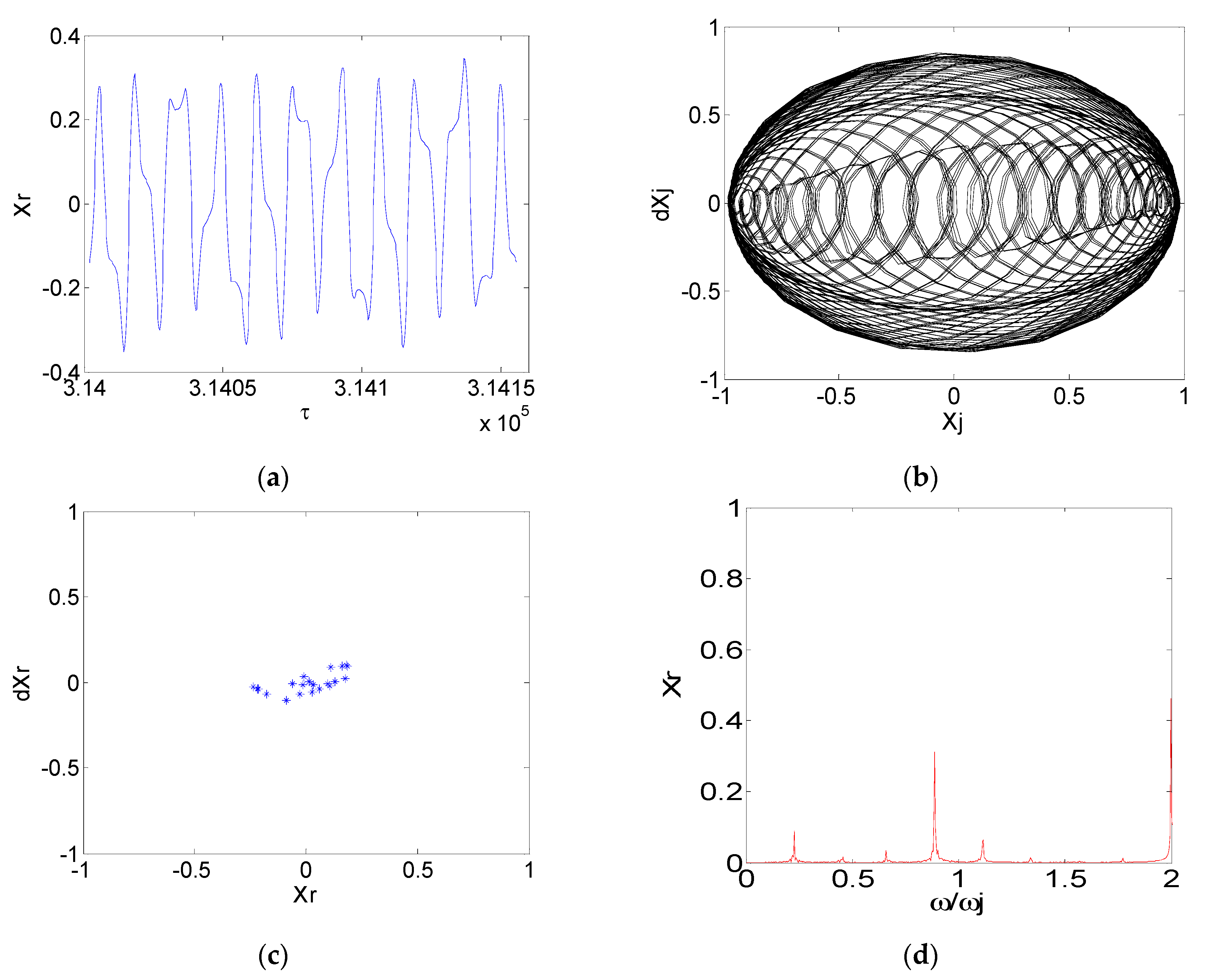
3. Numerical Simulation and Result Analysis
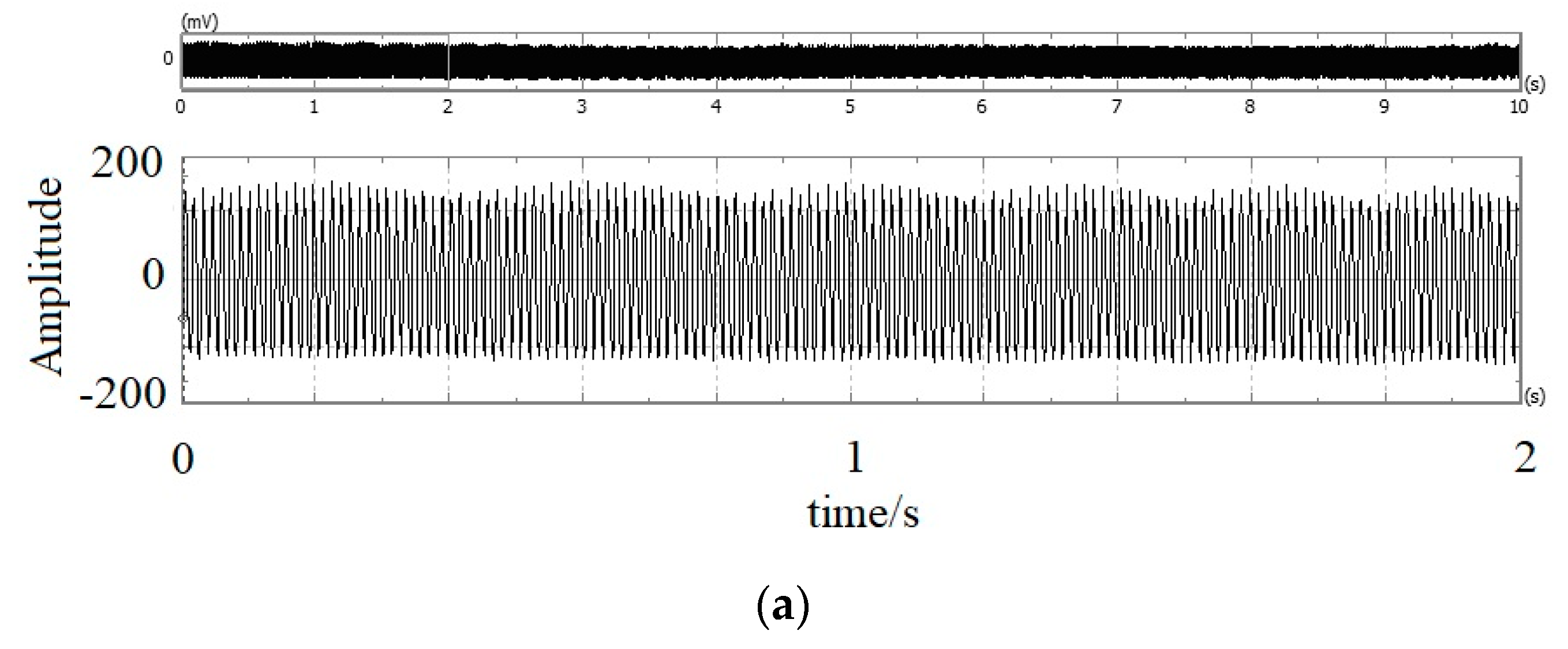
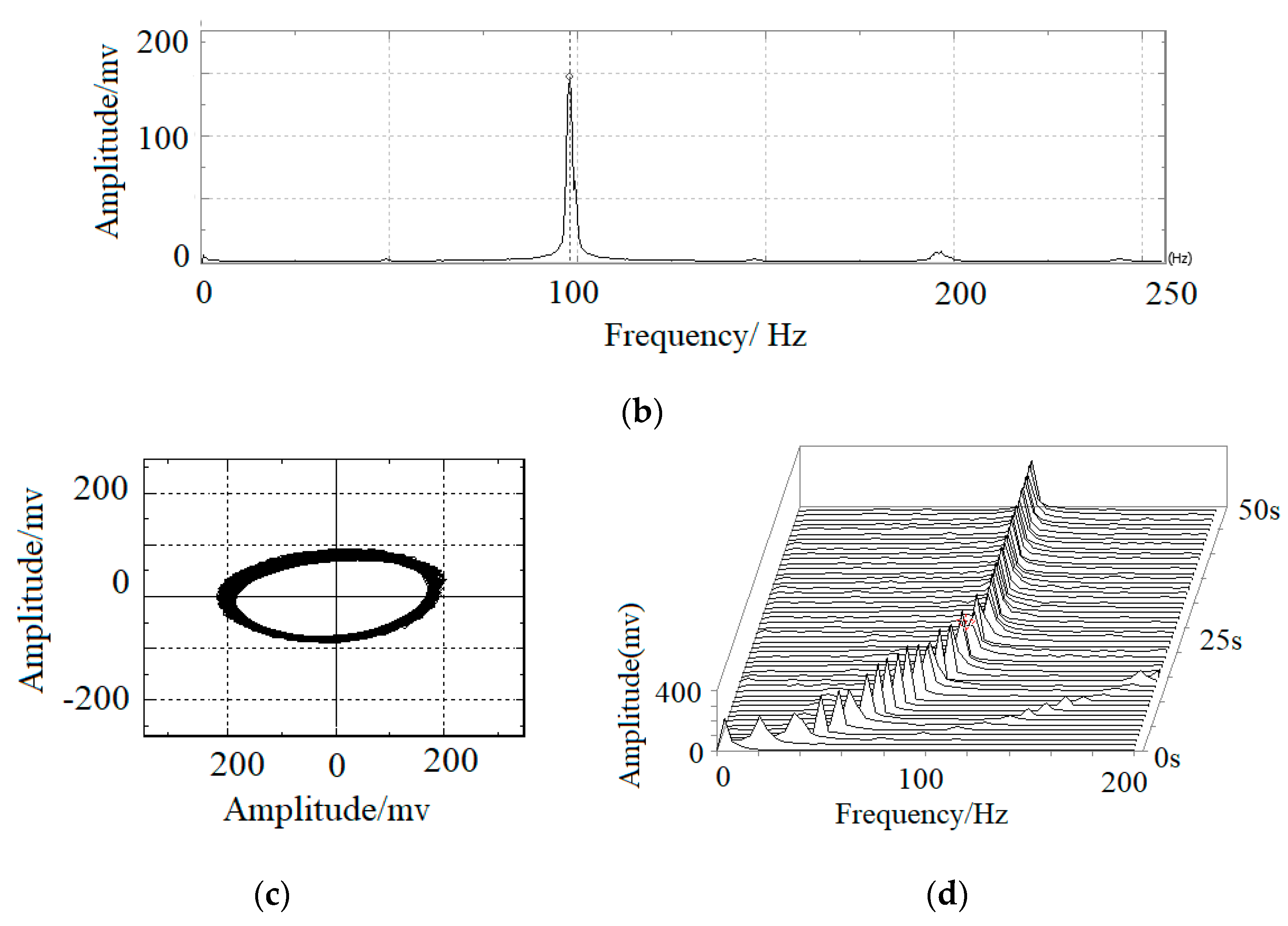
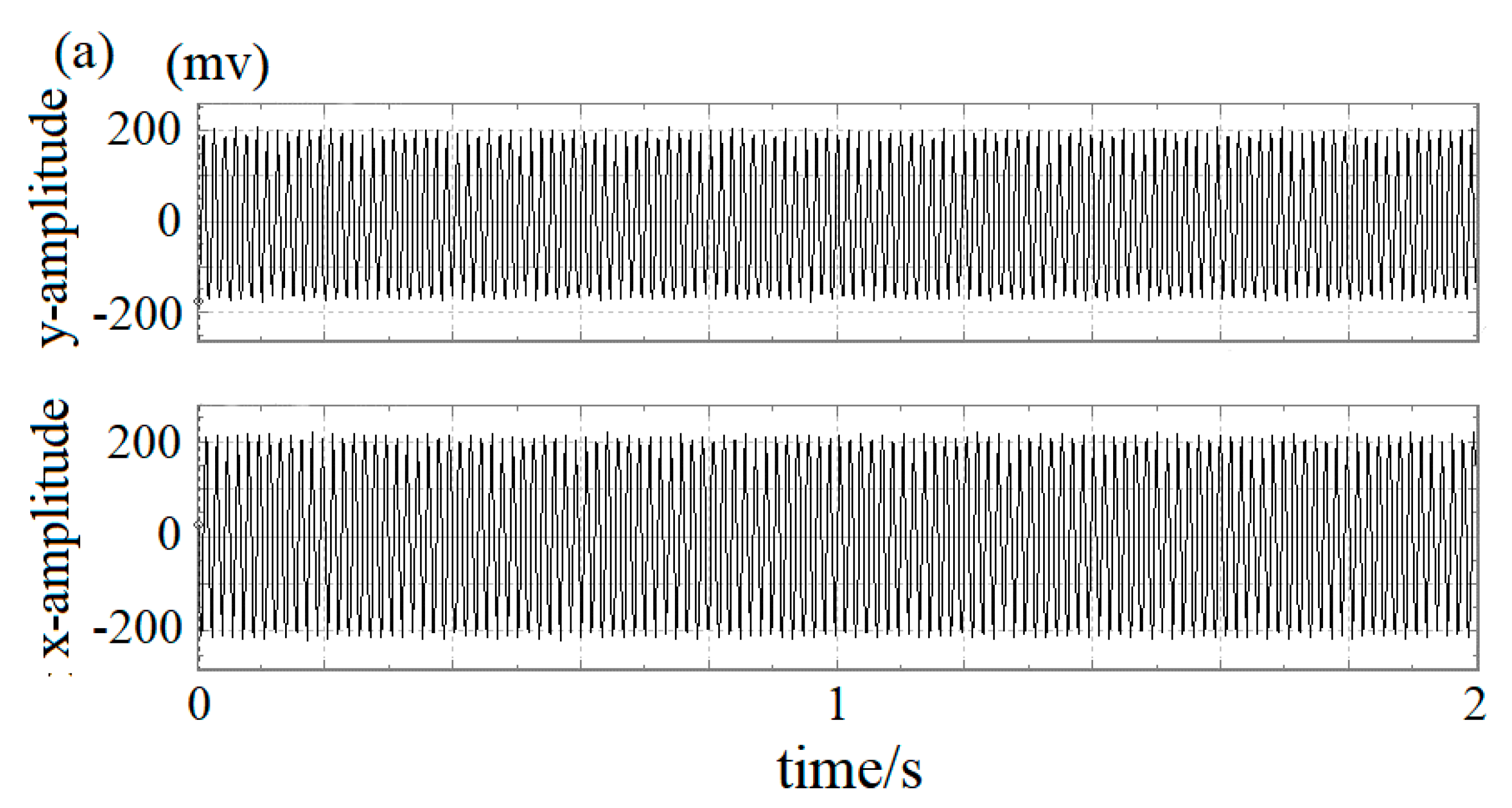
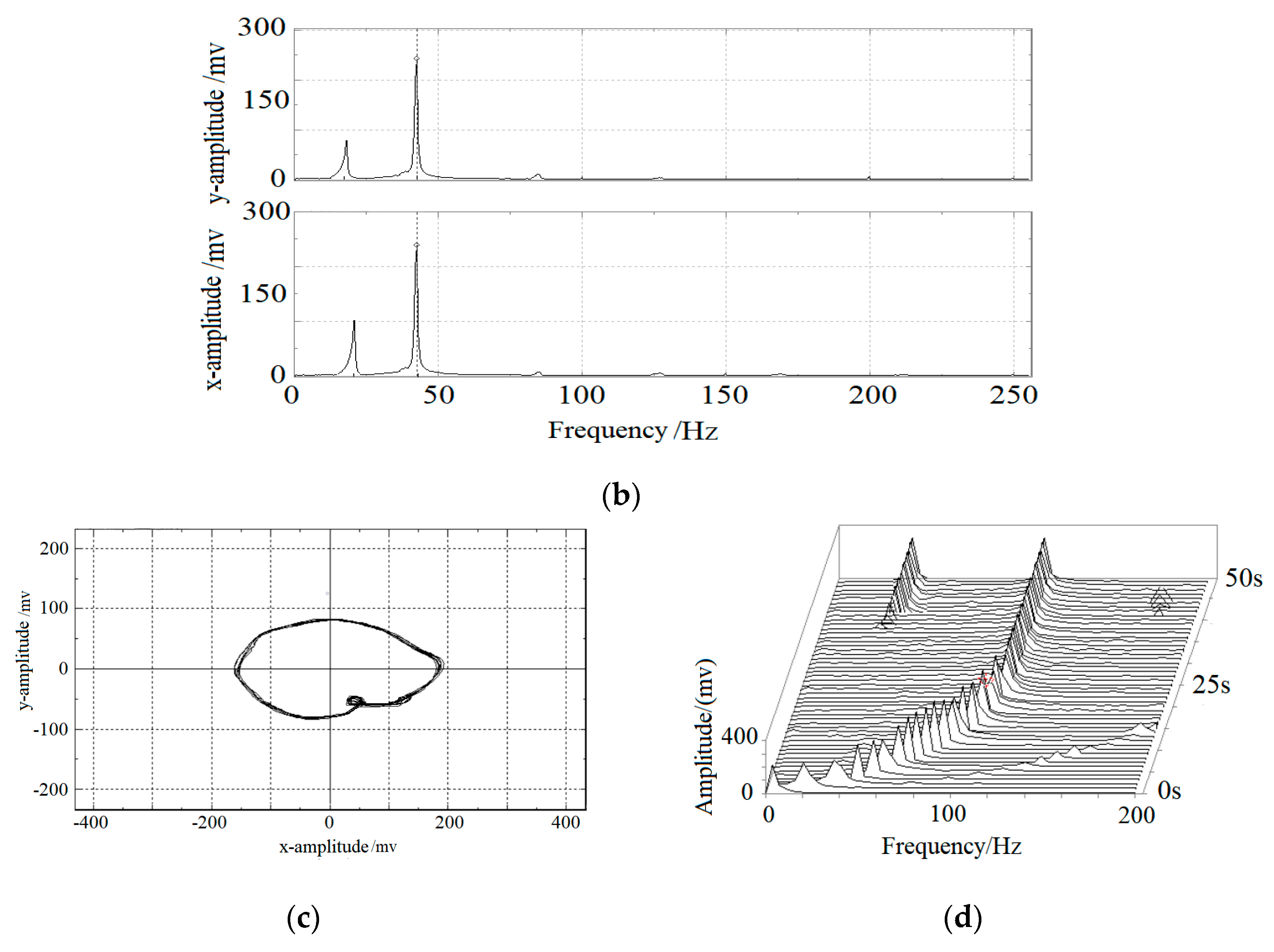
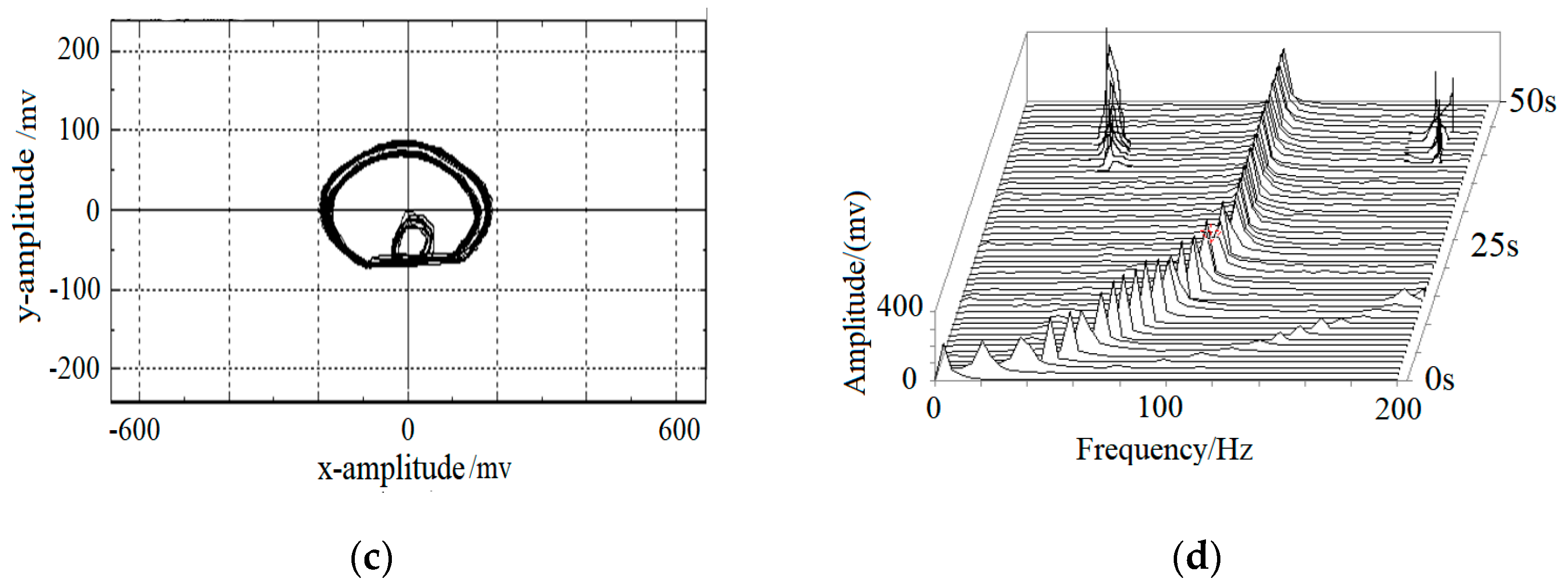
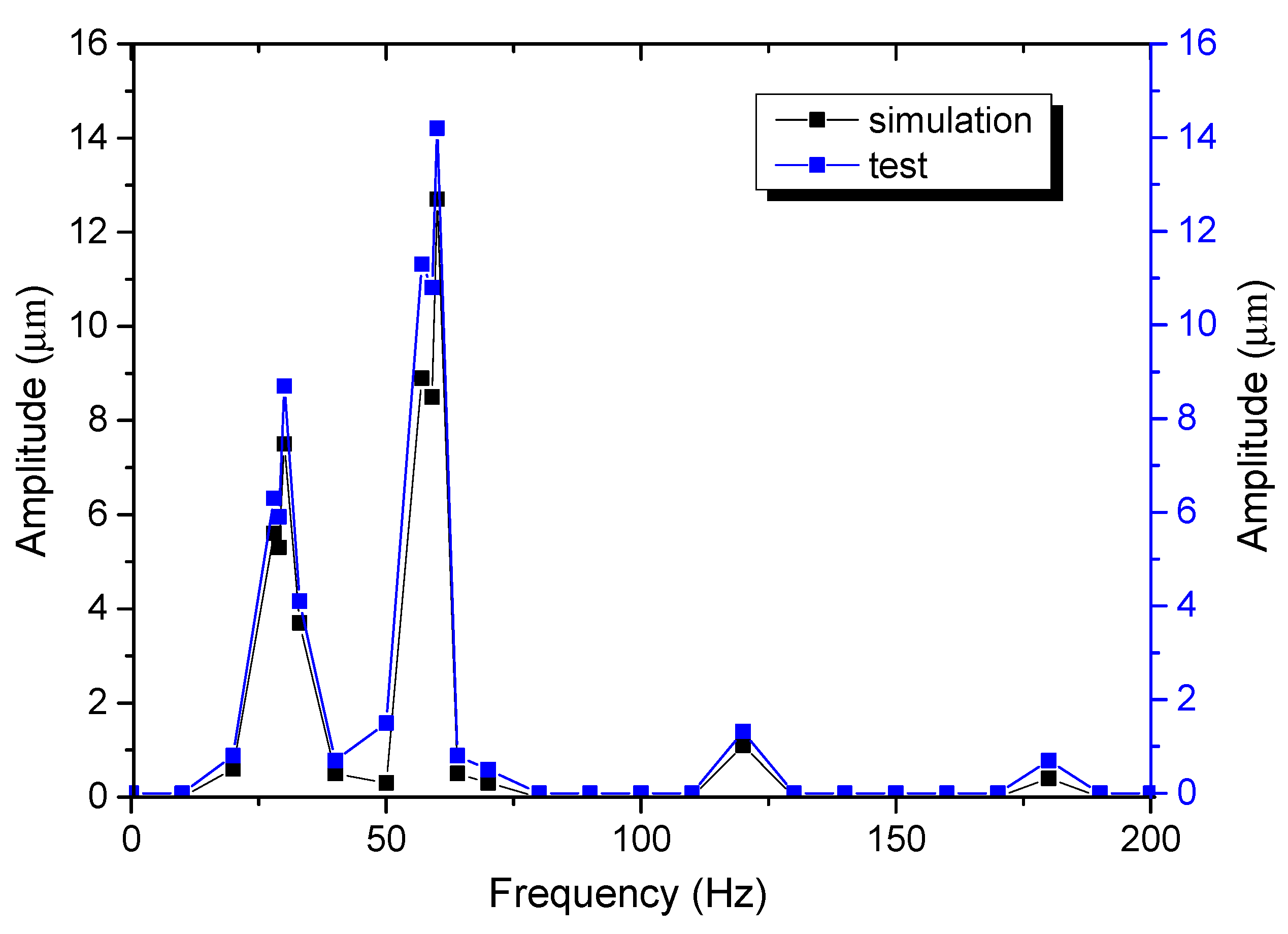
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, W.; Wei, D.G.; Zhu, L.; Hu, M.L. Study on effects of clearance ratio of inner to outer oil film on turbocharger rotor instability. Chin. J. Auto. Eng. 2014, 33, 130–136. [Google Scholar]
- Huang, R.; Zhang, W.L.; Xing, W.D.; Zhang, Y. Gas excitation’s influence on dynamic behavior of a turbo-charger rotor-ball bearing system. J. Vib. Shock. 2014, 33, 140–146. [Google Scholar]
- Liao, A.H.; Sui, Y.F.; Wu, C.H. Dynamic characteristics analysis of turbocharger rotor based on gyro effect. Chin. Int. Combust. Engine Eng. 2009, 4, 68–73. [Google Scholar]
- Zhu, L.; Wei, D.G.; Shi, W. Effects of eccentricity on rotor dynamics charac-teristic of turbocharger. Chin. J. Auto. Engin. 2013, 4, 282–286. [Google Scholar]
- Dyk, Š.; Smolík, L.; Rendl, J. Predictive capability of various linearization approaches for floating-ring bearings in nonlinear dynamics of turbochargers. Mech. Mach. Theory 2020, 149, 103843. [Google Scholar] [CrossRef]
- Pei, S.; Xu, H.; Yun, M.; Shi, F.; Hong, J. Effects of surface texture on the lubrication performance of the floating ring bearing. Tribol. Int. 2016, 102, 143–153. [Google Scholar] [CrossRef]
- Pavel, N.; Petr, Š.; Jura, H. The effective computational model of the hydrodynamics journal floating ring bearing for simulations of long transient regimes of turbocharger rotor dynamics. Inter. J. Mech. Sci. 2018, 148, 611–619. [Google Scholar]
- Luboš, S.; Štěpán, D. Towards efficient and vibration-reducing full-floating ring bearings in turbochargers. Int. J. Mech. Sci. 2020, 175, 105516. [Google Scholar]
- Sitae, K.; Alan, B.P. Effects of thermo hydro dynamic (THD) floating ring bearing model on rotor dynamic bifurcation. Inter. J. Non-Linear Mech. 2017, 95, 30–41. [Google Scholar]
- Tian, L.; Wang, W.; Peng, Z. Nonlinear effects of unbalance in the rotor-floating ring bearing system of turbochargers. Mech. Syst. Signal Process. 2013, 34, 298–320. [Google Scholar] [CrossRef]
- Xie, Z.; Zhu, W. An investigation on the lubrication characteristics of floating ring bearing with consideration of multi-coupling factors. Mech. Syst. Signal Process. 2021, 162, 108086. [Google Scholar] [CrossRef]
- Papadopoulos, C.I.; Kaiktsis, L.; Fillon, M. Computational fluid dynamics thermo hydrodynamic analysis of three-dimensional sector-pad thrust bearings with rectangular dimples. J. Tribol. 2014, 136, 11702. [Google Scholar] [CrossRef]
- Braun, D.; Greiner, C.; Schneider, J.; Gumbsch, P. Efficiency of laser surface texturing in the reduction of friction under mixed lubrication. Tribol. Int. 2014, 77, 142–147. [Google Scholar] [CrossRef]
- Qiu, Y.; Khonsari, M. Experimental investigation of tribological performance of laser textured stainless steel rings. Tribol. Int. 2011, 44, 635–644. [Google Scholar] [CrossRef]
- Etsion, I. State of the art in laser surface texturing. J. Trib. 2009, 127, 761–762. [Google Scholar] [CrossRef]
- Wang, Q.J.; Zhu, D. Virtual texturing: Modeling the performance of lubricated contacts of engineered surfaces. J. Tribol. 2005, 127, 722–729. [Google Scholar] [CrossRef]
- Xie, Z.; Song, P.; Hao, L.; Shen, N.; Zhu, W.; Liu, H.; Shi, J.; Wang, Y.; Tian, W. Investigation on effects of Fluid-Structure-Interaction (FSI) on the lubrication performances of water lubricated bearing in primary circuit loop system of nuclear power plant. Ann. Nucl. Energy 2020, 141, 107355. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, N.; Zhu, W.; Liu, H.; Shi, J.; Wang, Y.; Tian, W. Dynamic characteristics analysis of the hydro-hybrid liquid Sodium lubricated bearing-rotor coupled system in the two-circuit main loop liquid sodium pump system. Ann. Nucl. Energy 2019, 136, 107059. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, N.; Ge, J.; Zhu, W.; Song, P.; Liu, H.; Hao, L.; Tian, W. Analysis of the flow noises of the nuclear main pump caused by the high temperature liquid Sodium in the two-circuit main loop liquid Sodium pump system. Ann. Nucl. Energy 2020, 145, 107550. [Google Scholar] [CrossRef]
- Schweizer, B. Total instability of turbocharger rotors—Physical explanation of the dynamic failure of rotors with full-floating ring bearings. J. Sound Vib. 2009, 328, 156–190. [Google Scholar] [CrossRef]
- Schweizer, B. Dynamics and stability of turbocharger rotors. Arch. Appl. Mech. 2009, 80, 1017–1043. [Google Scholar] [CrossRef]
- Tian, L.; Wang, W.J.; Peng, Z.J. Effects of bearing outer clearance on the dynamic behaviors of the full floating ring bearing supported turbocharger rotor. Mech. Syst. Signal Process. 2012, 31, 155–175. [Google Scholar] [CrossRef]
- Woschke, E.; Daniel, C.; Nitzschke, S. Excitation mechanisms of non-linear rotor systems with floating ring bearings—Simulation and validation. Int. J. Mech. Sci. 2017, 134, 15–27. [Google Scholar] [CrossRef]
- Zhang, C.; Men, R.; He, H.; Chen, W. Effects of circumferential and axial grooves on the nonlinear oscillations of the full floating ring bearing supported turbocharger rotor. Proc. Inst. Mech. Eng. Part J. J. Eng. Tribol. 2018, 233, 741–757. [Google Scholar] [CrossRef]
- Wen, B.C.; Gu, J.L. Advanced Rotor Dynamics: Theory, Technology and Application; Mach Press: Beijing, China, 1999. [Google Scholar]
- Nicholas, V.; Alan, R.C.; Balakumar, B. Nonlinear dynamics of a Jeffcott rotor with torsional deformations and rotor-stator contact. Int. J. Non-Linear Mech. 2017, 92, 102–110. [Google Scholar]
- Saurabh, K.B.; Anubhab, S.; Arun, K.S.; Ranjan, B. Dynamics of a rotor shaft driven by a non-ideal source through a universal joint. J. Sound Vib. 2021, 499, 115992. [Google Scholar]
- Kandil, A.; Sayed, M.; Saeed, N.A. On the nonlinear dynamics of constant stiffness coefficients 16-pole rotor active magnetic bearings system. Eur. J. Mech.-A/Solids 2020, 84, 104051. [Google Scholar] [CrossRef]
- Zeise, P.; Schweizer, B. Dynamics, stability and bifurcation analysis of rotors in air ring bearings. J. Sound Vib. 2021, 116392. [Google Scholar] [CrossRef]
- Capone, G.; Russo, M.; Russo, R. Dynamic characteristics and stability of a journal bearing in a non-laminar lubrication regime. Tribol. Int. 1987, 20, 255–260. [Google Scholar] [CrossRef]
- Adiletta, G.; Guido, A.R.; Rossi, C. Chaotic motions of a rigid rotor in short journal bearings. Nonlinear Dyn. 1996, 10, 251–269. [Google Scholar] [CrossRef] [Green Version]
- Orcutt, F.K.; Ng, C.E. Steady-State and dynamic prosperities of the floating-ring journal bearing. ASME J. Jubr. Technol.-Trans. 1968, 90, 243–253. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, Z.Q.; Zhen, D.; Gu, F.S.; Ball, A. Stability analysis of a turbocharger rotor system supported on floating ring bearings. J. Physics Conf. Ser. 2012, 364, 012032. [Google Scholar] [CrossRef] [Green Version]
- Tian, L.; Wang, W.J.; Peng, Z.J. Dynamic behaviors of a full floating ring bearing supported turbocharger rotor with engine excitation. J. Sound Vib. 2011, 330, 4851–4874. [Google Scholar] [CrossRef]


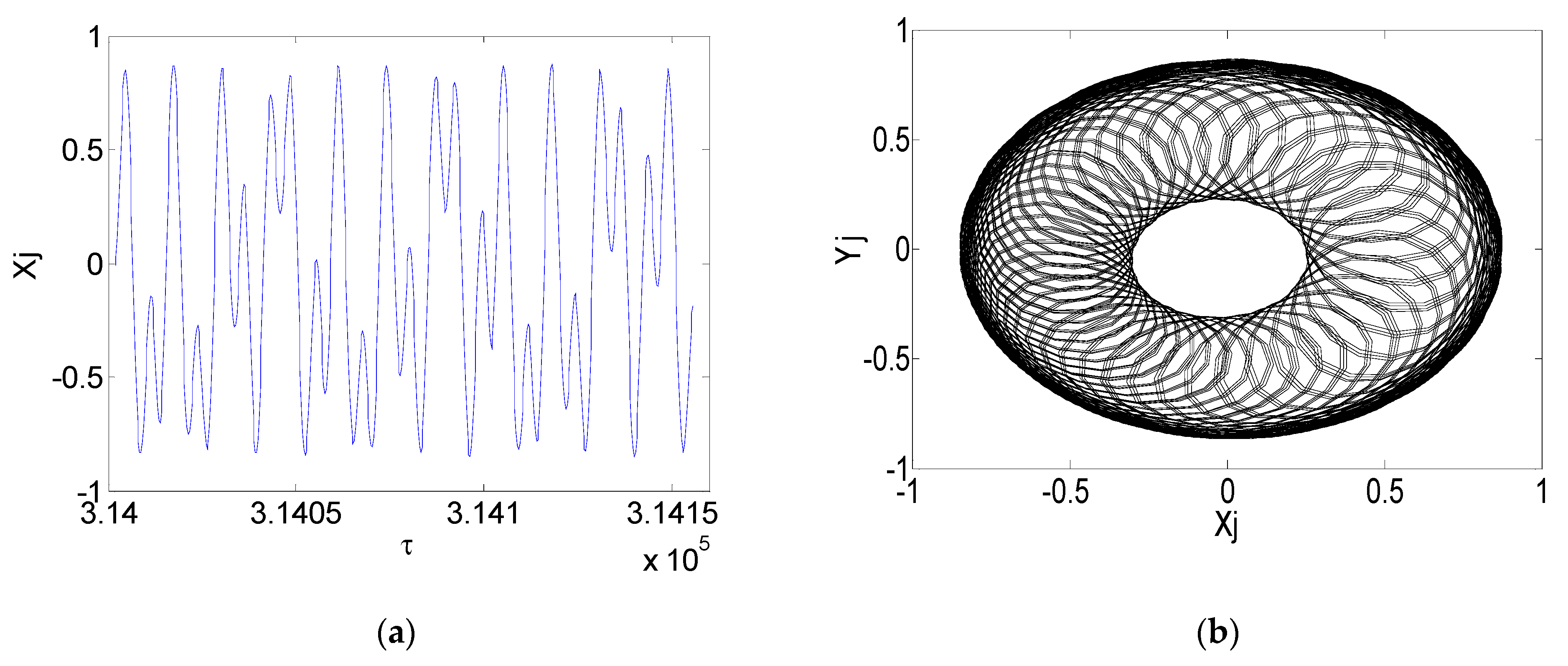



| Parameters | Numerical Value |
|---|---|
| Quality (kg) | m1 = m3 = 0.005, m2 = 0.1078 |
| Moment of inertia (10−6 kg·m2) | Jp = 18.75, Ja = 10.62 |
| Shaft length (mm) | L1 = L2 = 36 |
| Spindle diameter (mm) | D = 7 |
| Axis eccentric (mm) | e1 = e2 = 0.002 |
| The first critical speed (rad/s) | ω0 = 2π × 692.5 |
| Parameters | Numerical Value |
|---|---|
| Oil-film viscosity (Pa·s) | μ = 0.01 (25 °C) |
| Inner and outer radius of floating ring (mm) | Ri = 3.5; Ro = 6.5 |
| Floating ring length (mm) | L = 7.6 |
| Floating ring mass (g) | m = 6.7 |
| Moment of inertia (10−6 kg·m2) | I = 0.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, L.; Zheng, H.; Shi, Z. Performance of Relative Clearance Ratio of Floating Ring Bearing for Turbocharger-Rotor System Stability. Machines 2021, 9, 285. https://doi.org/10.3390/machines9110285
Peng L, Zheng H, Shi Z. Performance of Relative Clearance Ratio of Floating Ring Bearing for Turbocharger-Rotor System Stability. Machines. 2021; 9(11):285. https://doi.org/10.3390/machines9110285
Chicago/Turabian StylePeng, Liqiang, Huiping Zheng, and Zhanqun Shi. 2021. "Performance of Relative Clearance Ratio of Floating Ring Bearing for Turbocharger-Rotor System Stability" Machines 9, no. 11: 285. https://doi.org/10.3390/machines9110285
APA StylePeng, L., Zheng, H., & Shi, Z. (2021). Performance of Relative Clearance Ratio of Floating Ring Bearing for Turbocharger-Rotor System Stability. Machines, 9(11), 285. https://doi.org/10.3390/machines9110285





