The Deterministic Nature of Sensor-Based Information for Condition Monitoring of the Cutting Process
Abstract
:1. Introduction
2. Theoretical Background on Non-Linear Indicators
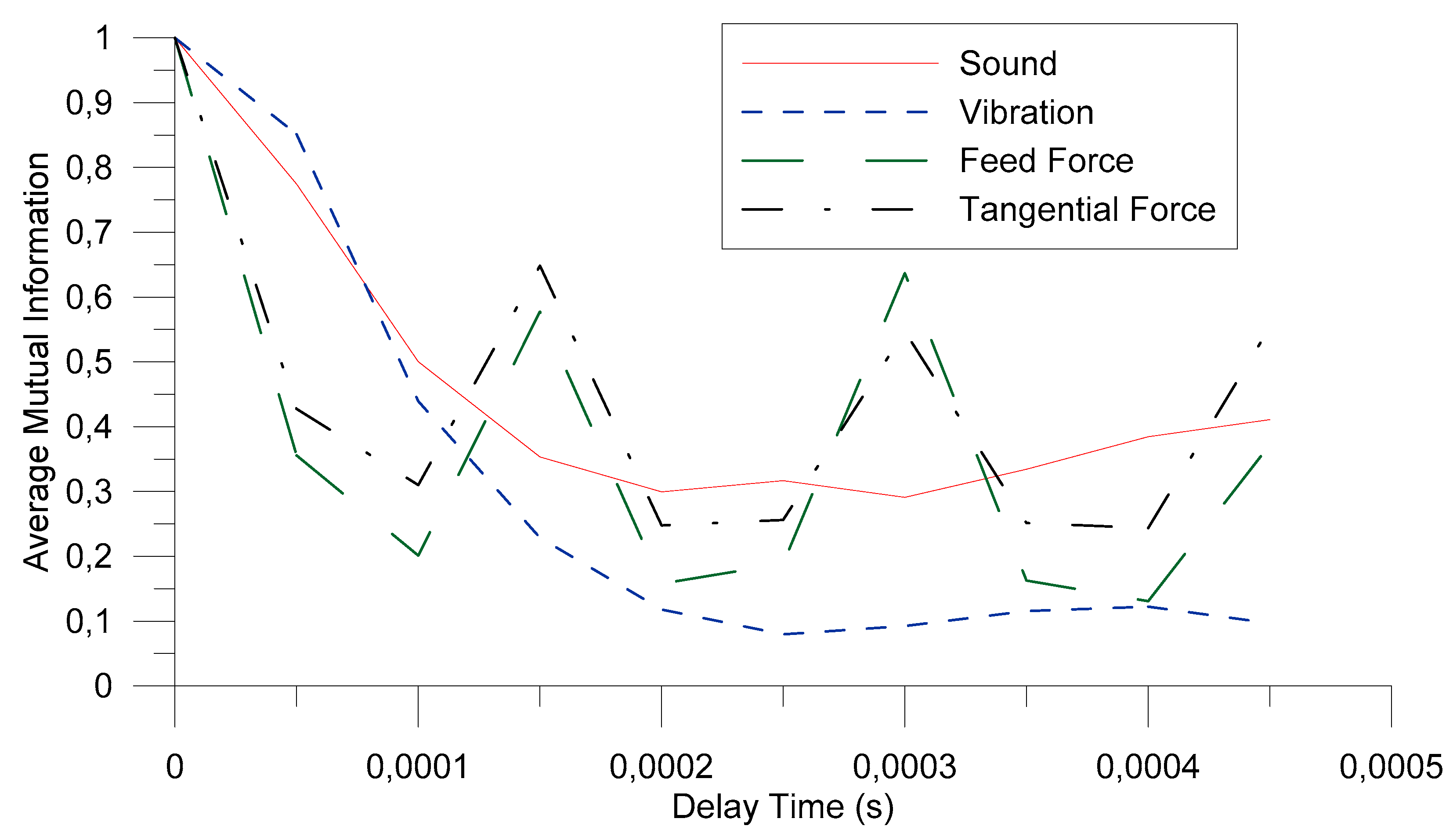
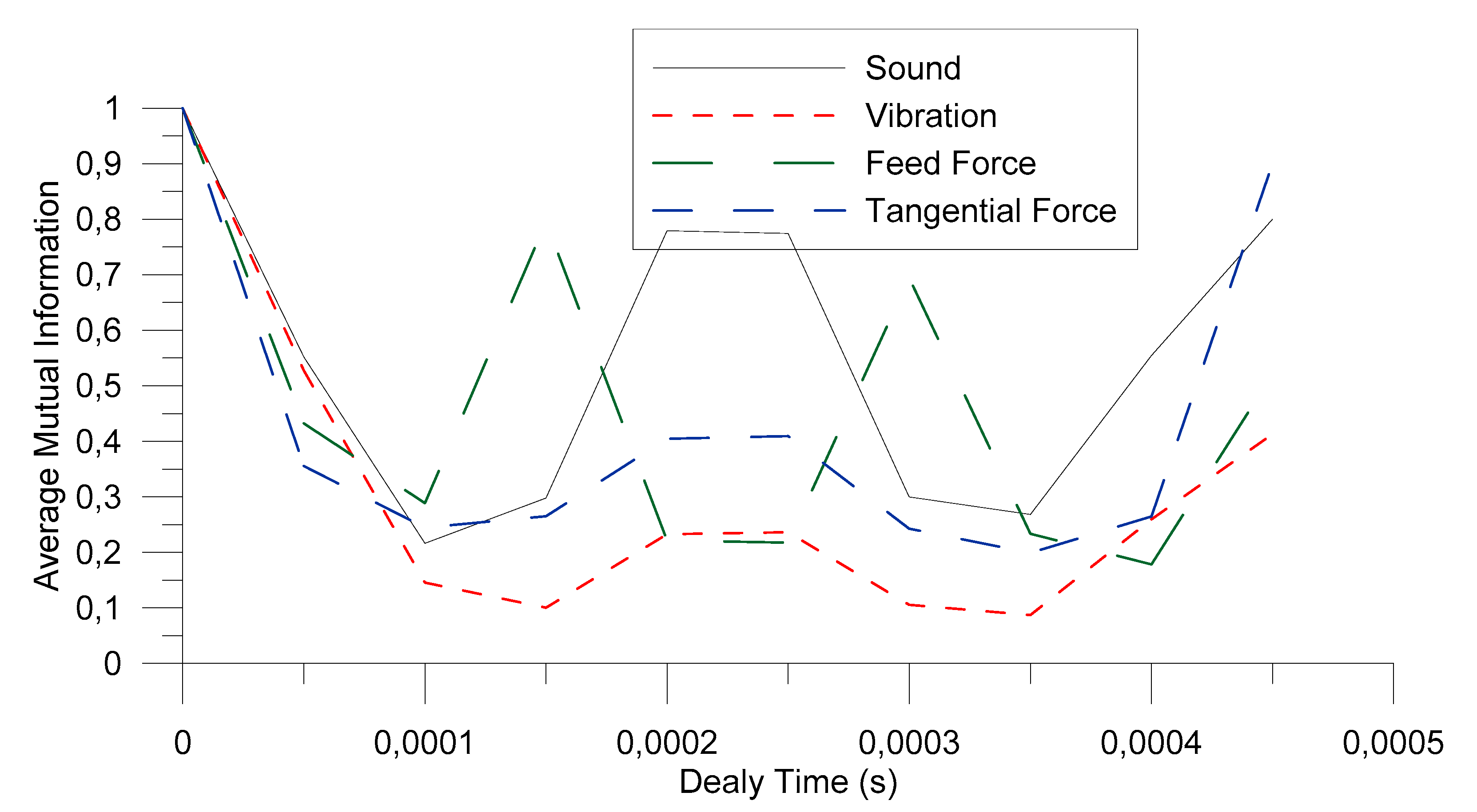
2.1. Average Mutual Information
2.2. Lyapunov Exponents
2.3. Recurrence Plots
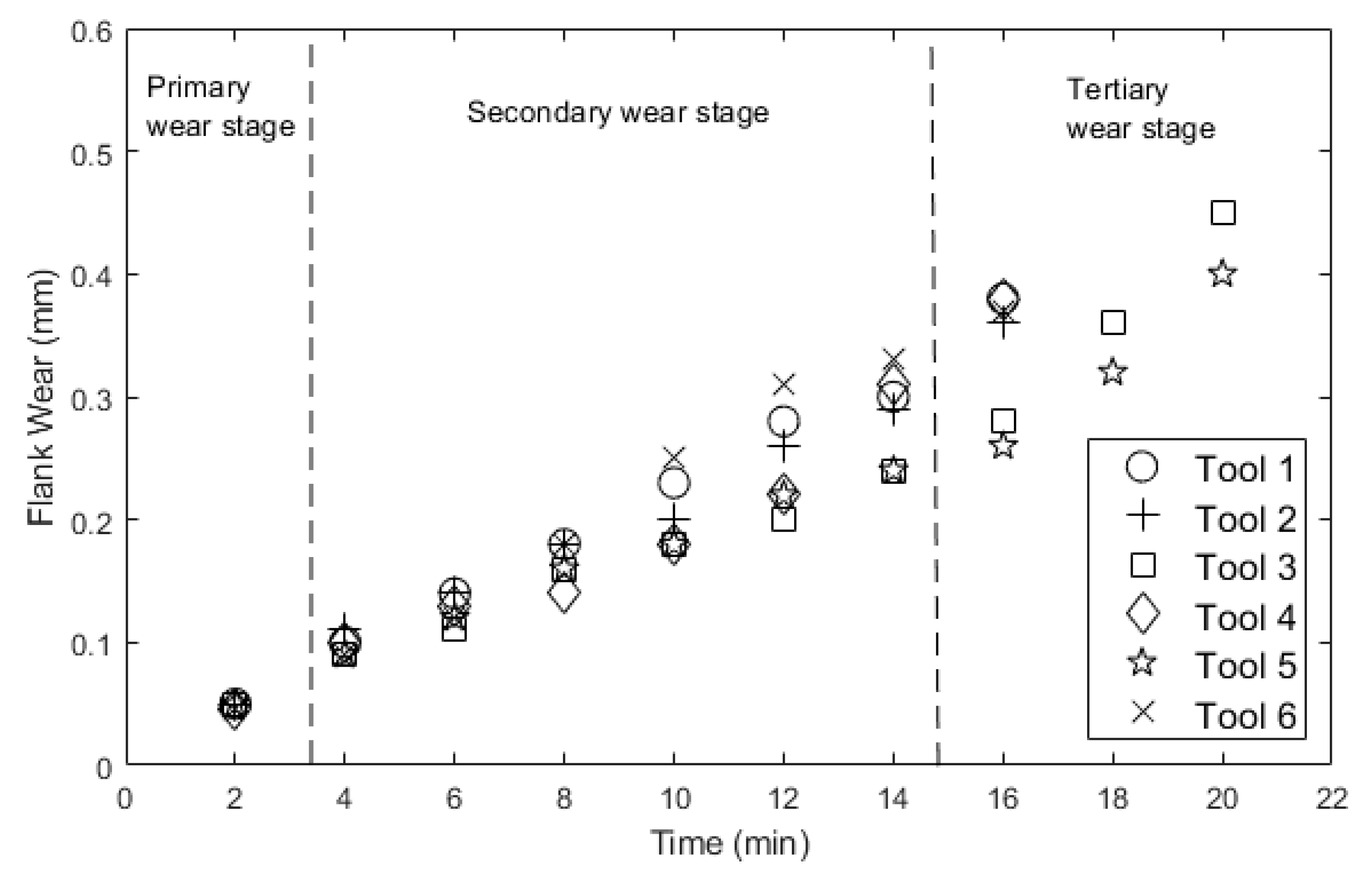
3. Materials and Methods
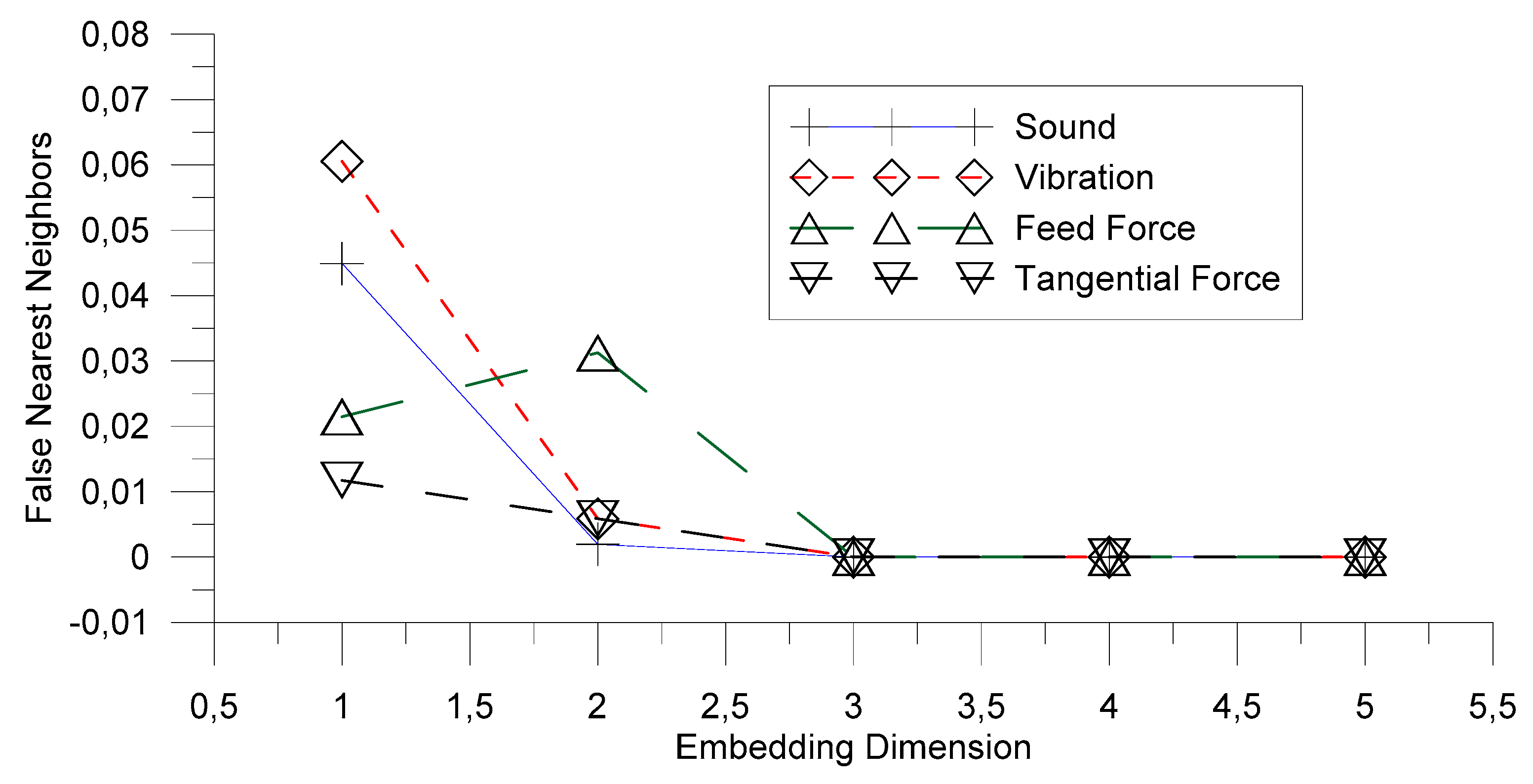
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ambhore, N.; Kamble, D.; Chinchanikar, S.; Wayal, V. Tool condition monitoring system: A review. Mater. Today Proc. 2015, 2, 3419–3428. [Google Scholar] [CrossRef]
- Siddhpura, A.; Paurobally, R. A review of flank wear prediction methods for tool condition monitoring in a turning process. Int. J. Adv. Manuf. Technol. 2013, 65, 371–393. [Google Scholar] [CrossRef]
- Wang, G.F.; Yang, Y.W.; Zhang, Y.C.; Xie, Q.L. Vibration sensor based tool condition monitoring using ν support vector machine and locality preserving projection. Sens. Actuators A Phys. 2014, 209, 24–32. [Google Scholar] [CrossRef]
- Wang, G.; Guo, Z.; Yang, Y. Force sensor based online tool wear monitoring using distributed Gaussian ARTMAP network. Sens. Actuators A Phys. 2013, 192, 111–118. [Google Scholar] [CrossRef]
- Silva, R.G.; Wilcox, S.J. Feature evaluation and selection for condition monitoring using a self-organizing map and spatial statistics. Artif. Intell. Eng. Des. Anal. Manuf. 2018, 33, 1–10. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Zhu, K.P.; Wong, Y.S.; Hong, G.S. Wavelet analysis of sensor signals for tool condition monitoring: A review and some new results. Int. J. Mach. Tools Manuf. 2009, 49, 537–553. [Google Scholar] [CrossRef]
- Silva, R.G.; Reuben, R.L.; Baker, K.J.; Wilcox, S.J. Tool wear monitoring of turning operations by neural network and expert system classification of a feature set generated from multiple sensors. Mech. Syst. Signal Process. 1998, 12, 319–332. [Google Scholar] [CrossRef]
- Snr, D.E.D. Sensor signals for tool-wear monitoring in metal cutting operations—A review of methods. Int. J. Mach. Tools Manuf. 2000, 40, 1073–1098. [Google Scholar]
- Duro, J.A.; Padget, J.A.; Bowen, C.R.; Kim, H.A.; Nassehi, A. Multi-sensor data fusion framework for CNC machining monitoring. Mech. Syst. Signal Process. 2016, 66–67, 505–520. [Google Scholar] [CrossRef] [Green Version]
- Weller, E.J.; Scrier, H.M.; Weichbrodt, B. What Sound Can Be Expected from a Worn Tool? ASME Pap. 1969, 91, 525–534. [Google Scholar] [CrossRef]
- McNulty, G.J.; Popplewell, N. Health Monitoring of Cutting Tools Through Noise Spectra. In Proceedings of the 1st Joint Polytechnic Symposium on Manufacturing Engineering, Leicester, UK, 12–16 July 1997. [Google Scholar]
- Lee, L.C. A study of noise emission for tool failure prediction. Int. J. Mach. Tool Des. Res. 1986, 26, 205–215. [Google Scholar] [CrossRef]
- Ya, W.; Shiqiu, K.; Shuzi, Y.; Qilin, Z.; Shanxiang, X.; Yaozu, W. An Experimental Study of Cutting Noise Dynamics. Mach. Dyn. Elem. Vib. 1991, 36, 313–318. [Google Scholar]
- Dimla, D.; Lister, P. On-line metal cutting tool condition monitoring. Int. J. Mach. Tools Manuf. 2000, 40, 769–781. [Google Scholar] [CrossRef]
- Huang, P.M.; Lee, C.H. Estimation of tool wear and surface roughness development using deep learning and sensors fusion. Sensors 2021, 21, 5338. [Google Scholar] [CrossRef] [PubMed]
- Ferrando Chacón, J.L.; de Fernández Barrena, T.; García, A.; de Sáez Buruaga, M.; Badiola, X.; Vicente, J. A Novel Machine Learning-Based Methodology for Tool Wear Prediction Using Acoustic Emission Signals. Sensors 2021, 21, 5984. [Google Scholar] [CrossRef] [PubMed]
- Orellana, R.; Carvajal, R.; Escárate, P.; Agüero, J.C. On the uncertainty identification for linear dynamic systems using stochastic embedding approach with gaussian mixture models. Sensors 2021, 21, 3837. [Google Scholar] [CrossRef]
- Parlos, A.G.; Rais, O.T.; Atiya, A.F. Multi-step-ahead prediction using dynamic recurrent neural networks. Neural Netw. 2000, 13, 765–786. [Google Scholar] [CrossRef]
- Li, X. A brief review: Acoustic emission method for tool wear monitoring during turning. Int. J. Mach. Tools Manuf. 2002, 42, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Silva, R.G.; Baker, K.J.; Wilcox, S.J.; Reuben, R.L. the Adaptability of a Tool Wear Monitoring System Under Changing Cutting Conditions. Mech. Syst. Signal Process. 2000, 14, 287–298. [Google Scholar] [CrossRef]
- Rusinek, R.; Wiercigroch, M.; Wahi, P. Modelling of frictional chatter in metal cutting. Int. J. Mech. Sci. 2014, 89, 167–176. [Google Scholar] [CrossRef]
- Chen, H.Y.; Lee, C.H. Deep learning approach for vibration signals applications. Sensors 2021, 21, 3929. [Google Scholar] [CrossRef]
- Brili, N.; Ficko, M.; Klančnik, S. Tool condition monitoring of the cutting capability of a turning tool based on thermography. Sensors 2021, 21, 6687. [Google Scholar] [CrossRef]
- Wang, R.; Song, Q.; Liu, Z.; Ma, H.; Gupta, M.K.; Liu, Z. A novel unsupervised machine learning-based method for chatter detection in the milling of thin-walled parts. Sensors 2021, 21, 5779. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, M.; Xiao, W.; Li, B. A method of using turning process excitation to determine dynamic cutting coefficients. Int. J. Mach. Tools Manuf. 2014, 87, 49–60. [Google Scholar] [CrossRef]
- Balazinski, M.; Czogala, E.; Jemielniak, E.; Leski, J. Tool condition monitoring using artificial intelligence methods. Eng. Appl. Artif. Intell. 2002, 15, 73–80. [Google Scholar] [CrossRef]
- Silva, R.G. Condition monitoring of the cutting process using a self-organizing spiking neural network map. J. Intell. Manuf. 2009, 21, 823–829. [Google Scholar] [CrossRef]
- Karatasou, S.; Santamouris, M. Detection of low-dimensional chaos in buildings energy consumption time series. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1603–1612. [Google Scholar] [CrossRef]
- Pham, T.D.; Thang, T.C.; Oyama-Higa, M.; Sugiyama, M. Mental-disorder detection using chaos and nonlinear dynamical analysis of photoplethysmographic signals. Chaos Solitons Fractals 2013, 51, 64–74. [Google Scholar] [CrossRef]
- Keane, C. Chaos in collective health: Fractal dynamics of social learning. J. Theor. Biol. 2016, 409, 47–59. [Google Scholar] [CrossRef] [PubMed]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M.; Acosta Del Campo, O.R. A RGB image encryption algorithm based on total plain image characteristics and chaos. Signal Process. 2015, 109, 119–131. [Google Scholar] [CrossRef]
- Khatibi, R.; Sivakumar, B.; Ali, M.; Kisi, O.; Koçak, K. Investigating chaos in river stage and discharge time series. J. Hydrol. 2012, 414–415, 108–117. [Google Scholar] [CrossRef]
- Lorenz, E. Deterministic non-periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Devaney, R.L. An Introduction to Chaotic Dynamical Systems; Addison-Wesley Publishing Company, Inc.: Redwood City, CA, USA, 1989. [Google Scholar]
- Letellier, C. Chaos in nature. In World Scientific Series on Nonlinear Science Series A: Volume 81, 1st ed.; World Scientific: Singapore, 2012; ISBN-10: 9814374423, ISBN-13: 978-9814374422. [Google Scholar]
- Grabec, I. Chaos generated by the cutting process. Phys. Lett. A 1986, 117, 384–386. [Google Scholar] [CrossRef]
- Grabec, I. Chaotic dynamics of the cutting process. Int. J. Mach. Tools Manuf. 1988, 28, 19–32. [Google Scholar] [CrossRef]
- Zakovorotny, V.L.; Lukyanov, A.D.; Gubanova, A.A.; Hristoforova, V. V Bifurcation of stationary manifolds formed in the neighborhood of the equilibrium in a dynamic system of cutting. J. Sound Vib. 2016, 368, 174–190. [Google Scholar] [CrossRef]
- Siddhpura, M.; Paurobally, R. A review of chatter vibration research in turning. Int. J. Mach. Tools Manuf. 2012, 61, 27–47. [Google Scholar] [CrossRef]
- Quintana, G.; Ciurana, J. Chatter in machining processes: A review. Int. J. Mach. Tools Manuf. 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Moon, F.C.; Abarbanel, H. Evidence for chaotic dynamics in metal cutting, and classification of chatter in lathe operations. In Summary Report of a Workshop on Nonlinear Dynamics and Material Processes and Manufacturing; Moon, F.C., Ed.; Institute for Mechanics and Materials, University of California: San Diego, CA, USA, 1995; pp. 11–12. [Google Scholar]
- Science, N.; Phenomena, C.; Alves, P.R.L.; Duarte, L.G.S.; Mota, L.A.C.P. Chaos, Solitons and Fractals A new characterization of chaos from a time series. Chaos Solitons Fractals Interdiscip. J. Nonlinear Sci. Nonequilibrium Complex Phenom. 2017, 104, 323–326. [Google Scholar]
- Eckman, J.A.; Kampshort, S.O.; Ruelle, D. Recurrence Plots of Dynamical Systems. Europhys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef] [Green Version]
- Wąż, P. New indicators of chaos. Appl. Math. Comput. 2014, 227, 449–455. [Google Scholar]
- Awrejcewicz, J.; Krysko, V.A.; Kutepov, I.E.; Vygodchikova, I.Y.; Krysko, A.V. Quantifying chaos of curvilinear beams via exponents. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 81–92. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. Dyn. Syst. Turbul. Lect. Notes Math. 1981, 898, 366–381. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Babloyantz, A. Estimation of Correlation Dimensions from Single and Multichannel Recordings—A Critical View. In Brain Dynamics: Progress and Perspectives; Başar, E., Bullock, T.H., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 122–130. ISBN 978-3-642-74557-7. [Google Scholar]
- Liebert, W.; Schuster, H.G. Proper choice of the time delay for the analysis of chaotic time series. Phys. Lett. A 1989, 142, 107–111. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D. Determining embedding dimension for phase space. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [Green Version]
- Abarbanel, H.D.I.; Brown, R.; Kennel, M.B. Lyapunov exponents in chaotic systems: Their importance and their evaluation using observed data. Int. J. Mod. Phys. B 1991, 5, 1347–1375. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Marwan, N.; Thiel, M.; Nowaczyk, N.R. Nonlinear Processes in Geophysics. Nonlinear Process. Geophys. 2002, 9, 325–331. [Google Scholar] [CrossRef]
- Kerry, R.; Oliver, M.A. Determining the effect of asymmetric data on the variogram. I. Underlying asymmetry. Comput. Geosci. 2007, 33, 1212–1232. [Google Scholar] [CrossRef]
- Lauro, C.H.; Brandão, L.C.; Baldo, D.; Reis, R.A.; Davim, J.P. Monitoring and processing signal applied in machining processes—A review. Measurement 2014, 58, 73–86. [Google Scholar] [CrossRef]
- ISO. International Standard ISO 3685: Tool-Life Testing with Single-Point Turning Tools; International Standards Organization (ISO): Geneva, Switzerland, 1993. [Google Scholar]
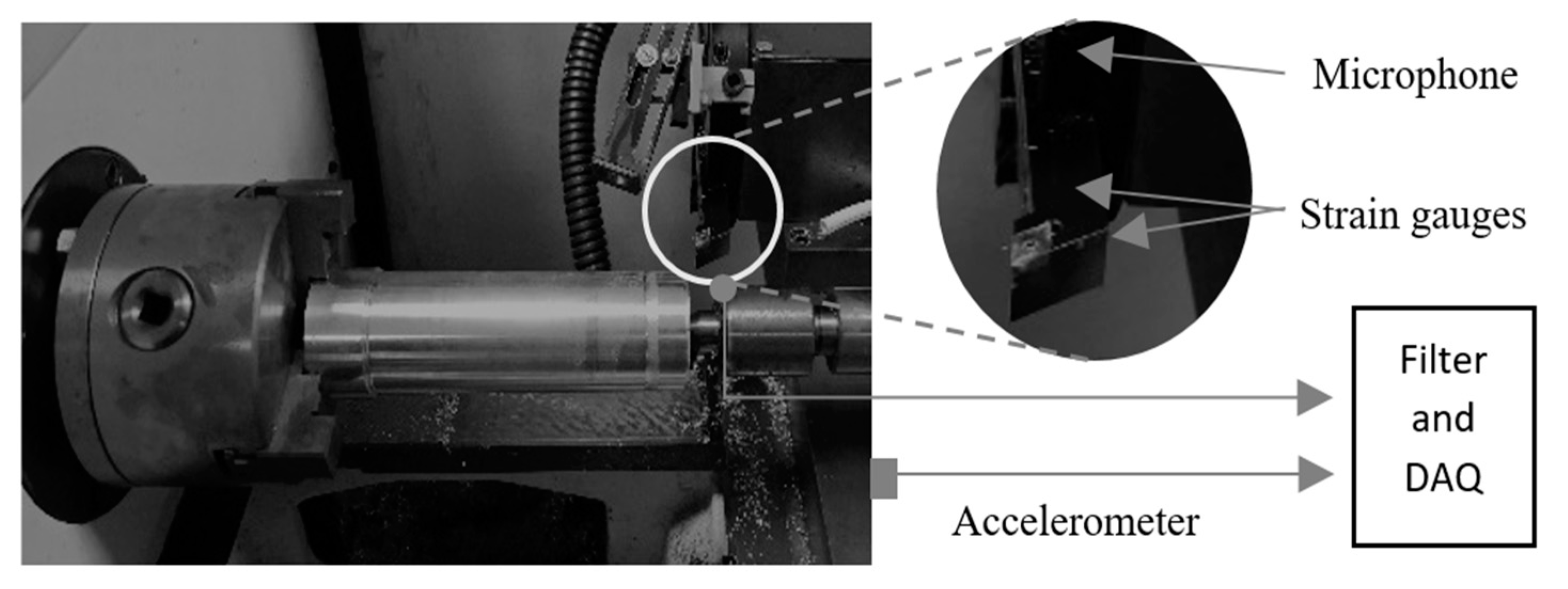


| Scheme | Type | Characteristics | Mounting |
|---|---|---|---|
| Accelerometer | Piezotron Kistler 8752A50 | Coupler–Kistler 5108, mounted resonant frequency 32.6 kHz, transverse sensitivity 1.6%, range ±50 g, and sensitivity 100.2 mV/g | Measuring Vertical vibration–Mounted on the base. |
| Microphone | ECM-1028 | Matching amplifier. | 10 cm from cutting insert. |
| Strain gauge | - | Feed and tangential force measurement–two half wheatstone bridge (amplification–RS 435–692) mounting | Tool holder-feed and tangential direction. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, R.; Araújo, A. The Deterministic Nature of Sensor-Based Information for Condition Monitoring of the Cutting Process. Machines 2021, 9, 270. https://doi.org/10.3390/machines9110270
Silva R, Araújo A. The Deterministic Nature of Sensor-Based Information for Condition Monitoring of the Cutting Process. Machines. 2021; 9(11):270. https://doi.org/10.3390/machines9110270
Chicago/Turabian StyleSilva, Rui, and António Araújo. 2021. "The Deterministic Nature of Sensor-Based Information for Condition Monitoring of the Cutting Process" Machines 9, no. 11: 270. https://doi.org/10.3390/machines9110270
APA StyleSilva, R., & Araújo, A. (2021). The Deterministic Nature of Sensor-Based Information for Condition Monitoring of the Cutting Process. Machines, 9(11), 270. https://doi.org/10.3390/machines9110270






