Using the Box–Behnken Response Surface Method to Study Parametric Influence to Improve the Efficiency of Helical Gears
Abstract
1. Introduction
2. Gear Power-Loss Analysis and Equations
2.1. Windage Loss
2.2. Bearing Churning Loss
2.3. Churning Loss
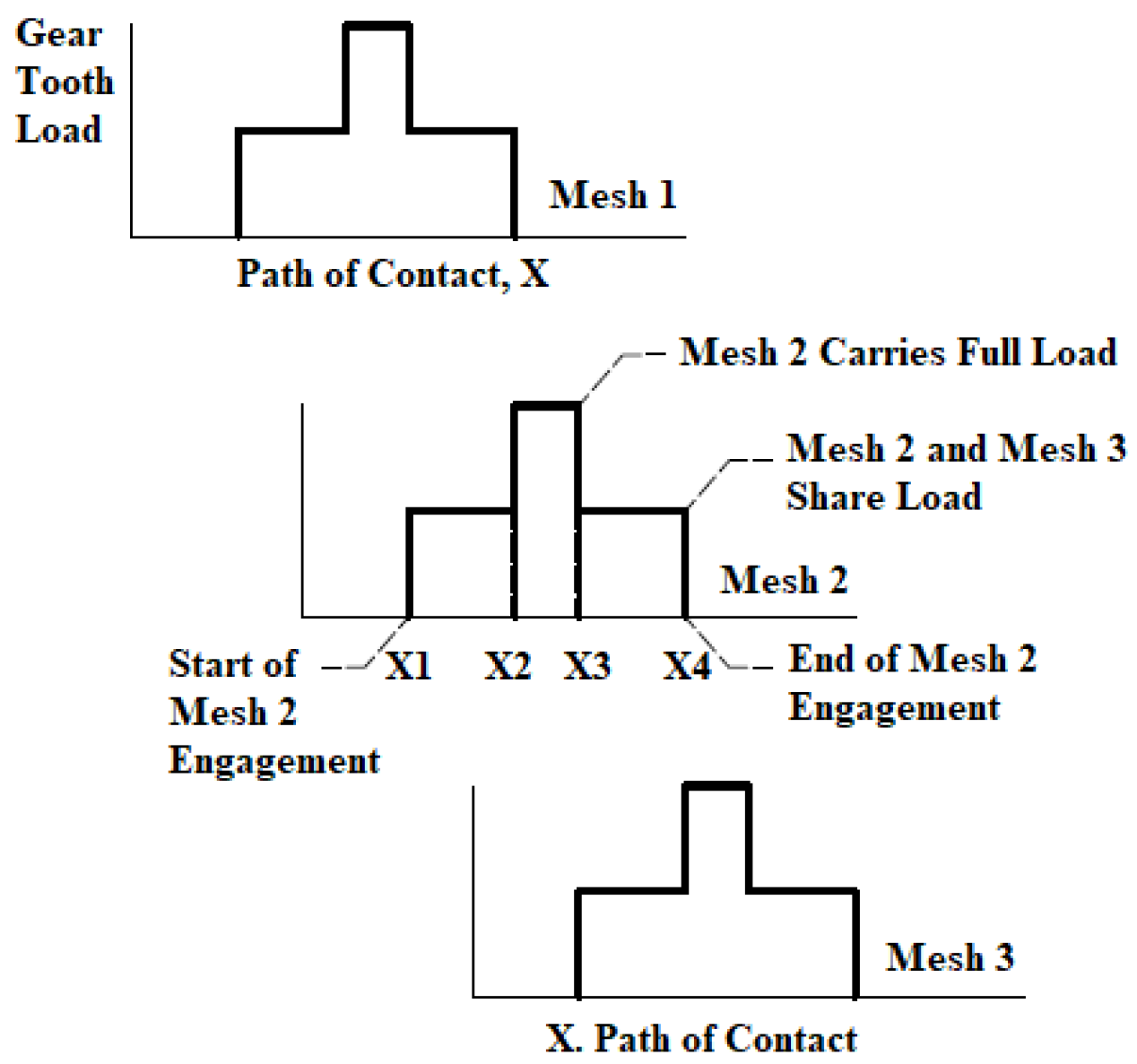
2.4. Meshing Losses
2.5. Rolling and Sliding Velocities
- the lubricant absolute viscosity η, dynamic viscosity μ, and kinematic viscosity v, which remain constant;
- the geometrical parameters da1, da2, db1, db2, etc., calculated from the specified quantities;
- the numbers z1 and z2 of teeth, the normal pressure angle α, the helix angle β, the gear ratio u, the module m, the normal force F exerted on the teeth, the torque T, and the rotation speed n, all of which are changeable parameters.
3. Design of Experiments
3.1. Screening Design
3.2. Box–Behnken Design
3.3. Highest and Lowest Gear Efficiencies
4. Results and Discussion
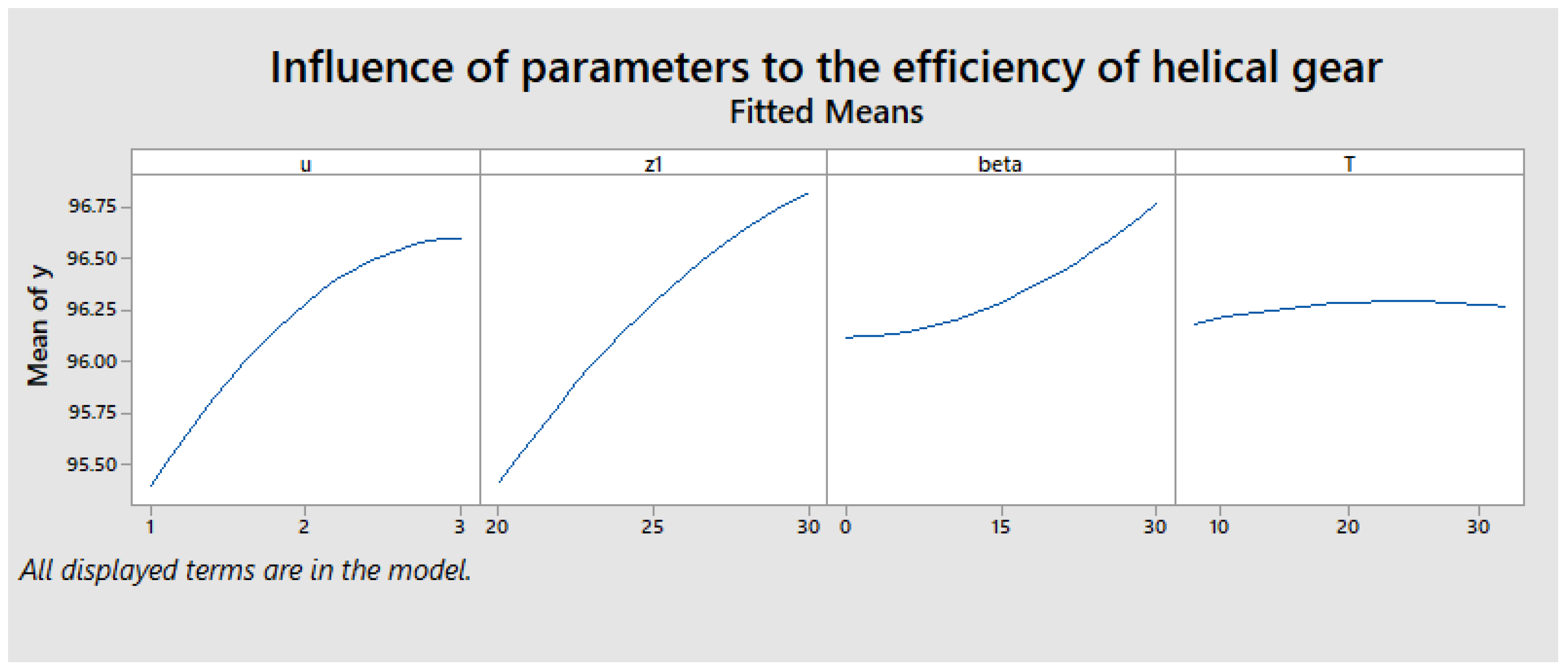
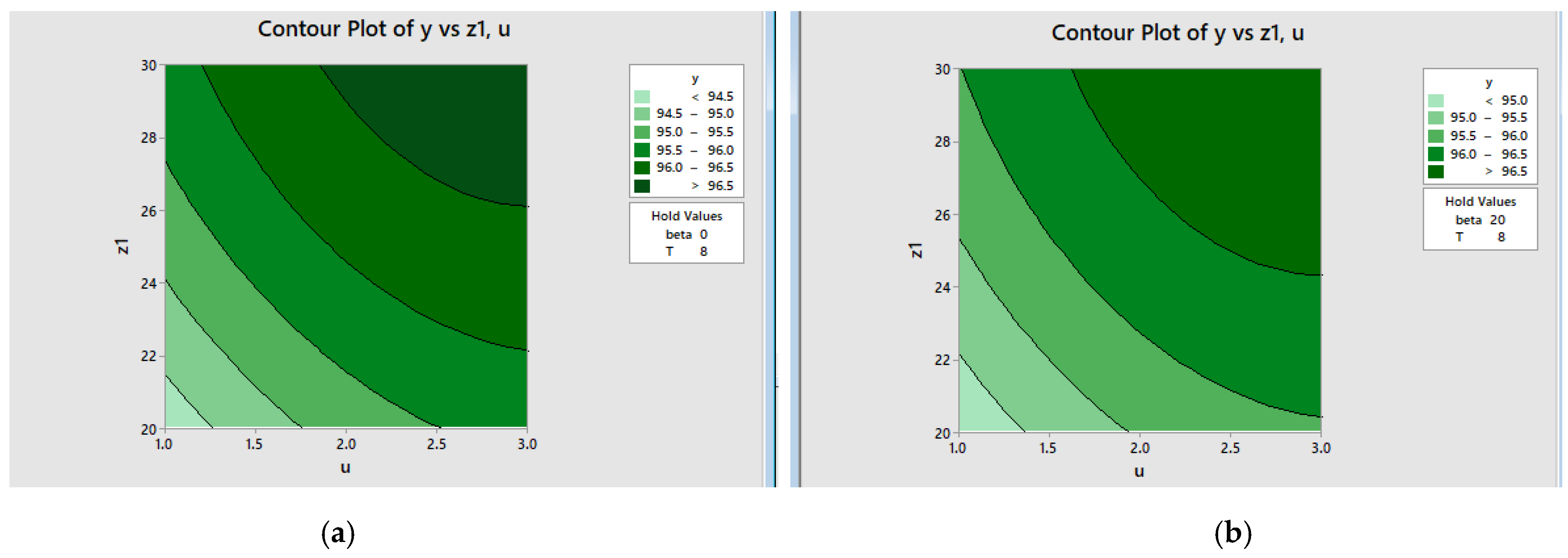
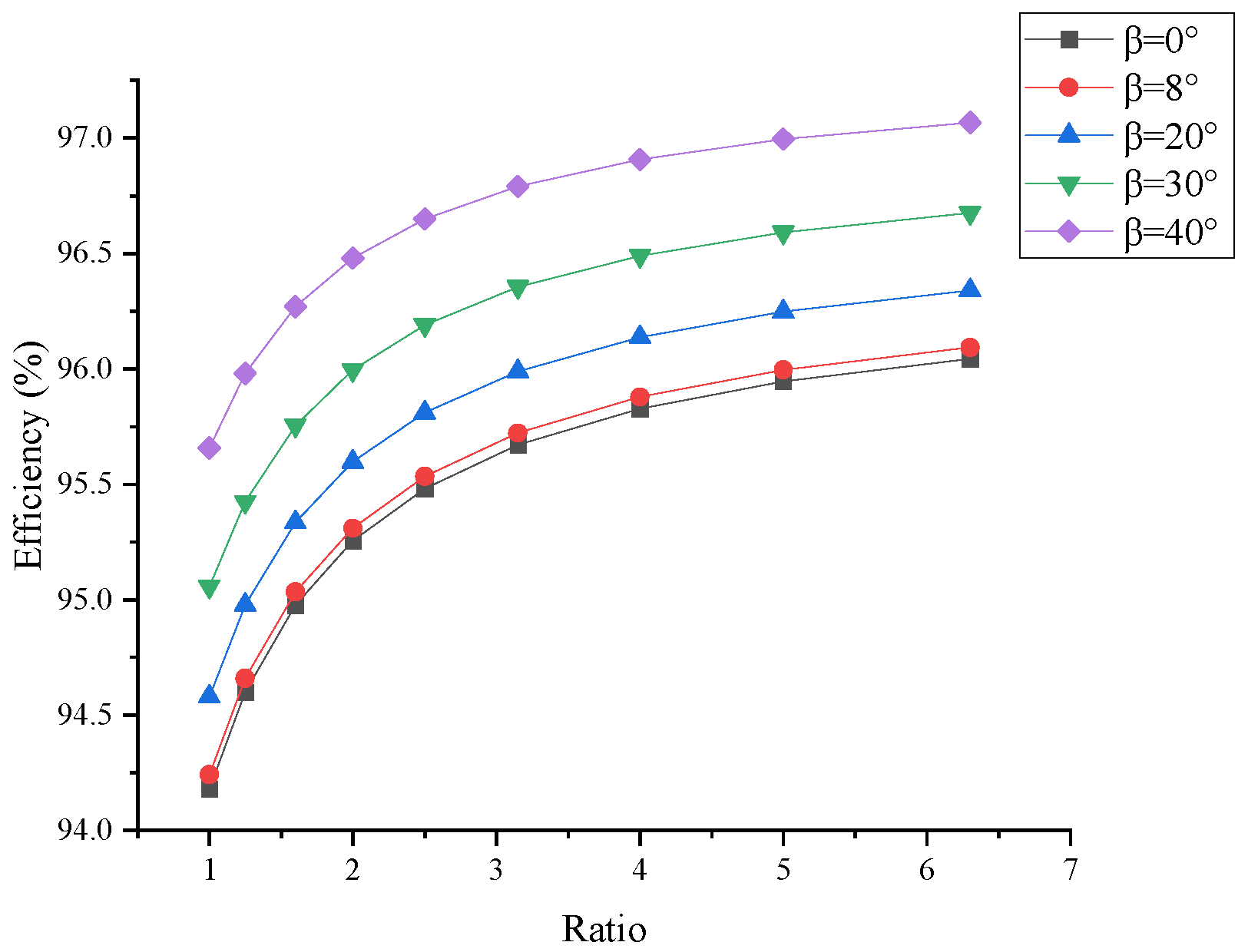
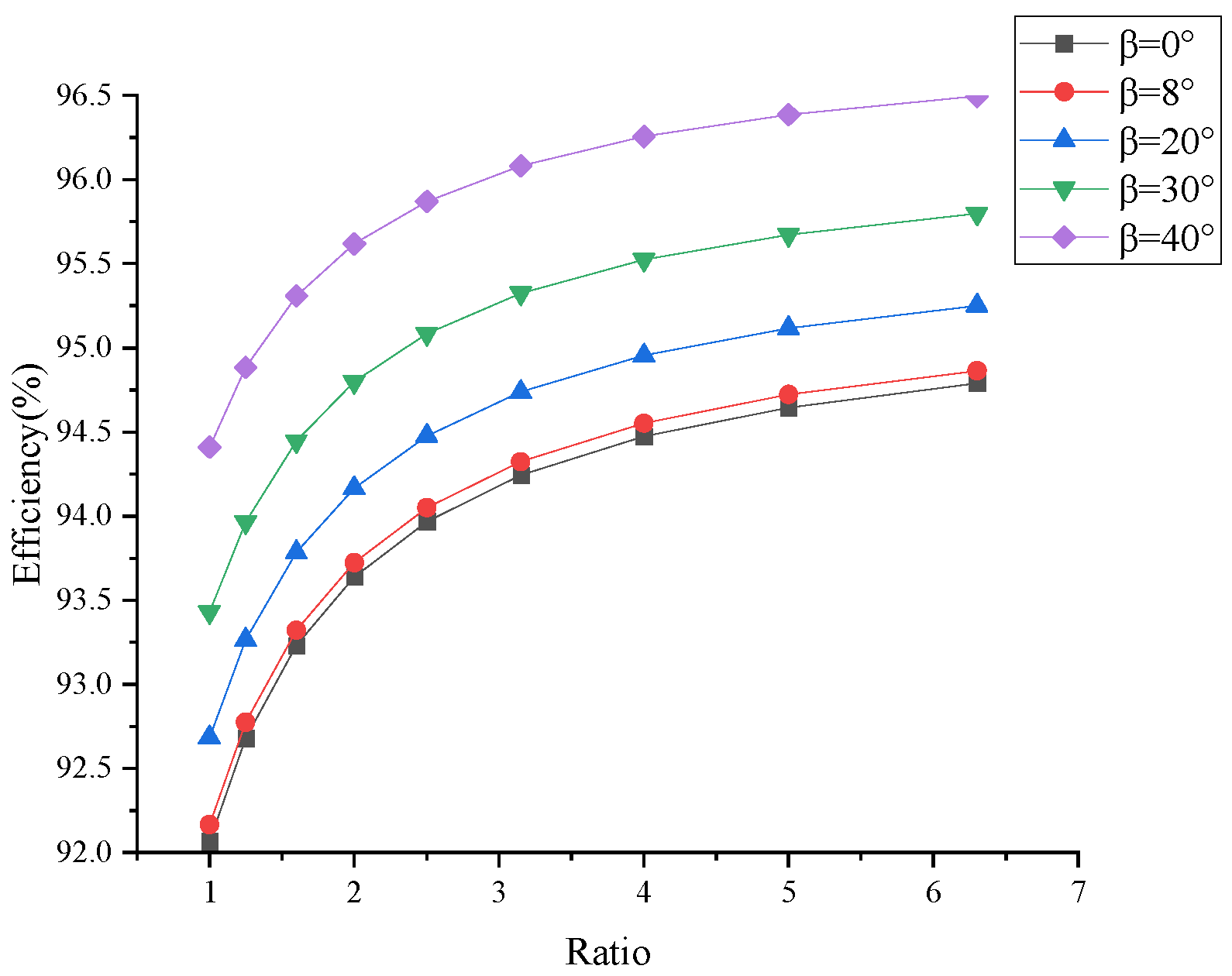
4.1. Lookup Tables for Gear Ratio u and Gear Efficiency η
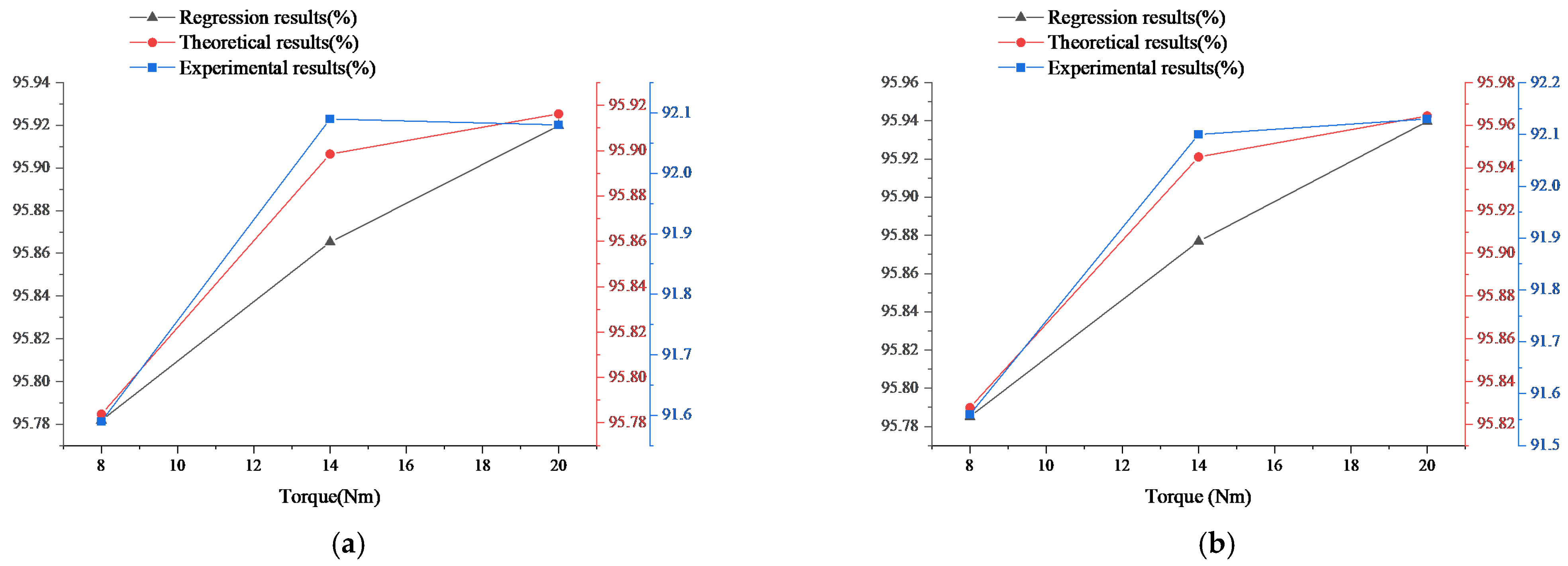
4.2. Experimental Verification
4.3. Comparison of Experimental and Theoretical Regression Model Results
- errors in size, parallelism, perpendicularity, concentricity, and other aspects during manufacturing;
- assembly errors when putting parts together;
- there are many calculation steps in the theoretical calculation process, and rounding at each step generates discrepancies in the theoretical calculation results;
- the torque is generated by weights, and the torque value is inaccurate;
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dudley, D.W. Gear Handbook: The Design, Manufacture and Application of Gears, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1962; pp. 14.1–14.52. [Google Scholar]
- Fernandes, C.M.C.G.; Marques, P.M.T.; Martins, R.C.; Seabra, J.H.O. Influence of gear loss factor on the power loss prediction. Mech. Sci. 2015, 6, 81–88. [Google Scholar] [CrossRef][Green Version]
- Hohn, B.-R.; Michaelis, K.; Hinterstoisser, M. Influence factors on gearbox power loss. In Proceedings of the 3rd International Conference on Integrity, Reliability and Failure, Porto, Portugal, 20–24 July 2009. [Google Scholar]
- Anderson, M. An Experimental Investigation of Spur Gear Efficiency and Temperature. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 2017. [Google Scholar]
- Vaidyanathan, A. An Experimental Investigation of Helical Gear Efficiency. Master’s Thesis, Ohio State University, Columbus, OH, USA, 2009. [Google Scholar]
- Guan, D.; Jing, L.; Han, X.; Wang, L.; Gong, J. Theoretical modeling and numerical simulation of dynamic contact characteristics of a spherical pump with variable friction coefficient. Proc. Inst. Mech. Eng. Part. J J. Eng. Tribol. 2021, 2021, 13506501211016201. [Google Scholar]
- Bashta, O.; Nosko, P.; Nosko, P.; Boyko, G.; Golovin, A.; Stebeletska, N. Power losses of gear systems. Probl. Frict. Wear 2017, 4, 107–116. [Google Scholar]
- Anderson, N.E.; Loewenthal, S.H.; Black, J.D. Spur-Gear-System Efficiency at Part and Full Load; NASA Technical Paper; NASA: Washington DC, WA, USA, 1980. [Google Scholar]
- Ziegltrum, A.; Lohner, T.; Stahl, K. TEHL Simulation on the Influence of Lubricants on Load-Dependent Gear Losses. Tribiol. Int. 2016, 113, 252–261. [Google Scholar] [CrossRef]
- Wang, C.; Shi, Z. A dynamic calculation method of sliding friction losses for a helical gear pair. J. Braz. Soc. Mech. Sci. Eng. 2016, 39, 1521–1528. [Google Scholar] [CrossRef]
- Jurkschat, T.; Lohner, T.; Stahl, K. Improved calculation method for load-dependent gear losses. Forsch Ing. 2017, 81, 109–115. [Google Scholar] [CrossRef]
- Voeltzel, N.; Marchesse, Y.; Changenet, C.; Ville, F.; Velex, P. On the influence of helix angle and face width on gear windage losses. Proc. IMechE Part. C J. Mech. Eng. Sci. 2016, 230, 1101–1112. [Google Scholar] [CrossRef]
- Jurkschat, T.; Lohner, T.; Stahl, K. Improved calculation of load-dependent gear losses by consideration of so far disregarded influences. Proc. IMechE Part. J J. Eng. Tribol. 2018, 233, 509–519. [Google Scholar] [CrossRef]
- Zeng, Q.-L.; Sun, Z.Y.; Wan, L.R.; Yang, Y.; Dai, H.Z.; Yang, Z.K. Research and comparative analysis of flow field characteristics and load-independent power losses of internal and external gear pairs. Math. Probl. Eng. 2020, 2020, 8860588. [Google Scholar] [CrossRef]
- Kahraman, A.; Houser, D.R.; Xu, H. Development of a Generalized Mechanical Efficiency Prediction Methodology for Gear Pairs. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2005. [Google Scholar]
- Heingartner, P.; Mba, D. Determining power losses in the helical gear mesh. Gear Technol. 2015, 22, 32–37. [Google Scholar]
- Nguyen, H.L. Design and Analysis of Experiments, 1st ed.; Publishing House, Vietnam National University: Ho Chi Minh City, Vietnam, 2020. [Google Scholar]
- Loc, N.H.; Hung, N.P. Utilizing response surface methods designs for optimization of technological parameters on the vibration amplitude of cnc router spindle. ASEAN Eng. J. 2021, 11, 34–44. [Google Scholar] [CrossRef]

| Level | |||||||
|---|---|---|---|---|---|---|---|
| N | Factor | Unit | Symbol | Code | −1 | 0 | +1 |
| 1 | Rotation speed | rpm | n | x1 | 200 | 400 | 600 |
| 2 | Gear ratio | - | u | x2 | 1 | 2 | 3 |
| 3 | Tooth number | - | z1 | x3 | 20 | 25 | 30 |
| 4 | Helix angle | ° | β | x4 | 0 | 15 | 30 |
| 5 | Normal pressure angle | ° | α | x5 | 20 | 25 | 30 |
| 6 | Module | mm | m | x6 | 2 | 2.5 | 3 |
| 7 | Torque | N∙m | T | x7 | 8 | 20 | 32 |
| Coded | Uncoded | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | x1 | x2 | x3 | x4 | x5 | x6 | x7 | n | u | z1 | β | α | m | T | Efficiency |
| 1 | +1 | −1 | +1 | −1 | −1 | −1 | +1 | 600 | 1 | 30 | 0 | 20 | 2 | 32 | 96.2245 |
| 2 | +1 | +1 | −1 | +1 | −1 | −1 | −1 | 600 | 3 | 20 | 30 | 20 | 2 | 8 | 96.5375 |
| 3 | −1 | +1 | +1 | −1 | +1 | −1 | −1 | 200 | 3 | 30 | 0 | 30 | 2 | 8 | 96.9777 |
| 4 | +1 | −1 | +1 | +1 | −1 | +1 | −1 | 600 | 1 | 30 | 30 | 20 | 3 | 8 | 95.4477 |
| 5 | +1 | +1 | −1 | +1 | +1 | −1 | +1 | 600 | 3 | 20 | 30 | 30 | 2 | 32 | 97.0477 |
| 6 | +1 | +1 | +1 | −1 | +1 | +1 | −1 | 600 | 3 | 30 | 0 | 30 | 3 | 8 | 94.7501 |
| 7 | −1 | +1 | +1 | +1 | −1 | +1 | +1 | 200 | 3 | 30 | 30 | 20 | 3 | 32 | 97.5257 |
| 8 | −1 | −1 | +1 | +1 | +1 | −1 | +1 | 200 | 1 | 30 | 30 | 30 | 2 | 32 | 96.8106 |
| 9 | −1 | −1 | −1 | +1 | +1 | +1 | −1 | 200 | 1 | 20 | 30 | 30 | 3 | 8 | 95.4031 |
| 10 | +1 | −1 | −1 | −1 | +1 | +1 | +1 | 600 | 1 | 20 | 0 | 30 | 3 | 32 | 95.6499 |
| 11 | −1 | +1 | −1 | −1 | −1 | +1 | +1 | 200 | 3 | 20 | 0 | 20 | 3 | 32 | 95.7151 |
| 12 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 200 | 1 | 20 | 0 | 20 | 2 | 8 | 93.8570 |
| Code | Uncode | Efficiency with Lubrication | FITS | RESI1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | x1 | x2 | x3 | x4 | u | z1 | β | T | |||
| 1 | −1 | −1 | 0 | 0 | 1 | 20 | 15 | 20 | 94.2958 | 94.3992 | −0.103402 |
| 2 | +1 | −1 | 0 | 0 | 3 | 20 | 15 | 20 | 95.7969 | 95.8505 | −0.053582 |
| 3 | −1 | +1 | 0 | 0 | 1 | 30 | 15 | 20 | 96.0755 | 96.0418 | 0.033658 |
| 4 | +1 | +1 | 0 | 0 | 3 | 30 | 15 | 20 | 97.0976 | 97.0141 | 0.083479 |
| 5 | 0 | 0 | −1 | −1 | 2 | 25 | 0 | 8 | 96.0530 | 96.0562 | −0.003234 |
| 6 | 0 | 0 | +1 | −1 | 2 | 25 | 30 | 8 | 96.5724 | 96.6252 | −0.052775 |
| 7 | 0 | 0 | −1 | +1 | 2 | 25 | 0 | 32 | 96.0885 | 96.0557 | 0.032851 |
| 8 | 0 | 0 | +1 | +1 | 2 | 25 | 30 | 32 | 96.7691 | 96.7858 | −0.016690 |
| 9 | −1 | 0 | 0 | −1 | 1 | 25 | 15 | 8 | 95.3570 | 95.3230 | 0.033981 |
| 10 | +1 | 0 | 0 | −1 | 3 | 25 | 15 | 8 | 96.4847 | 96.4670 | 0.017758 |
| 11 | −1 | 0 | 0 | +1 | 1 | 25 | 15 | 32 | 95.3303 | 95.3352 | −0.004909 |
| 12 | +1 | 0 | 0 | +1 | 3 | 25 | 15 | 32 | 96.5937 | 96.6148 | −0.021132 |
| 13 | 0 | −1 | −1 | 0 | 2 | 20 | 0 | 20 | 95.1904 | 95.1627 | 0.027651 |
| 14 | 0 | +1 | −1 | 0 | 2 | 30 | 0 | 20 | 96.7010 | 96.7319 | −0.030912 |
| 15 | 0 | −1 | +1 | 0 | 2 | 20 | 30 | 20 | 96.0221 | 95.9783 | 0.043762 |
| 16 | 0 | +1 | +1 | 0 | 2 | 30 | 30 | 20 | 97.2006 | 97.2154 | −0.014802 |
| 17 | −1 | 0 | −1 | 0 | 1 | 25 | 0 | 20 | 95.1816 | 95.1780 | 0.003620 |
| 18 | +1 | 0 | −1 | 0 | 3 | 25 | 0 | 20 | 96.4469 | 96.4769 | −0.029977 |
| 19 | −1 | 0 | +1 | 0 | 1 | 25 | 30 | 20 | 95.9517 | 95.9146 | 0.037051 |
| 20 | +1 | 0 | +1 | 0 | 3 | 25 | 30 | 20 | 97.0428 | 97.0393 | 0.003454 |
| 21 | 0 | −1 | 0 | −1 | 2 | 20 | 15 | 8 | 95.4491 | 95.4077 | 0.041383 |
| 22 | 0 | +1 | 0 | −1 | 2 | 30 | 15 | 8 | 96.5850 | 96.6221 | −0.037114 |
| 23 | 0 | −1 | 0 | +1 | 2 | 20 | 15 | 32 | 95.3432 | 95.2990 | 0.044188 |
| 24 | 0 | +1 | 0 | +1 | 2 | 30 | 15 | 32 | 96.8566 | 96.8909 | −0.034309 |
| 25 | 0 | 0 | 0 | 0 | 2 | 25 | 15 | 20 | 96.2855 | 96.2855 | 0.000000 |
| 26 | 0 | 0 | 0 | 0 | 2 | 25 | 15 | 20 | 96.2855 | 96.2855 | 0.000000 |
| 27 | 0 | 0 | 0 | 0 | 2 | 25 | 15 | 20 | 96.2855 | 96.2855 | 0.000000 |
| Term | Coef. | SE Coef. | T | P |
|---|---|---|---|---|
| Constant | 85.0307 | 0.804593 | 105.682 | 0.000 |
| u | 2.3496 | 0.185391 | 12.674 | 0.000 |
| z1 | 0.5125 | 0.052719 | 9.722 | 0.000 |
| β | 0.0298 | 0.011422 | 2.611 | 0.023 |
| T | −0.0281 | 0.014983 | −1.872 | 0.086 |
| u2 | −0.2895 | 0.025040 | −11.561 | 0.000 |
| z12 | −0.0068 | 0.001002 | −6.772 | 0.000 |
| β2 | 0.0007 | 0.000111 | 6.239 | 0.000 |
| T2 | −0.0004 | 0.000174 | −2.434 | 0.031 |
| uz1 | −0.0240 | 0.005783 | −4.142 | 0.001 |
| uβ | −0.0029 | 0.001928 | −1.506 | 0.158 |
| uT | 0.0028 | 0.002410 | 1.173 | 0.264 |
| z1β | −0.0011 | 0.000386 | −2.871 | 0.014 |
| z1T | 0.0016 | 0.000482 | 3.263 | 0.007 |
| βT | 0.0002 | 0.000161 | 1.394 | 0.189 |
| Model summary | S | R-sq. | R-sq. (adj.) | R-sq. (pred.) |
| 0.0578286 | 99.68% | 99.32% | 98.18% |
| β | Ratio | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.25 | 1.6 | 2 | 2.5 | 3.15 | 4 | 5 | 6.3 | |
| 00 | 94.18 | 94.60 | 94.98 | 95.26 | 95.48 | 95.67 | 95.83 | 95.95 | 96.04 |
| 80 | 94.24 | 94.66 | 95.03 | 95.31 | 95.53 | 95.72 | 95.88 | 96.00 | 96.09 |
| 200 | 94.58 | 94.98 | 95.34 | 95.60 | 95.81 | 95.99 | 96.14 | 96.25 | 96.34 |
| 300 | 95.06 | 95.42 | 95.75 | 96.00 | 96.19 | 96.35 | 96.49 | 96.59 | 96.68 |
| 400 | 95.66 | 95.98 | 96.27 | 96.48 | 96.65 | 96.79 | 96.91 | 97.00 | 97.07 |
| β | Ratio | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.25 | 1.6 | 2 | 2.5 | 3.15 | 4 | 5 | 6.3 | |
| 0° | 92.07 | 92.68 | 93.23 | 93.64 | 93.97 | 94.24 | 94.47 | 94.65 | 94.79 |
| 8° | 92.17 | 92.78 | 93.32 | 93.72 | 94.05 | 94.32 | 94.55 | 94.72 | 94.86 |
| 20° | 92.69 | 93.26 | 93.78 | 94.17 | 94.48 | 94.74 | 94.95 | 95.12 | 95.25 |
| 30° | 93.43 | 93.97 | 94.45 | 94.80 | 95.08 | 95.32 | 95.52 | 95.67 | 95.80 |
| 40° | 94.41 | 94.88 | 95.31 | 95.62 | 95.87 | 96.08 | 96.26 | 96.39 | 96.49 |
| Torque [N∙m] | Experimental Results [N∙m] | Variances | Efficiency [%] | |||
|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | Average | |||
| 8 | 0.683 | 0.661 | 0.674 | 0.673 | 0.0001225 | 91.59 |
| 14 | 1.108 | 1.120 | 1.094 | 1.107 | 0.0001695 | 92.09 |
| 20 | 1.611 | 1.583 | 1.552 | 1.583 | 0.0008725 | 92.08 |
| Torque [N∙m] | Experimental Results [N∙m] | Variances | Efficiency [%] | |||
|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | Average | |||
| 8 | 0.679 | 0.652 | 0.695 | 0.675 | 0.0004725 | 91.56 |
| 14 | 1.093 | 1.109 | 1.117 | 1.106 | 0.0001495 | 92.10 |
| 20 | 1.533 | 1.602 | 1.587 | 1.574 | 0.0013170 | 92.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.L.; Duy, L.T. Using the Box–Behnken Response Surface Method to Study Parametric Influence to Improve the Efficiency of Helical Gears. Machines 2021, 9, 264. https://doi.org/10.3390/machines9110264
Nguyen HL, Duy LT. Using the Box–Behnken Response Surface Method to Study Parametric Influence to Improve the Efficiency of Helical Gears. Machines. 2021; 9(11):264. https://doi.org/10.3390/machines9110264
Chicago/Turabian StyleNguyen, Huu Loc, and Le Thanh Duy. 2021. "Using the Box–Behnken Response Surface Method to Study Parametric Influence to Improve the Efficiency of Helical Gears" Machines 9, no. 11: 264. https://doi.org/10.3390/machines9110264
APA StyleNguyen, H. L., & Duy, L. T. (2021). Using the Box–Behnken Response Surface Method to Study Parametric Influence to Improve the Efficiency of Helical Gears. Machines, 9(11), 264. https://doi.org/10.3390/machines9110264





