Abstract
To gain fast dynamic response, high performance, and good tracking capability, several control strategies have been applied to synchronous reluctance motors (SynRMs). In this paper, a nonlinear advanced strategy of speed predictive control (SPC) based on the finite control set model predictive control (FCS-MPC) is proposed and simulated for nonlinear SynRMs. The SPC overcomes the limitation of the cascaded control structure of the common vector control by employing a novel strategy that considers all the electrical and mechanical variables in one control law through a new cost function to obtain the switching signals for the power converter. The SynRM flux maps are known based on finite element method (FEM) analysis to take into consideration the effect of the nonlinearity of the machine. To clear the proposed strategy features, a functional and qualitative comparison between the proposed SPC, field-oriented control (FOC) with an anti-windup scheme, and current predictive control (CPC) with outer PI speed control loop is presented. For simplicity, particle swarm optimization (PSO) is performed to tune all the unknown parameters of the control strategies. The comparison features include controller design, dynamic and steady-state behaviors. Simulation results are presented to investigate the benefits and limitations of the three control strategies. Finally, the proposed SPC, FOC, and CPC have their own merits, and all methods encounter the requirements of advanced high-performance drives.
1. Introduction
The control of AC electric machines is one of the most important challenging issues in electrical engineering. Presently with the high development of electric vehicles, this topic gains great interest in academia and industry. Additionally, the rapidly increasing computation capability of recently developed microprocessors provides the opportunity to use more powerful control techniques [1].
Furthermore, in the present time, rugged designed synchronous reluctance motors (SynRMs) are an alternative to permanent magnet synchronous motors and induction motors in some commercial and numerous industrial applications [2,3]. The features that support this choice are high reliability and efficiency, low cost, and easier field weakening capability [4,5,6]. Generally, SynRMs are highly nonlinear and there is a nonlinear relationship between the stator inductances and stator currents due to magnetic saturation and cross-coupling magnetizing effects (chapt. 14 in [7,8]). This causes problems for the control of the SynRM. Several strategies have been investigated to calculate and measure the motor electrical parameters as in [9,10]. The apparent defect in these methods, despite the ease of the measurement, is that they require an external circuit to implement. Recently, the finite element method (FEM) has been investigated to simulate and compute the parameters of the motor under ideal operating conditions. The FEM is a numerical strategy that investigates the performance and parameters of the machine based on the distribution of electromagnetic field in the electrical machine [11,12]. All the materials properties, geometrical dimensions, and windings data should be known. In this work, the FEM is employed to take the influence of the magnetic cross saturation for the motor through the flux maps computation.
Commonly, two types of control have been dominating the market during the previous decades. The first one is the field-oriented control FOC, which is a cascaded control and uses PWM to generate the required voltages to the motor. Due to its good performance at transient and steady-state conditions, FOC has been widely applied to electrical drives [1,5,13,14]. However, the use of many PI controllers in the external and inner loops that contain many parameters to tune is the weakness of this control scheme. The other type is the direct torque control (DTC) which provides a fast dynamic response with high torque ripples [1]. Due to the increase of digital signal processing and power converters, in which fast dynamic response and uncomplex control are favored, researchers have been made for the nonlinear control strategies. One of these is the finite control set model predictive control (FCS-MPC) [15,16,17].
FCS-MPC methods are classified into three major groups: current predictive control (CPC), torque predictive control (TPC), and speed predictive control (SPC) [18,19]. CPC and TPC apply the MPC only to the internal electric subsystem control (inner loops), while the outer speed loop is still controlled by a PI controller [20]. SPC combines the inner and outer loops of the common vector control in a full predictive control topology [21]. Several CPC and TPC topologies have been proposed for SynRMs in the literature [2,22,23,24,25]. In [2], model-free predictive current control of SynRM is proposed, which gives a better performance than the PI controller. An efficient predictive current control of SynRM based on online parameter estimation is presented in [3], which gives a superior response than the conventional current predictive control. However, in [3], the influence of the magnetic saturation is not considered in the model of SynRM. Predictive torque control of synchronous reluctance motor is presented in [22]. However, most topologies that have been developed in the literature concentrate either on current or torque control, which still requires the outer speed loop. Furthermore, the studies showed that CPC and TPC give a good steady-state routine and slightly enhance the system robustness under parameter variations. Though, the dynamic response is still comparatively slow due to the cascaded speed loop. Due to the limitations of CPC and TPC, many SPC schemes have been performed on electric drives. In [26], model predictive speed control of permanent magnet synchronous motor (PMSM) based on the finite control set is proposed. Speed predictive control with a short prediction horizon for PMSM is presented in [27]. However, the authors incorporated all the control objectives in a complicated cost function, with several numbers of weighting factors, which may become tough to tune. The speed predictive control of SynRM is proposed in [28]. However, the predictive control is only applied to the external loop while maintaining the PI controllers in the inner current loops. In conclusion, there are slight numbers of studies focus on speed predictive control of SynRM, which encouraged the authors to do this work.
Newly, tuning the weighting factors of the cost function and PI Controller factors is one of the most challenges to succeed a sufficient routine and robustness of the drive system [29,30]. Particle swarm optimization (PSO) is considered one of the new heuristic approaches use to compute the variables that needed to minimize or maximize a certain objective function through the travel over the search area of the particle’s problems [31,32,33,34]. It has found to be more active in solving many optimization problems with having fewer parameters to fine-tune.
In this work, a new method of the SPC for the SynRM with the impact of cross saturation is proposed and simulated. The proposed SPC is replaced all PI controllers (inner and outer loops) by one control law called cost function to generate the signals for the converter. Furthermore, the PSO algorithm is employed for tuning the weighting factors in the proposed cost function, i.e., the effort and time to tune these factors by trail-and-error is avoided. In addition, to show the benefits of the proposed method, a comprehensive comparison between the proposed strategy, FOC, and CPC is discussed. Also, FOC with an anti-windup scheme is used to decrease performance degradation and pulse-width modulation is employed to regulate the fundamental component of the motor voltages. CPC based on FCS-MPC is a nonlinear method to directly generate the voltage vectors in the absence of the modulator. For ensuring the fair comparison between the three strategies, a set of parameters are kept constant such as simulation configuration parameters, sampling time for the prediction models, and PI controller parameters for generating the reference electromagnetic torque. Furthermore, a convergent switching frequency has been obtained for all the strategies.
The paper is organized as follows: Section 2 displays the drive model of the inverter and SynRM modeling. In Section 3, the advanced control strategies are presented in detail. Section 4 illustrates the PSO for tuning. In Section 5, the simulation results and discussion are presented. Finally, the paper is concluded in Section 6.
2. Drive Model
This section presents the mathematical model of the three-phases two-level voltage source inverter (32L-VSI) and the nonlinear SynRM [4,8] and ([7], chapt. 14).
2.1. Inverter Model
The 32L-VSI is considered the most widespread inverter in low and medium power drive applications. The inverter is coupled with the SynRM to supply three-phase voltages as displayed in Figure 1a. The 32L-VSI produces eight voltage vectors categorized as , where two zero voltages , and six active vectors , as illustrated in Figure 1b. The output stator voltages of the SynRM can be given as a function of the switching vector of the inverter as [3,7,21]:
where and are the inverse Park and Clark transformations see [4] and ([7], chapt.14), and is the dc-link voltage.
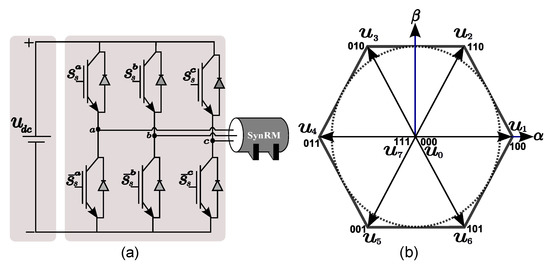
Figure 1.
Three-phase two-level VSI: (a) Topology, and (b) voltage space vectors.
2.2. Synchronous Reluctance Motor Modeling
In this paper, the nonlinear model of SynRM is considered, where the influence of magnetic saturation and cross-coupling magnetizing effects of the machine are considered based on the machine flux maps that obtained using FEM data (Courtesy of Prof Maarten Kamper, Stellenbosch University, ZA). The nonlinear relationship between stator flux linkages and stator currents is revealed in Figure 2. Furthermore, the inductances can be approximated by the differentiation of the stator fluxes with respect to the stator currents as displayed in Figure 3. Therefore, the look-up tables (LUTs) of the differential inductance matrix and flux linkages can be created and used for online adaptation of the control strategies. The continuous-time model of the SynRM in the reference frame can be written as [4] and ([7], chapt. 14):
where
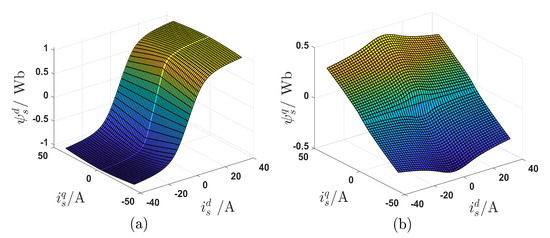
Figure 2.
The nonlinear flux linkages of a real 9.6 kW SynRM obtained from FEM data: (a) d-axis component , and (b) q-axis component .
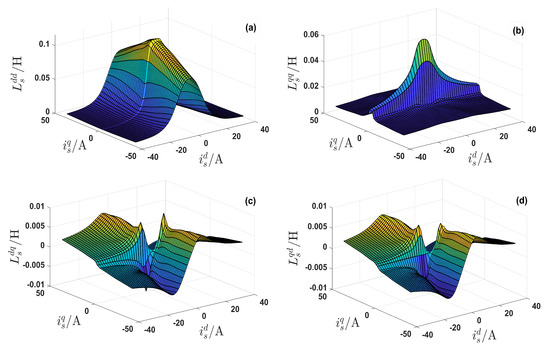
Figure 3.
Nonlinear differential inductances of a 9.6 kW SynRM (obtained from the FEM data): (a) d-axis inductance . (b) q-axis inductance . (c) Cross-coupling inductance . (d) Cross-coupling inductance .
The differential stator inductance matrix and time derivative of the stator flux linkages can be expressed as
3. Control Strategies
The theory of field-oriented control (FOC), current predictive control (CPC), and proposed speed predictive control (SPC) strategies of SynRM are discussed and investigated in this section.
3.1. Field-Oriented Control Strategy
3.1.1. Anti-Windup Scheme
When the input error to the PI controllers is high or remains non-zero for a long time. The output of the controller may be saturated, which makes the integrator output accumulated. For these reasons, the anti-windup is employed in the presence of saturation and to reduce the performance degradation. The block diagram of the PI controller with an anti-windup scheme is described in Figure 4. The decision function (conditional integration) for anti-windup is chosen to be ([7], chapt. 14) and [4,35]
where is the saturation limit.
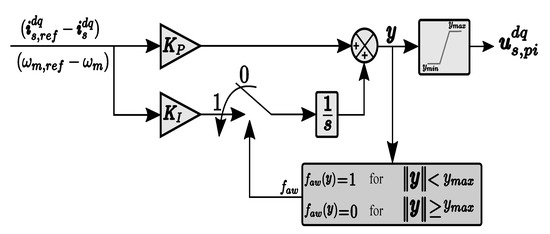
Figure 4.
PI controller with anti-windup block diagram [4].
3.1.2. Field-Oriented Control of Nonlinear SynRM
The main idea of the FOC strategy is to use an appropriate coordinate system to achieve independent control of flux and torque [1]. The whole block diagram of the FOC for SynRM is shown in Figure 5. The flux linkages and the differential matrix of stator inductance as displayed in Figure 2 and Figure 3, are known. Furthermore, the stator currents and motor electrical position and speed , are available for feedback. Usually, an optimal torque feedforward control must be implemented to compute the optimal and feasible current references which depend on the actual operating point and consider current, voltage and speed constraints [36]. In this paper, for simplicity, a constant d-current is fed to the underlying current control loops of FOC and CPC. Consequently, in the rotating reference frame , the reference value of direct stator current is set as a constant value, while the reference value of the quadrature stator current can be computed from the error between the reference and actual values of the speed and anti-windup scheme as follows
where is the decision function of the anti-windup approach as in Equation (7), and in this case , and and are the proportional and integral parameters for PI speed controller that obtained using the PSO algorithm (see Section 4). The references values of the stator voltages can be computed as [4]
where are the voltages from PI current controller with anti-windup approach as follows [4] and ([7], chapt. 14)
where as in Equation (7) and in this case , and is the integrator output of the PI controller and and are the proportional and integration gain matrices
The second part of Equation (9) is the disturbance compensation voltages, given by [4] and ([7], chapt. 14)
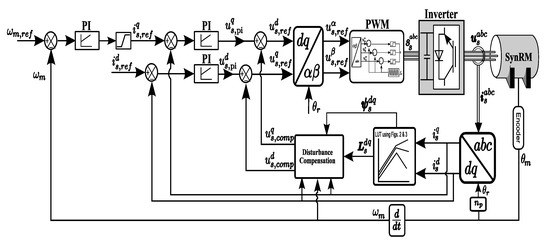
Figure 5.
Field-oriented control of synchronous reluctance motor [4].
Finally, the reference voltages as in Equation (9) are transformed to the stationary reference frame , and then fed to the modulator to generate the switching signals of the power converter.
3.2. Current Predictive Control Strategy
CPC strategy uses the error between the reference current and predicted currents based on a cost function to replace the inner PI controllers of the FOC strategy [1], while the control of the outer speed loop is still executed by the PI Controller as in Equation (8). The block diagram of the CPC of SynRM based on FCS-MPC is illustrated in Figure 6. To design the CPC, the discretization of Equation (5) with small sampling time by using the forward Euler method can be expressed as [3,23]
where
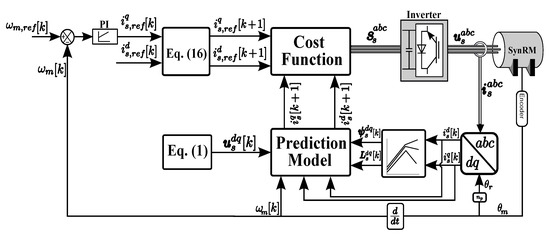
Figure 6.
Current predictive control of synchronous reluctance motor.
The stator voltages can be computed from Equation (1). The seven voltage vectors of the inverter can be applied to predict seven future values of the current according to Equation (13). The predicted currents are used in a cost function with soft constraints to select the optimal switching vector for the inverter. The following cost function formula is used [23]
where are switching states of the two-level inverter (see Table I in [3]), and represents the soft constraint set of the cost function and is given by
where is the maximum stator current of the SynRM, and are the reference stator currents. The references are obtained by using a second-order extrapolation as [2,3]
According to Equation (14), the optimal switching vector is selected such that
3.3. The Proposed Speed Predictive Control
In this section, a novel method for the SPC based on FCS-MPC is investigated, which overcomes the limitation of the cascaded linear control loops (PI controllers). Where the inner and outer loops are combined in one control law called the cost function. SPC principle predicts the future values of the speed and currents and obtains the optimal control signal for the inverter by minimizing the errors between the predicted and reference values in the cost function. The proposed cost function is easy and simple to execute and contains only two weighting factors to tune. The overall block diagram of the proposed SPC is shown in Figure 7. To design the SPC, the forward Euler method is applied to speed dynamic equation as in Equation (2) for discretization period as [26,28,37]
where is the machine electromagnetic torque at sampling instant , by assuming , it can be expressed as [36].
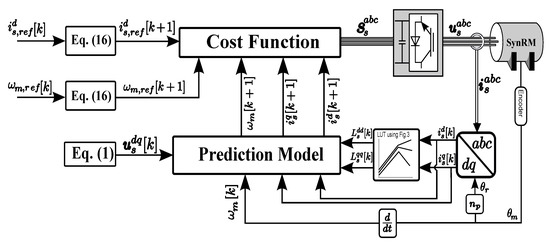
Figure 7.
Proposed speed predictive control of synchronous reluctance motor.
A cost function is favored to achieve a fast dynamic response and good tracking performance. The controller objective is concentrating on having a minimum speed error with minimum control input [38]. Subsequently, exploiting this objective, the cost function for the speed controller can be given as [28]
where and are weighting factors, and is the prediction horizon. is the mechanical reference speed and can be calculated from the previous values of speed as follows
To make the problem simple, is set to 1, and the new cost function can be written as
By neglecting the viscous friction , substitute Equation (18) into Equation (22), the cost function can be written as
Furthermore, Minimizing the cost function can be achieved by letting the derivative of Equation (23) be equal to zero.
Therefore, the reference electromagnetic torque can be calculated from speed error as
The reference direct current is set as a constant. Then, the reference quadrature current can be calculated from Equation (19) as
where is the torque factor, which can be calculated from Equation (19) by neglecting the cross magnetic saturation as follows
As the sampling time is very small, the change in the mechanical speed can be considered constant during a very short period of time, so it can be assumed that . By substituting Equations (28) and (26) into (27), the can be calculated as follows
The overall cost function for the proposed SPC can be concluded as
The cost function contains three terms: d-axis current error term, speed error term, and constraint term that is the same as in Equation (15). Finally, the optimal switching vector for the power converter is obtained by minimizing the overall cost function in Equation (30).
The execution of the investigated SPC can be summarized in the steps listed in Algorithm 1.
| Algorithm 1 The proposed DSPC |
3.4. The Difference of Control Strategies
In this section, the control designs and concepts are compared. In Figure 5, Figure 6 and Figure 7, the block diagrams of FOC, CPC, and proposed SPC of SynRM are displayed, respectively. According to the figures, two control methods need a PI speed controller for regulating the speed, while SPC does not require the PI speed controller. For FOC, two PI current controllers are used, while CPC judges the currents error of the stator, SPC assesses the speed and currents error. The three topologies require a coordinate transformation and consequently, the rotor angle is essential. FOC requires a modulator to treat with the continuous variable and the other two methods do not need a modulator. For tuning tasks, FOC has six factors to tune, while CPC and SPC need two factors to be chosen. Finally, the comparative elements of the different control techniques are summarized in Table 1.

Table 1.
Comparative elements in theory.
4. Particle Swarm Optimization
It can be exposed from the design of the different control strategies that the PI controllers factors and the weighting factors represent an important part in the performance of the whole drive system. Subsequently, tuning of these parameters is crucial, and tuning them by trial and error method consumes the time. Therefore, particle swarm optimization (PSO) is employed to select these parameters offline. PSO is considered the most active approach in solving many types of optimization problems with a slight number of parameters to regulate. Initially, PSO chooses a set of random values of the unknown parameters and each set is selected as a particle [33]. The fitness corresponding to each particle is computed. Then, the particle with the best fitness is chosen and recorded after each iteration of the approach, and lastly the global optimum solution is obtained [33]. The flow chart of the PSO is shown in Figure 8. Furthermore, the fitness functions which applied to choose the best parameters are
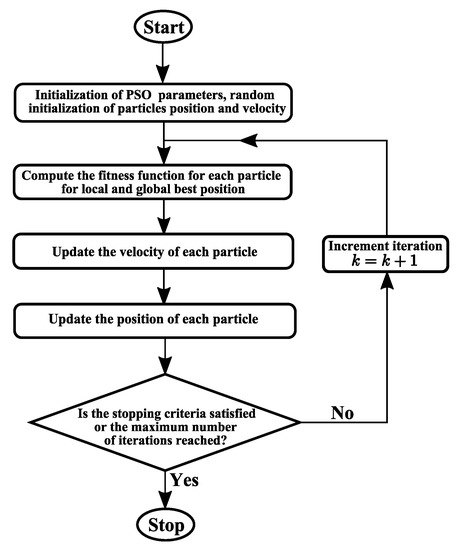
Figure 8.
Particle swarm optimization flow chart.
Applying PSO with control parameters vector the optimal parameters for FOC, CPC, and SPC are obtained as listed in Table 2.

Table 2.
Motor, execution, and controller data.
5. Simulation Results and Discussion
For the validation of the three control strategies, the block diagrams of FOC, CPC, and the proposed SPC as shown in Figure 5, Figure 6 and Figure 7 are verified, simulated, and compared at both dynamic and steady-state with the help of MATLAB/SIMULINK. The nominal parameters of SynRM are collected in Table 2. First, the unknown parameters of the control strategies are obtained through the PSO technique. The parameters of FOC, CPC, and proposed SPC are listed in Table 2. For a fair comparison, the sampling time for prediction models of the CPC and SPC is chosen to be , to obtain a similar switching frequency as in FOC. Furthermore, the PI speed controller parameters of the FOC and CPC have been set to the same values. The measured stator three-phase currents are transformed from the stationary frame to the rotating frame using a rotor angle obtained directly from the encoder. These currents are used as inputs to LUTs to obtain the inductances and flux linkages that represent the influence of magnetic saturation.
The simulation results are shown in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. Figure 9, reveals both the dynamic and steady-state responses of the different control strategies under the rotor mechanical speed of 500 rpm. This operation is accomplished at mechanical load torque of 10 N.m. According to the figure, the dynamic response of the SPC is the fastest compared to the FOC and CPC, where the settling times of FOC, CPC, and SPC are 65 ms, 56 ms, and 52 ms, respectively. Furthermore, it can be seen that the average tracking errors between the references and actual stator current in the frame and the frame are very small and approach zero. Also, FOC contains a clear percentage of the overshoot in the dynamic response of the speed and torque as a result of using the PI controllers, while this ratio disappears in CPC and SPC. The average switching frequency of the proposed SPC is approximately 3 kHz, while the CPC gives average switching frequency of 4 kHz, which means that the switching frequency of the SPC is lower than that of CPC and FOC. Figure 10 displays the current trajectories in the frame. There are two circles: the big circle represents the transient response with an amplitude of the current of 25 A, while the small one represents the steady-state response with an amplitude of the current of about 11 A. Also, as can be seen in Figure 10, the performance of the three topologies is satisfactory at dynamic and steady state. The steady-state errors (SSEs) between the actual values and reference values(, , and ) of the different control strategies for the same operating conditions as shown in Figure 9, are displayed in Figure 11. It can be seen that the average SSE of the speed using the SPC is remarkably smaller than the average SSEs of the CPC and FOC. The average SSEs of the stator currents in the three methods are almost similar, with large ripples in SPC and CPC methods due to the variable switching frequencies. In contrast, the torque ripples of the SPC and CPC are higher than the ripples of FOC.
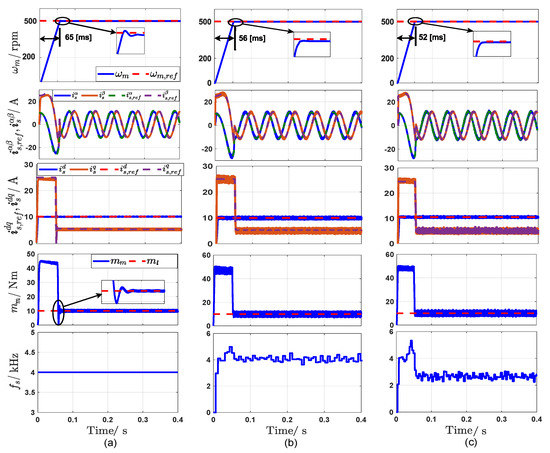
Figure 9.
Overall performance of the different control strategies under rotor mechanical speed 500 [rpm]: (a) FOC, (b) CPC, and (c) proposed SPC.
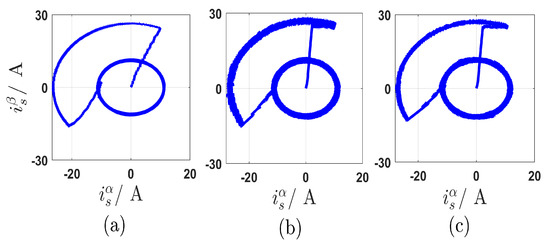
Figure 10.
Current trajectory in frame under rotor mechanical speed 500 [rpm]: (a) FOC, (b) CPC, and (c) Proposed SPC.
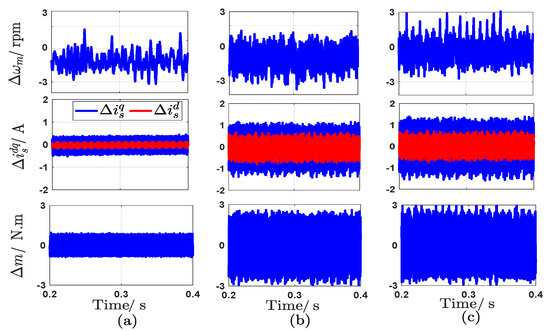
Figure 11.
Steady-state error performance of the different control strategies under rotor mechanical speed 500 rpm (from up to down): , , and : (a) FOC, (b) CPC, and (c) Proposed SPC.
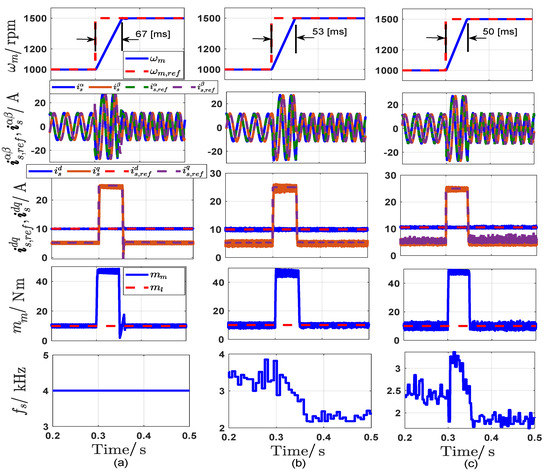
Figure 12.
Dynamic performance of the different control strategies under a step change of rotor mechanical speed form 1000 rpm to 1500 rpm: (a) FOC, (b) CPC, and (c) Proposed SPC.
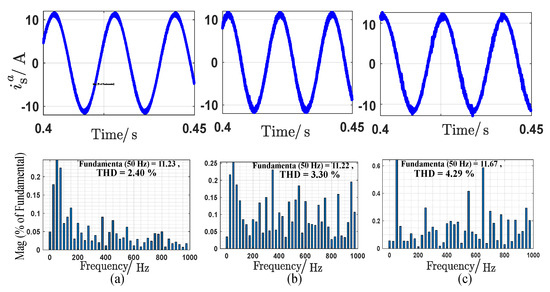
Figure 13.
Current THD of the different control strategies at 1500 rpm: (a) FOC, (b) CPC, and (c) Proposed SPC.
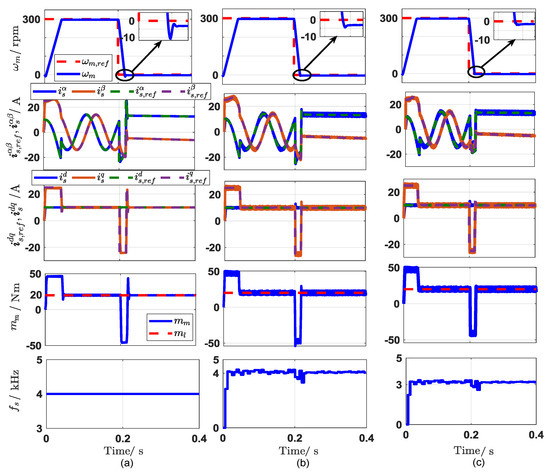
Figure 14.
Dynamic performance of the different control strategies under a step change of rotor mechanical speed form 300 rpm to mechanically stopped: (a) FOC, (b) CPC, and (c) Proposed SPC.
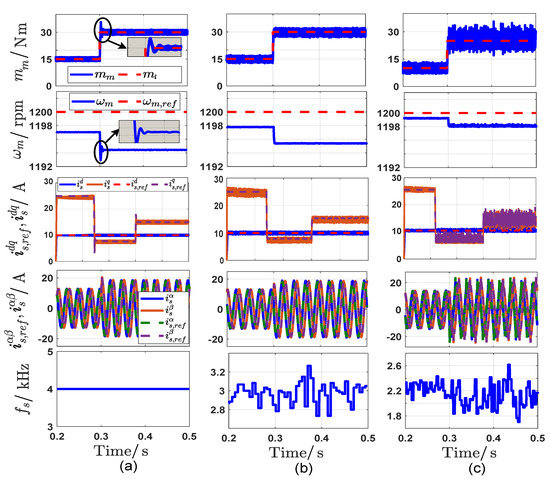
Figure 15.
Overall performance of the different control strategies under a step change of mechanical load torque under speed of 1200 rpm: (a) FOC, (b) CPC, and (c) Proposed SPC.
The different control methods are checked during the sudden change in speed. However, the rotor speed starts at 1000 rpm and increases to 1500 rpm at the time 0.3 s, as shown in Figure 12. From the figure, the dynamic response of SPC is faster than the other two strategies. Furthermore, for the proposed SPC and CPC, the speed reaches its reference value without any overshooting, while the overshoot is clear in FOC response especially in the torque and currents responses. Also, the tracking capability of the stator currents in both and frames, and electromagnetic torque for the three schemes is adequate and following the current references and the applied load torque very well, with noticeable high torque ripples in the proposed SPC. It also noticed that the average switching frequencies of the CPC and SPC are decreased by increasing the rotor speed. Figure 13 depicts the currents THD for the different control methods. It can be confirmed from the figure that the THD of SPC is slightly higher than of CPC and FOC. The dynamic and steady-state performance of the three control strategies are tested and compared when the rotor is suddenly stopped as shown in Figure 14. Where the mechanical speed starts with speed of 300 rpm and decreases to zero suddenly. This operation is executed under applying mechanical load torque 20 N.m. It can be seen from the figure that the different control strategies have a satisfactory response at both dynamic and steady state. Also, for the proposed SPC, the rotor speed reaches zero without overshooting, while in CPC a very low overshooting ratio is appeared due to the outer PI speed controller. In contrast, in FOC strategy, a clear ratio of the overshooting appears in speed, currents, and torque responses. The switching frequency of the proposed method is less than the other two methods. Eventually, the performance of the three control strategies is investigated during a sudden change in the mechanical load torque. Where the load torque changes from 15 N.m to 30 N.m at time 0.3 s under a rotor speed of 1200 rpm as depicted in Figure 15. It can be seen from the figure that the three control methods achieve a very good performance and high tracking ability at steady-state with a slight contrast between the three methods especially in the overshooting ratio, current/torque ripples, and switching frequency. The general comparison features between the FOC, CPC, and proposed SPC that are obtained from all the simulation figures are summarized in Table 3.

Table 3.
Comparison between the FOC, CPC, and SPC.
6. Conclusions
In this paper, three control strategies that achieve high-performance control of SynRM were presented and investigated. They have been compared in concepts and simulations and each control has its own merits. SPC is the proposed and newest strategy, it combines all the cascaded structure in one control law to obtain the switching vector by minimizing the predefined cost function. Its advantages are very fast dynamic response without overshooting and the average SSE is close to zero, while its disadvantages are the variable switching frequency and high current/torque ripples. FOC is the most popular control with cascaded PI controllers (current and speed), its advantages are constant switching frequency and low torque ripples, while its weakness is the slow dynamic response. CPC is the conventional predictive method; it replaces the PI current controllers with model predictive control. Its benefits are simple design and fast dynamic response, while its drawbacks are the variable switching frequency and high current/torque ripples. The simulation results reveal that all control strategies have a satisfactory performance for dynamic and steady-state responses during a wide speed range and meet the requirements of the application drives.
Author Contributions
A.F. and M.A. are conceived, designed, and implemented the control strategies and wrote the manuscript; C.M.H. was responsible for guidance in control theory and nonlinear modeling and provided the simulation model of the SynRM and revised the manuscript; R.K., A.S. (Amr Saleh) and A.S. (Adel Shaltout) were responsible for the guidance and a number of key suggestions. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Variables | |
| , | Stator voltages and currents in the rotating frame |
| , | Stator fluxes and inductances in the rotating frame |
| , | Stator resistance, rotor inertia, and viscous friction |
| , | Electrical position, electrical speed, and mechanical speed of the rotor () |
| Machine electromagnetic torque and load torque | |
| , | Pole pairs number, switching frequency, sample, and sampling time |
| Notation | |
| , , | Scalar, vector, and matrix, respectively |
References
- Wang, F.; Zhang, Z.; Mei, X.; Rodríguez, J.; Kennel, R. Advanced control strategies of induction machine: Field oriented control, direct torque control and model predictive control. Energies 2018, 11, 120. [Google Scholar] [CrossRef]
- Lin, C.K.; Lai, Y.S.; Yu, H.C. Improved model-free predictive current control for synchronous reluctance motor drives. IEEE Trans. Ind. Electron. 2016, 63, 3942–3953. [Google Scholar] [CrossRef]
- Farhan, A.; Abdelrahem, M.; Saleh, A.; Shaltout, A.; Kennel, R. Simplified Sensorless Current Predictive Control of Synchronous Reluctance Motor Using Online Parameter Estimation. Energies 2020, 13, 492. [Google Scholar] [CrossRef]
- Hackl, C.M.; Kamper, M.J.; Kullick, J.; Mitchell, J. Current control of reluctance synchronous machines with online adjustment of the controller parameters. In Proceedings of the 2016 IEEE 25th International Symposium on Industrial Electronics (ISIE), Santa Clara, CA, USA, 8–10 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 153–160. [Google Scholar]
- Farhan, A.; Saleh, A.; Shaltout, A. High performance reluctance synchronous motor drive using field oriented control. In Proceedings of the 2013 5th International Conference on Modelling, Identification and Control (ICMIC), Cairo, Egypt, 31 August–2 September 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 181–186. [Google Scholar]
- Lagerquist, R.; Boldea, I.; Miller, T.J. Sensorless-control of the synchronous reluctance motor. IEEE Trans. Ind. Appl. 1994, 30, 673–682. [Google Scholar] [CrossRef]
- Hackl, C.M. Non-Identifier Based Adaptive Control in Mechatronics: Theory and Application; Springer: Berlin/Heidelberg, Germany, 2017; Volume 466. [Google Scholar]
- Hackl, C.M.; Kamper, M.J.; Kullick, J.; Mitchell, J.; Nonlinear, P.I. Current control of reluctance synchronous machines. arXiv, 2015; arXiv:1512.09301. [Google Scholar]
- Hwang, S.H.; Kim, J.M.; Van Khang, H.; Ahn, J.W. Parameter identification of a synchronous reluctance motor by using a synchronous PI current regulator at a standstill. J. Power Electron. 2010, 10, 491–497. [Google Scholar] [CrossRef]
- Radimov, N.; Ben-Hail, N.; Rabinovici, R. Inductance measurements in switched reluctance machines. IEEE Trans. Magn. 2005, 41, 1296–1299. [Google Scholar] [CrossRef]
- Rafajdus, P.; Hrabovcova, V.; Lehocky, P.; Makys, P.; Holub, F. Effect of Saturation on Field Oriented Control of the New Designed Reluctance Synchronous Motor. Energies 2018, 11, 3223. [Google Scholar] [CrossRef]
- Arkadan, A.A.; Isaac, F.N.; Mohammed, O.A. Parameters evaluation of ALA synchronous reluctance motor drives. IEEE Trans. Magn. 2000, 36, 1950–1955. [Google Scholar] [CrossRef]
- Matsuo, T.; Lipo, T.A. Field oriented control of synchronous reluctance machine. In Proceedings of the IEEE Power Electronics Specialist Conference-PESC’93, Seattle, WA, USA, 20–24 June 1993; IEEE: Piscataway, NJ, USA, 1993; pp. 425–431. [Google Scholar]
- Ghaderi, A.; Hanamoto, T. Wide-speed-range sensorless vector control of synchronous reluctance motors based on extended programmable cascaded low-pass filters. IEEE Trans. Ind. Electron. 2010, 58, 2322–2333. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Two-vector-based model predictive torque control without weighting factors for induction motor drives. IEEE Trans. Power Electron. 2015, 31, 1381–1390. [Google Scholar] [CrossRef]
- Lin, C.K.; Liu, T.H.; Fu, L.C.; Hsiao, C.F. Model-free predictive current control for interior permanent-magnet synchronous motor drives based on current difference detection technique. IEEE Trans. Ind. Electron. 2013, 61, 667–681. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.M.; Kennel, R.; Rodriguez, J. Efficient direct-model predictive control with discrete-time integral action for PMSGs. IEEE Trans. Energy Convers. 2018, 34, 1063–1072. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Koh, B.K.; Lee, Y.I. A comparison of finite control set and continuous control set model predictive control schemes for speed control of induction motors. IEEE Trans. Ind. Inform. 2017, 14, 1334–1346. [Google Scholar] [CrossRef]
- Gonçalves, P.F.; Cruz, S.M.; Mendes, A.M. Comparison of model predictive control strategies for six-phase permanent magnet synchronous machines. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 5801–5806. [Google Scholar]
- Gonçalves, P.; Cruz, S.; Mendes, A. Finite control set model predictive control of six-phase asymmetrical machines—An overview. Energies 2019, 12, 4693. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.; Kennel, R.; Rodriguez, J. Sensorless predictive speed control of permanent-magnet synchronous generators in wind turbine applications. In PCIM Europe 2019, Proceedings of the International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 7–9 May 2019; VDE: Frankfurt, Germany, 2019; pp. 1–8. [Google Scholar]
- Morales-Caporal, R.; Pacas, M. A predictive torque control for the synchronous reluctance machine taking into account the magnetic cross saturation. IEEE Trans. Ind. Electron. 2007, 54, 1161–1167. [Google Scholar] [CrossRef]
- Farhan, A.; Saleh, A.; Shaltout, A.; Kennel, R. Encoderless Finite Control Set Predictive Current Control of Synchronous Reluctance Motor. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 692–697. [Google Scholar]
- Hadla, H.; Cruz, S. Predictive stator flux and load angle control of synchronous reluctance motor drives operating in a wide speed range. IEEE Trans. Ind. Electron. 2017, 64, 6950–6959. [Google Scholar] [CrossRef]
- Hadla, H.; Cruz, S. Active flux based finite control set model predictive control of synchronous reluctance motor drives. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; IEEE: Piscataway, NJ, USA, 2019; pp. 1–10. [Google Scholar]
- Preindl, M.; Bolognani, S. Model predictive direct speed control with finite control set of PMSM drive systems. IEEE Trans. Power Electron. 2012, 28, 1007–1015. [Google Scholar] [CrossRef]
- Kakosimos, P.; Abu-Rub, H. Predictive speed control with short prediction horizon for permanent magnet synchronous motor drives. IEEE Trans. Power Electron. 2017, 33, 2740–2750. [Google Scholar] [CrossRef]
- Liu, T.H.; Haslim, H.S.; Tseng, S.K. Predictive controller design for a high-frequency injection sensorless synchronous reluctance drive system. IET Electr. Power Appl. 2017, 11, 902–910. [Google Scholar] [CrossRef]
- Hackl, C.M.; Larcher, F.; Dötlinger, A.; Kennel, R.M. Is multiple-objective model-predictive control “optimal”? In Proceedings of the 2013 IEEE International Symposium on Sensorless Control for Electrical Drives and Predictive Control of Electrical Drives and Power Electronics (SLED/PRECEDE), Munich, Germany, 17–19 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–8. [Google Scholar]
- Bolognani, S.; Tubiana, L.; Zigliotto, M. Extended Kalman filter tuning in sensorless PMSM drives. IEEE Trans. Ind. Appl. 2003, 39, 1741–1747. [Google Scholar] [CrossRef]
- Solihin, M.I.; Tack, L.F.; Kean, M.L. Tuning of PID controller using particle swarm optimization (PSO). Proceeding of the International Conference on Advanced Science, Engineering and Information Technology, Bangi, Malaysia, 14–15 January 2011; Volume 1, pp. 458–461. [Google Scholar]
- Farhan, A.; Saleh, A.; Abdelrahem, M.; Kennel, R.; Shaltout, A. High-Precision Sensorless Predictive Control of Salient-Pole Permanent Magnet Synchronous Motor based-on Extended Kalman Filter. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 226–231. [Google Scholar]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernez, J.C.; Harley, R.G. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Calvini, M.; Carpita, M.; Formentini, A.; Marchesoni, M. PSO-based self-commissioning of electrical motor drives. IEEE Trans. Ind. Electron. 2014, 62, 768–776. [Google Scholar] [CrossRef]
- Ghoshal, A.; John, V. Anti-Windup Schemes for Proportional Integral and Proportional Resonant Controller. Proceedings of National Power Electronics Conference, Roorkee, India, 10–13 June 2010; pp. 1–6. [Google Scholar]
- Eldeeb, H.; Hackl, C.M.; Horlbeck, L.; Kullick, J. A unified theory for optimal feedforward torque control of anisotropic synchronous machines. Int. J. Control 2018, 91, 2273–2302. [Google Scholar] [CrossRef]
- Garcia, C.; Silva, C.; Rodriguez, J.; Zanchetta, P. Cascaded model predictive speed control of a permanent magnet synchronous machine. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2714–2718. [Google Scholar]
- Maciejowski, J.M.; PRedictive Control: With Constraints. Pearson Education. 2002. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/acs.736 (accessed on 15 June 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).