Kineto-Static Analysis of a Wrist Rehabilitation Robot with Compliance and Passive Joints for Joint Misalignment Compensation †
Abstract
1. Introduction
2. Methods
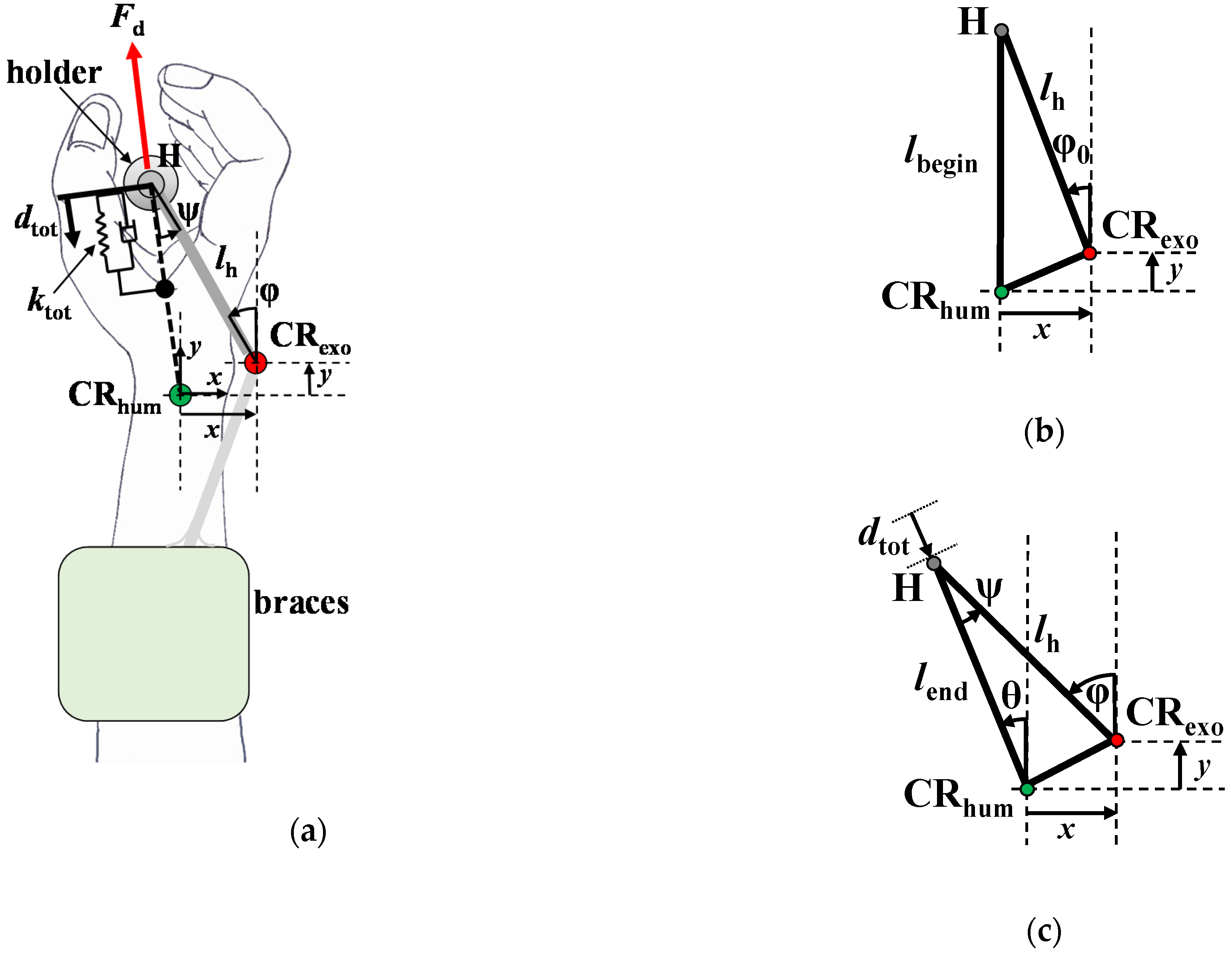
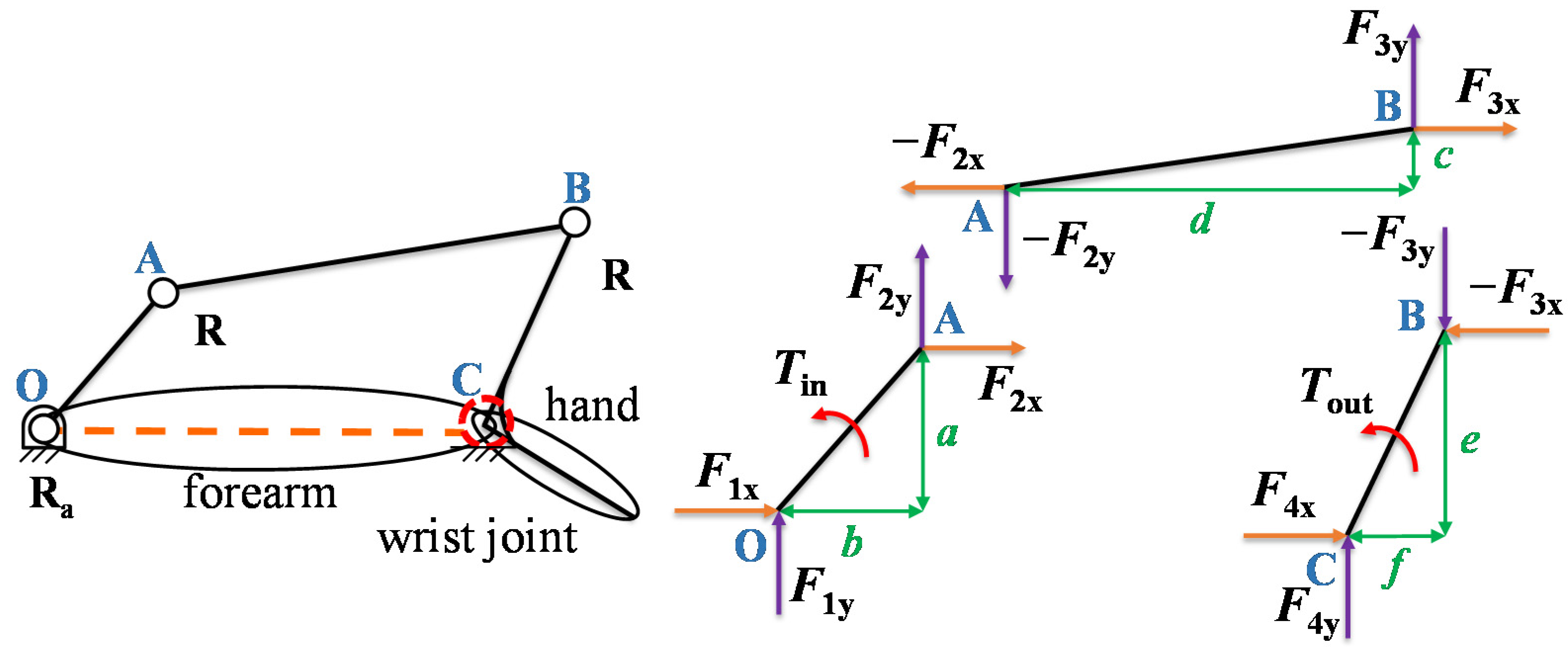
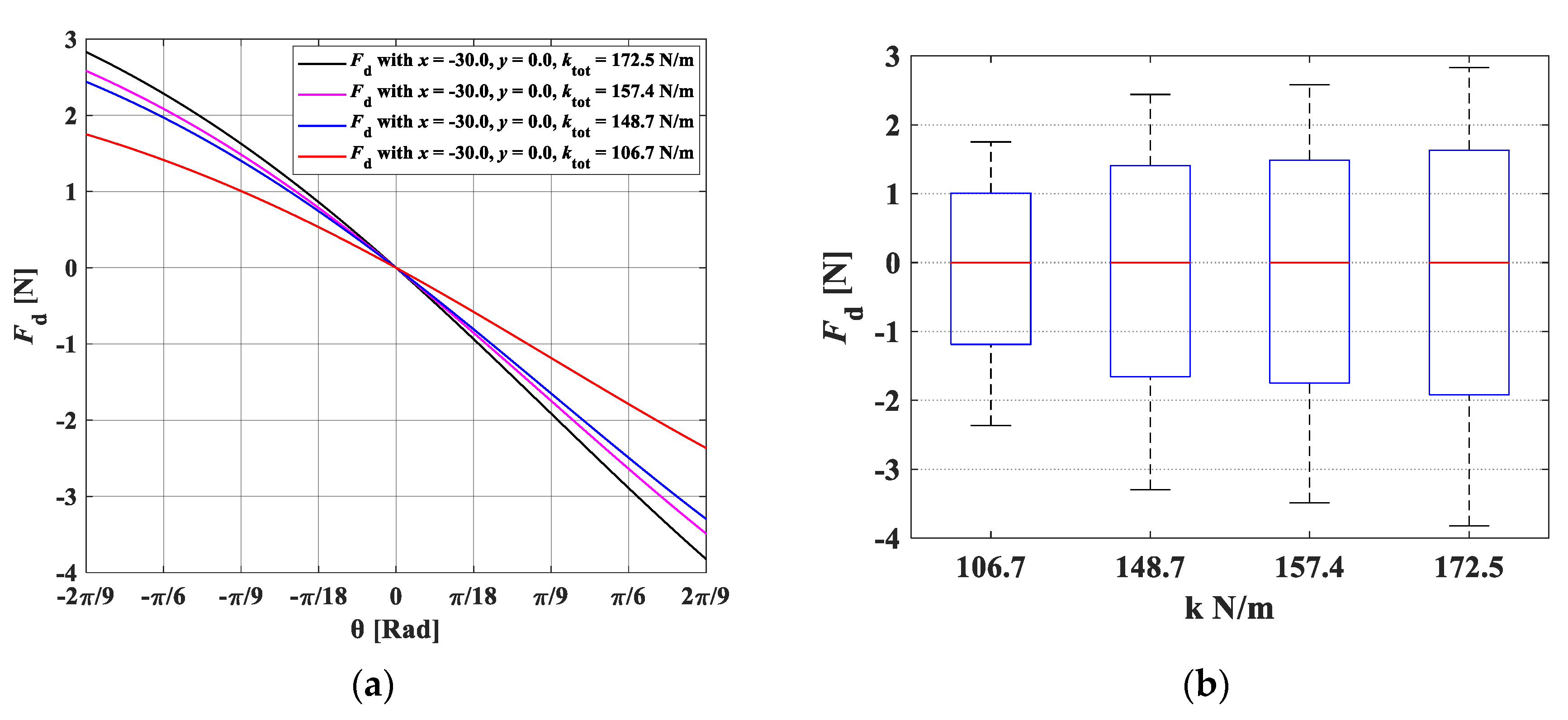
2.1. Static Force Analysis of a Wrist Rehabilitation Robot
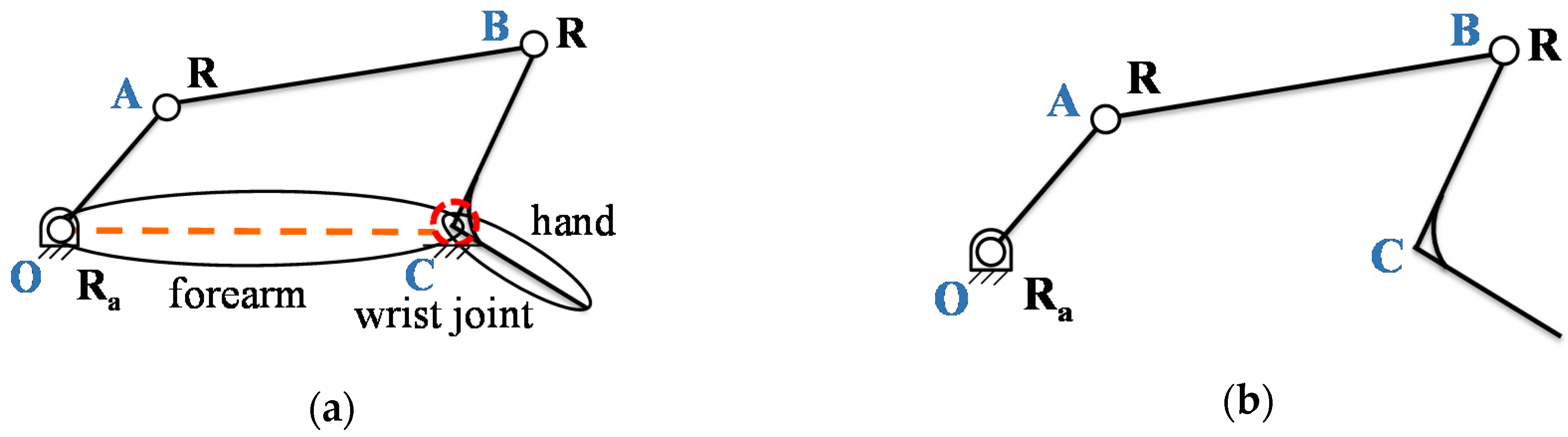
2.2. Addtion of Passive Joints
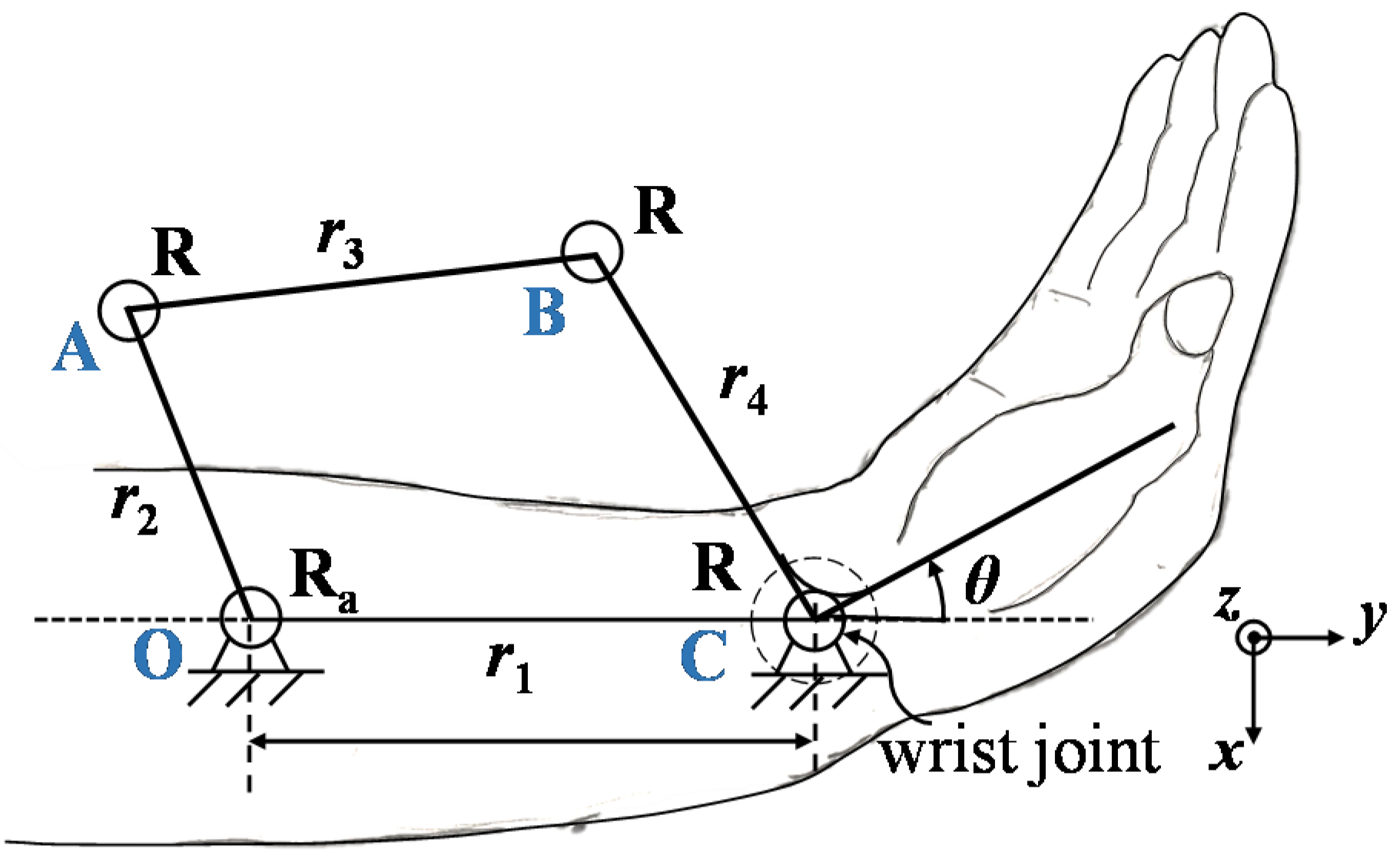
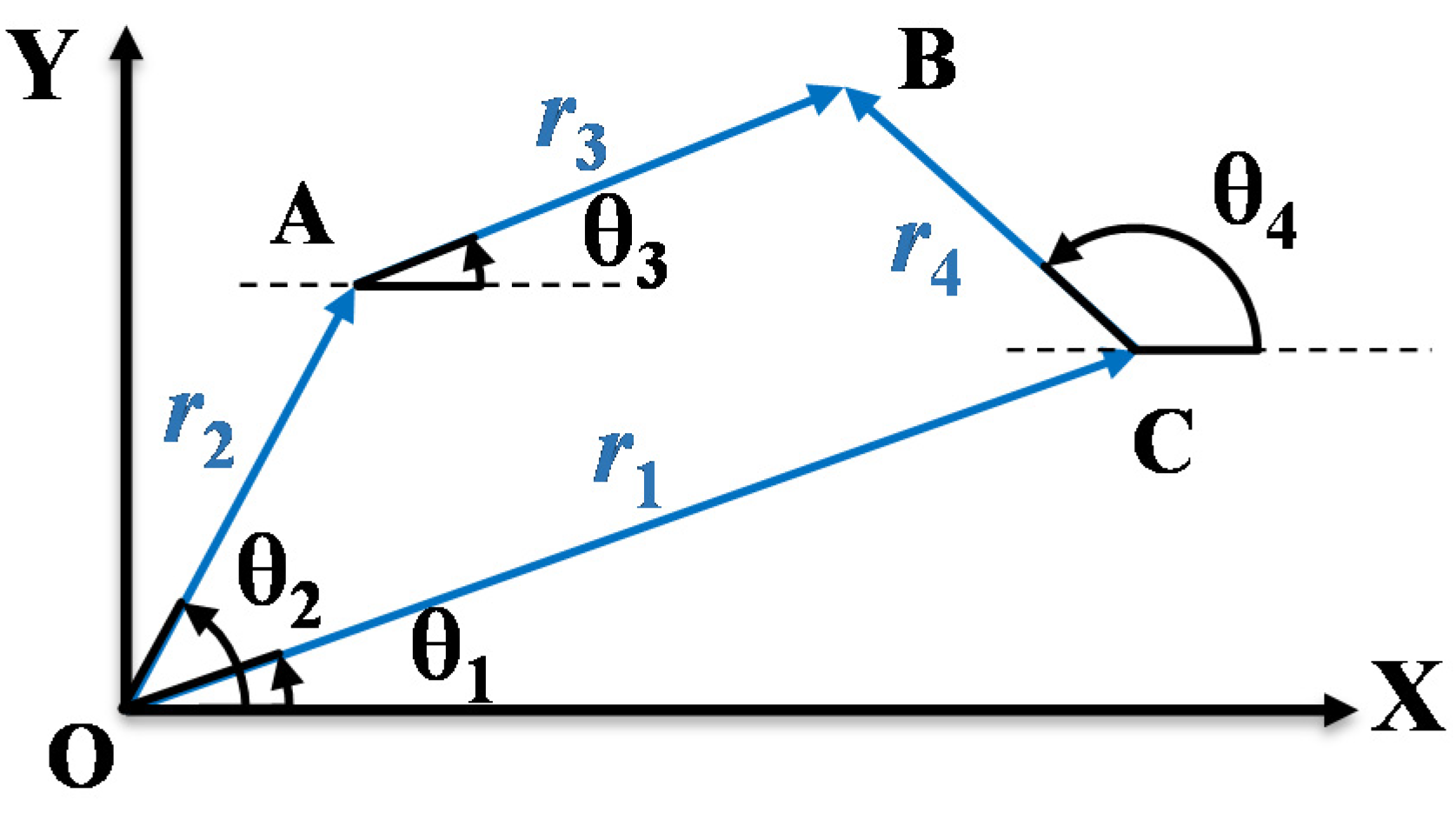
2.2.1. Four-Bar Linkage Design
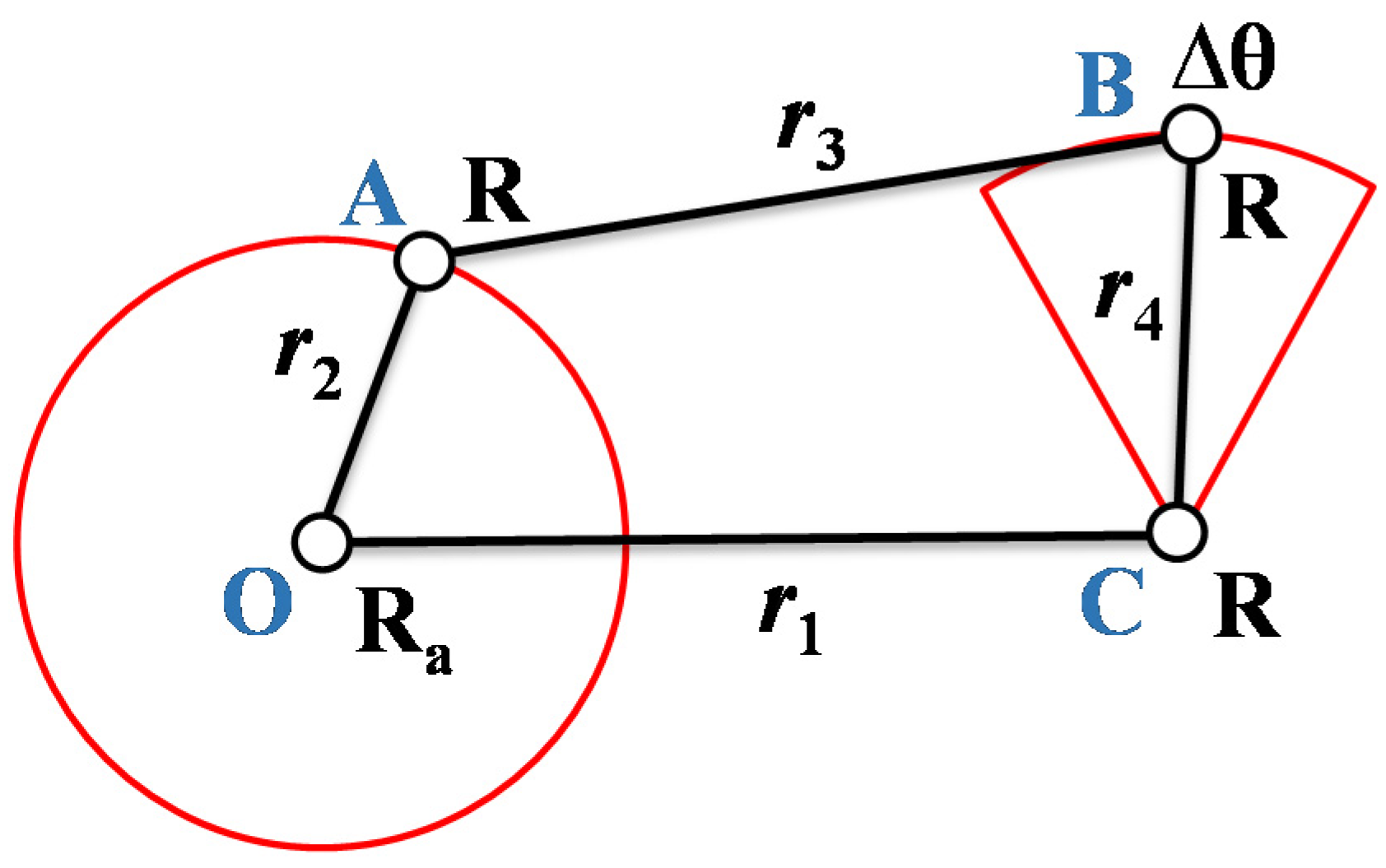
2.2.2. Kineto-Static Analysis
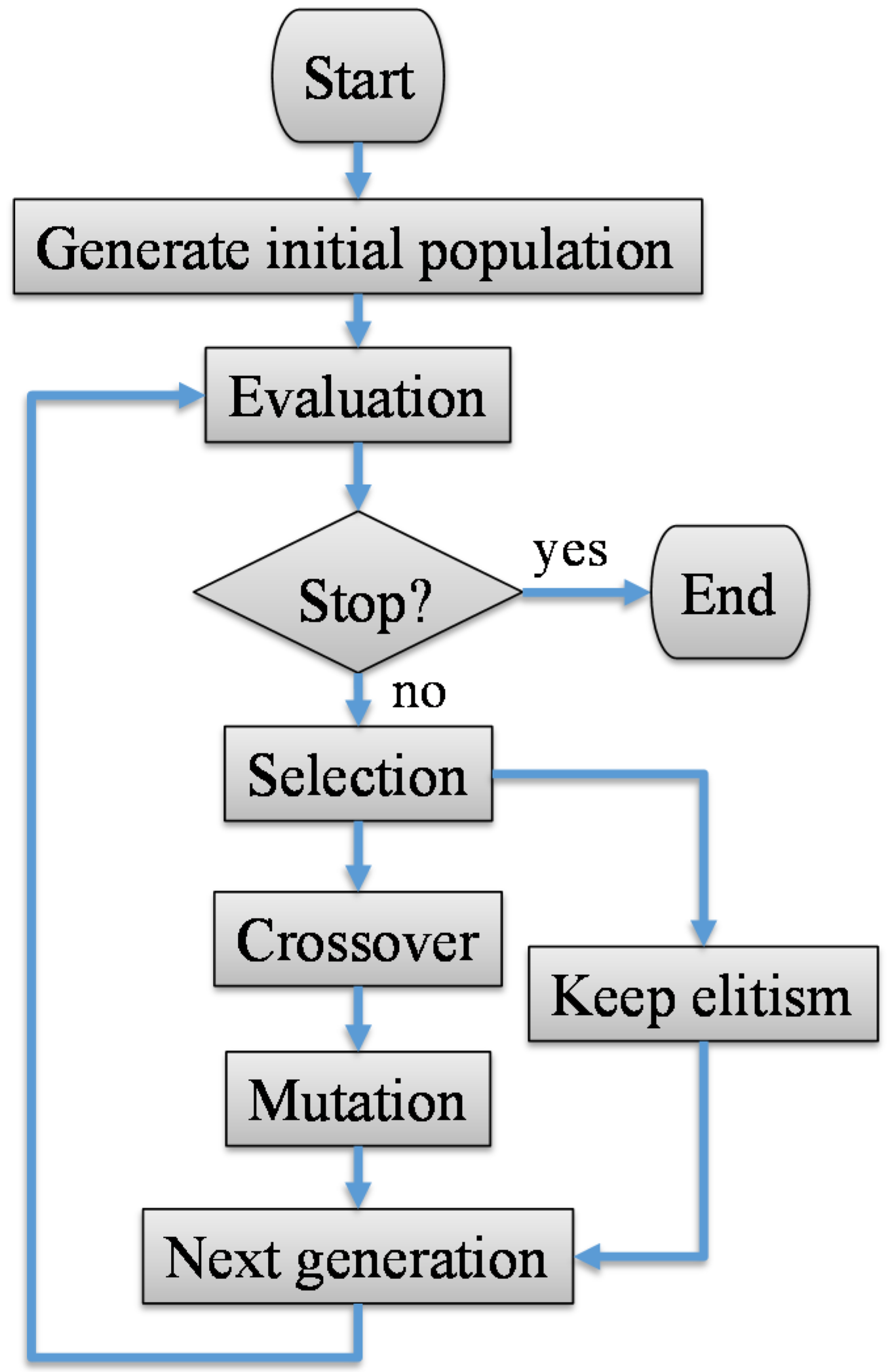
2.2.3. Optimization
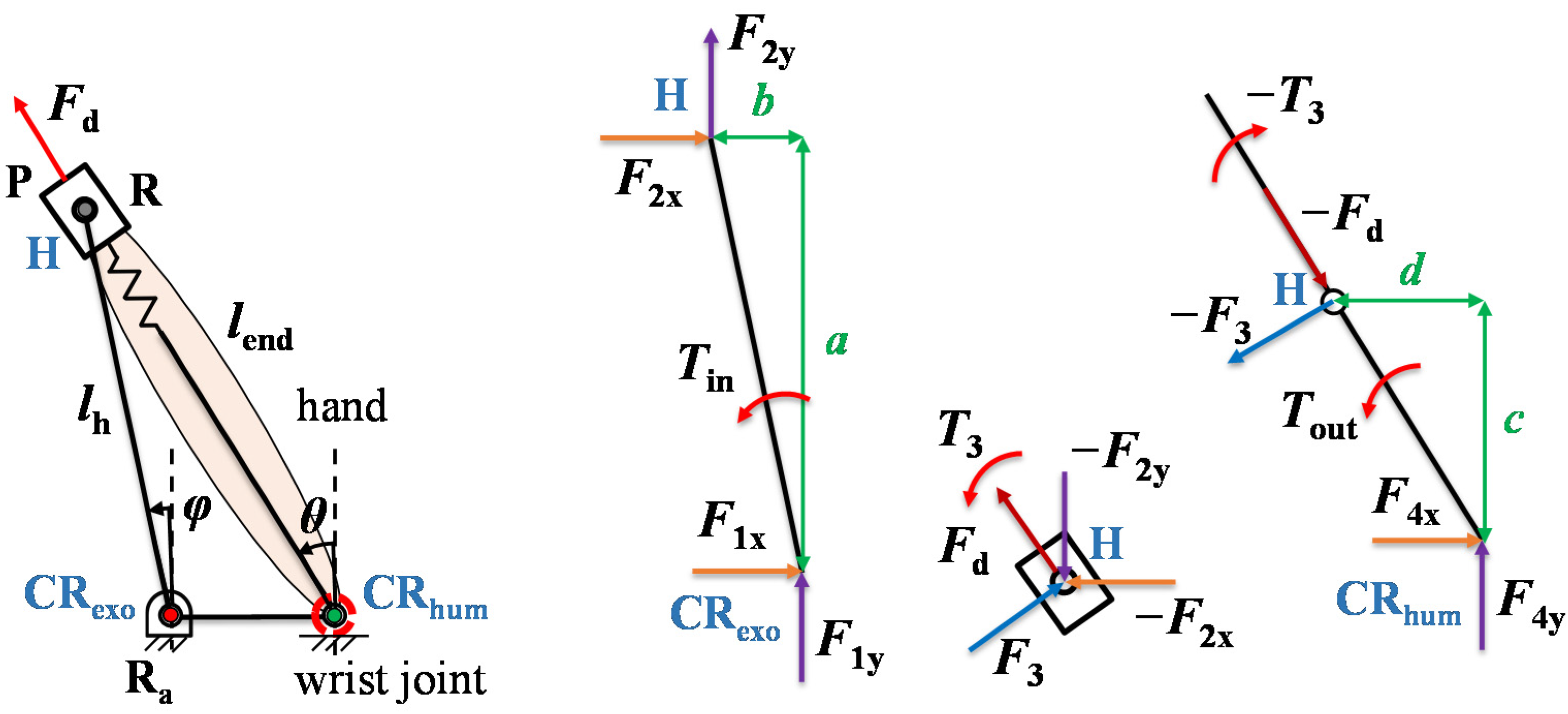
2.3. The Consideration of Human Soft Tissue
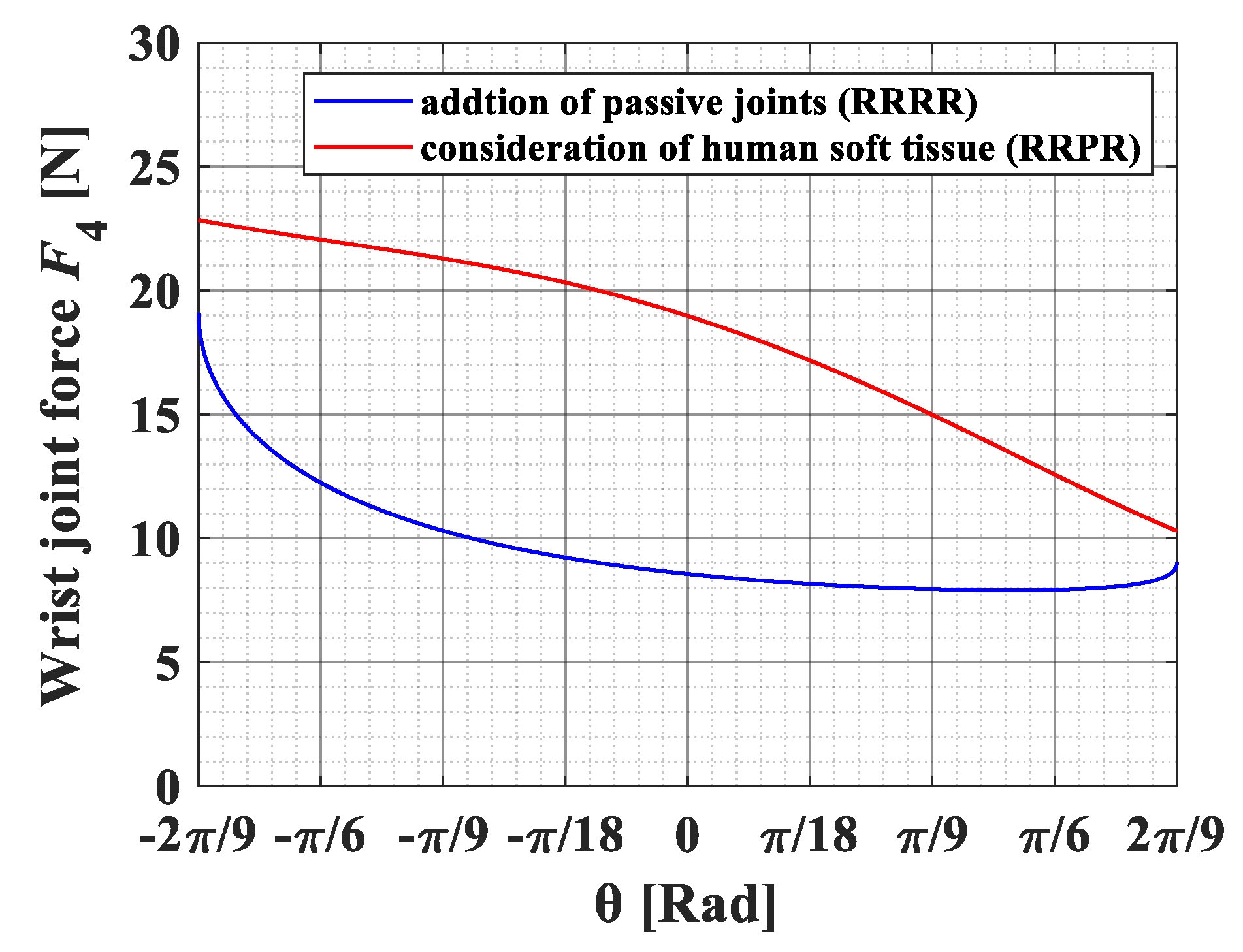
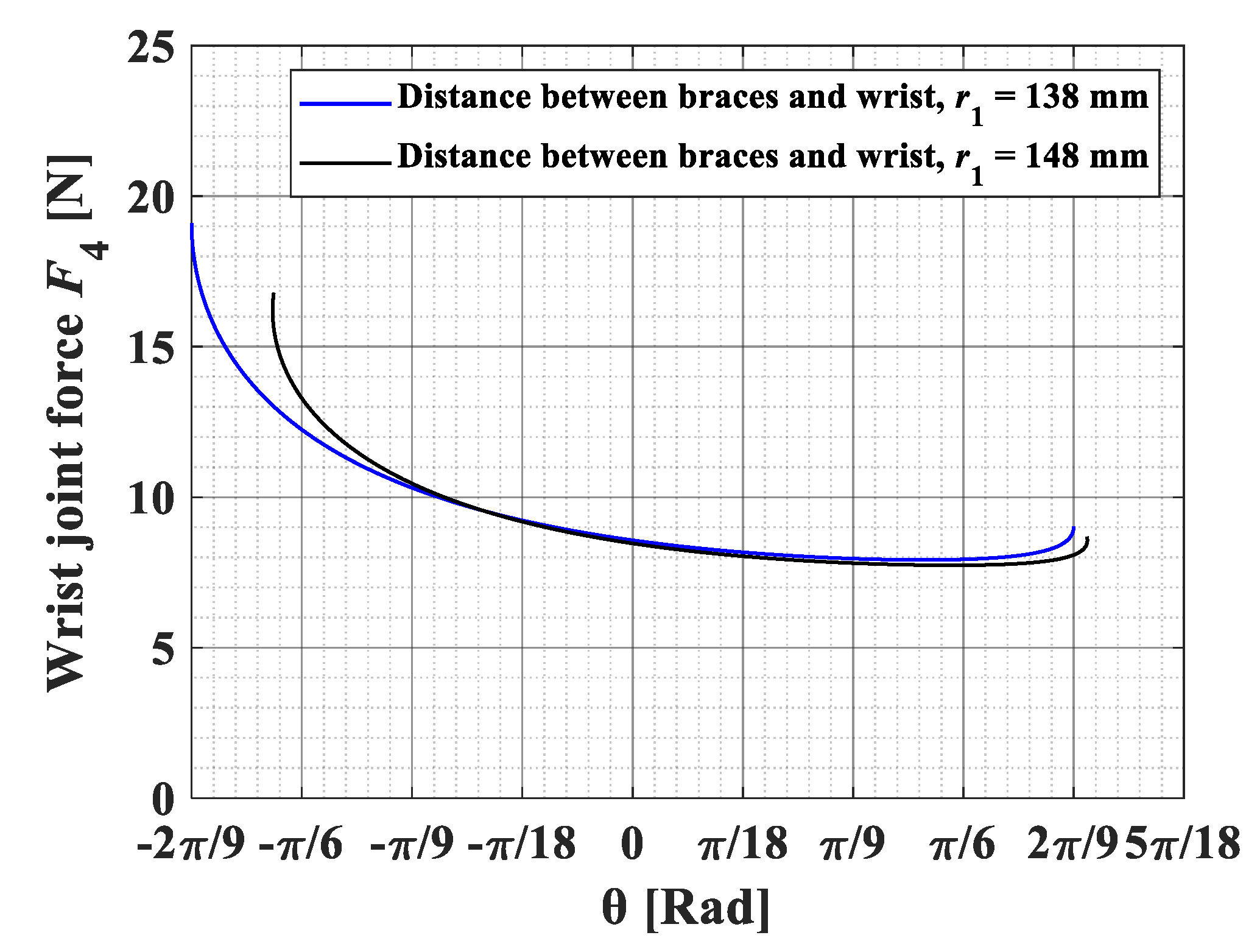
3. Results and Discussion
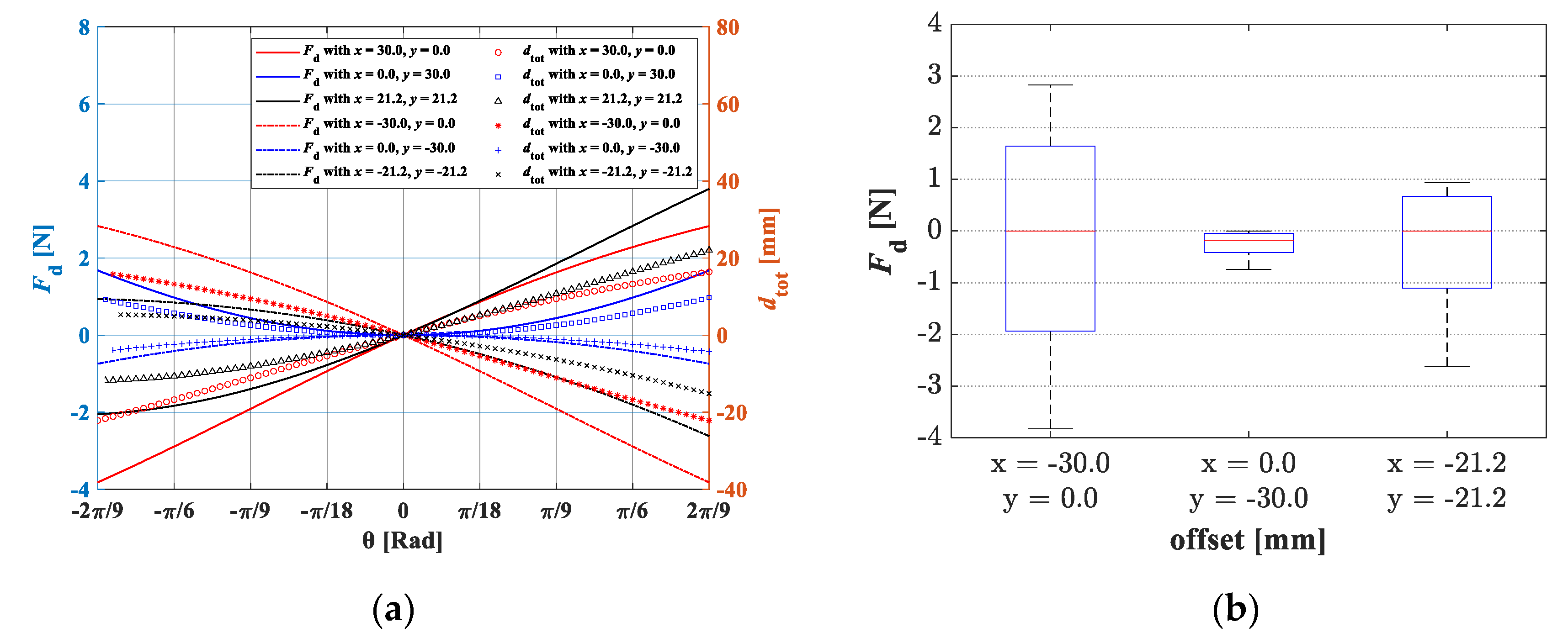
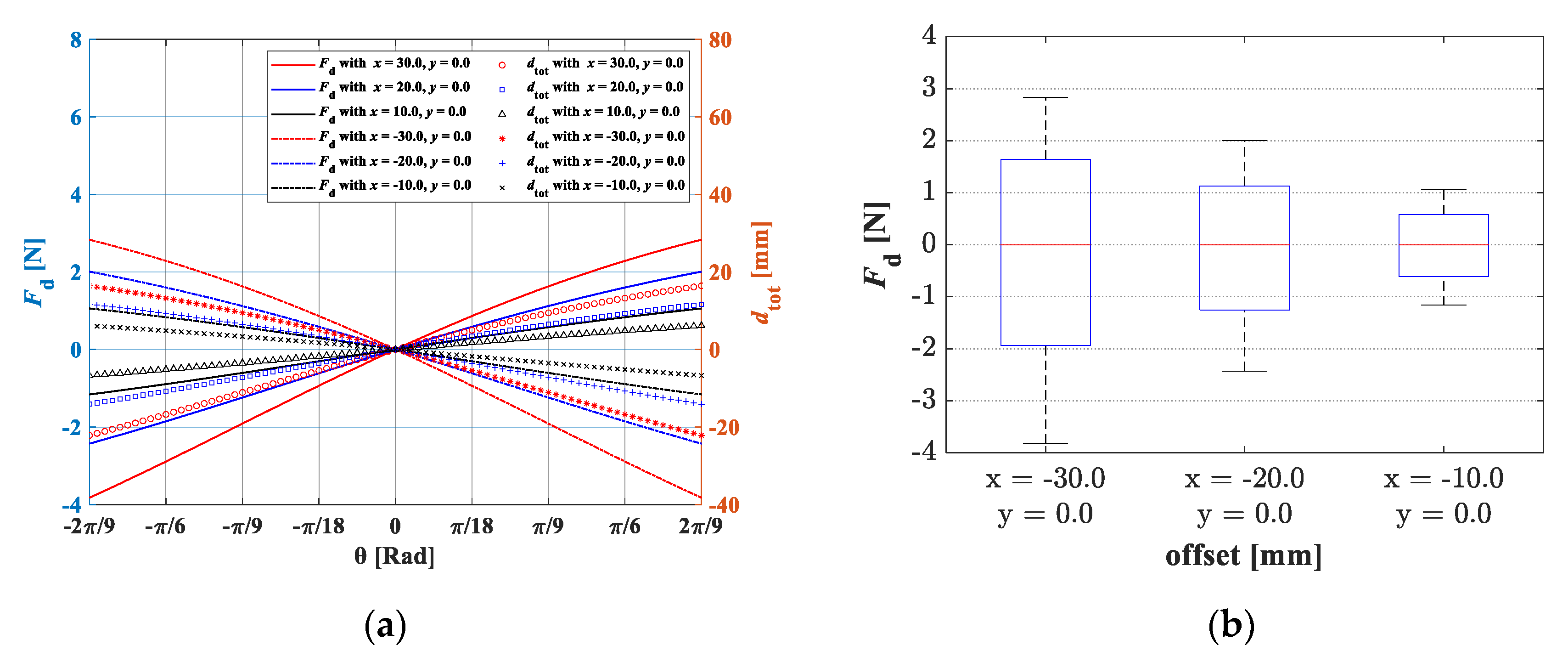
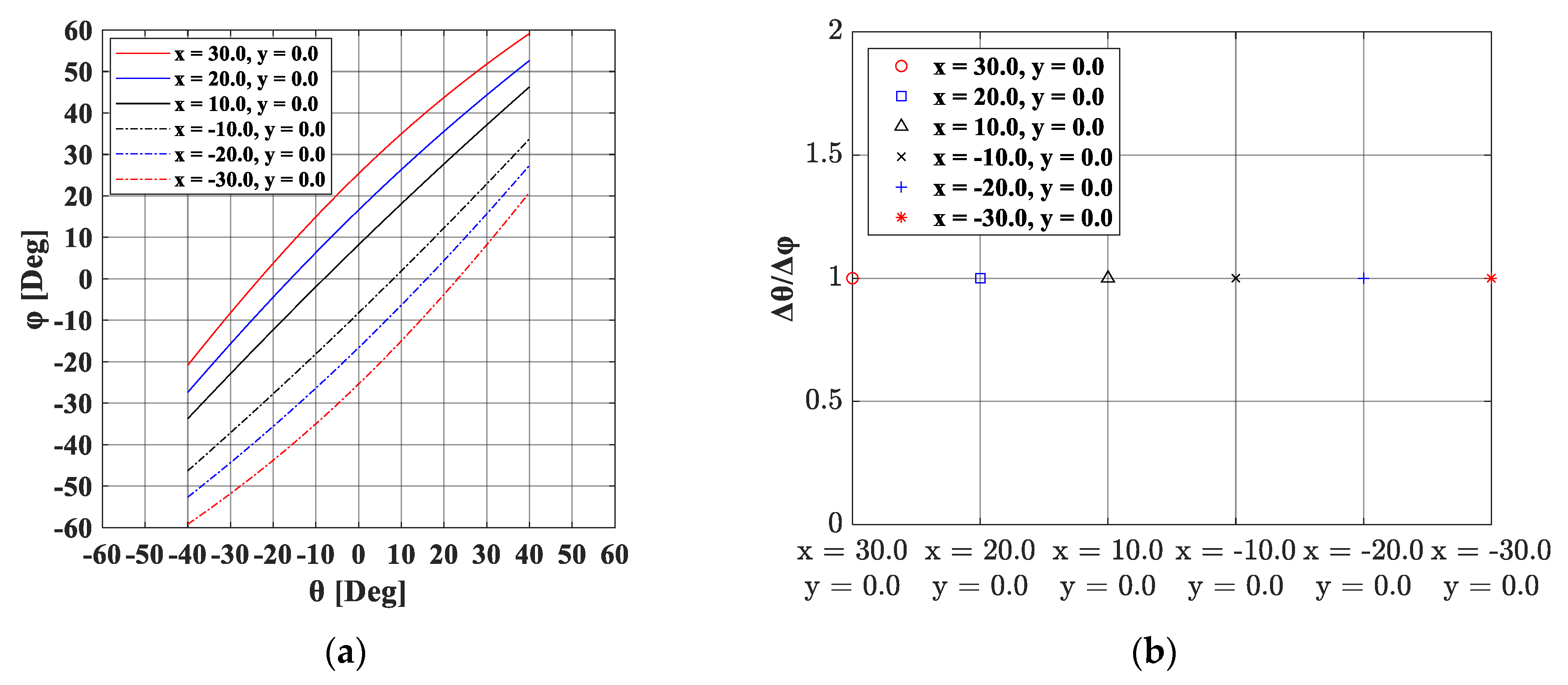
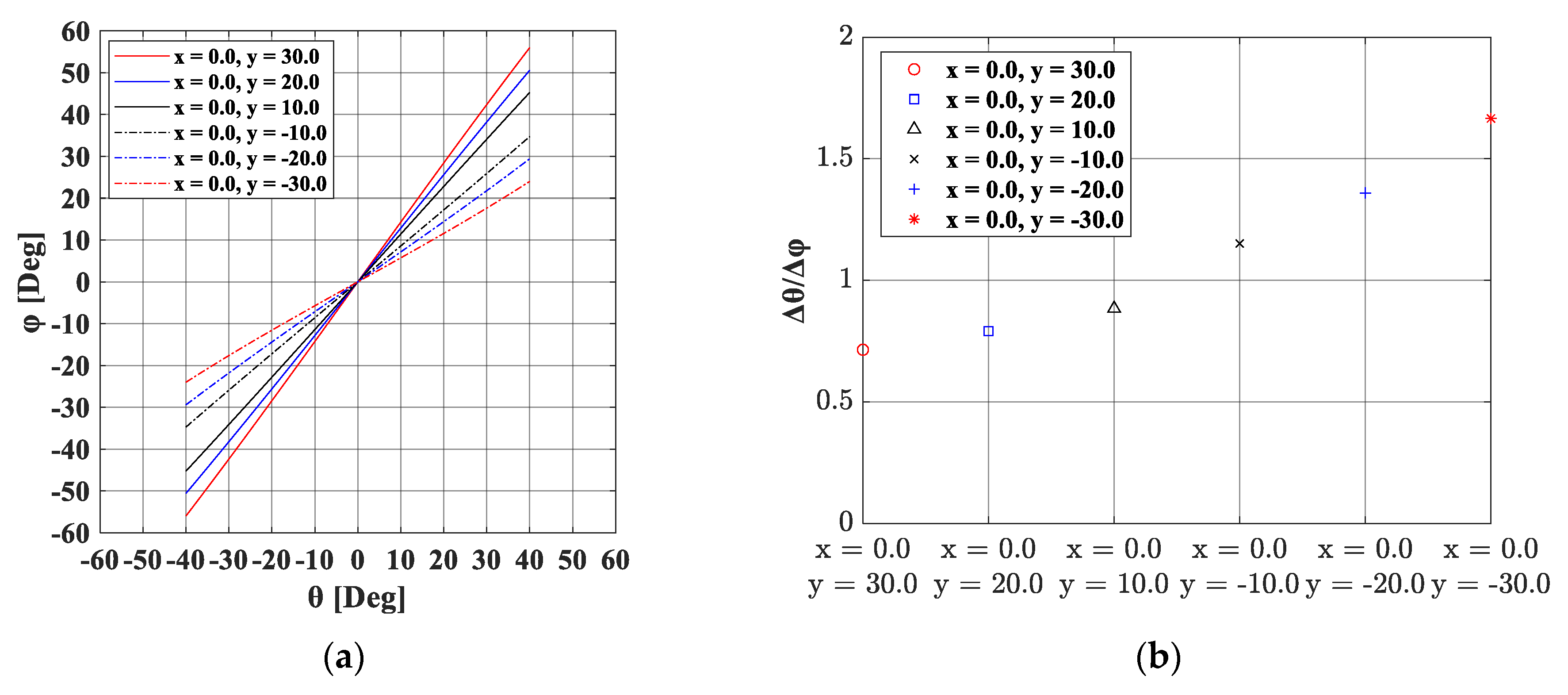
3.1. Static Force Analysis of a Wrist Rehabilitation Robot
3.2. Addition of Passive Joints and the Consideration of Human Soft Tissue
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maciejasz, P.; Eschweiler, J.; Gerlach-Hahn, K.; Jansen-Troy, A.; Leonhardt, S. A survey on robotic devices for upper limb rehabilitation. J. Neuroeng. Rehabil. 2014, 11, 3–31. [Google Scholar] [CrossRef] [PubMed]
- Molteni, F.; Gasperini, G.; Cannaviello, G.; Guanziroli, E. Exoskeleton and End-Effector Robots for Upper and Lower Limbs Rehabilitation: Narrative Review. PM&R 2018, 10, S174–S188. [Google Scholar]
- Norouzi-Gheidari, N.; Archambault, P.S.; Fung, J. Effects of robot-assisted therapy on stroke rehabilitation in upper limbs: Systematic review and meta-analysis of the literature. J. Rehabil. Res. Dev. 2012, 49, 479–496. [Google Scholar] [CrossRef] [PubMed]
- Ryu, J.; Cooney, W.P.; Askew, L.J.; An, K.-N.; Chao, E.Y.S. Functional Ranges of Motion of the Wrist Joint. J. Hand Surg. Am. 1991, 16, 409–419. [Google Scholar] [CrossRef]
- Pezent, E.; Rose, C.G.; Deshpande, A.D.; O’Malley, M.K. Design and characterization of the OpenWrist: A robotic wrist exoskeleton for coordinated hand-wrist rehabilitation. In Proceedings of the 2017 IEEE International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 720–725. [Google Scholar]
- McDaid, A.J. Development of an Anatomical Wrist Therapy Exoskeleton (AW-TEx). In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; pp. 434–439. [Google Scholar]
- Singh, N.; Saini, M.; Anand, S.; Kumar, N.; Srivastava, M.V.P.; Mehndiratta, A. Robotic Exoskeleton for Wrist and Fingers Joint in Post-Stroke Neuro-Rehabilitation for Low-Resource Settings. IEEE Trans Neural Syst. Rehabil. Eng. 2019, 27, 2369–2377. [Google Scholar] [CrossRef] [PubMed]
- Näf, M.B.; Junius, K.; Rossini, M.; Rodriguez-Guerrero, C.; Vanderborght, B.; Lefeber, D. Misalignment Compensation for Full Human-Exoskeleton Kinematic Compatibility: State of the Art and Evaluation. Appl. Mech. Rev. 2019, 70, 050802-1–050802-19. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Takeda, Y. Static Analysis of a Wrist Rehabilitation Robot with Consideration to the Compliance and Joint Misalignment between the Robot and Human Hand. In Proceedings of the Annual Conference of the Robotics Society of Japan 2019, Tokyo, Japan, 3–7 September 2019. [Google Scholar]
- Liu, Y.-C.; Takeda, Y. Kineto-static Analysis of a Wrist Rehabilitation Robot with Compliant Elements and Supplementary Passive Joints to Compensate the Joint Misalignment. In Proceedings of the 25th Jc-IFToMM Symposium, 2nd International Jc-IFToMM Symposium, Kanagawa, Japan, 25–26 October 2019. [Google Scholar]
- Takeda, Y.; Sugahara, Y.; Matsuura, D.; Matsuda, S.; Suzuki, T.; Kitagawa, M.; Liu, Y.-C. Introduction of Dynamic Pair to Modeling and Kinemato-Dynamic Analysis of Wearable Assist-Devices. In Proceedings of the JSME Annual Mechanical Engineering Congress 2019, Akita, Japan, 8–11 September 2019. [Google Scholar]
- Schiele, A. An explicit model to predict and interpret constraint force creation in pHRI with exoskeletons. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation (ICRA), Nice, France, 22–26 September 2008; pp. 1324–1330. [Google Scholar]
- Matsuura, D.; Ishida, S.; Koga, T.; Takeda, Y. Design of Ankle Rehabilitation Mechanism Using a Quantitative Measure of Load Reduction. Adv. Theory Pract. Robot. Manip. 2014, 22. [Google Scholar] [CrossRef]
- Szigeti, A.; Takeda, Y.; Matsuura, D. Portable design and range of motion control for an ankle rehabilitation mechanism capable of adjusting to changes in joint axis. Int. J. Mech. Robot. Syst. 2016, 3, 222–236. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; U Michigan Press: Oxford, UK, 1975. [Google Scholar]
- Faghihi, A.; Haghpanah, S.A.; Farahmand, F.; Jafari, M. Design and fabrication of a robot for neurorehabilitation; Smart RoboWrist. In Proceedings of the 2nd International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 5–7 November 2015; pp. 447–450. [Google Scholar]
- Srinivas, M.; Patnaik, L.M. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man. Cybern. 1994, 24, 656–667. [Google Scholar] [CrossRef]
- Gomi, H.; Koike, Y.; Kawato, M. Human hand stiffness during discrete point-to-point multi-joint movement. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS), Paris, France, 29 October–1 November 1992; pp. 1628–1629. [Google Scholar]
- Yu, T.F.; Wilson, A.J. A passive movement method for parameter estimation of a musculo-skeletal arm model incorporating a modified hill muscle model. Comput. Methods Programs Biomed. 2014, 114, 46–59. [Google Scholar] [CrossRef] [PubMed]


| Bit Length of One Variable | Population Size | Crossover Rate | Mutation Rate |
|---|---|---|---|
| 40 | 70 | 0.7 | 0.02 |
| Description | Parameter | Value | Unit |
|---|---|---|---|
| Optimal distance between braces and wrist joint | r1 | 138.0 | mm |
| Optimal length of crank link | r2 | 71.6 | mm |
| Optimal length of coupler link | r3 | 199.8 | mm |
| Optimal length of rocker link | r4 | 161.3 | mm |
| Spring constant of forearm | k | 143 | N/m |
| Output torque | Tout | 1.2 | N·m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-C.; Takeda, Y. Kineto-Static Analysis of a Wrist Rehabilitation Robot with Compliance and Passive Joints for Joint Misalignment Compensation. Machines 2020, 8, 23. https://doi.org/10.3390/machines8020023
Liu Y-C, Takeda Y. Kineto-Static Analysis of a Wrist Rehabilitation Robot with Compliance and Passive Joints for Joint Misalignment Compensation. Machines. 2020; 8(2):23. https://doi.org/10.3390/machines8020023
Chicago/Turabian StyleLiu, Ying-Chi, and Yukio Takeda. 2020. "Kineto-Static Analysis of a Wrist Rehabilitation Robot with Compliance and Passive Joints for Joint Misalignment Compensation" Machines 8, no. 2: 23. https://doi.org/10.3390/machines8020023
APA StyleLiu, Y.-C., & Takeda, Y. (2020). Kineto-Static Analysis of a Wrist Rehabilitation Robot with Compliance and Passive Joints for Joint Misalignment Compensation. Machines, 8(2), 23. https://doi.org/10.3390/machines8020023





