Fault Tolerant Control Based on an Observer on PI Servo Design for a High-Speed Automation Machine
Abstract
1. Introduction
2. Materials and Methods
2.1. Dynamics Modelling of Feed Drive with DC Servomotor
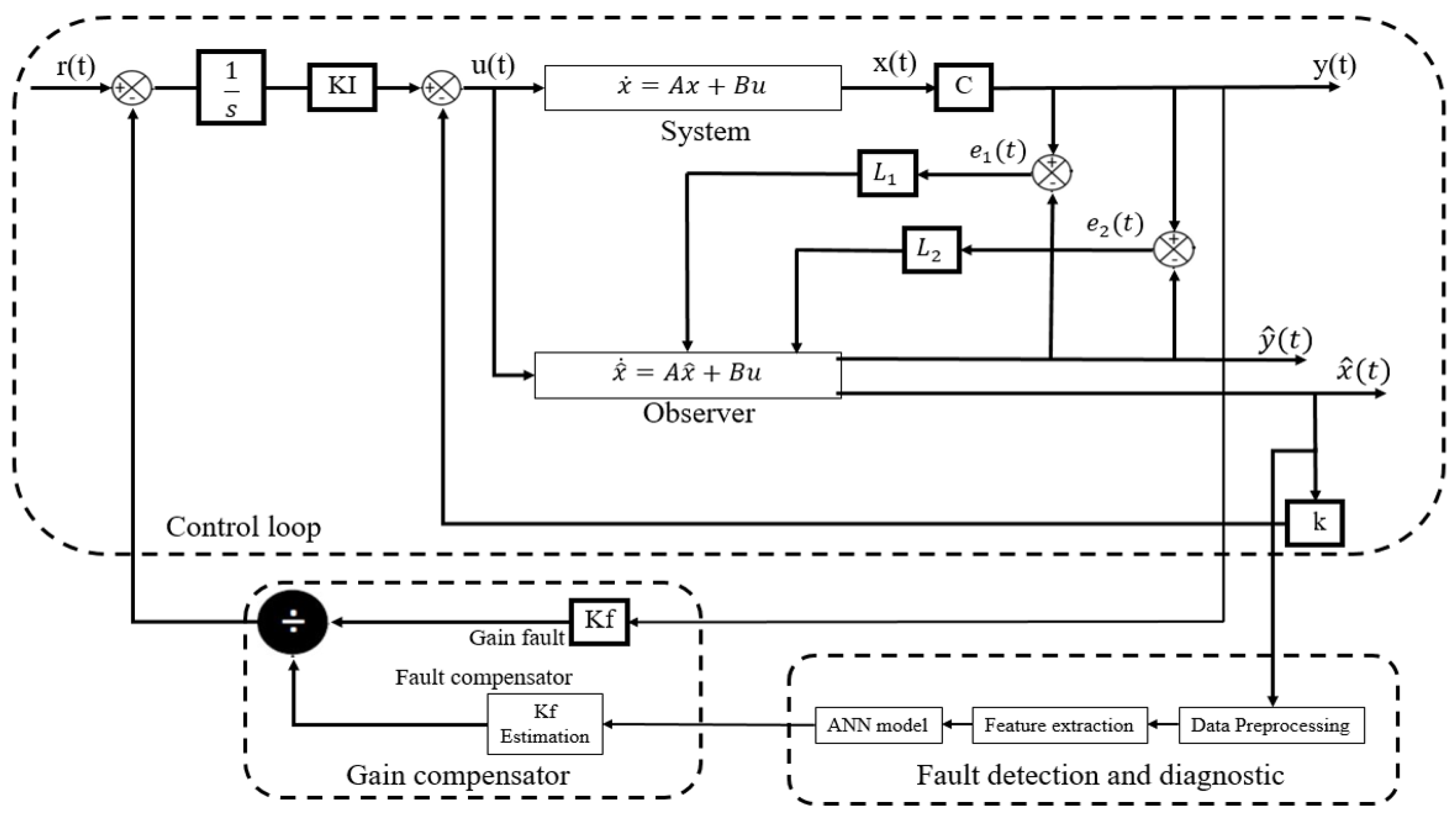
2.2. Fault Tolerant Control by the Artificial Neural Network (ANN) based on the PI Servo System and Observer
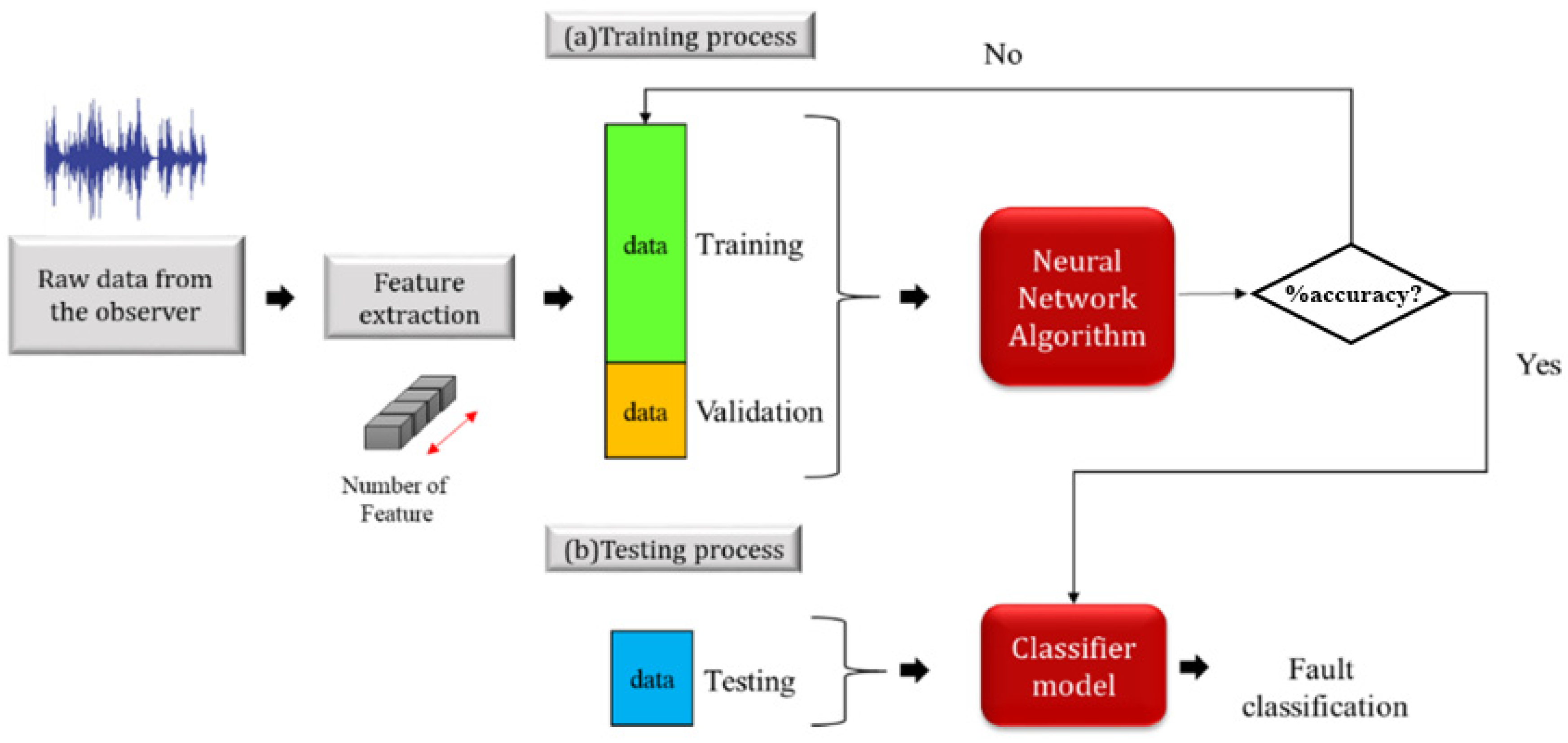
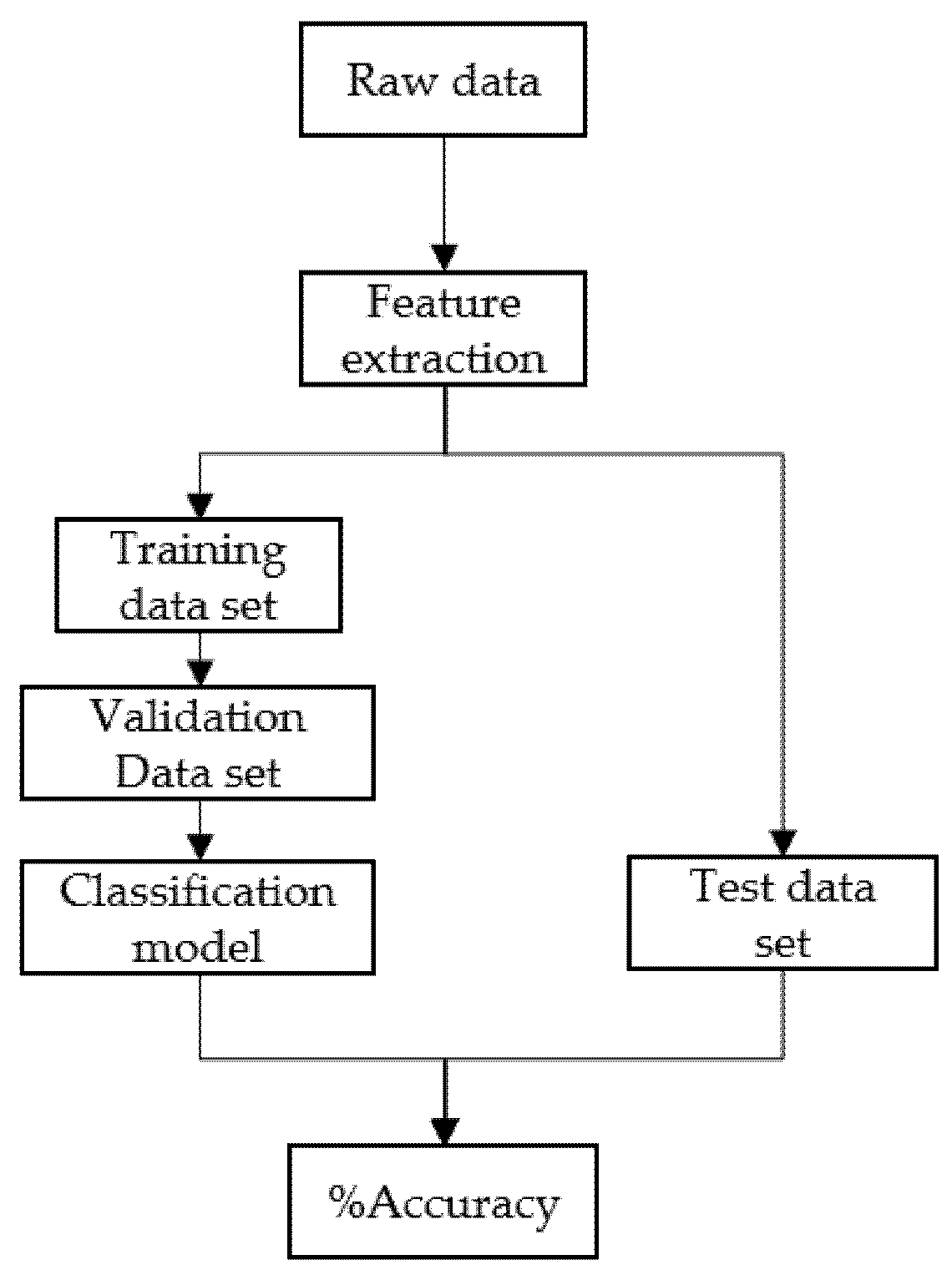
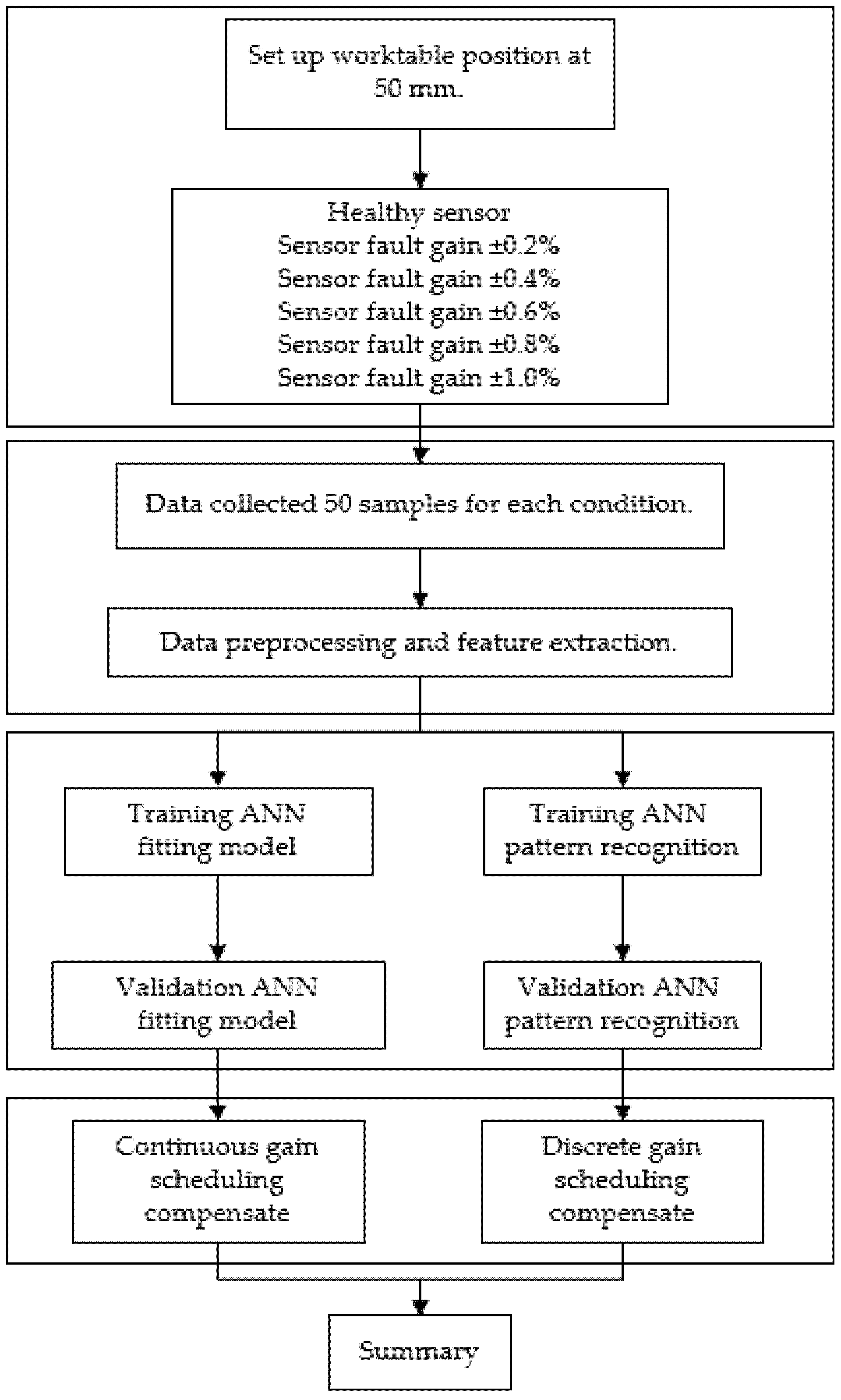
2.3. Data Manipulation
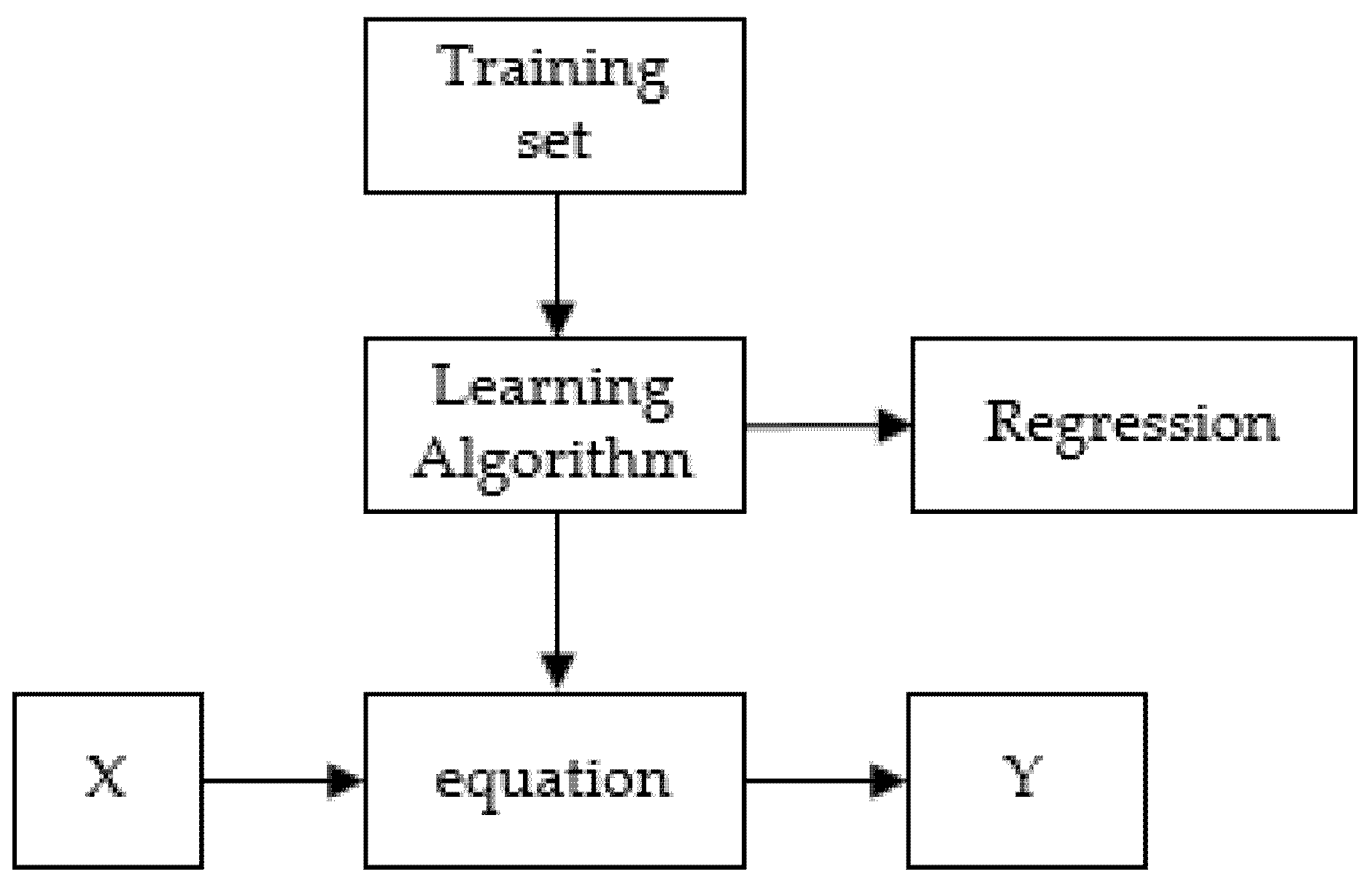
2.4. Artificial Neural Network (ANN)
2.4.1. ANN Pattern Recognition
2.4.2. ANN Model Fitting
2.5. Gain Scheduling
2.5.1. Discrete Gain Scheduling
2.5.2. Continuous Gain Scheduling
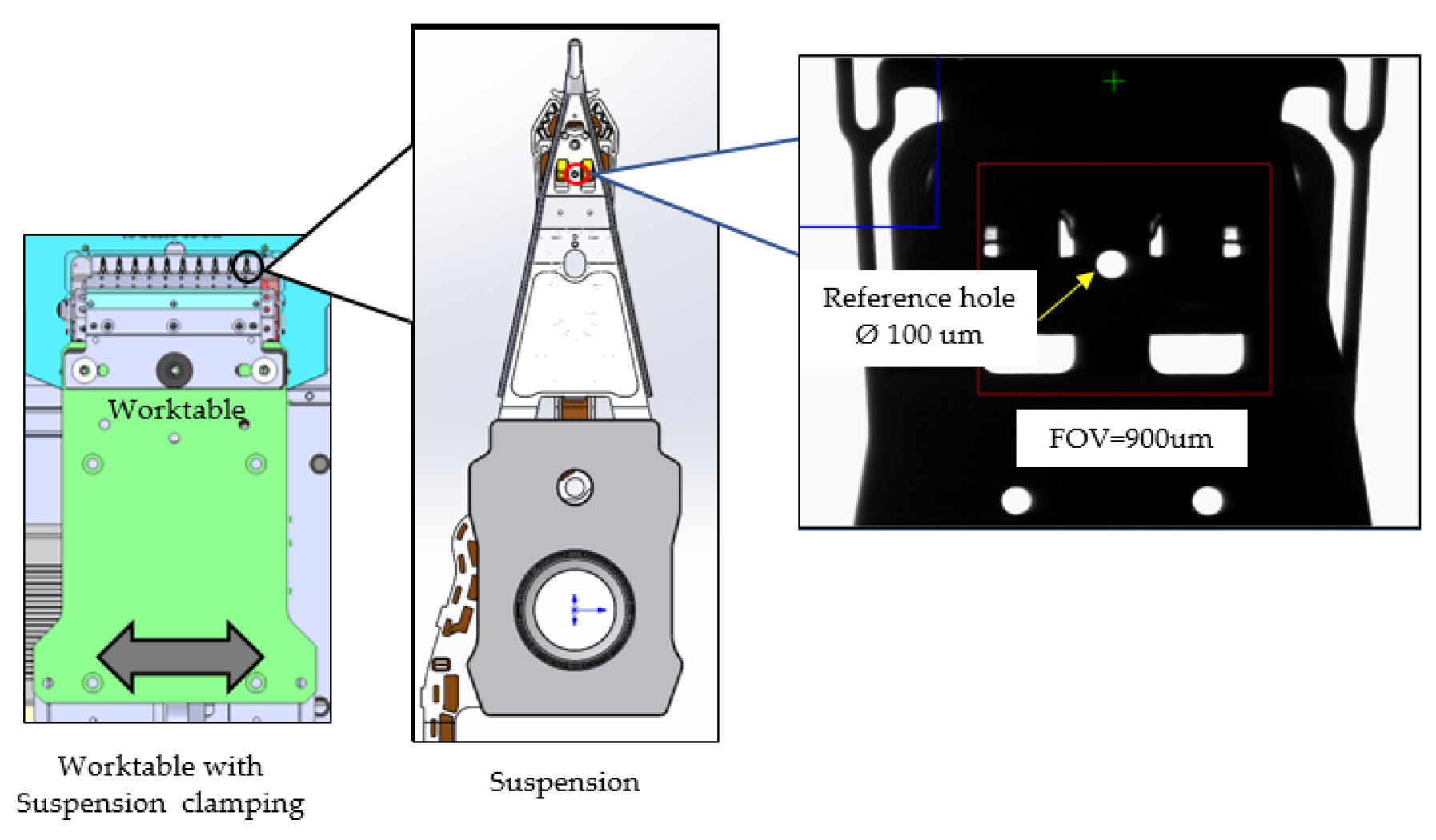
3. Experimental Setup
4. Results and Discussion
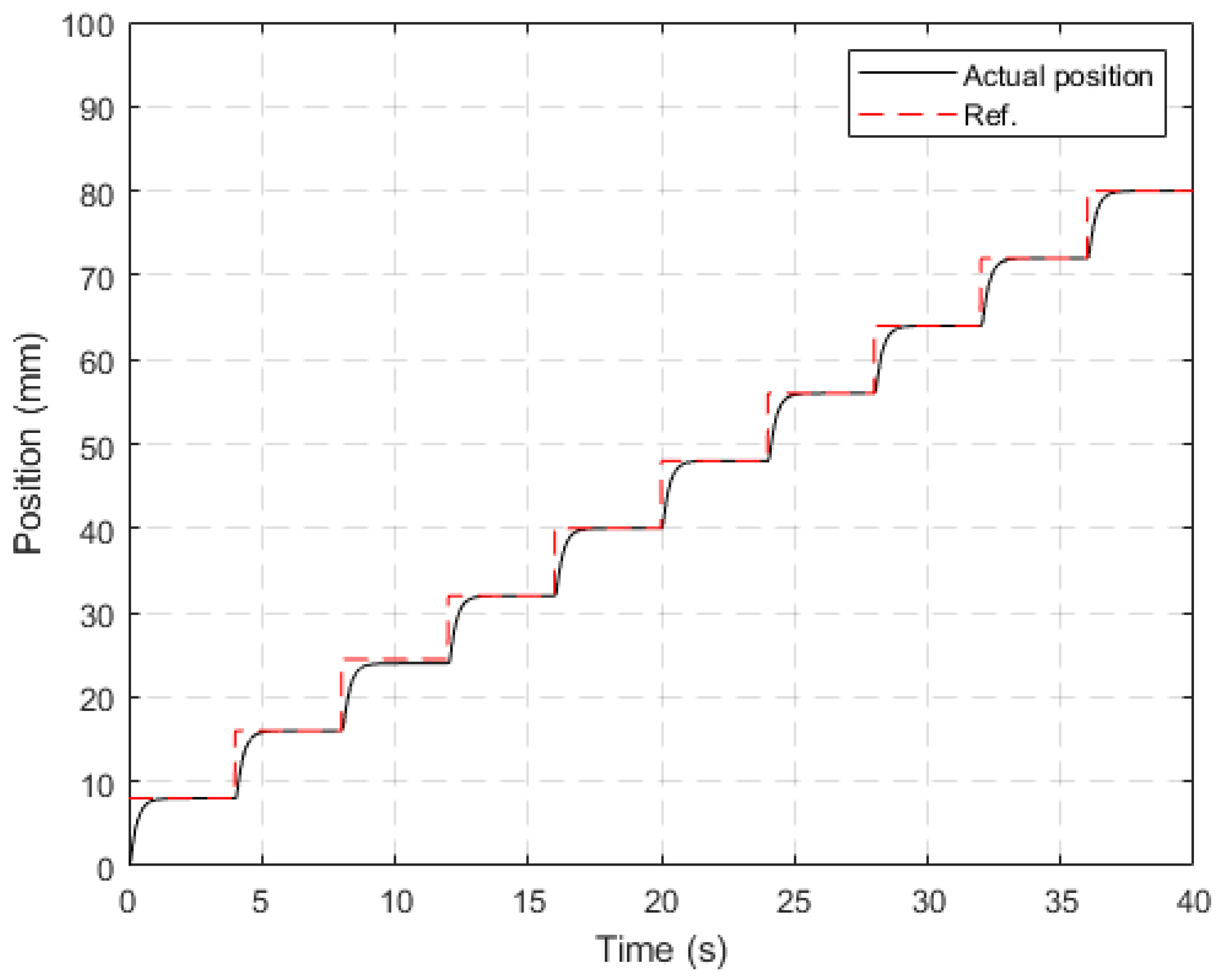
4.1. Response Tracking and Observer Performance
4.2. Data Collection and Preprocessing
4.3. Fault Detection and Diagnostic Experiment Result
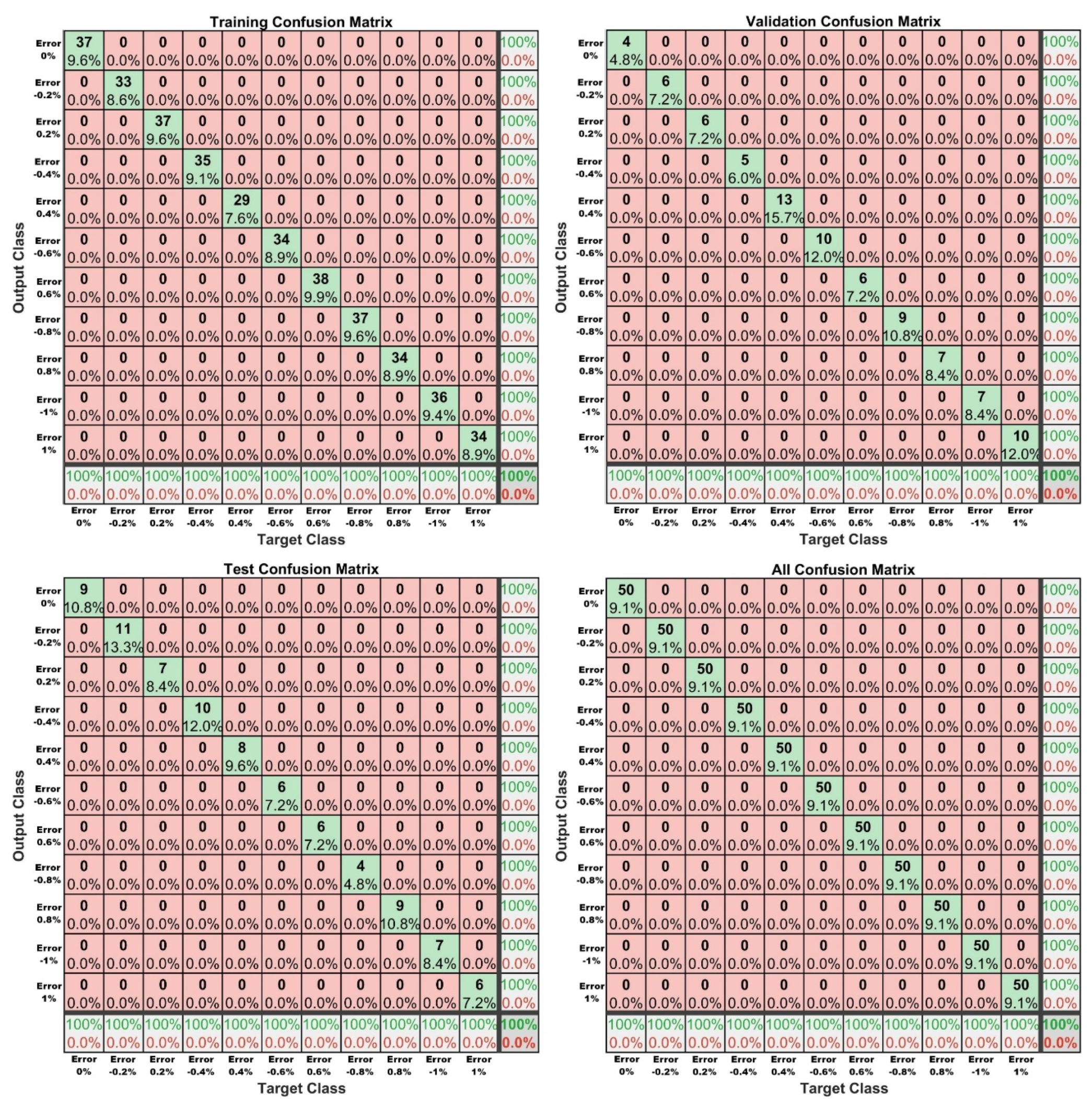
4.3.1. Fault Detection by ANN Pattern Recognition
4.3.2. Fault Detection by ANN Model Fitting
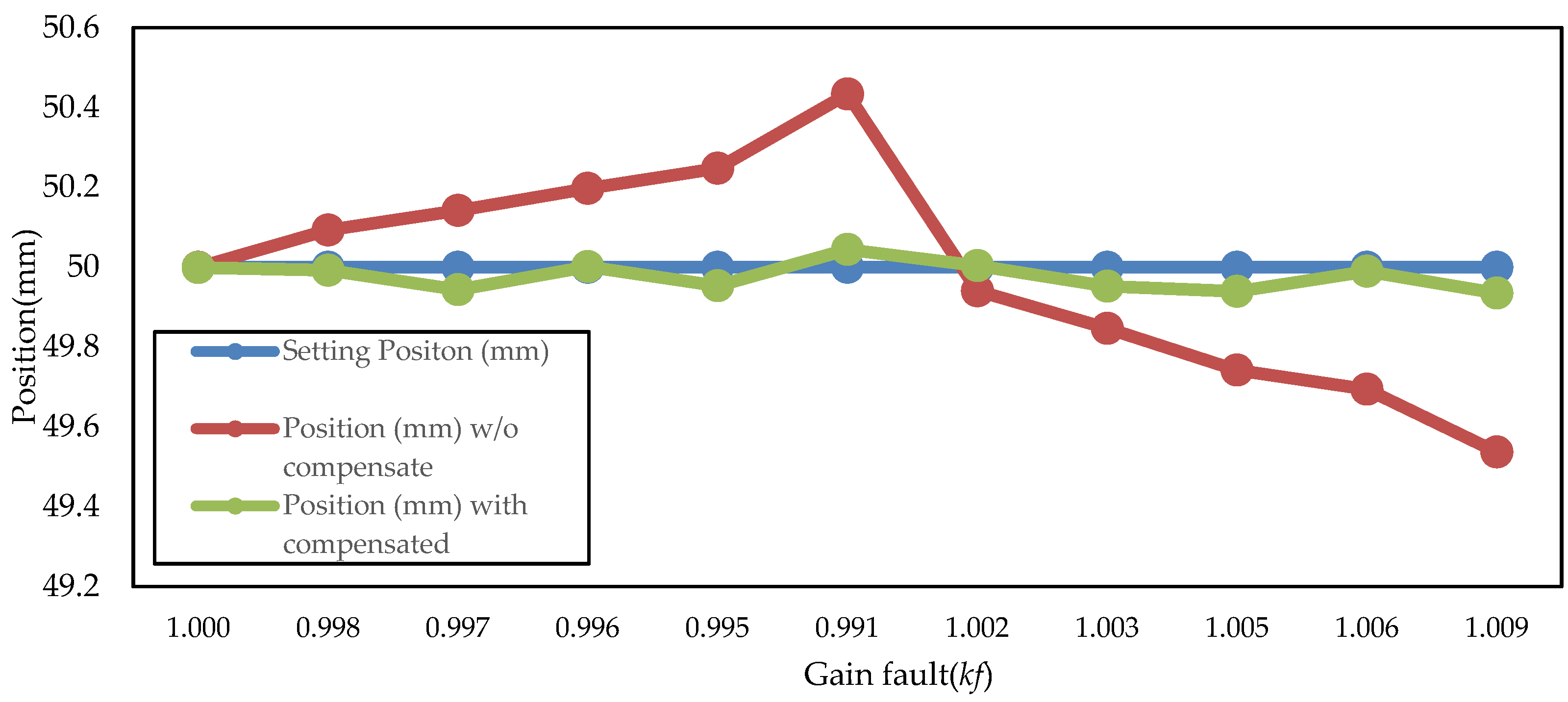
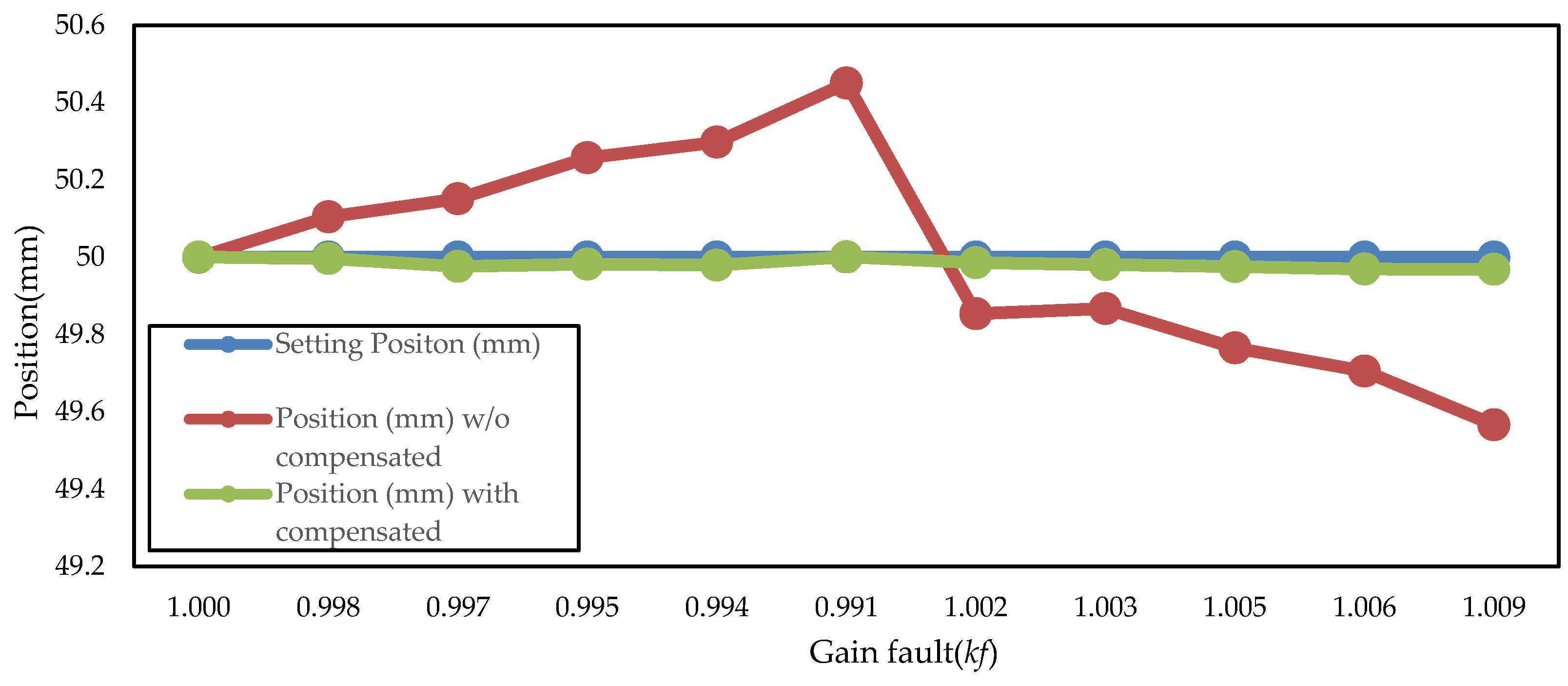
4.4. Gain Compensation Experiment Result
4.4.1. Result for Gain Compensation by Discrete Gain Scheduling
4.4.2. Result for Gain Compensation by Continuous Gain Scheduling
5. Conclusions
- The tracking response of the controller by the PI servo system with state estimation based on an observer was found to provide effective enhancement in position control and was able to track reference inputs, which compensated and significantly reduced errors, leading to the desired step response.
- For the fault detection and diagnostics of linear encoder faults by the ANN pattern recognition and model fitting, by using the observer error signal from the observer, the approaches successfully classified the sensor fault condition with an accuracy of 100% for the pattern recognition method and an R-square of 99.99% for the model fitting technique.
- Both gain compensation techniques—continuous gain scheduling and discrete gain scheduling—were shown to successfully compensate the gain value to maintain the position error of the worktable, moving it back to the desired position, as shown as Table 6. With discrete gain scheduling, position error was reduced from 0.228 mm to 0.031 mm (86% reduction), while the continuous gain scheduling reduced the error from 0.228 mm to 0.017 mm (93% reduction) compared with the system without gain compensation.
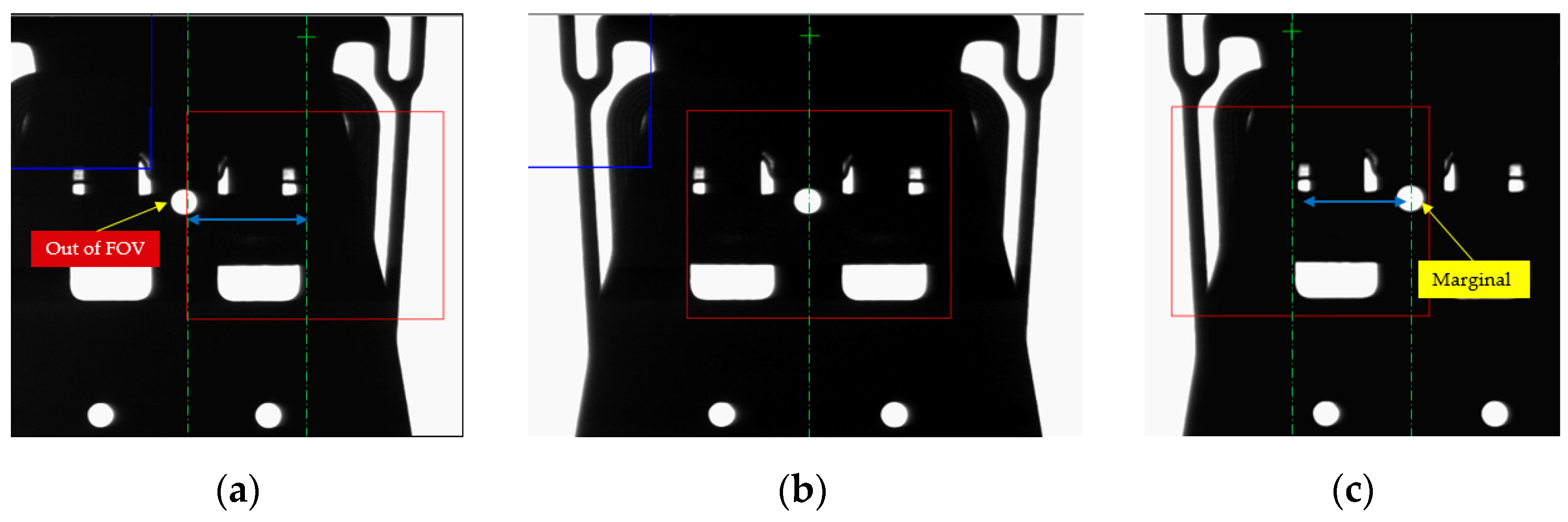
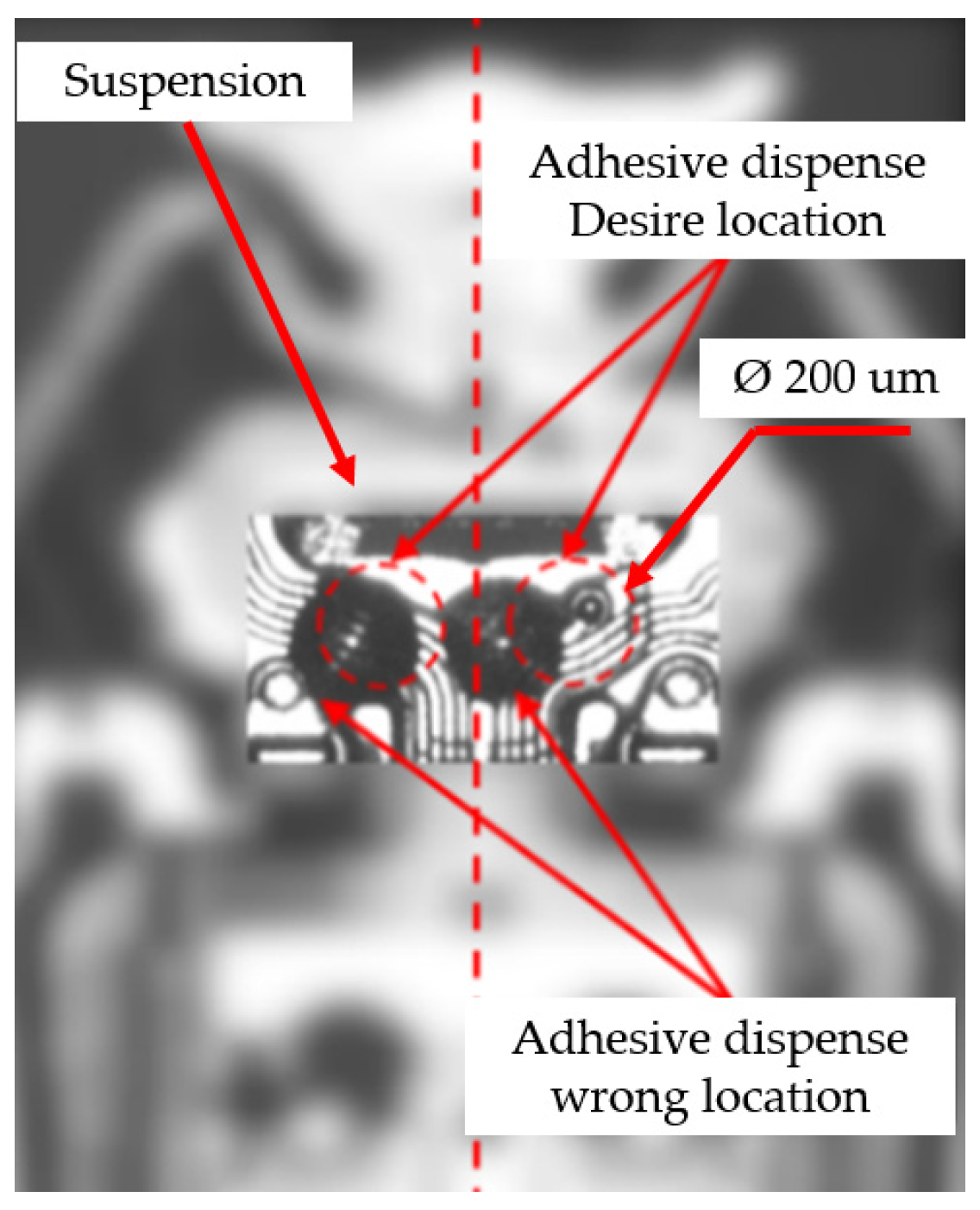
- Fault tolerant control based on PI servo design with an observer by using the ANN and gain compensation technique exceeded the process requirements in controlling the position of the worktable, maintaining the suspension reference hole position within the FOV for slider attachment and the adhesive dispensing process.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Soontaree, S.; Prawanta, S.; Odngam, S.; Srisertpol, J. Pl-Servo with State-D Feedback and Observer for Magnetic Stirrer Machine In 2017 International Conference on Circuits, Devices and Systems (ICCDS); IEEE: Piscataway, NJ, USA, 2017; pp. 6–10. [Google Scholar]
- Aunsiri, T.; Numanoy, N.; Hemsuwan, W.; Srisertpol, J. Servo System Using Pole-Placement with State Observer for Magnetic Levitation System. Lect. Notes Electr. Eng. 2014, 309, 921–926. [Google Scholar]
- Dong, X.; Jian-Qu, Z.; Feng, W. Fuzzy PID Control to Feed Servo System of CNC Machine Tool. Procedia Eng. 2012, 29, 2853–2858. [Google Scholar] [CrossRef]
- Jamaludin, Z.; Van Brussel, H.; Swevers, J. Friction Compensation of an XY Feed Table Using Friction-Model-Based Feedforward and an Inverse-Model-Based Disturbance Observer. IEEE Trans. Ind. Electron. 2009, 56, 3848–3853. [Google Scholar] [CrossRef]
- Dubey, R.; Agrawal, D. Bearing fault classification using ANN-based Hilbert footprint analysis. IET Sci. Meas. Technol. 2015, 9, 1016–1022. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, T.; Chu, F. Deep convolutional neural network based planet bearing fault classification. Comput. Ind. 2019, 107, 59–66. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, S.; Chen, X.-D.; Li, C.; Sánchez, R.-V.; Qin, H. Deep neural networks-based rolling bearing fault diagnosis. Microelectron. Reliab. 2017, 75, 327–333. [Google Scholar] [CrossRef]
- Prathan, C.; Lawbootsa, S.; Srisertpol, J. Fault Detection of Linear Bearing in Auto Core Adhesion Mounting Machine Using Artificial Neural Network. WSEAS Trans. Syst. Control 2019, 14, 31–42. [Google Scholar]
- Noura, H.; Sauter, D.; Hamelin, F.; Theilliol, D. Fault-tolerant control in dynamic systems: Application to a winding machine. IEEE Control. Syst. 2000, 20, 33–49. [Google Scholar]
- Xu, L.; Li, J.; Ouyang, M.; Hua, J.; Li, X. Active fault tolerance control system of fuel cell hybrid city bus. Int. J. Hydrog. Energy 2010, 35, 12510–12520. [Google Scholar] [CrossRef]
- Wanglomklang, T.; Chommaungpuck, P.; Srisertpol, J. Linear Bearing Fault Detection Using an Artificial Neural Network Based on a PI Servo System with the Observer for High-Speed Automation Machine. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 717, p. 012011. [Google Scholar]
- Lin, C.-Y.; Lee, C.-H. Remote Servo Tuning System for Multi-Axis CNC Machine Tools Using a Virtual Machine Tool Approach. Appl. Sci. 2017, 7, 776. [Google Scholar] [CrossRef]
- Saad, S.B.M.; Andrew, A.M.; Shakaff, A.Y.M.; Saad, A.R.M.; Yusof, A.M.; Zakaria, A. Classifying Sources Influencing Indoor Air Quality (IAQ) Using Artificial Neural Network (ANN). Sensors 2015, 15, 11665–11684. [Google Scholar] [CrossRef] [PubMed]
- Mohamad, K.; Wallbaum, H.; Nägeli, C.; Ostermeyer, Y. Feasibility of solar energy in south Sweden: Artificial Neural Network modeling. Int. Multidiscip. Sci. GeoConf. SGEM Surv. Geol. Min. Ecol. Manag. 2016, 3, 273–280. [Google Scholar]
- Luwei, K.C.; Yunusa-Kaltungo, A.; Sha’Aban, Y. Integrated Fault Detection Framework for Classifying Rotating Machine Faults Using Frequency Domain Data Fusion and Artificial Neural Networks. Machines 2018, 6, 59. [Google Scholar] [CrossRef]
- Setyawan, W.; Suryasa, I.N.; Fajarianto, O.; Abdullah, K.A.b.; Rahim, M.S.M.; Priyandoko, G.; Budaya, G.A. Wood Texture Detection with Conjugate Gradient Neural Network Algorithm. In 2017 4th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI); IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Hamed, B.; Zhang, Y.; Hong, H. Fault-Tolerant Control Design for a Large off-Shore Wind Turbine Using Fuzzy Gain-Scheduling and Signal Correction. In 2013 American Control Conference; IEEE: Piscataway, NJ, USA, 2013; pp. 1448–1453. [Google Scholar]
- Manjula, S.; Nirosha, H.; Sheeparamatti, B.G. Artificial Neural Network Modeling of MEMS Cantilever Resonator Using Levenberg Marquardt Algorithm. In 2016 2nd International Conference on Applied and Theoretical Computing and Communication Technology (ICATccT); IEEE: Piscataway, NJ, USA, 2016; pp. 808–811. [Google Scholar]
- Hong-Bo, Z.; Pei, H.; Chen, B. Observer-Based Gain Scheduling Control of Robotic Helicopter. In 2009 International Conference on Artificial Intelligence and Computational Intelligence; IEEE: Piscataway, NJ, USA, 2009; Volume 2, pp. 297–302. [Google Scholar]
- Llins, L.I.H.; Assunção, E.; Teixeira, M.C.M.; Cardim, R.; Cadalso, M.R.R.; De Oliveira, D.R.; Da Silva, E.R.P. Design of Gain Scheduling Control Using State Derivative Feedback. Math. Probl. Eng. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
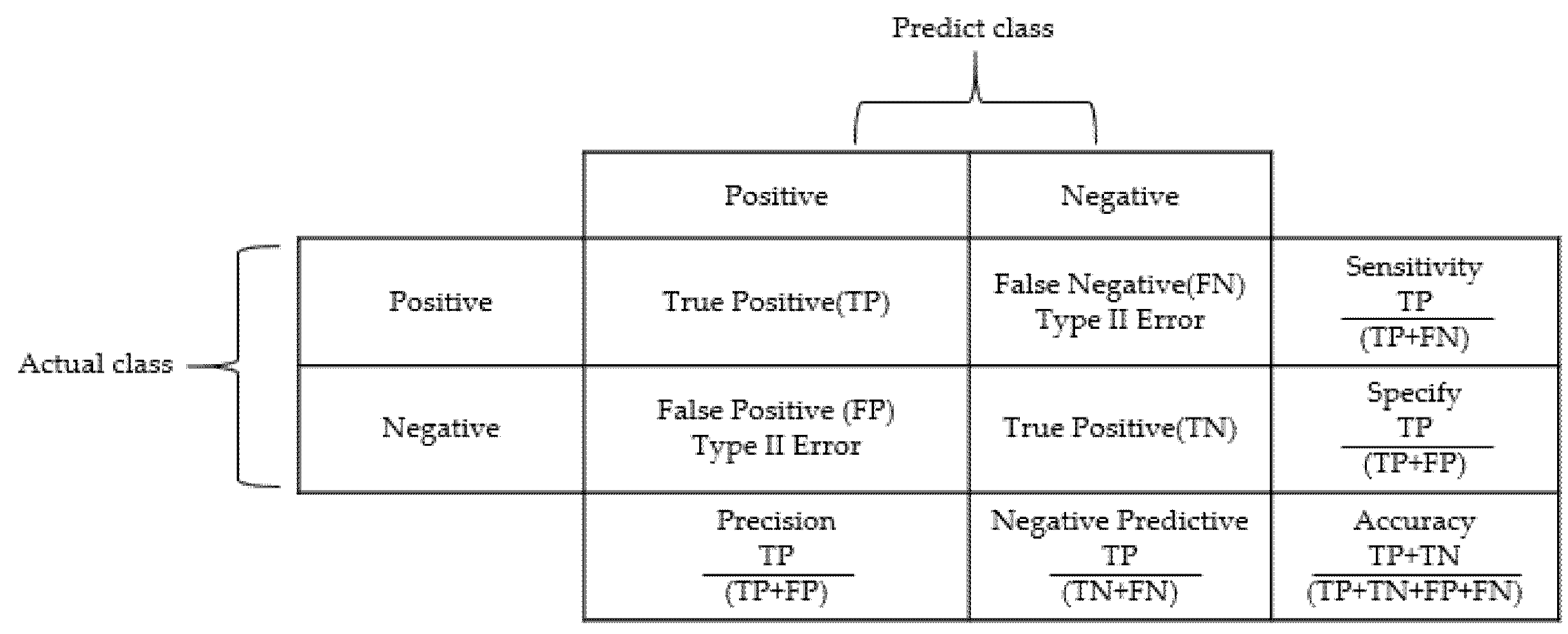
- Plot Classification Confusion Matrix-MATLAB Plotconfusion. Available online: https://www.mathworks.com/help/deeplearning/ref/plotconfusion.html (accessed on 16 April 2020).
- GeeksforGeeks. Confusion Matrix in Machine Learning. 15 October 2017. Available online: https://www.geeksforgeeks.org/confusion-matrix-machine-learning/ (accessed on 16 April 2020).










| Description | Parameter | Value | Unit |
|---|---|---|---|
| Moment of inertia | 10.27 | kgm2 | |
| Armature resistance | 1165.2 | Ω | |
| Torque coefficient | 7.3892 × 106 | Nm/A | |
| Viscous friction coefficient | 6.474 | Nms/rad | |
| Back electromotive force coefficient | 0.0294 | Vs/rad | |
| Total of worktable mass | 7 | kg | |
| Coefficient of the damping of the lead screw | 10566 | Ns/m | |
| Coefficient stiffness of the lead screw | 5.18 × 106 | N/m | |
| Coefficient of motor rotation converts to lead screw | R | 0.7958 | - |
| Gain Error (Kf) | Observer Error Range (mm.) | Gain Compensation (Kf Estimate) | |
|---|---|---|---|
| Min | Max | ||
| −1.00% | −0.0437 | −0.0381 | 0.990 |
| −0.80% | −0.0358 | −0.0232 | 0.992 |
| −0.80% | −0.0358 | −0.0232 | 0.992 |
| −0.60% | −0.0171 | −0.0128 | 0.994 |
| −0.40% | −0.006 | −0.002 | 0.996 |
| −0.20% | 0.0047 | 0.0098 | 0.998 |
| 0.00% | 0.0167 | 0.0205 | 1.000 |
| 0.20% | 0.0276 | 0.032 | 1.002 |
| 0.40% | 0.0396 | 0.0438 | 1.004 |
| 0.60% | 0.051 | 0.0556 | 1.006 |
| 0.80% | 0.0599 | 0.0656 | 1.008 |
| 1.00% | 0.0733 | 0.0779 | 1.010 |
| ANN Method | Accuracy/R-Squared |
|---|---|
| Pattern recognition | 100% |
| Model fitting | 99.99% |
| Gain Fault (Kf) | Position (mm) without Compensation | Gain Estimate (Kf) | Position (mm) with Compensation | Position Error (mm) | |
|---|---|---|---|---|---|
| without Compensation | with Compensation | ||||
| 1.000 | 50.000 | 1.000 | 49.999 | 0.000 | 0.001 |
| 0.998 | 50.093 | 0.998 | 49.992 | 0.093 | 0.008 |
| 0.997 | 50.142 | 0.996 | 49.944 | 0.142 | 0.056 |
| 0.996 | 50.198 | 0.996 | 50.002 | 0.198 | 0.002 |
| 0.995 | 50.248 | 0.994 | 49.953 | 0.248 | 0.047 |
| 0.991 | 50.434 | 0.992 | 50.044 | 0.434 | 0.044 |
| 1.002 | 49.941 | 1.002 | 50.004 | 0.059 | 0.004 |
| 1.003 | 49.847 | 1.002 | 49.952 | 0.153 | 0.048 |
| 1.005 | 49.743 | 1.004 | 49.940 | 0.257 | 0.060 |
| 1.006 | 49.694 | 1.006 | 49.990 | 0.306 | 0.010 |
| 1.009 | 49.537 | 1.008 | 49.935 | 0.463 | 0.065 |
| Gain Fault (Kf) | Position (mm) without Compensation | Gain Estimate (Kf) | Position (mm) with Compensation | Position Error (mm) | |
|---|---|---|---|---|---|
| without Compensation | with Compensation | ||||
| 1.000 | 50.000 | 1.000 | 50.000 | 0.000 | 0.000 |
| 0.998 | 50.104 | 0.998 | 49.996 | 0.104 | 0.004 |
| 0.997 | 50.151 | 0.997 | 49.976 | 0.151 | 0.024 |
| 0.996 | 50.257 | 0.994 | 49.982 | 0.257 | 0.018 |
| 0.995 | 50.298 | 0.994 | 49.979 | 0.298 | 0.021 |
| 0.991 | 50.450 | 0.991 | 50.001 | 0.450 | 0.001 |
| 1.002 | 49.854 | 1.001 | 49.986 | 0.146 | 0.014 |
| 1.003 | 49.867 | 1.002 | 49.981 | 0.133 | 0.019 |
| 1.005 | 49.765 | 1.004 | 49.976 | 0.235 | 0.024 |
| 1.006 | 49.706 | 1.005 | 49.970 | 0.294 | 0.030 |
| 1.009 | 49.567 | 1.008 | 49.969 | 0.433 | 0.031 |
| Condition | Position Error (mm) | % Position Error Reduction |
|---|---|---|
| Without compensate | 0.228 | - |
| Discrete gain scheduling | 0.031 | 86% |
| Continuous gain scheduling | 0.017 | 93% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chommuangpuck, P.; Wanglomklang, T.; Tantrairatn, S.; Srisertpol, J. Fault Tolerant Control Based on an Observer on PI Servo Design for a High-Speed Automation Machine. Machines 2020, 8, 22. https://doi.org/10.3390/machines8020022
Chommuangpuck P, Wanglomklang T, Tantrairatn S, Srisertpol J. Fault Tolerant Control Based on an Observer on PI Servo Design for a High-Speed Automation Machine. Machines. 2020; 8(2):22. https://doi.org/10.3390/machines8020022
Chicago/Turabian StyleChommuangpuck, Prathan, Thanasak Wanglomklang, Suradet Tantrairatn, and Jiraphon Srisertpol. 2020. "Fault Tolerant Control Based on an Observer on PI Servo Design for a High-Speed Automation Machine" Machines 8, no. 2: 22. https://doi.org/10.3390/machines8020022
APA StyleChommuangpuck, P., Wanglomklang, T., Tantrairatn, S., & Srisertpol, J. (2020). Fault Tolerant Control Based on an Observer on PI Servo Design for a High-Speed Automation Machine. Machines, 8(2), 22. https://doi.org/10.3390/machines8020022






