Effects of Ultra-High Reynolds Number and Low Mach Number Compressibility on the Static Stall Behavior of a Wind Turbine Airfoil
Abstract
1. Introduction
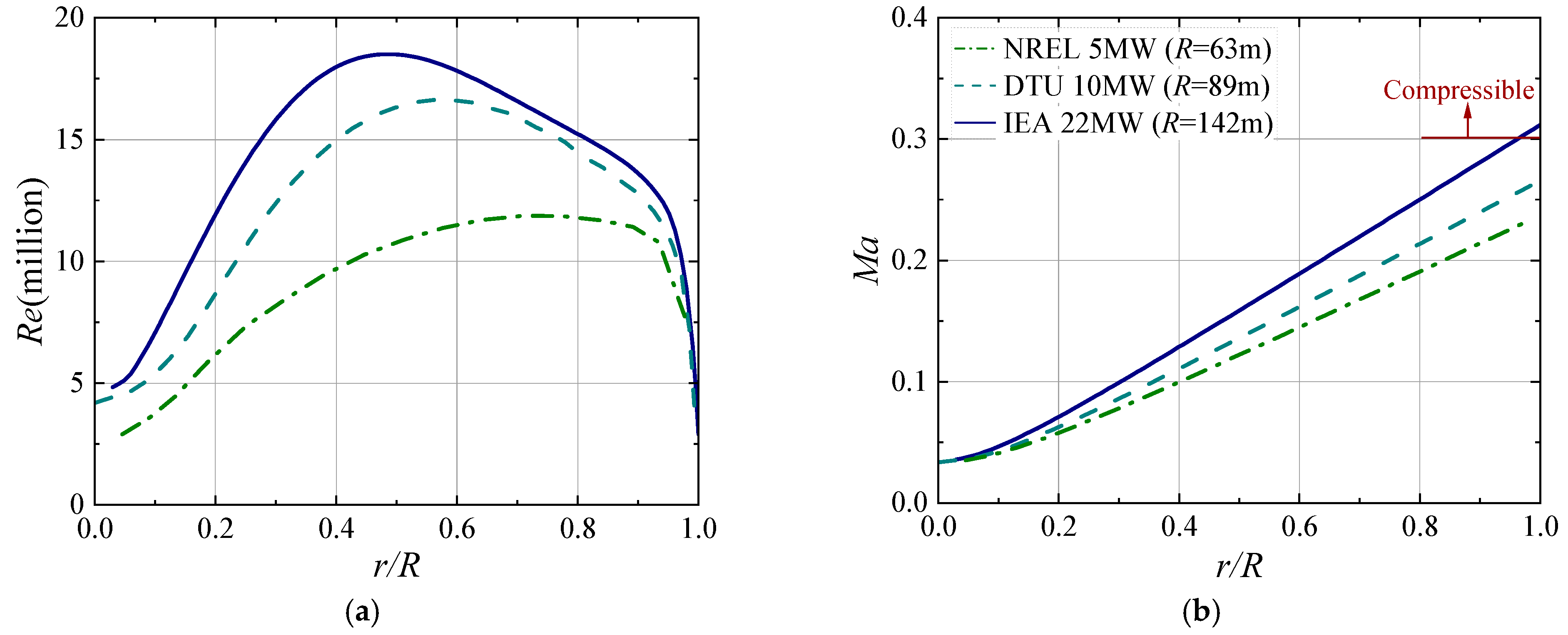
2. Relationship and Decoupling of Reynolds Number and Mach Number
2.1. High Reynolds Number Effect
2.2. Compressible Effect
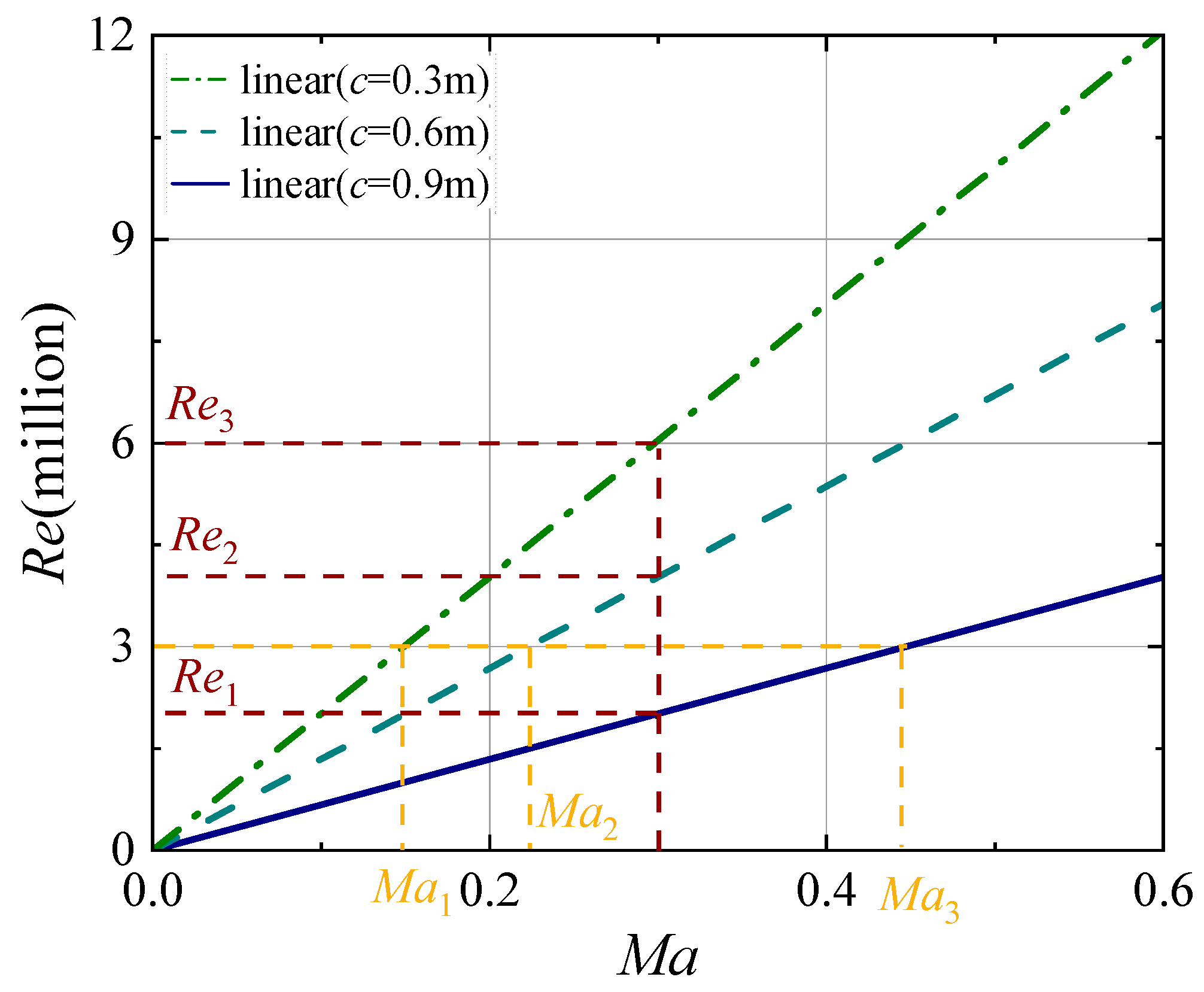
2.3. Decoupling Between Reynolds Number and Mach Number
3. Numerical Modeling of Airfoil Static Stall
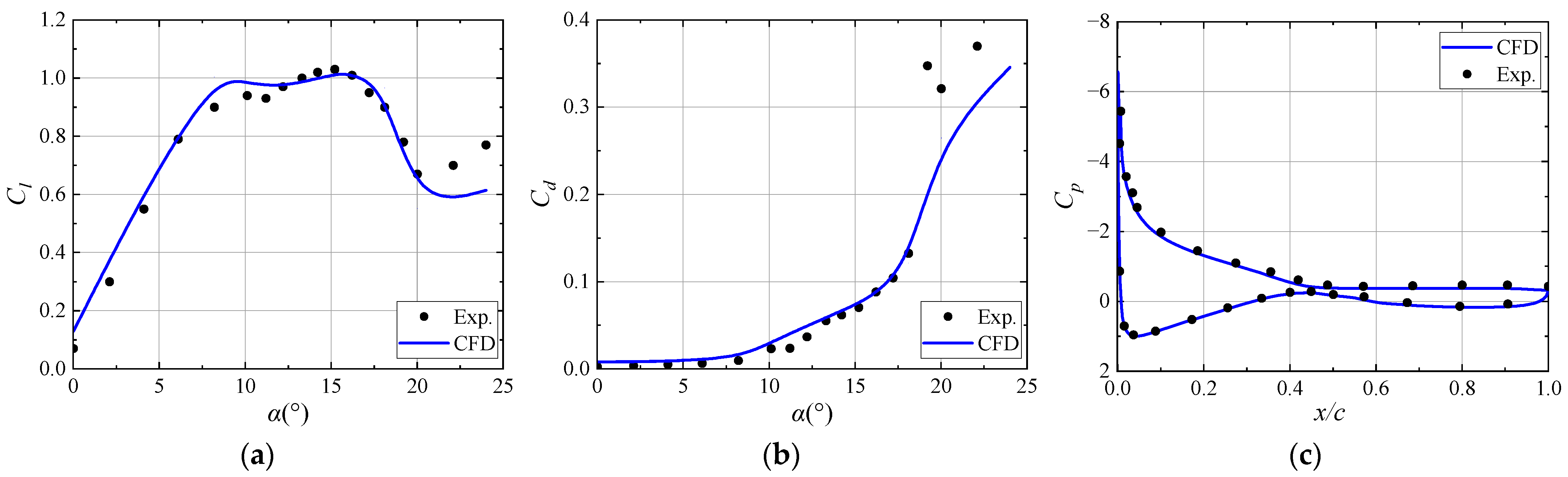
4. Validation of Numerical Modeling
5. Clarification of Numerical Uncertainty
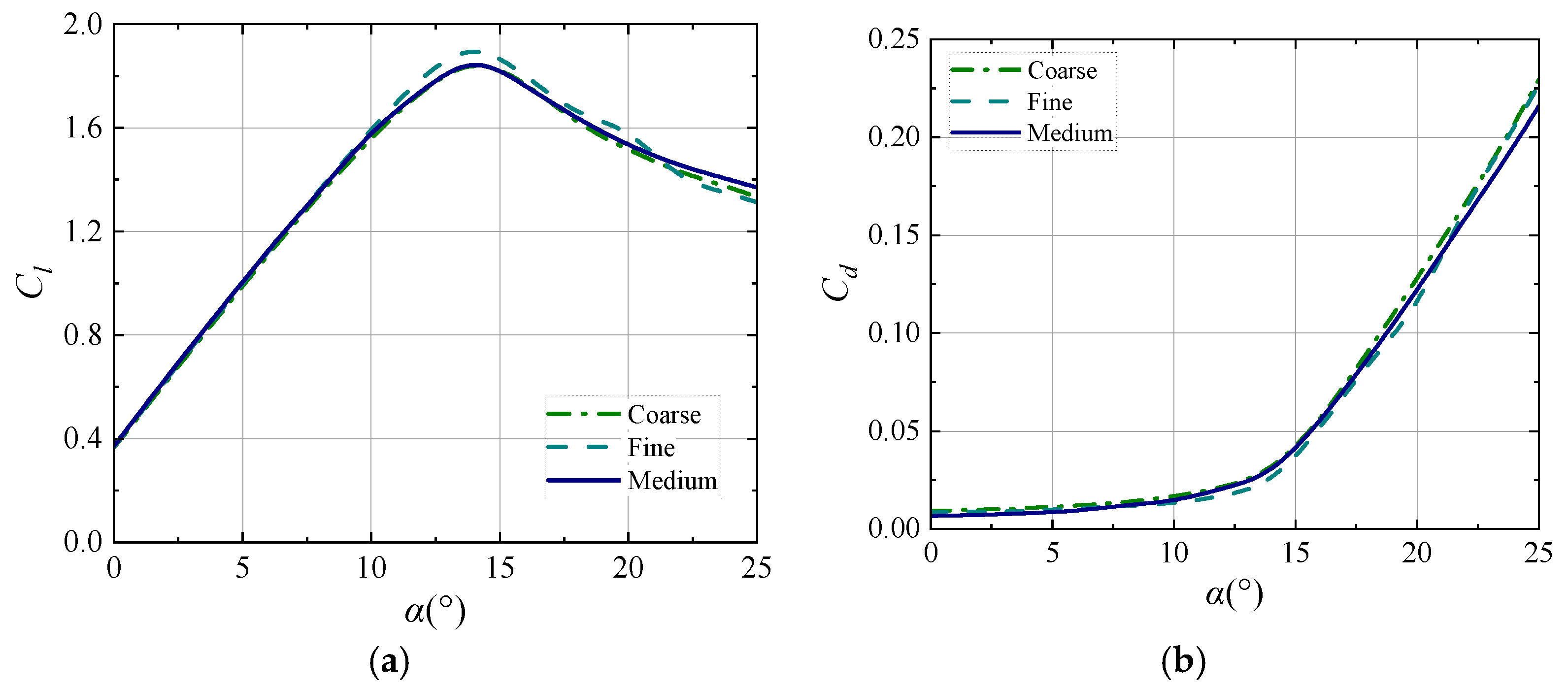
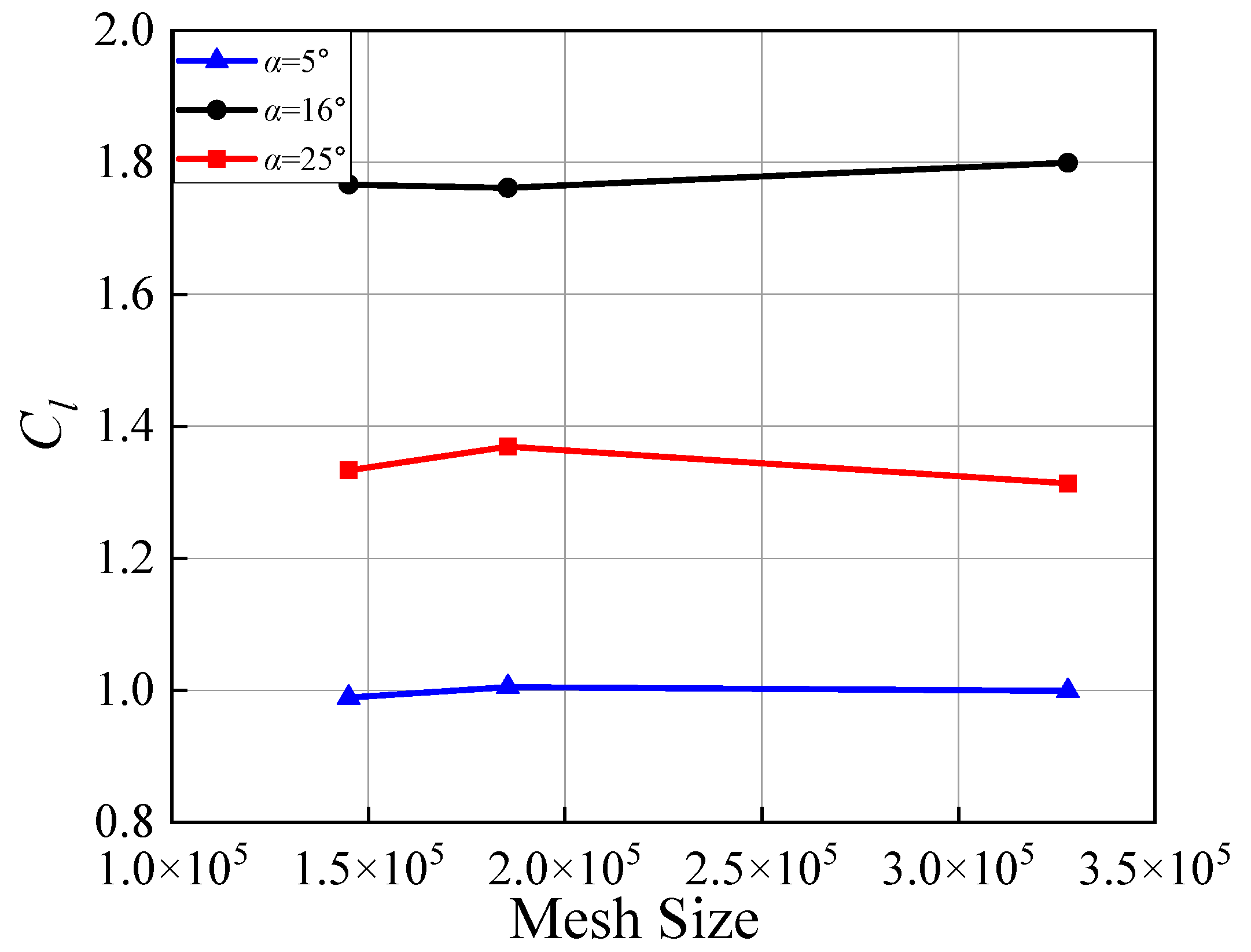
5.1. Verification of Grid Independence
5.2. Turbulence Model Sensitivity
5.3. Numerical Error
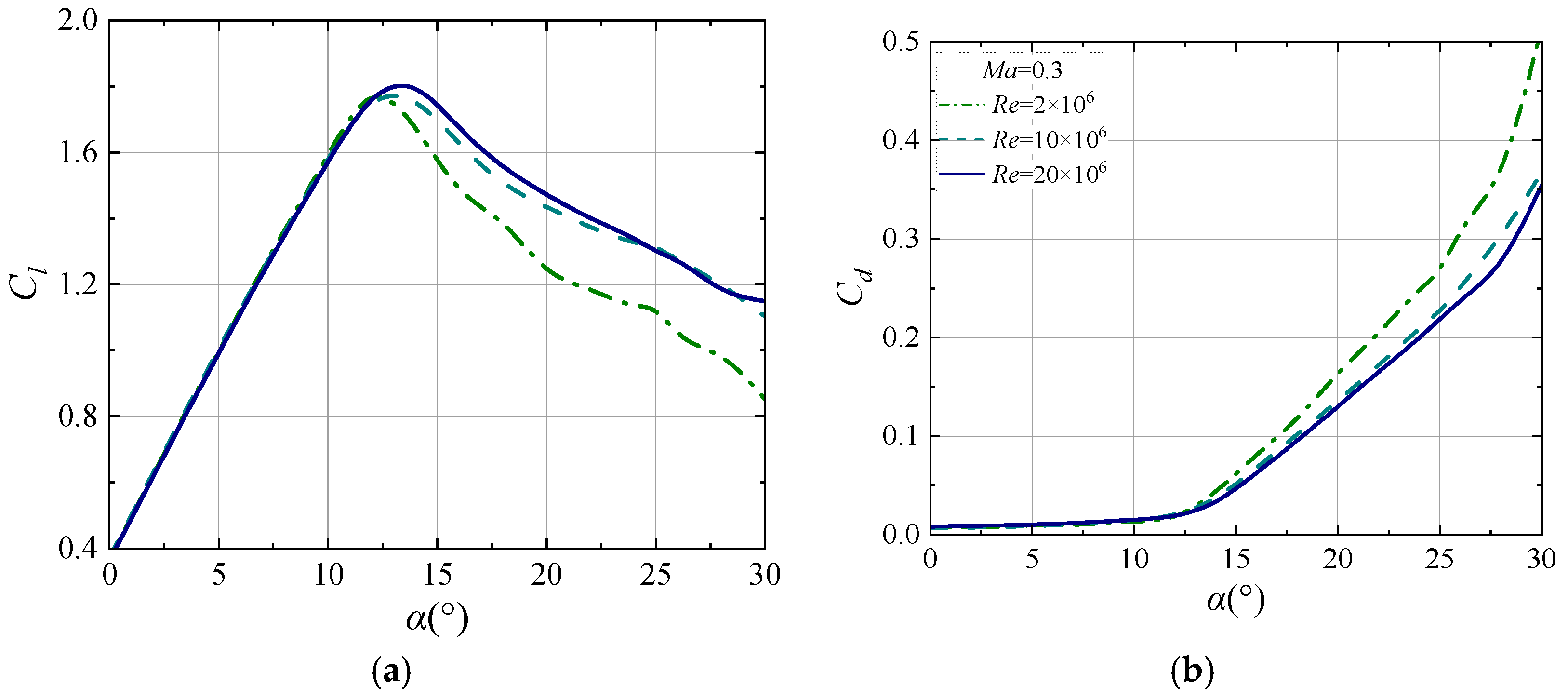
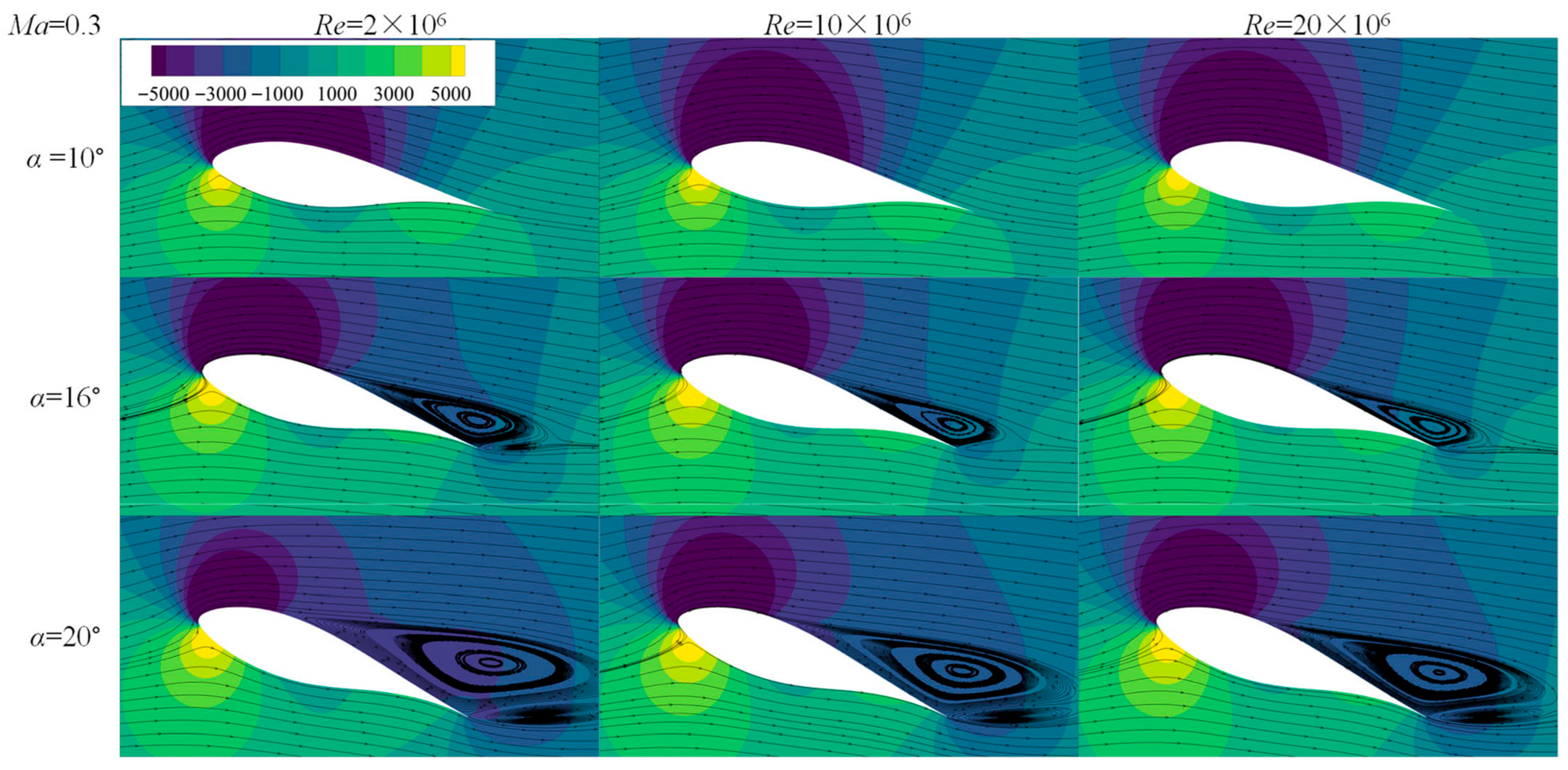
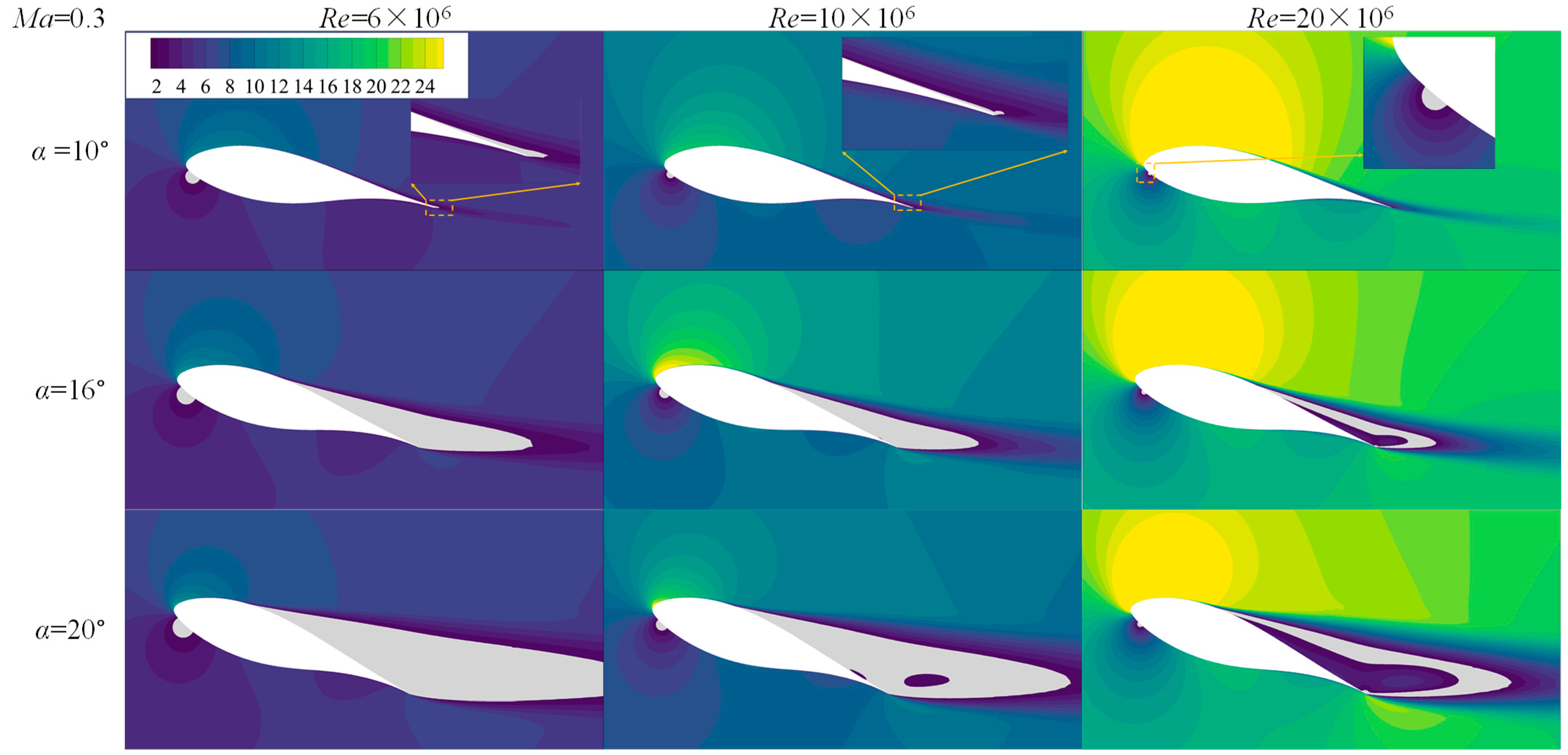
6. High Re-Turbulent Separation Control Delays Static Stall
6.1. Static Stall Behaviors
6.2. Flow Field Development
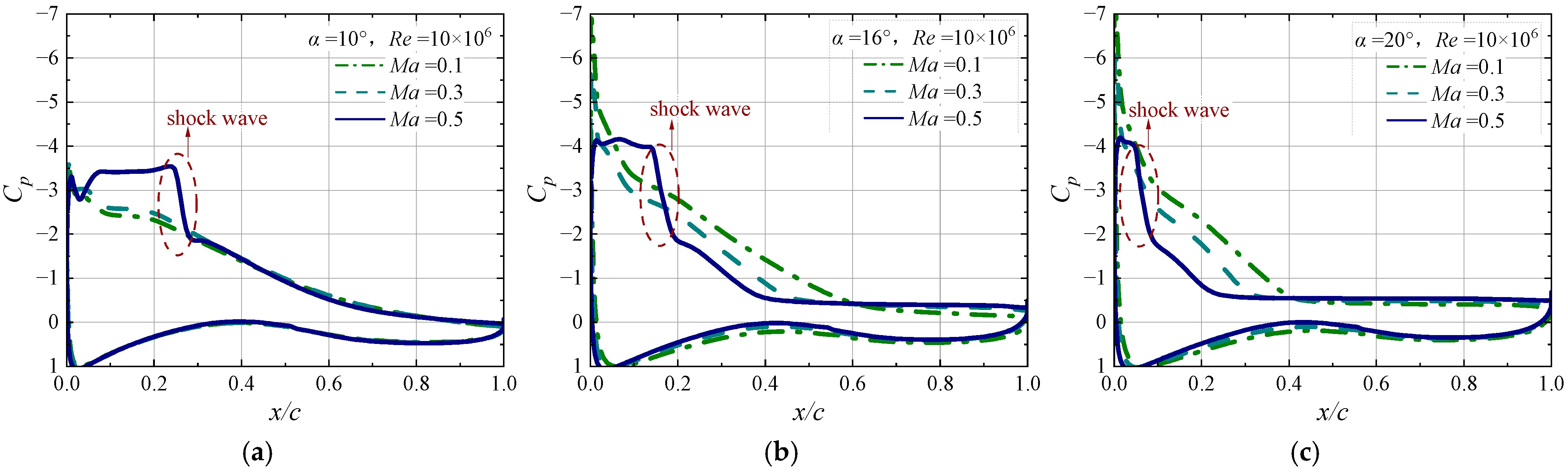
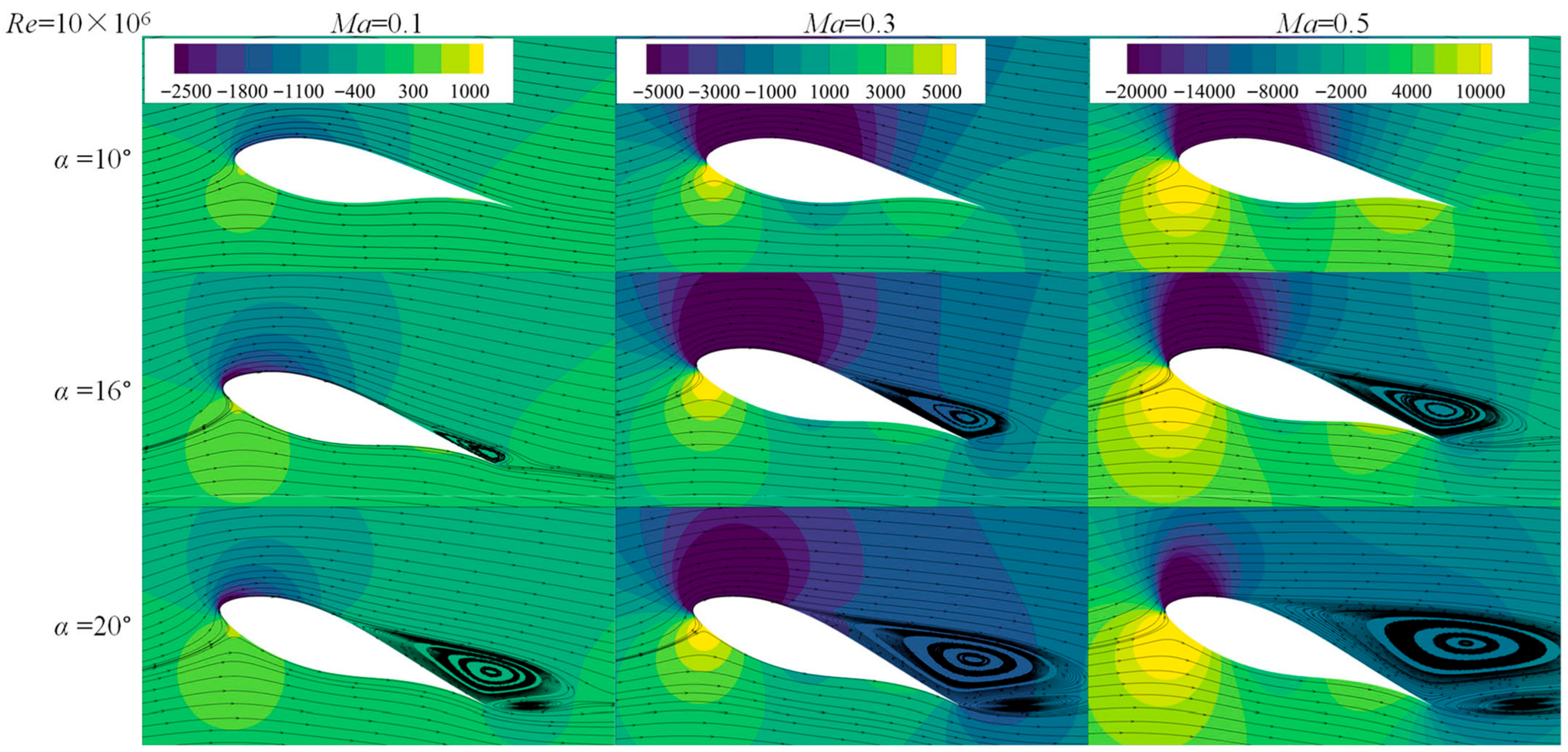
7. Low-Mach Shock Interaction Induces Premature Stall
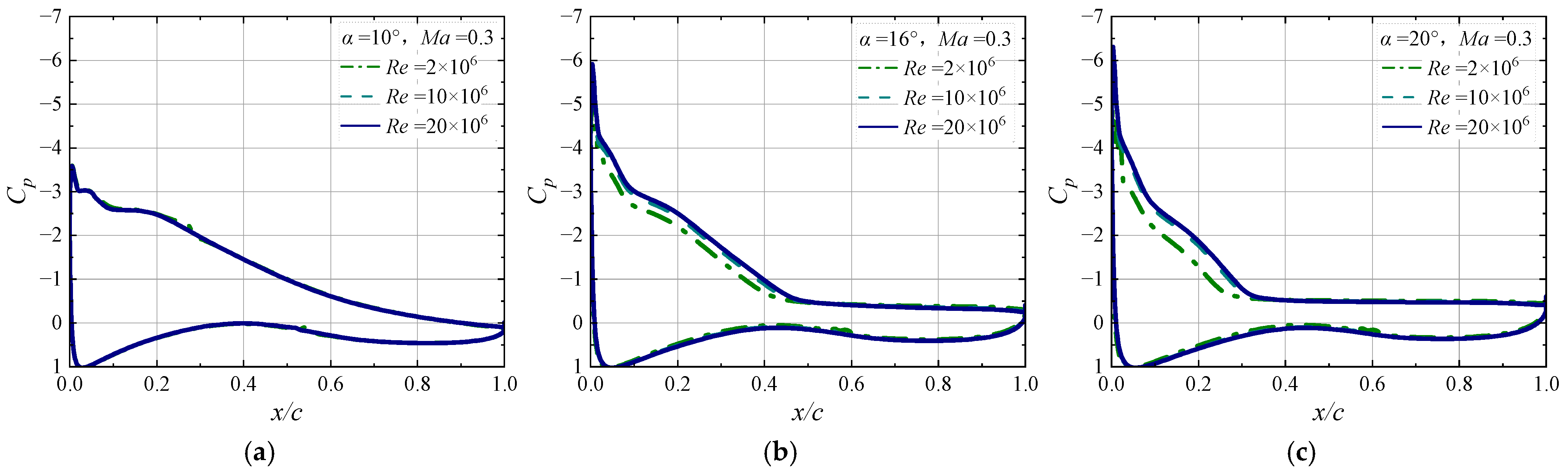
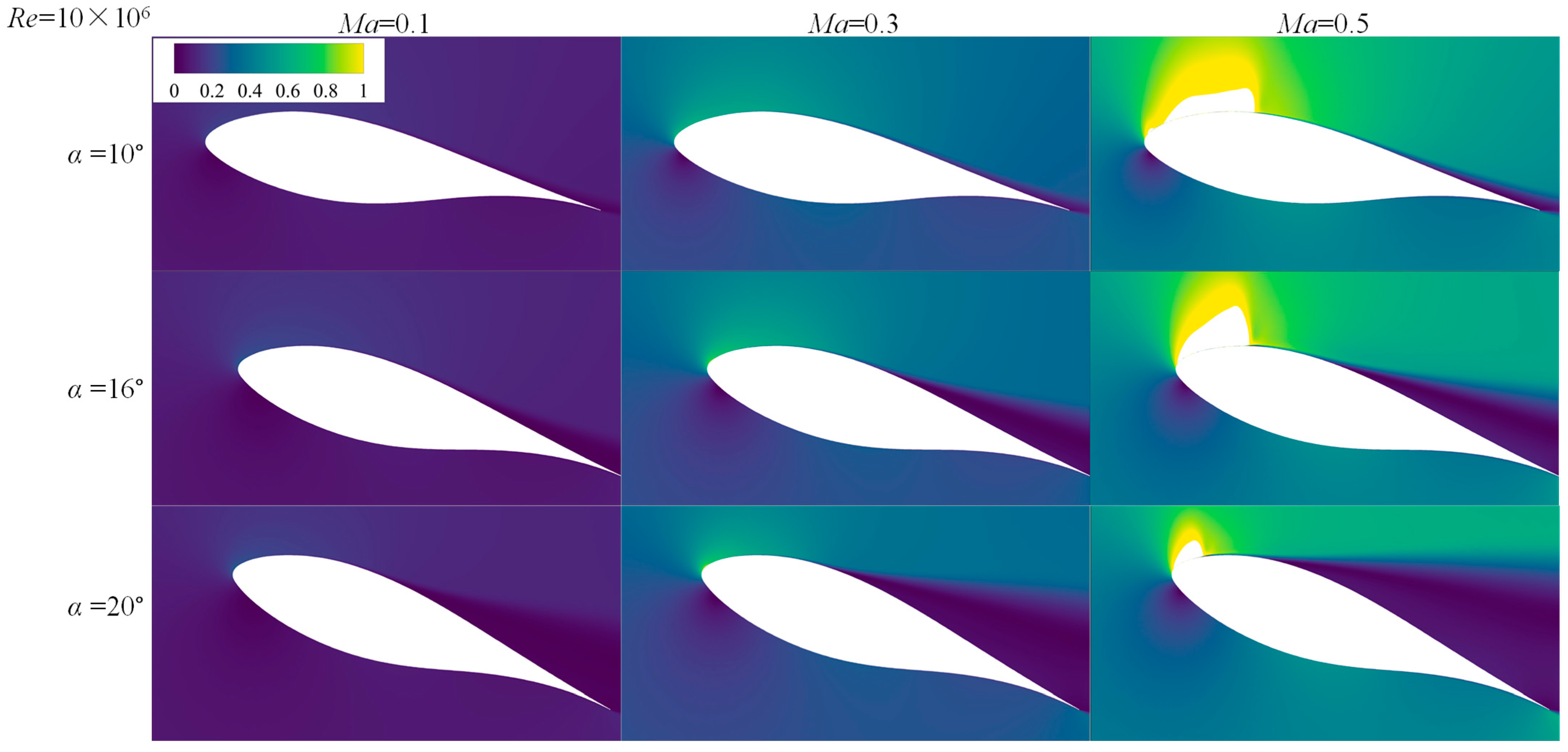
7.1. Static Stall Behaviors
7.2. Flow Field Development
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Vitulano, M.C.; De Tavernier, D.A.M.; De Stefano, G.; Von Terzi, D.A. Numerical Analysis of Transonic Flow over the FFA-W3-211 Wind Turbine Tip Airfoil. Wind Energy Sci. 2025, 10, 103–116. [Google Scholar] [CrossRef]
- Zahle, F.; Barlas, A.; Loenbaek, K.; Bortolotti, P.; Zalkind, D.; Wang, L.; Labuschagne, C.; Sethuraman, L.; Barter, G. Definition of the IEA Wind 22-Megawatt Offshore Reference Wind Turbine; Department of Wind and Energy Systems: Roskilde, Denmark, 2024. [Google Scholar]
- Kim, H.R.; Printezis, J.A.; Ahrens, J.D.; Seume, J.R.; Wein, L. Characterization of Dynamic Stall on Large Wind Turbines. Wind Energy Sci. 2025, 10, 161–175. [Google Scholar]
- Akhtar, N.; Geyer, B.; Schrum, C. Larger wind turbines as a solution to reduce environmental impacts. Sci. Rep. 2024, 14, 6608. Available online: https://www.nature.com/articles/s41598-024-56731-w (accessed on 15 July 2025). [CrossRef]
- Gudmundsson, S. The Anatomy of the Airfoil. In General Aviation Aircraft Design; Elsevier: Amsterdam, The Netherlands, 2014; pp. 235–297. Available online: https://linkinghub.elsevier.com/retrieve/pii/B9780123973085000088 (accessed on 15 July 2025).
- Lei, W.; Zhao, K.; Yang, H.; Xie, L.; Zhang, C.; Bai, J. Research progress on reynolds number effects in the design of large aircraft. Acta Aerodyn. Sin. 2025, 43, 1–17. [Google Scholar] [CrossRef]
- Vitulano, M.C.; De Tavernier, D.; De Stefano, G.; Von Terzi, D. Numerical analysis of static and dynamic wind turbine airfoil characteristics in transonic flow. J. Phys. Conf. Ser. 2024, 2767, 022013. Available online: https://iopscience.iop.org/article/022010.021088/021742-026596/022767/022012/022013 (accessed on 15 July 2025). [CrossRef]
- Brusca, S.; Cucinotta, F.; Galvagno, A.; Sfravara, F.; Chillemi, M. Development of a numerical characterization method for a ducted savonius turbine with power augmenters. Energies 2025, 18, 1142. Available online: https://www.mdpi.com/1996-1073/18/5/1142 (accessed on 15 July 2025). [CrossRef]
- Sfravara, F.; Barberi, E.; Bongiovanni, G.; Chillemi, M.; Brusca, S. Development of a predictive model for evaluation of the influence of various parameters on the performance of an oscillating water column device. Sensors 2024, 24, 3582. Available online: https://www.mdpi.com/1424-8220/24/11/3582 (accessed on 15 July 2025). [CrossRef] [PubMed]
- Jamieson, P. Innovation in Wind Turbine Design; Wiley: Hoboken, NJ, USA, 2018; Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9781119137924 (accessed on 15 July 2025).
- Hansen, M.O.L. Aerodynamics of Wind Turbines; Routledge: London, UK, 2015; Available online: https://www.taylorfrancis.com/books/edit/10.4324/9781315769981/aerodynamics-wind-turbines-martin-hansen (accessed on 16 July 2025).
- Burton, T.L.; Jenkins, N.; Bossanyi, E.; Sharpe, D.; Graham, M. Wind Energy Handbook, 3rd ed.; Wiley: Hoboken, NJ, USA, 2021; Available online: https://www.wiley.com/en-cn/Wind+Energy+Handbook%2C+3rd+Edition-p-9781119451167 (accessed on 16 July 2025).
- Yin, J.; Shen, W.Z.; Sun, Z.; Zhu, W.J.; Cho, H. A new Blade Element Momentum theory for both compressible and incompressible wind turbine flow computations. Energy Convers. Manag. 2025, 328, 119619. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0196890425001426 (accessed on 16 July 2025). [CrossRef]
- Aditya, A.; De Tavernier, D.; Schrijer, F.; Van Oudheusden, B.; Von Terzi, D. Experimental investigation of the occurrence of transonic flow effects on the FFA-W3-211 airfoil. J. Phys. Conf. Ser. 2024, 2767, 022031. Available online: https://iopscience.iop.org/article/022010.021088/021742-026596/022767/022032/022031 (accessed on 16 July 2025). [CrossRef]
- Cao, J.; Qin, Z.; Ju, Y.; Chen, Y.; Shen, W.Z.; Shen, X.; Ke, S. Study of air compressibility effects on the aerodynamic performance of the IEA-15 MW offshore wind turbine. Energy Convers. Manag. 2023, 282, 116883. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0196890423002297 (accessed on 16 July 2025). [CrossRef]
- De Tavernier, D.; Terzi, D.V. The emergence of supersonic flow on wind turbines. J. Phys. Conf. Ser. 2022, 2265, 042068. Available online: https://iopscience.iop.org/article/042010.041088/041742-046596/042265/042064/042068 (accessed on 16 July 2025). [CrossRef]
- Glauert, H. The effect of compressibility on the lift of an aerofoil. Proc. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character 1928, 118, 113–119. Available online: https://royalsocietypublishing.org/doi/10.1098/rspa.1928.0039 (accessed on 16 July 2025).
- Pires, O.; Munduate, X.; Ceyhan, O.; Jacobs, M.; Snel, H. Analysis of high Reynolds numbers effects on a wind turbine airfoil using 2D wind tunnel test data. J. Phys. Conf. Ser. 2016, 753, 022047. Available online: https://iopscience.iop.org/article/022010.021088/021742-026596/022753/022042/022047 (accessed on 16 July 2025). [CrossRef]
- Zhu, C.; Yang, H.; Qiu, Y.; Zhou, G.; Wang, L.; Feng, Y.; Shen, Z.; Shen, X.; Feng, X.; Wang, T. Effects of the reynolds number and reduced frequency on the aerodynamic performance and dynamic stall behaviors of a vertical axis wind turbine. Energy Convers. Manag. 2023, 293, 117513. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0196890423008592 (accessed on 16 July 2025). [CrossRef]
- Campobasso, M.S.; Sanvito, A.G.; Drofelnik, J.; Jackson, A.; Zhou, Y.; Xiao, Q.; Croce, A. Compressible navier-stokes analysis of floating wind turbine rotor aerodynamics. In Proceedings of the ASME 2018 1st International Offshore Wind Technical Conference, San Francisco, CA, USA, 4–7 November 2018; Available online: https://asmedigitalcollection.asme.org/OMAE/proceedings/IOWTC2018/51975/San%51920Francisco,%51920California,%51920USA/275559 (accessed on 16 July 2025).
- Cheng, X. Development of wind energy model and application of CFD in wind energy assessment. Acta Aerodyn. Sin. 2023, 41, 1–15. Available online: http://kqdlxxb.xml-journal.net/en/article/doi/10.7638/kqdlxxb-2023.0011 (accessed on 20 July 2025).
- Gharali, K.; Johnson, D.A. Numerical modeling of an S809 airfoil under dynamic stall, erosion and high reduced frequencies. Appl. Energy 2012, 93, 45–52. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0306261911002595 (accessed on 20 July 2025). [CrossRef]
- Qian, Y.; Zhang, Y.; Sun, Y.; Wang, T. Numerical investigations of the flow control effect on a thick wind turbine airfoil using deformable trailing edge flaps. Energy 2023, 265, 126327. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0360544222032133 (accessed on 20 July 2025). [CrossRef]
- McAlister, K.W.; Pucci, S.L.; McCroskey, W.J.; Carr, L.W. An Experimental Study of Dynamic Stall on Advanced Airfoil Section. Volume 2: Pressure and Force Data; NASA Ames Research Center: Moffett Field, CA, USA, 1982. Available online: https://ntrs.nasa.gov/citations/19830003778 (accessed on 20 July 2025).
- Amjith, L.; Bavanish, B. A review on biomass and wind as renewable energy for sustainable environment. Chemosphere 2022, 293, 133579. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0045653522000686 (accessed on 20 July 2025). [CrossRef] [PubMed]
- Souza, L.F.d.; Miotto, R.F.; Wolf, W.R. Active flow control of vertical-axis wind turbines: Insights from large-eddy simulation and finite-time resolvent analysis. arXiv 2025, arXiv:2507.08625. [Google Scholar]
- Chellini, S.; De Tavenier, D.; Von Terzi, D. Impact of dynamic stall model tailoring on wind turbine loads and performance prediction. J. Phys. Conf. Ser. 2024, 2767, 022016. Available online: https://iopscience.iop.org/article/022010.021088/021742-026596/022767/022012/022016 (accessed on 20 July 2025). [CrossRef]
- Corke, T.C.; Thomas, F.O. Dynamic Stall in Pitching Airfoils: Aerodynamic Damping and Compressibility Effects. Annu. Rev. Fluid Mech. 2015, 47, 479–505. Available online: https://www.annualreviews.org/content/journals/10.1146/annurev-fluid-010814-013632 (accessed on 20 July 2025). [CrossRef]
- Leishman, J.G. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2006; Available online: https://assets.cambridge.org/97811070/13353/frontmatter/9781107013353_frontmatter.pdf (accessed on 20 July 2025).
- McCroskey, W.J. The Phenomenon of Dynamic Stall; Ames Research Center: Moffett Field, CA, USA, 1981.
- Yan, C.; Archer, C.L. Assessing compressibility effects on the performance of large horizontal-axis wind turbines. Appl. Energy 2018, 212, 33–45. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0306261917317348 (accessed on 22 July 2025). [CrossRef]
- Sørensen, N.N.; Bertagnolio, F.; Jost, E.; Lutz, T. Aerodynamic effects of compressibility for wind turbines at high tip speeds. IOPscience 2018, 1037, 022003. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/1037/2/022003 (accessed on 22 July 2025).
- Zunaid, M.; Mustafa, M.G. Mathematical analysis of wind turbine blade at various angle of attack and reynold number. IOP Conf. Ser. Mater. Sci. Eng. 2020, 804, 012005. Available online: https://iopscience.iop.org/article/012010.011088/011757-012899X/012804/012001/012005 (accessed on 22 July 2025). [CrossRef]
- Mereu, R.; Passoni, S.; Inzoli, F. Scale-resolving CFD modeling of a thick wind turbine airfoil with application of vortex generators: Validation and sensitivity analyses. Energy 2019, 187, 115969. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0360544219316597 (accessed on 22 July 2025). [CrossRef]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of darrieus wind turbines. Renew. Energy 2016, 85, 419–435. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0960148115300719 (accessed on 22 July 2025). [CrossRef]
- Wang, H.; Zhang, B.; Qiu, Q.; Xu, X. Flow control on the NREL S809 wind turbine airfoil using vortex generators. Energy 2017, 118, 1210–1221. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0360544216315924 (accessed on 22 July 2025). [CrossRef]
- Cai, X.; Gu, R.; Pan, P.; Zhu, J. Unsteady aerodynamics simulation of a full-scale horizontal axis wind turbine using CFD methodology. Energy Convers. Manag. 2016, 112, 146–156. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0196890416000145 (accessed on 22 July 2025). [CrossRef]
- Carrion, M. Low Mach Number CFD for Wind Turbine Analysis; University of Liverpool: Liverpool, UK, 2015. [Google Scholar]
- Bai, C.-J.; Wang, W.-C. Review of computational and experimental approaches to analysis of aerodynamic performance in horizontal-axis wind turbines (HAWTs). Renew. Sustain. Energy Rev. 2016, 63, 506–519. Available online: https://linkinghub.elsevier.com/retrieve/pii/S1364032116301903 (accessed on 22 July 2025). [CrossRef]


| Solver Setting Item | Parameter/Selection Value |
|---|---|
| Solver type | Pressure-Based Solver |
| Time type | Steady |
| Energy equation | Ma ≤ 0.3, off |
| Ma > 0.3, on | |
| Density | Ma ≤ 0.3, constant |
| Ma > 0.3, ideal-gas | |
| Turbulence modeling | SST k-ω model |
| Transition modeling | γ-Reθ model |
| Spatial discretization | Second-order upwind scheme |
| Temporal discretization | Unbounded second-order implicit scheme |
| Pressure-velocity coupling | Coupled algorithm |
| Courant number | 20 |
| Number of Iterations | 4000 |
| Reporting Interval | 10 |
| Grid Accuracy | Mesh Distribution on the Upper/Lower Surface | First Layer Height | Growth Rate |
|---|---|---|---|
| coarse | 150 | 2.0 × 10−6 | 1.07 |
| medium | 250 | 2.0 × 10−6 | 1.05 |
| fine | 350 | 2.0 × 10−6 | 1.03 |
| Re (Million) | Slope of the Linear Segment of the Cl | αStall (°) | Cl,max |
|---|---|---|---|
| 2 | 0.1180 | 12 | 1.76 |
| 10 | 0.1159 | 14 | 1.75 |
| 20 | 0.1172 | 14 | 1.79 |
| α (°) | Re (Million) | Cl | Cd | Cl/Cd | ft/c | fs/c | Cp,min | h/c |
|---|---|---|---|---|---|---|---|---|
| 10 | 2 | 1.592 | 0.0132 | 120.7 | 26.88% | --- | −3.60 | --- |
| 10 | 1.579 | 0.0146 | 108.2 | 5.29% | --- | −3.58 | --- | |
| 20 | 1.571 | 0.0151 | 103.9 | 0.96% | --- | −3.57 | --- | |
| 16 | 2 | 1.491 | 0.0805 | 18.5 | 2.18% | 43.62% | −4.94 | 17.26% |
| 10 | 1.628 | 0.0675 | 24.1 | 1.31% | 47.15% | −5.67 | 13.37% | |
| 20 | 1.675 | 0.0625 | 26.8 | 0.79% | 48.72% | −5.92 | 12.82% | |
| 20 | 2 | 1.248 | 0.1631 | 7.7 | 1.80% | 25.82% | −4.84 | 40.37% |
| 10 | 1.435 | 0.1357 | 10.6 | 0.96% | 31.97% | −6.06 | 33.53% | |
| 20 | 1.473 | 0.1299 | 11.3 | 0.82% | 32.97% | −6.31 | 32.50% |
| Ma | Slope of the Linear Segment of the Cl | αstall (°) | Cl,max |
|---|---|---|---|
| 0.1 | 0.1139 | 16 | 1.91 |
| 0.3 | 0.1159 | 14 | 1.75 |
| 0.5 | 0.1221 | 12 | 1.82 |
| α (°) | Ma | Cl | Cd | Cl/Cd | ft/c | fs/c | Cp,min | h/c |
|---|---|---|---|---|---|---|---|---|
| 10 | 0.1 | 1.514 | 0.0137 | 110.6 | 4.34% | --- | −3.49 | --- |
| 0.3 | 1.579 | 0.0146 | 108.2 | 5.29% | --- | −3.58 | --- | |
| 0.5 | 1.736 | 0.0210 | 82.8 | 22.20% | --- | −3.54 | --- | |
| 16 | 0.1 | 1.908 | 0.0354 | 54.0 | 1.01% | 68.09% | −6.90 | 5.61% |
| 0.3 | 1.628 | 0.0675 | 24.1 | 1.10% | 47.15% | −5.67 | 13.37% | |
| 0.5 | 1.585 | 0.0994 | 16.0 | 3.10% | 40.49% | −4.16 | 21.11% | |
| 20 | 0.1 | 1.682 | 0.0942 | 17.8 | 0.77% | 42.31% | −7.24 | 23.06% |
| 0.3 | 1.435 | 0.1357 | 10.6 | 0.82% | 31.97% | −6.06 | 33.53% | |
| 0.5 | 1.207 | 0.2017 | 6.0 | 4.85% | 23.50% | −4.19 | 51.86% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Huang, X.; Zhang, Z.; Zhu, Z.; Qiu, Y.; Wang, T.; Zhu, C. Effects of Ultra-High Reynolds Number and Low Mach Number Compressibility on the Static Stall Behavior of a Wind Turbine Airfoil. Machines 2025, 13, 847. https://doi.org/10.3390/machines13090847
Zhang Z, Huang X, Zhang Z, Zhu Z, Qiu Y, Wang T, Zhu C. Effects of Ultra-High Reynolds Number and Low Mach Number Compressibility on the Static Stall Behavior of a Wind Turbine Airfoil. Machines. 2025; 13(9):847. https://doi.org/10.3390/machines13090847
Chicago/Turabian StyleZhang, Zijian, Xiufeng Huang, Zijie Zhang, Zeling Zhu, Yingning Qiu, Tongguang Wang, and Chengyong Zhu. 2025. "Effects of Ultra-High Reynolds Number and Low Mach Number Compressibility on the Static Stall Behavior of a Wind Turbine Airfoil" Machines 13, no. 9: 847. https://doi.org/10.3390/machines13090847
APA StyleZhang, Z., Huang, X., Zhang, Z., Zhu, Z., Qiu, Y., Wang, T., & Zhu, C. (2025). Effects of Ultra-High Reynolds Number and Low Mach Number Compressibility on the Static Stall Behavior of a Wind Turbine Airfoil. Machines, 13(9), 847. https://doi.org/10.3390/machines13090847







