3.2. CFD Validation and Application of the Proposed Method for Turbine Characterization
The initial simulation was performed under no-load conditions to determine the maximum rotational velocity. In
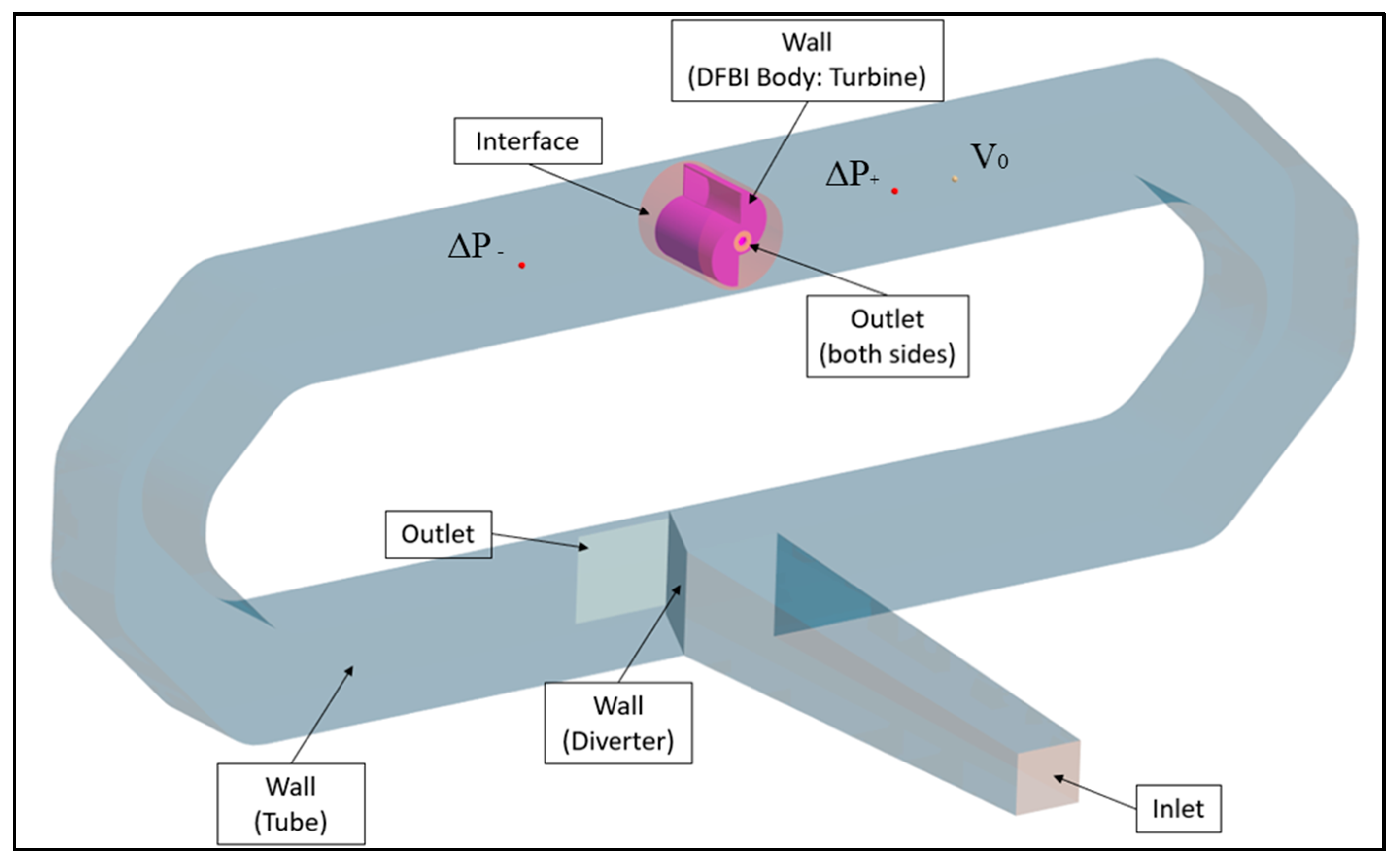
Figure 11, a streamlines map extracted from the simulation without Power Augmenters is represented. As expected, the flow is deflected from the diverter, passes through the bends of the test tube, impacts the turbine, and exits from its sides and from the back of the structure.
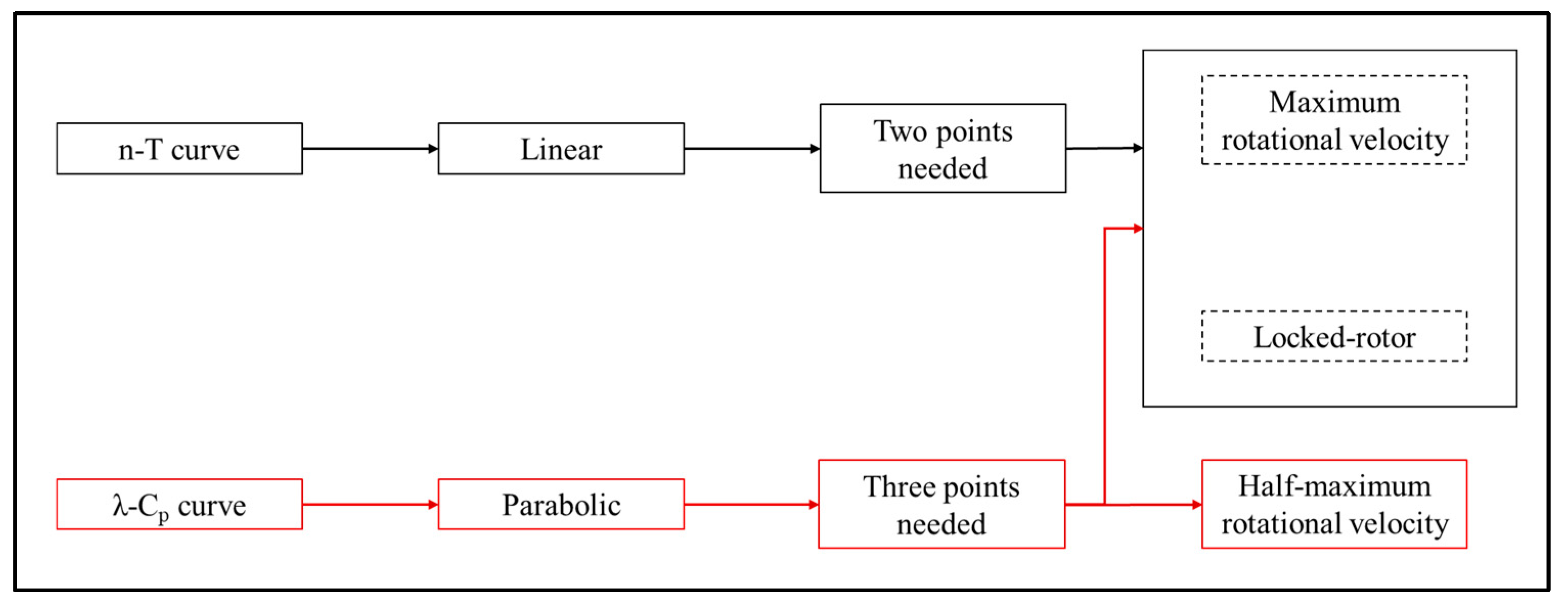
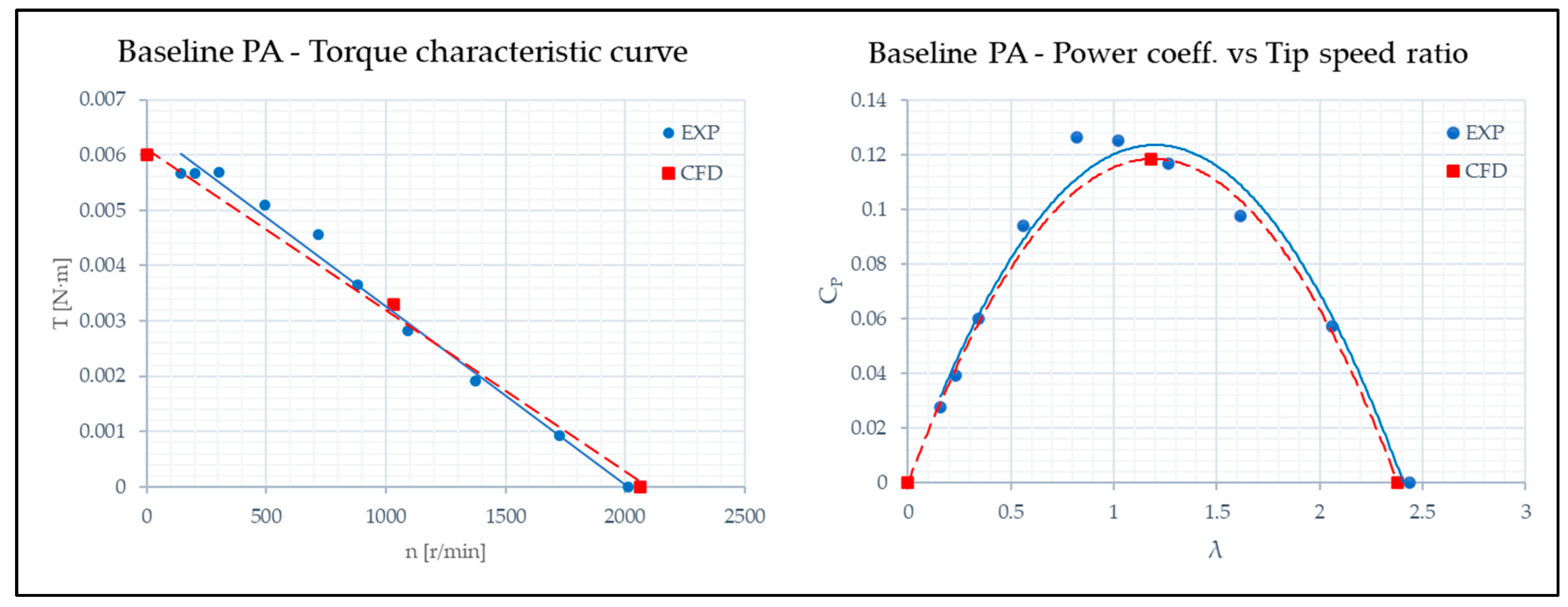
Subsequently, simulations corresponding to the conditions representing the operating states at maximum tip speed ratio, half of the maximum tip speed ratio, and a locked rotor condition were conducted. These simulations were essential for predicting the performance curves both with and without ramps.
The results of the simulations are listed in
Table 8,
Table 9,
Table 10 and
Table 11. Using these results, the
n–
C and the
λ–
Cp curves can both be constructed.
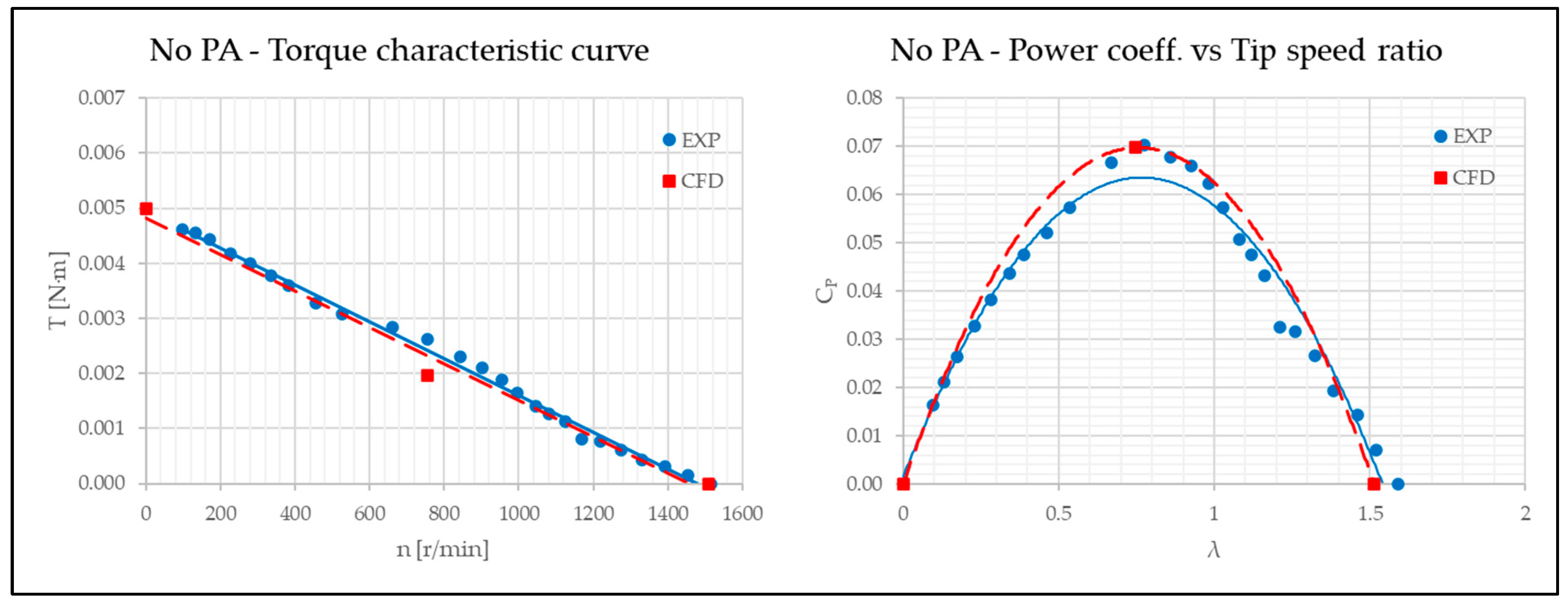
To demonstrate that the CFD curve based on three points provides a reliable prediction of the turbine’s actual behaviour, the R2 value of the experimental points relative to the CFD curve was calculated without and with the Power Augmenters.
The determination coefficient
R2 is calculated using the following formula:
where
- -
are the experimentally observed values;
- -
are the values predicted by the regression curve;
- -
is the mean of the observed values;
- -
is the Residual Sum of Squares;
- -
is the Total Sum of Squares.
The values were calculated by solving the equations corresponding to each parabolic regression curve, considering the same λ values of the experimental tests.
The first analysed configuration is the one without PA. Equation (24) is the equation of the CFD curve relative to this case.
The obtained determination coefficient is equal to 0.9165.
Equation (25) represents the equation of the CFD curve in the configuration with the Baseline Bell-Metha PA.
The obtained determination coefficient with the Baseline PA is equal to 0.9478.
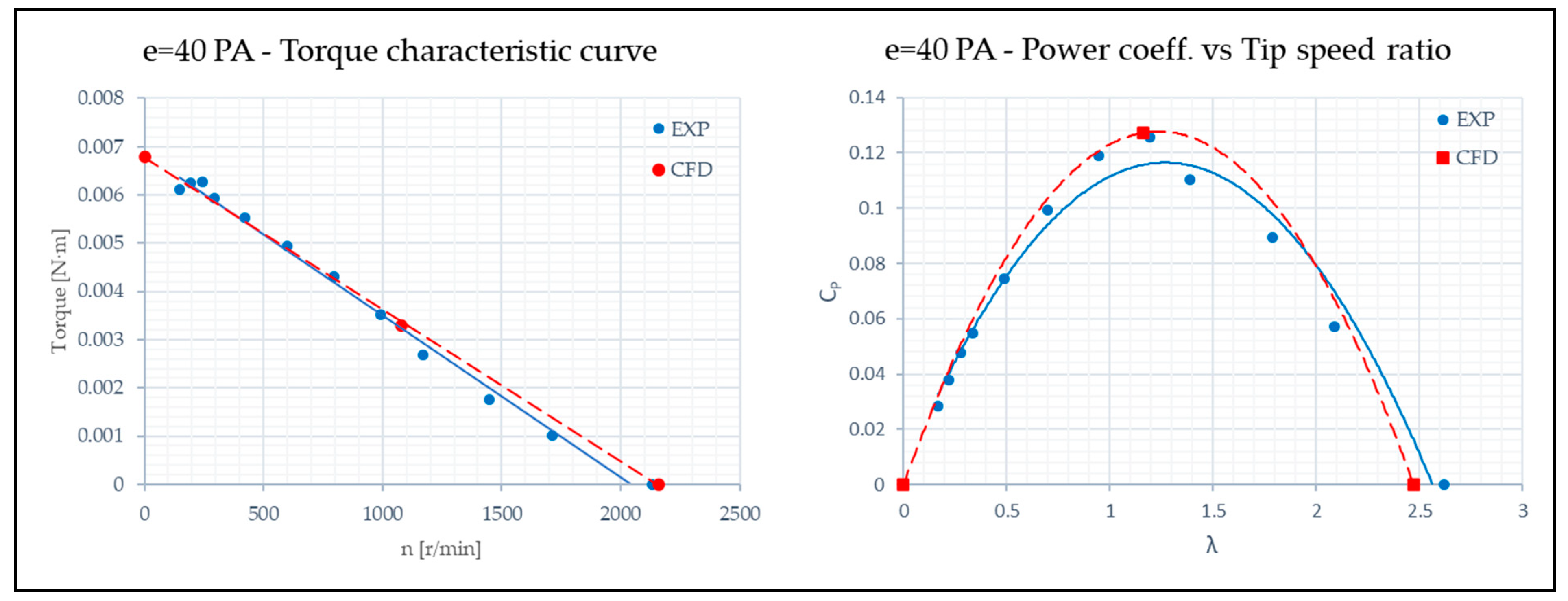
Equation (26) is relative to the case with PA 2.
The obtained determination coefficient with PA 2 is 0.9451.
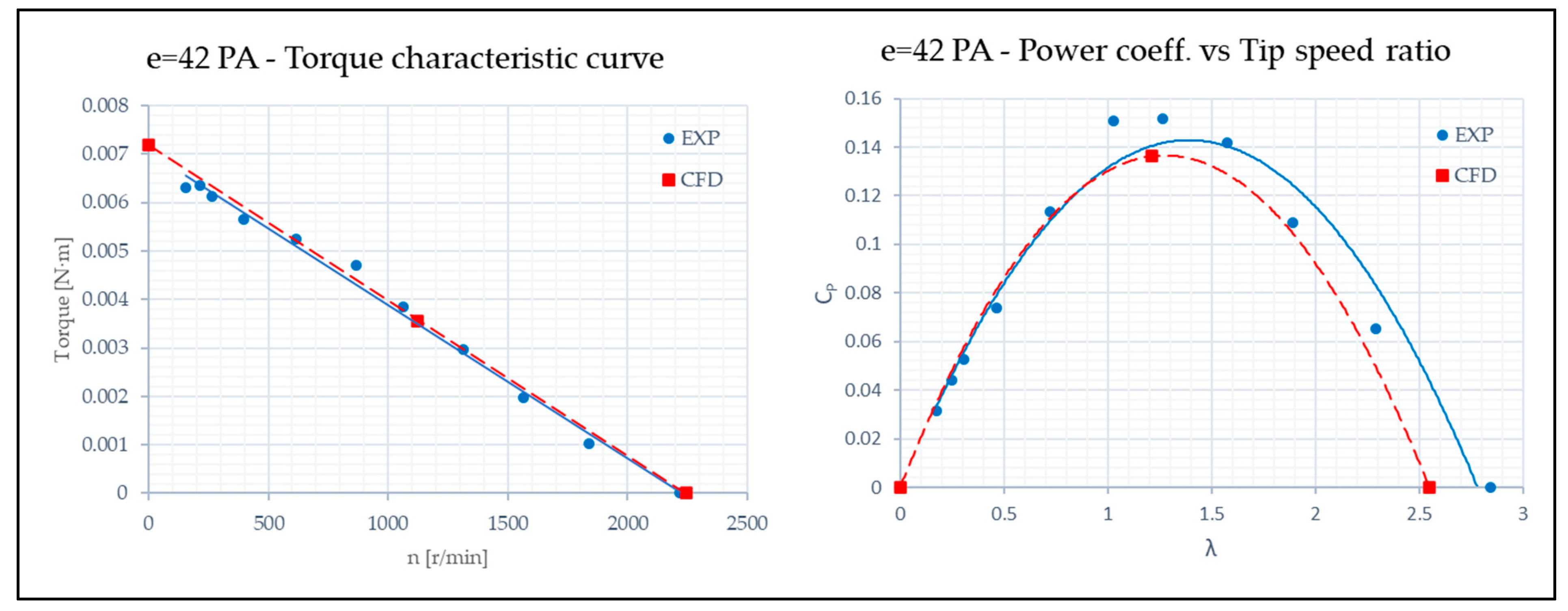
The last configuration is the one with PA 3. The CFD curve is described by Equation (27).
The determination coefficient with PA 3 is 0.9389.
The coefficient of determination has an acceptable value for all configurations, with a minimum value of 0.9165 corresponding to the case without the PA. The values then improve and remain consistently high for all cases with the PA, reaching a maximum of 0.9594 for the configuration with PA 2.
There are multiple factors influencing these results, as the values of the power coefficient and the tip speed ratio depend on variables, such as velocity or pressure, which are also characterized by measurement uncertainties in the experimental data.
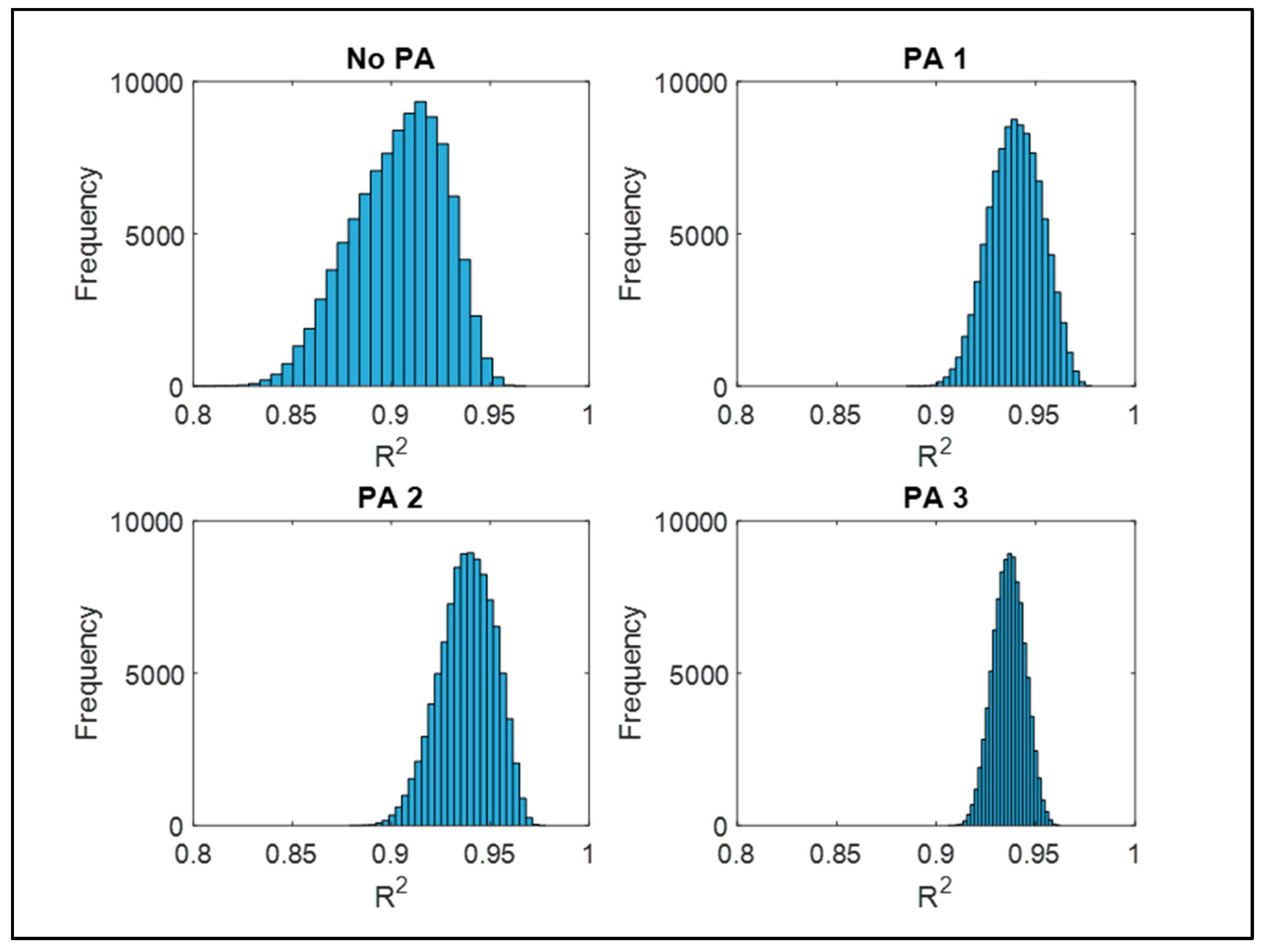
To assess the effect of measurement uncertainties on the determination coefficient, the Monte Carlo method [
31] was applied by perturbing the experimental C
p data using the standard deviations reported in
Section 3.1. The perturbed data were then compared with the numerical curve obtained using the proposed method.
By doing so, a distribution of R
2 was obtained, performing 10,000 trials for each configuration (
Figure 16).
Analysing these plots, it can be observed that the R2 value calculated using the unperturbed mean experimental curve falls, for each configuration, within the range of the most frequently occurring values.
The tests conducted with a PA exhibit a lower standard deviation, which consequently leads to a smaller variation in R2.
In all configurations, however, the R2 value calculated with the mean curve remains within an acceptable variability range.
Therefore, the result is very promising because a calculation methodology has been defined that provides reliable results with only three CFD simulations.
3.3. Analysis on the Influence of the Power Augmenters
In
Figure 17,
Figure 19,
Figure 21 and
Figure 23 a comparison of velocity vector fields obtained using line integral convolution on the symmetry plane at maximum rotational velocity is presented. The scenes were extracted from the no-load condition simulations.
They are useful to explain how the presence of the PA significantly affects the velocity distribution both upstream of the turbine and in its wake, consequently altering the pressure drop, rotational speed, and generated torque.
Velocity scenes for all configurations have been analysed in the two positions of particular interest: the one with the highest aerodynamic resistance and the one with the lowest resistance, where the blades are aligned parallel to the flow.
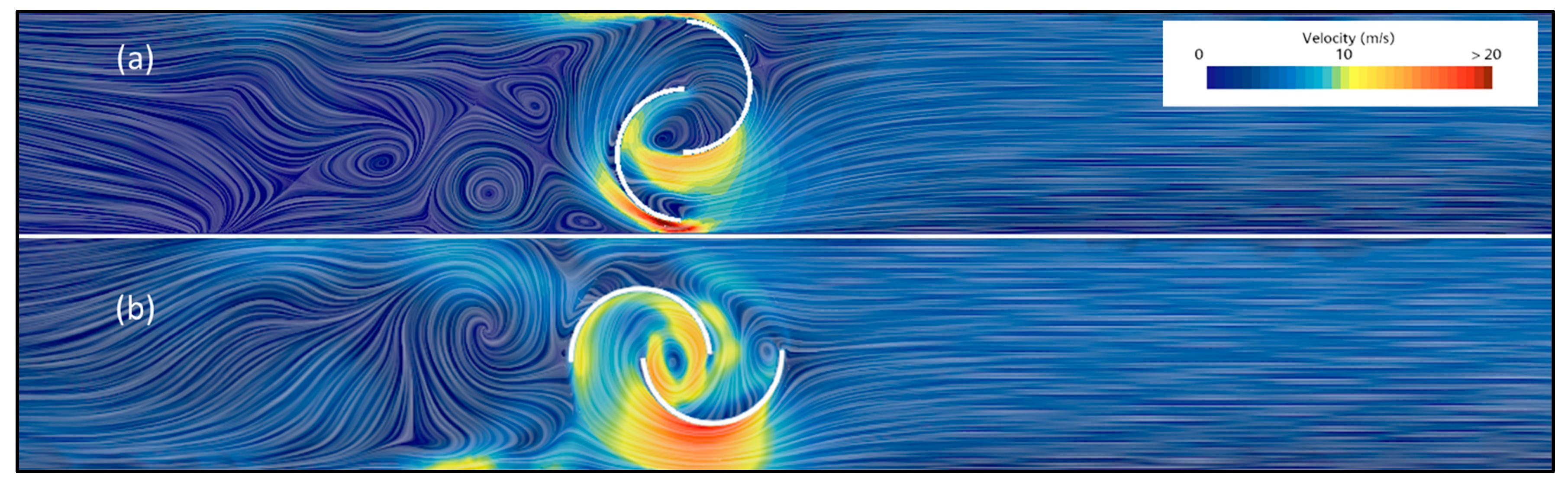
In
Figure 17a, the turbine is directly impacted by the incoming flow without any shielding. In this high aerodynamic resistance configuration, the flow striking the resisting blade separates, generating turbulent vortices. Part of the flow is redirected towards the motor blade, contributing to torque generation, while another portion leaks through the gap between the upper wall of the test tube and the turbine.
In
Figure 17b, in the low resistance condition, multiple vortices and high-velocity peaks are observed inside the turbine. The wake is characterized by the formation of a large-scale vortex, indicating a more streamlined interaction between the flow and the turbine structure.
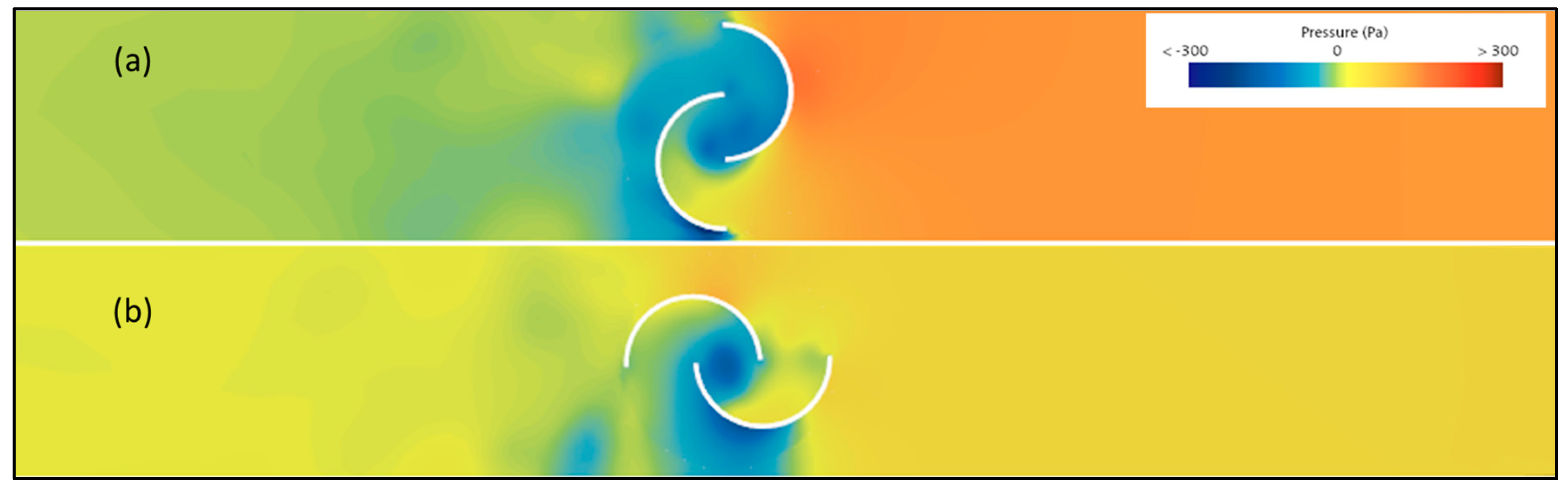
In
Figure 18a,b, from a visual impact perspective, it is evident that the presence of the turbine acts as a barrier in the position of maximum resistance, whereas it has a lesser effect on the pressure drop inside the test tube in the position of minimum resistance.
Figure 17.
Velocity scene comparison without PA between high (a) and low (b) resistance positions.
Figure 17.
Velocity scene comparison without PA between high (a) and low (b) resistance positions.
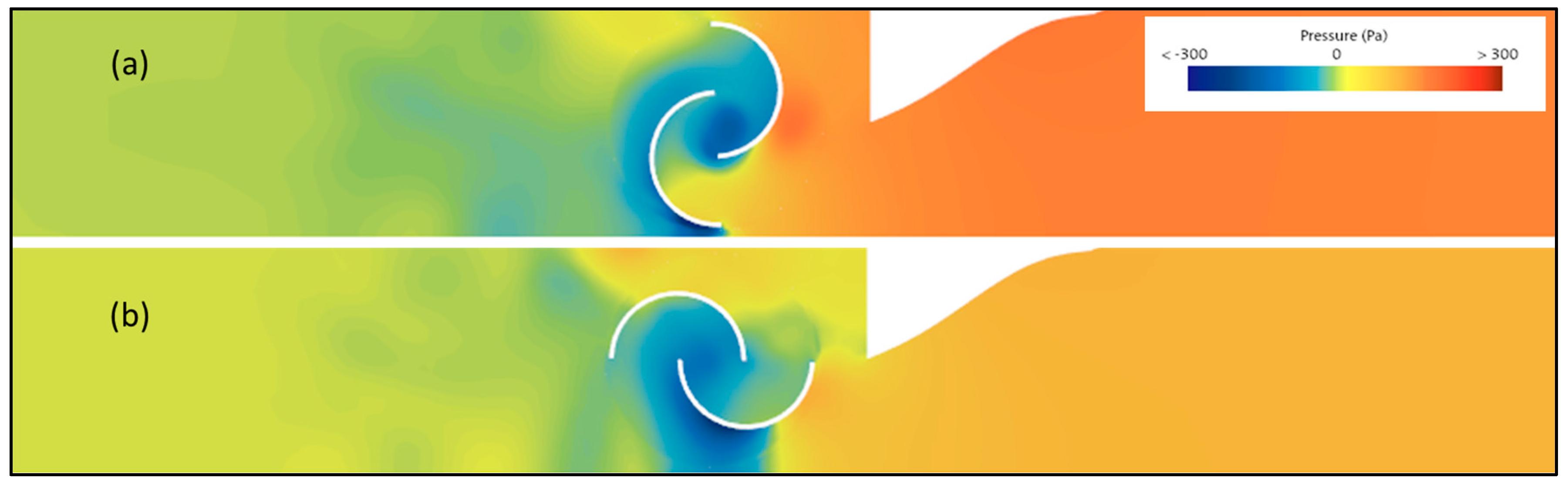
Figure 18.
Pressure scene comparison without PA between high (a) and low (b) resistance positions.
Figure 18.
Pressure scene comparison without PA between high (a) and low (b) resistance positions.
By adding the Baseline Bell-Metha PA, in the condition shown in
Figure 19a, the resisting blade is largely shielded, thereby reducing the generated aerodynamic resistance. Compared to
Figure 17a, the velocity in front of the blade behind the PA is generally lower and the flow is less turbulent. Another beneficial effect of the PA is the redirection of the airflow onto the motor blade, which reaches it in a more organized manner and at a higher velocity than in the case without the PA.
A clear improvement is also observed in the condition shown in
Figure 19b: almost half of the turbine remains shielded by the PA, and in the wake, the formation of less extensive vortices is noticeable.
Figure 19.
Velocity scene comparison with Baseline Bell-Metha PA between high (a) and low (b) resistance positions.
Figure 19.
Velocity scene comparison with Baseline Bell-Metha PA between high (a) and low (b) resistance positions.
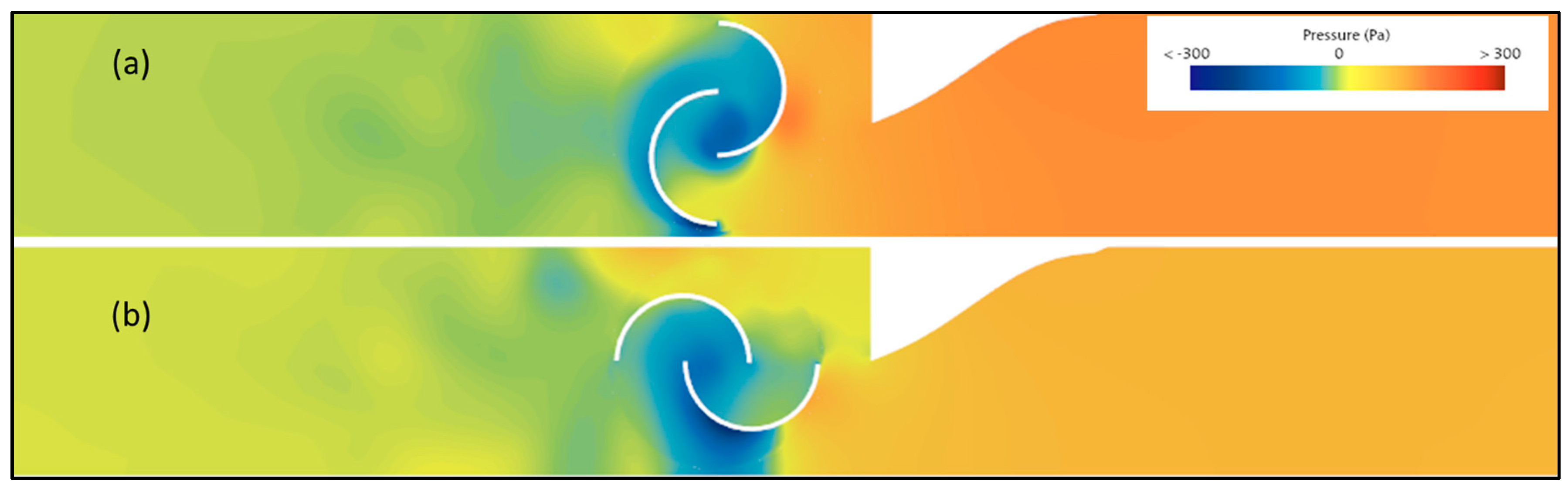
Considering the pressure distribution,
Figure 20a illustrates how the stagnation zone on the resisting blade, which is more extensive in the case without the PA, is now reduced and localized at the lower end of the same blade. Additionally, the presence of the PA creates a low-pressure zone in front of the resisting blade, effectively pulling the turbine while simultaneously increasing the overpressure on the driving blade.
Figure 20b shows that even in the condition of lower resistance, the overpressure zone on the upper blade is reduced. However, stagnation on the lower blade, positioned beneath the PA, becomes more pronounced. Although this effect is not desirable, its overall impact is minimal, and the presence of the PA remains advantageous.
Figure 20.
Pressure scene comparison with Baseline Bell-Metha PA between high (a) and low (b) resistance positions.
Figure 20.
Pressure scene comparison with Baseline Bell-Metha PA between high (a) and low (b) resistance positions.
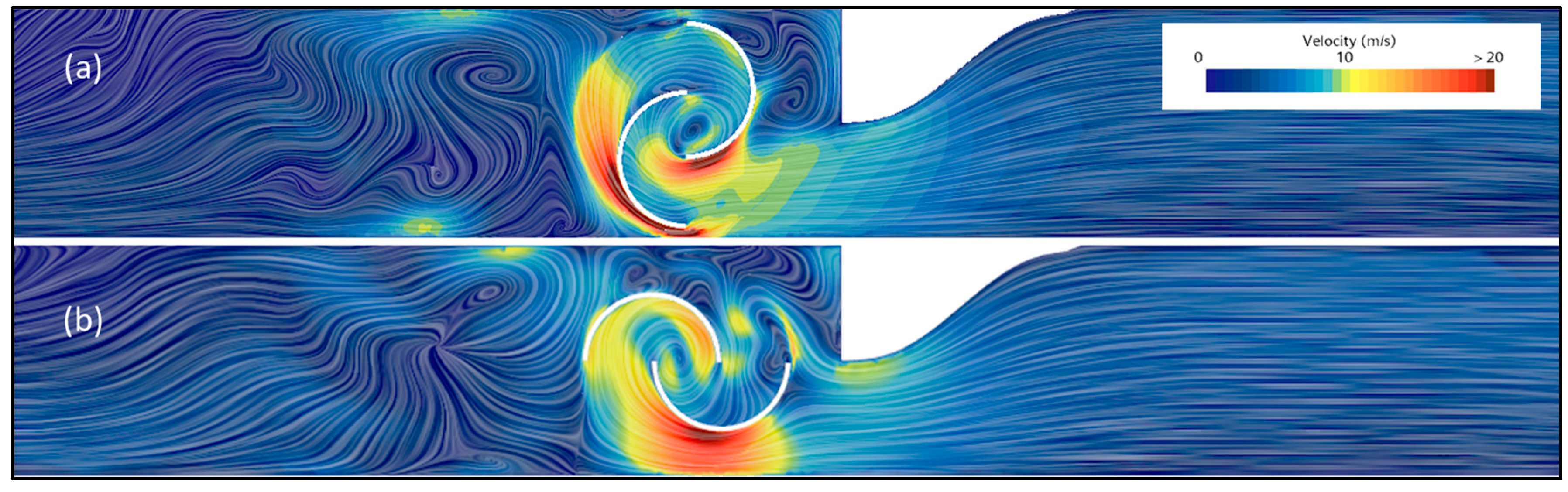
The Baseline Bell-Metha PA improves performance, but the fully horizontal outlet defined by the original polynomial is not very effective, as a small portion of the flow is not properly directed and still impacts the resisting blade. By introducing a slope at the end of the PA with the PA 2, as shown in
Figure 21a, more of the resisting blade is shielded and the velocity of the flow reaching the motor blade is even higher.
In
Figure 21b, it can be observed that the tangential outlet helps guide the flow along the curvature of the lower blade, allowing it to continue smoothly downstream.
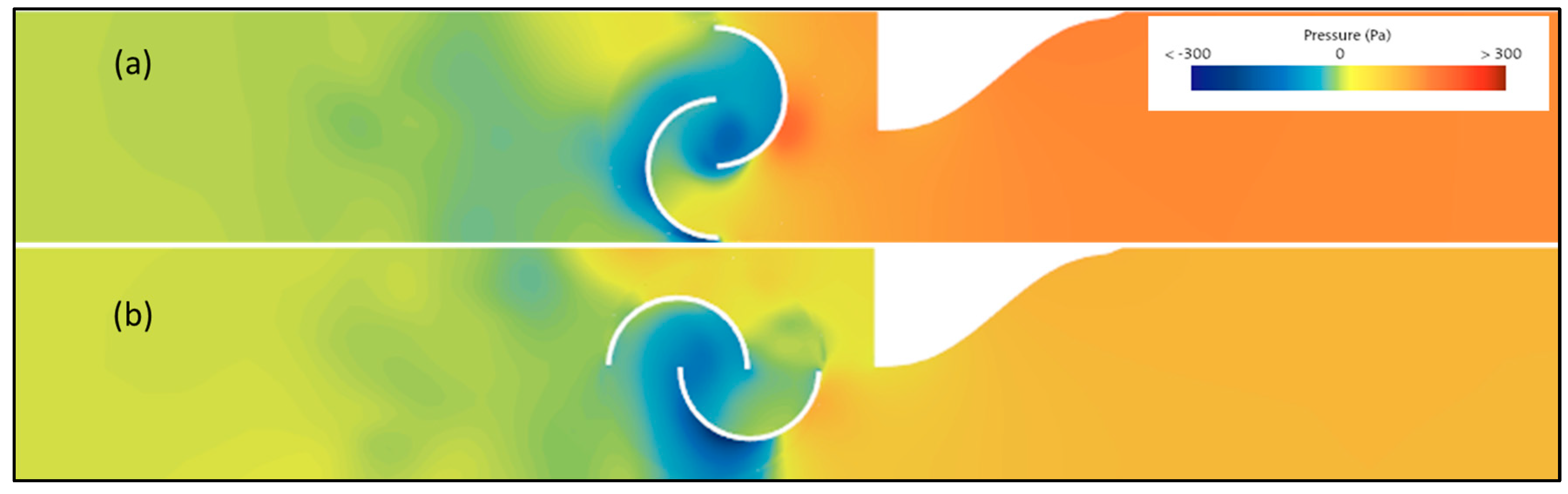
Figure 22a highlights how the inclination of the PA shifts the stagnation point on the resisting blade, guiding the flow more naturally towards the motor blade. Meanwhile, the overpressure generated by the Baseline Bell-Metha PA, as seen in
Figure 20b, is reduced due to the exit slope (
Figure 22b).
Figure 21.
Velocity scene comparison with PA 2 between high (a) and low (b) resistance positions.
Figure 21.
Velocity scene comparison with PA 2 between high (a) and low (b) resistance positions.
Figure 22.
Pressure scene comparison with PA 2 between high (a) and low (b) resistance positions.
Figure 22.
Pressure scene comparison with PA 2 between high (a) and low (b) resistance positions.
By increasing the inclination with the PA 3, the beneficial effects already observed in the PA 2 case are further maximized.
As shown in
Figure 23a,b, the velocity distribution is even more regular in both cases compared to the previous configurations. Specifically, in
Figure 23a, the flow is now guided exactly onto the motor blade, completely avoiding the resistant blade due to its inertia.
Figure 24a shows how PA 3 further reduces the overpressure on the resisting blade. Additionally, among all configurations, this is the one where the overpressure zone on the motor blade is the most extensive.
Figure 24b reveals that the benefits of this PA are also present in the condition of lower resistance, with the overpressure zone on the lower blade being the smallest among all the studied configurations.
Figure 23.
Velocity scene comparison with PA 3 between high (a) and low (b) resistance positions.
Figure 23.
Velocity scene comparison with PA 3 between high (a) and low (b) resistance positions.
Figure 24.
Pressure scene comparison with PA 3 between high (a) and low (b) resistance positions.
Figure 24.
Pressure scene comparison with PA 3 between high (a) and low (b) resistance positions.
If the outlet inclination is increased too much, the PA would start acting as a barrier, reducing the velocity and energy of the flow reaching the turbine.
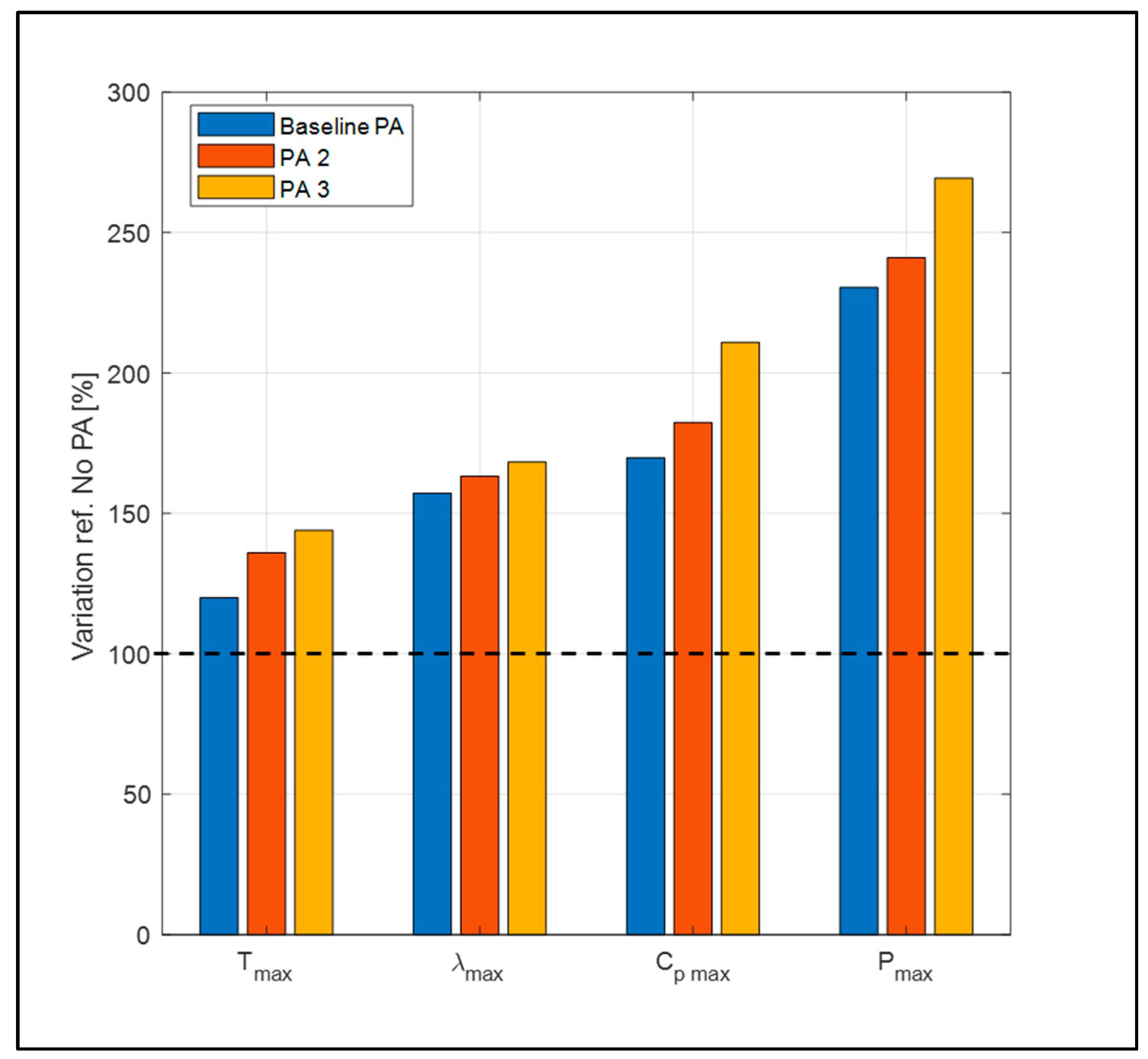
To better understand the impact of integrating various PAs (PA) on the system’s behaviour, the maximum values of torque, tip speed ratio, power coefficient, and power output were analysed and plotted in
Figure 25.
The comparison was carried out by normalizing each value in all the configurations with PAs with respect to their corresponding value in the configuration without a PA. The configuration that maximizes all these values is PA 3, which is the most inclined among those tested.
This numerical comparison confirms the findings from the characteristic curve analysis and the velocity and pressure field visualization. Specifically, with PA 3, the torque is 144% of the baseline value, the tip speed ratio reaches 168%, the power coefficient is 210%, and the power output is 269%.
Thus, PA 3 expanded the operational range of the turbine in terms of maximum rotational speed while also increasing the maximum power coefficient. The Baseline PA and PA 2 configurations also led to significant improvements, but to a lesser extent than PA 3.
Figure 25.
Comparison between configurations with Power Augmenters.
Figure 25.
Comparison between configurations with Power Augmenters.