Fault Diagnosis of In-Wheel Motors Used in Electric Vehicles: State of the Art, Challenges, and Future Directions
Abstract
1. Introduction
2. IWMs and Fault Types
2.1. Types of IWMs
2.2. Common Fault Types
2.2.1. Mechanical Faults
2.2.2. Electrical Faults
2.2.3. Magnetic Faults
2.2.4. Fault Comparison Between Axial-Flux and Radial-Flux IWMS
2.3. Section Summary of IWMs and Fault Types
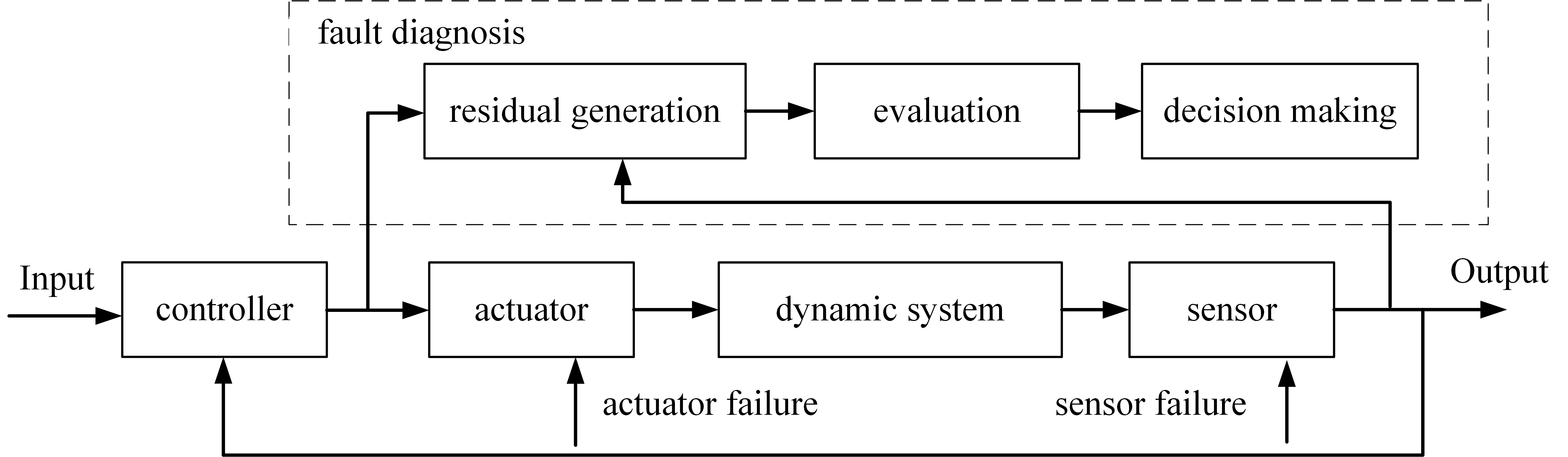
3. Fault Diagnosis for IWMs
3.1. Model-Based Diagnosis
3.1.1. Parameter Estimation-Based Methods
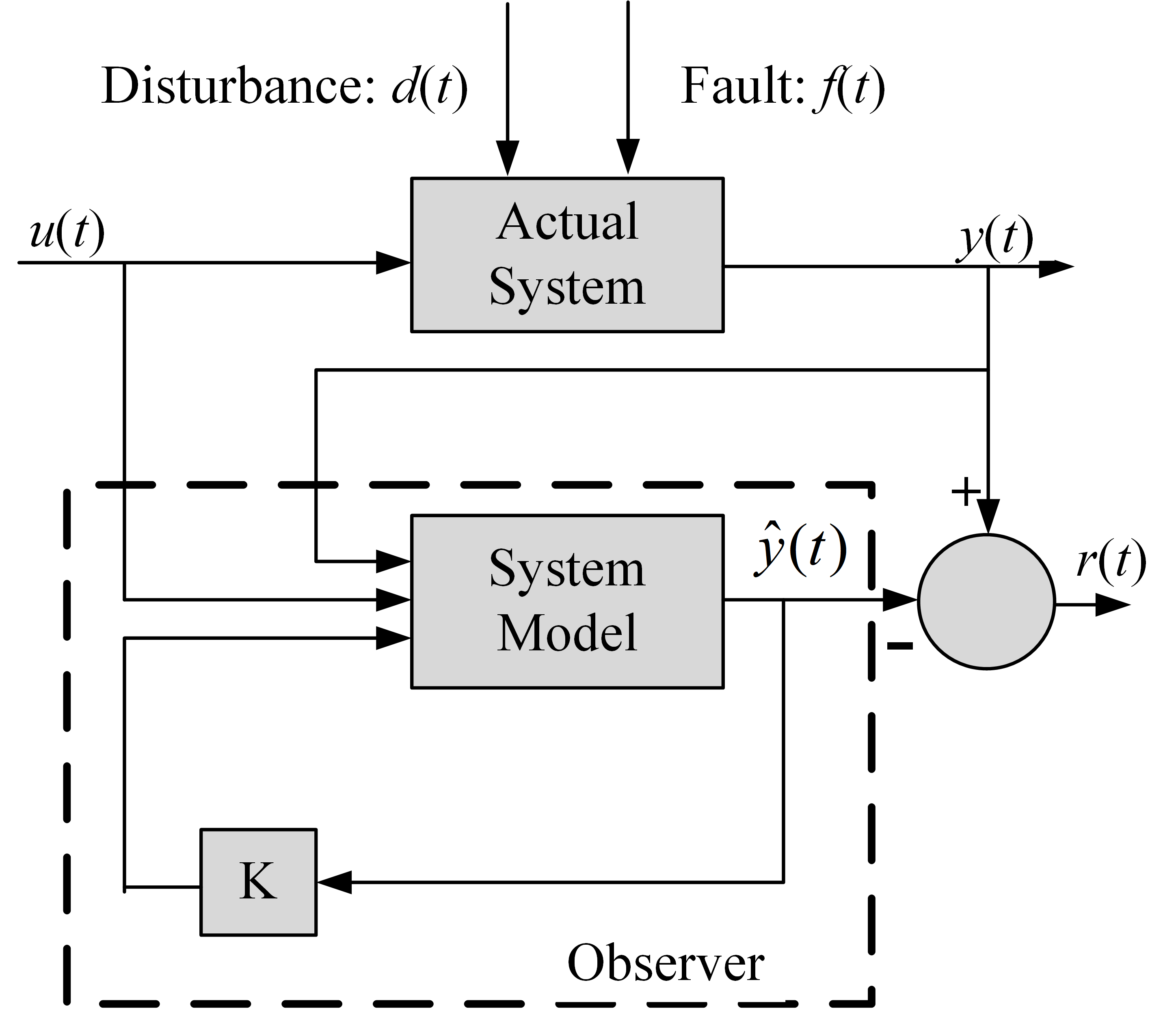
3.1.2. State Estimation-Based Methods
- a.
- Kalman Filtering
- b.
- Observers
3.1.3. Limitations and Challenges
3.2. Signal-Based Diagnostic Methods
3.2.1. Time-Domain and Frequency-Domain Analysis
3.2.2. Time–Frequency Analysis
3.2.3. Fault Component Extraction Techniques
3.2.4. Limitations and Challenges
3.3. Knowledge-Based Diagnostic Methods
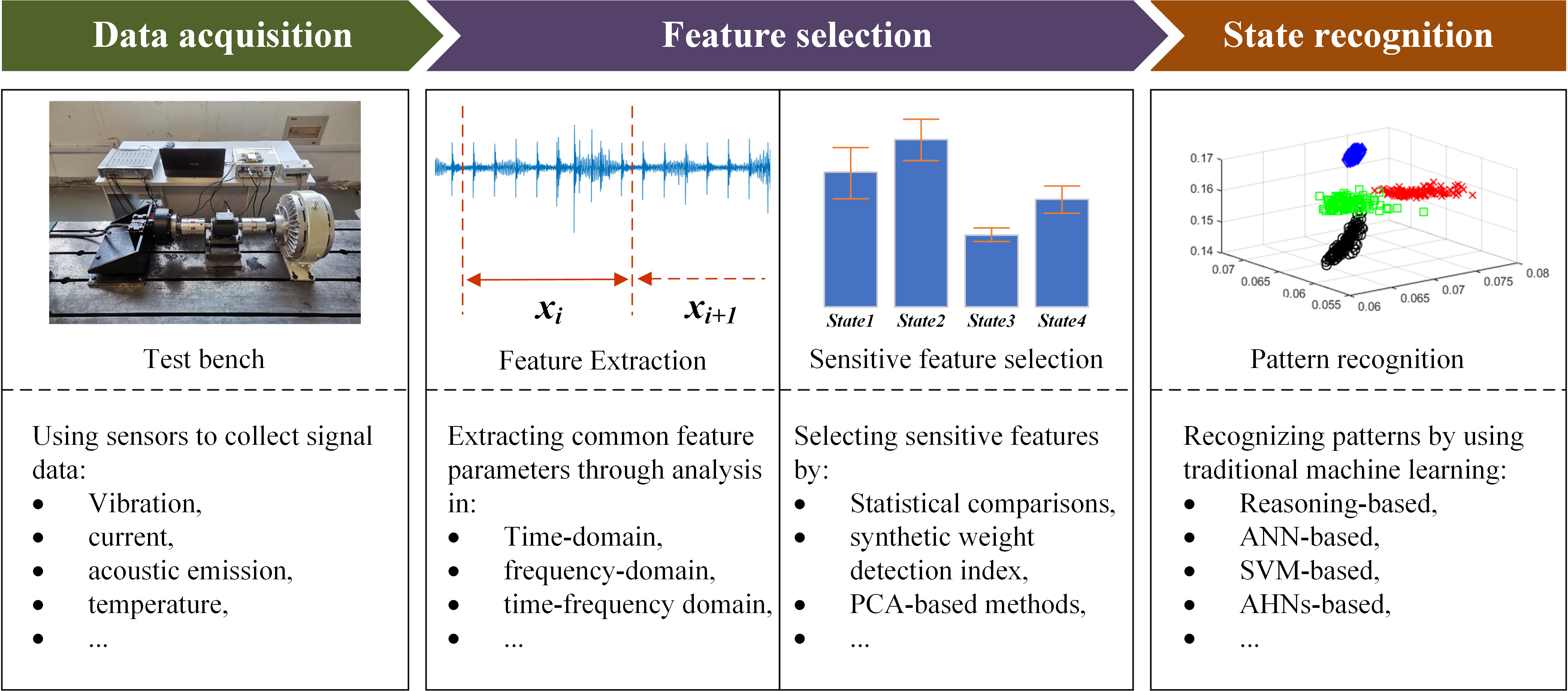
3.3.1. Traditional Machine Learning Methods
- a.
- Data Acquisition and Feature Selection
- b.
- State Recognition
- (1)
- Reasoning-based Methods
- Fuzzy Logic Reasoning
- Probabilistic Reasoning
- (2)
- Artificial Neural Network (ANN)-based Methods
- (3)
- Support Vector Machine (SVM)-based Methods
- (4)
- Other Approaches
3.3.2. Deep Learning Methods
- a.
- Representation Learning Models
- b.
- Temporal Dynamic Networks
- c.
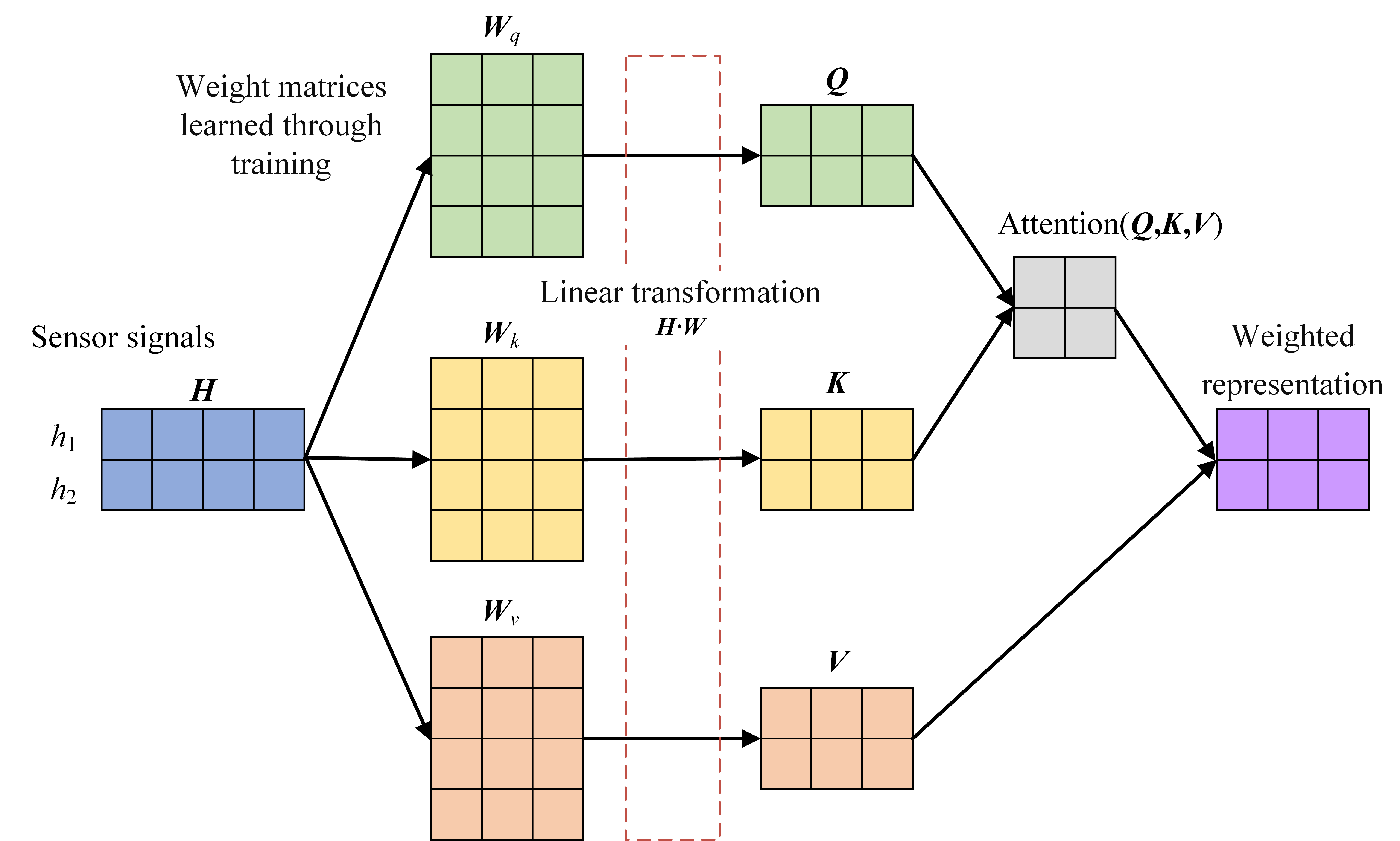
- Attention-enhanced Models
- (1)
- Attention Integration
- (2)
- Transformer
3.3.3. Limitations and Challenges
3.4. Section Summary of Fault Diagnosis for IWMs
4. Diagnostic Challenges and Future Research Directions
4.1. Toward More Accurate Modeling: Digital Twin-Driven Diagnosis
4.2. Handling Noise and Disturbances: Nonstationary Signal Analysis and Multi-Wheel Cooperative Processing
4.3. Coping with Complex Working Conditions: Condition-Invariant Representation Learning
4.4. Enhancing Generalization: Transferable and Data-Efficient Diagnostic Knowledge
4.5. Towards Practical Deployment: Efficiency and Interpretability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cai, S.; Kirtley, J.L.; Lee, C.H.T. Critical review of direct-drive electrical machine systems for electric and hybrid electric vehicles. IEEE Trans. Energy Convers. 2022, 37, 2657–2668. [Google Scholar] [CrossRef]
- Li, L.; Dai, L.; Niu, S.; Fu, W.; Chau, K.T. Critical review of direct-drive in-wheel motors in electric vehicles. Energies 2025, 18, 1521. [Google Scholar] [CrossRef]
- Hori, Y. Future Vehicle Driven by electricity and control-research on four-wheel-motored “UOT Electric March II”. IEEE Trans. Ind. Electron. 2004, 51, 954–962. [Google Scholar] [CrossRef]
- Deepak, K.; Frikha, M.A.; Benômar, Y.; El Baghdadi, M.; Hegazy, O. In-Wheel Motor Drive Systems for Electric Vehicles: State of the Art, Challenges, and Future Trends. Energies 2023, 16, 3121. [Google Scholar] [CrossRef]
- Zhang, H.; Hua, W. Overview of in-wheel traction machine and its key techniques for distributed-driving system. Proc. Chin. Soc. Electr. Eng. 2024, 44, 2871–2885. [Google Scholar] [CrossRef]
- Guan, T.; Liu, D.; He, Y. Review on development of permanent magnet in-wheel motors. Trans. China Electrotech. Soc. 2024, 39, 378–396. [Google Scholar] [CrossRef]
- Deng, Z.; Li, X.; Liu, T.; Zhao, S. Modeling and suppression of unbalanced radial force for in-wheel motor driving System. J. Vib. Control. 2022, 28, 3108–3119. [Google Scholar] [CrossRef]
- Sun, J.; Cong, J. Optimization and Control of Vehicle Vertical system with suspended in-wheel motor. Mechanics 2022, 28, 103–112. [Google Scholar] [CrossRef]
- Zhang, H.; Wan, S.; Zhang, M.; Guo, J. Analysis on coupled vibration characteristics of electric vehicles in-wheel motor with random excitation. J. Mach. Des. 2024, 41, 146–152. [Google Scholar] [CrossRef]
- Zhao, Z.; Taghavifar, H.; Du, H.; Qin, Y.; Dong, M.; Gu, L. In-wheel motor vibration control for distributed-driven electric vehicles: A review. IEEE Trans. Transp. Electr. 2021, 7, 2864–2880. [Google Scholar] [CrossRef]
- Iizuka, S.; Akatsu, K. A Thermal Dissipation Characteristics of Integrated In-Wheel Motor Using SiC Power Module. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and Ecce Asia, Kaohsiung, Taiwan, 3–7 June 2017; pp. 1251–1255. [Google Scholar]
- Li, L.; Zhu, G.; Zhao, Y.; Jia, N.; Xue, M.; Li, Y. Design and analysis of different cooling schemes of a flux-modulated permanent magnet in-wheel motor for electric vehicle applications. IET Electr. Power Appl. 2021, 15, 348–358. [Google Scholar] [CrossRef]
- Mutoh, N.; Nakano, Y. Dynamics of front-and-rear-wheel-independent-drive-type electric vehicles at the time of failure. IEEE Trans. Ind. Electron. 2012, 59, 1488–1499. [Google Scholar] [CrossRef]
- Wanner, D.; Drugge, L.; Trigell, A.S. Fault classification method for the driving safety of electrified vehicles. Veh. Syst. Dyn. 2014, 52, 704–732. [Google Scholar] [CrossRef]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Chai, F.; Yu, Y.; Pei, Y. State-of-the-art technology and prospects of permanent magnet in-wheel motors for electric drive vehicles. Acta Armamentarii 2022, 42, 2060–2074. [Google Scholar]
- Hang, P.; Chen, X. Towards autonomous driving: Review and perspectives on configuration and control of four-wheel independent drive/steering electric vehicles. Actuators 2021, 10, 184. [Google Scholar] [CrossRef]
- Li, Y.; Adeleke, O.P.; Xu, X. Methods and applications of energy saving control of in-wheel motor drive system in electric vehicles: A comprehensive review. J. Renew. Sustain. Energy 2019, 11, 062701. [Google Scholar] [CrossRef]
- He, S.; Fan, X.; Wang, Q.; Chen, X.; Zhu, S. Review on torque distribution scheme of four-wheel in-wheel motor electric vehicle. Machines 2022, 10, 619. [Google Scholar] [CrossRef]
- Xu, X.; Qiao, X.; Zhang, N.; Feng, J.; Wang, X. Review of intelligent fault diagnosis for permanent magnet synchronous motors in electric vehicles. Adv. Mech. Eng. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- Khaneghah, M.Z.; Alzayed, M.; Chaoui, H. Fault detection and diagnosis of the electric motor drive and battery system of electric vehicles. Machines 2023, 11, 713. [Google Scholar] [CrossRef]
- Zaaraoui, L.; Mansouri, A. New design and optimization of an in-wheel permanent magnet motor with tangentially magnetized magnets and unequal stator teeth. J. Electr. Eng. 2023, 74, 228–239. [Google Scholar] [CrossRef]
- Chang, J.; Yu, K.; Ding, Y.; Lu, X. Design and optimization of a novel external-rotor axial flux motor for in-wheel application. J. Electr. Eng. Technol. 2024, 19, 2473–2479. [Google Scholar] [CrossRef]
- Saavedra, H.; Romeral, L.; Riba, J.-R. Optimal Design of a Three-Phase AFPM for In-Wheel Electrical Traction. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014. [Google Scholar]
- Gong, J.; Wang, X.; Zhao, B.; Tan, F.; Semail, E.; Nguyen, N.K.; Bracikowski, N. Design, analysis of a seven-phase fault-tolerant bi-harmonic permanent magnet machine with three active air gaps for in-wheel traction applications. IEEE Trans. Energy Convers. 2024, 39, 263–276. [Google Scholar] [CrossRef]
- Gong, J.; Zhao, B.; Huang, Y.; Semail, E.; Nguyen, N.K. Quantitative comparisons of outer-rotor permanent magnet machines of different structures/phases for in-wheel electrical vehicle application. Energies 2022, 15, 6688. [Google Scholar] [CrossRef]
- Nishanth, F.N.U.; Van Verdeghem, J.; Severson, E.L. A review of axial flux permanent magnet machine technology. IEEE Trans. Ind. Appl. 2023, 59, 3920–3933. [Google Scholar] [CrossRef]
- Nandagopal, S.; Chokkalingam, L.N. External rotor permanent magnet-less electric motors for traction application: A review. Int. J. Veh. Des. 2022, 90, 142–195. [Google Scholar] [CrossRef]
- Cetinceviz, Y. Optimal design, electromagnetic–thermal analysis and application of in-wheel permanent magnet BLDC motor for e-mobility. Appl. Sci. 2025, 15, 3258. [Google Scholar] [CrossRef]
- Tashakori, A.; Ektesabi, M.; Hosseinzadeh, N. Characteristics of suitable drive train for electric vehicle. In Proceedings of the 2011 International Conference on Instrumentation, Measurement, Circuits and Systems (ICIMCS 2011), Hong Kong, China, 12–13 December 2011; pp. 51–57. [Google Scholar]
- Wang, Y.; Xu, Y.; Wang, Y.; Zhang, Y. Outer-rotor switched reluctance motor and its control system used in electric vehicles. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–4. [Google Scholar]
- Boldea, I.; Tutelea, L.N.; Parsa, L.; Dorrell, D. Automotive electric propulsion systems with reduced or no permanent magnets: An overview. IEEE Trans. Ind. Electron. 2014, 61, 5696–5711. [Google Scholar] [CrossRef]
- Abdo, T.M.; Adly, A.A. The outer solid rotor induction motor as an alternative for electric vehicle traction applications. In Proceedings of the 2022 Joint MMM-Intermag Conference (INTERMAG), New Orleans, LA, USA, 10–14 January 2022; pp. 1–4. [Google Scholar]
- Sui, Y.; Zheng, P.; Wu, F.; Wang, P.; Cheng, L.; Zhu, J. A novel five-phase fault-tolerant modular in-wheel permanent-magnet synchronous machine for electric vehicles. J. Appl. Phys. 2015, 117, 17B521. [Google Scholar] [CrossRef]
- Zheng, P.; Wu, F.; Lei, Y.; Sui, Y.; Yu, B. Investigation of a novel 24-Slot/14-Pole six-phase fault-tolerant modular permanent-magnet in-wheel motor for electric vehicles. Energies 2013, 6, 4980–5002. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Ye, H.; Zhou, W. A Review of Permanent Magnet Synchronous Motor Fault Diagnosis. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014. [Google Scholar]
- Chen, Y.; Liang, S.; Li, W.; Liang, H.; Wang, C. Faults and diagnosis methods of permanent magnet synchronous motors: S review. Appl. Sci. 2019, 9, 2116. [Google Scholar] [CrossRef]
- Xue, H.; Wang, M.; Li, Z.; Chen, P. Sequential fault detection for sealed deep groove ball bearings of in-wheel motor in variable operating conditions. J. Vibroengineering 2017, 19, 5947–5959. [Google Scholar] [CrossRef]
- Tao, Y.; Ge, C.; Feng, H.; Xue, H.; Yao, M.; Tang, H.; Liao, Z.; Chen, P. A novel approach for adaptively separating and extracting compound fault features of the in-wheel motor bearing. ISA Trans. 2025, 159, 337–351. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Ji, K.; Zhu, R. A fault diagnosis method for a differential inverse gearbox of a crawler combine harvester based on order analysis. Agriculture 2022, 12, 1300. [Google Scholar] [CrossRef]
- Wu, G.; Yu, Y.; Tu, W. Review of research on fault diagnosis of permanent magnet synchronous motor. Chin. J. Eng. Des. 2022, 28, 548–558. [Google Scholar]
- Ma, C.; Gao, Y.; Degano, M.; Wang, Y.; Fang, J.; Gerada, C.; Zhou, S.; Mu, Y. Eccentric position diagnosis of static eccentricity fault of external rotor permanent magnet synchronous motor as an in-wheel motor. IET Electr. Power Appl. 2020, 14, 2263–2272. [Google Scholar] [CrossRef]
- Wu, H.; Zheng, L.; Li, Y.; Zhang, Z.; Yu, Y. Robust control for active suspension of hub-driven electric vehicles subject to in-wheel motor magnetic force oscillation. Appl. Sci. 2020, 10, 3929. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Yu, Y.; Liu, J. Research on unbalanced characteristics of axial-varying eccentric rotor based on signal demodulation. Mech. Syst. Signal Proc. 2024, 220, 111647. [Google Scholar] [CrossRef]
- Wang, Z.; He, Z.; Cai, J. Study on torque ripple suppression of permanent magnetic in-wheel motor under rotor eccentricity by separated harmonic current injection. Int. J. Appl. Electrom. 2021, 65, 561–577. [Google Scholar] [CrossRef]
- Ifedi, C.J.; Mecrow, B.C.; Brockway, S.T.M.; Boast, G.S.; Atkinson, G.J.; Kostic-Perovic, D. Fault-tolerant in-wheel motor topologies for high-performance electric vehicles. IEEE Trans. Ind. Appl. 2013, 49, 1249–1257. [Google Scholar] [CrossRef]
- Sumislawska, M.; Gyftakis, K.N.; Kavanagh, D.F.; McCulloch, M.; Burnham, K.J.; Howey, D.A. The Impact of Thermal Degradation on Electrical Machine Winding Insulation. In Proceedings of the 2015 IEEE 10th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September 2015; pp. 232–238. [Google Scholar]
- Tan, D.; Xue, H.; Yang, K.; Li, A.; Wang, H. Study on the thermal characteristics of in-wheel motor drive system based on driving cycles. IEEE Access 2019, 7, 14463–14471. [Google Scholar] [CrossRef]
- Yang, C.; Yuan, C.; Wang, Y.; Qiu, H.; Chen, S.; Lian, Z.; Zhu, Z. Analysis of inter-turn-short fault in high-speed permanent magnet generators considering effect of structure windings. IEEE Trans. Ind. Appl. 2025, 61, 3007–3015. [Google Scholar] [CrossRef]
- Tabarniarami, Z.; Ghods, M.; Faiz, J.; Abedini, M. Online diagnosis of short-circuit faults of permanent magnet synchronous generator by short-time analysis of the three phase amplitude-phase signal based on analytical modeling. IEEE Trans. Transp. Electrif. 2024, 10, 10029–10042. [Google Scholar] [CrossRef]
- Kavanagh, D.F.; Gyftakis, K.N.; McCulloch, M.D. Thermal degradation phenomena of polymer film on magnet wire for electromagnetic coils. IEEE Trans. Ind. Appl. 2021, 57, 458–467. [Google Scholar] [CrossRef]
- Ge, Y.; Mollet, Y.; Song, B.; Gyselinck, J. Detection and Isolation of Asymmetrical Short-Circuit Faults in Permanent-Magnet Synchronous Machines. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–6. [Google Scholar]
- Zhang, X.; Zheng, X.; Li, X.; Wang, H.; Jin, S.; Wu, X. An improved mean phase currents method of open-circuited faults diagnosis for nine-phase permanent synchronous motor systems. Proc. Chin. Soc. Electr. Eng. 2023, 43, 1589–1597. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, X.; Liu, X.; Yuan, X. A new signal-based diagnosis method for current sensor and open-circuited faults of a nine-phase open-end winding PMSM. IEEE Trans. Transp. Electrif. 2025, 11, 1214–1222. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Cheng, M. Common model predictive control for permanent-magnet synchronous machine drives considering single-phase open-circuit fault. IEEE Trans. Power Electron. 2017, 32, 5862–5872. [Google Scholar] [CrossRef]
- Tang, Y.; Chai, F.; Xie, Y.; Cai, W. Design of a modular in-wheel motor with high fault-tolerant performance and low MMF space harmonic. IEEE Trans. Ind. Electron. 2023, 70, 6574–6584. [Google Scholar] [CrossRef]
- Tang, Y.; Chai, F.; Chen, L. Investigation of open-circuit fault-tolerant strategy in a modular permanent magnet synchronous in-wheel motor based on electromagnetic–thermal analysis. IEEE Trans. Ind. Electron. 2022, 8, 1085–1093. [Google Scholar] [CrossRef]
- Hang, J.; Shu, X.; Ding, S.; Huang, Y. Robust open-circuit fault diagnosis for PMSM drives using wavelet convolutional neural network with small samples of normalized current vector trajectory graph. IEEE Trans. Ind. Electron. 2023, 70, 7653–7663. [Google Scholar] [CrossRef]
- Saavedra, H. Detection of inter-turn faults in five-phase permanent magnet synchronous motors. Adv. Electr. Comp. Eng. 2014, 14, 49–54. [Google Scholar] [CrossRef]
- Wang, Q.; Li, R.; Xu, W.; Zhao, Z.; Liu, S. Evolutionary characteristics of magnetic field for the permanent magnet in-wheel motor under time-dependent demagnetization. IEEE Access 2024, 12, 76673–76681. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Qu, C.; Zhou, C. Temperature field and demagnetization analysis of in-wheel motors based on magneto-thermal two-way coupling. J. Power Electron. 2024, 24, 227–238. [Google Scholar] [CrossRef]
- Bae, J.C.; Cho, H.R.; Yadav, S.; Kim, S.C. Cooling effect of water channel with vortex generators on in-wheel driving motors in electric vehicles. Energies 2022, 15, 722. [Google Scholar] [CrossRef]
- Yu, D.; Huang, X.; Ma, J.; Fang, Y. A Comparative Study on Two Outer Rotor PMSMs for In-Wheel Direct Drive Under Short-Circuit Faults. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017. [Google Scholar]
- Yang, S.; Baker, N.J.; Mecrow, B.C.; Smith, D.; Atkinson, G.; Hilton, C.; Perovic, D.K.; Kakavas, I.; Sooriyakumar, G.; Harvey, P. Magnet Losses and Demagnetisation in a Permanent Magnet In-Wheel Electric Vehicle Traction Motor. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1831–1837. [Google Scholar]
- Xiang, P.; Yan, L.; Liu, X.; He, X.; Du, N.; Wang, H. Structural topology design for electromagnetic performance enhancement of permanent-magnet machines. Chin. J. Mech. Eng. 2025, 38, 26. [Google Scholar] [CrossRef]
- Bin Tarek, M.T.; Das, S.; Sozer, Y. Comparative Analysis of Static Eccentricity Faults of Double Stator Single Rotor Axial Flux Permanent Magnet Motors. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 3223–3228. [Google Scholar]
- Ajily, E.; Ardebili, M.; Abbaszadeh, K. Magnet defect and rotor eccentricity modeling in axial flux permanent-magnet machines via 3-D field reconstruction method. IEEE Trans. Energy Convers. 2016, 31, 486–495. [Google Scholar] [CrossRef]
- Guo, B.; Du, Y.; Peng, F.; Huang, Y. Magnetic field calculation in axial flux permanent magnet motor with rotor eccentricity. IEEE Trans. Magn. 2022, 58, 1–4. [Google Scholar] [CrossRef]
- Tong, W.; Dai, S.; Li, S.; Li, J.; Tang, R. Modeling and analysis of axial flux permanent magnet machines with coexistence of rotor radial deviation and angular eccentricity. IEEE Trans. Energy Convers. 2020, 35, 2181–2190. [Google Scholar] [CrossRef]
- Farrokh, F.; Vahedi, A.; Torkaman, H.; Banejad, M.; Jafer Mahdi, A.; Jamal Mohammed, M. Demagnetization and fault-tolerance analysis in dual-stator axial-field flux-switching permanent magnet motor. IEEE Access 2024, 12, 102579–102591. [Google Scholar] [CrossRef]
- Rallabandi, V.; Taran, N.; Ionel, D.M. Multilayer concentrated windings for axial flux PM machines. IEEE Trans. Magn. 2017, 53, 8103104. [Google Scholar] [CrossRef]
- Li, T.; Liang, Y.; Yang, Y.; Tian, J.; Fan, L. Thermal analysis and research of a yokeless and segmented armature axial flux in-wheel motor with an amorphous magnetic metal stator. IEEE Access 2025, 13, 48672–48682. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Zeng, T.; Wang, H.; Chan, S.-C.; Ran, L. Wind turbine generator failure analysis and fault diagnosis: A review. IET Renew. Power Gener. 2024, 18, 3127–3148. [Google Scholar] [CrossRef]
- Solís, R.; Torres, L.; Pérez, P. Review of methods for diagnosing faults in the stators of BLDC motors. Processes 2023, 11, 82. [Google Scholar] [CrossRef]
- Xu, Y.; Ge, X.; Shen, W.; Yang, R. A soft short-circuit diagnosis method for lithium-ion battery packs in electric vehicles. IEEE Trans. Power Electron. 2022, 37, 8572–8581. [Google Scholar] [CrossRef]
- Muenchhof, M.; Beck, M.; Isermann, R. Fault-tolerant actuators and drives—Structures, fault detection principles and applications. Annu. Rev. Control. 2009, 33, 136–148. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J. Fault-tolerant control with active fault diagnosis for four-wheel independently driven electric ground vehicles. IEEE Trans. Veh. Technol. 2011, 60, 4276–4287. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, Y.; Yu, S.; Chen, H. Gain-Scheduled Fault Diagnosis of In-Wheel Motor Electric Vehicles. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 4093–4098. [Google Scholar]
- Lee, J.; Moon, S.; Jeong, H.; Kim, S.W. Robust diagnosis method based on parameter estimation for an interturn short-circuit fault in multipole PMSM under high-speed operation. Sensors 2015, 15, 29452–29466. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Lin, K.; Zhang, X.; Wang, S.; Ai, J.; Lin, M. An online estimation method for both stator inductance and rotor flux linkage of SPMSM without dead-time influence. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1627–1638. [Google Scholar] [CrossRef]
- Park, B.-G.; Kim, R.-Y.; Hyun, D.-S. Open circuit fault diagnosis using stator resistance variation for permanent magnet synchronous motor drives. J. Power Electron. 2013, 13, 985–990. [Google Scholar] [CrossRef]
- Lee, J.; Jeon, Y.-J.; Choi, D.; Kim, S.; Kim, S.W. Demagnetization Fault Diagnosis Method for PMSM of Electric Vehicle. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON 2013), Vienna, Austria, 10–13 November 2013; pp. 2709–2713. [Google Scholar]
- Sarikhani, A.; Mohammed, O.A. Inter-turn fault detection in PM synchronous machines by physics-based back electromotive force estimation. IEEE Trans. Ind. Electron. 2013, 60, 3472–3484. [Google Scholar] [CrossRef]
- Feng, H.; Tao, Y.; Feng, J.; Zhang, Y.; Xue, H.; Wang, T.; Xu, X.; Chen, P. Fault-tolerant collaborative control of four-wheel-drive electric vehicle for one or more in-wheel motors’ faults. Sensors 2025, 25, 1540. [Google Scholar] [CrossRef]
- Jeon, N.; Lee, H. Integrated fault diagnosis algorithm for motor sensors of in-wheel independent drive electric vehicles. Sensors 2016, 16, 2106. [Google Scholar] [CrossRef]
- Liu, H.; Niu, W.; Guo, Y. Direct torque control for PMSM based on the RBFNN surrogate model of electromagnetic torque and stator flux linkage. Control. Eng. Pract. 2024, 148, 105943. [Google Scholar] [CrossRef]
- Tang, L.; Wang, W.; Zhang, C.; Wang, Z.; Ge, Z.; Yuan, S. Linear active disturbance rejection control system for the travel speed of an electric reel sprinkling irrigation machine. Agriculture 2024, 14, 1544. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Zhou, D. Diagnosis and prognosis for complicated industrial systems—Part I. IEEE Trans. Ind. Electron. 2016, 63, 2501–2505. [Google Scholar] [CrossRef]
- Zhao, Z.; Jin, M.; Tian, C.; Qin, F. Molecular diagnostics of copper-transporting protein mutations allows early onset individual therapy of Menkes disease. Int. J. Agric. Biol. Eng. 2019, 12, 81–86. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Chen, B.C.; Yin, D.; Huynh, P.S. Active Fault Tolerant Torque Distribution Control of 4 In-Wheel Motors Electric Vehicles Based on Kalman Filter Approach. In Proceedings of the 2017 International Conference on System Science and Engineering (ICSSE), Ho Chi Minh City, Vietnam, 21–23 July 2017; pp. 360–364. [Google Scholar]
- Naseri, F.; Schaltz, E.; Lu, K.; Farjah, E. Real-time open-switch fault diagnosis in automotive permanent magnet synchronous motor drives based on Kalman Filter. IET Power Electron. 2020, 13, 2450–2460. [Google Scholar] [CrossRef]
- Romdhane, M.; Naoui, M.; Mansouri, A. PMSM inter-turn short circuit fault detection using the fuzzy-extended Kalman Filter in electric vehicles. Electronics 2023, 12, 3758. [Google Scholar] [CrossRef]
- Dan, L. EKF-based fault detection and isolation for PMSM inverter. Sustain. Energy Technol. Assess. 2022, 52, 101846. [Google Scholar] [CrossRef]
- Aboelhassan, A.; El Sayed, W.; Hebala, A.; Galea, M.; Bozhko, S. Fault Tolerant Control Strategy Based on Model Predictive Control and Unscented Kalman Filter for Permanent Magnet Synchronous Motor. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021; pp. 153–159. [Google Scholar]
- Zhou, N.; He, H.; Liu, Z.; Zhang, Z. UKF-Based Sensor Fault Diagnosis of PMSM Drives in Electric Vehicles. In Proceedings of the 9th International Conference on Applied Energy, Cardiff, UK, 21–24 August 2017; Volume 142, pp. 2276–2283. [Google Scholar]
- Sun, J.; Wang, Z.; Ding, S.; Xia, J.; Xing, G. Adaptive disturbance observer-based fixed time nonsingular terminal sliding mode control for path-tracking of unmanned agricultural tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Hang, J.; Hu, Q.; Sun, W.; Ren, X.; Ding, S.; Huang, Y.; Hua, W. A voltage-distortion-based method for robust detection and location of interturn fault in permanent magnet synchronous machine. IEEE Trans. Power Electron. 2022, 37, 11174–11186. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Jlassi, I.; Marques Cardoso, A.J.; Yahia, K.; Sahraoui, M. Inter-turn short-circuit faults diagnosis in synchronous reluctance machines, using the Luenberger state observer and current’s second-order harmonic. IEEE Trans. Ind. Electron. 2022, 69, 8420–8429. [Google Scholar] [CrossRef]
- Chen, Z.; Liang, D.; Jia, S.; Yang, S. Model-based data normalization for data-driven PMSM fault diagnosis. IEEE Trans. Power Electron. 2024, 39, 11596–11612. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J. Actuator-redundancy-based fault diagnosis for four-wheel independently actuated electric vehicles. IEEE Trans. Intell. Transp. Syst. 2014, 15, 239–249. [Google Scholar] [CrossRef]
- Li, F.; Chen, Y.; Tang, H.; Xia, F.; Luo, J.; Du, C. Event-triggered adaptive fault tolerant sliding mode control for FWID-EV. IEEE Trans. Transp. Electrif. 2024, 10, 9192–9208. [Google Scholar] [CrossRef]
- Salehifar, M.; Salehi Arashloo, R.; Moreno-Eguilaz, M.; Sala, V.; Romeral, L. Observer-based open transistor fault diagnosis and fault-tolerant control of five-phase permanent magnet motor drive for application in electric vehicles. IET Power Electron. 2015, 8, 76–87. [Google Scholar] [CrossRef]
- Hashemi, M.; Stolz, M.; Watzenig, D. Super-Twisting Algorithm-Based Sliding Mode Observer for Open-Circuit Fault Diagnosis in PWM Voltage Source Inverter in an In-Wheel Motor Drive System. In Proceedings of the 2023 IEEE International Conference on Mechatronics (ICM), Loughborough, UK, 15–17 March 2023. [Google Scholar]
- Zhao, K.; Leng, A.; Zhou, R.; Dai, W.; Wu, S.; Li, T. Demagnetization fault reconstruction for six-phase permanent magnet synchronous motor by improved super-twisting algorithm-based sliding-mode observer. Measurement 2021, 172, 108905. [Google Scholar] [CrossRef]
- Xue, H.; Ding, D.; Zhang, Z.; Wu, M.; Wang, H. A fuzzy system of operation safety assessment using multimodel linkage and multistage collaboration for in-wheel motor. IEEE Trans. Fuzzy Syst. 2022, 30, 999–1013. [Google Scholar] [CrossRef]
- Wang, L.; Wang, G.; Zhai, X.; Tang, Z.; Wang, B.; Li, P. Response characteristics of harvester bolts and the establishment of the strongest response structure’s kinetic model. Agriculture 2024, 14, 1174. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Z.; Zhang, Z.; Song, Z.; Liu, Y.; Li, Y.; Xu, L. Durable testing and analysis of a cleaning sieve based on vibration and strain signals. Agriculture 2023, 13, 2232. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Hao, S.; Tang, Z.; Guo, S.; Ding, Z.; Su, Z. Model and method of fault signal diagnosis for blockage and slippage of rice threshing drum. Agriculture 2022, 12, 1968. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics-a tutorial. Mech. Syst. Signal Proc. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Nandi, S.; Toliyat, H.A.; Li, X. Condition monitoring and fault diagnosis of electrical motors—A review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Javan Roshtkhari, M.; Faiz, J.; Khatami, S.V. Advanced eccentricity fault recognition in permanent magnet synchronous motors using stator current signature analysis. IEEE Trans. Ind. Electron. 2014, 61, 2041–2052. [Google Scholar] [CrossRef]
- Espinosa, A.G.; Rosero, J.A.; Cusido, J.; Romeral, L.; Ortega, J.A. Fault detection by means of Hilbert–Huang transform of the stator current in a PMSM with demagnetization. IEEE Trans. Energy Convers. 2010, 25, 312–318. [Google Scholar] [CrossRef]
- Liang, H.; Chen, Y.; Liang, S.; Wang, C. Fault detection of stator inter-turn short-circuit in PMSM on stator current and vibration signal. Appl. Sci. 2018, 8, 1677. [Google Scholar] [CrossRef]
- Skora, M.; Ewert, P.; Kowalski, C.T. Selected rolling bearing fault diagnostic methods in wheel embedded permanent magnet brushless direct current motors. Energies 2019, 12, 4212. [Google Scholar] [CrossRef]
- Tashakori, A.; Ektesabi, M. Fault Diagnosis of In-Wheel BLDC Motor Drive for Electric Vehicle Application. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium (IV), Gold Coast, QLD, Australia, 23–26 June 2013; pp. 925–930. [Google Scholar]
- Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H. Signals & Systems; Pearson Education: London, UK, 1997; ISBN 978-970-17-0116-4. [Google Scholar]
- Maldonado Ruelas, V.A.; Villalobos Pina, F.J.; Alvarez Salas, R.; Morones Alba, J.A.; Ortiz Medina, R.A. Multiple criteria fault detection of BLDC (brushless direct current) motor. Dyna 2018, 93, 556–562. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999; ISBN 978-0-08-052083-4. [Google Scholar]
- Choudhary, A.; Mian, T.; Fatima, S.; Panigrahi, B.K. Fault diagnosis of electric two-wheeler under pragmatic operating conditions using wavelet synchrosqueezing transform and CNN. IEEE Sens. J. 2023, 23, 6254–6263. [Google Scholar] [CrossRef]
- Xu, K.; Wu, X.; Wang, D.; Liu, X. Error analysis of instantaneous frequency estimation of second-order SST and its application on analyzing gear meshing stiffness from motor current. IEEE Trans. Instrum. Meas. 2024, 73, 3507812. [Google Scholar] [CrossRef]
- Yuan, J.; Dong, X.; Niu, G.; Ge, X. Fault detection of synchronous motor inter-turn short circuit based on current residual harmonic characteristics. Proc. Inst. Mech. Eng. Part C J. Eng. Mech. Eng. Sci. 2025, 239, 6238–6257. [Google Scholar] [CrossRef]
- Cui, L.; Chen, J.; Liu, D.; Zhen, D. Fault diagnosis of offshore wind turbines based on component separable synchroextracting transform. Ocean Eng. 2024, 291, 116275. [Google Scholar] [CrossRef]
- Wang, X.-B.; Luo, L.; Tang, L.; Yang, Z.-X. Automatic representation and detection of fault bearings in in-wheel motors under variable load conditions. Adv. Eng. Inform. 2021, 49, 101321. [Google Scholar] [CrossRef]
- Ge, C.; Song, Z.; Shang, J.; Xue, H.; Wang, T. MIWF-2DCNN diagnosis method for bearing fault of in-wheel motor. J. Electron. Meas. Instrum. 2024, 38, 127–135. [Google Scholar]
- Ding, D.; Xue, H.; Liu, B. Feature extraction method based on optimized SSD and enhance MOMEDA for bearing faults of in-wheel motor. Proc. CSEE 2024, 43, 9721–9732. [Google Scholar]
- Rosero, J.A.; Romeral, L.; Ortega, J.A.; Rosero, E. Short-circuit detection by means of empirical mode decomposition and Wigner Ville distribution for PMSM running under dynamic condition. IEEE Trans. Ind. Electron. 2009, 56, 4534–4547. [Google Scholar] [CrossRef]
- Shen, Y.; Gao, J.; Jin, Z. Research on acoustic signal identification mechanism and denoising methods of combine harvesting loss. Agronomy 2024, 14, 1816. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Z.; Li, Y.; Sun, Q. Open-circuit fault diagnosis of six-phase permanent magnet synchronous motor drive system based on empirical mode decomposition energy entropy. IEEE Access 2021, 9, 91137–91147. [Google Scholar] [CrossRef]
- Dogan, Z.; Tetik, K. Diagnosis of inter-turn faults based on fault harmonic component tracking in LSPMSMs working under nonstationary conditions. IEEE Access 2021, 9, 92101–92112. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Q.; Gao, L.; Miao, Y.; Cai, H.; Zhao, Y. ITSC fault diagnosis for PMSM by using adaptive filtering and tree-structured parzen estimator optimized-automated random forest. Electr. Eng. 2025, 107, 4711–4725. [Google Scholar] [CrossRef]
- Ji, K.; Li, Y.; Liu, Y.; Yu, Z.; Cheng, J. Vibration signal extraction and analysis of combine harvester based on low-pass filter-EEMD combination. Eng. Agric. 2024, 44, e20240006. [Google Scholar] [CrossRef]
- Xia, Y.; Li, X.; Luo, Y. Inter-turn short circuit fault detection of PMSM based on wavelet packet energy spectrum and CEEMDAN-HT. J. Electr. Eng. Technol. 2024, 19, 1379–1393. [Google Scholar] [CrossRef]
- Mahmoud, T.; Dong, Z.Y.; Ma, J. Integrated optimal active and reactive power control scheme for grid connected permanent magnet synchronous generator wind turbines. IET Electr. Power Appl. 2018, 12, 474–485. [Google Scholar] [CrossRef]
- Dai, D.; Chen, D.; Wang, S.; Li, S.; Mao, X.; Zhang, B.; Wang, Z.; Ma, Z. Compilation and extrapolation of load spectrum of tractor ground vibration load based on CEEMDAN-POT model. Agriculture 2023, 13, 125. [Google Scholar] [CrossRef]
- Yu, Z.; Li, Y.; Du, X.; Liu, Y. Threshing cylinder unbalance detection using a signal extraction method based on parameter-adaptive variational mode decomposition. Biosyst. Eng. 2024, 244, 26–41. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Shi, J.; Shen, C.; Huang, W.; Zhu, Z. A coarse-to-fine decomposing strategy of VMD for extraction of weak repetitive transients in fault diagnosis of rotating machines. Mech. Syst. Signal Proc. 2019, 116, 668–692. [Google Scholar] [CrossRef]
- Xia, Y.-K.; Wang, W.-T.; Li, X.-Y. Adaptive parameter selection variational mode decomposition based on Bayesian optimization and its application to the detection of ITSC in PMSM. IEEE Access 2024, 12, 38594–38614. [Google Scholar] [CrossRef]
- Li, X.; Zhang, M.; Liu, M.; Yan, X.; Xu, L. Drive power allocation strategy for electric tractor based on adaptive multiresolution analysis. Trans. Chin. Soc. Agric. Eng. 2024, 39, 55–66. [Google Scholar]
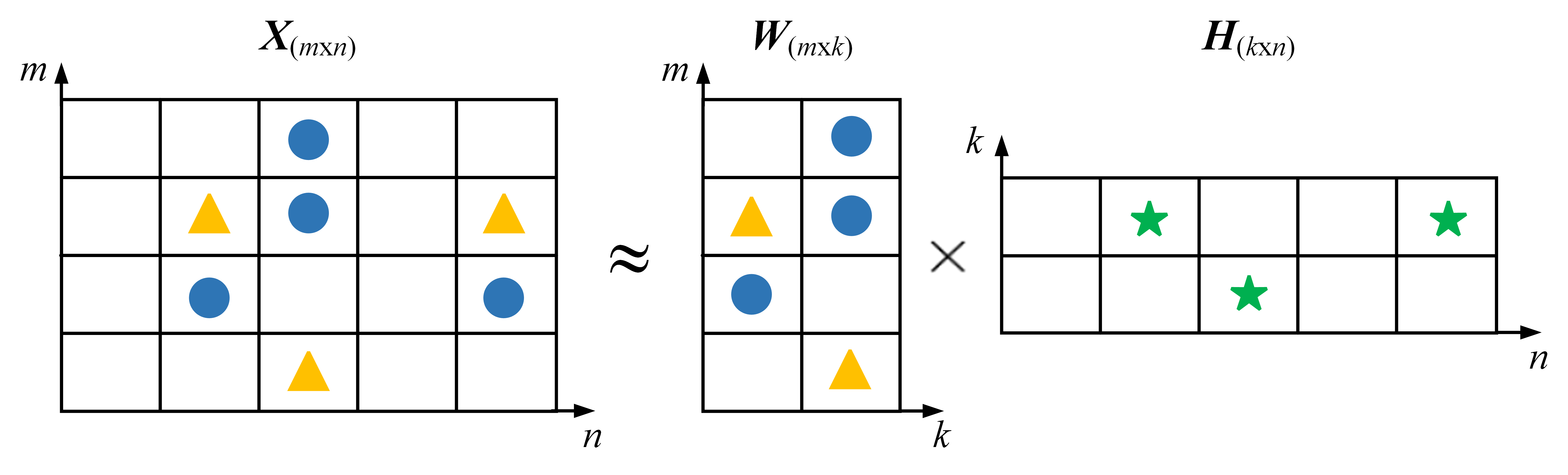
- Lee, D.; Seung, H.S. Algorithms for Non-Negative Matrix Factorization. In Proceedings of the Advances in Neural Information Processing Systems, Cambridge, MA, USA; 2000; Volume 13. [Google Scholar]
- Xue, H.; Ding, D.; Li, R.; Xu, X. Feature extraction method based on component weighted reconstruction and sparse NMF for bearing compound faults of in-wheel motor. J. Mech. Eng. 2023, 59, 146–156. [Google Scholar]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Duan, Z.; Wu, T.; Guo, S.; Shao, T.; Malekian, R.; Li, Z. Development and trend of condition monitoring and fault diagnosis of multi-sensors information fusion for rolling bearings: A review. Int. J. Adv. Manuf. Technol. 2018, 96, 803–819. [Google Scholar] [CrossRef]
- Li, L.; Xie, S.; Ning, J.; Chen, Q.; Zhang, Z. Evaluating green tea quality based on multisensor data fusion combining hyperspectral imaging and olfactory visualization systems. J. Sci. Food Agric. 2019, 99, 1787–1794. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y.; Hu, Q. Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAs. Mech. Syst. Signal Process. 2007, 21, 2280–2294. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Xue, H.; Yin, S. Online diagnosis method for mechanical fault of in-wheel motor based on DBNs. J. Vib. Meas. Diagn. 2020, 40, 643–649. [Google Scholar]
- Zhu, Z.; Zeng, L.; Chen, L.; Zou, R.; Cai, Y. Fuzzy adaptive energy management strategy for a hybrid agricultural tractor equipped with HMCVT. Agriculture 2022, 12, 1986. [Google Scholar] [CrossRef]
- Wu, X.; Wu, B.; Sun, J.; Yang, N. Classification of apple varieties using near infrared reflectance spectroscopy and fuzzy discriminant c-means clustering model. J. Food Process Eng. 2017, 40, e12355. [Google Scholar] [CrossRef]
- Yan, H.; Xu, Y.; Cai, F.; Zhang, H.; Zhao, W.; Gerada, C. PWM-VSI fault diagnosis for a PMSM drive based on the fuzzy logic approach. IEEE Trans. Power Electron. 2019, 34, 759–768. [Google Scholar] [CrossRef]
- Moosakunju, S.; Mini, V.P.; Ushakumari, S.; Mayadevi, N.; Harikumar, R. A hybrid fault detection and diagnosis algorithm for five-phase PMSM drive. Arab. J. Sci. Eng. 2023, 48, 6507–6519. [Google Scholar] [CrossRef]
- Yu, Y.; Hao, S.; Guo, S.; Tang, Z.; Chen, S. Motor torque distribution strategy for different tillage modes of agricultural electric tractors. Agriculture 2022, 12, 1373. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Y.; Yan, K.; Zhou, K.; Zhang, C.; Zhang, X. Probabilistic graphical models in energy systems: A review. Build. Simul. 2022, 15, 699–728. [Google Scholar] [CrossRef]
- Cai, B.; Wang, Z.; Zhu, H.; Liu, Y.; Hao, K.; Yang, Z.; Ren, Y.; Feng, Q.; Liu, Z. Artificial intelligence enhanced two-stage hybrid fault prognosis methodology of PMSM. IEEE Trans. Ind. Inform. 2022, 18, 7262–7273. [Google Scholar] [CrossRef]
- Cai, B.; Zhao, Y.; Liu, H.; Xie, M. A data-driven fault diagnosis methodology in three-phase inverters for PMSM drive systems. IEEE Trans. Power Electron. 2017, 32, 5590–5600. [Google Scholar] [CrossRef]
- Cai, B.; Hao, K.; Wang, Z.; Yang, C.; Kong, X.; Liu, Z.; Ji, R.; Liu, Y. Data-driven early fault diagnostic methodology of permanent magnet synchronous motor. Expert Syst. Appl. 2021, 177, 115000. [Google Scholar] [CrossRef]
- Li, Z.; Qin, X.; Xue, H. In-wheel motor fault diagnosis method based on BN and improved DST. J. Huazhong Univ. Sci. Technol. Nat. Sci. 2021, 49, 27–32. [Google Scholar]
- Xue, H.; Zhou, J.; Tong, P. Mechanical fault diagnosis method of in-wheel motor based on WMM-HMM. J. Huazhong Univ. Sci. Technol. Nat. Sci. 2021, 49, 32–37. [Google Scholar]
- Xue, H.; Liu, B.; Ding, D.; Zhou, J.; Cui, X. Diagnosis method based on hidden Markov model and Weibull mixture model for mechanical faults of in-wheel motors. Meas. Sci. Technol. 2022, 33, 114002. [Google Scholar] [CrossRef]
- Zhang, J.; Zhan, W.; Ehsani, M. Diagnosis and fault-tolerant control of permanent magnet synchronous motors with interturn short-circuit fault. IEEE Trans. Control Syst. Technol. 2023, 31, 1909–1916. [Google Scholar] [CrossRef]
- Zhang, J.; Zhan, W.; Ehsani, M. On-line diagnosis of inter-turn short circuit fault for DC brushed motor. ISA Trans. 2018, 77, 179–187. [Google Scholar] [CrossRef]
- Zhu, W.; Feng, Z.; Dai, S.; Zhang, P.; Wei, X. Using UAV multispectral remote sensing with appropriate spatial resolution and machine learning to monitor wheat scab. Agriculture 2022, 12, 1785. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Zhou, Z.; Zhang, Y.; Wang, X. Detection method for tomato leaf mildew based on hyperspectral fusion terahertz technology. Foods 2023, 12, 535. [Google Scholar] [CrossRef]
- Huang, X.; Yu, S.; Xu, H.; Aheto, J.H.; Bonah, E.; Ma, M.; Wu, M.; Zhang, X. Rapid and nondestructive detection of freshness quality of postharvest spinaches based on machine vision and electronic nose. J. Food Saf. 2019, 39, e12708. [Google Scholar] [CrossRef]
- Lale, T.; Gumus, B. An Effective Torque-based method for automatic turn fault detection and turn fault severity classification in permanent magnet synchronous motor. Electr. Eng. 2024, 106, 2865–2876. [Google Scholar] [CrossRef]
- Moosavi, S.S.; Djerdir, A.; Ait-Amirat, Y.; Khaburi, D.A. ANN based fault diagnosis of permanent magnet synchronous motor under stator winding shorted Turn. Electr. Power Syst. Res. 2015, 125, 67–82. [Google Scholar] [CrossRef]
- Kang, J.-K.; Yoo, D.-W.; Hur, J. Application and verification of voltage angle-based fault diagnosis method in six-phase IPMSM. IEEE Trans. Ind. Appl. 2024, 60, 426–438. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Faiz, J.; Roshtkhari, M.J. Static-, dynamic-, and mixed-eccentricity fault diagnoses in permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2009, 56, 4727–4739. [Google Scholar] [CrossRef]
- Aktas, M.; Aygun, H. Comparison of DC link current and stator phase current in inverter switching faults detection of PMSM drives in HEVs. Eng. Sci. Technol. 2018, 21, 664–671. [Google Scholar] [CrossRef]
- Mahafzah, K.A.A.; Obeidat, M.A.A.; Mansour, A.M.M.; Al-Shetwi, A.Q.Q.; Ustun, T.S. Artificial-Intelligence-Based Open-Circuit Fault Diagnosis in VSI-Fed PMSMs and a Novel Fault Recovery Method. Sustainability 2022, 14, 16504. [Google Scholar] [CrossRef]
- Nyanteh, Y.; Edrington, C.; Srivastava, S.; Cartes, D. Application of artificial intelligence to real-time fault detection in permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2013, 49, 1205–1214. [Google Scholar] [CrossRef]
- Belfore, L.A.; Arkadan, A. A methodology for characterizing fault tolerant switched reluctance motors using neurogenetically derived models. IEEE Trans. Energy Convers. 2002, 17, 380–384. [Google Scholar] [CrossRef]
- Pang, Y.; Li, H.; Tang, P.; Chen, C. Irrigation scheduling of pressurized irrigation networks for minimizing energy consumption. Irrig. Drain. 2023, 72, 268–283. [Google Scholar] [CrossRef]
- Siddique, M.F.; Zaman, W.; Ullah, S.; Umar, M.; Saleem, F.; Shon, D.; Yoon, T.H.; Yoo, D.-S.; Kim, J.-M. Advanced Bearing-fault diagnosis and classification using mel-scalograms and FOX-optimized ANN. Sensors 2024, 24, 7303. [Google Scholar] [CrossRef] [PubMed]
- Bonah, E.; Huan, X.; Yi, R.; Aheto, J.H.; Osae, R.; Golly, M. Electronic nose classification and differentiation of bacterial foodborne pathogens based on support vector machine optimized with particle swarm optimization algorithm. J. Food Process Eng. 2019, 42, e13236. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, X.; Mao, H.; Wu, X.; Zhang, X.; Li, Q. Discrimination of pesticide residues in lettuce based on chemical molecular structure coupled with wavelet transform and near infrared hyperspectra. J. Food Process Eng. 2017, 40, e12509. [Google Scholar] [CrossRef]
- Liang, S.; Chen, Y.; Liang, H.; Li, X. Sparse representation and SVM diagnosis method for inter-turn short-circuit fault in PMSM. Appl. Sci. 2019, 9, 224. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, H.; Zhou, S.; Pan, Y.; Zhang, K.; Liu, P.; Yang, H.; Zhao, Z.; Madyira, D.M. Rotor faults diagnosis in PMSMs based on branch current analysis and machine learning. Actuators 2023, 12, 145. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Wu, Q.; Pei, H.; Diao, L. A data-driven intelligent fault diagnosis framework for permanent magnet in PMSM. Alex. Eng. J. 2025, 113, 331–346. [Google Scholar] [CrossRef]
- Kong, L.; Mao, Y.; Zhang, T.; Chen, X.; Wang, Z.; Wang, X. Online data-driven diagnosis for common electrical and sensor faults in dual three-phase PMSM drives. IEEE Trans. Instrum. Meas. 2025, 74, 2507510. [Google Scholar] [CrossRef]
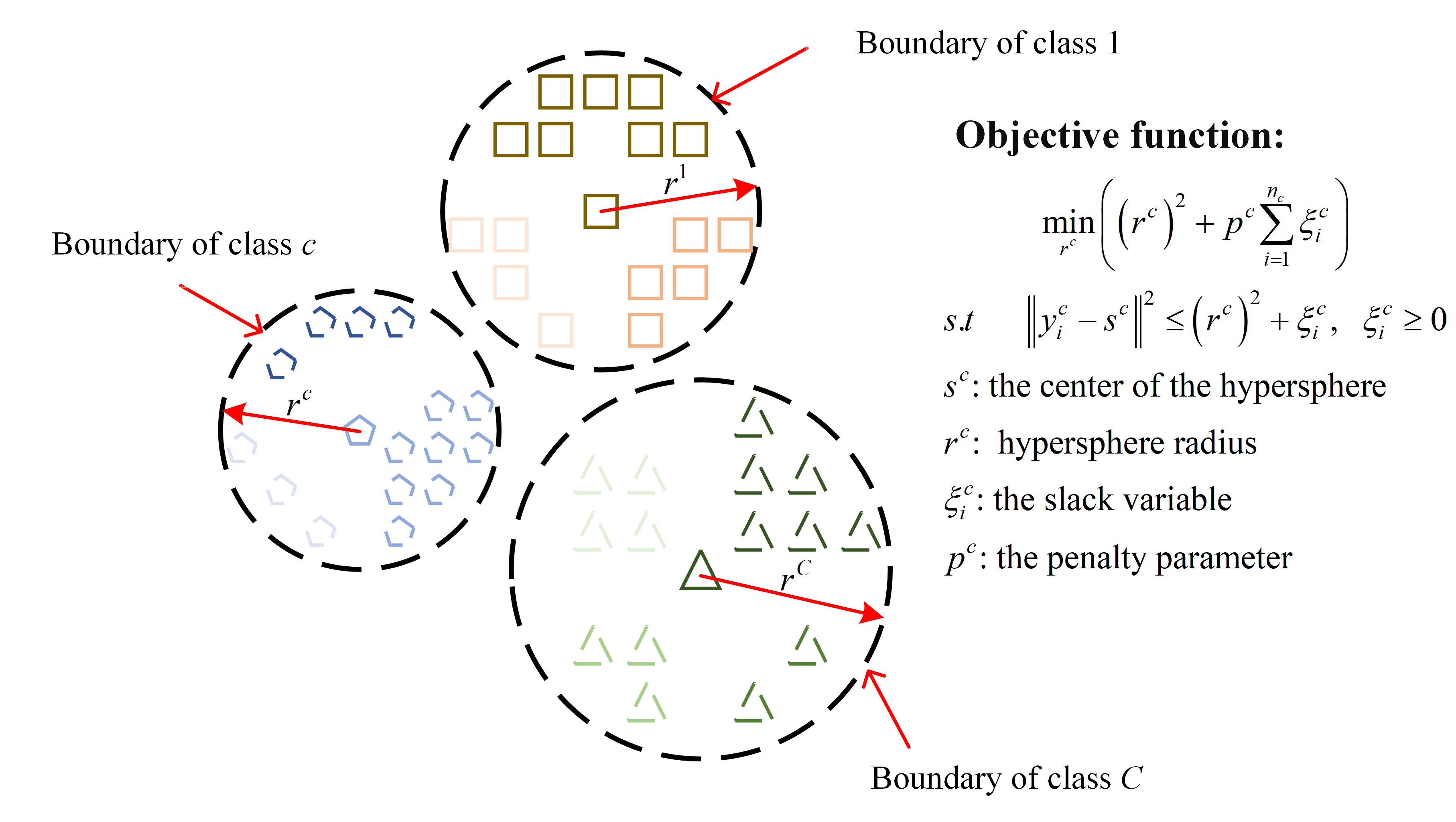
- Liu, B.; Xue, H.; Ding, D.; Sun, N.; Chen, P. In-wheel motor fault diagnosis using affinity propagation minimum-distance discriminant projection and weibull-kernel-function-based SVDD. Sensors 2023, 23, 4021. [Google Scholar] [CrossRef]
- Li, Z.; Xi, S.; Xue, H.; Zhu, F. Research on condition recognition method based on DK-SVDD for in-wheel motor bearing. J. Vib. Meas. Diagn. 2023, 43, 1121–1128. [Google Scholar]
- Wang, B.; Tang, Z.; Wang, K.; Li, P. Failure feature identification of vibrating screen bolts under multiple feature fusion and optimization method. Agriculture 2024, 14, 1433. [Google Scholar] [CrossRef]
- Xue, H.; Wu, M.; Zhang, Z.; Zhou, H.; Wang, H. Condition recognition method based on K-AHNs for in-wheel motor. J. Mech. Eng. 2024, 59, 207–214. [Google Scholar]
- Xue, H.; Wang, M.; Li, Z.; Chen, P. Fault Feature Extraction Based on Artificial Hydrocarbon Network for Sealed Deep Groove Ball Bearings of In-Wheel Motor. In Proceedings of the 2017 Prognostics and System Health Management Conference (PHM-Harbin), Harbin, China, 9–12 July 2017; pp. 417–421. [Google Scholar]
- Xue, H.; Song, Z.; Wu, M.; Sun, N.; Wang, H. Intelligent diagnosis based on double-optimized artificial hydrocarbon networks for mechanical faults of in-wheel motor. Sensors 2022, 22, 6316. [Google Scholar] [CrossRef]
- Xue, H.; Wu, M.; Zhang, Z.; Wang, H. Intelligent diagnosis of mechanical faults of in-wheel motor based on improved artificial hydrocarbon networks. ISA Trans. 2022, 120, 360–371. [Google Scholar] [CrossRef] [PubMed]
- Ponce, H.; Miralles-Pechuán, L.; Martínez-Villaseñor, M.D.L. A flexible approach for human activity recognition using artificial hydrocarbon networks. Sensors 2016, 16, 1715. [Google Scholar] [CrossRef] [PubMed]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep Neural Networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72–73, 303–315. [Google Scholar] [CrossRef]
- Lin, H.; Pan, T.; Li, Y.; Chen, S.; Li, G. Development of analytical method associating near-infrared spectroscopy with one-dimensional convolution neural network: A case study. Food Meas. 2021, 15, 2963–2973. [Google Scholar] [CrossRef]
- Ouyang, Q.; Fan, Z.; Chang, H.; Shoaib, M.; Chen, Q. Analyzing TVB-N in snakehead by Bayesian-optimized 1D-CNN using molecular vibrational spectroscopic techniques: Near-infrared and Raman spectroscopy. Food Chem. 2025, 464, 141701. [Google Scholar] [CrossRef]
- Wang, B.; Deng, J.; Jiang, H. Markov Transition field combined with convolutional neural network improved the predictive performance of near-infrared spectroscopy models for determination of aflatoxin B1 in maize. Foods 2022, 11, 2210. [Google Scholar] [CrossRef] [PubMed]
- Pietrzak, P.; Wolkiewicz, M.; Orlowska-Kowalska, T. PMSM stator winding fault detection and classification based on bispectrum analysis and convolutional neural network. IEEE Trans. Ind. Electron. 2023, 70, 5192–5202. [Google Scholar] [CrossRef]
- Yu, Y.; Yuan, C.; Zeng, D.; Carbone, G.; Hu, Y.; Yang, J. Conceptual approach to permanent magnet synchronous motor turn-to-turn short circuit and uniform demagnetization fault diagnosis. Actuators 2024, 13, 511. [Google Scholar] [CrossRef]
- Zhang, Q.; Cui, J.; Xiao, W.; Mei, L.; Yu, X. Demagnetization fault diagnosis of a PMSM for electric drilling tools using GAF and CNN. Electronics 2024, 13, 189. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Z.; Cao, J. A novel method of combining generalized frequency response function and convolutional neural network for complex system fault diagnosis. PLoS ONE 2020, 15, e0228324. [Google Scholar] [CrossRef]
- Song, Q.; Wang, M.; Lai, W.; Zhao, S. Multiscale kernel-based residual CNN for estimation of inter-turn short circuit fault in PMSM. Sensors 2022, 22, 6870. [Google Scholar] [CrossRef] [PubMed]
- Lv, K.; Wang, D.; Huang, W.; Liu, H.; Jiang, Y.; Hu, J. Multiple fault diagnosis of PMSM based on stator tooth flux and parallel residual convolutional neural network. IEEE Trans. Transp. Electrif. 2024, 10, 9727–9738. [Google Scholar] [CrossRef]
- Zhu, J.; Ouyang, X.; Jiang, Z.; Xu, Y.; Xue, H.; Yue, H.; Feng, H. In-wheel motor fault diagnosis method based on two-stream 2DCNNs with DCBA module. Sensors 2025, 25, 4617. [Google Scholar] [CrossRef]
- Song, Q.; Wang, M.; Lai, W.; Zhao, S. On bayesian optimization-based residual CNN for estimation of inter-turn short circuit fault in PMSM. IEEE Trans. Power Electron. 2023, 38, 2456–2468. [Google Scholar] [CrossRef]
- Wei, L.; Yang, H.; Niu, Y.; Zhang, Y.; Xu, L.; Chai, X. Wheat biomass, yield, and straw-grain ratio estimation from multi-temporal UAV-based RGB and multispectral images. Biosyst. Eng. 2023, 234, 187–205. [Google Scholar] [CrossRef]
- Rehman, M.M.U.; Liu, J.; Nijabat, A.; Faheem, M.; Wang, W.; Zhao, S. Leveraging convolutional neural networks for disease detection in vegetables: A comprehensive review. Agronomy 2024, 14, 2231. [Google Scholar] [CrossRef]
- Lale, T.; Yueksek, G. Identification and classification of turn short-circuit and demagnetization failures in PMSM using LSTM and GRU methods. Bull. Pol. Acad. Sci. Tech. Sci. 2025, 73, e151958. [Google Scholar] [CrossRef]
- Taha, M.F.; Mao, H.; Mousa, S.; Zhou, L.; Wang, Y.; Elmasry, G.; Al-Rejaie, S.; Elwakeel, A.E.; Wei, Y.; Qiu, Z. Deep learning-enabled dynamic model for nutrient status detection of aquaponically grown plants. Agronomy 2024, 14, 2290. [Google Scholar] [CrossRef]
- Shifat, T.A.; Jang-Wook, H. Remaining useful life estimation of BLDC motor considering voltage degradation and attention-based neural network. IEEE Access 2020, 8, 168414–168428. [Google Scholar] [CrossRef]
- Seker, S.; Ayaz, E.; Türkcan, E. Elman’s recurrent neural network applications to condition monitoring in nuclear power plant and rotating machinery. Eng. Appl. Artif. Intell. 2003, 16, 647–656. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, W.; Steibel, J.; Siegford, J.; Han, J.; Norton, T. Classification of drinking and drinker-playing in pigs by a video-based deep learning method. Biosyst. Eng. 2020, 196, 1–14. [Google Scholar] [CrossRef]
- Tang, M.; Liang, L.; Zheng, H.; Chen, J.; Chen, D. Anomaly detection of permanent magnet synchronous motor based on improved DWT-CNN multi-current fusion. Sensors 2024, 24, 2553. [Google Scholar] [CrossRef] [PubMed]
- Ertargin, M.; Yildirim, O.; Orhan, A. Mechanical and electrical faults detection in induction motor across multiple sensors with CNN-LSTM deep learning model. Electr. Eng. 2024, 106, 6941–6951. [Google Scholar] [CrossRef]
- Qi, L.; Zhang, Q.; Xie, Y.; Zhang, J.; Ke, J. Research on wind turbine fault detection based on CNN-LSTM. Energies 2024, 17, 4497. [Google Scholar] [CrossRef]
- Eang, C.; Lee, S. Predictive maintenance and fault detection for motor drive control systems in industrial robots using CNN-RNN-based observers. Sensors 2025, 25, 25. [Google Scholar] [CrossRef]
- Encalada-Davila, A.; Moyon, L.; Tutiven, C.; Puruncajas, B.; Vidal, Y. Early fault detection in the main bearing of wind turbines based on gated recurrent unit (GRU) neural networks and SCADA data. IEEE-ASME Trans. Mechatron. 2022, 27, 5583–5593. [Google Scholar] [CrossRef]
- Kong, Z.; Tang, B.; Deng, L.; Liu, W.; Han, Y. Condition monitoring of wind turbines based on spatio-temporal fusion of SCADA data by convolutional neural networks and gated recurrent units. Renew. Energy 2020, 146, 760–768. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Zhu, J.; Xu, F. Fault diagnosis of motor vibration signals by fusion of spatiotemporal features. Machines 2022, 10, 246. [Google Scholar] [CrossRef]
- Ji, W.; Pan, Y.; Xu, B.; Wang, J. A real-time apple targets detection method for picking robot based on shufflenetV2-YOLOX. Agriculture 2022, 12, 856. [Google Scholar] [CrossRef]
- Tao, K.; Wang, A.; Shen, Y.; Lu, Z.; Peng, F.; Wei, X. Peach flower density detection based on an improved CNN incorporating attention mechanism and multi-scale feature fusion. Horticulturae 2022, 8, 904. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, Y.; Fan, W.; Liu, J. An improved YOLOv8 model for lotus seedpod instance segmentation in the lotus pond environment. Agronomy 2024, 14, 1325. [Google Scholar] [CrossRef]
- Zhao, S.; Peng, Y.; Liu, J.; Wu, S. Tomato leaf disease diagnosis based on improved convolution neural network by attention module. Agriculture 2021, 11, 651. [Google Scholar] [CrossRef]
- Chen, X.; Hassan, M.; Yu, J.; Zhu, A.; Han, Z.; He, P.; Chen, Q.; Li, H.; Ouyang, Q. Time series prediction of insect pests in tea gardens. J. Sci. Food Agric. 2024, 104, 5614–5624. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Peng, D.; Zuo, M.J. Interpretable convolutional neural network with multilayer wavelet for noise-robust machinery fault diagnosis. Mech. Syst. Signal Proc. 2023, 195, 110314. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, L.; Wang, M.; Wei, L.; Li, M. Adaptive sparse attention wavelet network for the robust open-circuit fault diagnosis in PMSM drives. IEEE Trans. Instrum. Meas. 2024, 73, 3514611. [Google Scholar] [CrossRef]
- Cheng, J.; Sun, J.; Shi, L.; Dai, C. An effective method fusing electronic nose and fluorescence hyperspectral imaging for the detection of pork freshness. Food Biosci. 2024, 59, 103880. [Google Scholar] [CrossRef]
- Wang, M.; Lai, W.; Sun, P.; Li, H.; Song, Q. Severity estimation of inter-turn short-circuit fault in PMSM for agricultural machinery using Bayesian optimization and enhanced convolutional neural network architecture. Agriculture 2024, 14, 2214. [Google Scholar] [CrossRef]
- Qin, S.; Tao, J.; Zhao, Z. Fault diagnosis of wind turbine pitch system based on LSTM with multi-channel attention mechanism. Energy Rep. 2023, 10, 4087–4096. [Google Scholar] [CrossRef]
- He, Q.; Li, S.; Bai, Q.; Zhang, A.; Yang, J.; Shen, M. A Siamese vision transformer for bearings fault diagnosis. Micromachines 2022, 13, 1656. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Sun, J.; Wang, S.; Shen, J.; Yang, K.; Zhou, X. Identifying field crop diseases using transformer-embedded convolutional neural network. Agriculture 2022, 12, 1083. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, M.; Qiu, L.; Wang, L.; Yu, Y. An arrhythmia classification model based on vision transformer with deformable attention. Micromachines 2023, 14, 1155. [Google Scholar] [CrossRef] [PubMed]
- Xie, F.; Guo, Z.; Li, T.; Feng, Q.; Zhao, C. Dynamic task planning for multi-arm harvesting robots under multiple constraints using deep reinforcement learning. Horticulturae 2025, 11, 88. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, X.; Cai, N.; Zhou, S.; Wang, H. IC packaging material identification via a hybrid deep learning framework with CNN–transformer bidirectional interaction. Micromachines 2024, 15, 418. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, B. Comparative study of popular deep learning models for machining roughness classification using sound and force signals. Micromachines 2021, 12, 1484. [Google Scholar] [CrossRef]
- He, S.; Yu, M.; Chen, Y.; Zhou, Z.; Yu, L.; Zhang, C.; Ni, Y. Prediction of IGBT gate oxide layer’s performance degradation based on MultiScaleFormer network. Micromachines 2024, 15, 985. [Google Scholar] [CrossRef]
- Ji, W.; Zhai, K.; Xu, B.; Wu, J. Green apple detection method based on multidimensional feature extraction network model and transformer module. J. Food Prot. 2025, 88, 100397. [Google Scholar] [CrossRef]
- Parvin, F.; Faiz, J.; Qi, Y.; Kalhor, A.; Akin, B. A comprehensive interturn fault severity diagnosis method for permanent magnet synchronous motors based on transformer neural networks. IEEE Trans. Ind. Inform. 2023, 19, 10923–10933. [Google Scholar] [CrossRef]
- Lang, W.; Hu, Y.; Zhang, Z.; Gan, C.; Si, J.; Wen, H. Few-shot learning with residual current for EV inverter fault diagnosis of EV powertrain. IEEE Trans. Transp. Electrif. 2024, 10, 9316–9327. [Google Scholar] [CrossRef]
- Li, M.; Geng, Y.; Wang, W.; Tu, M.; Wu, X. Permanent magnet synchronous motor inter-turn short circuit diagnosis based on physical-data dual model under oil-drilling environment. Eng. Appl. Artif. Intell. 2024, 132, 107938. [Google Scholar] [CrossRef]
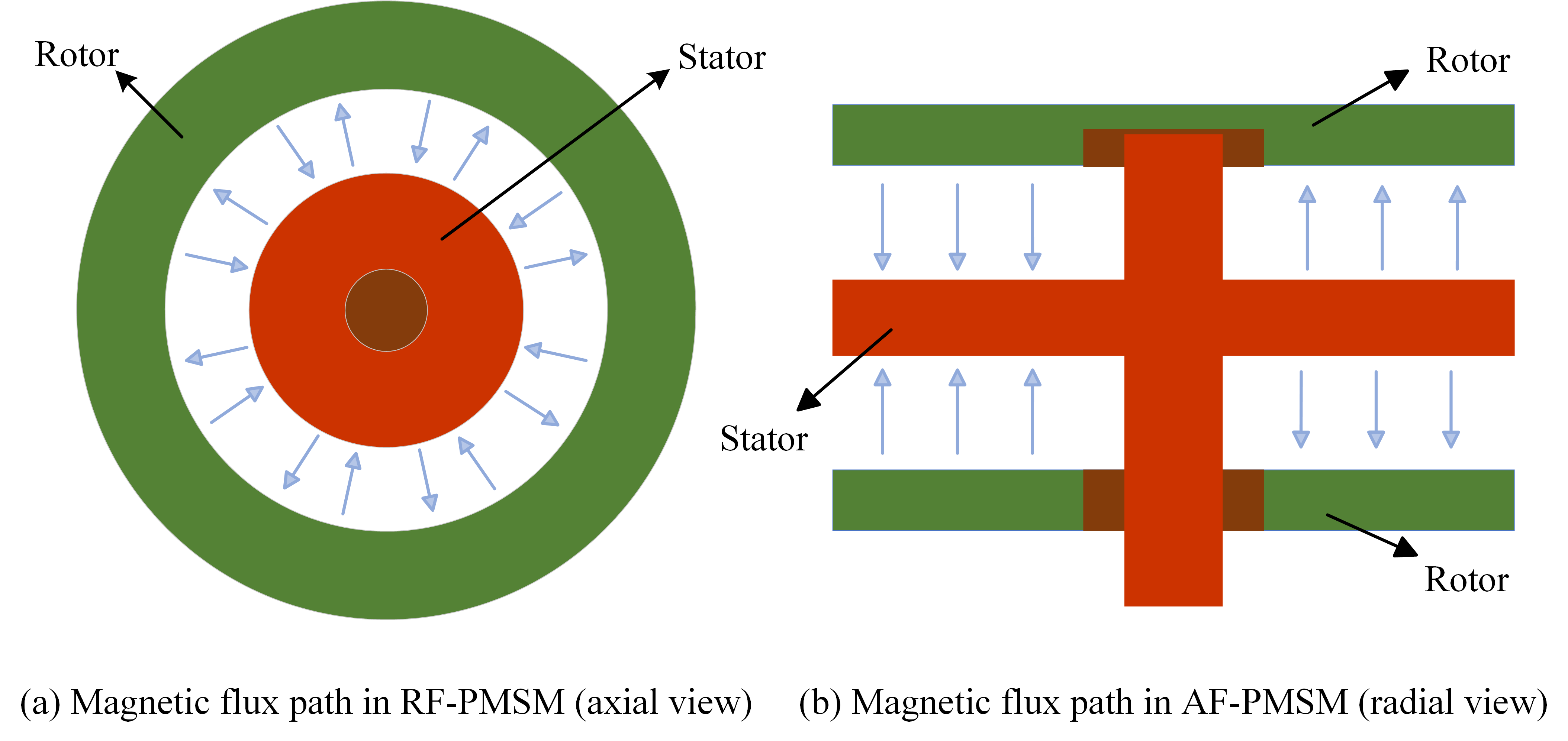
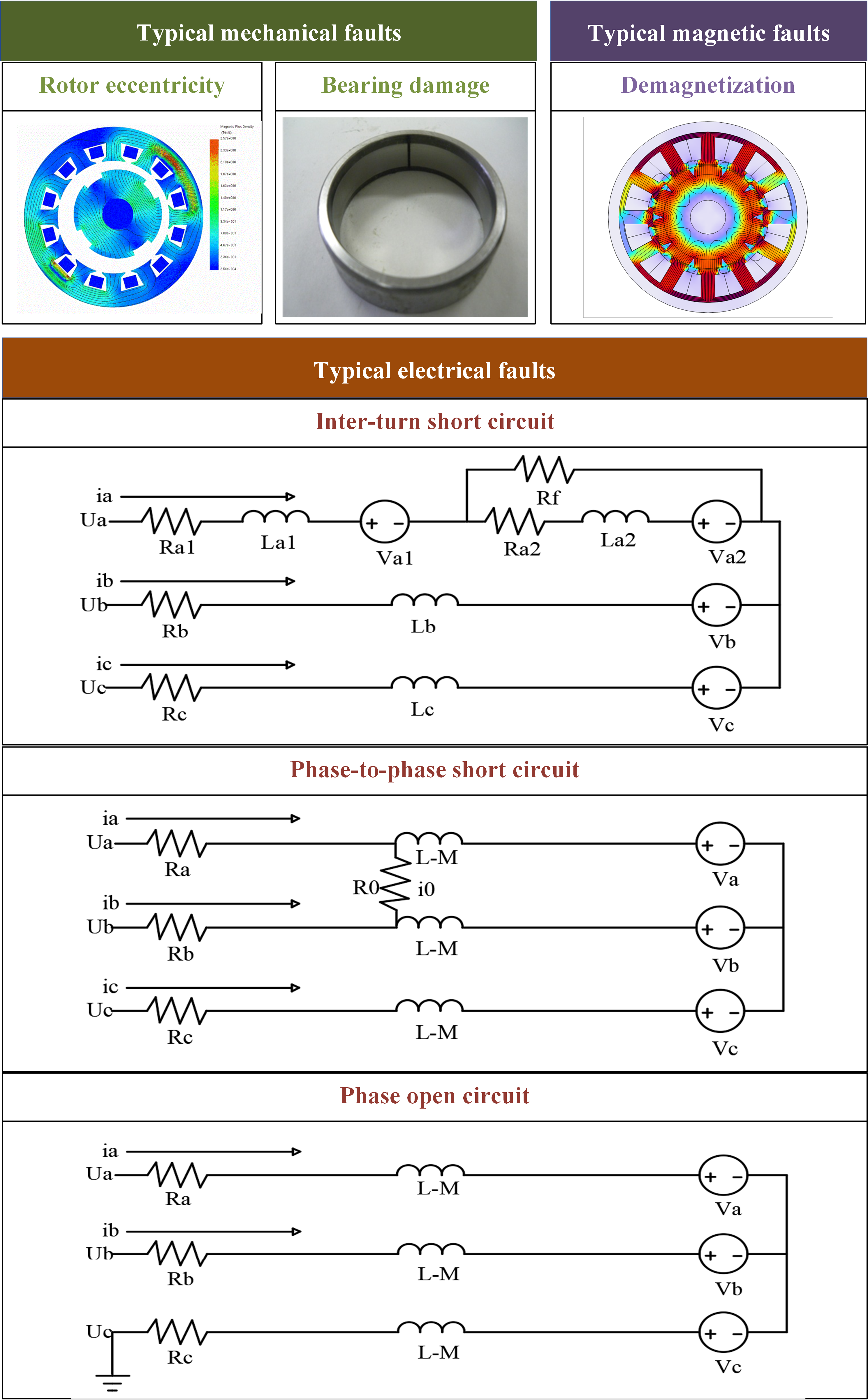




| Fault Types | Similar Faults | AF-PMSM Specific Manifestation |
|---|---|---|
| Mechanical | Bearing faults, rotor eccentricity, mechanical deformation | Axial deflection caused by disk-shaped structure; more prone to axial vibration and end-face deformation |
| Electrical | Inter-turn short circuit, phase-to-phase short circuit, open-circuit fault | End-windings more susceptible to fatigue damage and insulation degradation, due to planar winding layout |
| Magnetic | Demagnetization | Uneven temperature distribution may lead to local demagnetization due to insufficient heat dissipation |
| Method Category | Definition | Advantages | Disadvantages |
|---|---|---|---|
| Model-based | Establishes mathematical or physical models of the system to detect faults via residuals or state deviations |
|
|
| Signal-based | Extracts fault features from measured signals using time-domain, frequency-domain, time–frequency, or decomposition methods |
|
|
| Knowledge-based | Uses machine learning or deep learning to build data-driven models that learn fault patterns from data |
|
|
| Model Type | Fundamental Formula | Variable Description |
|---|---|---|
| Voltage (d–q frame) | ud/q: stator voltage, id/q: stator current, ψd/q: flux linkage, Rs: stator resistance, ωe: electrical angular speed | |
| Flux linkage model | Ld/q: inductance, ψd/q: permanent magnet flux linkage | |
| Electromagnetic torque | Te: electromagnetic torque, p: number of pole pairs | |
| Mechanical model | J: inertia, B: damping coefficient, ωm: mechanical speed, TL: load torque | |
| Thermal model | T: winding temperature, Tamb: ambient temperature, Cth: thermal capacitance, Rth: thermal resistance, Ploss: power loss | |
| Longitudinal vehicle dynamics | vx: longitudinal velocity, Fx: traction force, Fr/Fa/Fg: rolling/air/slope resistance force | |
| Lateral vehicle dynamics (2 DoF) | vy: lateral velocity, r: yaw rate, Fyf/ Fyr: lateral tire forces, a, b: CG distances, Iz: yaw moment of inertia | |
| Inverter switching model | Vdc: DC link voltage, si: switching state (0 or 1) | |
| FOC control | i*d/q: current references, u*d/q: voltage references, ω/ω*: actual and reference rotor speeds, Kpi/Kii: proportional and integral gains of the current loop, Kpv/Kiv: proportional and integral gains of the speed loop |
| Signal Type | Fault Types | Characteristic Frequencies | Note |
|---|---|---|---|
| Current | Inter-turn short circuit | Unbalanced currents cause high-order harmonics, with a significant third harmonic. | |
| Rotor eccentricity | Uneven air gap affects magnetomotive force (MMF) and modulates base frequency. | ||
| Demagnetization | Permanent magnet demagnetization leads to MMF distortion, with prominent low-frequency modulation. | ||
| Vibration | Magnetic field asymmetry | UMP causes abnormal harmonic components in addition to the normal stator vibration frequency of 2f0. | |
| Bearing fault | Characteristic bearing frequencies depend on structure-related parameters. |
| Category | Representative Models | Key Characteristics |
|---|---|---|
| Representation Learning Models | AE, DBN, CNN |
|
| Temporal Dynamic Networks | RNN, LSTM, GRU |
|
| Attention-Enhanced Models | Attention + CNN/LSTM, Transformer |
|
| Method Type | Accuracy | Response Speed | Interpretability | Deployment Cost | Data Requirement | Suitable Scenarios |
|---|---|---|---|---|---|---|
| Model-based | Medium | Medium | High | Medium–High | Low | Fault localization, embedded systems, data-scarce environments |
| Signal-based | Medium | High | Medium | Low | Low–Medium | Rapid fault detection without modeling, moderate noise conditions |
| Traditional ML | High | High | Low–Medium | Medium | Medium | Stable conditions with partial labels, limited deployment cost |
| Deep Learning | Very High | Medium | Low | High | High | Complex patterns, large-scale data, multi-condition recognition |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Wang, X.; Zhang, L.; Bao, X.; Xue, H.; Yue, H.; Feng, H.; Yang, D. Fault Diagnosis of In-Wheel Motors Used in Electric Vehicles: State of the Art, Challenges, and Future Directions. Machines 2025, 13, 711. https://doi.org/10.3390/machines13080711
Tao Y, Wang X, Zhang L, Bao X, Xue H, Yue H, Feng H, Yang D. Fault Diagnosis of In-Wheel Motors Used in Electric Vehicles: State of the Art, Challenges, and Future Directions. Machines. 2025; 13(8):711. https://doi.org/10.3390/machines13080711
Chicago/Turabian StyleTao, Yukun, Xuan Wang, Liang Zhang, Xiaoyi Bao, Hongtao Xue, Huiyu Yue, Huayuan Feng, and Dongpo Yang. 2025. "Fault Diagnosis of In-Wheel Motors Used in Electric Vehicles: State of the Art, Challenges, and Future Directions" Machines 13, no. 8: 711. https://doi.org/10.3390/machines13080711
APA StyleTao, Y., Wang, X., Zhang, L., Bao, X., Xue, H., Yue, H., Feng, H., & Yang, D. (2025). Fault Diagnosis of In-Wheel Motors Used in Electric Vehicles: State of the Art, Challenges, and Future Directions. Machines, 13(8), 711. https://doi.org/10.3390/machines13080711






