Abstract
High-precision measurement of water turbine flow is critical for ensuring the stable operation of hydropower stations and enhancing power generation efficiency. Ultrasonic transit-time flow meters, owing to their non-intrusive measurement capability and robust environmental adaptability, have gained widespread application in flow monitoring within hydropower settings. However, under complex operating conditions, their measurement accuracy remains susceptible to constraints imposed by installation environments, construction quality, and intrinsic device performance limitations. This review systematically examines the fundamental principles, system architecture, and typical classifications of ultrasonic transit-time flow meters for flow measurement. It critically evaluates key techniques for field deployment and methodologies for the accurate acquisition of geometric parameters. A primary focus lies in synthesizing and categorizing the principal sources of error affecting measurement accuracy, alongside an analysis of their underlying causes. Building upon this analysis, the review explores and summarizes current key technological pathways and engineering solutions aimed at enhancing ultrasonic transit-time flow meters’ measurement precision. Furthermore, it critically assesses the associated application challenges and emerging development trends (exploration of cutting-edge directions). Collectively, this work offers comprehensive theoretical reference and technical guidance to support the high-reliability application and optimized design of ultrasonic transit-time flow meters within the complex environments characteristic of hydropower stations.
1. Introduction
Hydropower, as the pillar of low-carbon electricity, plays a pivotal role in the global power structure, accounting for approximately 15% of the world’s total power generation [1]. At this stage, the precise quantification of the hydropower conversion efficiency in hydropower stations has become the foundation for optimizing their operation. The core prerequisite to achieve this goal is the high-precision measurement of the water energy utilization efficiency in hydropower stations.
The efficiency of hydro energy utilization in power stations is determined by turbine performance, whose evaluation requires accurate flow measurement. Among the dozen established measurement techniques—including current-meter, thermodynamic, and ultrasonic methods—the current-meter method demonstrates the highest prevalence in China due to its well-established methodology [2]. This method is based on the rotational response of a velocity probe influenced by water flow, where the relationship between the blade’s rotational speed and flow velocity forms a calibration function, enabling quantitative flow measurement. Its strengths include a well-established methodology with high accuracy (±1.2–1.5%) under ideal conditions. Its limitations include the need to shut down the pipeline and work under dry conditions; sensitivity to water quality (e.g., particulate matter); and unsuitability for continuous monitoring. The pressure–time method, also widely applied, is grounded in Newton’s second law and fundamental fluid dynamics equations [3]. It measures the pressure difference between two points in a pipeline over a defined time interval and utilizes pipeline geometry to calculate the fluid’s average velocity and volumetric flow rate. Its strengths include robustness for medium- and high-head stations (with a ±1.5% error). Limitations include inapplicability to low-head stations; non-continuous operation; and accuracy that hinges on pipeline geometry. The thermodynamic method, initially proposed by Cattaert [4], proposed the principle of energy conservation applying Bernoulli’s equation to analyze energy exchange between the water and the turbine. It integrates the thermodynamic properties of water and parameters including pressure, temperature, flow velocity, and water level to infer turbine efficiency [5,6]. Its strengths include indirectly inferring efficiency through energy conservation (with an error of ±0.7–1.8%) and effectiveness for high-head units (≥100 m). Its limitations include complex installation; the requirement for pre-reserved measurement points during the design phase; and high dependence on temperature. The Winter–Kennedy method (also referred to as the volute pressure difference method or W–K method) is a pragmatic technique [7]. It employs differential pressure sensors at two points on the volute and, through a pre-established calibration curve, converts the measured differential pressure into a relative flow value. Its strengths include simple real-time monitoring (with a ±0.5–1.0% error). Limitations include the need for external calibration and inability to operate independently. The ultrasonic method is a non-invasive technique based on the propagation characteristics of acoustic waves. Among various ultrasonic techniques, the time-of-flight (TOF) method measures upstream/downstream acoustic wave transit-time differences to calculate flow velocity, enabling flow rate quantification. Its strengths include being non-intrusive, having no upper velocity limit, adaptability to large diameters and high flows, and enabling real-time monitoring with minimal pressure loss. Limitations include accuracy (±2.0%), being highly sensitive to installation conditions (e.g., straight pipe length, transducer alignment) and flow field distortions. During efficiency testing, turbine efficiency can be derived through integration of generator active power and turbine net head and other parameters [8,9]. Table 1 summarizes and compares the applicability ranges, primary instrumentation, and measurement accuracy of the aforementioned flow measurement methods.

Table 1.
Comparison of several flow measurement methods.
Although ultrasonic flow meters have been widely adopted in hydropower stations due to advantages such as simplified installation, minimal pressure loss, and broad applicability across pipe diameters, their measurement accuracy is highly sensitive to installation conditions, specifically insufficient upstream/downstream straight pipe lengths—frequently overlooked during design/construction phases. Moreover, uncontrolled on-site construction quality frequently causes sensor misalignment, flow profile distortion, and increased system uncertainty. GB/T 20043-2005 [11] requires total system uncertainty ≤ |2.0%|, yet operational deviations frequently exceed this threshold. To address these issues, researchers have systematically analyzed various sources of error—such as acoustic path deviation, installation inaccuracies, flow field distortion, and signal processing precision—and have proposed several optimization strategies aimed at improving measurement accuracy and environmental adaptability, thereby enhancing the reliability of ultrasonic flow meters under complex hydraulic conditions [12].
Extensive technological evolution has established robust ultrasonic flow measurement principles and diversified techniques [13]. The transit-time method calculates flow velocity from differences in the downstream and upstream directions. This technique is well-suited for clean liquids and offers high accuracy, good repeatability, and strong adaptability for large-diameter pipelines, making it the most widely used method in hydropower stations today [14]. The Doppler method utilizes the frequency shift of sound waves scattered by particles or bubbles in the fluid. Though applicable to contaminated fluids, accuracy diminishes with particle distribution/concentration variations, limiting primary use to wastewater/industrial flows [15]. The cross-correlation method estimates flow velocity by analyzing the time delay of disturbance signals detected at different receiving points. It requires advanced signal processing capabilities and is mainly applied in research and low-speed flow scenarios [16]. The beam deflection method derives velocity from flow-induced acoustic path deflection. Despite theoretical precision, system complexity confines it largely to experimental research [12].
In summary, different ultrasonic flow measurement methods are applicable to various fluid conditions. Among them, the transit-time method is increasingly becoming the mainstream approach in hydropower applications due to its overall superior performance. Therefore, this review aims to provide a systematic analysis of ultrasonic transit-time flow measurement technology in hydraulic and hydroelectric applications, with a focus on overcoming accuracy limitations under complex operating conditions. The specific objectives are
- (1)
- To comprehensively review the fundamental principles, system architectures, and classifications of ultrasonic transit-time flow meters, highlighting their engineering adaptability in hydropower settings;
- (2)
- To critically analyze the dominant sources of measurement errors (e.g., geometric parameter deviations, transducer-induced flow disturbances, and flow-field distortions) and their coupling mechanisms;
- (3)
- To synthesize and evaluate emerging technological pathways for enhancing accuracy, including hardware innovations (e.g., transducer design), CFD-driven flow-field optimization, and multi-method collaborative calibration;
- (4)
- To identify challenges (e.g., non-axisymmetric flows, calibration–field discrepancies) and outline future research directions for high-reliability applications in large-scale hydropower systems.
These objectives establish a framework for assessing the state of the art and guiding advancements in ultrasonic flow measurement for sustainable hydropower operation.
2. Ultrasonic Transit-Time Flow Measurement Technology
This section systematically analyzes the core components of ultrasonic transit-time flow measurement technology, given the non-intrusive measurement advantages of ultrasonic methods under complex working conditions. The technical principles and equipment selection serve as critical support for achieving high-precision flow measurement.
First, Section 2.1 shows the review methodology. Section 2.2 elucidates the acoustic measurement principles and mathematical models of the transit-time method. Then, Section 2.3 categorically discusses the engineering adaptability of transducer structures, channel configurations, and installation forms. Finally, Section 2.4–2.6 focus on precise acquisition methods for geometric parameters in field deployment, laying a theoretical foundation for subsequent error analysis and accuracy optimization.
2.1. Review Methodology
To ensure a systematic and transparent analysis of error sources and optimization strategies for ultrasonic transit-time flow measurement in hydraulic and hydroelectric applications, a structured literature review methodology was employed.
- (1)
- Literature Search: Comprehensive searches were conducted across major scientific databases, including ScienceDirect (Elsevier), SpringerLink and CNKI Data. Key search terms and their combinations encompassed “ultrasonic flow meter”, “transit-time method”, “time-of-flight”, “flow measurement error”, “measurement accuracy”, “uncertainty”, “hydropower”, “hydroelectric”, “water turbine”, “penstock”, “flow disturbance”, “installation effect”, “geometric parameter”, “error source”, “accuracy improvement”, “optimization”, “CFD”, and “multi-method calibration”, along with their Chinese equivalents. The search focused primarily on literature published from 2000 onwards to capture recent advancements, while seminal earlier works were also considered. Relevant international and national standards (e.g., IEC, GB/T) and proceedings of key conferences in fluid mechanics and hydropower engineering were also reviewed. Backward snowballing (tracking references from retrieved articles) was utilized to identify additional pertinent studies.
- (2)
- Study Selection: Inclusion criteria required studies to ① explicitly focus on ultrasonic transit-time flow measurement technology; ② investigate sources of measurement error, their mechanisms, influencing factors, and/or strategies/technologies for improving measurement accuracy; ③ be applicable or relevant to the context of hydropower/hydraulic engineering (large diameters, specific flow conditions); ④ comprise peer-reviewed journal articles, conference papers, dissertations, technical reports from reputable institutions, or standards. Studies primarily dealing with other flow meter types (e.g., electromagnetic, Doppler ultrasonic) or lacking substantive details on error analysis or optimization methods were excluded.
- (3)
- Data Extraction and Synthesis: Information pertaining to identified error sources (type, magnitude, causes), proposed optimization strategies (hardware, software, installation, calibration), experimental/simulation conditions, and main findings was extracted from the selected literature. Thematic analysis was used to identify, categorize, and synthesize recurring themes and patterns related to error mechanisms and accuracy enhancement approaches.
2.2. Ultrasonic Transit-Time Flow Measurement Devices
Transit-time ultrasonic flow meters primarily consist of three components: ultrasonic transducers, electronic signal processing units, and flow rate display/accumulation systems. The ultrasonic transducers emit sound waves under electrical excitation and convert received ultrasonic signals back into electrical signals. The electronic unit processes acoustic wave transit-time differences to calculate fluid velocity and volumetric flow rate. Based on the number and configuration of acoustic paths formed by transducer placement within the flow channel, transit-time ultrasonic flow meters are classified into single-path and multi-path types:
- (1)
- Single-path ultrasonic flow meters: Tang et al. [17] pioneered a flow measurement scheme employing a pair of transducers to form a single acoustic path, establishing the foundation for ultrasonic flow measurement technology. This simple design suits stable flow conditions and is well-suited for relatively stable flow conditions. Subsequently, Irving [18] introduced a flow velocity detection method based on ultrasonic phase shift, further expanding the principles of ultrasonic flow measurement. As the field advanced, the United States successfully developed the world’s first commercial ultrasonic flow meter, “MAXSON”, which implemented the “sing-around” technique in aviation fuel measurement, initiating ultrasonic engineering applications [19].
- (2)
- Multi-path ultrasonic flow meters: In 1963, Schima et al. [20] developed an ultrasonic flow meter featuring a symmetric dual-path configuration, which significantly reduced velocity-profile-induced errors. This milestone established multi-path technology’s origin. With the evolution of microprocessors and digital signal processors, multi-path configurations have progressed toward higher precision and intelligent functionality. In recent years, to address challenges such as non-axisymmetric flow fields and large-diameter pipelines, researchers have continually optimized acoustic path layouts, transducer materials, and structural designs, thereby improving the robustness and adaptability of multi-path ultrasonic flow meters [21].
According to the transducer installation position and method within the flow channel, transit-time ultrasonic flow meters can be further categorized into clamp-on, surface-mounted, insertion, and portable types [10]. The clamp-on type—also known as external or strap-on—uses coupling agents to attach transducers to the outer surface of the pipeline, allowing for non-invasive installation without interrupting the flow. This configuration is easy to install, does not damage the pipeline, and facilitates convenient maintenance [22]. In contrast, surface-mounted ultrasonic flow meters require installation during pipeline construction, typically via welding or bolting the transducers to the inner wall. This type demands a high degree of surface smoothness, involves complex installation procedures, and necessitates periodic replacement due to sensor exposure to corrosion and fluid-induced wear [23]. Insertion-type ultrasonic flow meters involve drilling into the pipe to insert transducer probes directly into the flow channel using specialized tools. These are suitable for conditions involving severe internal scaling or when deep penetration into the flow medium is required. However, they pose risks of pipeline damage and are vulnerable to clogging or contamination, which can lead to measurement deviations [24]. Portable ultrasonic flow meters are designed for mobile use and are commonly employed for flow calibration and temporary measurements. They offer high adaptability and rapid deployment, making them particularly valuable for on-site verification and online calibration of flow meters in hydropower stations [25].
In practical applications within hydropower stations, multi-path configurations have gradually become mainstream due to their superior accuracy and anti-interference capabilities under complex flow conditions. Clamp-on and portable types are also widely used for flow monitoring and equipment calibration in large-diameter, low-velocity pipelines due to their minimal impact on system operation and high flexibility. Looking ahead, with the continuous development of intelligent control systems and digital signal processing technologies, transit-time ultrasonic flow meters are expected to evolve toward configurations characterized by “multi-path + high precision + modularization” [26].
2.3. Principle of Ultrasonic Transit-Time Flow Measurement
Figure 1 illustrates the fundamental working principle of the transit-time ultrasonic flow meter. This method is based on the principle that the propagation speed of ultrasonic waves in a fluid differs depending on the flow direction. When the ultrasonic wave propagates in the same direction as the fluid flow (downstream), its velocity increases and the travel time decreases. Conversely, when propagating against the flow direction (upstream), the wave slows down, resulting in a longer travel time. By measuring the time difference between upstream and downstream propagation, the fluid velocity can be accurately determined [27].
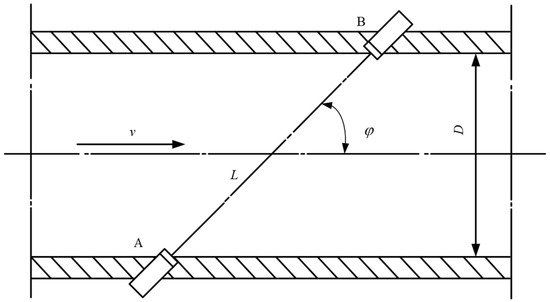
Figure 1.
Flow measurement principle of transit-time ultrasonic flow meter.
To further explain this principle, the mathematical expressions for the ultrasonic wave propagation time in the downstream and upstream directions (Note: ‘Upstream/downstream’ herein refers to acoustic wave direction relative to flow, not physical pipe segments) are given as follows:
The upstream transit time is
The downstream transit time is
In the equations, L is the length of the acoustic path, D is the diameter of the pipe, c is the speed of sound in a stationary fluid, φ is the angle between the acoustic path and the pipe axis, v is the average axial velocity of the fluid to be measured, and tdown and tup are the propagation times in the downstream and upstream directions, respectively. From the above two equations, the expression for the axial flow velocity of the fluid can be derived:
For a multi-channel ultrasonic flow meter, the flow measurement principle involves arranging several acoustic paths in parallel at different heights (i.e., positions relative to the center of the flow channel) within the flow path. The axial flow velocity vi (i = 1, 2, …, n) measured by each acoustic path represents the average flow velocity over a certain area in that region. By combining the axial flow velocity values from multiple acoustic paths, a more accurate estimate of the overall average flow velocity of the flow path can be made, which can then be used to calculate the flow rate. The calculation formula is
In the equation, Q is the volumetric flow rate; A is the cross-sectional area of the flow path, which is related to the pipe diameter D; n is the number of acoustic paths; ai is the weighting factor corresponding to the i-th acoustic path, and its precise form depends on the specific arrangement of the acoustic paths and the numerical integration method used.
2.4. On-Site Installation
For flow meter selection, single-channel or crossed dual-channel ultrasonic flow meters are typically employed for small- to medium-sized pipelines or channels where extremely high measurement accuracy is not required. In contrast, multi-path ultrasonic flow meters are preferred for large-diameter pipelines or flow fields with complex velocity distributions. In hydropower plants, when measuring flow through turbines, multi-path ultrasonic flow meters are generally adopted, usually configured with at least four acoustic paths. Zhang et al. [27] recommend that for ultrasonic flow meters installed in intake tunnels and buried sections of pressure steel pipelines, internally mounted types should be prioritized. For flow meters installed in exposed sections of pressure steel pipelines, either insertion-type or internally mounted configurations are considered appropriate. In hydropower plants, the pressure pipes upstream of turbine volutes are typically of large diameter. When ultrasonic flow meters are installed in such pressure pipes, internally mounted flow meters are usually preferred in buried sections (i.e., non-exposed flow paths), with the transducers and cable clamps welded directly to the inner pipe wall. In exposed sections, the selection between insertion-type and internally mounted flow meters should be based on factors such as pipe diameter, accuracy requirements, and installation conditions [28]. In general, internally mounted ultrasonic flow meters are suitable for pipes with diameters greater than or equal to 1.6 m, whereas insertion-type flow meters are typically recommended for pipes with diameters above 0.8 m.
Due to the susceptibility of ultrasonic waves to interference from factors such as air bubbles and turbulence during propagation, local resistance elements—such as elbows, reducers, valves, and throttling devices—can cause pressure drops. This often leads to gas separation within the flow, resulting in attenuation of the ultrasonic signal and increased noise, which in turn degrades the accuracy of flow measurement [29,30]. Therefore, the installation location of the flow meter plays a critical role in ensuring measurement accuracy. To obtain stable and reliable readings, transducers should be placed in undisturbed flow regions—in areas where the velocity distribution is relatively uniform, the pressure is stable, and installation conditions are favorable. Additionally, it is important to avoid installing transducers at weld seams or on irregular pipe sections to minimize the impact of flow anomalies on acoustic signal propagation. Different installation positions impose specific requirements on the flow meter [10]:
- External clamp-on ultrasonic flow meters require a certain length of exposed pipe and support pipe diameters up to 6 m. These devices typically employ two crossed acoustic paths, allowing measurement only at the central layer of the pipe, resulting in lower accuracy. Under ideal flow conditions, measurement errors can be within 1%; however, in disturbed flow, errors may exceed 2%.
- External insertion-type ultrasonic flow meters also require an exposed pipe section and involve drilling a hole into the pipe wall. They are unsuitable for high-pressure applications (e.g., above 2 MPa).
- Internally mounted ultrasonic flow meters do not require exposed pipe segments and are capable of operating under relatively high pressure (up to 4 MPa or more). These are typically used in large-scale hydropower facilities.
2.5. Transducer Layout
Ultrasonic flow meters typically employ three transducer configurations based on installation geometry—the Z-method, V-method, and W-method—as illustrated in Figure 2. In Figure 2a, the Z-method places two transducers on opposite horizontal sides of the pipeline, with their centerline aligned parallel to the pipeline axis. The ultrasonic signal travels directly across the pipe without reflection, thereby minimizing signal loss. This configuration is particularly suitable for large-diameter pipelines or those with smooth internal surfaces. Figure 2b,c show the V-method and W-method, respectively. These configurations extend the acoustic path length by introducing one and three reflections, causing the ultrasonic signal to traverse the fluid twice and four times, respectively. While these methods enhance measurement accuracy by reducing cross-flow interference, the additional reflections lead to greater signal attenuation, making them more appropriate for medium- and small-diameter pipelines.
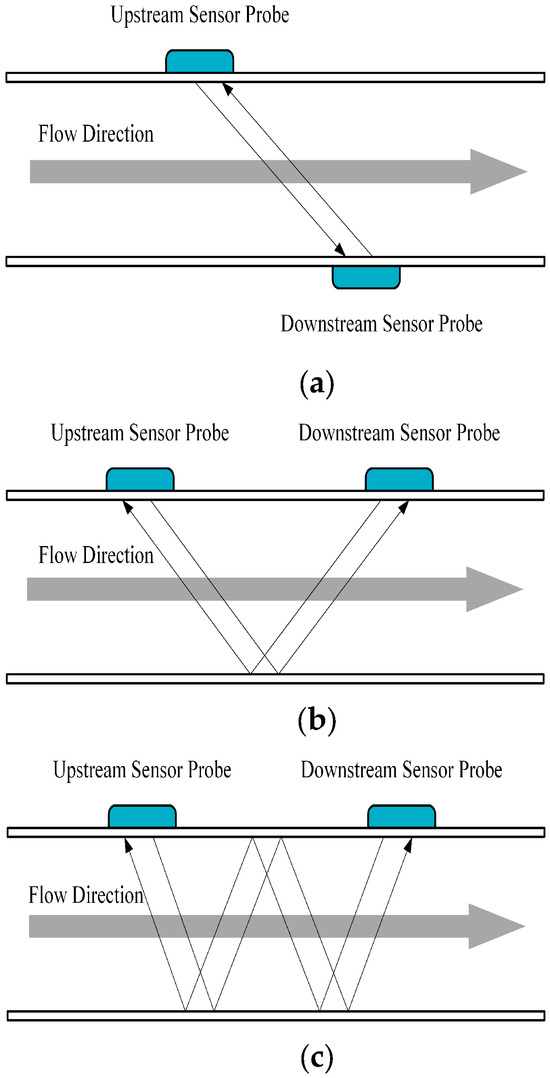
Figure 2.
Schematic diagram of common installation methods for flow meters. (a) Z-Method. (b) V-Method. (c) W-Method.
As noted in [31], under complex conditions—such as large-diameter pipelines, fluid containing suspended particles, or pipes with heavily scaled pipes or thick-lined pipes—the V-method may malfunction due to insufficient signal strength. In such cases, the Z-method is preferred to ensure measurement reliability. Li et al. [32] conducted comparison tests between standard flow meters and portable ultrasonic flow meters on large-diameter calibration platforms with various pipe sizes (DN150, DN250, DN400). The results showed that when the pipe diameter does not exceed DN150, the V-method yields good consistency and accuracy, with minimal relative error between the portable and standard flow meters. However, each reflection introduces signal attenuation; therefore, the number of reflections should be carefully limited. The V-method and W-method are particularly effective for pipes with diameters below 50 mm, where they significantly enhance accuracy. However, the W-method requires the ultrasonic beam’s reflection path inside the pipe to remain stable and reliable, which places higher demands for pipeline alignment and transducer fixation [33].
2.6. Geometric Parameter Measurement
As a critical technique for flow measurement in hydropower stations, the accuracy of ultrasonic transit-time flow metering is highly dependent on the precision of pipeline geometry and the geometric parameters of each acoustic channel. Standard GB/T 35717-2024 [34] provides specifications for channel height and angle across different acoustic channel configurations, employing the Gauss–Jacobi integration method to define precise requirements. Following the installation of transducers, it is essential to re-measure the relevant geometric parameters to ensure the accuracy of input data, as prescribed by these standards. According to Standard IEC 60041 [35], geometric parameter uncertainty typically contributes 30% to 50% of the total uncertainty in comprehensive flow measurement uncertainty assessments. This indicates that the accuracy of geometric parameter acquisition plays a decisive role in determining overall measurement accuracy. Although current ultrasonic flow meters can achieve accuracy levels of up to 0.5%, such performance is attainable only if all geometric parameters are precisely measured and strictly controlled [36]. Therefore, during on-site installation and commissioning, high-precision measurement tools and methods must be employed to accurately determine critical parameters—including transducer positions, channel angles, pipe diameters, and acoustic path lengths—to minimize the impact of geometric error on the final flow measurement results.
For large-diameter ultrasonic flow meters used in hydropower stations, Stefan [37] summarized commonly applied methods for geometric parameter measurement, including steel tape (or laser distance meter), theodolite, and total station methods. The steel tape method measures the distance between transducers and calculates the acoustic path length, angle, and height based on geometric relationships. The theodolite method determines the relevant channel parameters by recording horizontal and vertical angles using angle measurement instruments. Figure 3 illustrates the standard installation of a mechanical theodolite, while Figure 4 shows a setup using a total station theodolite.
Figure 3.
The schematic of an installation setup with a mechanical theodolite [37].
Figure 4.
The schematic of an installation setup with a total station theodolite [37].
Hu et al. [38] found that the three geometric measurement methods yield similar accuracy in length measurements, with error margins around 0.1%. However, their angle measurement accuracies vary significantly, with precision values of approximately 0.5°, 0.1°, and 0.05%, respectively. In recent years, advanced measurement instruments such as three-coordinate arms and laser trackers have been increasingly adopted for geometric parameter acquisition. Compared to traditional tools, both the laser tracker and the total station employ non-contact measurement techniques, which effectively eliminate errors caused by physical contact and reduce uncertainties related to human intervention [39]. In pipelines accessible to personnel, geometric parameters of ultrasonic flow meters are typically measured using a combination of steel tape and theodolite, or by employing a total station directly [38,39,40]. Under favorable site conditions and with proper instrument handling, the use of a theodolite introduces a flow measurement uncertainty of approximately 0.5%, whereas a total station can reduce this uncertainty to about 0.2% [40]. For ultra-large-diameter pipelines that are inaccessible to personnel, transducer positioning is often performed using marking methods, and geometric parameters are either calculated geometrically or substituted with theoretical values. Some manufacturers also provide calibrated positioning systems to improve layout accuracy. Currently, three-coordinate arms and laser trackers offer robust non-contact external measurement solutions, significantly enhancing installation accuracy and the reliability of parameter acquisition.
In multi-path ultrasonic flow measurement, determining geometric parameters essentially involves performing a velocity-weighted integration across the pipeline cross-section to compute the average flow velocity and volumetric flow rate, constituting a typical one-dimensional or two-dimensional numerical integration problem. Compared to traditional techniques such as the trapezoidal rule or Simpson’s rule, Gauss-type numerical integration is favored for its superior accuracy, particularly when using a limited number of sampling points. To enhance the accuracy and efficiency of integration, researchers often optimize the spatial placement and weighting coefficients of the acoustic channels based on representative velocity distribution profiles. Studies have shown that the Gauss–Jacobi integration method, which relies on Jacobi polynomials, is highly suitable for conditions involving relatively regular velocity distributions, offering high numerical stability and ease of implementation. Conversely, the OWICS (Optimal Weighting for Ideal Circular Section) method utilizes numerical optimization algorithms to minimize integration errors, making it more appropriate for real-world complex asymmetric flow fields. This method is particularly effective in achieving high-accuracy measurements in large-diameter pipelines and under high-Reynolds-number conditions [41,42,43].
Deviations arising from three-dimensional coordinate measurement errors during geometric parameter acquisition are major contributors to the overall uncertainty in ultrasonic flow meter results. To evaluate the impact of such errors on parameter fitting accuracy, the Monte Carlo simulation method is frequently employed in uncertainty propagation analysis. This technique assumes that measurement errors in three-dimensional coordinates follow a known probability distribution. It then generates a large number of simulated data points randomly within a virtual model and repeatedly fits and statistically analyzes key geometric parameters—such as pipe radius and axial orientation—to estimate their uncertainty intervals [40]. Figure 5 presents a schematic diagram of cylindrical pipe fitting using measured spatial points, illustrating the process of deriving geometric parameters using spatial coordinate data.
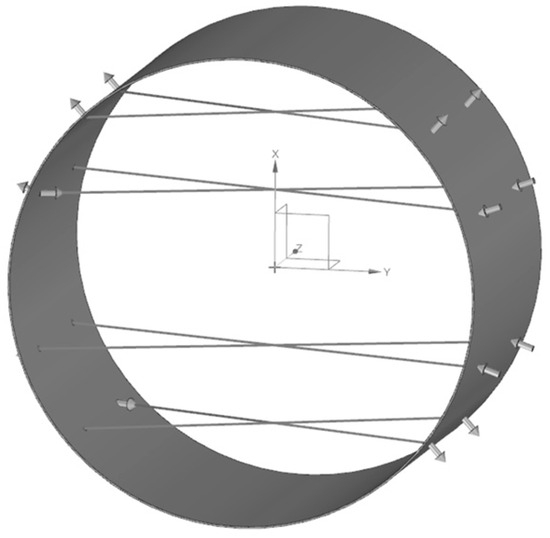
Figure 5.
Diagram of cylindrical fitting for pipeline measurement points [40].
Previous studies have employed total station instruments to capture the coordinates of characteristic points on the pipeline wall, followed by cylindrical fitting using the Lukács algorithm [44]. The Monte Carlo method was subsequently applied to analyze the propagation of errors associated with these measurement points. Results indicated that uncertainties in pipeline radius and axial orientation are positively correlated with the accuracy of individual measurement points and negatively correlated with both the number of measurement points and the axial measurement span. In other words, the uncertainty in pipe radius and axial direction increases as point accuracy decreases and decreases with increased measurement points and axial span. These findings emphasize the importance of utilizing high-precision instruments and applying optimized measurement point distributions to minimize overall geometric uncertainty.
Therefore, in practical applications, the optimal selection of ultrasonic flow meter installation methods should be determined based on evaluation of pipe diameter, required measurement accuracy, and site-specific conditions. For medium- and small-diameter pipelines or scenarios with moderate accuracy demands, the external clamp-on method is generally more practical due to its simplicity in installation and maintenance. In contrast, for large-diameter pipelines or applications requiring high-precision flow measurement, internal or insertion-type configurations should be prioritized to enhance measurement stability and accuracy. Furthermore, to ensure long-term, reliable system operation, it is essential to strictly adhere to relevant technical standards and operating protocols throughout all stages of flow meter installation, geometric parameter acquisition, and subsequent maintenance.
3. Measurement Errors
Despite the theoretical advancement of the ultrasonic transit-time method, practical engineering applications still face multiple error challenges: geometric parameter measurement deviations (Section 2.5 has indicated that it contributes 30–50% uncertainty) interact with complex flow fields, leading to core issues such as transducer-induced flow disturbance (Section 3.1) and flow field distortion (Section 3.2). This section will quantitatively reveal the generation mechanisms and coupling effects of these errors, particularly focusing on the substantial impact of installation condition deviations from ideal states on measurement accuracy, so as to clarify the key directions for accuracy improvement.
3.1. Local Disturbances of the Transducer
In the design and engineering application of ultrasonic flow meters, parameters such as pipeline diameter, acoustic path length, and the incidence angle of the acoustic beam significantly influence the measurement accuracy of the instrument [45]. Any deviation of the transducer from its intended position, or errors in related geometric parameters, can directly distort the projection of the flow velocity vector, thereby affecting the measured volumetric flow rate. For insertion-type transducers commonly used in large hydropower plants, minor protrusions or recessions formed during installation may disturb the boundary layer, thereby altering the local velocity distribution. Additionally, during operation, solid particle deposition or biological fouling on the surface of the transducer or pipe wall can further modify the local flow pattern, introducing unexpected measurement errors. Surface contamination of the transducer can also lead to signal attenuation and a reduced signal-to-noise ratio, ultimately degrading system stability and accuracy [46].
Existing studies have shown that the influence of the transducer on measurement error is governed by the flow Reynolds number and the pipe wall roughness. Staubli et al. [47] found that under high-Reynolds-number conditions, even slight geometric deviations within the pipeline could lead to substantial measurement errors. Voser et al. [48] performed a systematic investigation using Computational Fluid Dynamics (CFD) simulations to assess the impact of protruding transducer structures in an eight-channel configuration, introducing the concept of a “protrusion coefficient.” They observed that, for conditions where the pipe diameter exceeds 2 m and flow velocity is greater than 0.1 m/s, errors caused by protrusions are generally within ±0.5%. However, in small- and medium-diameter pipelines, such errors may become significantly amplified. Hu et al. [49] conducted measurements on a DN100 system and reported a measurement error reaching −5%. Zhang et al. [50], using Fluent simulations, revealed that regions near the transducer are prone to the formation of recirculation zones, resulting in diminished integration values and a negative system bias. Their research further indicated that, in large-diameter applications, a 65° incidence angle performs better than a 45° angle in avoiding disturbed flow regions, thereby enhancing measurement accuracy. Zheng et al. [51] noted that both “full extension” and “full retraction” layouts of insertion-type transducers introduce negative errors, with the fully extended configuration offering slightly better performance. They also evaluated six channel configurations in a DN100 system and found that increasing the number of channels corresponded to higher system error, as shown in Table 2 and Table 3.

Table 2.
Measurement errors for single-channel configuration.

Table 3.
Measurement errors for cross-channel configuration.
Liu et al. [52] pointed out that in DN400 pipelines, although there is an error with the full contraction configuration, high precision can still be achieved through correction algorithms. Additionally, Wang et al. [53], through a combination of experiments and numerical simulations, found that as the pipe diameter increases, the error tends to decrease, with shorter path channels exerting greater influence on integral errors. The above studies indicate that structural deviations in the transducer and its interference with the flow field are more likely to cause significant errors in small- and medium-diameter pipelines. These errors become more pronounced as the pipe diameter decreases, the number of channels increases, and the local flow pattern becomes more complex.
3.2. Rectifying Effect of Flow Regulators and Calibration Differences
In industrial applications, installation components such as elbows, control valves, and welded flanges often induce disturbances in the flow field, causing the ultrasonic flow meter to operate under non-ideal conditions and introducing significant measurement errors [54]. While flow velocity distribution correction factors can compensate for certain deviations, their effectiveness is typically limited under highly turbulent flow conditions. Although in situ calibration methods can detect the specific influence of installation-related disturbances on measurement error [55], they do not fundamentally enhance the intrinsic accuracy of the instrument. Therefore, investigating and addressing the dynamic characteristics of non-ideal flow fields has become a critical avenue for improving measurement precision. Inside the pipeline, axial flow is the predominant component; however, in curved sections such as elbows, centrifugal forces induce secondary radial flows that interfere with the ultrasonic measurement path, leading to errors [56]. Previous studies have systematically analyzed the effects of installation components—such as elbows and flow conditioners—on measurement accuracy and have developed real-time monitoring systems to track key parameters including axial velocity, sound velocity, and signal-to-noise ratio. This enables timely identification of operational condition changes and instrument abnormalities [57].
To improve flow conditions and enhance measurement accuracy, flow rectifiers are commonly installed upstream of the ultrasonic flow meter to reduce the required straight pipe length. This practice has been widely adopted. By optimizing the internal flow structure, flow rectifiers can effectively suppress vortices and asymmetric velocity profiles, thereby improving the velocity distribution and reducing measurement errors associated with flow field non-uniformities. However, rectifier design must optimize the balance between rectification efficiency and structural complexity, while also accounting for manufacturing tolerances. For optimal performance, combining vane structures with orifice plates has been shown to effectively mitigate measurement errors under certain operating conditions. Nevertheless, their influence on pressure loss and flow distortion must be carefully evaluated [58]. As such, optimizing flow rectifier design and developing adaptive flow conditioners applicable to various operational scenarios are key strategies for enhancing overall system performance.
In practical engineering contexts, constraints related to pipeline structure, limited installation space, and layout costs often prevent ideal flow conditions from being realized. Consequently, flow calibration methods are employed to verify measurement errors under different pre-installation conditions, thereby quantifying relationships between instrument performance and pipe layout characteristics. This approach is widely used in high-precision metering applications and can effectively assess the influence of actual flow conditions on measurement accuracy [59]. However, due to discrepancies between field versus laboratory conditions, traditional models based on ideal flow field assumptions often fail to accurately represent complex field environments: especially in large-diameter pipeline systems where flow disturbances cannot be entirely eliminated. This mismatch between the measurement model and the actual flow field further amplifies measurement uncertainty [60].
In summary, internal channel disturbances, installation-induced flow disturbances, and calibration-to-field condition discrepancies constitute the primary sources of measurement error in ultrasonic transit-time flow measurement. Addressing these challenges requires systematic research in hardware optimization, flow characteristic modeling, and measurement technology innovation—establishing an integrated accuracy assurance framework spanning the instrument lifecycle.
4. Precision Improvements
To address the aforementioned error sources (e.g., the −10% negative deviation caused by transducer-induced flow disturbance in Section 3.1 and calibration mismatch triggered by flow field installation effects in Section 3.2), it is urgent to break through the accuracy bottleneck from three dimensions: hardware innovation, flow field regulation, and algorithm integration.
Section 4 will sequentially investigate high-stability transducer design and signal processing technologies (Section 4.1); CFD-driven flow field optimization and channel adaptive weighting strategies (Section 4.2); and collaborative calibration mechanisms of multi-flow measurement technologies (Section 4.3). These efforts aim to construct a holistic accuracy enhancement pathway covering the full chain of “device–flow field–system”.
4.1. Hardware Improvements
In industrial applications, installation components such as elbows, control valves, and welded flanges often cause flow field disturbances, leading to the ultrasonic flow meter compromising measurement performance. Improving hardware is essential for achieving high-precision ultrasonic transit-time flow measurements and primarily involves two aspects: transducer optimization and electronic circuitry improvements.
The core performance of an ultrasonic transducer is primarily determined by the characteristics of its piezoelectric material. Studies have shown that rigid piezoelectric ceramics such as PZT-5H/PZT-8, known for their high electromechanical coupling coefficients and thermal stability, are well-suited for high-precision ultrasonic flow measurement applications [61]. In recent years, single-crystal materials such as PMN-PT (lead magnesium niobate–lead titanate) have attracted considerable interest due to their superior piezoelectric properties, improving transducer sensitivity by approximately 20% [62].
From a structural design perspective, advancements such as matching layer technology, modifications to transducer installation methods, and enhanced temporal resolution have significantly enhanced acoustic energy transmission efficiency. The quarter-wavelength matching layer design proposed by Sadeghi et al. [63] increased transmission efficiency from 60% to 85%. Gururaja [64] utilized high-impedance tungsten powder–epoxy resin composite backing layers to effectively suppress residual vibrations, reducing pulse width by approximately 30% and thereby enhancing precision and reliability of time delay estimation. According to Lynnworth [65], oblique incidence configurations—typically at 45° or 60°—produce higher signal amplitudes and higher signal-to-noise ratios than direct incidence. Willatzen [66], through numerical simulations, found that optimizing the installation angle can mitigate measurement deviations caused by asymmetric velocity distributions, reducing system errors by up to 15%. Zhang [67] developed a high-precision time measurement system based on a Time-to-Digital Converter (TDC), achieving a time resolution of 20 ps using the TDC-GPX chip. Robert [68] further developed an FPGA-based multi-cycle averaging system, reducing timing uncertainty to ±50 ps. Digital signal processing technologies have also proven effective in improving system resilience to noise. Balazs et al. [69] proposed a wavelet-based time delay estimation algorithm, achieving measurement precision within ±0.1% even under low signal-to-noise conditions. In addition, adaptive filtering algorithms have been introduced to suppress pipeline vibration noise, resulting in a signal quality improvement of up to 20 dB [70].
Temperature compensation and thermal stability are also crucial factors. Temperature fluctuations alter fluid sound velocity and induce electronic time-based drift in the time base of electronic components. Guo et al. [71] designed a real-time compensation system integrated with a temperature sensor, which dynamically corrected the temperature term in the sound velocity calculation, reducing temperature-induced measurement errors from 1.5% to 0.2%. The use of low-drift oscillators and other high-stability components further improves the system’s environmental adaptability and operational stability [72].
4.2. CFD Applications
In practical applications, ultrasonic flow meters are frequently affected by complex flow field conditions, disturbances from pipeline components, and multiphase flows, leading to significant measurement errors [73]. Traditional design approaches based on empirical formulas and ideal flow assumptions are no longer sufficient to meet the growing demand for high-precision flow measurement in modern industrial environments. In recent years, CFD has emerged as a powerful high-resolution numerical simulation tool that enables detailed analysis of the operating mechanisms of ultrasonic flow meters, supports structural optimization of measurement systems, and enhances measurement accuracy. In large-scale engineering environments such as hydropower plants, CFD has been extensively applied to evaluate and improve the performance of flow measurement systems. This section focuses on recent advances in CFD applications in three key areas: analysis of flow field characteristics, structural optimization of instruments, and improvements in signal processing methods.
4.2.1. Flow Field Characteristic Analysis
The accuracy of transit-time ultrasonic flow meters is highly dependent on the symmetry and uniformity of the velocity field along the acoustic path. Zhao et al. [74] used CFD simulations to compare velocity profiles in laminar, fully developed turbulent, and transitional flow regimes, and found that non-ideal velocity distributions can lead to ≤5% measurement deviations. Kurniadi et al. [75] simulated the evolution of flow fields under varying installation conditions, quantifying the degree of velocity asymmetry caused by structural disturbances and evaluating its influence on measurement accuracy. Piechota et al. [76] further investigated vortex structures generated by local disturbances and analyzed their attenuation along the flow path, which provides a theoretical foundation for optimizing ultrasonic flow meter installation standards.
Currently, most CFD analyses are based on solving the Navier–Stokes equations using the Reynolds-Averaged Navier–Stokes (RANS) method, typically in combination with the standard k-ε turbulence model, which is effective for simulating the complex flow states commonly encountered in engineering applications [77]. Previous studies have shown that in DN100 pipelines, even under conditions of fully developed turbulence, deviations between the actual velocity profile and the ideal parabolic distribution can cause measurement errors of 1.5–3% [78]. For transient flow analyses that require higher temporal and spatial resolution, some researchers have adopted the Large Eddy Simulation (LES) method to capture detailed turbulence structures, providing valuable insights for the development of dynamic compensation models and algorithms [79].
4.2.2. Optimizing the Design of Ultrasonic Flow Meters
Leveraging CFD technology, researchers can systematically evaluate the effects of various structural parameters on the performance of ultrasonic flow meters in a virtual environment, thereby facilitating more efficient and precise instrument design. Tang et al. [80] employed parametric CFD simulations to analyze the impact of the transducer installation angle on the signal-to-noise ratio, revealing that a properly optimized angle can significantly enhance signal quality. Chen et al. [81] integrated genetic algorithms with CFD to develop an optimized transducer arrangement strategy tailored to non-standard pipeline diameters. Wang [82] emphasized that flow field irregularities pose a universal challenge for all ultrasonic flow meters. Their study found that when the actual flow field closely matches design assumptions or when the installation angle is optimized, the performance of the ultrasonic flow meter improves significantly. In a separate investigation, Zhang [60] employed CFD simulations to compare the measurement performance of five different single-path channel configurations—radial, V-method, triangular, square, and pentagonal—under varying flow resistance conditions. As illustrated in Figure 6, their results showed that the triangular configuration exhibited the highest adaptability in downstream flow conditions influenced by single elbows. Overall, the triangular channel layout demonstrated superior measurement performance across a range of disturbed flow conditions.
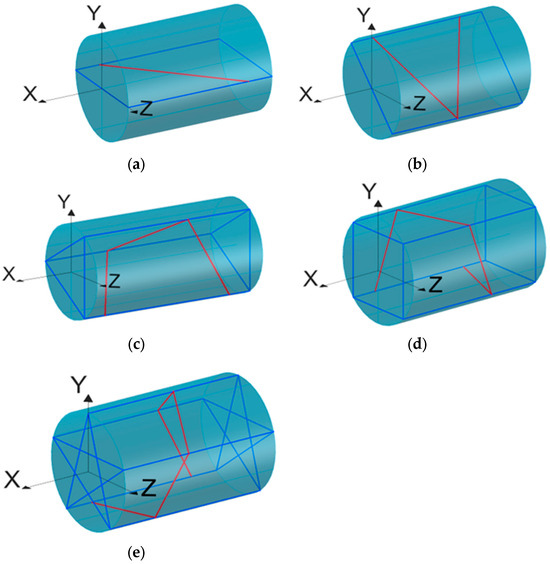
Figure 6.
Five different channel configurations. (a) Radial Shape. (b) V Shape. (c) Triangular Shape. (d) Square Shape. (e) Pentagonal Shape.
Mousavi et al. [83] further proposed an adaptive channel weighting algorithm based on CFD simulation results to enhance the robustness of flow measurements. In addition, they [84] designed a novel structure incorporating a streamlined flow director, which effectively improved the velocity distribution near the transducer region. For low-Reynolds-number conditions, Guo et al. [85] developed a spiral acoustic channel arrangement that significantly enhanced measurement linearity under low-flow-rate conditions.
In terms of algorithmic optimization, gradient-based optimization methods have been predominantly employed [86,87,88]. For example, the adjoint method—well-suited for continuous design spaces due to its high computational efficiency—has been applied to improve the sensitivity of transducer angle settings to measurement linearity. In more complex or discontinuous design spaces, researchers have integrated genetic algorithms with CFD simulations to facilitate the automatic generation and topological optimization of acoustic channel structures across varying pipeline diameters. Furthermore, particle swarm optimization (PSO), characterized by its simple implementation and fast convergence, has demonstrated promising results in optimizing transducer positioning [89,90,91,92]. The hybrid application of multiple optimization strategies has proven to be an effective approach for improving both the structural design and measurement accuracy of ultrasonic flow meters.
To further reduce computational costs during the optimization process, surrogate modeling techniques have gained increasing attention. Among them, the radial basis function (RBF) method, when combined with mesh deformation techniques, enables efficient parametric modeling of complex geometries [93,94,95,96]. With the advances of artificial intelligence, deep learning methods are increasingly being applied to structural optimization tasks. Adaptive optimization strategies based on deep reinforcement learning, in conjunction with the emerging digital twin technology, are paving the way for the next generation of intelligent ultrasonic flow meter design, offering novel insights and breakthrough opportunities [97,98].
4.2.3. Signal Processing and Error Compensation Methods Supported by CFD
In addition to its role in structural optimization, CFD also plays a pivotal role in the development of ultrasonic signal processing and error compensation algorithms. Liu et al. [99] established a coupled simulation model integrating acoustic wave propagation with fluid dynamics, providing a theoretical framework for analyzing acoustic characteristics in complex flow fields. Petris et al. [100] extended this approach by incorporating fluid compressibility and viscous dissipation mechanisms, elucidating their effects on the modulation of ultrasonic signal waveforms. Building on CFD analysis, Liu et al. [101] investigated how non-uniform temperature fields influence sound velocity and propagation paths. They proposed a temperature field reconstruction method that utilizes CFD-based prior information to compensate for measurement errors caused by thermal gradients.
Zhang [73] conducted a comprehensive analysis of environmental factors—including temperature, pressure, and non-uniform fluid velocity distributions—and their impact on flow measurement accuracy. They developed a temperature compensation model using least-squares surface fitting, which is based on mathematical modeling and parameter optimization techniques, as illustrated in Figure 7.
Figure 7.
Temperature model based on least-squares [73].
In recent years, the emergence of data-driven modeling approaches has facilitated significant advancements in ultrasonic signal processing through the integration of CFD simulations and machine learning techniques. Researchers [102] trained deep neural networks using flow field characteristic data generated from CFD simulations, enabling high-precision prediction of time-of-flight propagation under complex flow conditions. Another research group [103] further integrated real-time CFD simulation outputs with online measurement data to develop a digital twin-based ultrasonic flow meter system, which enables dynamic state monitoring and real-time error correction.
These developments underscore that CFD technology has become a core enabler for improving the measurement accuracy of ultrasonic time-of-flight flow meters, with notable progress achieved in flow field modeling, structural optimization, signal processing, and error compensation. Nevertheless, in practical engineering applications, it remains challenging to strike a balance between multiphysics coupling accuracy, computational efficiency, and operational adaptability [104]. Future research should aim to establish high-precision, multi-scale, and multi-field-coupled CFD modeling frameworks to support broader engineering deployments and the intelligent advancement of ultrasonic flow measurement systems.
4.3. Advances in Flow Measurement Technology
As field conditions become increasingly complex, researchers have increasingly recognized the limitations of individual flow measurement technologies in terms of both accuracy and adaptability. This has led to efforts to integrate flow measurement techniques with simulation models, as well as combining different measurement methodologies to enhance overall performance. To improve flow measurement accuracy, researchers have coupled simulation models with ultrasonic measurement techniques. Alexander et al. [105] proposed a turbulent flow field model specifically designed for ultrasonic cross-correlation flow measurement. Massaad Jack introduced the concept of nonlinear wave propagation, demonstrating that combining the second harmonic and fundamental wave components—both exhibiting similar time-of-flight differences—can yield more accurate flow measurements than using only the fundamental component [106]. Landskron Johannes developed a method utilizing acoustic signals along multiple propagation paths to evaluate the influence of fluid temperature and pipe wall thickness. A finite element model was used to identify calibration curves under various simulated temperature and wall thickness scenarios, thereby enabling flow measurement corrections by adjusting the waveguide resolution based on experimental data [107]. The corresponding experimental results are illustrated in Figure 8.
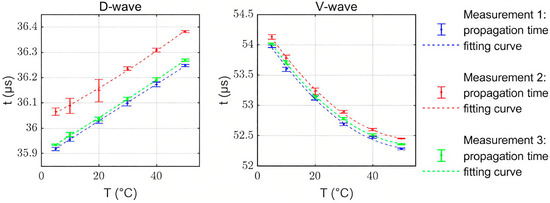
Figure 8.
Experimentally measured propagation times tD and tV depending on the temperature in a range from 5 °C to 50 °C. The vertical offset in the curves is related to variations in the transducer attachment on the different sensors or variations in limescale layer thickness [107].
Hong [108] designed an ultrasonic flow meter incorporating adaptive Kalman filtering for time-of-flight measurements. The system employs an optimized Sage–Husa adaptive Kalman filter algorithm to process time-of-flight data, dynamically updating system noise and process covariance matrices to estimate and correct measurement errors. This approach significantly improves the accuracy of flow measurements. The integration of multiple flow measurement techniques has proven effective in enhancing both accuracy and robustness. For instance, velocity probes provide localized velocity distribution data, which complement the average velocity obtained from the ultrasonic transit-time method. A combined flow measurement technique employing cross-correlation and optical flow methods was proposed [109]. In this method, cross-correlation is first applied to detect velocity vectors between two consecutive river images, followed by dense optical flow to refine the initial velocity estimation. This hybrid approach achieved a relative error of only 4.3% for average velocity and 3.9% for total flow rate. Zhao et al. [110] conducted absolute and relative efficiency tests on pump turbines using ultrasonic flow meters or spiral casing differential pressure transmitters (calibrated for absolute flow). Combined with other key operational parameters, these measurements were used to evaluate the efficiency and output characteristics of the turbines. A software system was developed to test the efficiency characteristics of pump turbines, as shown in Figure 9. This system enables real-time acquisition and transmission of experimental parameters via RS232/485 serial communication, supporting data analysis, calculation, and graphical visualization.
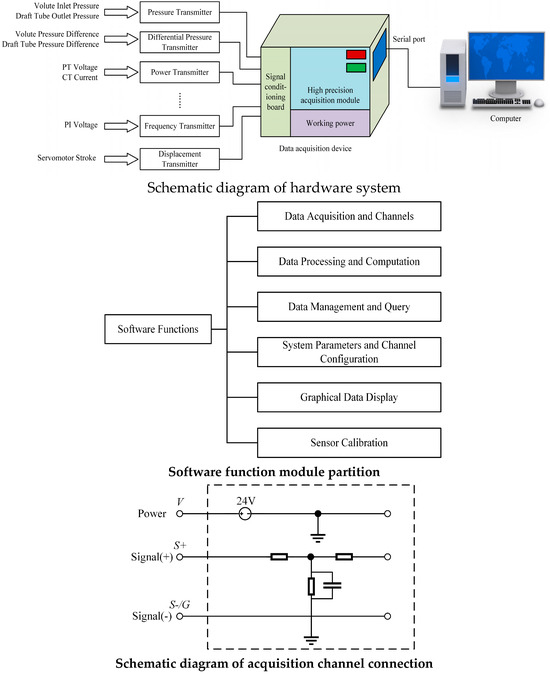
Figure 9.
Software system developed for testing efficiency characteristics of water pump turbines.
The integration of multiple flow measurement methods has become an increasingly important strategy; see Figure 10. Researchers at the China Institute of Water Resources and Hydropower, led by Zhou Ye, are conducting efficiency tests on turbine units at the Wu-dongde Hydroelectric Station. This testing integrates the ultrasonic time-of-flight method with the thermodynamic method and the spiral casing differential pressure method. Preliminary results have shown that the integration of multiple methods can effectively improve the efficiency of hydropower plant units.
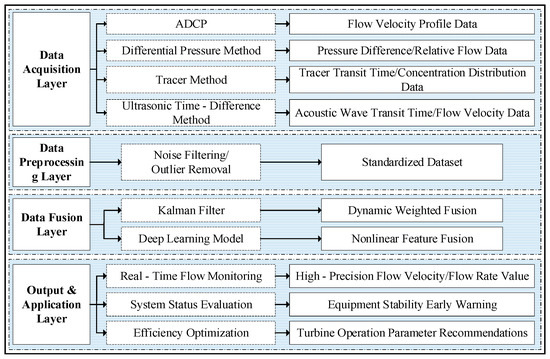
Figure 10.
Flow chart of integration technology for ultrasonic time-of-flight method, thermodynamic method, and spiral casing differential pressure method.
In summary, acoustic channel structural parameters, localized flow disturbances, and transducer results are the primary sources of errors in ultrasonic flow measurement. Furthermore, discrepancies between the installed flow field conditions, calibration parameters, and actual operating regimes significantly contribute to measurement errors. Enhancing measurement accuracy has relied critically on hardware refinements and optimized signal processing techniques. CFD simulation has demonstrated significant potential for flow meter design optimization and reducing errors. Consequently, future research should prioritize the integration of diverse optimization approaches and investigation of their synergistic effects to further enhance both the precision and reliability of ultrasonic time-of-flight flow measurement.
To provide a clear and concise overview of the key performance metrics associated with the accuracy-improving technologies discussed in this section, Table 4 summarizes the core parameters—including measurement accuracy, frequency-related characteristics, and flow rate adaptability—derived from the empirical findings of cited studies. This table systematically consolidates the quantitative and qualitative performance data of hardware optimization, CFD-driven strategies, and multi-method integration, offering a direct reference for comparing the practical effectiveness of different technologies in hydropower ultrasonic flow measurement scenarios.

Table 4.
Key parameters of ultrasonic transit-time flow measurement linked to accuracy-improving technologies.
To systematically consolidate the diverse accuracy-improving technologies discussed in this section, Table 5 provides a concise summary of key strategies categorized by their technical pathways. This table encapsulates the core methods, critical findings, and supporting references for hardware optimization, CFD-driven innovations, and multi-method integration, offering a structured overview to facilitate quick comprehension of the landscape of precision-enhancing approaches. By distilling the complexities of each technology into accessible entries, it serves as a practical reference for researchers and engineers seeking to select or advance accuracy-improving strategies in ultrasonic transit-time flow measurement for hydropower systems.

Table 5.
Summary of existing accuracy-improving technologies for ultrasonic transit-time flow measurement.
5. Summary and Outlook
With the increasing demand for higher flow measurement accuracy, real-time monitoring capabilities, and long-term stability in hydropower plants, ultrasonic transit-time flow measurement technology has gained widespread application in turbine flow measurement due to its non-contact nature, structural flexibility, and capacity for online monitoring. This paper provides a systematic review of the development, key structural configurations, primary sources of error, and strategies for accuracy enhancement, summarized as follows:
- (1)
- To address the objective of “comprehensively reviewing the fundamental principles, system architectures, and classifications of ultrasonic transit-time flow meters, and clarifying their engineering adaptability in hydropower scenarios,” this study systematically sorts out the core components of transit-time ultrasonic flow meters (ultrasonic transducers, signal processing units, and display systems). It categorizes and elaborates on the characteristics of single-path and multi-path configurations, as well as installation types such as clamp-on and insertion types. Combined with complex environments in hydropower engineering (e.g., penstocks, volutes), it analyzes the applicable scenarios of different types of flow meters (e.g., the advantages of multi-path configurations in non-ideal flow fields, and the flexibility of clamp-on types in large-diameter pipelines), thus defining their boundaries of engineering applications.
- (2)
- Regarding the objective of “analyzing the main sources of measurement errors and their coupling mechanisms,” this study identifies key error sources, including geometric parameter deviations (accounting for 30–50% of total uncertainty), localized flow disturbances caused by transducers (e.g., recirculation zones due to protrusions/recessions), and flow field distortions (e.g., secondary flows induced by elbows). By integrating CFD simulations and experimental data, it reveals the coupling effects of various error sources (e.g., installation deviations and flow field distortions jointly amplify measurement biases) and quantifies their impacts on measurement accuracy (e.g., transducer interference in small-diameter pipelines can lead to a −5% error).
- (3)
- For the objective of “comprehensively evaluating technological pathways for accuracy improvement,” this study systematically summarizes three core optimization methods: hardware-level improvements (PMN-PT single-crystal transducers improve sensitivity by 20%, and TDC technology enhances time measurement accuracy to ±20 ps), CFD-driven optimizations (flow field correction reduces errors in disturbed flows by ≤5%, and optimized transducer layouts reduce system errors by 15%), and multi-method collaborative calibration (the integration of ultrasonic and thermodynamic methods reduces uncertainty to ±0.8%). Through comparative analysis, it clarifies the applicable conditions and effects of different technologies.
- (4)
- Concerning the objective of “identifying challenges and proposing future directions,” this study points out the limitations of current technologies in adapting to non-axisymmetric flow fields and discrepancies between calibration and on-site conditions. Based on existing research results, it proposes that future efforts should focus on developing array-based transducers (enabling real-time reconstruction of three-dimensional flow fields), multi-physical field coupling correction models (integrating temperature, pressure, and flow velocity), and improving industry standards, thus providing a reference path for high-reliability applications in large-scale hydropower systems.
- (5)
- In the future, research should prioritize the development of array-based transducers capable of adapting to complex flow pattern variations, for real-time reconstruction of three-dimensional flow fields. Concurrently, establishing multi-physical field correction models that dynamically integrate temperature, pressure, and flow velocity is essential. Furthermore, advancing national/industry standards for ultrasonic flow measurement in hydropower applications would enhance technological consistency and facilitate broader implementation.
Author Contributions
Conceptualization, L.L. and Y.Z.; methodology, L.L.; formal analysis, L.L. and H.Z.; investigation, L.L., H.Z. and Y.Y.; resources, B.X.; data curation, L.L. and Y.Y.; writing—original draft preparation, L.L.; writing—review and editing, Y.Z. and B.X.; visualization, H.Z.; supervision, Y.Z.; project administration, Y.Z.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Basic and Applied Basic Research Foundation of Guangdong Province (Project Number: 2021A1515110552). Project Name: Research on the Impact of Multi-energy Complementary Mode on the Speed Control of Pumped Storage Units: Boundary Conditions and Control Strategies.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFD | Computational Fluid Dynamics |
References
- Wang, R.; Xiao, Q.; Chen, Y.; Liu, Y.; Wang, X. Development Trend and Exploration of Core Control System of Hydropower Units in New Power System. New Type Power Syst. 2025, 3, 33–44. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, Y. Discussion of Turbine Efficiency Testing of a Nepal Hydropower Station by Thermodynamic Method. Mech. Electr. Tech. Hydropower Stn. 2020, 43, 8–10. [Google Scholar] [CrossRef]
- Cao, D.; Zhou, Y.; Pan, L.; Liu, Y. Absolute Discharge Measurement of Bulb Turbine Based on Current-Meter Method. Water Resour. Power 2021, 39, 190–193. [Google Scholar] [CrossRef]
- Cattaert, A.E. High Pressure Pump Efficiency Determination from Temperature and Pressure Measurements. In Proceedings of the 2007 IEEE Power Engineering Society Conference and Exposition in Africa—PowerAfrica, Johannesburg, South Africa, 16–20 July 2007; pp. 1–8. [Google Scholar] [CrossRef]
- IS/IEC 41; Field Acceptance Tests to Determine the Hydraulic Performance of Hydraulic Turbines, Storage Pumps and Pump Turbines. Bureau of Indian Standards (BIS): New Delhi, India, 1991. Available online: https://archive.org/details/gov.in.is.iec.41.1991 (accessed on 27 March 2025).
- Lu, C. Field Acceptance Tests of Pump-turbine with Thermodynamics and its Discussions. Water Power 2005, 31, 59–66. [Google Scholar]
- Baidar, B.; Nicolle, J.; Gandhi, B.K.; Cervantes, M.J. Sensitivity of the Winter-Kennedy Method to Different Guide Vane Openings on an Axial Machine. Flow Meas. Instrum. 2019, 68, 101585. [Google Scholar] [CrossRef]
- Zhou, B.; Tian, T.T.; Zhu, G.; Zhao, J.B.; Liu, D.H. An Ultrasonic Testing Method for Wall Thickness of Turbine Blades. Measurement 2022, 198, 111357. [Google Scholar] [CrossRef]
- Yang, Y.X. Measurement and Energy Efficiency Analysis of Hydraulic Turbine Based on CFD and Ultrasonic Method. Master’s Thesis, Xinjiang Agricultural University, Wulumuqi, China, 2021. [Google Scholar]
- Zhang, N. The Principle and Application of Ultrasonic Flowmeter. Ind. Metrol. 2019, 29, 36–38. [Google Scholar] [CrossRef]
- GB/T 20043-2005; Field Acceptance Test to Determine the Hydraulic Performance of Hydraulic Turbine, Storage Pumps and Pump-Turbines. China Standards Press: Beijing, China, 2005. Available online: https://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=34BCCE2D14AC8DB07993B6235FA1F919 (accessed on 27 March 2025).
- Sanderson, M.L.; Yeung, H. Guidelines for the Use of Ultrasonic Non-Invasive Metering Techniques. Flow Meas. Instrum. 2002, 13, 125–142. [Google Scholar] [CrossRef]
- Baker, R.C. Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, P.; Wang, R.; Niu, Z.; Zhang, K. Signal Processing Method of Ultrasonic Gas Flowmeter Based on Transit-Time Mathematical Characteristics. Measurement 2025, 239, 115485. [Google Scholar] [CrossRef]
- Tan, C.; Murai, Y.; Liu, W.; Tasaka, Y.; Dong, F.; Takeda, Y. Ultrasonic Doppler Technique for Application to Multiphase Flows: A Review. Int. J. Multiph. Flow 2021, 144, 103811. [Google Scholar] [CrossRef]
- Ren, R.; Wang, H.; Sun, X.; Quan, H. Design and Implementation of an Ultrasonic Flowmeter Based on the Cross-Correlation Method. Sensors 2022, 22, 7470. [Google Scholar] [CrossRef]
- Tang, X.; Xie, X.; Fan, B.; Sun, Y. A Fault-Tolerant Flow Measuring Method Based on PSO-SVM with Transit-Time Multipath Ultrasonic Gas Flowmeters. IEEE Trans. Instrum. Meas. 2018, 67, 992–1005. [Google Scholar] [CrossRef]
- Irving, W. Air Speed Indicator. U.S. Patent 2274262A, 31 May 1939. [Google Scholar]
- Raine, A.B.; Aslam, N.; Underwood, C.P.; Danaher, S. Development of an Ultrasonic Airflow Measurement Device for Ducted Air. Sensors 2015, 15, 10705–10722. [Google Scholar] [CrossRef] [PubMed]
- Schima, H.; Huber, L.; Schmallegger, H.; Drost, C.J.; Droudt, A.; Wieselthaler, G.; Losert, U. Flow Measurement at the Pump Head of Centrifugal Pumps: Comparison of Ultrasonic Transit Time and Ultrasonic Doppler Systems. Artif. Organs. 1997, 21, 808–815. [Google Scholar] [CrossRef] [PubMed]
- Zhao, N.N.; Hu, L.; Peng, X.X. A Method Combining Measurement Tool and Numerical Simulation for Calculating Acoustic Signals of Ultrasonic Flowmeter. IEEE Sens. J. 2019, 19, 11805–11813. [Google Scholar] [CrossRef]
- Marco, D.; Mauro, C.; Matteo, D. Measurement of High-Pressure Natural Gas Flow Using Ultrasonic Flowmeters. Measurement 1997, 20, 75–89. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, F.; Yang, W. The Application of Ultrasonic Wave Meter in Puding Hydropower Station. Power Syst. Big Data 2018, 21, 85–88. [Google Scholar] [CrossRef]
- Fang, W.G. Application of Plug-in Ultrasonic Flowmeter in Online Continuous Flow Replacement Situation. Water Purif. Technol. 2020, 39, 151–154. [Google Scholar] [CrossRef]
- Cascetta, F. Application of a Portable Clamp-on Ultrasonic Flowmeter in the Water Industry. Flow Meas. Instrum. 1994, 5, 191–194. [Google Scholar] [CrossRef]
- Dadashnialehi, A.; Moshiri, B. Online Monitoring of Transit-Time Ultrasonic Flowmeters Based on Fusion of Optical Observation. Measurement 2011, 44, 1028–1037. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, G.; Liu, J. Application of Ultrasonic Flowmeter in Hydropower Station. Northwest Hydropower 2021, 05, 94–97. [Google Scholar] [CrossRef]
- Yang, J. Application of Pipe Flow Meter of Multi-Path Time Difference Method in Manla Hydropower Station. Water Resour. Informatiz. 2014, 06, 47–50. [Google Scholar] [CrossRef]
- Zhang, R.; Li, G. The Application of Ultrasonic Flowmeter in Liquid Transmission Metering. J. Langfang Norm. Univ. 2003, 19, 95–97. [Google Scholar] [CrossRef]
- Qiu, S.; Xu, K. Research on the Detection Method of Pipeline Natural Gas Ultrasonic Flow Meter. China Insp. Body Lab. 2024, 32, 35–40. [Google Scholar] [CrossRef]
- Zheng, D.D.; Zhang, P.Y.; Xu, T.S. Study of Acoustic Transducer Protrusion and Recess Effects on Ultrasonic Flowmeter Measurement by Numerical Simulation. Flow Meas. Instrum. 2011, 22, 488–493. [Google Scholar] [CrossRef]
- Li, Q.; Ma, H.; Liu, H.; Li, Y. Experimental Study on Online Detection of Portable Ultrasonic Flowmeter. Metrol. Sci. Technol. 2017, 08, 46–48. [Google Scholar] [CrossRef]
- Cavuoto, G.; Romeo, R.; Lago, S.; Giuliano, A. Towards the Validation of Ultrasonic Flowmeters Operating in Hydrogen-Enriched Natural Gas Mixtures through Speed of Sound Measurements Obtained by a Clamp-On Meter. Int. J. Hydrogen Energy 2025, 105, 1178–1185. [Google Scholar] [CrossRef]
- GB/T 35717-2024; Discharge Measurement for Hydraulic Turbines, Storage Pumps and Pump-Turbines—Ultrasonic Transit-Time Method. China Standards Press: Beijing, China, 2024. Available online: https://max.book118.com/html/2025/0103/5322002023012023.shtm (accessed on 27 March 2025).
- IEC 60041:1991; Field Acceptance Tests to Determine the Hydraulic Performance of Hydraulic Turbines, Storage Pumps and Pump-Turbines. International Electrotechnical Commission (IEC): Geneva, Switzerland, 1991. Available online: https://webstore.iec.ch/en/publication/154 (accessed on 27 March 2025).
- Broquet, P.; Conti, L.; Vaterlaus, H.P. Use of Total Station Theodolite for the Installation of Ultrasonic Flowmeters in Large Diameter Penstocks. In Proceedings of the 3rd International Conference ICHEM, Lucerne, Switzerland, 10–12 July 2000. [Google Scholar]
- Stefan, B. Discussion of Installation Methods and Errors of Multipath Acoustic Discharge Measurements in Closed Conduits. In Proceedings of the 5rd International Conference ICHEM, Lucerne, Switzerland, 14–16 July 2004. [Google Scholar]
- Hu, H.; Wang, C.; Meng, T.; Cui, L. Study on Geometric Parameter Calculation Method and Uncertainty Estimation of Ultrasonic Flowmeter. Chin. J. Sci. Instrum. 2010, 31, 1583–1587. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, C.W.; Lin, J. Effects of Velocity Profiles on Measuring Accuracy of Transit-Time Ultrasonic Flowmeter. Appl. Sci. 2019, 9, 1648. [Google Scholar] [CrossRef]
- Meng, T.; Hu, H.; Wang, C.; Chen, H.; Zhuang, T. Geometric Parameter Measurement of Large Ultrasonic Flowmeter Based on Total Station. ACTA Metrol. Sin. 2010, 31, 59–62. [Google Scholar] [CrossRef]
- Hu, H.; Meng, T.; Wang, C. Theoretical Analysis of Integration Error of Ultrasonic Flowmeter in the Disturbed Flow Condition. ACTA Metrol. Sin. 2011, 32, 198–202. [Google Scholar] [CrossRef]
- Cui, H. Research and Application of Online Precision Measurement Method for Geometric Parameters of Ultrasonic Flow Measuring Device. Master’s Thesis, China Jiliang University, Hangzhou, China, 2019. [Google Scholar] [CrossRef]
- Renaldas, R. Investigation of The Flow Velocity Profile in a Metering Section of an Invasive Ultrasonic Flowmeter. Flow Meas. Instrum. 2006, 17, 201–206. [Google Scholar] [CrossRef]
- Lukács, G.; Martin, R.; Marshall, D. Faithful Least-Squares Fitting of Spheres, Cylinders, Cones and Tori for Reliable Segmentation. In Proceedings of the 15th European Conference on Computer Vision, Freiburg, Germany, 1–5 June 1998; pp. 671–686. [Google Scholar] [CrossRef]
- Zhu, W.J.; Xu, K.J.; Fang, M.; Shen, Z.W.; Tian, L. Variable Ratio Threshold and Zero-Crossing Detection-Based Signal Processing Method for Ultrasonic Gas Flow Meter. Measurement 2017, 103, 343–352. [Google Scholar] [CrossRef]
- Chen, H. Influence of the Upstream Pipe Bends on the Measurement Errors of an Ultrasonic Flowmeter. Master’s Thesis, China Jiliang University, Hangzhou, China, 2014. [Google Scholar]
- Staubli, T.; Tresch, T.; Gruber, P. A Discussion of Uncertainties and of Potential for Improvement of the Acoustic Transit Time Method; Hydro Porto: Oslo, Norway, 2004. [Google Scholar]
- Voser, A.; Bruttinch, C.; Prenat, J.; Staubli, T. Improving Acoustic Flow Measurement. Int. Water Power Dam Constr. 1996, 48, 30–34. [Google Scholar]
- Hu, Y.; Zhang, T.; Zheng, D.D. Estimation of the Influence of Ultrasonic Flowmeter Probe Installation Intrusion Length on Measurement Accuracy. J. Tianjin Univ. (Sci. Technol.) 2013, 46, 776–783. [Google Scholar] [CrossRef]
- Zhang, P.Y.; Zheng, D.D.; Xu, T.S. Study on the Influence of Ultrasonic Probes on Flow Field and Measurement Performance of Ultrasonic Flowmeter. Exp. J. Exp. Fluid Mech. 2011, 25, 60–65. [Google Scholar]
- Zheng, D.D.; Zhao, D. Study on Mechanism of Flow Disturbance Caused by Acoustic Transducers in Flow Measurement. J. Mech. Eng. 2014, 50, 20–22. [Google Scholar] [CrossRef]
- Liu, D.; Liu, H.; Gan, M. Development and Test of Combined Standard Meter Flow Standard Device. Ind. Metrol. 2024, 34, 46–49. [Google Scholar] [CrossRef]
- Wang, B.; Cui, Y.; Liu, W. Study of Transducer Installation Effects on Ultrasonic Flow Metering Using Computational Fluid Dynamics. Adv. Mater. Res. 2013, 629, 676–681. [Google Scholar] [CrossRef]
- Goltsman, A.; Saushin, I. The Resulting Effect of Flow Pulsations on Calibration Constant of Acoustic Path in Ultrasonic Flowmeters. Sensors 2022, 22, 2815. [Google Scholar] [CrossRef]
- Martin, H.; Jacob, S.; Jerker, D. Simulation of Flow Meter Calibration Factors for Various Installation Effects. Measurement 1995, 15, 235–244. [Google Scholar] [CrossRef]
- Lin, J.Z. Turbulent Dynamics; Zhejiang University Press: Hangzhou, China, 2000. [Google Scholar]
- Hallanger, A.; Saetre, C.; Frøysa, K.E. Flow Profile Effects Due to Pipe Geometry in an Export Gas Metering Station-analysis by CFD Simulations. Flow Meas. Instrum. 2018, 61, 56–65. [Google Scholar] [CrossRef]
- Spearman, E.P.; Sattary, J.A.; Reader-Harris, M.J. Comparison of Velocity and Turbulence Profiles Downstream of Perforated Plate Flow Conditioners. Flow Meas. Instrum. 1996, 7, 181–199. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, H.; Meng, T.; Han, C. Experimental Study on the Measurement Performance of Dual Channel Ultrasonic Flowmeter under Obstruction Conditions. Ind. Metrol. 2013, 23, 33–36. [Google Scholar] [CrossRef]
- Zhang, P. Research on the Adaptability of Ultrasonic Flowmeter in the Non-Ideal Flow Field. Master’s Thesis, Tianjin University, Tianjin, China, 2012. [Google Scholar]
- Smith, W.A.; Auld, B.A. Modeling 1-3 Composite Piezoelectrics: Thickness-Mode Oscillations. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1991, 38, 40–47. [Google Scholar] [CrossRef]
- Zhang, S.; Li, F. High Performance Ferroelectric Relaxor-PbTiO3 Single Crystals: Status and Perspective. J. Appl. Phys. 2012, 111, 031301. [Google Scholar] [CrossRef]
- Sadeghi, S.; Najafabadi, M.A.; Javadi, Y. Using Ultrasonic Waves and Finite Element Method to Evaluate Through-Thickness Residual Stresses Distribution in the Friction Stir Welding of Aluminum Plates. Mater. Des. 2013, 52, 870–880. [Google Scholar] [CrossRef]
- Gururaja, T.R. Piezoelectric Composite Materials for Ultrasonic Transducer Applications. Part I: Resonant Modes of Vibration of PZT Rod-Polymer Composites. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1985, 32, 481–498. [Google Scholar] [CrossRef]
- Lynnworth, L.C. Ultrasonic Measurements for Process Control: Theory, Techniques, Applications; Academic Press: Cambridge, MA, USA, 1989. [Google Scholar]
- Willatzen, M. Ultrasonic Flowmeters: Half-Century Progress Report, 1955–2005. Ultrasonics 2006, 44, 1371–1378. [Google Scholar] [CrossRef]
- Zhang, J. A High-Resolution Time-to-Digital Converter Implemented in Field-Programmable-Gate-Arrays. IEEE Trans. Nucl. Sci. 2006, 53, 236–241. [Google Scholar] [CrossRef]
- Robert, H. Time Delay Estimation of Random Signals Using Cross-correlation with Hilbert Transform. Measurement 2019, 146, 792–799. [Google Scholar] [CrossRef]
- Balazs, T.; Attila, B.; Sándor, Z.; Gabor, V.; Gabor, P. Cross-correlation based time delay estimation for turbulent flow velocity measurements: Statistical considerations. Phys. Plasmas 2011, 18, 122304. [Google Scholar] [CrossRef]
- Manuchehri, M.S.; Setarehdan, S.K. A Robust Time Delay Estimation Method for Ultrasonic Echo Signals and Elastography. Comput. Biol. Med. 2021, 136, 104653. [Google Scholar] [CrossRef] [PubMed]
- Guo, R.; Chen, D.; Fei, C.; Li, D.; Zhang, Q.; Feng, W.; Yang, Y. Optimization Design of High-Frequency Ultrasonic Transducer Based on ANFIS and Particle Swarm Optimization Algorithm. Appl. Acoust. 2022, 187, 108507. [Google Scholar] [CrossRef]
- International Electrotechnical Commission (IEC). IEC 61000-4-1: 2006—Electromagnetic Compatibility (EMC)—Part 4-1: Testing and Measurement Techniques—General Guide on the Limits of Electromagnetic Interference; IEC: Geneva, Switzerland, 2006. [Google Scholar]
- Zhang, Y. Research on Measurement Error Compensation of Multi-Channel Ultrasonic Flow Meter. New Technol. New Prod. China 2024, 22, 8–10. [Google Scholar] [CrossRef]
- Zhao, H.; Peng, L.; Stephane, S.A.; Ishikawa, H.; Shimizu, K.; Takamoto, M. CFD-Aided Investigation of Multipath Ultrasonic Gas Flow Meter Performance under Complex Flow Profile. IEEE Sens. J. 2014, 14, 897–907. [Google Scholar] [CrossRef]
- Kurniadi, D.; Trisnobudi, A. A Multi-Path Ultrasonic Transit Time Flow Meter Using a Tomography Method for Gas Flow Velocity Profile Measurement. Part. Part. Syst. Charact. 2006, 23, 330–338. [Google Scholar] [CrossRef]
- Piechota, P.; Synowiec, P.; Andruszkiewicz, A.; Wędrychowicz, W. Selection of the Relevant Turbulence Model in a CFD Simulation of a Flow Disturbed by Hydraulic Elbow—Comparative Analysis of the Simulation with Measurements Results Obtained by the Ultrasonic Flowmeter. J. Therm. Sci. 2018, 27, 413–420. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Xia, X.X.; Li, Y.C.; Cai, F.Y. Ultrasonic Tunable Focusing by a Stretchable Phase-Reversal Fresnel Zone Plate. Appl. Phys. Lett. 2020, 117, 021904. [Google Scholar] [CrossRef]
- Alvarez-Arenas, T.E.G.; Camacho, J.; Fritsch, C. Passive Focusing Techniques for Piezoelectric Air-Coupled Ultrasonic Transducers. Ultrasonics 2016, 67, 85–93. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Lu, W.; Cui, Y.; Sun, T.; Wu, C.; Xu, Y.; Li, P. Field Simulation and Measurement of Effective Radiating Area of Planar Non-Focused Therapeutic Ultrasound Transducers. Measurement 2025, 254, 117907. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, W.; Shen, P.; Wang, C.; Jiang, Y. A Fault Diagnosis Method for Ultrasonic Flow Meters Based on KPCA-CLSSA-SVM. Processes 2024, 12, 809. [Google Scholar] [CrossRef]
- Wang, W.T. Multi-Channel Gas Ultrasonic Flowmeter Flow Field Adaptability. Master’s Thesis, Northeast Petroleum University, Daqing, China, 2011. [Google Scholar]
- Mousavi, S.F.; Hashemabadi, S.H.; Jamali, J. Calculation of Geometric Flow Profile Correction Factor for Ultrasonic Flow Meter Using Semi-3D Simulation Technique. Ultrasonics 2020, 106, 106165. [Google Scholar] [CrossRef]
- Joshi, S.G. Ultrasonic Flow Meter Using Mode Coupling Transducers. Ultrasonics 2021, 116, 106497. [Google Scholar] [CrossRef]
- Guo, S.; Xiang, N.; Li, B.; Wang, F.; Zhao, N.; Zhang, T. Integration Method of Multipath Ultrasonic Flowmeter Based on Velocity Distribution. Measurement 2023, 207, 112388. [Google Scholar] [CrossRef]
- Hon, S.F.; Kwok, K.W.; Li, H.L. Self-Focused Acoustic Ejectors for Viscous Liquids. Rev. Sci. Instrum. 2010, 81, 065102. [Google Scholar] [CrossRef]
- LeMay, G.S.; Askari, D. A New Method for Ultrasonic Detection of Peel Ply at the Bondline of Out-of-Autoclave Composite Assemblies. J. Compos. Mater. 2019, 53, 245–259. [Google Scholar] [CrossRef]
- Aeinfar, S.; Serteser, N. Parametric Study of Energy Optimization and Airflow Management in High-Rise Buildings with Double-Skin Façade Using a Genetic Algorithm and CFD. J. Build. Eng. 2025, 105, 112441. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Wu, G. An Acoustic Pressure-Gradient MEMS Vector Hydrophone System Based on Piezoelectric Micromachined Ultrasonic Transducer Array. Microelectron. J. 2024, 151, 106332. [Google Scholar] [CrossRef]
- Javadi, Y.; Pirzaman, H.S.; Raeisi, M.H. Ultrasonic Inspection of a Welded Stainless Steel Pipe to Evaluate Residual Stresses Through Thickness. Mater. Des. 2013, 49, 591–601. [Google Scholar] [CrossRef]
- Javadi, Y.; Pirzaman, H.S.; Raeisi, M.H. Ultrasonic Evaluation of Welding Residual Stresses in Stainless Steel Pressure Vessel. J. Press. Vessel Technol.-Trans. ASME 2013, 135, 041502. [Google Scholar] [CrossRef]
- He, X.L.; Duan, Y.X.; Fan, Q.W. Correction of Coupling Error in Contact-Type Ultrasonic Evaluation of Bolt Axial Stress. Ultrasonics 2022, 124, 106763. [Google Scholar] [CrossRef] [PubMed]
- Rincón, M.J.; Reclari, M.; Yang, X.; Abkar, M. Validating the Design Optimization of Ultrasonic Flow Meters Using Computational Fluid Dynamics and Surrogate Modelling. Int. J. Heat Fluid Flow 2023, 100, 109112. [Google Scholar] [CrossRef]
- Liang, F.; Hang, Y.; Yu, H.; Gao, J. Identification of Gas-Liquid Two-Phase Flow Patterns in a Horizontal Pipe Based on Ultrasonic Echoes and RBF Neural Network. Flow Meas. Instrum. 2021, 79, 101960. [Google Scholar] [CrossRef]
- Murai, Y.; Tasaka, Y.; Nambu, Y.; Takeda, Y.; Gonzalez, S. Ultrasonic Detection of Moving Interfaces in Gas–Liquid Two-Phase Flow. Flow Meas. Instrum. 2010, 21, 356–366. [Google Scholar] [CrossRef]
- Wang, X.F.; Tang, Z.A. Note: Ultrasonic Gas Flowmeter Based on Optimized Time-of-Flight Algorithms. Rev. Sci. Instrum. 2011, 82, 1371–1384. [Google Scholar] [CrossRef]
- Zou, Z.Y.; Hao, Y.P.; Tian, F.Y. An Ultrasonic Longitudinal Through-Transmission Method to Measure the Compressive Internal Stress in Epoxy Composite Specimens of Gas-Insulated Metal-Enclosed Switchgear. Energies 2020, 13, 1428. [Google Scholar] [CrossRef]
- Liu, L.; Li, B.; Liu, S.; Wang, K.; Gu, H. Recognition of Gas-Liquid Flow Regimes in Helically Coiled Tube Using Wire-Mesh Sensor and KNN Algorithm. Int. J. Multiph. Flow 2022, 154, 104144. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Z.; Yu, F.; Yan, T.; He, B. Computational Fluid Dynamics Driven Surrogate Model to Predict Hydrodynamic and Acoustic Properties of Propeller Boss Cap Fins. Appl. Ocean Res. 2024, 153, 104293. [Google Scholar] [CrossRef]
- Petris, G.; Cianferra, M.; Armenio, V. Full Acoustic Analogy of the Fluid-Dynamics Noise of an Immersed Cube. Ocean Eng. 2024, 300, 117433. [Google Scholar] [CrossRef]
- Liu, W.; Wang, X.; Peng, Z.; Guo, F. Optimized Kalman Filter Techniques for Ultrasonic Flow Measurement. J. Phys. Conf. Ser. 2024, 2897, 012039. [Google Scholar] [CrossRef]
- Safikhani, H.; Esmaeili, F.; Rezvani, S. Extracting a Smart Model for Determining Defrost Time in Household Refrigerators Using a Combination of CFD, Experimental Data, and GMDH Type Artificial Neural Network. Int. J. Refrig. 2025, 176, 52–56. [Google Scholar] [CrossRef]
- Mazzuto, G.; Ciarapica, F.E.; Ortenzi, M.; Bevilacqua, M. The Digital Twin Realization of an Ejector for Multiphase Flows. Energies 2021, 14, 5533. [Google Scholar] [CrossRef]
- Li, M.; Li, Z.; Li, C. In-use Measurement of Ultrasonic Flowmeter Based on Machine Learning. Measurement 2023, 223, 113721. [Google Scholar] [CrossRef]
- Alexander, Y.G.; Mikhail, G.G.; Yuri, G.G.; Armando, M.L. Synthetic Turbulence Modeling for Evaluation of Ultrasonic Cross-correlation Flow Measurement. Flow Meas. Instrum. 2018, 60, 134–143. [Google Scholar] [CrossRef]
- Jack, M.; Paul, L.M.J.; Douwe, M.W.; Nicolaas, J.; Michiel, A.P.P.; Martin, D.V. Exploiting Nonlinear Wave Propagation to Improve the Precision of Ultrasonic Flow Meters. Ultrasonics 2021, 116, 106476. [Google Scholar] [CrossRef]
- Landskron, J.; Dötzer, F.; Benkert, A.; Mayle, M.; Drese, K.S. Acoustic Limescale Layer and Temperature Measurement in Ultrasonic Flow Meters. Sensors 2022, 22, 6648. [Google Scholar] [CrossRef]
- Hong, L. Design of Time Difference Ultrasonic Flowmeter Based on Adaptive Kalman Filter. Master’s Thesis, Huaiyin Institute of Technology, Huai’an, China, 2024. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Yang, X.H. Fusion of Cross-correlation Method and Optical Flow Method for Flow Measurement. China Water Transp. 2023, 23, 98–100. [Google Scholar]
- Zhao, Y.; Dong, K.; Liu, G.; Liu, X.; Min, Z.; Li, Z.; Ma, X.; Gao, L. Development and Field Application of Reversible Pump Turbine Efficiency Testing Software Based on Ultrasonic Method and Spiral Case Differential Pressure Method. Water Resour. Power 2015, 33, 159–162. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).