A Scoping Review of Energy Consumption in Industrial Robotics

Abstract

The increasing adoption of industrial robots has significantly advanced manufacturing efficiency and flexibility. However, this expansion introduces new energy consumption challenges, especially as electricity has become the dominant energy source in automated systems. As the industrial sector faces rising energy costs and ambitious sustainability goals, understanding and minimizing the energy consumption of robotic systems is imperative. This review presents a structured analysis of energy consumption in industrial robots, linking mechanical design, actuation systems, and control strategies to their energetic effects. We first discuss different industrial robot types and their kinematic configurations, identifying how structural characteristics influence energy use. The article then categorizes energy consumption optimization strategies into software-based and hardware-based approaches. A comparative SWOT analysis highlights the strengths and limitations of each approach. The review also explores emerging trends such as DC microgrid integration. The future directions underline the need for standardized energy assessment frameworks and the development of hybrid optimization strategies that combine the reviewed approaches, suitable for being applied in real-world industrial robot applications. This work provides a comprehensive foundation for establishing best practices in energy consumption optimization for industrial robots.

1. Introduction

The adoption of Industry 4.0 technologies has driven a rapid increase in the use of industrial robots (IRs) over the past decade. According to the International Federation of Robotics (IFR), more than 4 million IRs were installed globally by 2024—a 10% increase from 2023 and nearly three times the amount in 2014 [1]. This surge reflects the growing demand for automation to improve productivity, quality, and operational flexibility across manufacturing sectors.

ISO 8373:2021 defines an IR as “an automatically controlled, reprogrammable multipurpose manipulator, programmable in three or more axes, which can be either fixed in place or fixed to a mobile platform for use in automation applications in an industrial environment” [2]. This definition encompasses not only the manipulator but also its actuators, the robot controller, including all associated hardware, software communication interfaces, and the teach pendant. The term reprogrammable indicates that the robot’s motion instructions can be modified through software without any physical changes to the system, while multipurpose underscores the robot’s versatility across a range of applications.

Energy efficiency has become a central priority for industrial manufacturing, particularly in light of rising energy costs and climate goals. The European Union (EU) has committed to reducing overall energy consumption by at least 11.7% by 2030 [3]. In 2022, the industrial sector was the third-largest energy consumer in the EU, accounting for 25.1% of final energy use, with electricity comprising the largest share at 33% [4]. Improving energy performance in industrial operations is therefore crucial not only for meeting sustainability targets but also for reducing manufacturing costs and maintaining competitiveness.

Recognizing this challenge, the IFR has identified sustainability and energy efficiency as key trends shaping the future of robotics [5]. When properly integrated, robotic systems can enhance production efficiency and resource utilization [6]. Robots often execute tasks with greater efficiency and consistency, which enables increased production throughput, ultimately contributing to improved energy efficiency [7,8]. Additionally, as noted in [9], fully automated facilities can implement “lights-out” manufacturing, where operations proceed without human intervention. This approach further reduces energy usage by eliminating non-essential energy consumers such as lighting and other support systems. Recent studies demonstrate that the application of IRs plays a significant role in optimizing energy consumption within the entire manufacturing company [10]. This impact underscores the importance of integrating robots in the evolving industrial landscape and modern energy transition strategies.

However, the widespread deployment of IRs may increase overall energy demand. IRs are complex electromechanical systems that consume significant energy during operation. They require power to drive actuators, control electronics, auxiliary components, and end effectors. Numerous studies have explored energy consumption optimization (ECO) in industrial robotics from various angles, including dynamic modeling, trajectory planning, control strategy optimization, and hardware-level improvements, as stated in recent topical reviews [11,12,13,14]. Relatively few works have demonstrated how their findings are implemented in real-world IR applications within manufacturing settings like in [15]. While ECO in IRs has been studied from various perspectives, including various control algorithms, trajectory planning, and hardware enhancements, relatively little attention has gone towards how the kinematic structure of IRs, together with its controllable aspects, influences energy usage. This constitutes a crucial gap in the literature, especially considering the diverse kinematic configurations in use today. This review aims to bridge that gap.

A literature search was performed to conduct this scoping review using the databases Google Scholar, IEEE Xplore, and Scopus. The search strategy involved combinations of keywords such as “industrial robot”, “energy optimization”, “energy consumption”, “energy-efficient control”, “energy-efficient trajectory”, and “kinematic structure”. The search included peer-reviewed journal articles, conference papers, and preprints, published in the English language. Studies were considered eligible if they addressed energy consumption or energy optimization in the context of IRs, with a focus on either control strategies, mechanical design, or system-level considerations. Papers that focused solely on mobile robots, legged robots, or service robots were excluded. The selection followed the PRISMA 2020 guidelines [16], specifically the extension for scoping review (PRISMA-ScR) [17]. Titles and abstracts were screened for relevance, followed by full-text review. Articles lacking technical depth or applicability to IRs were removed.

The remainder of this paper is organized as follows: Section 2 presents an overview of IR types and kinematic structures, linking mechanical design with energetic characteristics. Section 3 presents a comprehensive review of ECO strategies, encompassing both software-based approaches, such as parameter tuning, task scheduling, and trajectory planning, and hardware-based methods, including structural design, energy recovery systems, and the application of functional redundancy. Additionally, a SWOT analysis is provided to compare the various software- and hardware-based approaches. This is followed by a discussion and suggestions for future research directions in Section 4.

2. Background: Characteristics of Industrial Robots

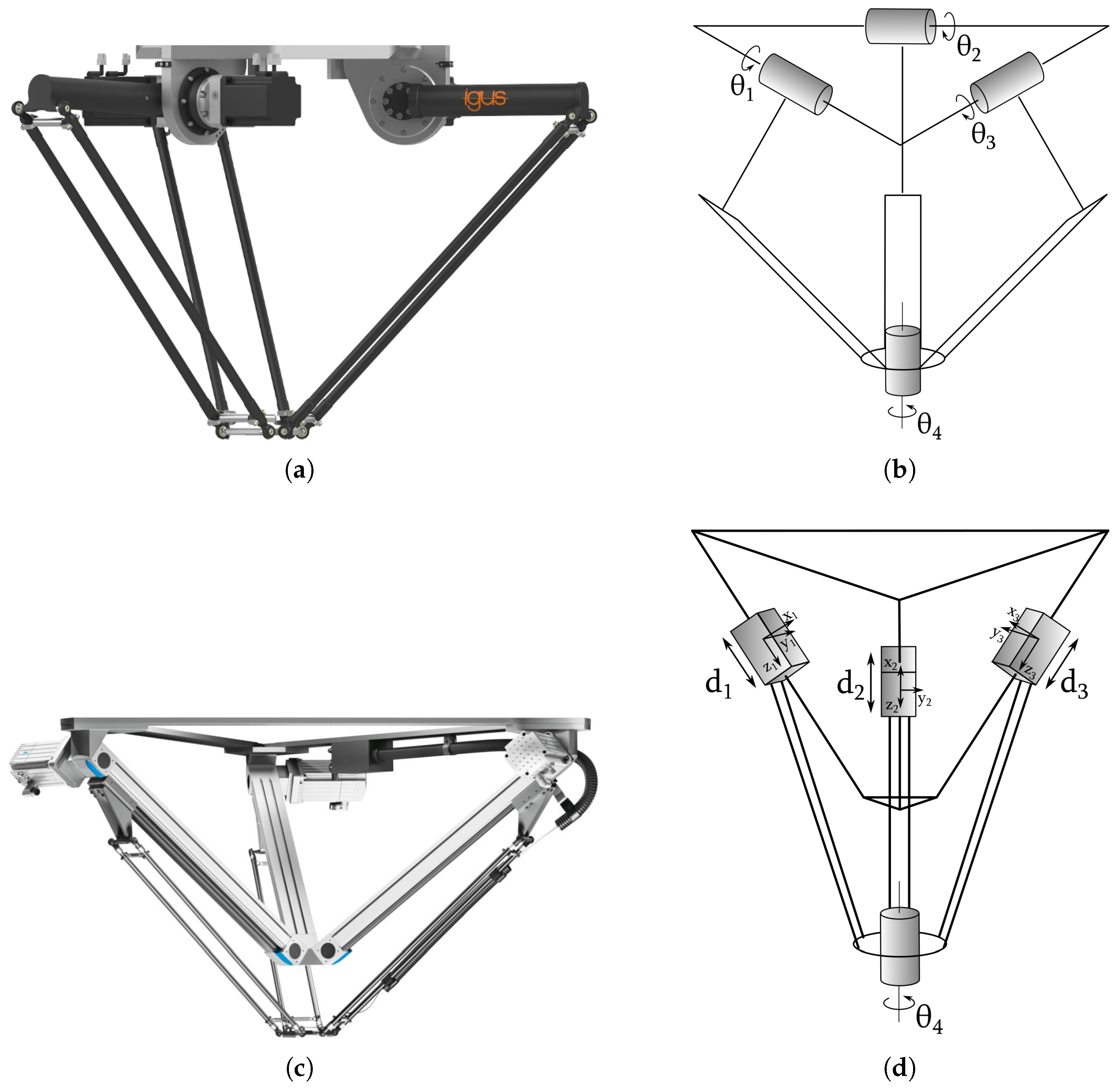
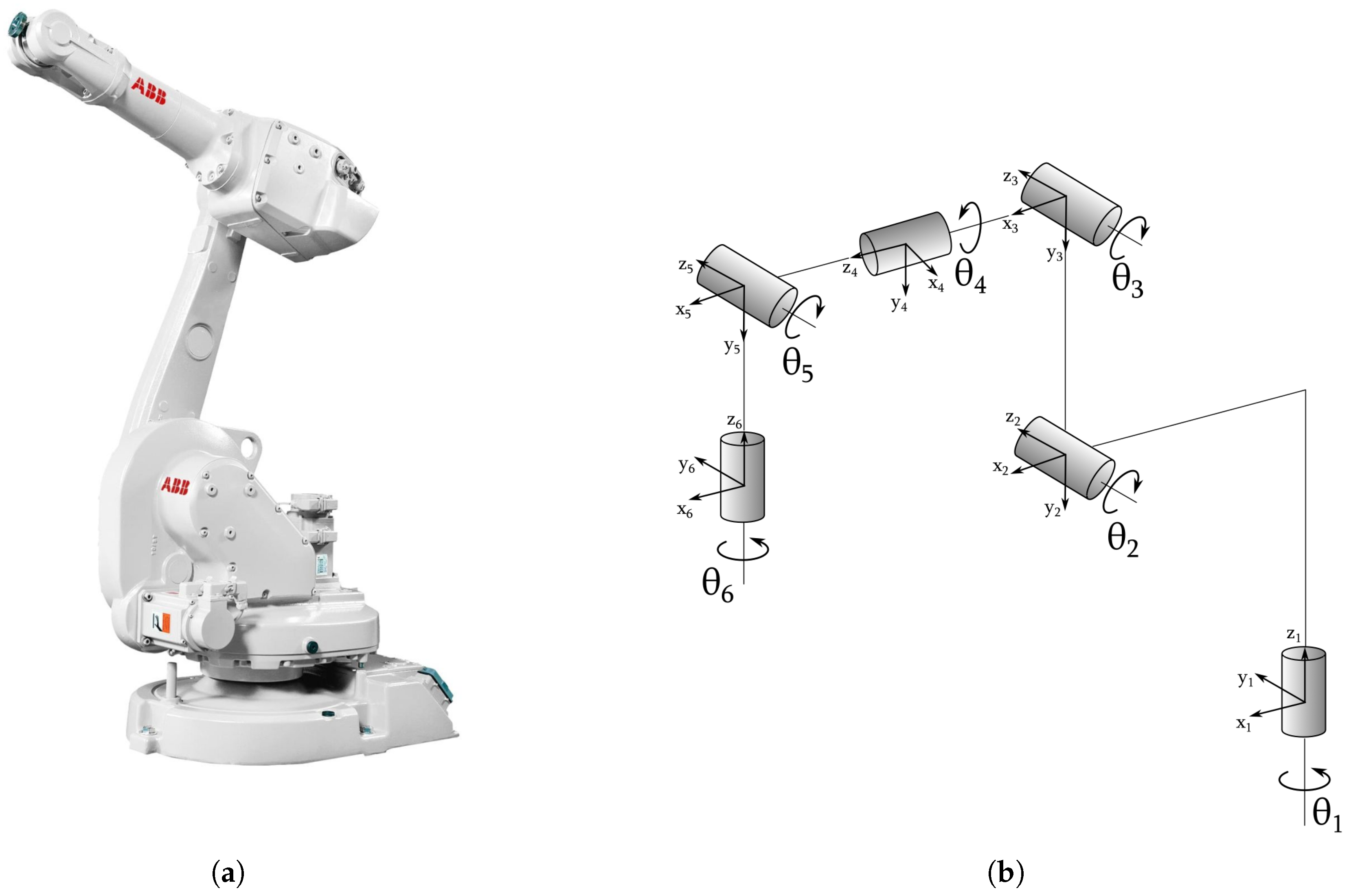
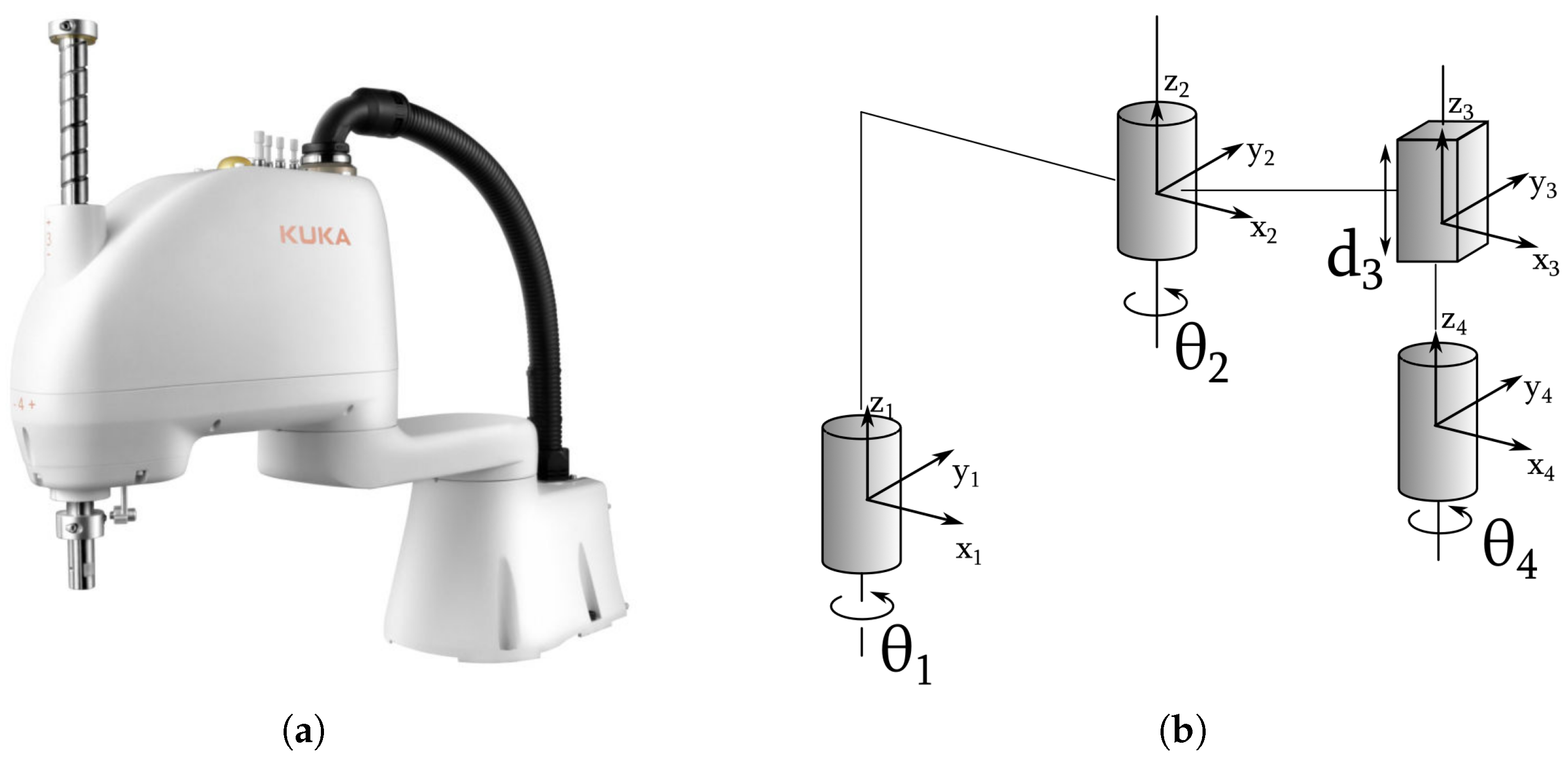
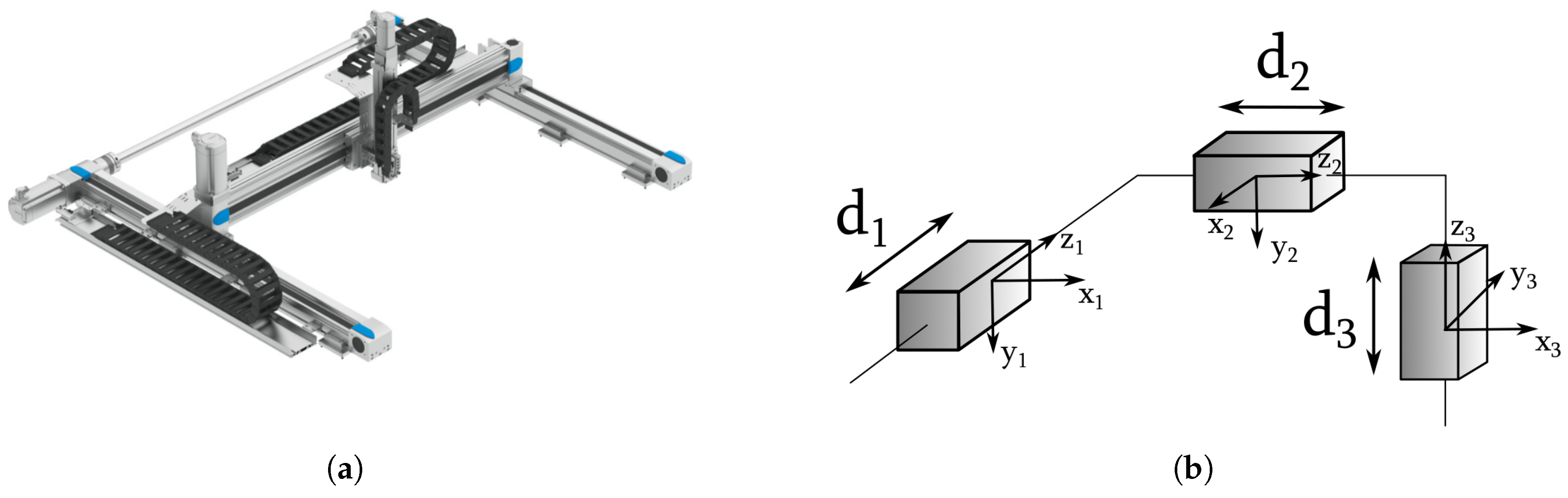
2.1. Definition and Types of Industrial Robots

According to IFR, IRs can be categorized based on their mechanical structure into the following types [18]:

• Articulated robot;
• SCARA robot;
• Cartesian robot;
• Parallel/Delta robot;
• Cylindrical robot;
• Polar robot.

Articulated robots are among the most widely deployed robot types in industrial settings, primarily due to their high versatility [19]. This is largely enabled by their kinematic structure, which allows for functional redundancy, and a wide range of motion relative to their physical size. Articulated robots are built from several interconnected links, which are connected through revolute joints (Figure 1). Each joint provides the robot one degree of freedom (DOF). The most common configurations of articulated robots are 4-DOF to 6-DOF. Articulated robots are adaptable to various automation tasks that require complex motions. However, complex configuration means more complex programming, as well as higher costs and more frequent maintenance for the robot.

A SCARA (Selective Compliance Assembly Robot Arm) robot usually consists of three revolute and one prismatic joint (Figure 2). SCARA robots are mainly designed for tasks requiring high-speed, precise, and repeatable movements within a horizontal plane. The term “selective compliance” comes from the characteristic compliance of the joints in the X-Y direction, which makes the robot best suited for assembly applications; yet they are extensively used in material handling and pick-and-place tasks as well. Thanks to their compact size, simple design, and cost effectiveness, SCARA robots excel in environments with limited space and high throughput demands.

A Cartesian robot, also known as a linear robot or gantry robot, operates on three prismatic joints perpendicular to each other, forming a rectangular coordinate system (Figure 3). This simple design provides high precision and repeatability, making Cartesian robots ideal for applications such as CNC machining and 3D printing, as well as simple pick-and-place tasks. Their structure allows for scalability, enabling larger workspaces and higher payload capacities compared to other robot types. Cartesian robots are widely used in manufacturing, logistics, and laboratory automation due to their straightforward programming and efficiency in tasks requiring linear movements.

A Delta robot is a high-speed parallel robot with a lightweight structure. Most commonly, the robot comprises three arms with a parallelogram structure connected to revolute joints at the base allowing three DOFs (Figure 4). Some configurations also use prismatic joints instead of the revolute joints in the form of linear axes to drive the arms [23].

The structural characteristics that make Delta robots effective in industrial applications include symmetry, distributed actuation, and rigid constraint-based motion. These principles can be more generally described through the framework of parallel mechanism synthesis [24,25], which allows for the systematic exploration of alternative limb configurations and constraint arrangements that achieve similar or expanded motion capabilities. The Delta robot is typically implemented using a 3-RRR configuration (Figure 4b). However, other topologies, such as the 3-PRR configuration shown in Figure 4d, belong to the same family of parallel mechanisms.

These unique designs keep the orientation of the end effector unchanged, and the structure provides high stability, high-speed operation, and low inertia. In most cases, the end plate is equipped with an additional revolute joint to allow rotational movement for the end effector. The robot excels in performing precise and rapid movements and is often used in tasks requiring quick pick-and-place operations, sorting, and packaging in industries such as food processing, pharmaceuticals, and electronics.

Figure 4. (a) Igus Delta LCA-DR1000-04 robot [26], (b) kinematic diagram of delta robot with rotational links, (c) Festo EXPT-45-E1 robot [27], (d) kinematic diagram of Delta robot with linear links.

Figure 4. (a) Igus Delta LCA-DR1000-04 robot [26], (b) kinematic diagram of delta robot with rotational links, (c) Festo EXPT-45-E1 robot [27], (d) kinematic diagram of Delta robot with linear links.

Cylindrical and polar robots are generally regarded as obsolete in contemporary industrial applications due to their limited usage. A modern alternative to cylindrical robots is the 4-axis articulated robot, which is widely employed in industry today, particularly for palletizing tasks [28]. Polar robots share a similar workspace configuration with higher DOF articulated robots, offering comparable reach and motion capabilities, although with reduced flexibility and precision.

The kinematic design of an IR plays an important role in its energy consumption. Robots with serial kinematics, such as articulated robots, often experience cumulative inertial effects along their kinematic chain. Each additional joint must support the mass and movement of all subsequent joints, which leads to higher torque requirements, especially in the base joints. This increases the demand for more powerful motors and leads to higher energy consumption during dynamic operations. Strategies such as robot positioning to minimize gravitational torque are applicable here to minimize the consumed energy, especially during standstill [29,30].

Another notable characteristic of articulated manipulators is kinematic redundancy, which provides additional degrees of freedom beyond those minimally required for a given task. This redundancy enhances the robot’s flexibility, as the system has multiple possible configurations to reach the same end-effector pose. However, this also introduces challenges in energy-efficient control, as not all configurations are energetically equivalent. Choosing a posture that minimizes joint torques becomes important for reducing energy consumption, while intelligent path-planning algorithms can exploit the redundancy to optimize not only for time and collision avoidance but also for energy [31,32]. Hence, the presence of redundancy affects the control system as well as the joint and link design that can efficiently execute a range of configurations.

In parallel robot architectures, the payload is supported directly by all actuators, which can typically be positioned on or near the robot base. This configuration allows the connecting links between the base and the mobile platform to be significantly lighter, resulting in a substantially higher payload-to-robot-mass ratio [33]. In terms of accuracy and repeatability, parallel robots offer clear advantages over serial counterparts. In serial manipulators, errors such as backlash, friction, and joint compliance accumulate along the kinematic chain, with greater influence from joints located closer to the base. Parallel robots avoid this cascading error effect and exhibit high structural rigidity, even with lightweight components. Additionally, due to their favorable payload-to-mass ratio and reduced joint coupling, parallel robots demonstrate superior dynamic performance compared to serial configurations [34]. Some recent studies have also investigated energy minimization strategies for Delta robots [35,36].

The researchers in [37] showed that parallel manipulators tend to be on average more energy efficient than serial manipulators with similar work capacity. The energetic characteristic of parallel robots is mostly affected by the actuator placement and load distribution. In many parallel configurations, the heavy actuators are fixed to the base, which significantly reduces the moving mass [38]. This, in turn, leads to lower inertia [39], meaning less energy is required for acceleration and deceleration. Furthermore, the symmetry and rigidity of the structure allow for efficient force transmission, and the closed-loop kinematics enable multiple limbs to share the load, reducing peak actuator demand [40].

Variations in kinematic structure directly affect component selection, especially regarding motors, gearboxes, and power electronics. For example, a robot designed for high-speed operations with short reach and low payload may utilize low-inertia motors and harmonic drives to achieve a desired efficiency [41,42]. On the other hand, a long-reach articulated robot operating under high payload demands requires high-torque motors and robust gearboxes, which may increase both energy consumption and system complexity [42]. These design decisions represent a balance between functional versatility and energy cost, emphasizing the need for an integrated co-design approach that merges mechanical architecture with energy-aware component selection. Motor sizing and gear ratio choices must accommodate worst-case torque demands, which in turn contribute substantially to the overall energy budget of the system.

In high-precision applications such as welding, assembly, or machining, energy consumption is often secondary to motion accuracy and repeatability. In these cases, trajectory smoothness and tool-path precision are prioritized, sometimes at the expense of optimal energy use. With optimization techniques such as trajectory planning or workstation redesign, studies have shown that the possible energy savings are modest, typically in the range of 10% [43,44].

Applications involving high-speed, repetitive motions, and larger movements—such as sorting, palletizing, and packaging—present greater opportunities for energy consumption optimization. These tasks typically involve predictable motion patterns and shorter cycle times, making them ideal for various ECO strategies. Generally, reported savings in such use cases are substantially higher—up to 30% in palletizing [28], 45% in pick-and-place, and 25% in bin-picking scenarios [45], and in moderate-complexity operations such as drilling, energy reductions approaching 18% have been achieved when optimization strategies are applied [45].

Table 1. Comparison of industrial robot configurations by degrees of freedom, typical application areas, and relative energy optimization potential. The energy optimization priority reflects how suitable or critical energy consumption strategies are for each robot type and task context.

DOF/Motors	Robot Type	Typical Use Cases	ECO Priority
3	Cartesian	CNC machining, 3D printing	Low
4	SCARA, Delta, Articulated	High-speed assembly, sorting, packaging, pick-and-place, palletizing	High
5	Articulated	Pick and place, palletizing	High
6	Articulated	Welding, painting, machining, assembly	Low-Medium
7	Articulated	Human-robot collaboration, flexible tasks	Medium

summarizes typical application areas in relation to different kinematic configurations of IRs. It is important to note that the listed use cases refer to the kinds of applications that can be realized with a given kinematic structure—not to the specific systems themselves. The ECO priority levels presented in the table offer a reasoned estimation of how critical or suitable energy optimization strategies are for each use case. However, these assessments are not yet universally validated. The literature in this domain remains limited, often relying on isolated case studies.

2.2. Fundamentals of Energy Consumption in Industrial Robots

IRs are complex systems composed of various interconnected components, each having a specific function in the robotic system. These components—such as motors, transmissions, controllers, sensors, and end effectors—work together to make the robot move with high accuracy and efficiency as is desired in a manufacturing environment. The total energy consumption of an IR is not determined by any single component but rather by the interaction between all of them; however, the drive system, which is responsible for robot motion, is the primary contributor to the overall energy consumption [46].

Traditionally, the actuators have been powered by three primary sources: electrical, pneumatic, and hydraulic systems [47,48]. Hydraulic actuators were preferred for IRs during the early stages of robotics development [49,50] due to their high power-to-weight ratio, robustness, and ability to handle large payloads with rapid dynamics and precise positioning. These systems operate by converting pressurized fluid energy into mechanical force, typically using oil as the working fluid. Hydraulic robots are especially prevalent in heavy machinery and construction equipment, where high strength and quick response are essential. However, they tend to be complex, nonlinear, and require careful control design to manage their dynamics effectively [51].

Pneumatic actuators, sharing a similar working principle as hydraulic systems, are often favored in automation environments requiring clean and dry conditions, focusing primarily on the gripping mechanisms of IRs [52,53]. Pneumatic systems are generally lighter and simpler than hydraulic ones but face challenges in precise control due to the air compressibility and hysteresis effects inherent in the actuators [47]. However, the power delivery in pneumatic systems is continuous via compressors, and the systems in general tend to have low efficiencies [54]. Energy consumption in Europe of pneumatic systems accounts for around 10% of total industrial power consumption [55].

Electric actuation systems in IRs convert electrical energy directly into mechanical motion, typically through servo motors coupled with various transmission mechanisms. Electric actuation is by far the most common source used in IRs [47]. They offer advantages in the smoothness of motion, precise velocity and acceleration control, and energy efficiency. Electric actuators are widely used in applications requiring high precision and repeatability. Compared to fluid power systems, electric actuators generally have a smaller footprint and produce less noise, making them suitable for a broad range of industrial tasks [51].

In electrically powered robots, energy is supplied primarily through an AC grid connection, which is internally converted to a DC supply via power electronics. This DC bus powers the robot’s servo drives, which in turn control brushless AC servo motors at each joint [56]. These motors are responsible for executing precise motions, with varying torque and velocity demands depending on the task dynamics and the robot’s kinematic structure. In addition to the actuator system, electrical energy also supports the robot’s control system, including the central processing unit, safety modules, sensors, human–machine interfaces (HMIs), and cooling mechanisms [56]. While the control-side consumption remains relatively constant, the majority of electrical energy is expended in driving the manipulator joints [46], where the efficiency is influenced by factors such as joint kinematics, mechanical transmission efficiency, motion profiles, and dynamic loads [29]. Therefore, analyzing and optimizing electrical power consumption at the manipulator level is crucial for developing energy-efficient robotic systems.

One of the emerging trends in industrial automation is the integration of DC microgrids with robotic systems, aimed at improving energy efficiency, system modularity, and renewable energy compatibility [57,58,59]. Unlike traditional AC-based distribution, DC microgrids offer several advantages in robotic applications, including reduced conversion losses, simplified power electronics, and better compatibility with onboard energy storage and regenerative braking systems [60]. IRs, particularly those operating in multi-robot cells or high-speed repetitive tasks, can generate significant amounts of regenerative energy during deceleration phases. When integrated into a shared DC microgrid, this energy can be redistributed to other robots or stored locally for later use, minimizing dissipation through braking resistors [60,61]. Moreover, DC microgrids facilitate the seamless integration of renewable sources [57], capacitive storage [60], and intelligent energy management systems [61]. These solutions shift toward a holistic energy management system in manufacturing environments, where IRs function not only as energy consumers but also as active participants in decentralized, intelligent energy networks.

Figure 5 inspired by [56] shows a schematic of the power distribution within an IR system. A standard 6-DOF articulated IR is actuated by a multi-drive servo system including six servo motors in each joint and the related power converters, composed of a rectifier (AC/DC), DC-bus, and inverters (DC/AC), which are usually referred to as servo drives.

The overall power fed from the main grid $P_{ac}$ is converted at the rectifier $P_{dc}$ and divided between the power delivered to the servo drives $P_{sd}$, to the control cabinet $P_{cab}$ and to the electromechanical brakes $P_{br}$. $P_{sd}$ contributes to the motors $P_m$. Each conversion stage is associated with relevant electric power losses ($P_{rec,loss},P_{sd,loss},P_{m,loss}$). Mechanical power $P_{mech}$ is delivered via motor shafts to the robot’s mechanical structure to move the joints ($P_{jnt}$) and the payload ($P_{pyl}$). Mechanical power loss $P_{mech,loss}$ also exists due to mechanical friction within the manipulator.

The term $P_{cab}$ refers to the load-independent power required to operate the robot’s control infrastructure, including the controller, teach pendant, cooling systems, and other auxiliary electronics. This also includes the constant power requirements of internal control components, such as the rectifier ($P_{rec,const}$) and the servo drives ($P_{sd,const}$). Losses ($P_{cab,loss}$) also exist here. The DC-bus capacitance ($C_{dc}$) functions as an energy buffer during regenerative braking events, storing the recuperated energy. However, due to the limited storage capacity of the capacitor, surplus energy that cannot be buffered is dissipated through the DC-bus balancing resistor ($R_{dc}$) to prevent over-voltage [60].

The relationship between the joint torques of an industrial manipulator and the changes in its joint positions can be characterized through inverse dynamics computations, which can be represented by the function

$$\mathit{\tau }=f(\mathbf{q},\dot{\mathbf{q}},\ddot{\mathbf{q}}),$$

(1)

where $\mathit{\tau }\in {\mathbb{R}}^n$ (n—number of joints) is the vector of joint torques, $\mathbf{q}\in {\mathbb{R}}^n$ is a vector of joint positions, $\dot{\mathbf{q}}\in {\mathbb{R}}^n$ is a vector of joint velocities, $\ddot{\mathbf{q}}\in {\mathbb{R}}^n$ is a vector of joint accelerations.

The dynamic behavior of serial manipulators with revolute joints in joint space is commonly described by a generalized nonlinear differential equation [62]

$$\mathit{\tau }=\mathbf{M}\left(\mathbf{q}\right)\ddot{\mathbf{q}}+\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}+\mathbf{G}\left(\mathbf{q}\right)+{\mathbf{F}}_{\mathbf{f}}\left(\dot{\mathbf{q}}\right),$$

(2)

where $\mathbf{M}\left(\mathbf{q}\right)\in {\mathbb{R}}^{n\times n}$ is the generalized inertia matrix, $\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}$ denotes the Coriolis and centrifugal forces, $\mathbf{G}\left(\mathbf{q}\right)$ is a vector of gravity terms, and ${\mathbf{F}}_{\mathbf{f}}\left(\dot{\mathbf{q}}\right)$ represents friction effects in the system. This equation captures how joint torques must compensate for inertia, Coriolis and centrifugal forces, gravity, and mechanical friction to follow a desired motion trajectory.

Parallel robots feature closed-loop kinematic chains where multiple limbs simultaneously support and actuate the end effector. This structural difference affects both the dynamic behavior and the control complexity of such systems. The closed-loop nature introduces kinematic constraints that must be respected at all times. These constraints relate the motion of different joints and ensure that the end effector follows a physically valid path. For parallel robots, the general dynamic model can be expressed as [63,64]

$$\mathit{\tau }+{\mathbf{J}}^T\left(q\right)\mathit{\lambda }=\mathbf{M}\left(\mathit{q}\right)\ddot{\mathit{q}}+\mathbf{C}(\mathit{q},\dot{\mathit{q}})\dot{\mathit{q}}+\mathbf{G}\left(\mathit{q}\right)+{\mathbf{F}}_{\mathbf{f}}\left(\dot{\mathbf{q}}\right).$$

(3)

The constraint forces are incorporated into the dynamic model through the Jacobian, ${\mathbf{J}}^T\left(q\right)$, and the vector of Lagrange multipliers, $\mathit{\lambda }$, which are associated with the closed-loop kinematic constraints. Physically, the Lagrange multipliers represent the internal constraint forces required to maintain the closed-loop structure, and these forces are mapped to individual actuators via the Jacobian [65].

Cartesian robots are composed exclusively of orthogonal prismatic joints. Their dynamics are inherently simpler than those of articulated or parallel manipulators because of their linear and decoupled nature of motion. Coriolis or centrifugal effects are minimal or absent. The dynamic model thus reduces to a set of second-order linear differential equations, where actuator forces directly control axis accelerations. We can generalize the model as [66]

$$\mathit{F}=\mathbf{M}\ddot{\mathbf{p}}+\mathbf{G}\left(\mathbf{p}\right)+{\mathbf{F}}_{\mathbf{f}}\left(\dot{\mathbf{p}}\right),$$

(4)

where $\mathbf{p}$ is a vector of Cartesian position. The gravitational term mainly affects the vertical $\left(z\right)$ axis. Cartesian structures are often more energy efficient due to simpler dynamics and lower internal motion losses.

The torque exerted by the robot joints is linked to instantaneous mechanical power

$$P\left(t\right)=\sum _{i=1}^n{\tau }_i\left(t\right)·{\dot{q}}_i\left(t\right),$$

(5)

and the mechanical energy consumption

$$E={\int }_{t_0}^{t_f}P\left(t\right)dt={\int }_{t_0}^{t_f}\sum _{i=1}^n{\tau }_i\left(t\right)·{\dot{q}}_i\left(t\right)dt.$$

(6)

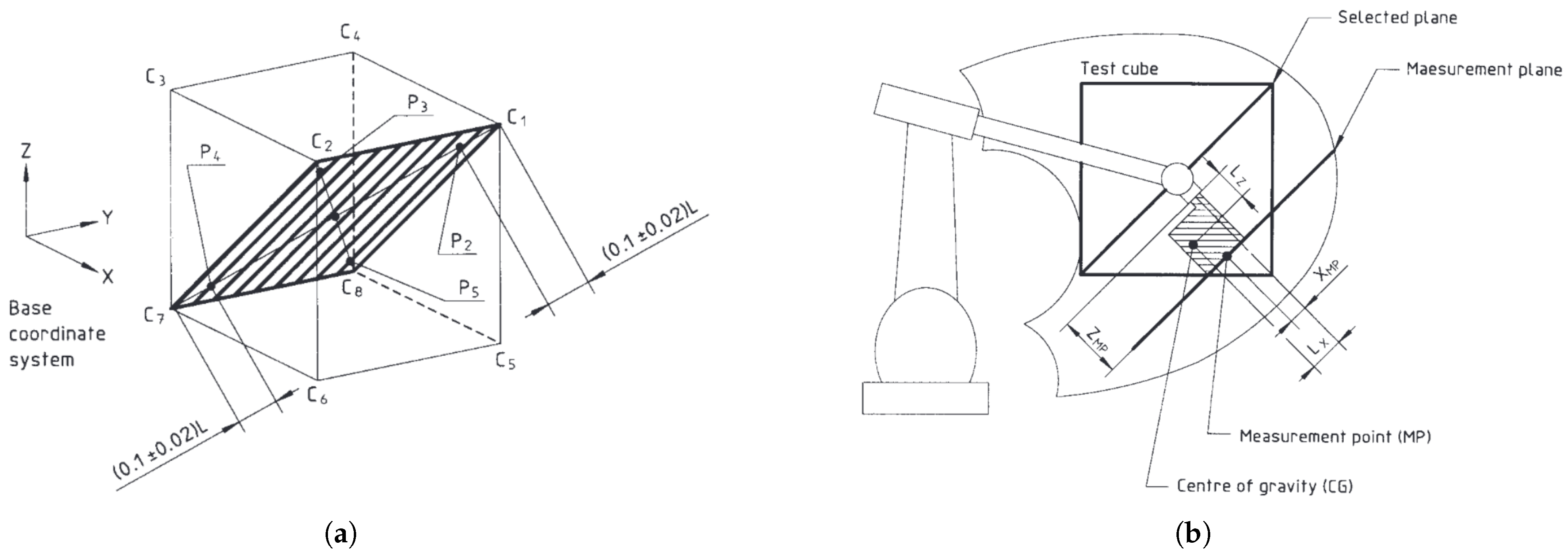
2.3. Assessing the Energy Performance of an IR

ISO 9283:1998 [67] describes the methods for testing various performance characteristics for IRs, such as pose accuracy and pose repeatability. The performance is tested using a defined cubical volume within the robot’s workspace (Figure 6). The test trajectories must be contained within that cube. There are certain constraints that must be applied. Firstly, the cube must be located in a portion of the workspace with the greatest anticipated use. Secondly, the cube must have the maximum possible volume with the edges parallel to the base coordinate system. One diagonal plane is then selected. The measurement plane, on which five measurement points are selected for testing, must be parallel to the selected diagonal plane.

Some robot manufacturers have taken this procedure to assess the energy consumption of their robots and present it in the data sheet [68]. However, this solution does not represent an objective view on the EC, as the specific position of the cube is selected by the user and not all of the motion parameters are defined for the robot. The use of an ISO-cube to assess the energy consumption in an IR is shown in [46].

VDMA 24608:2013-11 [69] outlines a standardized methodology for energy measurements in 6-axis IRs, which is directly derived from ISO 9283:1998 [67]. In this approach, the reference cube is also defined to occupy the largest possible volume within the robot’s working envelope, with its edges aligned parallel to the base coordinate frame, but the side lengths must be multiples of 200 mm. Trajectory points $P2$ to $P5$ are positioned inward from the cube’s edges by 10% of the cube’s diagonal length (Figure 6a), while $P1$ is recorded as the center point, providing a fixed spatial reference for the test.

Static and dynamic measurements are then conducted as specified by the test procedure. During the static measurement, the robot is held at point $P1$, and energy is recorded under conditions with the motor drives activated and deactivated. For dynamic measurements, the test cycle is defined as $30\times (P2-P3-P4-P5-P2)$, executed at maximum speed under nominal load, which is defined by the maximum load at the wrist as per the manufacturer’s data sheet [69].

While the documentation indicates that the type of interpolation (linear or joint motion) can be randomly selected for the motion of the IR [69], multiple studies have shown that the interpolation method can affect energy consumption under certain operating conditions [29,70].

The article [71] presents another standardized methodology for the comparison of 6-axis IRs, developed by Fraunhofer IWU in collaboration with German automotive automation initiative (AIDA). The aim here was to develop the methodology to compare IRs used particularly in the automotive industry.

The core of the method is an energy consumption evaluation based on a standardized reference trajectory. Additionally, IRs are categorized into six load-capacity classes, ranging from 0 to 250 kg in 50 kg increments, with a separate class for robots exceeding 250+ kg [71]. The reference trajectory was derived by statistically analyzing the operational parameters, such as point coordinates, movement types, trajectory lengths, velocities, accelerations, and path approximation values used in real robot programs in automotive body shops [72].

To ensure realistic testing conditions in terms of used payload, tool data were also analyzed to determine representative average values for each load-capacity class. Based on this, a configurable loading tool was developed to simulate standardized and comparable load conditions across reference trajectories for consistent energy evaluation [71,72].

The methodology includes three trajectory variants [71]:

• Standard—baseline cycle with fixed parameters defined by the statistical data used to create the reference trajectory.
• Performance—cycle with maximum speed and acceleration to analyze the maximal performance.
• Efficient—cycle with incrementally reduced velocity and acceleration to explore energy–cycle time trade-offs and identify optimal operating points.

The authors in [71] propose to compile the results into a data sheet, which includes detailed energy metrics of the IR, such as active, reactive, and apparent power, power factor, and energy per cycle, enabling transparent comparison between different robot models and manufacturers.

3. Comparative Review of ECO Techniques

Several previous reviews have categorized energy optimization strategies into hardware and software solutions, typically defining hardware as the selection of correct robot type, component replacements or additions, and software as encompassing trajectory and operation planning [11,12,13]. This review proposes a refined classification that focuses more specifically on the individual IR system level. The intention is to present a system-centric perspective that links the robot’s physical structure and control strategy directly to its energy optimization potential. Our approach is schematically presented in Figure 7. Within software-based approaches, the strategies are divided into parameter optimization (e.g., tuning speed, acceleration, and jerk values along a predefined path) and trajectory optimization (e.g., shaping or modifying the path itself). While these two are closely interrelated and often employed together, they represent distinct levels of decision-making in energy-aware planning. A third category, task scheduling, focuses on the energy-efficient arrangement of tasks. Hardware-based optimization emphasizes the electrical and mechanical design of IRs, including structural design, the use of energy-efficient components, and, emerging in recent literature, the integration of energy regeneration units. The selected strategies are discussed in more detail in the following sections with relevant references to the existing research.

3.1. Software

3.1.1. Parameter Optimization

Parameter optimization focuses on identifying the most energy-efficient operating parameters, most commonly velocity and acceleration, that minimize energy consumption in IRs without compromising task performance. These parameters are directly linked to motion profiles and actuator loads during operation. Some studies also consider external factors such as payload and drive lubricant temperature, which influence both mechanical performance under varying conditions.

Guerra-Zubiaga and Luong [73] focused on determining how linear speed, acceleration, payload, and temperature affect the IR energy consumption. The researchers used a Kawasaki ZZX130L IR in a simulated pick-and-place task. The results show that linear speed and acceleration contribute to 95% of energy consumption, while changes in payload and temperature have minor impacts. Additionally, higher speeds and accelerations are generally more energy efficient because of their effect on reducing cycle times.

Garcia et al. [29] investigated the impact of motion parameters on robot energy consumption also through simulations. Three experiments were conducted focusing on standstill energy use, motion paths, and the effects of load, speed, and lubricant temperature. The findings highlighted, as expected, that minimizing dwell times and using energy-efficient positions (positions with low gravity torques) during standstill reduces idle energy consumption. Speeds between 50 and 100% of the maximum were identified to balance cycle time and energy use, with continuous motion paths preferred to avoid excessive deceleration–acceleration transitions. Payloads were most efficient when limited to 80% of the maximum, particularly at lower speeds.

Izagirre et al. [30] also investigated idle-time energy consumption, proposing a torque-based methodology to find the most optimal robot poses during standstill. By minimizing the torque applied to robot joints, this approach reduces both mechanical stress and energy consumption. Their experiments used a genetic algorithm to identify optimal poses, starting with tests on KUKA KR3 robot in a controlled laboratory environment. Validation was carried out on ABB IRB 6400R robot in a real assembly line, where the results showed a 31.37% reduction in average torque, highlighting its potential in practical applications. An analytical friction model in the third experiment showed that while speed remains the dominant factor, lower speeds reduced consumption in friction-model-based scenarios, i.e., load torque was not considered. High lubricant temperatures were found to lower friction-related consumption at high speeds. Applying these findings to an industrial welding robot demonstrated an energy reduction of 11–16% [30].

Torayev et al. [45] proposed a black-box model-based method that enables parameter optimization in real time without stopping production. Their algorithm starts with an initial guess of input parameters—velocity and acceleration—and then iteratively searches for more optimal parameters using various well-known optimization algorithms. When an optimal set of new parameters is found, the new parameters are set in the IR. They demonstrated the applicability of the solution on three applications—pick-and-place, bin picking, and drilling—and demonstrated significant energy savings compared to baseline parameters, which were defined as the minimum and maximum allowable parameter configurations for each task. Energy reductions were 44.59% in pick-and-place, 25% in bin picking, and 17.64% in drilling, where the focus was on the end-effector spindle speed and feed rate optimization of the IR [45].

Carabin and Scalera [74] presented an analytical model and experimental results on finding minimum-energy motion parameters by adjusting the acceleration time, deceleration time, and total motion duration. They considered two optimization scenarios: one with fixed acceleration and deceleration times and free total time, and another with fixed total time and free acceleration/deceleration times. Their experiments were conducted on two robotic systems: a linear axis of a Cartesian manipulator and a 1-DOF system composed of two coupled servomotors, either directly connected or coupled via a planetary gear. The Cartesian robot experiments demonstrated a potential of up to 33.6% reduction in energy consumption.

Pellicciari et al. [75] demonstrated a method for the electromechanical modeling of serial and parallel manipulators to compute energy-optimal trajectories based on predefined TCP position profiles, specifically focusing on pick-and-place operations. The approach optimized the task execution time of predefined joint trajectories, i.e., maintaining the same TCP position profiles while adjusting the speed of task execution. They conducted an experimental validation to highlight the existence of an energy consumption minimum in a pick-and-place application on ABB IRB6600. For the mathematical optimization problem, they implemented two simulation case studies, one involving a PUMA 560 serial manipulator and another involving a Delta robot. Both case studies confirmed the efficacy of the time-scaling method, showing reductions in energy consumption of up to 7.7% for the PUMA arm and 9.8% for the Delta robot.

The reviewed studies consistently emphasize velocity and acceleration as the most influential parameters in determining energy consumption in IRs. Optimal operating ranges typically fall between 50% and 80% of the robot’s rated maximums. While secondary factors like payload and lubricant temperature have smaller overall effects, they may become critical under specific task or environmental conditions. Furthermore, several studies highlight the importance of reducing idle-time losses. These findings suggest strong potential for energy savings through parameter tuning—particularly in repetitive, short-cycle applications—without the need for major hardware modifications. However, practical implementation faces challenges such as limited access to low-level control parameters in commercial robot controllers, the need for parameter tuning across varying payload conditions, and ensuring that cycle time constraints are still met.

3.1.2. Task Scheduling

In multi-robot manufacturing environments, task scheduling plays a pivotal role in ensuring efficient system coordination. Traditionally, scheduling strategies have aimed to optimize productivity by sequencing robot operations to avoid collisions, reduce cycle time, and ensure timely task completion [76,77,78]. However, recent studies have demonstrated that these methods can be extended to support ECO without compromising throughput or violating operational constraints. A key energy-saving strategy is to coordinate robot actions in ways that reduce idle times, balance workload across robots, and activate power-saving modes during non-productive periods.

The researchers in [15] introduced a mathematical model that incorporates robot speeds, positions, operational order, and power-saving modes. A mixed-integer linear programming formulation was applied; however, this was only suitable for instances with a small number of robots. For larger robot cells, the authors propose a hybrid heuristic algorithm, which uses parallelization for faster and more efficient computations. The proposed method was tested on a real IR cell containing six robots. The method achieved approximately a 20% reduction in energy consumption [15].

In [79] the researchers formulated a similar mixed-integer linear programming approach but integrated IR energy consumption models with production constraints. This approach allowed for the allocation of tasks and synchronization of multiple robots to avoid collisions and idle periods, thereby reducing unnecessary energy usage. The scheduling model incorporated variables such as operation start and stop times, cycle times, and energy consumption during active and idle states, enabling a holistic optimization of the robotic cell’s energy profile [79].

In addition to task sequencing, trajectory time-scaling methods have been investigated for non-process-critical movements, such as transitions to and from home positions. Meike et al. [80] showed that adjusting the velocity of these movements and leveraging the earlier release of mechanical brakes during idle states can reduce energy consumption without affecting cycle time or process quality. These techniques are practical for deployment, as they require minimal changes to existing robot programs and no additional hardware modifications.

Task scheduling appears as a practical strategy for energy optimization in multi-robot production systems. By incorporating energy consumption models into scheduling algorithms, researchers have demonstrated energy reductions of up to 20% in real-world robotic cells [15]. Approaches combining scheduling with time-scaling and brake-release strategies further enhance efficiency without disrupting existing workflows [80]. Compared to other optimization strategies, task scheduling benefits from its system-level perspective, allowing coordinated adjustments across robots and tasks. However, challenges remain mainly regarding the scalability of the methods. Mixed-integer linear programming-based models offer precise optimization but face computational limitations as system complexity increases. Heuristic and learning-based methods show promise but require further validation and benchmarking. Additionally, expanding these methods to accommodate dynamic environments and unstructured tasks will be essential for broader industrial adoption.

3.1.3. Trajectory Optimization

Trajectory planning for IRs is a critical control strategy with significant potential for reducing energy consumption. Instead of following predefined paths, these approaches reformulate the motion of the IR as an optimization problem that considers energy efficiency alongside task constraints, dynamic feasibility, and limitations. By leveraging detailed kinematic and dynamic models, trajectory optimization enables IRs to reduce energy usage without compromising task performance. This subsection highlights the key contributions from recent research, showcasing the range of strategies and their reported effectiveness.

Liu et al. [28] introduced an energy-optimal trajectory planning method for palletizing robots, beginning with developing a rigid-flexible coupling dynamics model of the 4-DOF palletizing robot for torque prediction. The model was verified against a virtual model of the robot to ensure consistency. To identify the energy-efficient trajectory, the researchers formulated a mathematical optimization problem with boundary conditions specifying zero velocity and acceleration at both the start and end points—ensuring the robot begins and finishes each motion from a standstill. In addition to trajectory optimization, the study also considers determining the optimal pick position to minimize energy usage. Experimental results demonstrated that the proposed trajectory optimization method reduces energy consumption by approximately 15%, and optimal pick point selection can further enhance efficiency, achieving up to a 30% reduction in total energy use for palletizing tasks [28]. Similarly, the work in [81] employed B-spline functions and a detailed robot model including robot dynamics, friction losses, servo drive losses, and energy exchange between axes through DC-bus coupling to optimize PTP trajectories, highlighting the importance of considering servo drive and inverter losses for realistic energy savings. The model was applied to KUKA KR 210-2 IR, where a reduction of up to 10% in energy consumption was achieved.

Otani et al. [82] proposed a novel method to find the energy-efficient trajectory under task deadline constraints. The method enables robots to adopt energy-efficient postures within the trajectory by low joint torque loads before proceeding to task completion within the specified cycle time. Unlike conventional approaches that focus on minimizing task duration or reducing acceleration and deceleration along predefined paths, their method allows the robot to adopt intermediate postures with low joint torque demands before proceeding to task completion within the given cycle time. By discretizing the end effector’s position in both spatial and temporal dimensions, the search space for trajectory planning is expanded. This enables the optimization to identify energy-efficient configurations where the robot can momentarily remain stationary in low-torque postures, rather than strictly following the most direct or time-optimal route. The approach exploits the structural characteristics of the IR, such as link length and mass, to minimize torque requirements during the entire motion. Simulation results using models including the PUMA500 IR demonstrated a 10% reduction in total torque required in the new trajectory for executing the predefined task.

Garriz and Domingo [83] focused on maximizing manipulator performance while minimizing electrical energy consumption in an industrial sealing solution featuring a KUKA KR30-3 IR. In this application, trajectory optimization is critical for ensuring quality sealer application. The authors proposed a multiobjective optimization method based on the Kalman algorithm, which iteratively adjusts trajectories by balancing manipulability and energy consumption criteria. The cost function incorporates constraints such as joint limits or velocity restrictions. The method integrates the kinematic and dynamic model of the IR and applies an objective function with experimentally determined weights to guide optimization. Simulation results for three different trajectories demonstrated significant improvements, with electrical energy consumption reduced by up to 70.65%, and trajectory times shortened by up to 10.75%. The approach outperforms several previous methods in both manipulability and energy efficiency.

Some approaches consider energy recuperation and collision avoidance strategies within motion planning. Knöchelmann et al. [84] address the challenge of reducing energy consumption in industrial multi-robot cells through trajectory optimization while ensuring collision avoidance and exploiting energy sharing between robots over a common DC circuit. They implemented a two-level optimization approach, where the first level determines the optimal task sequence among the robots, and the second level refines individual robot trajectories to coordinate and balance energy flow across the shared DC-bus. The trajectory optimization incorporates a nonlinear collision detection constraint to prevent infeasible trajectories that could cause collisions in the packed robot cell. Simulation results on a three-robot system demonstrate that trajectory optimization without collision detection yields approximately 12.7% energy savings but results in collisions, whereas incorporating collision detection maintains around 9% energy savings.

Energy optimization can also be achieved along a fixed trajectory by adjusting motion timing. Li et al. [85] proposed a computationally efficient method that combines dynamic time-scaling with an energy characteristic parameter model to optimize energy use without altering the path itself. Their approach achieved 33.7% energy savings compared to the initial trajectory, while also reducing the computational cost associated with typical dynamic programming methods. This work highlights the potential of time-domain optimization techniques to achieve significant improvements in energy consumption within fixed motion paths.

Smart trajectory optimization offers a robust software-based solution for improving energy efficiency in IRs without hardware modifications. The reviewed methods generally frame the problem as multi-objective optimization, balancing energy use with additional goals such as manipulability [83], task timing [82], or collision avoidance [84]. These strategies leverage detailed physical and electrical models, yielding energy savings typically in the range of 10–30%, and in some cases even higher. However, computational complexity and the need for accurate system modeling can limit real-time deployment.

As discussed in [86], the computational speed of trajectory planning is a critical factor for practical deployment, particularly in dynamic or time-sensitive environments. One of the key challenges arises as the number of DOFs in the robot increases—the dimensionality of the optimization space grows, leading to significantly higher computational complexity [86]. This problem extends when additional constraints are introduced, such as joint limits, obstacle avoidance, or energy consumption bounds. These constraints increase the nonlinearity of the problem, often requiring more sophisticated solvers [86,87]. Furthermore, optimization outcomes are often task- and system-specific and not easily generalized.

Despite these challenges, trajectory optimization is a promising direction—especially when combined with energy-sharing mechanisms and adaptive scheduling.

Table 2. SWOT analysis—software ECO strategies.

Strengths	Weaknesses
Software based optimization can significantly reduce energy consumption without altering hardware.	Performance is highly dependent on accurate models; Artificial intelligence (AI) and machine learning (ML) based methods may require extensive training data.
Universally effective for wide variety of applications.	Optimization strategies may vary significantly by task and robot type.
Online and real-time optimization techniques enable adaptation to varying operational conditions.	Implementation complexity increases when integrating real-time optimization within existing control systems.
Can be applied at different levels–motion, task scheduling, and trajectory–offering multi-layered efficiency gains.	May conflict with other goals such as cycle time or throughput if not well balanced.
Opportunities	Threats
Integration with AI and ML allows adaptive, context-aware optimization.	Over-reliance on complex algorithms may reduce interpretability and increase system debugging difficulty.
Scalable to multi-robot cells through task scheduling and robot coordination.	For large-scale robot systems, computational time or model complexity may become cumbersome.
Trajectory optimization can take advantage of electromechanical energy recovery (e.g., regenerative braking, DC bus coupling) highlighting the opportunity for hybrid strategies.	Lack of standardization in optimization methods can hinder adoption across robot types and manufacturers.
Combining real-time sensor data with optimization models could enable closed-loop energy-aware control.	Some algorithms do not scale efficiently. As the number of robots, tasks, or decision variables increases, the computational complexity can grow exponentially, making real-time or large-scale implementation impractical

concludes an analysis of the main software-based ECO strategies’ characteristics.

3.2. Hardware

3.2.1. Structural Design

One of the primary hardware-oriented strategies for enhancing energy efficiency in IRs involves optimizing the structural design to reduce the mass and inertia of moving components. Lighter moving elements directly translate to lower joint torque requirements, which in turn reduces actuator effort and overall energy consumption during operation. This is especially relevant for articulated robots, where each joint not only drives its own link but also bears the weight of mechanically linked actuators, as actuators are mounted directly at the joints. To address this, several studies propose relocating actuators closer to the robot base and transmitting motion through cable- or belt-driven systems [88,89,90]. In parallel, structural optimization through material selection, topology refinement, and dimensional adjustments has shown promising results in improving energy efficiency while maintaining stiffness and precision [91,92].

Aziz et al. [88] designed a lightweight 3-DOF planar industrial manipulator aimed at reducing the torque requirements and overall weight of the robotic arm by locating all motors at the base. This configuration transfers motor motion via belts, aluminum pulleys, and bearings to the links, resulting in lighter links, allowing the potential use of smaller motors. Simulation results showed a significant reduction in joint torques, which is up to 3.8 times lower compared to traditional manipulators, demonstrating the effectiveness of this design for more efficient operation in industrial automation. A similar design of a cable-driven robotic arm was presented in [89].

Nguyen et al. [90] introduced a low-cost, 6-DOF cable-driven robotic arm designed to achieve low inertia movement comparable in scale and payload capacity to the UR5 robotic arm. The design relocates the heavy wrist motors to the shoulder base, significantly reducing the wrist’s weight, thereby decreasing torque demands on the elbow and shoulder motors. A hybrid actuation approach is employed, with direct-drive mechanisms at the shoulder and elbow joints to ensure precise positional repeatability, while the wrist’s three degrees of freedom are cable-driven through a sophisticated differential gear mechanism. Experimental evaluations demonstrated the arm’s capability to manipulate a 5 kg payload with positional repeatability under 0.1 mm, alongside effective load handling, cable longevity, and precise manipulation, all achieved with a lightweight carbon fiber frame and cost-effective materials.

Jia and Sun [91] presented a comprehensive methodology for the structural optimization of IRs by integrating topological and dimensional parameter design. The proposed method aims to reduce the mass of robot components—particularly the lower arm—while maintaining structural stiffness and minimizing deformation. Their study models stiffness–mass relationships and employs a multi-objective genetic algorithm for optimization, reducing mass by 15% while achieving a deformation of less than 0.352 mm, confirming its viability for real-world application.

Another structural optimization strategy was described in [92], where the authors selected aluminum as the primary lightweight material for the robot structure. DC brushless motors were combined with harmonic drive gearboxes to enhance dynamic performance and achieve a compact design. The results demonstrated that their approach led to a 15.7% reduction in total mass and enabled the effective use of motors with up to 57% lower power ratings.

These studies highlight the significant impact that structural design has on energy consumption in IRs. Designs that relocate actuators to the base using cable- or belt-driven transmissions can dramatically reduce joint torques, and incorporating lightweight materials, such as aluminum or carbon fiber, and applying optimization algorithms to minimize link mass and deformation further enhance efficiency. Reductions in total system mass and the possibility of using less powerful motors have been demonstrated. These findings confirm that structural optimization, when approached holistically, can play a pivotal role in developing energy-efficient robots. However, retrofitting existing IRs with optimized structures is rarely feasible. Lightweight designs may introduce compliance or reduce vibration damping, necessitating additional suppression strategies [93]. Cable- or belt-driven solutions, while reducing inertia, also introduce additional maintenance and control complexity. Such solutions may also not meet the strict IP ratings required in harsh industrial environments.

3.2.2. Energy Recovery and Reuse

Energy recovery strategies aim to reclaim the electrical and kinetic energy that is typically lost during robotic operations, particularly during deceleration, braking, or idle phases [29]. In conventional IR systems, regenerative braking energy is briefly buffered in the internal capacitors of the DC-bus (Figure 5) [60]. Recent advancements aim to improve reusing or storing the recovered energy through mechanisms such as shared DC-bus architectures [60,94], external energy storage, and compliant or elastic recovery elements [36,95,96], demonstrating the feasibility of integrating both passive and active energy recovery systems in real-world applications.

Meike et al. [60] presented two complementary strategies to reduce energy consumption in IRs through capacitive energy buffering and robot-to-robot energy sharing. The first strategy involves the use of external capacitor banks connected to the DC-bus of a single robot controller. The results demonstrate energy savings of up to 20% during dynamic tasks. However, due to robots spending a comparatively small fraction of production time in motion, the return on investment for this hardware is relatively long; therefore, a more scalable approach involves connecting multiple robot controllers via a shared DC-bus, allowing braking energy from one robot to be reused by another robot. Simulations with 20 robots show that energy dissipation on brake resistors dropped from 24% to below 0.5%. This method offers similar energy savings as capacitive buffering but without the need for expensive energy storage hardware.

Building on the energy buffering concept, the researchers in [94] explored the use of a shared storage capacitor connected to a common DC-bus among multiple IRs. Simulation results demonstrated that such a configuration could lead to energy savings of up to 30%, highlighting the potential of using buffer capacitors in multi-robot systems.

Another study by Meike et al. [61] introduced a smart power converter that builds upon the concept of a shared DC-bus across multiple robotic systems. The proposed system enables each robot’s drive to store recuperated energy within an independent DC subgrid and to return the stored energy only when required. Experimental validation with two high-payload IRs demonstrated energy savings exceeding 20%.

Palomba et al. [95] proposed a method to add energy-recovering and energy-storing devices in the form of regenerative drives and compliant elements (springs that store elastic energy) that would function together to lower the energy consumption in mechanisms performing cyclic tasks. The compliant elements would reduce the necessary load from the actuators to drive the system. However, the compliant element needs to be designed optimally in terms of stiffness and preload to fit each system. The solution was tested on a Five-Bar Mechanism where an overall energy reduction of 70% was achieved, and on a SCARA robot, where the energy consumption was reduced by 60%. The approach works with an arbitrary motion trajectory and aims for universal applicability.

Scalera et al. [96] demonstrated the use of torsional springs to enhance energy efficiency in a parallel robot designed for pick-and-place tasks. The springs are mounted in parallel with the motors, enabling conversion between elastic and kinetic energy to reduce actuator torque demands. The results showed an energy consumption reduction of up to 67.8%.

Expanding here, the work in [36] demonstrated the use of variable stiffness springs in a parallel configuration with the motors. Similarly, one end of each spring is connected to the motor, while the other is linked to the robot joint; however, the stiffness of the springs is dynamically tunable with a dedicated motor, allowing the spring to adapt to different conditions during each phase of the robot’s motion. Their aim was to target the braking phases of the robot’s motion, where the energetic losses are usually the highest. The results show that energy consumption is minimized by up to 70% compared to the standard configuration without the springs.

The literature highlights multiple hardware-oriented strategies for recovering otherwise wasted energy in IRs. Capacitive buffering on the DC-bus of a single robot controller can yield some energy savings during motion-intensive operations, while multi-robot shared DC-bus systems can reduce brake resistor losses significantly, making them highly scalable for energy reuse across collaborative cells. Complementary to electrical strategies, mechanical solutions involving elastic or variable-stiffness elements have also shown good results. However, electrical energy recovery systems often involve additional hardware costs and complex system integration, and mechanical recovery methods must be carefully tuned to task-specific dynamics, requiring sophisticated control schemes and introducing additional maintenance complexity. Therefore, future work should aim to generalize these strategies across robot types and tasks. Ultimately, hybrid approaches combining electrical and mechanical recovery with intelligent software-based methods stand as a promising direction. From a deployment perspective, energy recovery systems often necessitate physical modifications to the robot’s hardware and drive architecture as shown in [97]. Capacitive storage elements or shared DC-bus configurations may pose compliance challenges and require certification from system vendors to meet regulations.

3.2.3. Functional Redundancy

Functional redundancy refers to the intentional design or exploitation of additional DOFs beyond what is strictly necessary to achieve a task. This redundancy enables multiple kinematic solutions for the same end-effector position and orientation, allowing the optimization of secondary criteria such as joint torque, positioning [98], or energy consumption [31,32]. Beyond this, parallel redundancy introduces an additional layer of flexibility, where robot links are actuated by more than one actuator [99]. Though not presented as a standalone category in this review’s ECO classification, functional and parallel redundancies offer a compelling example of a hybrid energy optimization strategy combining structural design with motion planning and control.

Boscariol et al. [31] explored how functional redundancy can lead to energy efficiency through smart motion planning. By building the dynamic and electrical model of the UR5 robot, they could simulate the energy consumption. Energy optimization can be achieved by adjusting the redundant degrees of freedom according to some task-specific constraints. Tasks with high inertial forces benefit the most from the proposed method, achieving up to 20.8% reduction in energy consumption [31].

Another work by the same author [32] explored the use of kinematic redundancy focusing on a SCARA robot integrated with an additional linear unit. The proposed method optimizes the trajectory by adjusting time parameters between via-points and motion profile parameters for the added axis, forming a numerical optimization problem. A detailed inverse dynamic and electromechanical model allows the precise estimation of energy drawn by each joint and the linear unit. Results show that introducing redundancy via an external axis enables both faster execution and energy savings—up to 33% [32].

While the earlier work in [32] focuses on hardware-extended redundancy by adding an external linear unit, the research in [31] shifts the focus to software-based functional redundancy, leveraging redundant degrees of freedom in joint configurations without modifying the robot structure. Both works use dynamic modeling and trajectory optimization but address redundancy from complementary angles—hardware augmentation versus internal joint-space exploitation.

Lee et al. [99] proposed an energy-saving strategy for parallel robotic manipulators by utilizing redundant parallel mechanical actuation. The concept is based on adding more actuators to the robot structure than functional DOFs, allowing the distribution of joint torques. This redundancy enables the optimization of actuator torques to minimize energy losses in three key areas: regenerative power dissipation, electric power loss, and frictional losses in reducers.

Using a 2-DOF parallel manipulator—structurally comparable to traditional palletizing robots with parallel linkage architecture—the researchers in [28] developed detailed kinematic and dynamic models and analyzed energy consumption in both non-redundant and redundant configurations. Their findings showed that redundant actuation reduced total energy consumption by 26.1%, mainly due to decreased frictional losses (26.7%) and regenerative power dissipation (75.3%) [99]. The optimized torque distribution also allows for the use of smaller motors and gearboxes, reducing the mechanical load and improving energy efficiency.

Functional redundancy presents the intersection of hardware and software strategies for energy optimization. In its simplest form, redundancy can be exploited entirely at the software level—particularly in articulated robots—by optimizing joint configurations without requiring any physical hardware modification. This makes it a highly accessible and low-cost solution for improving energy efficiency in existing systems. On the other hand, hardware-extended parallel redundancy, such as the integration of additional actuated axes or parallel actuators, can yield even greater energy savings by enabling more flexible and distributed force generation. However, these approaches require modifications to the robot’s physical structure, making them less feasible in commercial IRs. The need for custom mechanical design, additional components, and integration complexity limits their practical deployment in standardized manufacturing environments. Both approaches underscore the importance of co-optimizing robot structure and control strategy. Future work should explore the development of scalable frameworks that combine internal functional redundancy with adaptive motion planning and real-time optimization with AI-based methods.

Table 3. SWOT analysis—hardware ECO strategies.

Strengths	Weaknesses
Significant reduction in joint torques by relocating actuators to the base	Increased mechanical complexity in transmission systems.
Lightweight materials and optimized link design reduce inertia and enable use of smaller motors	Maintenance and calibration of cable- or belt-driven systems may be more demanding.
Structural optimization through multi-objective algorithms yields stiffness-mass-efficient designs	Trade-offs between weight reduction and structural rigidity or load capacity.
Enables safer and more precise motion due to lower moving mass	Topology optimization requires high computational resources.
Opportunities	Threats
Potential integration with energy recuperation systems	Increased design complexity may limit applicability in cost-sensitive or compact environments.
Applicable to a wide range of robots and payload classes	Cable or belt fatigue and durability could limit long-term performance.
Functional redundancy can be leveraged for further energy optimization via smart motion planning	Dependence on highly specific mechanical configurations may limit modularity or scalability.
	Structures with optimized topologies often feature open or exposed geometries, which can compromise their suitability for harsh industrial environments by reducing their ingress protection (IP) rating.

concludes an analysis of the main hardware-based ECO strategies’ characteristics.

4. Discussion

Automation technologies are undergoing a rapid increase in adoption, following a similar trend observed in the electric vehicle (EV) sector, where sustainability and energy efficiency have become central priorities [100,101]. Just as EVs have urged the creation of standardized testing protocols and frameworks to support transparent performance evaluation, a similar shift is needed in IRs. However, in the field of IRs, the evaluation of energy performance remains fragmented. The reported energy savings in previous studies are often referenced against baseline or worst-case conditions (e.g., maximum speed and acceleration, and unoptimized trajectories), which limits the ability to make consistent comparisons across robot types, tasks, or manufacturers. This variability complicates the objective assessment of energy optimization strategies and slows the establishment of best practices within the field. Currently, there is no universally accepted framework for evaluating or reporting the energy performance of IRs. As a result, researchers as well as integrators and end-users lack reliable tools for benchmarking and decision-making regarding energy-efficient robot deployment. To address this gap, future research should advocate for the development of the following:

• Standardized benchmarking procedures as an expansion of ISO 9283 [67] or VDMA [69];
• Development of a universal energy optimization tool that is usable with standardized robotic hardware across multiple manufacturers.

This standardization would simplify the comparisons of energy performance and promote transparency in the energy-related specifications provided by IR manufacturers. It would also form the foundation for developing industry-relevant ECO strategies that go beyond academic simulations and can be embedded into real-world manufacturing environments.

While the majority of energy optimization research in IRs has emerged from academic studies, often centered on dynamic modeling, simulation-based optimization, or laboratory-scale experiments, there is a growing need to transition these findings into practical, scalable solutions for industrial environments. Academic methods frequently emphasize efficiency gains under idealized conditions. This advocates for a shift toward implementation-focused research that considers integration into existing robotic systems, user accessibility, and maintainability.

An example of such an industry-oriented solution is the patented method by Björkman et al. [102], which introduces a software control method to dynamically switch between energy optimization mode and time optimization mode during robot program execution. The optimization can be started through an energy-optimization block within the program code, allowing energy-wise optimization over portions of the program. The energy is minimized under the constraint of a fixed path.

Building upon this, future research directions should prioritize the integration of hybrid energy optimization strategies and adaptive control algorithms that enable real-time decision-making. Current control-based ECO techniques often rely on static or predefined motion parameter sets, which may not be optimal under changing operational or environmental conditions. These approaches must not only respond dynamically to variations in the production environment, task load, cycle time, and robot condition but also integrate seamlessly into existing IR workflows.

In this context, the growing use of AI-based tools offers new opportunities to enhance the effectiveness of hybrid optimization. AI-based algorithms can analyze large volumes of sensory and operational data to continuously adjust motion parameters, predict energy demand, or identify inefficient behaviors [103]. When deployed within closed-loop IR systems, such intelligence can dynamically coordinate between control, scheduling, and actuation components. Prior research has explored data-driven techniques for motion planning [104,105], and even from an energy-efficiency point of view [106], as well as the optimization of motion parameters [107,108]. However, most of these studies have focused on offline or simulation-based applications. Applying AI methods in real-time optimization contexts where energy usage is monitored and minimized during robot operation remains an open research problem.

Recent developments indicate that AI-based methods are increasingly capable of bridging the gap between offline energy optimization and real-time application in industrial robotics. For instance, the use of long short-term memory (LSTM) deep neural networks for predicting energy consumption in IRs has been demonstrated in [109]. In some cases, LSTM models have been integrated with model-based approaches to estimate energy use based on joint torques and velocities [110]. Dona’ et al. [111] proposed a real-time trajectory generation method that produces near-optimal energy profiles with significantly reduced computation time. Other studies have addressed real-time optimization under unknown payload conditions, such as the method proposed in [112], which combines LSTM-based load estimation with particle swarm optimization (PSO) for online trajectory tuning. Their approach achieved more than 50% energy savings in simulated environments. Extending such strategies to real-world applications such as pick-and-place and palletizing holds strong potential for practical impact.

Real-time optimization would benefit from integrating power measurement directly at the manipulator–controller interface, rather than at the whole system input. Typical experimental validations assess power consumption at the full system level (including controllers, cooling systems, and auxiliary electronics), masking the relevant electromechanical losses specific to the manipulator.

Despite this progress, most studies remain limited to offline or simulation-based settings. The application of AI techniques in real-time energy optimization—where energy usage is monitored and minimized continuously during robot operation—remains largely unexplored. Progress in this area would benefit from integrating direct power measurements at the manipulator–controller interface as opposed to measuring system-wide energy consumption. Current experimental validations typically assess power usage at the full system level, which includes controllers, cooling units, and auxiliary electronics, thereby obscuring the electromechanical losses that are directly attributable to the manipulator.

By proper estimation of the consumed power at the manipulator interface, it is possible to isolate energy flow through the actuators, drive systems, and mechanical linkages, aligning the experimental data more closely with the assumptions and focus of dynamic modeling. This opens the door for training more accurate data-driven models, developing predictive analytics for joint-specific losses, and enabling closed-loop AI agents to learn and apply energy-aware behaviors in real time. In such a framework, the models could infer energy-optimal motion trajectories and parameters in dynamic industrial environments.

The application of high-resolution energy monitoring and intelligent control architecture could redefine energy optimization in IR, shifting the paradigm from pre-planned static simulation-based tuning to responsive, autonomous, and self-improving systems. Herein, the authors propose a standalone power measurement and energy optimization tool that can be integrated between the manipulator and the control system, effectively isolating the mechanical subsystem to enable precise evaluation of energy losses within the manipulator itself. Furthermore, connecting the tool to the IR control system would allow for continuous monitoring, dynamic evaluation, and real-time optimization of energy usage, specifically facilitating joint-level measurement. In this context, AI integration would be well-suited to enhance energy-aware trajectory planning, motion parameter tuning, and task scheduling.

5. Conclusions

As the usage of IRs continues to expand across manufacturing sectors, optimizing their energy consumption has become increasingly critical for achieving both economic efficiency and environmental sustainability. This review provided a detailed exploration of the controllable aspects of energy use in IRs, linking kinematic structures, component-level characteristics, and control strategies to energy performance. Through the classification of energy optimization approaches into software- and hardware-based strategies, the review has highlighted the different methods available for reducing energy consumption, from motion parameter tuning and trajectory planning to structural redesign, energy recovery systems, and applying functional redundancy. A comparative SWOT analysis further clarified the trade-offs and complementarities between these strategies.

Software-based energy optimization methods offer a flexible and non-intrusive approach to improving energy efficiency in IRs. These strategies can be implemented without altering the IR hardware and are generally applicable across various robot types and applications. Their compatibility with AI and ML models enable advanced predictive and adaptive control, especially when integrated with real-time sensor feedback. Furthermore, software-based methods are usable in multi-robot environments, allowing coordination and optimization at the task level. However, the effectiveness of these techniques heavily relies on the accuracy of the dynamic and energy models of the IR. Optimization outcomes may vary depending on the complexity of the task, and there can be trade-offs between energy efficiency and other priorities such as cycle time or precision. Some algorithms may suffer from limited scalability and increased computational demands, potentially impacting system responsiveness and interpretability.

Hardware-based strategies offer substantial energy savings by directly reducing joint torques, moving masses, and inertial loads, thereby enhancing the baseline energy efficiency of IRs independent of control strategies. Structural optimizations can also improve motion precision and contribute to safer and more responsive robotic behavior due to reduced moving masses. The integration of energy recuperation mechanisms, such as regenerative braking or compliant elements, presents further opportunities for capturing and reusing otherwise wasted energy, especially in cyclic tasks. However, implementing hardware modifications typically requires physical redesign, retrofitting, or the adoption of non-standard components. This may be impractical in existing industrial settings due to cost, downtime, integration complexity, or environmental constraints. Their effectiveness also varies depending on the application domain of the IR, and they may introduce additional mechanical complexity or maintenance requirements.

Emerging trends such as the integration of DC microgrids and regenerative energy sharing point toward a future in which robots not only consume energy efficiently but also participate actively in intelligent energy ecosystems. Equally important is the role of modular power measurement systems that enable precise energy monitoring and continuous feedback, creating the foundation for real-time optimization.

Looking ahead, the convergence of these developments with AI and ML presents a powerful opportunity: the creation of hybrid, adaptive, and context-aware energy optimization frameworks that are capable of scaling to complex, real-world applications, with the control layer in particular. ML models can dynamically adjust motion parameters, select energy-efficient trajectories, or even predict system behavior under varying workloads. Reinforcement learning and neural network-based controllers may eventually enable robots to autonomously fine-tune their actions in response to changes in task complexity, load, or workspace configuration. However, the successful deployment of such systems will depend on robust real-time data acquisition, especially at the manipulator level.

Taking into account the growing trend in automatization, similar to that observed in the EV industry, future efforts should also address the open question of how to develop standardized energy certification schemes and publicly accessible consumption profiles for commercial IRs. These initiatives would promote transparency, support benchmarking, and drive manufacturers toward designing inherently more energy-efficient IR systems. By synthesizing current research, technological advances, and future directions, this review aims to support the development of best practices and inspire further innovation toward energy-aware IRs.