Abstract
This paper proposes a dynamic adaptation of the crossover parameter (CR) in Differential Evolution (DE) using Type-3 fuzzy logic. The strategy involves adjusting the CR value according to the progress of the algorithm by employing a Type-3 fuzzy system (T3FS) to handle the uncertainty and variability inherent in this parameter. To assess the effectiveness of the proposed approach, an inverted pendulum system controlled by a T3FS is employed. The controller parameters are optimized using an enhanced DE algorithm. The results demonstrate that dynamically adapting the crossover rate parameter significantly enhances both the efficiency and accuracy of the DE algorithm, compared to traditional static adjustments. Specifically, the proposed approach achieved an RMSE of 0.0127, outperforming traditional static adjustment methods, which resulted in an RMSE of 0.732. In addition, the results exhibit an improvement in the consistency of the outcomes, with a significantly lower standard deviation (0.0111) compared to conventional methods. These findings underscore the potential of Type-3 fuzzy systems (T3FSs) in enhancing evolutionary algorithms for optimizing fuzzy controllers in highly uncertain nonlinear systems. Furthermore, this emphasizes the capability of T3FSs to enhance evolutionary algorithms in optimizing fuzzy controllers for nonlinear systems subject to significant uncertainty.
1. Introduction
The optimization of complex and nonlinear problems is a field of great interest in automatic control and computational intelligence. In this area, the Differential Evolution (DE) algorithm has established itself as a powerful tool due to its simplicity and effectiveness in exploring and exploiting the solution space [1]. However, the performance of DE critically depends on the proper configuration of its parameters, such as the scaling factor (F), population size, and particularly the crossover parameter (CR), which controls the exchange of information between candidate solutions. An inappropriate selection of these parameters can lead to premature convergence or a limited exploration of the search space.
To address this limitation, various adaptive strategies have been proposed to dynamically adjust the parameters during the evolutionary process. Among these strategies, the use of fuzzy logic-based systems has proven promising, especially for managing uncertainty and the nonlinear nature of problems [2,3,4,5]. Type-1 fuzzy logic allows modeling uncertainties through traditional membership functions [6], in control [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22], in real-time prediction [23], and in hybrid fuzzy-expert system control [24,25]. Type-2 fuzzy logic extends this capability by handling uncertainties within the membership functions themselves [26]. Some of the most recent applications with Type-2 fuzzy logic are mentioned below: energy-efficient routing [27], hydropower system management [28], and tracking for photovoltaic systems [29,30,31] and control systems [32,33]. Recently, Type-3 fuzzy logic has emerged as an innovative approach that incorporates an additional level of flexibility to handle more complex uncertainties through second-order interval fuzzy sets, enhancing representation and adjustment capabilities [34]. Some recent applications with Type-3 fuzzy logic (T3FL) have been in areas such as deep learning [35], diagnosis of mental disorders [36], control systems [37,38], and clustering [39].
In this context, this work proposes a strategy for the dynamic adaptation of CR in DE using a Type-3 fuzzy system (T3FS). The strategy consists of adjusting the CR value based on the algorithm’s progress, allowing for a more precise adaptation to the problem characteristics and the evolutionary process. To evaluate the effectiveness of the proposed approach, an inverted pendulum plant is used as a classic nonlinear system in automatic control, which is controlled through an interval Type-3 Sugeno fuzzy system. This plant offers significant challenges due to its inherent instability and the need for fast and precise responses.
Despite advances in fuzzy control, significant limitations remain in the ability of traditional approaches to handle complex and dynamic uncertainties in nonlinear systems. Controllers based on Type-1 and Type-2 fuzzy logic exhibit constraints in terms of precision and robustness under scenarios with high levels of noise or uncertainty. This research gap highlights the need for more adaptive and efficient strategies, such as those offered by Type-3 fuzzy logic. In this context, the main contributions of our work are as follows:
- Proposal of a Type-3 fuzzy logic framework: We introduce an innovative approach that enables dynamic adaptation of the CR parameter, enhancing the system’s response to complex uncertainties.
- Evaluation in a classical nonlinear system: We validate the performance of the approach in a well-known system, the inverted pendulum, demonstrating its effectiveness and robustness.
- Comprehensive comparison: We conduct a comparative analysis of the proposed method’s performance against controllers based on Type-1 and Type-2 fuzzy logic, considering both noisy and noise-free scenarios.
The structure of this paper is as follows: Section 2 offers an overview of interval Type-3 fuzzy sets and their theoretical foundation. Section 3 describes the Differential Evolution algorithm, highlighting its relevance for optimization problems. Section 4 outlines the proposed methodology, integrating an IT3FS with DE to design a novel control strategy. Section 5 outlines the experimental setup and discusses the results obtained from various simulations. Section 6 offers a discussion of results. Finally, Section 7 summarizes the key findings.
2. Interval Type-3 Fuzzy Sets
Interval Type-3 fuzzy logic (IT3FL) is an extension of Type-2 fuzzy logic that provides an additional level of flexibility for modeling complex uncertainties. In general terms, fuzzy logic allows representing imprecise or uncertain information through fuzzy sets.
Evolution of Fuzzy Logic
Type-1: This uses well-defined membership functions to model uncertainty.
Type-2: This introduces second-order fuzzy sets, where membership functions can also be uncertain (defined by a range of values instead of a single value).
Type-3: This further extends the concept by incorporating third-order fuzzy sets, enabling the handling of more complex uncertainties in knowledge representation and decision-making.
The main characteristics of T3FL are as follows:
- Greater capacity for representing uncertainty, as it manages not only variability in data but also in rules and membership functions;
- Increased flexibility and robustness in decision-making compared to Type-1 and Type-2 approaches;
- Applications in complex problems, such as adaptive control, artificial intelligence, and optimization in highly uncertain environments.
The mathematical structure of fuzzy logic is presented in detail in various existing works in the literature [35]; for this work, some important mathematical aspects of Type-3 fuzzy logic are presented: a set is represented by the plot of a trivariate function, given by the membership function (MF) in the Cartesian product, where the universe is defined in the primary variable . The MF is expressed by a function, and it is called a Type-3 membership function (T3MF).
Here, represents the universe for the secondary variable , and denotes the universe for the tertiary variable . A Type-3 fuzzy set can also be defined as follows:
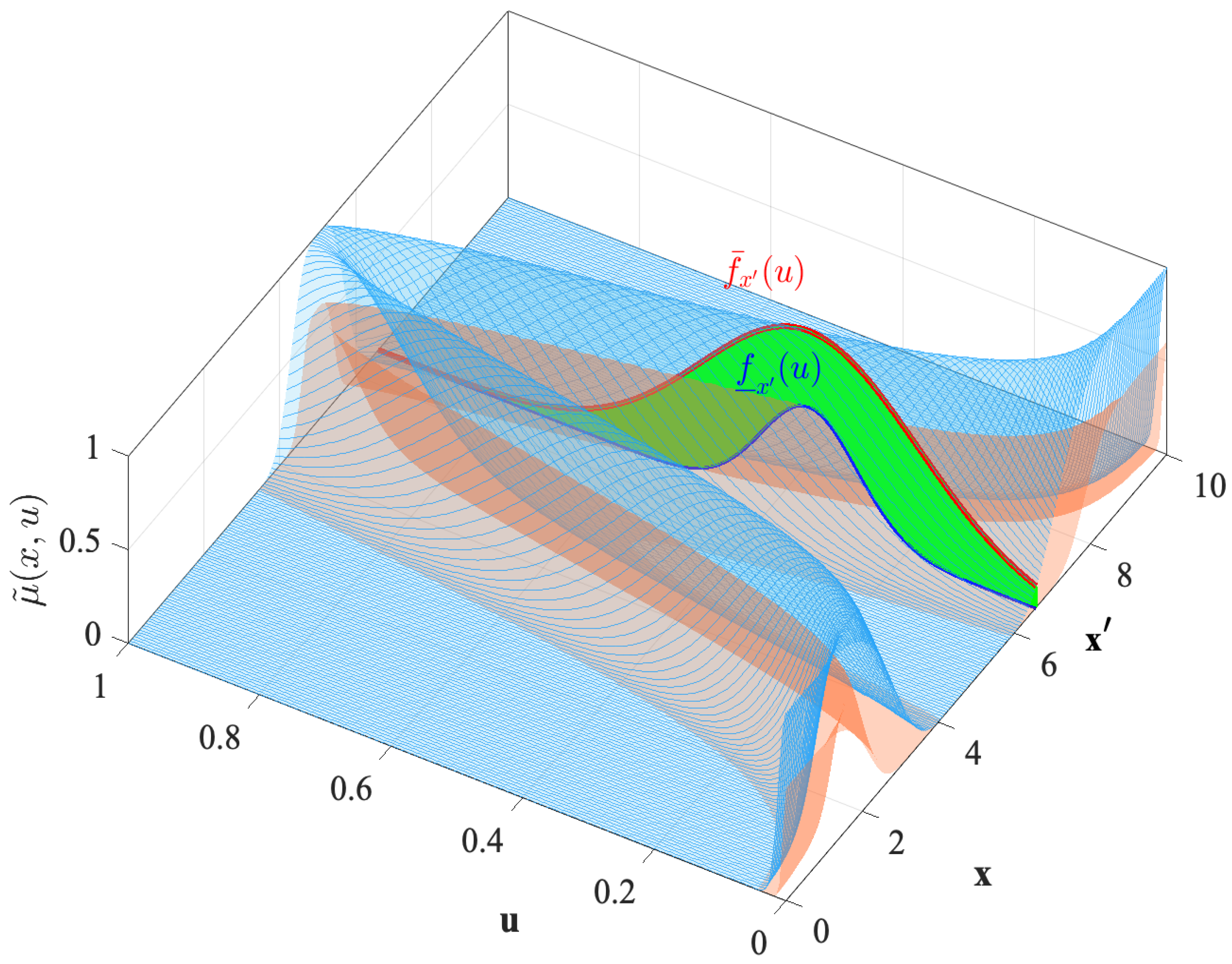
Figure 1 illustrates a graphical representation of a membership function for a T3FS, with its corresponding mathematical expression provided as follows:
where .
where is a T2FS.
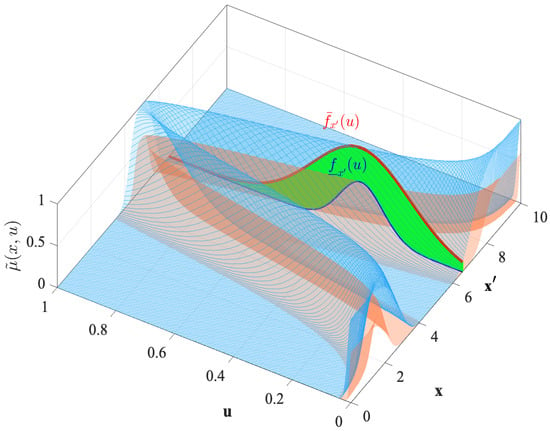
Figure 1.
Graphical view of a T3FS membership function with a mathematical expression.
3. Differential Evolution
The DE algorithm is a population-based method that belongs to the family of evolutionary algorithms. Its goal is to find the best solution to a problem by minimizing (or maximizing) an objective function through operations inspired by biological evolution, such as mutation, recombination, and selection [1].
3.1. Initialization
An initial population of N individuals (solution vectors) of dimension D is generated, where each individual is represented as
3.2. Mutation
For each individual , a mutant vector is generated from three randomly selected individuals, and (different from ):
where F is a scaling factor (typically in the range [0, 1]) that controls the magnitude of the mutation.
3.3. Crossover
The mutant vector is crossed with the individual to produce an offspring vector , using a crossover parameter CR (in the range [0, 1]):
3.4. Selection
The new vector is evaluated using the objective function . If the offspring has a better value than the parent, it replaces the individual in the next generation:
The Differential Evolution algorithm offers several advantages, including its simplicity, ease of implementation, and the need for only a few parameters to tune. It is particularly efficient for continuous optimization problems as it does not require derivative information, making it suitable for a wide range of applications. DE is widely used in function optimization, automatic control, neural network training, and parameter tuning in dynamic systems, among other fields where robust and adaptive optimization techniques are needed.
4. Proposed Methodology
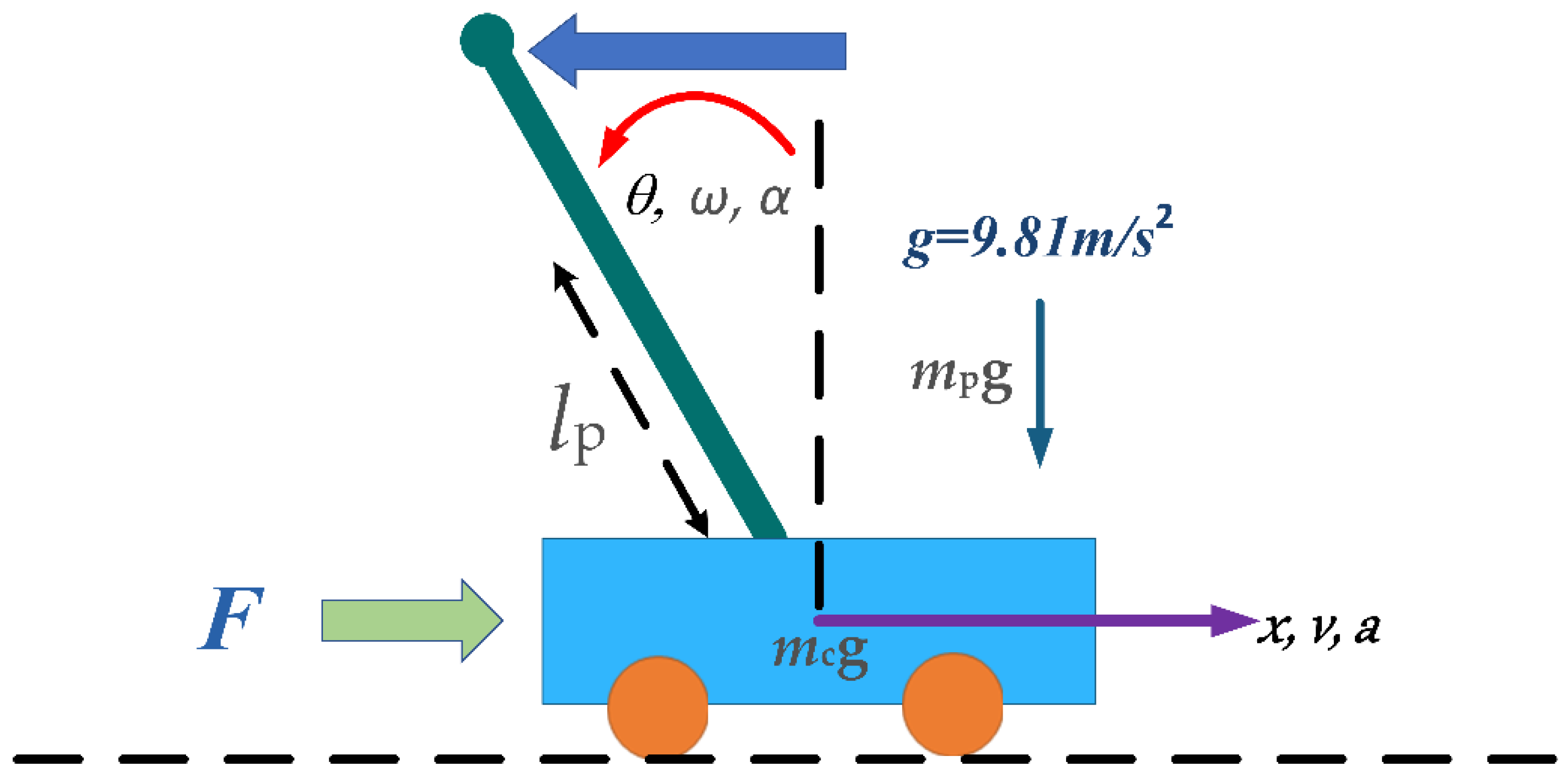
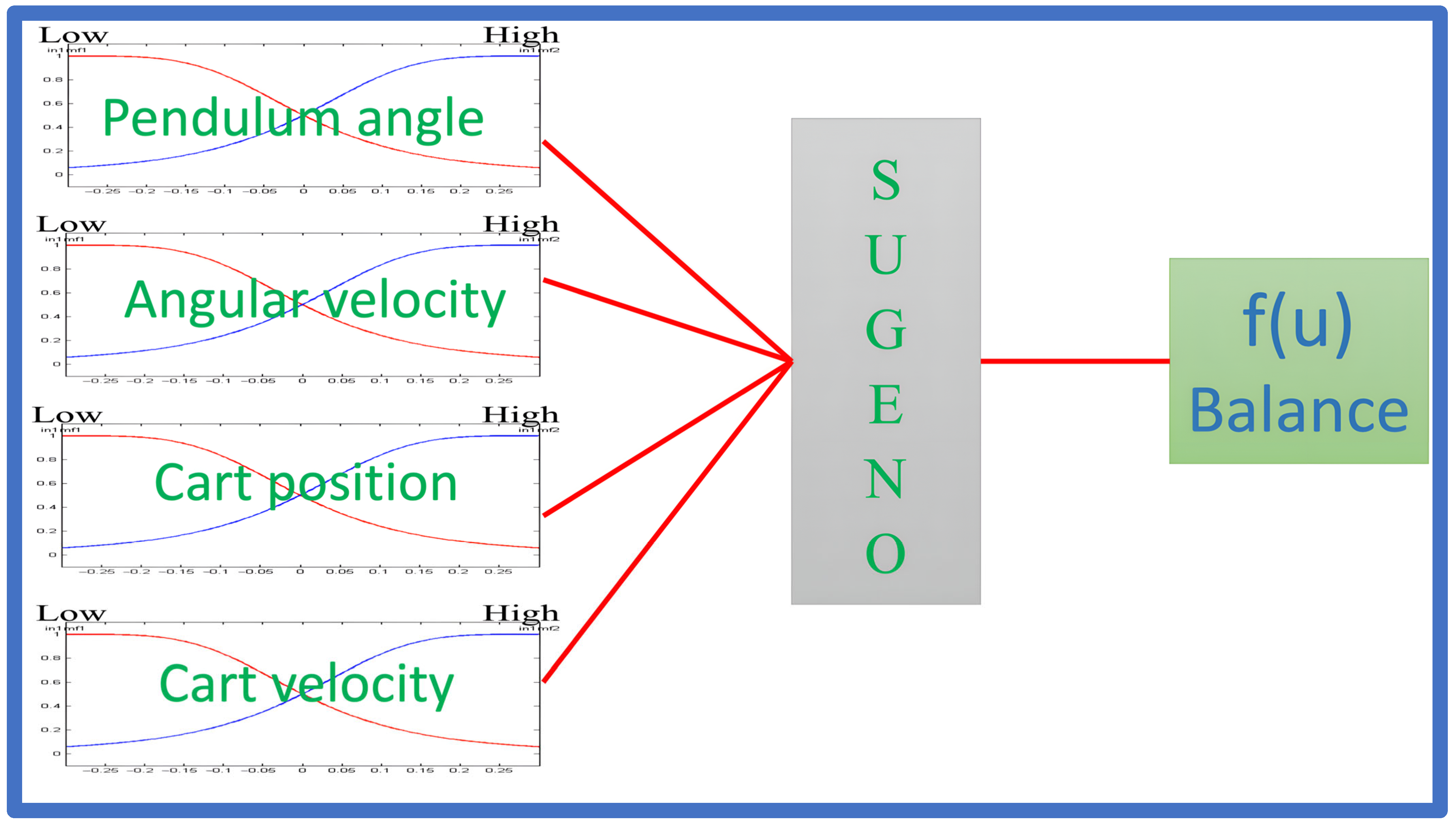
The inverted pendulum controlled with a Sugeno-type fuzzy system is a classic approach in automatic control that employs fuzzy logic to stabilize an inherently unstable system. In some related works, a Takagi–Sugeno model has been used [40,41,42,43,44,45]. In this method, the Sugeno fuzzy controller receives system variables as inputs, such as the pendulum’s angle and angular velocity, and generates a control output that adjusts the force applied to the cart to maintain the pendulum’s balance. The Sugeno Type-1 fuzzy system has proven effective in controlling the inverted pendulum since it can generate a fast and stable response without requiring an exact model of the system. However, its performance can be affected by parameter uncertainties or variations in system conditions. Figure 2 provides a visual representation of the controller, while Figure 3 illustrates the structure of the original Type-1 fuzzy system. As shown, the system has four inputs, follows a Sugeno-type approach, and includes a single output corresponding to the balance.
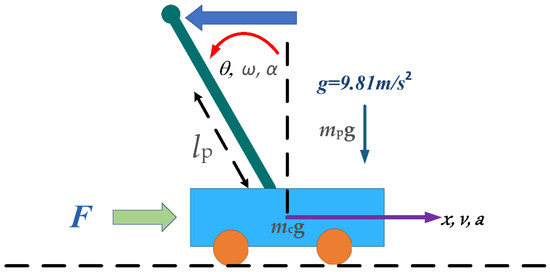
Figure 2.
Inverted pendulum controller.
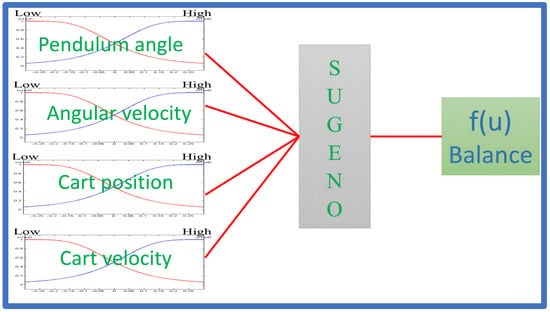
Figure 3.
Structure of the original Type-1 fuzzy system with a Sugeno approach.
The goal of this problem is to maintain the pendulum’s balance without it falling from the cart. The system consists of a straight-line rail, a cart, a pendulum, and a driving unit. The cart is free to move left or right along the rail, while the pendulum is attached at the center of the cart’s top surface and can rotate around its pivot within the same vertical plane as the rail. Assuming the system is frictionless, Equations (12) and (13) describe the mathematical model of the inverted pendulum.
The parameters mc and mp correspond to the mass of the cart and the pendulum, respectively, measured in kilograms [kg]. The gravitational acceleration is given as The parameter lp represents the distance from the center of the pendulum to the pivot, measured in meters [m], and is equal to half the length of the pendulum. The variable F denotes the driving force applied horizontally to the cart, measured in newtons [N]. The variables θ, ω, and α indicate, respectively, the pendulum’s angle from the upright position, its angular velocity, and its angular acceleration, where the clockwise direction is considered positive. Similarly, the variables x, v, and a represent the cart’s position relative to the rail’s origin, its velocity, and its acceleration, with the rightward direction taken as positive. Figure 4 presents the rule set for this controller, which models the vehicle’s behavior on the cart to keep it balanced.

Figure 4.
Rule set for the inverted pendulum controller modeling vehicle behavior.
To enhance the controller’s robustness against more complex uncertainties, this work develops three Type-3 fuzzy systems, varying the Lower Scale parameter with values of 0.1, 0.4, and 0.8. Each of these configurations is represented through images that illustrate the structures of the T3FSs, allowing visualization of how the variation of the Lower Scale parameter affects uncertainty representation and, consequently, the controller’s performance.
Three fuzzy systems have been developed for the control of the inverted pendulum, all sharing the same structure but differing in the configuration of the LowerScale parameter. This parameter influences the representation of uncertainty within the system, and in this study, three different values have been considered: 0.1, 0.4, and 0.8.
Figure 5, Figure 6 and Figure 7 illustrate the membership functions of the inputs for each of these systems, showing how the variation in Lower Scale affects the dispersion and overlap of the fuzzy sets. This analysis allows for the evaluation of the impact of uncertainty on the controller’s performance.
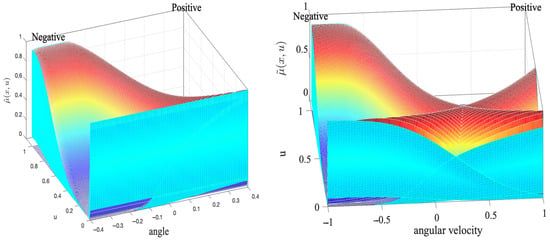
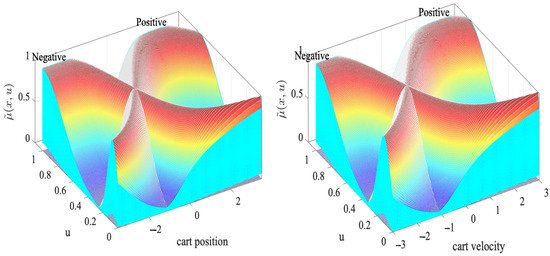
Figure 5.
MFs of the inputs with Lower Scale of 0.1.
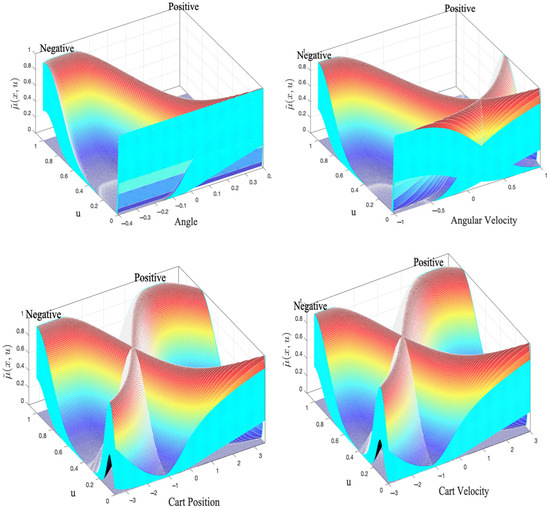
Figure 6.
MFs of the inputs with Lower Scale of 0.4.
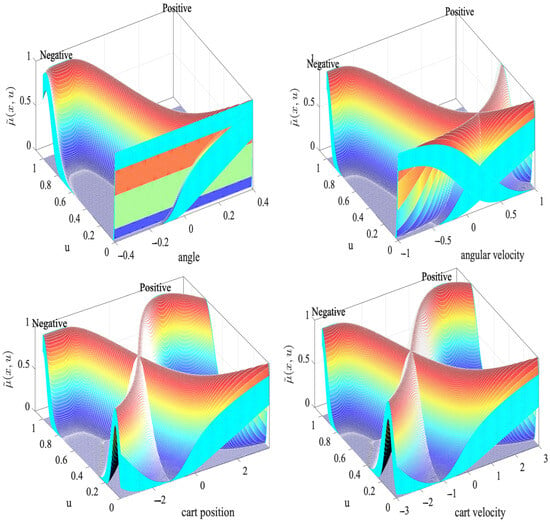
Figure 7.
MFs of the inputs with Lower Scale of 0.8.
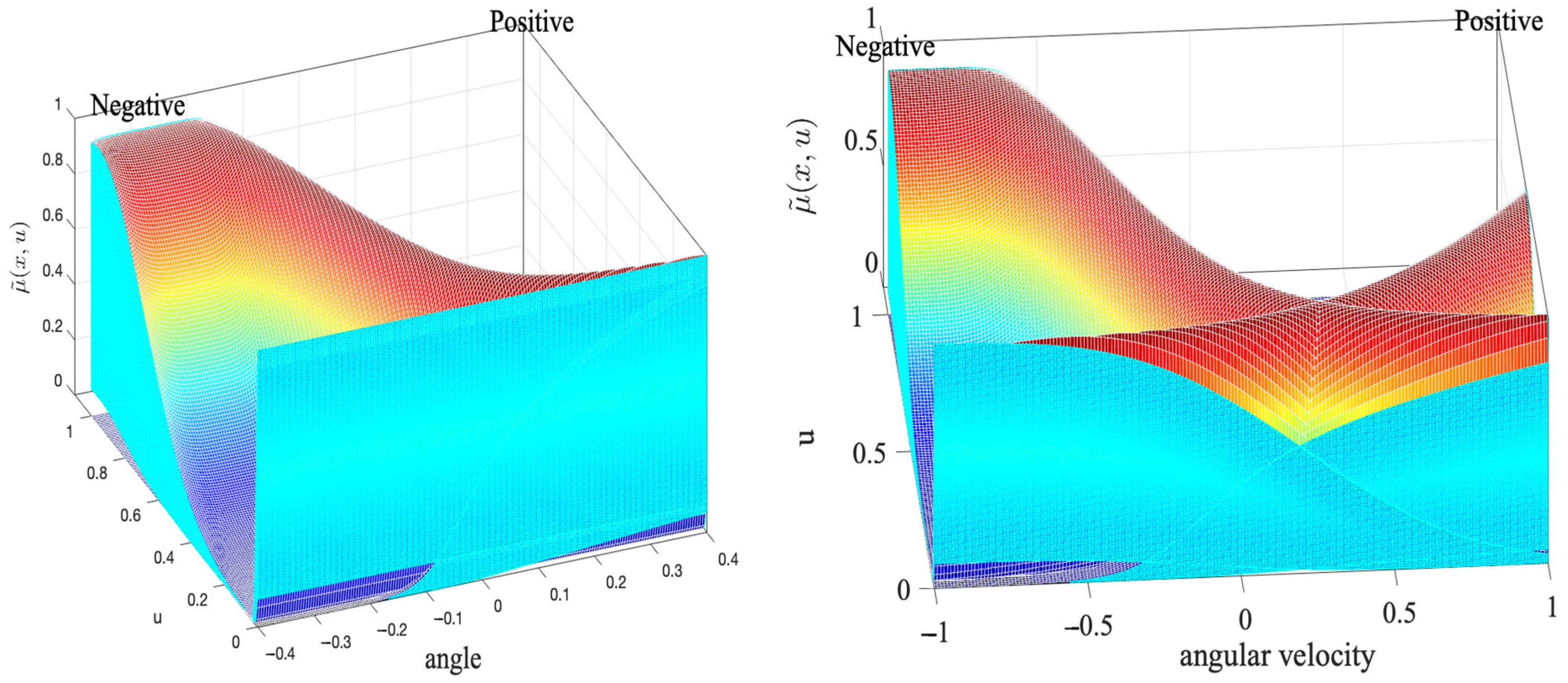
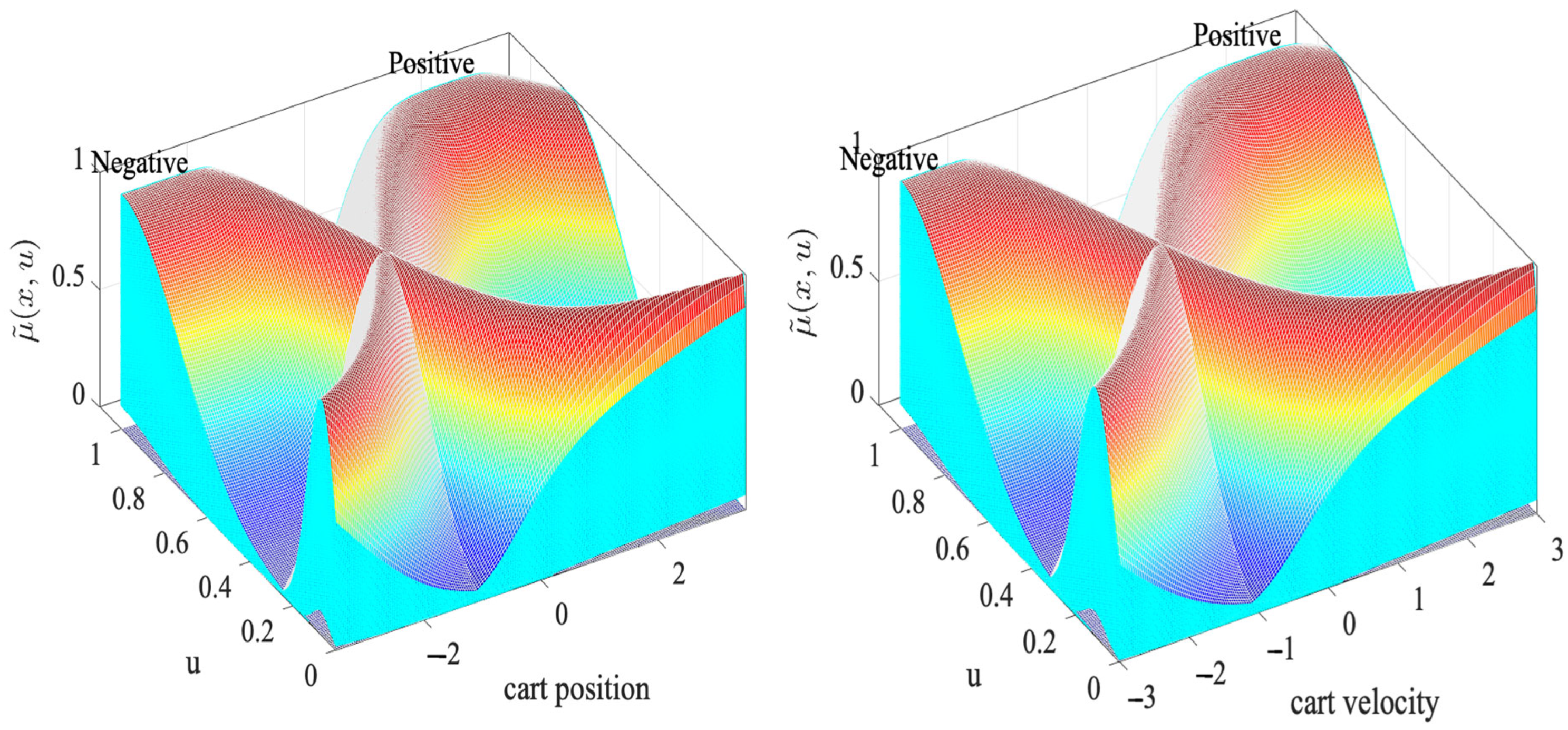
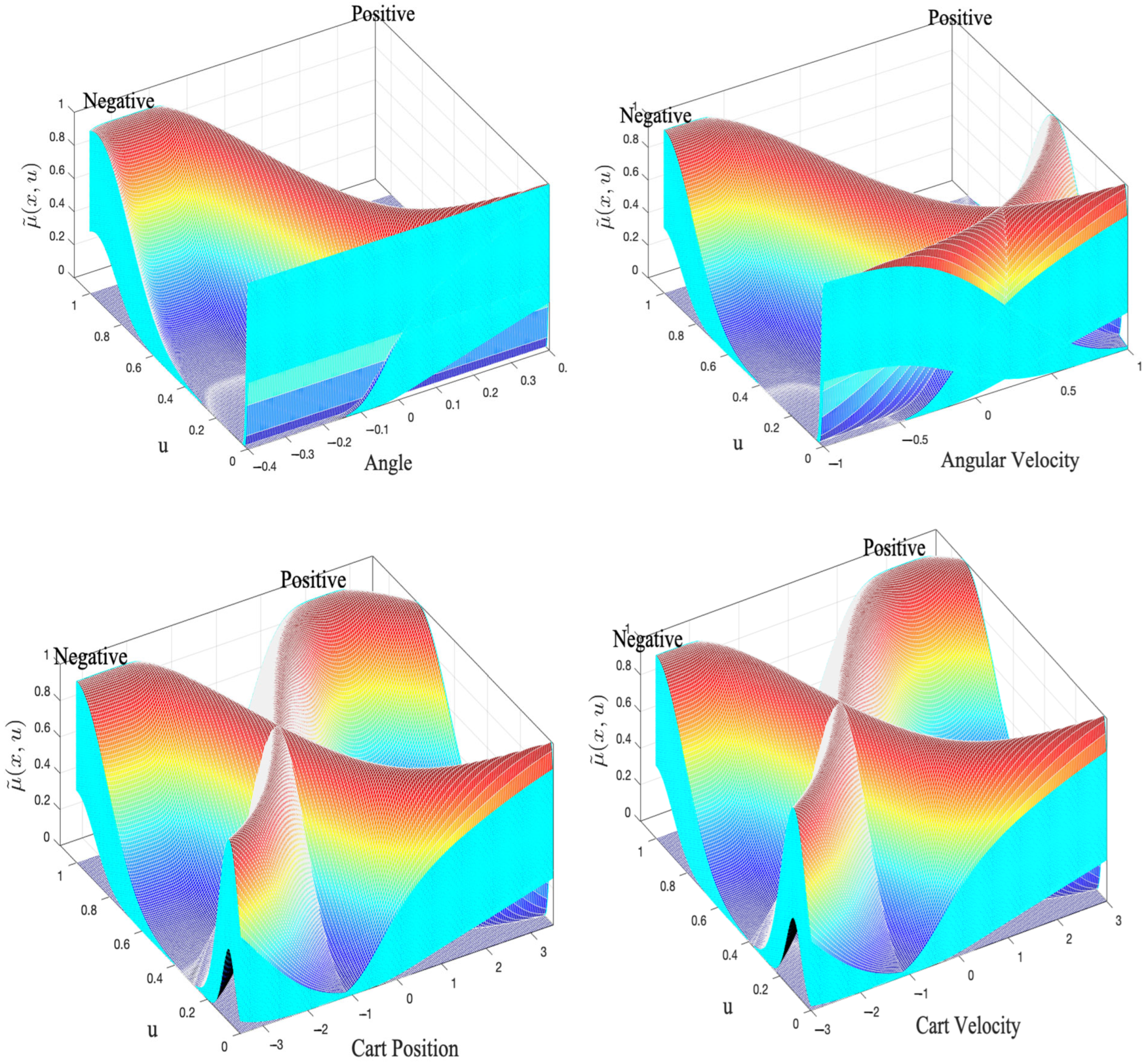
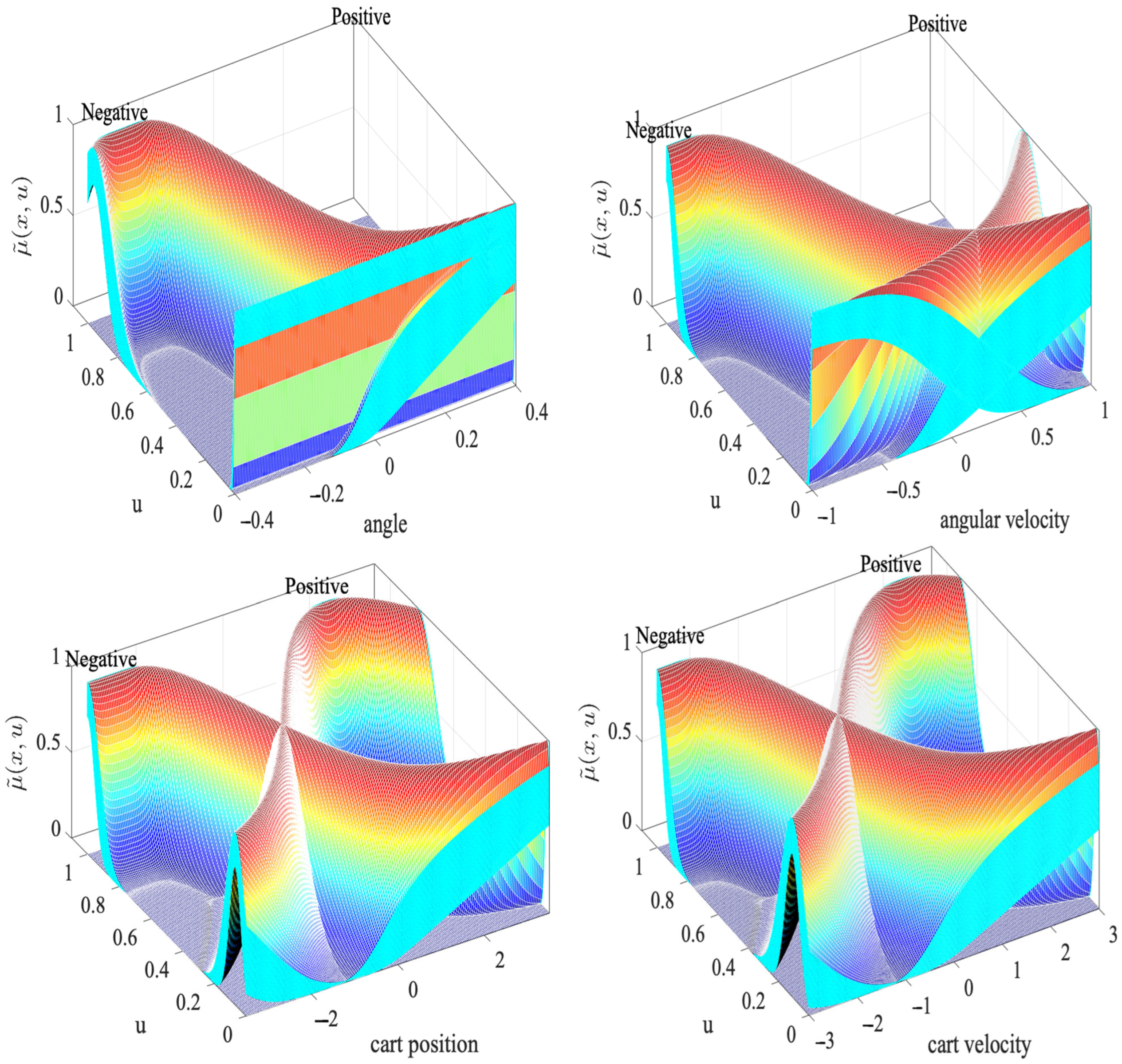
Figure 8 depicts the response surface of the fuzzy systems used for controlling the inverted pendulum. Since both the inputs and the rule set remain constant across the three evaluated systems, the shape of the surface does not change. This indicates that despite the variation in the Lower Scale parameter, the relationship between the input variables and the system’s output remains the same, ensuring consistency in the controller’s behavior.
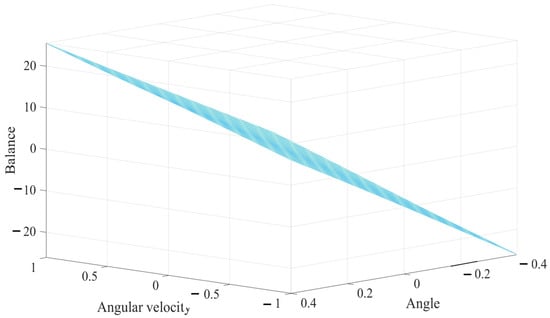
Figure 8.
Response surface of the fuzzy control systems.
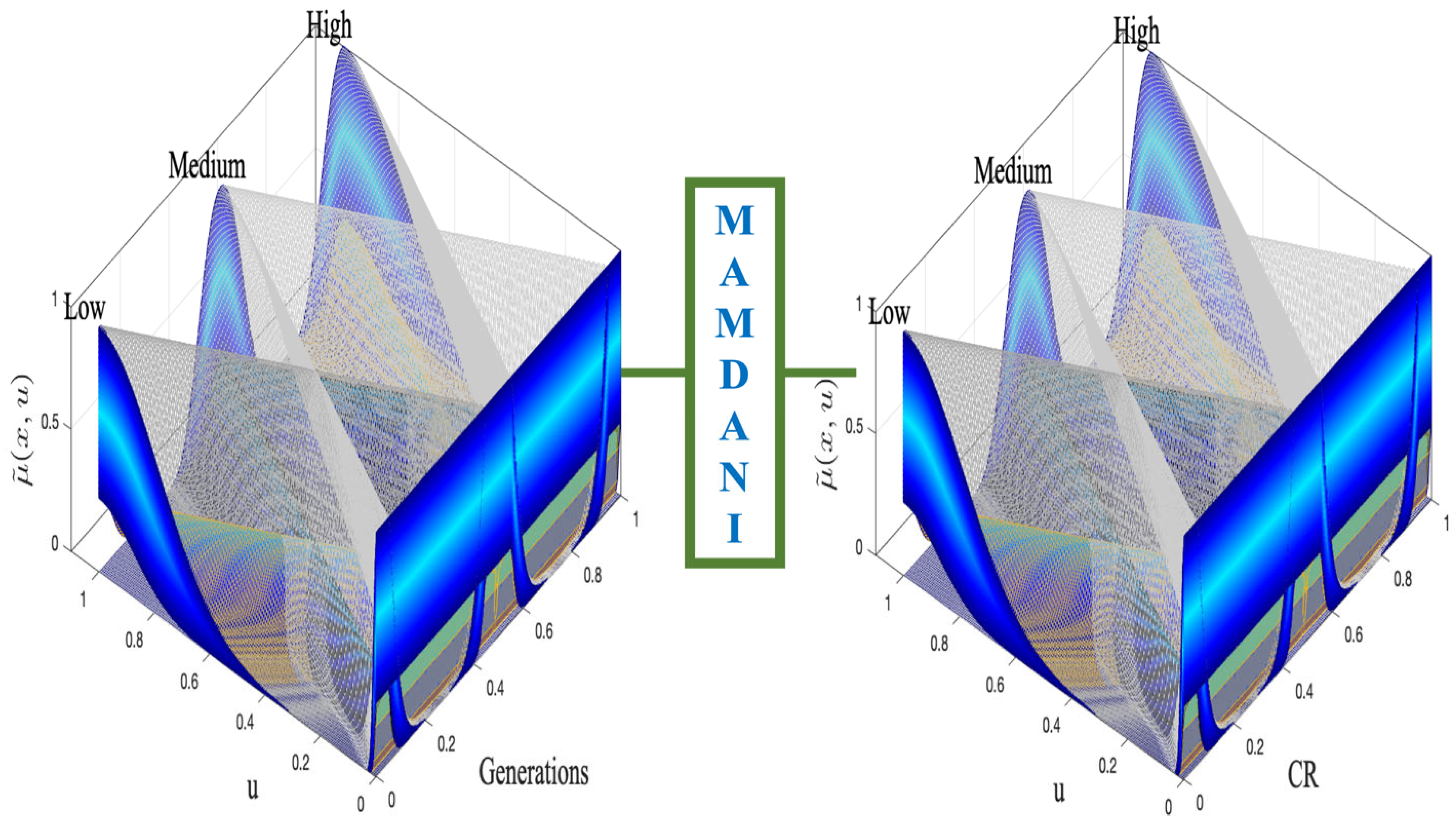
In the context of enhancing the adaptability of the DE algorithm, an interval T3FS was designed to dynamically adjust the crossover rate (CR) during the optimization process. This system aims to improve the convergence behavior and performance of DE by responding to changes in the number of generations. Figure 9 illustrates the internal structure of the fuzzy system, where the input variable represents the current generation count and the output corresponds to the dynamically adjusted CR value. The idea of employing fuzzy logic to tune the DE parameters has been explored in several works [46,47,48], and this allows the algorithm to adapt its exploration and exploitation balance throughout the optimization.
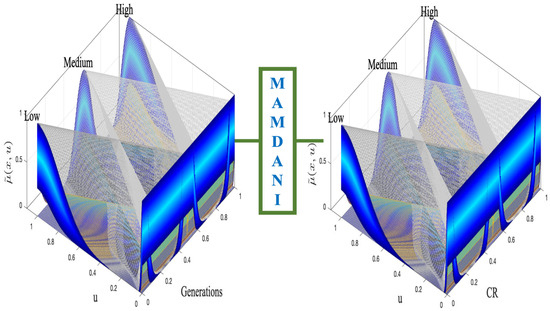
Figure 9.
Interval T3FS for CR adjustment in Differential Evolution.
The fuzzy rules of the system were designed based on expert knowledge and previous research in the field. These rules are of a decreasing nature, meaning that as the number of generations increases, the value of the crossover rate (CR) is gradually reduced. This approach aims to encourage exploration in the early stages of the evolutionary process and promote exploitation in later stages.
Equation (14) shows how the CR value is computed through a weighted average of the consequent values, using the membership degrees of each rule. The input variable (generations) is normalized to the interval [0, 1] to maintain consistency across different runs.
The fuzzy rule base is composed of three rules that define the relationship between the number of generations and the crossover rate (CR). These rules are structured as follows:
Rule 1: If the generation is low, then the CR is high;
Rule 2: If the generation is medium, then the CR is medium;
Rule 3: If the generation is high, then the CR is low.
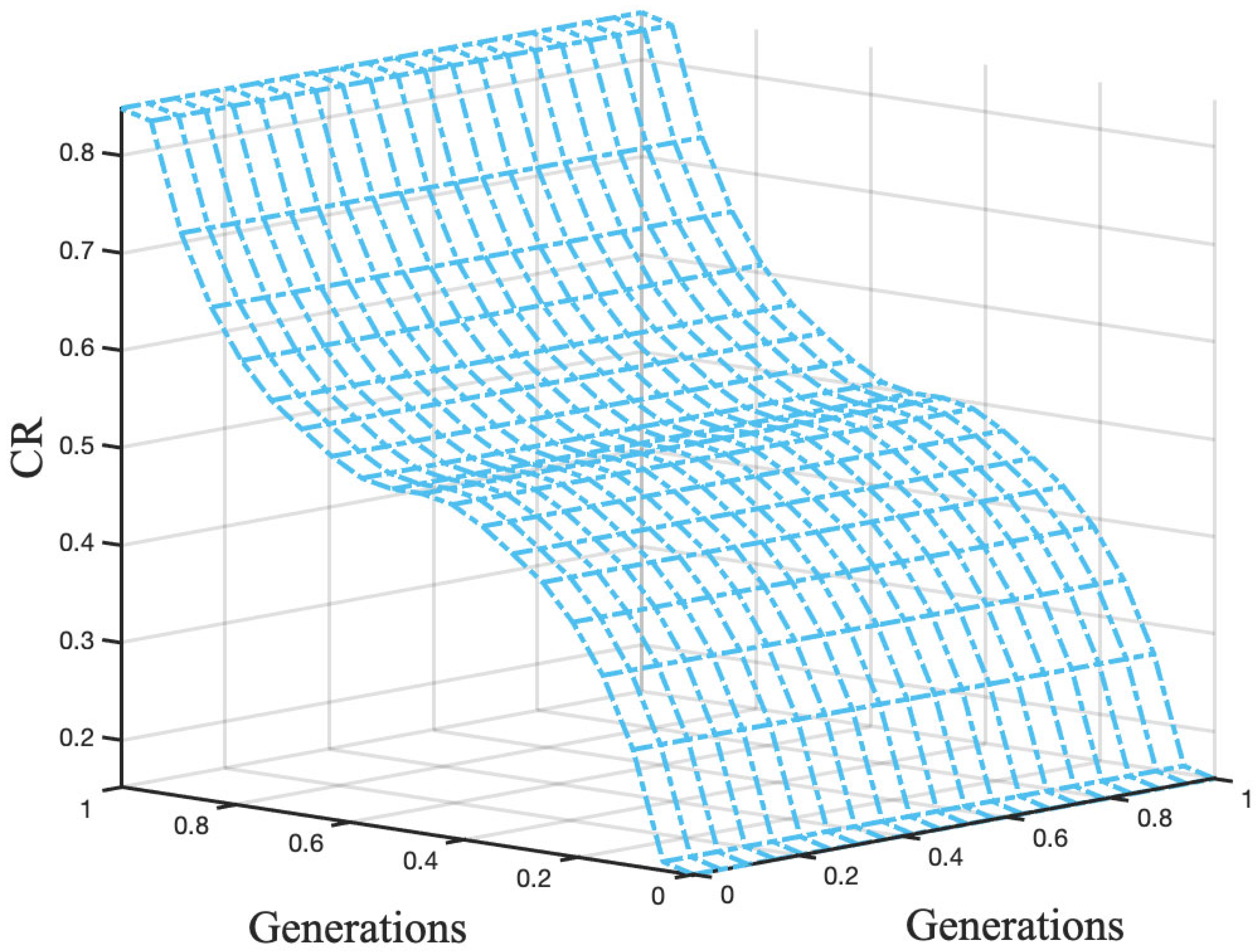
This rule configuration reflects a decreasing strategy, where the crossover rate is initially high to encourage exploration and is gradually reduced as generations increase to promote exploitation. The following figure, Figure 10, illustrates the surface generated by the previously described fuzzy system. This surface graphically represents the relationship between the input (number of generations) and the output (CR parameter value), showing how the crossover rate evolves as the algorithm progresses.
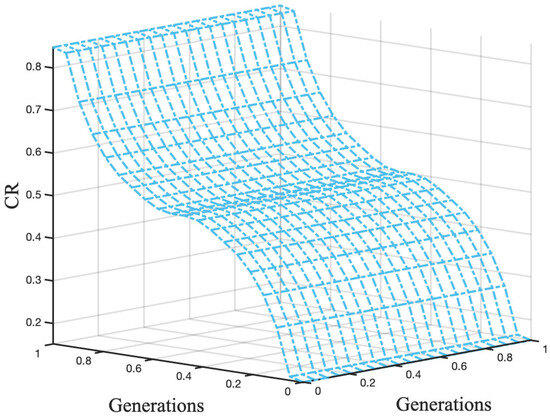
Figure 10.
Surface of the fuzzy system for dynamic CR adjustment based on generations.
5. Experimental Setup and Results
For the experimentation of the fuzzy controller applied to the inverted pendulum system, the following metrics were used along with their respective performance equations to evaluate the system’s performance:
Among these metrics, the root-mean-square error (RMSE) was chosen as the objective function for the experimentation, as it provides a direct measure of the model’s accuracy in terms of mean squared error.
Moreover, to assess the practical feasibility of the proposed method, it is relevant to analyze its computational complexity from both the inference system perspective and the execution environment.
Type-3 Fuzzy Inference System:
Type-3 fuzzy logic introduces a higher computational load compared to Type-1 and Type-2 systems due to the increased dimensionality of the footprint of uncertainty. However, to mitigate this load, a simplified inference structure based on α-plane representation is employed, which significantly reduces the number of operations required during the type reduction process. Furthermore, by using a Sugeno-type model, the inference stage is further simplified, as the outputs are linear functions, which enhances computational efficiency.
Simulation Environment:
The controller has been evaluated exclusively in a simulation environment, which allows for the computational load associated with both the Type-3 fuzzy logic and the optimization algorithm to be handled without difficulty. Since the system is not executed in real time, the type reduction and rule evaluation processes do not pose a practical limitation. Therefore, the system’s complexity does not compromise the viability of the proposed approach within the experimental framework used.
The first step in the experimental process was to validate three different fuzzy systems. In this phase, the LowerScale parameter in the inverted pendulum controller was adjusted to analyze its impact on performance. Each of the fuzzy systems was implemented, and the results obtained for each system are presented in Table 1.

Table 1.
Experimental results of the fuzzy controller with Lower Scale adjustments.
Based on the results presented in Table 1, the performance of the three evaluated fuzzy systems was analyzed. Considering RMSE as the main comparison criterion, it was observed that the fuzzy system with a Lower Scale value of 0.1 achieved the lowest error. Therefore, this configuration was selected for further development and experimentation, as it demonstrated superior performance in terms of control accuracy.
Once the T3FS for the inverted pendulum controller was defined—referred to as T3IP (Type-3 inverted pendulum)—the experimentation phase was carried out with the objective of evaluating its performance under different operating conditions. To this end, the original DE algorithm was used and applied to the simulation of the T3IP controller.
The experimentation was conducted in two main phases. In the first phase, simulations were performed without the presence of noise (DE + T3IP), allowing the system’s behavior to be analyzed under ideal conditions. In the second phase, noise was introduced into the input signal—specifically a uniform random number—resulting in the DE + T3IP + N configuration. The noise level was set to 0.50 to assess the robustness and stability of the controller under external disturbances.
The experimental setup parameters are provided in Table 2, and the results of the experimentation are shown in Table 3, where the performance of the DE+T3IP and DE + T3IP + N algorithms is compared. The table includes the best, worst, mean, and standard deviation values obtained over 30 independent experiments, allowing a comprehensive evaluation of consistency and performance under both ideal and noisy conditions.

Table 2.
Parameter configuration.

Table 3.
Evaluation metrics for the Type-3 fuzzy controller with and without noise.
Overall Accuracy (Mean RMSE): The controller configuration DE+T3IP+N achieves a significantly lower average RMSE compared to DE+T3IP, indicating better general performance even in the presence of noise. This suggests that the Type-3 fuzzy system responds more flexibly and adaptively to noisy inputs—a key advantage of higher-order fuzzy systems.
Best Case (Lowest RMSE): The best RMSE was also achieved with the noisy configuration (0.302 vs. 0.732), reinforcing the idea that introducing noise might help the system avoid local minima and reach more optimal solutions.
Worst Case (Highest RMSE): Interestingly, the worst-case performance with noise (4.500) is slightly better than that without noise (5.680), suggesting that the controller maintains acceptable behavior even under perturbations.
Consistency (Standard Deviation): The standard deviation is slightly higher with noise (0.277 compared to 0.226), indicating slightly more variability across the 30 runs. However, this increased variability is moderate and acceptable considering the significant reduction in average error.
The next phase of the experimentation involves applying the DE algorithm with T3FL, where the CR parameter is dynamically adapted. The parameters used for this stage are presented in Table 4.

Table 4.
Parameters used for the experimentation with adaptive DE.
Table 5 shows the results obtained from this approach applied to the Type-3 inverted pendulum system, under two different configurations:

Table 5.
Performance results of the T3DE+T3IP controller with and without noise.
T3DE+T3IP: Differential Evolution with Type-3 fuzzy logic adapting CR, without noise;
T3DE + T3IP + N: The same configuration, but with the addition of uniform random noise with a noise level of 0.5 applied to the input signal.
The table reports the best, worst, mean, and standard deviation values obtained from 30 experimental runs, to assess the controller’s accuracy, robustness, and stability under both ideal and noisy conditions.
To further evaluate the performance of the proposed controller, Table 5 presents the results obtained from 30 experimental runs under both noise-free (T3DE + T3IP) and noisy (T3DE + T3IP + N) conditions. The analysis includes the best, worst, mean, and standard deviation of the RMSE metric. These results allow us to assess the controller’s accuracy, robustness, and consistency when facing external disturbances.
Best Case Performance: The T3DE + T3IP + N configuration achieved the best individual result (0.0127), indicating that introducing noise significantly enhanced the controller’s performance in the best-case scenario.
Worst Case Performance: While both configurations show performance degradation in the worst case, the worst result of T3DE + T3IP + N (0.235) is still substantially better than that of T3DE + T3IP (0.397).
Average Performance (Mean): The average RMSE drops from 0.122 to 0.0245, demonstrating a considerable overall improvement in performance when noise is introduced.
Standard Deviation (Std): The standard deviation also decreases from 0.136 to 0.0111, indicating that the system with noise is more consistent and less variable.
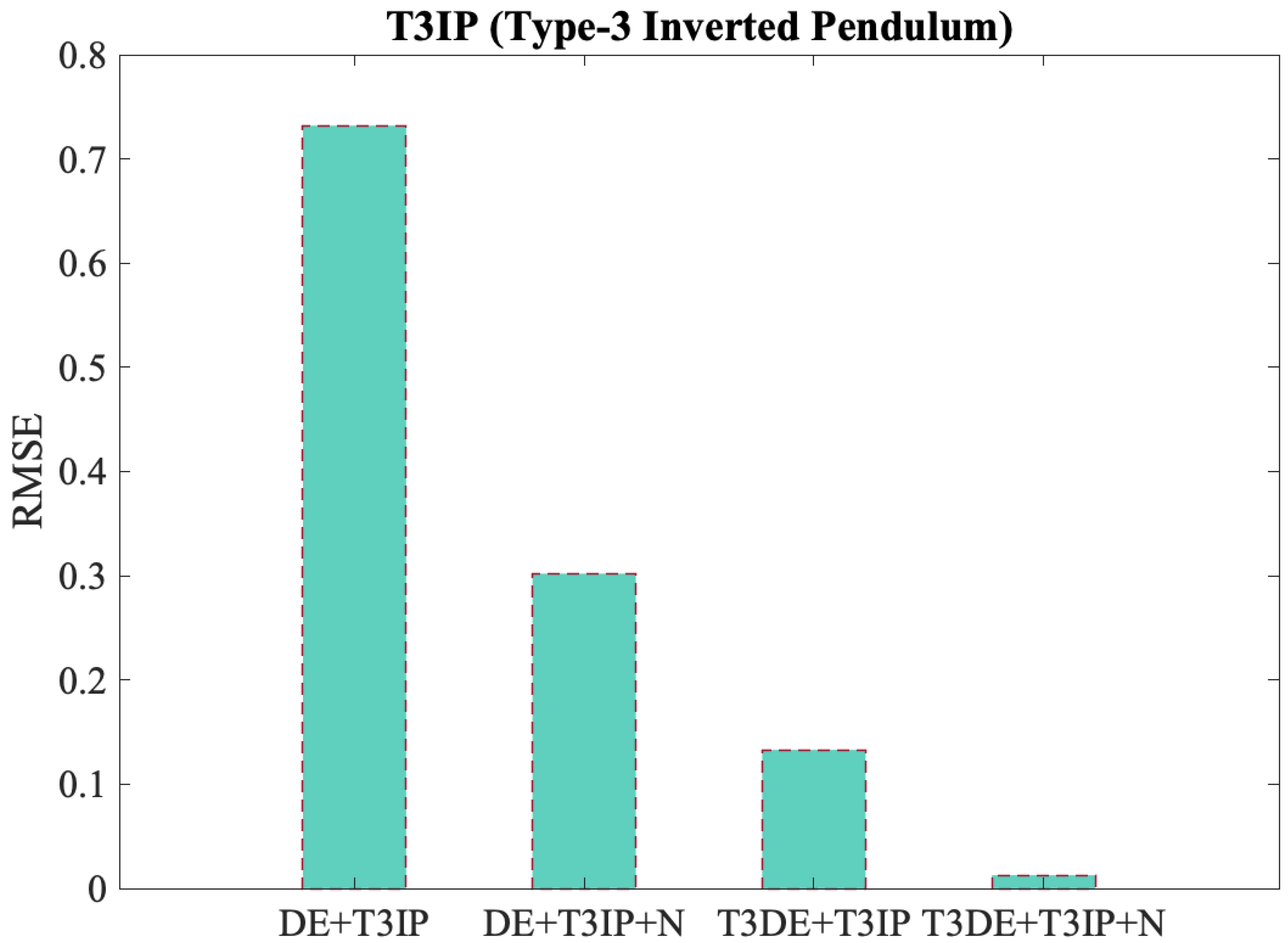
To compare the performance of the Type-3 inverted pendulum controller under different experimental configurations, the results presented in Table 3 and Table 5 were analyzed. These tables show the system’s performance using the Differential Evolution algorithm in both its original form and in the variant with dynamic adaptation of the CR parameter, evaluated under both noise-free and noisy conditions. To facilitate comparison, Table 6 summarizes the best RMSE values obtained in each configuration. Additionally, Figure 11 provides a graphical representation of these results, allowing for a clear and direct visualization of the controller’s performance differences under the evaluated conditions.

Table 6.
Comparison of the best RMSE results of the T3IP controller.
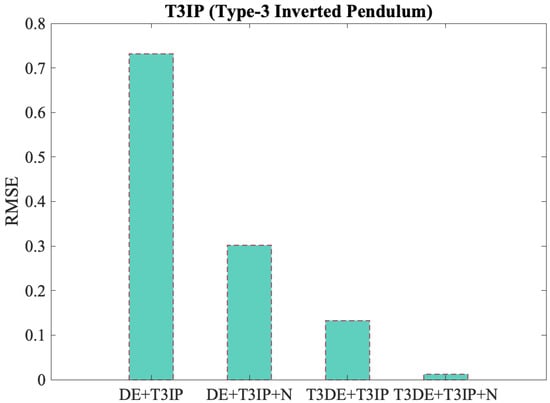
Figure 11.
Comparison of best RMSE results for DE with different variables on the Inverted Pendulum.
The RMSE results indicate that the T3IP controller significantly improves its performance when using the adaptive Type-3 Fuzzy Differential Evolution algorithm (T3DE). This improvement is evident in both ideal and noisy conditions, where the lowest error (0.0127) is achieved, demonstrating greater precision and robustness of the system.
To validate the results obtained, two independent statistical tests were conducted to compare the performance of the controller under different configurations:
First Statistical Test: This test compares DE + T3IP + N (µ1) against DE + T3IP (µ2), based on the hypothesis that introducing noise improves the controller’s performance, meaning that DE + T3IP + N yields a lower error than DE + T3IP.
Second Statistical Test: This comparison evaluates T3DE + T3IP + N (µ1) versus T3DE + T3IP (µ2), under the hypothesis that the Type-3 fuzzy controller with dynamic CR adaptation performs better when noise is introduced, implying that T3DE + T3IP + N achieves a lower error than T3DE + T3IP.
For both comparisons, a one-tailed (left-tailed) Z-test was used, since the goal is to determine whether the configuration with noise significantly reduces the error. The parameters used for these statistical tests are presented in Table 7.

Table 7.
Specifications of the test parameters.
Table 8 shows the results of the statistical tests conducted to compare the controller’s performance under different configurations. Two independent one-tailed (left-sided) Z-tests were applied to determine whether the inclusion of noise significantly reduces the RMSE.

Table 8.
Z-test results for the T3IP system.
In the first case, DE+T3IP+N was compared with DE+T3IP, and in the second case, T3DE+T3IP+N was compared with T3DE+T3IP. In both tests, the alternative hypothesis assumes that the configuration with noise (μ1) produces a lower error than the configuration without noise (μ2). The calculated Z values were −28.0987 and −3.9137, respectively, both indicating statistically significant differences in favor of the noisy configurations.
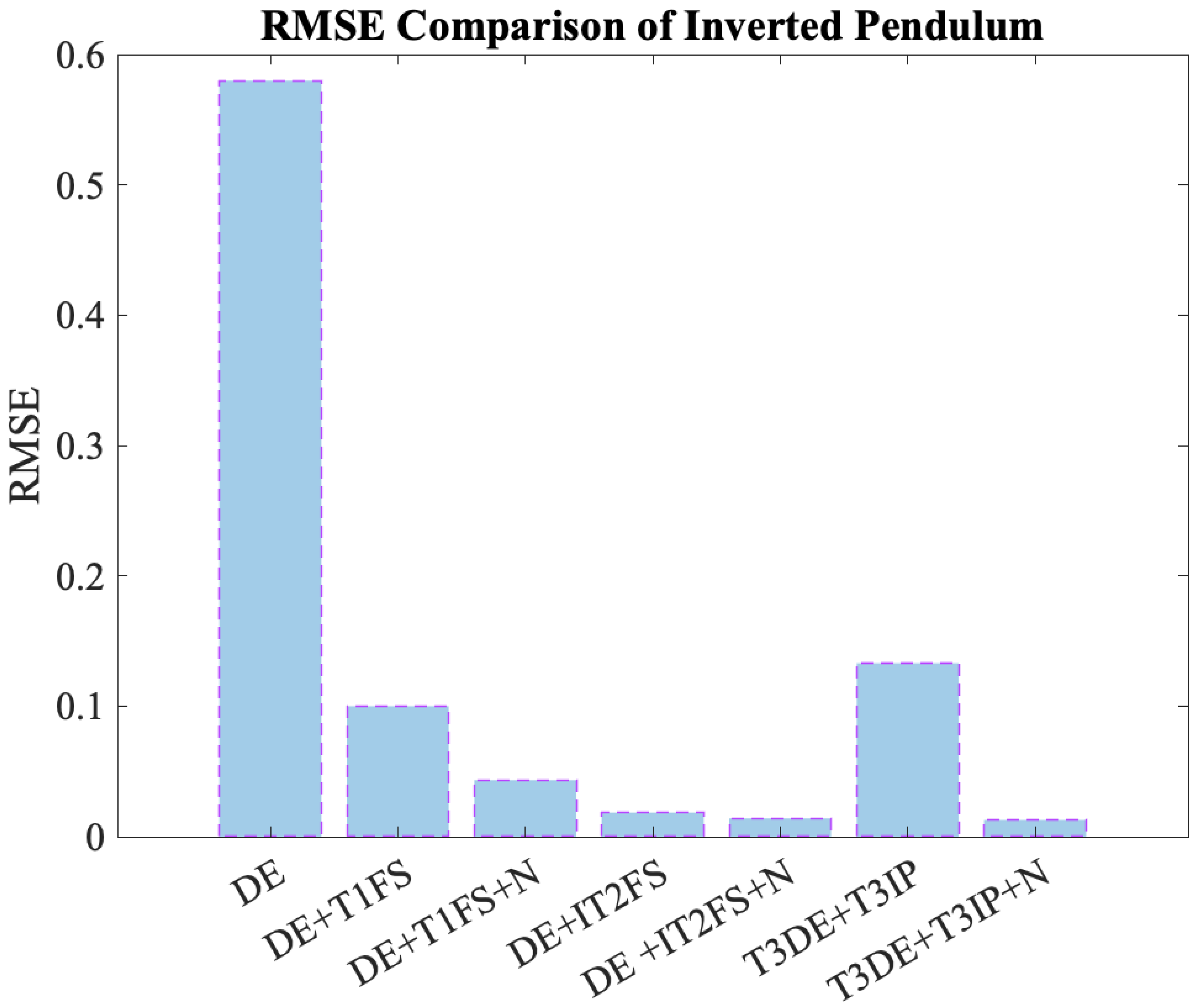
Finally, a comparison was made with a previous study in which the inverted pendulum controller was implemented using the Differential Evolution (DE) algorithm under various experimental configurations [49]. Table 9 presents the RMSE values obtained for each configuration, including the best, worst, mean, and standard deviation.

Table 9.
Performance comparison of the controller with previous and current configurations.
To contextualize the performance of the approach, a direct comparison is presented with configurations previously reported in the literature. The table includes various combinations of DE with Type-1, Type-2, and Type-3 fuzzy systems, both with and without noise. The following section analyzes the performance of each configuration based on the obtained RMSE values.
Performance evolution with higher-order fuzzy systems: There is a clear performance improvement when moving from pure DE (mean RMSE of 1.4) to more sophisticated fuzzy systems such as the T1FS, IT2FS, and ultimately T3IP.
Effect of noise (N): The inclusion of noise consistently improves performance across all configurations. For instance, DE+T1FS has a mean RMSE of 0.43, which drops to 0.33 with DE+T1FS+N. A similar pattern is observed with the IT2FS and T3IP.
Proposed controller (T3DE+T3IP+N): This configuration shows the best overall performance among all evaluated approaches:
Best RMSE: 0.0127;
Lowest mean RMSE: 0.0245;
Smallest standard deviation: 0.0111.
These results indicate that the controller based on T3FL with dynamic CR adaptation and added noise not only enhances accuracy but also improves stability and consistency.
Comparison with IT2FS: Although IT2FS-based configurations perform better than the T1FS, they still do not reach the performance levels achieved by the proposed controller. This highlights the advantages of T3FSs for nonlinear control tasks.
Based on the best RMSE values reported in Table 9 for each of the evaluated configurations, Figure 12 was generated to provide a comparative graphical representation of these results. This visualization clearly highlights the impact of different control approaches and the role of noise on the system’s performance.
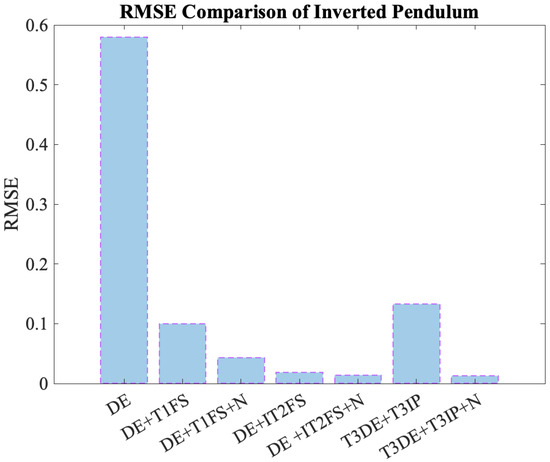
Figure 12.
Comparison of the best RMSE results.
6. Discussion of Results
The results presented in this study demonstrate the effectiveness of the Type-3 fuzzy logic framework in addressing the limitations of traditional Type-1 and Type-2 fuzzy control systems. The proposed approach exhibits superior performance in terms of accuracy (measured by RMSE) and robustness, particularly under noisy conditions. These findings align with recent advances in adaptive control methodologies, further validating the potential of Type-3 fuzzy logic as a viable solution for complex nonlinear systems.
Compared to related studies, our framework provides a more flexible mechanism to handle dynamic uncertainties. Unlike previous approaches, which rely heavily on fixed or less adaptable parameters, the dynamic adaptation of the CR parameter in our method ensures consistent performance across a wide range of operational scenarios. Additionally, the results presented in Table 9 highlight the comparative advantages of the proposed approach under both noisy and noise-free conditions, reinforcing its robustness and adaptability. Another aspect to consider is the complexity involved in selecting and calibrating the additional parameters inherent in the Type-3 framework. Although the parameter selection process described in Section 4 provides a systematic approach, future research could explore automated or hybrid optimization techniques to simplify this process.
This work presented the design and evaluation of a control strategy based on an interval Type-3 fuzzy system (IT3FS) for the inverted pendulum system, with the main objective of minimizing the RMSE. Initially, the influence of the LowerScale parameter was analyzed, and the configuration with LowerScale = 0.1 yielded the best RMSE (1.4), making it the selected setup for the controller. Subsequently, experiments were conducted using the inverted pendulum system in two phases:
- Using a standard Differential Evolution (DE) algorithm with the Type-3 fuzzy controller (T3IP), both with and without noise.
- Using an enhanced Differential Evolution (T3DE) version, where the crossover rate (CR) is dynamically adjusted using a Type-3 fuzzy logic system.
The following RMSE results were obtained:
- DE + T3IP: 0.732;
- DE + T3IP + N: 0.302;
- T3DE + T3IP: 0.133;
- T3DE + T3IP + N: 0.0127.
These results show a substantial improvement in performance, particularly in the presence of noise. The T3DE+T3IP+N configuration outperformed all others, confirming that integrating T3FL both in the controller and in the parameter adaptation of the evolutionary algorithm enhances robustness and accuracy. To further assess the effectiveness of the proposal, a comparative analysis was conducted against previous fuzzy control strategies, including the following:
- DE;
- DE with Type-1 fuzzy systems (T1FSs);
- DE with interval Type-2 fuzzy systems (IT2FSs).
The comparison, summarized in terms of the best, worst, mean, and standard deviation RMSE values, showed that the proposed T3DE + T3IP approach achieved the following:
- The lowest mean RMSE: 0.0245;
- The best performance in noisy environments: 0.0127;
- The lowest variability: standard deviation of 0.0111.
Compared to the previous best (DE + IT2FS + N), which had a best-case RMSE of 0.014, the proposed method improved both the average performance and the consistency of the results. This demonstrates the advantage of using Type-3 fuzzy systems not only for control, but also for dynamic parameter tuning in optimization algorithms.
7. Conclusions
In conclusion, the dual application of T3FL, both within the controller and in the evolutionary optimization process, proved to be a robust and effective strategy for controlling nonlinear systems under uncertain and noisy conditions. The comparative results clearly validate the superiority of the proposal over traditional DE and lower-order fuzzy logic-based approaches.
As a main line of future work, we propose to further explore the Differential Evolution algorithm enhanced with Type-3 fuzzy logic, investigating alternative strategies for dynamic parameter adaptation and hybridization with other optimization techniques. This could lead to improved performance in complex and highly uncertain environments.
Additionally, it is considered promising to extend Type-3 fuzzy logic to other types of controllers, such as adaptive PID, predictive, or neuro-fuzzy controllers, aiming to enhance their robustness against disturbances and noise. This would allow for the development of more flexible and accurate control schemes.
Finally, a key goal is to apply these developments to real-world problems, such as the control of robotic systems, autonomous vehicles, industrial processes, or energy applications. This would not only validate the practical utility of the proposed approach but also open new opportunities for designing intelligent control systems based on T3FL.
This study has presented a Type-3 fuzzy logic framework that demonstrates significant advantages over traditional Type-1 and Type-2 approaches in terms of accuracy and robustness, especially under noisy conditions. However, like any approach, the proposed method has limitations that must be considered:
Limitations:
- Computational cost: The implementation of the Type-3 framework involves higher computational costs compared to Type-1 and Type-2 approaches. This could limit its application in systems with restricted computational resources or those requiring real-time responses.
- Parameter selection complexity: The need to select and calibrate several additional parameters can pose a challenge, particularly in systems with high dimensionality or changing conditions.
Future directions:
- Computational optimization: Future research could focus on improving the computational efficiency of the method, developing simplified versions, or leveraging specialized hardware such as GPUs.
- Automation of parameter selection: The use of automatic optimization techniques, such as evolutionary algorithms or machine learning, could simplify the parameter tuning process and enhance the framework’s usability.
Author Contributions
P.O., C.P. and O.C. conducted the state-of-the-art and literature reviews, conducted the formal analysis, and developed the main idea. P.M. contributed to the formal analysis and methodology. O.C. and Z.W.G. provided supervision. Z.W.G. acquired funding. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy, Republic of Korea (RS-2024-00441420; RS-2024-00442817).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank the Tijuana Institute of Technology and TECNM for their support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Price, K.V.; Storn, R.M.; Lampinen, J.A. Differential Evolution; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Pytel, K. Fuzzy logic applied to tuning mutation size in evolutionary algorithms. Sci. Rep. 2025, 15, 1937. [Google Scholar] [CrossRef] [PubMed]
- Bingol, M.C. A Safe Navigation Algorithm for Differential-Drive Mobile Robots by Using Fuzzy Logic Reward Function-Based Deep Reinforcement Learning. Electronics 2025, 14, 1593. [Google Scholar] [CrossRef]
- Li, K.; Liu, X. Fuzzy Adaptive Cooperative Prescribed Time Control for Nonlinear Vehicular Platoon Systems. IEEE Trans. Fuzzy Syst. 2025, 33, 1568–1577. [Google Scholar] [CrossRef]
- Yilmaz, B.M.; Tatlicioglu, E.; Selim, E. Velocity observer design for a class of uncertain nonlinear mechanical systems: A self-adaptive fuzzy logic-based approach. Int. J. Syst. Sci. 2025, 56, 423–433. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Grasa, P.; Polyakhov, N. The direct adaptive trajectory control of robot manipulators via fuzzy logic algorithm. WIT Trans. Inf. Commun. Technol. 2025, 1, 9. [Google Scholar]
- Zhao, X.; Zhao, Q.; Peng, J. Research on improved dynamic window approach based on fuzzy logic for adaptive obstacle avoidance control in unmanned surface vehicles. In Proceedings of the Fifth International Conference on Signal Processing and Computer Science (SPCS 2024) SPIE, Kaifeng, China, 23–25 August 2024; Volume 13442, pp. 643–651. [Google Scholar]
- Cavus, M.; Dissanayake, D.; Bell, M. Deep-Fuzzy Logic Control for Optimal Energy Management: A Predictive and Adaptive Framework for Grid-Connected Microgrids. Energies 2025, 18, 995. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Yu, J. Lyapunov-derived fuzzy temperature control for thermoelectric cooling system using dynamic updating law. Appl. Therm. Eng. 2025, 258, 124600. [Google Scholar] [CrossRef]
- Li, H.; Chou, W.; Meng, L. Finite-Time Adaptive Fuzzy Prescribed Performance Control for Teleoperation With Asymmetric Time Delays and Uncertainties. Int. J. Robust. Nonlinear Control 2025, 35, 2982–2995. [Google Scholar] [CrossRef]
- Elnaghi, B.E.; Ismaiel, A.M.; El Sayed Abdel-Kader, F.; Abelwhab, M.N.; Mohammed, R.H. Validation of energy valley optimization for adaptive fuzzy logic controller of DFIG-based wind turbines. Sci. Rep. 2025, 15, 711. [Google Scholar] [CrossRef]
- Madebo, N.W. Enhancing Intelligent Control Strategies for UAVs: A Comparative Analysis of Fuzzy Logic, Fuzzy PID, and GA-Optimized Fuzzy PID Controllers. IEEE Access 2025, 13, 16548–16563. [Google Scholar] [CrossRef]
- Mohammad, S.I.; Yogeesh, N.; Raja, N.; Chetana, R.; Ramesha, M.S.; Vasudevan, A. Optimizing MIMO Antenna Performance Using Fuzzy Logic Algorithms. Appl. Math. 2025, 19, 349–364. [Google Scholar]
- Jiang, Q.; Wang, P. A fuzzy logic-based coordinated adaptive control method for megawatt novel nuclear power systems. Ann. Nucl. Energy 2025, 215, 111245. [Google Scholar] [CrossRef]
- Hosny, M.; Marei, M.I.; Mohamad, A.M. Adaptive hybrid virtual inertia controller for PMSG-based wind turbine based on fuzzy logic control. Sci. Rep. 2025, 15, 3757. [Google Scholar] [CrossRef]
- Li, Z.; Dewantoro, G.; Xiao, T.; Swain, A. A Comparative Analysis of Fuzzy Logic Control and Model Predictive Control in Photovoltaic Maximum Power Point Tracking. Electronics 2025, 14, 1009. [Google Scholar] [CrossRef]
- Zhang, W. Predefined-Time Fuzzy Control for Robotic Manipulators Driven by Compliant Actuators. Int. J. Fuzzy Syst. 2025, 27, 1–10. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.; Wu, D. Force–vision fusion fuzzy control for robotic batch precision assembly of flexibly absorbed pegs. Robot. Comput.-Integr. Manuf. 2025, 92, 102861. [Google Scholar] [CrossRef]
- Pérez-Juárez, J.G.; García-Martínez, J.R.; Medina Santiago, A.; Cruz-Miguel, E.E.; Olmedo-García, L.F.; Barra-Vázquez, O.A.; Rojas-Hernández, M.A. Kinematic Fuzzy Logic-Based Controller for Trajectory Tracking of Wheeled Mobile Robots in Virtual Environments. Symmetry 2025, 17, 301. [Google Scholar] [CrossRef]
- Kumar, V.; Mistri, A. Fuzzy logic-based synchronization of trajectory planning and obstacle avoidance for RRP SCARA robot. Int. J. Interact. Des. Manuf. 2025, 19, 3039–3052. [Google Scholar] [CrossRef]
- Shufian, A.; Shib, S.K.; Dipto, D.R.; Rahman, M.T.; Hannan, N.; Fattah, S.A. Fuzzy logic-controlled three-phase dynamic voltage restorer for enhancing voltage stabilization and power quality. Int. J. Electr. Power Energy Syst. 2025, 166, 110517. [Google Scholar] [CrossRef]
- Zheng, Y.; Na, Z.; Ji, W.; Lu, Y. An Adaptive Fuzzy SIR Model for Real-Time Malware Spread Prediction in Industrial Internet of Things Networks. IEEE Internet Things J. 2025; in press. [Google Scholar] [CrossRef]
- Chotikunnan, P.; Roongprasert, K.; Chotikunnan, R.; Pititheeraphab, Y.; Puttasakul, T.; Wongkamhang, A.; Thongpance, N. Hybrid Fuzzy-Expert System Control for Robotic Manipulator Applications. J. Robot. Control (JRC) 2025, 6, 155–165. [Google Scholar] [CrossRef]
- Nasir, N.M.; Ghani NM, A.; Nasir AN, K.; Ahmad, M.A.; Tokhi, M.O. Neuro-modelling and fuzzy logic control of a two-wheeled wheelchair system. J. Low. Freq. Noise Vib. Act. Control 2025, 44, 588–602. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.; Liu, F. Interval Type-2 Fuzzy Logic Systems Made Simple. IEEE Trans. Fuzzy Syst. 2006, 14, 808–821. [Google Scholar] [CrossRef]
- Ambareesh, S.; Chavan, P.; Supreeth, S.; Nandalike, R.; Dayananda, P.; Rohith, S. A secure and energy-efficient routing using coupled ensemble selection approach and optimal type-2 fuzzy logic in WSN. Sci. Rep. 2025, 15, 38. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Hussein, Z.A.; Chyad, M.H.; Farhadi, A.; Yu, J.; Rahbarimagham, H. Integrating type-2 fuzzy logic controllers with digital twin and neural networks for advanced hydropower system management. Sci. Rep. 2025, 15, 5140. [Google Scholar] [CrossRef]
- Boudia, A.; Messalti, S.; Zeghlache, S.; Harrag, A. Type-2 fuzzy logic controller-based maximum power point tracking for photovoltaic system. Electr. Eng. Electromech. 2025, 1, 16–22. [Google Scholar] [CrossRef]
- Rinesh, S.; Arun, M.; Kumar, S.N.; Prajitha, C.; Kumar, A.S. Evaluating the type 2 fuzzy logic controller with multilayer perceptrons for optimal tracking of solar photovoltaic systems. Int. J. Low-Carbon. Technol. 2025, 20, 394–403. [Google Scholar] [CrossRef]
- Belhadj, S.M.; Meliani, B.; Benbouhenni, H.; Zaidi, S.; Elbarbary ZM, S.; Alammer, M.M. Control of multi-level quadratic DC-DC boost converter for photovoltaic systems using type-2 fuzzy logic technique-based MPPT approaches. Heliyon 2025, 11, e42181. [Google Scholar] [CrossRef]
- Hashim AA, A.; Ghani NM, A.; Ahmad, S.; Hashim, M.R.; Naharuddin NZ, A.; Irawan, A. Optimized Type-2 Fuzzy Logic Control for Low-Speed Vehicle Pedal Pressing Automation Using Hybrid Spiral Sine Cosine Algorithm. IIUM Eng. J. 2025, 26, 563–584. [Google Scholar] [CrossRef]
- Benbrahim, M.; Bouhentala, M.; Ghanai, M.; Chafaa, K.; Essounbouli, N. Generalization to Type 2 of PSO-Optimized Type 1 PD Fuzzy Controller and its Application to a Quadrotor UAV. Eng. Technol. Appl. Sci. Res. 2025, 15, 21658–21664. [Google Scholar] [CrossRef]
- Castillo, O.; Castro, J.R.; Melin, P. Interval type-3 fuzzy logic systems (IT3FLS). In Interval Type-3 Fuzzy Systems: Theory and Design; Springer International Publishing: Cham, Switzerland, 2022; pp. 45–49. [Google Scholar]
- Sabahi, K.; Panahi, S.; Shokri Kalandaragh, Y.; Mohammadzadeh, A. Deep reinforcement learning tuned type-3 fuzzy PID controller: AC microgrid case study. Electr. Eng. 2005, 107, 1–14. [Google Scholar] [CrossRef]
- Melin, P.; Castillo, O. A Type-3 Fuzzy-Fractal Approach for Diagnosis of Mental Disorders. In Type-3 Fuzzy Logic and Fractal Theory for Medical Diagnosis; Springer Nature Switzerland: Cham, Switzerland, 2025; pp. 47–55. [Google Scholar]
- Sabetahd, R.; Mohammadzadeh, A.; Jafarzadeh, O.; Taghavifar, H.; Sakthivel, R.; Zhang, C. Applied Type-3 Fuzzy Logic Systems and Controllers; Studies in Fuzziness and Soft Computing; Springer: Cham, Switzerland, 2025. [Google Scholar]
- Li, S.; Mohammadzadeh, A.; Zhang, C. An Applied Type-3 Fuzzy Controller for Gyroscopes. Int. J. Fuzzy Syst. 2025, 27, 1–18. [Google Scholar] [CrossRef]
- Mozaffari, M.; Mazinani, S.M.; Khazaei, A.A. An energy efficient grid-based clustering algorithm using type-3 fuzzy system in wireless sensor networks. Wirel. Netw. 2025, 31, 109–125. [Google Scholar] [CrossRef]
- Chen, F.; Qiu, X.; Alattas, K.A.; Mohammadzadeh, A.; Ghaderpour, E. A new fuzzy robust control for linear parameter-varying systems. Mathematics 2022, 10, 3319. [Google Scholar] [CrossRef]
- Maraslidis, G.S.; Kottas, T.L.; Tsipouras, M.G.; Fragulis, G.F. Design of a Fuzzy Logic Controller for the Double Pendulum Inverted on a Cart. Information 2022, 13, 379. [Google Scholar] [CrossRef]
- Shirgir, S.; Farahmand-Tabar, S. An enhanced optimum design of a Takagi-Sugeno-Kang fuzzy inference system for seismic response prediction of bridges. Expert. Syst. Appl. 2025, 266, 126096. [Google Scholar] [CrossRef]
- Zaman, M.Q.; Wu, H.M. Genetic Algorithm Based Takagi-Sugeno Fuzzy Modelling of a Mecanum Wheeled Mobile Robot. Int. J. Control Autom. Syst. 2025, 23, 907–919. [Google Scholar] [CrossRef]
- Gu, S.; Wang, Y.; Chou, Y.; Cong, J.; Lu, M.; Jiao, Z. Interpretable Style Takagi-Sugeno-Kang Fuzzy Clustering. arXiv 2025, arXiv:2504.05125. [Google Scholar]
- Pérez-del-Notario, I.; González, X.; Horanska, L.; Oria, P.; Fernandez, J.; Dimuro, G.; Bustince, H. Flexible fusion models for improving the early warning of river floodings, based on a generalization of Takagi-Sugeno-Kang inference system. Expert. Syst. Appl. 2025, 240, 121539. [Google Scholar]
- Zhang, S.X.; Liu, Y.H.; Hu, X.R.; Zheng, L.M.; Zheng, S.Y. Fully Informed Fuzzy Logic System Assisted Adaptive Differential Evolution Algorithm for Noisy Optimization. IEEE Trans. Fuzzy Syst. 2025; in press. [Google Scholar]
- Mehmood, A.; Raja MA, Z. Fuzzy-weighted differential evolution computing paradigm for fractional order nonlinear wiener systems. Chaos Solitons Fractals 2022, 159, 112160. [Google Scholar] [CrossRef]
- Shukla, S.; Pandit, M. An optimum multi-objective dynamic scheduling strategy for a hybrid microgrid system using fuzzy rank-based modified differential evolution algorithm. In Artificial Intelligence and Sustainable Computing: Proceedings of ICSISCET 2020; Springer: Singapore, 2021; pp. 175–188. [Google Scholar]
- Ochoa, P.; Castillo, O.; Soria, J. Optimization of fuzzy controller design using a differential evolution algorithm with dynamic parameter adaptation based on type-1 and interval type-2 fuzzy systems. Soft Comput. 2020, 24, 193–214. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).