Abstract
Reinforcement learning plays a crucial role in the field of robotic arm grasping, providing a promising approach for the development of intelligent and adaptive grasping strategies. Due to distribution shift and local optimum in action, traditional online reinforcement learning is difficult to use existing grasping datasets, leading to low sample efficiency. This study proposes an improved QT-Opt algorithm for robotic arm grasping based on offline reinforcement learning. This improved algorithm proposes the Particle Swarm Optimization (PSO) to identify the action with the highest value within the robotic arm’s action space. Furthermore, a regularization term is proposed during the value iteration process to facilitate the learning of a conservative Q-function, enabling precise estimation of the robotic arm’s action values. Experimental results indicate that the improved QT-Opt algorithm achieves higher average grasping success rates when trained on multiple offline grasping datasets and demonstrates improved stability throughout the training process.
1. Introduction
Robotic arms are the most widely utilized automated mechanical devices in the field of robotics technology, with extensive applications in industries such as manufacturing and healthcare. For robotic systems, the arm itself performs manipulation tasks, while grippers or other end-effectors are dedicated to object interaction functions such as grasping, clamping–unclamping, and release. In industrial production, robotic arms typically operate within structured environments and are limited to traditional grasping tasks. To grasp arbitrary objects in unstructured environments, robotic arms need more sophisticated control algorithms [1].
Reinforcement learning, a prominent technology in the field of artificial intelligence, demonstrates enhanced generalization and autonomous decision-making capabilities. It is recognized as a robust self-learning methodology for robotic arms. In complex and dynamic environments, the reinforcement learning approach enables robotic arms to make intelligent decisions and optimizations [2].
The robotic arm grasping task is complex and requires continuous control. For such tasks, reinforcement learning algorithms with an Actor-Critic architecture are often chosen. However, with sparse reward settings, the training of algorithms with this architecture can be unstable. The QT-Opt algorithm [3] abandons the Actor-Critic architecture and adopts a more stable Q-learning algorithm architecture. It selects optimal actions through stochastic optimization algorithms, making it more suitable for robotic arm grasping tasks in a continuous action space.
However, the original QT-Opt algorithm is an online off-policy reinforcement learning algorithm that requires continuous exploration and data collection in the environment. In an offline setting, due to distribution shift, its grasping performance will be significantly degraded. Additionally, the employed action optimization algorithm is prone to getting stuck in local optima.
This study proposes an improved QT-Opt algorithm that transitions from online to offline learning for robotic arm grasping tasks. Specifically, the PSO algorithm substitutes the original optimization approach, facilitating a more effective search for high-value actions within the robotic arm’s action space. Furthermore, a regularization term is integrated into the value iteration process to mitigate Q-value overestimation caused by distribution shift, ensuring accurate action-value estimation. Experimental results demonstrate that the improved QT-Opt algorithm achieves superior grasping performance and stability when trained on multiple offline datasets.
The rest of this paper is organized as follows. Section 2 gives an overview of end-to-end grasping methods and approaches to address distribution shift. Section 3 defines the robotic arm grasping problem. Section 4 describes how the robotic arm grasping task is modeled as a Markov Decision Process. The improved QT-Opt algorithm is introduced in Section 5. Section 6 presents the experimental results that evaluate the performance of the improved algorithm. Finally, the conclusion is given in Section 7.
2. Related Work
The end-to-end grasping method based on visual-motor control strategies primarily applies deep reinforcement learning technology and has become a popular research direction. Kalashnikov et al. proposed the QT-Opt robotic arm grasping algorithm, which has achieved a success rate 96% on unknown objects [3]. In densely packed object scenarios, Zeng et al. proposed a synergistic robotic arm control algorithm that integrates pushing and grasping [4]. Quillen et al. conducted benchmark tests for robotic arm grasping in simulated environments, exploring the performance of different reinforcement learning algorithms on grasping tasks [5]. Joshi et al. proposed a robotic arm grasping method that employs an off-policy reinforcement learning framework to develop grasping policies [6]. Zhang et al. developed two distinct networks designed to learn grasping and stacking policies [7]. Shukla et al. employed a genetic algorithm to estimate the grasping position and designed a deep Q-network for grasping orientation [8]. Zhang et al. proposed a Gaussian Parameterized Deep Deterministic Policy Gradient algorithm based on a weighted autoencoder [9]. Chen et al. presented a grasping system that integrates deep reinforcement learning algorithms with object detection technique [10]. Chen et al. employed the YOLO algorithm to detect and classify all objects of interest within the camera’s field of view [11]. Tang proposed a safe grasping policy network with an attention module to intrinsically identify safe areas within the field of view, facilitating the learning of safe grasping actions [12]. Zuo et al. introduced a graph-structured deep reinforcement learning model to efficiently explore occluded objects and enhance the grasping success rate through collaborative grasping and pushing actions [13].
The online reinforcement learning requires a significant amount of time and resources, leading to low sample efficiency. The application of offline reinforcement learning in robotic arm grasping has attracted the attention of scholars. Offline reinforcement learning focuses on learning policies solely from previously collected static datasets, without interacting with the environment [14]. However, due to distribution shift, many reinforcement learning algorithms often fail to train effectively in offline settings.
Many researchers have imposed constraints on policies to mitigate the issue of distribution shift. Fujimoto et al. proposed the BCQ algorithm, which has demonstrated high performance on multiple control tasks in the MuJoCo environment [15]. Kumar et al. proposed the BEAR algorithm, which can learn good policies even from datasets collected with suboptimal behavior policies [16]. Fujimoto et al. combined the TD3 algorithm [17] with behavioral cloning, adding only a behavioral cloning regularization term to the value function and normalizing the states. Experimental results indicate that this method is highly effective across multiple tasks and significantly reduces training time [18].
Another approach is to directly constrain the value function, making its value estimates for out-of-distribution actions more conservative. Kumar et al. introduced Conservative Q-Learning (CQL), which achieves good performance on the D4RL benchmark [19]. Lyu et al. proposed Moderately Conservative Q-Learning, which actively trains on out-of-distribution actions by assigning them appropriate pseudo Q-values [20]. Qiu et al. introduced Adaptive Conservative Q-Learning, which utilizes the Q-value distribution of each fixed datasets to design a highly generalizable metric that balances the relationship between conservative constraints and training objectives [21].
3. Definition of the Robotic Arm Grasping Problem
This study considers a common top-down 2D planar grasping scenario in the industrial field. The robotic arm perceives the environment through an RGB-D camera mounted on its wrist. This camera configuration can capture clearer images of objects and is more robust to camera positioning. Furthermore, the grasping process is completed by directly controlling the pose of the end effector.
The implementation scenario consists of four key elements: a UR10 robotic arm equipped with an RGB-D camera and a pneumatic soft gripper, a robotic arm controller, a basket containing objects to be grasped, and a high-performance workstation. An example of robotic arm grasping is shown in Figure 1.

Figure 1.
An example of robotic arm grasping.
Due to the high costs associated with data collection and experimentation in the real-world environment, a simulated grasping scenario [22,23,24] similar to the real-world environment is constructed within the Isaac Gym simulation environment to accelerate the training process. Isaac Gym [25] is a high-performance robotic simulation platform that utilizes PhysX to accelerate physical simulations. In Isaac Gym, observations and rewards are stored as tensors directly on the GPU. This method eliminates the necessity for repeated data transfers between the CPU memory and the GPU throughout the training process, thereby expediting the overall training procedure. The workflow is shown in Figure 2.
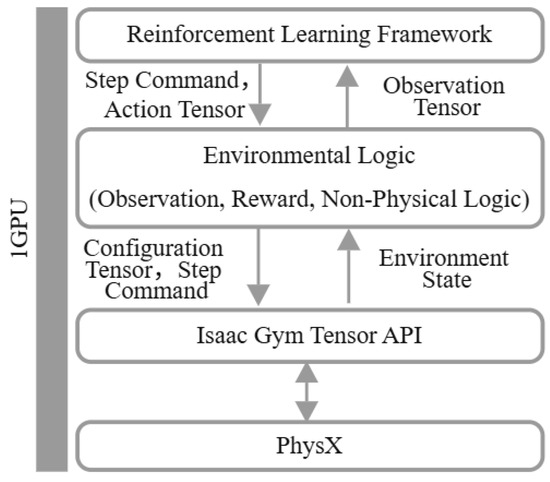
Figure 2.
Workflow of Isaac Gym.
In the Isaac Gym simulation environment, both single-object and multi-object grasping scenarios are established, as shown in Figure 3. In the multi-object grasping scenario, five objects are randomly selected and positioned at random locations within the grasping-ready area before the commencement of each grasping episode. Conversely, in the single-object grasping scenario, a single object is randomly chosen and placed at a random location.
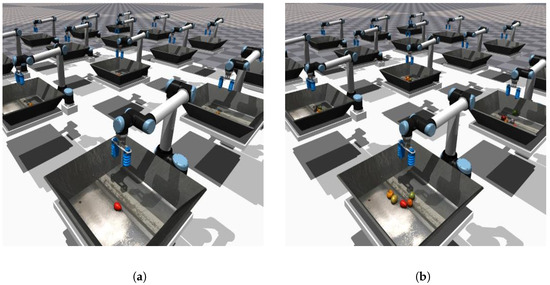
Figure 3.
Robotic arm grasping scenario: (a) single-object grasping scenario, (b) multi-object grasping scenario.
4. Markov Modeling
The QT-Opt algorithm is a robotic arm grasping algorithm based on reinforcement learning. First, the robotic arm grasping task needs to be modeled as a Markov Decision Process [26]. In a grasping episode with a maximum time step , at any time step t, after observing the current state , the robotic arm executes an action according to the grasping policy , receives a reward , and observes the next state , repeating this process. When the time step reaches the maximum or the end effector’s position is below a set height, the gripper will automatically close and then lift to the initial height to determine if the object has been successfully grasped, marking the end of the grasping episode. The state of the robotic arm at the current time step includes visual information captured by the hand-mounted camera (raw RGB images) and the current time step t. The action space of the robotic arm consists of the displacement and rotation angle of the end effector, , where represents the movement of the end effector in the Cartesian coordinate system and represents the rotation of the end effector around an axis. The reward function adopts a sparse reward form, where the robotic arm receives a reward of 1 if it successfully grasps any object at the final time step of the grasping episode, and 0 otherwise. The Markov-modeled robotic arm grasping process is shown in Equation (1), where T represents the actual length of the grasping episode.
The ultimate goal of the robotic arm grasping task is to learn an optimal grasping policy. When executing actions based on this policy, the robotic arm can maximize the expected discounted return of the grasping episode, as shown in Equation (2), where is the discount factor.
The QT-Opt algorithm is based on the Q-learning algorithm framework and obtains the optimal grasping policy by learning the optimal action-value function. The action-value function and the optimal action-value function are shown in Equations (3) and (4), where represents the discounted return at the current time step.
The optimal action-value function is obtained through iterating the optimal Bellman equation, as shown in Equation (5). The optimal action-value function provides the value of each action in the robotic arm’s action space for a given state. Continuously selecting the action with the highest value to execute constitutes the optimal grasping policy , as shown in Equation (6).
5. Improved QT-Opt Algorithm with Offline Reinforcement Learning
The QT-Opt algorithm is a Q-learning method designed for continuous action spaces, specifically utilized to train policies for vision-based robotic arm grasping. It approximates the optimal Q-function through the use of neural networks, which evaluate each action within the grasping task’s action space. Additionally, it employs the Cross-Entropy Method (CEM) [27] to identify the action with the highest Q-value in this space. When learning a grasping policy from static, offline grasping datasets, the robotic arm cannot collect new grasping data through active exploration in the grasping environment. If the previously collected grasping datasets do not encompass all states and actions, the algorithm may struggle to accurately estimate the value of state–action pairs that are absent or infrequently represented in the datasets during the learning process. This distribution shift can lead to suboptimal training performance or even the failure of the grasping algorithm.
The overall structure of the improved QT-Opt grasping algorithm consists of offline grasping datasets, Q-network, PSO algorithm, and conservative estimation of target Q-value, as shown in Figure 4. Grasping data are sampled from offline grasping datasets to update the network, thereby approximating the optimal Q-function. A target network with soft updates is used to stabilize the training process. Furthermore, a regularization term is integrated into the value iteration process to facilitate the learning of a conservative Q-function. In the offline setting, this conservative Q-function provides more accurate estimates of the robotic arm’s action values. During the network update process, the PSO algorithm is utilized to identify the action with the highest value in the robotic arm’s action space to achieve policy improvement. In the grasping test phase, at each time step, the trained network evaluates each action in the robotic arm’s action space, and the PSO algorithm is used to search for and execute the action with the highest value again. The details are given as follows.
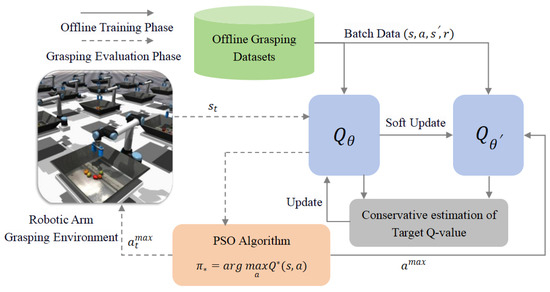
Figure 4.
Structure of the improved QT-Opt grasping algorithm.
5.1. Offline Grasping Datasets
Offline reinforcement learning cannot explore and perform trial-and-error in the environment. Its performance is heavily reliant on the offline dataset. Consequently, constructing offline grasping datasets with diverse characteristics is important for evaluating grasping algorithms based on offline reinforcement learning.
In this study, random policy, mixed policy, and expert policy are employed to collect multiple offline grasping datasets under different grasping scenarios. The specific definitions of each policy are as follows.
- (a)
- Random Policy: For the robotic arm grasping task, the purely random sampling strategy results in excessively low grasping success rates and the collected data has limited value. Therefore, a heuristic random strategy is adopted for data collection. This strategy directs the gripper to move approximately towards the vicinity of the object while maintaining an open position. Upon descending below a predetermined height threshold, the gripper automatically closes and returns to the starting position.
- (b)
- Expert Policy: During the online reinforcement learning training process, the policy is continuously updated, and the data collected throughout this process are consistently added to the experience replay buffer. Consequently, the replay buffer can be regarded as a dataset compiled from a mixture of multiple behavior policies. An online reinforcement learning algorithm can be utilized to train the robotic arm grasping policy, resulting in a grasping dataset generated by a hybrid policy. Given that the robotic arm grasping task relies on high-dimensional visual information as input, the DrQ-v2 algorithm [28], which performs effectively in visual tasks, is employed for the online training of the grasping policy. Upon completion of the training, the experience replay buffer is preserved as an offline grasping dataset generated by the hybrid policy.
- (c)
- Mixed Policy: For online reinforcement learning algorithms, pretraining on expert datasets can significantly enhance the efficiency of the learning process for the agent. Therefore, we adopt a high-success-rate grasping policy trained using the DrQ-v2 algorithm as the expert policy for collecting grasping data. The rewards in the collected grasping trajectories consist only of a sparse reward given at the final step.
The DrQ-v2 algorithm underwent a training regimen consisting of 150,000 iterations, with each iteration involving a single stochastic gradient descent step. Training began after collecting 200 steps of environment interaction data. Every 200 training steps, the average episode reward and average grasping success rate over the last 100 episodes were documented. The reward curves and grasping success rate curves for various grasping scenarios are illustrated in Figure 5.
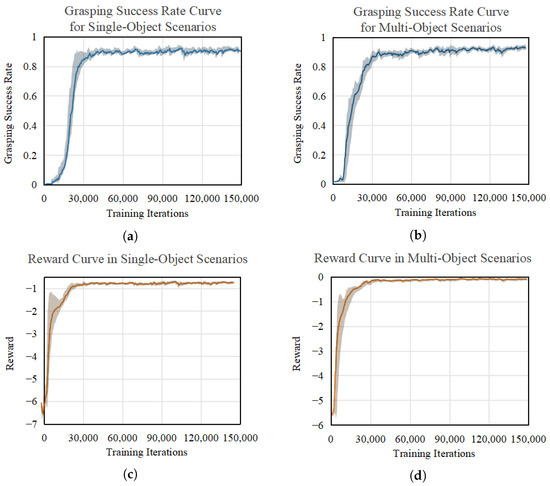
Figure 5.
Grasping success rate curves and reward curves of the DrQ-v2 algorithm trained in different grasping scenarios: (a) grasping success rate curve for single-object scenarios, (b) grasping success rate curve for multi-object scenarios, (c) reward curve in single-object scenarios, (d) reward curve in multi-object scenarios.
As shown in Figure 5, in the single-object grasping scenario, the algorithm demonstrated convergence, with the curves stabilizing after approximately 30,000 training steps. Conversely, the training process for the multi-object grasping scenario exhibited more pronounced fluctuations, with the curves reaching stability after about 40,000 steps.
After the training is completed, the first 20,000 trajectories from the experience replay buffer are saved as the grasping datasets collected using a mixed strategy. Concurrently, 20,000 grasping trajectories are collected in both single-object and multi-object grasping scenarios utilizing both random and expert policies. The comparison of the grasping datasets collected by each grasping strategy is shown in Table 1.

Table 1.
Comparison of offline grasping datasets collected using different strategies.
5.2. Q-Network
For robotic arm grasping tasks that take visual images as input, convolutional neural networks are typically employed to learn a parameterized Q-function. To this end, a Q-network (robotic arm action-value network) is designed, the structure of which is shown in Figure 6. This network takes as input the image captured by the camera at the wrist of the robotic arm at time step t, the current time step t, and the robotic arm action , and outputs the value of the action at the current time step, i.e., it evaluates the value (Q-value) of the action based on the current state of the robotic arm. The network utilizes three convolutional blocks to extract features from the image state, each block comprising a convolutional layer with a stride of 2, followed by batch normalization and an activation function. The current time step is replicated to match the dimensions of the image feature vector, after which a channel concatenation operation is performed to create a feature vector that incorporates the current time step information. The action is processed through a linear block to generate a latent vector, which includes a fully connected layer, layer normalization, and an activation function. This latent vector is subsequently combined with the previously obtained feature vector and flattened. Finally, it passes through two linear blocks and is mapped to a scalar using a fully connected layer. The scalar is then transformed to a specific range using a Sigmoid function to yield the output Q-value.
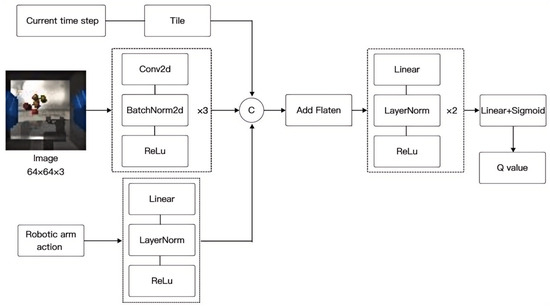
Figure 6.
Structure of Q-network.
5.3. PSO Algorithm
For robotic arm grasping tasks, the optimal Q-function is often quite intricate. The CEM optimization algorithm used in the QT-Opt algorithm may become trapped in local optima when dealing with complex objective functions, consequently hindering the identification of the action with the highest value. This study adopts the PSO algorithm to search for the action with the highest value in the robotic arm’s action space. Particle Swarm Optimization [29] is an optimization algorithm based on swarm intelligence. Its core idea is to gradually optimize the value of the objective function by simulating swarm behavior and obtain the optimal solution. Compared to the CEM, its mechanism of sharing information among the swarm helps to escape local optima. The general process is as follows:
- (a)
- Before initiating the iteration process, it is essential to determine the number of particles and to initialize their respective positions and velocities. Typically, the positions of the particles are randomly distributed within the search space, while their initial velocities are set to zero. Each particle serves as a potential solution. The position and velocity of each particle are denoted as and , respectively.
- (b)
- The objective function can be defined as a mathematical expression that quantifies the performance of a solution. In each iteration, the fitness value of all particles is evaluated according to this objective function. Subsequently, the personal best position of each particle is updated based on its current fitness value. Finally, the global best position is determined by selecting the position with the highest fitness value from all particles’ personal best positions. The personal best position is denoted as , and the global best position of all particles is denoted as .
- (c)
- The last step is to update the velocity of each particle according to Equation (7), where represents the inertia weight, is the individual learning factor, is the social learning factor, and and are random numbers within the range [0, 1]. After determining the velocity of each particle, update its position according to Equation (8).
To enable particles to achieve a higher velocity in the early stages to explore more areas and a lower velocity in the later stages, an inertia weight decay strategy is introduced during the iteration process of the PSO algorithm. The inertia weight is shown in Equation (9), where represents the initial value of the inertia weight, k is the total number of iterations, and is a coefficient that adjusts the decay rate.
5.4. Conservative Estimation of Target Q-Value
In scenarios where actions fall outside the distribution of static datasets, the Q-function’s ability to accurately estimate their values diminishes. As iterations continue, it tends to overestimate the Q-values associated with out-of-distribution actions. Within the context of offline reinforcement learning, the robotic arm is unable to engage with the environment to gather supplementary data or receive real rewards based on environmental feedback. Consequently, the overestimated Q-values remain uncorrected, which can result in instability or even failure during the training of the grasping algorithm.
The Conservative Q-learning algorithm [19] effectively addresses the overestimation issue by introducing an additional penalty term derived from the Bellman error. The value iteration formula with the penalty term is shown in Equation (10). This penalty term is designed to minimize the expected Q-value associated with a specific state–action pair distribution. The standard Q-function training only considers states that are present in the dataset, thereby neglecting unseen states. This limitation restricts the matching process to the marginal distribution of states represented in the dataset, i.e., , where is the behavior policy that generated the offline datasets D. When , by updating Equation (10), a true lower bound of the Q-function can be obtained, where is the Bellman optimality operator and c is the weight coefficient.
An additional penalty term may lead to a Q-function that is overly conservative. To address this issue, an incentive term is introduced to maximize the Q-values of actions within the distribution of the datasets, as shown in Equation (11).
To accelerate the policy learning process, we can use to approximately maximize the policy for the current Q-function iteration. To this end, an optimization problem as shown in Equation (12) can be defined, where represents the divergence between a given and a prior distribution .
Solving for the maximum in Equation (12) can be abstracted as a constrained optimization problem, as shown in Equation (13). The solution to this problem can be obtained using the Lagrange multiplier method, and the optimal solution is given by Equation (14), where Z represents the normalization factor.
6. Experiments
6.1. Experimental Metrics
For robotic arm grasping tasks, the grasping success rate is undoubtedly the most important metric. The grasping success rate of a grasping strategy can be defined as the proportion of successful grasping episodes out of the total number of grasping episodes when using this strategy for multiple trials. The grasping success rate (GSR) is calculated as shown in Equation (16), where represents the number of successful episodes and represents the total number of episodes.
To more accurately evaluate the performance of grasping algorithms, the Area Under the Grasping Success Rate Curve (AUGSRC) is introduced. During the algorithm training process, the success rate curves are plotted with training iterations on the x-axis and grasping success rate on the y-axis. Assuming the curve is plotted using N points, the AUGSRC is calculated as shown in Equation (17).
To measure the stability of the training process of a grasping algorithm, the Coefficient of Variation (CV) is introduced, as shown in Equation (18). Here, y represents the value of each data point in the grasping success rate curve, represents the mean of this set of data, and N is the number of data points. A lower Coefficient of Variation indicates that the data points are more concentrated relative to the mean, suggesting a more stable training process for the grasping algorithm.
6.2. Experimental Results
The performance of the grasping algorithm is evaluated through training on multiple offline grasping datasets constructed in Section 5.1. The grasping tests are conducted in the simulated grasping scenarios described in Section 3. If the algorithm is trained on a multi-object grasping dataset, the grasping tests during the training process are carried out in a multi-object grasping scenario. Conversely, if trained on a single-object grasping dataset, the grasping tests are performed in a single-object grasping scenario.
6.2.1. Ablation Experiment
To evaluate the impact of the two proposed improvements on the grasping performance of the QT-Opt algorithm, three sets of experiments were designed: QT-Opt(CEM), QT-Opt(PSO), and QT-Opt(PSO)+Regular. The first set employs the CEM to search for the action with the highest value in the action space, while the second set employs the PSO algorithm to search for the action with the highest value in the action space. When using the PSO algorithm, the hyperparameter ranges are first defined, and grid search is then applied to optimize the hyperparameter. The third set not only searches for actions using the PSO algorithm but also introduces a regularization term during the value iteration process to conservatively estimate the value of robotic arm actions.
All grasping algorithms were trained for 20,000 iterations, with one stochastic gradient descent performed per iteration, and tests were conducted every 200 iterations, consisting of 100 grasping episodes in the grasping scenario. To mitigate contingency effects, the experiments were conducted using various random seeds. The grasping success rate curves for different grasping algorithms on various grasping datasets are compared in Figure 7. For better visualization, all curves have been smoothed, with shaded areas representing the standard deviation of experimental results. The AUGSRC and CV metrics are employed for evaluation, as shown in Table 2.
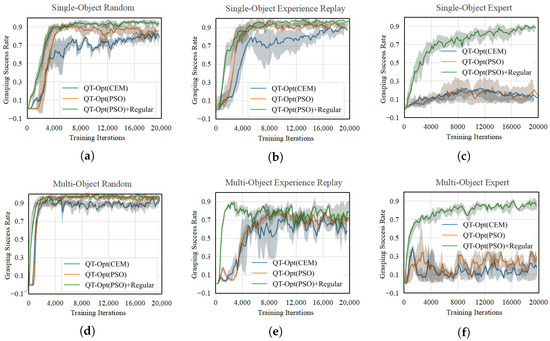
Figure 7.
Comparison of grasping success rate curves in the ablation experiment: (a) random datasets of single-object, (b) experience replay datasets of single-object, (c) expert datasets of single-object, (d) random datasets of multi-object, (e) experience replay datasets of multi-object, (f) expert datasets of multi-object.

Table 2.
Comparison of performance metrics.
As shown in Figure 7 and Table 2, the AUGSRC metric of the QT-Opt(PSO) grasping algorithm consistently surpasses that of the QT-Opt(CEM) grasping algorithm across most grasping datasets. Such results reflect the superior optimization capabilities of the PSO algorithm in an offline setting. Furthermore, in certain grasping datasets, the training outcomes of the QT-Opt(CEM) algorithm display greater fluctuations, indicating heightened sensitivity to initial parameters. Across all grasping datasets, the QT-Opt(PSO) grasping algorithm, augmented by the inclusion of a regularization term, demonstrates faster convergence, and displays the most effective grasping performance. Additionally, its lower CV metric signifies a more stable training process, thereby validating the effectiveness of incorporating a regularization term during the value iteration process. In addition, QT-Opt(CEM) achieves an inference latency of 3.17 ms per action, while QT-Opt(PSO) requires 4.66 ms per action. Both algorithms meet the real-time performance requirements for robotic grasping tasks.
6.2.2. Comparative Experiment
To validate the applicability of the improved QT-Opt algorithm for robotic arm grasping tasks, we selected the DrQ-v2 algorithm and the Decision Transformer (DT) algorithm [30], which perform well in vision-based tasks, for comparative experiments.
All algorithms were trained offline for 20,000 iterations under multiple different random seeds. Every 200 training iterations, 100 grasping trials are conducted for testing in the grasping scenario. Due to the faster convergence of the improved QT-Opt algorithm and the DT algorithm, only one stochastic gradient descent step was executed per training iteration for them, whereas five stochastic gradient descent steps were required for the DrQ-v2 algorithm. Since training the DT algorithm on datasets collected through an expert policy can be viewed as a form of imitation learning, the practical significance is limited. Therefore, training is concentrated solely on datasets obtained using random policies and hybrid policies for comparison with the DT algorithm. The grasping success rate curves of different algorithms on diverse datasets are shown in Figure 8 and Figure 9.
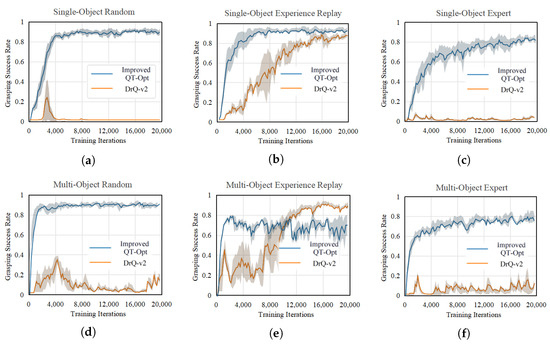
Figure 8.
Comparison of grasping success rate curves between improved QT-Opt and DrQ-v2: (a) random datasets of single-object, (b) experience replay datasets of single-object, (c) expert datasets of single-object, (d) random datasets of multi-object, (e) experience replay datasets of multi-object, (f) expert datasets of multi-object.
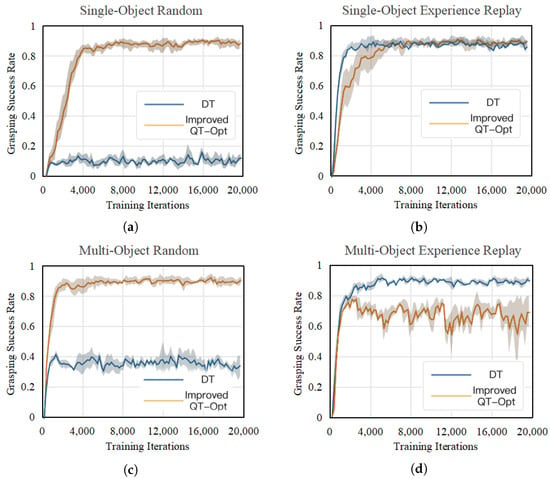
Figure 9.
Comparison of grasping success rate curves between improved QT-Opt and DT: (a) random datasets of single-object, (b) experience replay datasets of single-object, (c) random datasets of multi-object, (d) experience replay datasets of multi-object.
As shown in Figure 8, the DrQ-v2 algorithm can only be effectively trained on experience replay datasets. This is due to the fact that experience replay datasets are generated through interactions with the environment during the online training process, which minimizes the potential for distribution shifts during training. Conversely, other datasets experience an accumulation of errors resulting from distribution shifts, which ultimately hinders the training efficacy of the DrQ-v2 algorithm. The improved QT-Opt algorithm demonstrates enhanced training performance across most datasets and exhibits a more stable training process. Previous ablation experiments have indicated that even the QT-Opt(PSO) algorithm, which operates without regularization, can achieve relatively high grasping performance when trained on random datasets. In contrast, the DrQ-v2 algorithm fails completely to train on such datasets. This discrepancy arises because the Actor-Critic architecture of the DrQ-v2 algorithm relies heavily on accurate policy gradient information. In control tasks like robotic arm grasping, where rewards are sparse, no rewards are generated during intermediate steps. This lack of feedback hinders the Critic network’s ability to provide accurate gradient information, leading to slow convergence or even non-convergence of the algorithm. This demonstrates that the improved QT-Opt algorithm, which employs a Q-learning architecture, performs more stably in robotic arm grasping tasks, converges more rapidly, and is better suited for scenarios characterized by sparse rewards.
As shown in Figure 9, the trajectory quality of the grasping dataset collected using a random policy is relatively low. Consequently, the DT algorithm struggles to effectively model the relationship between rewards and the interplay of states and actions. As a result, its grasping performance, when trained on such datasets, falls significantly short compared to that of the improved QT-Opt algorithm. On the single-object experience replay dataset, following training convergence, the improved QT-Opt algorithm exhibits slightly superior grasping performance relative to the DT algorithm. In contrast, on the multi-object experience replay dataset, the DT algorithm achieves better training performance. Overall, the improved QT-Opt algorithm demonstrates superior grasping capabilities compared to the DT algorithm.
6.2.3. Q-Function Visualization Analysis
The trajectories of grasping are determined by the existing policy, which is subsequently evaluated using the Q-function. To investigate the impact of different trajectories on the grasping success rate, a comprehensive analysis centered on Q-values is performed. Notably, the grasping performance trained on the expert dataset is found to be inferior to that trained on the random dataset. Therefore, the trained Q-functions for the multi-object random grasping dataset and the multi-object expert grasping dataset are visualized. The last two dimensions in the action space are fixed, and the Q-values of the robot arm’s end effector in the horizontal direction during the same grasping trial are evaluated.
As shown in Figure 10, the Q-function trained on the multi-object random grasping dataset is visualized. The brightness of the color in an area corresponds to the Q-value, indicating the action value associated with that region. During the first step of the grasping round, the majority of the action space exhibits high Q-values, indicating that the directionality of the actions produced by the policy is not distinctly pronounced. As the number of steps increases, the region with elevated Q-values gradually diminishes, and the action directionality becomes more pronounced, indicating that the robotic arm gains increased certainty regarding which object to grasp. This stable approach towards the target movement trajectory correlates with a higher grasping success rate.
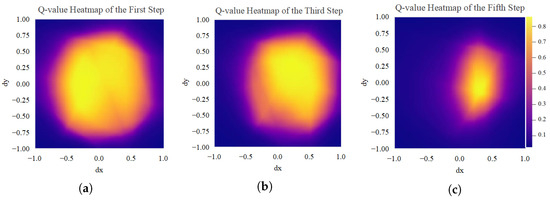
Figure 10.
Q-value heatmaps trained on the multi-object random grasping dataset: (a) the first step, (b) the third step, (c) the fifth step.
The Q-function, derived from training on the multi-object expert grasping dataset, is shown in Figure 11. In the initial step of the grasping process, the Q-function exhibits a more irregular shape. As the number of steps increases, the high-Q-value region diminishes sharply, leading the robotic arm to oscillate with greater amplitude during the first few steps. This unstable movement trajectory prolongs the adjustment time of the robotic arm and adversely impacts the stability of the grasping process.
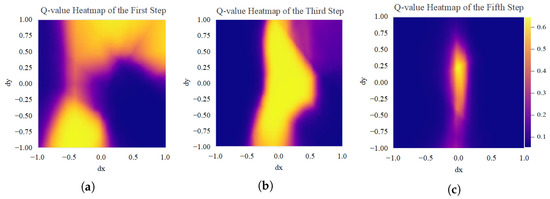
Figure 11.
Q-value heatmaps trained on the multi-object expert grasping dataset: (a) the first step, (b) the third step, (c) the fifth step.
7. Conclusions
This study addresses the challenges of low data utilization and high interaction costs associated with traditional online reinforcement learning methods in robotic arm grasping scenarios. We propose a robotic arm grasping approach based on an improved QT-Opt algorithm. First, the PSO algorithm is employed to identify the action with the highest value within the action space. Additionally, a regularization term is incorporated during the value iteration process to address the issue of Q-value overestimation resulting from distribution shifts. The ablation and comparative experimental results indicate that the improved QT-Opt algorithm not only achieves superior grasping performance when trained on multiple offline grasping datasets but also exhibits a more stable training process. However, the Q-function trained on datasets collected using expert policies displayed a relatively irregular shape, which adversely affected the stability of the grasping process. Consequently, for such datasets, it is imperative to design alternative grasping algorithms.
Author Contributions
Conceptualization, H.Z.; Methodology, H.Z.; Software, H.Z.; Writing—original draft, H.Z.; Writing—review and editing, S.Z., Y.H., H.H., and Z.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tian, H.; Song, K.; Li, S.; Ma, S.; Xu, J.; Yan, Y. Data-driven robotic visual grasping detection for unknown objects: A problem-oriented review. Expert Syst. Appl. 2023, 211, 118624. [Google Scholar] [CrossRef]
- Newbury, R.; Gu, M.; Chumbley, L.; Mousavian, A.; Eppe, C.; Leitner, J. Deep learning approaches to grasp synthesis: A review. IEEE Trans. Robot. 2023, 39, 1–22. [Google Scholar] [CrossRef]
- Kalashnikov, D.; Ipran, A.; Pastor, P.; Ibarz, J.; Herzog, A.; Jang, E.; Quillen, D.; Holly, E.; Kalakrishnam, M.; Vanhoucke, V.; et al. QT-Opt: Scalable deep reinforcement learning for vision-based robotic manipulation. In Proceedings of the 2nd Conference on Robot Learning, Zürich, Switzerland, 29–31 October 2018; pp. 651–673. [Google Scholar]
- Zeng, A.; Song, S.; Welker, S.; Lee, J.; Rodriguez, A.; Funkhouser, T. Learning synergies between pushing and grasping with self-supervised deep reinforcement learning. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4238–4245. [Google Scholar]
- Qi, L.; Jang, E.; Nachum, O.; Finn, C.; Ibarz, J. Deep reinforcement learning for vision-based robotic grasping: A simulated comparative evaluation of off-policy methods. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6284–6291. [Google Scholar]
- Shi, S.; Kumra, S.; Sahin, F. Robotic grasping using deep reinforcement learning. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1461–1466. [Google Scholar]
- Zhang, J.; Zhang, W.; Song, R.; Ma, L.; Li, Y. Grasp for stacking via deep reinforcement learning. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2543–2549. [Google Scholar]
- Shukla, P.; Kumar, H.; Nandi, G.C. Robotic grasp manipulation using evolutionary computing and deep reinforcement learning. Int. Serv. Robot. 2021, 14, 61–77. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Wang, J.; Cui, B. Robot grasping method optimization using improved deep deterministic policy gradient algorithm of deep reinforcement learning. Rev. Sci. Instrum. 2021, 92, 2. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Lu, W. Deep reinforcement learning based moving object grasping. Inf. Sci. 2021, 565, 62–76. [Google Scholar] [CrossRef]
- Chen, Y.L.; Cai, Y.R.; Cheng, M.Y. Vision-based robotic object grasping—A deep reinforcement learning approach. Machines 2023, 11, 275. [Google Scholar] [CrossRef]
- Tang, Z.; Shi, Y.; Xu, X. CSGP: Closed-loop safe grasp planning via attention-based deep reinforcement learning from demonstrations. IEEE Rob. Autom. 2023, 8, 3158–3165. [Google Scholar] [CrossRef]
- Zuo, G.; Tong, J.; Wang, Z.; Gong, D. A graph-based deep reinforcement learning approach to grasping fully occluded objects. Cogn. Comput. 2023, 15, 36–49. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Yao, Y.; Yang, X.; Zhong, M. Research Status of Robotic Grasping Detection Technology. Control Decis. 2020, 35, 2817–2828. [Google Scholar]
- Fujimoto, S.; Meger, D.; Precup, D. Off-policy deep reinforcement learning without Exploration. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 2052–2062. [Google Scholar]
- Kumar, A.; Fu, J.; Tucker, G.; Levine, S. Stabilizing off-policy q-learning via bootstrapping error reduction. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic Methods. In Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Fujimoto, S.; Gu, S.S. A minimalist approach to offline reinforcement learning. Adv. Neural Inf. Process. Syst. 2021, 34, 20132–20145. [Google Scholar]
- Kumar, A.; Zhou, A.; Tucker, G.; Levine, S. Conservative q-learning for offline reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 1179–1191. [Google Scholar]
- Lyu, J.; Ma, X.; Li, X.; Lu, Z. Mildly conservative q-learning for offline reinforcement learning. Adv. Neural Inf. Process. Syst. 2022, 35, 1711–1724. [Google Scholar]
- Qiu, L.; Li, X.; Liang, L.; Sun, M.; Yan, J. Adaptive Conservative Q-Learning for Offline Reinforcement Learning. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Xiamen, China, 13–15 October 2023; pp. 200–212. [Google Scholar]
- Bousmalis, K.; Vezzani, G.; Rao, D.; Devin, C.; Lee, A.X.; Bauza, M.; Davchev, T.; Zhou, Y.; Gupta, A.; Raju, A.; et al. RoboCat: A Self-Improving Generalist Agent for Robotic Manipulation. arXiv 2023, arXiv:2306.11706. [Google Scholar]
- Black, K.; Nakamoto, M.; Atreya, P.; Walke, H.; Finn, C.; Kumar, A.; Levine, S. Zero-shot robotic manipulation with pretrained image-editing diffusion models. arXiv 2023, arXiv:2310.10639. [Google Scholar]
- Chi, C.; Feng, S.; Du, Y.; Xu, Z.; Cousineau, E.; Burchfiel, B.; Song, S. Diffusion Policy: Visuomotor Policy Learning via Action Diffusion. In Proceedings of the Robotics: Science and Systems (RSS), Daegu, Republic of Korea, 10–14 July 2023; pp. 1–10. [Google Scholar]
- Du, G.; Wang, K.; Lian, S.; Zhao, K. Vision-based robotic grasping from object localization, object pose estimation to grasp estimation for parallel grippers: A review. Artif. Intell. Rev. 2021, 54, 1677–1734. [Google Scholar] [CrossRef]
- Bellman, R. A Markov decision process. Indiana Univ. Math. J. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Rubinstein, R.Y.; Kroese, D.P. A Tutorial Introduction to the Cross-Entropy Method. In The Cross-Entropy Method: A Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation, and Machine Learning; Rubinstein, R.Y., Kroese, D.P., Eds.; Springer: New York, NY, USA, 2004; pp. 147–148. [Google Scholar]
- Yarats, D.; Fergus, R.; Lazaric, A.; Pinto, L. Mastering visual continuous control: Improved data augmented reinforcement learning. arXiv 2021, arXiv:2107.09645. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 1–27 August 1995; pp. 1942–1948. [Google Scholar]
- Chen, L.; Lu, K.; Rajeswaran, A.; Lee, K.; Grover, A.; Laskin, M.; Abbeel, P.; Srinivas, A.; Mordatch, I. Decision transformer: Reinforcement learning via sequence modeling. Adv. Neural Inf. Process. Syst. 2021, 34, 15084–15097. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).