Sensitivity Analysis Based on E-TOPSIS Combined with MORIME-Based Multi-Objective Optimization for Sprayer Frame Design Optimization
Abstract
1. Introduction
2. Finite Element Simulation and Experimental Testing of the Frame
2.1. Construction of the Frame’s 3D Model
2.2. Finite Element Modeling of the Sprayer Frame
2.3. Mechanical Properties Evaluation of the Frame
2.3.1. Mechanical Properties Under Fully Loaded Bending Condition
2.3.2. Mechanical Properties Under Extreme Torsional Loading Conditions
2.4. Modal Analysis and Experimental Validation
2.4.1. Modal Analysis of the Frame Under Free Boundary Conditions
2.4.2. Modal Test and Validation of the Frame
3. Lightweight Frame Optimization Process
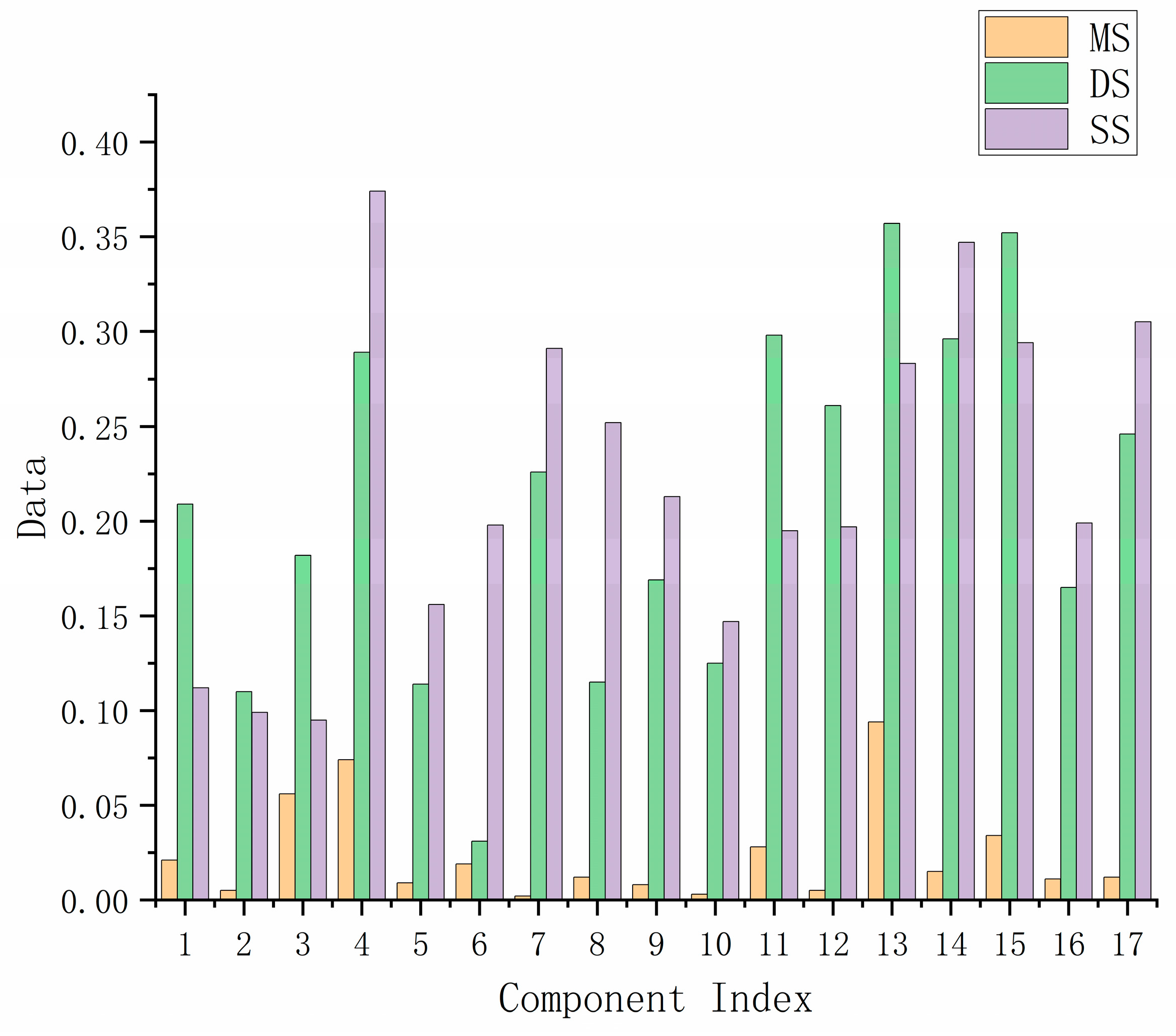
3.1. Component Sensitivity Analysis
3.2. Screening of Design Variables Using Entropy Weighting and TOPSIS Methods
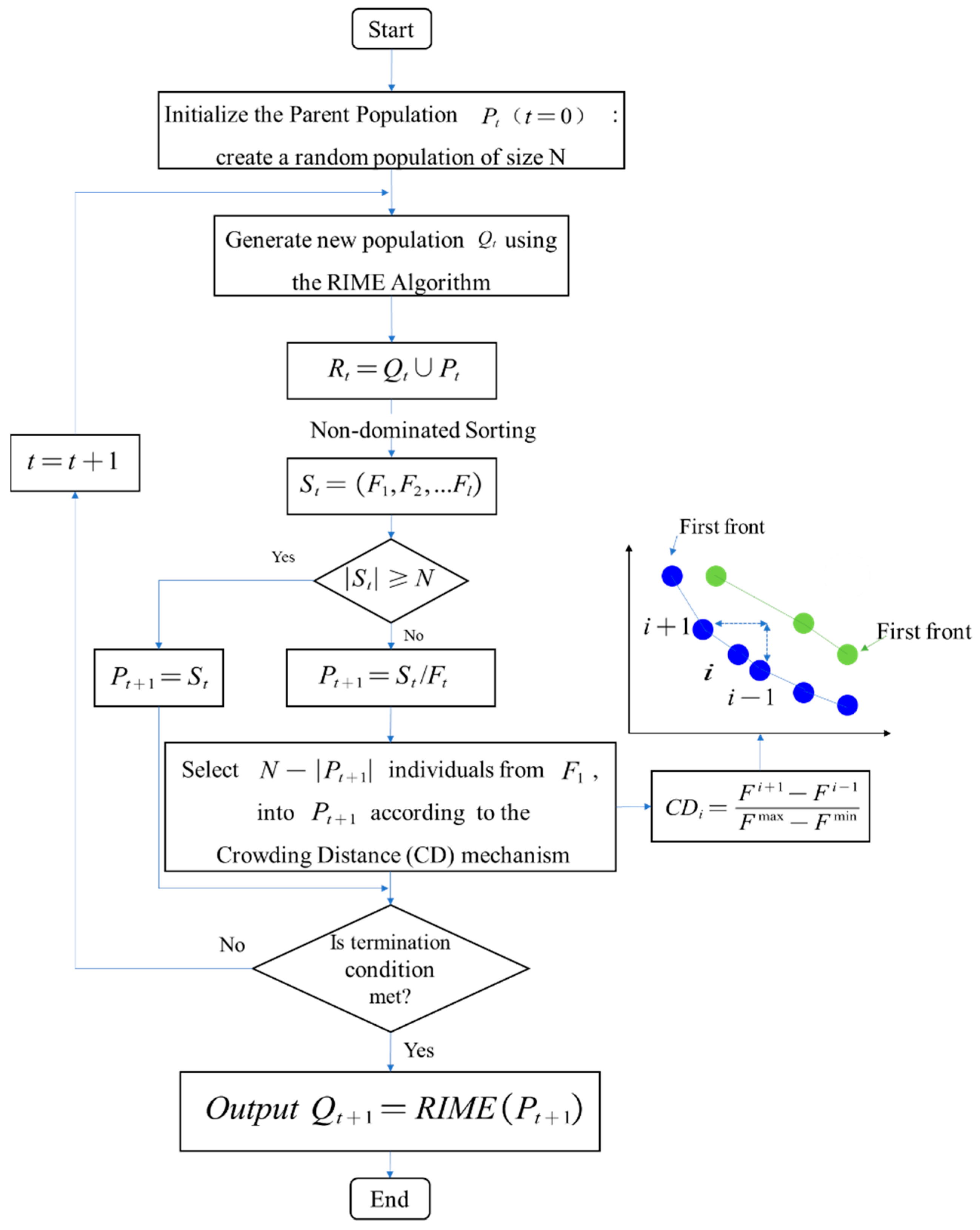
3.3. Size Optimization Design Using the MORIME Algorithm
- Initialization: The population is initialized by randomly generating an initial parent population of size , denoted as . An offspring population of the same size, , is then created using the standard RIME algorithm, denoted as .
- Non-Dominated Sorting: The parent and offspring populations ( and ) are merged to form a new population, , of size . The merged populations are sorted according to their dominance levels , and are sequentially merged into a new population . If the size of exceeds N, then, . Otherwise, .
- Crowding Distance Sorting: The population is sorted based on crowding distance, and the selection process continues to supplement until individuals are reached.
- Iteration: Steps 2 and 3 are repeated until the maximum number of iterations is reached.
4. Results
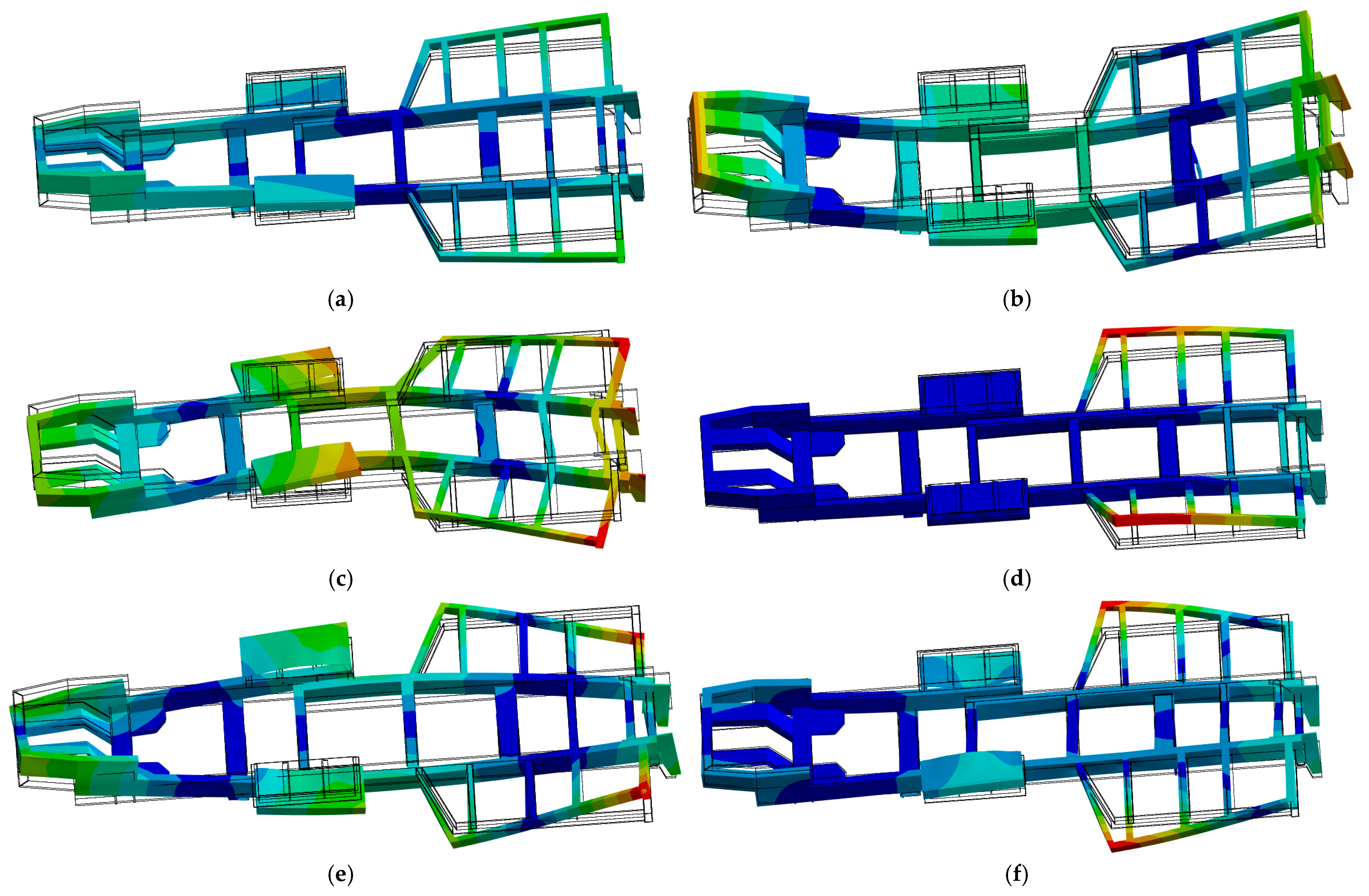
4.1. Static Analysis
4.2. Modal Analysis and Experimental Validation
4.3. Multi-Objective Optimization Outcomes
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| E-TOPSIS | Entropy-based TOPSIS |
| FT | First-order torsion |
| FB | First-order bending |
| TBC | Bending and torsion combinations |
| MS | Mass sensitivity |
| DS | Deformation sensitivity |
| SS | Stress sensitivity |
| MSTC | Maximum Stress in torsion condition |
| MSBC | Maximum Stress in bending condition |
| DTC | Deformation in torsion condition |
| DBC | Deformation in bending condition |
| FOM | First-order modal |
References
- Tang, P.; Yang, R.; Ni, X.; Zhao, H.; Xu, F. Research on a Lightweight Unmanned Sightseeing Vehicle Frame Based on Multi-Condition and Multi-Objective Optimization. Adv. Mech. Eng. 2022, 14, 16878132221131748. [Google Scholar] [CrossRef]
- Hosseini, S.E.; Karimi, O.; AsemanBakhsh, M.A. Experimental Investigation and Multi-Objective Optimization of Savonius Wind Turbine Based on Modified Non-Dominated Sorting Genetic Algorithm-II. Wind Eng. 2024, 48, 446–467. [Google Scholar] [CrossRef]
- Liu, S.; Du, Y.; Lin, M. Study on Lightweight Structural Optimization Design System for Gantry Machine Tool. Concurr. Eng. 2019, 27, 170–185. [Google Scholar] [CrossRef]
- Cui, W.; Feng, J.; Zhu, G.; Liu, B.; Ge, Z.; Luo, X. Multi-objective Optimization Design of a Centrifugal Fan Based on the Blade Loading Distribution. J. Eng. Thermophys. 2024, 45, 1949–1959. [Google Scholar]
- Zhou, X.; Tan, W.; Sun, Y.; Huang, T.; Yang, C. Multi-Objective Optimization and Decision Making for Integrated Energy System Using STA and Fuzzy TOPSIS. Expert Syst. Appl. 2024, 240, 122539. [Google Scholar] [CrossRef]
- Li, H.; Liu, Z.; Zhu, P. An Improved Multi-Objective Optimization Algorithm with Mixed Variables for Automobile Engine Hood Lightweight Design. J. Mech. Sci. Technol. 2021, 35, 2073–2082. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, X. Application of the Preference Selection Index Method in Multi-Objective Lightweight Design of Heavy Commercial Vehicle Frames. Eng. Optim. 2023, 55, 1020–1039. [Google Scholar] [CrossRef]
- Ebrahimi-Nejad, S.; Kheybari, M.; Borujerd, S.V.N. Multi-Objective Optimization of a Sports Car Suspension System Using Simplified Quarter-Car Models. Mech. Ind. 2020, 21, 412. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D. Research on Crashworthiness and Lightweight of B-Pillar Based on MPSO with TOPSIS Method. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 498. [Google Scholar] [CrossRef]
- Ni, X.; Li, Y.; Sun, R.; Xu, Y. Multi-Parameter Optimization Analysis of Permanent Magnet Couplings Using Response Surface Methodology and Genetic Algorithm. J. Mech. Sci. Technol. 2024, 38, 6279–6286. [Google Scholar] [CrossRef]
- Adjei, R.A.; Fan, C. Multi-Objective Design Optimization of a Transonic Axial Fan Stage Using Sparse Active Subspaces. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2325488. [Google Scholar] [CrossRef]
- Li, S.; Bei, J.; Jiang, Z.; Zhang, D. Lightweight design of integrated engine hood based on FAHP-TOPSIS method. J. Vib. Shock 2024, 43, 125–133. [Google Scholar]
- Chen, P. Effects of the Entropy Weight on TOPSIS. Expert Syst. Appl. 2021, 168, 114186. [Google Scholar] [CrossRef]
- Rezaei, J. Best-Worst Multi-Criteria Decision-Making Method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Liu, W. Application on Floor Water Inrush Evaluation Based on AHP Variation Coefficient Method with GIS. Geotech. Geol. Eng. 2018, 36, 2799–2808. [Google Scholar] [CrossRef]
- Zhang, J.; He, J. Matching Evaluation of Integrated Energy Services and Users Based on FA-E-TOPSIS-GRA. In Proceedings of the 2023 International Conference on Power System Technology (PowerCon), Jinan, China, 21–22 September 2023; pp. 1–5. [Google Scholar]
- Fu, G. Re-Ranking and TOPSIS-Based Ensemble Feature Selection with Multi-Stage Aggregation for Text Categorization. Pattern Recognit. Lett. 2023, 168, 47–56. [Google Scholar] [CrossRef]
- Nguyen, V.-C.; Vu, D.-T.; Tran, Q.-H. Optimizing EDM for Titanium Alloys: An In-Depth Comparison of Five MCDM Techniques. EUREKA Phys. Eng. 2024, 5, 89–98. [Google Scholar] [CrossRef]
- Jiang, R.; Zhang, T.; Sun, H.; Liu, D.; Chen, H.; Wang, D. Study on Lightweighting of CFRP Bumper Beam Using Entropy-Based TOPSIS Approach. Automot. Eng. 2021, 43, 421–428. [Google Scholar]
- Chen, T.; Liu, Y.; Jia, R.; Tang, C. Wear State Evaluation Method Based on Improved Entropy-weighted TOPSIS for Power-shift Steering Transmission. J. Hunan Univ. Sci. 2024, 51, 10–18. [Google Scholar]
- Yang, W.; Yong, T.; Wang, X.; Liu, W.; Yang, F. Creation and Application of Corn—Soybean Belt Compound Planting Technology System. China High-Tech. 2020, 15, 15. [Google Scholar]
- Wu, G.; Wu, X. To Adopt the Loads of Passenger Car Body on Strength Analysis by Finite Element Method. J. Mech. Eng. 1997, 5, 84–88. [Google Scholar]
- Pandya, S.B.; Kalita, K.; Jangir, P.; Cep, R.; Migdady, H.; Chohan, J.S.; Abualigah, L.; Mallik, S. Multi-Objective RIME Algorithm-Based Techno Economic Analysis for Security Constraints Load Dispatch and Power Flow Including Uncertainties Model of Hybrid Power Systems. Energy Reports. Energy Rep. 2024, 11, 4423–4451. [Google Scholar] [CrossRef]
- Su, H. RIME: A Physics-Based Optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Cai, L.; Ma, S.; Zhao, Y.; Liu, Z.; Yang, W. Finite Element Modeling and Modal Analysis of Heavy-Duty Mechanical Spindle under Multiple Constraints. J. Mech. Eng. 2012, 48, 165–173. [Google Scholar] [CrossRef]
- Xiong, F.; Wang, D.; Ma, Z.; Chen, S.; Lv, T.; Lu, F. Structure-Material Integrated Multi-Objective Lightweight Design of the Front End Structure of Automobile Body. Struct. Multidiscip. Optim. 2018, 57, 829–847. [Google Scholar] [CrossRef]
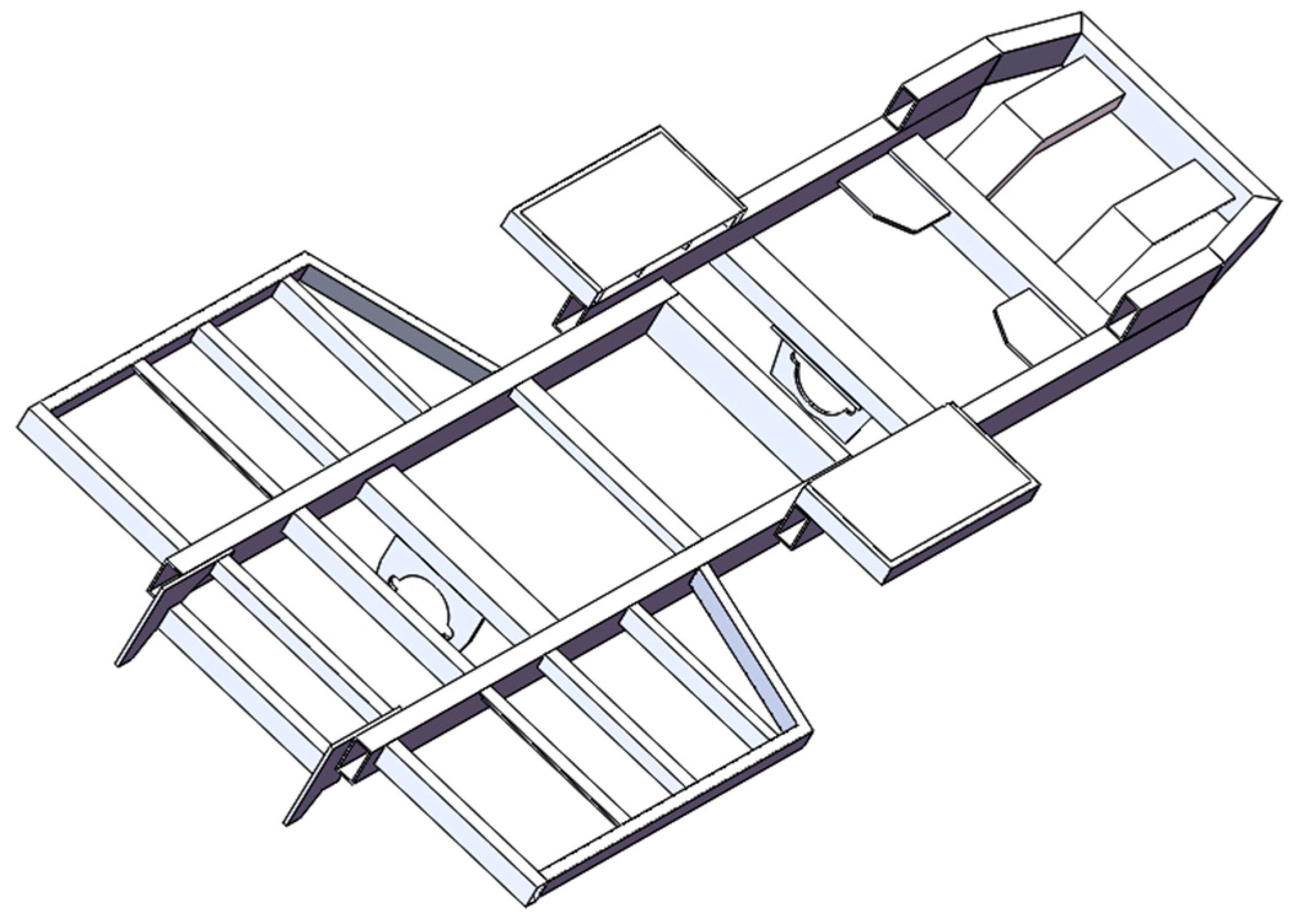

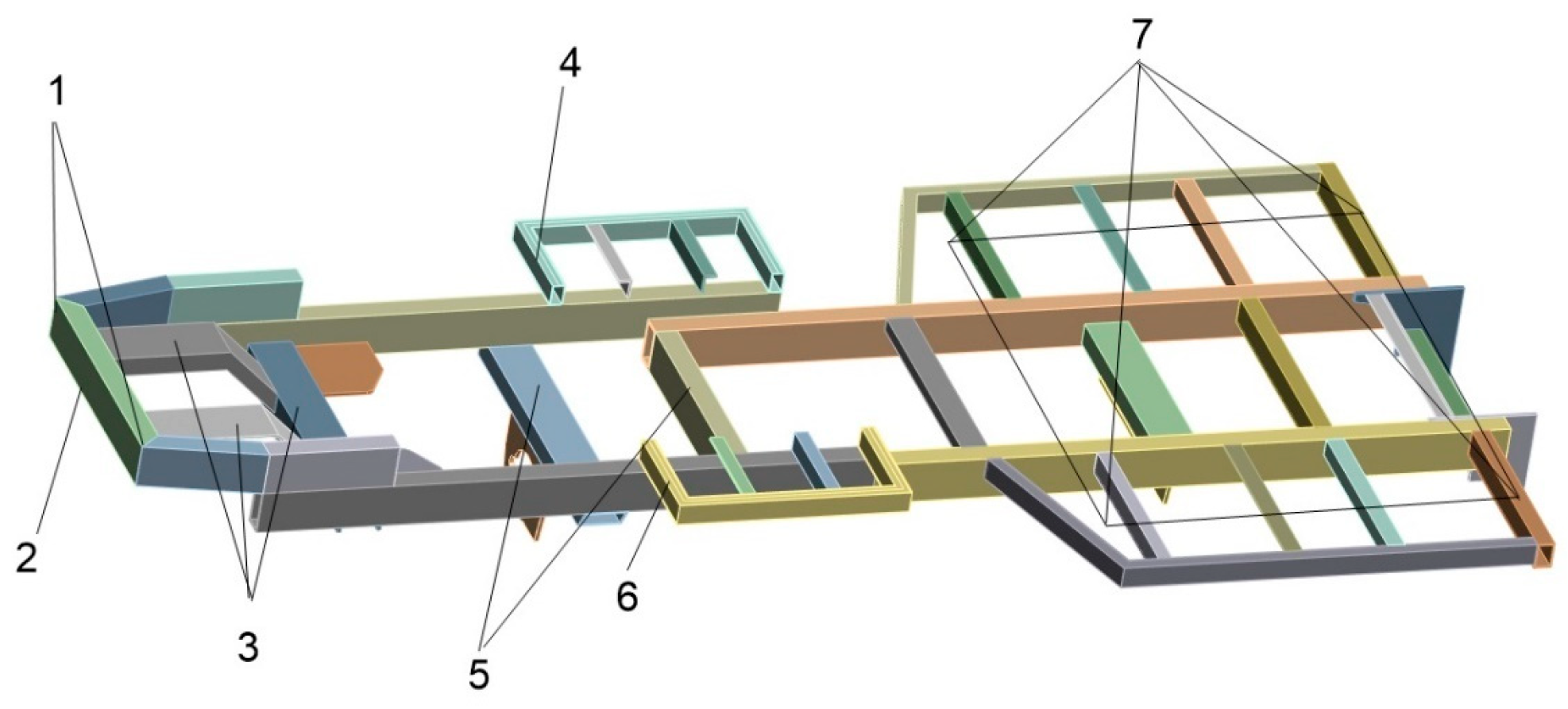
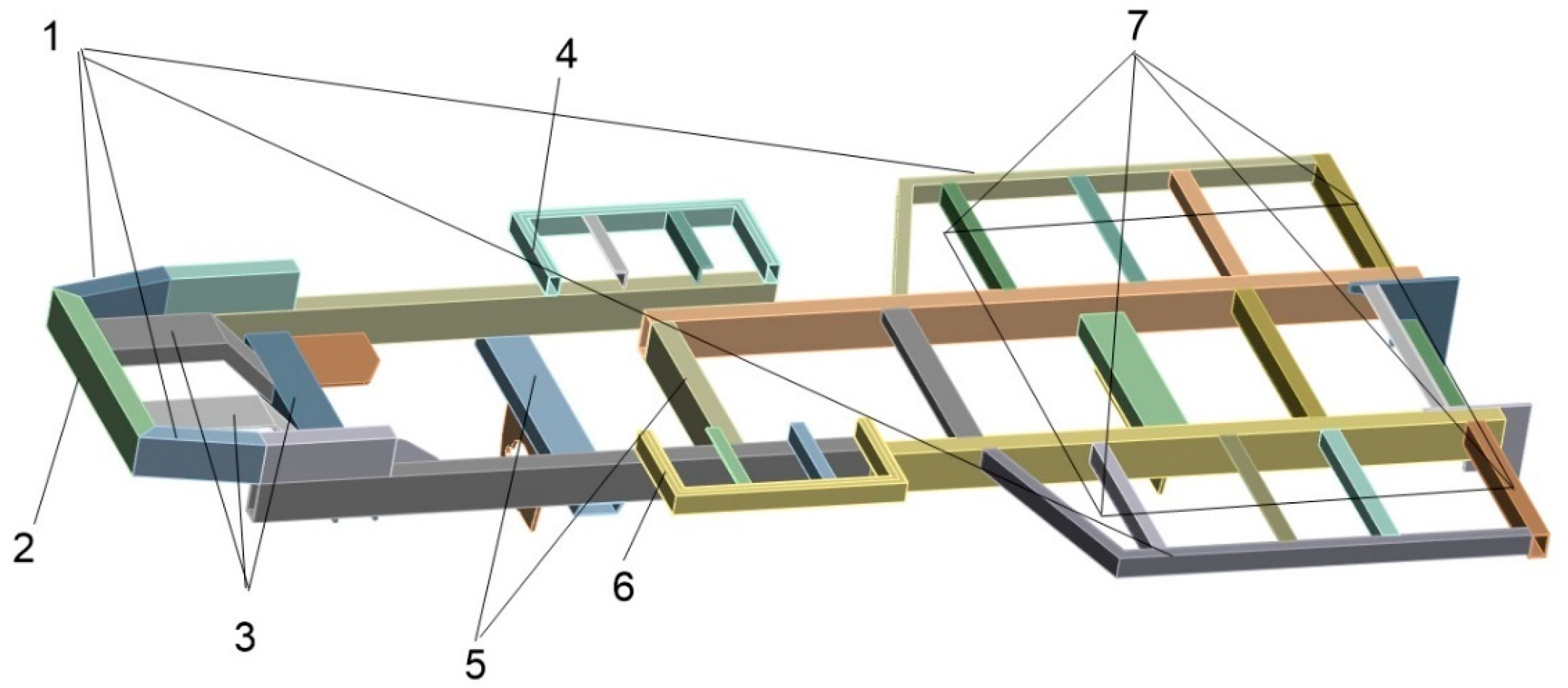

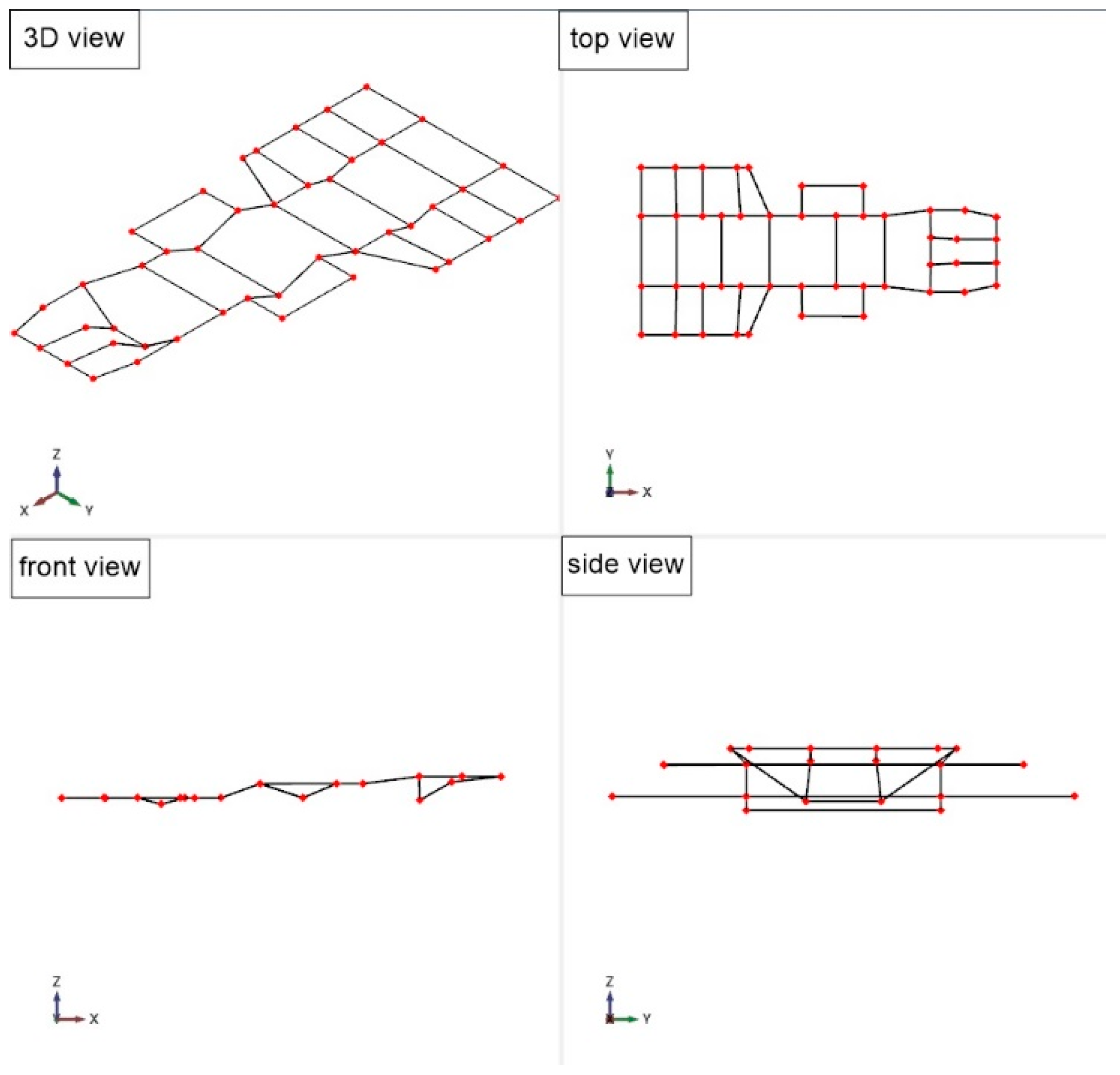

| The Sprayer Components | Weights/kg |
|---|---|
| suspensions | 80 |
| nozzle | 220 |
| motor | 250 |
| oil tank | 50 |
| water box | 40 |
| cabs | 300 |
| medicine cabinet (full) | 600 |
| Part Number | MS | DS | SS |
|---|---|---|---|
| 1 | 0.021 | −0.209 | 0.112 |
| 2 | 0.005 | 0.110 | 0.099 |
| 3 | 0.056 | 0.182 | 0.095 |
| 4 | 0.074 | −0.289 | 0.374 |
| 5 | 0.009 | −0.114 | −0.156 |
| 6 | 0.019 | −0.031 | −0.198 |
| 7 | 0.002 | −0.226 | 0.291 |
| 8 | 0.012 | −0.115 | 0.252 |
| 9 | 0.008 | 0.169 | 0.213 |
| 10 | 0.003 | 0.125 | 0.147 |
| 11 | 0.028 | 0.298 | −0.195 |
| 12 | 0.005 | −0.261 | −0.197 |
| 13 | 0.094 | −0.357 | 0.283 |
| 14 | 0.015 | −0.296 | 0.347 |
| 15 | 0.034 | −0.352 | 0.294 |
| 16 | 0.011 | 0.165 | 0.199 |
| 17 | 0.012 | 0.246 | 0.305 |
| Performance Indicators | Weight Coefficient |
|---|---|
| Mass | 0.5042 |
| Equivalent Stress | 0.2552 |
| Total Deformation | 0.2406 |
| Part Number | Comprehensive Contribution |
|---|---|
| 1 | 0.2065 |
| 3 | 0.5870 |
| 4 | 0.7826 |
| 6 | 0.1848 |
| 8 | 0.1087 |
| 11 | 0.2826 |
| 13 | 1.0000 |
| 14 | 0.1413 |
| 15 | 0.3478 |
| 17 | 0.1087 |
| Modal Order | Frequency/Hz | Vibration Type |
|---|---|---|
| 1 | 32.532 | FT |
| 2 | 38.292 | FB |
| 3 | 69.213 | TBC |
| 4 | 73.936 | FT |
| 5 | 74.170 | TBC |
| 6 | 92.752 | TBC |
| Modal Order | Simulation Frequency/Hz | Experimental Frequency/Hz |
|---|---|---|
| 1 | 39.532 | 37.007 |
| 2 | 45.292 | 48.626 |
| 3 | 59.213 | 69.892 |
| 4 | 63.936 | 71.350 |
| 5 | 70.170 | 76.632 |
| 6 | 82.752 | 89.932 |
| Part Number | Optimized Thickness | Rounded Value |
|---|---|---|
| 1 | 4.72108 | 4.7 |
| 3 | 4.59229 | 4.6 |
| 4 | 7.53861 | 7.5 |
| 6 | 2.35219 | 2.4 |
| 8 | 4.78118 | 4.8 |
| 11 | 9.72451 | 9.7 |
| 13 | 4.42859 | 4.4 |
| 14 | 3.52281 | 3.5 |
| 15 | 5.16852 | 5.2 |
| 17 | 4.71954 | 4.7 |
| Mass \kg | MSTC \MPa | MSBC \MPa | DTC \mm | DBC \mm | FOM \Hz | |
|---|---|---|---|---|---|---|
| Before Opt. | 178.367 | 180.23 | 203.61 | 1.4723 | 1.728 | 39.532 |
| After Opt. | 155.613 | 200.65 | 206.71 | 2.1193 | 2.335 | 41.225 |
| Variation | −22.754 | +20.64 | +3.10 | +0.647 | +0.607 | +1.693 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Chen, Q.; Zhang, L. Sensitivity Analysis Based on E-TOPSIS Combined with MORIME-Based Multi-Objective Optimization for Sprayer Frame Design Optimization. Machines 2025, 13, 201. https://doi.org/10.3390/machines13030201
Zhou S, Chen Q, Zhang L. Sensitivity Analysis Based on E-TOPSIS Combined with MORIME-Based Multi-Objective Optimization for Sprayer Frame Design Optimization. Machines. 2025; 13(3):201. https://doi.org/10.3390/machines13030201
Chicago/Turabian StyleZhou, Shaohao, Qi Chen, and Lihua Zhang. 2025. "Sensitivity Analysis Based on E-TOPSIS Combined with MORIME-Based Multi-Objective Optimization for Sprayer Frame Design Optimization" Machines 13, no. 3: 201. https://doi.org/10.3390/machines13030201
APA StyleZhou, S., Chen, Q., & Zhang, L. (2025). Sensitivity Analysis Based on E-TOPSIS Combined with MORIME-Based Multi-Objective Optimization for Sprayer Frame Design Optimization. Machines, 13(3), 201. https://doi.org/10.3390/machines13030201




