Optimization of Desired Multiple Resonant Modes of Compliant Parallel Mechanism Using Specific Frequency Range and Targeted Ratios
Abstract
1. Introduction
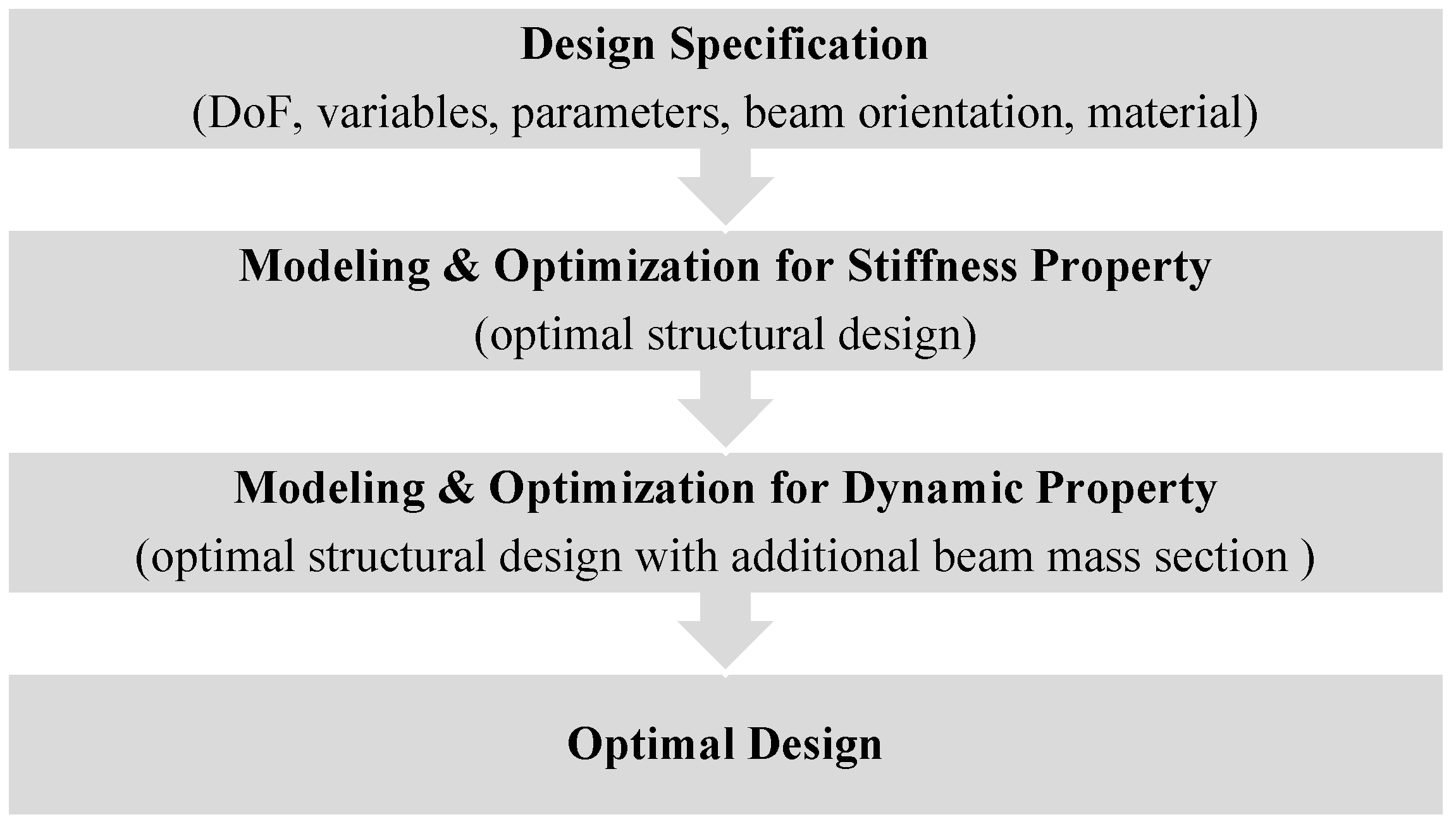
2. Synthesis of the 6-DoF CPM with Specified Resonant Modes
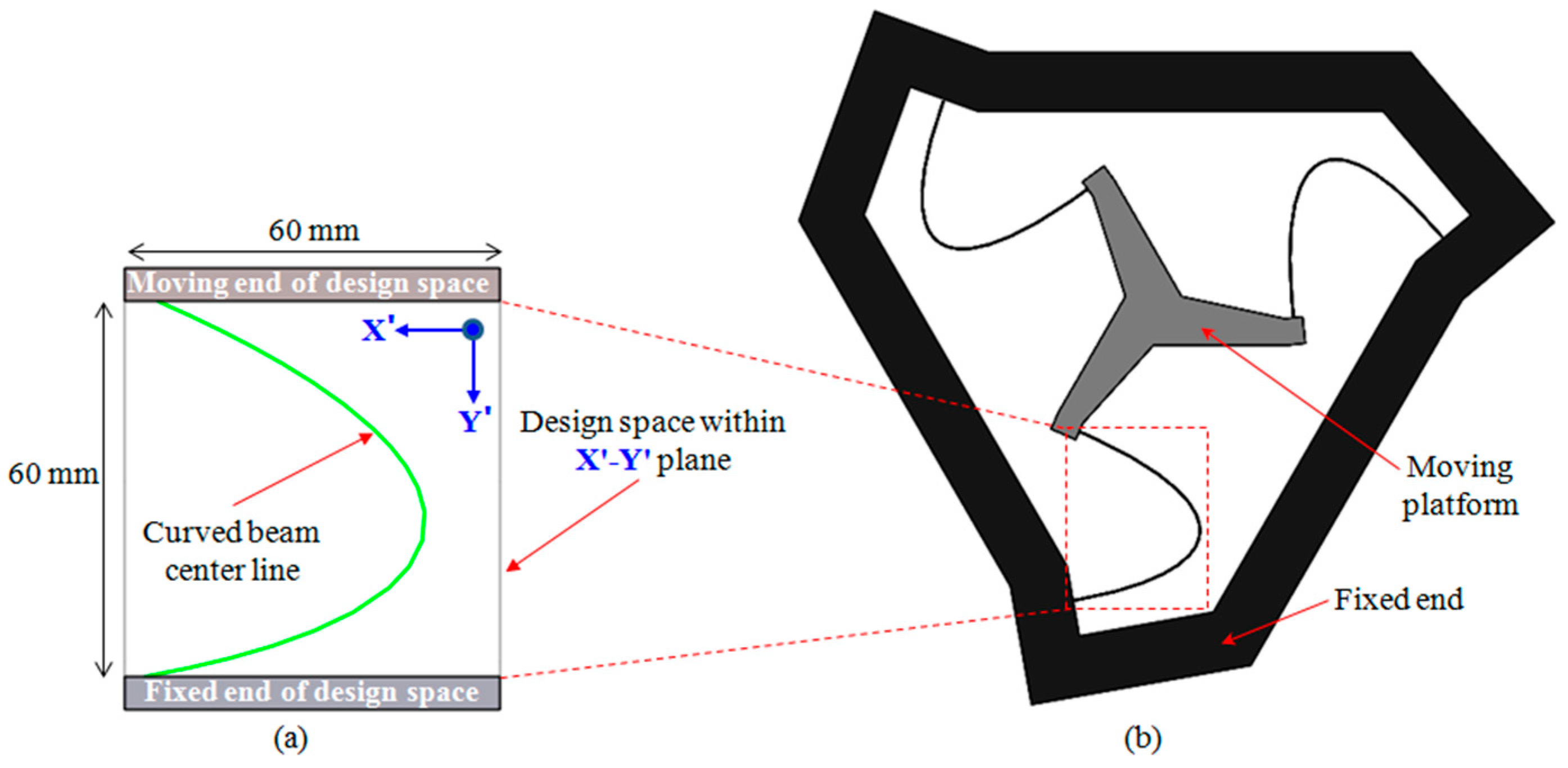
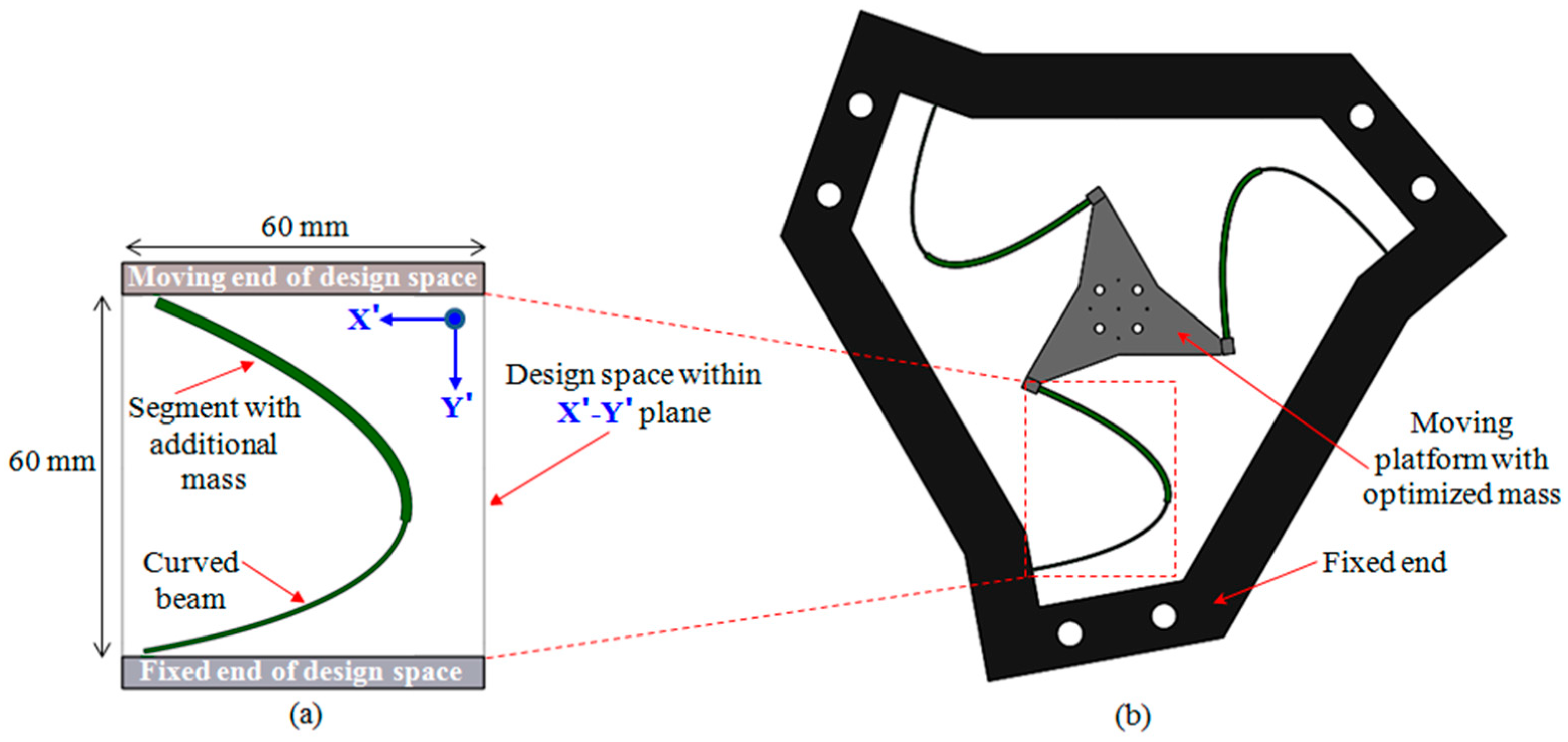
2.1. Synthesis Process
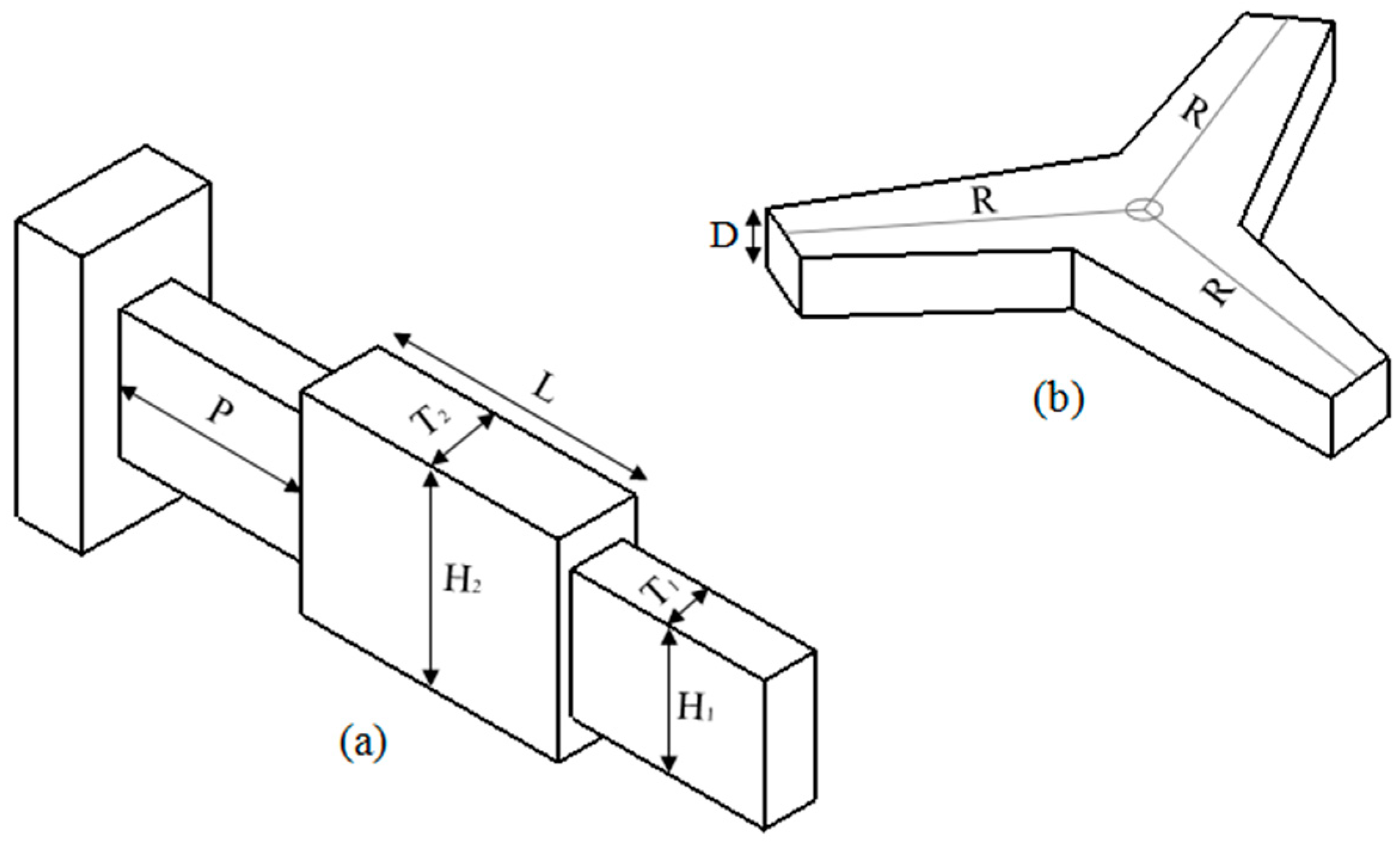
2.2. Stiffness Modeling and Optimization of the 6-DoF CPM
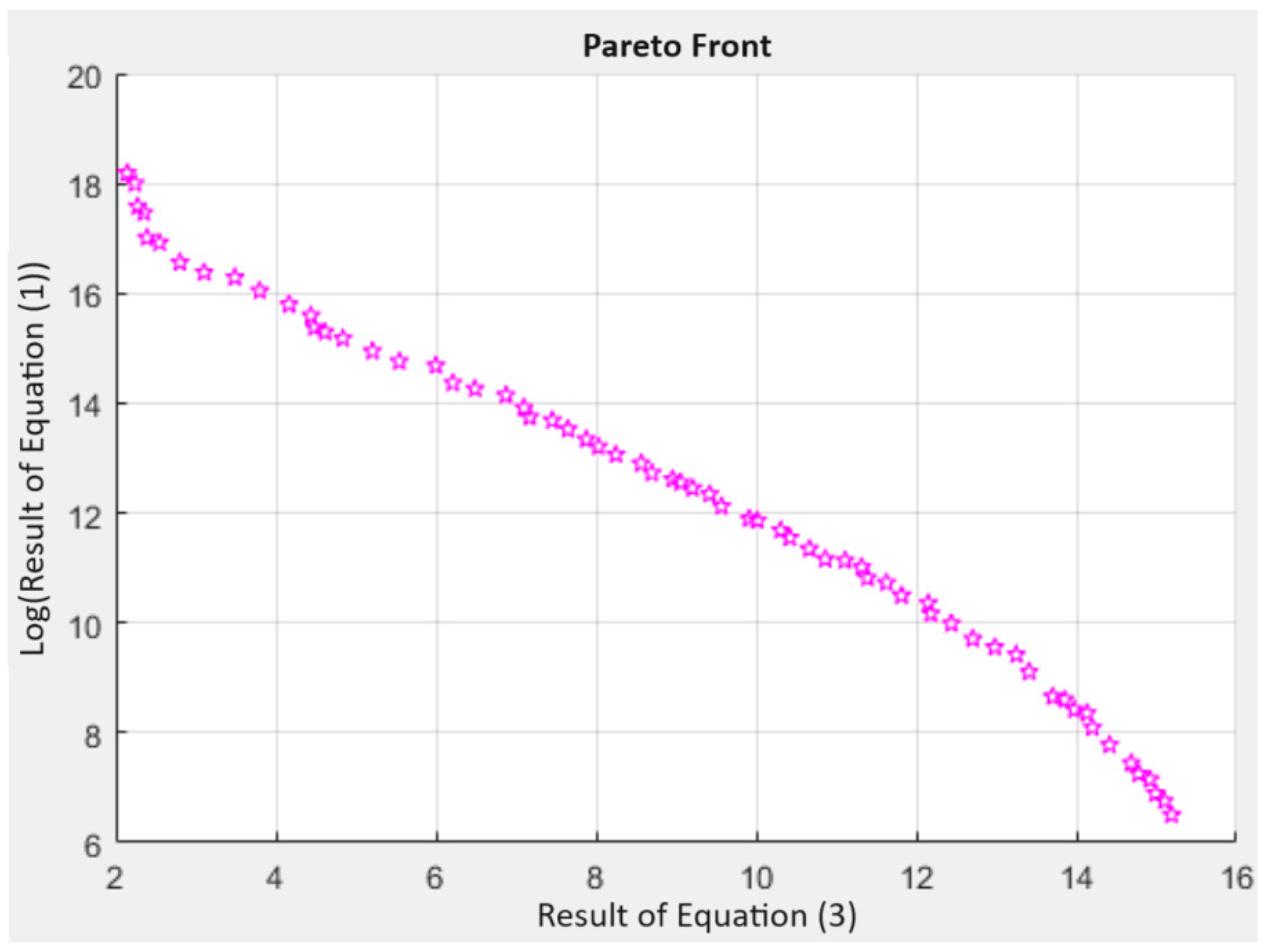
2.3. The Novel Objective Function for Optimizing Multiple Resonant Frequencies
2.4. Dynamic Modeling and Optimization of 6-DoF CPM
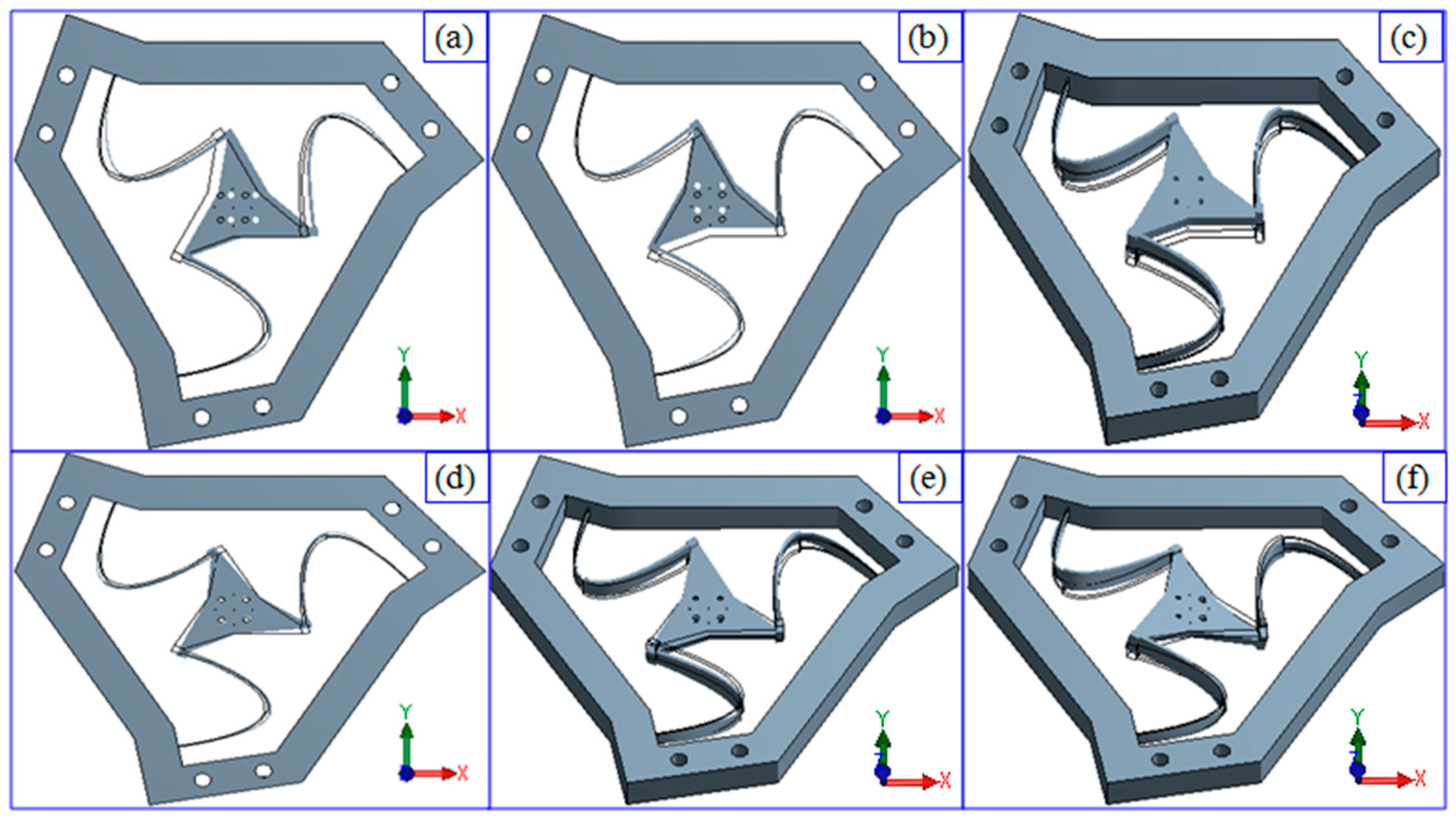
2.5. Summary of Results
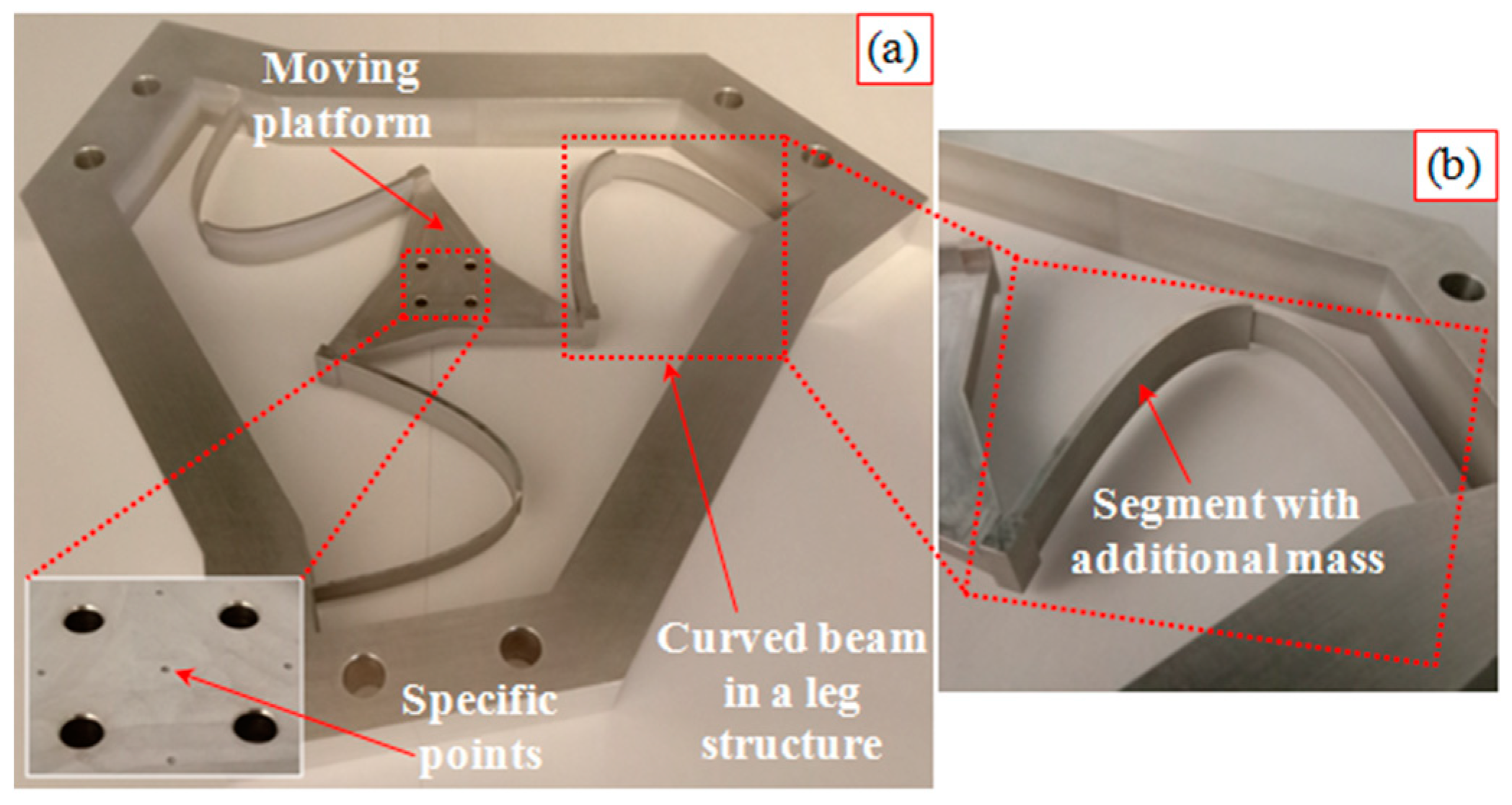
3. Experimental Investigation of the 6-DoF CPM Prototype
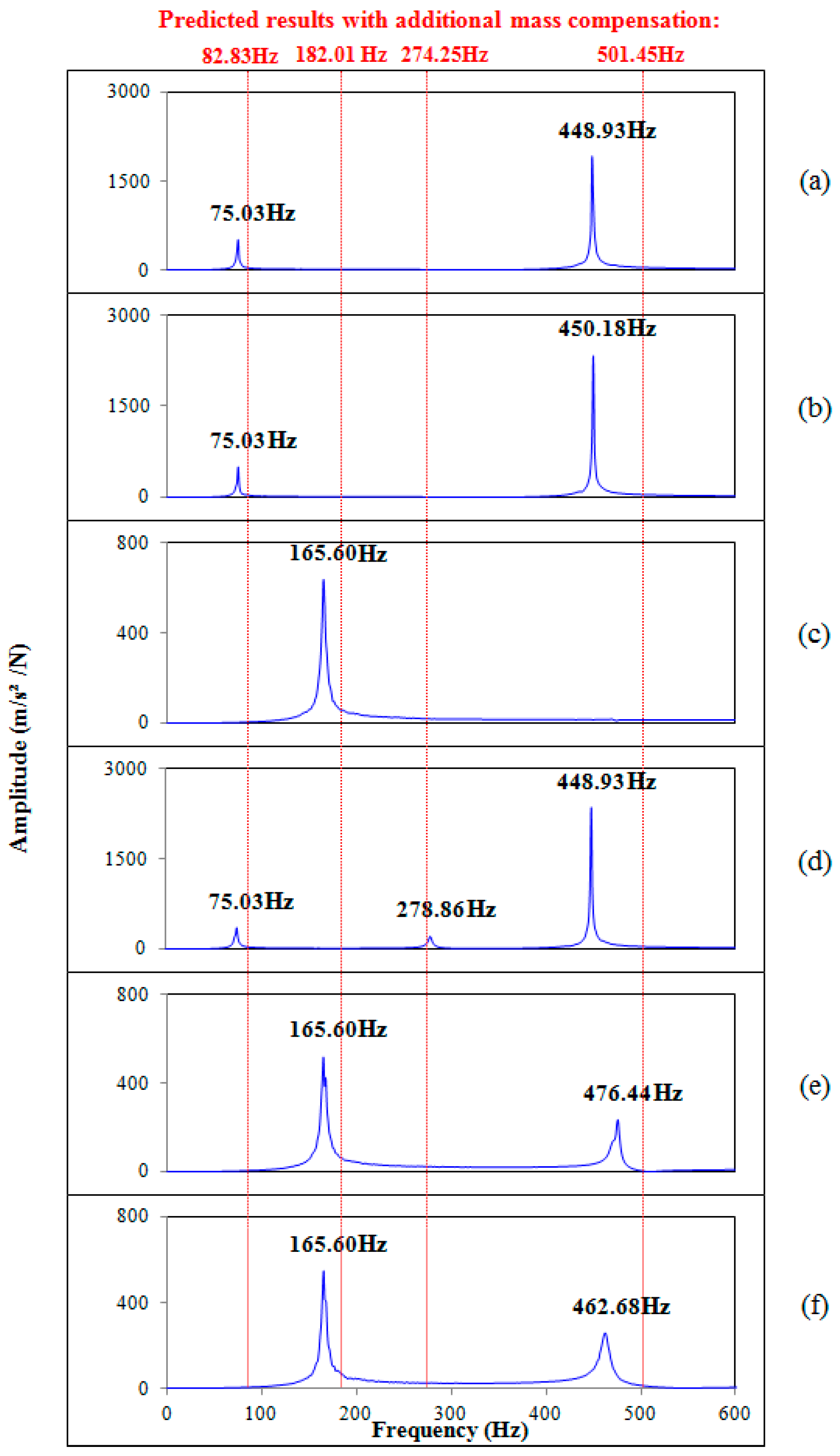
3.1. Dynamic Experiment of the Prototype
3.2. Compliance Experiment of the Prototype
4. Discussion of the Results
5. Conclusion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, X.-C.; Lu, Y.; Duan, X.-C.; Zhang, D.; Deng, W.-Y. Design and DOF Analysis of a Novel Compliant Parallel Mechanism for Large Load. Sensors 2019, 19, 828. [Google Scholar] [CrossRef]
- Paniselvam, V.; Tan, N.Y.J.; Anantharajan, S.K. A Review on the Design and Applications of Compliant Mechanism-Based Fast-Tool Servos for Ultraprecision Machining. Machines 2023, 11, 450. [Google Scholar] [CrossRef]
- Zhan, W.-H.; He, X.-H.; Yang, J.-M.; Lai, J.-H.; Zhu, D.-C. Optimal design method for 3-DOF planar compliant mechanisms based on mapping matrix constraints. Structures 2020, 26, 1–5. [Google Scholar] [CrossRef]
- Thomas, T.L.; Venkiteswaran, V.K.; Anathasureh, G.K.; Misra, S. Surgical Applications of Compliant Mechanisms—A Review. J. Mech. Robot. 2021, 13, 020801. [Google Scholar] [CrossRef]
- Ling, M.-X.; Cao, J.-Y.; Howell, L.L.; Zeng, M.-H. Kinetostatic modeling of complex compliant mechanisms with serial-parallel substructures: A semi-analytical matrix displacement method. Mech. Mach. Theory 2018, 125, 169–184. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, H.-J.; Liao, Q.-Z. Mobility criteria of compliant mechanisms based on decomposition of compliance matrices. Mech. Mach. Theory 2014, 79, 80–93. [Google Scholar] [CrossRef]
- Teo, T.J.; Yang, G.-L.; Chen, I.-M. Compliant Manipulators. In Handbook of Manufacturing Engineering and Technology; Springer: London, UK, 2014; pp. 1–63. [Google Scholar]
- Wang, R.-Z.; Zhang, X.-M. Optimal design of a planar parallel 3-DOF nanopositioner with multi-objective. Mech. Mach. Theory 2017, 112, 61–83. [Google Scholar] [CrossRef]
- Zhang, X.-Z.; Xu, Q.-S. Design and Analysis of a Compound Constant-Force Mechanism for Compliant Gripper. In Proceedings of the 2018 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Nagoya, Japan, 4–8 July 2018. [Google Scholar]
- Ai, W.-J.; Xu, Q.-S. New Structural Design of a Compliant Gripper Based on the Scott-Russell Mechanism. Int. J. Adv. Robot. Syst. 2014, 11, 192. [Google Scholar] [CrossRef]
- Zhu, W.-L.; Zhu, Z.-W.; Guo, P.; Ju, B.-F. A novel hybrid actuation mechanism based XY nanopositioning stage with totally decoupled kinematics. Mech. Syst. Signal Process 2018, 99, 747–759. [Google Scholar] [CrossRef]
- Li, Y.-M.; Xiao, S.-L.; Xi, L.-Q.; Wu, Z.-G. Design, Modeling, Control and Experiment for a 2-DOF Compliant Micro-Motion Stage. Int. J. Precis. Eng. Manuf. 2014, 15, 735–744. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, C. Design and Analysis of a 3-DOF Planar Flexure-based Parallel Mechanism with Large Motion Range. In Proceedings of the IEEE International Conference on Robotics and Biometrics, Kuala Lumpur, Malaysia, 12–15 December 2018. [Google Scholar]
- Bhagat, U.; Shirinzadeh, B.; Clark, L.; Chea, P.; Qin, Y.-D.; Tian, Y.-L.; Zhang, D.-W. Design and analysis of a novel flexure-based 3-DOF mechanism. Mech. Mach. Theory 2014, 74, 173–187. [Google Scholar] [CrossRef]
- Chen, X.-G.; Li, Y.-M.; Xie, Y.-L.; Wang, R.-B. Design and analysis of new ultra compact decoupled XYZθ stage to achieve large-scale high precision motion. Mech. Mach. Theory 2022, 167, 104527. [Google Scholar] [CrossRef]
- Ahn, D.-H.; Choi, Y.-M.; Jeong, J.-H. Design of a four-degree-of-freedom nano positioner utilizing electromagnetic actuators and flexure mechanisms. Rev. Sci. Instrum. 2015, 86, 035101. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.-P.; Luo, X.; Wang, S.-L.; Li, X.-J. Dynamic Analysis of a 5-DOF Flexure-Based Nanopositioning Stage. Math. Probl. Eng. 2019, 2019, 8501583. [Google Scholar] [CrossRef]
- Zhang, D.; Gao, Z. Performance analysis and optimization of a five-degrees-of-freedom compliant hybrid parallel micromanipulator. Robot. Comput. Integr. Manuf. 2015, 34, 20–29. [Google Scholar] [CrossRef]
- Lin, C.; Zheng, S.; Li, P.-Y.; Jiang, M.-D. Kinetostatic analysis of 6-DoF compliant platform with a multi-stage condensed modeling method. Microsyst. Technol. 2021, 27, 2153–2166. [Google Scholar] [CrossRef]
- Ghafarian, M.; Shrinzadesh, B.; Das, T.K.; Al-Jodah, A.; Wei, W.-C. Design of a novel parallel monolithic 6-DOF compliant micromanipulation mechanism. In Proceedings of the IEEE/ASME International Conference on AIM, Auckland, New Zealand, 9–12 July 2018. [Google Scholar]
- Ghafarian, M.; Shirinzadeh, B.; Al-Jodah, A.; Das, T.K.; Pinskier, J. FEA-based optimization of a complete structure of a monolithic z/tip/tilt micromanipulator. J. Micro-Bio Robot. 2020, 16, 93–110. [Google Scholar] [CrossRef]
- Pham, M.T.; Teo, T.J.; Yeo, S.H. Synthesis of multiple degrees-of-freedom spatial-motion compliant parallel mechanisms with desired stiffness and dynamics characteristics. Precis. Eng. 2017, 47, 131–139. [Google Scholar] [CrossRef]
- Pham, M.T.; Yeo, S.H.; Teo, T.J.; Wang, P.; Nai, M.L.S. A Decoupled 6-DOF Compliant Parallel Mechanism with Optimized Dynamic Characteristics Using Cellular Structure. Machines 2021, 9, 5. [Google Scholar] [CrossRef]
- Low, V.; Yeo, S.H.; Pham, M.T. Synthesis of Compliant Parallel Mechanisms Using an Improved Beam-Based Method with the Optimization of Multiple Resonant Modes. Machines 2023, 11, 731. [Google Scholar] [CrossRef]




| Resonant Mode | Targeted Ratio | Obtained Ratio | Deviation (%) |
|---|---|---|---|
| 1 | 1 | 0 | |
| 2 | 1.89 | 5.50 | |
| 3 | 3.15 | 5.00 | |
| 5 | 5.22 | 4.40 | |
| 5 | 5.22 | 4.40 |
| Actuating Direction | Predicted Resonant Frequency (Hz) | FEA Resonant Frequency (Hz) | Deviation (%) |
|---|---|---|---|
| Along X—axis | 96.15 | 95.31 | 0.87 |
| Along Y—axis | 96.15 | 95.33 | 0.85 |
| Along Z—axis | 182.01 | 179.75 | 1.24 |
| About Z—axis | 302.88 | 298.86 | 1.33 |
| About X—axis | 501.45 | 496.89 | 0.91 |
| About Y—axis | 501.45 | 497.07 | 0.87 |
| Actuating Direction | Predicted Compliance (m/N) or (rad/Nm) | FEA Compliance (m/N) or (rad/Nm) | Deviation (%) |
|---|---|---|---|
| Along X—axis | 1.96 | ||
| Along Y—axis | 1.96 | ||
| Along Z—axis | 1.35 | ||
| About X—axis | 1.79 | ||
| About Y—axis | 1.79 | ||
| About Z—axis | 2.55 |
| Actuating Direction | Along X-Axis | Along Y-Axis | Along Z-Axis | About X-Axis | About Y-Axis | About Z-Axis |
|---|---|---|---|---|---|---|
| Full Range of Motion (±Range of Motion) | 10.0 mm (±5.0 mm) | 8.8 mm (±4.4 mm) | 4.6 mm (±2.3 mm) | 4.6° (±2.3°) | 4.4° (±2.2°) | 10.8° (±5.4°) |
| Actuating Direction | Along X-Axis | Along Y-Axis | Along Z-Axis | About Z-Axis | About X-Axis | About Y-Axis |
|---|---|---|---|---|---|---|
| Resonant Frequency (Hz) | 82.83 | 82.83 | 182.01 | 274.25 | 501.45 | 501.45 |
| Actuating Direction | Predicted Resonant Frequency (Hz) | Experimental Resonant Frequency (Hz) | Deviation (%) |
|---|---|---|---|
| Along X—axis | 82.83 | 75.03 | 9.42 |
| Along Y—axis | 82.83 | 75.03 | 9.42 |
| Along Z—axis | 182.01 | 165.60 | 9.02 |
| About Z—axis | 274.25 | 278.86 | 1.68 |
| About X—axis | 501.45 | 476.44 | 4.99 |
| About Y—axis | 501.45 | 462.68 | 7.73 |
| Actuating Direction | Predicted Compliance (m/N) or (rad/Nm) | Experimental Compliance (m/N) or (rad/Nm) | Deviation (%) |
|---|---|---|---|
| Along X—axis | 0.98 | ||
| Along Y—axis | 5.88 | ||
| Along Z—axis | 10.77 | ||
| About X—axis | 5.36 | ||
| About Y—axis | 6.25 | ||
| About Z—axis | 2.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Low, V.; Yeo, S.H.; Pham, M.T. Optimization of Desired Multiple Resonant Modes of Compliant Parallel Mechanism Using Specific Frequency Range and Targeted Ratios. Machines 2024, 12, 585. https://doi.org/10.3390/machines12080585
Low V, Yeo SH, Pham MT. Optimization of Desired Multiple Resonant Modes of Compliant Parallel Mechanism Using Specific Frequency Range and Targeted Ratios. Machines. 2024; 12(8):585. https://doi.org/10.3390/machines12080585
Chicago/Turabian StyleLow, Vin, Song Huat Yeo, and Minh Tuan Pham. 2024. "Optimization of Desired Multiple Resonant Modes of Compliant Parallel Mechanism Using Specific Frequency Range and Targeted Ratios" Machines 12, no. 8: 585. https://doi.org/10.3390/machines12080585
APA StyleLow, V., Yeo, S. H., & Pham, M. T. (2024). Optimization of Desired Multiple Resonant Modes of Compliant Parallel Mechanism Using Specific Frequency Range and Targeted Ratios. Machines, 12(8), 585. https://doi.org/10.3390/machines12080585






