Abstract
Driven by the rise of intelligent manufacturing and Industry 4.0, the manufacturing industry faces significant challenges in adapting to flexible and efficient production methods. This study presents an innovative approach to solving the Flexible Job-Shop Scheduling Problem (FJSP) by integrating Heterogeneous Graph Neural Networks based on Relation (HGNNR) with Deep Reinforcement Learning (DRL). The proposed framework models the complex relationships in FJSP using heterogeneous graphs, where operations and machines are represented as nodes, with directed and undirected arcs indicating dependencies and compatibilities. The HGNNR framework comprises four key components: relation-specific subgraph decomposition, data preprocessing, feature extraction through graph convolution, and cross-relation feature fusion using a multi-head attention mechanism. For decision-making, we employ the Proximal Policy Optimization (PPO) algorithm, which iteratively updates policies to maximize cumulative rewards through continuous interaction with the environment. Experimental results on four public benchmark datasets demonstrate that our proposed method outperforms four state-of-the-art DRL-based techniques and three common rule-based heuristic algorithms, achieving superior scheduling efficiency and generalization capabilities. This framework offers a robust and scalable solution for complex industrial scheduling problems, enhancing production efficiency and adaptability.
1. Introduction
The manufacturing industry is currently experiencing a number of significant challenges and opportunities as a result of globalization and technological innovation [1]. The advent of intelligent manufacturing and Industry 4.0 is driving a shift from traditional large-scale production to flexible and intelligent production modes, which allows for rapid adaptation to changing market demands [2,3]. This transformation necessitates that manufacturing systems maintain high efficiency and flexibility to cope with the continuous changes in production tasks and environments [4,5,6].
In this context, the Flexible Job-shop Scheduling Problem (FJSP) is crucial. The objective is to plan the execution sequence of production tasks and resource allocation in order to maximize efficiency and reduce costs [7]. The complexity of FJSP arises from the need to determine task sequences, select suitable machines, and consider various constraints and uncertainties [8,9]. FJSP solutions can be applied in a variety of fields, including manufacturing [10], cloud computing centers [11], logistics [12], and supply chain management [13], to improve flexibility and efficiency while increasing competitiveness and customer satisfaction.
FJSP is an NP-hard problem, which means that its computational complexity increases exponentially with the size of the problem, making it difficult to find an optimal or near-optimal solution [14]. Traditional methods, including exact, heuristic, and metaheuristic approaches, have various advantages and limitations [15]. Exact algorithms, while accurate, struggle with scalability and generalization [16]. Heuristic methods, though flexible and fast, often only achieve local optima [17]. Metaheuristic methods balance global and local searches but require precise parameter tuning and can be computationally intensive [18].
Recent advancements in machine learning and artificial intelligence, particularly Deep Reinforcement Learning (DRL), offer unique advantages in solving complex decision-making problems like FJSP [19]. DRL can learn and adapt through continuous environmental interaction, but effectively extracting and utilizing state features for large-scale FJSP remains a challenge [20,21]. Researchers have explored various state representation methods, including integrated features [22], disjunctive graphs [23], and heterogeneous graphs [24], each with its strengths and limitations.
Graph Neural Networks (GNNs) provide an innovative solution by handling graph-structured data, capturing complex relationships, and providing detailed state representations for DRL [25,26]. GNNs overcome traditional methods’ limitations, enhancing scheduling performance and the application potential of DRL in intelligent manufacturing [27,28,29]. However, challenges remain in comprehensively modeling flexible shop floor states and fully capturing the static and dynamic features necessary for optimal scheduling decisions.
To address these challenges, this study proposes an end-to-end scheduling framework that comprehensively models FJSP states and effectively extracts features to make reinforcement learning-based scheduling decisions. By modeling the FJSP state as a heterogeneous graph, machines and operations are mapped to nodes in the graph, with directed and undirected arcs representing dependencies and compatibilities, preserving the rich features and structural information of the FJSP. Various representative dynamic and static features are selected to enrich the representation of FJSP. This study designs a Heterogeneous Graph Neural Network based on Relation (HGNNR) to fully exploit the relationship information in the heterogeneous graph. Both machine and operation node feature extraction is accomplished using HGNNR. Subgraph embeddings are extracted through subgraph decomposition based on relation and Graph Convolution Network, then integrated using a multi-head attention mechanism. This method effectively extracts subtle features of nodes and captures complex interactions, providing rich information for scheduling decisions. Finally, combined with the Proximal Policy Optimization (PPO) algorithm, this framework aims to minimize the maximum completion time, i.e., makespan, as the optimization objective, constructing a Markov Decision Process (MDP) and learning effective scheduling strategies from the node and graph embeddings through continuous interaction with the environment. This framework balances algorithm performance, solution efficiency, and generalization ability, validating its superiority over existing methods on public benchmark datasets.
The main contributions of this article can be summarized as follows:
- This study comprehensively models the FJSP using the heterogeneous graph, effectively capturing the internal structure and diverse relationships within the FJSP. This method ensures the retention of essential static features such as processing time and operation dependencies while also detailing dynamic features like workpiece progress and machine status.
- An HGNNR is introduced in this study, specifically designed to extract rich and detailed feature information from heterogeneous graphs. This model enhances the understanding of inter-process dependencies and improves the capture of compatibility between operations and machines, offering a robust theoretical basis for the design and optimization of scheduling algorithms.
- This study integrates HGNNR with DRL to create an end-to-end scheduling framework. This innovative framework not only delivers efficient solutions for FJSP but also demonstrates its effectiveness through validation on custom synthetic datasets and publicly available benchmark datasets. The framework successfully balances algorithm performance, solution efficiency, and generalization capability, proving its practicality and wide applicability in addressing real-world complex scheduling problems.
The following content arrangement is as follows. Section 2 reviews recent research progress on the FJSP, including traditional methods and DRL-based scheduling strategies. Section 3 defines FJSP and describes its representation of a heterogeneous graph. Section 4 details the proposed methods, including the construction of MDP, the design of HGNNR, and the training and updating of PPO. Section 5 presents experimental results and analysis. Finally, Section 6 concludes the article.
2. Related Work
In this section, we review the existing methods for solving the FJSP, categorizing them into conventional and DRL-based methods.
2.1. Conventional Methods
Traditional methods for solving the FJSP can be categorized into exact, heuristic, and metaheuristic methods [15].
Exact methods, such as Mixed-Integer Linear Programming (MILP), achieve precise solutions by using mathematical models. For instance, in [30], six MILP models were developed to optimize production activities, focusing on energy efficiency. However, exact methods, including the models proposed in [31,32], often lack generalization capability and are suitable only for specific cases due to their high computational complexity. To overcome these limitations, our study introduces heterogeneous graph models, enhancing generalization and applicability across various FJSP scenarios.
Heuristic methods provide quick, feasible solutions based on local information. The authors of [33] proposed a hybrid search strategy using Petri nets, while in [34,35], methods focusing on Total Weighted Tardiness and green scheduling were introduced, respectively. Despite their speed, heuristic methods like those discussed in [36] often only guarantee locally optimal solutions, limiting their performance in complex environments. By integrating GNN and DRL, our approach extracts both global and local features, improving decision-making and overcoming traditional heuristic limitations.
Metaheuristic methods, such as Genetic Algorithms (GA), balance global and local searches. Studies [37,38,39] demonstrate the effectiveness of GA variants in solving FJSP. However, these methods require precise parameter tuning and can be computationally intensive. To address these challenges, we utilize DRL to enhance computation speed and adaptability, significantly improving the efficiency of metaheuristic approaches in handling complex FJSP.
2.2. DRL-Based Methods
Numerous studies have applied various neural network models to extract features for improving scheduling decisions in the FJSP. For instance, ref. [40] proposed a DRL actor–critic framework using Convolutional Neural Networks (CNNs) to model the problem as a Markov Decision Process (MDP). This approach effectively extracts features, aiding optimal decision-making. Ref. [41] introduced a 3D separable graph-based end-to-end framework utilizing a modified pointer network with attention mechanisms and Recurrent Neural Networks (RNNs, excelling in feature extraction. Ref. [42] presented a novel framework using a lightweight Multi-Layer Perceptron (MLP) for state embedding, reducing computational complexity while effectively reflecting state features.
Traditional neural network models like CNN, RNN, and MLP, though effective for fixed-structure inputs, struggle with heterogeneous and complex graph-structured data inherent in FJSP. They often fail to capture intricate process dependencies and machine selections, limiting their application scope.
In response, ref. [43] combined GNN and MLP, using GNN for state embedding and MLP for operation sequence and machine allocation, optimized via the asynchronous advantage actor–critic (A3C) algorithm. Ref. [44] proposed a Graph Isomorphism Network (GIN) to learn Priority Dispatching Rules (PDRs) for Job Shop Scheduling Problems (JSSPs), trained with the PPO algorithm. However, this approach ignores shop floor state heterogeneity. Ref. [24] employed a Heterogeneous Graph Neural Network (HGNN) to capture complex relationships between operations and machines, utilizing PPO for policy optimization.
Despite these advancements, existing research often overlooks the complex relationships in FJSP. This study proposes a relation-based heterogeneous graph neural network that decomposes the entire graph into relation-specific subgraphs, applying Graph Convolutional Networks (GCNs) to each subgraph and using a multi-head attention mechanism to dynamically integrate subgraph features. This approach enhances the model’s understanding and adaptability to the complex dynamics of the shop floor, significantly improving optimization and generalization capabilities.
This study analyzes existing research to identify key limitations in exact, heuristic, and metaheuristic methods. Exact methods struggle with scalability and generalization, heuristic methods often find only locally optimal solutions, and metaheuristic methods require precise parameter tuning and can be computationally intensive. Existing DRL methods face challenges in feature extraction and state representation for heterogeneous, complex data.
To address these challenges, our study proposes an end-to-end scheduling framework integrating HGNNR and DRL. This framework enhances efficiency, accuracy, adaptability, and generalization, offering a comprehensive solution for FJSP, pushing the boundaries of intelligent manufacturing and complex scheduling problem-solving.
3. Preliminaries
This section provides the foundational concepts and definitions essential for understanding the proposed methods. It begins with an overview of the FJSP, detailing its complexity and key components. Following this, we introduce the heterogeneous graph representation of FJSP, explaining how it captures the intricate relationships and dependencies within the scheduling environment. These preliminaries set the stage for the subsequent sections, where the proposed methods and algorithms are elaborated upon.
3.1. Flexible Job-Shop Scheduling Problem
In the framework of FJSP, we consider an instance with n jobs and m machines, where these machines and jobs form sets and , respectively. Each job consists of a series of operations that must be completed in a specific order, denoted by set , and each operation can be executed on any compatible machine , with an uninterrupted processing time . The objective is to assign suitable machines and start times for each operation in order to minimize the maximum completion time of all jobs. In solving the FJSP, we make the following assumptions:
- All machines are initially idle.
- All jobs can start processing immediately.
- Once an operation starts, it must be completed without interruption.
- Each machine can process only one operation at a time.
- Setup times between operations are neglected or included in processing times.
Based on the problem description and the model proposed in [45], the mathematical model of FJSP can be represented as follows:
Decision variables:
Objective function:
Constraints:
The optimization goal of minimizing the maximum completion time is defined by Equation (3); Equations (4) and (5) indicate priority constraints between adjacent operations of the same process; each machine is confined to processing a single operation at a moment by Equations (6) and (7), where Z is an enormous constant; Equation (8) is also a machine constraint, ensuring that each operation is processed by only one machine at a time.
3.2. Heterogeneous Graph
The heterogeneous graph offers a structured representation of the FJSP, effectively illustrating the characteristics of multi-machine processing and the diversity of operations. This heterogeneous graph is denoted as , where includes all operations along with two virtual nodes: Start and End. The set consists of machine nodes, with each machine represented as a node. While consists of undirected arcs that show possible combinations of machines and operations, collection contains directed arcs that show process sequences among operations. Each arc connects operation to a machine and includes the corresponding processing time as an attribute.
In Figure 1, part (a) represents an instance of FJSP, where dashed lines between operation and machine nodes indicate potential compatibility. Part (b) illustrates the final scheduling solution, with solid lines representing the actual assignments between operations and machines.
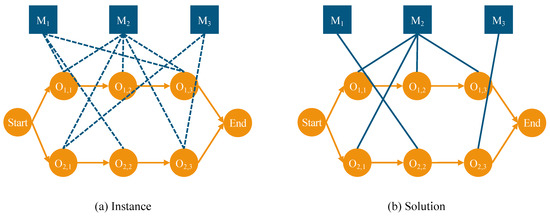
Figure 1.
Heterogeneous Graph Representation for FJSP.
For each state , we define the following original feature vectors to capture detailed information about operations, machines, and arcs during the scheduling process:
Original features of operation nodes: Each actual operation node is described by feature vector , containing the following information:
- Status: whether the operation is scheduled in the current timestep t (a binary value);
- Number of adjacent machines: the number of available adjacent machines;
- Processing time: if scheduled, the specific processing time ; otherwise, the expected average processing time ;
- Starting time: the operation’s predicted or real start time in the incomplete schedule ;
- Number of predecessor operations: the total amount of operations in the currently selected job that precede ;
- Number of successor operations: the count of operations that succeed in the current job;
- Proportion of unscheduled operations: the ratio of operations not yet scheduled in the current job;
- Job completion time: estimated or actual completion time of the job.
Original features of machine nodes: Each machine node is described by feature vector containing:
- Available time: the available time after completing all assigned operations;
- Number of adjacent operations: the number of directly adjacent operations that can be processed on ;
- Utilization rate: the utilization rate up to the current timestep t, ranging from zero to one.
Original features of O-M arcs: The feature vector of each O-M arc contains a single element: processing time . This processing time represents the duration required for operation to be completed on machine .
4. Method
In this section, we present the comprehensive methodology for our proposed framework to FJSP. This section details the design of HGNNR and its integration with deep reinforcement learning techniques. The aim is to develop an efficient and effective end-to-end scheduling framework that leverages advanced machine learning techniques to optimize scheduling decisions.
Figure 2 offers an overview of the proposed framework. The process begins with a Flexible Job-Shop Instance, where raw data about operations and machines are collected. From this instance, we extract the heterogeneous graph along with the raw node and arc information, capturing the essential details of operations and machines in the job shop environment. The extracted data are then fed into the HGNNR, which begins with Subgraph Decomposition, breaking down the heterogeneous graph into relation-specific subgraphs. This is followed by Feature Preprocessing, which includes two steps: standardization, where raw data are normalized to ensure consistency, and dimension alignment using MLP to prepare the features for further analysis. Graph Convolution is then applied to extract deep features from the nodes within each subgraph. Finally, Cross-Relation Feature Fusion integrates features from different subgraphs using a multi-head attention mechanism, resulting in a comprehensive representation of the data. After the graph convolution and feature fusion steps, Mean Pooling is used to obtain the global feature representation from the integrated node embeddings. These global features, along with the local features extracted by HGNNR, are then used by the PPO Algorithm for decision-making and training updates. The PPO algorithm iteratively updates parameters based on rewards calculated from actions taken. Both local and global features contribute to the decision-making process, enhancing the accuracy and efficiency of the scheduling strategy. Finally, the framework produces an optimized Scheduling Solution, efficiently allocating operations to machines and maximizing production efficiency.
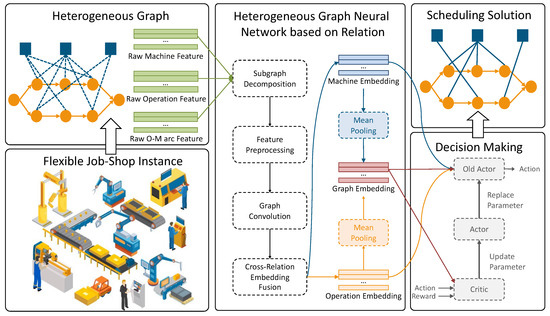
Figure 2.
Overview of Proposed Scheduling Framework.
4.1. Markov Decision Process
To explore the solution path for the FJSP, this study adopts a reinforcement learning framework and designs an MDP to intelligently schedule operations and allocate machines. With this method, at each decision point t (i.e., at start-up or after every operation is finished), the agent can decide based on the current environment state . In particular, the agent starts the starting time from timestep t and chooses a machine that is available to allocate to the anticipated operation. After that, the environment moves on to the following decision point, , and so on, iterating until all operations are scheduled.
State: At each step t of the MDP, system state comprehensively presents the real-time status of each job and machine. The initial state is determined by sampling from the distribution of FJSP instances, establishing the benchmark for the scheduling process. For each state , the system tracks part of schedule , including the actual processing time of scheduled jobs and the estimated processing time of unscheduled jobs. If operation is scheduled, represents the actual start time ; if not scheduled, predictions are made based on the status of preceding operations and available machines. For example, if the preceding operation is started on machine , then ; otherwise, the average processing time in the optional machine set for operation is used for prediction. The state provides a global view, facilitating wise scheduling decisions under complete information.
Action: This work combines machine allocation and job selection into a single decision approach to solve the FJSP efficiently. The definition of action at timestep t is an appropriate operation-machine pair , where is available and is to be executed. The action set varies at each timestep and comprises all feasible operation–machine pairs available at that moment.
State Transition: State transitions are determined by the current state and action , replicating the dynamics of scheduling. Various states are distinguished by the heterogeneous graph’s structure and characteristics, offering a flexible and robust representation for scheduling. This deterministic transition allows for a clear and predictable evolution of the scheduling environment as decisions are made.
Reward: The reward is determined by the completion time difference between consecutive states and . Specifically, , where represents the maximum completion time. This reward mechanism encourages the agent to complete jobs as quickly as possible, aiming to improve scheduling efficiency and maximize cumulative rewards.
Policy: Policy defines a probability distribution for actions in each state. Through DRL algorithms, policy is parameterized in the form of a neural network to optimize the expected cumulative reward and solve the complex FJSP. The continuous iteration and optimization of the policy allow the agent to make efficient decisions in a versatile production environment, thereby contributing to improved production efficiency.
4.2. Heterogeneous Graph Neural Networks Based on Relation
The nodes in include various types of neighbors for operation node , such as direct predecessor , direct successor , and multiple machine nodes belonging to the set . Specifically, with directed arcs pointing in opposing directions, and are connected to , revealing the sequential dependencies between operations, while machine nodes are associated with it through undirected arcs, demonstrating the pairing relationship between operations and machines. Traditional attention mechanisms struggle to efficiently handle heterogeneous graphs with rich relationship types, and existing methods for heterogeneous graph learning often focus on the propagation of node representations without fully exploring the intrinsic properties of different relationships. To fully exploit the multiple relations in heterogeneous graphs and achieve deep fusion of node features, we design a framework specifically for heterogeneous graphs, i.e., HGNNR, aiming to enhance the identification and utilization of different relationship types, thereby optimizing the quality and granularity of node representations, improving the accuracy and efficiency of scheduling strategy formulation, and providing a more powerful and flexible tool for solving the FJSP.
This component aims to process the heterogeneous graph and the corresponding node feature matrix extracted for any operation node as the target node, ultimately obtaining the updated feature representation for the operation node and for the machine node. It ensures that for any operation node and any machine node , the updated node features have rich information density and relevance, providing precise and detailed feature support for Reinforcement Learning decisions, further enriching the functionality and application scope of the model. As shown in Figure 3, the proposed HGNNR is composed of four stages: (1) Subgraph Decomposition based on Relation, which divides the heterogeneous graph into subgraphs based on different types of relationships, simplifying the complexity of the problem; (2) Preprocessing of Node Features, where original features are transformed into high-dimensional vectors suitable for graph neural network processing; (3) Relation-Specific Graph Convolution, which applies graph convolution to extract and aggregate features specific to each relationship type; and (4) Cross-Relation Feature Fusion, which integrates the features from various subgraphs using a multi-head attention mechanism to generate a comprehensive node representation. The implementation details of these four stages are explained as follows.
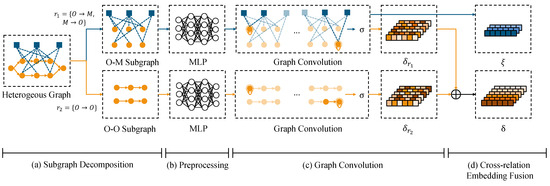
Figure 3.
Feature Extraction Process Using HGNNR.
Subgraph Decomposition based on Relation. Throughout the full manufacturing process, the FJSP consists in complex relationships among several machines and operations. We first divide the many graph representations of FJSP into several subgraphs depending on different kinds of relationships, such as operation–operation (O-O) subgraphs and operation–machine (O-M) subgraphs, so enabling us to fully understand and control these links. Simplifying the heterogeneous graph of the problem is the key component of this decomposition approach since it enables a more targeted and precise investigation and control of many kinds of interactions.
Every node in the O-O subgraph represents a different operation; the edges show the sequential links between these processes. This provides important contextual information for extracting characteristics from operation nodes and helps us to understand and describe the sequence of events in the manufacturing process. We investigate the potential allocation linkages between operations and the currently accessible machines within the O-M subgraph. While edges show the possibility of operations to be carried out on specific machines, nodes are operations and machines. This clarifies for the model the possibilities and constraints of resource allocation and machine choice for every operation.
For further feature extraction and graph structure research, this decomposition technique presents a unique and focused viewpoint. It not only helps to simplify the complexity of the problem but also facilitates the feature extraction and analysis for several kinds of relationships. This prepares the ground strongly for the next phases of the algorithm. Furthermore, this decomposition approach helps us to independently observe and clarify the particular effects of various relationships on scheduling decisions, so enabling a more effective comprehension and improvement of scheduling strategies.
Preprocessing of Node Features. After completing the subgraph decomposition, this stage focuses on transforming the original features of each node into high-dimensional feature vectors suitable for processing by Graph Neural Networks through normalization and feature enhancement mappings. This process not only optimizes the scale and distribution of features but also enhances their expressive power, preparing for capturing deeper graph structural information.
In this stage, the features of all machine nodes and operation nodes are first normalized to ensure a unified numerical range among different features, improving the stability of model training and reducing learning biases due to feature scale differences [27]. Subsequently, we enhance the node features through MLP, which not only learns the nonlinear relationships between features but also maps these features to a higher-dimensional space [46]. For machine nodes, the MLP explores the intrinsic connections and complexity of machine features, providing a comprehensive and representative high-dimensional feature vector. Meanwhile, for operation nodes, the MLP takes into account the intrinsic properties of operation nodes and their potential connections with other nodes, achieving deep enhancement and high-dimensional mapping of operation features.
This preprocessing of features not only enriches and makes the node features more representative but also provides a solid foundation for the subsequent learning and analysis by graph neural networks. Through this process, the model can more effectively understand the roles and interactions of each node in the FJSP, thereby achieving higher accuracy and efficiency in solving scheduling problems.
Relation-Specific Graph Convolution. After preprocessing the node features, the next key step is to perform graph convolution on subgraphs of different relationship types, namely Relation-Specific Graph Convolution. Graph Convolution Network is a powerful neural network architecture that operates directly on graph-structured data and can effectively extract and aggregate features of nodes in the graph [47]. We adopt a generic graph convolution computation method that can adapt to different types of relationships and subgraph structures. For every given relationship type r, the formula below shows the method of updating node characteristics using graph convolution on the corresponding subgraph:
where the node features produced following graph convolution are shown by matrix . By adding adjacency matrix of the subgraph to identity matrix I, we generate matrix . Self-loops in this addition help to maintain the node self-features. Every vertex in graph has a degree shown by matrix . Graph convolution uses weight matrix to retain the parameters. Nonlinearity is introduced and the expressive capacity of the model is increased by means of the Rectified Linear Unit (ReLU) activation function.
Any node can effectively examine input from all connected nodes throughout this process, therefore gathering comprehensive contextual information while preserving its own properties and providing strong support for further optimization and decision-making.
Cross-Relation Feature Fusion. This stage aims to merge node properties from several subgraphs thereby generating a complete node representation. Capturing the complex links among the several diverse network nodes depends on this. Cross-relation feature fusion uses a multi-head attention method to integrate elements from several subgraphs, hence improving the adaptability of the model. This method helps the model to independently learn the significance weights of various subgraph features, hence generating optimal feature representations for every node in several environments [48]. More exactly, for every operation node and subject, we combine the features from the O-O and O-M subgraphs and apply a multi-head attention layer for additional processing. Every head in the model adds a different feature perspective; the weights learnt by each head are aggregated to provide a complete node feature. One may characterize the process of aggregating the outputs from several sources by means of the following equation:
where each head is calculated as follows:
where correspond to query, key, and value derived from linear transformations and splitting into multiple heads. Query (Q) represents the current node’s feature, Key (K) represents the features of nodes connected to it, and Value (V) contains relevant information about nodes used to update the query node’s feature. are parameter matrices corresponding to each head, and is the weight matrix for linear transformation of the outputs of all heads. d is the output dimension of each head, usually determined by the total model dimension L and the number of heads z, i.e., .
In this step, the attention weights calculated for each head provide information about the importance of each head, and by concatenating the outputs of each head and performing the linear transformation, a comprehensive feature representation that incorporates information from all heads is obtained, serving as the updated embedding representation for operation .
This comprehensive node feature representation captures the roles and information of each node under different relationships, providing a comprehensive perspective for the next decision-making step. In this way, the model can consider the execution sequence of operations, the status of machines, and the resource allocation requirements when making decisions, thereby achieving more effective and accurate scheduling in FJSP.
4.3. Pooling
In this study, we adopted a unified pooling strategy, namely mean pooling, for the operation nodes and machine nodes. This approach allows for the model to maintain computational efficiency and model simplicity when processing both types of nodes. Through mean pooling, we can effectively extract global features from the operation nodes and machine nodes , which reflect the average state of the entire system without emphasizing the influence of any specific node.
After extracting features from operation node and machine node , updated operation node features and machine node features are obtained. The heterogeneous graph state is represented by embedding , which is formed by concatenating the two L-dimensional vectors obtained by mean pooling these two features:
A heterogeneous graph of various sizes can be converted into a fixed-dimensional embedding using the procedure described above. We let the set of all HGNNR parameters be .
4.4. Proximal Policy Optimization
In our study, to address the job-shop scheduling problem, we developed a deep learning framework incorporating a policy network that can effectively select operation–machine pairs. The key to this framework lies in utilizing HGNN to extract high-quality embedding representations, which can simplify the state space and facilitate rapid learning of the policy network. To train this network, we employed the PPO algorithm, which utilizes an actor–critic architecture for reinforcement learning.
The policy network accepts the updated features of operation nodes, the updated features of machine nodes, and the global features obtained from mean pooling as inputs, and outputs the probability of selecting the operation–machine pair. Formally, we let be the feature vector for an operation node, be the feature vector for a machine node, and be the global feature vector. The input to the policy network is , and the output is probability for selecting the operation–machine pair .
Next, the actor network applies the softmax function to the probabilities of all operation–machine pairs. During training mode, it uses a sampling strategy to select actions, while in validation and testing modes, the action with the highest probability is chosen directly by using a greedy strategy.
In training mode, actions are sampled from the probability distribution:
In validation and testing modes, the action with the highest probability is selected:
The value function accepts the global feature as input and outputs the value estimate :
The critic network constructs the optimization objective and loss function based on the actions, rewards, and value estimates to perform gradient updates. The goal is to maximize the expected cumulative reward, and the loss function takes into account both the policy loss and the value function loss. The policy loss is defined using the clipped surrogate objective to stabilize training:
where is the probability ratio, is the advantage estimate, and is a hyperparameter controlling the clipping range.
The value function loss is defined as
where is the discounted reward at time t.
The total loss function for PPO is a combination of the policy loss and the value function loss, often with an entropy bonus to encourage exploration:
where the entropy bonus and the loss of the value function are balanced using coefficients and . The entropy of the policy is denoted by expression , which discourages certainty in the choice of behavior hence fostering experimentation.
The system runs constantly throughout the training phase to validate and maximize the policy throughout numerous runs. This approach helps the model to efficiently control the trade-off between exploration and exploitation, thereby optimizing the efficiency in practical workshop scheduling conditions.
5. Experiment
This section aims to show the practical relevance and efficacy of our proposed scheduling system by means of extensive evaluation. We use both synthetic and benchmark datasets to reach this so that we may verify the universality, resilience, and effectiveness of our method throughout several situations. There are multiple subsections in this part, each covering a certain facet of the experimental examination.
We start with Experimental Settings, where we describe synthetic datasets for training and public benchmark datasets for testing. We also outline the several action choosing techniques used in the training and testing stages, thereby balancing the need of exploration during training with the need of best performance during testing. Moreover, we present the reinforcement learning techniques and scheduling guidelines applied as baselines for evaluation using our suggested method.
The impact of three fundamental hyperparameters on the performance of our scheduling system is then investigated using Parameter Sensitivity Analysis. This study clarifies how these factors affect the outcomes and supports the identification of the ideal values for maximizing performance. The results of this study are meant to help readers and other investigators comprehend and reproduce our efforts. All of the next comparison studies are carried out using this ideal parameter setting.
At last, we report Performance Comparison, in which we evaluate our approach against four DRL techniques and three common rule-based heuristic algorithms over four datasets. The data unequivocally show that our strategy constantly beats the others and produces better outcomes in all examined conditions.
5.1. Experimental Settings
Here, we offer a thorough summary of the experimental setup, stressing the main characteristics and setups followed in our investigations. This is a description of the used datasets, including public benchmark datasets used for validation and testing and synthetic datasets created especially for training needs. Along with the training and evaluation strategies applied to guarantee a thorough assessment of our technique, we also describe the hardware environment used for the experiments.
Furthermore, we introduce the baseline methods against which our proposed framework is evaluated. These include four advanced DRL methods and three heuristic scheduling algorithms based on predefined rules. By comparing our method with these approaches, we aim to demonstrate the relative strengths and effectiveness of our scheduling framework.
5.1.1. Evaluation Instances
Following the ideas suggested in [24], we created a sequence of synthetic datasets for training in this work. These datasets guarantee thorough training of the system by covering FJSP events of several scales. The training set consists of three-scale events representing small, medium, and big datasets, respectively: , , and .
The number of operations per job () for the training set is consistently between 4 and 6 for instances and between 8 and 12 for both and . For examples, the number of suitable machines () ranges from 1 to 5; for and , from 1 to 10. For every operation, the processing time () falls consistently between 1 and 20 over all training set scales.
To choose appropriate cases for additional testing, we also thoroughly examined publically accessible datasets. From the Brandimarte dataset suggested in [49], we selected the MK01-10 instances from the Edata, Rdata, and Vdata versions of the Hurink dataset by [50]. This choice guaranteed a wide spectrum of FJSP situations with different issue sizes and operation-to-machine assignment flexibility, therefore strengthening our basis for the assessment of our method.
The described benchmark datasets include MKdata, Edata, Rdata, and Vdata, each of which is used to evaluate the performance of our proposed scheduling framework. As shown in Table 1, MKdata comprises 21 instances with task counts of either 10 or 15, machine counts ranging from 11 to 18, and operations per job between 10 and 15. The processing times in MKdata vary from 5 to 100, with a flexibility range of 1.07 to 1.3. Each of the Edata, Rdata, and Vdata sets consists of 66 instances, with task counts ranging from 6 to 30, machine counts from 4 to 15, and operations per job ranging from 4 to 15. Processing times in these datasets vary from 10 to 100. Specifically, Edata has a flexibility range of 1 to 1.15, Rdata runs from 1 to 2, and Vdata ranges from 1 to 7.5.

Table 1.
Descriptions of Benchmark Instances.
These datasets cover a broad spectrum of FJSP situations, allowing us full assessment under several settings of the generalization and performance capacity of our suggested approach.
5.1.2. Configuration
When developing strategy networks for action selection, there are often two primary methods to consider: a probability-based sampling strategy and a greedy strategy that chooses the action with the highest likelihood. Each of these strategies has its own advantages and is suitable for different scenarios and goals. In this paper, we carefully designed the interaction between the policy network and the environment to utilize the most appropriate strategy during the training and evaluation phases.
During the training phase, we employed a probability-based sampling strategy. This strategy allowed for the policy network to randomly select actions at each decision point based on the current policy’s probability distribution. Although the policy network already shows a preference for some activities, the main goal of using the sample technique is to improve exploration, so offering an option for additional activities to be selected. The policy network’s ability to find and adopt new successful strategies depends critically on the exploration mechanism, which helps to prevent early convergence to inadequate solutions. Following this strategy ensures a broad spectrum of viewpoints and completeness in the training process, therefore enhancing the strength and efficiency of the resulting policy.
We used the greedy strategy in the validation and testing stages, meaning that at every decision point, we regularly selected the action with the highest likelihood. We selected this method to evaluate, in a given environment, the most efficient performance of the trained policy network. By always selecting the actions with the highest confidence, the greedy approach helps us to evaluate the maximum performance that the policy network can obtain in deterministic situations, thereby defining a definite performance criterion. Furthermore, using the greedy approach during the assessment process reduces the degree of uncertainty in the results, thereby producing a more consistent and similar performance. This approach ensures that, in practical applications or next research, we may exactly measure and understand the capacity of the trained policy network.
By means of a sampling strategy for exploration during the training phase and a greedy technique for performance benchmarking during the validation and testing phases, we essentially constructed a policy network that effectively learns and can be appropriately evaluated. Aiming to balance exploration and exploitation, the selection of this approach is one of the cores of the policy network design in this study, ensuring that the policy network can achieve efficient learning in complicated environments and show outstanding performance.
The entire evaluation was carried out on a PC running 64-bit Ubuntu 22.04, equipped with an Intel Core i5-12600KF, 32GB RAM, and an Nvidia GeForce RTX 2060 GPU.
5.1.3. Baselines
In this study, to comprehensively evaluate the performance of the proposed scheduling framework, we compared it with various methods widely recognized and applied in both industry and academia. These comparative methods include an efficient constraint solver, four classical PDR, multiple genetic algorithm variants, and several latest DRL-based techniques. Such comparisons aim to demonstrate the advantages and applicability of our method in handling complex scheduling problems, particularly achieving a good balance between optimization capability and applicability. Specific comparative methods include:
- FIFO + EET (First In First Out + Earliest End Time): This strategy first schedules jobs in the order they arrive (FIFO). Then, it assigns operations to the machine that can complete the task the earliest (EET).
- MWKR + EET (Most Work Remaining + Earliest End Time): This method prioritizes jobs with the most remaining work (MWKR). After selecting a job, it uses EET to assign the machine that can finish the operation the earliest.
- MOPNR + EET (Most Operations Not Ready + Earliest End Time): This approach first selects jobs with the fewest remaining operations (MOPNR). Then, it applies EET to choose the machine that can complete the current operation soon.
- Ref. [41]: A 3D discrete graph-based DRL framework is presented in this paper. It encodes and decodes the FJSP using an improved pointer network combined with attention mechanisms. The pointer network maps sequences to sequences through an encoder–decoder architecture and GRU RNN, while the attention mechanism dynamically adjusts the model’s focus at each decoding step to different parts of the input.
- Ref. [23]: This article uses a disjunctive graph for state representation and employs a multi-pointer graph network (MPGN) for state feature extraction, consisting of two encoder–decoder components. The job operation action policy and machine action policy are learned through the multi-Proximal Policy Optimization (multi-PPO) algorithm, optimizing the model parameters to handle FJSP instances effectively.
- Ref. [43]: This article proposes a disjunctive graph for state representation and graph neural networks (GNNs) for state feature extraction. An MLP and scheduling rules are used for action selection. The asynchronous advantage actor–critic (A3C) algorithm optimizes the model parameters.
- Ref. [51]: This article proposes an actor–critic framework, with a dynamic action space of parameterized priority rules. The state representation incorporates characteristics such as the utilization of machines and the rates at which jobs are completed, while the reward function is designed to reflect the average machine utilization and work completion rate in order to direct the learning process.
5.2. Parameter Sensitivity Analysis
In this section, we apply a thorough analysis of parameter sensitivity to assess the influence of three crucial factors on the effectiveness of our model in solving the FJSP. The parameters encompass the learning rate, the number of heads in the multi-head attention mechanism, and the output feature vector dimension of the HGNNR. The makespan is observed by methodically varying each parameter, which provides insights into how these factors influence the model’s ability to properly capture and utilize the deep relationships within the data. We smoothed the original data to help with observation and study of these impacts. The lighter-colored lines in the comparison curves below show the raw data; the darker-colored lines show the smoothed data, therefore highlighting the trends and simplifying their interpretation. This study helps in determining the ideal configurations that strike a balance between model intricacy and performance. Ultimately, we compile the primary hyperparameters employed in our trials, drawing from the results of this sensitivity analysis.
Figure 4 shows the influence of different learning rates on makespan for solving the FJSP across various training set sizes. For all training set sizes, an excessively high learning rate (e.g., ) leads to poor model convergence and suboptimal performance. As the learning rate decreases (e.g., and ), performance improves significantly, indicating that the model can learn patterns in the heterogeneous graph more stably. However, when the learning rate is further reduced to or , performance declines again, suggesting that an overly low learning rate slows down the training process, preventing the model from learning effectively. This trend is consistent across all training set sizes, with a learning rate of showing the best performance, particularly for large training sets. In summary, selecting an appropriate learning rate is crucial for optimizing the model’s performance in solving the FJSP. A moderate learning rate ensures effective learning and stable training, while both excessively high and low learning rates negatively impact the model’s final performance.
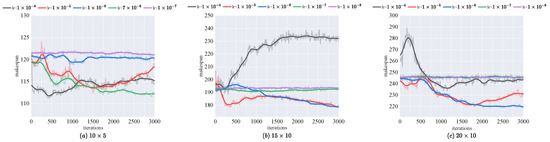
Figure 4.
Performance of various learning rates on different training datasets.
Figure 5 demonstrates the impact of the number of heads in the multi-head attention mechanism on makespan for solving the FJSP across various training set sizes. For all training set sizes, using a single head leads to suboptimal performance, indicating that the model is unable to effectively capture the complex interactions of nodes in the entire heterogeneous graph. As the number of heads increases (e.g., 2, 4, and 8), performance improves significantly, suggesting that the model benefits from the enhanced capability to attend to different aspects of the heterogeneous graph simultaneously. However, when the number of heads is further increased to 16, performance declines, likely due to the overfitting or increased complexity that hampers the model’s ability to generalize. This trend is consistent across all training set sizes, with 8 heads showing the best performance, particularly for larger training sets. In summary, selecting an appropriate number of heads in the multi-head attention mechanism is crucial for optimizing the model’s performance in solving the FJSP. A moderate number of heads ensures effective learning and better capturing of data dependencies, while both too few and too many heads negatively impact the model’s final performance.
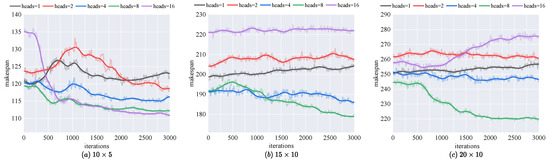
Figure 5.
Performance of various numbers of heads on different training datasets.
Figure 6 illustrates the impact of the output feature vector dimension of the HGNNR on makespan for solving the FJSP across various training set sizes. When the dimension is set to 8, the model’s performance is suboptimal, as it struggles to capture the complexity of the data. Increasing the dimension to 16, 32, and 64 leads to significant performance improvements, indicating that a higher-dimensional feature space allows for the model to better represent and utilize the data’s intricate relationships. However, further increasing the dimension to 128 results in a decline in performance, likely due to overfitting or increased computational complexity that hinders generalization. This trend is consistent across all training set sizes, with a dimension of 64 showing the best performance, particularly for larger datasets. Choosing the right output feature vector dimension for HGNNR is essential for maximizing the model’s effectiveness in solving the FJSP. An optimal dimension size facilitates efficient learning and accurately captures data dependencies. Conversely, dimensions that are either too small or too large have a detrimental influence on the model’s overall performance.
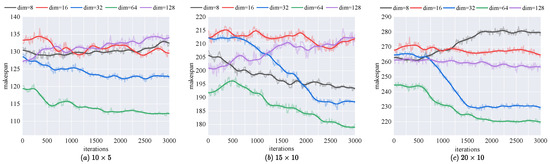
Figure 6.
Performance of various dimensions of actor and critic on different training datasets.
The main hyperparameters used in our experiments to solve the FJSP are compiled in Table 2. With a focus on achieving the highest potential performance of the model, the choices of these hyperparameters were guided by the results of our extensive study on parameter sensitivity. The parameters include the learning rate, discount factor, clip ratio, coefficients for policy and value loss, input and hidden dimensions of the actor and critic networks, optimizer, maximum iterations, embedding dimension, and the number of heads in the multi-head attention mechanism. The precise selection of these hyperparameters significantly enhanced the overall robustness and efficiency of our FJSP system. Furthermore, the subsequent comparative experiments were all conducted based on this optimal set of hyperparameters, ensuring that the results are both replicable and comprehensible for readers and researchers.

Table 2.
The main hyperparameters of the experiment.
5.3. Performance Comparison
This part aims to assess the efficacy of our proposed scheduling framework by means of a comparison of many scheduling techniques over four different datasets: Brandimarte, Hurink (Rdata), Hurink (Edata), and Hurink (Vdata). The greatest completion time of all the jobs in any instance——represents a fundamental metric employed in this comparison. The efficiency of scheduling methods depends on this statistic. The tables show the percentage difference between the answer our model offers and the upper bound (UB), theoretically optimal or best-known solution for every instance. Reflecting the quantity and complexity of the synthetic data used for training, the word “ours ” denotes our model trained on a synthetic dataset with a configuration. Furthermore, in the tables, the bolded values show the best makespan—that is, the lowest —attained among all the approaches for a particular case. This highlights the cases when our model reduces the maximum completion time and shows its excellence over the other techniques.
In the Brandimarte dataset (Table 3), our proposed model, particularly the configuration, achieves the lowest average makespan () of 197.5 and the smallest optimality gap of 14.36%. This performance significantly outperforms other DRL-based methods and rule-based heuristic methods, demonstrating the model’s robustness and efficiency across various problem instances. The model excels in providing near-optimal solutions consistently.

Table 3.
Performance comparison on the Brandimarte dataset.
In the Hurink (Rdata) dataset (Table 4), our model maintains superior performance with the configuration, achieving an average makespan of 1058.78 and an optimality gap of 13.33%. This again surpasses other DRL-based methods and heuristic methods. The heuristic methods exhibit higher makespans and gaps, underscoring the effectiveness of our DRL approach in solving complex scheduling problems more efficiently.

Table 4.
Performance comparison on the Hurink dataset (Rdata).
For the Hurink (Edata) dataset (Table 5), our DRL-based methods demonstrate strong performance, with the configuration achieving an average makespan of 1212.40 and an optimality gap of 17.84%. Although heuristic methods show some competitiveness in individual instances, they generally fall behind our proposed models in both makespan and optimality gap, indicating the robustness of our methods.

Table 5.
Performance comparison on the Hurink dataset (Edata).
In the Hurink (Vdata) dataset (Table 6), our configuration achieves the lowest average makespan of 963.73 and the smallest optimality gap of 4.81%. This dataset further confirms the superior performance of our proposed methods compared to heuristic methods, which display higher makespans and larger gaps. The consistency across different instances highlights our model’s adaptability and precision in scheduling.

Table 6.
Performance comparison on the Hurink dataset (Vdata).
The model trained on a dataset with size of consistently outperforms all other datasets, which is a noteworthy result. This shows that the design efficiently generalizes over many instances of the problem since it reaches an ideal equilibrium between the complexity of the model and the size of the training data. The consistent performance of our suggested method shows its capacity to efficiently adjust to several scheduling difficulties.
Moreover, the experimental plan used in this work makes use of publicly accessible databases for testing and generated data for training. This environment provides significant proof to justify the general relevance of our suggested scheduling approach in several situations. The robustness of our proposed approach in generalizing to other scenarios is shown by the good performance of our model in publicly accessible datasets, which deviate from the artificially produced training data. This ensures that the model can adequately manage a varied variety of real-world scheduling problems rather than only overfitting to the contrived data.
All things considered, our study of performance on the Brandimarte and Hurink datasets (Rdata, Edata, Vdata) shows that the solutions we propose often outperform existing methods dependent on DRL and rule-based heuristics. Our models show a better degree of precision and dependability in generating almost perfect solutions for different scheduling problems since they often offer solutions with shorter average makespans and lesser optimality gap. The results show the possibility of our proposed solutions in maximizing difficult scheduling activities with higher efficiency and effectiveness than current heuristic solutions. Furthermore underlining the strength and versatility of our scheduling concept are the repeated success of the arrangement and the exhibited ability to use synthetic training data for public testing datasets.
5.4. Average Scheduling Time Analysis
This part aims to investigate, over datasets of different scales, the average scheduling time of the proposed scheduling model. This study seeks to offer understanding of how the performance of the model scales with data amount and complexity. The generated datasets for this work follow a technique described in [24]. Six separate scales comprise these datasets: , , , , , and . Every dataset has 50 cases; the average number of operations across all the datasets is roughly 50, 100, 150, 200, 300, and 400, respectively. To estimate the average scheduling time needed for every scale, we evaluated the suggested scheduling model on these six datasets. This study clarifies how the computational requirements of the model rise in scale and complexity of the scheduling problem.
With rows representing models trained on datasets of diverse scales and columns corresponding to different test datasets, Table 7 below shows the average scheduling times for several models. For the corresponding model on the given test set, every cell has the average scheduling time—in seconds. Under each dataset, the bolded numbers show the shortest scheduling time among the three models, so emphasizing the model with most efficiency under those particular circumstances.

Table 7.
Average scheduling time for different models among various datasets (unit: s).
Table 7 shows that the model trained on the dataset not only exhibits one of the shortest average scheduling times over the other test datasets but also displays the greatest performance in terms of scheduling efficiency. This emphasizes the better performance of our suggested model, which effectively balances fast computation times with good scheduling efficiency. The model keeps this balance even with before-unheard-of data, therefore highlighting its dependability and resilience in several scheduling conditions.
As the dataset size rises, the observed scheduling times show a nearly linear rise. This pattern implies that, without a disproportionate rise in computing complexity, the suggested approach preserves good efficiency while scaling to bigger datasets.
Furthermore, the constantly short scheduling times—all less than one second—show that the model can react in real-time in useful manufacturing environments. In settings where quick decisions are required to maximize manufacturing processes and reduce delays, this degree of performance is absolutely vital. The model fits for pragmatic uses since its average scheduling time falls within a reasonable range.
Although the existing results show promise, more optimization is feasible. Further reduction in scheduling times and increase in the applicability of the model in even more demanding manufacturing environments would be by upgrading the hardware (e.g., using higher-performance GPUs) or by sharping the algorithm (e.g., including more efficient graph processing techniques or parallel computation).
6. Conclusions
This study proposes a novel method to solve the FJSP by integrating the HGNNR and DRL. This method not only considers the complex dependencies between operations but also fully explores the connections between operations and machines, thereby achieving efficient and flexible task allocation and resource optimization in a complex production scheduling environment.
Our experimental results demonstrate that this method performs well on FJSP instances of different scales, showing superior scheduling efficiency and lower maximum completion times compared to traditional scheduling algorithms and some existing advanced methods. Furthermore, we find that through the continuous learning capability of DRL, this method can continuously optimize scheduling strategies, adapt to changes in the production environment, and quickly find near-optimal solutions on unknown new instances, ultimately achieving a delicate balance between algorithm performance, solution efficiency, and generalization ability.
Overall, our research not only expands the theoretical solutions to FJSP but also provides strong technical support for practical production scheduling. Considering that the heterogeneous graph in the scheduling process is constantly evolving and HGNNR possesses a certain capability to handle dynamic events, we will explore the potential of HGNNR in real-world applications by investigating its ability to manage dynamic changes in operation priorities, machine statuses, and random task arrivals, extending the applicability of our approach to dynamic and unpredictable production environments in the future. Additionally, we will further investigate special constraints in actual production scenarios and explore research on multiple optimization objectives to comprehensively improve production efficiency. We plan to delve deeper into the integration of HGNNR and DRL to enhance the model’s generalization ability and its capability to solve more complex scheduling problems, thus driving the realization of intelligent manufacturing and Industry 4.0 and achieving the goal of intelligent, automated, and efficient production management.
Author Contributions
Conceptualization, H.T. and J.D.; methodology, J.D.; software, J.D.; validation, H.T. and J.D.; formal analysis, H.T. and J.D.; investigation, J.D.; resources, H.T.; data curation, J.D.; writing—original draft preparation, H.T. and J.D.; writing—review and editing, H.T. and J.D.; visualization, J.D.; supervision, H.T.; project administration, H.T.; funding acquisition, H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Outstanding Young Science and Technology Worker of Science and Technology Projects in Tongzhou District (Beijing (JCQN2024007)), the General Program of Science and Technology Development Project of Beijing Municipal Education Commission of China (KM202410037005) and the School level Youth Research Fund Project (2024XJQN22).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support this research are available from the corresponding author upon request.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FJSP | Flexible Job-shop Scheduling Problem |
| DRL | Deep Reinforcement Learning |
| GNN | Graph Neural Network |
| HGNNR | Heterogeneous Graph Neural Network based on Relation |
| PPO | Proximal Policy Optimization |
| MDP | Markov Decision Process |
| MILP | Mixed-Integer Linear Programming |
| GA | Genetic Algorithm |
| MLP | Multi-Layer Perceptron |
| A3C | Asynchronous Advantage Actor–Critic |
| GIN | Graph Isomorphism Network |
| PDRs | Priority Dispatching Rules |
| JSSP | Job Shop Scheduling Problem |
| HGNN | Heterogeneous Graph Neural Network |
| GCN | Graph Convolutional Network |
References
- Attaran, M.; Attaran, S.; Celik, B.G. The impact of digital twins on the evolution of intelligent manufacturing and Industry 4.0. Adv. Comput. Intell. 2023, 3, 11. [Google Scholar] [CrossRef] [PubMed]
- Oztemel, E.; Gursev, S. Literature review of Industry 4.0 and related technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- Cañas, H.; Mula, J.; Díaz-Madroñero, M.; Campuzano-Bolarín, F. Implementing industry 4.0 principles. Comput. Ind. Eng. 2021, 158, 107379. [Google Scholar] [CrossRef]
- Frank, A.G.; Dalenogare, L.S.; Ayala, N.F. Industry 4.0 technologies: Implementation patterns in manufacturing companies. Int. J. Prod. Econ. 2019, 210, 15–26. [Google Scholar] [CrossRef]
- Cannavacciuolo, L.; Ferraro, G.; Ponsiglione, C.; Primario, S.; Quinto, I. Technological innovation-enabling industry 4.0 paradigm: A systematic literature review. Technovation 2023, 124, 102733. [Google Scholar] [CrossRef]
- Xue, F.; Tang, H.; Su, Q.; Li, T. Task allocation of intelligent warehouse picking system based on multi-robot coalition. KSII Trans. Internet Inf. Syst. (TIIS) 2019, 13, 3566–3582. [Google Scholar]
- Nwasuka, N.C.; Uchechukwu, N. Computer-based Production Planning, Scheduling and Control: A Review. J. Eng. Res. 2023, 12, 275–280. [Google Scholar] [CrossRef]
- Luan, F.; Li, R.; Liu, S.Q.; Tang, B.; Li, S.; Masoud, M. An improved sparrow search algorithm for solving the energy-saving flexible job shop scheduling problem. Machines 2022, 10, 847. [Google Scholar] [CrossRef]
- Li, X.; Guo, X.; Tang, H.; Wu, R.; Wang, L.; Pang, S.; Liu, Z.; Xu, W.; Li, X. Survey of integrated flexible job shop scheduling problems. Comput. Ind. Eng. 2022, 174, 108786. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, S.; Yang, B.; He, Y.; Pang, Z.; Gao, Y. A coupling optimization method of production scheduling and logistics planning for product processing-assembly workshops with multi-level job priority constraints. Comput. Ind. Eng. 2024, 190, 110014. [Google Scholar] [CrossRef]
- Chitgar, N.; Jazayeriy, H.; Rabiei, M. Improving cloud computing performance using task scheduling method based on vms grouping. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; pp. 2095–2099. [Google Scholar]
- Nouiri, M.; Bekrar, A.; Trentesaux, D. An energy-efficient scheduling and rescheduling method for production and logistics systems. Int. J. Prod. Res. 2020, 58, 3263–3283. [Google Scholar] [CrossRef]
- Ceylan, Z.; Tozan, H.; Bulkan, S. A coordinated scheduling problem for the supply chain in a flexible job shop machine environment. Oper. Res. 2021, 21, 875–900. [Google Scholar] [CrossRef]
- Al Aqel, G.; Li, X.; Gao, L. A modified iterated greedy algorithm for flexible job shop scheduling problem. Chin. J. Mech. Eng. 2019, 32, 21. [Google Scholar] [CrossRef]
- Xie, J.; Gao, L.; Peng, K.; Li, X.; Li, H. Review on flexible job shop scheduling. IET Collab. Intell. Manuf. 2019, 1, 67–77. [Google Scholar] [CrossRef]
- Stanković, A.; Petrović, G.; Ćojbašić, Ž.; Marković, D. An application of metaheuristic optimization algorithms for solving the flexible job-shop scheduling problem. Oper. Res. Eng. Sci. Theory Appl. 2020, 3, 13–28. [Google Scholar] [CrossRef]
- Türkyılmaz, A.; Şenvar, Ö.; Ünal, İ.; Bulkan, S. A research survey: Heuristic approaches for solving multi objective flexible job shop problems. J. Intell. Manuf. 2020, 31, 1949–1983. [Google Scholar] [CrossRef]
- Bożejko, W.; Uchroński, M.; Wodecki, M. Parallel hybrid metaheuristics for the flexible job shop problem. Comput. Ind. Eng. 2010, 59, 323–333. [Google Scholar] [CrossRef]
- Elsayed, E.K.; Elsayed, A.K.; Eldahshan, K.A. Deep reinforcement learning-based job shop scheduling of smart manufacturing. Comput. Mater. Contin. 2022, 73, 5103–5120. [Google Scholar]
- Mousavi, S.S.; Schukat, M.; Howley, E. Deep reinforcement learning: An overview. In Proceedings of SAI Intelligent Systems Conference (IntelliSys) 2016: Volume 2; Springer: Berlin/Heidelberg, Germany, 2018; pp. 426–440. [Google Scholar]
- Zhang, J.; Ding, G.; Zou, Y.; Qin, S.; Fu, J. Review of job shop scheduling research and its new perspectives under Industry 4.0. J. Intell. Manuf. 2019, 30, 1809–1830. [Google Scholar] [CrossRef]
- Hu, H.; Jia, X.; He, Q.; Fu, S.; Liu, K. Deep reinforcement learning based AGVs real-time scheduling with mixed rule for flexible shop floor in industry 4.0. Comput. Ind. Eng. 2020, 149, 106749. [Google Scholar] [CrossRef]
- Lei, K.; Guo, P.; Zhao, W.; Wang, Y.; Qian, L.; Meng, X.; Tang, L. A multi-action deep reinforcement learning framework for flexible Job-shop scheduling problem. Expert Syst. Appl. 2022, 205, 117796. [Google Scholar] [CrossRef]
- Song, W.; Chen, X.; Li, Q.; Cao, Z. Flexible job-shop scheduling via graph neural network and deep reinforcement learning. IEEE Trans. Ind. Inform. 2022, 19, 1600–1610. [Google Scholar] [CrossRef]
- Munikoti, S.; Agarwal, D.; Das, L.; Halappanavar, M.; Natarajan, B. Challenges and opportunities in deep reinforcement learning with graph neural networks: A comprehensive review of algorithms and applications. IEEE Trans. Neural Netw. Learn. Syst. 2023. Early Access. [Google Scholar] [CrossRef] [PubMed]
- Almasan, P.; Suárez-Varela, J.; Rusek, K.; Barlet-Ros, P.; Cabellos-Aparicio, A. Deep reinforcement learning meets graph neural networks: Exploring a routing optimization use case. Comput. Commun. 2022, 196, 184–194. [Google Scholar] [CrossRef]
- Park, J.; Chun, J.; Kim, S.H.; Kim, Y.; Park, J. Learning to schedule job-shop problems: Representation and policy learning using graph neural network and reinforcement learning. Int. J. Prod. Res. 2021, 59, 3360–3377. [Google Scholar] [CrossRef]
- Cao, Z.; Deng, X.; Yue, S.; Jiang, P.; Ren, J.; Gui, J. Dependent Task Offloading in Edge Computing Using GNN and Deep Reinforcement Learning. IEEE Internet Things J. 2024, 11, 21632–21646. [Google Scholar] [CrossRef]
- Huang, J.P.; Gao, L.; Li, X.Y. An end-to-end deep reinforcement learning method based on graph neural network for distributed job-shop scheduling problem. Expert Syst. Appl. 2024, 238, 121756. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, C.; Shao, X.; Ren, Y. MILP models for energy-aware flexible job shop scheduling problem. J. Clean. Prod. 2019, 210, 710–723. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, C.; Ren, Y.; Zhang, B.; Lv, C. Mixed-integer linear programming and constraint programming formulations for solving distributed flexible job shop scheduling problem. Comput. Ind. Eng. 2020, 142, 106347. [Google Scholar] [CrossRef]
- Özgüven, C.; Özbakır, L.; Yavuz, Y. Mathematical models for job-shop scheduling problems with routing and process plan flexibility. Appl. Math. Model. 2010, 34, 1539–1548. [Google Scholar] [CrossRef]
- Huang, B.; Sun, Y.; Sun, Y. Scheduling of flexible manufacturing systems based on Petri nets and hybrid heuristic search. Int. J. Prod. Res. 2008, 46, 4553–4565. [Google Scholar] [CrossRef]
- Sobeyko, O.; Mönch, L. Heuristic approaches for scheduling jobs in large-scale flexible job shops. Comput. Oper. Res. 2016, 68, 97–109. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, G.; Pan, R.; Ge, H. A novel heuristic method for the energy-efficient flexible job-shop scheduling problem with sequence-dependent set-up and transportation time. Eng. Optim. 2022, 54, 1646–1667. [Google Scholar] [CrossRef]
- Ziaee, M. A heuristic algorithm for the distributed and flexible job-shop scheduling problem. J. Supercomput. 2014, 67, 69–83. [Google Scholar] [CrossRef]
- Driss, I.; Mouss, K.N.; Laggoun, A. An effective genetic algorithm for the flexible job shop scheduling problems. In Proceedings of the 11th Congres Int. de Genine Industriel–CIGI2015, Quebec, QC, Canada, 26–28 October 2015; pp. 26–28. [Google Scholar]
- Rooyani, D.; Defersha, F.M. An efficient two-stage genetic algorithm for flexible job-shop scheduling. IFAC-PapersOnLine 2019, 52, 2519–2524. [Google Scholar] [CrossRef]
- Xie, J.; Li, X.; Gao, L.; Gui, L. A hybrid genetic tabu search algorithm for distributed flexible job shop scheduling problems. J. Manuf. Syst. 2023, 71, 82–94. [Google Scholar] [CrossRef]
- Elsayed, A.K.; Elsayed, E.K.; Eldahshan, K.A. Deep reinforcement learning based actor-critic framework for decision-making actions in production scheduling. In Proceedings of the 2021 Tenth International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 5–7 December 2021; pp. 32–40. [Google Scholar]
- Han, B.; Yang, J. A deep reinforcement learning based solution for flexible job shop scheduling problem. Int. J. Simul. Model. 2021, 20, 375–386. [Google Scholar] [CrossRef]
- Yuan, E.; Wang, L.; Cheng, S.; Song, S.; Fan, W.; Li, Y. Solving flexible job shop scheduling problems via deep reinforcement learning. Expert Syst. Appl. 2023, 245, 123019. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, X.; Bai, C. A Deep Reinforcement Learning Approach to Flexible Job Shop Scheduling. In Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic, 9–12 October 2022; pp. 884–890. [Google Scholar]
- Zhang, C.; Song, W.; Cao, Z.; Zhang, J.; Tan, P.S.; Chi, X. Learning to dispatch for job shop scheduling via deep reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 1621–1632. [Google Scholar]
- Fattahi, P.; Saidi Mehrabad, M.; Jolai, F. Mathematical modeling and heuristic approaches to flexible job shop scheduling problems. J. Intell. Manuf. 2007, 18, 331–342. [Google Scholar] [CrossRef]
- Liu, C.L.; Huang, T.H. Dynamic job-shop scheduling problems using graph neural network and deep reinforcement learning. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6836–6848. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, T.; Li, Y.; Zhang, Y.; Wu, F. Multi-modality cross attention network for image and sentence matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10941–10950. [Google Scholar]
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
- Hurink, J.; Jurisch, B.; Thole, M. Tabu search for the job-shop scheduling problem with multi-purpose machines. Oper. 1994, 15, 205–215. [Google Scholar] [CrossRef]
- Zhao, C.; Deng, N. An actor-critic framework based on deep reinforcement learning for addressing flexible job shop scheduling problems. Math. Biosci. Eng. 2024, 21, 1445–1471. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).