From Innovation to Standardization—A Century of Rolling Bearing Life Formula
Abstract
1. Introduction
2. General Considerations
3. Life Theory Was Born
4. The Paper “Die Lebensdauer von Kugellagern” by N.A. Palmgren [1]
4.1. Life Function
4.2. Equivalent Radial Load
4.3. Variable Load
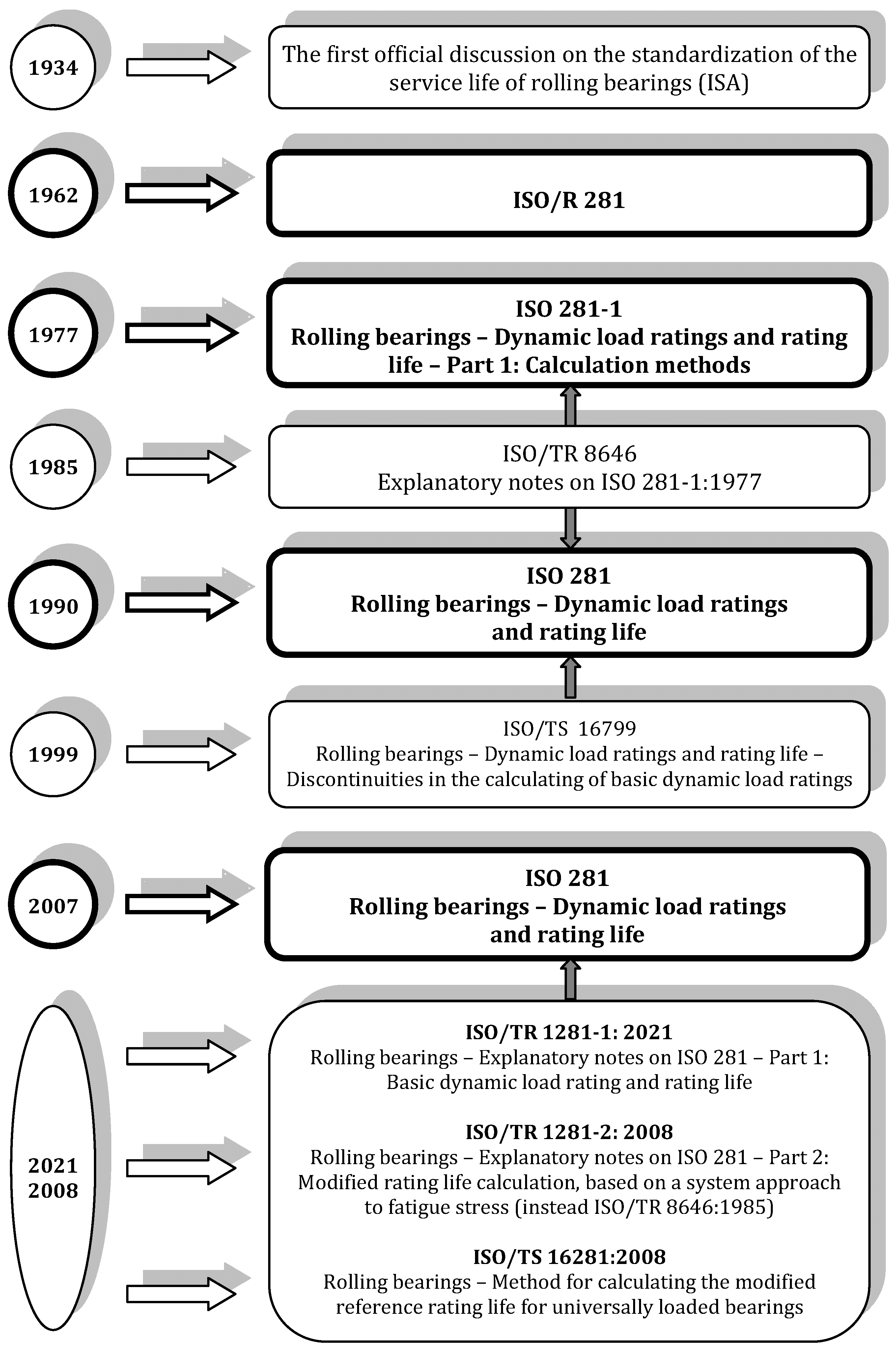
5. ISO
5.1. History
5.2. ISO Technical Committee TC 4, Subcommittee SC 8
- ISO 76:2006 “Rolling bearings—static load ratings”
- ISO 76:2006/AMD 1:2007 “Rolling bearings—Static load ratings—Amendment 1”
- ISO 1281-1:2007 “Rolling bearings—Dynamic load ratings and rating life”
- ISO/TR 1281-1:2021 “Rolling bearings—Explanatory notes on ISO 281—Part 1: Basic dynamic load rating and basic rating life”
- ISO/TR 1281-2:2008 “Rolling bearings—Explanatory notes on ISO 281—Part 2: Modified rating life calculation, based on a systems approach to fatigue stresses”
- ISO/TR 1281-2:2008/COR 1:2009 “Rolling bearings—Explanatory notes on ISO 281—Part 2: Modified rating life calculation, based on a systems approach to fatigue stresses—Technical Corrigendum 1”
- ISO/TR 10657:2021 “Explanatory notes on ISO 76”;
- ISO 14728-1:2017 “Rolling bearings—Linear motion rolling bearings—Part 1: Dynamic load ratings and rating life”
- ISO 14728-2:2017 “Rolling bearings—Linear motion rolling bearings—Part 2: Static load ratings”
- ISO 15312:2018 “Rolling bearings—Thermal speed rating—Calculation”
- ISO/TS 16281:2008 “Rolling bearings—Methods for calculating the modified reference rating life for universally loaded bearings”
- ISO/TS 16281:2008/COR 1:2009 “Rolling bearings—Methods for calculating the modified reference rating life for universally loaded bearings—Technical Corrigendum 1”
- ISO 20015:2017 “Spherical plain bearings—Method for the calculation of static and dynamic load ratings”
- ISO/TR 20051:2020 “Spherical plain bearings—Derivation of the load rating factors”;
- ISO 20056-1:2017 “Rolling bearings—Load ratings for hybrid bearings with rolling elements made of ceramic—Part 1: Dynamic load ratings”
- ISO 20056-2:2017 “Rolling bearings—Load ratings for hybrid bearings with rolling elements made of ceramic—Part 2: Static load ratings”
- ISO/DIS 16281 Rolling bearings—Methods for calculating the modified reference rating life for universally loaded rolling bearings
- ISO/DIS 17956 Rolling bearings—Method for calculating the effective static safety factor for universally loaded rolling bearings
- ISO/AWI TR 25165 10657 Rolling Bearings—Method for calculating the rating life with additional consideration of surface distress
5.3. Evolution of the ISO 281 Standard
- ISO 281:1990/AMD 1:2000 “Rolling bearings—Dynamic load ratings and rating life—Amendment 1”
- ISO/281:1990/AMD 2:2000 “Rolling bearings—Dynamic load ratings and rating life—Amendment 2: Life modification factor aXYZ”.
- ISO/TR 1281-1:2021 “Explanatory notes on ISO 281—Part 1: Basic dynamic load rating and basic rating life”
- ISO/TR 1281-2:2008 “Explanatory notes on ISO 281—Part 2: Modified rating life calculation, based on a systems approach to fatigue stresses”.
- determining the reliability modification factor a1 and the modification factor of systems approach aISO
- presentation of the contamination level of lubricants from the ISO 4466 standard, applied in ISO 281
- impact of wear
- the influence of the corrosive environment on the service life of the bearing
- the fatigue load limit of the bearing
- influence of circular stress, temperature, and hardness of contamination particles on the service life of the bearing
- determination of lubricant viscosity parameters
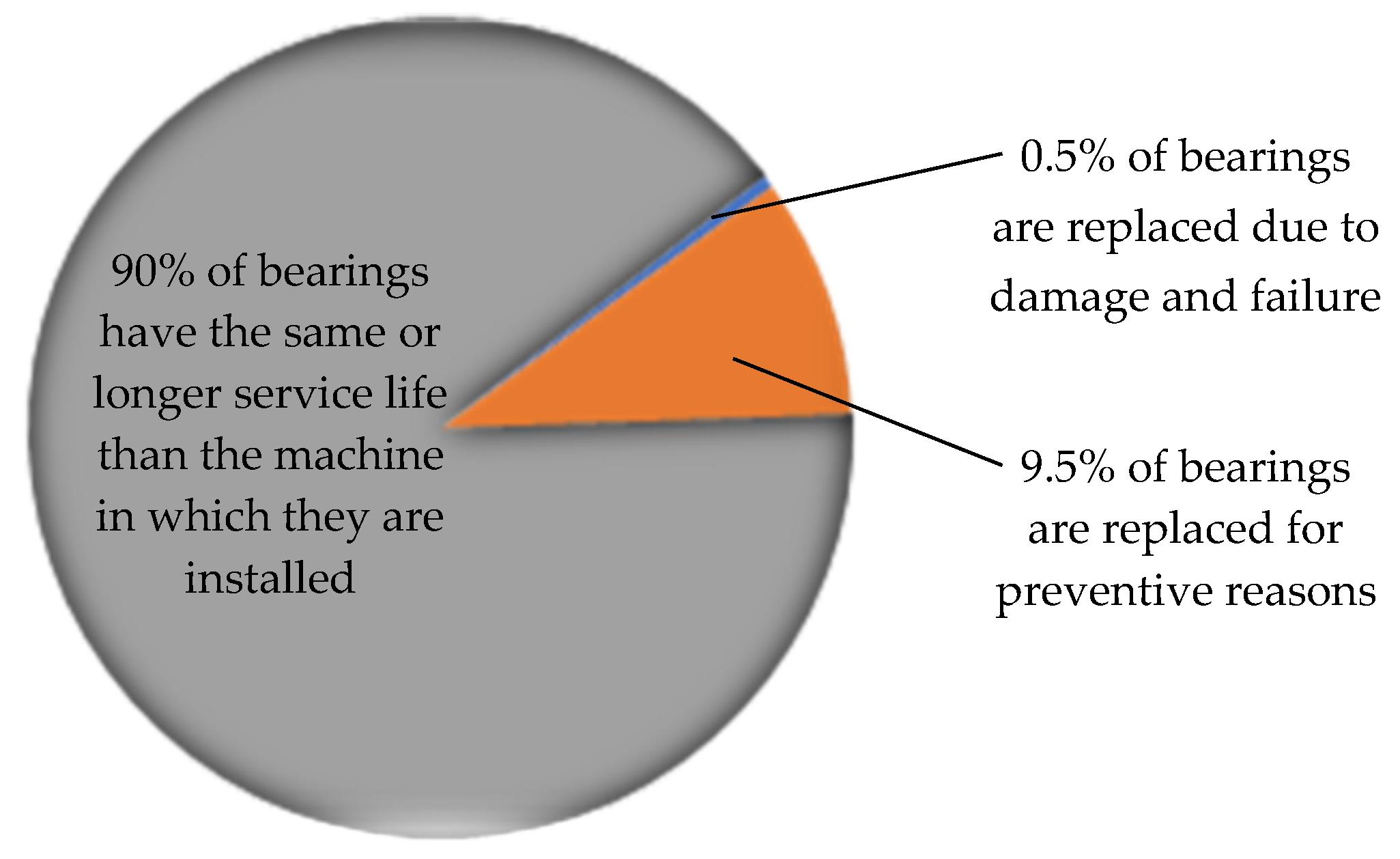
6. Briefly about the Rolling Bearings Service Life
6.1. Causes of Rolling-Bearing Failures
6.2. A Stochastic Approach to Service Life Estimation
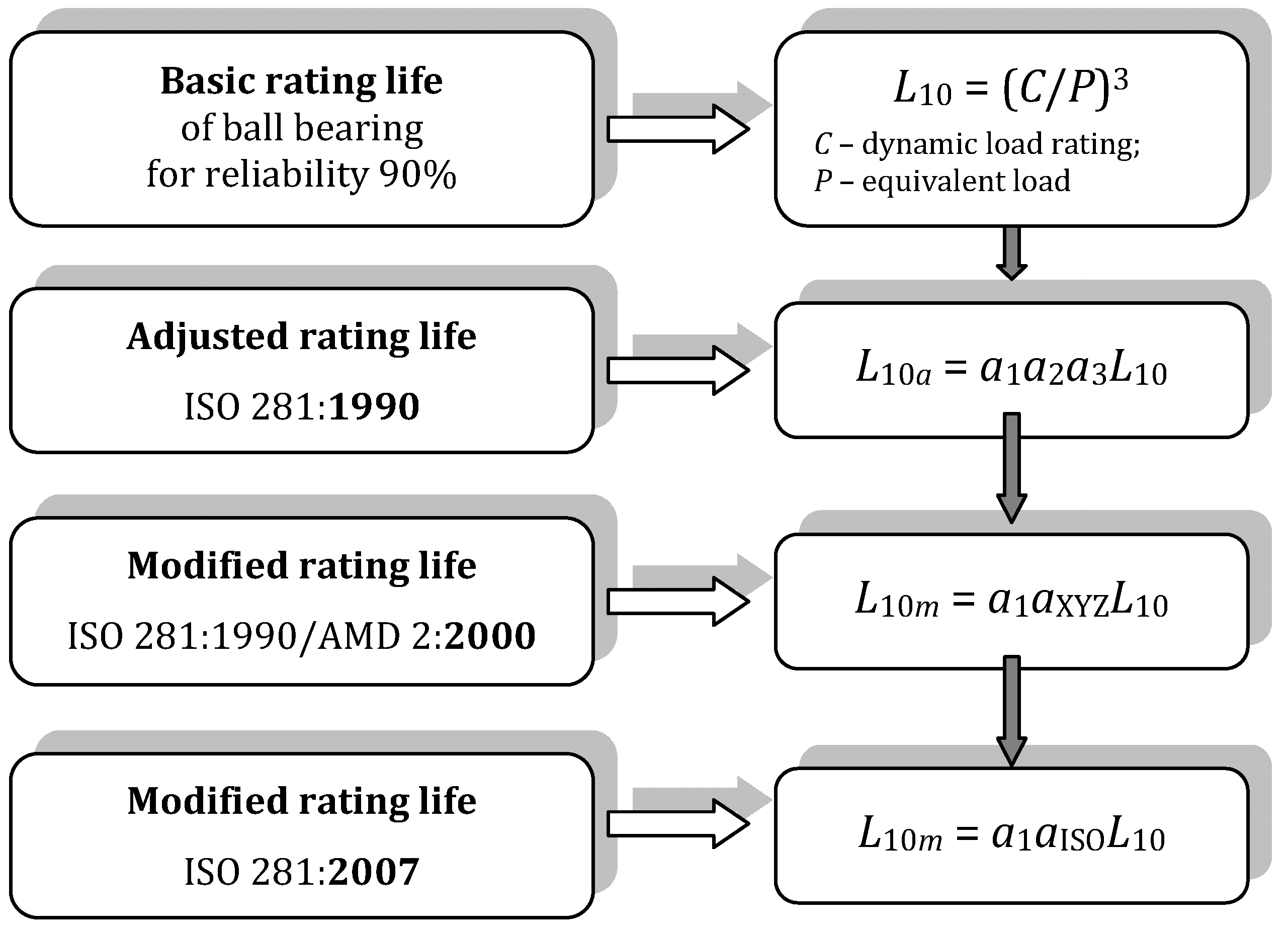
6.3. Basic Rating Life
6.3.1. Dynamic Load Rating
6.3.2. Dynamic Equivalent Load
6.4. Modified Rating Life
6.4.1. Modification Factor a1
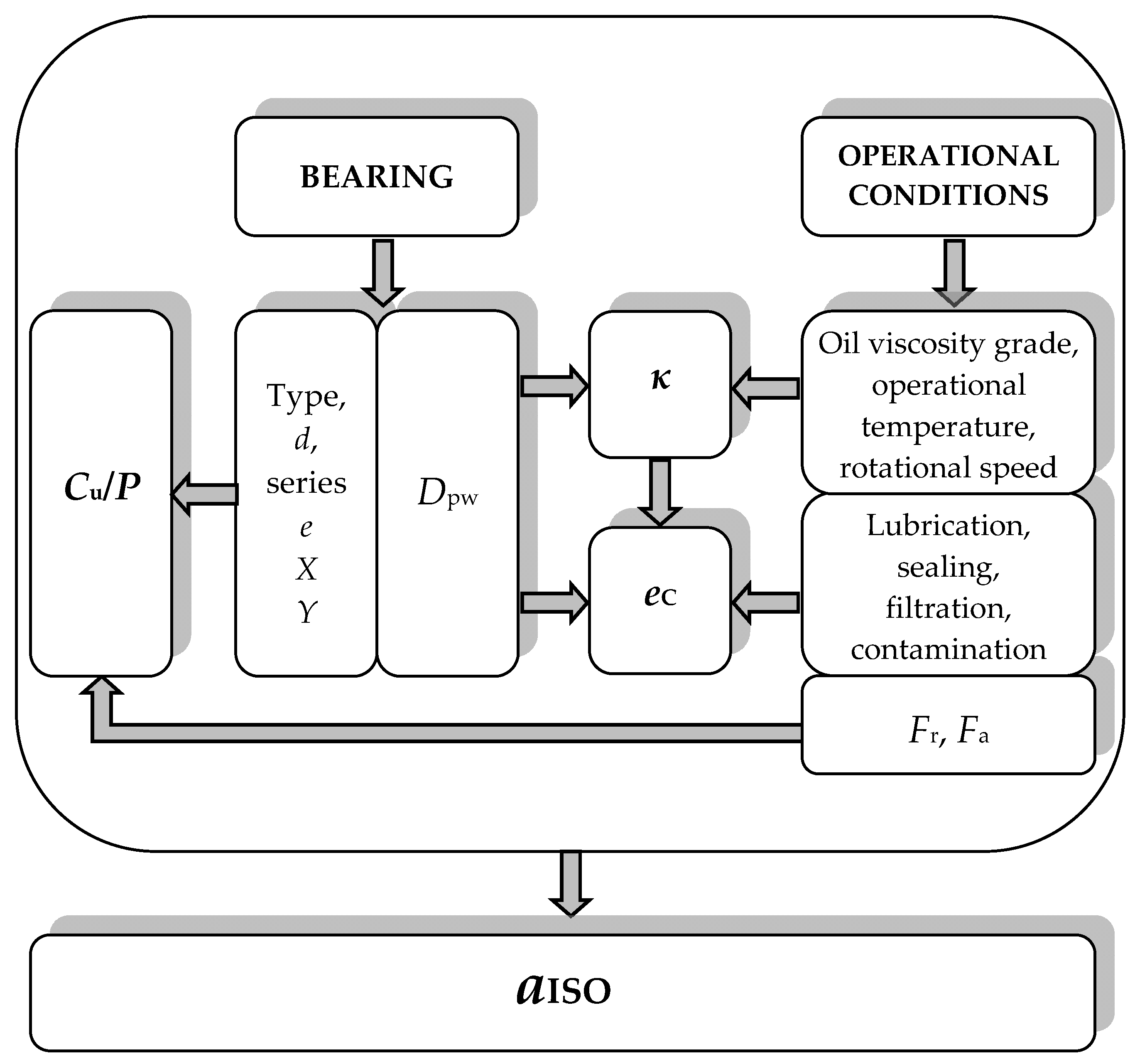
6.4.2. Modification Factor aISO
- The factor aISO depends on the bearing properties and operating conditions.
- The factor aISO is a function of three quantities: the viscosity ratio of the lubricant κ, the contamination factor eC, and the Cu/P ratio of the fatigue load limit and the bearing equivalent operating load.
- The viscosity ratio of the lubricant κ depends on the operating conditions (the degree of viscosity of the applied oil at a temperature of 40 °C, bearing operating temperature, and the bearing rotation speed) and on the bearing size (the pitch diameter, which is a function of the bore diameter and bearing outer diameter).
- The contamination factor eC depends on the operating conditions: lubrication method (with circulating oil, oil bath, or grease) and sealing, the efficiency of filtering (if implemented), contamination level of the working environment with hard particles, and the bearing size but also the viscosity ratio of the lubricant κ.
- The Cu/P ratio of the fatigue load limit and bearing operating load depends on the bearing properties (type—internal geometry, size, series, and material) and the intensity and character of the bearing load (radial, axial, combined).
6.4.3. Other Influences
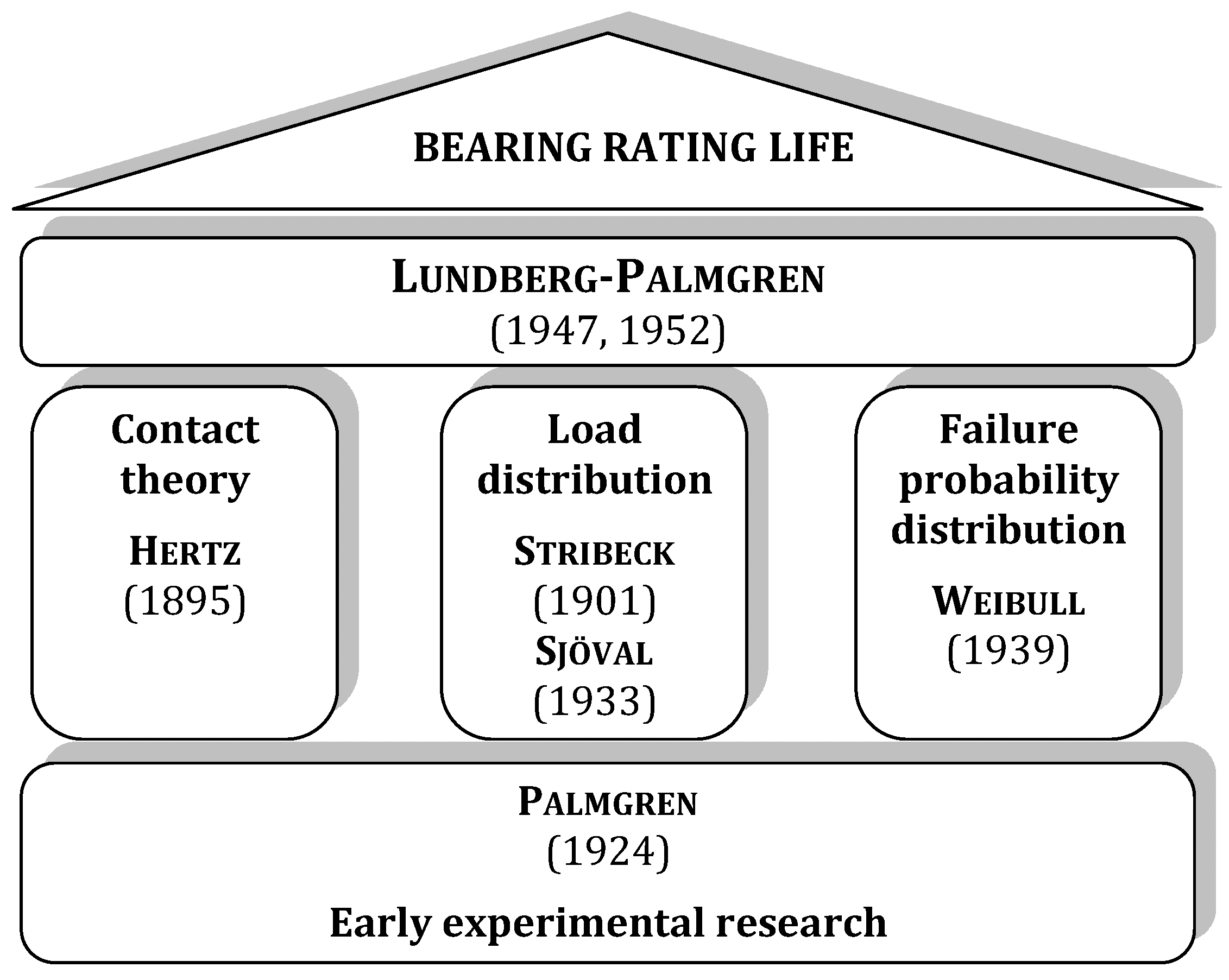
7. Research of Bearing Life through the Century
7.1. Basic Life Theories
7.2. Other Main Contributions
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Palmgren, A. Die Lebensdauer von Kugellagern. Zeitscrift Vereines Dtsch. Ingenieure 1924, 68, 339–341. [Google Scholar]
- International Standard ISO 281:2007; Rolling Bearings—Dynamic Load Ratings and Rating Life. International Organization for Standardization: Geneva, Switzerland, 2007.
- Lundberg, G.; Palmgren, A. Dynamic Capacity of Rolling Bearings. Acta Polytech. 1947, 1, 1–50. [Google Scholar] [CrossRef]
- Lundberg, G.; Palmgren, A. Dynamic Capacity of Roller Bearings. Acta Polytech. 1952, 2, 1–33. [Google Scholar]
- Available online: https://evolution.skf.com/the-skf-formula-for-rolling-bearing-life/ (accessed on 29 May 2024).
- Palmgren, A.; Lundberg, G. Investigation of the Load Capacity of Ball Bearings. Tek. Tidskr. Mek. 1919, 49. [Google Scholar]
- Palmgren, A. Note on the theoretical and practical methods of calculation the carrying capacity of ball bearings. Proc. Inst. Automob. Eng. 1923. [Google Scholar]
- Stribeck, R. Kugellager für beliebige Belastungen. In Zeitschrift des Vereines deutscher Ingenieure; Buchdruckerei A.W. Schade: Berlin, Germany, 1901; p. 45. [Google Scholar]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Angewandte. Math. 1881, 92, 156–171. [Google Scholar]
- Sjövall, H. Belastningsfordelningen inom kul-och rullager vid givna yttre radial-och axialbelastningar. Tek. Tidskr. Mek. 1933, 9, 97–102. [Google Scholar]
- Lazović, T.; Ristivojević, M.; Mitrović, R. Mathematical model of load distribution in rolling bearing. FME Trans. 2008, 36, 189–196. [Google Scholar]
- Lazović, T.; Marinković, A.; Popović, V. Influence of Load and Design Conditions on Lubricant Film Thickness in the Deep Groove Ball Bearing. J. Chin. Soc. Mech. Engineers. Trans. Chin. Inst. Eng 2021, 42, 381–392. [Google Scholar]
- Weibull, W. A Statistical Theory of the Strength of Materials; Royal Swedish Institute for Engineering Research: Stockholm, Sweden, 1939; Volume 151, pp. 1–45. [Google Scholar]
- Zaretsky, E. Rolling Bearing Life Prediction, Theory, and Application; NASA/TP-2013-215305; NASA, Glenn Research Center: Cleveland, OH, USA, 2013.
- Explanatory Notes on ISO 281/1-1977; Technical Report ISO/TR 8646-1985. International Organization for Standardization: Geneva, Switzerland, 1985.
- Technical Report ISO/TR 1281-1:2021; Rolling Bearings—Explanatory Notes on ISO 281—Part 1: Basic Dynamic Load Rating and Basic Rating Life. International Organization for Standardization: Geneva, Switzerland, 2021.
- Lazović, T.; Topalović, I. Evolution of rolling bearing life rating through the standardization. Int. Sci. J. Mach. Technol. Mater. 2020, 14, 222–225. [Google Scholar]
- International standard ISO 281:1990; Rolling Bearings—Dynamic Load Ratings and Rating Life. International Organization for Standardization: Geneva, Switzerland, 1990.
- Technical Specification ISO/TS 16799:1999; Rolling Bearings—Dynamic Load Ratings and Rating Life—Discontinuities in the Calculating of Basic Dynamic Load Ratings. International Organization for Standardization: Geneva, Switzerland, 1999.
- Ioannides, E. Life prediction in rolling element bearings. In Proceedings of the I World Tribology Congress, London, UK, 8–12 September 1997. [Google Scholar]
- Ioannides, E.; Harris, T.A. A new fatigue life model for rolling bearings. ASME J. Tribol. 1985, 107, 367–378. [Google Scholar] [CrossRef]
- Amendment ISO 281:1990/AMD 1:2000; Rolling Bearings—Dynamic Load Ratings and Rating Life—Amendment 1. International Organization for Standardization: Geneva, Switzerland, 2000.
- Amendment ISO/281:1990/AMD 2:2000; Rolling Bearings—Dynamic Load Ratings and Rating Life—Amendment 2: Life Modification Factor aXYZ. International Organization for Standardization: Geneva, Switzerland, 2000.
- Anonymous. Cover story: ISO 281:2007 bearing-life standard—and the answer is? Tribol. Lubr. Technol. 2010, 66, 34–41. [Google Scholar]
- Technical Report ISO/TR 1281-2:2008; Rolling Bearings—Explanatory Notes on ISO 281—Part 2: Modified Rating Life Calculation, Based on a Systems Approach to Fatigue Stresses. International Organization for Standardization: Geneva, Switzerland, 2008.
- Technical Corrigendum ISO/TR 1281-1:2008/COR 1:2009; Rolling Bearings—Explanatory notes on ISO 281—Part 1: Basic Dynamic Load Rating and Basic Rating Life. International Organization for Standardization: Geneva, Switzerland, 2009.
- Technical Report ISO/TR 1281-1:2008; Rolling Bearings—Explanatory Notes on ISO 281—Part 1: Basic Dynamic Load Rating and Basic Rating Life. International Organization for Standardization: Geneva, Switzerland, 2008.
- Technical Corrigendum ISO/TR 1281-2:2008/COR 1:2009; Rolling Bearings—Explanatory Notes on ISO 281—Part 1: Modified Rating Life Calculation, Based on a Systems Approach to Fatigue Stresses. International Organization for Standardization: Geneva, Switzerland, 2009.
- Technical Specification ISO/TS 16281:2008; Rolling Bearings—Methods for Calculating the Modified Reference Rating Life for Universally Loaded Bearings. International Organization for Standardization: Geneva, Switzerland, 2008.
- SKF Publication: Bearing Damage and Failure Analysis, SKF Group. 2017. Available online: https://cdn.skfmediahub.skf.com/api/public/0901d1968064c148/pdf_preview_medium/0901d1968064c148_pdf_preview_medium.pdf (accessed on 23 June 2024).
- International Standard ISO 15243:2017; Rolling Bearings—Damage and Failures—Terms, Characteristics and Causes. International Organization for Standardization: Geneva, Switzerland, 2017.
- Lai, J.; Kadin, Y. Towards a better understanding of material imperfections. SKF Evol. Mag. 2018, 3, 26–30. [Google Scholar]
- Kuhnell, B. Wear in rolling element bearings and gears—How age and contamination affect them. Mach. Lubr. 2004, 9. Available online: https://www.machinerylubrication.com/Read/664/wear-bearings-gears (accessed on 29 May 2024).
- Deutsche norm DIN 51819-1:1999; Testing Rolling Bearing Lubricants Using the FE 8 War Test Machine—Principle. Deutsche Institut für Normung: Berlin, Germany, 1999.
- International Standard ISO 76:2006; Rolling Bearings—Static Load Ratings. International Organization for Standardization: Geneva, Switzerland, 2006.
- Lazović, T. Service Life of Ball Bearings; Faculty of Mechanical Engineering, University of Belgrade: Belgrade, Serbia, 2021. (In Serbian) [Google Scholar]
- Zaretsky, E.V.A. Palmgren Revisited—A Basis for Bearing Life Prediction. In Proceedings of STLE Annual Meeting, Kansas City, MO, USA, 18–22 May 1997. [Google Scholar]
- Lieblein, J.; Zelen, M. Statistical Investigation of the Fatigue Life of Deep-Groove Ball Bearings. J. Res. Natl. Bur. Stand. 1956, 57, 273–316. [Google Scholar] [CrossRef]
- Tallian, T.E. Prediction of Rolling Bearing Contact Fatigue Life in Contamined Lubricant: Part I—Mathematical Model. Trans. ASME J. Lubr. Technol. 1976, 98F, 251–257. [Google Scholar] [CrossRef]
- Tallian, T.E. Prediction of Rolling Bearing Contact Fatigue Life in Contamined Lubricant: Part II—Experimental. Trans. ASME J. Lubr. Technol. 1976, 98, 384–392. [Google Scholar] [CrossRef]
- Gabelli, A.; Doyer, A.; Morales-Espejel, G. The Modified Life Rating of Rolling Bearings: A Criterion for Gearbox Design and Reliability Optimization. Power Transm. Eng. 2015, 2015, 46–54. [Google Scholar]
- Weibull, W. The Phenomenon of Rupture in Solids; Royal Swedish Institute for Engineering Research: Stockholm, Sweden, 1939; Volume 153. [Google Scholar]
- Zaretsky, E.V. 2. Rolling bearing life prediction, theory, and application. In Recent Developments in Wear Prevention, Friction and Lubrication; Research Signpost: Kerala, India, 2010; pp. 45–136. [Google Scholar]
- Thomas, H.R.; Hoersch, V.A. Stresses Due to the Pressure of One Elastic Solid upon Another with Special Reference to Railroad Wheels; Bulletin 212; Engineering Experimental Station, University of Illinois: Urbana, IL, USA, 1930. [Google Scholar]
- Zaretsky, E.V.; Poplawski, J.V.; Miller, C.R. Rolling Bearing Life Prediction—Past, Present, and Future. In Proceedings of the International Tribology Conference, Nagasaki, Japan, 29 October–2 November 2000. [Google Scholar]
- Ioannides, E.; Bergling, G.; Gabelli, A. An analytical formulation for the life of rolling bearings. Acta Polytech. Scand. Mech. Eng. Ser. 1999, 137, 1–77. [Google Scholar]
- Zaretsky, E.V.; Poplawski, J.; Peters, S. Comparison of Life Theories for Rolling-Element Bearings; NASA Technical Memorandum 106585; Society of Tribologists and Lubrication Engineers: Chicago, IL, USA, 1995. [Google Scholar]
- Zaretsky, E.V. Fatigue criterion to system design, life and reliability. AIAA J. Propuls. Power 1987, 107, 76–83. [Google Scholar] [CrossRef]
- Gabelli, A.; Kerrigan, A.M.; De Bilc, E. HN Treated Rolling Bearings for Extended Service Life, Progress in Heat Treatment and Surface Engineering. In Proceedings of the 5th ASM Heat Treatment Conference, Gothenburg, Sweden, 7–9 June 2000; pp. 397–408. [Google Scholar]
- Takemura, H.; Matsumoto, Y.; Murakami, Y. Development of New Life Equation for Ball and Roller Bearings. Motion Control. 2001, 11, 1–10. [Google Scholar]
- Mitrović, R.; Ristivojević, M.; Lazović, T. Influence of internal radial clearance on service life of deep groove ball bearing. In Proceedings of XVII International Conference on Material Flow, Machines and Devices in Industry, Belgrade, Serbia, 12–13 September 2002. [Google Scholar]
- Mitrovic, R.; Lazovic, T. Influence of wear on deep groove ball bearing service life. Facta Univ. Ser. Mech. Eng. 2002, 1, 1112–1117. [Google Scholar]
- Bakić, G.; Đukić, M.; Lazović, T.; Prokić-Cvetković, R.; Popović, O.; Rajičić, B. New methodology for monitoring and prevention of rotating parts failures. FME Trans. 2007, 35, 195–200. [Google Scholar]
- Zaretsky, E.V.; Poplawski, J.V.; Root, L.E. Reexamination of Ball-Race Conformity Effects on Ball Bearing Life; Technical Memorandum NASA 2007, TM-2007-212635. Available online: https://ntrs.nasa.gov/api/citations/20080001446/downloads/20080001446.pdf (accessed on 23 June 2024).
- Zaretsky, E.V.; Poplawski, J.V.; Root, L.E. Relation between Hertz Stress-Life Exponent, Ball-Race Conformity, and Ball Bearing Life, Technical Memorandum NASA 2008, TM-2008-214265. Available online: https://ntrs.nasa.gov/api/citations/20080000851/downloads/20080000851.pdf (accessed on 23 June 2024).
- Lazovic, T.; Mitrovic, R.; Marinkovic, A. Influence of Abrasive Wear on the Ball Bearing Service Life. In Proceedings of the European Conference on Tribology—ECOTRIB 2009, Pisa, Italy, 7–10 June 2009; pp. 387–392. [Google Scholar]
- Lazovic, T.; Mitrovic, R.; Ristivojevic, M. Influence of internal radial clearance on the ball bearing service life. In Proceedings of the 3rd International Conference Power Transmissions 09, Kallithea-Chalkidiki, Greece, 1–2 October 2009; pp. 441–444. [Google Scholar]
- Lazovic, T.; Marinković, A. Influence of wear rate on the rolling bearing life, Solving Friction and Wear Problems. In Proceedings of the 17th International Colloquium Tribology, Stuttgart/Ostfildern, Germany, 19–21 January 2010. [Google Scholar]
- Lazović, T.; Mitrović, R.; Ristivojević, M. Influence of internal radial clearance on the ball bearing service life. J. Balk. Tribol. Assoc. 2010, 16, 1–8. [Google Scholar]
- Morales-Espejel, G.; Gabelli, A.; Ioannides, S. Lubrication and Contamination Effects on Bearing Life. SKF Evol. Mag. 2010, 2, 25–31. [Google Scholar]
- Oswald, F.B.; Zaretsky, E.V. Interference-Fit Life Factors for Ball Bearings; Technical Memorandum NASA 2010, TM-2010-216913. Available online: https://ntrs.nasa.gov/api/citations/20110000529/downloads/20110000529.pdf (accessed on 23 June 2024).
- Kwofie, S.; Rahbar, N. A fatigue driving stress approach to damage and life prediction under variable amplitude loading. Int. J. Damage Mech. 2012, 22, 393–404. [Google Scholar] [CrossRef]
- Kim, H.-E.; Tan, A.C.C.; Mathew, J.; Choi, B.-K. Bearing fault prognosis based on health state probability estimation. Expert Syst. Appl. 2012, 39, 5200–5213. [Google Scholar] [CrossRef]
- Lai, J.; Lund, T.; Rydén, K.; Gabelli, A.; Strandel, I. The fatigue limit of bearing steels—Part I: A pragmatic approach to predict very high cycle fatigue strength. Int. J. Fatigue 2012, 37, 155–168. [Google Scholar] [CrossRef]
- Gabelli, A.; Lai, J.; Lund, T.; Rydén, K.; Strandel, I. The fatigue limit of bearing steels—Part II: Characterisation for life rating standards. Int. J. Fatigue 2012, 38, 169–180. [Google Scholar] [CrossRef]
- Soualhi, A.; Razik, H.; Clerc, G.; Doan, D.D. Prognosis of Bearing Failures Using Hidden Markov Models and the Adaptive Neuro-Fuzzy Inference System. IEEE Trans. Ind. Electron. 2014, 61, 2864–2874. [Google Scholar] [CrossRef]
- Needelman, W.M.; Zaretsky, E.V. Recalibrated Equation for Determining Effect of Oil Filtration on Rolling Bearing Life. Tribol. Trans. 2015, 58, 786–800. [Google Scholar] [CrossRef]
- Morales-Espejel, G.E.; Gabelli, A.; De Vries, A.J.C. A Model for Rolling Bearing Life with Surface and Subsurface Survival—Tribological Effects. Tribol. Trans. 2015, 58, 894–906. [Google Scholar] [CrossRef]
- Gupta, P.K.; Oswald, F.B.; Zaretsky, E.V. Comparison of Models for Ball Bearing Dynamic Capacity and Life. Tribol. Trans. 2015, 58, 1039–1053. [Google Scholar] [CrossRef]
- Londhe, N.D.; Arakere, N.K.; Haftka, R.T. Reevaluation of Rolling Element Bearing Load-Life Equation Based on Fatigue Endurance Data. Tribol. Trans. 2015, 58, 815–828. [Google Scholar] [CrossRef]
- Balan, M.R.; Tufescu, A.; Cretu, S.S. A case study on relation between roughness, lubrication and fatigue life of rolling bearings. In Proceedings of the 7th International Conference on Advanced Concepts in Mechanical Engineering, Iasi, Romania, 9–10 June 2016. [Google Scholar]
- Morales Espejel, G.; Gabelli, A. A model for rolling bearing life with surface and subsurface survival: Sporadic surface damage from deterministic indentations. Tribol. Int. 2016, 96, 279–288. [Google Scholar] [CrossRef]
- Gabelli, A.; Morales-Espejel, G. Improved Fatigue Life Analysis of Pre-Dented Raceways Used in Bearing Material Testing, Bearing Steel Technologies: Advances in Steel Technologies for Rolling Bearings; Beswick, J.M., Ed.; ASTM International: West Conshohocken, PA, USA, 2017; Volume 11. [Google Scholar]
- Sharma, A.; Amarnath, M.; Kankar, P.K. Life assessment and health monitoring of rolling element bearings: An experimental study. Life Cycle Reliab. Saf. Eng. 2018, 7, 97–114. [Google Scholar] [CrossRef]
- Gupta, P.K.; Zaretsky, E.V. New Stress-Based Fatigue Life Models for Ball and Roller Bearings. Tribol. Trans. 2018, 61, 304–324. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2018, 99, 1–12. [Google Scholar] [CrossRef]
- Romanowicz, P.J.; Szybiński, B. Fatigue Life Assessment of Rolling Bearings Made from AISI 52100 Bearing Steel. Materials 2019, 12, 371. [Google Scholar] [CrossRef]
- Gao, C.; Lv, K.; Wu, T.; Si, J.; Yihua, H. Method for Determining Starting Point of Rolling Bearing Life Prediction Based on Linear Regression. Electronics 2019, 8, 923. [Google Scholar] [CrossRef]
- Cui, L. A new fatigue damage accumulation rating life model of ball bearings under vibration load. Ind. Lubr. Tribol. 2020, 72, 1205–1215. [Google Scholar] [CrossRef]
- Morales Espejel, G.; Gabelli, A. Rolling bearing performance rating parameters: Review and engineering assessment. Proc. Inst. Mech. Engineers. Part C J. Mech. Eng. Sci. 2020, 234, 3064–3077. [Google Scholar] [CrossRef]
- Lazović, T.; Simonović, I.; Marinković, A. Service Life of Universally Loaded Deep Groove Ball Bearing Depending on Internal Clearance: In Machine and Industrial Design in Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2022; Volume 109. [Google Scholar]
- Fu, Y.; Fu, H.; Wu, Q. A Reliable Life Consumption Assessment and Individual Life Monitoring Method for Rolling Bearings. Machines 2023, 11, 742. [Google Scholar] [CrossRef]
- Morales-Espejel, G. Surface Life Modelling of Tribological Components—From Surface Roughness to Bearings and Gear Life. Tribol. Online Jpn. Soc. Tribol. 2023, 18, 255–267. [Google Scholar] [CrossRef]
- Sauer, B.; Beck, T.; Blinn, B.; Foko Foko, F.; Ostermayer, P.; Rüth, L. Influence of the Surface Morphology on Rolling Bearing Life Under Mixed Lubrication; Component Surfaces, Series in Advanced Manufacturing; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Chen, L.; Bu, D.T.; Feng, Z.B.; Liu, H.B. Fatigue Life Analysis of Remanufactured Radial Rolling Bearing with the Replaced Loading Zone. J. Eng. 2023, 3, 1–11. [Google Scholar] [CrossRef]
- Mahamad, A.K.; Saon, S.; Hiyama, T. Predicting remaining useful life of rotating machinery based artificial neural network. Comput. Math. Appl. 2010, 60, 1078–1087. [Google Scholar] [CrossRef]
- Hinchi, A.Z.; Tkiouat, M. Rolling element bearing remaining useful life estimation based on a convolutional long-short-term memory network. Procedia Comput. Sci. 2018, 127, 123–132. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Zuo, M.J. Predicting Remaining Useful Life of Rolling Bearings Based on Deep Feature Representation and Transfer Learning. IEEE Trans. Instrum. Meas. 2020, 69, 1594–1608. [Google Scholar] [CrossRef]
- Li, Q.; Yan, C.; Chen, G.; Wang, H.; Li, H.; Wu, L. Remaining Useful Life prediction of rolling bearings based on risk assessment and degradation state coefficient. ISA Trans. 2022, 129 Pt B, 413–428. [Google Scholar] [CrossRef]
- Zhong, Z.; Zhao, Y.; Yang, A.; Zhang, H.; Zhang, Z. Prediction of Remaining Service Life of Rolling Bearings Based on Convolutional and Bidirectional Long- and Short-Term Memory Neural Networks. Lubricants 2022, 10, 170. [Google Scholar] [CrossRef]
- Ye, Z.; Zhang, Q.; Shao, S.; Niu, T.; Zhao, Y. Rolling Bearing Health Indicator Extraction and RUL Prediction Based on Multi-Scale Convolutional Autoencoder. Appl. Sci. 2022, 12, 5747. [Google Scholar] [CrossRef]
- Guo, D.; Cao, Z.; Fu, H.; Li, Z. Remaining Useful Life Estimation for Rolling Bearings Using MSGCNN-TR. IEEE Sens. J. 2022, 22, 24333–24343. [Google Scholar] [CrossRef]
- Lu, Q.; Li, M. Digital Twin-Driven Remaining Useful Life Prediction for Rolling Element Bearing. Machines 2023, 11, 678. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Ren, M.; Xu, T.; Lu, C.; Zhao, Z. Remaining Useful Life Prediction of Rolling Bearings Based on Multi-scale Permutation Entropy and ISSA-LSTM. Entropy 2023, 25, 1477. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Yang, J.; Yang, X. Residual Life Prediction of Rolling Bearings Based on a CEEMDAN Algorithm Fused with CNN-Attention-Based Bidirectional LSTM Modeling. Processes 2024, 12, 8. [Google Scholar] [CrossRef]
- Wen, H.; Zhang, L.; Sinha, J. Early Prediction of Remaining Useful Life for Rolling Bearings Based on Envelope Spectral Indicator and Bayesian Filter. Appl. Sci. 2024, 14, 436. [Google Scholar] [CrossRef]
- Yang, L.; Jiang, Y.; Zeng, K.; Peng, T. Rolling Bearing Remaining Useful Life Prediction Based on CNN-VAE-MBiLSTM. Sensors 2024, 24, 2992. [Google Scholar] [CrossRef]
- Cao, S.; Zhang, F.; Zhao, J.; Duan, Y.; Guo, X. Remaining Useful Life Prediction of Rolling Bearing Based on Multi-Domain Mixed Features and Temporal Convolutional Networks. Appl. Sci. 2024, 14, 2354. [Google Scholar] [CrossRef]


| Viscosity Ratio | A | B |
|---|---|---|
| 0.1 ≤ κ < 0.4 | 2.2649 | 0.054381 |
| 0.4 ≤ κ < 1.0 | 1.9987 | 0.190870 |
| 1.0 ≤ κ < 4.0 | 1.9987 | 0.071739 |
| Lubrication Method and Level of Lubricant Contamination | E | F |
|---|---|---|
| Circulation oil lubrication with online filters: | ||
| β 6(c) = 200; ISO 4406 code –/13/10 | 0.5663 | 0.0864 |
| β 12(c) = 200; ISO 4406 code –/15/12 | 0.9987 | 0.0432 |
| β 25(c) ≥ 75; ISO 4406 code –/17/14 | 1.6329 | 0.0288 |
| β 40(c) ≥ 75; ISO 4406 code –/19/16 | 2.3362 | 0.0216 |
| Oil lubrication without filtration or with offline filters: | ||
| ISO 4406 code –/13/10 | 0.6796 | 0.0864 |
| ISO 4406 code –/15/12 | 1.141 | 0.0288 |
| ISO 4406 code –/17/14 | 1.67 | 0.0133 |
| ISO 4406 code –/19/16 | 2.5164 | 0.00864 |
| ISO 4406 code –/21/18 | 3.8974 | 0.0411 |
| Grease lubrication: | ||
| High cleanliness | 0.6796 | 0.0864 |
| Normal cleanliness | 1.141 | 0.0432 |
| Slight to typical contamination, Dpw < 500 mm | 1.887 | 0.0177 |
| Slight to typical contamination, Dpw ≥ 500 mm | 1.677 | 0.0177 |
| Severe contamination | 2.662 | 0.0115 |
| Very severe contamination | 4.06 | 0.00617 |
| Reliability | Life Formula | |
|---|---|---|
| Weibull | ||
| Lundberg–Palmgren | ||
| Ioannides–Harris | ||
| Zaretsky |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lazović, T.; Marinković, A.; Atanasovska, I.; Sedak, M.; Stojanović, B. From Innovation to Standardization—A Century of Rolling Bearing Life Formula. Machines 2024, 12, 444. https://doi.org/10.3390/machines12070444
Lazović T, Marinković A, Atanasovska I, Sedak M, Stojanović B. From Innovation to Standardization—A Century of Rolling Bearing Life Formula. Machines. 2024; 12(7):444. https://doi.org/10.3390/machines12070444
Chicago/Turabian StyleLazović, Tatjana, Aleksandar Marinković, Ivana Atanasovska, Miloš Sedak, and Blaža Stojanović. 2024. "From Innovation to Standardization—A Century of Rolling Bearing Life Formula" Machines 12, no. 7: 444. https://doi.org/10.3390/machines12070444
APA StyleLazović, T., Marinković, A., Atanasovska, I., Sedak, M., & Stojanović, B. (2024). From Innovation to Standardization—A Century of Rolling Bearing Life Formula. Machines, 12(7), 444. https://doi.org/10.3390/machines12070444










