Multi-Objective Optimization Study on the Coupling Mechanism of Underwater Wireless Power Transfer Systems
Abstract
1. Introduction
2. Modeling of Magnetically Coupled Resonant Wireless Power Transfer System
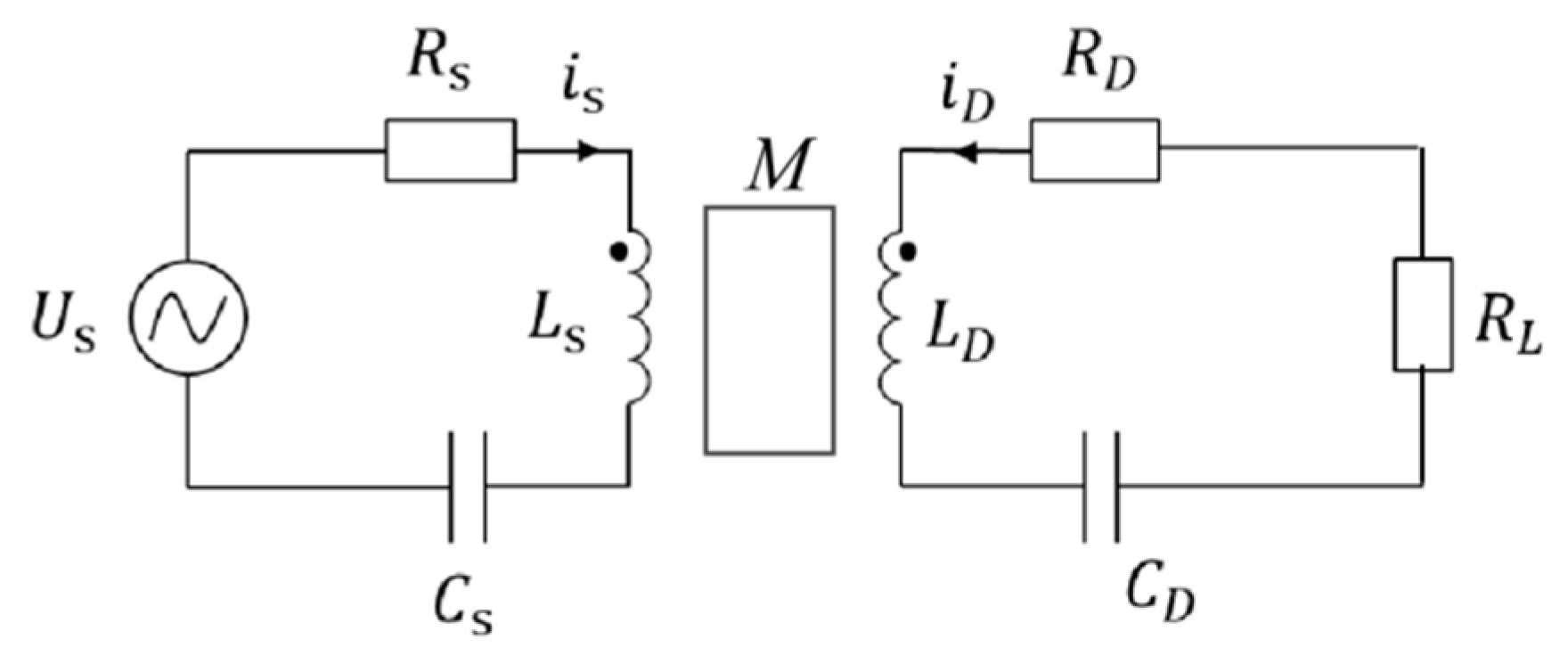
2.1. Equivalent Circuit Model of MCR-WPT System
2.2. Variations in Self-Inductance and Mutual Inductance of Underwater Coils
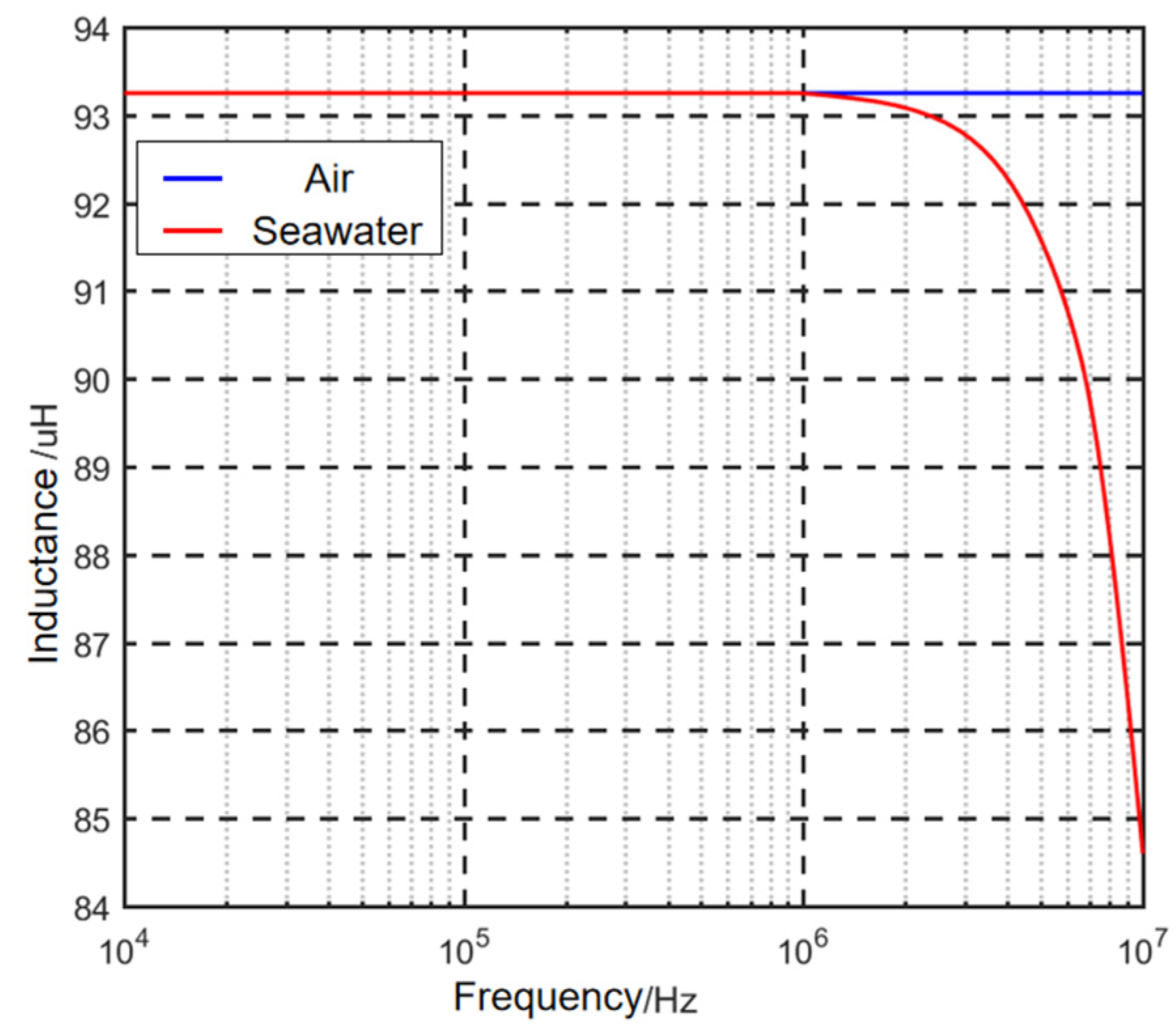
2.2.1. Variations in Self-Inductance of Underwater Coils
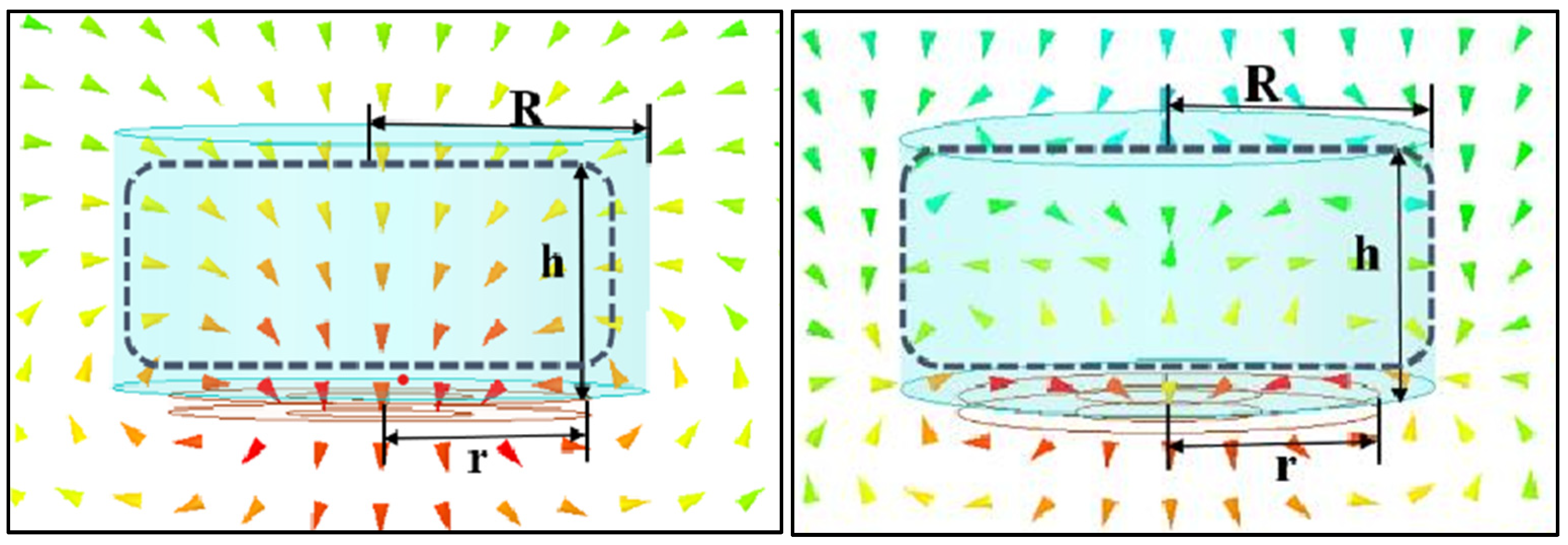
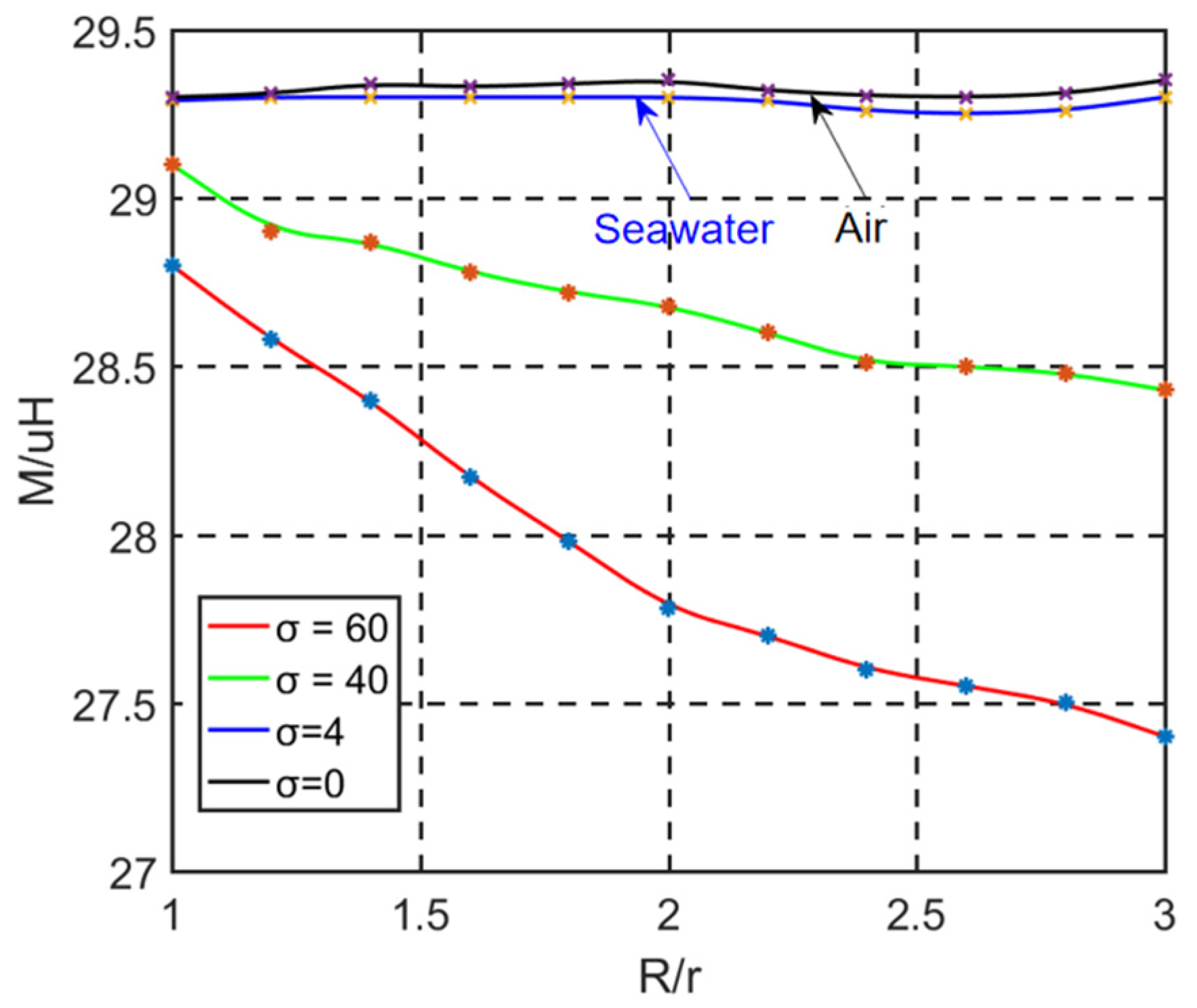
2.2.2. Variations in Mutual Inductance of Underwater Coils
2.3. Radio Energy Transmission Underwater Correction Model
3. Orthogonal Experimental Design
3.1. Self-Inductance Orthogonal Test
3.2. Mutual Inductance Orthogonal Experiment
4. Regression Prediction Based on RBF Neural Network
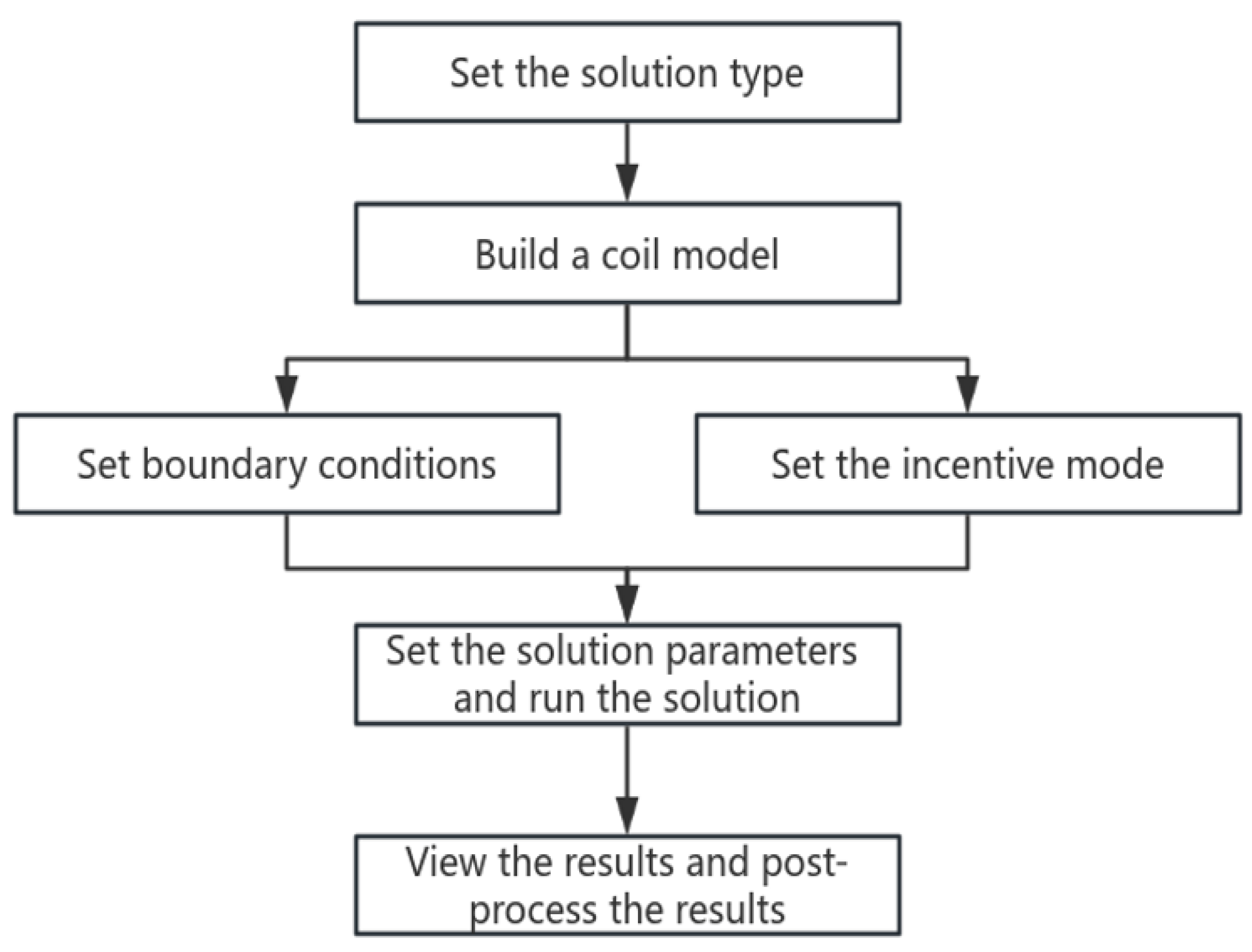
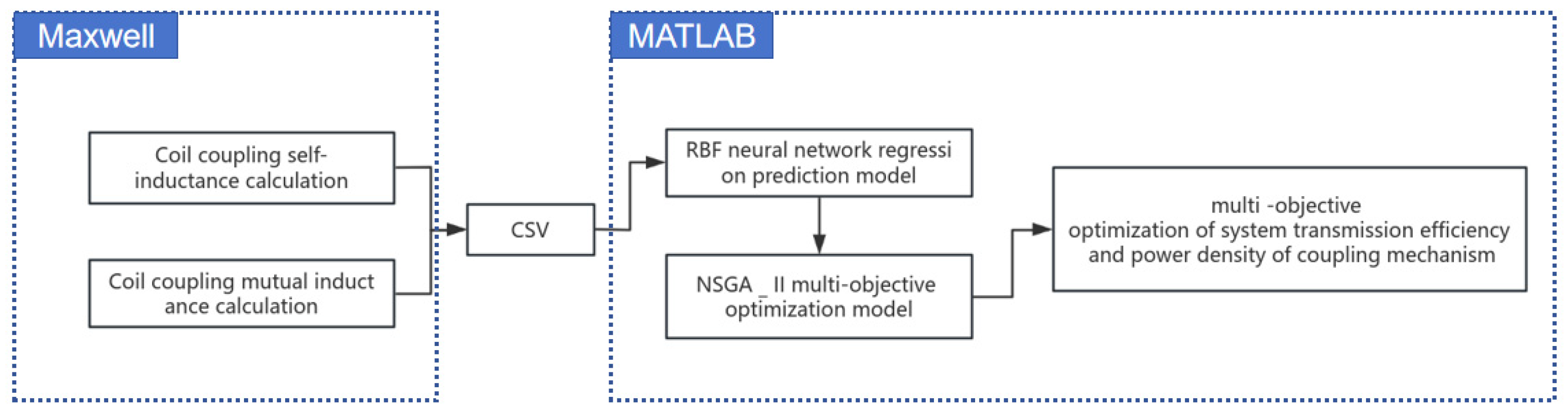
4.1. Integrated Simulation Platform
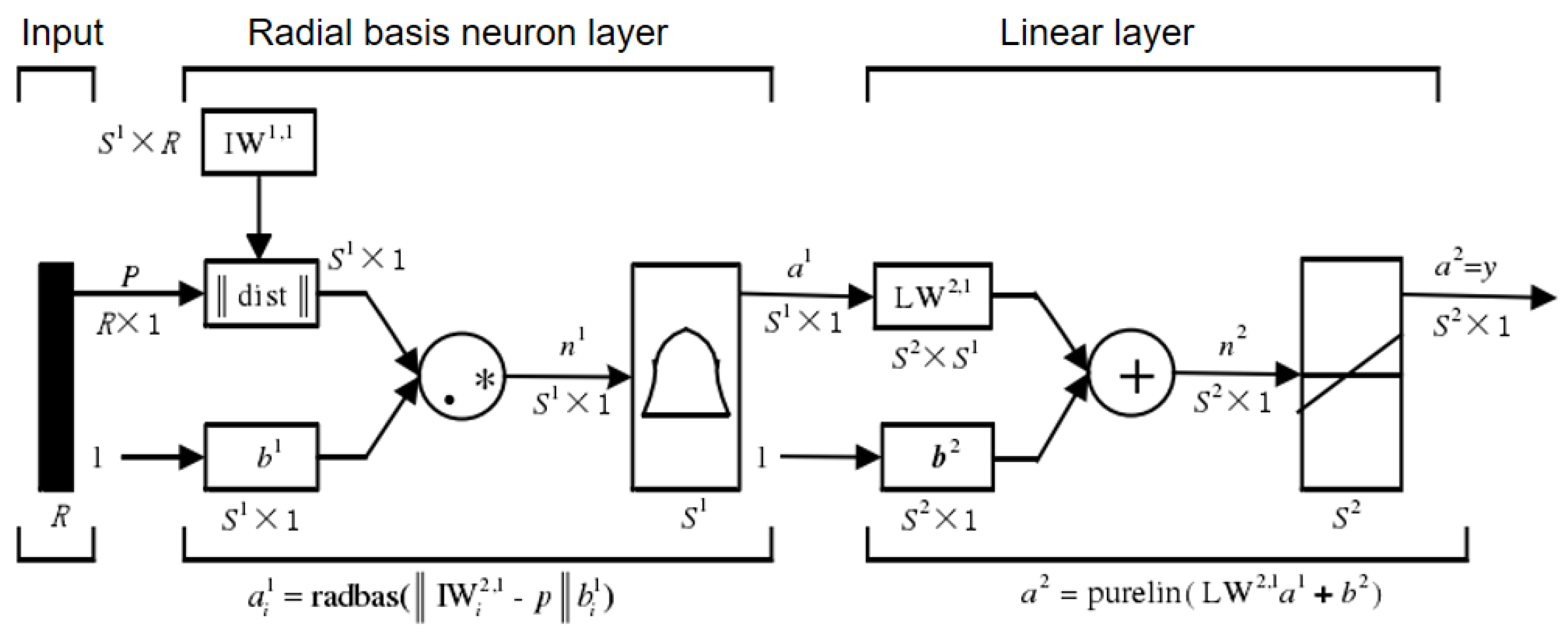
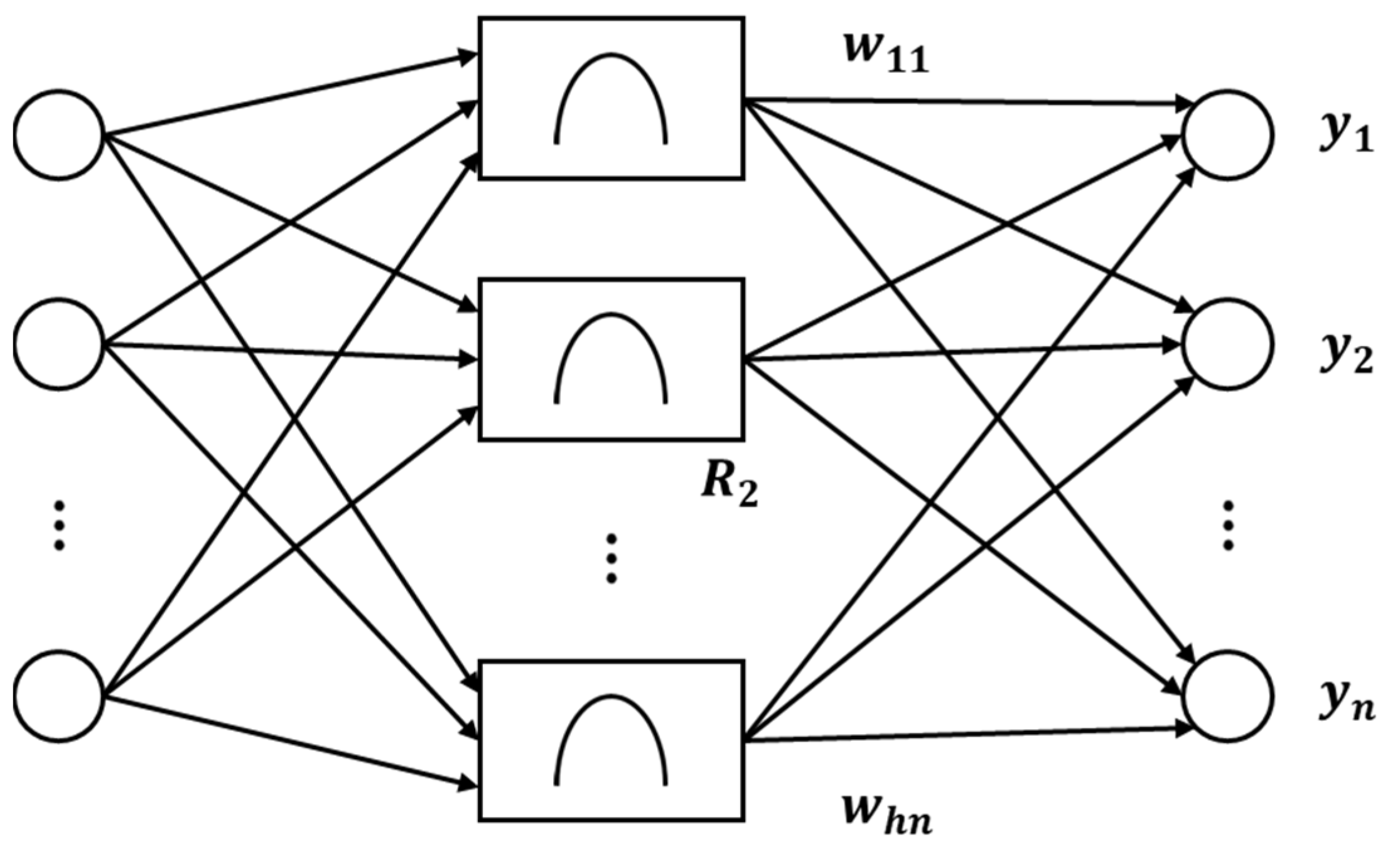
4.2. Neural Network Model
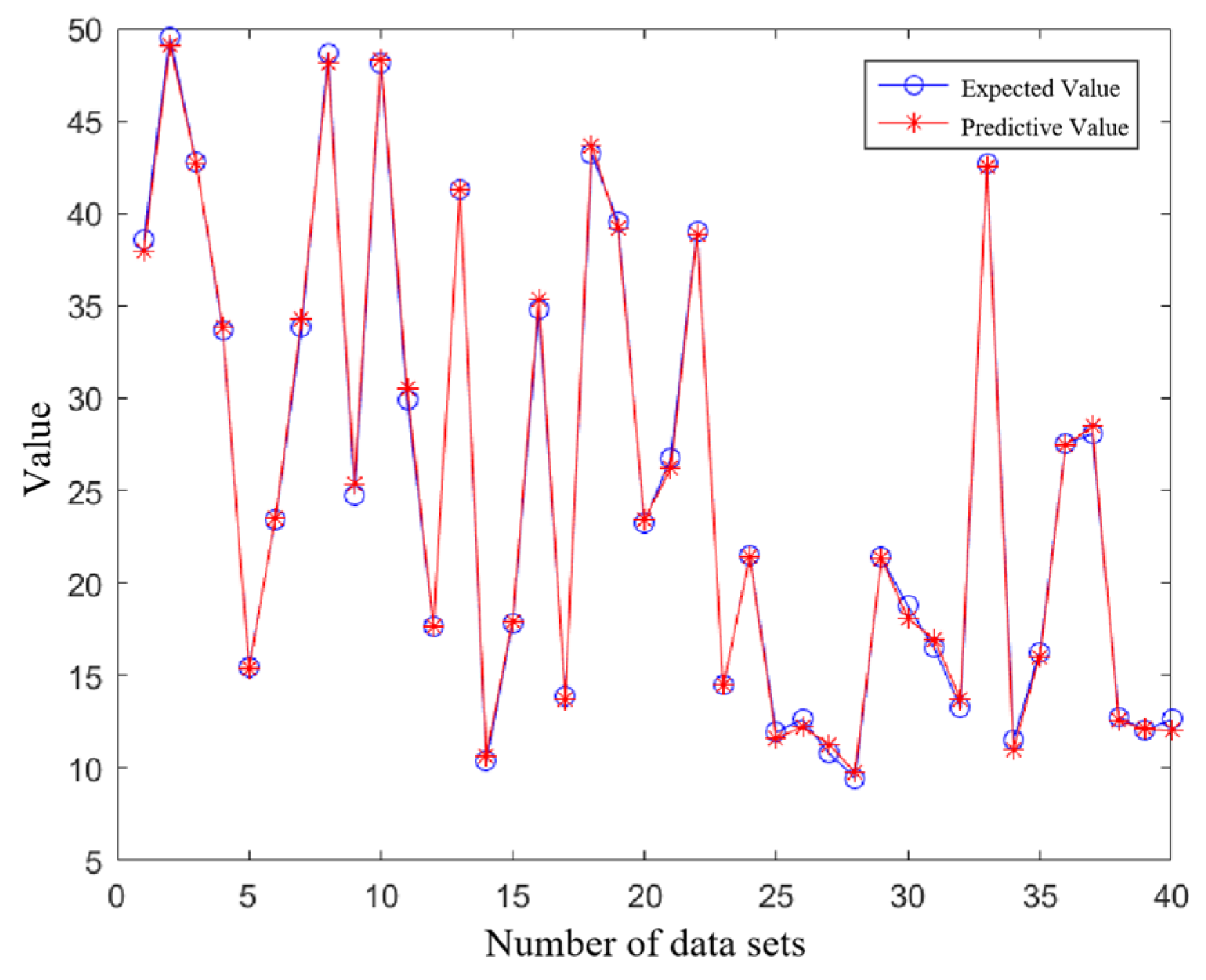
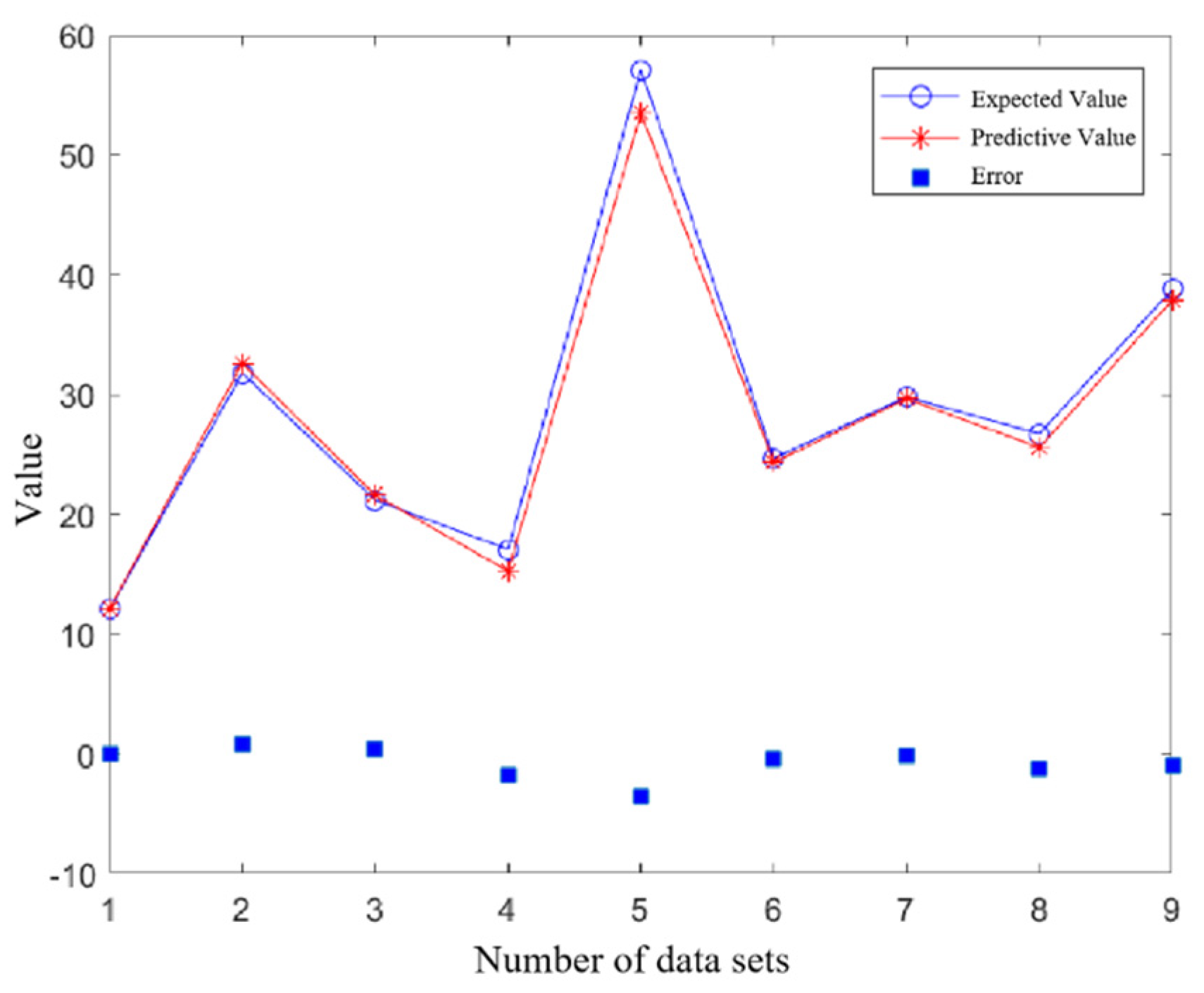
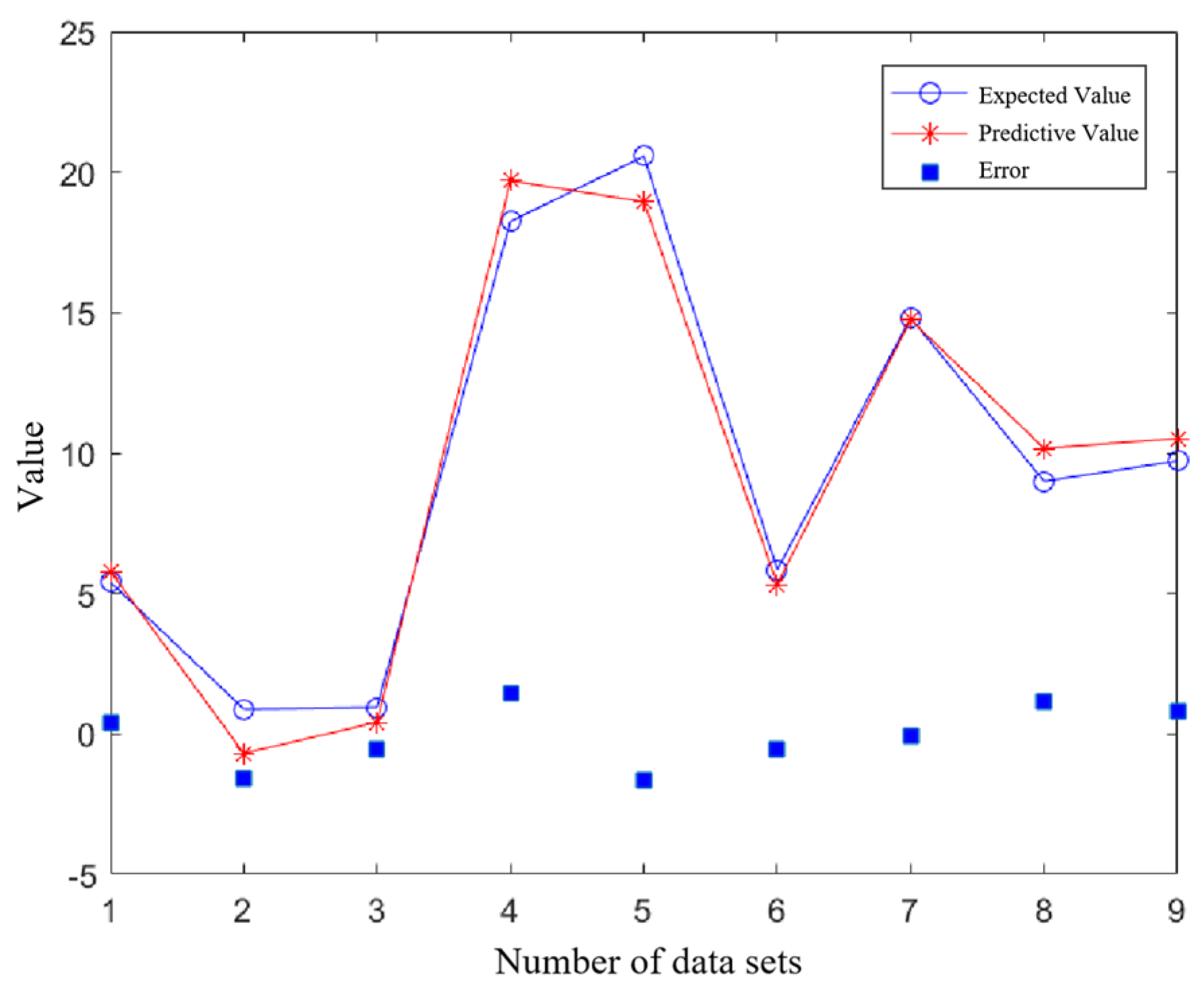
4.3. Regression Result Prediction
4.3.1. Self-Inductance Regression Prediction
4.3.2. Mutual Inductance Regression Prediction
5. Multi-Objective Optimization of Coupling Mechanisms
5.1. NSGA-II Non-Dominated Sorting Genetic Algorithm
5.2. Coupling Mechanism Multi-Objective Optimization Model
5.2.1. Defining the Optimization Objectives
5.2.2. Selection of Design Variables
5.2.3. Constraint Analysis
5.2.4. Establishment of Optimization Model
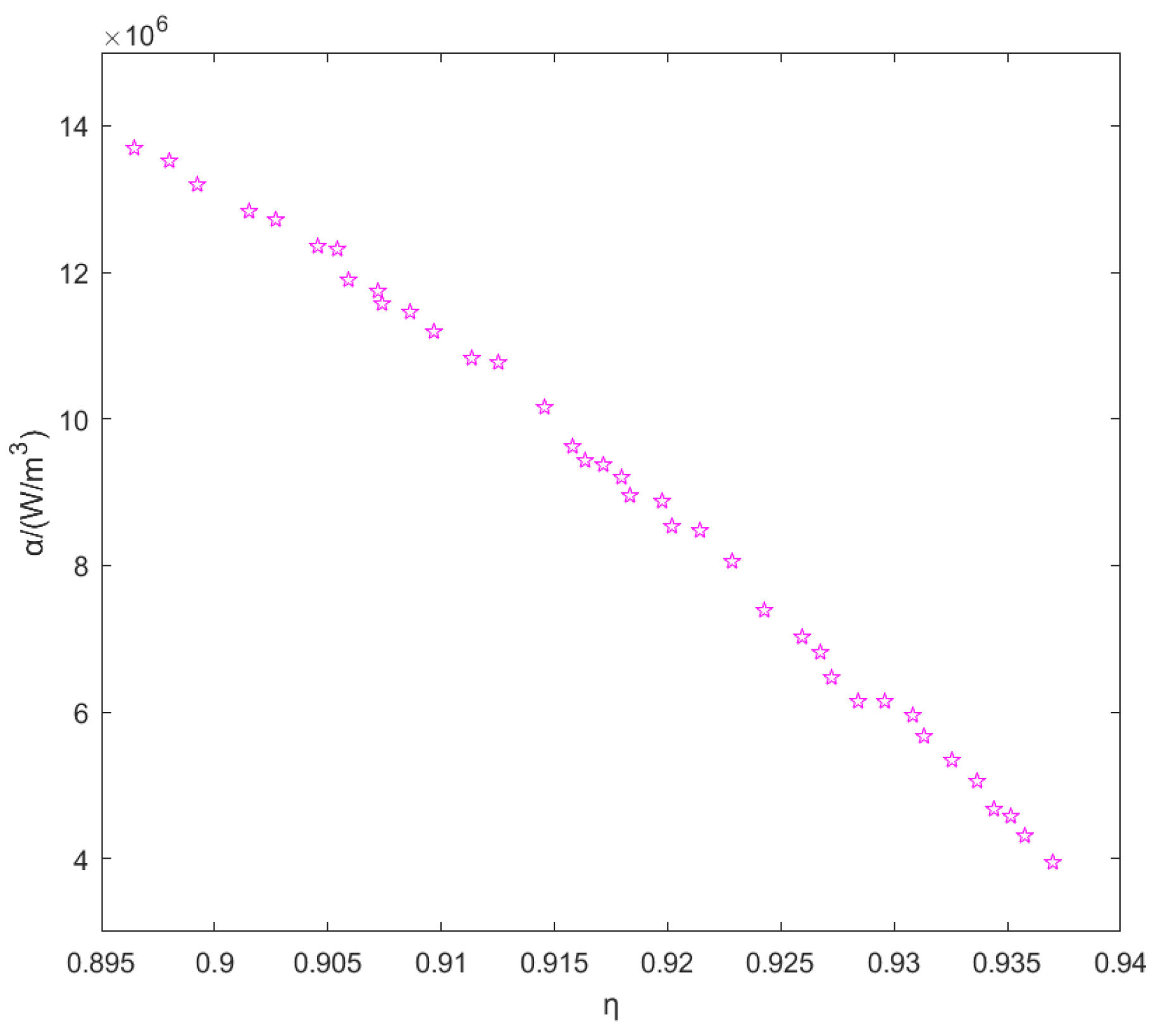
5.3. Multi-Objective Optimization Results
6. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohsan, S.A.H.; Islam, A.; Khan, M.A.; Mahmood, A.; Rokia, L.S.; Mazinani, A.; Amjad, H. A Review on Research Challenges, Limitations and Practical Solutions for Underwater Wireless Power Transfer. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 554–562. [Google Scholar] [CrossRef]
- Yu, L.; Sun, H.; Su, S.; Tang, H.; Sun, H.; Zhang, X. Review of Crucial Problems of Underwater Wireless Power Transmission. Electronics 2023, 12, 163. [Google Scholar] [CrossRef]
- Lyu, F.; Cai, T.; Huang, F. A universal wireless charging platform with novel bulged-structure transmitter design for multiple heterogeneous autonomous underwater vehicles (AUVs). IET Power Electron. 2023, 16, 2162–2177. [Google Scholar] [CrossRef]
- Feng, H.; Tavakoli, R.; Onar, O.C.; Pantic, Z. Advances in High-Power Wireless Charging Systems: Overview and Design Considerations. IEEE Trans. Transp. Electrif. 2020, 6, 886–919. [Google Scholar] [CrossRef]
- Teeneti, C.R.; Truscott, T.T.; Beal, D.N.; Pantic, Z. Review of Wireless Charging Systems for Autonomous Underwater Vehicles. IEEE J. Ocean. Eng. 2021, 46, 68–87. [Google Scholar] [CrossRef]
- Mukherjee, S.; Galigekere, V.P.; Onar, O.; Ozpineci, B.; Su, G.J. Control of Output Power in Primary Side LCC and Secondary Series Tuned Wireless Power Transfer System without Secondary Side Sensors. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020. [Google Scholar]
- McGinnis, T.; Henze, C.P.; Conroy, K. Inductive power system for autonomous underwater vehicles. In Proceedings of the OCEANS 2007, Aberdeen, Scotland, 18–21 June 2007; pp. 1–5. [Google Scholar]
- Pyle, D.; Granger, R.; Geoghegan, B.; Lindman, R.; Smith, J. Leveraging a large UUV platform with a docking station to enable forward basing and persistence for light weight AUVs. In Proceedings of the 2012 OCEANS, Rhodes, Greece, 17–23 June 2012; pp. 1–8. [Google Scholar]
- Granger, R.P.; Baer, C.M.; Gabriel, N.H.; Labosky, J.J.; Galford, T.C. Non-contact wet mateable connectors for power and data transmission. In Proceedings of the 2013 OCEANS, San Diego, CA, USA, 23–26 September 2013; pp. 1–4. [Google Scholar]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Sandhu, S.; Beiker, S.; Sassoon, R.; Fan, S. Wireless energy transfer with the presence of metallic planes. Appl. Phys. Lett. 2011, 99, 214102. [Google Scholar] [CrossRef]
- Moon, S.; Kim, B.-C.; Cho, S.-Y.; Ahn, C.-H.; Moon, G.-W. Analysis and design of a wireless power transfer system with an intermediate coil for high efficiency. IEEE Trans. Ind. Electron. 2014, 61, 5861–5870. [Google Scholar] [CrossRef]
- Shi, J.-g.; Li, D.-j.; Yang, C.-j. Design and analysis of an underwater inductive coupling power transfer system for autonomous underwater vehicle docking applications. J. Zhejiang Univ. Sci. C 2014, 15, 51–62. [Google Scholar] [CrossRef]
- Tran, D.H.; Choi, W. Design of a high-efficiency wireless power transfer system with intermediate coils for the on-board chargers of electric vehicles. IEEE Trans. Power Electron. 2017, 33, 175–187. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.; Jin, X.; Li, H. Modeling and Application of Magnetic Induction Wireless Power Transmission in Sea Water. In Proceedings of the 2021 International Conference on Power System Technology (POWERCON), Haikou, China, 10–11 November 2021; pp. 2172–2177. [Google Scholar]
- Zhang, K.-H.; Zhu, Z.-B.; Song, B.-W.; Xu, D.-M. A power distribution model of magnetic resonance WPT system in seawater. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–4. [Google Scholar]
- Yeo, T.-D.; Kwon, D.; Khang, S.-T.; Yu, J.-W. Design of maximum efficiency tracking control scheme for closed-loop wireless power charging system employing series resonant tank. IEEE Trans. Power Electron. 2016, 32, 471–478. [Google Scholar] [CrossRef]
- Wheeler, H.A. Simple Inductance Formulas for Radio Coils. Proc. Inst. Radio Eng. 1928, 16, 1398–1400. [Google Scholar] [CrossRef]
- Kraichman, M.B. Impedance of a circular loop in an infinite conducting medium. J. Res. Nat. Bur. Stand. D. Radio Propag. 1962, 66, 499–503. [Google Scholar] [CrossRef]
- Guan, Y.; Sun, X.; Jiang, X.; Sa, R.; Zhou, L.; Huang, Y.; Liu, Y.; Li, X.; Lu, R.; Wang, C. The effect of Fe-Mn minerals and seawater interface and enrichment mechanism of ore-forming elements of polymetallic crusts and nodules from the South China Sea. Acta Oceanol. Sin. 2017, 36, 34–46. [Google Scholar] [CrossRef]
- Tippmann, J.; Sarkar, J.; Verlinden, C.; Hodgkiss, W.; Kuperman, W. Toward ocean attenuation tomography: Determining acoustic volume attenuation coefficients in seawater using eigenray amplitudes. J. Acoust. Soc. Am. 2016, 140, EL247–EL250. [Google Scholar] [CrossRef] [PubMed]
- Mazlouman, S.J.; Mahanfar, A.; Kaminska, B. Mid-range wireless energy transfer using inductive resonance for wireless sensors. In Proceedings of the 2009 IEEE International Conference on Computer Design, Lake Tahoe, CA, USA, 4–7 October 2009; pp. 517–522. [Google Scholar]
- Montazer, G.A.; Giveki, D.; Karami, M.; Rastegar, H. Radial basis function neural networks: A review. Comput. Rev. J. 2018, 1, 52–74. [Google Scholar]
- Tian, W.; Bao, Y.; Liu, W. Wind power forecasting by the BP neural network with the support of machine learning. Math. Probl. Eng. 2022, 2022, 7952860. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
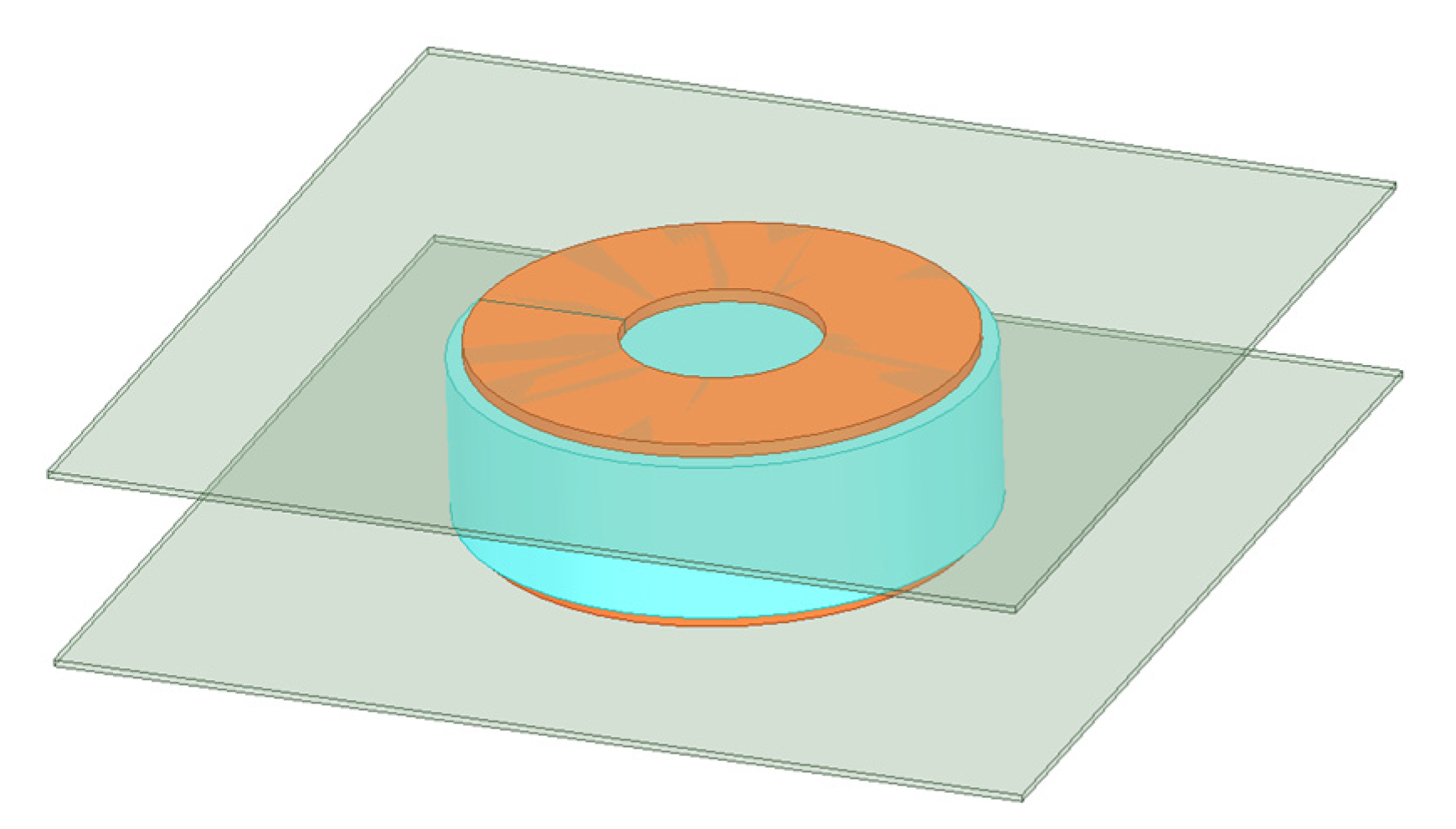


| Parameter | Seawater |
|---|---|
| Number of turns | 11 |
| Number of layers | 1 |
| Coil inner diameter (mm) | 35 |
| Coil outer diameter (mm) | 75 |
| Wire radius (mm) | 2 |
| Transmission distance (mm) | 30 |
| Experiment Number | Factor A | Factor B | Factor C | Factor D | Self-Inductance (μH) |
|---|---|---|---|---|---|
| 1 | 60 | 7 | 4 | 0.5 | 13.263 |
| 2 | 60 | 7 | 4 | 1 | 12.066 |
| 3 | 60 | 7 | 4 | 1.5 | 12.632 |
| 4 | 60 | 7 | 4.5 | 1.5 | 10.814 |
| 5 | 60 | 8 | 4 | 1.5 | 13.884 |
| 6 | 60 | 8 | 5.5 | 1.5 | 9.426 |
| 7 | 60 | 9 | 5 | 0.5 | 12.623 |
| … | … | … | … | … | … |
| 42 | 100 | 12 | 5 | 1 | 48.635 |
| 43 | 110 | 7 | 4.5 | 1 | 27.564 |
| 44 | 110 | 7 | 4.5 | 1.5 | 26.796 |
| 45 | 110 | 8 | 4 | 2 | 33.686 |
| 46 | 110 | 9 | 4 | 1 | 43.175 |
| 47 | 110 | 10 | 5.5 | 0.5 | 42.651 |
| 48 | 110 | 11 | 5 | 1.5 | 48.116 |
| 49 | 110 | 12 | 5 | 0.5 | 57.101 |
| Experiment Number | Factor A | Factor B | Factor C | Factor D | Factor E | Mutual Inductance (μH) |
|---|---|---|---|---|---|---|
| 1 | 60 | 7 | 4 | 0.5 | 30 | 6.686 |
| 2 | 60 | 7 | 4.5 | 0.5 | 90 | 0.892 |
| 3 | 60 | 7 | 4.5 | 1 | 70 | 1.459 |
| 4 | 60 | 7 | 5.5 | 1.5 | 30 | 4.161 |
| 5 | 60 | 8 | 4.5 | 1 | 50 | 3.056 |
| 6 | 60 | 8 | 5 | 1.5 | 50 | 2.511 |
| 7 | 60 | 9 | 4 | 0.5 | 70 | 2.201 |
| … | … | … | … | … | … | … |
| 42 | 100 | 12 | 4.5 | 1.5 | 90 | 8.109 |
| 43 | 110 | 7 | 4 | 1.5 | 30 | 15.223 |
| 44 | 110 | 7 | 5 | 1 | 50 | 9.500 |
| 45 | 110 | 8 | 4.5 | 0.5 | 70 | 8.478 |
| 46 | 110 | 9 | 5.5 | 2 | 90 | 5.846 |
| 47 | 110 | 10 | 4.5 | 1.5 | 30 | 28.005 |
| 48 | 110 | 11 | 4 | 1 | 50 | 21.865 |
| 49 | 110 | 12 | 5 | 0.5 | 70 | 9.030 |
| Parameter | Range of Values |
|---|---|
| Outer Diameter/mm | [60, 110] |
| Number of Turns N | [7, 15] |
| Pitch (mm)/mm | [2, 10] |
| Wire Radius (mm)/mm | [0.5, 2.5] |
| Parameter | Values |
|---|---|
| 300 | |
| 15 | |
| 15 | |
| 50 | |
| 50 |
| Design Variables | Objective Function Values | ||||
|---|---|---|---|---|---|
| Outer Diameter/mm | Number of Turns | Turn-to-Turn Spacing/mm | Wire Diameter/(mm) | ||
| 105.84 | 11.4 | 2.43 | 1.18 | 93.0% | 5.94 |
| 106.33 | 11.4 | 2.62 | 1.29 | 93.2% | 5.33 |
| 107.79 | 11.5 | 2.96 | 1.35 | 93.4% | 4.66 |
| 108.43 | 11.7 | 3.05 | 1.43 | 93.6% | 4.30 |
| 109.65 | 11.8 | 3.12 | 1.55 | 93.7% | 3.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Zheng, M.; Li, Z.; Qin, Y.; Huang, J.; Ou, Y. Multi-Objective Optimization Study on the Coupling Mechanism of Underwater Wireless Power Transfer Systems. Machines 2024, 12, 445. https://doi.org/10.3390/machines12070445
Hu Q, Zheng M, Li Z, Qin Y, Huang J, Ou Y. Multi-Objective Optimization Study on the Coupling Mechanism of Underwater Wireless Power Transfer Systems. Machines. 2024; 12(7):445. https://doi.org/10.3390/machines12070445
Chicago/Turabian StyleHu, Qiong, Meiling Zheng, Zhenfu Li, Yu Qin, Junqiang Huang, and Yujia Ou. 2024. "Multi-Objective Optimization Study on the Coupling Mechanism of Underwater Wireless Power Transfer Systems" Machines 12, no. 7: 445. https://doi.org/10.3390/machines12070445
APA StyleHu, Q., Zheng, M., Li, Z., Qin, Y., Huang, J., & Ou, Y. (2024). Multi-Objective Optimization Study on the Coupling Mechanism of Underwater Wireless Power Transfer Systems. Machines, 12(7), 445. https://doi.org/10.3390/machines12070445






