3. Experiment Setup
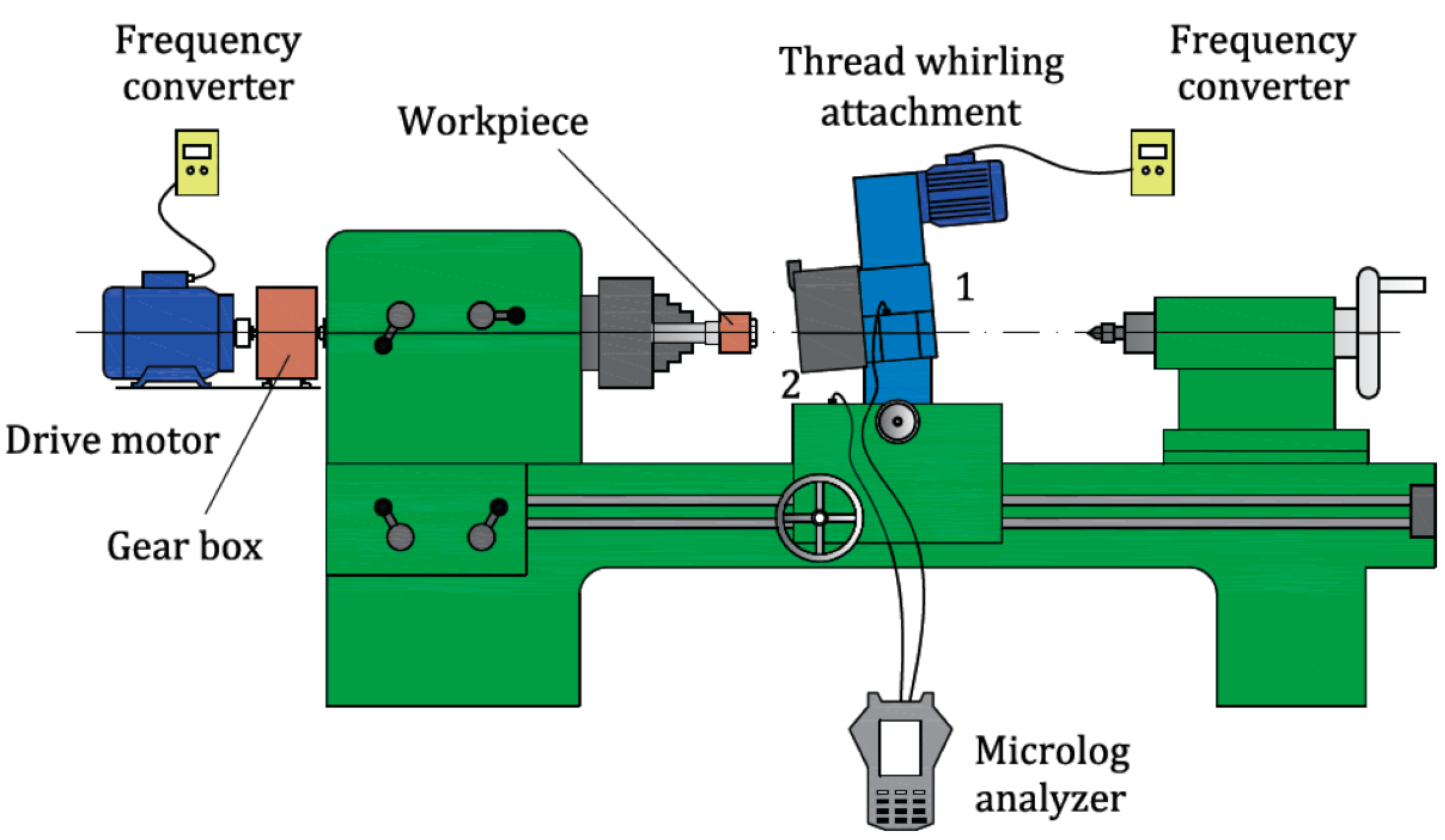
The thread-whirling attachment was fastened to the lathe carrier on the front side via four hexagon-socked head screws placed in the groves, which secured the compound rest to the cross slide of the lathe machine. On the back side, for fastening, two non-standard-shaped screws were placed in the groves of the cross slide. This enabled sufficiently rigid clamping of the thread whirling attachment and, thus, stable processing.
The accuracy of the transversal carrier of the lathe was 0.1 mm, which influenced the accuracy of position settling in the radial direction of the cutting tool in the whirling device. The speed of the main lathe spindle could be varied from 11.2 to 2240 rpm. Using a frequency converter, the lowest speed (11.2 rpm) was reduced by 90% (to 1.12 rpm). Further reduction was not possible due to torque loss and the cessation of main spindle rotation. The cutting tool and blank exhibited the same direction of rotation as in down-milling.
A gearbox with a 1:15 gear ratio (
Figure 3) was used to reduce the workpiece rotation from 1.12 to 0.075 rpm. The main lathe motor was removed, and the lathe main spindle was operated with the aid of another drive motor using a frequency converter connected to the gearbox with simple coupling. The material removal rate was thus lowered, as was the feed rate per tool.
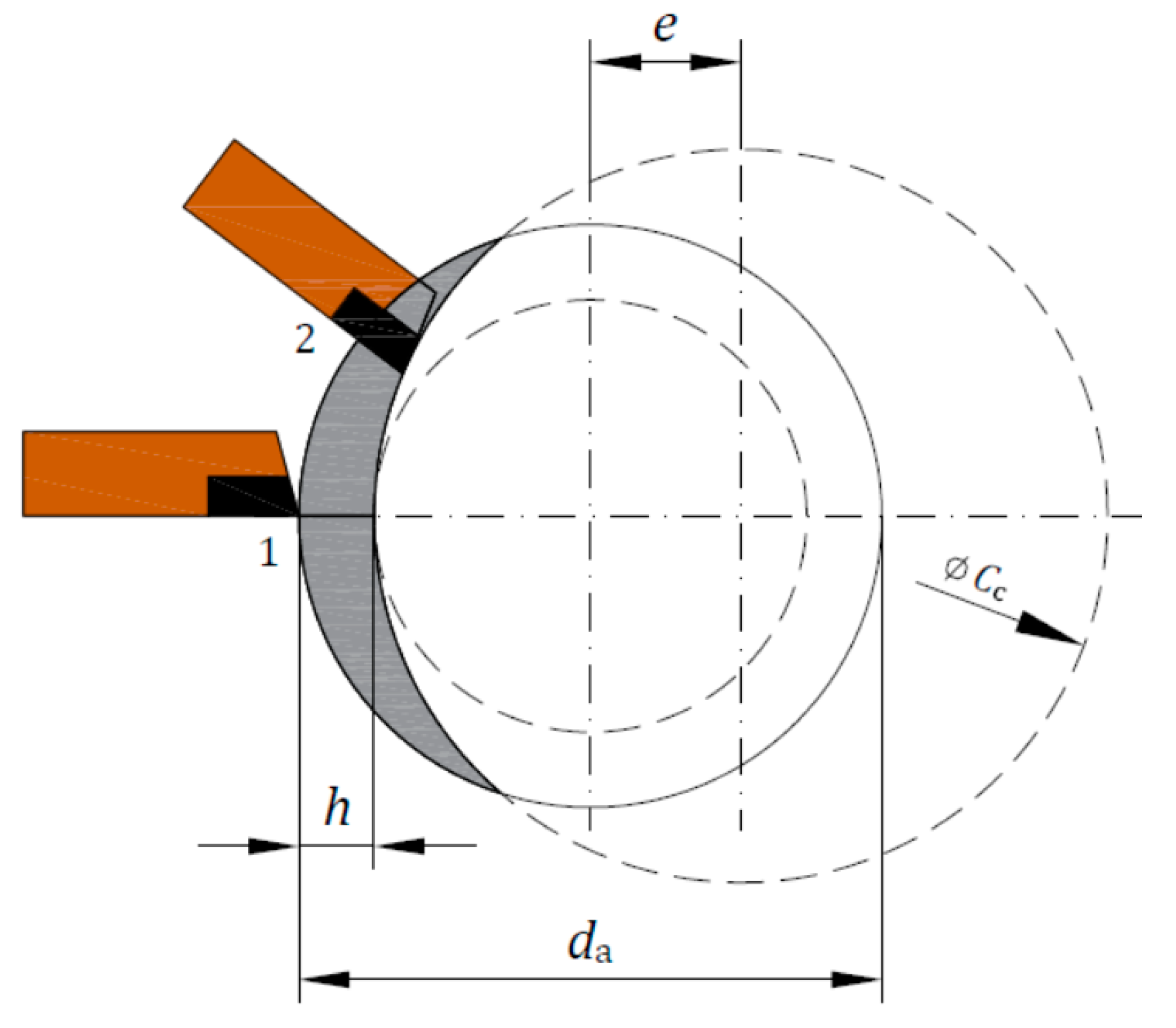
The cutting head rpm
n2 is given by
where
n1 is the rpm of the electric motor,
d1 is the diameter of the driving pulley, and
d2 is the diameter of the driven pulley.
The cutting speed is therefore:
where
Cc is the diameter of the cutting circle.
Four cutting speeds were used by changing the rpm of the electric motor that powered the whirling attachment (
Table 1).
The dimensions of the screw are listed in
Table 2.
Rather than 16MnCr5 material, 11SMn30 material was used for processing (
Table 3). The latter is marked by good machinability on machine tools and by easy fragmentation of chips; thus, its machined surface was expected to be of better quality. Due to their high sulfur and phosphorus content, free-cutting steels not destined for heat treatment generally are not recommended for welding. The chemical composition of the 11SMn30 material was as follows: C max 0.14, Si max 0.05, Mn 0.9–1.3, P max 0.11, and S 0.27–0.33.
Processing was performed without any support due to the risk of interference between the driven pulley and the revolving center. The cutting tool was cooled during machining with a bonderite L-MR 72 coolant trough hollow in the driven pulley of the whirling attachment. The temperature of the tool remained low during machining; the amount of energy directed into the workpiece was also small. The generated heat was removed from the cutting area, primarily with chips and partially with coolant, because the workpiece temperature remained low during the course of machining. This allowed for the use of higher cutting speeds without the danger of exceeding the temperature resistance of the cutting tool or overheating the workpiece.
Cuts were made at a certain cutting speed to a depth of 8 mm over two passes at three cutting depths. In the first pass, the screw was processed to depths of 6, 7.2, and 7.8 mm; in the second pass, processing continued to yield the final screw dimensions (
Table 4).
Before the initiation of machining, vibrations were measured on the whirling attachment and the lathe carriage (
Figure 3). Vibrations also were measured after the cutting tool fully entered the material, approximately 15 mm from the screw’s beginning. The vibration was reduced when machining was performed against the feed rate because the main component of the cutting force opposed the feed rate movement and assumed control of movements from the main shaft of the lathe.
To allow comparisons, two more screws were made in one pass at the lowest cutting speed (screws 13 and 14). The main shaft speed is a parameter directly related to the longitudinal feed rate of the lathe sleeve and was a constant value for the machining of all 14 screws. The productivity of machining in this case was relatively low; however, the main goal was to achieve the best possible surface quality.
The cutting tool was a carbide insert brazed on the body, which was prismatic in shape (16 mm × 16 mm) and ground into the corresponding shape (
Figure 4).
The tool profile had the same profile as the hollow profile of the screw. The blade was fastened to the cutting ring with a special holder using a grove and four socked bolts (
Figure 5). This allowed for easy dismantling of the tool for sharpening after the completion of screw machining.
Two tools were used for machining; when one tool was processing material, the other was sharpening. The determination of the cutting tool holder radial runout was accomplished using a dial gauge with a value of 0.05 mm. The maximum value of blank tightening on the mandrel of the three-yaw chuck was 0.03 mm.
The cutting tool was sharpened on a universal diamond grinder (granulation 100) after each tool pass. Twelve screws were fabricated using different cutting parameters, and two screws required one tool pass.
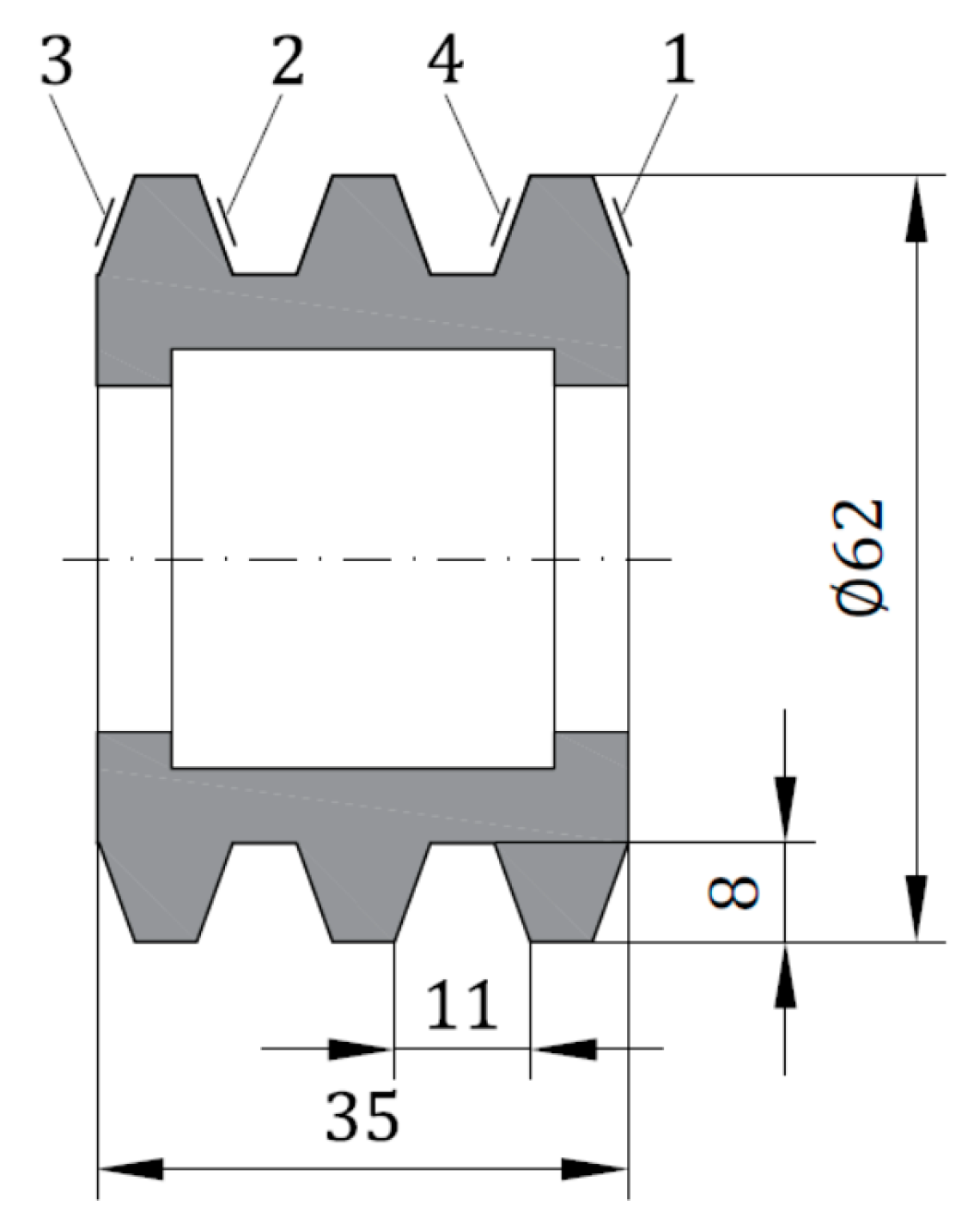
Processing quality was measured at four points (
Figure 6), at the beginning and end of the screw.
Points 1 and 4 are further from, and 2 and 3 are closer to, the chuck of the lathe.
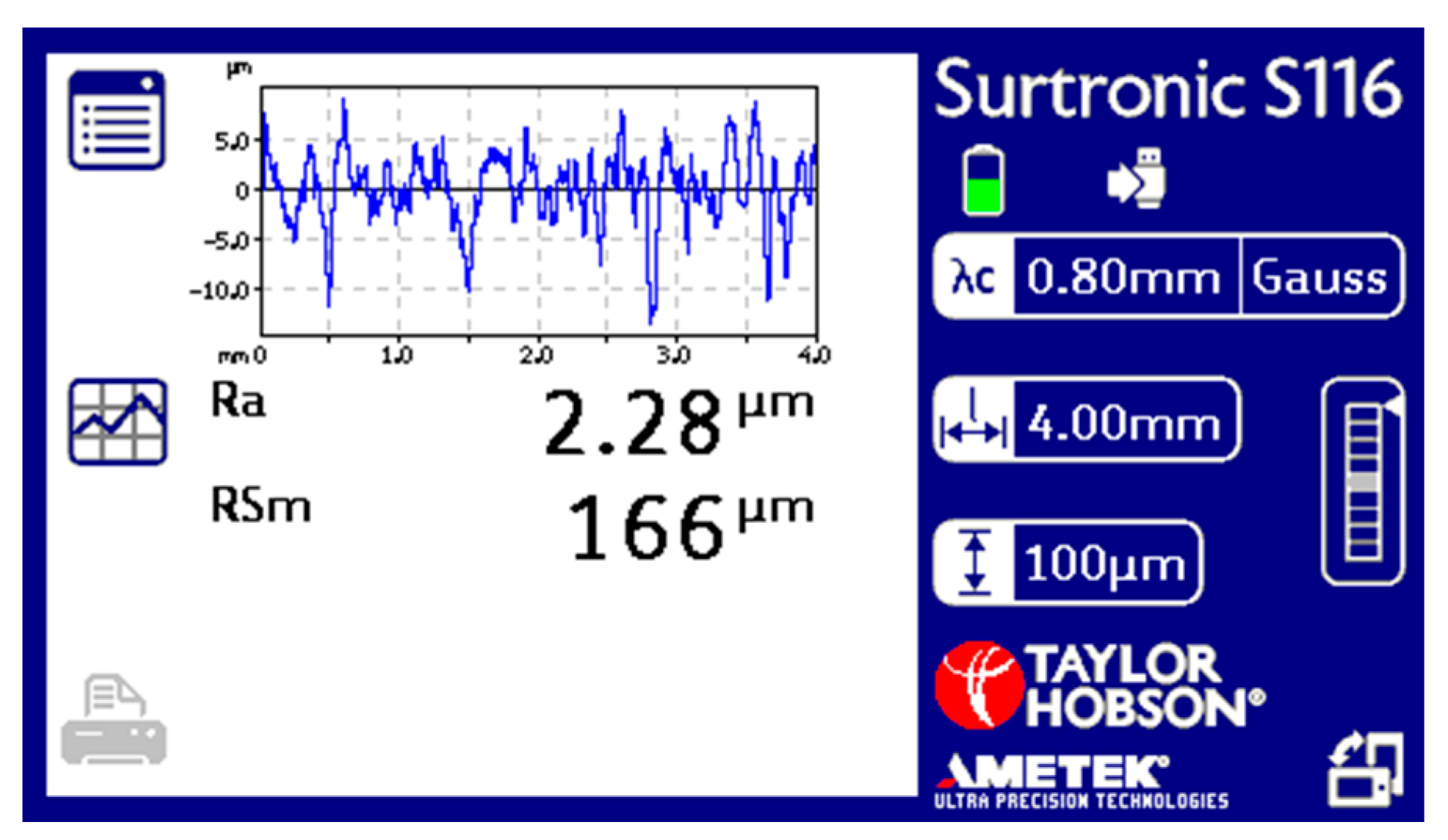
Roughness was measured using a Surtronic S-116 device (Taylor Hobson) at a screw profile length of 4 mm. The instrument can measure roughness in any orientation within 25 mm of the evaluation length. In addition to roughness data, it is possible to measure waviness parameters, parameters on the raw profile, and parameters obtained by double filtering. The instrument resolution and reading accuracy are 0.01 μm and 2%, respectively. Before the measurement, the instrument was calibrated using a reference specimen type 112/534 with 6.0 μm roughness. An example of the measurement is shown in
Figure 7. A Gaussian filter was used for the measurement.
The arithmetical mean height (Ra) and the mean width of the profile elements (Rsm) were also measured. To ensure the right position (height) between the measuring device and the screw surface, a special device that allowed the measurement of all screws in the same place was constructed, depending on the keyway of the screw.
During machining, CMSS 2200 vibration acceleration sensors were placed in two locations, as shown in
Figure 3, and the data were logged by an SKF Microlog gx CMXA 75 analyzer. The sensors are designed for exceptionally low noise levels for low frequencies in the temperature range of −50 °C to 120 °C, with a sensitivity of 100 mV/g and precision of ±5%.
Initially, the maximum amplitude was extracted from each vibration profile as proposed in the literature [
16]. After further consideration, the RMS value was chosen as a better representation of the total energy of the vibration profile.
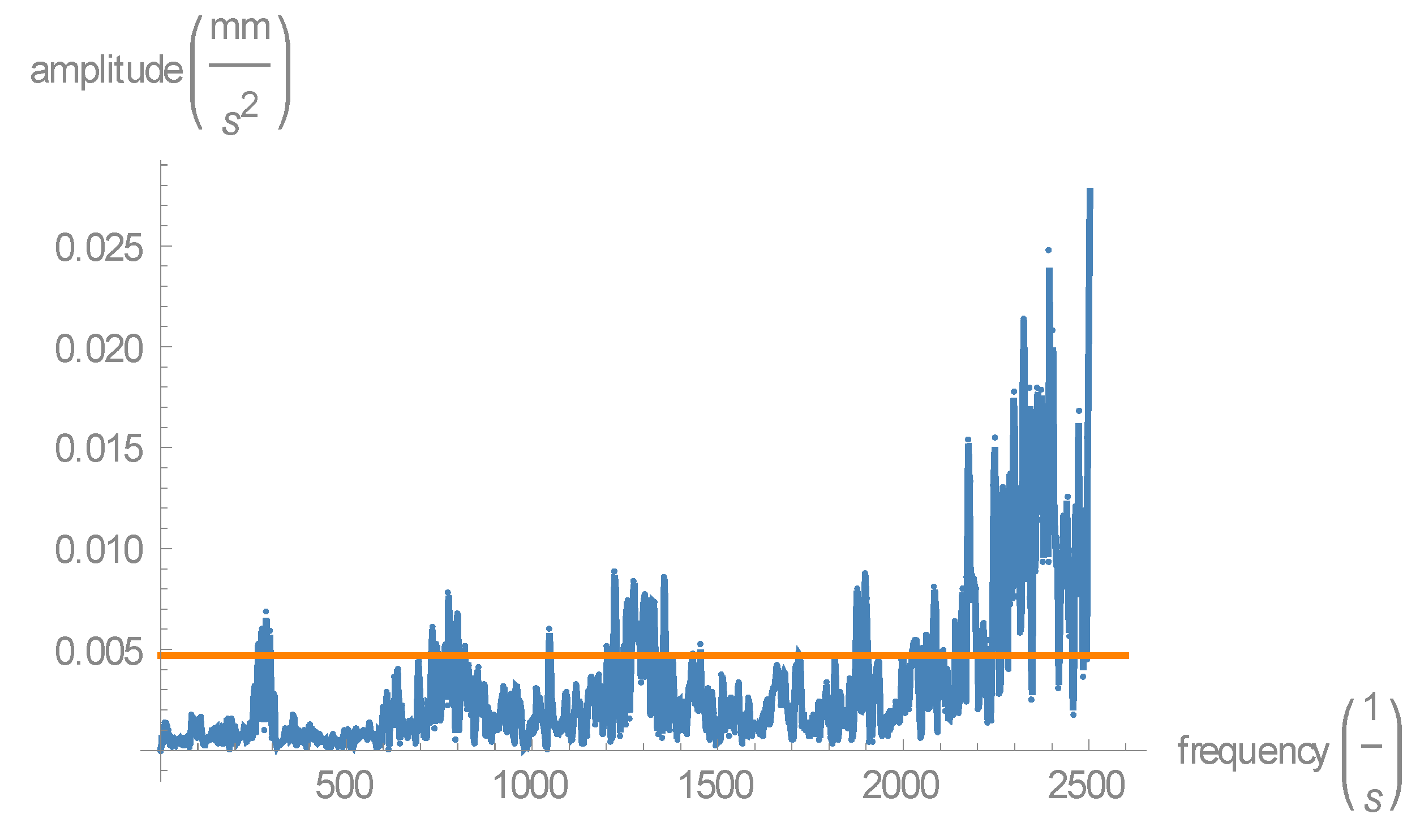
The RMS value of a set of vibration amplitudes is the square root of the arithmetic mean of the squares of the values of amplitudes, also known as the quadratic mean of the amplitude.
The blue lines in
Figure 8 represent the amplitude at each frequency of vibration as a multiplier of
g, gravitational acceleration, and the orange line is the RMS value for this dataset. This figure is a graphical representation of one set of data from which the RMS value was calculated. This type of data set was obtained for each set of input parameters from which the RMS value was extracted.
4. Results and Discussion
The roughness measurements are shown in
Table 5. The lowest surface roughness parameter
Ra was reached at points 2 and 3 (
Figure 6), as expected, considering that these points are closer to the lathe chuck. Considering the cutting parameters, the lowest average surface roughness parameter,
Ra, was reached at a cutting speed of 322.73 m/min and a depth of cut of 0.2 mm, although the vibration amplitudes (
Table 6) were not the lowest values.
The accuracy of the worm and the nut steering of the lathe on which the thread whirling attachment is mounted influence the accuracy of the worm thread surface, primarily with respect to the screw pitch. In this study, the primary goal was the achievement of better surface quality; deviations in screw pitch and helix profile error were not determined. Notably, this information is unimportant for screw functionality; the small length of the screw also ensured that this error was negligible.
The machined surface was observed using a stereo microscope Olympus SZX 10, with two apochromatic objective lenses (
Figure 9b). The surface of the screw made by whirling had a much lower roughness compared with the screw made by turning (
Figure 9c).
Deviation of the lateral cutting face angle depends on the correct shape of all cutting edges of the cutting tool, as well as the correct disposal of the whirling device on the lathe carriage. When sharpening the cutting tool, the inclination angles of the body of the sharpening device must be very accurate. At the time of grinding, the cutting tool was clamped in a two-axis machine vice; thus, the correct shape of the cutting edges of the tool depended on the accuracy of the division scale on the machine vice.
The results of RMS amplitudes for each dataset were calculated from the measured amplitudes stored in the Microlog device and are listed in
Table 6.
Wolfram Mathematica was used to analyze the experimental data.
The first part of the numerical analysis resulted in a series of RMS data in the algorithm VIBRACIJE
VIBRACIJE
vibracije[naslov_, broj_, opcija_, pod_] :=
Module[
{ naslovstr = naslov, dataXYraw, \[CapitalDelta]f, dataaX, dataaY1,
ii, duzina, tabmx, rjesenjaaa, rjesenjaaaa, rjesenjaaaaa, plot0,
plot1, plot2, fff, pozmaksf, maksimumf, maksimumf1, prikaz, rms,
iii, op = opcija, podd = pod, dataaYY1, dataaYY2, plot3, frms,
prikaz1},
dataXYraw = Import[naslovstr, "Data"][[
1]][[61 ;; 861, 1 ;; 3]];
\[CapitalDelta]f = 3.125;
dataaX = dataXYraw[[All, 1]];
dataaYY1 = dataXYraw[[All, 2]];
dataaYY2 = dataXYraw[[All, 3]];
dataaY1 = Which[podd == 1, dataaYY1, podd == 2, dataaYY2];
ii = Range[Dimensions[dataaX]] // Flatten;
duzina = Dimensions[dataaX][[
1]];
iii = Table[i/i, {i, 1, Dimensions[dataaX][[
1]], 1}];
tabmx = Table[{dataaX[[i]], dataaY1[[i]]}, {i, duzina}];
fff = Interpolation[tabmx, InterpolationOrder -> 1];
pozmaksf[n_] :=
Position[dataaY1, RankedMax[dataaY1, n]][[
1]][[
1]] - 1;
maksimumf[n_] := {pozmaksf[n], \[CapitalDelta]f*pozmaksf[n],
RankedMax[dataaY1, n]};
maksimumf1[n_] := {\[CapitalDelta]f*pozmaksf[n],
RankedMax[dataaY1, n]};
rjesenjaaa = Table[maksimumf[i], {i, 1, broj}];
rjesenjaaaa = Table[maksimumf1[i], {i, 1, broj}];
rjesenjaaaaa = SortBy[rjesenjaaaa, First];
rms = RootMeanSquare[dataaY1];
frms[x_] = rms;
plot0 =
Plot[fff[x], {x, 1, \[CapitalDelta]f*duzina}, PlotRange -> All,
AxesOrigin -> {0, 0},
AxesLabel -> {frequency [s^-1], amplitude [mm/s^2]}];
plot1 = ListPlot[tabmx, PlotRange -> All, AxesOrigin -> {0, 0}];
plot2 =
ListPlot[rjesenjaaaaa, Filling -> Axis, PlotStyle -> Red,
AxesOrigin -> {0, 0}];
plot3 = Plot [frms[x], {x, 0, 2600}, PlotStyle -> Orange];
prikaz = Show[plot0, plot1, plot2];
prikaz1 = Show[plot0, plot1, plot3];
Which[op == 1, iii, op == 2, Print[prikaz], op == 3, rms, op == 4,
rjesenjaaaaa, op == 5, Print[prikaz1]]
]
From a series of RMS data matrices, rezultati and arezultati, appropriate for further analysis, were constructed as shown in the algorithm REZULTATI.
REZULTATI
RMSrez = Table[i/i, {i, 1, Dimensions[nazivi][[
1]], 1}];
Do[RMSrez[[i]] = vibracije[nazivi[[i]], 1, 3, 1], {i, n}];
RMSrez = Table[vibracije[nazivi[[i]], 1, 3, 1], {i, n}]
rezultati =
Table[{pojasnjvc[[i]], pojasnjA1[[i]], RMSrez[[i]]}, {i, 1, n}]
RMSrez1 = Table[vibracije[nazivi[[i]], 1, 3, 2], {i, n}]
arezultati =
Table[{pojasnjvc[[i]], pojasnjA1[[i]], RMSrez1[[i]]}, {i, 1, n}]
To determine the functions of response surfaces or a data model, Mathematica 10 is equipped with a Fit function. Fit is also used for linear regression and least squares fit analyses. Fit is typically applied to fit combinations of functions to data, including polynomials and exponentials. As a particularly simple way to model measurement data, the Fit function minimizes the sum of squares:
Fit[data,{
f1,…,
fn},{
x,
y,…}] finds a fit
a1 f1 +…+
an fn to a list of data for functions
f1,…,
fn of variables {
x,
y,…} [
17]. The following algorithm (ISPIS) uses the Fit function to find the models.
ISPIS
lpr = ListPlot3D[rezultati]
Fit[rezultati, {1, x, y, x^2, x y, y^2}, {x, y}]
model1 = Fit[rezultati, { 1, x, y, x y, x^2, y^2}, {x, y}]
Show[lpr, Graphics3D[{Red, PointSize[0.02], Map[Point, rezultati]}]]
Show[Plot3D[model1, {x, 230, 400}, {y, 0, 30},
PlotStyle -> Opacity[.5], PlotRange -> {0, 0.02},
AxesLabel -> {vc, A2, RMSY1}],
Graphics3D[{Red, PointSize[0.02], Map[Point, rezultati]}]]
pr1 = ListPlot3D[arezultati]
model12 = Fit[arezultati, {1, x, y, x^2, x y, y^2, x^3, y^3}, {x, y}]
Show[pr1, Graphics3D[{Red, PointSize[0.02], Map[Point, arezultati]}]]
Show[Plot3D[model12, {x, 230, 370}, {y, 0, 30},
PlotStyle -> Opacity[.5], PlotRange -> {0, 0.005},
AxesLabel -> {vc, A2, RMSY2}],
Graphics3D[{Red, PointSize[0.02], Map[Point, arezultati]}]]
Figure 10,
Figure 11 and
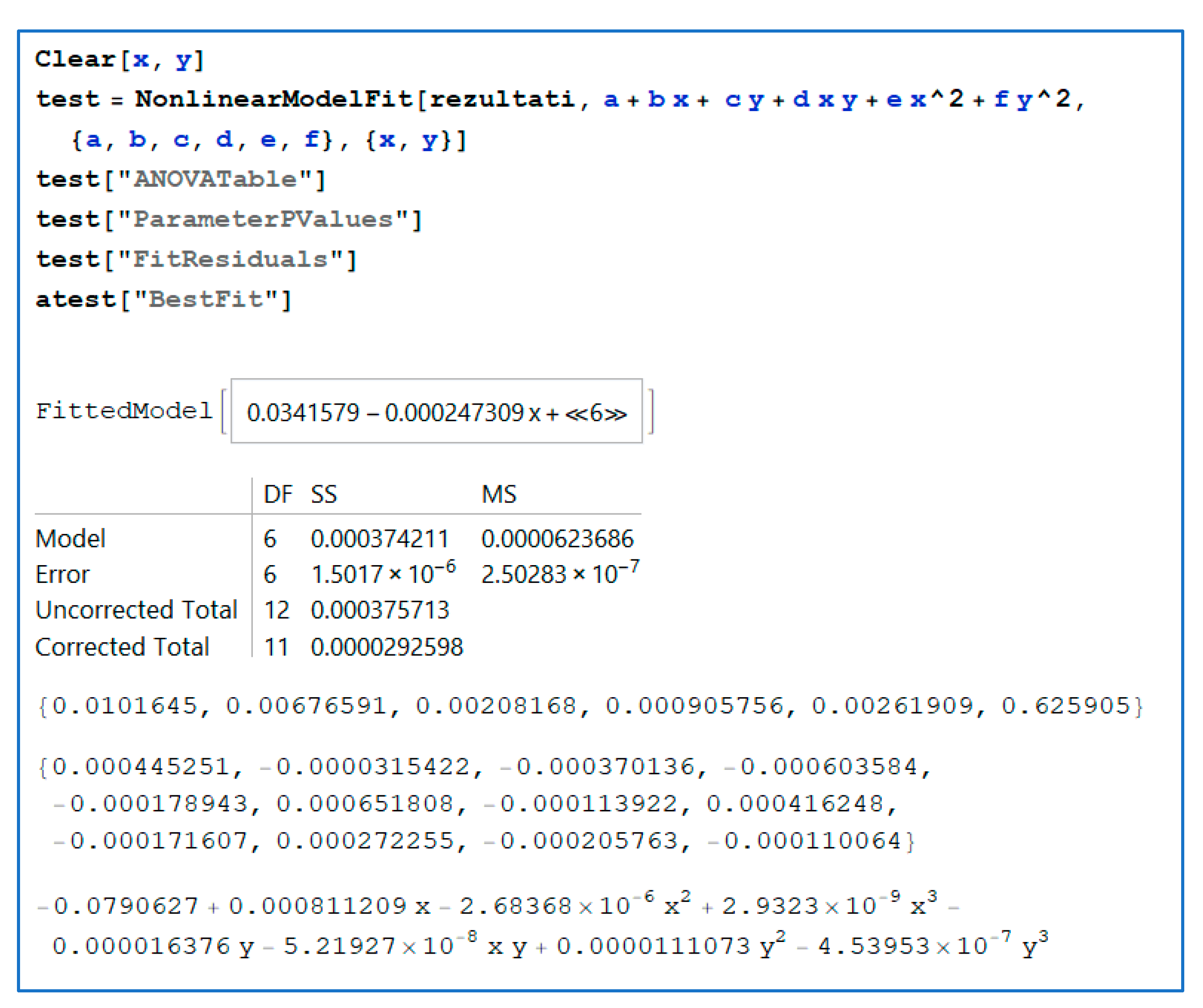
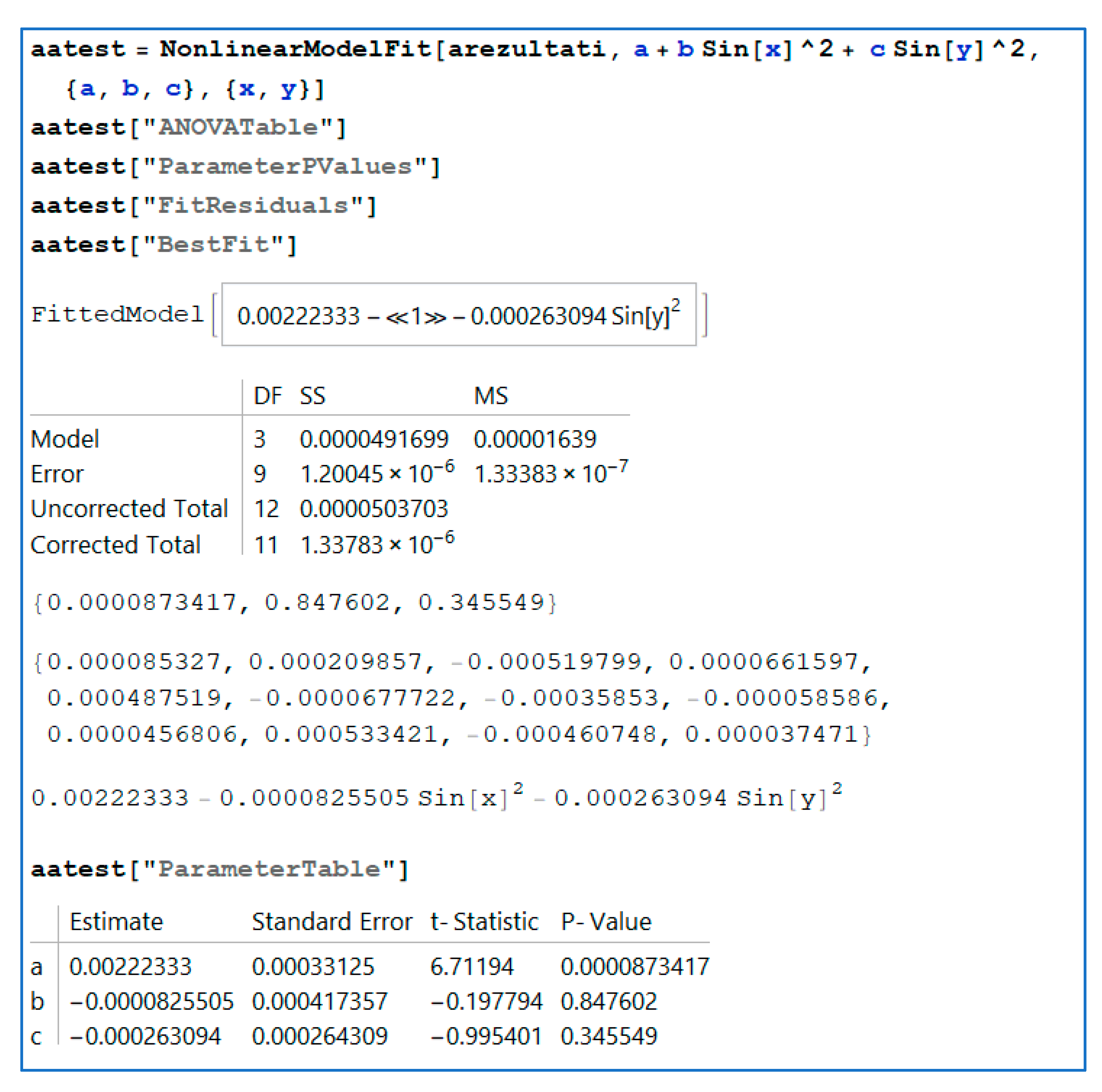
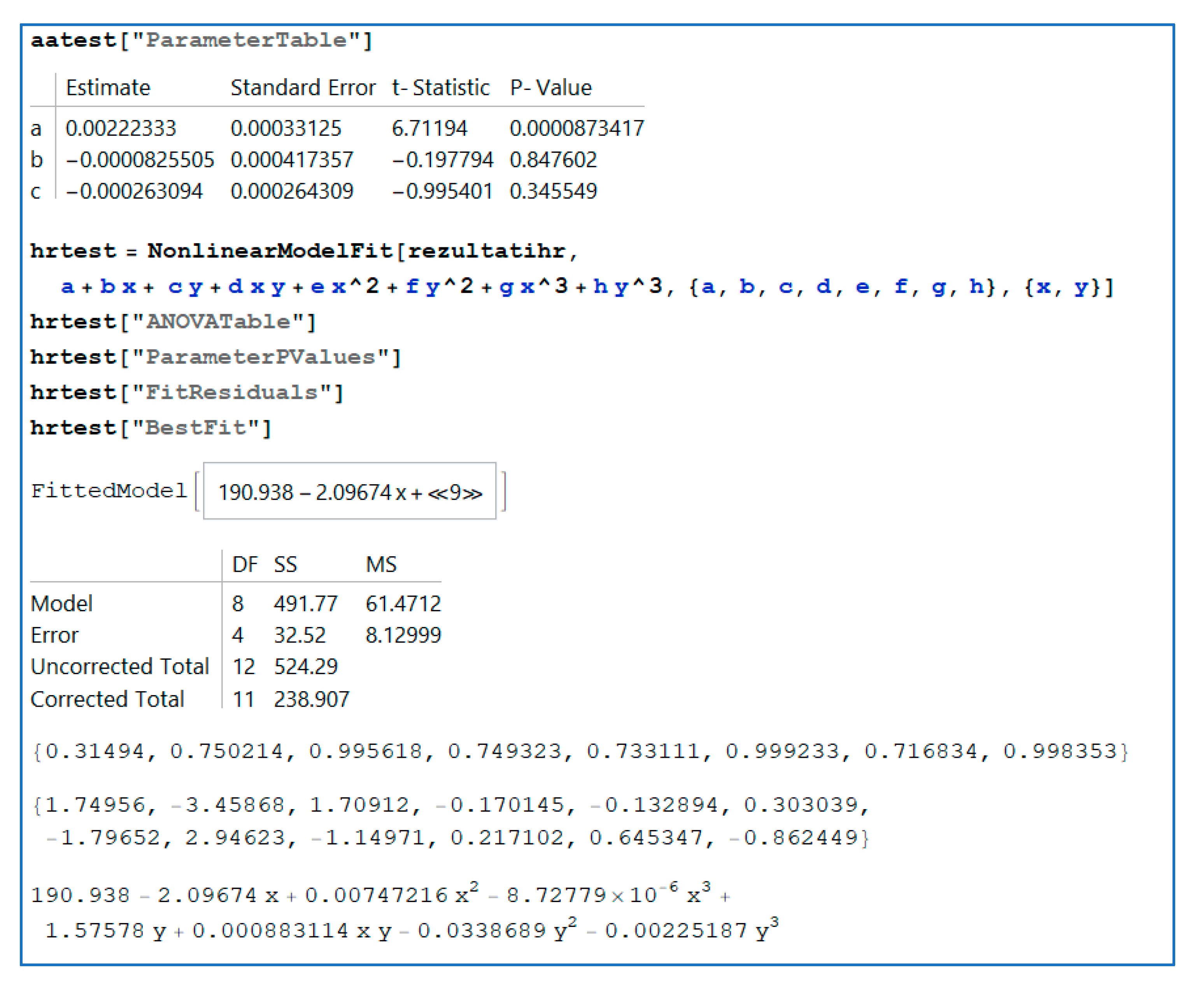
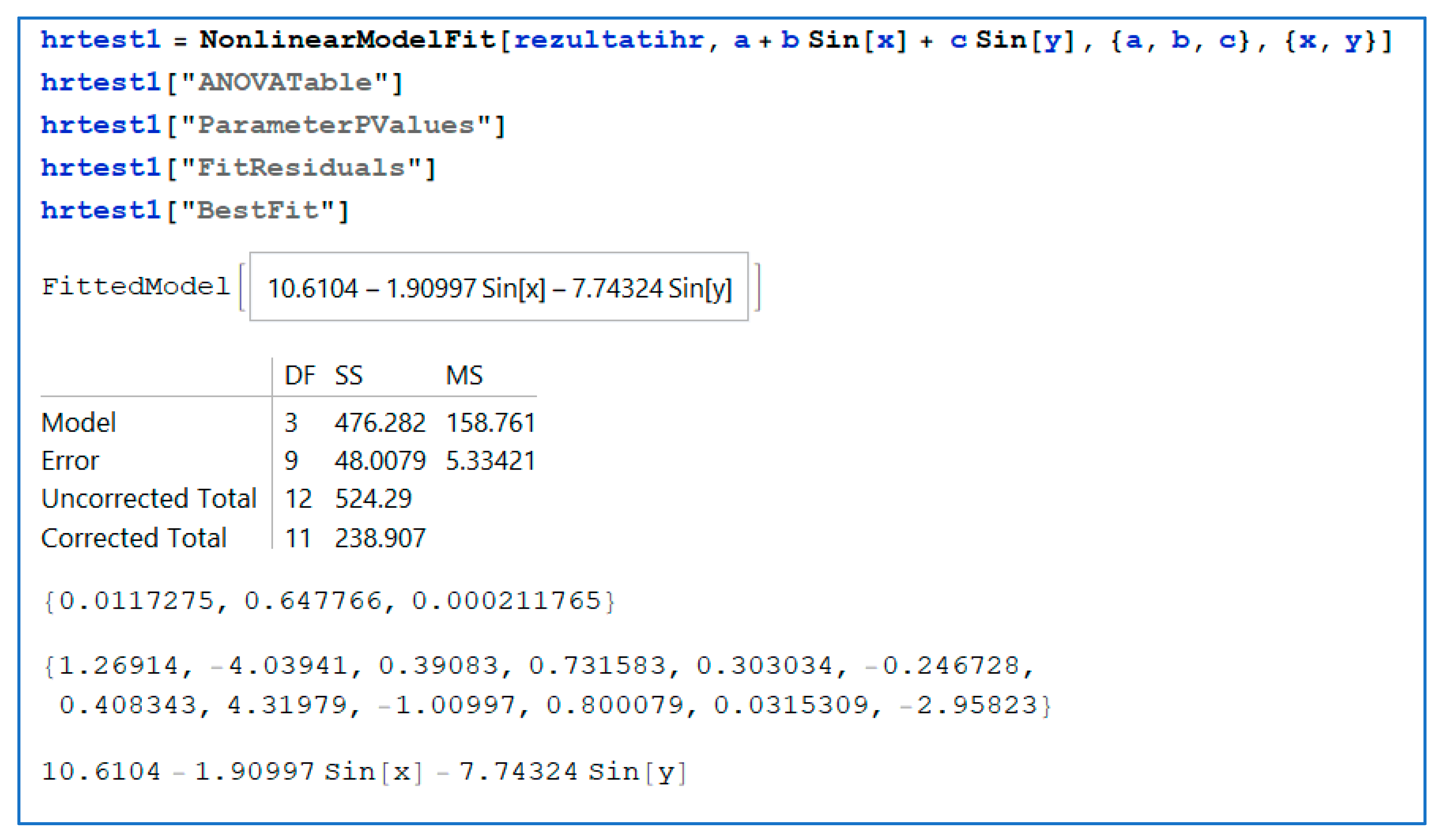
Figure 12 show the code for the analysis of variance (ANOVA) test for each data set or matrix. Matrix rezultati stores the analyzed vibration data from sensor 1, matrix arezultati stores the analyzed data from vibration sensor 2, and matrix rezultatihr stores data from the surface roughness analysis. With the appropriate function (NonlinearModelFit), ANOVA was performed; the ANOVA table, parameter
p values, and residuals were extracted for each prepared set of data.
Figure 11 and
Figure 12 show fitted models and the ANOVA results. The ANOVA tests revealed good statistical significance in the first and second sets of vibration data, whereas models of surface roughness indicated that the model was insignificant. However, for this experiment, we proceeded with obtaining the fit function. Further measurements are planned to improve model significance. In particular, the surface roughness will be measured for more levels of input parameters to determine whether the increased number of input parameters would influence the resulting model and increase the level of significance; otherwise, it would prove that the machining parameters do not impact the surface roughness of the workpiece. Additional data transformation may also improve model significance; this will be explored in future research efforts.
Using the data-fitting function of Wolfram Mathematica 10.2 on the data obtained from each acceleration amplitude sensor, the following mathematical models were obtained.
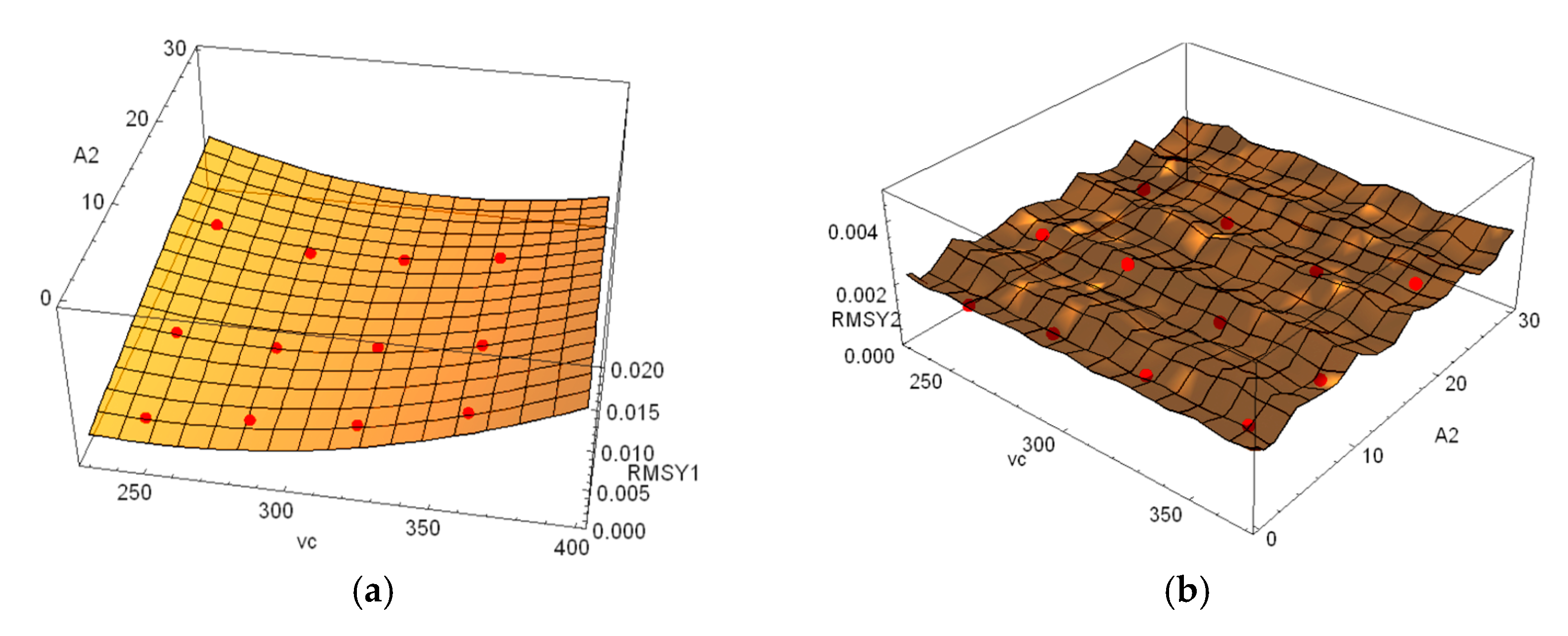
The response surfaces, and measurement points used to derive vibration measurement data for each sensor are shown in
Figure 13. The obtained surfaces and three-dimensional graphs show how the machining parameters impact vibration amplitude levels.
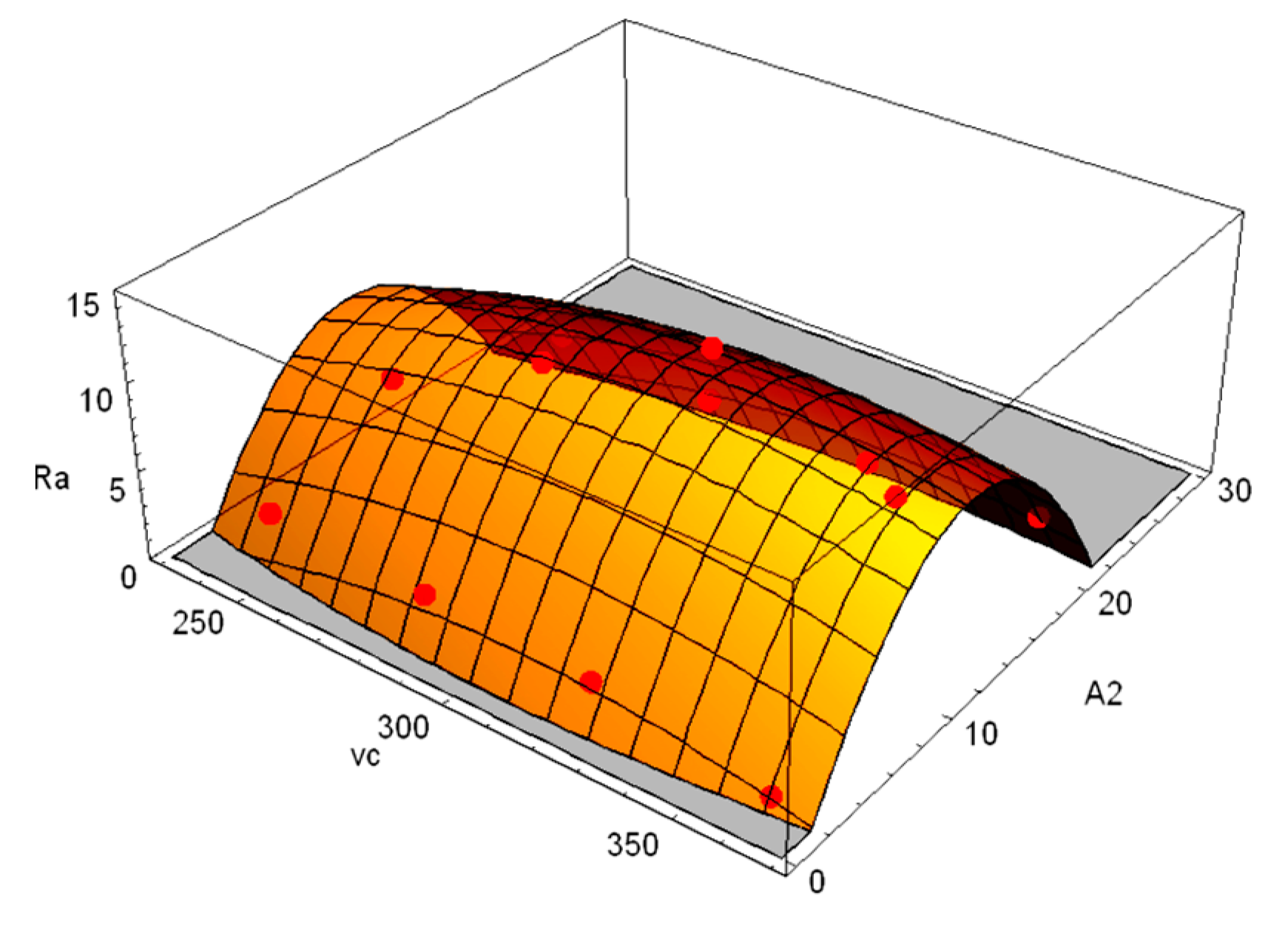
In a similar manner, the
Ra value for surface roughness was determined; the response surface is shown in
Figure 14. For simplicity, physical units on the following graphs are omitted and can be identified using
Table 6.
The current model z2 has a form that significantly differs from the response surface of sensor 1. Further measurements are planned to obtain more accurate results for the real model.
The Wolfram Mathematica 10.2 function was also used to establish the response surface model from roughness measurement data. The impact of machining parameters on surface roughness is shown in
Figure 14. Although upon modification of the prediction model, the ANOVA showed an improvement in model significance (
Figure 15), the sinusoidal model may not provide the best representation of the data. Additional tests with more input variable levels might improve model significance or help to entirely dismiss the chosen model.
The model obtained using the surface roughness data is as follows:
The response surfaces of the vibration data and surface roughness data were compared. Based on the chosen models, it is apparent that the lowest roughness and vibration values of the surface cross-sections are those that occur at higher cutting speeds and larger A2 values.