Experimental Evaluation of Flexible Fixture Stiffness for Steering Knuckles When Loading a Milling Machine Tool

Abstract

In the conditions of the increase in the range of products in the automobile and aircraft industry, there is a tendency to increase the scope of application of flexible fixtures. Thus, in the current article, it was proposed to consider a new concept of a flexible fixture for location parts of a complex shape. The stress and deflection of the steering knuckle elements were calculated using finite element modeling. During the experiment on the static loading, the deflection of the steering knuckle elements was measured, and the results of finite element modeling were validated. It was determined that the stiffness of the proposed flexible fixture ensures compliance with the tolerances of the mutual location of the surfaces of the part, making it reasonable for feature research the novel flexible fixture design during milling.

1. Introduction

The inaccuracies are recognized in dimensions, shapes, and mutual position. Inaccuracy can also be defined as deviations from ideal dimensions, shapes, and the relative position of the part’s surface. The physical causes of deviations from the desired dimensions, shapes, and position of parts surfaces during machining are inaccuracies in the mutual adjustment of the tool, i.e., the workpiece [1], flexibility of the machine–fixture–workpiece system, temperature deformations of the machine–fixture–workpiece system, dimensional wear of the tool, internal tension of the workpiece [2], and deformations caused by clamping forces [3]. Another aspect that affects inaccuracy, form, and size deviations are cutting parameters [4]. Among which cutting speed, feed rate, and depth of cut are the most significant ones. Their influence has a complex effect on machining, i.e., it can lead to high vibrations, cutting tool thermal expansion, or rapid wear. However, in many cases, accuracy of basing in fixture dominates under the cutting parameters effect [5].

State of the Art

Machining of parts with complex forms is often associated with inaccuracy, which corresponds to workpiece deflection under high cutting forces, which may occur because of the allowance deviation [6]. The clamping force also plays a significant role in ensuring minimal deformation of the workpiece, which can be achieved by properly positioning fixture elements [7,8].

The location of parts during machining is an essential aspect of ensuring quality when machining [9]. They provide a rigid and stationary position of the workpiece during machining, which guarantees the accuracy of the dimensions and geometry of the finished part [10]. The correct design of the fixture determines the method of fixing the workpiece, the use of technological capabilities of the machine tool, the choice of cutting parameters [11], and the trajectory of the tool [12]. It significantly affects the setup time of mechanical operations [13]. Currently, approximately fifty-two fixture concepts have been developed. These concepts can be classified into two main groups, i.e., dedicated and standard fixtures. The group of dedicated fixtures is rapidly growing and offers more advantages for the industry. Dedicated fixtures can be component-integrated fixture features (CFFs), feature-based fixturing (FBF), robot-based fixtures (RBFs), flexible fixtures (FFs), modular + singular flex and fixture systems (M + SFFSs), and fixture change systems (FCSs). Though the number of product variants in the automobile industry will not change significantly in the long-term trend, the trend of individualization of part geometry will increase the diversity in shapes and forms of the automobile [14] and aeroengine [15] components. The rapid development of dedicated fixtures is also explained by their potential to be quickly adopted in computer-integrated manufacturing environments [16]. Combined with machine learning techniques, the configuration of flexible fixtures can be optimized to improve clamping schemes [17]. Good potential for structural optimization has a transformable pin array fixture system, comprised of reconfigurable pin array fixtures, that locates and holds parts for assembly and supports parts of different shapes adaptably [18]. Also, dedicated self-adaptive fixtures are available in airplane turbine production [19,20].

One of the crucial directions in investigations of flexible fixture construction is evaluating their stiffness [9,21,22] and stress–strain states [23]. Currently, the most promising tools of fixture research are digital twin technology, artificial intelligence, finite element methods, topology, and parameter optimization [24]. In particular, the technology of digital twins allows the creation of virtual models of machine tools that simulate their behavior in actual conditions and is an effective research tool for optimizing the characteristics of machine tools without the risk of damage to physical equipment [25]. It can also be used to predict component service life and vibration. With the help of an artificial neural network, the data on the fixture’s operation and the layout of fixture fasteners were analyzed [26]. However, the artificial neural network can also be used for a multi-objective approach for automated fixture synthesis [27], deformation force monitoring methods during machining in dedicated fixtures [28], clamping force prediction [29], and even for evaluating the effect of cutting parameters on hole accuracy during machining. Topology optimization appears to be a good solution to improve the shape of fixture parts. As a result of topology optimization utilization, it is possible to improve the trajectory of the cutting tool [30], improve the quality of parts, and reduce the consumption of materials during its production [31]. Feature optimization of the structure design of dedicated fixtures can reduce the positioning error up to 4 µm [32].

Currently, finite element modeling (FEM) is one of the most reliable methods of investigation of deflection and stress–strain states. Complex assemblies can be designed manually or using Feeman chain code [33]. Li E. et al. developed a deformation prediction method based on the spatiotemporal correlation evolution of workpiece geometry, cutting loads, and deformation. Such a calculational setup converts quantities of geometric and physical parameters related to machining deformation [34,35]. A proper clamping scheme can reduce the axial deformation of the part when welding, which was calculated via FEM in SYSWELD software [36]. Based on the FEM calculated and facilitated with optimization of the loading scheme, the proper position of clamps to avoid workpiece deflection was proposed [37]. The impact of alignment uncertainty on workpiece positioning can be evaluated by geometric dimensions and tolerance models using Monte Carlo simulation [38]. At the same time, via the combination of FEM and machine learning techniques, the optimal position of the workpiece fixture was determined [39]. Another application of FEM in the evaluation of the quality parameters of the machining process is the definition of surface flatness and elastic deformation during machining [40]. Weichang G. et al. conducted FEM milling in ABAQUS software based on the dynamic model of mechanical/magnetorheological composite clamping milling. In such a way, the natural frequency ω_w and dynamic displacement q_w, m(t) of the workpiece were defined [41]. Another application of FEM for flexible fixtures calculates the deformation and fixture of the elastic diaphragm. The system was determined to ensure up to 4 µm location accuracy [3,42]. One more aspect that was studied with FEM was machining error during milling [43]. The developed methodology helped evaluate the fixture scheme’s effect on cutting force and machining error [6]. The finite element analysis study evaluated the effect of clamping force on the von Misses stress and workpiece deformation [44,45].

The current paper is focused on the FEM and experimental validation of techniques for validation workpiece deflection at the milling machine tool. The present research proposes that the dedicated, flexible fixture can provide sufficient processing accuracy and that stress in various steering knuckle components under static load be evaluated. Based on these calculations, it is proposed to evaluate the allowable margin for movements at individual transition ranges for each element of the steering knuckle to define the maximum allowable error of machining. In such a way, positioning error and accuracy of basing for the proposed dedicated fixture concept for machining steering knuckles will be defined.

2. Materials and Methods

The present study proposed that the deflection and stress state of the steering knuckle in the dedicated flexible fixture be investigated. For that purpose, the following research methodology was proposed:

(1)

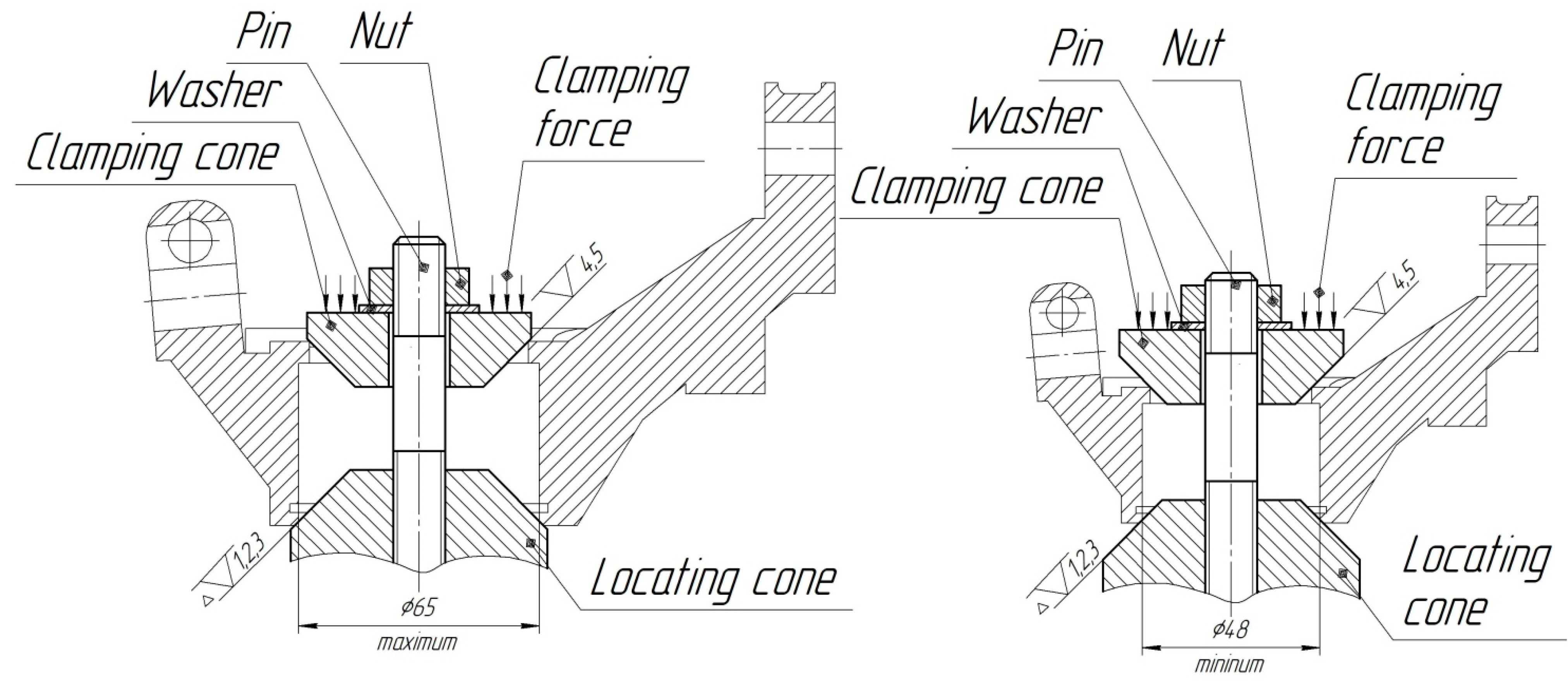
To develop the design of the flexible fixture based on the principles of incomplete locating for machining the maximum number of surfaces of the steering knuckle in one setup.

(2)

To conduct a study of the stress–strain state of the proposed construction using FEM methods.

(3)

Perform experimental studies of the developed design of the flexible fixture and compare them with the results of FEM.

The steering knuckle is a crucial element of the front steering system. It transmits rotational movement to the wheels relative to their vertical axis from the steering wheel through the steering system, enabling them to turn at the desired angle.

The steering knuckles have a rather complex spatial geometric shape, which is due to their purpose and the need to be a connecting link between many parts of the car steering system, such as ball bearings, hubs, ends of the steering rods, shock absorber assemblies, and brackets of the brakes. The steering knuckle plays a significant role in the running system because it contains a wheel hub bearing in its housing. It belongs to the running system, but it includes steering control elements. Generally, the steering knuckle is made of Steel 41Cr4 AISI 5140 with the following chemical composition (

Table 1. Chemical composition of Steel 41Cr4 ISO683-2:2018 by weight [46].

C, %	P, %	S, %	Si, %	Mn, %	Cr, %	Cu, %	Ni, %	Fe, %
0.41	0.035	0.04	0.2	0.8	0.25	0.4	0.25	97.615

) and mechanical properties (

Table 2. Mechanical properties of Steel 41Cr4 ISO683-2:2018 [46].

Young’s Modulus, GPa	Poisson’s Ratio	Density, kg/m3	Tensile Strength, MPa	The Ultimate Strength of the Compression, MPa	Yield Strength, MPa	Hardness, (HRC)
200	0.3	7850	950	950	726	45

) considered during finite element modeling.

The factors as mentioned above, as well as the analysis of the designs of several rotary jaws of cars and all-terrain vehicles (ATVs) (Figure 1), indicate that this part refers to the parts of a complex geometric shape, which contains from three to six smooth holes of conical or cylindrical shape and from five to ten threaded holes. At the same time, the holes and surfaces of the nuts are located at angles in different coordinate planes, which significantly complicates the machining process and requires the use of 5-axis CNC machine tools. However, the number of holes may be more significant depending on the complexity of the product.

Steering knuckles must withstand constant mechanical loads without the risk of part deformation, so the main requirements for the knuckle material are its sufficient hardness and, at the same time, high bending strength.

Thus, the bracket in the unit only rotates around the axis; high runout tolerances of its surfaces are not required. However, position tolerance of the steering knuckle surfaces must be ensured. This condition must be secured at the manufacturing steps of machining. At the same time, the main base is the hole for the hub bearing.

The object of the study was the steering knuckles of middle-class cars and powerful quad bikes (Figure 1), which have the following parameters:

-

Overall dimensions: l × b × h = 120 × 80 × 70–180 × 105 × 100 mm.

-

Mass, m = 1.1–2.5 kg.

-

Accuracy of the central holes—IT 7.

-

Accuracy of the auxiliary holes—IT 7–IT9.

-

Roughness of the auxiliary hole walls and flat surfaces, Ra 1.6–3.2 µm.

In this article, the most common design of steering knuckles was considered (Figure 1), with two main arms equidistant from the axis of the central hole and four auxiliary arms, one of which is located at an angle to the other in the vertical plane (Figure 1d), which in one or another modification is widely used in light-class cars with a capacity of up to 100 horsepower or an engine of up to 1800 cm³.

Currently, there is a wide variety of cars of the light class and other equipment, which includes steering knuckles, on the world markets and in the use of the population. However, as can be seen from Figure 1. Their designs are very similar, and the difference can only be in standard sizes and some design parameters. Therefore, the machining is given a range of products of these parts in one device can be implemented. It is advisable to machine such parts on modern five-axis CNC machines, which have the function of automatic binding to the machine’s workpiece and can be oriented in any way relative to the machine elements. This makes it possible to depart from the principle of complete orientation of the workpiece in the device, ensuring sufficiently reliable clamping and excluding any displacements during the machining.

This approach to the design of flexible fixtures using the example of connecting rods [13,47] and forks [48] has shown its effectiveness in terms of achieving minimum deformation rates and not exceeding their permissible values arising under the influence of loads from cutting forces acting on the surface finish in the “fixture–workpiece” system.

In previous studies [13,47] based on maximal stress and deflection evaluation by a physical measurement and FEM calculations, it was found that both of these parameters can be ensured within appropriate limits. In such a way, the proposed concept of incomplete orientation can be utilized for other complex form parts, for example, steering knuckles. The locating chart of the steering knuckles consists of locating points on the top and clamping points on the bottom (Figure 2).

This setup scheme provides only two surfaces for the workpiece bases for machining the holes on the heads’ surfaces on the steering knuckles’ shoulders. The surface of the central hole’s internal chamfer contacts the fixture’s external conical surface. The conical surface of the fixture centers the workpiece from displacement on the sides and downwards in the axial direction. Another annular surface of the ledge on the upper part of the workpiece in contact with the corresponding external conical surface of the fixture washer will center the workpiece against lateral displacement.

Thus, only one degree of freedom remains free, namely the workpiece’s rotation around the central hole’s axis. Clamping of the workpiece is carried out by evenly applying force to the annular surface of the opening of the outer ledge.

Thus, based on the location chart (Figure 2), the design of the flexible fixture that allows the implementation of this scheme is proposed. The proposed flexible fixture is intended for the setup of steering knuckles of different sizes in the range of diameters of the central hole 48–65 mm (Figure 2). The height of the central part of the steering knuckles between the end of the outer ledge and the end of the landing surface from the side of the central hole is 30–80 mm. The adjustment of the range is carried out by screwing the nut, which provides both a change in the distance between the supporting cones of the device and the clamping force for the workpiece between the cones. The lower and upper support cones are made with grooves for better clamping of the workpiece during machining and to prevent rotation.

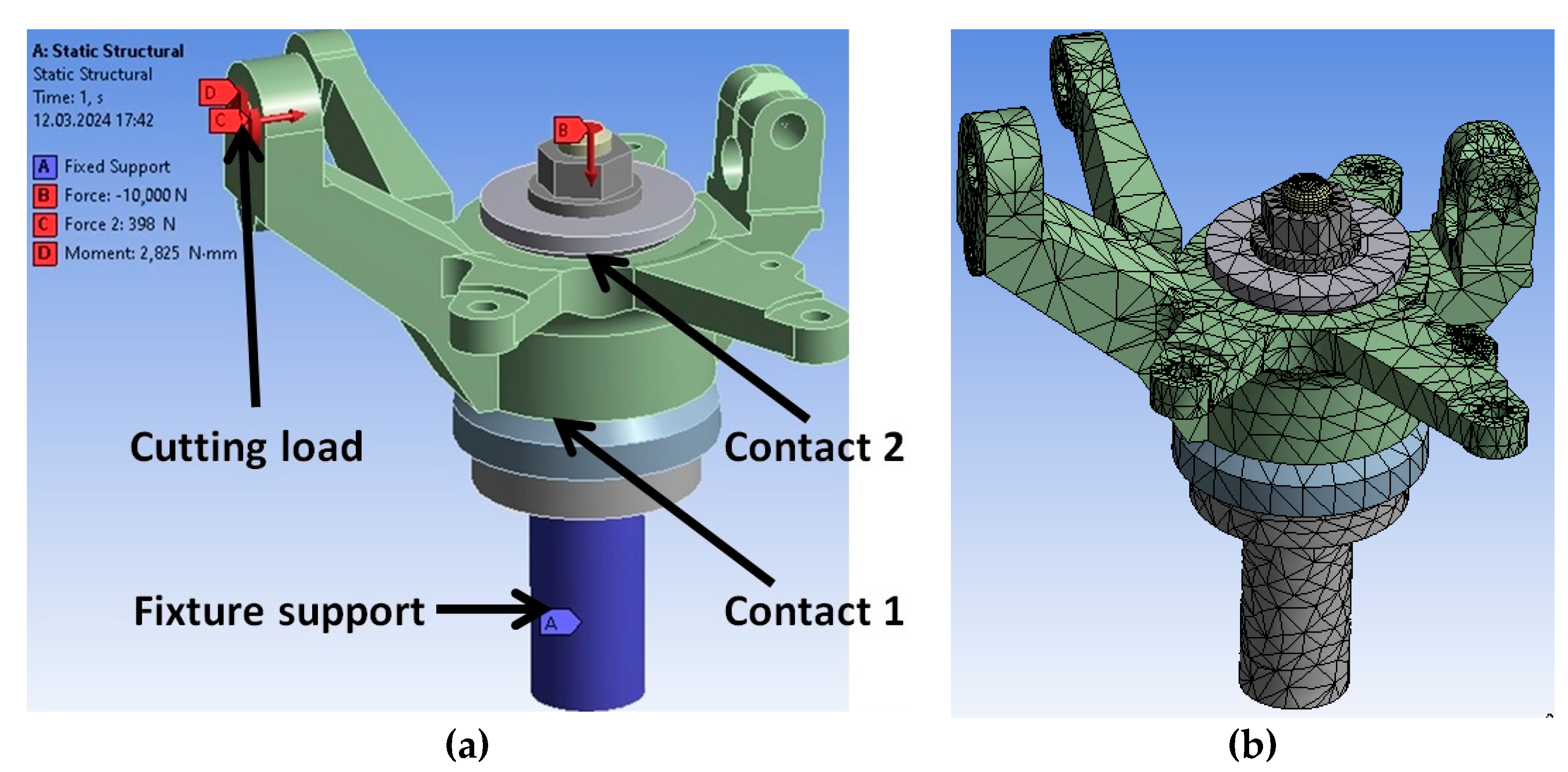
2.1. Set Up of the Finite-Element Method Calculations

The improved flexible fixture was investigated using numerical simulation of the stress–strain state in the Static Structural module of the ANSYS ver. 19 Workbench Software (ANSYS, Inc., Canonsburg, PA, USA). At the same time, the deflection of the movement of the machined surfaces of the part (marked in red in Figure 3) relative to their initial position will also be evaluated.

During the FEM calculations, several boundary conditions were established (

Table 3. Contact conditions of improved fixtures for steering knuckles.

Parameters of Implemented Contact Groups
Contact	Contact Surface	Type of Contacting Surface	Friction Coefficient
1	working surface of the bottom cone/cone surface of the steering knuckles	corrugated/machined	0.7 [13]
2	the working surface of the top cone/cylindrical surface of the top face of the steering knuckles	corrugated/unmachined	0.3 [13]

) [13,48].

Since the fixture will be operated under normal conditions and the type of production will be small and medium series, the recommended material for producing fixture parts is C45 steel, with the following chemical composition (

Table 4. Chemical composition of Steel C45 BS EN 10083 by weight [49].

C, %	P, %	S, %	Mn, %	Cr, %	Fe, %
0.45	0.025	0.035	0.8	0.5	98.19

) and mechanical properties (

Table 5. Mechanical properties of Steel C45 for the workpiece and fixture elements [49].

Young’s Modulus, GPa	Poisson’s Ratio	Density, kg/m3	Tensile Strength, MPa	The Ultimate Strength of the Compression, MPa	Yield Strength, MPa	Hardness, (HRC)
200	0.3	7850	932	932	784	33

). These mechanical properties were considered in finite element modeling.

The calculation model also considers the Coulomb friction between the contact surfaces of the fixture parts with a coefficient of 0.1 since they have approximately the same roughness in the Ra 1.6–3.2 μm. The surface for location that was proposed in the current device is the shank (surface A in Figure 3). This type of fastening simulates its rigid clamping in the chuck on the machine table using the Fixture Support contact type, which assumes its complete immobility (in this case, the entire technological system is not investigated, but only the “fixture–workpiece” system).

During the FEM, the contact type of the other elements that have an abutment with each other, except for the contact of the lower support cone and the workpiece and the upper extraction cone and the workpiece, was set as bonded. The contacts of the lower support cone and the workpiece and the upper extraction cone and the workpiece were set as frictional, with the corresponding coefficient of friction (Table 3), because the surfaces of these cones have grooves that will help keep the workpiece in place due to force friction, which will be created by the normal force that will act when the nut is tightened [2]. A hexahedral finite element (SOLID 185) was used for calculating plasticity, hyperelasticity, stress stiffening, creep, large deflection, and significant strain capabilities, which properly fit the purposes of structural analysis [50].

Since the machined surface has no requirements for accuracy higher than 0.2 mm, the size of the finite-element mesh cannot be set less than this value. The mesh was generated using an additive software algorithm that automatically creates mesh for each surface depending on its design parameters and the basic settings of the ANSYS Workbench. As a result, the finite element mesh with 32,606 elements and 88,197 nodes was generated.

During FEM, loading forces and moments were applied to each surface one by one. First, the force was applied to one surface and the results were determined; then, the force was excluded from the calculation and another design force was applied to the other surface. Since CNC machines are usually single-spindle for greater versatility, they are typically machined with one tool. The value of cutting forces at different manufacturing steps varied within 25–398 N and torques 1105–2825 N · mm depending on the method and stage of machining. At the same time, an axial clamping force of 10,000 N was applied to the pin, which, with a pin strength class of 10.9, does not exceed 30% tensile strength.

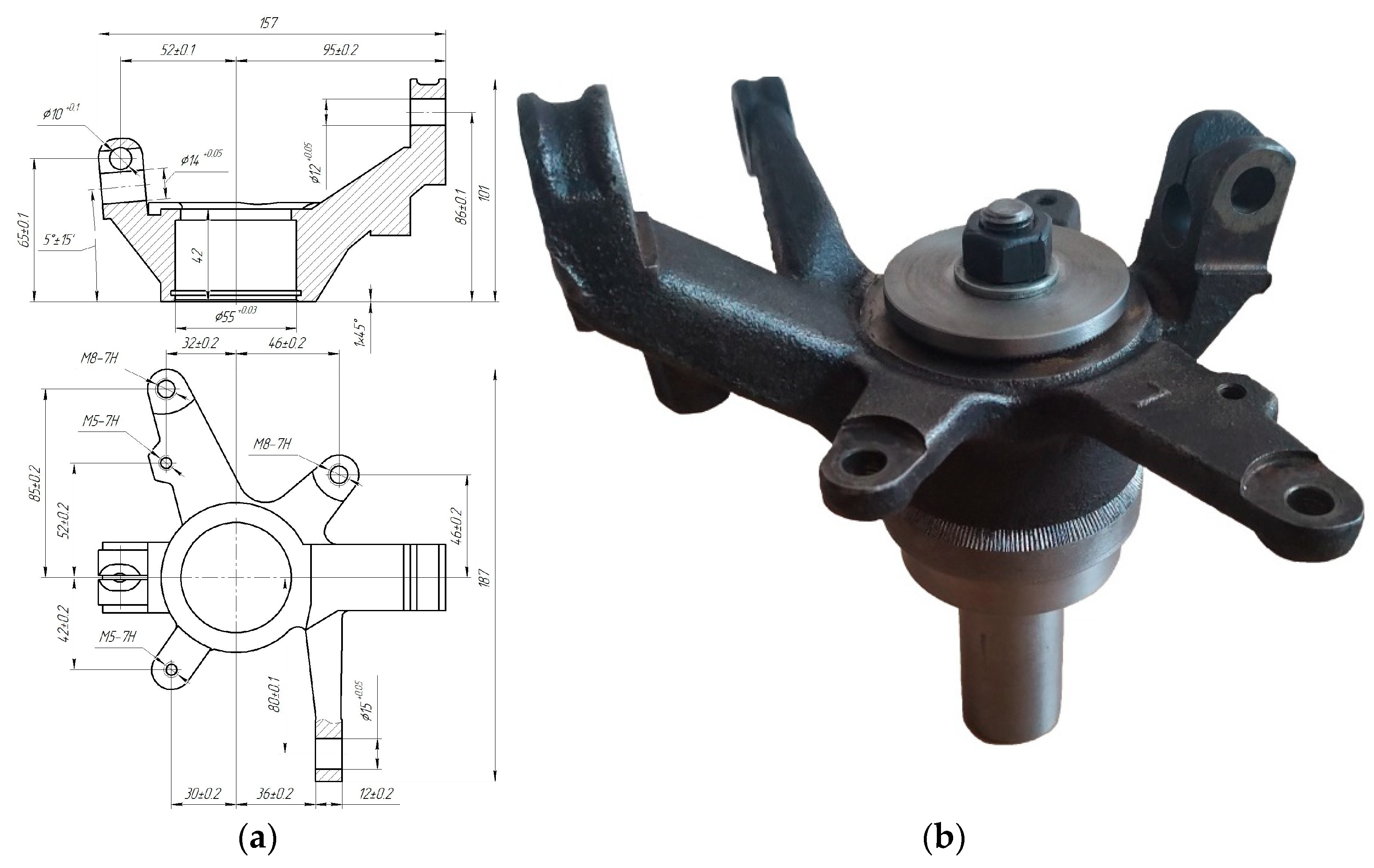
2.2. Physical Measurement of Steering Knuckle Deflections

Experimental studies of the stress–strain state of the “fixture–workpiece” system are an intermediate stage between FEM and machining. A static experiment is also necessary to check the adequacy of the finite element analysis results by comparing them with the results of physical experiments. A fixture and its parts were manufactured based on 3D models of the fixture concept. Accuracy of fixture parts manufacturing and assembling was ensured according to the [51]. The steering knuckle of the BRP Can-AM Outlander L Max 500 DPS ATV was taken as an experimental sample (Figure 4).

Static loading of the part was conducted to investigate the value of part elements’ deflection under the force applied to specific machined areas. A custom test setup (Figure 5) was built to recreate the effect of a milling machine (Model 676P) load on the steering knuckle elements during machining [18].

The experimental setup (Figure 5) consists of the flexible fixture (1), which was clamped into a three-jaw chuck (2) mounted on the machine table. A force was loaded on the workpiece using a mandrel installed in the machine spindle (3). Additional interchangeable mandrels (4) were used on the steering knuckles to mount a mechanical dynamometer (5). This dynamometer is a calibrated spring device from Mohr and Federhaff (Mannheim, Germany) and has a known stiffness of 6 N/μm. The mandrel deflection was measured with a dial gauge with a graduation of 1 μm. The deflection of steering knuckle elements was measured with another dial gauge (6) (Shahe (5310-10) 0–12.7 mm, graduation of 1 μm) (Wenzhou Sanhe Measuring Instrument Co., Ltd., Wenzhou, China) installed on the opposite side of the loaded surface. The loading of elements was repeated three times.

3. Results

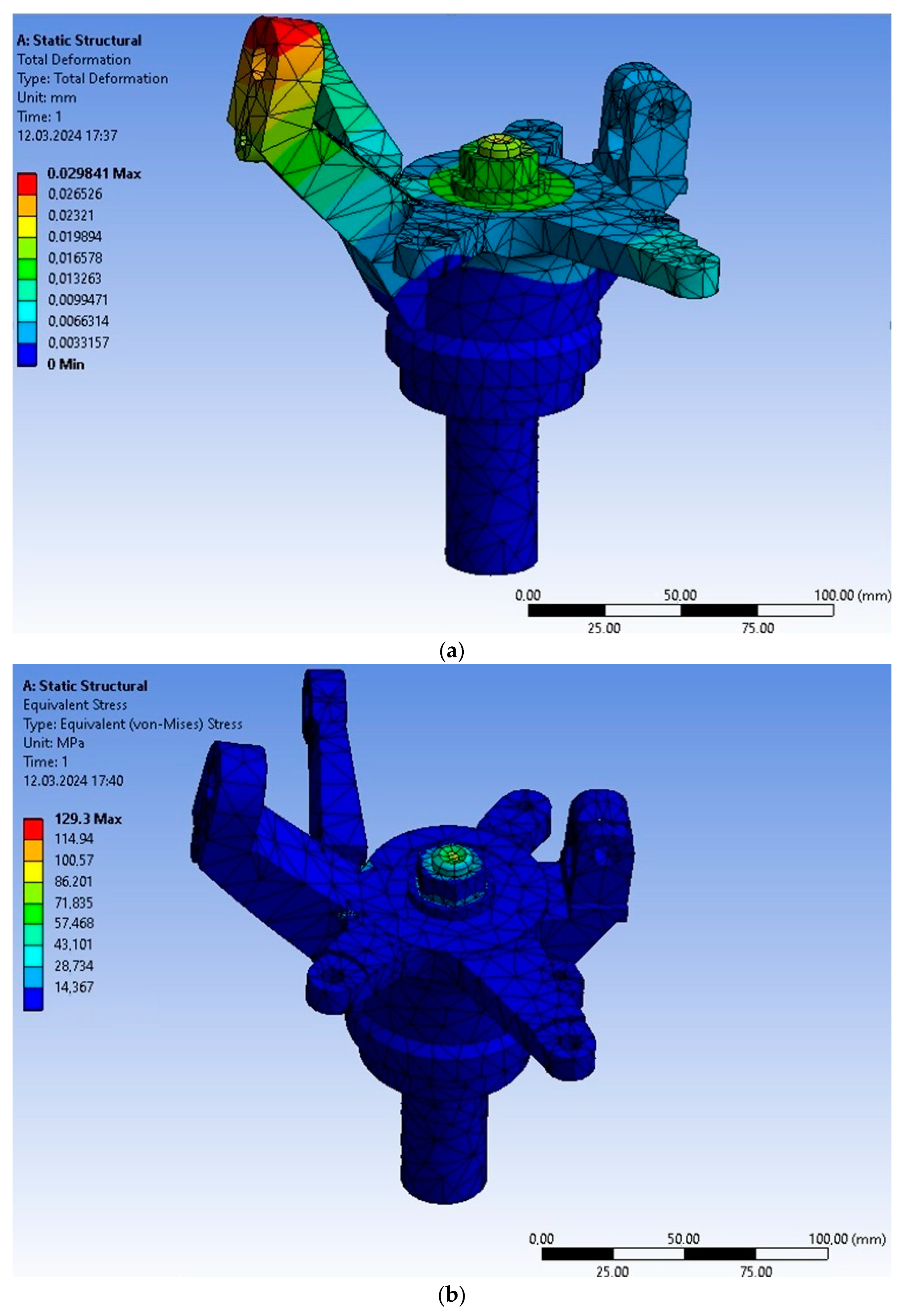
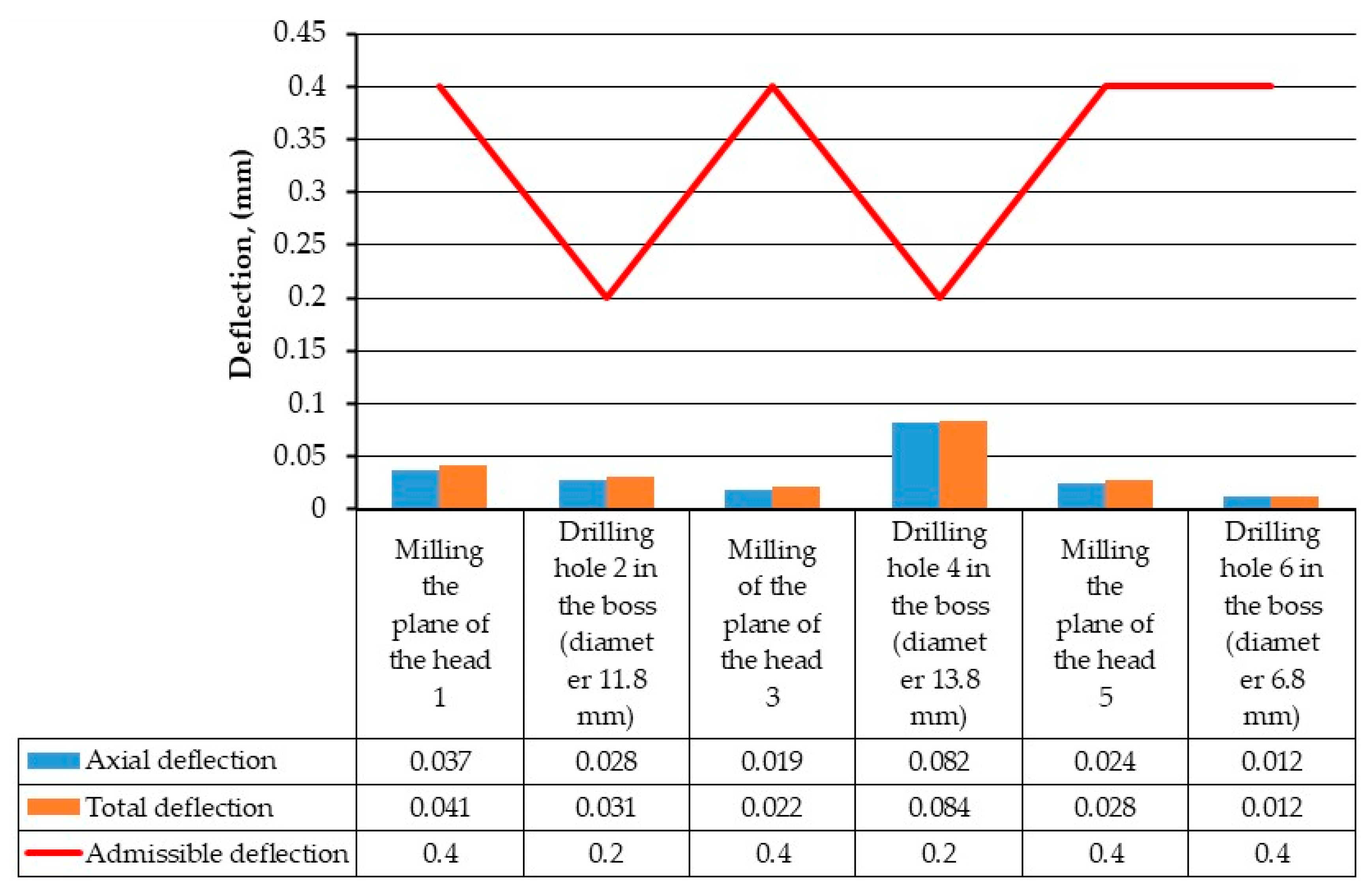
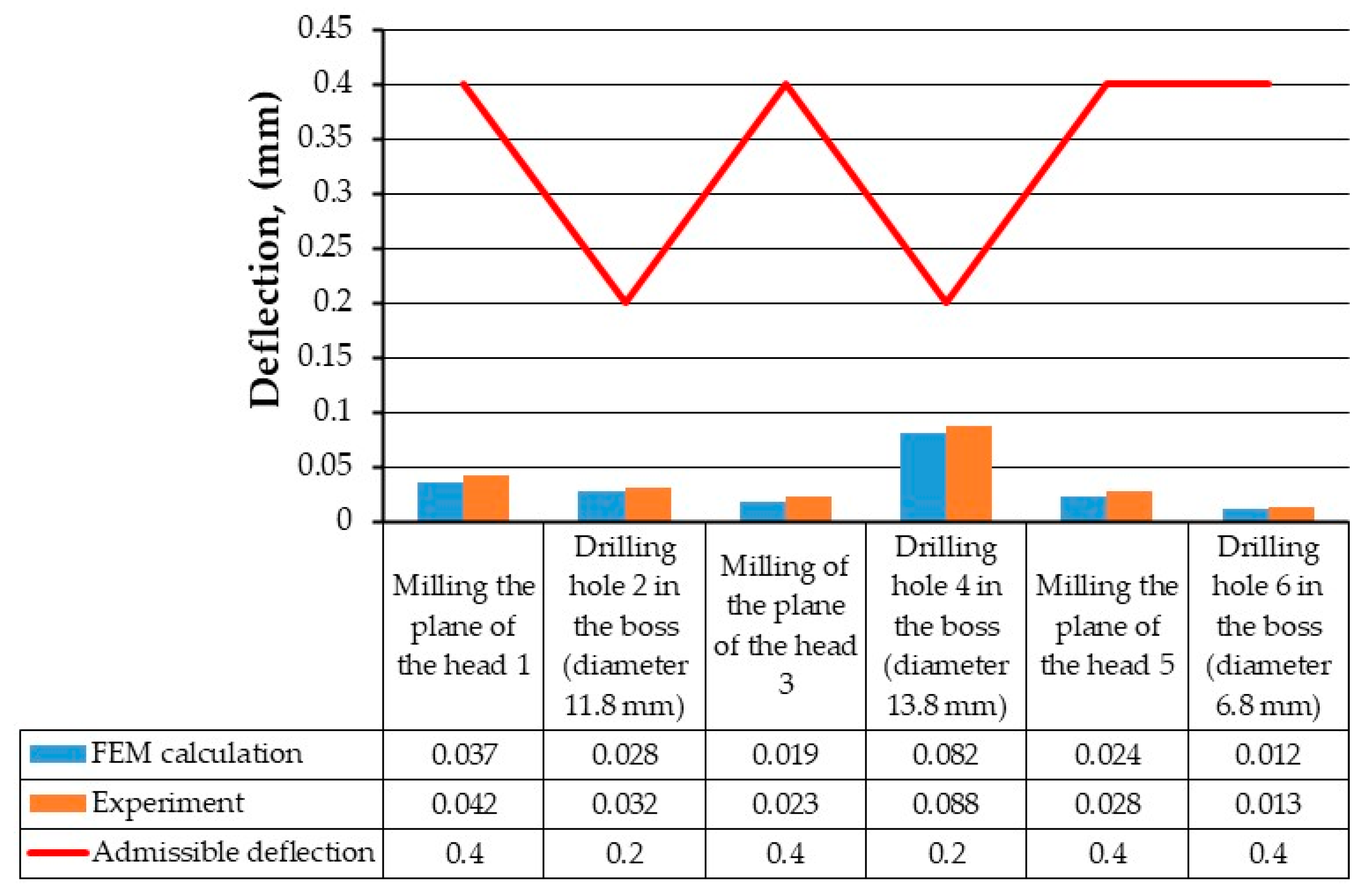
Analysis of the Finite Element Modeling

Setting these boundary conditions ensured proper setup fixture static loading with forces and torque. Load modeling was performed for the most loaded transitions and in those places where the fastening force was at the maximum distance from the machined surface (Figure 6). The values of the maximum equivalent stresses according to the IV hypothesis of Mises’s strength and maximum deflection of the elements of the “fixture–workpiece” system were obtained. The process of FEM was carried out similarly as in [13,48], the results of which showed their adequacy in confirmation by the results of physical experiments [47].

It can be seen from the results of the stress diagrams obtained in the “machine tool–workpiece” system (Figure 7b) that all the parts of the device and the workpiece are of uniform strength, except for the pin, where the maximum Mises stress is 129 MPa, because its stretching causes this as a result of applying the necessary fastening force to ensure reliable retention of the workpiece. The magnitudes of the general deformations (Figure 7a) indicate that the maximum displacements are expected at the processing point at the maximum distance from the attachment point and the fixture, respectively. However, simultaneously, the values of total displacements and displacements along the coordinate axes do not exceed a third of the size tolerance in the worst case of the FEM of a flexible fixture with an incomplete location for steering knuckles (deflection) (Figure 7a).

In general, the flexible fixture design based on the static analysis results looks relatively rigid, and the design features of the workpiece itself determine the maximum movements. However, there is no need for additional support because all loads are within permissible limits. This indicates that the process is not a force, but the difficulties in the manufacture and creation of special devices for almost each of the transitions of mechanical processing are determined not by the need to increase rigidity but only by the equipment’s capabilities at that time.

For loads at various manufacturing steps, the deflection of steering knuckles varied from 0.012 to 0.082 mm (Figure 8). Maximal axial deflection is characterized by a maximal axial load equivalent to the drilling of a 13.8 mm hole, which correlates to values of equivalent stress (Figure 9). Neither limits of admissible deflection nor admissible stress were broken under loads during static testing.

The results FEM of the main transitions of machining in the proposed flexible fixture showed that it is possible to achieve the required dimensional accuracy since the total deflection, as well as the values along the coordinate axes in the corresponding direction of the load, do not exceed the absolute limit values. Static stresses during the application of loads are also within acceptable limits according to the characteristics of the corresponding materials. The most stressed element of the system is the workpiece, where the arms of the steering knuckles are attached to the center of the part.

As a result, data on parts’ element deflection were collected and compared with the results of the FEM (Figure 10).

The values of deflection obtained experimentally do not exceed the allowed values, although they are higher than those obtained in FEM. The deviation of FEM and experimental results varied in the range of 6.8–17.3%, depending on the force load. The measurement uncertainty of the measuring tool and approximation of FEM results can explain this. However, in this case, the maximum relative error was less than 20%, despite the size of the margin to the allowed values of displacements being quite significant compared with the actual values of displacements at specific stages.

4. Discussion

Based on the results of FEM, the magnitudes of stresses and displacements in the proposed machine tool for processing parts of the steering knuckle type, using the principles of incomplete location, theoretically prove that the values of stresses in the structural elements do not exceed the permissible values according to the mechanical characteristics of the materials of the parts machine stand and workpiece. At the same time, the value of the maximum stresses at the transition with the most significant loads is 238 MPa, which is 2.5 times less than the permissible values. It was also established that the values of the total displacements of the processed surfaces in the proposed machine tool do not exceed the tolerances on the processed surfaces, and at the same time, there is a significant margin of accuracy for the performance of this technological operation because the displacement during processing is less than the permissible values from 2.4 to 30 times depending on specific transitions. According to the drawing, the values of movements along the coordinate axes along which the load was applied also do not exceed the allowable values.

From the experimental results, it can be seen that the design of the developed machined device for processing steering knuckles can provide the necessary accuracy of processing under static load since the magnitudes of displacements are, albeit, more significant than during numerical modeling by 1–6 μm, which in relative terms is 6.8–17.4% depending on the value of force load but still do not exceed the allowed values.

As for the comparison with the other authors research in this field, in particular, in the article [27], the authors present a multi-purpose approach to the synthesis of machine tools in a discrete area, where the criteria of efficiency are accuracy of basing, disconnection of reference points, deformation workpieces, degree and dispersion of reaction loads, and distance between contact points. This approach has been tested and proven effective for automating the reliable design selection of a machine tool for a prismatic workpiece. However, studies have not been conducted on other types of blanks. Experimental verification was also not performed.

The work [52] shows the development of new algorithms and machine learning with the possibility of using regression methods to create realistic, fast, and reliable equivalent models instead of modeling based on the finite element method. The paper also presents a new method that allows for the optimization of clamping concepts and the machine tool’s design with machine learning to help reduce errors during the production of parts and to obtain increased rigidity and accuracy of processing. However, as an example for modeling, a box-shaped workpiece with a stiffening rib in the middle was chosen, which cannot describe all types of interaction of the workpiece with device elements, and the simulation results were not confirmed experimentally.

Based on the results of theoretical and experimental studies, it was established that the proposed scientific approach to designing machine tools with incomplete location and ensuring the necessary stable position during processing due to clamping forces allows obtaining the specified accuracy. This proves the correctness of the working hypothesis [13,47] that devices with incomplete locations can ensure the specified processing accuracy, and this article is a logical continuation of previous research in this area and confirms this hypothesis experimentally.

5. Conclusions

In the current paper, the evaluation of static stiffness of steering knuckles in the flexible fixture was carried out using the finite element method and an experimental static tensile test. that the following was found out:

• A flexible fixture with an incomplete location for steering knuckles provides sufficient accuracy at all transitions of a multi-purpose operation. Using FEM methods, it was evaluated that the maximum stresses of 238 MPa at the most loaded transition and the smallest part of the workpiece do not exceed the tensile strength, and at the same time, a margin of 2.5 times is preserved.
• The proposed flexible fixture for machining parts steering knuckles can ensure the necessary accuracy under static loading since the movements do not exceed the permissible values on the corresponding surfaces according to the drawing. Although they are more significant than the results of FEM, in the worst case, by 17.4%, this allows to discuss the prospects of introducing fixtures with incomplete basing for machining other types of complexly shaped parts such as brackets, rockers, etc.
• Validation of FEM and experimental results evaluated that a scientific approach to designing fixtures with incomplete locations allows obtaining the specified processing accuracy while ensuring the necessary stable position exclusively by clamping forces.
• Further research will focus on the experimental determination of fixtures’ accuracy and stiffness characteristics of steering knuckles in dynamic mode during machining.