Erosion Analysis and Optimal Design of Sand Resistant Pipe Fittings
Abstract
1. Introduction
2. Erosion Analysis
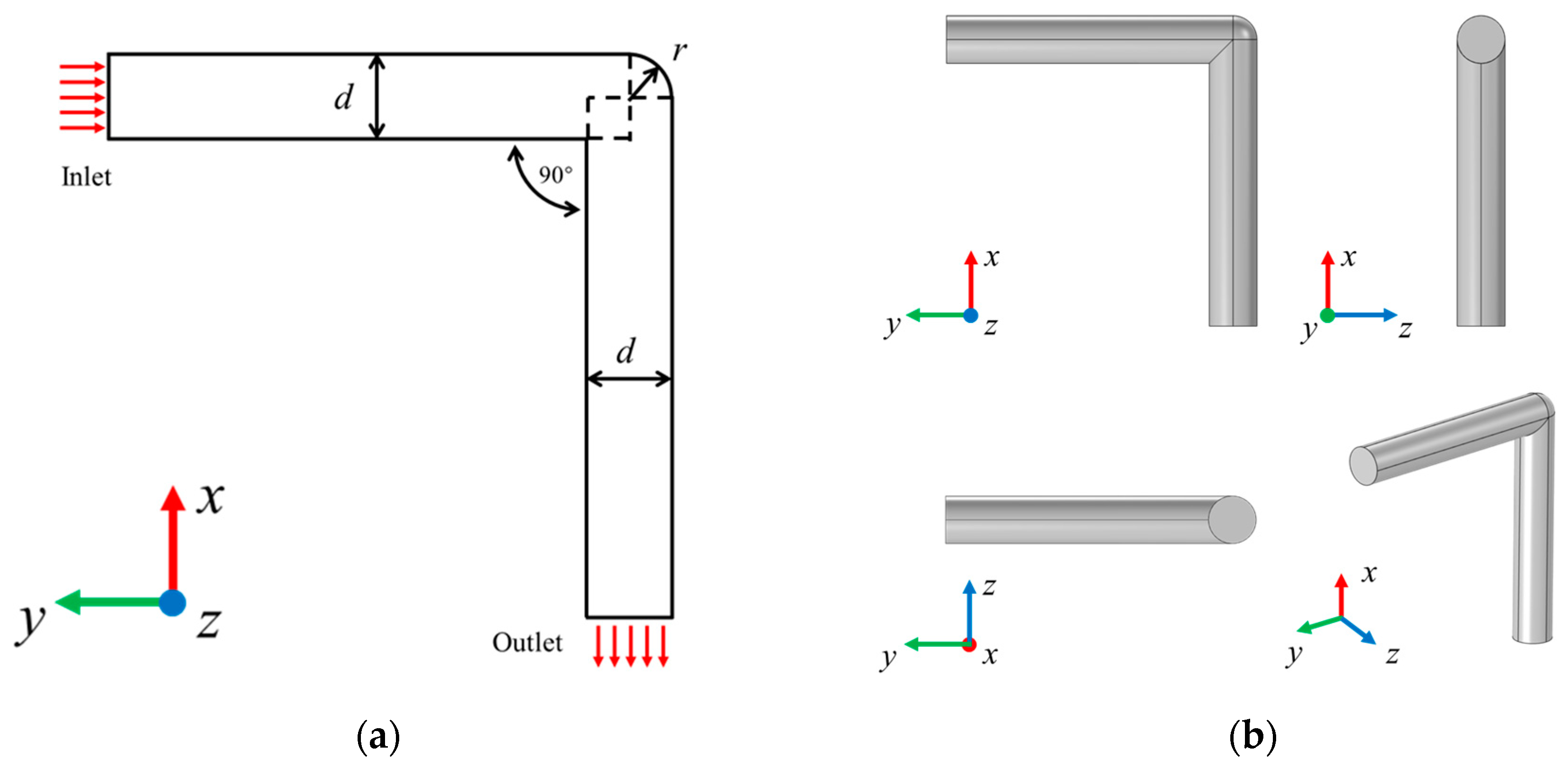
2.1. Geometric Construction
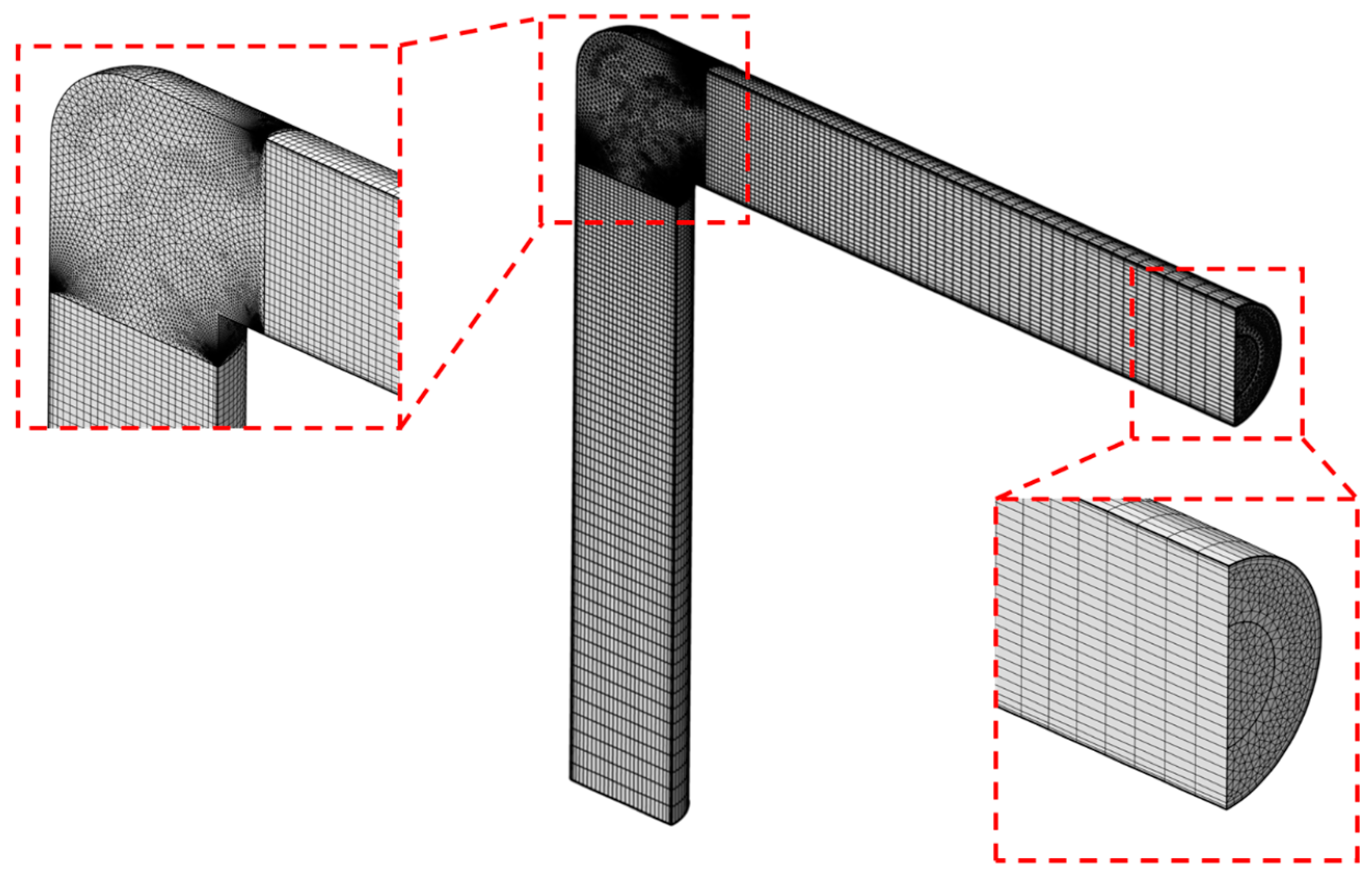
2.2. Numerical Model
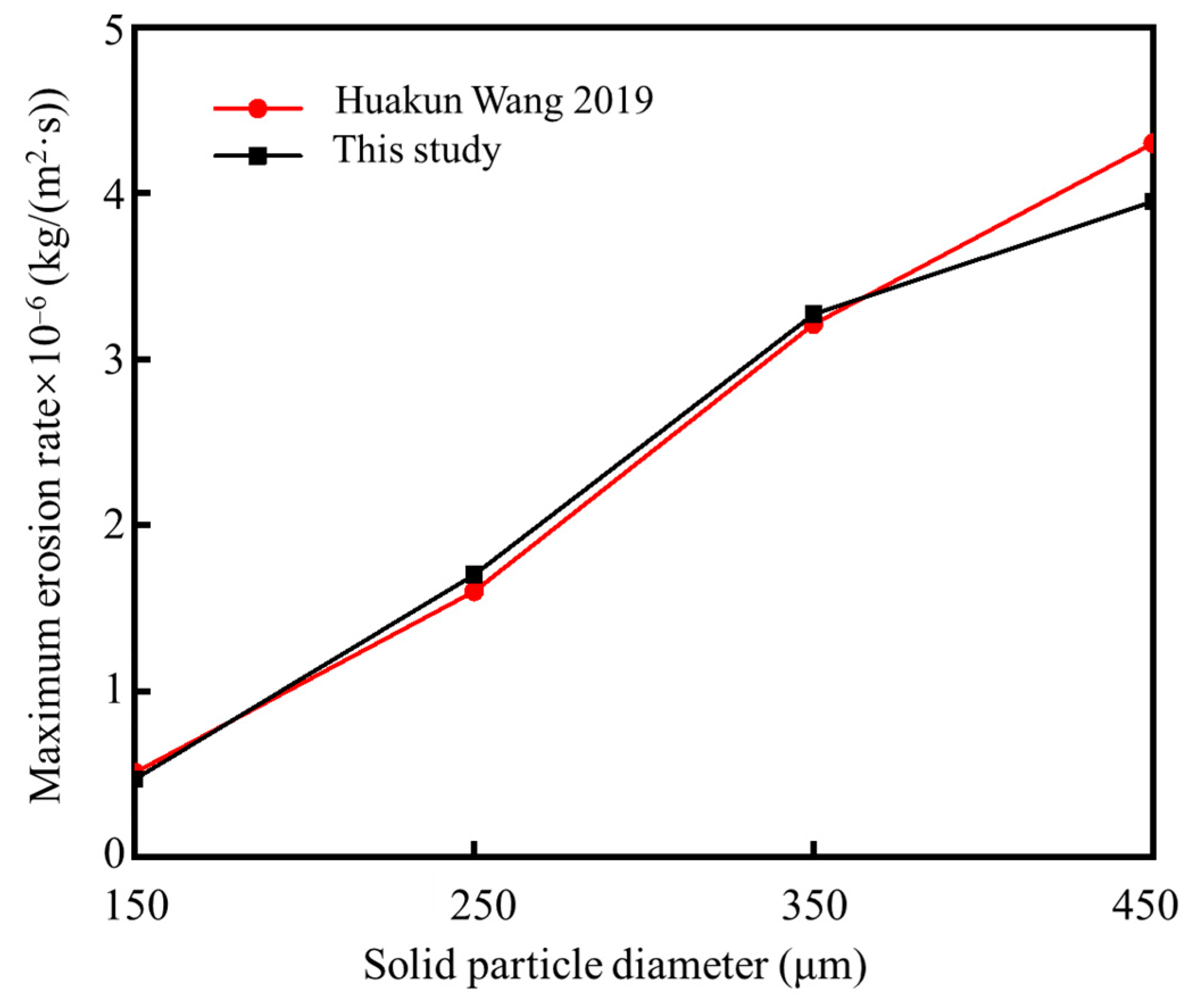
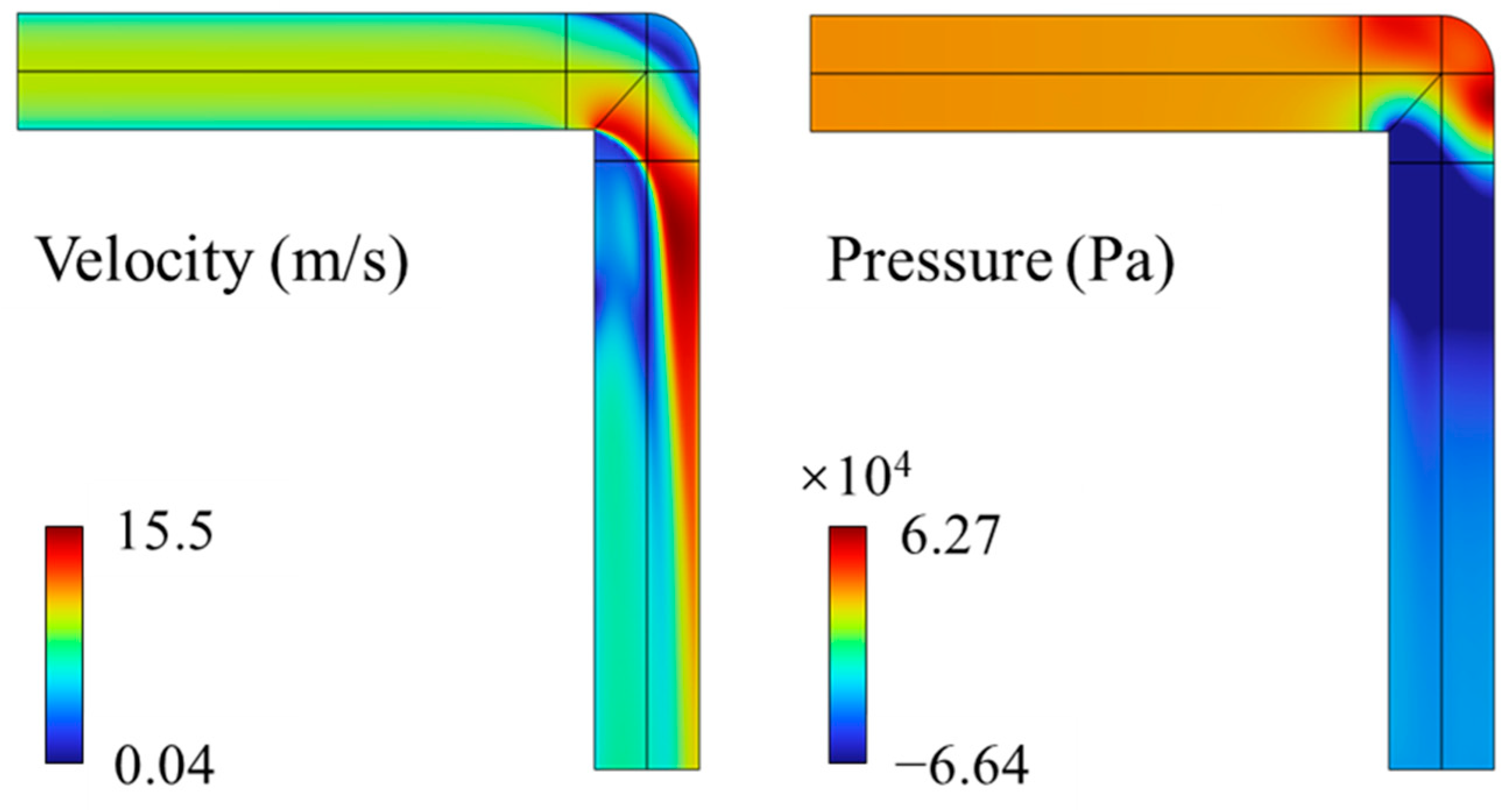
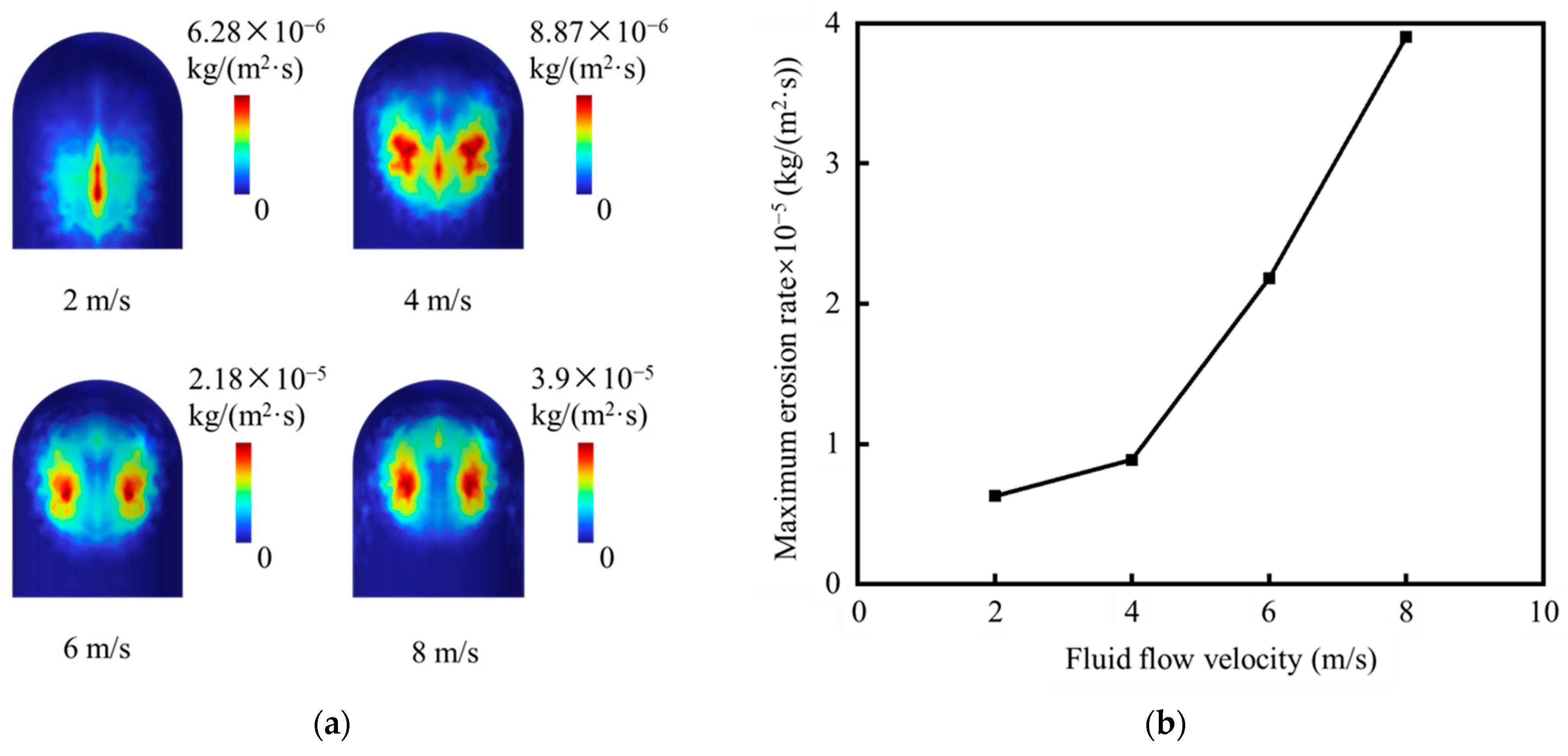
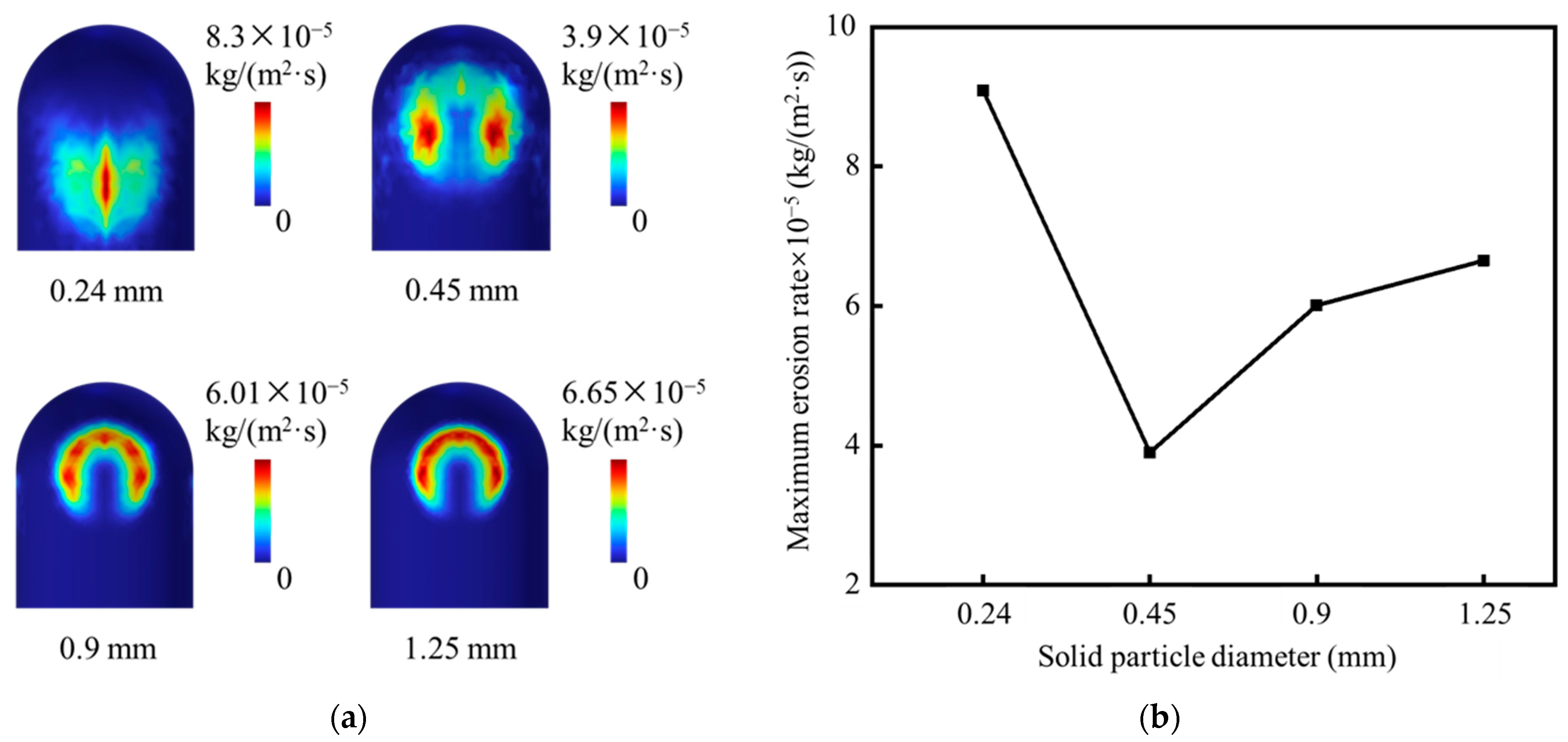
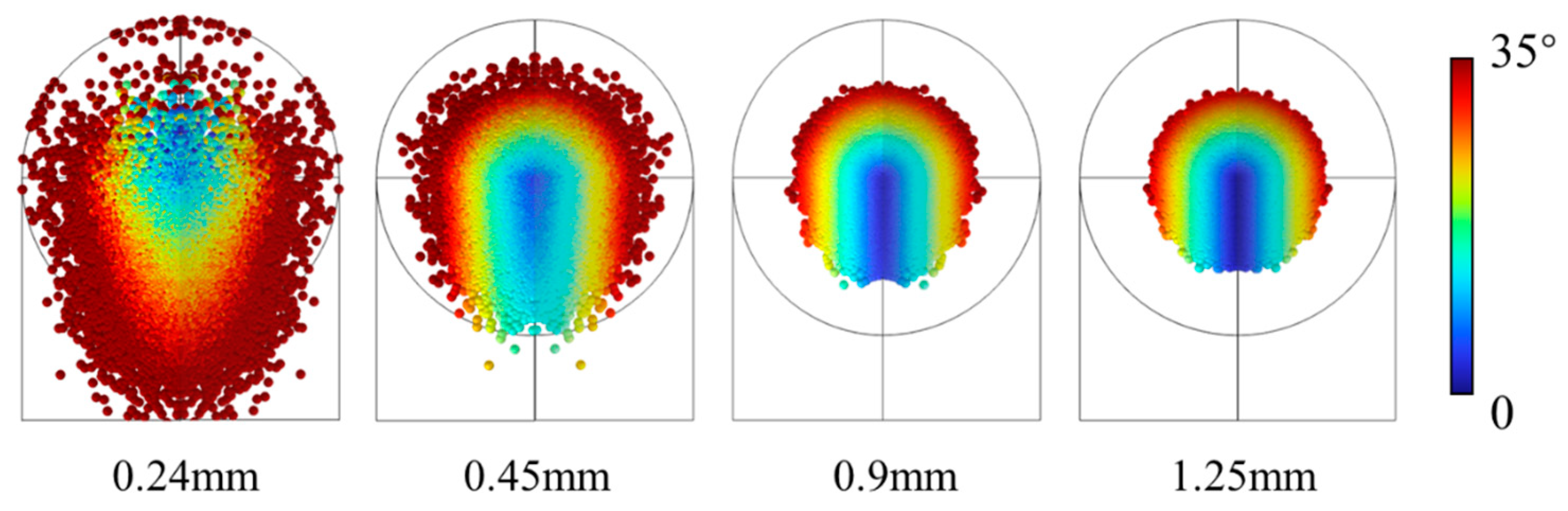
2.3. Results and Analysis
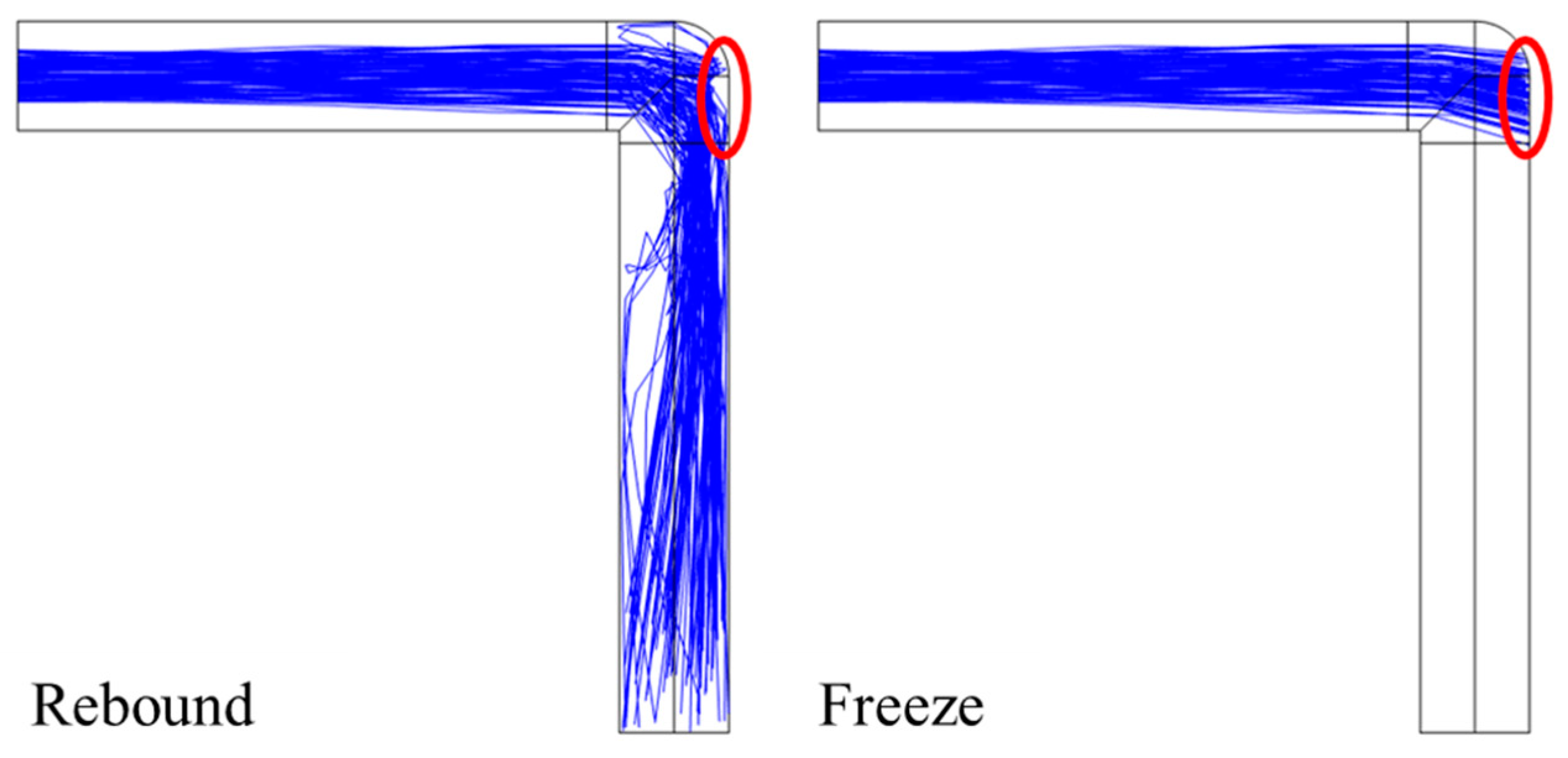
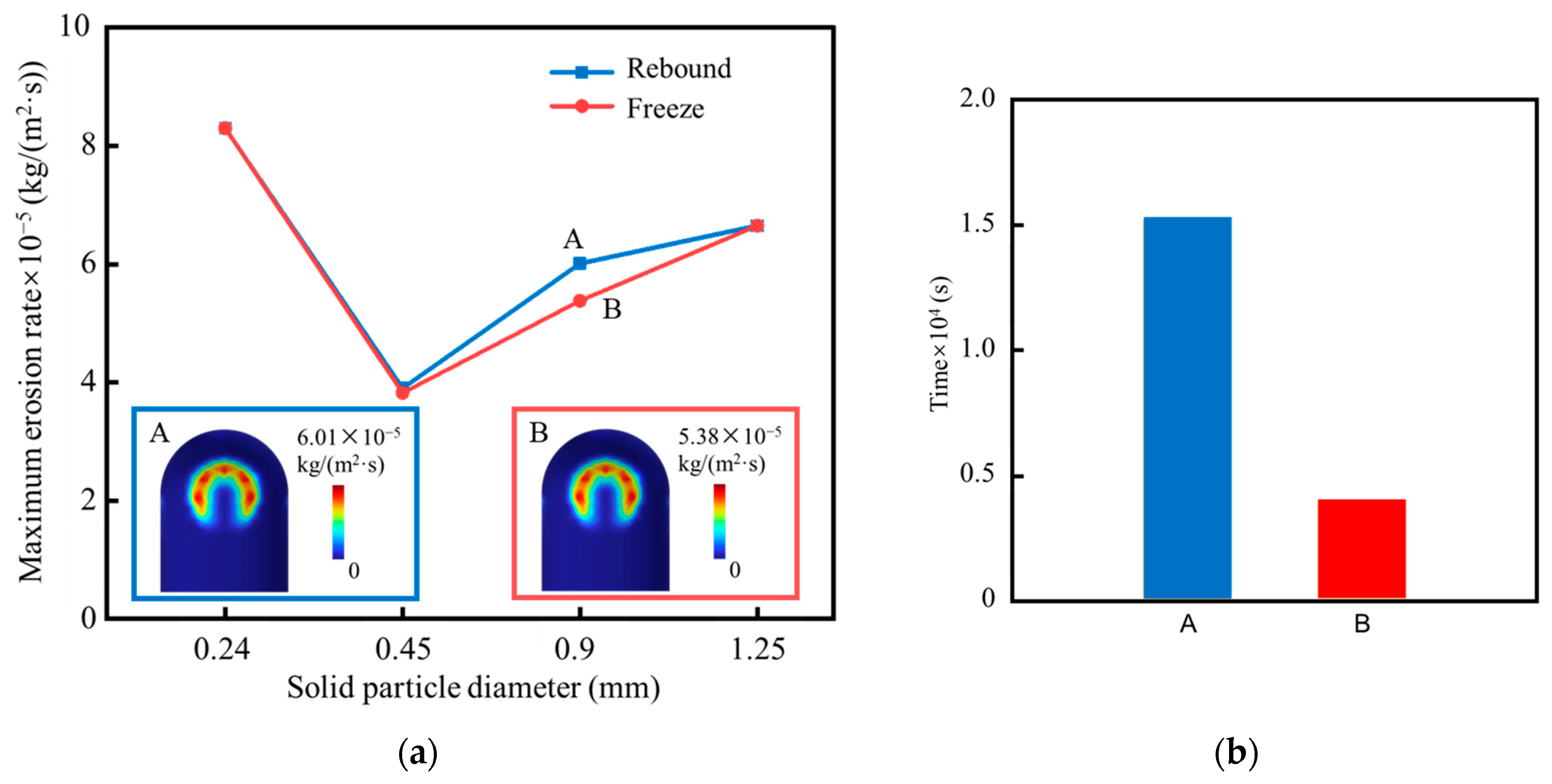
3. Comparation of Rebound and Freeze Boundary Conditions
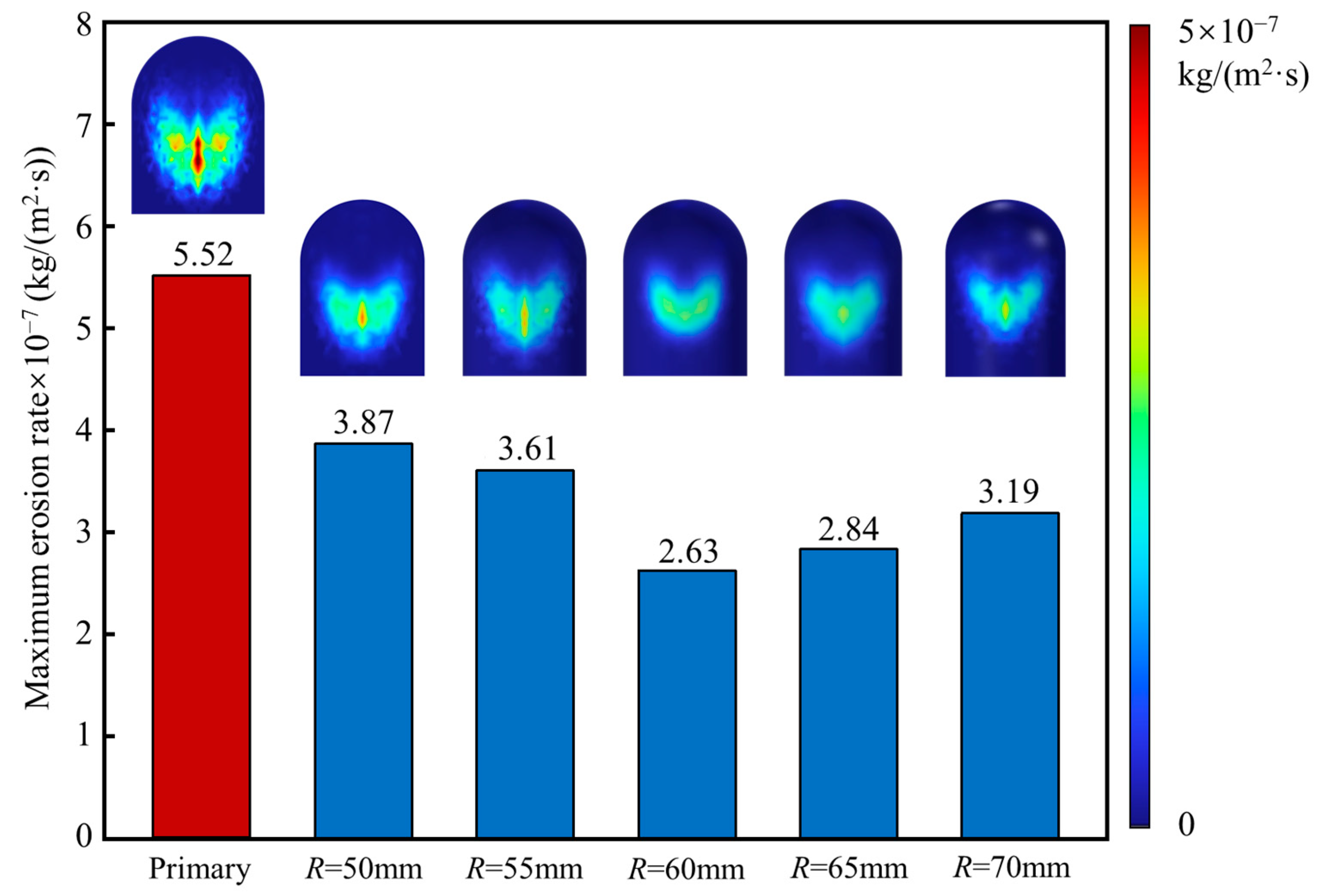
4. Optimal Design
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fetzer, R.; Weisenburger, A.; Mueller, G. Turbulent flow of liquid lead alloy in oxygen-controlled corrosion erosion test facility. AIP Adv. 2021, 11, 075303. [Google Scholar] [CrossRef]
- Ma, S.; Li, X.; Wang, H.; Ma, J.; Du, M.; Li, F.; Ren, J. Experimental and simulation study on anti-erosion properties of ductile materials. AIP Adv. 2022, 12, 025224. [Google Scholar] [CrossRef]
- Zhou, W.; Yin, Y.; Sun, Z.; Ma, P.; Shi, X. Numerical simulation of particle erosion in the internal flow field of solid rocket motor nozzle using Rocstar. AIP Adv. 2022, 12, 025224. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Yu, J.; Xu, W.; Li, X.; Yu, S. Numerical simulation of the erosion of pipe bends considering fluid-induced stress and surface scar evolution. Wear 2019, 440–441, 203043. [Google Scholar] [CrossRef]
- Wu, T.; Chen, Y.; Deng, Z.; Shen, L.; Xie, Z.; Liu, Y.; Zhu, S.; Liu, C.; Li, Y. Oil pipeline leakage monitoring developments in China. J. Pipeline Sci. Eng. 2023, 3, 100129. [Google Scholar] [CrossRef]
- Edwards, J.K.; McLaury, B.S.; Shirazi, S.A. Modeling Solid Particle Erosion in Elbows and Plugged Tees. J. Energy Resour. Technol. 2001, 123, 277–284. [Google Scholar] [CrossRef]
- Yu, H.; Liu, H.; Zhang, S.; Zhang, J.; Han, Z. Research progress on coping strategies for the fluid-solid erosion wear of pipelines. Powder Technol. 2023, 422, 118457. [Google Scholar] [CrossRef]
- Li, S.; Zhang, B.; Yang, L.; Zhang, J.; Wang, Y.; Kang, W. Study on Wear Properties of the Graphite-Sealing Surfaces in a Triple Eccentric Butterfly Valve Based on EDEM-Fluent Coupling. Machines 2023, 11, 463. [Google Scholar] [CrossRef]
- Wang, Q.; Ba, X.; Huang, Q.; Wang, N.; Wen, Y.; Zhang, Z.; Sun, X.; Yang, L.; Zhang, J. Modeling erosion process in elbows of petroleum pipelines using large eddy simulation. J. Petrol. Sci. Eng. 2022, 211, 110216. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Shang, P.; Xu, Z.; Huang, Q. A numerical study of the slurry erosion in 90° horizontal elbows. J. Pipeline Sci. Eng. 2023, 100149, in press. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, L.; Fan, J.; Sun, B. Experimental study on erosion behavior of fracturing pipeline involving tensile stress and erosion prediction using random forest regression. J. Nat. Gas Sci. Eng. 2021, 87, 103760. [Google Scholar] [CrossRef]
- Zhang, R.; Sun, L.; Li, Y.; Yin, J. Numerical analysis of solid particle erosion caused by slurry in dredging pipelines based on a particle separation method. Powder Technol. 2023, 428, 118826. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, K.; Liu, Y.; Liu, H. A general numerical method for solid particle erosion in gas–liquid two-phase flow pipelines. Ocean Eng. 2023, 267, 113305. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, W.L.; Chen, J. An improved EMMS model for turbulent flow in pipe and its solution. Particuology 2023, 76, 1–12. [Google Scholar] [CrossRef]
- Yao, L.; Liu, Y.; Xiao, Z.; Chen, Y. An algorithm combining sedimentation experiments for pipe erosion investigation. Energy 2023, 270, 126891. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Jia, P.; Liu, H.; Yun, F.; Li, Z.; Wang, L. Orthogonal Experimental Design Based Nozzle Geometry Optimization for the Underwater Abrasive Water Jet. Machines 2022, 10, 1243. [Google Scholar] [CrossRef]
- Li, A.; Wang, Z.; Zhu, L.; Wang, Z.; Shi, J.; Yang, W. Design optimization of guide vane for mitigating elbow erosion using computational fluid dynamics and response surface methodology. Particuology 2022, 63, 83–94. [Google Scholar] [CrossRef]
- Duarte, C.A.R.; de Souza, F.J.; dos Santos, V.F. Mitigating elbow erosion with a vortex chamber. Powder Technol. 2016, 288, 6–25. [Google Scholar] [CrossRef]
- Farokhipour, A.; Mansoori, Z.; Rasteh, A.; Rasoulian, M.A.; Saffar-Avval, M.; Ahmadi, G. Study of erosion prediction of turbulent gas-solid flow in plugged tees via CFD-DEM. Powder Technol. 2019, 352, 136–150. [Google Scholar] [CrossRef]
- Yu, H.; Shao, L.; Zhang, S.; Zhang, J.; Han, Z. A new erosive wear resistance strategy for curved surfaces based on combined bionics. Tribol. Int. 2023, 180, 108226. [Google Scholar] [CrossRef]
- Duarte, C.A.R.; de Souza, F.J. Innovative pipe wall design to mitigate elbow erosion: A CFD analysis. Wear 2017, 380–381, 176–190. [Google Scholar] [CrossRef]
- Kannojiya, V.; Kumar, S. Assessment of Optimum Slurry Pipe Design for Minimum Erosion. Sci. Iran. 2019, 27, 2409–2418. [Google Scholar] [CrossRef]
- Liu, E.-B.; Huang, S.; Tian, D.-C.; Shi, L.-M.; Peng, S.-B.; Zheng, H. Experimental and numerical simulation study on the erosion behavior of the elbow of gathering pipeline in shale gas field. Pet. Sci. 2023, in press. [Google Scholar] [CrossRef]
- Zolfagharnasab, M.H.; Salimi, M.; Zolfagharnasab, H.; Alimoradi, H.; Shams, M.; Aghanajafi, C. A novel numerical investigation of erosion wear over various 90-degree elbow duct sections. Powder Technol. 2021, 380, 1–17. [Google Scholar] [CrossRef]
- Khan, R.; Mourad, A.H.I.; Seikh, A.H.; Petru, J.; H.Ya, H. Erosion impact on mild steel elbow pipeline for different orientations under liquid-gas-sand annular flow. Eng. Fail. Anal. 2023, 153, 107565. [Google Scholar] [CrossRef]
- Wang, S.; Shi, J.; Han, X.; Zhu, L.; Bi, J.; Wang, J.; Wang, S.; Ma, Z.; Wang, Z. Effect of pipe orientation on erosion of π-shaped pipelines. Powder Technol. 2022, 408, 117769. [Google Scholar] [CrossRef]
- Karthik, S.; Amarendra, H.J.; Rokhade, K.K.; Prathap, M.S. Experimental and numerical approach to predict slurry erosion in jet erosion test rig. Int. J. Refract. Met. Hard Mater. 2022, 105, 105807. [Google Scholar] [CrossRef]
- Jia, W.; Zhang, Y.; Li, C.; Luo, P.; Song, X.; Wang, Y.; Hu, X. Experimental and numerical simulation of erosion-corrosion of 90° steel elbow in shale gas pipeline. J. Nat. Gas Sci. Eng. 2021, 89, 103871. [Google Scholar] [CrossRef]
- Xu, L.; Wu, F.; Ren, H.; Zhou, W.; Yan, Y. Experimental and numerical investigation on erosion of circular and elliptical immersed tubes in fluidized bed. Powder Technol. 2022, 409, 117820. [Google Scholar] [CrossRef]
- Chen, J.; Cao, L.; Song, G. Detection of the pipeline elbow erosion by percussion and deep learning. Mech. Syst. Sig. Process. 2023, 200, 110546. [Google Scholar] [CrossRef]
- Hong, B.; Li, Y.; Li, Y.; Gong, J.; Yu, Y.; Huang, A.; Li, X. Numerical simulation of solid particle erosion in the gas-liquid flow of key pipe fittings in shale gas fields. Case Stud. Therm. Eng. 2023, 42, 102742. [Google Scholar] [CrossRef]
- Parsi, M.; Najmi, K.; Najafifard, F.; Hassani, S.; McLaury, B.S.; Shirazi, S.A. A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications. J. Nat. Gas Sci. Eng. 2014, 21, 850–873. [Google Scholar] [CrossRef]
- Finnie, I. Some observations on the erosion of ductile metals. Wear 1972, 19, 81–90. [Google Scholar] [CrossRef]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Grant, G.; Tabakoff, W. Erosion Prediction in Turbomachinery Resulting from Environmental Solid Particles. J. Aircr. 1975, 12, 471–478. [Google Scholar] [CrossRef]
- Zeng, L.; Zhang, G.A.; Guo, X.P. Erosion–corrosion at different locations of X65 carbon steel elbow. Corros. Sci. 2014, 85, 318–330. [Google Scholar] [CrossRef]
- Homicz, G.F. Computational Fluid Dynamics simulations of pipe elbow flow. SAND2004-3467. 2004; pp. 3–28. Available online: https://www.osti.gov/servlets/purl/919140 (accessed on 1 August 2004).



| Maximum Mesh Size (mm) | Number of Mesh | Pressure (Pa) |
|---|---|---|
| 7 | 139,131 | 66,400 |
| 4 | 203,756 | 64,300 |
| 2.77 | 317,450 | 62,700 |
| 2.4 | 410,279 | 61,500 |
| Truncated Particle Fraction ci | Normal and Tangential Force Ratio K | Surface Hardness HV (GPa) | Surface Mass Density ρ (kg/m3) | Particle Radius rP (mm) | Sand Mass Flow Rate mp (kg/s) |
|---|---|---|---|---|---|
| 0.1 | 2 | 1.2 | 3900 | 0.225 | 0.1 |
| Truncated Particle Fraction ci | Normal and Tangential Force Ratio K | Surface Hardness HV (GPa) | Surface Mass Density ρ (kg/m3) | Grain Density ρP (kg/m3) | Fluid Velocity u (m/s) |
|---|---|---|---|---|---|
| 0.1 | 2 | 1.96 | 7860 | 2850 | 16.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Mi, K.; Lei, Y.; Li, Z.; Yan, D. Erosion Analysis and Optimal Design of Sand Resistant Pipe Fittings. Machines 2024, 12, 177. https://doi.org/10.3390/machines12030177
Song X, Mi K, Lei Y, Li Z, Yan D. Erosion Analysis and Optimal Design of Sand Resistant Pipe Fittings. Machines. 2024; 12(3):177. https://doi.org/10.3390/machines12030177
Chicago/Turabian StyleSong, Xiaoning, Kaifu Mi, Yu Lei, Zhengyang Li, and Dongjia Yan. 2024. "Erosion Analysis and Optimal Design of Sand Resistant Pipe Fittings" Machines 12, no. 3: 177. https://doi.org/10.3390/machines12030177
APA StyleSong, X., Mi, K., Lei, Y., Li, Z., & Yan, D. (2024). Erosion Analysis and Optimal Design of Sand Resistant Pipe Fittings. Machines, 12(3), 177. https://doi.org/10.3390/machines12030177





