Implementation of Grey Wolf, Multi-Verse and Ant Lion Metaheuristic Algorithms for Optimizing Machinability of Dry CNC Turning of Annealed and Hardened UNIMAX® Tool Steel
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of Experiments
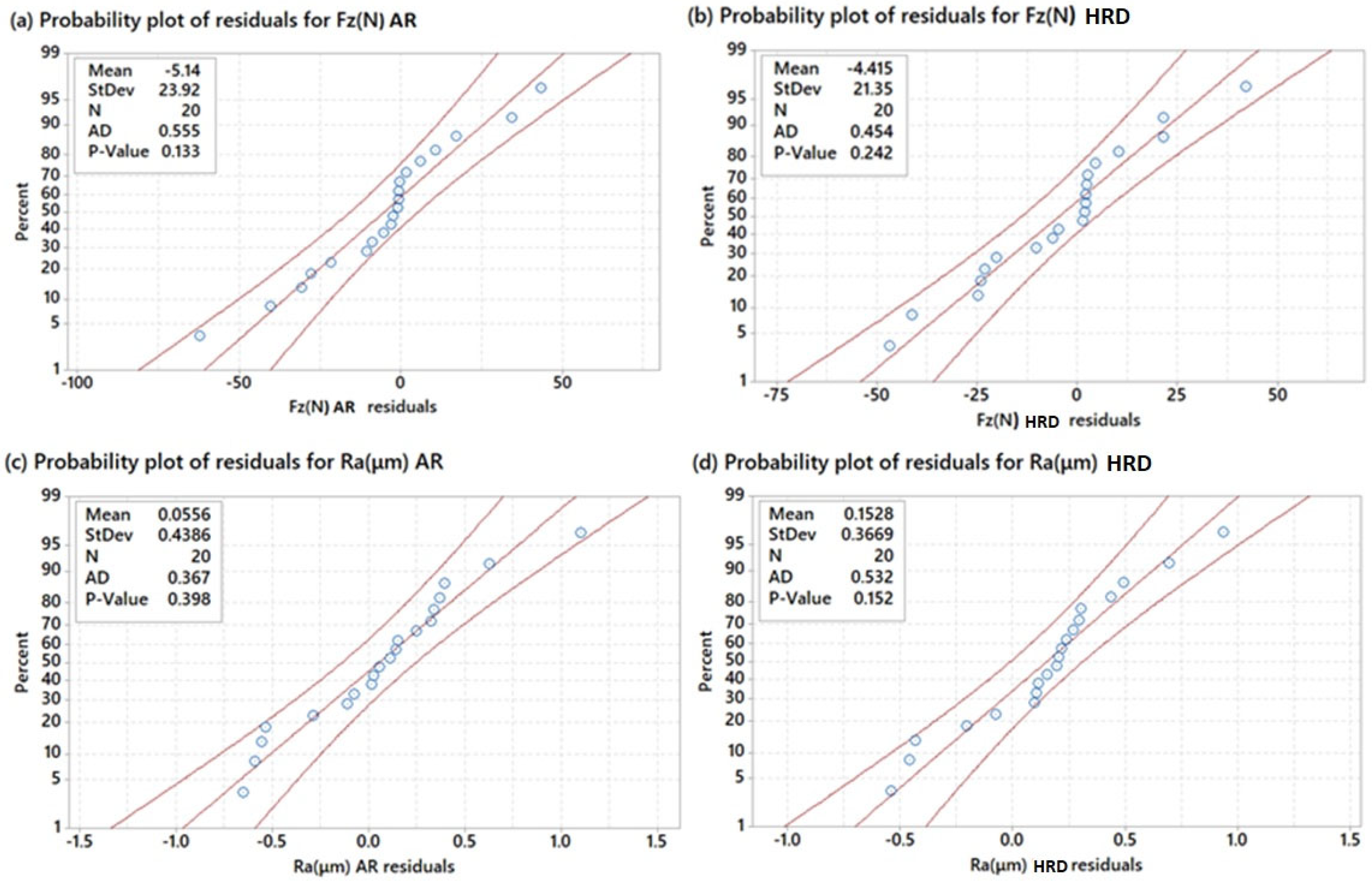
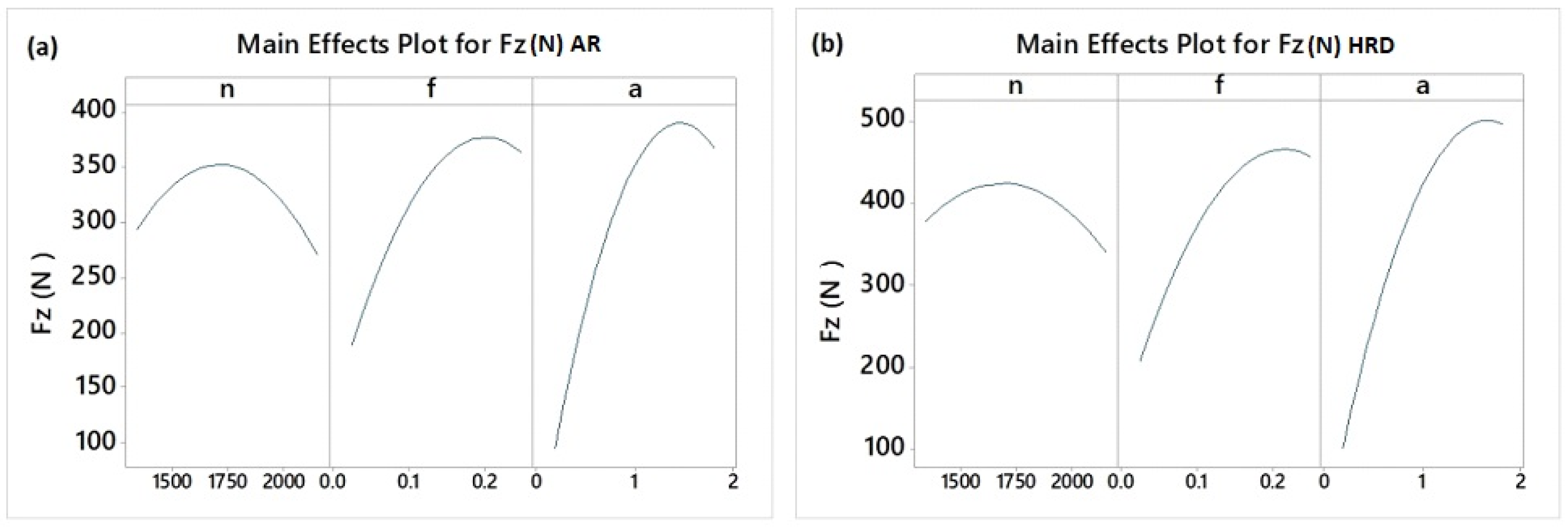
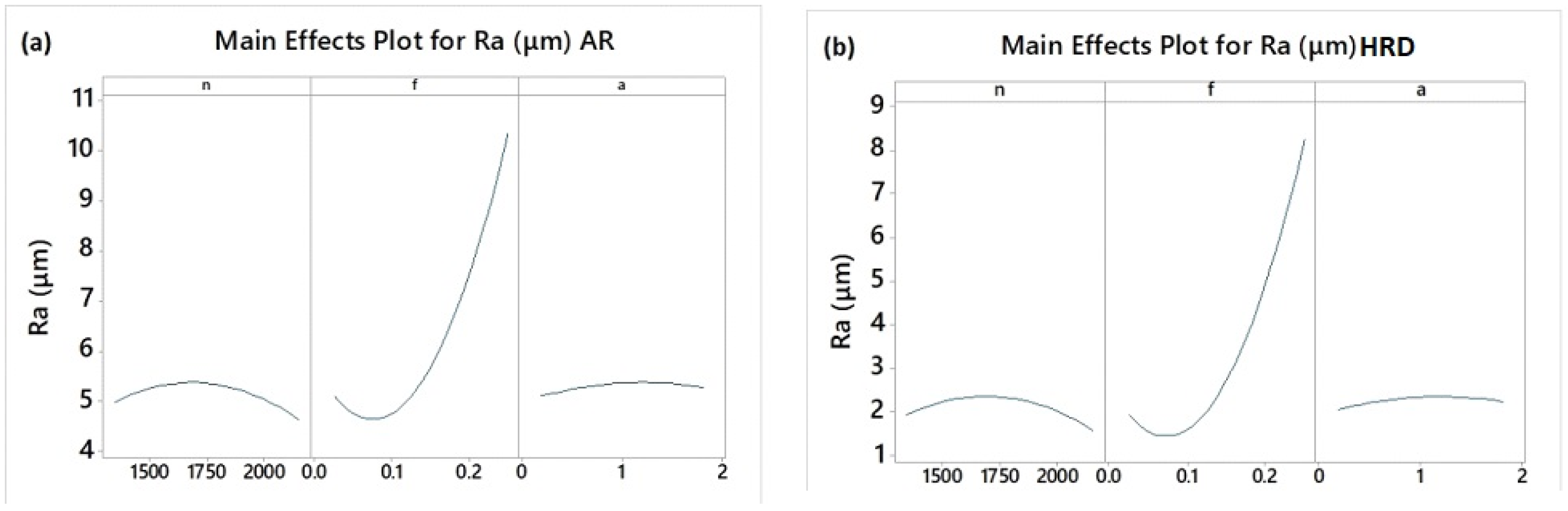
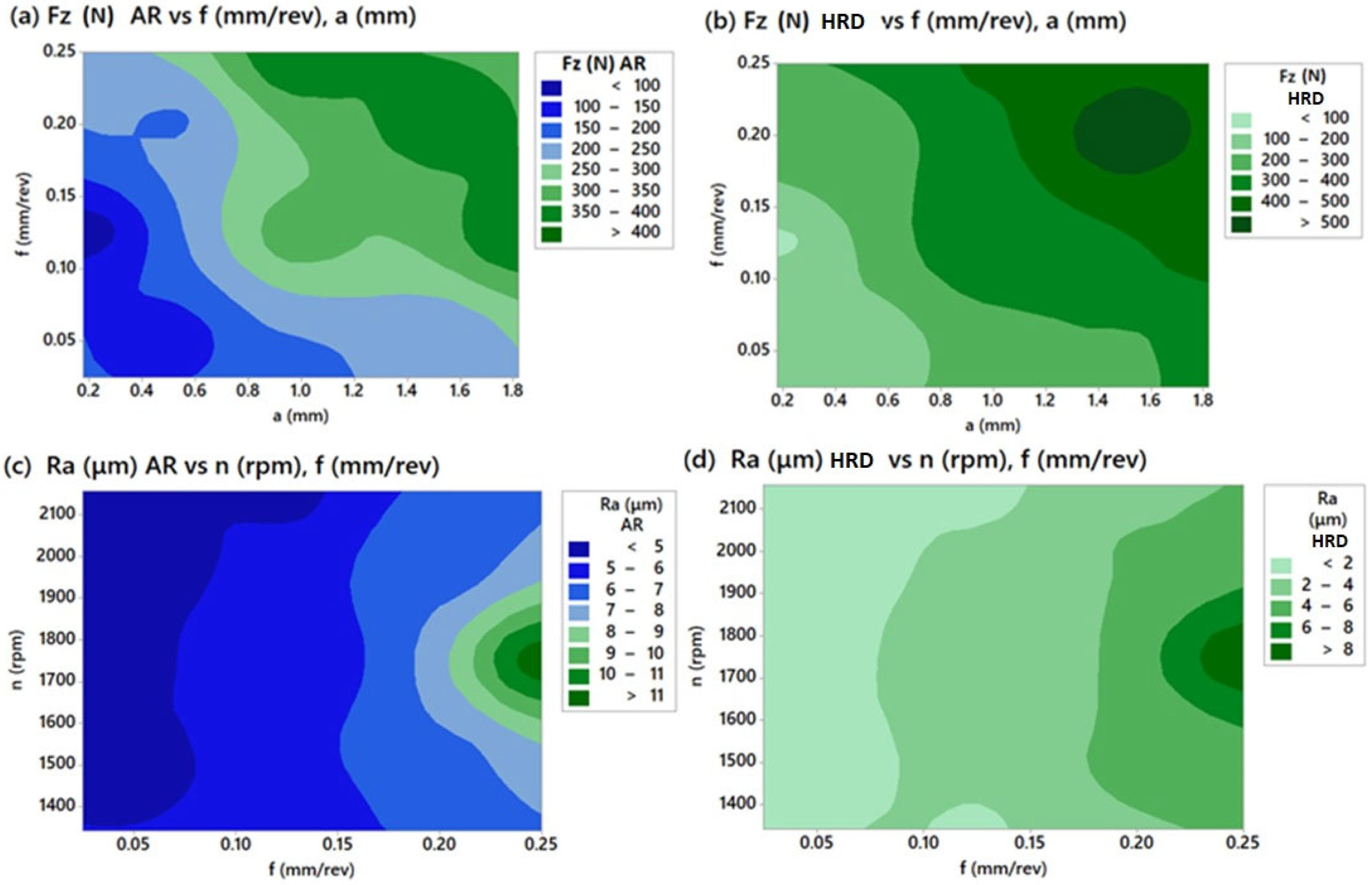
2.2. Experimental Results
n × a + 595 × f × a
n × a + 905 × f × a
0.00048 × n × a − 1.43 × f × a
0.00052 × n × a −1.61 × f × a
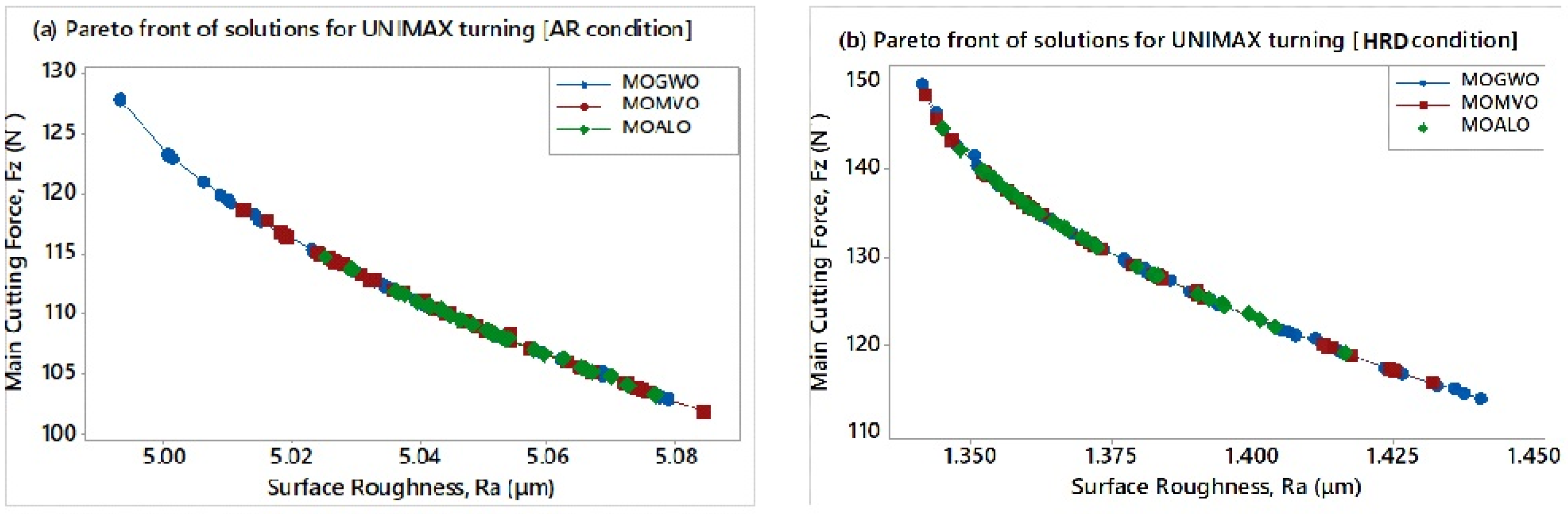
3. Multi-Objective Optimization
4. Conclusions
- When finish-turning the UNIMAX® in its hardened “HRD” condition, main cutting force Fz is approximately 19% larger than the one corresponding to the “AR” (soft-annealed) state. Yet, surface roughness is reduced to 47.1% providing a superior surface finish.
- According to the analysis of variance, the hierarchy of the effects of the cutting parameters in terms of cutting force suggests the linear terms, the square terms, and finally the interaction terms, regardless of the material conditions.
- Depth of cut and feed rate are influential cutting parameters for main cutting force, whilst feed rate and spindle speed are influential cutting parameters for surface roughness, regardless of the material conditions. Both objectives of main cutting force Fz and surface roughness Ra alter their experimental trends from one condition to another with quite high complexity. This can justify the implementation of intelligent algorithms to solve multi-objective optimization problems.
- There is no clear superiority in the application of multi-objective intelligent algorithms to this case of the machinability optimization problem. However, the different algorithms may exhibit different performance behavior affecting computational costs depending on the problem under question. Algorithms should be tested by conducting several evaluations and examining their statistical outputs to gain a clear understanding of their performance. Final selections for the settings of advantageous machining parameters to facilitate all objectives under study should be based on requirements corresponding to the production and shop floor’s resources.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ezugwu, E.O.; Da Silva, R.B.; Bonney, J.; Machado, A.R. Evaluation of the performance of CBN tools when turning Ti–6Al–4V alloy with high pressure coolant supplies. Int. J. Mach. Tools Manuf. 2005, 45, 1009–1014. [Google Scholar] [CrossRef]
- Armendia, M.; Garay, A.; Iriarte, L.M.; Arrazola, P.J. Comparison of the machinabilities of Ti6Al4V and TIMETAL® 54M using uncoated WC–Co tools. J. Mater. Process. Technol. 2010, 210, 197–203. [Google Scholar] [CrossRef]
- Kalpakjian, S.; Schmid, S.R. Manufacturing Processes for Engineering Materials, 6th ed.; Pearson: London, UK, 2022. [Google Scholar]
- Hoyle, G. Electroslag Processes: Principles and Practice; Applied Science: London, UK, 1983. [Google Scholar]
- Roberts, G.; Kraus, G.; Kennedy, R. Tool Steel, 5th ed.; ASM International: Materials Park, OH, USA, 2000. [Google Scholar]
- Kumar, P.; Chauhan, S.R. Machinability Study on Finish Turning of AISI H13 Hot Working Die Tool Steel with Cubic Boron Nitride (CBN) Cutting Tool Inserts Using Response Surface Methodology (RSM). Arab. J. Sci. Technol. 2015, 40, 1471–1485. [Google Scholar] [CrossRef]
- Boy, M.; Yaşar, N.; Çiftçi, İ. Experimental investigation and modelling of surface roughness and resultant cutting force in hard turning of AISI H13 Steel. IOP Conf. Ser. Mater. Sci. Eng. 2016, 161, 012039. [Google Scholar] [CrossRef]
- Hosseini, A.; Hussein, M.; Kishawy, H.A. On the machinability of die/mold D2 steel material. Int. J. Adv. Manuf. Technol. 2016, 85, 735–740. [Google Scholar] [CrossRef]
- Elbestawi, M.A.; Chen, L.; Becze, C.E.; El-Wardany, T.I. High-speed milling of dies and molds in their hardened state. CIRP Ann. 1997, 46, 57–62. [Google Scholar] [CrossRef]
- Abbas, A.T.; El Rayes, M.M.; Luqman, M.M.; Naeim, N.; Hegab, H.; Elkaseer, A. On the Assessment of Surface Quality and Productivity Aspects in Precision Hard Turning of AISI 4340 Steel Alloy: Relative Performance of Wiper vs. Conventional Inserts. Materials 2020, 20, 2036. [Google Scholar] [CrossRef]
- Ghani, M.U.; Abukhashim, N.A.; Sheikh, M.A. An investigation of heat partition and tool wear in hard turning of H13 tool steel with CBN cutting tools. Int. J. Adv. Manuf. Technol. 2008, 39, 874–888. [Google Scholar] [CrossRef]
- Outeiro, J.C. Surface integrity predictions and optimisation of machining conditions in the turning of AISI H13 tool steel. Int. J. Mach. Mach. Mater. 2014, 15, 122–134. [Google Scholar] [CrossRef]
- Pathak, H.; Das, S.; Doley, R.; Kashyap, S. Optimization of Cutting Parameters for AISI H13 Tool Steel by Taguchi Method and Artificial Neural Network. Int. J. Mater. Form. Mach. Process. 2015, 2, 47–65. [Google Scholar] [CrossRef]
- Mia, M.; Królczyk, G.; Maruda, R.; Wojciechowski, S. Intelligent Optimization of Hard-Turning Parameters Using Evolutionary Algorithms for Smart Manufacturing. Materials 2019, 12, 879. [Google Scholar] [CrossRef]
- Kumar, A.; Pradhan, S.K. Investigations into hard turning process using wiper tool inserts. Proc. Mater. Today 2018, 5 Pt 2, 12579–12587. [Google Scholar] [CrossRef]
- Schaal, N.; Wegener, K. Comparison of ground and laser machined wiper geometry on carbide inserts for high performance finishing. Proc. CIRP 2016, 46, 623–626. [Google Scholar] [CrossRef]
- D’Addona, D.M.; Raykar, S.J. Analysis of surface roughness in hard turning using wiper insert geometry. Proc. CIRP 2016, 41, 841–846. [Google Scholar] [CrossRef]
- M’Saoubi, R.; Guddat, J.; Alm, P.; Meyer, D. Hard turning of AISI 52100 using PCBN wiper geometry inserts and the resulting surface integrity. Proc. Eng. 2011, 19, 118–124. [Google Scholar]
- Balestrassi, P.P.; Paiva, E.J.; Lopes, L.G.D.; Ferreira, J.R.; Campos, P.H.; Paiva, A.P. A multivariate robust parameter design approach for optimization of AISI 52100 hardened steel turning with wiper mixed ceramic tool. Int. J. Refract. Met. Hard Mater. 2012, 30, 152–163. [Google Scholar]
- Gaitonde, V.N.; Karnik, S.R.; Figueira, L.; Davim, J.P. Performance comparison of conventional and wiper ceramic inserts in hard turning through artificial neural network modeling. Int. J. Adv. Manuf. Technol. 2011, 52, 101–114. [Google Scholar] [CrossRef]
- Kurniawan, D.; Noordin, M.Y.; Sharif, S. Hard machining of stainless steel using wiper coated carbide: Tool life and surface integrity. J. Mater. Manuf. Process. 2010, 25, 370–377. [Google Scholar] [CrossRef]
- Gaitonde, V.N.; Karnik, S.R.; Figueira, L.; Davim, J.P. Machinability investigations in hard turning of AISI D2 cold work tool steel with conventional and wiper ceramic inserts. Int. J. Refract. Met. Hard Mater. 2009, 27, 754–763. [Google Scholar] [CrossRef]
- He, X.; Wu, S.; Kratz, H. Forces in Hard Turning of 51CrV4 with Wiper Cutting Tool. Tsinghua Sci. Technol. 2006, 11, 501–506. [Google Scholar] [CrossRef]
- Markopoulos, A.P.; Georgiopoulos, S.; Manolakos, D.E. On the use of back propagation and radial basis function neural networks in surface roughness prediction. J. Ind. Eng. Int. 2016, 12, 389–400. [Google Scholar] [CrossRef]
- Markopoulos, A.P.; Manolakos, D.E.; Vaxevanidis, N.M. Artificial neural network models for the prediction of surface roughness in electrical discharge machining. J. Intell. Manuf. 2008, 19, 283–292. [Google Scholar] [CrossRef]
- Karagiannis, S.; Stavropoulos, P.; Ziogas, C.; Kechagias, J. Prediction of surface roughness magnitude in computer numerical controlled end milling processes using neural networks, by considering a set of influence parameters: An aluminium alloy 5083 case study. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2014, 228, 233–244. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Papacharalampopoulos, A.; Vasiliadis, E.; Chryssolouris, G. Tool wear predictability estimation in milling based on multi-sensorial data. Int. J. Adv. Manuf. Technol. 2016, 82, 509–521. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-Objective Grey Wolf Optimizer: A Novel Algorithm for Multi-Criterion Optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Mirjalili, S.Z.; Saremi, S.; Trivedi, I.N. Optimization of Problems with Multiple Objectives Using the Multi-Verse Optimization Algorithm. Knowl.-Based Syst. 2017, 134, 50–71. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Saremi, S. Multi-Objective Ant Lion Optimizer: A Multi-Objective Optimization Algorithm for Solving Engineering Problems. Appl. Intell. 2017, 46, 79–95. [Google Scholar] [CrossRef]



| Central Composite Design of Experiments | |||||
|---|---|---|---|---|---|
| Parameter | Symbol | Level | |||
| Low (−1) | Center (0) | High (1) | Unit | ||
| Spindle speed (Cutting speed) | n (Vc) | 1500 (141) | 1750 (165) | 2000 (188) | rpm (m/min) |
| Feed rate | f | 0.050 | 0.125 | 0.200 | mm/rev |
| Depth of cut | a | 0.500 | 1.000 | 1.500 | mm |
| No. | n/(Vc) (rpm)/(m/min) | f (mm/rev) | a (mm) | Fz (N) AR | Fz (N) HRD | Ra (μm) AR | Ra (μm) HRD |
|---|---|---|---|---|---|---|---|
| 1 | 1500 (141) | 0.050 | 0.50 | 140.760 | 120.644 | 4.499 | 1.291 |
| 2 | 2000 (188) | 0.050 | 0.50 | 98.581 | 120.270 | 4.453 | 1.261 |
| 3 | 1500 (141) | 0.200 | 0.50 | 170.008 | 280.139 | 6.778 | 4.279 |
| 4 | 2000 (188) | 0.200 | 0.50 | 220.991 | 250.178 | 6.587 | 4.081 |
| 5 | 1500 (141) | 0.050 | 1.50 | 220.166 | 320.886 | 4.931 | 1.753 |
| 6 | 2000 (188) | 0.050 | 1.50 | 200.773 | 270.034 | 4.511 | 1.325 |
| 7 | 1500 (141) | 0.200 | 1.50 | 430.855 | 580.945 | 6.863 | 4.362 |
| 8 | 2000 (188) | 0.200 | 1.50 | 320.351 | 570.847 | 6.563 | 4.040 |
| 9 | 1750 (165) | 0.125 | 1.00 | 340.837 | 410.206 | 5.134 | 2.349 |
| 10 | 1750 (165) | 0.125 | 1.00 | 340.263 | 410.124 | 5.122 | 2.251 |
| 11 | 1750 (165) | 0.125 | 1.00 | 340.936 | 410.553 | 4.996 | 1.969 |
| 12 | 1750 (165) | 0.125 | 1.00 | 340.957 | 410.326 | 4.819 | 1.612 |
| 13 | 1342 * (126) | 0.125 | 1.00 | 280.011 | 340.845 | 5.054 | 1.846 |
| 14 | 2158 * (203) | 0.125 | 1.00 | 295.215 | 300.899 | 4.782 | 1.574 |
| 15 | 1750 (165) | 0.025 * | 1.00 | 180.069 | 210.112 | 4.468 | 1.260 |
| 16 | 1750 (165) | 0.250 * | 1.00 | 400.445 | 410.702 | 11.434 | 9.226 |
| 17 | 1750 (165) | 0.125 | 0.18 * | 80.407 | 90.524 | 5.205 | 1.997 |
| 18 | 1750 (165) | 0.125 | 1.82 * | 392.834 | 430.412 | 5.384 | 2.176 |
| 19 | 1750 (165) | 0.125 | 1.00 | 340.529 | 410.353 | 5.358 | 2.150 |
| 20 | 1750 (165) | 0.125 | 1.00 | 340.023 | 410.152 | 5.251 | 2.043 |
| St.Dev. | 102.768 | 135.341 | 1.575 | 1.863 | |||
| Mean | 273.751 | 337.958 | 5.610 | 2.642 | |||
| Median | 307.783 | 375.485 | 5.128 | 2.02 | |||
| Range | 350.448 | 490.421 | 6.981 | 7.966 | |||
| Source | DF | Seq.SS | Contribution % | Adj.SS | Adj.MS | F-Val. | p-Val. |
|---|---|---|---|---|---|---|---|
| Model | 9 | 188,566 | 93.97 | 188,566 | 20,951.8 | 17.32 | <0.005 |
| Linear | 3 | 137,073 | 68.31 | 128,711 | 42,903.6 | 35.46 | <0.005 |
| n (rpm) | 1 | 696 | 0.35 | 657.0 | 657.0 | 0.54 | 0.478 |
| f (mm/rev) | 1 | 53,315 | 26.57 | 41,005 | 41,004.9 | 33.89 | <0.005 |
| a (mm) | 1 | 83,062 | 41.39 | 87,049 | 87,048.9 | 71.95 | <0.005 |
| Square | 3 | 45,100 | 22.48 | 45,100 | 15,033.3 | 12.43 | 0.001 |
| n2 | 1 | 6729 | 3.35 | 9252 | 9251.6 | 7.65 | 0.020 |
| f2 | 1 | 11,057 | 5.51 | 12,192 | 12,192.4 | 10.08 | 0.010 |
| a2 | 1 | 27,314 | 13.61 | 27,314 | 27,314.2 | 22.58 | 0.001 |
| 2-way int. | 3 | 6393 | 3.19 | 6393 | 2131.0 | 1.76 | 0.218 |
| n × f | 1 | 1 | 0 | 1 | 0.5 | 0 | 0.984 |
| n × a | 1 | 2405 | 1.20 | 2405 | 2404.7 | 1.99 | 0.189 |
| f × a | 1 | 3988 | 1.99 | 3988 | 3987.6 | 3.30 | 0.100 |
| Error | 10 | 12,098 | 6.03 | 12,098 | 1209.8 | ||
| Lack-of-fit | 5 | 12,097 | 6.03 | 12,097 | 2419.5 | 6.56 | 0.235 |
| Pure error | 5 | 1 | 0 | 1 | 0.1 | ||
| Total | 19 | 200,664 | 100 | ||||
| R2 | 93.97% |
| Source | DF | Seq.SS | Contribution % | Adj.SS | Adj.MS | F-Val. | p-Val. |
|---|---|---|---|---|---|---|---|
| Model | 9 | 339,052 | 97.42 | 339,052 | 37,672 | 41.99 | <0.005 |
| Linear | 3 | 280,464 | 80.59 | 269,026 | 89,675 | 99.95 | <0.005 |
| n (rpm) | 1 | 1837 | 0.53 | 1687 | 1687 | 1.88 | 0.200 |
| f (mm/rev) | 1 | 103,913 | 29.86 | 83,447 | 83,447 | 93.01 | <0.005 |
| a (mm) | 1 | 174,714 | 50.20 | 183,892 | 183,892 | 204.97 | <0.005 |
| Square | 3 | 49,244 | 14.15 | 49,244 | 16,415 | 18.30 | <0.005 |
| n2 | 1 | 5102 | 1.47 | 7466 | 7466 | 8.32 | 0.016 |
| f2 | 1 | 15,623 | 4.49 | 16,996 | 16,996 | 18.94 | <0.005 |
| a2 | 1 | 28,519 | 8.19 | 28,519 | 28,519 | 31.79 | <0.005 |
| 2-way int. | 3 | 9345 | 2.69 | 9345 | 3115 | 3.47 | 0.059 |
| n × f | 1 | 16 | 0 | 16 | 16 | 0.02 | 0.898 |
| n × a | 1 | 117 | 0.03 | 117 | 117 | 0.13 | 0.725 |
| f × a | 1 | 9212 | 2.65 | 9212 | 9212 | 10.27 | 0.009 |
| Error | 10 | 8972 | 2.58 | 8972 | 897 | ||
| Lack-of-fit | 5 | 8972 | 2.58 | 8972 | 1794 | 4.25 | 0.244 |
| Pure error | 5 | 0 | 0 | 0 | 0 | ||
| Total | 19 | 348,024 | 100 | ||||
| R2 | 97.42% |
| Source | DF | Seq.SS | Contribution % | Adj.SS | Adj.MS | F-Val. | p-Val. |
|---|---|---|---|---|---|---|---|
| Model | 9 | 43.4157 | 92.12 | 43.4157 | 4.8240 | 12.98 | <0.005 |
| Linear | 3 | 30.8937 | 65.55 | 36.7643 | 12.2548 | 32.98 | <0.005 |
| n (rpm) | 1 | 0.1473 | 0.31 | 0.1421 | 0.1421 | 0.38 | 0.550 |
| f (mm/rev) | 1 | 30.6931 | 65.12 | 36.5846 | 36.5846 | 98.46 | <0.005 |
| a (mm) | 1 | 0.0533 | 0.11 | 0.0375 | 0.0375 | 0.10 | 0.757 |
| Square | 3 | 12.4698 | 26.46 | 4.1566 | 4.1566 | 11.19 | 0.002 |
| n2 | 1 | 0.6894 | 1.46 | 0.5614 | 0.5614 | 1.51 | 0.247 |
| f2 | 1 | 11.7276 | 24.88 | 11.6648 | 11.6648 | 31.39 | <0.005 |
| a2 | 1 | 0.0529 | 0.11 | 0.0529 | 0.0529 | 0.14 | 0.714 |
| 2-way int. | 3 | 0.0522 | 0.11 | 0.0174 | 0.0174 | 0.05 | 0.986 |
| n × f | 1 | 0.0001 | 0.00 | 0.0001 | 0.0001 | 0.00 | 0.989 |
| n × a | 1 | 0.0230 | 0.06 | 0.0292 | 0.0292 | 0.08 | 0.785 |
| f × a | 1 | 3.7158 | 0.05 | 0.0230 | 0.0230 | 0.06 | 0.809 |
| Error | 10 | 3.5361 | 7.88 | 0.3716 | 0.3716 | ||
| Lack-of-fit | 5 | 0.1797 | 7.50 | 0.7072 | 0.7072 | 1.68 | 0.187 |
| Pure error | 5 | 0.1797 | 0.38 | 0.0359 | 0.0359 | ||
| Total | 19 | 47.1315 | 100 | ||||
| R2 | 92.12% |
| Source | DF | Seq.SS | Contribution % | Adj.SS | Adj.MS | F-Val. | p-Val. |
|---|---|---|---|---|---|---|---|
| Model | 9 | 62.9558 | 95.47 | 62.9558 | 6.9951 | 23.44 | <0.005 |
| Linear | 3 | 45.9046 | 69.62 | 54.2317 | 18.0772 | 60.57 | <0.005 |
| n (rpm) | 1 | 0.1517 | 0.23 | 0.1485 | 0.1485 | 0.50 | 0.497 |
| f (mm/rev) | 1 | 45.6974 | 69.30 | 54.0454 | 54.0454 | 181.09 | <0.005 |
| a (mm) | 1 | 0.0555 | 0.08 | 0.0377 | 0.0377 | 0.13 | 0.730 |
| Square | 3 | 16.9874 | 25.76 | 16.9874 | 5.6625 | 18.97 | <0.005 |
| n2 | 1 | 0.8127 | 1.23 | 0.6532 | 0.6532 | 2.19 | 0.170 |
| f2 | 1 | 16.0906 | 24.40 | 15.9990 | 15.9990 | 53.61 | <0.005 |
| a2 | 1 | 0.0841 | 0.13 | 0.0841 | 0.0841 | 0.28 | 0.607 |
| 2-way int. | 3 | 0.0638 | 0.10 | 0.0638 | 0.0213 | 0.07 | 0.974 |
| n × f | 1 | 0.0005 | 0.00 | 0.0005 | 0.0005 | 0.00 | 0.969 |
| n × a | 1 | 0.0341 | 0.05 | 0.0341 | 0.0341 | 0.11 | 0.742 |
| f × a | 1 | 0.0293 | 0.04 | 0.0293 | 0.0293 | 0.10 | 0.761 |
| Error | 10 | 2.9845 | 4.53 | 2.9845 | 0.2984 | ||
| Lack-of-fit | 5 | 2.6471 | 4.01 | 2.6471 | 0.5294 | 3.85 | 0.204 |
| Pure error | 5 | 0.3373 | 0.51 | 0.3373 | 0.0675 | ||
| Total | 19 | 65.9403 | 100 | ||||
| R2 | 95.47% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fountas, N.A.; Papantoniou, I.; Manolakos, D.E.; Vaxevanidis, N.M. Implementation of Grey Wolf, Multi-Verse and Ant Lion Metaheuristic Algorithms for Optimizing Machinability of Dry CNC Turning of Annealed and Hardened UNIMAX® Tool Steel. Machines 2024, 12, 156. https://doi.org/10.3390/machines12030156
Fountas NA, Papantoniou I, Manolakos DE, Vaxevanidis NM. Implementation of Grey Wolf, Multi-Verse and Ant Lion Metaheuristic Algorithms for Optimizing Machinability of Dry CNC Turning of Annealed and Hardened UNIMAX® Tool Steel. Machines. 2024; 12(3):156. https://doi.org/10.3390/machines12030156
Chicago/Turabian StyleFountas, Nikolaos A., Ioannis Papantoniou, Dimitrios E. Manolakos, and Nikolaos M. Vaxevanidis. 2024. "Implementation of Grey Wolf, Multi-Verse and Ant Lion Metaheuristic Algorithms for Optimizing Machinability of Dry CNC Turning of Annealed and Hardened UNIMAX® Tool Steel" Machines 12, no. 3: 156. https://doi.org/10.3390/machines12030156
APA StyleFountas, N. A., Papantoniou, I., Manolakos, D. E., & Vaxevanidis, N. M. (2024). Implementation of Grey Wolf, Multi-Verse and Ant Lion Metaheuristic Algorithms for Optimizing Machinability of Dry CNC Turning of Annealed and Hardened UNIMAX® Tool Steel. Machines, 12(3), 156. https://doi.org/10.3390/machines12030156









