Investigation of Dynamic Behavior and Process Stability at Turning of Thin-Walled Tubular Workpieces Made of 42CrMo4 Steel Alloy
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Process
2.1.1. Behavior Law
2.1.2. Friction Law Model
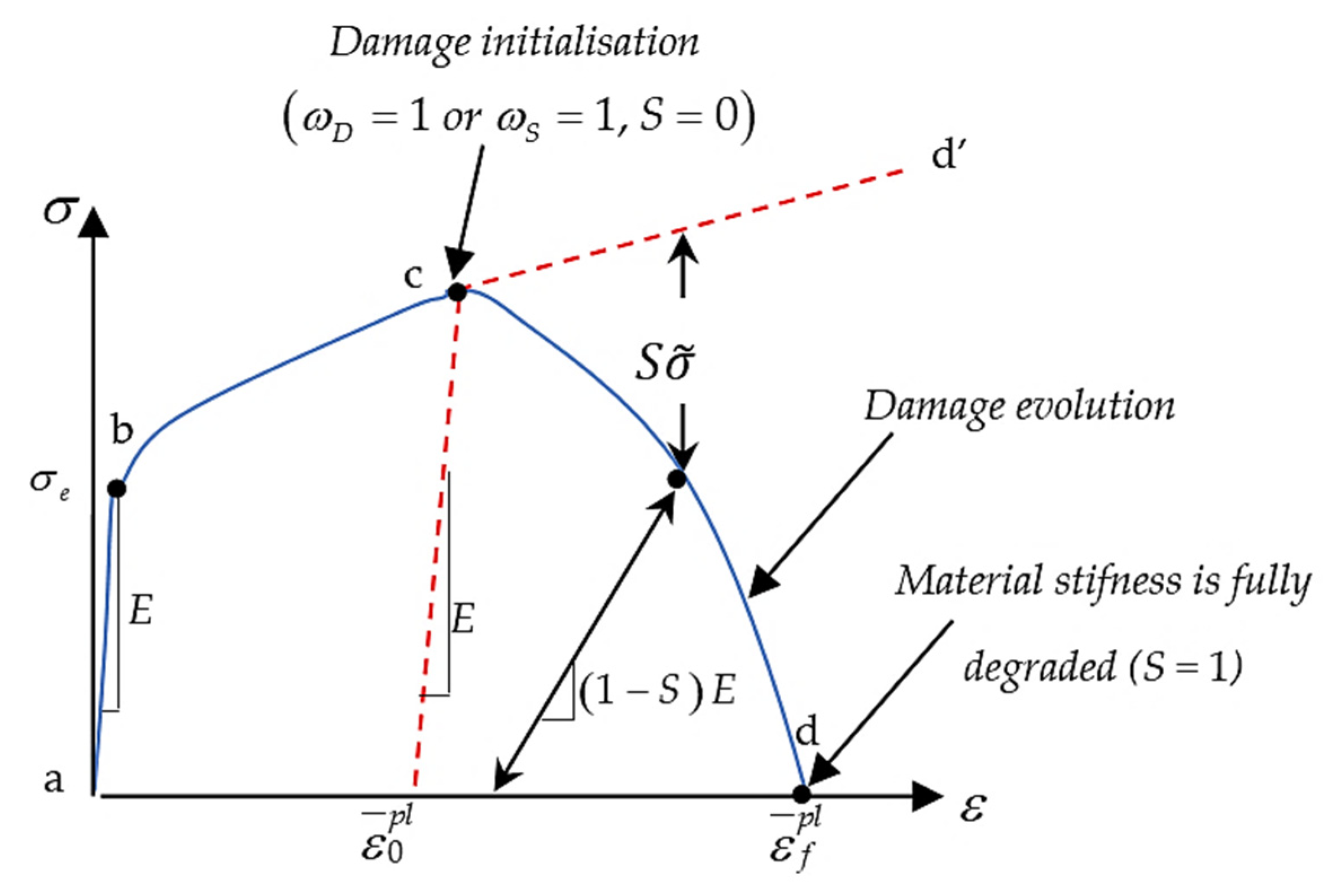
2.1.3. Damage Law Model
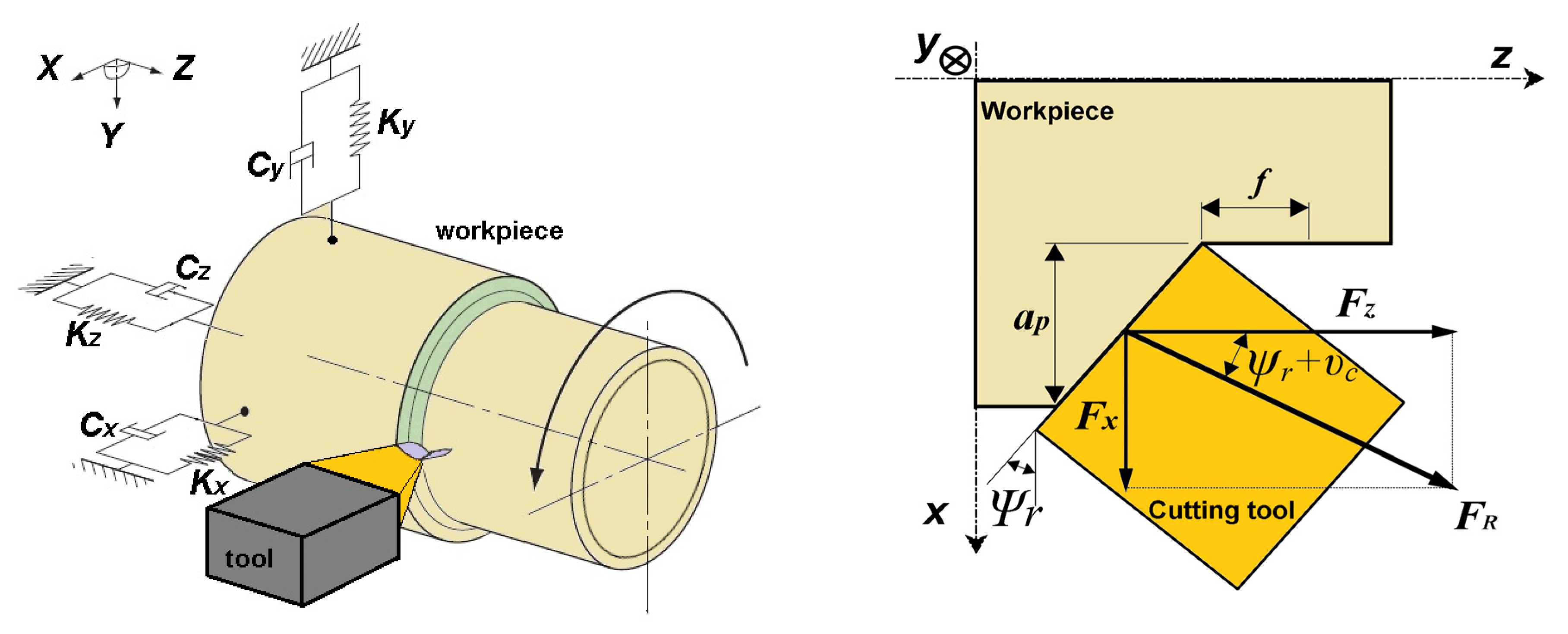
2.1.4. Dynamic Model of Cutting Forces
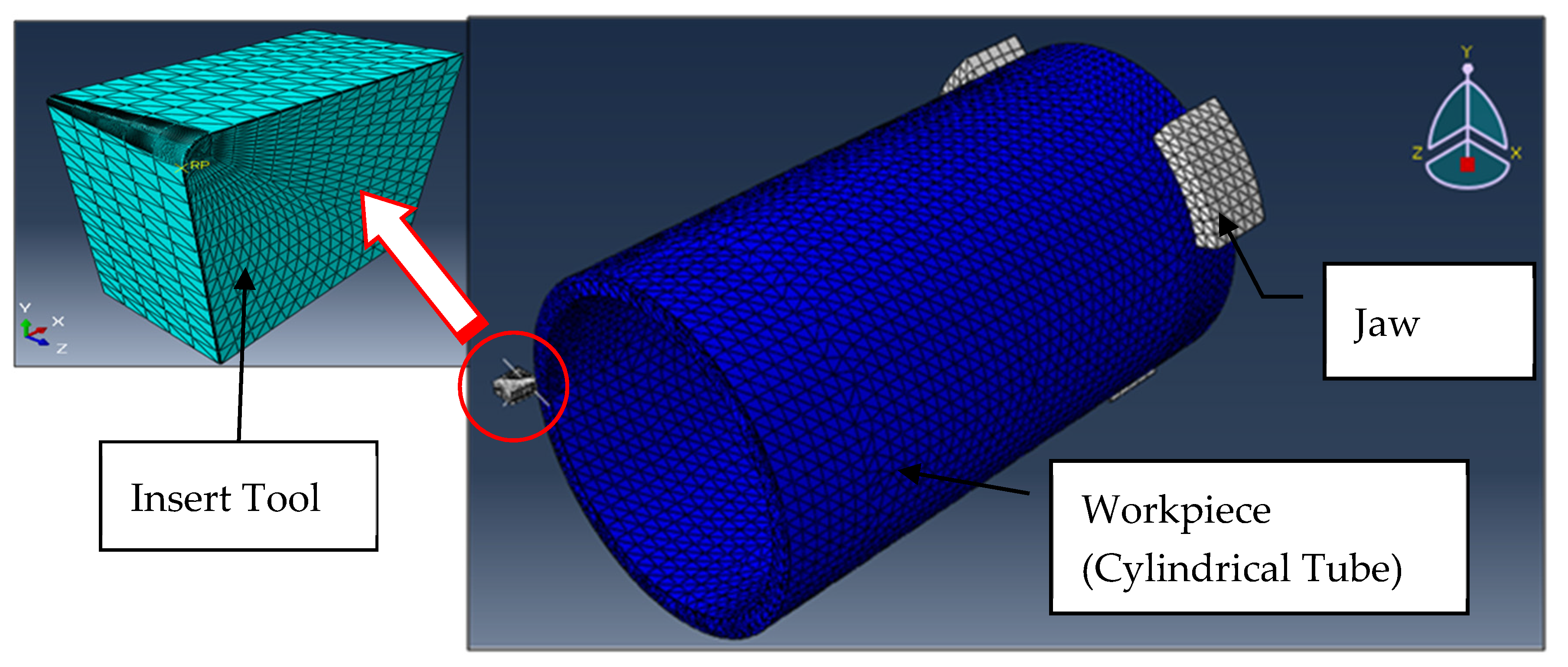
2.1.5. Numerical Model
2.2. Experimental Procedure
3. Results and Discussions
3.1. Analysis of the Cutting Force and Radial Vibration of the Workpiece Wall
- The average values of the cutting forces and the radial displacement of the workpiece wall are proportional to the chip cross-section ap × f (mm2). These average values are slightly influenced by the wall thickness of the machined parts. For the finishing tests (small chip cross-section), the average values are lower than those for the roughing tests (large chip cross-section). Indeed, an increase in the feed rate f from 0.2 mm/rev to 0.4 mm/rev is accompanied by a significant increase in the average values of , , and : for the workpiece of 3 mm thick, , , and increase by 102%, 80%, and 79%, respectively. For the workpiece of 4.5 mm thick, the increase in , , and is, respectively, 104%, 78%, and 75%. Finally, for the workpiece of 6 mm thick, , , and increased by 102%, 79%, and 78%, respectively;
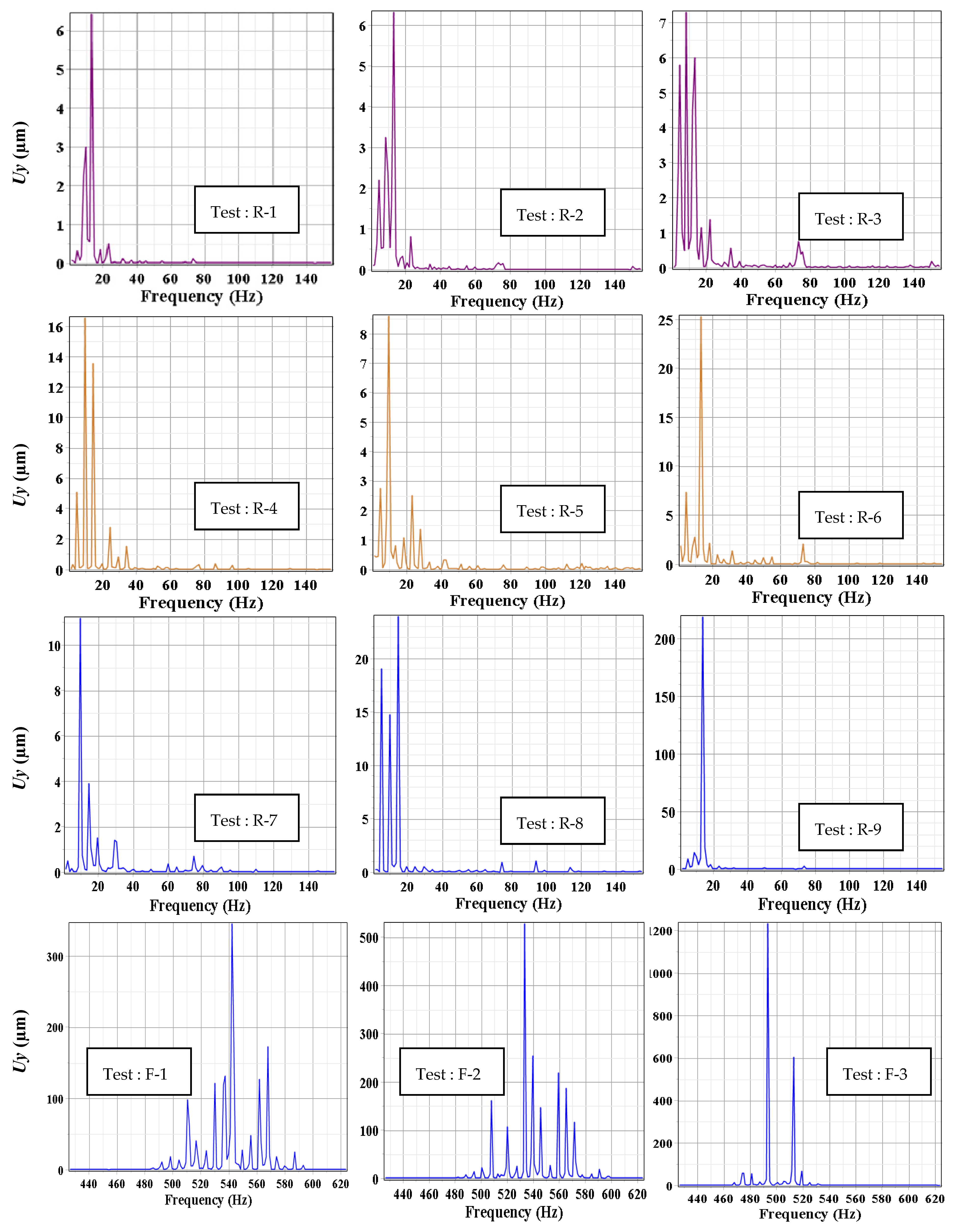
- The variation of the radial, tangential, and axial components , , and of the cutting force, as well as the radial displacement of the workpiece wall around their average value, is low for the roughing tests where the wall thickness . However, this variation intensifies for the finishing tests where the wall thickness . These variations have a significant effect on the quality of the surface finish of the workpiece wall;
- For the roughing operations, no vibrated surfaces were observed except for test “R-9”. In this case, the flexibility of the workpiece limits the chip cross-section value without vibrations. For the other tests, variations of the dynamic cutting forces were measured. The variations are situated from ±10% to ±23% of the average value.
3.2. Stability Analysis
3.3. FFT Spectra Analysis
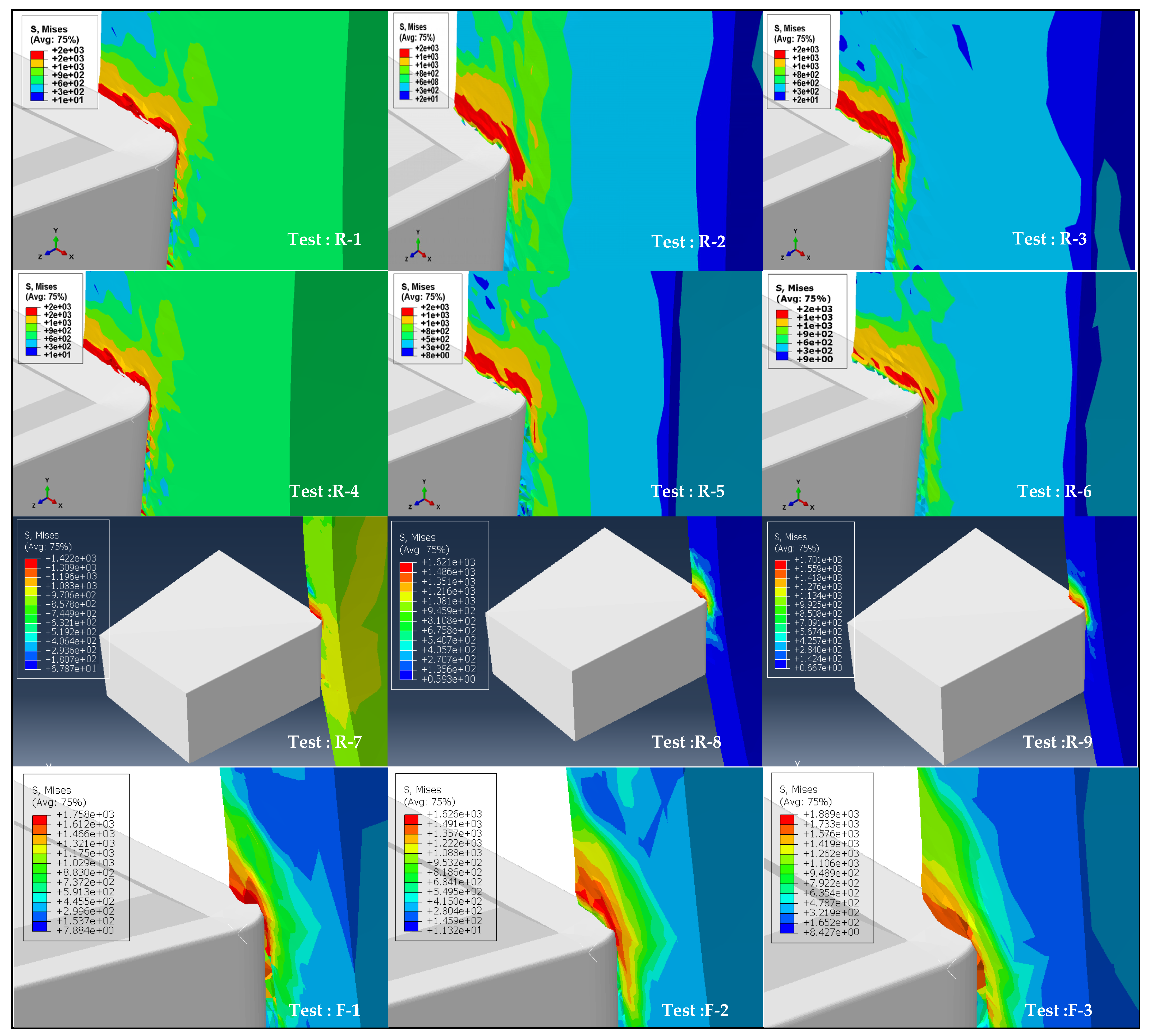
3.4. Von Mises Stress Field Distribution
4. Conclusions
- Cutting forces and the quality of the machined surface depend not only on the choice of the feed rate but also on the dynamic behavior of thin-walled parts due to their low rigidity and low structural damping during the machining operation;
- The average values of the cutting forces and the radial displacement of the workpiece wall are proportional to the feed rate. These average values are slightly influenced by the wall thickness of the machined parts;
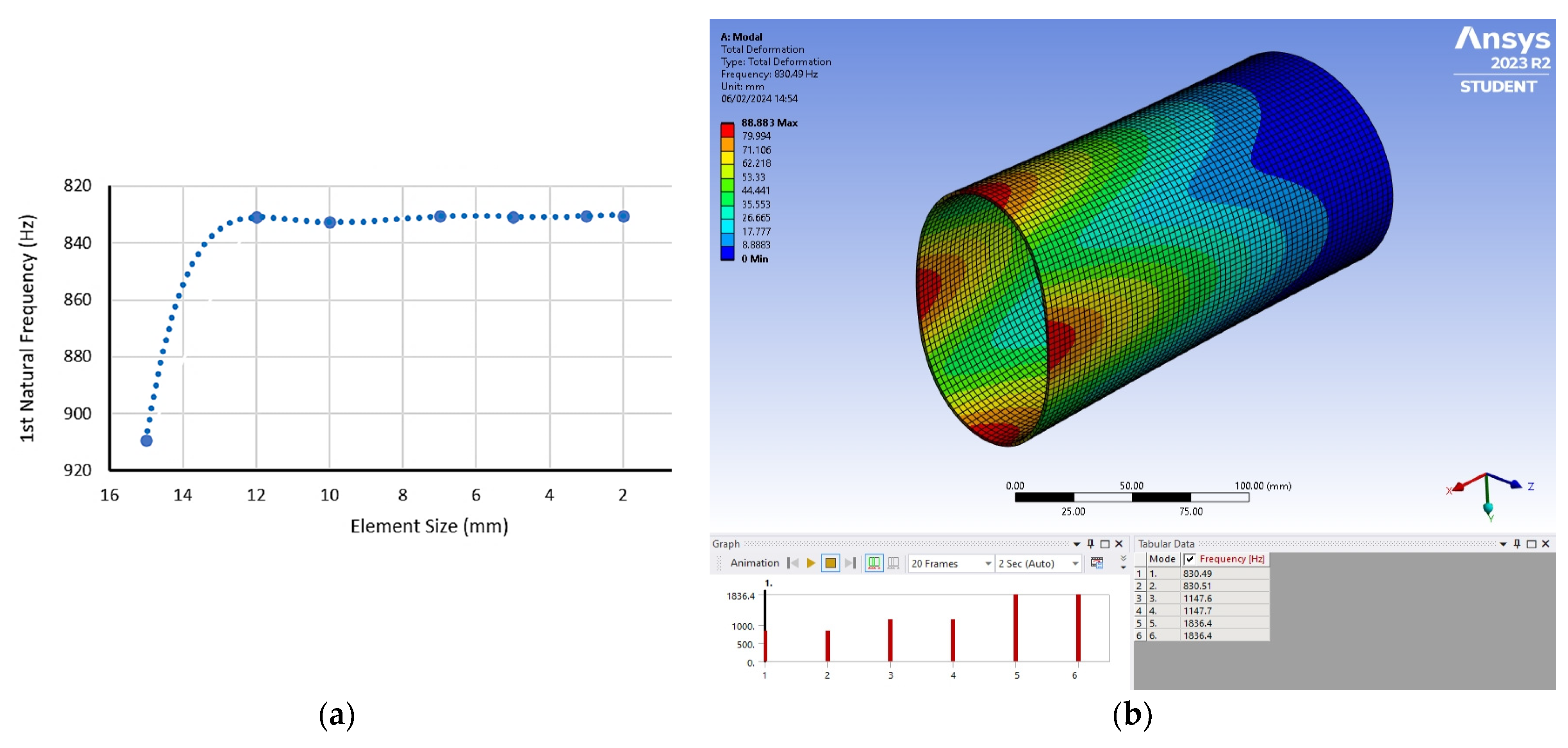
- The results of the modal analysis confirmed that the instability of the cutting process under the given conditions is not caused by the resonance of the workpiece but is influenced by the parameters of the technological process;
- The variation of the radial, tangential, and axial components of the cutting force, as well as the radial displacement of the workpiece wall around their average value, is low for the roughing tests where the wall thickness is considered large. However, this variation intensifies for the finishing tests where the wall thickness is thin. These variations have a significant effect on the quality of the surface finish of the workpiece wall;
- The stress distribution is concentrated in the cutting zone. It reaches its maximum value at the cutting-edge contact of the tool and workpiece. Analysis of results allowed deducing the existence of shear zones at the edge of the tool throughout the cut.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mabrouki, T.; Courbon, C.; Zhang, Y.; Rech, J.; Nélias, D.; Asad, M.; Hamdi, H.; Belhadi, S.; Salvatore, S. Some insights on the modelling of chip formation and its morphology during metal cutting operations. Comptes Rendus Mécanique 2016, 344, 335–354. [Google Scholar] [CrossRef]
- Siddhpura, M.; Paurobally, R. Experimental Investigation of Chatter Vibrations in Facing and Turning Processes. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2013, 7, 968–973. [Google Scholar]
- Cao, H.; Zhou, K.; Chen, X. Stability-based selection of cutting parameters to increase material removal rate in high-speed machining process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 227–240. [Google Scholar] [CrossRef]
- Li, A.; Zhao, J.; Luo, H.; Pei, Z.; Wang, Z. Progressive tool failure in high-speed dry milling of Ti-6Al-4V alloy with coated carbide tools. Int. J. Adv. Manuf. Technol. 2012, 58, 465–478. [Google Scholar] [CrossRef]
- Ezugwu, E.O.; Wang, Z.M. Titanium alloys and their machinability. J. Mater. Process. Technol. 1997, 68, 262–274. [Google Scholar] [CrossRef]
- Tan, L.; Yao, C.; Li, X.; Fan, Y.; Cui, M. Effects of Machining Parameters on Surface Integrity when Turning Inconel 718. J. Mater. Eng. Perform. 2022, 31, 4176–4186. [Google Scholar] [CrossRef]
- Joshi, S.; Tewari, A.; Joshi, S.S. Microstructural Characterization of Chip Segmentation Under Different Machining Environments in Orthogonal Machining of Ti6Al4V. J. Mater. Process. Technol. 2015, 137, 011005. [Google Scholar] [CrossRef]
- Dikshit, M.K.; Puri, A.B.; Maity, A. Modelling and application of response surface optimization to optimize cutting parameters for minimizing cutting forces and surface roughness in high-speed, ball-end milling of Al2014-T6. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 5117–5133. [Google Scholar] [CrossRef]
- Alajmi, M.S.; Almeshal, A.M. Prediction and Optimization of Surface Roughness in a Turning Process Using the ANFIS-QPSO Method. Materials 2020, 13, 2986. [Google Scholar] [CrossRef]
- Xu, Y.; Wan, Z.; Zou, P.; Huang, W.; Zhang, G. Experimental study on cutting force in utrasoninc vibration-assisted turning of 304 austenitic stainless steel. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 235, 494–513. [Google Scholar] [CrossRef]
- Dutta, S.; Kumar, S.; Narala, R. Investigations on machining characteristics and chip morphology in turning Al-Mn (AM) alloy using finite element simulation. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 1608–1617. [Google Scholar] [CrossRef]
- Grzesik, W.; Bartoszuk, M.; Nieslony, P. Finite Element Modeling of Temperature Distribution in the Cutting Zone in Turning Processes with Differently Coated Tools. J. Mater. Process. Technol. 2005, 164–165, 1204–1211. [Google Scholar] [CrossRef]
- Twardowski, P.; Wiciak-Pikuła, M. Prediction of Tool Wear Using Artificial Neural Networks during Turning of Hardened Steel. Materials 2019, 12, 3091. [Google Scholar] [CrossRef]
- Liu, C.; Wan, M.; Zhang, W.; Yang, Y. Chip Formation Mechanism of Inconel 718: A Review of Models and Approaches. Chin. J. Mech. Eng. 2021, 34, 34. [Google Scholar] [CrossRef]
- Duan, C.Z.; Doul, T.; Cai, Y.J.; Li, Y.Y. Finite Element Simulation and Experiment of Chip Formation Process during High Speed machining of AISI 1045 Hardned Steel. Int. J. Recent Trends Eng. 2009, 1, 46–50. [Google Scholar]
- Abushawashi, Y.; Xiao, X.; Astakhov, V.P. FEM simulation of metal cutting using a new approach to model chip formation. Int. J. Adv. Mach. Form. Oper. 2011, 3/2, 71–92. [Google Scholar]
- Zhang, Y.; Outeiro, J.C.; Mabrouki, T. On the selection of Johnson-Cook constitutive model parameters for Ti-6Al-4V using three types of numerical models of orthogonal cutting. Procedia Cirp 2015, 31, 112–117. [Google Scholar] [CrossRef]
- Shuang, F.; Chen, X.; Ma, W. Numerical analysis of chip formation mechanisms in orthogonal cutting of Ti6Al4V alloy based on a CEL model. Int. J. Mater. Form. 2018, 11, 185–198. [Google Scholar] [CrossRef]
- Pantale, O. 2D and 3D numerical models of metal cutting with damage effects. Comput. Methods Appl. Mech. Eng. 2004, 193, 4383–4399. [Google Scholar] [CrossRef]
- Mabrouki, T.; Girardin, F.; Asad, M.; Rigal, J.F. Numerical and experimental study of dry cutting for an aeronautic aluminum alloy (A2024-T351). Int. J. Mach. Tools Manuf. 2008, 48, 1187–1197. [Google Scholar] [CrossRef]
- Yue, C.X. 3D Finite Element Simulation of Hard Turning. Adv. Mater. Res. 2009, 69–70, 11–15. [Google Scholar] [CrossRef]
- Schermann, T.; Marsolek, J.; Schmidt, C.; Fleischer, J. Aspects of the simulation of a cutting process with ABAQUS/Explicit including the interaction between the cutting process and the dynamic behavior of the machine tool. CIRP Int. Workshop Model. Mach. Oper. 2006, 9, 163–170. [Google Scholar]
- Bagheri, B.; Abdollahzadeh, A.; Abbasi, M.; Kokabi, A.H. Effect of vibration on machining and mechanical properties of AZ91 alloy during FSP: Modeling and experiments. Int. J. Mater. Form. 2021, 14, 623–640. [Google Scholar] [CrossRef]
- Mehdi, K.; Rigal, J.F.; Play, D. Dynamic behavior of a thin wall cylindrical workpiece during the turning process Part I: Cutting Process Simulation. J. Manuf. Sci. Eng. 2002, 124, 562–568. [Google Scholar] [CrossRef]
- Mehdi, K.; Rigal, J.F.; Play, D. Dynamic behavior of a thin wall cylindrical workpiece during the turning process Part II: Experimental approach and validation. J. Manuf. Sci. Eng. 2002, 124, 569–580. [Google Scholar] [CrossRef]
- Lorong, P.; Larue, A.; Perez Duarte, A. Dynamic Study of Thin Wall Part Turning. Adv. Mater. Res. 2011, 223, 591–599. [Google Scholar] [CrossRef]
- Gerasimenko, A.; Guskov, M.; Duchemin, J.; Lorong, P.; Gouskov, A. Variable compliance-related aspects of chatter in turning thin-walled tubular parts. Procedia CIRP. 2015, 31, 58–63. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, D.H.; Wu, B.H.; Zhou, X. Material removal process optimization for milling of flexible workpiece considering machining stability. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 1263–1272. [Google Scholar] [CrossRef]
- Sahraoui, Z.; Mehdi, K.; Ben Jaber, M. Analytical and experimental stability analysis of AU4G1 thin-walled tubular workpieces in turning process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 1007–1018. [Google Scholar] [CrossRef]
- Del Sol, I.; Rivero, A.; López de Lacalle, L.N.; Gamez, A.J. Thin-Wall Machining of Light Alloys: A Review of Models and Industrial Approaches. Materials 2019, 12, 2012. [Google Scholar] [CrossRef]
- Amigo, F.J.; Urbikain, G.; Pereira, O.; Fernández-Lucio, P.; Fernández-Valdivielso, A.; López de Lacalle, L.N. Combination of high feed turning with cryogenic cooling on Haynes 263 and Inconel 718 superalloys. J. Manuf. Process. 2020, 58, 208–222. [Google Scholar] [CrossRef]
- Grolleau, V. Approche de la Validation Expérimentale des Simulations Numériques de la Coupe Avec Prise en Compte Des Phénomènes Locaux à L’arête de L’outil. Ph.D. Thesis, École Centrale de Nantes, Nantes, France, 1996. (In French). [Google Scholar]
- Zhang, D.-W.; Ou, H. Relationship between friction parameters in a Coulomb–Tresca friction model for bulk metal forming. Tribol. Int. 2016, 95, 13–18. [Google Scholar] [CrossRef]
- Das, M.K.; Tobias, S.A. The Relation between the Static and the Dynamic Cutting of Metals. Int. J. Mach. Tool Des. Res. 1967, 7, 63–89. [Google Scholar] [CrossRef]
- Sission, T.R.; Kegg, R.L. An Explanation of Low Speed Chatter Effects. J. Manuf. Sci. Eng. 1969, 91, 951–958. [Google Scholar] [CrossRef]
- Wu, D.W. A new approach of formulating the transfer function for dynamic cutting processes. Trans. ASME J. Eng. Ind. 1989, 111, 37–47. [Google Scholar] [CrossRef]
- Chiou, R.Y.; Liang, S.Y. Chatter Stability of a Slender Cutting Tool in Turning with Wear Effect. Internaional J. Mach. Tools Manuf. 1998, 38, 315–327. [Google Scholar] [CrossRef]
- Kegg, R.L. Cutting Dynamics in Machine tool Chatter, Contribution to Machine tool Chatter Research 3. Trans. ASME J. Eng. Ind. 1965, 87, 464–470. [Google Scholar] [CrossRef]
- Kayhan, M.; Budak, E. An experimental investigation of chatter effects on tool life. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 1455–1463. [Google Scholar] [CrossRef]
- Barge, M. Simulation numérique de la coupe orthogonale. 7ème Colloq. Natl. En Calc. Des Struct. Giens Fr. 2005, 2, 371–376. (In French) [Google Scholar]
- Arrazola, P.J.; Ugarte, D.; Montoya, J.; Villar, A.; Marya, S. Finite element modeling of chip formation process with Abaqus/Explicit 6.3. In Proceedings of the 8th International Conference on Computational Plasticity, Barcelona, Spain, 5–7 September 2005. [Google Scholar]
- Tlusty, J.; Polacek, M. The stability of the machine tool against self-excited vibration in machining. Mach. Sci. Technol. 1963, 1, 465–474. [Google Scholar]
- Insperger, T.; Stepan, G. Stability analysis of turning with periodic spindle speed modulation via semidiscretization. J. Vib. Control. 2004, 10, 1835–1855. [Google Scholar] [CrossRef]
- Technical Datasheet 42CrMo4 Steel, Swiss Steel Group; Steeltec AG/Steeltec GmbH: Emmenbrücke, Switzerland; Düsseldorf, Germany; Gebze, Türkiye, 2023.



| Parameter | Value |
|---|---|
| Young’s modulus E (GPa) | 211 |
| Poisson’s ratio υ | 0.29 |
| Density ρ (kg/m3) | 7850 |
| A (MPa) | 598 |
| B (MPa) | 768 |
| C | 0.0137 |
| n | 0.2092 |
| m | 0.807 |
| (s−1) | 0.001 |
| Machining Operation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Roughing | Finishing | |||||||||||
| Test Ref. | R-1 | R-2 | R-3 | R-4 | R-5 | R-6 | R-7 | R-8 | R-9 | F-1 | F-2 | F-3 |
| Wall thickness ep (mm) | 6 | 6 | 6 | 4.5 | 4.5 | 4.5 | 3 | 3 | 3 | 1.5 | 1.5 | 1.5 |
| Depth of cut ap (mm) | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 0.5 | 0.5 | 0.5 |
| Feed rate f (mm/rev) | 0.2 | 0.3 | 0.4 | 0.2 | 0.3 | 0.4 | 0.2 | 0.3 | 0.4 | 0.1 | 0.125 | 0.16 |
| Cutting speed vc (m/min) | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 200 | 200 | 200 |
| Parameters | Machining Operation | |
|---|---|---|
| Roughing | Finishing | |
| Tool insert reference (ISO) | CNMG 120408 QMGC 415 | CNMG 120404 QFGC 425 |
| Tools noise radius: R (mm) | 0.8 | 0.4 |
| Acuity radius of the cutting edge: r (mm) | 0.04 | 0.03 |
| Rake angle: γ (°) | 7 | 2 |
| Clearance angle: α (°) | 6 | 6 |
| Cutting edge angle: χr (°) | 95 | 95 |
| Complementary angle of the cutting edge direction: ψr (°) | −5 | −5 |
| Test Ref. | (mm) | (N) | (N) | (N) | dep (μm) | Observed Surface |
|---|---|---|---|---|---|---|
| R-1 | 0.2 | 260 | 791 | 391 | −61 | N. V. |
| R-2 | 0.3 | 360 | 1091 | 491 | −95 | N. V. |
| R-3 | 0.4 | 482 | 1465 | 574 | −132 | N. V. |
| R-4 | 0.2 | 255 | 780 | 392 | −63 | N. V. |
| R-5 | 0.3 | 319 | 1040 | 455 | −81 | N. V. |
| R-6 | 0.4 | 530 | 1408 | 684 | −119 | N. V. |
| R-7 | 0.2 | 256 | 790 | 387 | −69 | N. V. |
| R-8 | 0.3 | 359 | 1076 | 505 | −119 | N. V |
| R-9 | 0.4 | 492 | 1462 | 662 | −135 | L. V. |
| F-1 | 0.1 | 91 | 249 | 141 | −39 | V. |
| F-2 | 0.125 | 98 | 250 | 100 | −34 | V. |
| F-3 | 0.16 | 156 | 307 | 168 | −49 | V. |
(err%) | (err%) | (err%) | (err%) | (err%) | (err%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| R-1 | 260 | 277 (6) | 53 (80) | 791 | 787 (1) | 774 (2) | 391 | 381 (3) | 239 (39) |
| R-2 | 360 | 359 (0) | 63 (82) | 1091 | 1088 (0) | 1034 (5) | 491 | 495 (1) | 263 (47) |
| R-3 | 482 | 435 (10) | 94 (81) | 1465 | 1445 (1) | 1271 (13) | 574 | 599 (4) | 312 (46) |
| R-4 | 255 | 211 (17) | 23 (91) | 780 | 779 (0) | 800 (3) | 392 | 406 (4) | 244 (38) |
| R-5 | 319 | 280 (12) | 46 (86) | 1040 | 1044 (0) | 900 (13) | 455 | 537 (18) | 260 (43) |
| R-6 | 530 | 390 (26) | 77 (85) | 1408 | 1393 (1) | 1225 (13) | 684 | 748 (9) | 304 (55) |
| R-7 | 256 | 217 (15) | 30 (88) | 790 | 790 (0) | 705 (11) | 387 | 416 (8) | 231 (40) |
| R-8 | 359 | 292 (19) | 35 (90) | 1076 | 1079 (0) | 1005 (7) | 505 | 559 (11) | 241 (52) |
| R-9 | 492 | 406 (18) | 96 (81) | 1462 | 1416 (3) | 1350 (8) | 662 | 777 (17) | 310 (53) |
| F-1 | 91 | 89 (2) | 17 (81) | 249 | 248 (0) | 176 (29) | 141 | 148 (5) | 93 (34) |
| F-2 | 98 | 96 (3) | 22 (78) | 250 | 246 (2) | 190 (24) | 100 | 110 (11) | 93 (7) |
| F-3 | 156 | 157 (0) | 23 (85) | 307 | 306 (1) | 216 (30) | 168 | 181 (8) | 99 (41) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehdi, K.; Monka, P.P.; Monkova, K.; Sahraoui, Z.; Glaa, N.; Kascak, J. Investigation of Dynamic Behavior and Process Stability at Turning of Thin-Walled Tubular Workpieces Made of 42CrMo4 Steel Alloy. Machines 2024, 12, 120. https://doi.org/10.3390/machines12020120
Mehdi K, Monka PP, Monkova K, Sahraoui Z, Glaa N, Kascak J. Investigation of Dynamic Behavior and Process Stability at Turning of Thin-Walled Tubular Workpieces Made of 42CrMo4 Steel Alloy. Machines. 2024; 12(2):120. https://doi.org/10.3390/machines12020120
Chicago/Turabian StyleMehdi, Kamel, Peter Pavol Monka, Katarina Monkova, Zied Sahraoui, Nawel Glaa, and Jakub Kascak. 2024. "Investigation of Dynamic Behavior and Process Stability at Turning of Thin-Walled Tubular Workpieces Made of 42CrMo4 Steel Alloy" Machines 12, no. 2: 120. https://doi.org/10.3390/machines12020120
APA StyleMehdi, K., Monka, P. P., Monkova, K., Sahraoui, Z., Glaa, N., & Kascak, J. (2024). Investigation of Dynamic Behavior and Process Stability at Turning of Thin-Walled Tubular Workpieces Made of 42CrMo4 Steel Alloy. Machines, 12(2), 120. https://doi.org/10.3390/machines12020120








