Analysis of Roughness, the Material Removal Rate, and the Acoustic Emission Signal Obtained in Flat Grinding Processes
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Grinding Experiments
2.3. Experimental Setup
2.4. Roughness Measurements
2.5. Determination of the Material Removal Rate (MRR)
2.6. Measurement of the AE Signal
2.7. Analysis of the AE Signal
- -
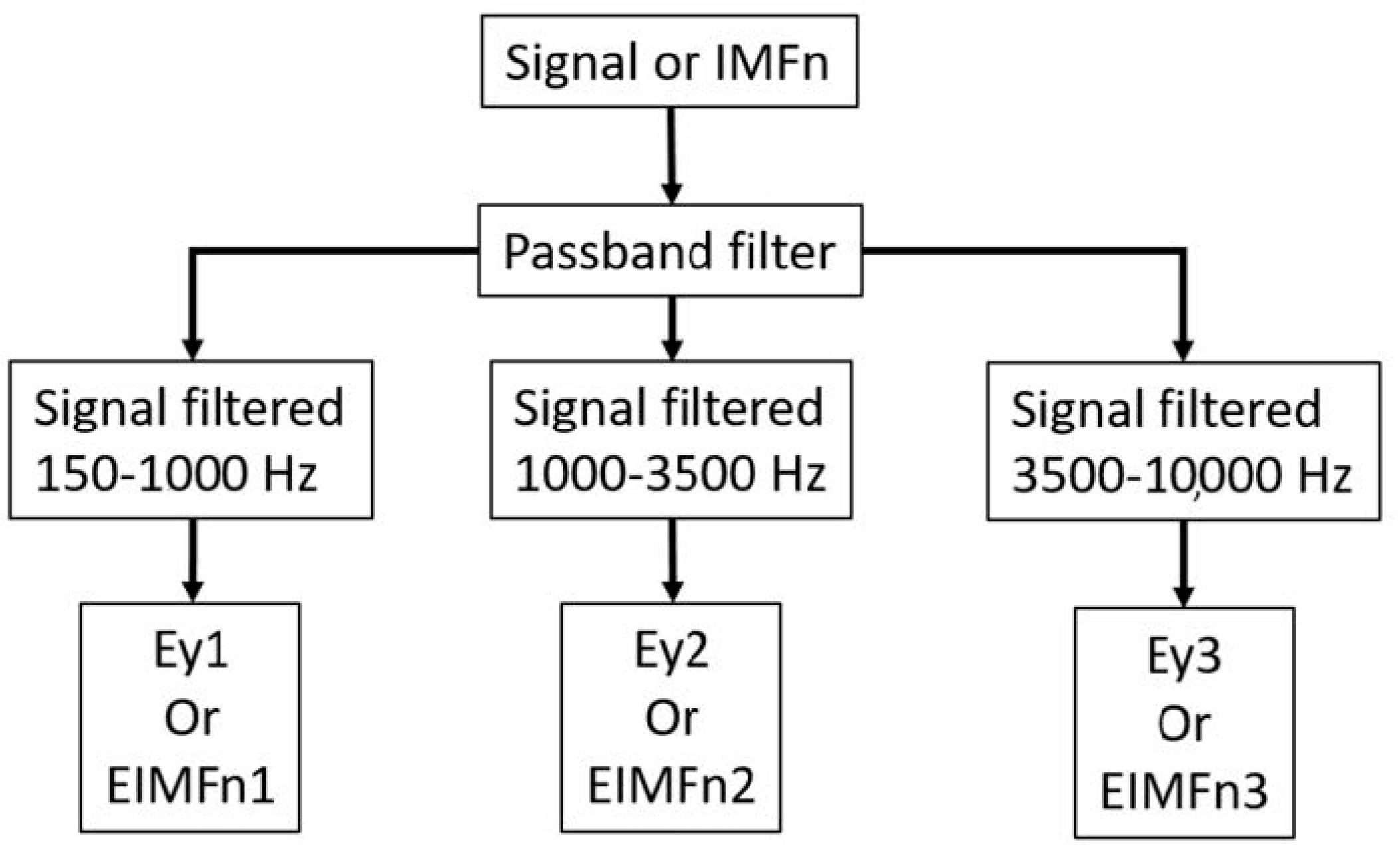
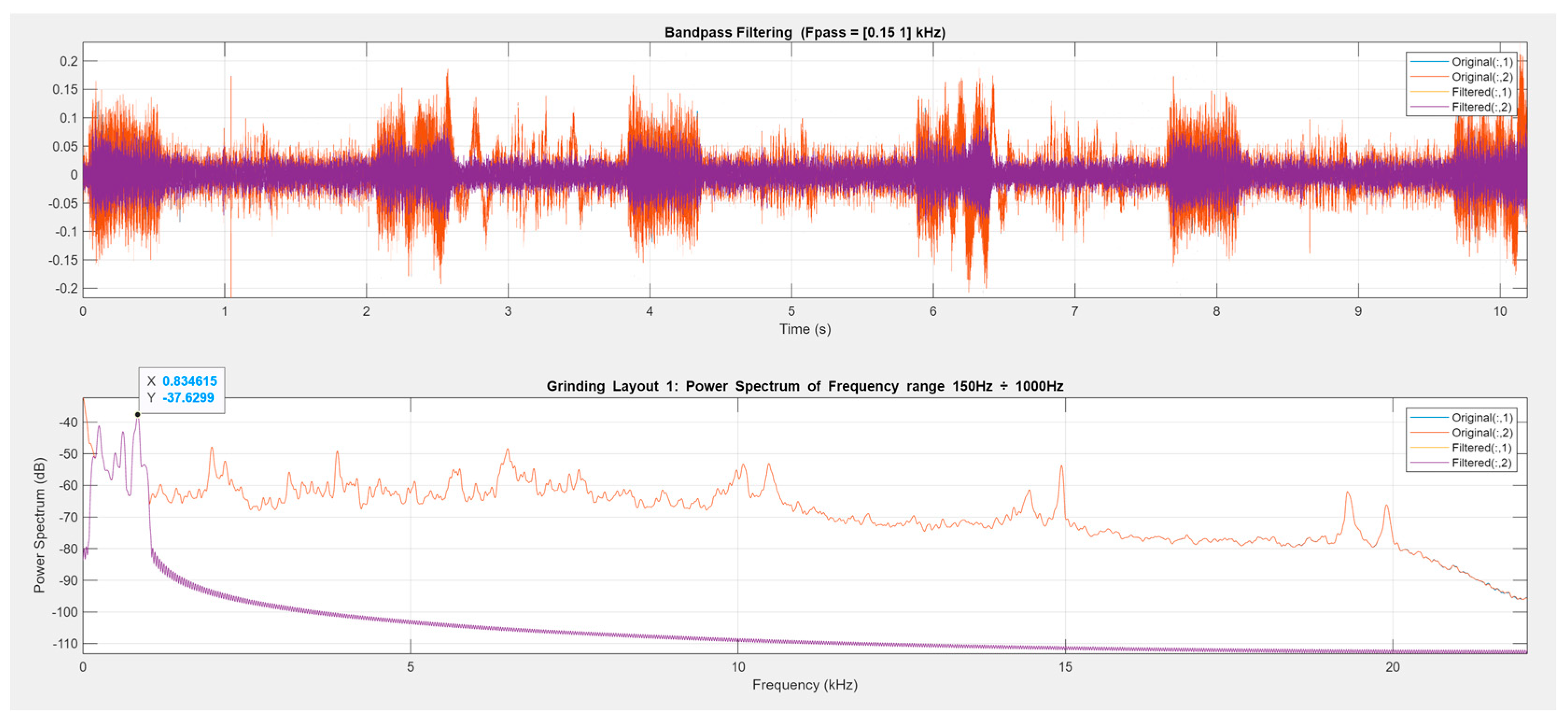
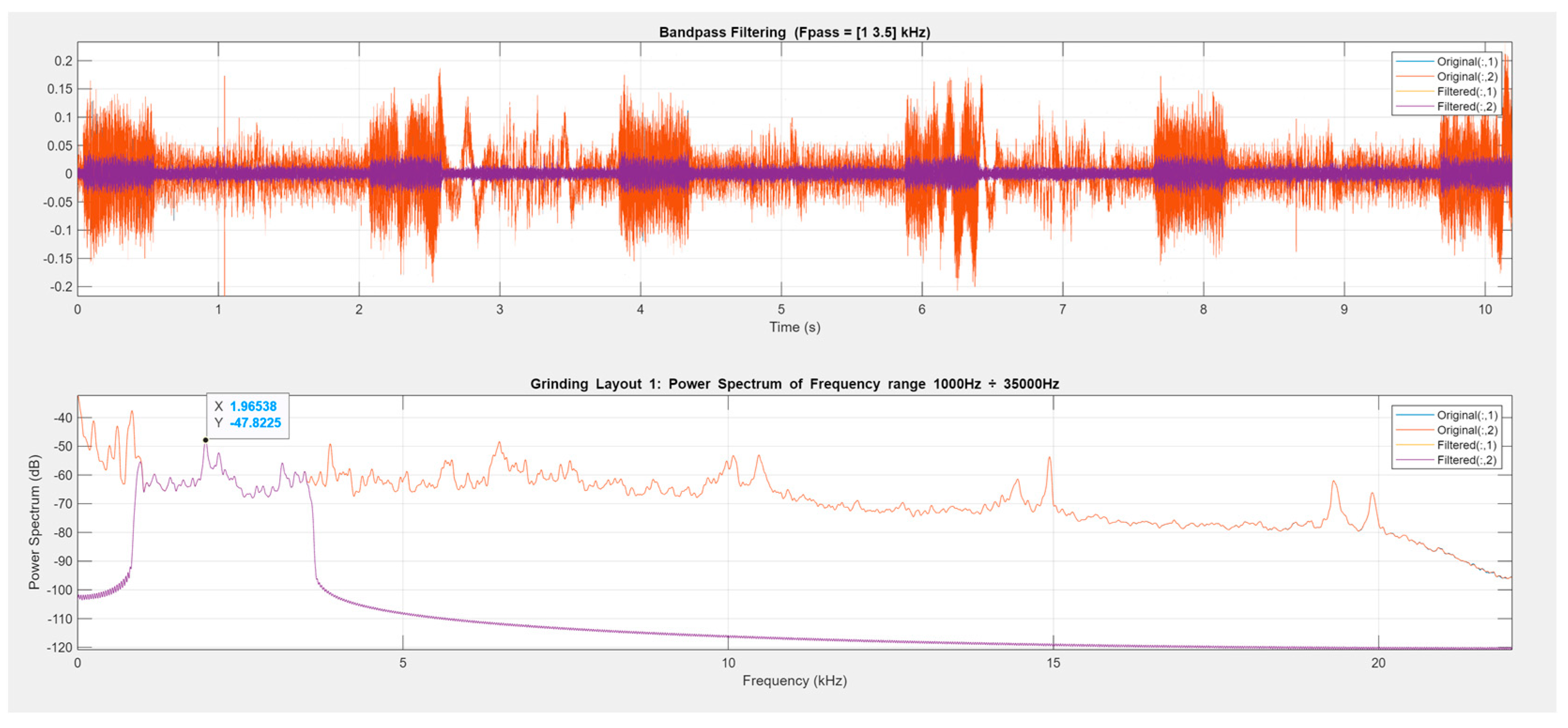
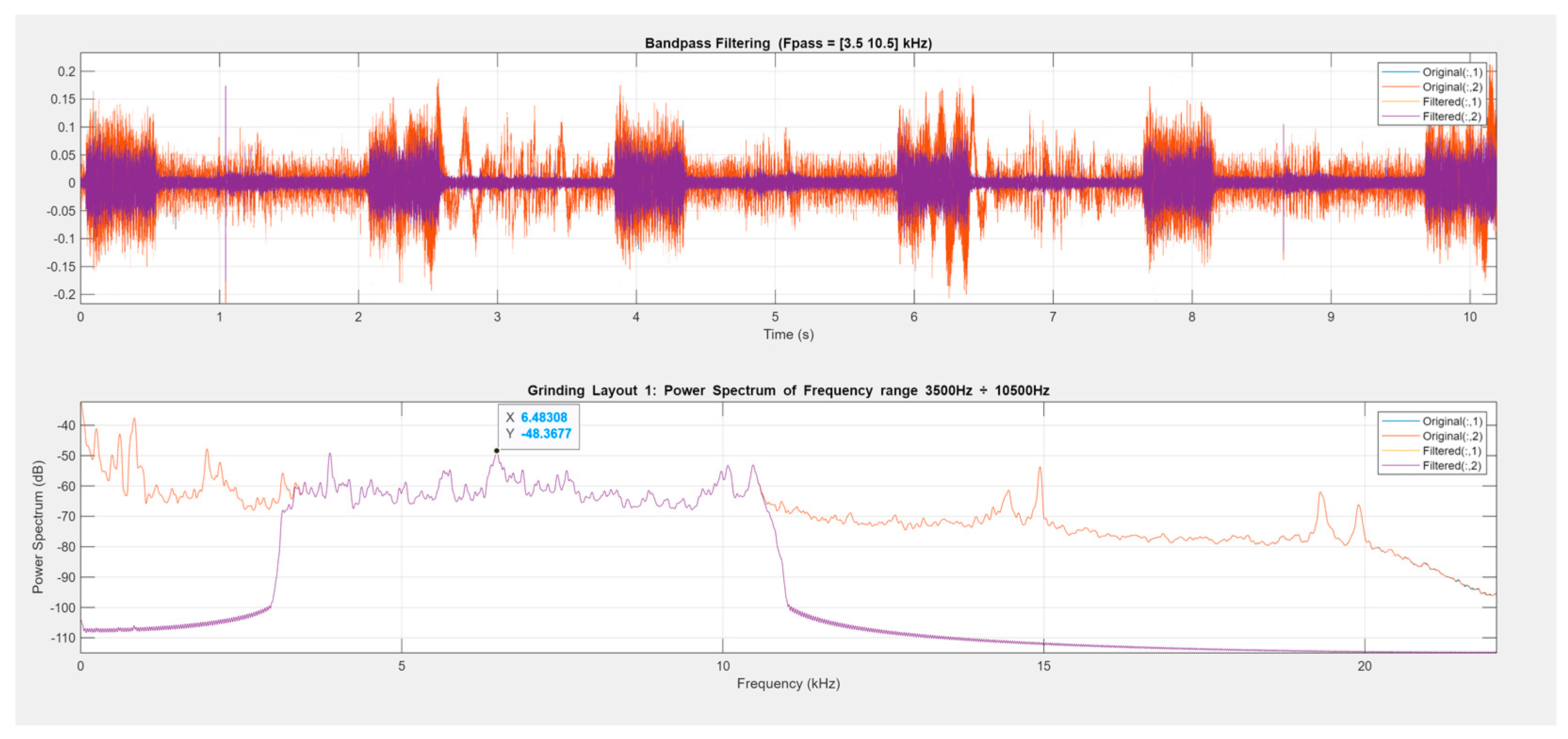
- First, the frequency bands are established. The signal is decomposed into three different signals, using band pass filters. In this case, the selected frequency ranges were as follows: for the first band, 150 to 1000 Hz; for the second band, 1000 to 3500 Hz; and for the third band, 3500 to 10,000 Hz. Other values can be established depending on the type of machining or machining conditions. Alternatively, IMFs can be used instead of the signal. They are obtained with the empirical mode decomposition (EMD) method.
- -
- The next step is to measure the power spectrum for the different frequency ranges of the analyzed AE signals.
- -
- In addition, X is calculated as the frequency of the highest peak of the filtered signal (in kHz), while Y is the power spectrum in dB.
3. Results and Discussion
3.1. The Material Removal Rate and Surface Roughness
3.2. Ey1, Ey2, Ey3, X1, Yy, X2, Y2, X3, and Y3
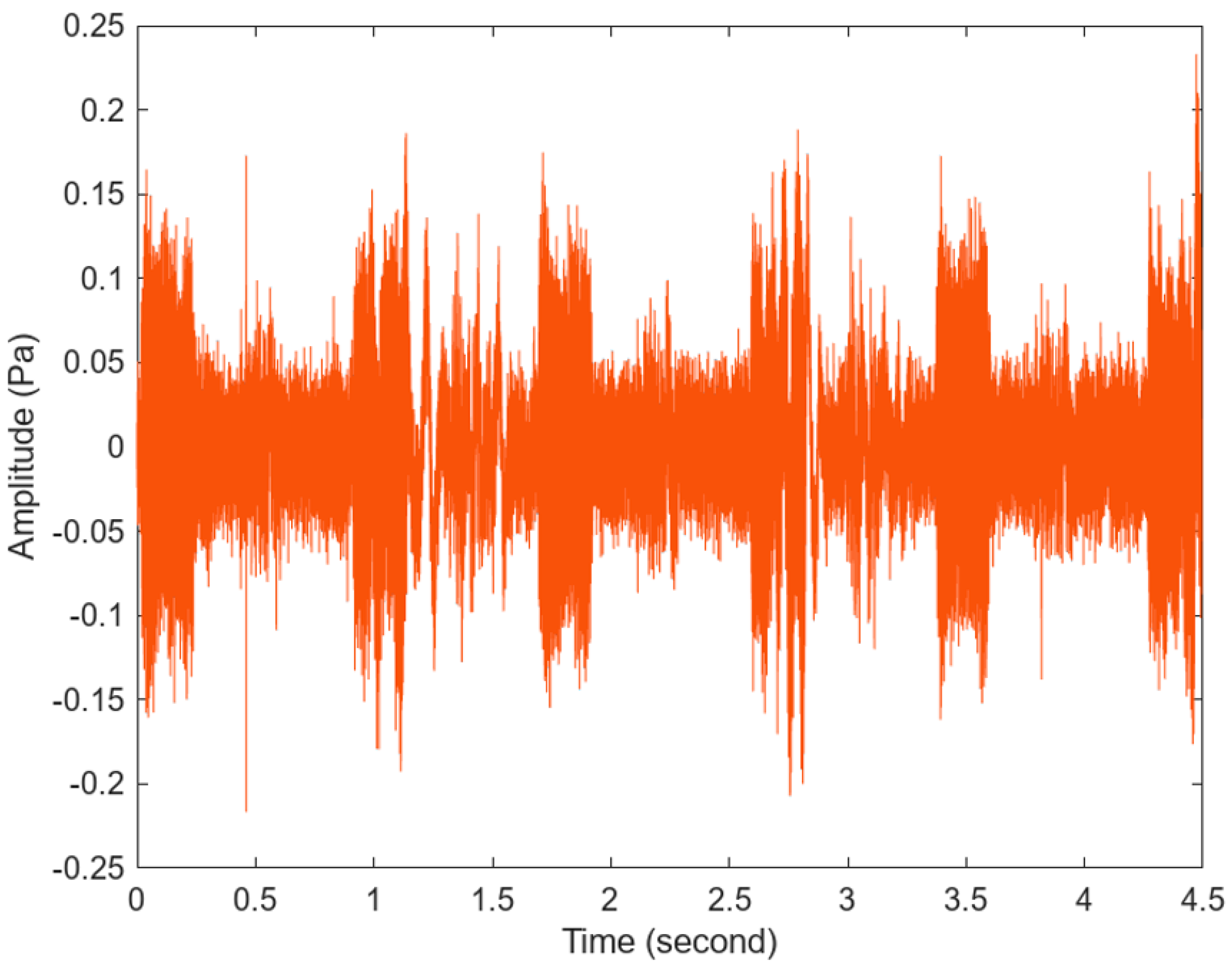
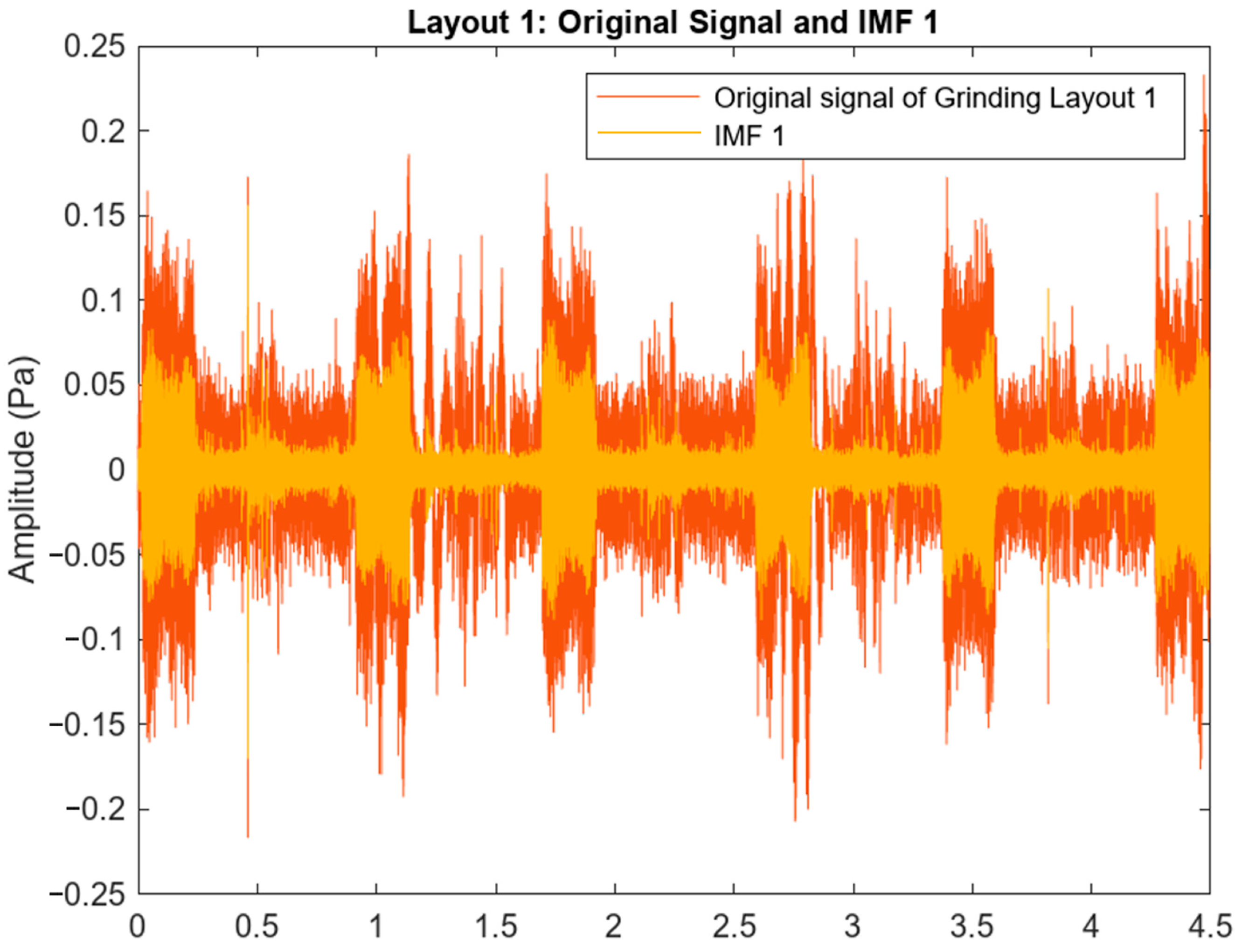
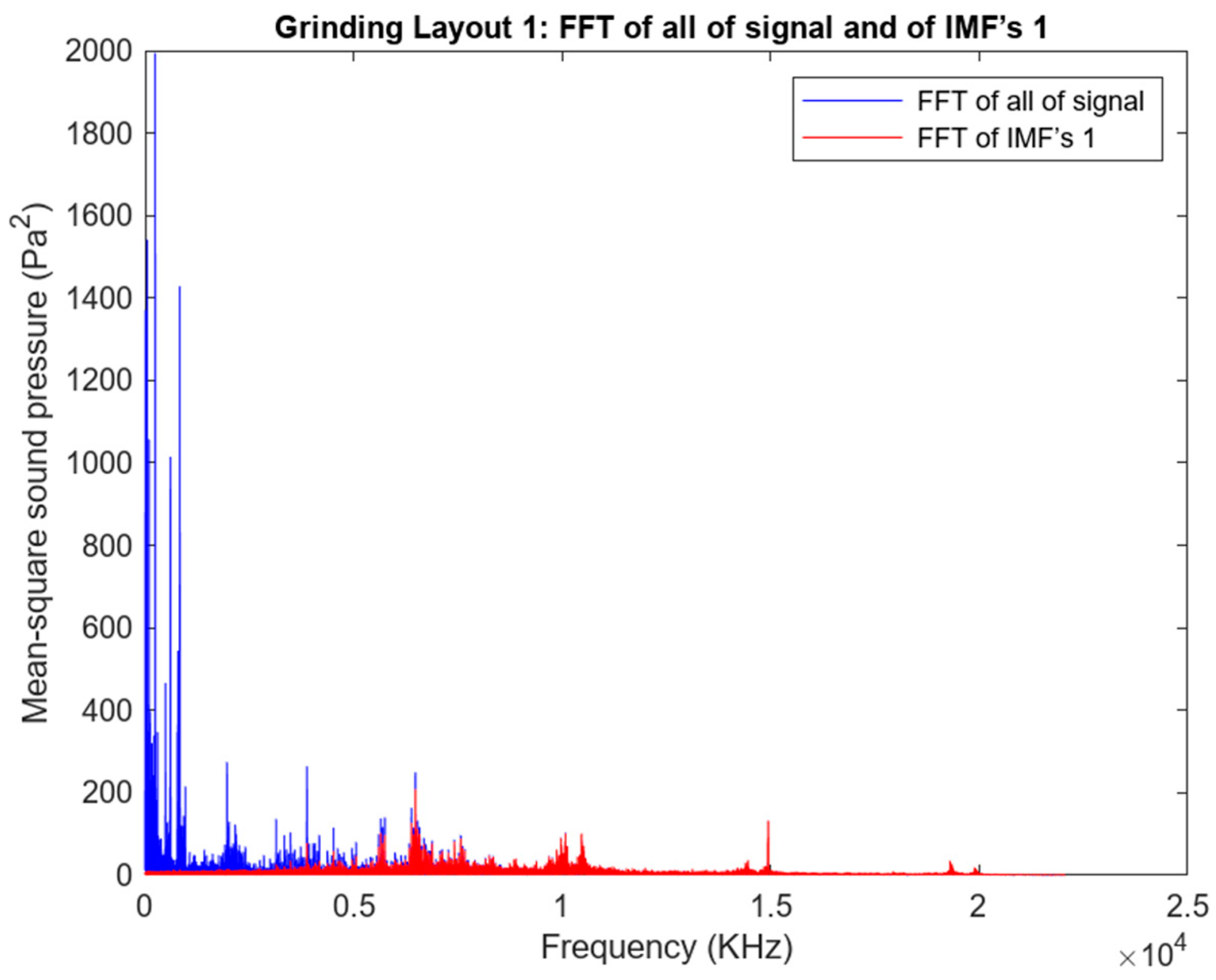
3.3. Analysis of the Acoustic Emission (AE) Signal for Experiment 1
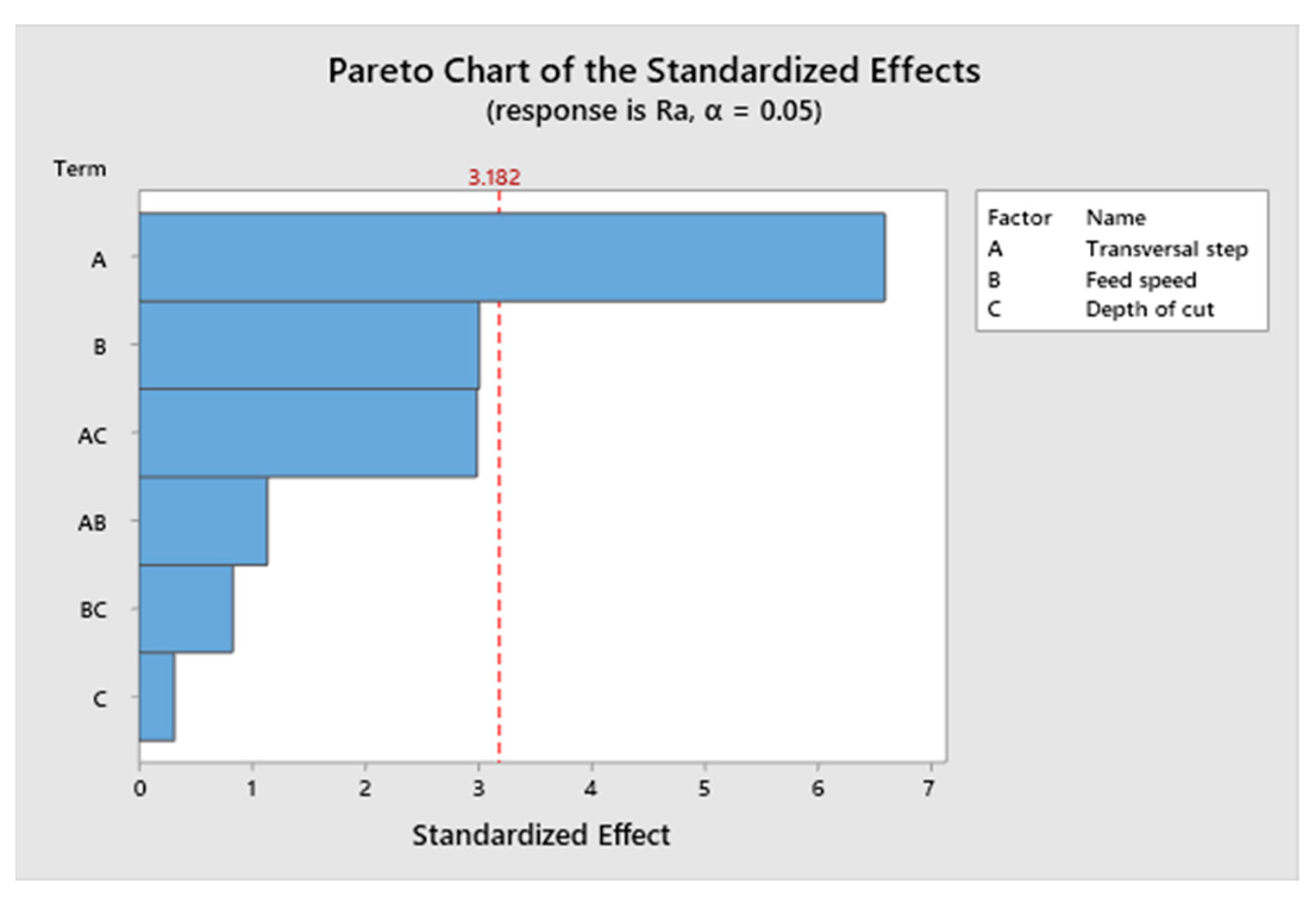
3.4. Factorial Regression Analysis
3.4.1. Model for Ra
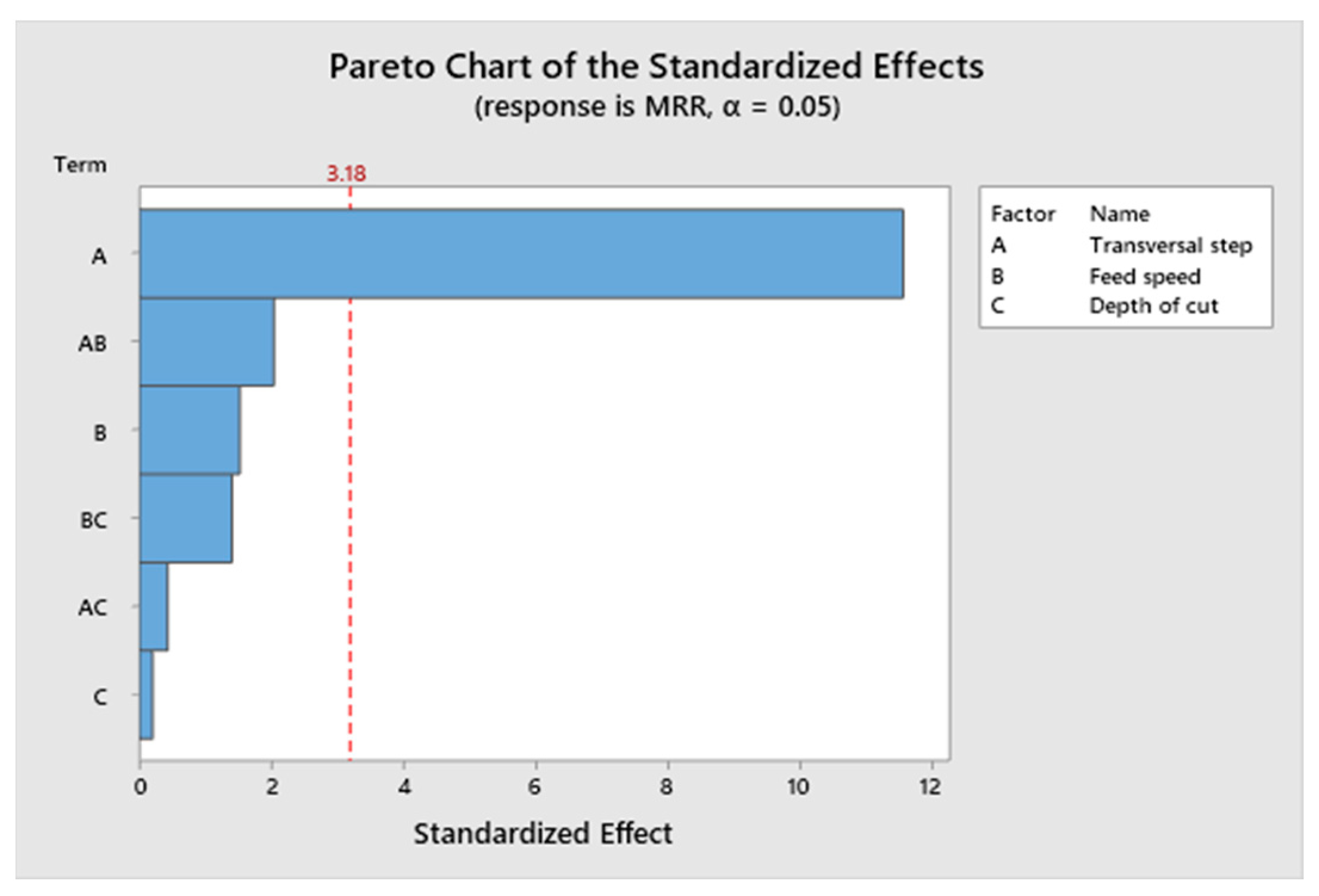
3.4.2. Model for the MRR
3.5. Multi-Objective Optimization
4. Conclusions
- Analysis of AE signal using filtration in three different frequency ranges is a useful method to analyze the grinding process. In this case, three modes were considered. As a general trend, the higher the depth of cut, the higher the energy values. The highest frequency of each frequency group tends to decrease with the depth of cut.
- The greatest influence on the Ra parameter is the transversal step followed by feed speed and the mutual effect of depth of cut and the transversal step.
- Within the ranges studied, the material removal rate depends mainly on the transversal step.
- In order to simultaneously obtain low roughness and a high MRR, a high transversal step and feed speed and a low depth of cut are recommended.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klocke, F. Manufacturing Processes 2-Grinding, Honing, Lapping; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Liang, S.Y.; Shih, A.J. Analysis of Machining and Machine Tools; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Adeniji, D.; Oligee, K.; Schoop, J. A Novel Approach for Real-Time Quality Monitoring in Machining of Aerospace Alloy through Acoustic Emission Signal Transformation for DNN. J. Manuf. Mater. Process. 2022, 6, 18. [Google Scholar] [CrossRef]
- Barylski, A.; Sender, P. The proposition of an automated honing cell with advanced monitoring. Machines 2020, 8, 70. [Google Scholar] [CrossRef]
- Ferrando Chacón, J.L.; Fernández de Barrena, T.; García, A.; Sáez de Buruaga, M.; Badiola, X.; Vicente, J. A Novel Machine Learning-Based Methodology for Tool Wear Prediction Using Acoustic Emission Signals. Sensors 2021, 21, 5984. [Google Scholar] [CrossRef] [PubMed]
- Rimpault, X.; Chatelain, J.F.; Klemberg-Sapieha, J.E.; Balazinski, M. Fractal Analysis of Cutting Force and Acoustic Emission Signals during CFRP Machining. Procedia CIRP 2016, 46, 143–146. [Google Scholar] [CrossRef]
- Gómez, M.P.; Hey, A.M.; Ruzzante, J.E.; D’Attellisc, C.E. Tool wear evaluation in drilling by acoustic emission. Phys. Procedia 2010, 3, 819–825. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Aslan, A.; Pimenov, D.Y.; Usca, Ü.A.; Salur, E.; Gupta, M.K.; Mikolajczyk, T.; Giasin, K.; Kapłonek, W.; Sharma, S. A review of indirect tool condition monitoring systems and decision-making methods in turning: Critical analysis and trends. Sensors 2021, 21, 108. [Google Scholar] [CrossRef]
- Murat, Z.; Brezak, D.; Augustin, G.; Majetic, D. Frequency domain analysis of acoustic emission signals in medical drill wear monitoring. In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), Porto, Portugal, 21–23 February 2017; Volume 4, pp. 173–177. [Google Scholar]
- Nahornyi, V.; Panda, A.; Valíček, J.; Harničárová, M.; Kušnerová, M.; Pandová, I.; Legutko, S.; Palková, Z.; Lukáč, O. Method of Using the Correlation between the Surface Roughness of Metallic Materials and the Sound Generated during the Controlled Machining Process. Materials 2022, 15, 823. [Google Scholar] [CrossRef]
- Sio-Sever, A.; Lopez, J.M.; Asensio-Rivera, C.; Vizan-Idoipe, A.; de Arcas, G. Improved Estimation of End-Milling Parameters from Acoustic Emission Signals Using a Microphone Array Assisted by AI Modelling. Sensors 2022, 22, 3807. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, X.; Wang, T.; He, Y. Tool Wear Condition Monitoring Method Based on Deep Learning with Force Signals. Sensors 2023, 23, 4595. [Google Scholar] [CrossRef]
- The Ho, Q.N.; Do, T.T.; Minh, P.S.; Nguyen, V.T.; Nguyen, V.T.T. Turning Chatter Detection Using a Multi-Input Convolutional Neural Network via Image and Sound Signal. Machines 2023, 11, 644. [Google Scholar] [CrossRef]
- Huda, F.; Darman, D.; Rusli, M. Chatter detection in turning process using sound signal and simple microphone. IOP Conf. Ser. Mater. Sci. Eng. 2020, 830, 42027. [Google Scholar] [CrossRef]
- Nikhare, C.P.; Conklin, C.; Loker, D.R. Understanding acoustic emission for different metal cutting machinery and operations. J. Manuf. Mater. Process. 2017, 1, 7. [Google Scholar] [CrossRef]
- Nourizadeh, R.; Rezaei, S.M.; Zareinejad, M.; Adibi, H. Comprehensive investigation on sound generation mechanisms during machining for monitoring purpose. Int. J. Adv. Manuf. Technol. 2022, 121, 1589–1610. [Google Scholar] [CrossRef]
- Papacharalampopoulos, A.; Stavropoulos, P.; Doukas, C.; Foteinopoulos, P.; Chryssolouris, G. Acoustic emission signal through turning tools: A computational study. Procedia CIRP 2013, 8, 426–431. [Google Scholar] [CrossRef]
- Perrelli, M.; Cosco, F.; Gagliardi, F.; Mundo, D. In-Process Chatter Detection Using Signal Analysis in Frequency and Time-Frequency Domain. Machines 2022, 10, 24. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Z. A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components. Mech. Syst. Signal Process. 2012, 28, 258–279. [Google Scholar] [CrossRef]
- Leaman, F.; Vicuña, C.M.; Clausen, E. Potential of Empirical Mode Decomposition for Hilbert Demodulation of Acoustic Emission Signals in Gearbox Diagnostics. J. Vib. Eng. Technol. 2022, 10, 621–637. [Google Scholar] [CrossRef]
- Amarnath, M.; Praveen Krishna, I.R. Local fault detection in helical gears via vibration and acoustic signals using EMD based statistical parameter analysis. Meas. J. Int. Meas. Confed. 2014, 58, 154–164. [Google Scholar] [CrossRef]
- Deja, M. Method of Monitoring of the Grinding Process with Lapping Kinematics Using Audible Sound Analysis. J. Mach. Eng. 2022, 22, 157255. [Google Scholar] [CrossRef]
- Sender, P.; Buj-Corral, I. Influence of Honing Parameters on the Quality of the Machined Parts and Innovations in Honing Processes. Metals 2023, 13, 140. [Google Scholar] [CrossRef]
- Warren Liao, T. Feature extraction and selection from acoustic emission signals with an application in grinding wheel condition monitoring. Eng. Appl. Artif. Intell. 2010, 23, 74–84. [Google Scholar] [CrossRef]
- Pilný, L.; Bissacco, G.; De Chiffre, L.; Ramsing, J. Acoustic Emission Based In-process Monitoring in Robot Assisted Polishing. Int. J. Comput. Integr. Manuf. 2016, 29, 1218–1226. [Google Scholar] [CrossRef]
- Mirifar, S.; Kadivar, M.; Azarhoushang, B. First steps through intelligent grinding using machine learning via integrated acoustic emission sensors. J. Manuf. Mater. Process. 2020, 4, 35. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Vuong, T.H.; Nguyen, Q.T. Feature representation of audible sound signal in monitoring surface roughness of the grinding process. Prod. Manuf. Res. 2022, 10, 606–623. [Google Scholar] [CrossRef]
- Hatami, O.; Sayadi, D.; Razbin, M.; Adibi, H. Optimization of Grinding Parameters of Tool Steel by the Soft Computing Technique. Comput. Intell. Neurosci. 2022, 2022, 3042131. [Google Scholar] [CrossRef] [PubMed]
- Demir, H.; Gullu, A.; Ciftci, I.; Seker, U. An investigation into the influences of grain size and grinding parameters on surface roughness and grinding forces when grinding. Stroj. Vestnik/J. Mech. Eng. 2010, 56, 447–454. [Google Scholar]
- Wang, C.; Wang, G.; Shen, C. Analysis and Prediction of Grind-Hardening Surface Roughness Based on Response Surface Methodology-BP Neural Network. Appl. Sci. 2022, 12, 12680. [Google Scholar] [CrossRef]
- Wen, X.; Li, J.; Gong, Y. Simulation and experimental research on grinding force and grinding surface quality of TiC-coated micro-grinding tools. Int. J. Adv. Manuf. Technol. 2023, 128, 1337–1351. [Google Scholar] [CrossRef]
- Ying, J.; Yin, Z.; Zhang, P.; Zhou, P.; Zhang, K.; Liu, Z. An Experimental Study of the Surface Roughness of SiCp/Al with Ultrasonic Vibration-Assisted Grinding. Metals 2022, 12, 1730. [Google Scholar] [CrossRef]
- Kwak, J.S.; Ha, M.K. Neural network approach for diagnosis of grinding operation by acoustic emission and power signals. J. Mater. Process. Technol. 2004, 147, 65–71. [Google Scholar] [CrossRef]
- Ruzzi, R.d.S.; da Silva, R.B.; da Silva, L.R.R.; Machado, Á.R.; Jackson, M.J.; Hassui, A. Influence of grinding parameters on Inconel 625 surface grinding. J. Manuf. Process. 2020, 55, 174–185. [Google Scholar] [CrossRef]
- Ma, L.J.; Gong, Y.D.; Chen, X.H.; Duan, T.Y.; Yang, X.Y. Surface roughness model in experiment of grinding engineering glass-ceramics. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 228, 1563–1569. [Google Scholar] [CrossRef]
- Patel, D.K.; Goyal, D.; Pabla, B.S. Optimization of parameters in cylindrical and surface grinding for improved surface finish. R. Soc. Open Sci. 2018, 5, 171906. [Google Scholar] [CrossRef]
- König, W.; von Arciszewski, A. Continuous Dressing-Dressing Conditions Determine Material Removal Rates and Workpiece Quality. CIRP Ann.-Manuf. Technol. 1988, 37, 303–307. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, A.; Singh, P. Optimization of Process Parameters in Surface Grinding using Response Surface Methodology. IJRMET 2013, 3, 245–252. [Google Scholar]
- Walton, I.M.; Stephenson, D.J.; Baldwin, A. The measurement of grinding temperatures at high specific material removal rates. Int. J. Mach. Tools Manuf. 2006, 46, 1617–1625. [Google Scholar] [CrossRef]
- Wei, C.; He, C.; Chen, G.; Sun, Y.; Ren, C. Material removal mechanism and corresponding models in the grinding process: A critical review. J. Manuf. Process. 2023, 103, 354–392. [Google Scholar] [CrossRef]
- Singh, K.; Singh, B.; Kumar, M. Experimental Investigation of Machining Characteristics of AISI D3 Steel with Abrasive Assisted Surface Grinding. Int. Res. J. Eng. Technol. 2015, 2, 269. [Google Scholar]
- Yin, G.; Wang, J.; Guan, Y.; Wang, D.; Sun, Y. The prediction model and experimental research of grinding surface roughness based on AE signal. Int. J. Adv. Manuf. Technol. 2022, 120, 6693–6705. [Google Scholar] [CrossRef]
- Webster, J.; Marinescu, I.; Bennett, R.; Lindsay, R. Acoustic Emission for Process Control and Monitoring of Surface Integrity during Grinding. CIRP Ann.-Manuf. Technol. 1994, 43, 299–304. [Google Scholar] [CrossRef]
- Klocke, F. Grinding. In Manufacturing Processes 2; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Aguiar, P.R.; Cruz, C.E.; Paula, W.C.; Bianchi, E.C. Predicting Surface Roughness in Grinding Using Neural Networks. In Advances in Robotics, Automation and Control; IntechOpen Limited: London, UK, 2008. [Google Scholar]
- Zhang, S.; Zhang, G.; Ran, Y.; Wang, Z.; Wang, W. Multi-objective optimization for grinding parameters of 20CrMnTiH gear with ceramic microcrystalline corundum. Materials 2019, 12, 1352. [Google Scholar] [CrossRef] [PubMed]
- Öpöz, T.T.; Chen, X. Experimental study on single grit grinding of Inconel 718. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 713–726. [Google Scholar] [CrossRef]
- Khangarot, H.; Sharma, S.; Vates, U.K.; Singh, G.K.; Kumar, V. Optimization of surface grinding process parameters through RSM. In Proceedings of the International Conference on Modern Research in Aerospace Engineering. Lecture Notes in Mechanical Engineering; Singh, S., Raj, P., Tambe, S., Eds.; Springer: Singapore, 2018; pp. 291–302. [Google Scholar] [CrossRef]




| Run Order | Transversal Step (mm) | Feed Speed (m/min) | Depth of Cut (mm) | Ra (µm) | MRR (mm/min) |
|---|---|---|---|---|---|
| 1 | 3 | 12 | 0.010 | 0.447 | 0.0178 |
| 2 | 9 | 12 | 0.010 | 0.554 | 0.0310 |
| 3 | 3 | 20 | 0.010 | 0.395 | 0.0231 |
| 4 | 9 | 20 | 0.010 | 0.442 | 0.0308 |
| 5 | 3 | 12 | 0.020 | 0.378 | 0.0202 |
| 6 | 9 | 12 | 0.020 | 0.601 | 0.0307 |
| 7 | 3 | 20 | 0.020 | 0.350 | 0.0211 |
| 8 | 9 | 20 | 0.020 | 0.536 | 0.0300 |
| 6 | 16 | 0.015 | 0.456 | 0.0242 |
| Run Order | Ey1 (dB) | Ey2 (dB) | Ey3 (dB) | X1 (Hz) | Y1 (dB) | X2 (Hz) | Y2 (dB) | X3 (Hz) | Y3 (dB) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 187.33 | 30.70 | 85.74 | 834.62 | −37.63 | 1965.38 | −47.82 | 6483.08 | −48.37 |
| 2 | 233.80 | 156.35 | 373.87 | 834.62 | −36.12 | 2213.08 | −41.34 | 6515.38 | −43.92 |
| 3 | 724.60 | 75.60 | 379.47 | 818.46 | −24.23 | 1970.77 | −47.12 | 6515.38 | −41.52 |
| 4 | 296.08 | 47.57 | 154.97 | 829.23 | −33.24 | 2040.77 | −49.40 | 6477.69 | −47.11 |
| 5 | 595.29 | 315.84 | 494.91 | 813.08 | −33.63 | 1992.31 | −43.54 | 6515.38 | −46.08 |
| 6 | 650.16 | 157.10 | 420.11 | 823.85 | −36.37 | 2040.77 | −43.71 | 6499.23 | −44.29 |
| 7 | 364.03 | 73.98 | 277.28 | 818.47 | −28.40 | 974.62 | −36.64 | 4469.23 | −36.92 |
| 8 | 701.53 | 177.95 | 402.66 | 818.46 | −32.21 | 1997.69 | −39.25 | 4113.85 | −44.88 |
| 530.54 | 220.19 | 442.63 | 816.67 | −30.93 | 2006.67 | −44.12 | 5878.21 | −43.93 |
| Term | Effect | Coef | SE Coef | T-Value | p-Value | VIF |
|---|---|---|---|---|---|---|
| Constant | 0.4629 | 0.0107 | 43.39 | 0.000 | ||
| Transversal step | 0.1408 | 0.0704 | 0.0107 | 6.60 | 0.007 | 1.00 |
| Feed speed | −0.0642 | −0.0321 | 0.0107 | −3.01 | 0.057 | 1.00 |
| Depth of cut | 0.0067 | 0.0034 | 0.0107 | 0.32 | 0.772 | 1.00 |
| Transversal step·feed speed | −0.0242 | −0.0121 | 0.0107 | −1.14 | 0.338 | 1.00 |
| Transversal step·depth of cut | 0.0637 | 0.0319 | 0.0107 | 2.99 | 0.058 | 1.00 |
| Feed speed·depth of cut | 0.0178 | 0.0089 | 0.0107 | 0.83 | 0.466 | 1.00 |
| Ct Pt | −0.0065 | 0.0204 | −0.32 | 0.770 | 1.00 |
| Constant | 0.025587 | 0.000435 | 58.78 | 0.000 | ||
| Transversal step | 0.010075 | 0.005038 | 0.000435 | 11.57 | 0.001 | 1.00 |
| Feed speed | 0.001325 | 0.000663 | 0.000435 | 1.52 | 0.225 | 1.00 |
| Depth of cut | −0.000175 | −0.000087 | 0.000435 | −0.20 | 0.854 | 1.00 |
| Transversal step·feed speed | −0.001775 | −0.000888 | 0.000435 | −2.04 | 0.134 | 1.00 |
| Transversal step·depth of cut | −0.000375 | −0.000188 | 0.000435 | −0.43 | 0.696 | 1.00 |
| Feed speed·depth of cut | −0.001225 | −0.000613 | 0.000435 | −1.41 | 0.254 | 1.00 |
| Ct Pt | −0.001421 | 0.000834 | −1.70 | 0.187 | 1.00 |
| Importance | Transversal Step (mm) | Feed Speed (mm/min) | Depth of Cut (mm) | MRR (mm/min) | Ra (µm) | Composite Desirability |
|---|---|---|---|---|---|---|
| Equal | 9 | 20 | 0.010 | 0.0313 | 0.464 | 0.7385 |
| 10 times higher Ra | 3 | 20 | 0.020 | 0.0216 | 0.330 | 0.8927 |
| 10 times higher MRR | 9 | 20 | 0.010 | 0.0313 | 0.464 | 0.9464 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sender, P.; Buj-Corral, I.; Álvarez-Flórez, J. Analysis of Roughness, the Material Removal Rate, and the Acoustic Emission Signal Obtained in Flat Grinding Processes. Machines 2024, 12, 110. https://doi.org/10.3390/machines12020110
Sender P, Buj-Corral I, Álvarez-Flórez J. Analysis of Roughness, the Material Removal Rate, and the Acoustic Emission Signal Obtained in Flat Grinding Processes. Machines. 2024; 12(2):110. https://doi.org/10.3390/machines12020110
Chicago/Turabian StyleSender, Piotr, Irene Buj-Corral, and Jesús Álvarez-Flórez. 2024. "Analysis of Roughness, the Material Removal Rate, and the Acoustic Emission Signal Obtained in Flat Grinding Processes" Machines 12, no. 2: 110. https://doi.org/10.3390/machines12020110
APA StyleSender, P., Buj-Corral, I., & Álvarez-Flórez, J. (2024). Analysis of Roughness, the Material Removal Rate, and the Acoustic Emission Signal Obtained in Flat Grinding Processes. Machines, 12(2), 110. https://doi.org/10.3390/machines12020110








