Finite-Time Adaptive Control for Electro-Hydraulic Braking Gear Transmission Mechanism with Unilateral Dead Zone Nonlinearity
Abstract
1. Introduction
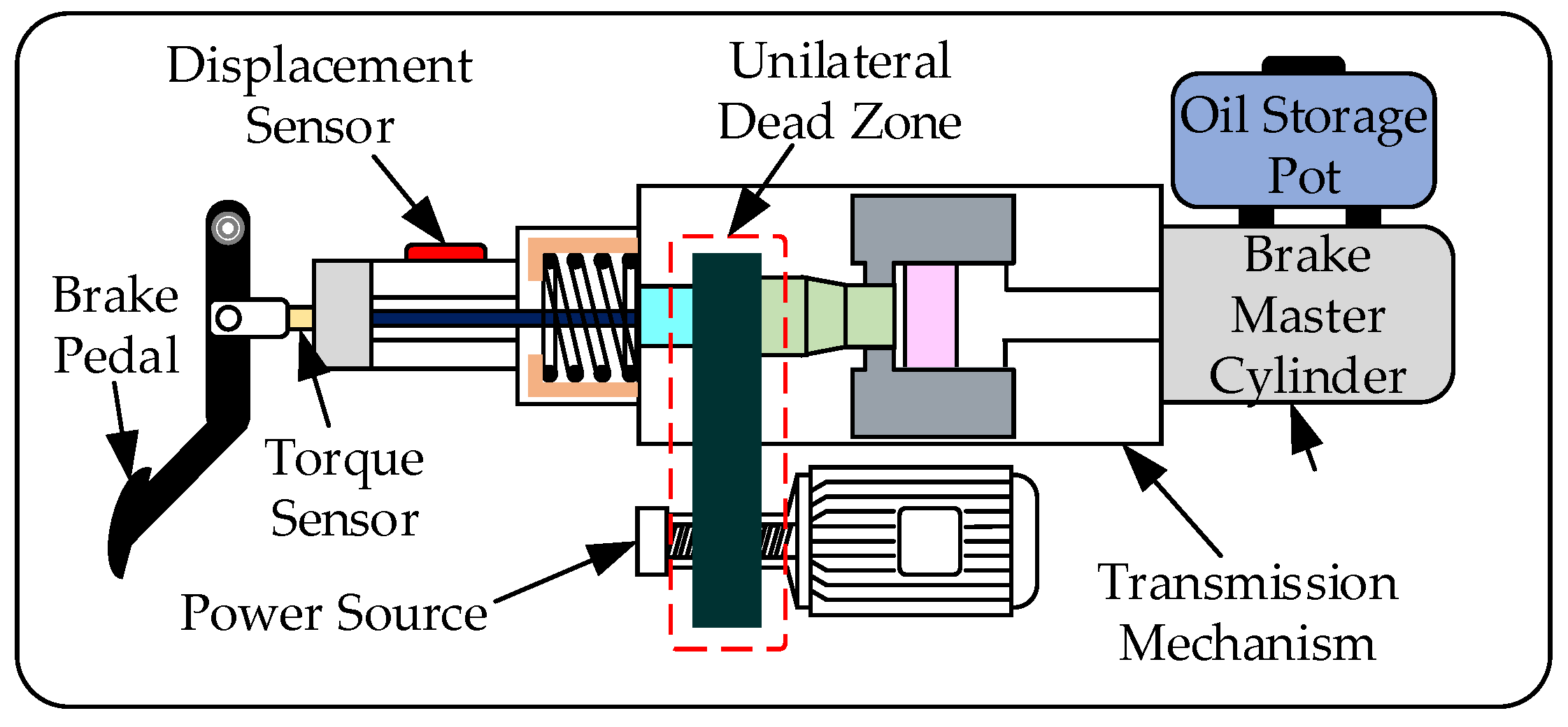
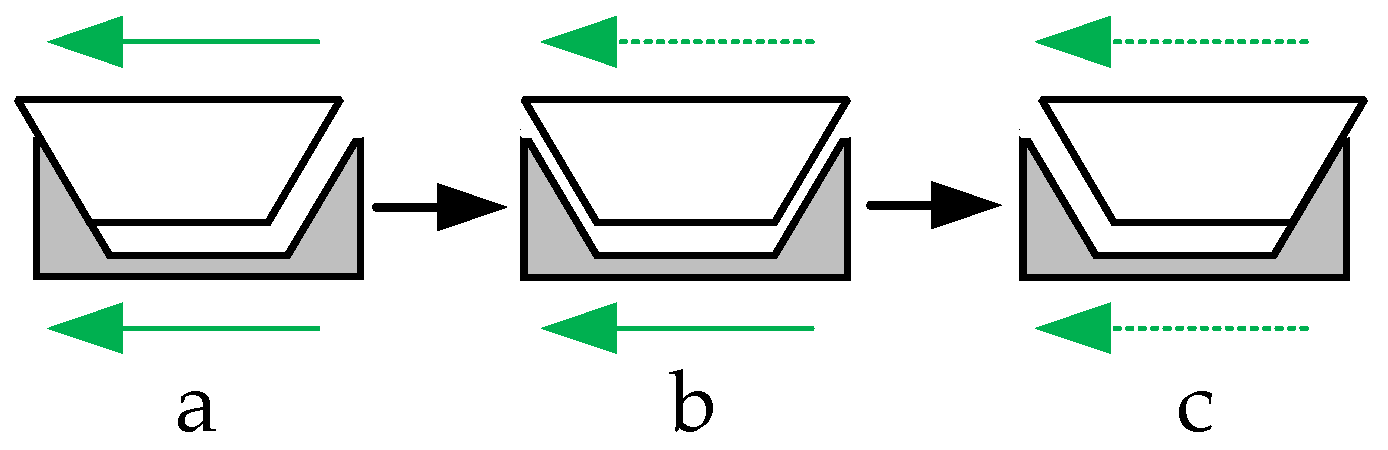
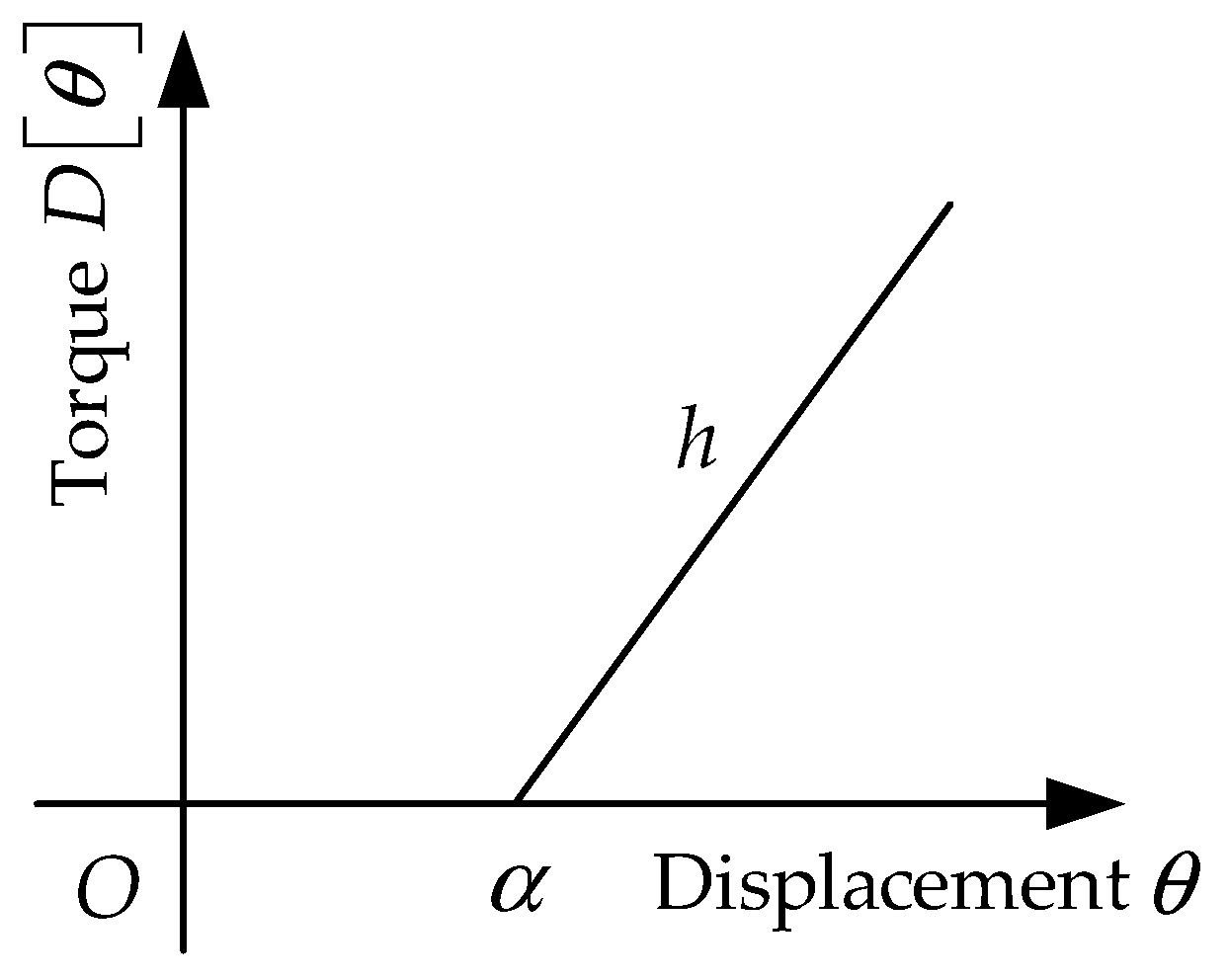
2. System Modeling and Problem Description
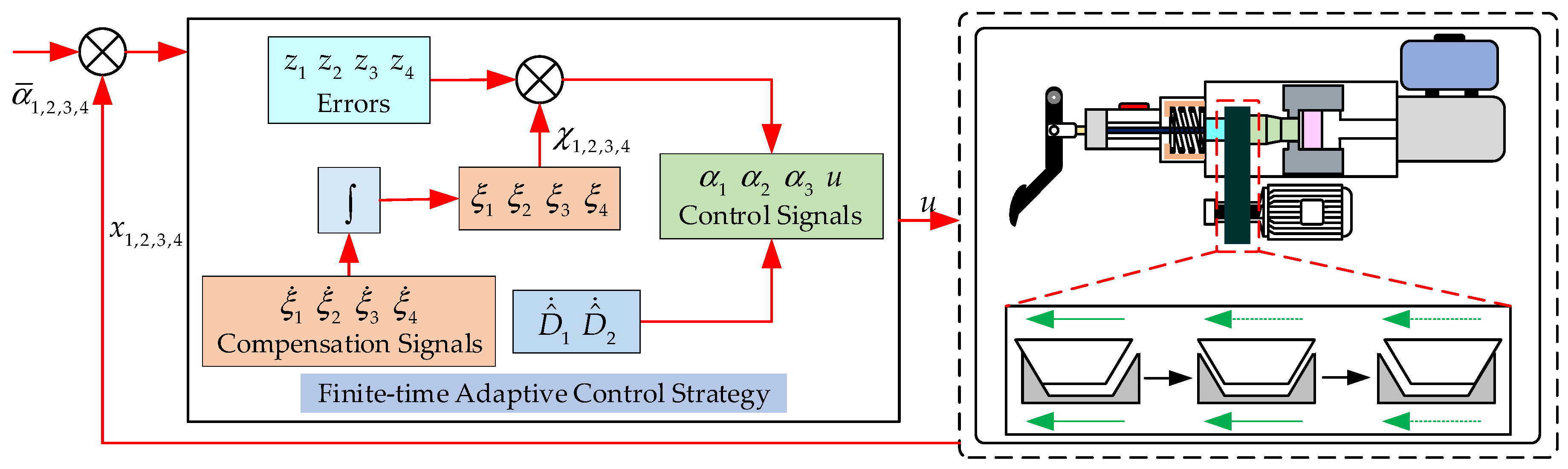
3. Controller Design and Stability Analysis
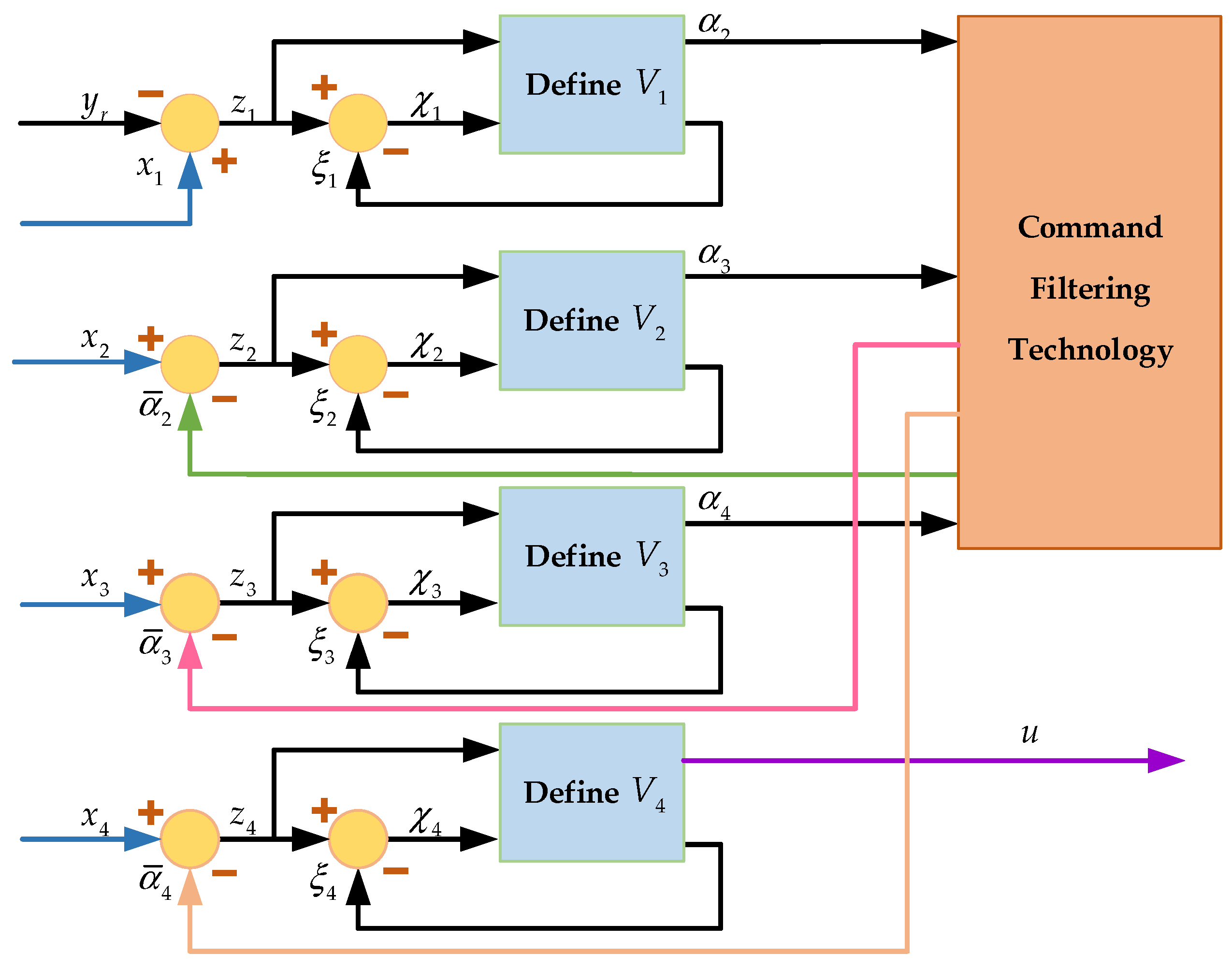
3.1. Design of the Controller
3.2. Stability Analysis
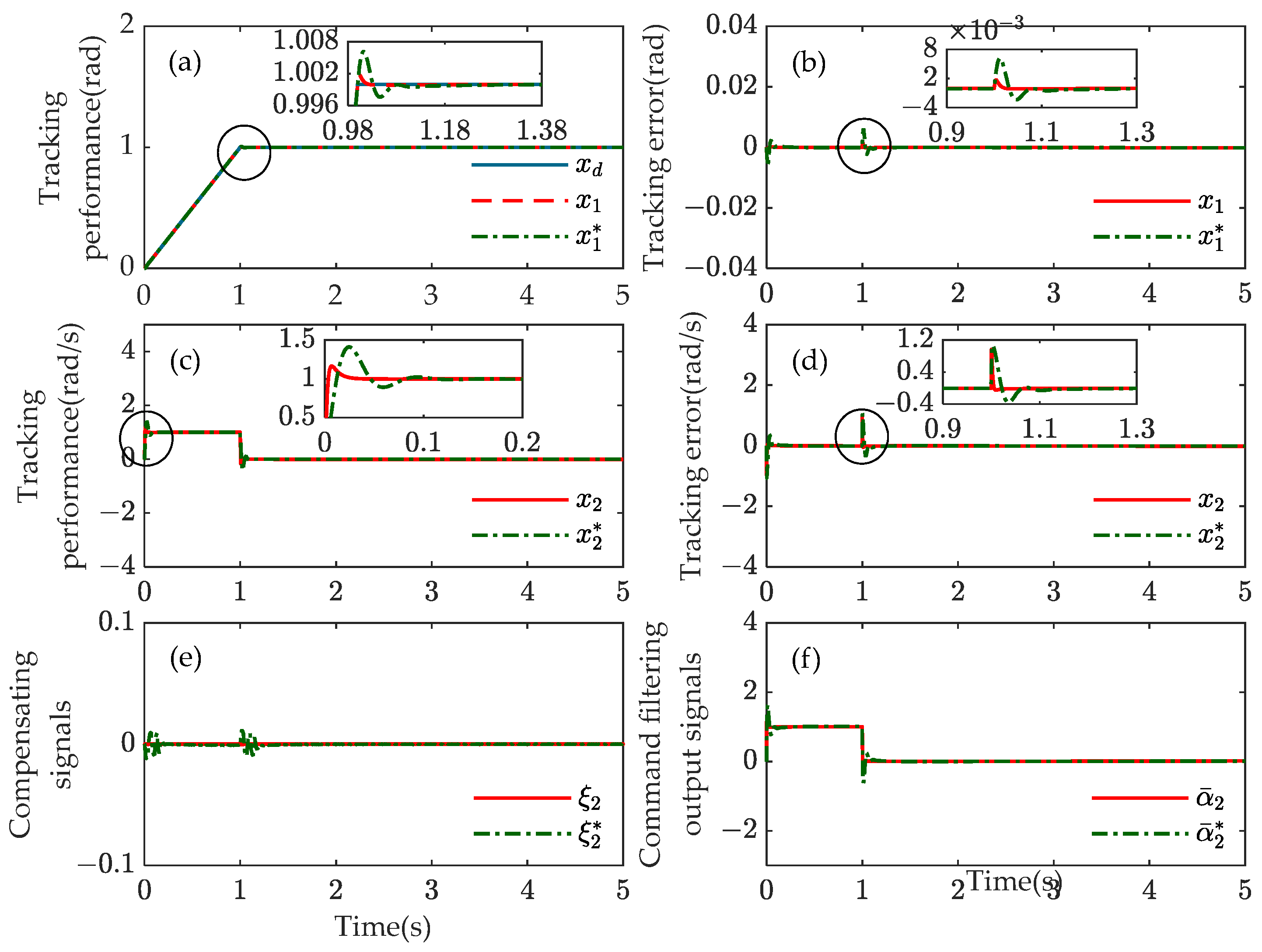
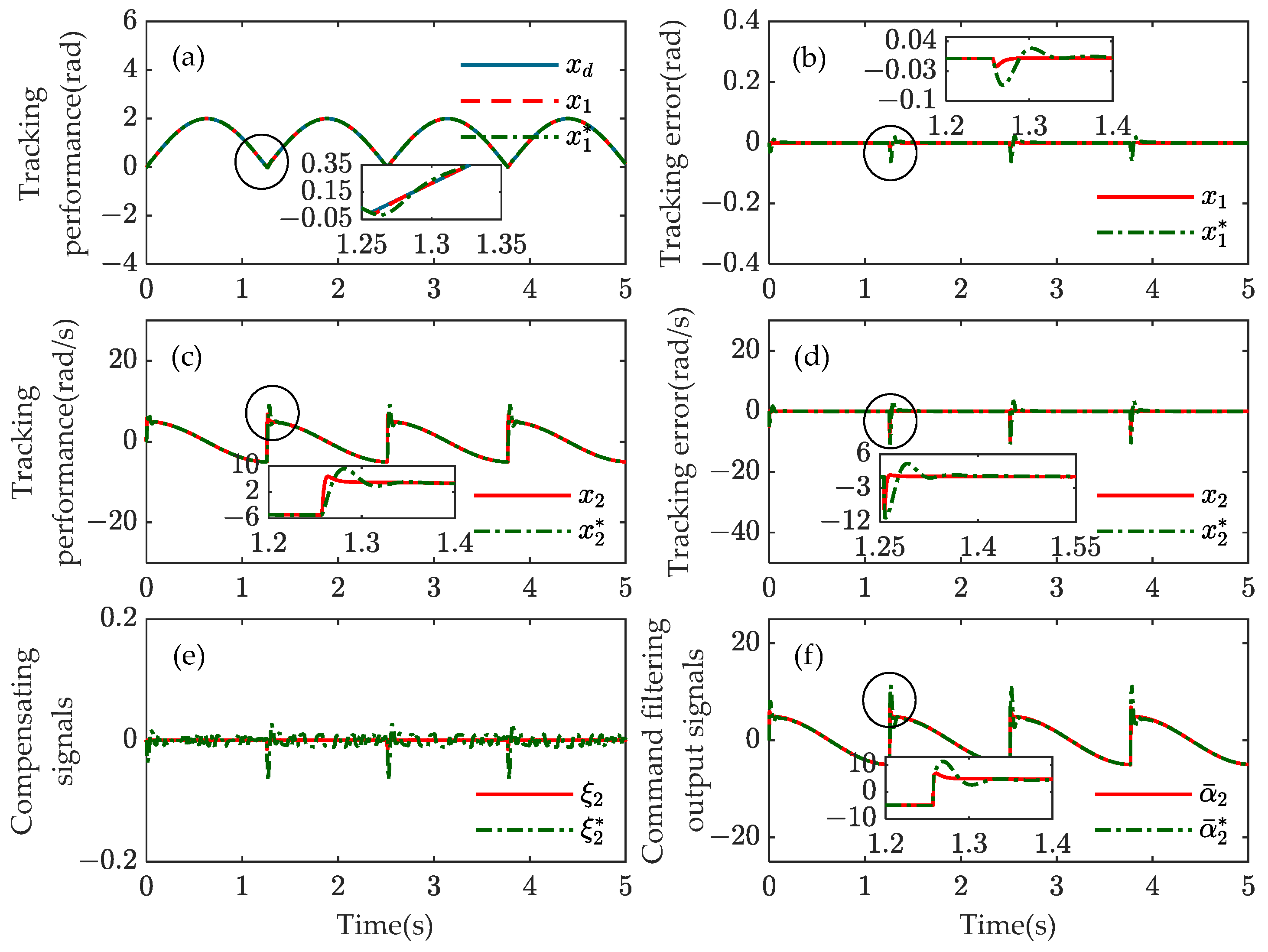
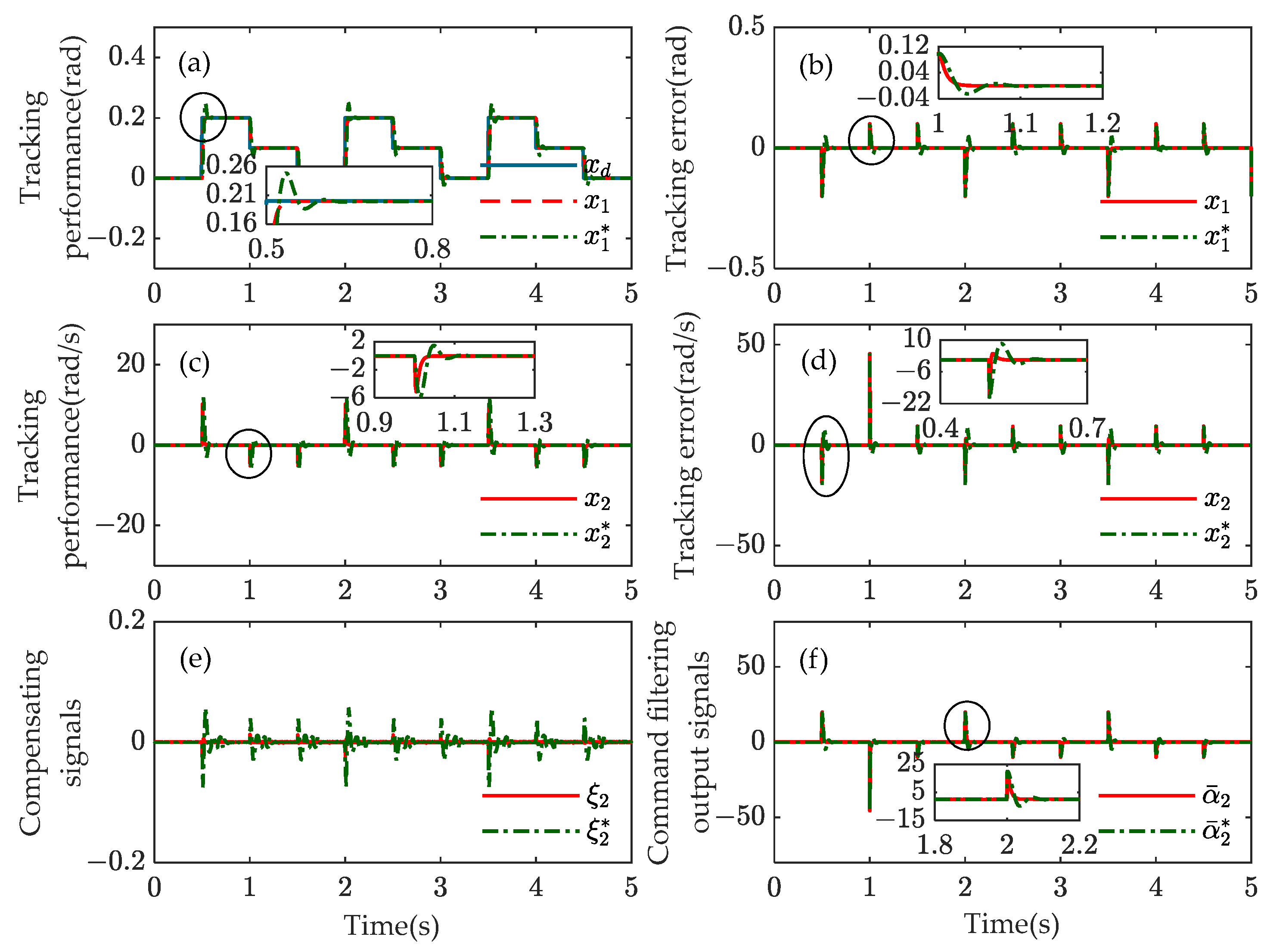
4. Simulation Results
- Experiment 1: The desired trajectory in experiment 1 is shown in (61).
- Experiment 2: The desired trajectory in experiment 2 is shown in (62).
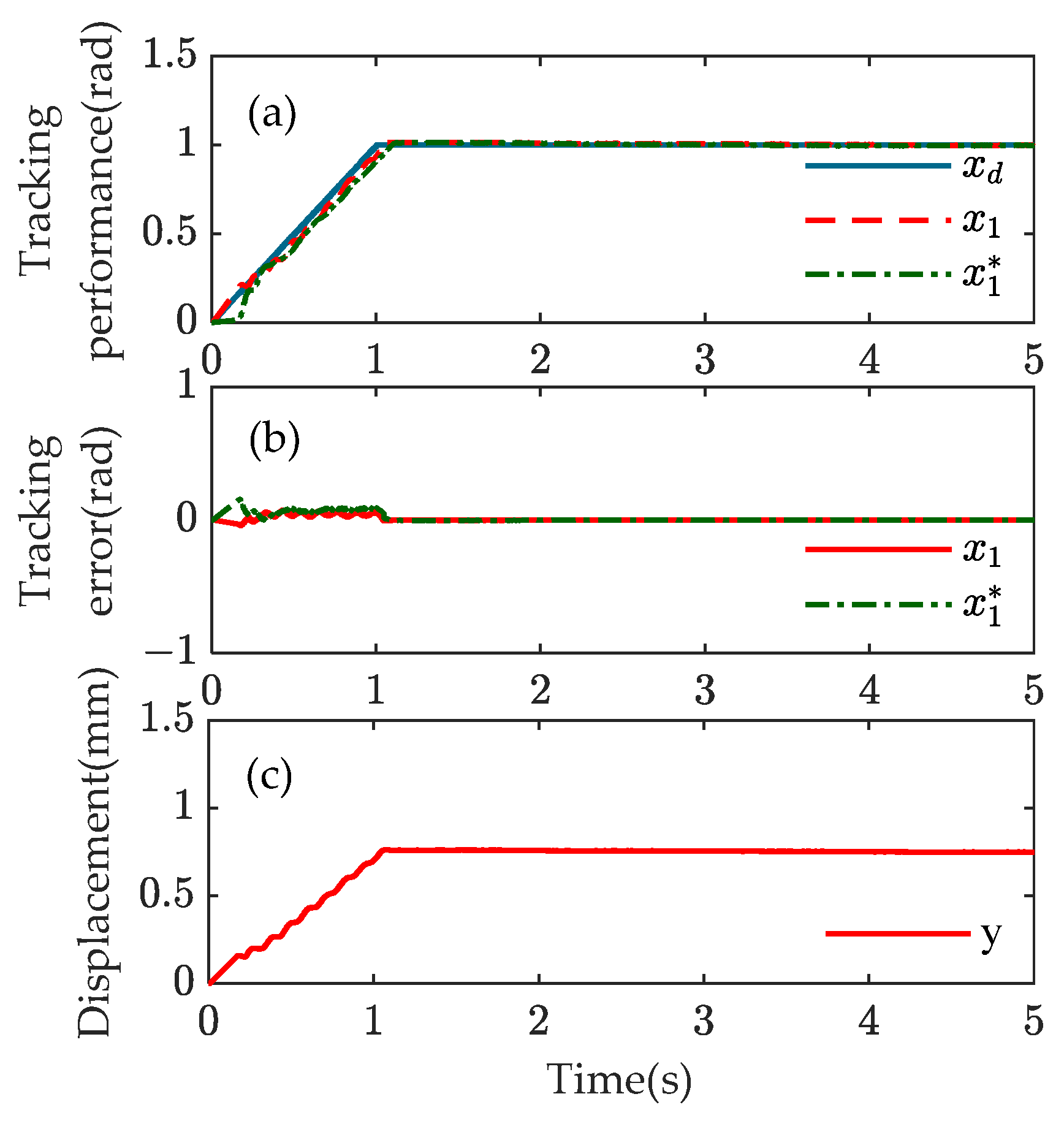
- Experiment 3: The desired trajectory in experiment 3 is a step function. The value of the function in 0~0.5 s is 0, the value of the function in 0.5~1 s is 0.2, and the value of the function in 1~1.5 s is 0.1. The period is set to 1.5 s and ends after 5 s.
5. HIL Experiments and Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, J.; Lu, Y.; Yin, G.; Fang, Z.; Zhuang, W.; Ren, Y.; Xu, L.; Li, Y. A distributed integrated control architecture of AFS and DYC based on MAS for distributed drive electric vehicles. IEEE Trans. Veh. Technol. 2021, 70, 5565–5577. [Google Scholar] [CrossRef]
- Liang, J.; Feng, J.; Fang, Z.; Lu, Y.; Yin, G.; Mao, X.; Wu, J.; Wang, F. An energy-oriented torque-vector control framework for distributed drive electric vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 4014–4031. [Google Scholar] [CrossRef]
- Liang, J.; Feng, J.; Lu, Y.; Yin, G.; Zhuang, W.; Mao, X. A direct yaw moment control framework through robust TS fuzzy approach considering vehicle stability margin. IEEE/ASME Trans. Mechatron. 2023, 29, 166–178. [Google Scholar] [CrossRef]
- Liang, J.; Lu, Y.; Feng, J.; Yin, G.; Zhuang, W.; Wu, J.; Xu, L.; Wang, F. Robust shared control system for aggressive driving based on cooperative modes identification. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6672–6684. [Google Scholar] [CrossRef]
- Liang, J.; Tian, Q.; Feng, J.; Pi, D.; Yin, G. A polytopic model-based robust predictive control scheme for path tracking of autonomous vehicles. IEEE Trans. Intell. Veh. 2023, 9, 3928–3939. [Google Scholar] [CrossRef]
- Zheng, H.Y.; He, R.; Zong, C.F. Research of electric vehicle regenerative braking control strategy based on EHB system. Adv. Mater. Res. 2013, 724, 1436–1439. [Google Scholar] [CrossRef]
- Zhao, J.; Du, J.; Zhu, B.; Chen, Z. Adaptive Dual-loop Pressure Control for an Integrated Electro-hydraulic Brake System Considering Uncertain Nonlinear Characteristics. IEEE Trans. Transp. Electrif. 2024; Early Access. [Google Scholar]
- Xiong, L.; Han, W.; Yu, Z. Adaptive sliding mode pressure control for an electro-hydraulic brake system via desired-state and integral-antiwindup compensation. Mechatronics 2020, 68, 102359. [Google Scholar] [CrossRef]
- Pei, X.; Pan, H.; Chen, Z.; Guo, X.; Yang, B. Coordinated control strategy of electro-hydraulic braking for energy regeneration. Control Eng. Pract. 2020, 96, 104324. [Google Scholar] [CrossRef]
- Shi, Q.; He, L. A model predictive control approach for electro-hydraulic braking by wire. IEEE Trans. Ind. Inform. 2022, 19, 1380–1388. [Google Scholar] [CrossRef]
- Zhao, Z.; Ahn, C.K.; Li, H.X. Dead zone compensation and adaptive vibration control of uncertain spatial flexible riser systems. IEEE/ASME Trans. Mechatron. 2020, 25, 1398–1408. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, P.; Zhao, Z.; Yang, J.; Zou, T. Adaptive fault-tolerant boundary control for a flexible string with unknown dead zone and actuator fault. IEEE Trans. Cybern. 2021, 52, 7084–7093. [Google Scholar] [CrossRef] [PubMed]
- Vörös, J. Modeling and identification of systems with backlash. Automatica 2010, 46, 369–374. [Google Scholar] [CrossRef]
- Margielewicz, J.; Gąska, D.; Litak, G. Modelling of the gear backlash. Nonlinear Dyn. 2019, 97, 355–368. [Google Scholar] [CrossRef]
- Su, H.; Zhao, X.; Zhang, W. Prescribed performance adaptive fuzzy control for nonstrict-feedback nonlinear systems with dead zone outputs. Int. J. Adapt. Control Signal Process. 2021, 35, 567–590. [Google Scholar] [CrossRef]
- Azhdari, M.; Binazadeh, T. Output tracker design for uncertain nonlinear sandwich systems with sandwiched dead-zone nonlinearity based on adaptive finite-time control. Int. J. Syst. Sci. 2021, 52, 596–611. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Y.; Lv, M.; Zuo, R. Adaptive accurate tracking control of HFVs in the presence of dead-zone and hysteresis input nonlinearities. Chin. J. Aeronaut. 2021, 34, 642–651. [Google Scholar] [CrossRef]
- Shi, Z.G.; Huo, W. Robust tracking for BLDCM system based on unknown differentiable deadzone nonlinearity. Appl. Mech. Mater. 2013, 313, 530–534. [Google Scholar] [CrossRef]
- Shi, Z.; Zuo, Z. Backstepping control for gear transmission servo systems with backlash nonlinearity. IEEE Trans. Autom. Sci. Eng. 2014, 12, 752–757. [Google Scholar] [CrossRef]
- Zuo, Z.; Ju, X.; Ding, Z. Control of gear transmission servo systems with asymmetric deadzone nonlinearity. IEEE Trans. Control Syst. Technol. 2015, 24, 1472–1479. [Google Scholar] [CrossRef]
- Shi, Z.; Zuo, Z.; Liu, H. Backstepping control for gear transmission servo systems with unknown partially nonsymmetric deadzone nonlinearity. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2580–2589. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, H.; Miao, F. An adaptive backstepping nonsingular fast terminal sliding-mode control for the electromechanical brake system with backlash nonlinearity compensation. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2023, 237, 858–870. [Google Scholar] [CrossRef]
- Cai, M.; Shi, P.; Yu, J. Adaptive neural finite-time control of non-strict feedback nonlinear systems with non-symmetrical dead-zone. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 1409–1414. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Hu, J. Adaptive robust control of a class of motor servo system with dead zone based on neural network and extended state observer. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 236, 1724–1737. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Yao, S.; Qu, C.; Wang, H. Adaptive backstepping control of primary permanent magnet linear motor via radial basis function neural network and command filter. Comput. Electr. Eng. 2023, 109, 108774. [Google Scholar] [CrossRef]
- Ge, Z.; Man, Z.; Wang, Z.; Bai, X.; Wang, X.; Xiong, F.; Li, D. Robust adaptive sliding mode control for path tracking of unmanned agricultural vehicles. Comput. Electr. Eng. 2023, 108, 108693. [Google Scholar] [CrossRef]
- Ding, S.; Huang, C.; Ding, C.; Wei, X. Straight-line tracking controller design of agricultural tractors based on third-order sliding mode. Comput. Electr. Eng. 2023, 106, 108559. [Google Scholar] [CrossRef]
- Zirkohi, M.M. Command filtering-based adaptive control for chaotic permanent magnet synchronous motors considering practical considerations. ISA Trans. 2021, 114, 120–135. [Google Scholar] [CrossRef]
- Li, Y.X. Command filter adaptive asymptotic tracking of uncertain nonlinear systems with time-varying parameters and disturbances. IEEE Trans. Autom. Control 2021, 67, 2973–2980. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Deng, W.; Yao, J. Command filtered adaptive tracking control of nonlinear systems with prescribed performance under time-variant parameters and input delay. Int. J. Robust Nonlinear Control 2023, 33, 2840–2860. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, J.; Liu, J.; Zhou, Q.; Xia, J.; Sun, W.; He, X. Command-filter-adaptive-based lateral motion control for autonomous vehicle. Control Eng. Pract. 2022, 121, 105044. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, X. Command filter and universal approximator based backstepping control design for strict-feedback nonlinear systems with uncertainty. IEEE Trans. Autom. Control 2019, 65, 1310–1317. [Google Scholar] [CrossRef]
- Shi, M.; Yu, J.; Zhang, T. Command filter-based adaptive control of flexible-joint manipulator with input saturation and output constraints. Asian J. Control 2024, 26, 42–55. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, L.; Zou, W.; Ding, D.W. Robust adaptive control of uncertain nonlinear systems with unmodeled dynamics using command filter. Int. J. Robust Nonlinear Control 2021, 31, 7764–7784. [Google Scholar] [CrossRef]
- He, Y.; Chang, X.H.; Wang, H.; Zhao, X. Command-filtered adaptive fuzzy control for switched MIMO nonlinear systems with unknown dead zones and full state constraints. Int. J. Fuzzy Syst. 2023, 25, 544–560. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Y. Adaptive finite-time stabilization for uncertain nonlinear systems with unknown control coefficients. Automatica 2023, 149, 110845. [Google Scholar] [CrossRef]
- Wang, S.; Cao, Q.; Ma, F.; Wu, J. EHB Gear-Drive Symmetric Dead-Zone Finite-Time Adaptive Control. Machines 2023, 11, 1002. [Google Scholar] [CrossRef]
- Lu, S.; Wang, X.; Li, Y. Adaptive neural network finite-time command filtered tracking control of fractional-order permanent magnet synchronous motor with input saturation. J. Frankl. Inst. 2020, 357, 13707–13733. [Google Scholar] [CrossRef]
- Wang, X.; Niu, B.; Gao, Y.; Shang, Z. Adaptive finite time output feedback bipartite tracking control for nonlinear multiagent systems. IEEE Trans. Autom. Sci. Eng. 2023. [Google Scholar]
- Gao, Y.; Sun, W.; Su, S.F.; Zhao, X. Finite-time command filtered control for multiagent systems with unknown control gains and quantized inputs. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 7165–7176. [Google Scholar] [CrossRef]
- Xu, K.; Wang, H.; Liu, P.X. Adaptive fuzzy finite-time tracking control of nonlinear systems with unmodeled dynamics. Appl. Math. Comput. 2023, 450, 127992. [Google Scholar] [CrossRef]
- Li, Y.X. Finite time command filtered adaptive fault tolerant control for a class of uncertain nonlinear systems. Automatica 2019, 106, 117–123. [Google Scholar] [CrossRef]
- Farrell, J.A.; Polycarpou, M.; Sharma, M.; Dong, W. Command filtered backstepping. IEEE Trans. Autom. Control 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
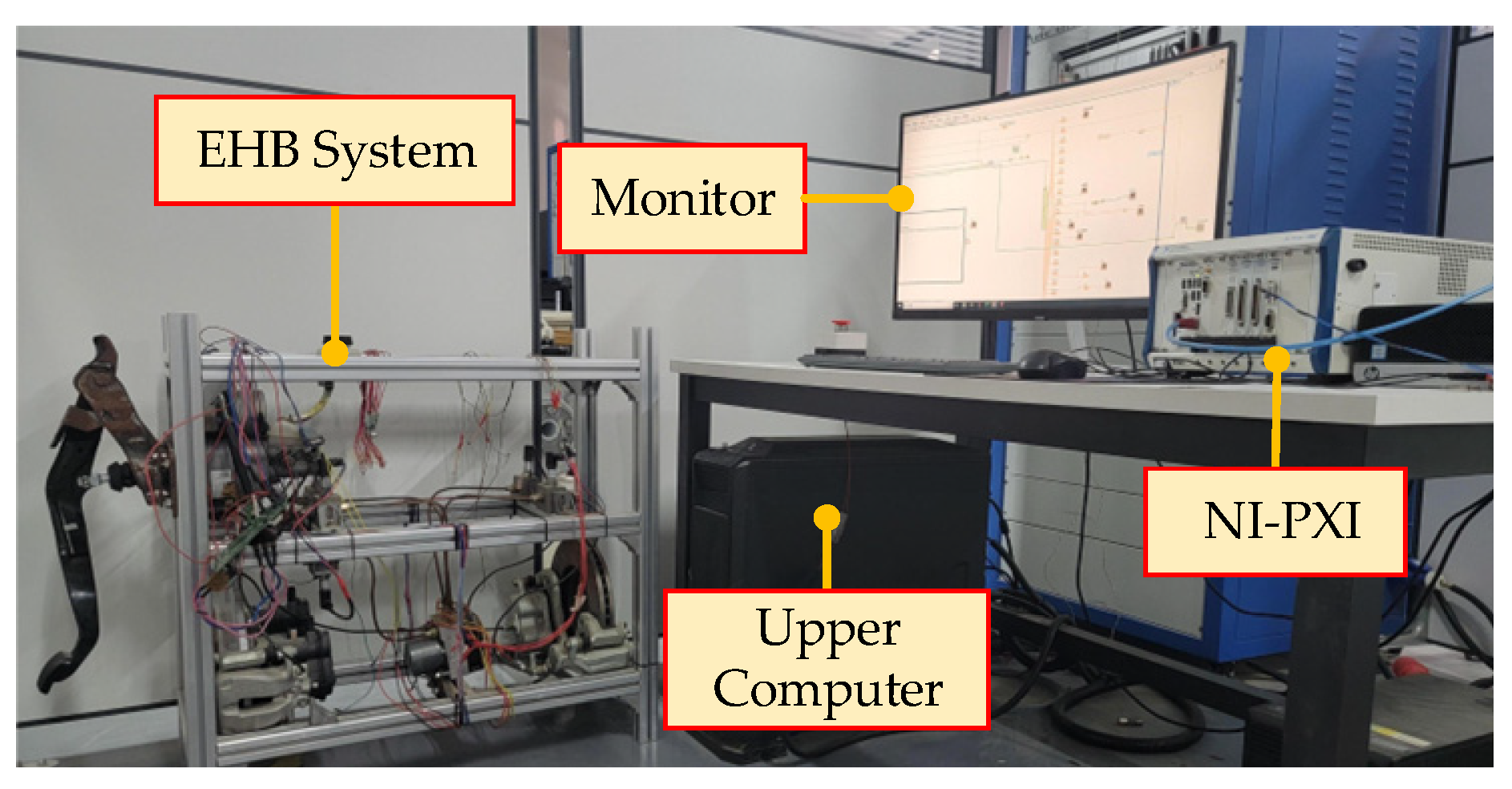

| Symbol | Parameters | Value | Units |
|---|---|---|---|
| Moment of inertia of the load end | 0.5 | kg·m2 | |
| Moment of inertia of the driving end | 0.01 | kg·m2 | |
| Viscous friction coefficient of the load end | 0.12 | Nm/rad | |
| Viscous friction coefficient of the driving end | 0.1 | Nm/rad | |
| Transmission ratio | 5 | Nm/rad | |
| Rigidity coefficient | 0.2 | null |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Q.; Wu, J.; Xu, F.; Miao, X.; Guo, M.; Chu, Y. Finite-Time Adaptive Control for Electro-Hydraulic Braking Gear Transmission Mechanism with Unilateral Dead Zone Nonlinearity. Machines 2024, 12, 698. https://doi.org/10.3390/machines12100698
Cao Q, Wu J, Xu F, Miao X, Guo M, Chu Y. Finite-Time Adaptive Control for Electro-Hydraulic Braking Gear Transmission Mechanism with Unilateral Dead Zone Nonlinearity. Machines. 2024; 12(10):698. https://doi.org/10.3390/machines12100698
Chicago/Turabian StyleCao, Qinghua, Jian Wu, Fuxing Xu, Xinhong Miao, Mingjie Guo, and Yuan Chu. 2024. "Finite-Time Adaptive Control for Electro-Hydraulic Braking Gear Transmission Mechanism with Unilateral Dead Zone Nonlinearity" Machines 12, no. 10: 698. https://doi.org/10.3390/machines12100698
APA StyleCao, Q., Wu, J., Xu, F., Miao, X., Guo, M., & Chu, Y. (2024). Finite-Time Adaptive Control for Electro-Hydraulic Braking Gear Transmission Mechanism with Unilateral Dead Zone Nonlinearity. Machines, 12(10), 698. https://doi.org/10.3390/machines12100698







