Abstract
This article proposes event-triggered cruise control in platoons of connected automated vehicles (CAVs) with heterogeneous input limitations. A distributed control protocol is developed to ensure the stability and performance of the platoon, explicitly addressing varying levels of input saturation among vehicles. To further enhance communication efficiency, a centralized event-triggered mechanism is introduced, activating control updates only when necessary, effectively preventing Zeno behaviors through a predefined threshold. The proposed approach not only achieves global asymptotic stability but also significantly reduces communication demands, making it suitable for real-world driving conditions characterized by input constraints. Simulation results validate the effectiveness and robustness of the proposed control strategy, demonstrating its potential for practical implementation in intelligent transportation systems.
1. Introduction
Connected automated vehicle (CAV) technology has emerged as a transformative innovation in modern transportation systems, garnering considerable attention due to its potential to revolutionize traffic management [1,2]. By integrating communication, automation, and control systems, CAVs promise significant improvements in traffic flow, road safety, emission reduction, and fuel efficiency [3]. Among the array of control strategies developed for CAVs, platooning stands out as a pivotal approach for realizing these advantages [4]. Recent European research projects, such as 5GHEART and ENSEMBLE, have made significant advancements in the field of platooning, focusing on enhancing communication infrastructure and cooperative vehicle technologies for improved safety and efficiency in CAV systems [5,6]. In platooning, a group of vehicles travels in close coordination, maintaining optimal speeds and inter-vehicle distances through vehicle-to-vehicle (V2V) communication. This rapid exchange of information—encompassing acceleration, braking, and velocity data—facilitates synchronized vehicle movement, thereby reducing aerodynamic drag, minimizing stop-and-go traffic, and enhancing overall road capacity [7].
Vehicle platoon control generally aims to maintain a desired time headway or space headway between successive vehicles through V2V communication, while stabilizing the entire platoon at a desired speed with ensured safety [8]. From a control theory perspective, the vehicle platoon control problem can be regarded as a consensus problem for networked multi-agent systems [9]. This viewpoint has inspired researchers to develop novel consensus-based control methods for vehicle platoon systems. For example, Zhang et al. [10] proposed a hierarchical framework for tracking control in uncertain vehicle platoons subject to external disturbances. Likewise, AddP-CACC strategies were utilized in [11] to address the string stability of vehicle platoons under network losses and delays. To handle dynamic heterogeneity, which is modeled as time-varying parameters, a hierarchical vehicle platoon control framework was developed featuring a finite-time local controller for each connected vehicle to address tracking issues [12]. Additionally, a distributed feedforward tube-based model predictive control (MPC) strategy, coupled with a disturbance-compensation feedback control approach, was proposed to ensure stability with performance in heterogeneous vehicle platoons, accounting for disturbances and modeling errors [13]. Given the inherent differences in powertrain components and vehicular structures, dynamic heterogeneity is an unavoidable factor in the practical implementation of vehicular platoons.
The deployment of cruise control strategies in CAV platoons presents several challenges, primarily related to communication efficiency and physical input constraints. Traditional control approaches typically depend on continuous information exchange among vehicles to ensure cohesive platoon behavior. However, this continuous communication can be computationally intensive and may cause network congestion, particularly in dense traffic conditions. Such communication demands not only place stress on network infrastructure but also elevate the risk of data packet loss and transmission delays, potentially compromising the stability and safety of the platoon [14,15]. As the number of CAVs grows, maintaining a robust and scalable communication framework becomes increasingly difficult, underscoring the need for control strategies that balance performance with communication efficiency [16]. Beyond communication constraints, physical limitations such as actuator saturation, rate constraints, and nonlinear dynamics also impact CAV control performance. Actuator saturation, for example, restricts the system’s capacity to implement large or rapid adjustments in acceleration, braking, or steering, which are often essential for maintaining desired speeds and inter-vehicle distances [17]. These limitations introduce nonlinearity into the system, complicating the design and stability analysis of the control strategies [18]. Therefore, effectively addressing such input constraints is critical for ensuring the practical feasibility and reliability of cruise control systems in real-world CAV platoons.
To tackle these challenges, event-triggered control has emerged as a promising solution that optimizes communication demands while maintaining the desired control performance [19,20,21]. Unlike traditional time-triggered control, which involves information exchange at regular intervals, event-triggered control initiates communication only when specific event conditions are met—such as when deviations from the desired state exceed a predefined threshold [22]. This approach markedly reduces communication frequency among vehicles, thereby easing network congestion and improving overall system efficiency [23]. Moreover, event-triggered control frameworks are designed to prevent Zeno behaviors, where an infinite number of events could occur within a finite time, thus ensuring their practical applicability in real-world scenarios [24,25]. By triggering control updates only when necessary, event-triggered mechanisms naturally adapt to the dynamic nature of driving conditions, making them well-suited to address both communication and physical input constraints. This not only facilitates efficient information exchange among CAVs but also ensures the stability and safety of the platoon across varying driving conditions, even in the presence of input limitations like actuator saturation.
In this paper, we propose an event-triggered cruise control strategy specifically designed to manage CAV platoons under input limitations. The primary objective of this strategy is to ensure asymptotic stability of the vehicular platoon in the presence of input constraints while improving communication and control efficiency. The main contributions of this study are threefold: (1) the development of a distributed control protocol is designed that explicitly accounts for input constraints such as actuator saturation, providing a systematic way to handle saturation nonlinearity and maintain desired performance levels; (2) the implementation of a centralized event-triggering mechanism is proposed to decrease communication loads by activating control updates only when the deviation from the desired state exceeds a predefined threshold, thereby enhancing communication efficiency and reducing bandwidth usage; and (3) a comprehensive set of simulations is conducted to validate the proposed control strategy’s effectiveness across heterogeneous input limitations.
2. Problem Statement
Consider a platoon of vehicles traveling on a horizontal road, as depicted in Figure 1. The platoon is led by the vehicle indexed as 0, while the remaining N vehicles are indexed sequentially from 1 to N. The lead vehicle shares its information with at least one following vehicle. Additionally, the following vehicles participate in bidirectional communication, exchanging information with both their immediate predecessor and successor within the platoon.
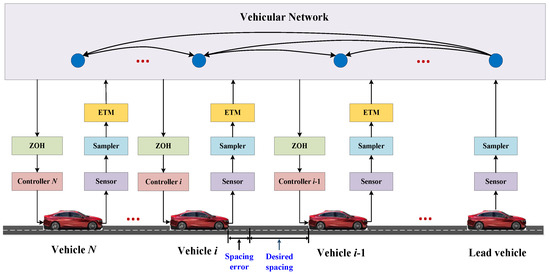
Figure 1.
Scenario of vehicular platoon driving on a straight lane.
2.1. Notations
The set of real numbers and the N-dimensional real vector space are denoted by and , respectively. The space spanned by a vector is defined as . The vector represents the N-dimensional all-ones vector. denotes the N-dimensional identity matrix. The symbol represents the Euclidean norm, while denotes the i-th eigenvalue of matrix H, sorted in ascending order.
2.2. Graph Theory
Graph theory is employed to represent the information exchange relationships among CAVs within a platoon. The interaction among vehicles, including one leader and N followers, can be represented by a graph . The interactions among the N followers are described by a graph , where represents the set of nodes (vehicles), and denotes the set of edges, indicating the directions of information flow.
The adjacency matrix associated with the graph is denoted as , where:
An edge indicates that vehicle i can receive information from vehicle j. The graph is undirected if for all .
The neighbor set of node i, denoted as , is defined as:
This means that vehicle j is considered a neighbor of vehicle i if and only if .
The Laplacian matrix associated with graph is denoted as , where the diagonal elements are given by:
and the off-diagonal elements are expressed as:
Additionally, the pinning matrix , associated with graph , represents the information flow from the leader to the followers. It is defined as:
where if the edge , indicating that follower i receives information from the leader; otherwise, .
Assumption A1.
Under the leader–following bidirectional topology, the graphs and are connected and undirected.
2.3. Longitudinal Vehicle Dynamics
This study aims to regulate the longitudinal motion of vehicles on a straight lane to maintain stable car-following behavior. Typically, the longitudinal dynamics of vehicles are influenced by several nonlinear factors, including powertrain dynamics, longitudinal tire forces, rolling resistance, gravitational forces, and aerodynamic drag [26,27]. For analytical simplicity, these nonlinear dynamics are often linearized using the input–output linearization technique [28].
In this paper, we utilize a second-order vehicle dynamic model that incorporates input saturation, as detailed in [29]:
where and represent the displacement and velocity of vehicle i, respectively, while denotes the control input. The saturation function is defined as
where and represent the lower and upper bounds of the control input, corresponding to acceleration and deceleration limits in real-world driving scenarios.
The saturation function serves to restrict the control inputs, considering physical powertrain limitations, as well as driver comfort and safety requirements, thus better aligning with actual driving behavior. Furthermore, this function accommodates heterogeneous vehicles, as it allows independent saturation bounds for each vehicle, making it adaptable to diverse traffic scenarios involving different vehicle types.
The platoon of the following vehicles is regulated to track a lead vehicle, whose dynamics are defined as:
where and represent the displacement and velocity of the lead vehicle, respectively.
Remark 1.
In real-world applications, vehicles within a platoon often exhibit diverse actuator limits due to variations in vehicle types, powertrain configurations, and operational constraints. This heterogeneity in actuator saturation may influence the stability and performance of the control strategy, especially under high-variance conditions. While our study assumes uniform post-saturation response dynamics for simplicity, the variation in actuator limits can lead to distinct transient behaviors across individual vehicles, potentially impacting overall platoon stability and coordination. To address these challenges, future research could explore adaptive control strategies that adjust control gains or utilize vehicle-specific saturation models to better capture individual vehicle responses.
Remark 2.
In autonomous vehicle (AV) platoons, non-linear dynamics such as actuator saturation, time-varying delays, and input-dependent non-linearities often lead to complex system behavior. These factors become particularly critical during sudden maneuvers or emergency braking, where transient responses may deviate significantly from linear predictions, impacting system stability and safety. While our study employs a linearized model to facilitate analysis, we acknowledge that input non-linearities could introduce unexpected behavior under such dynamic conditions. Future work could extend this research by incorporating non-linear control techniques or adaptive gain adjustments to better handle input non-linearities.
2.4. Control Objective
This manuscript aims to develop an event-triggered control scheme that enables the grouped vehicle system to achieve the desired platoon configuration, even in the presence of heterogeneous input saturation. Specifically, the proposed control strategy ensures that each following vehicle maintains a consistent speed and achieves the desired inter-vehicle distance with its neighbors:
where represents the desired inter-vehicle distance between the i-th vehicle and its predecessor , d and l denote the desired spacing and vehicle length, respectively.
3. Main Results
In this section, we focus on proposing an event-triggered mechanism (ETM) to achieve the control objective (4) subject to heterogeneous input saturation. Before exploring the event-triggered control strategy, the following useful lemmas are given.
Lemma 1
([30]). Under Assumption 1, is positive definite and has full rank.
To enable the design of the event-triggered approach, we propose a sampling-based control protocol, formulated as follows:
where , represents the k-th updating time, and denote the position and velocity deviations, respectively, between the following vehicle and the lead vehicle, The parameters and are the control gains.
To prevent Zeno behavior, we introduce a predefined minimum triggering interval , which ensures that the control input is not updated within after the last triggering time. As a result, the event-triggered condition can only be activated once the interval has elapsed. The update process of the control inputs adheres to the following rules:
- For , the control inputs will remain unchanged.
- For , the event-triggered condition becomes active, and the next update time is determined bywhere the event-triggered function satisfieswith , , , , and denotes a constant.
Remark 3.
In the proposed event-triggered control mechanism, a centralized event-triggering function, as defined in (7), is formulated to incorporate the velocity and control information of all vehicles. Event updates are managed uniformly, ensuring that the control inputs of all vehicles are updated simultaneously. This approach enhances implementation and management simplicity while improving coordination efficiency.
Based on the proposed event-triggered control mechanism, the following result can be derived.
Theorem 1.
Let Assumption 1 hold. The platoon control objective (4) can be achieved with control protocol (5) and the proposed event-triggered control mechanism if the following conditions hold
Then, each following vehicle can maintain a consistent speed and achieve the desired inter-vehicle distance with its neighbors.
Proof.
Combining the vehicle dynamics (1) and (3) with control protocol (5), we have the following closed-loop system
For (9), construct the following Lyapunov functional candidate
It can be derived that
Note that the eigenvalues of are given by , . Given that , it follows that for all , which implies . Thus, , and from , we obtain . Since is full rank, this leads to , implying that .
Next, let us first consider the moment , at which point we have
For convenience, let , , and . Then,
Furthermore,
Now we focus on the item . The eigenvalues of this matrix are
Note that
then
Therefore, we obtain . Moreover, it follows from that .
If , then ; otherwise, consider . Since is activated, the derivative of becomes
Through the above discussions, we have , and equality holds only when . Thus, the sequence is monotonically bounded and converges as . Consequently,
Furthermore,
which implies:
According to Lemma 1, it follows that and for all as . This indicates that the platoon control objective (4) can be achieved. □
4. Simulation Example
In this section, a simulation example is provided to evaluate the performance of the proposed event-triggered control strategies for regulating a vehicular platoon under input constraints. The scenario involves seven vehicles, including a lead vehicle and six following vehicles, driving along a one-dimensional lane. The communication topology of the vehicular platoon is illustrated in Figure 2.

Figure 2.
The communication topology of the vehicular platoon in the simulation case.
Initially, the states of the seven vehicles, including position and velocity, are defined as follows:
- -
- Lead vehicle (Vehicle 0) at ;
- -
- Vehicle 1 at ;
- -
- Vehicle 2 at ;
- -
- Vehicle 3 at ;
- -
- Vehicle 4 at ;
- -
- Vehicle 5 at ;
- -
- Vehicle 6 at .
The Laplacian matrix corresponding to this communication topology is given by:
and the Pinning matrix is given as
The saturation function for each vehicle, which constrains the control input within specified bounds, is defined as follows:
The simulation is carried out over a period of 30 s with a sampling interval of 0.05 s. The main parameter settings are presented in Table 1. With these parameters, the proposed controllers are tested using the event-triggered mechanism to evaluate the control performance of the seven vehicles, particularly under the constraints imposed by heterogeneous input saturation.

Table 1.
Parameter Settings.
The triggering interval and weight are chosen to balance communication efficiency and system stability while satisfying the conditions of Theorem 1. A shorter triggering interval would increase the communication frequency, while a longer interval might lead to delayed responses and potential instability. The selected interval represents a practical trade-off, ensuring effective communication without compromising control performance. With these parameters, feasible control gains and are determined, meeting the theoretical requirements for stability under heterogeneous input saturation. Figure 3, Figure 4, Figure 5 and Figure 6 present the performance of the event-triggered platoon control strategy for the seven vehicles under heterogeneous input saturation. Figure 3 shows the displacement trajectories of the vehicles moving along a straight lane, indicating that the vehicles maintain stable and orderly movement while preserving the desired spacing between them. This stability is crucial for safety and efficient traffic flow in practical applications, particularly in dynamic scenarios. Figure 4 depicts the velocity trajectories of the vehicles. While some fluctuations are observed due to the event-triggered nature of the control, the vehicles achieve relatively synchronized speeds. These minor fluctuations, which do not compromise overall stability, reflect the adaptive nature of the event-triggered mechanism and contribute to minimizing fuel consumption and aerodynamic drag, key benefits in real-world platooning. Figure 5 illustrates the control input variations for each vehicle under heterogeneous input saturation constraints. The results show that the control inputs remain within actuator saturation limits and gradually approach equilibrium, demonstrating the robustness of the control strategy and its ability to respect physical vehicle constraints. Figure 6 highlights the spacing errors between each pair of preceding and following vehicles, denoted as , showing that the spacing errors converge to zero over time. This convergence ensures asymptotic stability, meaning the vehicles consistently maintain the desired inter-vehicle distance, which is essential for smooth platoon operation and safety in diverse traffic conditions. In practice, asymptotic stability implies that the platoon can recover from initial disturbances or minor external disruptions while maintaining cohesion, safety, and operational efficiency. Overall, the results validate the proposed event-triggered control strategy, demonstrating its ability to ensure global asymptotic stability in the vehicular platoon even under heterogeneous input saturation. The event-triggered mechanism effectively manages minor fluctuations while maintaining desired performance and safety standards, making it suitable for practical implementation in intelligent transportation systems.
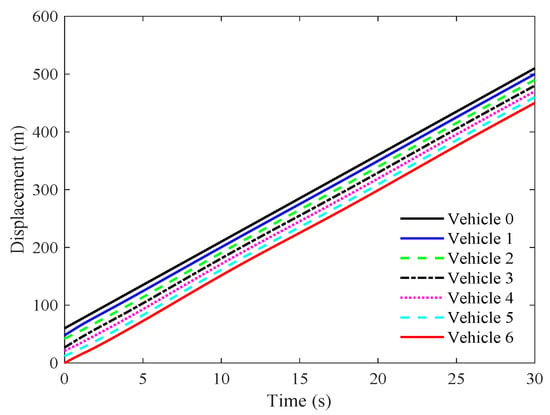
Figure 3.
The displacement trajectory of the seven vehicles under the proposed event-triggered controller.
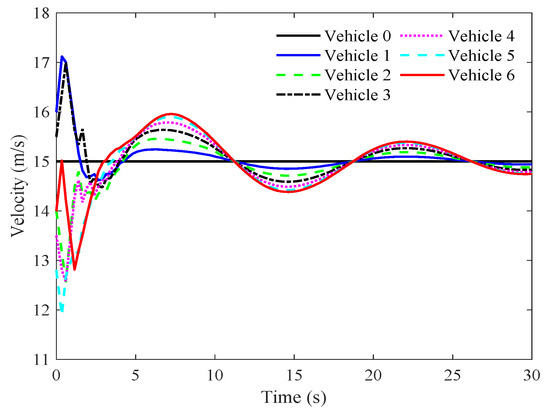
Figure 4.
The velocity trajectory of the seven vehicles under the proposed event-triggered controller.
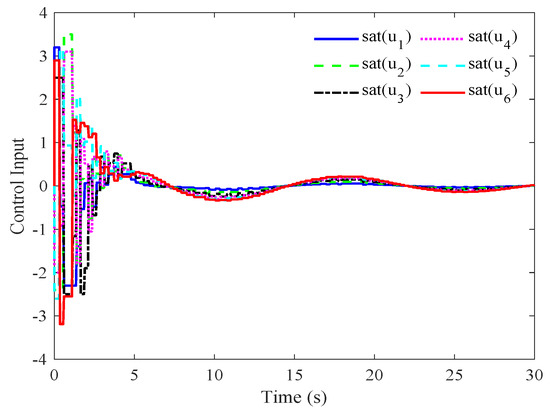
Figure 5.
The control input curves of the seven vehicles under the proposed event-triggered controller.
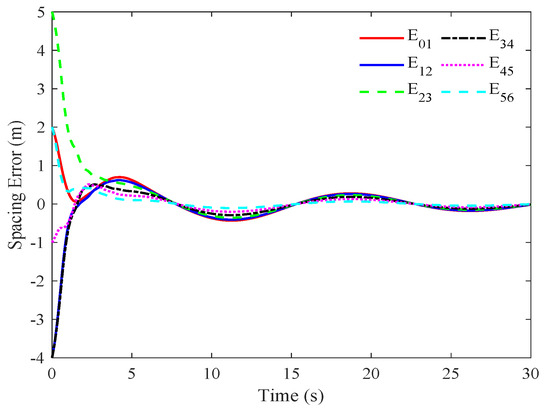
Figure 6.
The spacing errors of the seven vehicles under the proposed event-triggered controller.
Figure 7 presents the event-triggering sequence and the response curve of the triggering intervals under the proposed event-triggered control strategy. A key observation from the figure is that the controller updated only 94 times over the 30-second simulation period. In contrast, the time-triggered control protocol, with the same sampling interval of seconds, updated the control input 600 times within the same period. This substantial reduction in the number of control updates demonstrates the efficiency of the proposed event-triggered strategy. By updating the control input only when necessary, the communication and computational load of the control system is significantly reduced. This efficiency gain makes the event-triggered control approach particularly advantageous for large-scale, high-density multi-vehicle traffic scenarios, where minimizing communication overhead and computational demands is crucial. Overall, this makes the proposed method a promising solution for real-world applications, especially in environments with limited communication bandwidth or processing capacity.
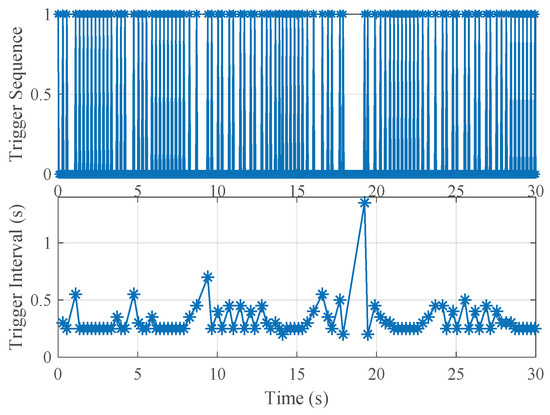
Figure 7.
The trigger sequence and interval under the proposed event-triggered controller.
5. Conclusions
This paper presents an event-triggered control strategy for the cruise control of CAV platoons, focusing on addressing input limitations such as actuator saturation. The proposed approach ensures global asymptotic stability while significantly reducing communication and computational demands. Simulation results validate the robustness of the strategy in maintaining desired inter-vehicle spacing and synchronized velocities under heterogeneous input constraints. Additionally, results demonstrate the efficiency of the strategy, with the controller updating only 94 times over a 30-s period, compared to 600 updates required by a time-triggered protocol with the same sampling interval. This substantial reduction in control updates highlights the communication efficiency and scalability of the method, making it particularly advantageous for large-scale, high-density traffic scenarios. These findings confirm the potential of the proposed control strategy for practical deployment in intelligent transportation systems, offering a reliable solution to balance system performance and resource efficiency in communication-constrained environments.
Practical implementations in vehicular ad hoc networks (VANETs) often face challenges such as packet loss, delays, and cyber attacks, which can disrupt timely control updates and impact overall platoon stability. To address these issues, future research could explore adaptive strategies that dynamically adjust event-triggering thresholds based on real-time network conditions, enhancing robustness under fluctuating environments. Additionally, incorporating realistic network scenarios, such as variable delays, packet loss, cyber attacks, into practical experiments or simulations would provide deeper insights into the system’s reliability and stability across diverse conditions.
Author Contributions
Conceptualization C.Z. and Q.L.; methodology, C.Z. and J.G.; writing—original draft, C.Z.; writing—review and editing, J.G. and J.L.; funding acquisition, C.Z. and Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by The National Natural Science Foundation (NNSF) of China under Grant 52025121, 52362054, and 52372379.
Data Availability Statement
Measurement data are available from the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, Y.; Gong, D.; Wen, S.; Ding, L.; Guo, G. A Privacy-preserving-based distributed collaborative scheme for connected autonomous vehicles at multi-lane signal-free intersections. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6824–6835. [Google Scholar] [CrossRef]
- He, J.Y.; Cheng, Z.Q.; Li, C.; Xiang, W.; Chen, B.; Luo, B.; Geng, Y.; Xie, X. Damo-streamnet: Optimizing streaming perception in autonomous driving. arXiv 2023, arXiv:2303.17144. [Google Scholar]
- Gong, J.; Zhao, Y.; Cao, J.; Huang, W.; Chen, W.; Abdel-Aty, M. Resilient automated intersection control of connected vehicles under denial of service attacks. Eng. Appl. Artif. Intell. 2024, 136, 108950. [Google Scholar] [CrossRef]
- Liang, J.; Li, Y.; Yin, G.; Xu, L.; Lu, Y.; Feng, J.; Shen, T.; Cai, G. A MAS-based hierarchical architecture for the cooperation control of connected and automated vehicles. IEEE Trans. Veh. Technol. 2022, 72, 1559–1573. [Google Scholar] [CrossRef]
- Kim, H.; Pinola, J. Transport Use Case Trials of 5G-HEART Project. In Proceedings of the 2021 IEEE 5G for Connected and Automated Mobility (CAM), Wellington, New Zealand, 30 November–2 December 2021. [Google Scholar]
- Gonzalez, A.J.; Xie, M.; Lehne, P.H.; Grønsund, P. Achieving high throughput and low latency with 5g: A real implementation experience. IEEE Commun. Mag. 2021, 59, 84–90. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Z.; Wong, W.S. Resilient platoon control of vehicular cyber physical systems under DoS attacks and multiple disturbances. IEEE Trans. Intell. Transp. Syst. 2021, 23, 10945–10956. [Google Scholar] [CrossRef]
- Ding, L.; Li, J.; Ye, M.; Zhao, Y. Fully distributed resilient cooperative control of vehicular platoon systems under DoS attacks. IEEE/CAA J. Autom. Sin. 2022, 9, 937–940. [Google Scholar] [CrossRef]
- Gong, J.; Cao, J.; Zhao, Y.; Wei, Y.; Guo, J.; Huang, W. Sampling-based cooperative adaptive cruise control subject to communication delays and actuator lags. Math. Comput. Simul. 2020, 171, 13–25. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, J.; Orosz, G. Hierarchical design of connected cruise control in the presence of information delays and uncertain vehicle dynamics. IEEE Trans. Control Syst. Technol. 2017, 26, 139–150. [Google Scholar] [CrossRef]
- Oliveira, R.; Montez, C.; Boukerche, A.; Wangham, M.S. Co-design of consensus-based approach and reliable communication protocol for vehicular platoon control. IEEE Trans. Veh. Technol. 2021, 70, 9510–9524. [Google Scholar] [CrossRef]
- Du, C.; Bian, Y.; Liu, H.; Ren, W.; Lu, P.; Liu, X. Cooperative startup control for heterogeneous vehicle platoons: A finite-time output tracking-based approach. IEEE Trans. Control Netw. Syst. 2021, 8, 1767–1777. [Google Scholar] [CrossRef]
- Luo, Q.; Nguyen, A.T.; Fleming, J.; Zhang, H. Unknown input observer based approach for distributed tube-based model predictive control of heterogeneous vehicle platoons. IEEE Trans. Veh. Technol. 2021, 70, 2930–2944. [Google Scholar] [CrossRef]
- Shen, Z.; Liu, Y.; Li, Z.; Wu, Y. Distributed vehicular platoon control considering communication delays and packet dropouts. J. Frankl. Inst. 2024, 361, 106703. [Google Scholar] [CrossRef]
- Zhan, J.; Zhang, L.; Chen, Y. Asynchronous platoon control for connected vehicles with intermittent and delayed information transmission. IEEE Trans. Autom. Control 2023, 68, 6875–6882. [Google Scholar] [CrossRef]
- Lin, Y.; Tiwari, A.; Fabien, B.; Devasia, S. Constant-spacing connected platoons with robustness to communication delays. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3370–3382. [Google Scholar] [CrossRef]
- Lin, S.; Liu, L. Observer-based adaptive control of vehicle platoon with uncertainty and input constraints. IET Control Theory Appl. 2024, 18, 1846–1853. [Google Scholar] [CrossRef]
- Wei, J.; Liu, Y.J.; Chen, H.; Liu, L. Fuzzy adaptive control for vehicular platoons with constraints and unknown dead-zone input. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4403–4412. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, Z.; Xue, L.; Ahn, C.K.; Liu, J. Stabilization of complex networks under asynchronously intermittent event-triggered control. Automatica 2024, 161, 111493. [Google Scholar] [CrossRef]
- Yao, W.; Wang, C.; Sun, Y.; Gong, S.; Lin, H. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Netw. 2023, 164, 67–80. [Google Scholar] [CrossRef]
- Tan, Y.; Yuan, Y.; Xie, X.; Tian, E.; Liu, J. Observer-based event-triggered control for interval type-2 fuzzy networked system with network attacks. IEEE Trans. Fuzzy Syst. 2023, 31, 2788–2798. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, C.; Ding, C.; Yu, B.; Cui, S. Observer-based event-triggered adaptive platooning control for autonomous vehicles with motion uncertainties. Transp. Res. Part C Emerg. Technol. 2024, 159, 104462. [Google Scholar] [CrossRef]
- Ding, L.; Ye, M.; Yue, D. Communication-efficient distributed Nash equilibrium seeking under switching topologies: A decentralized gradient-based event-triggered scheme. Automatica 2024, 167, 111738. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.L.; Ding, L.; Wang, Y.L.; Zhang, X.M. Dynamic event-triggered distributed coordination control and its applications: A survey of trends and techniques. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3112–3125. [Google Scholar] [CrossRef]
- Su, Y.; Yang, X.; Shi, P.; Wen, G.; Xu, Z. Consensus-based vehicle platoon control under periodic event-triggered strategy. IEEE Trans. Syst. Man Cybern. Syst. 2023, 54, 533–542. [Google Scholar] [CrossRef]
- Gong, J.; Zhao, Y.; Cao, J.; Guo, J.; Abdel-Aty, M.; Huang, W. A virtual spring strategy for cooperative control of connected and automated vehicles at signal-Free intersections. IEEE Trans. Intell. Transp. Syst. 2024, 25, 1430–1444. [Google Scholar] [CrossRef]
- Wang, J.; Deng, X.; Guo, J.; Luo, Y.; Li, K. A fully distributed antiwindup control protocol for intelligent-connected electric vehicles platooning with switching topologies and input saturation. IEEE/ASME Trans. Mechatron. 2022, 28, 1683–1694. [Google Scholar] [CrossRef]
- Zhou, C.; Gong, J.; Zhou, Z.; Ling, Q. Resilient automated intersection control of CAVs subject to DoS Attacks. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 6388–6395. [Google Scholar]
- Chen, J.; Liang, H.; Li, J.; Lv, Z. Connected automated vehicle platoon control with input saturation and variable time headway strategy. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4929–4940. [Google Scholar] [CrossRef]
- Meng, Z.; Zhao, Z.; Lin, Z. On global leader-following consensus of identical linear dynamic systems subject to actuator saturation. Syst. Control Lett. 2013, 62, 132–142. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).